Abstract
A correct reproduction of a motorcycle rider’s movements during driving is a crucial and the most influential aspect of the entire motorcycle–rider system. The rider performs significant variations in terms of body configuration on the vehicle in order to optimize the management of the motorcycle in all the possible dynamic conditions, comprising cornering and braking phases. The aim of the work is to focus on the development of a technique to estimate the body configurations of a high-performance driver in completely different situations, starting from the publicly available videos, collecting them by means of image acquisition methods, and employing machine learning and deep learning techniques. The technique allows us to determine the calculation of the center of gravity (CoG) of the driver’s body in the video acquired and therefore the CoG of the entire driver–vehicle system, correlating it to commonly available vehicle dynamics data, so that the force distribution can be properly determined. As an additional feature, a specific function correlating the relative displacement of the driver’s CoG towards the vehicle body and the vehicle roll angle has been determined starting from the data acquired and processed with the machine and the deep learning techniques.
1. Introduction
Human body movement is an object of a crucial interest, especially in the biomedical field [,]. Technological evolution has allowed considerable progress, especially in motor rehabilitation techniques in sports, in the study of motor problems related to behavioral pathologies and in the analysis of dynamic systems in which a person interacts with the surrounding environment both it real or virtual situations.
The fields of application of such a discipline can be various and most of the related issues concern the study of the balance characteristics of a human body and the determination of its center of gravity during motion, which is fundamental for a proper calculation of the inertial components and to evaluate the load distribution in motion phases [,]. In particular, the vehicular simulation field nowadays is lacking robust and usable methodologies to account for the driver/rider position in the vehicle, and for the two-wheel domain the problem is even deeper, due to the significant influence that the rider’s mass has on the overall rider + vehicle system [].
Due to the difficulty in sensing the rider with specific sensors aimed to measure the CoG position, the optimal method to acquire data on his position is based on image-processing. For this reason, an analysis aimed to obtain a preliminary comprehension of the state of the art in such a field has been carried out.
In recent years, motion analysis has evolved substantially, alongside major technological advances, and there is growing demand for faster and more sophisticated techniques for capturing motion in a wide range of contexts, ranging from clinical gait assessment [] to videogame animation.
Biomechanical tools have greatly developed, from manual image annotation to marker-based optical trackers, inertial sensor-based systems, and marker-free systems using sophisticated human body models, by double energy X-ray absorptiometry (DXA) [], machine vision, and machine learning algorithms. With such scope, the use of sophisticated sensors based on the presence of physical markers applied to humans’ bodies allows one to measure the physical quantities (force, speed, acceleration and displacement) linked to the different movements made by the body which, for example, in the sports field, allows one to carry out studies aiming at the improvement of the athlete’s performance [,].
An alternative method, markerless motion capture, based on the use of video acquisitions processed by machine learning techniques, aims to identify the positions of various key points belonging to the human body starting from a singular video frame or images, with no need of uncomfortable and impractical physical markers [,].
The major difficulty of this technique is that some body parts cover some others during the movement or in some given postures. As a result, automatic and markerless identification of body segments faces many difficulties that turn it into a complex problem [].
In recent years, thanks to the evolution of image-processing tools, the interest in marker-free motion capture systems has significantly increased and different software methods allowing one to automatically identify the anatomical landmarks have been developed, among them the OpenPose software []. The OpenPose package is capable of performing real-time skeleton tracking on a large number of subjects analyzing 2D images [].
Starting from the research output of the collaboration between the University of Messina and the University of Naples Federico II [], based on the employment of the OpenPose software aiming to predict the center of gravity (CoG) of a human subject posing in a specific set of 2D images, the present work focuses on a motorcycle rider adopting the images acquired from a motorcycle simulation game, MotoGP19.
The work aims to develop of a technique employing the neural network technology for correlation with vehicle data, applied in a deep learning environment, which, starting from a partial capture of the driver position acquired in each video frame, allows one to determine the key points not visible from the camera and corresponding to the entirety of the driver’s body. Starting from the information collected, the calculation of the CoG of the driver’s body is evaluated by adopting deep learning technology. The neural network technique is then employed to determine the correlation between the relative displacement of the driver’s center of gravity and the motorcycle’s body roll angle. The continuous availability of information on the position of the driver/rider’s CoG is fundamental in the motorcycle industry, both for racing and safety applications, due to the need to consider the influence of the human body on the rider + vehicle system in design and simulations activities [,].
2. Materials and Methods
The presented work aims to illustrate a methodologic approach, developed by using data acquired from a reference scenario, that will eventually be substituted by real video data. Each rider moves in a different way, as the driving style of racing riders demonstrates, and once the methodology is validated, the developed algorithms can be trained for each different rider, reproducing their typical motion and style, with the final aim of determining the continuous position of the center of gravity, which is fundamental for simulation activities and usually hard to determine for motorcycles. Such consideration has been better expressed in the text. In order to obtain a reliable dataset with repeatable and robust data, an approach based on the use of the MotoGP19 simulation videogame has been chosen in the acquisition phase, in which several runs have been captured. The video frames acquired in the various dynamic conditions of the motorcycle and the body driver configuration constitute a suitable and repeatable dataset on which the OpenPose software processing has been employed to calculate all the necessary body markers’ positions and, therefore, the center of gravity of the driver’s body. The particular choice to start with the videogame is motivated by the fact that modern simulation and sports games are generally very faithful to the real movements of the athletes and drivers, since their modelling is based on the extrapolation of Active Marker Mocap real data [,,]. As a result, the simulation output reproduces all the athlete’s movements in a realistic way, and in the particular case under analysis, it allows one to have a great coherence with the real movements assumed by motorcycle riders during the operation of the motorcycle even in extreme dynamic conditions. Eventual distortions and inaccuracies of the virtual camera did not represent a particular issue, due to the methodologic spirit of the study, whose data can be progressively improved in terms of quality in the following activities, keeping the value of the demonstrated feasibility.
Modern gyroscopic cameras, represented in Figure 1a, installed on racing motorcycles provide only a partial shape of the driver’s body, being limited to acquiring the movement information regarding only of the upper part of the rider’s body (as shown in Figure 1b). The missing part, mainly comprising legs and the bottom part of the torso, becomes necessary to correctly evaluate the CoG of the rider’s body [,,,].
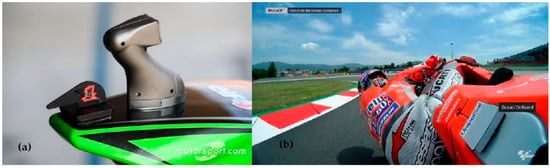
Figure 1.
(a) Gyroscopic camera; (b) rear shot with gyroscopic camera.
2.1. Acquisition of the Video Frames
A series of simulations were carried out via MotoGP19 on different tracks in order to explore as many dynamic conditions as possible concerning the motorcycle behavior and the driver’s body configurations.
For each track under analysis, the best track lap was selected as a reference and was recorded in two different video acquisitions using the two different points of view available in the simulator game:

Figure 2.
(a) Rear view camera 1; (b) rear view camera 2.
The video was subsequently processed via the OpenPose package as described later.
2.2. OpenPose Processing
OpenPose is an open source software package for the detection of multiperson key points in real time starting from video frame acquisitions. It is able to jointly detect the key points of the human body, namely the hands, face and feet on individual images, up to a total of 135 key points [].
It is capable of processing, in real time, single frames or direct videos in the input, providing, in output, the same images and videos with a further level of physics represented by the key points detected and added to the input frames.
For the recognition of key points, OpenPose uses a preadded neural convolution network (CNN) called Vggnet [,]. The network accepts a color image as input (Figure 3a), returning 2D positions of the key points for each person in the frame (Figure 3b). The additional processing layer, representing the extracted points, is represented in Figure 3c.
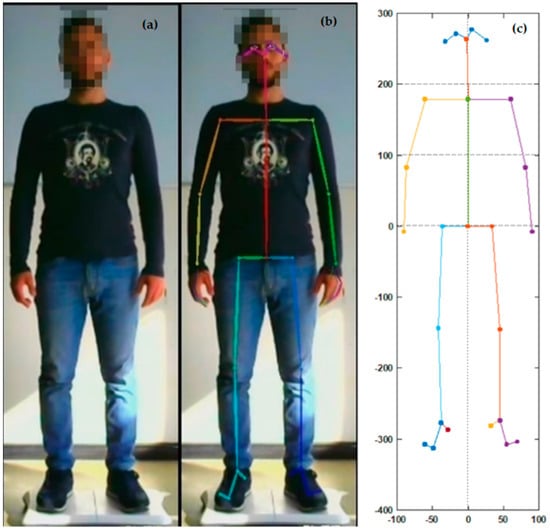
Figure 3.
(a) Original frame; (b) postprocessed frame by OpenPose; (c) plot of the key points.
3. Training Dataset
The output data obtained by means of the OpenPose package were divided into two key points sets depending on their positions towards the human body to constitute suitable datasets of input and target indispensable for the machine learning training. In particular, the processed key points have been split as follows:
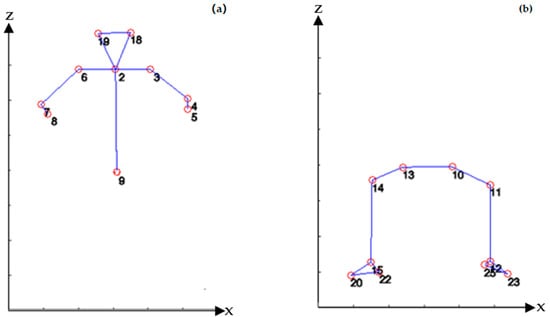
Figure 4.
(a) The top 10 points as network input; (b) the bottom 10 points as a network target.
The neural network is set to evaluate 10 points relative to the lower part of the body, starting from the 10 key points of the upper part acquired through camera 2 (Figure 2b).
Due to the different framings between the two chosen cameras, it was necessary to scale the shapes obtained from the two different sets of key points to the same proportions.
Furthermore, the data were divided into x and z coordinates because it is necessary to train two distinct neural networks for the x and z coordinates, respectively, to optimize the calibration algorithms response. In the y-direction, the hypothesis of the fixed CoG coordinate has been introduced, due to the lower variability of the rider’s motion in said direction. Four distinct matrices of points have thus been prepared for the training procedure:
- x coordinates of the upper points;
- z coordinates of the upper points;
- xcoordinates of the lower points;
- zcoordinates of the lower points.
3.1. Assessment of the Centre of Gravity of the Driver’s Body
Assuming that the body density is constant and all the body parts can be described by simple geometrical features, the calculation of the center of gravity can be easily achieved geometrically [].
However, it has to be taken into account that the human body is characterized by a nonuniform distribution of density between each couple of defined markers. With such reference, specific methodologies and more accurate methods for calculating the center of gravity could be employed [].
Schematizing the human body as a series of discrete mass parts, the center of gravity can be assessed as follows:
where:
- mi is the mass of i-th element;
- M is the mass of body (including clothing).
In order to employ the described equivalent system method, it is necessary to individuate the position of the CoG of each individual part of the human body, as described in Table 1, obtained by processing data available from the literature. It was designed to describe body segment mass as a proportion of total body mass and the location k of each segment’s center of mass as a proportion of segment length, in the three transverse, sagittal and longitudinal planes. Among the papers that provide such data, obtainable through experimental tests, this works adopts the approach described by Zatsiorsky et al. in [], modified by de Leva in [,].

Table 1.
Percentage values of mass and position of the center of gravity in adult men and women [,] (copyright has been permitted).
In particular, two procedures to evaluate the CoG are compared: the geometric method and the kinematic method [].
The overall procedure consists, therefore, of the following steps:
- Capture of video frames from the MotoGP19 simulator (rear camera 2);
- Data processing with OpenPose software to evaluate the center of gravity of the individual body elements;
- Evaluation of the center of gravity of the whole body using the data in Table 1.
3.2. Application on the Acquired Data
The recorded video was processed with the OpenPose software for both rear cameras, available in the MotoGP19 simulator, as illustrated in Figure 5 (rear camera 1, including data regarding the bottom part of the rider’s body) and in Figure 6 (rear camera 2, simulating the capabilities of a common onboard camera):

Figure 5.
OpenPose postprocessing of MotoGP19 rear camera 1.

Figure 6.
OpenPose postprocessing of MotoGP19 rear camera 2.
The processing of the acquisitions performed with camera 1 has a good quality with little presence of corrupt frames and undetected key points. On the contrary, the processing of the acquisition with camera 2 presents several corrupt frames, in which the algorithm is not able to recognize parts of the body shape, as illustrated in Figure 7.

Figure 7.
Errors in the OpenPose processing of the MotoGP19 frame regarding rear camera 2.
3.3. Machine Learning Technique
The data used to train the neural network consist of point arrays from OpenPose processing. Machine learning algorithms employing the MATLAB neural fitting tool [] have been used to train the neural network. In particular, 20 different runs, each one comprising about 10 laps, for a global acquired time of 20,000 s, with an acquisition frequency of 20 Hz, have been used to build the global dataset. The data have been organized into 10 input points of the upper body and 10 target points of the lower body, while the hidden and the output layers of the neural network have the dimensions of 6 and 10 neurons, respectively [,], as reported in Figure 8.
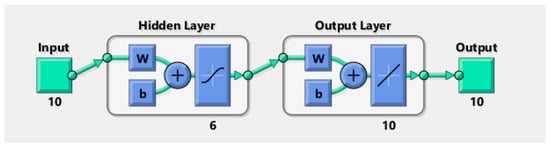
Figure 8.
Neural network layout.
The designed neural network is a two-layered feed-forward network with six hidden neurons based on the sigmoid (activation function of the nonlinear “neuron”) and with 10 linear output neurons (linear regression output function).
The training process of the neural networks is substantially based on a trial-and-error approach. Therefore, it is usually necessary to train the network several times varying its parameters until converging to the desired results. The dataset was divided into training, validation, and testing sets, assigning 60%, 35% and 5% of data to the three subsets, respectively, obtaining the datasets showed in Figure 9. Such figure shows the results of the training process, highlighting the convergence obtained for both x and z coordinates of the target points belonging to the lower part of the driver’s body.
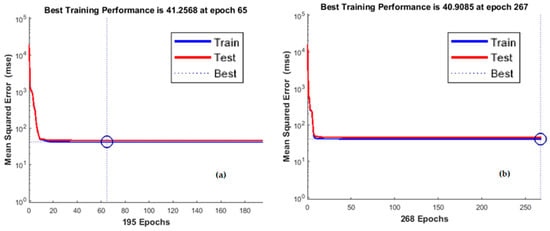
Figure 9.
Best training performance (a) x coordinates; (b) z coordinates.
The neural network outputs in terms of the entire body representation are illustrated in Figure 10, focusing in particular on the validation of the lower points calculated by means of the described technique, which are in a good agreement with the ones acquired in the same frames from a different point of view. The plot reports the best performance obtained, defined as the lowest validation error.
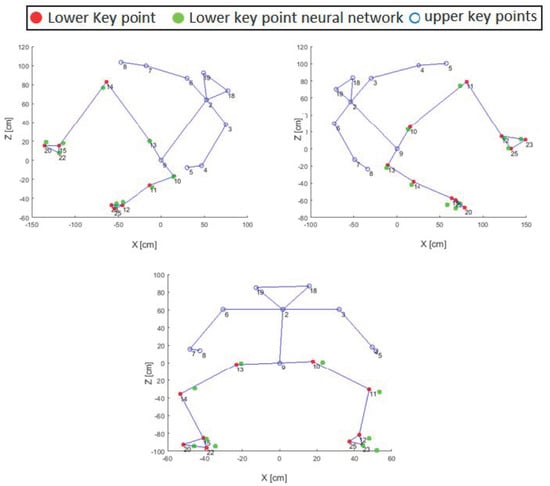
Figure 10.
Comparison between estimated and acquired key points in different body configurations.
Two distinct acquisitions were made, relating to the same lap, through the use of the two cameras:
Using the formulations described in Equation (1), an example of the points position, in terms of the center of gravity, obtained thanks to the OpenPose processing and thanks to the machine learning techniques (starting from the OpenPose estimated data) are represented in Figure 11 and Figure 12.
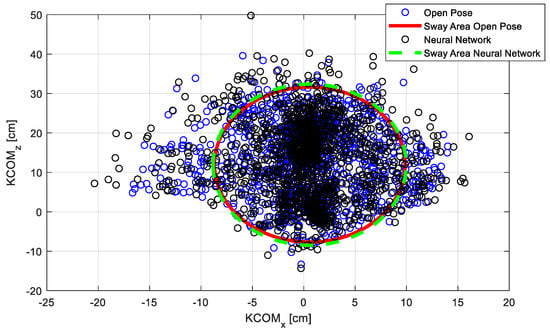
Figure 11.
Dispersion of points obtained thanks to OpenPose software compared with the neural network results (for acquisition 1).
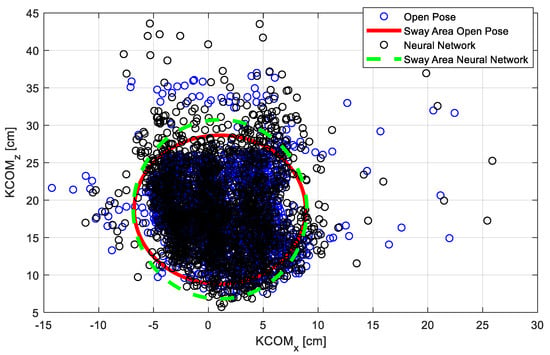
Figure 12.
Dispersion of points obtained thanks to OpenPose software compared with the neural network results (for acquisition 2).
In such figures, the confidence ellipse (or sway area) is depicted. It represents the surface that contains (with 86% probability) the positions of the calculated centers of gravity [].
Table 2 evidences the further similarity, in terms of standard deviation, relating to the x and z coordinates, between the OpenPose calculations and the results of the machine learning techniques, starting from the same OpenPose raw dataset.

Table 2.
Standard deviation value comparison highlighting consistency between the points acquired and processed by means of OpenPose and estimated by means of neural network.
3.4. Correlation with Roll Angle
The capacity to predict the motorcycle rider’s behavior becomes crucial when it comes to correctly define and design the dynamic characteristics of the entire motorcycle rider system [,]. The center of gravity of a motorcycle body can be determined through geometric and dynamic parameters, usually already available during the design phase and partly extrapolated through data acquisition systems [,].
Regarding the driver inertia system, it varies instant by instant depending on the driving style and the specific dynamic maneuver []. For this reason, one of the aims of this work is to understand if there is any correlation between the driver’s configuration and the main telemetry channels, the rolling angle being among them. The study has regarded the relative movement between the motorcycle and rider systems, calculated as the minimum distance “d” between the driver’s center of gravity and the vehicle rolling axle, the straight line belonging to the symmetric geometrical plane ISO-xz of the moving frame of the vehicle, as illustrated in Figure 13.
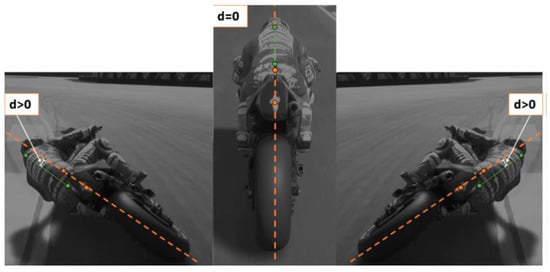
Figure 13.
Distance d between the driver’s center of gravity and the vehicle’s rolling axle.
The explicit equation of the distance “d” is defined in Equation (2).
The value of d was calculated as the minimum distance between a point and a straight line using the equation in explicit form (Equation (2)) per each video frame:
where:
- xp,yp represent the coordinates of point P;
- m is the angular coefficient of the straight line r;
- q is the intercept on the ordinate.
Figure 14a shows the trend of the quantity “d” as a function of the roll angle relative to the points acquired and processed by OpenPose. Figure 14b, in analogy, shows the trend of the quantity “d” as a function of the roll angle relative to the points estimated by means of the machine learning technique. In both cases, steady state conditions have been selected and reproduced with a third order polynomial to fit the main trends, highlighting similar shapes. The low availability of acquired vehicle channels did not allow us to produce a clear fitting and to provide further correlations, but the qualitative results encourage persisting with following studies, able to involve also other variables and a wider dataset.
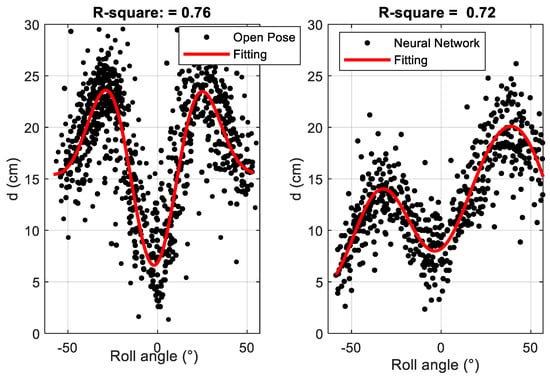
Figure 14.
Correlation of roll angle vs. “d” with Fourier fitting curve: OpenPose (a) and neural network (b).
The negative and positive values of the roll angle represent the vehicle cornering on the left and on the right, respectively.
Performing a specific data processing technique, consisting in removing the nonphysical outliers and transient stages with tresholds on “d” at 50 cm and on the roll angle derivative, filtering the data with a 1Hz low-pass filter, reporting the rolling angle values in the positive quadrant, and performing a linear regression, a preliminary trend of the distance d with the roll angle could be pointed out, as highlighted in Figure 15.
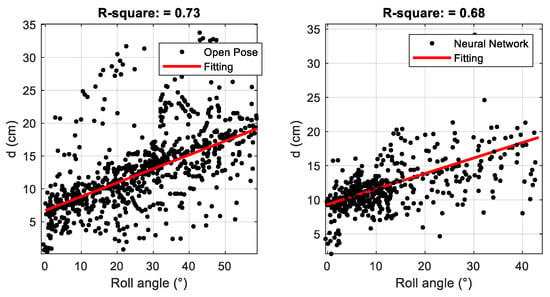
Figure 15.
Linear regression line: OpenPose (on left) and neural network (on right).
It can be clearly seen how, in order to better tackle the corners, the riders move their bodies internally in order to achieve a lower centre of gravity of the entire driver–motorcycle inertial system, therefore allowing the vehicle to achieve a greater forward speed during cornering for the level of the roll angle. All this is strictly related to the travel speed and relative forces, longitudinal and lateral, exchanged between the tire and the asphalt, designed to ensure the balance of the motorcycle when cornering.
Finally, the points where the roll angle values are high and the “d” values are very small are due to the intrinsic characteristics of the rider’s movements during the direction change maneuvers. Points (0,0) of the diagrams, expected to be physical (the rider position should be symmetrical at zero roll angle) in Figure 15, do not belong to the linear regression because it interpolates the data giving priority to the linear part of the dataset at roll angles > 3°.
4. Conclusions
The objective of determining the motion of a motorcycle rider using machine learning algorithms processing images through CNN motion capture techniques has been pursued in this paper, due to the complexity of developing and run physical-based algorithms, and the difficulty in parameterization, vehicle design and performance optimization applications.
The CoG parameter plays, in fact, a fundamental role in vehicle dynamics simulations and in the design phase of the motorcycle, since the rider and the motorcycle are not two separate systems, but fully integrated bodies whose deep understanding is a starting point to achieve maximum performance both in terms of safety and racing competitiveness.
The application of a technique based on the use of neural networks has made it possible to identify the position of several key points belonging to the human body, starting from the video frames acquired at the rear edge of a motorcycle from a gaming simulator. Such a choice was made because the reliability of the video data is not a main focus of the work, which aims to set a methodology that will be then replicated with real vehicle video data.
The quality of the results obtained is closely linked with the OpenPose software potential, which, as illustrated, could have significant limits in the recognition of key points in particular positions. Despite such an aspect, the presented activity presents a methodologic approach which could be further improved in terms of data quality, thanks to the availability of a more reliable acquisition system, retaining its feasibility.
The training of a neural network, even applied to frames reproducing partial visibility of the driver, allowed us to determine the key points not visible to the camera, thus also guaranteeing the calculation of the center of gravity in conditions in which such a task could hardly be achievable.
Finally, a preliminary function, linking the relative displacement of the driver’s center of gravity towards the vehicle rolling axis as a function of the roll angle, has been proposed.
The determination of the driver’s center of gravity plays a fundamental role in the overall dynamics of the system. Video analysis techniques represent a novel and under development discipline, through which it will be increasingly possible to better understand the motorcycle–rider relationship.
The practical implications of the presented study will involve the use of the developed algorithms in activities regarding vehicle design and motorsport analysis, for which the continuous and correct information on the rider’s CoG is an element of crucial interest as concerns the effect of the body motion on vehicle dynamics and the ride/handling attitude of the vehicle to be virtually prototyped.
Author Contributions
Data curation, F.C.; Funding acquisition, G.R.; Methodology, D.S.; Software, D.D.; Supervision, F.F.; Validation, A.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kourtzi, Z.; Shiffrar, M. Dynamic representations of human body movement. Perception 1999, 28, 49–62. [Google Scholar] [CrossRef] [PubMed]
- Kanda, T.; Ishiguro, H.; Imai, M.; Ono, T. Body movement analysis of human-robot interaction. IJCAI 2003, 3, 177–182. [Google Scholar]
- Panjan, A.; Sarabon, N. Review of Methods for the Evaluation of Human Body Balance. Sport Sci. Rev. 2012, 19, 131. [Google Scholar] [CrossRef]
- Catena, R.D.; Chen, S.H.; Chou, L.S. Does the anthropometric model influence whole-body center of mass calculations in gait? J. Biomech. 2017, 59, 23–28. [Google Scholar] [CrossRef] [PubMed]
- Cheli, F.; Mazzoleni, P.; Pezzola, M.; Ruspini, E.; Zappa, E. Vision-based measuring system for rider’s pose estimation during motorcycle riding. Mech. Syst. Signal Process. 2013, 38, 399–410. [Google Scholar] [CrossRef]
- Cimolin, V.; Galli, M. Summary measures for clinical gait analysis: A literature review. Gait Posture 2014, 39, 1005–1010. [Google Scholar] [CrossRef]
- Durkin, J.L.; Dowling, J.J.; Andrews, D.M. The measurement of body segment inertial parameters using dual energy X-ray absorptiometry. J. Biomech. 2002, 35, 1575–1580. [Google Scholar] [CrossRef]
- Munoz, F.; Rougier, P.R. Estimation of centre of gravity movements in sitting posture: Application to trunk backward tilt. J. Biomech. 2011, 44, 1771–1775. [Google Scholar] [CrossRef]
- Jaffrey, M.A. Estimating Centre of Mass Trajectory and Subject-Specific Body Segment Parameters Using Optimisation Approaches; Victoria University: Melbourne, Australia, 2008; pp. 1–389. [Google Scholar]
- Mündermann, L.; Corazza, S.; Andriacchi, T.P. The evolution of methods for the capture of human movement leading to markerless motion capture for biomechanical applications. J. Neuro Eng. Rehabil. 2006, 3, 1–11. [Google Scholar] [CrossRef]
- Hasler, N.; Rosenhahn, B.; Thormählen, T.; Wand, M.; Gall, J.; Seidel, H.P. Markerless motion capture with unsynchronized moving cameras. IEEE Conf. Comput. Vis. Pattern Recognit. 2009, 224–231. [Google Scholar] [CrossRef]
- Bakhtiari, A.; Bahrami, F.; Araabi, B.N. Real Time Estimation and Tracking of Human Body Center of Mass Using 2D Video Imaging. In Proceedings of the 1st Middle East Conference on Biomedical Engineering 2011, Sharjah, United Arab Emirates, 21–24 February 2011. [Google Scholar] [CrossRef]
- Cronin, N.J.; Rantalainen, T.; Ahtiainen, J.P.; Hynynen, E.; Waller, B. Markerless 2D kinematic analysis of underwater running: A deep learning approach. J. Biomech. 2019, 87, 75–82. [Google Scholar] [CrossRef]
- Cao, Z.; Simon, T.; Wei, S.E.; Sheikh, Y. Realtime Multi-Person 2D Pose Estimation Using Part Affinity Fields. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, 21–26 July 2017; pp. 1302–1310. [Google Scholar] [CrossRef]
- D’Andrea, D.; Cucinotta, F.; Farroni, F.; Risitano, G.; Santonocito, D.; Scappaticci, L. Development of Machine Learning Algorithms for the Determination of the Centre of Mass. Symmetry 2021, 13, 401. [Google Scholar] [CrossRef]
- Rice, R.S. Rider skill influences on motorcycle maneuvering. SAE Trans. 1978. [Google Scholar] [CrossRef]
- Liu, T.S.; Wu, J.C. A Model for a Rider-Motorcycle System Using Fuzzy Control. IEEE Trans. Syst. Man Cybern. 1993, 23, 267–276. [Google Scholar] [CrossRef][Green Version]
- Wang, Q.; Kurillo, G.; Ofli, F.; Bajcsy, R. Evaluation of Pose Tracking Accuracy in the First and Second Generations of Microsoft Kinect. In Proceedings of the 2015 International Conference on Healthcare Informatics, Dallas, TX, USA, 21–23 October 2015. [Google Scholar] [CrossRef]
- Kirk, A.G.; O’Brien, J.F.; Forsyth, D.A. Skeletal Parameter Estimation from Optical Motion Capture Data. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005. [Google Scholar] [CrossRef]
- Zordan, V.B.; van der Horst, N.C. Mapping Optical Motion Capture Data to Skeletal Motion Using a Physical Model. In Proceedings of the 2003 ACM SIGGRAPH/Eurographics Symposium on Computer Animation, San Diego, CA, USA, 26–27 July 2003. [Google Scholar]
- Cossalter, V.; Lot, R.; Massaro, M. Motorcycle Dynamics. In Modelling, Simulation and Control of Two-Wheeled Vehicles; Wiley & Sons: London, UK, 2014. [Google Scholar]
- Boniolo, I.; Savaresi, S.M.; Tanelli, M. Roll angle estimation in two-wheeled vehicles. IET Control Theory Appl. 2009, 3, 20–32. [Google Scholar] [CrossRef]
- Schlipsing, M.; Schepanek, J.; Salmen, J. Video-Based Roll Angle Estimation for Two-Wheeled Vehicles. In Proceedings of the 2011 IEEE Intelligent Vehicles Symposium (IV), Baden-Baden, Germany, 5–9 June 2011. [Google Scholar] [CrossRef]
- Farroni, F.; Mancinelli, N.; Timpone, F. A real-time thermal model for the analysis of tire/road interaction in motorcycle applications. Appl. Sci. 2020, 10, 1604. [Google Scholar] [CrossRef]
- Czart, W.R.; Robaszkiewicz, S. Openpose. Acta Phys. Pol. A 2004. [Google Scholar] [CrossRef]
- Martinez, G.H. Single-Network Whole-Body Pose Estimation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 28 October 2019. [Google Scholar] [CrossRef]
- Osokin, D. Real-time 2D multi-person pose estimation on CPU: Lightweight OpenPose. arXiv 2018, arXiv:1811. [Google Scholar] [CrossRef]
- Frosali, G.; Minguzzi, E. Meccanica Razionale per l’Ingegneria; Esculapio: Lucca, Italy, 2015. [Google Scholar]
- Yoganandan, N.; Pintar, F.A.; Zhang, J.; Baisden, J.L. Physical properties of the human head: Mass, center of gravity and moment of inertia. J. Biomech. 2009, 42, 1177–1192. [Google Scholar] [CrossRef]
- Zatsiorsky, V.M.; King, D.L. An algorithm for determining gravity line location from posturographic recordings. J. Biomech. 1997, 31, 161–164. [Google Scholar] [CrossRef]
- de Leva, P. Adjustments to zatsiorsky-seluyanov’s segment inertia parameters. J. Biomech. 1996, 29, 1223–1230. [Google Scholar] [CrossRef]
- Bova, M.; Massaro, M.; Petrone, N. A three-dimensional parametric biomechanical rider model for multibody applications. Appl. Sci. 2020, 10, 4509. [Google Scholar] [CrossRef]
- Demuth, H.; Beale, M. Neural Network Toolbox—For Use with MATLAB. MathWorks 2002. [Google Scholar] [CrossRef]
- Pan, J.; Sayrol, E.; Giro, I.; Nieto, X.; McGuinness, K.; O’connor, N.E. Shallow and Deep Convolutional Networks for Saliency Prediction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 30 June 2016. [Google Scholar] [CrossRef]
- Schubert, P.; Kirchner, M. Ellipse area calculations and their applicability in posturography. Gait Posture 2014, 39, 518–522. [Google Scholar] [CrossRef]
- Sforza, A.; Lenzo, B.; Timpone, F. A state-of-the-art review on torque distribution strategies aimed at enhancing energy efficiency for fully electric vehicles with independently actuated drivetrains. Int. J. Mech. Control 2019, 20, 3–15. [Google Scholar]
- Sharifzadeh, M.; Farnam, A.; Timpone, F.; Senatore, A. Stabilizing a Vehicle Platoon with the Unidirectional Distributed Adaptive Sliding Mode Control. Int. Conf. Mechatron. Technol. ICMT 2019. [Google Scholar] [CrossRef]
- Pleß, R.; Will, S.; Guth, S.; Hofmann, M.; Winner, H. Approach to a Holistic Rider Input Determination for a Dynamic Motorcycle Riding Simulator. In Proceedings of the Bicycle and Motorcycle Dynamics Conference, Milwaukee, WI, USA, 21–23 September 2016. [Google Scholar]
- Cossalter, V.; Doria, A.; Fabris, D.; Maso, M. Measurement and identification of the vibration characteristics of motorcycle riders. In Proceedings of the Noise and Vibration Engineering: Proceedings of ISMA 2006, Leuven, Belgium, 18–20 September 2006. [Google Scholar]
- Nagasaka, K.; Ichikawa, K.; Yamasaki, A.; Ishii, H. Development of a Riding Simulator for Motorcycles; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2018. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).