Abstract
For decades, drivers and fleet managers have been impacted by the instability of fuel prices, the need to save resources and the duty to meet and attain environmental regulations and certifications. Aiming to increase performance and efficiency and reduce emissions and mileage costs, plug-in electric vehicles (PHEVs) have been pointed out as a viable option, but there are gaps related to tools that could improve the numerous existing conventional vehicles. This study presents the design of an aftermarket hybridization kit that converts a vehicle originally driven by a combustion engine into a PHEV. To achieve this goal, an optimization was conducted with the objective of decreasing the cost (regarding fuel consumption and battery charging) to perform a local driving cycle, while attenuating the tailpipe emissions and reducing the battery mass. The torque curves of the electric motors, the battery capacity, the parameters for a gear shifting strategy and the parameters for a power split control were the design variables in the optimization process. This study used the Campinas driving cycle, which was experimentally obtained in a real-world driving scenario. The use of a local driving cycle to tune the design variables of an aftermarket optimization kit is important to achieve a customized product according to the selling location. Among the optimum solutions, the best trade-off configuration was able to decrease the mileage cost in 22.55%, and reduce the tailpipe emissions by 28.4% CO, 33.55% NOx and 19.11% HC, with the addition of a 137 kg battery.
1. Introduction
Local and global environmental issues have resulted in the establishment of regulations to reduce vehicle emissions worldwide [1,2]. On the other hand, the instability of fuel prices leads customers to react by reducing consumption [3] or by changing energy source [4] when it is possible. Plugin hybrid electric vehicles are driven by electric motors (EMs) and internal combustion engines (ICE) and can be connected to the grid [5]. They are one of the solutions for mitigating local emissions [6] and absorbing fuel and electric energy price instabilities.
The relevance of the plug-in electric vehicles (PHEVs) in the current engineering is reflected by the recent scientific activities. Du et al. [7] optimized a plug-in hybrid bus to avoid excessive changes of operation modes, reducing the number of engine startups, the clutch abrasion and the jerk. Golpîra and Khan [8] pointed that the increasing use of PHEVs is an important issue to be taken into account in domestic energy power management, while Li et al. [9,10] investigated the advantages for the power distribution systems due to the optimum coordination of the PHEVs charging times. Furthermore, Mohammadi et al. [11] asserted that if the PHEVs are able to work in a bidirectional power mode (draining power from and supplying power to the grid), they can collaborate to regulate the grid voltage and frequency along a day. Zhang et al. [12] studied the integration between PHEVs, other kinds of electric vehicles and the road to achieve global ecodriving conditions. Liu et al. [13] proposed a mixed mutation strategy for a multiobjective optimization algorithm and demonstrated its effect by applying it on a PHEV problem. Wang et al. [14] optimized a 4-wheel drive PHEV considering the Federal Test Procedure (FTP) 72 driving cycle and achieved good results in three antagonistic objectives: −1.21% electric energy consumption, −6.18% fuel consumption and −5.49% acceleration time. Fu et al. [15] optimized a front traction PHEV under the New European Driving Cycle (NEDC), resulting in reductions about 3.45% fuel consumption, 6.15% NOx, 3.71% CO, and 3.57% HC.
Although in general, research is focused on the production and application of new hybrid vehicles, there are good results regarding the installation of aftermarket hybridization kits on combustion vehicles, turning them into PHEVs. Some of these solutions have already been patented [16,17,18,19], and companies are selling and installing such kits [20].
Researchers of the University of Salermo have developed an aftermarket hybridization kit by installing EMs in the rear wheels of a combustion vehicle originally driven only through the front wheels. The batteries of this kit can be loaded by regenerative braking, by plugging the kit to the grid, and by the energy acquired through solar panels installed on the vehicle roof [21]. In the best conditions, the resulting vehicle would have the fuel economy improved by 11% under the NEDC and 20.5% considering the FTP 72 driving cycle [21]. It is expected that 10% of vehicle owners are interested in installing this kit [22]. Furthermore, the kit improves the life cycle assessment of the vehicle in which it is installed, and the overall environmental impact is better than the purchase of a brand-new hybrid vehicle [23].
The Integrated System Laboratory (LabSIn) of the University of Campinas has worked on vehicle longitudinal dynamics issues and on the development of an aftermarket hybridization kit for the Brazilian scenario. The regional market is dominated by conventional vehicles, which are numerous (in 2018 there were 600,000 samples in Campinas City [24]; 18,200,000 in the São Paulo State [25]; and 54,700,000 in the whole country [26]).
Key contributions of LabSIn arose from the addition of two EMs to the rear wheels of a conventional vehicle (front wheel ICE traction); the effects on fuel consumption and on gear shifting strategy were experimentally evaluated [27,28]. Such experimental data were input to virtual analysis regarding the hybridization of a conventional vehicle [29,30]. As a result, suitable configurations were able to decrease by up to 34.18%, the cost of performing the combination of the FTP 75 and US06 driving cycles. However, the mentioned studies did not analyze the hybridization kit’s influence on the engine emissions. The increase in the ICE warm-up period is amplified by the addition of the extra electric traction system, which supplies a parcel of the power demand and therefore decreases the ICE torque that can increase the generated emissions if the power split between ICE and EMs is not properly defined [31]. Modifications in the standard driving behavior, e.g., changing the gear shifting strategy, can decrease the ICE fuel consumption and emissions [32,33].
In 2019, LabSIn [34] proposed and simulated an aftermarket hybridization kit shown in Figure 1. The EMs are powered by a battery that is charged by the electrical grid when the vehicle is parked. The optimization was conducted to find out the best gear shifting strategy, EMs torque curves and battery size according to different fuel and electric energy cost scenarios, and the robust solutions regarding cost variations were selected. It also was not considered a local driving cycle that may differ from the standard ones, and may result in further optimized vehicle solutions [35,36,37].
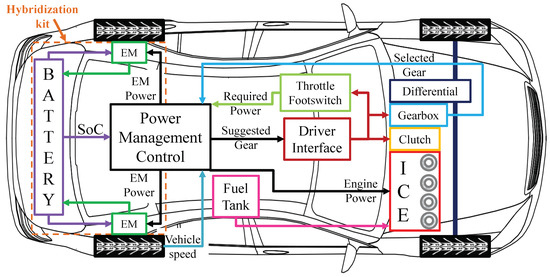
Figure 1.
Proposed assembly for the hybridization kit.
Therefore, the aim of the present study is to conduct a multi-objective optimization of the aftermarket hybridization kit. The optimization problem is formulated to decrease the mileage cost (in terms of fuel consumption and battery charging), mitigating the tailpipe emissions and decreasing the battery mass. The selected design variables are the EMs’ torque curves, the battery capacity, the parameters of the gear shifting strategy and the parameters of the power split control. Moreover, this study is based on the Campinas driving cycle [38], which was experimentally obtained in a real-world driving scenario. Local driving cycles allow a more realistic analysis of the possible gains of the aftermarket hybridization vehicle, focusing on the local costumer.
2. Simulation Model
In the literature, models of vehicle longitudinal dynamics and vehicle components are often implemented in MATLAB™ [37,39,40,41]. All the equations presented here have been implemented by the authors by means of MATLAB/Simulink™block diagrams. In this study, the vehicle longitudinal dynamics are modeled based on the equations presented by Gillespie [42]. However, some modifications were required to include the electric drive train in the model.
The vehicle required traction torque (Nm) is defined by Equation (1) as a function of the movement resistance forces caused by the gravitational acceleration g (m/s), vehicle mass M (kg) and required acceleration (m/s), the aerodynamic drag (N), the tires rolling resistance (N) and the climbing resistance that varies according to the road angle (rad).
The tire dynamic radius r (m) can be defined as proposed by Genta and Morello [43] as 98% of the geometric radius (m), that varies according to the tire standard geometry. The vehicle speed effects are also considered by means of the factor [44].
The rolling resistance (Equation (3)) and the aerodynamic drag (Equation (4)) increase with the vehicle speed V (m/s). Moreover, varies as a function of the air density (kg/m), the projection of the vehicle frontal area A (m) and the coefficient that represents the vehicle shape.
The required acceleration represents the driver behavior. In this paper, a local driving cycle of the city of Campinas, Brazil [38], is applied (Figure 2). The target speed (m/s) is defined as the cycle speed at one time step (s) ahead of the current simulation time. Therefore, the requested acceleration can be calculated by Equation (5).
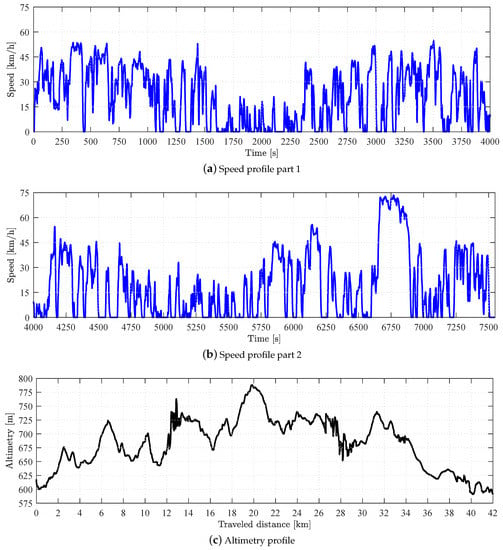
Figure 2.
Campinas Driving cycle [38].
As aforementioned, the main objective of the aftermarket hybridization kit is to add an extra propelling system in the conventional vehicle. Therefore, the power management control (PMC) defines the traction torque required by the engine (Nm) and the electric motors (Nm). In the same way, as presented by Eckert et al. [34], the extra electric motors act only as an auxiliary propelling system. Thus, the throttle pedal signal is acquired and the PMC splits the requested traction torque according to the factor (defined in the optimization problem). The engine torque and torque of the electric motors are defined by Equations (6) and (7) respectively, according to the engine inertia (kgm); gearbox and differential gear ratios and ; inertia (kgm) and (kgm); the frontal and real wheels inertia (kgm) and (kgm); and the overall powertrain efficiency .
2.1. ICE System Restrictions
Once the required traction torque parcel exerted by the engine is defined, it has to be compared to the available traction torque (Nm) that corresponds to the 100% throttle curve (Figure 3a). Moreover, the clutch transmissible torque limit (Nm) (that acts during the gear shifting) also is considered in the definition of the available traction torque.
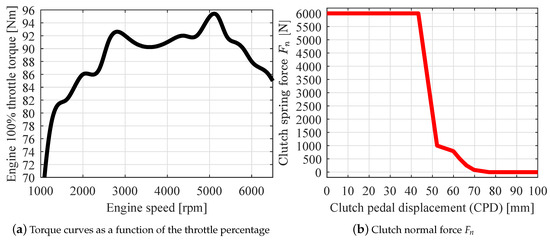
Figure 3.
Engine torque curve and clutch normal force (N) [45].
The clutch transmissible torque is calculated according to its friction coefficient , the number of clutch faces N (-) and internal and external disks radii (m) and (m) (see Equation (8)). Moreover, the spring force (N) (Figure 3b) controls the torque transmission according to the clutch pedal displacement (CPD).
It can be seen in Figure 3b that the clutch maximum value is applied when it is closed (CPD = 0). In this condition, the total engine output torque is transmitted to the gearbox. On the other hand, during the gear shifting process, the clutch disconnects the ICE from the gearbox (CPD = 0 to CPD = 100 mm) in 0.3 s. After the clutch fully opened (CPD = 100 mm), the gear ratio is changed in 0.2 s; then, the ICE is reconnected to the gearbox (CPD = 100 to CPD = 0 mm) in 0.5 s [32]. Therefore, the gearbox input torque (Nm) is defined according to the rules presented in Equation (9) and the available traction torque at the vehicle frontal wheels (Nm) is then defined by Equation (10).
2.2. Electric Drivetrain Restrictions
As the frontal propelling system, the electric drivetrain is also limited by the maximum torque of the EMs curves (Nm) according to their current speed. Therefore, if the required torque is higher than the sum of available torques of both in-wheel EMs, there will be performance losses. The available traction torque of the rear-drive system (Nm) is defined by the combination of Equations (11) and (12).
2.3. Traction Restrictions
Once the available traction torques and are defined, it is possible to verify whether the available torque can be transmitted through the tire/ground contact. The maximum transmissible torque for the frontal (Nm) and rear (Nm) wheels are defined by Equations (13) and (14) respectively [46]. represents the tire-ground peak friction coefficient, and L (m), h (m), b (m) and c (m) correspond respectively to the vehicle’s wheelbase; the height of its center of gravity; and the longitudinal distance between its front and rear axles.
2.4. Acceleration Iterative Process
With both effective traction torques, it is possible to define the vehicle current acceleration (m/s) by means of Equation (17), which is integrated by ODE5 of the Simulink™, to find out the current vehicle speed V and also the displacement.
Due to the many constraints presented, the vehicle acceleration may become lower than the requested . Therefore, it is necessary to perform an iterative process among Equations (1), (6), (7) and (9)–(17), considering until the convergence of the value. Moreover, the tire slipping has to be corrected in this iterative process. The coefficient e (Figure 4) estimates the difference between the tire tangential speed and the vehicle displacement speed as a function of the traction torque . This parameter changes the engine and EMs speeds, and therefore the maximum available torques according to the drivetrain respective curves.
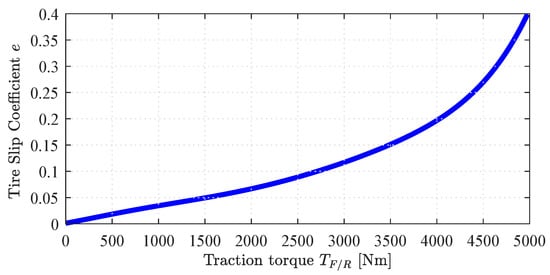
Figure 4.
Tire slip coefficient in function of the traction torque .
2.5. Fuel Consumption and Emissions
After the convergence, the engine effective torque (Nm) and speed are defined by the Equations (18) and (19).
These values correspond to the engine operation point, and are input to the ADVISOR™fuel converter block, which defines the ICE fuel consumption (l) and the tailpipe emissions HC (g/km) NOx (g/km) and CO (g/km) according to the ICE maps shown in Figure 5. ADVISOR™ [47] is a free vehicular simulation tool that considers the ICE transient regimes, simulating the combustion heat and its influence in the catalyst efficiency that significantly changes the generated tailpipe emissions [32].
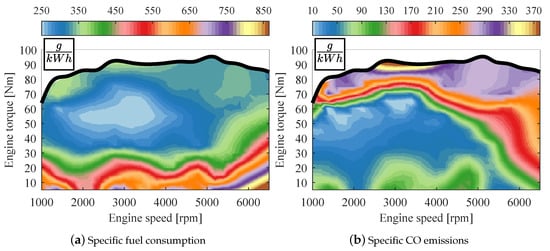
Figure 5.
Engine maps for fuel consumption and emissions [32,47].
2.6. Battery and Equivalent Fuel Consumption
As initially proposed by Eckert et al. [34], the hybridization kit contains a lead-acid battery pack with a nominal voltage of 48 V. This voltage value was selected because the hybridization kit must be adapted to conventional vehicles. Electrical systems above 60 V can represent a potential danger to the passenger [48], and therefore require a shock protection system [49] that would increase the cost of the kit. Furthermore, the lead-acid batteries were selected due to their maintenance-free, good recycling capacity [50] associated with easy manufacture and high-volume production [51] that decrease the final cost of the kit.
In the simulations, the lead-acid battery block from Simulink™database [34] is used. The developed control stops the use of the auxiliary electric drive train system when the battery state of charge is under 40% to avoid fatigue caused by deep discharge [34]. Aiming to define the best battery pack for the hybridization kit, its capacity (Ah) has to be defined and included as input to the Simulink™battery block. Moreover, the battery mass (kg) is also calculated by Equation (20) as a function of the lead-acid specific energy = 40 (Wh/kg) and added to the vehicle mass M. Thus, the resulting is added to the vehicle overall mass M.
Once the driving cycle is simulated, the final battery is used as an input to the charge simulation, which infers the cost of recharging the battery from the electric grid. As in Eckert et al. [34], the battery is recharged at constant current [52]—the maximum I (A) value that does not overcome the allowed battery voltage (V). The power consumption (W) to return the battery to 100% is defined by Equation (21), considering a charge efficiency that concerns the conversion from AC to DC and the heat losses.
Differences in the cost of the energy sources may impact the result of the optimization of vehicle solutions [53]. To allow a fair comparison between the conventional vehicles and the hybridized one, the cost of battery charge is converted in a equivalent fuel consumption (l) by Equation (22) according to the charging time (s) and the ratio between the fuel ($/l) and electric energy ($/Ws) costs. Finally, the is added to the engine fuel consumption , resulting in the total fuel consumption (l) used to compare the results.
2.7. Electric Motors
One of the goals of this study was to find out optimum in-wheel EMs to be applied in the aftermarket hybridization kit; a generic torque curve and efficiency map are presented in Figure 6 [34,54,55]. This approach allows for the definition of a theoretical torque curve, based on three main points. The first one is the EM maximum torque (Nm) and its respective speed (rad/s) at the constant torque phase. The second point is defined at the constant power phase, according to Tong [56], which defines the EM best operating region between and . In this paper, we adopt the upper limit of , as shown in Equation (24), and the EM speed of this point is defined by Equation (25). Finally, the last torque curve point represents the speed at which the EM reaches null torque, and it is defined by linear progression of the previously defined points (, ) and (, ).
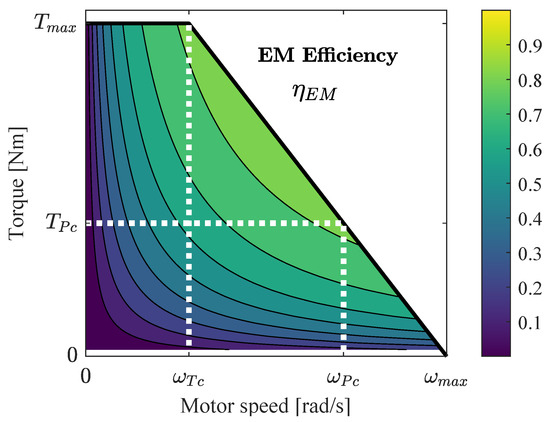
Figure 6.
Electric motor efficiency map and torque curve [34,54,55].
With the EM torque curve fully defined, the map that defines the EM efficiency is interpolated based on the data presented in Figure 6. Moreover, the EM inertia is interpolated based on some values presented by Corrêa et al. [57]. Finally, the inverter efficiency is obtained from Table 1 and the electric current I (A) results from the Equation (26).

Table 1.
Inverter efficiency map adapted from [58].
The EMs are able to regenerate some part of the kinetic energy during the braking. In this paper, the regenerative braking is limited to 10% of the EM maximum torque [54,59]. If the required braking torque exceeds the bounded, the remaining parcel is dissipated by the conventional brake of the vehicle [59].
2.8. Vehicle Parameters
The simulated vehicle is based on the 1.0L engine frontal traction Brazilian Chevrolet Celta™. The parameters used to model this conventional vehicle and the aftermarket hybridization kit in the simulations are presented in Table 2.

Table 2.
Simulated vehicle parameters [44,45].
2.9. Gear Shifting Strategy
Finally, the simulation parameters related to the applied gear shifting strategy have to be defined; they significantly influence the energy management [60], the vehicle performance, the fuel consumption and the emissions [32,33]. The use of an adequate gear shifting strategy improves the gains reached by the vehicle hybridization, once the electric motors decrease the ICE torque demand, allowing for the anticipation of the upshifts, moving the engine to a lower fuel consumption/better efficiency operation point [34]. On the other hand, anticipating the upshifts increases the ICE warm-up period, leading to poor catalyst efficiency and higher tailpipe emissions.
Therefore, the applied shifting strategy has to be carefully defined. The hybridization kit was developed to be adapted to a conventional vehicle a manual gearbox; the most adequate gear will be shown to the driver by means of a user interface adapted to the vehicle. As in previous works [32,34,45], the gear shifting strategy is based on speed limits; in other words, when the vehicle reaches one of these limits, the gear will be changed to the next (upshift) or previous gear (downshift). In the simulation the shifting process is controlled by the vector (Equation (27)) that contains the upshift speeds (km/h) and the speed interval (km/h) used to define the downshift speeds (km/h) (Equation (28)). This difference between and is necessary to prevent gear shifting instabilities, as highlighted by Xi et al. [61].
The gearbox transmission ratio is then defined according to the shifting rule present in Equation (29).
3. Optimization
As mentioned before, the hybridization kit is composed of two in-wheel electric motors assembled directly in the vehicle rear wheels and powered by a lead-acid battery. The main objective of this study is, focusing on a local drive cycle (Campinas, Brazil), to define the best configuration for the battery and electric motors and also the power split control and gear shifting strategy associated with each proposed configuration. To do that, a multi-objective optimization problem is formulated and solved by means of the interactive adaptive-weight genetic algorithm (i−AWGA) proposed by Gen, Cheng and Lin [62]. The i−AWGA technique performs a wide search for the best solution, and it is not limited to false minimums, as occurs in some other optimization techniques. Moreover, this method was applied in several previous works, regarding vehicle multi-objective optimization [32,33,34,59], reaching satisfactory results.
3.1. Problem Formulation
The first optimization criterion is the minimization of the total fuel consumption (Equation (23)) that represents the ICE fuel consumption and the conversion of the battery charge cost in hypothetical fuel (Equation (22)).
The second optimization criterion is the minimization of the engine carbon monoxide ( (g/km)), nitrogen oxide ( (g/km)) and hydrocarbon ( (g/km)) emissions. These emissions are combined in a single parameter named emission factor [32,33]. The value is defined by the adaptive-weight technique [62] according to Equation (30) as a function of the maximum and minimum values of each gas emission presented in the solution database.
Finally, the third optimization criterion is the minimization of the battery mass that represents the majority of the extra weight added by the hybridization kit to the vehicle and reduces the available space in the vehicle trunk where it is meant be assembled.
Therefore, the optimization criteria are:
subjected to the constraints C presented in Equation (34).
Besides the EMs and battery parameters used to narrow the optimization process, some extra constraints were included to ensure the correct behavior of the vehicle. The first one is the ICE operation range, which cannot be below the idle speed ( rad/s) and cannot overcome the maximum allowed speed ( rad/s).
The final constraints are included to avoid any configuration that presents poor acceleration performance caused by the fuel consumption minimization, and to prevent configurations that increase the tailpipe emissions due to the ICE warm-up delay. To be considered viable, the PHEV configuration cannot generate more CO, NOx and HC emissions than the conventional vehicle. Moreover, the vehicle performance is evaluated as the correlation coefficient R calculated by the Equation (35) [30,63] in which the simulated speed profile is compared to the standard driving cycle in discrete time steps of 0.1 s, and the analyzed PHEV must reach at least the same performance of the conventional vehicle , using a standard gear shifting strategy proposed by its manufacturer [64].
3.2. Genetic Algorithm
The optimization starts with the definition of chromosomes (Equation (36)) that constrain the design variables of a specific potential solution.
The initial solution database is composed of randomly defined chromosomes (considering the constrains C) that are simulated and included in the population if they reach the minimum required performance.
3.2.1. Selection, Crossover and Mutation
Once an initial solutions population is developed, the results are classified by the i−AWGA technique (Equation (37)), which compares the current result of each optimization criterion with the maximum and minimum values of the analyzed criterion presented in the population. Moreover, a penalty value is added to the dominated solutions, aiming to decrease their probability of reproduction. On the other hand, the non-dominated solutions (Pareto frontier) receive value, which increases their fitness value Ft(X), improving their selection probability as a function of the sum of all values according to the population size as shown by Equation (38).
The crossover process starts with the selection of two members of the population, which are named Member 1 () and Member 2 (). The values of the design variables of these selected chromosomes are then randomly combined, generating a new chromosome denominated which is simulated. It is included in the population if it respects the constraints C and if the minimum performance criteria are reached.
To provide diversity among the values of the design variables present in the population, the mutation process randomly changes some of the chromosomes values of the selected members and of the crossover chromosome , generating three new chromosomes , and that are evaluated by the constrains C. Table 3 shows the mutation rules according to the operator defined by the Matlab™function rand.

Table 3.
Mutation operator.
3.2.2. Population Control and Convergence Criterion
The initial population is composed of 100 members (randomly generated chromosomes), which are combined by the crossover and mutation operators. The addition of new solutions increases the population size until it reaches a limit value . Once the population limit is reached, the worst solutions (higher Pareto ranking) are eliminated from the population. If a population composed of exclusively non-dominated solutions (Pareto frontier) reaches , the limit is increased to avoid the elimination of the whole population.
The convergence is defined by the stagnation of the evolution process, which is characterized by the repetition of the Pareto frontier [33,59,65] for over 20 generations of 80 new simulated solutions (crossover and mutation).
Figure 7 shows the optimization flowchart according to the applied method.
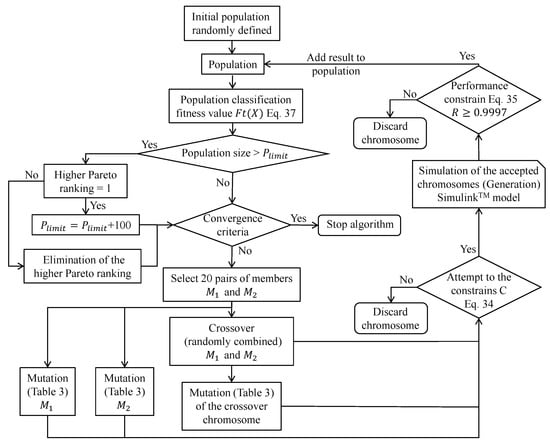
Figure 7.
Optimization flowchart.
4. Results and Discussion
After the convergence of the algorithm, the Pareto frontiers of non-dominated solutions are defined as optimum configurations with different compromise among the optimization criteria. Among these solutions, some of them are selected to be analyzed: the minimum energy cost solution and the minimum emissions , the minimum battery . Moreover, the solution presents the best trade-off ( value) among the analyzed criteria.
However, the (best trade-off) and present large batteries (up to ≈144 kg), representing the advantages of the electric powertrain system against the combustion one. On the other hand, the minimum battery solution was able to save fuel, but the tailpipe emissions were close to the ones of the conventional vehicle. In addition to these solutions, the Pareto frontier presents several other optimum solutions, and two of them were selected based on the decrease of the battery mass (criterion ). These extra solutions were named (making 50% more valuable: ) and (making 100% more valuable: ), increasing the importance of the value related to the battery mass minimization, selecting the lighter hybridization kit configurations.
Table 4 shows the results of the selected configurations and their respective chromosomes. Moreover, Figure 8 shows the Pareto frontier and highlights the selected configurations.

Table 4.
Optimized chromosomes and results.
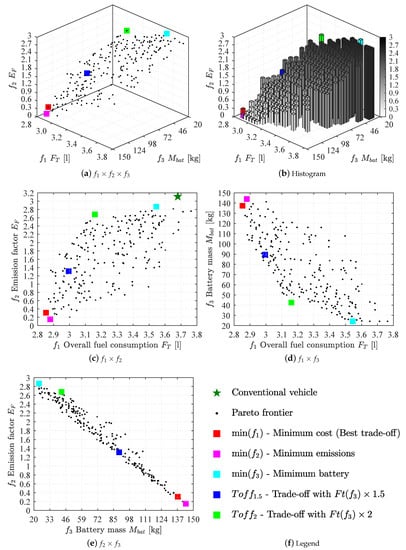
Figure 8.
Optimized solutions.
4.1. Standard Vehicle
The standard solution to be compared to the optimized PHEV configurations is the conventional vehicle configuration propelled only by the ICE and using a standard gear shifting strategy proposed by the vehicle manufacturer [64]. Figure 9 shows the ICE running time for each operation point (torque/speed), where it is possible to observe that the ICE presents several points close to the idle/low-speed regime, which is a characteristic of the Campinas driving cycle (Figure 2). The standard gear shifting strategy is shown in Figure 9; it represents the higher speed section of the cycle.
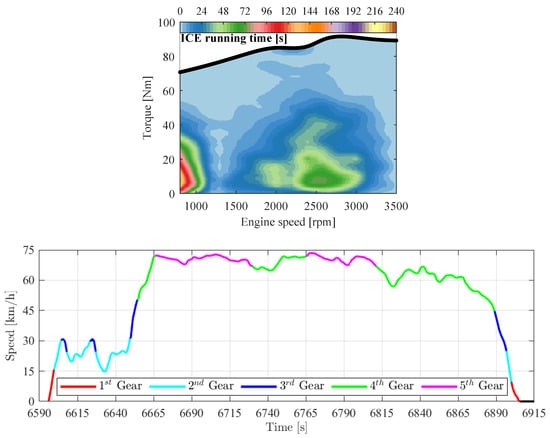
Figure 9.
Conventional (internal combustion engine (ICE)) vehicle results.
4.2. Minimum Battery Size Solution
The minimum battery size solution focuses on minimizing the EMs and battery, resulting in a more compact hybridization kit, with a 24.14 kg battery and low power EMs responsible only for 8.22% of the vehicle power demand. This configuration allows for the upshifting anticipation (Figure 10c) compared to the standard shifting procedure, which saves fuel by moving the ICE operation point to a low-speed/high-torque [32,33], as can be observed in Figure 10a. The EMs operation is presented in Figure 10b where it is possible to observe that in the majority of the time, the electric driving system is used only as a supplementary propelling system, which ensures the vehicle performance even with the upshifting anticipation, and decreases the ICE torque, saving fuel.
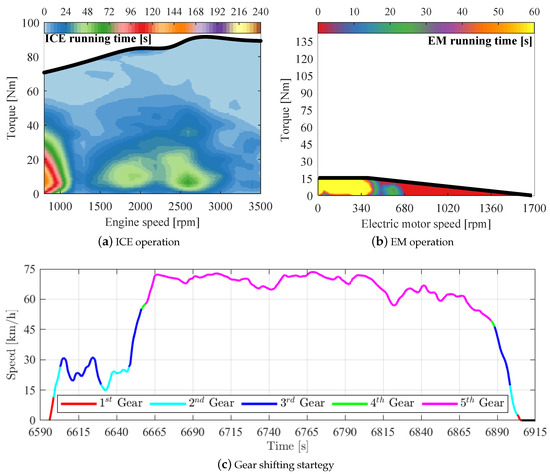
Figure 10.
Minimum battery size configuration powertrain behavior.
This configuration was able to reduce the equivalent fuel consumption () by 3.8%, and present tailpipe emissions close to the standard vehicle results (−3.03% , −2.3% and −1.57% ), as is shown in Table 4.
4.3. Minimum Emissions Solution
The minimum emission PHEV configuration() presents a high level of electrification of the vehicle propelling system, in which the EMs are responsible for 55.4% of the power demand. Therefore, the EMs present high torque, as shown in Figure 11b, in which it is possible to observe that these EMs operate at maximum torque for a large amount of time. Moreover, these high torque EMs also expressively decrease the ICE required torque (Figure 11a), associated with the upshifting anticipation (Figure 11c), keeping the ICE running under ≈ 2700 rpm.
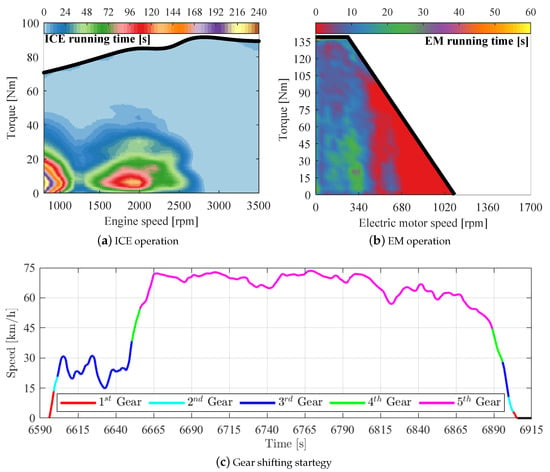
Figure 11.
Minimum emissions configuration powertrain behavior.
On the other hand, this configuration needs a large battery of ≈144 kg to ensure the availability of the electric propelling system during the 42 km of the analyzed driving cycle. Due to the mentioned minimization of the ICE using, it was possible to save 1.22 L of fuel, compared to the conventional vehicle, which represents 21.74% economy regarding the overall cost to perform the desired path. Due to the heavy use of the electric drivetrain system, this PHEV configuration results in −33.88% , −35.36% and −18.19% .
Regarding the cost relation between fuel and electricity, the presented results have shown a favorable scenario for vehicle electrification. However, the use of large batteries may lead to other issues, such as a higher cost of the aftermarket hybridization kit, difficulty of assembling the battery in the vehicle and possible interference in vehicle handling [34].
4.4. Minimum Cost Solution (Best Trade-Off)
Regarding the optimized scenario, the minimum cost solution , which represents the minimum equivalent fuel consumption () among the Pareto frontier is rated as the best-compromised solution (higher fitness value ). This PHEV configuration presents EMs that provide up to 105 Nm, which act similarly to the EMs, keeping the ICE running at a low speed and torque regime, which together, lead to fuel economy. The electric propelling system is responsible to fulfill 66.20% of the power demand, which results in a high concentration of EM operation points close to the maximum torque curve, as shown in Figure 12b. This configuration was able to decrease the cost to perform the driving cycle in 22.55% and generate −28.4% , −33.55% and −19.11% —fewer emissions compared to the conventional vehicle.
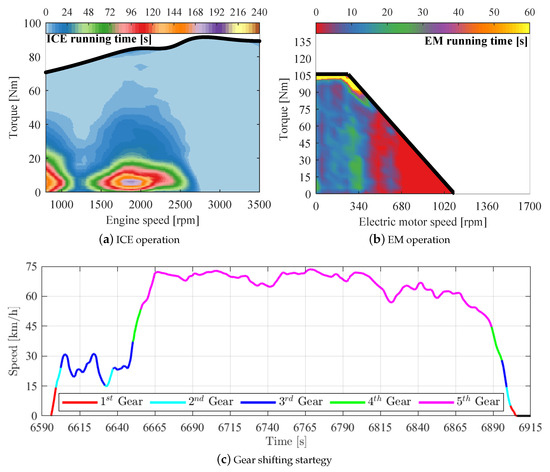
Figure 12.
Minimum cost solution powertrain behavior.
Besides the satisfactory reached results regarding cost end emissions of the configuration, this aftermarket hybridization kit needs a 137 kg battery, which implies in the same issues listed before regarding large batteries. Therefore, the configurations and analyzed below, are included to represent some alternative hybridization kits composed of lighter batteries and EMs, which can be more suitable in cases in which a lower powertrain electrification degree is desired.
4.5. Trade-Off Considering : The
The first of the selected trade-off solutions was defined by assigning 50% more weight to the battery mass minimization at Equation (37) that determines the fitness value, used to classify the population. This configuration is powered by a ≈ 90 kg battery and EMs able to perform up to 83 Nm, which operates the majority of the time at maximum torque regime, as shown in Figure 13b. Moreover, the power split control () was defined as 37.17% due to the lower EMs torque capacity compared to the and PHEV configurations. Similarly to the previously mentioned configurations, the keeps the ICE running at low torque and speed, which enables 950 mL fuel-saving and an equivalent fuel consumption 18.75% lower compared to the conventional vehicle. Furthermore, the solution also enhanced the ICE emissions, by decreasing 23.78% of the , 17.76% and 11.12% .
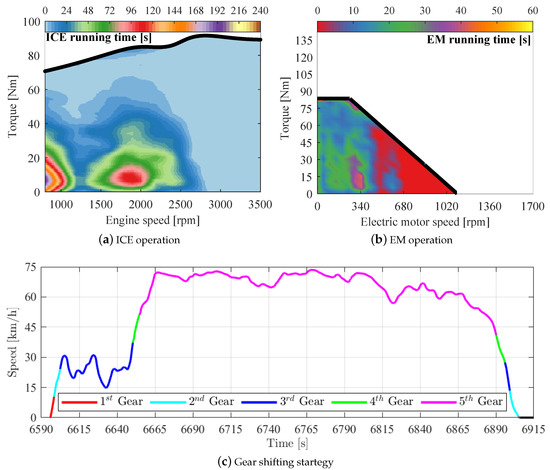
Figure 13.
Trade-off configuration () powertrain behavior.
4.6. Trade-Off Considering : The
Finally, the trade-off solution considering the calculated with , results in a PHEV configuration with 42.55 kg battery and EMs with 43.48 Nm torque capacity. This configuration decreases the equivalent fuel consumption in 14.13% and the emissions in 0.86% , 5.59% and 4.58% . The ICE and EMs operation points and the gear shifting strategy are presented in Figure 14.
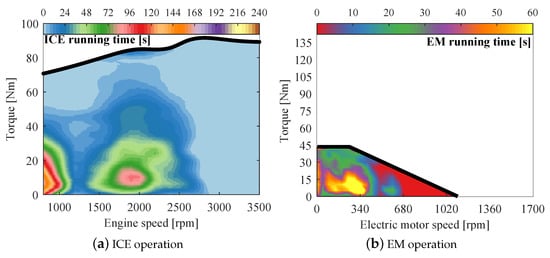
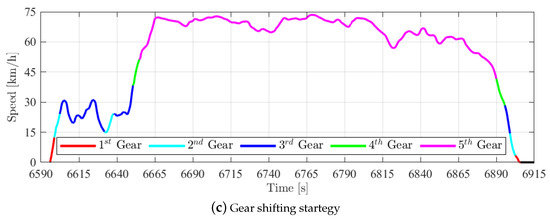
Figure 14.
Trade-off configuration () powertrain behavior.
The solution, in the same way as the minimum battery size PHEV configuration (), represents a lower powertrain electrification degree. Even with the lower gains in terms of energy consumption, these configurations may become good alternatives to provide cheaper hybridization kits due to their smaller batteries and electric motors, in addition to their lower interference in the vehicle weight distribution and drivability.
5. Conclusions
In this paper, an aftermarket hybridization kit that converts a vehicle originally driven by a combustion engine into a PHEV was proposed. An optimization problem was formulated, aiming to decrease the overall cost (regarding fuel consumption and battery charging) to perform a local driving cycle, attenuating the tailpipe emissions and reducing the battery mass, which leads to a low price hybridization kit. Some design variables were taken into account; they could change the capacity and the weight of the batteries, the power and the torque of the EMs, the gear shifting strategy and the PMC strategy. Considering the needs of the customer, the optimization of the kit was suitable to a local driving cycle, reflecting the real service loads that it would face.
After the driving cycle was set, an optimization process was conducted by means of the i−AWGA, which was able to find out a Pareto frontier of optimum configurations of the kit. Some of these solutions could be selected, such as the ones that further reduced the travel cost or emissions, resulting in vehicles with a high degree of electrification. These solutions were suitable for customers who were prone to adding more weight to their vehicles and buying a kit with a higher purchase price (due to the cost of large battery packs).
On the other hand, an optimum configuration with the minor battery weight could be found, which would result in a minor purchase price and would be less effective at reducing travel costs and emissions. If battery size was used as a rule, it would be possible to find other optimum solutions in the Pareto frontier to significantly reduce the wanted index but with a non-extravagant additional weight of the kit.
Furthermore, the optimization algorithm led to another aftermarket hybridization kit configuration which presented good trade-off among the optimization criteria. Each of these optimum configurations presented improvements in the overall energy cost (fuel and electricity) and engine emissions according to the applied electrification degree resulting from the assembled electric motors and battery.
Finally, the presented results have shown that it is possible to obtain expressive enhancements by converting a conventional vehicle propelled only by a combustion engine into a PREV. However, this study is only theoretical, and some other steps are necessary to ensure the feasibility of the proposed concept.
Our future work will guide the decisions among all the Pareto solutions. A study regarding the aftermarket hybridization kit cost, the purchase price and the consumer acceptation will contribute to define the kit setup for a certain local. Regarding the emissions, the electric energy mix and the kit material, manufacture and disposal must be taken into account in future analyses to ensure environmental gains. Moreover, the effectiveness of the hybridization kits should be evaluated under a set of different driving scenarios, to ensure the robustness of the designed devices. Finally, the real-time control for vehicle power management control also needs to be developed, aiming to make the hybridization kit feasible.
Author Contributions
Conceptualization, J.J.E. and F.G.D.; methodology, J.J.E. and L.C.d.A.e.S.; software, J.J.E.; formal analysis, J.J.E. and F.M.S.; writing—original draft preparation, J.J.E., F.M.S. and F.C.C.; writing—review and editing, F.M.S., L.C.d.A.e.S. and F.C.C.; visualization, J.J.E.; F.M.S. and F.C.C.; supervision, F.G.D. and L.C.d.A.e.S.; project administration, F.G.D. and L.C.d.A.e.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors wish to thank the State of São Paulo Research Foundation (FAPESP), Federal Technological University of Paraná—UTFPR, Ponta Grossa and the University of Campinas (UNICAMP) for financial support and scholarships.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Hooftman, N.; Messagie, M.; Mierlo, J.V.; Coosemans, T. A review of the European passenger car regulations—Real driving emissions vs local air quality. Renew. Sustain. Energy Rev. 2018, 86, 1–21. [Google Scholar] [CrossRef]
- Holjevac, N.; Cheli, F.; Gobbi, M. A simulation-based concept design approach for combustion engine and battery electric vehicles. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2019, 233, 1950–1967. [Google Scholar] [CrossRef]
- Shaw, C.; Hales, S.; Edwards, R.; Howden-Chapman, P.; Stanley, J. What can fuel price increases tell us about the air pollution health co-benefits of a carbon price? J. Transp. Health 2018, 8, 81–90. [Google Scholar] [CrossRef]
- Salvo, A. Flexible fuel vehicles, less flexible minded consumers: Price information experiments at the pump. J. Environ. Econ. Manag. 2018, 92, 194–221. [Google Scholar] [CrossRef]
- Mohammadi, F. Design, analysis, and electrification of a solar-powered electric vehicle. J. Sol. Energy Res. 2018, 3, 293–299. [Google Scholar]
- Holjevac, N.; Cheli, F.; Gobbi, M. Multi-objective vehicle optimization: Comparison of combustion engine, hybrid and electric powertrains. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2020, 234, 469–487. [Google Scholar] [CrossRef]
- Du, S.; Yang, Y.; Liu, C.; Muhammad, F. Multi-objective real-time optimization energy management strategy for plug-in hybrid electric vehicle. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2019, 233, 1067–1080. [Google Scholar] [CrossRef]
- Golpîra, H.; Khan, S.A.R. A multi-objective risk-based robust optimization approach to energy management in smart residential buildings under combined demand and supply uncertainty. Energy 2019, 170, 1113–1129. [Google Scholar] [CrossRef]
- Li, W.; Lin, Z.; Cai, K.; Zhou, H.; Yan, G. Multi-objective optimal charging control of plug-in hybrid electric vehicles in power distribution systems. Energies 2019, 12, 2563. [Google Scholar] [CrossRef]
- Li, W.; Lin, Z.; Zhou, H.; Yan, G. Multi-objective optimization for cyber-physical-social systems: A case study of electric vehicles charging and discharging. IEEE Access 2019, 7, 76754–76767. [Google Scholar] [CrossRef]
- Mohammadi, F.; Nazri, G.A.; Saif, M. A Bidirectional Power Charging Control Strategy for Plug-in Hybrid Electric Vehicles. Sustainability 2019, 11, 4317. [Google Scholar] [CrossRef]
- Zhang, F.; Hu, X.; Langari, R.; Cao, D. Energy management strategies of connected HEVs and PHEVs: Recent progress and outlook. Prog. Energy Combust. Sci. 2019, 73, 235–256. [Google Scholar] [CrossRef]
- Liu, M.; Wang, X.; Sheng, Y.; Wang, L. Improvement of multi-objective differential evolutionary algorithm and its application for Hybrid electric vehicles. In Proceedings of the 2019 Chinese Control And Decision Conference (CCDC), Nanchang, China, 3–5 June 2019; pp. 553–558. [Google Scholar]
- Wang, Z.; Cai, Y.; Zeng, Y.; Yu, J. Multi-Objective Optimization for Plug-In 4WD Hybrid Electric Vehicle Powertrain. Appl. Sci. 2019, 9, 4068. [Google Scholar] [CrossRef]
- Fu, X.; Zhang, Q.; Tang, J.; Wang, C. Parameter Matching Optimization of a Powertrain System of Hybrid Electric Vehicles Based on Multi-Objective Optimization. Electronics 2019, 8, 875. [Google Scholar] [CrossRef]
- Kydd, P.H. Electric Hybrid Vehicle Conversion. US Patent 7,681,676, 23 March 2010. [Google Scholar]
- Rodriguez, F.; Lukic, S.M.; Wirasingha, S.G.; Emadi, A. Hybrid Electric Conversion Kit for Rear-Wheel Drive, all Wheel Drive, and Four Wheel Drive Vehicles. US Patent 8,011,461, 6 September 2011. [Google Scholar]
- Vargas, J. Rechargeable Automobile Electric Power System Configured to Replace the Unpowered Rear Axle of a Front Wheel Drive Vehicle. US Patent 8,118,121, 21 February 2012. [Google Scholar]
- Kurdy, T. Electric Vehicle Conversion Kit. US Patent 9,308,810, 5 January 2016. [Google Scholar]
- Causton, M.S.; Wu, J. Aftermarket Vehicle Hybridization: Designing a Supply Network for a Startup Company. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2010. [Google Scholar]
- Rizzo, G.; Naddeo, M.; Pisanti, C. Upgrading conventional cars to solar hybrid vehicles. Int. J. Powertrains 2018, 7, 249–280. [Google Scholar] [CrossRef]
- De Luca, S.; Di Pace, R. Aftermarket vehicle hybridization: Potential market penetration and environmental benefits of a hybrid-solar kit. Int. J. Sustain. Transp. 2018, 12, 353–366. [Google Scholar] [CrossRef]
- Tiano, F.A.; Rizzo, G.; De Feo, G.; Landolfi, S. Converting a Conventional Car into a Hybrid Solar Vehicle: A LCA Approach. IFAC-PapersOnLine 2018, 51, 188–194. [Google Scholar] [CrossRef]
- IBGE. Campinas Fleet. Available online: https://cidades.ibge.gov.br/brasil/sp/campinas/pesquisa/22/28120 (accessed on 27 November 2019).
- IBGE. São Paulo Fleet. Available online: https://cidades.ibge.gov.br/brasil/sp/pesquisa/22/28120 (accessed on 27 November 2019).
- IBGE. Brazilian Fleet. Available online: https://cidades.ibge.gov.br/brasil/pesquisa/22/28120 (accessed on 27 November 2019).
- Costa, E.d.S.; Santiciolli, F.M.; Eckert, J.J.; Dionísio, H.J.; Dedini, F.G.; Corrêa, F.C. Computational and Experimental Analysis of Fuel Consumption of a Hybridized Vehicle; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2014. [Google Scholar] [CrossRef]
- Costa, E.d.S.; Eckert, J.J.; Santiciolli, F.M.; de Alkmin e Silva, L.C.; Corrêa, F.C.; Dedini, F.G. Economic and Energy Analysis of Hybridized Vehicle by Means of Experimental Mapping; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2016. [Google Scholar] [CrossRef]
- Correa, F.C.; Eckert, J.J.; Silva, L.C.; Costa, E.S.; Santiciolli, F.M.; Dedini, F.G. Gear shifting strategy to improve the parallel hybrid vehicle fuel consumption. In Proceedings of the 2015 IEEE Vehicle Power and Propulsion Conference (VPPC), Montreal, QC, Canada, 19–22 October 2015; pp. 1–6. [Google Scholar]
- Eckert, J.J.; Santiciolli, F.M.; Silva, L.C.; Costa, E.S.; Corrêa, F.C.; Dedini, F.G. Co-simulation to evaluate acceleration performance and fuel consumption of hybrid vehicles. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 53–66. [Google Scholar] [CrossRef]
- Eckert, J.J.; Santiciolli, F.M.; de Alkmin, L.C.; dos Santos Costa, E.; Bertoti, E.; Corrêa, F.C.; Dedini, F.G. Fuel consumption and emissions analysis for a hybridized vehicle. Blucher Eng. Proc. 2016, 3, 580–599. [Google Scholar]
- Eckert, J.J.; Santiciolli, F.M.; Bertoti, E.; Costa, E.d.S.; Corrêa, F.C.; Silva, L.C.d.A.e.; Dedini, F.G. Gear shifting multi-objective optimization to improve vehicle performance, fuel consumption, and engine emissions. Mech. Based Des. Struct. Mach. 2018, 46, 238–253. [Google Scholar] [CrossRef]
- Eckert, J.; Santiciolli, F.; Yamashita, R.; Correa, F.; Silva, L.C.A.; Dedini, F. Fuzzy Gear Shifting Control Optimization to Improve Vehicle Performance, Fuel Consumption and Engine Emissions. IET Control Theory Appl. 2019, 13, 2658–2669. [Google Scholar] [CrossRef]
- Eckert, J.J.; Silva, L.C.d.A.e.; Costa, E.d.S.; Santiciolli, F.M.; Corrêa, F.C.; Dedini, F.G. Optimization of electric propulsion system for a hybridized vehicle. Mech. Based Des. Struct. Mach. 2019, 47, 175–200. [Google Scholar] [CrossRef]
- Ho, S.H.; Wong, Y.D.; Chang, V.W.C. Developing Singapore Driving Cycle for passenger cars to estimate fuel consumption and vehicular emissions. Atmos. Environ. 2014, 97, 353–362. [Google Scholar] [CrossRef]
- Pitanuwat, S.; Sripakagorn, A. An Investigation of Fuel Economy Potential of Hybrid Vehicles under Real-World Driving Conditions in Bangkok. Energy Procedia 2015, 79, 1046–1053. [Google Scholar] [CrossRef]
- Jardin, P.; Esser, A.; Givone, S.; Eichenlaub, T.; Schleiffer, J.E.; Rinderknecht, S. The Sensitivity in Consumption of Different Vehicle Drivetrain Concepts Under Varying Operating Conditions: A Simulative Data Driven Approach. Vehicles 2019, 1, 5. [Google Scholar] [CrossRef]
- Oliveira, A.d.M.; Bertoti, E.; Eckert, J.J.; Yamashita, R.Y.; dos Santos Costa, E.; e Silva, L.C.d.A.; Dedini, F.G. Evaluation of Energy Recovery Potential through Regenerative Braking for a Hybrid Electric Vehicle in a Real Urban Drive Scenario; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2016. [Google Scholar]
- Mohammadi, F.; Nazri, G.A.; Saif, M. Modeling, Simulation, and Analysis of Hybrid Electric Vehicle Using MATLAB/Simulink. In Proceedings of the 2019 International Conference on Power Generation Systems and Renewable Energy Technologies (PGSRET), Istanbul, Turkey, 26–27 August 2019; pp. 1–5. [Google Scholar]
- Filgueira da Silva, S.; de Moura Fernandes, E.; de Amorim Junior, W.F. Simulation-Driven Model-Based Approach for the Performance and Fuel Efficiency Trade-Off Evaluation of Vehicle Powertrain; Automotive Technical Papers; SAE International: Warrendale, PA, USA, 2019. [Google Scholar]
- Blagojevic, M.; Djudurovic, M.; Bajic, B. Closed-Form Solution of a Special Case of a Vehicle Longitudinal Motion Model. Vehicles 2019, 1, 7. [Google Scholar] [CrossRef]
- Gillespie, T.D. Fundamentals of Vehicle Dynamics; SAE International: Warrendale, PA, USA, 1992. [Google Scholar]
- Genta, G.; Morello, L. The Automotive Chassis; Springer: Berlin, Germany, 2009; Volume 1. [Google Scholar]
- Reimpell, J.; Stoll, H.; Betzler, J. The Automotive Chassis: Engineering Principles; Butterworth-Heinemann: Oxford, UK, 2001. [Google Scholar]
- Eckert, J.J.; Corrêa, F.C.; Santiciolli, F.M.; Costa, E.d.S.; Dionísio, H.J.; Dedini, F.G. Vehicle gear shifting strategy optimization with respect to performance and fuel consumption. Mech. Based Des. Struct. Mach. 2016, 44, 123–136. [Google Scholar] [CrossRef]
- Jazar, R.N. Vehicle Dynamics; Springer: Berlin, Germany, 2008. [Google Scholar]
- Aaron, B.; Haraldsson, K.; Hendricks, T.; Johnson, V.; Kelly, K.; Kramer, B.; Markel, T.; O’Keefe, M.; Sprik, S.; Wipke, K.; et al. ADVISOR: A systems analysis tool for advanced vehicle modeling. J. Power Sources 2002, 110, 255–266. [Google Scholar]
- Kerler, M.; Burda, P.; Baumann, M.; Lienkamp, M. A concept of a high-energy, low-voltage EV battery pack. In Proceedings of the 2014 IEEE International Electric Vehicle Conference (IEVC), Florence, Italy, 17–19 December 2014; pp. 1–8. [Google Scholar]
- Bojoi, R.; Cavagnino, A.; Cossale, M.; Tenconi, A.; Vaschetto, S. Design trade-off and experimental validation of multiphase starter generators for 48v mini-hybrid powertrain. In Proceedings of the 2014 IEEE International Electric Vehicle Conference (IEVC), Florence, Italy, 17–19 December 2014; pp. 1–7. [Google Scholar]
- Pistoia, G. Electric and Hybrid Vehicles: Power Sources, Models, Sustainability, Infrastructure and the Market; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Jung, J.; Zhang, L.; Zhang, J. Lead-Acid Battery Technologies: Fundamentals, Materials, and Applications; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Young, K.; Wang, C.; Wang, L.Y.; Strunz, K. Electric vehicle battery technologies. In Electric Vehicle Integration into Modern Power Networks; Springer: Berlin, Germany, 2013; pp. 15–56. [Google Scholar]
- Björnsson, L.H.; Karlsson, S.; Sprei, F. Objective functions for plug-in hybrid electric vehicle battery range optimization and possible effects on the vehicle fleet. Transp. Res. Part C: Emerg. Technol. 2018, 86, 655–669. [Google Scholar] [CrossRef]
- Eckert, J.J.; Silva, L.C.d.A.e.; Santiciolli, F.M.; Costa, E.d.S.; Corrêa, F.C.; Dedini, F.G. Energy storage and control optimization for an electric vehicle. Int. J. Energy Res. 2018, 42, 3506–3523. [Google Scholar] [CrossRef]
- Eckert, J.J.; Silva, L.C.; Costa, E.S.; Santiciolli, F.M.; Dedini, F.G.; Corrêa, F.C. Electric vehicle drivetrain optimisation. IET Electr. Syst. Transp. 2017, 7, 32–40. [Google Scholar] [CrossRef]
- Tong, W. Mechanical Design of Electric Motors; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Correa, F.C.; Eckert, J.J.; Silva, L.C.; Santiciolli, F.M.; Costa, E.S.; Dedini, F.G. Study of Different Electric Vehicle Propulsion System Configurations. In Proceedings of the Vehicle Power and Propulsion Conference (VPPC), Montreal, QC, Canada, 19–22 October 2015; pp. 1–6. [Google Scholar]
- Rotering, N.; Ilic, M. Optimal charge control of plug-in hybrid electric vehicles in deregulated electricity markets. Power Syst. IEEE Trans. 2011, 26, 1021–1029. [Google Scholar] [CrossRef]
- Eckert, J.J.; Silva, L.C.A.; Dedini, F.G.; Correa, F.C. Electric Vehicle Powertrain and Fuzzy Control Multi-objective Optimization, considering Dual Hybrid Energy Storage Systems. IEEE Trans. Veh. Technol. 2020, 1. [Google Scholar] [CrossRef]
- Van Reeven, V.; Hofman, T. Multi-level energy management for hybrid electric vehicles—Part I. Vehicles 2019, 1, 2. [Google Scholar] [CrossRef]
- Lu, X.; Xu, X.; Liu, Y. Simulation of gear-shift algorithm for automatic transmission based on matlab. In Proceedings of the 2009 WRI World Congress on Software Engineering, Xiamen, China, 19–21 May 2009; Volume 2, pp. 476–480. [Google Scholar]
- Gen, M.; Cheng, R.; Lin, L. Network Models and Optimization: Multiobjective Genetic Algorithm Approach; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Barbosa, T.P.; da Silva, L.A.R.; Pujatti, F.J.P.; Gutiérrez, J.C.H. Hydraulic hybrid passenger vehicle: Fuel savings possibilities. Mech. Based Des. Struct. Mach. 2020, 1–19. [Google Scholar] [CrossRef]
- General Motors (GM). Owner Manual Chevrolet Celta 2013; Technical Report; GM: Saõ Paulo, Brazil, 2013. [Google Scholar]
- Lopes, M.V.; Eckert, J.J.; Martins, T.S.; Santos, A.A. Optimizing strain energy extraction from multi-beam piezoelectric devices for heavy haul freight cars. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 1–12. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).