2. Exploratory Graph Analysis
The most commonly applied network estimation method in the literature is the graphical least absolute shrinkage and selection operator (GLASSO) [
8,
9]. The GLASSO estimates a Gaussian Graphical Model (GGM) [
10], where edges are the partial correlation between two nodes given all other nodes in the network. The GLASSO penalizes and shrinks coefficients (with small coefficients going to zero) to provide more parsimonious results and lower the potential for spurious relations.
The GLASSO uses a regularization technique called the least absolute shrinkage and selection operator (LASSO) [
11]. The LASSO has a hyperparameter
, which controls the sparsity of the network. Lower values of
remove fewer edges, increasing the possibility of including spurious correlations, while larger values of
remove more edges, increasing the possibility of removing relevant edges. When
, the estimates are equal to the ordinary least squares solution for the partial correlation matrix.
A common approach in the network psychometrics literature is to compute models across several values of
(usually 100) and select the model that minimizes the extended Bayesian information criterion (EBIC) [
12,
13]. The EBIC has a hyperparameter (
), which controls how much it prefers simpler models (i.e., models with fewer edges) [
14]. Larger
values lead to simpler models, while smaller
values lead to denser models. When
, the EBIC is equal to the Bayesian information criterion. The EGA approach starts with
and lowers
by 0.25 if there are any unconnected nodes in the network (i.e., if a node does not have an edge to any other nodes). If
reaches zero, then the network is used regardless of whether there are unconnected nodes in the networks.
More recently, the triangulated maximally filtered graph (TMFG) [
15] has been applied as an alternative network estimation method in EGA [
2,
16]. The TMFG method uses a structural constraint that limits the number of zero-order correlations included in the network (
; where
n is the number of variables). The TMFG algorithm begins by identifying four variables that have the largest sum of correlations to all other variables. Then, it iteratively adds each variable with the largest sum of three correlations to nodes already in the network until all variables have been added to the network. The end result is a network of 3- and 4-node cliques (i.e., a set of connected nodes), which form the constituent elements of an emergent hierarchy in the network [
17].
In psychometric networks, clusters (or sets of many connected nodes) often emerge, forming distinct communities or sub-networks of related nodes. To estimate communities, community detection algorithms can be applied [
3,
18,
19]. The most commonly applied algorithm used in EGA is the Walktrap community detection algorithm. The Walktrap algorithm estimates the number and content of a network’s communities using “random walks” over the network [
20]. These random walks iteratively traverse over neighboring edges, with larger edge weights (i.e., partial correlations) being more probable paths of travel. Each node is repeatedly used as a starting point where
steps—a jump from one node over an edge to another—are taken away from that node, forming a community boundary. A node’s community is then determined by its proportion of many densely connected edges to few, sparsely connected edges (commonly optimized by a statistic known as
modularity) [
21]. The algorithm is deterministic, meaning the number and variable content of the communities are estimated without the researcher’s direction. These communities are shown to be consistent with latent factors of factor models [
1]. For more details about all network estimation methods and the Walktrap algorithm, see
Section 9.
3. EGA Compared to Factor Analytic Methods
There have been several simulation studies comparing EGA to factor analytic methods. In Golino and Epskamp’s [
1] seminal simulation, EGA was compared against several commonly used factor analytic methods, including the Kaiser–Guttman rule (eigenvalues > 1) [
22,
23], minimum average partial procedure [
24], and parallel analysis (PA) [
25]. Overall, EGA and PA with principal axis factoring (PAF) performed the best of the methods with 96% and 97% overall accuracy (respectively). EGA tended to perform better when there were fewer variables per factor (5) and moderate-to-high correlations between factors (0.50 and 0.70), while PA tended to perform better when there were more variables per factor (10) and moderate-to-high correlations between factors.
The second simulation expanded on the first by adding the TMFG network estimation method and PA with principal component analysis (PCA), estimating unidimensional structures, manipulating skew, factor loadings, and data categories (continuous and dichotomous variables) [
2]. Once again, EGA with GLASSO and PA with PCA and PAF had the best overall accuracy (88%, 82%, and 83%, respectively). EGA with TMFG was in the middle of the pack with an overall accuracy of 73%. The PA methods tended to perform better when there were more variables per factor (8 and 12), while EGA with GLASSO tended to perform better when there were fewer variables per factor (3 and 4). EGA with TMFG performed best when there were 4 and 8 variables per factor. EGA with GLASSO (96%) and PA with PCA (100%) performed better than PA with PAF when the data were unidimensional, while EGA with GLASSO (84%) and PA with PAF (83%) performed better than PA with PCA when the data were multidimensional. EGA with TMFG trailed behind all three with 79% accuracy for unidimensional structures and 73% accuracy for multidimensional structures.
A more recent simulation assessed different community detection algorithms (including the Walktrap) combined with EGA with GLASSO compared to the PA methods using continuous and polytomous (5-point Likert scale) data [
18]. In this study, factor loadings were drawn randomly from a uniform distribution between 0.40 and 0.70. The Louvain (90%) [
26], Fast-greedy (89%) [
27], and Walktrap (88%) [
20] algorithms had comparable overall accuracy with PA with PCA (88%) and PAF (85%). The number of factors had the biggest effects on performance, particularly when there were more factors (e.g., 4), where the Louvain and Fast-greedy algorithms were comparable to PA with PAF (around 90%), but the Walktrap was much less accurate (around 80%). In sum, EGA with GLASSO performs comparably to common factor analytic methods such as parallel analysis. Despite evidence of EGA’s effectiveness, there has yet to be an investigation into the stability of its results.
4. Bootstrap Approach
To address this issue, we introduce a novel approach called Bootstrap Exploratory Graph Analysis (bootEGA) to estimate the stability of dimensions identified by EGA. This approach allows for the consistency of dimensions and items to be evaluated across bootstrapped EGA results, providing information about whether the data are consistently organized in coherent dimensions or fluctuate between dimensional configurations. On the one hand, the number of dimensions identified may vary depending on the size of the sample or the sample being measured (e.g., measurement (in)variance). On the other hand, the number of dimensions might be consistent across samples, but some items may be identified in one dimension in one sample and in another dimension in a different sample. Even still, some sets of items may be forming completely separate dimensions.
Using a bootstrap approach, the bootEGA algorithm uses one of two data generation approaches: parametric or resampling (non-parametric). The parametric procedure begins by estimating the empirical correlation matrix. This correlation matrix is then used as the covariance matrix to generate data from a multivariate normal distribution. The resampling or non-parametric procedure is implemented by resampling with a replacement from the empirical dataset. The parametric procedure should be preferred when the underlying data are expected to follow a multivariate normal distribution. The resampling procedure should be preferred when the underlying distribution is unknown or non-normal. Regardless of procedure, the same number of cases as the original dataset is used to generate or resample data. For each replicate sample, EGA is applied, resulting in a sampling distribution of EGA results. This process continues iteratively until the desired number of samples is achieved (e.g., 500).
4.1. Descriptive Statistics
From this sampling distribution, several descriptive statistics are obtained. The median number of dimensions estimated from the replicate samples is computed. The standard deviation of the number of dimensions is used as the standard error. A normal approximation confidence interval is computed by using this standard error and multiplying it by the 2.5 and 97.5 percentile of a
t-distribution with iterations minus one degree of freedom [
28]. Finally, a percentile bootstrap confidence interval is computed using the same percentiles in the bootstrap quantiles [
29]. In addition, a median (or typical) network structure is estimated by computing the median value of each edge across the replicate networks, resulting in a single network. Such a network represents the “typical” network structure of the sampling distribution. The community detection algorithm was then applied, resulting in dimensions that would be expected for a typical network from the EGA sampling distribution.
4.2. Dimension and Item Stability
Because EGA assigns variables to dimensions, additional metrics related to the stability of dimensions and items across bootstrap replicates can be computed. bootEGA evaluates the stability of dimensions using a measure called structural consistency. We define structural consistency as the proportion of times that each empirically derived dimension (i.e., the result from the initial EGA) that was exactly recovered (i.e., identical item composition) from the replicate bootstrap samples was computed. Below, we provide an example of how structural consistency is computed.
Let
w be the placement of items in the empirical EGA communities:
where values
j denote dimensions (e.g., 1 denotes dimension 1). Let
be the bootstrap placement of items for the
iteration of bootEGA. For example, the first iteration:}
If all elements corresponding to the dimension of the empirical item placement and the bootstrap iteration placement match, then the dimension is given a value of 1 for the iteration; otherwise 0. For example, the first three elements of the empirical item placement w correspond to dimension 1. The first three elements of are also all 1 and therefore match (1). The next three elements of the empirical item placement w correspond to dimension 2. For , these elements are and therefore do not match (0). Finally, the last three elements of the empirical item placement w correspond to dimension 3. For , these elements are all 3 and therefore match (1).
Let
be a vector storing the values of whether the bootstrap placement of items match the empirical placement of items for dimension
j and iteration
i. For the example above,
. The structural consistency of each dimension is then defined as:
where
n is the number of iterations and
is the structural consistency of dimension
j.
Substantively, we interpret structural consistency as the extent to which a dimension is interrelated (internal consistency) and homogeneous (test homogeneity) in the presence of other related dimensions [
30]. Such a measure provides an alternative yet complementary approach to internal consistency measures in the factor analytic framework.
A complementary measure to structural consistency is item stability. Item stability quantifies the robustness of each item’s placement within each empirically derived dimension. Item stability is estimated by computing the proportion of times each item is placed in each dimension. This metric provides information about which items are leading to structural consistency (replicating often in their empirically derived dimension) or inconsistency (replicating often in other dimensions).
One obstacle for computing item stability is that item placement is not always consistent with the empirical placement. As demonstrated in
above, dimension 2 was only two elements and dimension 3 was four elements relative to both having three elements each in the empirical item placement. Below are several examples that can be compared with
w:
Starting with , the composition of w and are the same, but their number assignments differ. This is a common occurrence as EGA does not always assign dimension 1 to the label number 1 as it is in w. In this example, the solution is obvious: 3 becomes 1, 1 becomes 2, and 2 becomes 3.
For
, the categorization is not immediately clear. First, there are only two dimension labels (1 and 2). Second, the elements corresponding to the second empirical dimension overlap in
:
. To circumvent these issues, the item stability algorithm follows several steps to produce what we call “homogenized” item placements. First, the Adjusted Rand Index (ARI) [
31] is computed between each dimension’s elements of the item placement in the bootstrap iteration (
) and the corresponding elements for the empirical item placements (
w). The ARI is computed using the following formula:
where
a is the count of items placed into the same bootstrap and empirical community and
d is the count of items that are in different communities of both the bootstrap and empirical communities. Both
b and
c count the wrong placement of nodes between the bootstrap community and empirical community, respectively.
For dimension 1 of and the corresponding elements in w (), the ARI equals 0.4. For dimension 2 of and the corresponding elements in w (), the ARI equals 0.5. The next step orders the dimensions based on highest to lowest ARI first. Ties are decided based on the number of items in the respective dimensions from highest to lowest. This ordering ensures that (1) dimensions that correspond closest to the empirically defined dimensions (e.g., w) are handled first and (2) that dimensions that are most intact (i.e., that have more items) are handled prior to equivalent ARI values.
The final step is identifying the mode in which the respective elements of w belong to. For dimension 3 of , the mode is 1 and therefore converts all labels of 3 to 1. For dimension 2 of , the mode is 3 and therefore converts all labels of 2 to 3. The result is a “homogenized” item placement for of . Following these steps for , the result is . Once all bootstrap item placements have been homogenized with the empirical item placements, then item stability values can be computed. These values are computed by taking the number of times an item is assigned to each dimension and dividing it by the total number of bootstrap iterations.
5. Present Research
In the present paper, we introduce bootEGA to estimate the stability of dimensions identified by EGA. The goal of bootEGA is to provide a tool for assessing whether dimensions and items in a scale are generalizable. Unstable dimensions and items are important for diagnosing psychometric issues that may lead to inappropriate scale interpretations. Items sorting into different dimensions, for example, may be an issue of sample size, hint that the items are multidimensional, or that they are redundant with one another and are forming a minor factor [
32,
33]. Therefore, an approach that is able to assess the quality of EGA’s results is necessary and would allow researchers to examine how their results would be expected to generalize to other samples. Such an approach would not only lead to more accurate interpretations but also provide researchers with greater insights into the structure of their scales.
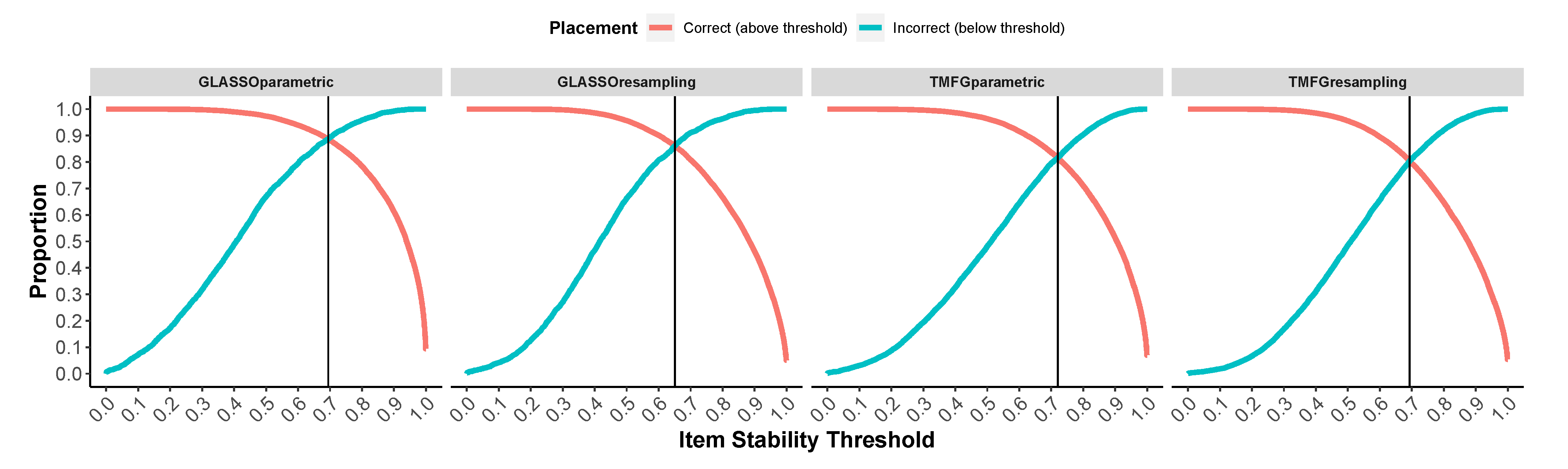
To investigate the validity of the bootEGA approach and item stability analysis, we conducted a large simulation study. In this study, we manipulated sample size (250, 500, and 1000), number of factors (2 and 4), number of variables per factor (4 and 8), correlations between factors (0.00, 0.30, 0.50, and 0.70), and data categories (continuous and polytomous). Importantly, we generated data with cross-loadings and factor loadings that varied randomly between 0.40 and 0.70. We also added skew to the polytomous data ranging from −2 to 2 on 0.5 increments. The first aim was to determine whether the typical structure of bootEGA could improve the accuracy of empirical EGA’s dimensionality accuracy and item placement. The second aim was to determine guidelines for what values of item stability reflect a “stable” item. For this latter aim, we used data from the largest sample size condition only to ensure the robustness of the guidelines we propose.
After, we provide an empirical example to show how to apply and interpret bootEGA output. In the example, we demonstrate that bootEGA can be used to improve the structural integrity of assessment instruments through the identification of problematic items. We show that problematic items can arise because several items are multidimensional (i.e., they replicate in other dimensions and cross-load onto more than one dimension). As part of the empirical example, we provide tutorial code that researchers can apply to their own data. The R code for the simulation, analyses, and example are available on our Open Science Framework repository:
https://osf.io/wxdk7/ (accessed on 24 April 2021).
7. Applied Example: Broad Autism Phenotype Questionnaire
To demonstrate how the bootEGA approach can be applied to investigate the stability of the structure of empirical data, we used data from the
Simons Simplex Collection (SSC), a core project and resource of the Simons Foundation Autism Research Initiative that established a permanent repository of genetic and phenotypic samples from 2600 simplex families. Each family has one child affected with an autism spectrum disorder with unaffected parents and siblings. Here, we used
Broad Autism Phenotype Questionnaire (BAPQ) [
35] data completed by mothers and fathers (
n = 5659) of children with an autism spectrum disorder. Before applying with the dataset, the reader will need to install and load the latest
EGAnet package:
After installing EGAnet, the reader should install, authenticate, download, and load data from our OSF:
With the correlation matrix of BAPQ loaded, EGA can be applied. Below, we use the default EGA approach, which is to use the GLASSO network estimation method with the Walktrap community detection algorithm:
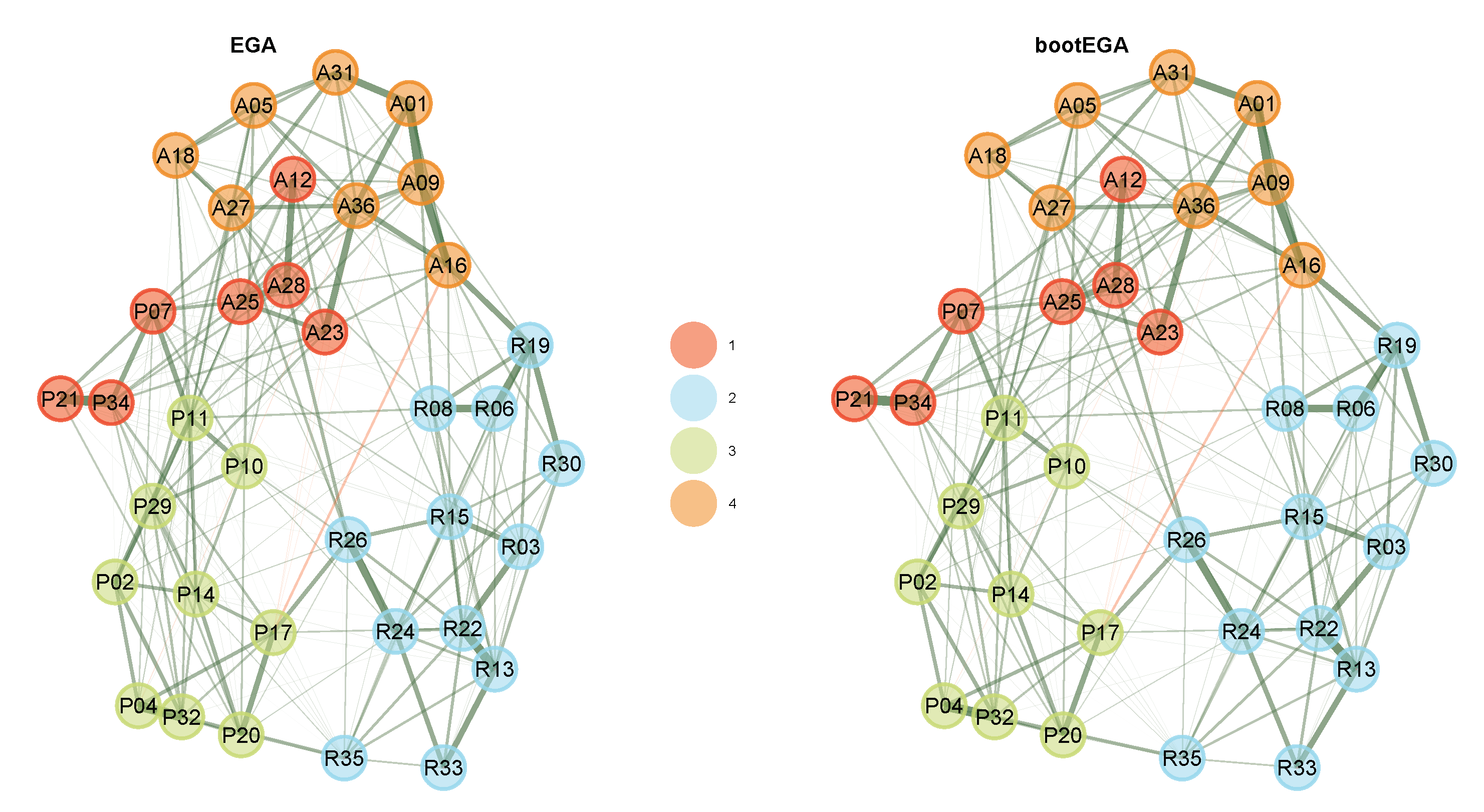
Exploratory Graph Analysis with the GLASSO network estimation method and the Walktrap community detection algorithm estimated four factors (
Figure 4), representing the theoretical factors. Dimension 2 is consistent with the rigid dimension (R3, R6, R8, R13, R15, R19, R22, R24, R26, R30, R33, R35). Dimension 3 is consistent with the pragmatic language dimension (P2, P4, P10, P11, P14, P17, P20, P21, P29, P32, P34). Dimension 4 is consistent with the aloof dimension (A1, A5, A9, A16, A18, A27, A31, A36). Dimension 1, however, represents a mix of the aloof (A12, A23, A25, A28) and pragmatic language (P7, P21, P34) dimensions.
Curiously, these items all reflect difficulty in social interactions with other people: A12 (“People find it easy to approach me”), A23 (“I am good at making small talk”), A25 (“I feel like I am really connecting with other people”), A28 (“I am warm and friendly in my interactions with others”), P07 (“I am ‘in-tune’ with the other person during conversation”), P21 (“I can tell when someone is not interested in what I am saying”) and P34 (“I can tell when it is time to change topics in conversation”). While we may be interested in interpreting this dimension, it is important to know whether these dimensions are stable and likely to reproduce in other samples. To achieve so, we can apply bootEGA for 500 iterations:
![Psych 03 00032 i005]()
Because our dataset is a correlation matrix, the resampling (non-parametric) bootstrap option is not available. Recall that the resampling requires shuffling cases with replacement. Proceeding with the parametric bootstrap, we find that the median network structure depicted in
Figure 4 has four dimensions, similar to the empirical EGA. To evaluate the stability of these dimensions, we can start first by checking the descriptive statistics (
Table 1):
Here, we can see that the median is four dimensions, mirroring the empirical EGA with a relatively narrow confidence interval (CI 95% [3.10, 4.90]). To get a better idea of this distribution, we can look at the frequency of each dimension solution (
Table 2):
With the frequencies, four dimensions were found 70.20% of the time or 351 of 500 bootstrap replicates while three dimensions were found 29.80% of the time or 149 of 500 bootstrap replicates. These results seem to suggest that the four dimension solution might be unstable. To get a better understanding of what dimensions in particular are unstable, we can compute structural consistency or how often the empirical EGA dimension is exactly replicated (identical item assignments) across the bootstrap replicates (
Table 3) [
30]:
![Psych 03 00032 i008]()
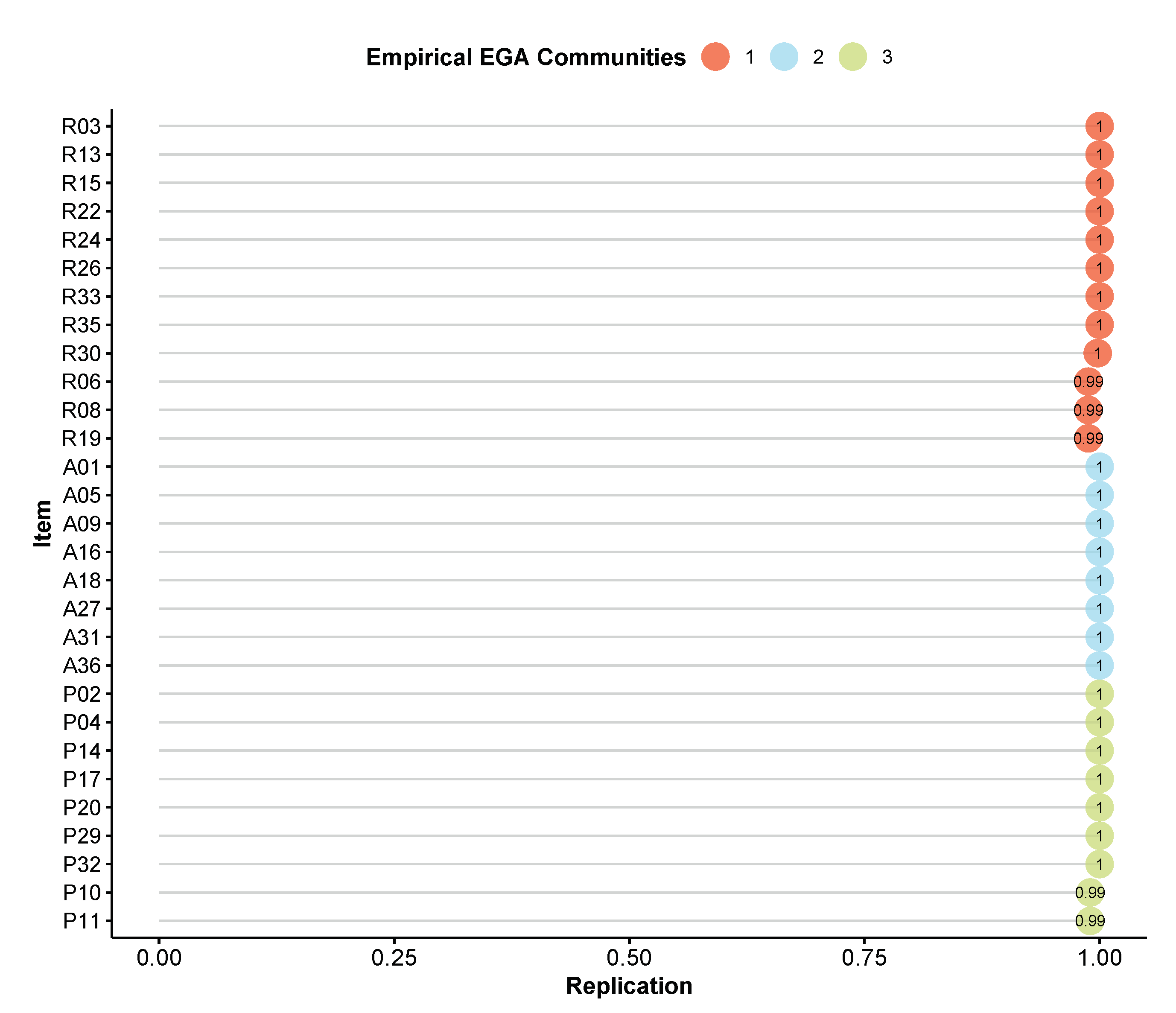
The structural consistency result shows that dimension 1, which represented the difficulty with social interactions, is very unstable. Indeed, this is confirmed when looking at the item stability values in the empirical dimensions (
Figure 5). All items from dimension 1 are at or below the range of 0.65–0.75, where they can be considered unstable.
Table 4 shows how the item stability values across each dimension in the replicate bootstrap samples (values of zero have been removed to facilitate interpretability). To probe this instability further, we can look at how these items are replicating across all bootstrap dimensions with the following code:
![Psych 03 00032 i009]()
Table 4 displays the item stability values across each dimension in the replicate bootstrap samples. From this table, it is clear that some items are unstable. Items A12, A23, A25, and A28 are sometimes replicating in dimension 4, which was their theoretical dimension of aloof. Items P7, P21, and P34 are sometimes replicating in dimension 3, which was the theoretical dimension of pragmatic language.
These results suggest that although these items are associated with their theoretical dimension, they share enough conceptual similarity that they form a separate dimension. These unstable items are clearly causing problems with the consistency of the dimensions of the BAPQ, which are likely due to their multidimensional features—that is, sharing an underlying difficulty with social interactions. To verify this, we looked at the average network loadings of these items across the bootstraps (example code:
bapq.dimstab$item.stability$item.stability$mean.loadings;
Table 5).
Based on the average network loadings, there are a couple of items that have cross-loadings worth consideration (≥0.15) [
36]: A23 (1 and 4) and A25 (1 and 4). Similarly, items P7 (0.13), A28 (0.13), and P34 (0.12) have a cross-loading approaching the same threshold. These results suggest that these items are indeed multidimensional. To resolve this issue, we can remove these items and reassess the structure of the BAPQ (
Figure 6 and
Figure 7).
![Psych 03 00032 i010]()
We can follow through with bootEGA to determine how stable the empirical EGA dimensions are after these items are removed. The bootEGA result found that three factors are being estimated in 99% of the bootstrapped samples, and
Figure 7 shows that the item stability values are now nearly all 1’s, demonstrating the robustness of the dimensionality solution estimated via EGA. The three factor structure estimated after removing the unstable items are very similar to the original three factor structure proposed by Hurley, Losh, Parlier, Reznick, and Piven [
35]. Dimension 1 is composed of items all rigid items (R), dimension 2 of all aloof items (A), and dimension 3 of all pragmatic language items (P).
This example demonstrates that multidimensional items can influence the stability of dimensions and lead to an unstable dimensional structure. Multidimensional items will replicate in two or more dimensions and can potentially be identified by examining the item stability and average network loadings across the bootstraps (e.g.,
Table 5). Removing these items cleans up the stability of the dimensions, leading to good structural consistency.
8. Discussion
In this paper, we present a novel approach for assessing the stability of dimensions in psychometric networks using EGA. Using a Monte Carlo simulation, we show that the typical structure of bootEGA is comparable to empirical EGA for estimating the number of dimensions but has as good or better item placement. From this simulation, we derived guidelines for acceptable item stability (≥0.70). Finally, we provide an empirical example with an associated R tutorial to demonstrate how to apply and interpret the bootEGA approach. We demonstrated that items with stability values lower than an acceptable value can lead to poor structural consistency. In our example, the poor stability of these items was due to multidimensionality. We show that removing these problematic items led to improved structural consistency.
bootEGA adds another approach to the network psychometric literature for assessing the robustness of network analysis results. Previous work has applied bootstrap approaches to assess the accuracy of estimated edge weights, stability of centrality measures, and test differences between edge weights and centrality values [
13]. Our approach expands reserachers’ capabilities to estimate network robustness by enabling them to verify the consistency of dimensions identified by EGA. Importantly, future work will need to examine whether bootEGA provides the same benefits when data have fewer categories than we tested here (i.e., <5). Dichotomous data, for example, may reveal greater differences in performance than the continuous and polytomous (i.e., 5-point Likert scale) data we generated.
As a part of our approach, bootEGA offers diagnostic information about the causes of poor dimensional stability. This has broad implications for scale development. For example, scales are intended to be developed to measure a single attribute. Often, attributes (measured by scales) are multifaceted with separate but related features (measured by subscales). While these features are related, there has yet to be an approach, to our knowledge, to assess the extent to which features remain cohesive (but see, [
37]). Such an approach is important for ensuring that each subscale is capturing a distinct feature of the attribute without being confounded by overlap with other features. In simpler language, our approach can help investigate whether the items are hanging together as researchers intend.
Our empirical example examined the BAPQ scale, which has mixed evidence for its internal structures. The BAPQ scale was intended to measure three separate but related factors of the broad autism phenotype. Previous validation studies of the BAPQ factors have shown that many items have sizable cross-loadings between factors [
38]. bootEGA’s dimension and item stabilities found that there were seven items belonging to the aloof and pragmatic language factors that were forming their own dimension related to difficulties with social interactions. These items were clarified using network loadings, revealing cross-loadings with considerable size. After removing these items, we identified a three-dimension structure that was structurally consistent and corroborated the theoretical factors. Future work using the BAPQ should strongly consider assessing the stability of the dimensionality of the scale before assuming the theoretical dimensions are being measured as intended.
In summary, bootEGA offers researchers several novel tools for assessing the structural integrity of their scales from the psychometric network perspective. Our approach represents both an advance in network psychometrics as well as constructs validation more generally. For network analysis, researchers can assess the stability of the dimensions of the networks. For the broader construct validation literature, researchers can assess whether the structure of their subscales remain homogeneous (i.e., unidimensional) in a multidimensional context.