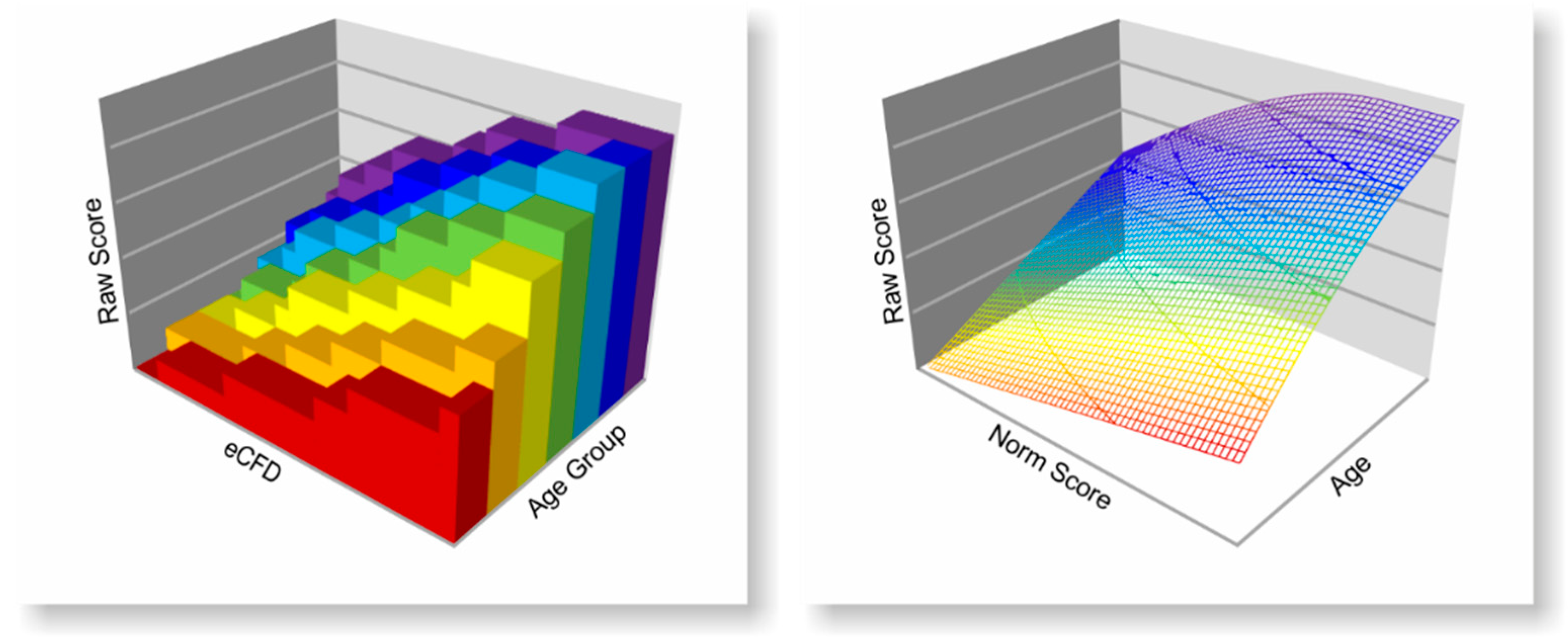
1. Introduction
Psychological tests are widely used instruments for measuring a variety of constructs such as intelligence, reading ability or personality. In most cases, a test raw score per se is not sufficient to assess the ability or personality trait of the test taker. Instead, the achieved raw scores have to be compared and interpreted in relation to an adequate reference population [
1]. Since critical life decisions such as school placement or diagnosis of mental retardation are based on such tests, psychological tests need to supply high quality norm scores [
1,
2]. Unfortunately, the exact distribution of test raw scores in the target population is usually unknown; therefore, the norm scores cannot be determined directly. Instead, they must be derived from test results of a norm sample, that is, a representative subsample of the target population, using statistical tools.
Over time, different norming approaches have been developed and used. For example, modelling the course of distribution parameters such as mean and standard deviation over age was used already early on in intelligence test construction (see [
1,
3,
4,
5,
6] for an overview). Subsequently, using the regression formula for the mean and the standard deviation, it was possible to estimate the norm score at any age. This approach however is based on very strong assumptions, e.g., normality, and it produces huge deviations especially at the upper and lower bounds of a scale. Moreover, mean and standard deviation were estimated independently, thus losing statistical power. This modelling approach was extended by including joint link functions and further parameters such as skew or by modelling non-normal distributions [
2]. Other approaches focus on modelling single percentile curves over age via quantile regression [
7]. Recently, regression-based approaches to directly model the raw score distributions [
3,
8] have become more and more popular. One of them is cNORM [
9], which was implemented in the R package of the same name. In the following section, we present the cNORM approach and its mathematical background. Moreover, the necessary steps for computing norms with the cNORM R package are explained and, finally, the norming process is demonstrated on the example of a concrete data set. We do, however, start this article with a short general introduction about norm scores and their relevance for decisions based on psychological tests.
2. Relevance of Norm Scores in Psychological Testing
To characterise the current state of methodological development in the field of norming, we would like to draw an analogy to the development of classical test theory (CTT) and item response theory (IRT). While, at present, there is a convergence between the development of both approaches and they have been perceived as rather complementary [
10] for a long time, IRT used to be seen as the more elaborate (but less used) framework for test development. To our understanding, a major reason for the perceived superiority of IRT was the simplistic assumption in former CTT that—apart from the measurement error—the distribution of the raw scores directly reflects the distribution of the ability or trait to be measured. Consequently, the major concern was to determine the error variance entailed in the raw score in order to infer the “true score” of a person or at least its confidence interval. In this sense, the “true score” approach of CTT leads to purely data-driven processing, without further explanations on how the test raw score results from the latent ability of a person. IRT in contrast always relied on the assumption that there is a probabilistic relationship between the latent ability of a person and the characteristics of an item. The test score does not directly represent the latent trait but the probabilistic outcome of the interaction between a person’s ability and the item’s difficulty—at least in the case of a 1PL IRT model.
In our view, calculating norm scores is far from being well enough understood and investigated so far. This shortcoming might be a consequence of the fact that many test constructors view norm scores as only referring to the manifest raw score distribution of a test scale. From this perspective, a norm score merely represents the location of a measured raw score in an empirical cumulative distribution function (eCDF); that is, it only conveys the information about the percentile rank regarding the eCDF of the raw scores in the norm sample. The mathematical processing of the eCDF therefore is usually limited to simple
z-standardisation of the raw scores (plus linear scaling where required) in case of normality or to an inverse normal rank-based transformation (INT) of the raw scores to approximate normality (e.g., [
11]). To put it yet another way, the significance of norm scores is limited to a manifest frequency information. Contrasting this notion, most test users probably see norm scores—at least implicitly—as an indicator of a latent trait, as for example in the case of the IQ scores in intelligence testing.
The notion that norm scores also represent latent traits is by no means an oversimplified assumption of psychometrically unskilled test users but is actually grounded in the definition of measurement itself. Measurement is defined as the homomorphous assignment of a numerical relative to an empirical relative (e.g., [
12], p. 47), or, with regard to psychometrics, numbers have to be assigned to traits in a way that the original relationship between the traits of different persons is preserved in the numbers. In the case of psychometric tests, the latent traits of different persons lead to different test scores. The numerical relations between the different test scores should therefore reflect the relations between the traits of the persons. Test raw scores do not necessarily reflect all relations between latent traits. For example, in many instances, they do not reflect the true intervals between latent traits. Moreover, they cannot be interpreted by themselves due to the missing frame of reference. However, what is represented in the eCDF of raw scores in the norm sample is the rank information, that is, information about the raw score that is expected for a certain rank of the latent trait [
13]. It should be noted here that just as in IRT, this is a relationship between the latent ability of a person and an expected outcome; however, unlike IRT, it is not the outcome of a single item but of the whole scale. If the rank information derived from the eCDF is projected onto a normal distribution (which is exactly what is achieved via INT) and the latent trait is in fact normally distributed, then the derived norm scores do represent the true intervals between latent traits. Therefore, norm scores derived via INT from the eCDF of the raw scores in the norm sample do not only represent frequency information of the raw score distribution. Instead, the relations between two different norm scores—apart from the individual measurement error—necessarily reflect the relations between the underlying latent traits as well.
Unfortunately, merely collecting data within a large norm sample and using INT to determine norm scores nevertheless entails numerous sources of error [
13]. First, sampling error contained in the raw scores is fully preserved in the norm scores. Therefore, to avoid imbalances in the data, each norm sample has to be representative and of a sufficient size. Second, in cases of tests that span a large age range, subsamples for different age groups must be collected, in order to control for the development of the latent ability across age. Since norm scores are usually determined for each of these groups separately, very large sample sizes are needed, making test construction utterly expensive. However, imbalances between subsamples can nonetheless occur, and the trajectories of the percentiles across age can exhibit jagged or even implausible courses (e.g., older children obtaining better norm scores for the same raw score than younger children, when normally a continuous increase in performance would be expected over age). Third, in many cases (e.g., in educational testing), it is hardly even possible to cover the complete age range with subsamples of sufficiently narrow intervals. Therefore, in many cases either the norm scores are extremely imprecise (e.g., the same scale used for a whole cohort or grade) or there are large gaps between the subsamples (e.g., tests normed only at the end of each school year). The more a person’s age deviates from the mean age of the respective subsample, the larger the bias becomes in the norm score [
8]. Finally, norm scores can only be specified for raw scores, which indeed occurred in the norm sample. In summary, conventional norming, that is, INT of the eCDF per subsample, leads to a huge amount of additional error—besides individual measurement error—contained in the norm scores [
1,
8,
13]. Therefore, the central assumptions of measurement are nevertheless frequently violated if norm scores are derived in an overly simplistic way.
We would therefore like to present a norming procedure (Implementation: R package
cNORM; [
9]), which is able address the abovementioned drawbacks, thereby substantially reducing the error variance usually introduced by the norming procedure while simultaneously requiring much smaller samples [
13]. We suggest to generally model the relation between a latent trait and the expected test raw score in the norming process with smooth functions, both per age and across age. In the simplest case, with a single norm sample, simple polynomial regression is used to model the monotonic function between raw scores and norm scores. In the case of additional explanatory variables such as, for example, age, a hyperplane is adjusted to the three-dimensional data map of person location (i.e., the rank information), raw score and explanatory variable [
1,
6,
8]. The hyperplane is adjusted by drawing on polynomial regression as well and represents a continuous statistical model extracting the functional relation between latent trait, raw score and explanatory variable from the manifest data. By drawing on the complete data set, imbalances of distinct subsamples are smoothed, thus reducing local violations of representativeness and raising statistical power. For a detailed description of the types of norming errors, please see [
13], where we could also show that continuously modelled norm scores more closely reflect the latent trait as compared to conventional test norms, retrieved via INT.
The approach makes only sparse assumptions on the nature of the latent trait and the data: First, we assume the existence of a latent trait, which is normally distributed at each level of the explanatory variable. Second, this latent trait interacts with the items of a scale, which—depending on the features of these items—leads to an expected raw score of each single test person and to an expected distribution of raw scores in the population. Note that this raw score distribution is not at all restricted to normality. Extreme floor and ceiling effects might, however, at some point be hard to model. Third, norm scores derived via INT from the eCDF mirror the normally distributed latent trait. Fourth, we further assume a bijective relationship between the norm scores and the expected raw scores at each level of the explanatory variable; that is, the relationship must be monotonic (e.g., higher latent traits consistently go along with higher expected raw scores or lower expected error rates at a fixed level of the explanatory variable). Finally, in the case of covariance between a latent trait and explanatory variable, the percentile curves must develop continuously and systematically, but not necessarily monotonically, across the explanatory variable. For example, the average raw scores of a test scale measuring fluid reasoning increase from childhood to early adulthood, but later, they decrease. Importantly, no further presumptions on the nature and course of this development are made. We outline the mathematical background of the procedure in the following section.
4. Generating Continuous Test Norms with cNORM
To generate test norms using the cNORM approach with the corresponding software package, several steps are necessary. The three steps include:
In the following section, these three steps are described and explained in detail both from a theoretical point of few as well as from the side of their practical application. Information about the installation of RStudio and the cNORM R package can be found here: [
20]. We will first explain the steps of the process in more detail, before demonstrating a comprehensive function that applies all steps in one process.
4.1. Data Preparation and Modelling
The basis of every norming process is a sufficiently large and representative norming sample. Therefore, some authors recommend using random sampling but emphasise that a stratification of the norm sample could be necessary in the case of unbalanced data sets, especially when using small samples [
13]. For example, to norm an intelligence test for a broad age range, it is necessary to stratify the norm sample with regard to the explanatory age variable, since an unbalanced set could lead to norming errors, especially in the underrepresented age intervals. One major advantage of using statistical continuous norming models instead of simply applying inverse normal transformation per age group is the increased statistical power, since the modelling draws on the complete data set. Consequently, smaller samples are already sufficient for obtaining a higher norm score precision compared to traditional norming approaches. For instance, with cNORM, 100 cases per age group already lead to more precise norms as compared to 250 cases in traditional norming [
13]. Choosing a modelling approach like cNORM can thus not only close the gaps between norm tables but can also render test norming projects more cost efficient while improving data quality. For more detailed information to the process of representative sampling, see [
21,
22].
After establishing a representative norm sample, the data must first be imported in the R environment. It is advisable to start with a simply structured data object of type data frame or even a numeric vector containing raw score and explanatory variable. Missing data in the norm sample should be excluded before the actual norming process. Since the explanatory variable in psychometric performance tests is usually age, the term ‘age’ as well as the shortcut
is used in the following to refer to the explanatory variable. In fact, the explanatory variable is not necessarily age but must in any case be an interval or nominal variable. Finally, a grouping variable is necessary to break down the norm sample into smaller subsamples (for example grades or age groups). The method is relatively robust to changes in the granularity of the group subdivision and has little effect on the quality of the norm scores [
8]. As a rule of thumb, the more the explanatory variable covaries with the measured test score, the more groups should be formed [
13]. Consequently, age groups need not necessarily be equidistant, or each contain a constant number of cases, but rather should increase in granularity at those areas where fast development of the latent ability occurs. By default, cNORM assigns the variable name ‘group’ to the grouping variable. To divide the norming sample into adequate groups, the ‘getGroups’ method can be used. By default, the function divides the sample into groups of equal size and returns a vector containing the group mean of the explanatory variable for every subject.
The next step is to rank each person in each group by using the ‘rankByGroup’ function, which returns percentiles and performs a normal-rank transformation using T-scores (M = 50, SD = 10) by default (z- or IQ-scores can also be used, and it is possible to define arbitrary scales by specifying mean and standard deviation). By doing so, every individual subject in the test sample is ranked in comparison to all other subjects in the same group. Different ranking methods (RankIt; Blom; Van der Warden; Tukey; Levenbach; Filliben; Yu and Hang) can also be used; however, by default RankIt was chosen. Instead of using a grouping variable respectively dividing the age variable into distinct age groups, one can also use the ‘rankBySlidingWindow’ method. This method draws on the continuous age variable and uses a sliding age interval to rank each subject in the norm sample relative to all other subjects whose age does not differ by more than half the width of the age interval from the age of the ranked subject. Grouping into distinct subgroups with the ‘getGroups’ function is thus not necessary. The width of the sliding age interval is set by specifying the function parameter ‘width’. For example, setting ‘width = 0.5’ by using age as a continuous variable in the unit ‘year’ means that the width of the age interval is six months, and therefore, every subject is assigned a rank based on all other subjects no more than three months younger or older than the person itself. The ranking by sliding window can be seen as a special case of ranking by group but with every subject being ranked with respect to all other subjects within a symmetric interval around the subject’s age value. Both ranking functions add the two columns ‘percentile’ and ‘normValue’ to the data, which are necessary for further computations. Moreover, descriptive information for every group such as group mean and standard deviation is added to the data.
The next step initiates the actual modelling process by determining a polynomial to express the raw score as a function of the estimated latent person parameter
and the explanatory variable a. As described in
Section 2 of this manuscript, we believe that the norm score assigned to a certain raw score reflects the estimated latent person parameter
In the following section, we do, however, refer to the norm scores as
for
location instead of
, because
is the abbreviation used in the R package. To retrieve the model, all powers of the variables
and
up to a certain exponent
together with all possible interactions are computed. To compute the desired powers, one should use the ‘computePowers’ method. Please note that using a power parameter
means to compute
new variables corresponding to the powers of
and
as well as their interactions. Therefore, the number of used predictors for modelling the regression function grows in a quadratic manner with respect to
. As a rule of thumb,
should be chosen to be smaller than 5; hence, higher values can lead to the overadjustment of the model. Alternatively, the power parameter for location and age can be set independently, with higher values for location and smaller powers for age, since age trajectories often can be modelled by quadratic or cubic polynomials. By default, cNORM uses
for both location and age, since practical application so far has shown a high goodness of fit with even a small number of predictors [
1,
8,
13], and it also provides methods for cross validation, verification of the model assumptions, visual model inspection and visualisation of percentiles to determine the optimal setting. Applying the method to the norm data adds
columns to the data set representing the values of all possible predictors of the raw scores.
The complete process of data preparation, containing ranking and computing powers can also be performed by using the function ‘prepareData’. Please note that when using this function, the names of the used grouping variable and raw score variable must be assigned to the parameters ‘group’ and ‘raw’, respectively.
To start the computation of the targeted regression model, the next step is to use the ‘bestModel’ function. There are several ways to use this function: By specifying , the function returns the model that satisfies this requirement with the smallest possible number of predictors. Instead, one can specify a fixed number of predictors, and the method in turn delivers the model with the highest to this number of predictors. Finally, a specific regression formula can be specified, and cNORM fits the regression weights accordingly. Since in most cases it is not possible to determine in advance how well the data can be modelled, the default settings are four for the number of predictors and 0.99 for . If the targeted precision of the regression model in terms of is not reached, the method returns the model with all allowed predictors. However, the threshold of is no ultimate criterion for model selection, since it depends on the covariance between the explanatory variable and the latent ability as well as on the size of the norm sample. It might even be suitable to reduce this value to 0.95 to smooth the percentiles and to avoid model overfitting. This can usually be achieved by reducing the power parameter k and/or the number of terms in the regression model.
4.2. Model Validation
The cNORM package contains a variety of methods for validating the resulting regression model. For this purpose, it is helpful to remember the main idea of the norming approach. From a graphical point of view, the resulting regression function represents a so-called hyperplane in three-dimensional space spanned by the three dimensions raw score, norm score and explanatory variable.
On the one hand, it is necessary to evaluate the model in terms of whether it is suitable to provide adequate test norms. If the resulting is sufficiently high, the hyperplane usually models the manifest norm data over a wide range of all variables very well. However, since the approach is based on a Taylor polynomial, which usually has a finite radius of convergence, it is possible that there are age or performance ranges for which the regression function no longer provides plausible values. With a high , this boundary of convergence is reached at the outer edges of the age or performance range of the norm sample or even beyond. These limits are not due to the used method only but also because the underlying test scales have only a limited validity range within which they are able to map a latent ability to a meaningful numerical test score (e.g., because of floor and ceiling effects and in general due to skewness of the raw score distributions). Therefore, norm tables and norm scores should generally only be issued within the validity range of the model. In addition, even if extrapolation to extreme raw scores that were not reached once in the norm sample yields plausible norm scores, such extrapolation should be carefully considered. For determining the limits of the regression model and for identifying model violations, cNORM provides graphical and numerical methods to investigate the possible limitations of the computed model. First, the ‘plotPercentile’ function of cNORM can be used to visually check the model fit. This function plots the manifest as well as the approximated relation between raw scores and percentiles as functions of the explanatory variable. By default, the maximum and minimum raw scores reached in the norm sample are used as the upper and lower limits of the plotted raw scores, but the range of plotted raw scores can also be set manually by using the function parameters ‘minRaw’ and ‘maxRaw’. It is important to make sure that the percentile lines do not intersect, because otherwise different percentile ranks would be assigned to the same raw score. As previously mentioned, intersecting percentile curves can occur when the regression model is extended to age or performance ranges that do not or only rarely occur in the norm sample. Moreover, intersecting percentile curves can be a sign of strong floor or ceiling effects in the test and are not necessarily due to the cNORM approach. From a mathematical point of view, intersecting percentile curves would implicate that the mapping from raw score to norm score is not unique for a fixed level of the explanatory variable. As a result, more than one norm score would be assigned to a given raw score, which would not only violate the model assumptions but also lead to problems in the practical application of norm scores. Second, one can use the ‘plotRaw’ function to compare fitted and manifest data for every group separately. The model fit is particularly good if all points are as close as possible to the bisecting line. However, it must be noted that deviations in the extremely upper and lower performance range often occur because, as already mentioned, the manifest data in these areas only rarely occur in the norm sample and are therefore afflicted with high measurement error. Alternatively, the ‘plotNorm’ method can be used, which delivers an equivalent plot as ‘plotRaw’ but uses norm scores instead of raw scores. Therefore, the plotted values should also approach the bisecting line as closely as possible. Both plots can be regarded as a graphical illustration of the accordance between predicted and observed values and, therefore, as a graphical visualisation of the model fit. Finally, to check the monotonicity of the mapping function between latent variable and raw score, the ‘plotDerivative’ method can be used, which plots the first-order derivative of the regression function with respect to . This method should be used to check whether there is any age or performance range with a zero-crossing, indicating a violation of the monotonicity. Please note that for example zero-crossings in the upper age and performance range do not necessarily mean that the modelling has completely failed, but that the test scale loses its ability to differentiate in this particular measurement range. This is important when subsequently norm tables are calculated from the model, since these performance ranges should be excluded from the tables. Alternatively, cNORM provides a ‘checkConsistency’ method, which scans all age and performance ranges numerically to find any violation of the bijectivity in the regression function. We recommend using both methods to find any violation of the model assumptions, especially intersecting percentiles, but as well contra intuitive age progression and undulating percentile curves as a sign of overfit.
Furthermore, it is also necessary to evaluate the model in terms of how well it fits the norm sample and whether it shows any signs of over- or under-fitting. For validating the derived model from a more statistical point of view, the ‘plotSubset’ function delivers additional information about and other information criteria, such as Mallow’s or , depending on the number of predictors with fixed parameter . Different charts are provided if the ‘type’ parameter is changed (1: , 2: , 3: ). The method can be especially helpful in case the resulting model seems to be invalid because of violations of consistencies in one or more measurement ranges. In addition, these information criteria can be particularly helpful in detecting any signs of over- or under-fitting. Depending on the specific parameter, the method returns a visualisation of the chosen information criterion as a function of the number of used predictors. Moreover, cNORM provides the ‘cnorm.cv’ method, which is a validation function to obtain an impression of the quality of the norming process. To this end, the method splits the data set into a training set (80%) and a validation set (20%), computes norming models with increasing numbers of predictors starting with one predictor up to a specified number (parameter ‘max’) based on the training set, and compares the predicted with the observed scores of the validation set in terms of the root mean squared error (RMSE) of the raw score as well as the adjusted of the norm score. Moreover, the method returns a crossfit value which can be used to identify the possible effects of under- or over-fitting. Crossfit values lower than one indicate signs of underfitting, while values greater than one suggest overfitting. By setting the parameter ‘repetition’, the number of validation cycles, that is, the number of times the sample is split, and the cross validation is repeated can be specified. Please note that for every repetition it is necessary to rank the training and validation set as well as to compute regression models with increasing numbers of predictors. For example, repeating the validation cycle ten times with a maximal number of predictors of twelve, the norm sample must be divided and ranked ten times, and regression models model must be computed. Consequently, the computational effort increases rapidly with the maximum number of predictors and the number of repetitions, leading to high computational duration. As a rule of thumb, crossfit values within are acceptable, while lower and, respectively, higher values should be seen as evidence of underfitting and, respectively, overfitting. Further research is necessary to investigate lower and upper bounds of crossfit values as indicators for under- and over-estimation in more detail
4.3. Generating Norm Tables
While the actual norming process provides a pure functional expression in a statistical sense, the cNORM package also contains methods to retrieve lists of norm scores for specific raw scores and, vice versa, raw scores for specific norm scores. Additionally, cNORM contains a variety of methods for the visualisation of norm curves.
First, cNORM provides the ‘getNormCurve’ method, which returns the fitted raw scores for a specific norm score. For example, specifying the norm score as T = 50 in terms of a T-score, the method plots the raw scores assigned to a norm score of T = 50 as a function of the explanatory variable (e.g., age). By default, the plotted range of the explanatory variable is limited by the corresponding range of the norm sample but can be specified using the parameters ‘minAge’ and ‘maxAge’ to set the desired values. Please note that the estimated norm scores can differ greatly from the true ones if the used age values are extrapolated to values that are not contained in the norm sample. Therefore, extrapolation should be used cautiously or at least be marked in the test manual.
Second, the ‘plotNormCurves’ method can be used to visualise norm curves for more than one norm score simultaneously. For example, setting the ‘normList’ parameter to ‘c(30, 40, 50, 60, 70)’ returns a visualisation of norm curves corresponding to the T-scores 30, 40, 50, 60 and 70 in one plot. In addition to the percentile curves mentioned above, the visualisation can also be used for checking the model validity, since intersecting norm curves would indicate a misspecification of the statistical model. Moreover, intersecting percentiles can emerge also due to floor and ceiling effects, for example, if the test cannot adequately discriminate in extreme performance ranges. In this case, the corresponding raw score should be assigned to a percentile range rather than to a single norm score to indicate that test scores in this performance range should be interpreted cautiously. This is especially important in extremely low norm ranges, since decisions about school placement and the like are often based on such norm scores.
Third, the ‘predictNorm’ function can be used to predict the norm score for a single raw score given a specific age. For considering the limits of the model validity, the minimum and maximum norm score can be specified by setting the parameters ‘minNorm’ and ‘maxNorm’ to the corresponding values. Likewise, the ‘predictRaw’ method returns the predicted raw score for a specific norm score and age.
When it comes to test application and automatised scoring and interpretation of test results, the statistical model is completely sufficient to provide norm scores with a prespecified precision for any level of the explanatory variable. In real-world scenarios, however, manual scoring is still very common, which is why in most cases norm tables must also be provided for users. One of the major advantages of statistical norming models is the possibility to also decide on the granularity of the norm tables and to provide norm scores even for those raw scores or levels of the explanatory variable for which no manifest data are at hand [
13]. In typical scenarios like achievement tests, the available norms are often referred to an entire grade level. By contrast, continuous norming methods like cNORM can, for example, provide norms per months or per week, theoretically even down to the exact day. Additionally, there are no missing values in the norm tables anymore, and there is even the possibility for cautious extrapolation to age or performance ranges not contained in the norm sample. To this end, cNORM provides functions to generate norm tables with either the assignment of norm scores to raw scores or vice versa: The ‘normTable’ method returns the corresponding raw scores for a specific age or vector of ages. Using the parameter ‘step’, the desired interval between two norm scores can be set. Furthermore, if a coefficient of reliability is entered, confidence intervals for the norm scores and the percentile ranks are also computed automatically.
In equivalence to the ‘normTable’ function, the ‘rawTable’ method can be used to assign predicted norm scores to a predefined series of raw scores at a certain age. The function is very useful in case the exact percentiles or the exact norm scores are to be determined for all raw scores that may occur in a given test scale and for a given range of the explanatory variable. By setting the parameter ‘step’, the desired precision for the raw scores can be specified. Since predicting the norm score for a given raw score and age requires an inversion of the regression function, with the latter being determined numerically, the computational of the ‘rawTable’ method increases with the higher precision and smaller step size.
5. Step-by-Step Example: Continuous Norming of a Reading Comprehension Test
To give a detailed example of the cNORM norming process following the already-mentioned three necessary steps, the norming sample of the sentence completion subtest of a German reading comprehension test named ELFE 1–6 [
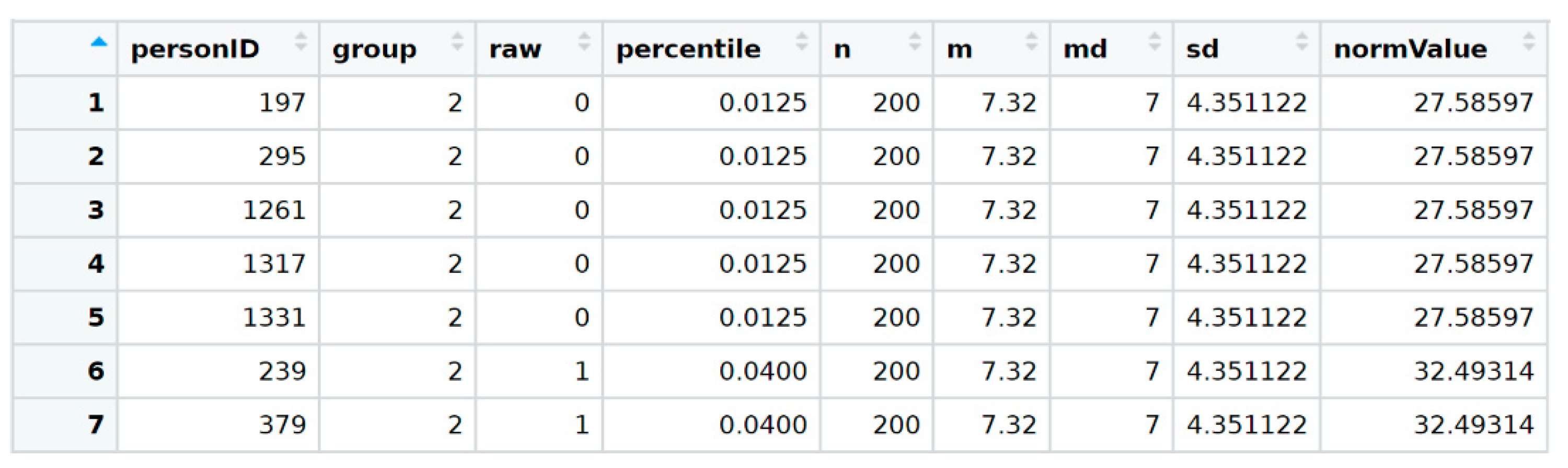
23] is used in what follows. The data set is already included in the cNORM R package and can directly be retrieved. In the first step, the data is assigned to the ‘data.elfe’ variable, and the ‘head’ method is used to obtain a first impression of the data set (
Figure 2).
As can be seen, there is no age variable in the data set, only person ID, a raw score, and a grouping variable. In this case, the grouping variable also serves as a continuous explanatory variable since children were only examined at the very beginning and the exact middle of the school year during the test standardisation. For example, a value of 2.5 indicates that the corresponding participants were examined in the middle of the second grade. Another possibility would have been to examine children throughout the entire school year instead and to use the schooling duration as a continuous variable. To build the grouping variable, the first and second half of each year could, for example, be aggregated into one group, respectively. Since the participants in this sample are grouped already, it is not necessary to use the ‘getGroups’ method. In the data set, there are seven groups with 200 cases each, totalling 1400 cases:
# Example dataset based on a reading comprehension test
data.elfe <- elfe
# Inspect the first six lines of the data set
head(elfe)
5.1. Data Preparation and Modelling
The next step is to apply the ‘rankByGroup’ method. Please note that the aforementioned ‘rankBySlidingWindow’ method is no valid alternative in this case, because the used explanatory variable is no continuous variable. The RankIt method is chosen as ranking method by setting the ‘method’ parameter to ‘4’. In addition, T-scores with M = 50 and SD = 10 are chosen as norm scale. As already mentioned, other scales can be used by specifying the mean and standard deviation as a vector to the ‘scale’ parameter of the method (for example, IQ-scale can be used by setting ‘scale = c(100, 15)’ instead). If the entire sample is to be ranked without a grouping or explanatory variable, the optional parameter ‘group’ must be set to ‘FALSE’. By doing so, the rank of every subject is determined with respect to the whole norming sample. If a grouping variable with a name other than “group” is to be used, the “group” parameter must be set to this very name:
# Rank by variable group and generate T scores
normData <- rankByGroup(data.elfe,
group = ’group’,
raw = ’raw’,
scale = ’T’,
method = 4)
# Inspect the resulting data set
head(normData)
A short inspection of the resulting data set shows that various columns such as manifest percentiles, mean and standard deviation of the corresponding group were added to the data set, as previously described (
Figure 3).
The last column contains the manifest norm scores with respect to the corresponding group, expressed as
T-scores. These values and the grouping variable are used in the next step of the data preparation procedure to calculate powers and interactions. To this end, the method ‘computePowers(normData)’ is used. The function appends the resulting powers and interactions of norm score and grouping variable to the data set as columns (
Figure 4).
As mentioned, cNORM calculates powers and interactions up to an exponent of by default. Thus, a total of predictors are added to the data set as additional columns. To start the actual modelling process, the ‘bestModel’ function is used with a default stopping criterion of . The resulting model contains four predictors plus an intercept and captures more than 99% of the variance of the norm data. For a more detailed summary, cNORM’s ‘summaryModel’ can be applied to the norm model:
# Compute best regression model, default R2 = 0.99
model <- bestModel(preparedData)
summaryModel(model)
# Output:
Final solution: 4 terms
R-Square Adj. = 0.991943
Final regression model: raw ~ L1A2 + L1A4 + L3 + L4A1
Regression function: raw ~ −6.598905 + 0.0379676 × L1A2 − 0.0006587483 × L1A4 + 9.255206e-05 × L3 − 2.910607e-07 × L4A1
Raw Score RMSE = 0.64069
The final solution, as chosen by the best subset approach, contains four predictors, namely
and
, as well as an intercept. The resulting polynomial regression function in this case is as follows:
Moreover, the deviation between observed and predicted raw scores seems to be sufficiently small with a root mean squared error of . In summary, the resulting regression model seems to cover a great amount of the variance in the norm data combined with a small, global prediction error.
5.2. Model Validation
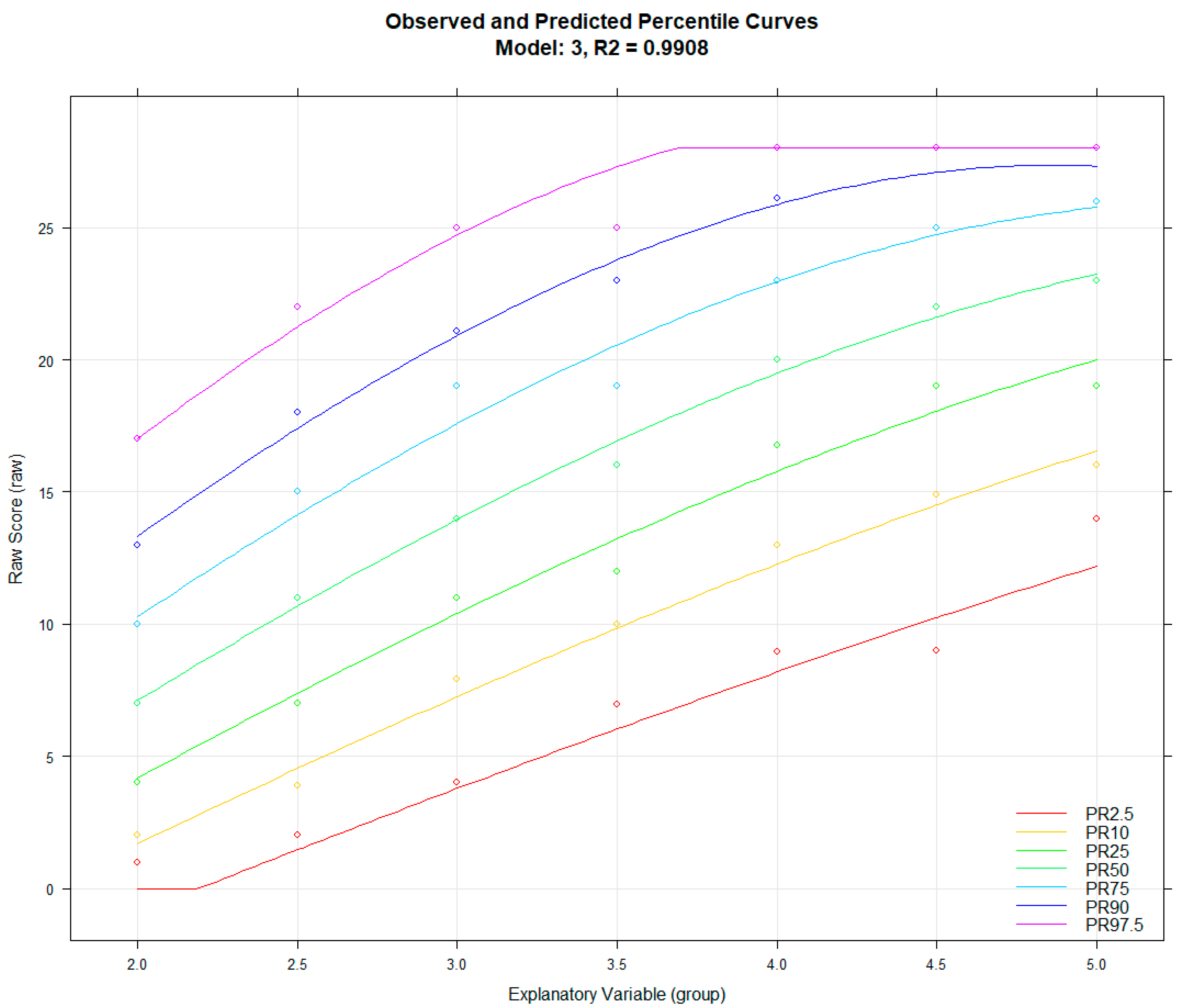
To obtain a first impression of the model fit in more detail, the ‘bestModel’ function automatically returns a visualisation of the observed and predicted percentile curves which can also be generated by using ‘plotPercentiles(model)’ (
Figure 5).
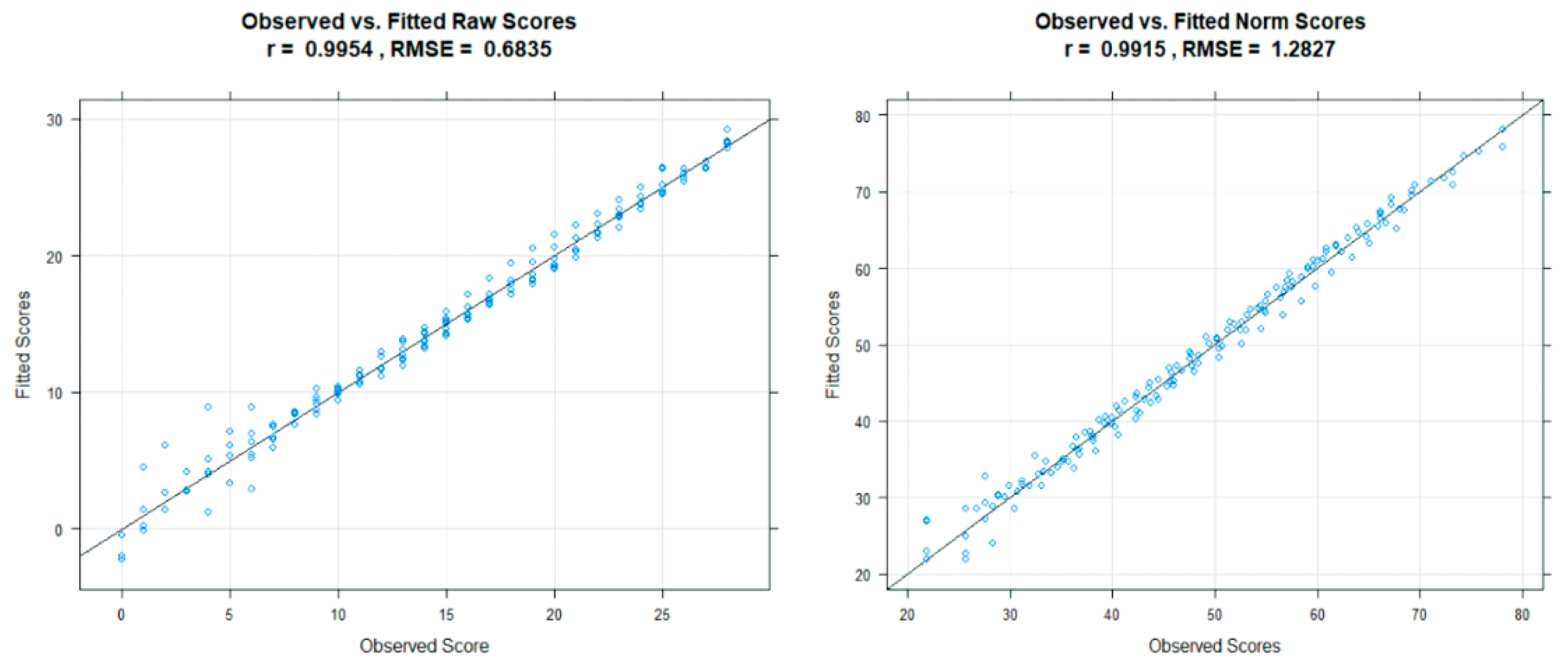
The plot shows only a small deviation between observed and predicted values, which can be interpreted as a first sign for a good model fit. Jagged or curvy trajectories, which are most likely the result of sampling error, are smoothed, leading to a better estimation of the latent ability per age. Specifically, no intersecting percentiles curves are predicted. Therefore, the mapping from raw score and explanatory variable to norm score seems to be unique within the observed range of age and raw scores. The opposite case would be a sign that the computed model is not valid for describing the norming sample. By default, the range of the explanatory variable is set to the minimum and maximum values of the used data set. As already mentioned before, we recommend using the computed model only for predictions within the range of the norm sample, since extrapolation can lead to large prediction errors. Another way to inspect the model is to compare the observed and fitted data in terms of the raw score with plotRaw(model). The method plots the observed against the predicted raw score and delivers information about the model fit in terms of correlation and RMSE (
Figure 6).
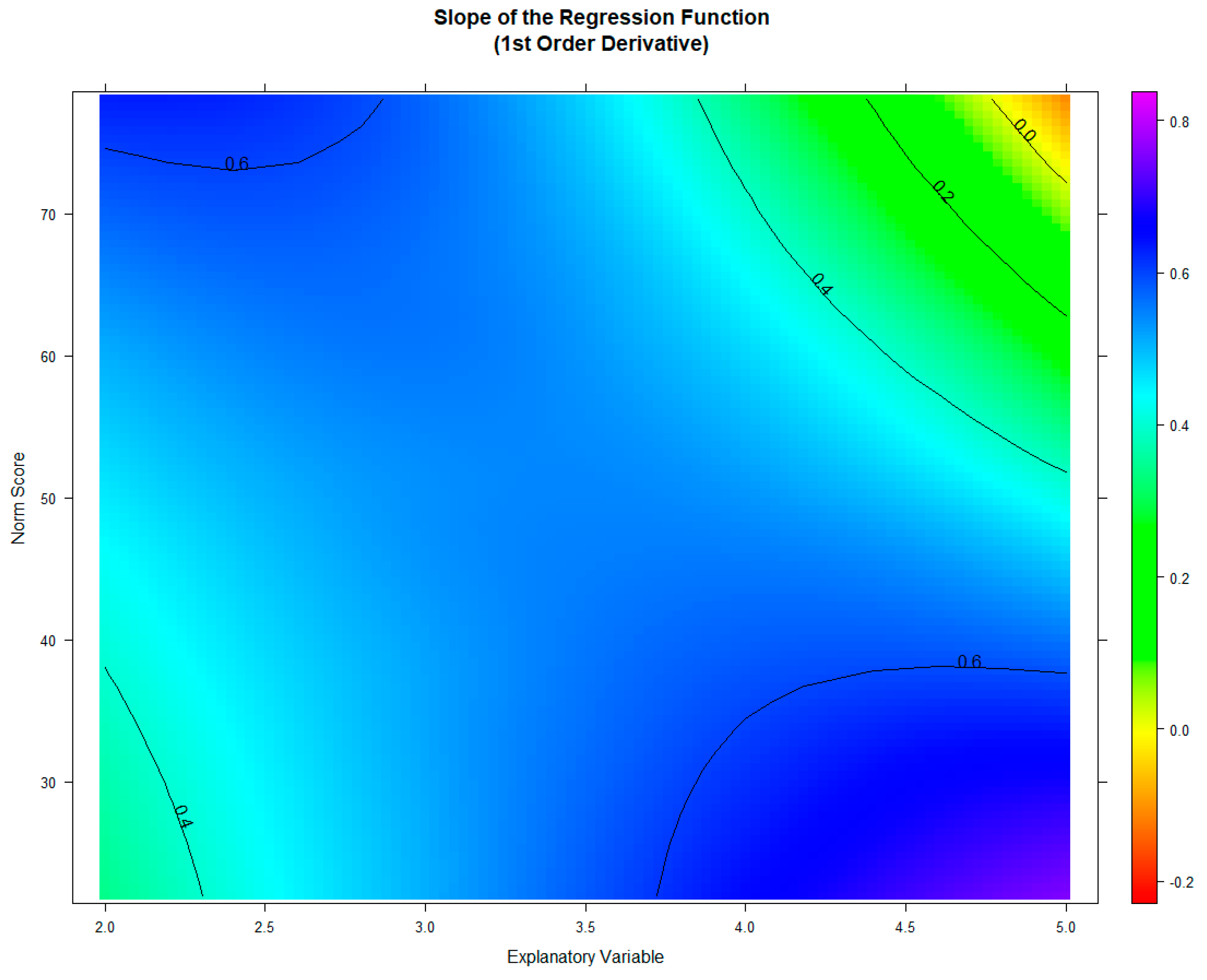
The visual inspection reveals only a small deviation between observed and predicted raw scores in line with a high correlation () and a small root mean squared error (). The ‘plotNorm’ functions deliver a nearly identical result. While the regression model seems to deliver nearly perfect predictions for the average performance range around T-scores of 50, higher deviation can be observed in the strongly below-average range of T < 30. Although the model seems to fit quite well overall in this case, the example still shows that the goodness of fit usually varies within the targeted measurement range. Higher deviations in the more extreme performance ranges may also be due to the fact that many tests contain only a low number of items that are very easy or very difficult. For investigating the model consistency in terms of monotonicity, the function checkConsistency(model) method may be used. The function examines whether model assumptions are violated using the derivative of the regression function and returns information as well as hints for exploring them further. In the case of the model of the example, it issues the following warning: “Violation of monotonicity at age 5. At least 1 violations of monotonicity found within the specified range of age and norm score. Use ’plotNormCurves’ to visually inspect the norm curve or ’plotDerivative’ to identify regions violating the consistency. Rerun the modelling with adjusted parameters or restrict the valid value range accordingly. Be careful with horizontal and vertical extrapolation. The original data for the regression model spanned from age 2 to 5, with a norm score range from 21.93 to 78.07. The raw scores range from 0 to 28.”
The procedure indicates a possible violation of the model assumptions in the fifth grade. (Please note that the variable
normally denotes age, but that in this particular case the grade level was used instead.) For further investigation, the ‘plotDerivative’ function can be used, which returns a visualisation of the derivative of the regression model with respect to
. In order to ensure a bijective relation of norm and raw scores, the slope must be either consistently positive or negative at all age and performance ranges. Zero-crossings indicate intersecting percentile lines. Thus, the yellow areas in this map indicate model violations or regions, where the model is less precise. In the current example, this is the case at high performance levels in the fifth grade, resulting from a ceiling effect of the test scale (
Figure 7, indicated in red in the right upper edge).
Consequently, in the fifth grade and in the highest performance range, higher raw scores lead to lower norm scores, which is a violation of the measurement assumptions. Obviously, the difficulty of the scale does not allow for differentiation in this performance range of grade five. The example shows that extrapolated norm scores should be used cautiously. Since the derivation shows no other zero-crossing, the regression model seems to be valid within all other ranges of the norm sample.
Please note that the slope depicted here relates to the first partial derivative of the regression function with respect to
not with respect to
. Negative slopes with respect to the explanatory variable, in contrast, are not a sign of model inconsistency. For example, in the case of fluid intelligence, empirical data show an increase in performance during childhood and adolescence but a decrease (i.e., negative slope) after the age of 25 years [
24]. This declining trajectory over age can usually be modelled with cNORM without problem. Therefore, the norming results should also be validated from a theoretical point of view regarding the measured latent ability.
5.3. Validation in Terms of Model Fit
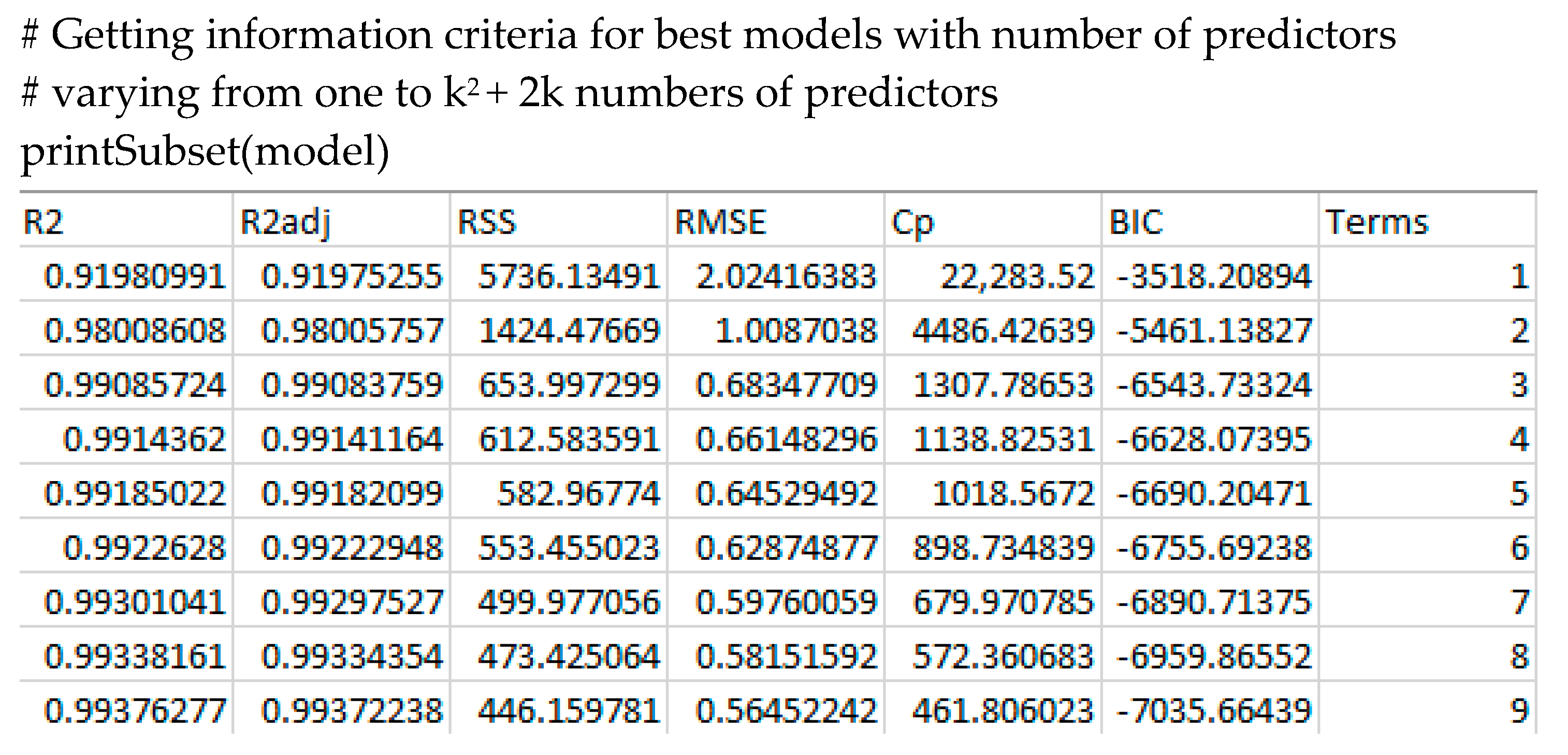
For validation in terms of different information criteria, the ‘printSubset(model)’ method can be used. The method returns a table containing adjusted
Mallow’s
,
and
for the best models chosen by the best subset regression in dependence of the number of contained parameters (
Figure 8).
As can be seen from
Figure 8, the criterion of
is only met when at least three predictors are in included in the regression function. These are the predictors returned by the ‘bestModel’ method, with a raw score
of
. For a graphical visualisation of the relationship between number of predictors and the model fit, the ‘plotSubset’ method returns an adequate illustration (
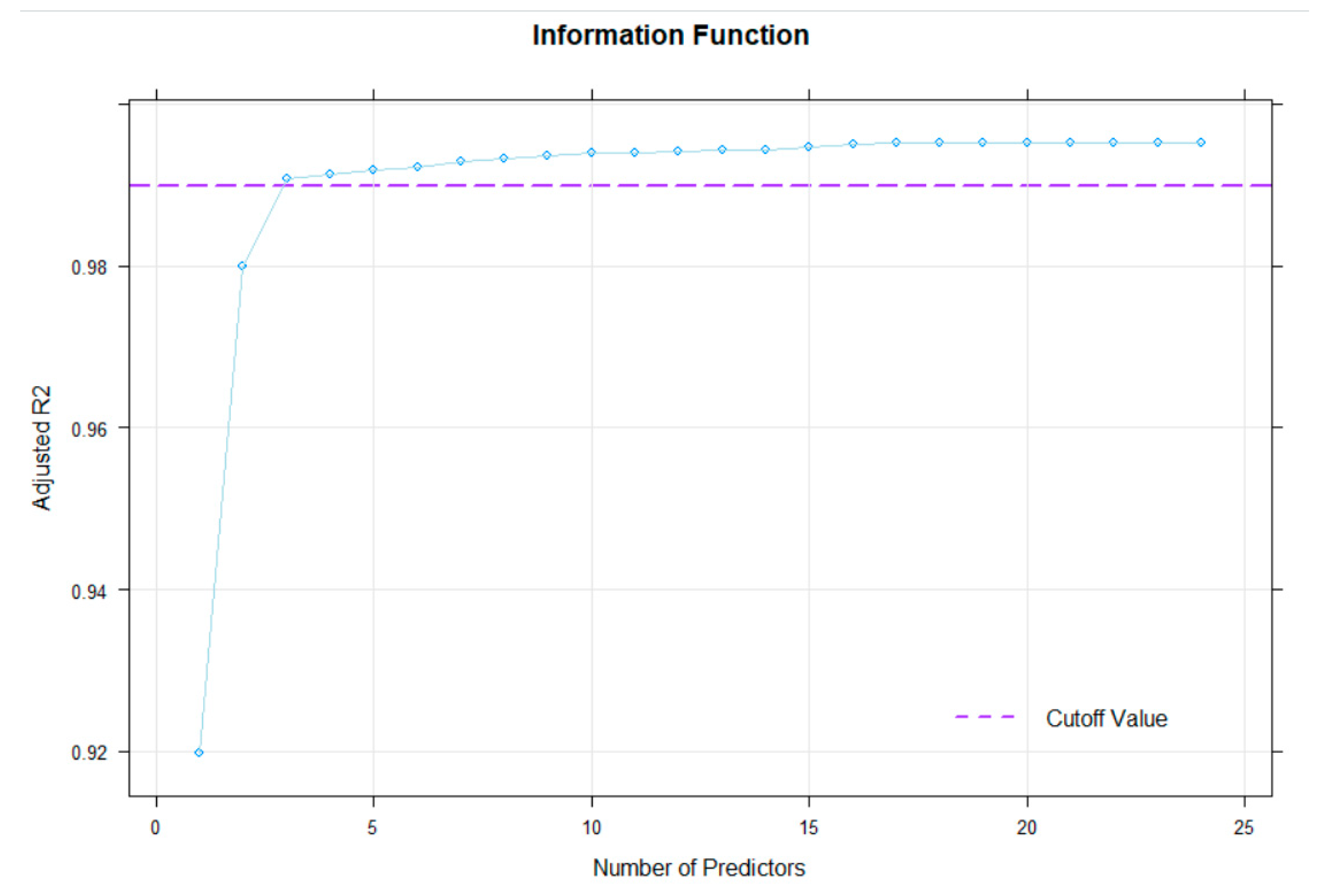
Figure 9).
As can be seen here, the cut-off is set to the default value of . As to be expected, increasing the number of predictors to more than three results is only a slight improvement of the adjusted . Therefore, the number of three or four terms chosen by the ‘bestModel’ method seems to deliver a sufficient norming model, while smoothing the percentile curves and cleaning sampling error variance. To investigate possible over- or under-fitting of the model with four predictors, cross validation of the regression model (function ‘cnorm.cv’) can be used:
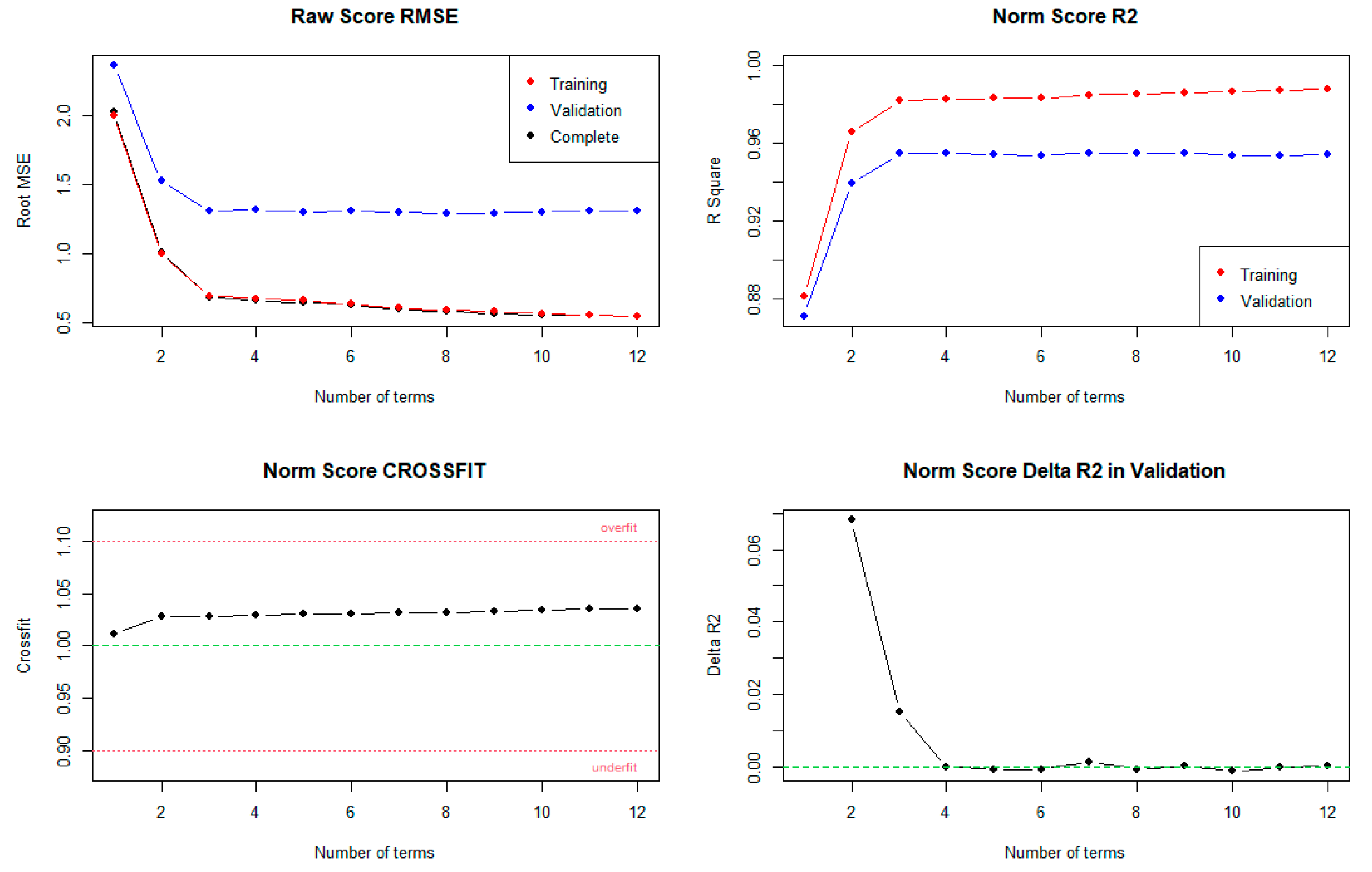
# Cross validation, repeated 10 times with an upper limit of 12 terms
cnorm.cv(preparedData, repetitions = 10, max = 12)
By using this method, the data set is divided into a training set containing 80% of the complete sample and a validation sample with 20% of the norming sample. Subsequently, the best regression models are computed with increasing numbers of terms starting from one until the specified number of predictors (by ‘max’ parameter). Finally, for every resulting training model, the model is projected on the validation data to independently estimate the model fit for data not included in the modelling process. This procedure is repeated n times (in this example: ten times), and the results are visualised, as can be seen in
Figure 10.
While none of the models shows serious signs of over- or under-fitting, of the norm scores increases only slightly when more than four predictors are used in the regression model, i.e., the model can barely be improved by including more than four predictors. This finding seems to be consistent with the aforementioned output of the ‘printSubset’ method. Therefore, the selected regression model is an adequate, parsimonious and efficient norming model.
5.4. Generating Norm Tables
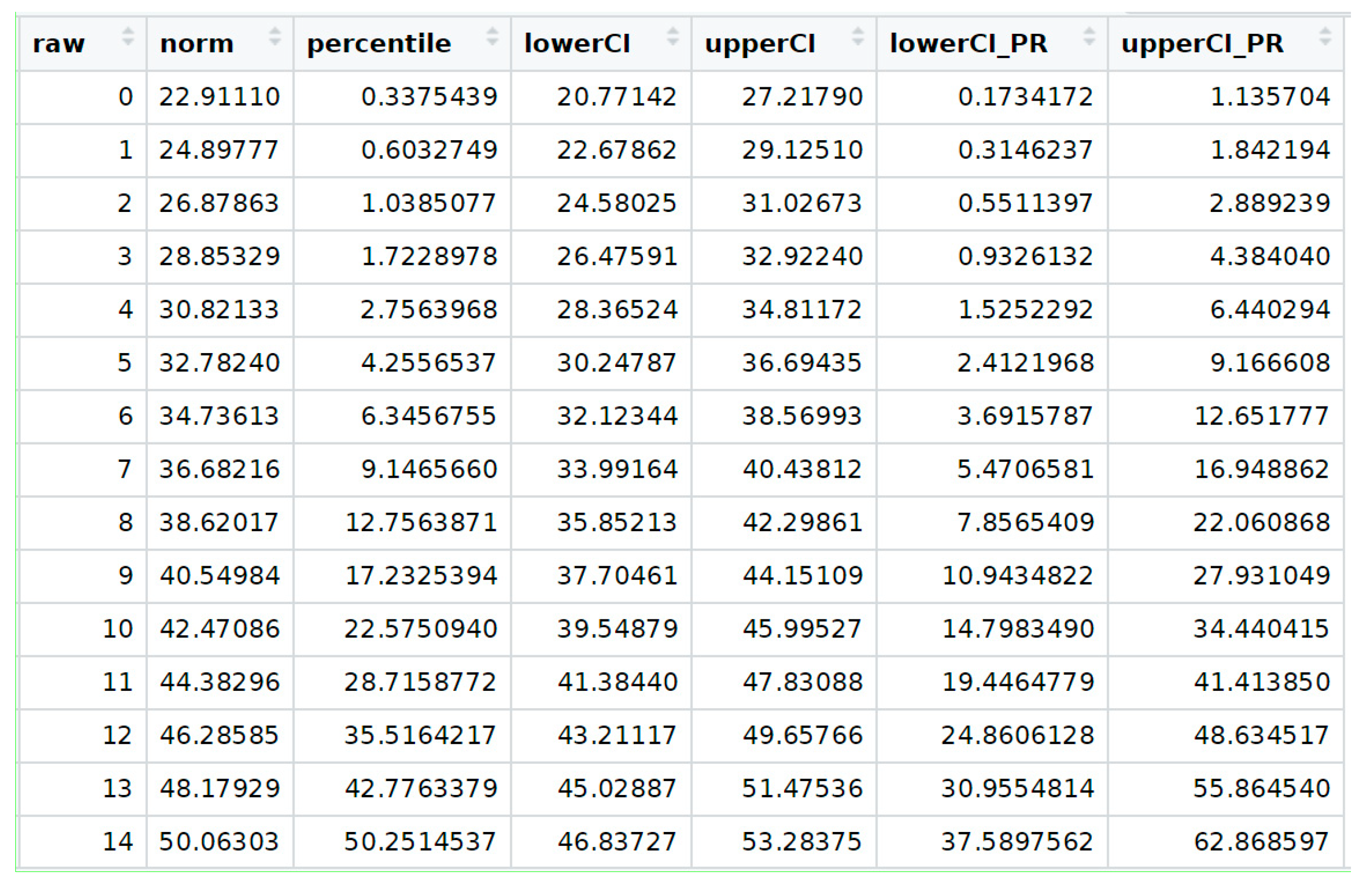
After selecting an adequate norming model, the final step of the norming procedure is to generate norm tables, which should be included in the test manual. For this purpose, we choose the ‘rawTable’ method to transform a series of raw scores, which can be specified by the user, into a series of norm scores as well as corresponding percentiles:
# Compute raw table for given age between T-scores 25 and 75 for age / grade 3
raw.table <- rawTable(3, model, rel = 0.96)
The table can be restricted in its range by specifying the minimum and maximum norm scores (minNorm, maxNorm) as well as the minimum and maximum raw scores (minRaw, maxRaw). By default, the function retrieves these boundaries based on the values in the data set. Increasing these values leads to extrapolation and elevates the risk of model violations. By specifying the scale reliability and confidence coefficient, the confidence intervals are included in the output both for the norm scores and the percentiles. Therefore, the lower and upper bounds are estimated by
The resulting raw table is illustrated in
Figure 11.
5.5. In a Nutshell
Besides these detailed steps, cNORM features convenience methods and standard S3 methods in R to abridge the process via the general function ‘cnorm’, as described in the following short syntax:
# In order to rank the data, compute powers and determine the regression function, the
# convenience method ‘cnorm’ can be used with numerical vectors. The resulting object
# includes the ranked data via object$data and model via object$model and it can be used
# with all plotting methods.
cnorm.elfe <- cnorm(raw = elfe$raw, group = elfe$group)
# Plot R2 of different model solutions in dependence of the number of predictors
plot(cnorm.elfe, "subset", type = 0) # plot R2
plot(cnorm.elfe, "subset", type = 3) # plot MSE
# To select a good fitting model, the analysis is usually rerun with a fixed number of terms,
# e. g. four. Avoid models with a high number of terms:
cnorm.elfe <- cnorm(raw = elfe$raw, group = elfe$group, terms = 4)
# Visual inspection of the percentile curves of the fitted model
plot(cnorm.elfe, "percentiles")
# Visual inspection of the observed and fitted raw and norm scores
plot(cnorm.elfe, "norm")
plot(cnorm.elfe, "raw")
# In order to check, how other models perform, plot series of percentile plots with
# ascending number of predictors, in this example up to 14 predictors.
plot(cnorm.elfe, "series", end = 14)
# Cross validation of number of terms with 20% of the data for validation and 80%
# training. Due to the time intensity, max terms is restricted to 10 in this example.
cnorm.cv(cnorm.elfe$data, max = 10, repetitions = 3)
# Cross validation with pre-specified terms, e. g. of an already existing model
cnorm.cv(cnorm.elfe, repetitions = 3)
# Print norm table (for grade 3, 3.2, 3.4, 3.6; see electronic Supplement Table S1)
normTable(c(3, 3.2, 3.4, 3.6), cnorm.elfe)
# The other way round: Print raw table (for grade 3; see electronic Supplement Table S2) together
# with 90% confidence intervals for a test with a reliability of 0.94
rawTable(3, cnorm.elfe, CI = 0.9, reliability = 0.94)
# cNORM includes a graphical user interface, based on shiny that runs locally in the
# browser and contains the most important functionality
cNORM.GUI()