Features of Synthesis, Crystal Structure, Thermal and Electrical Properties, XPS/NEXAFS Study of Pyrochlore-Type Bi2Cr0.5Co0.5Nb2O9+Δ
Abstract
1. Introduction
2. Experimental Section
3. Results and Discussion
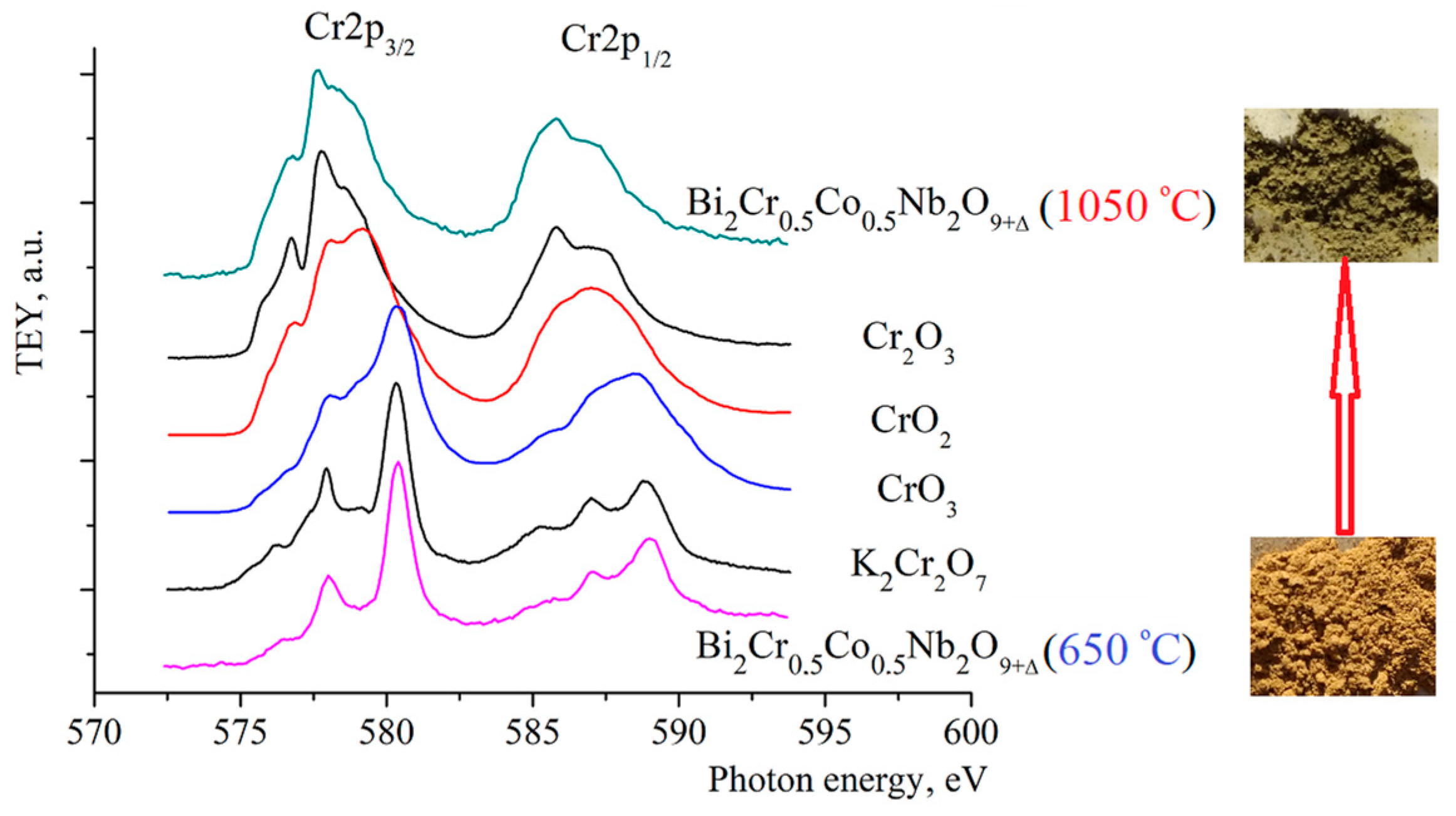
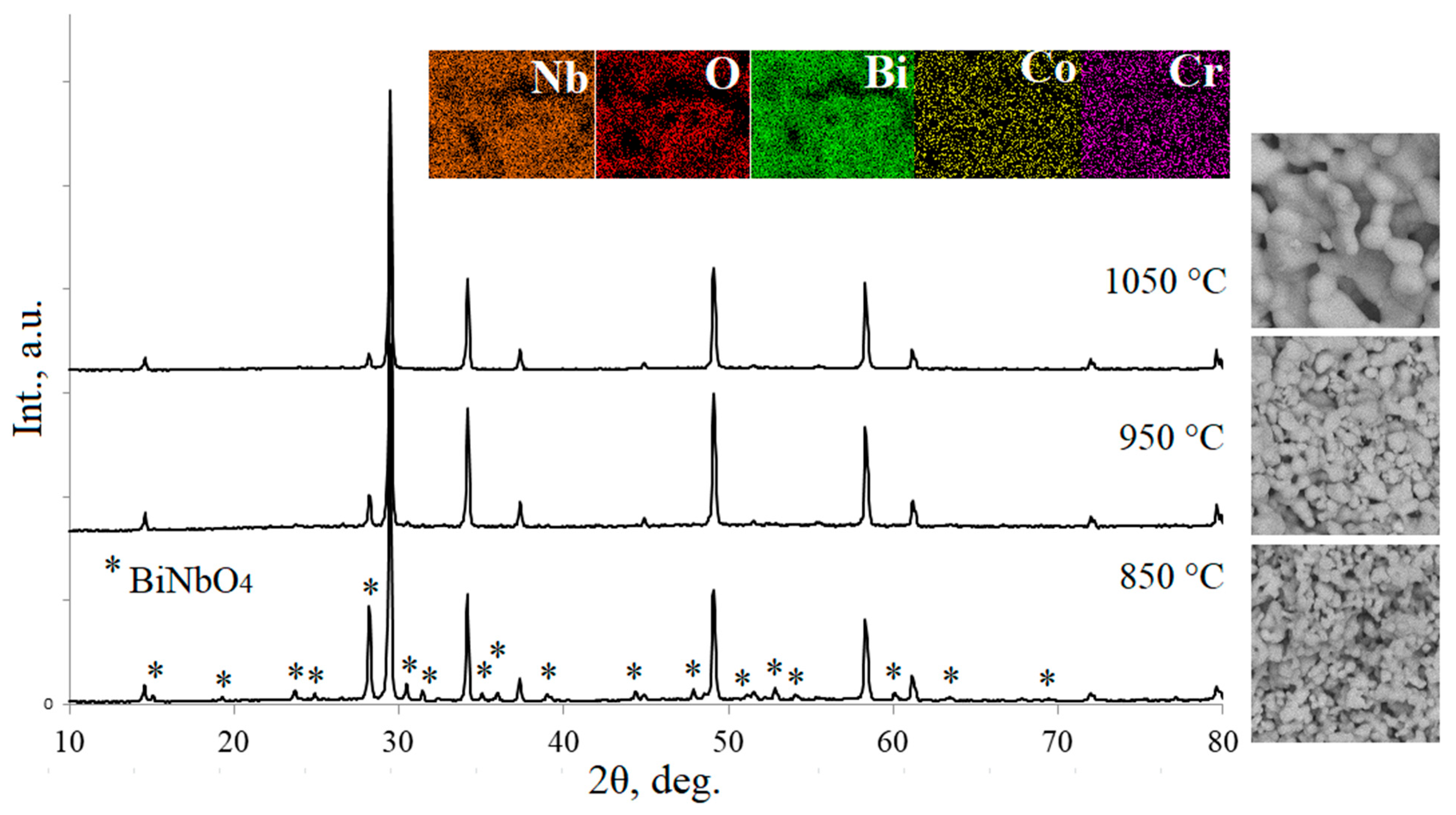
3.1. Synthesis by the Solid-Phase Reaction Method and the Pechini Method
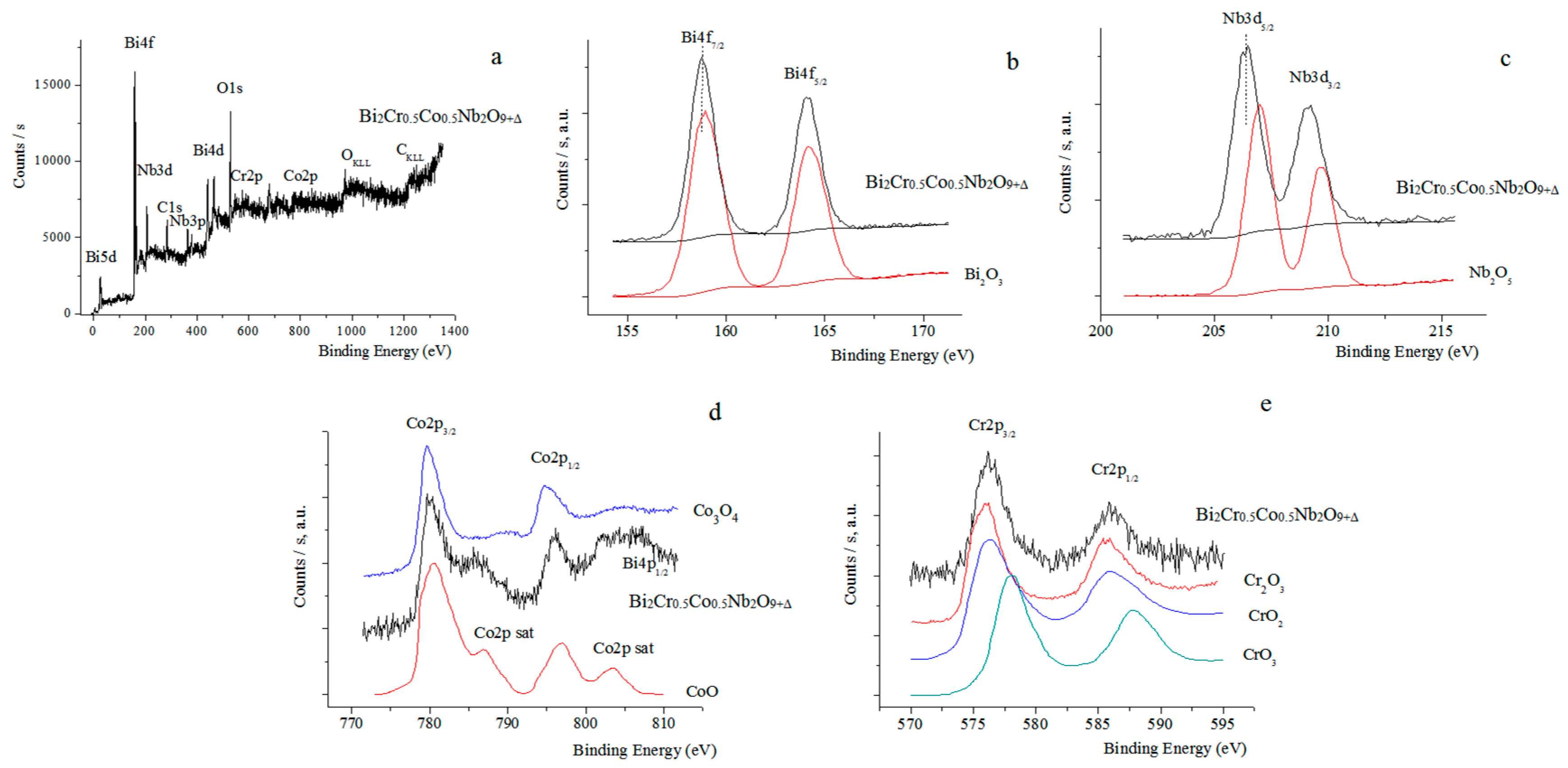
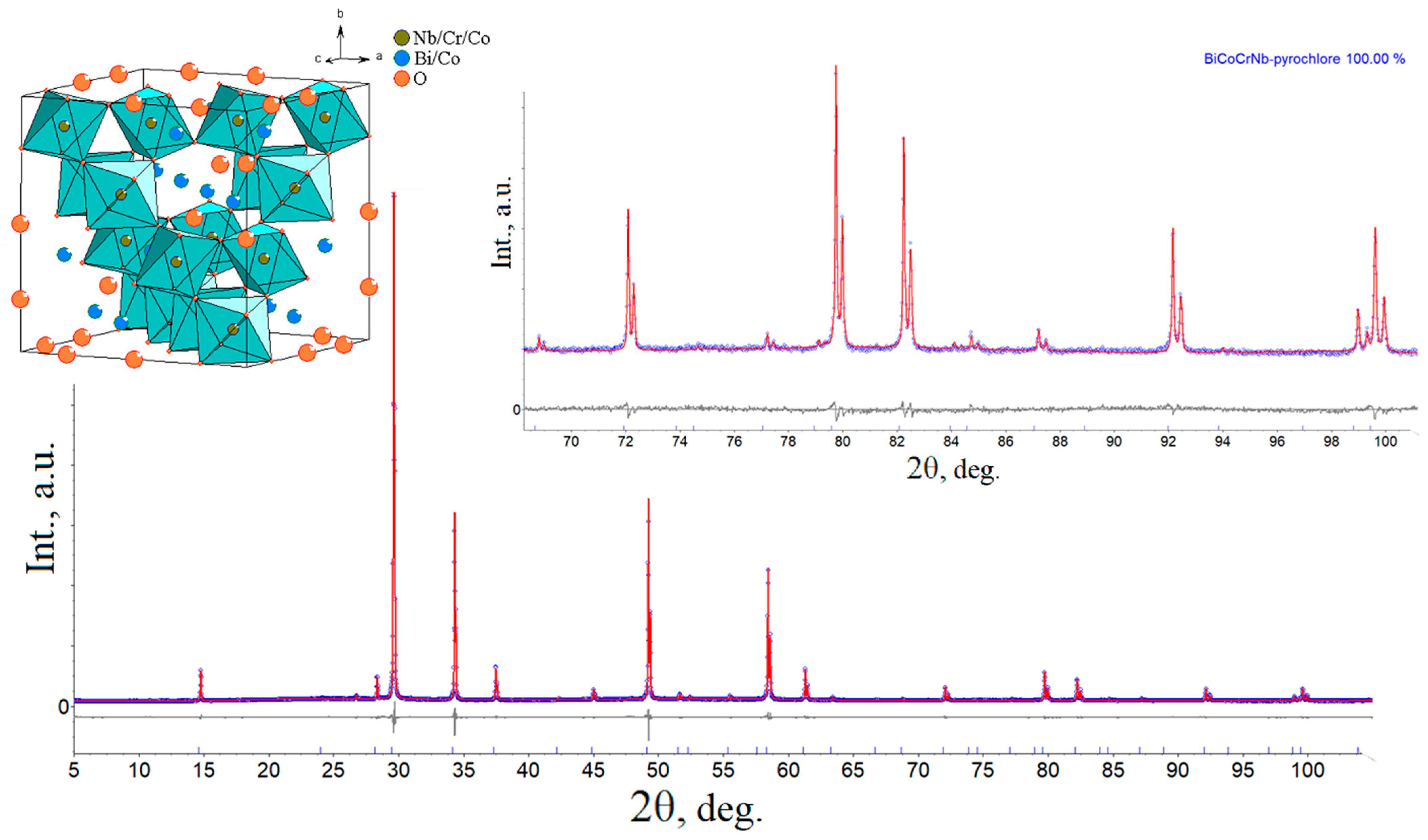
3.2. Crystal Structure
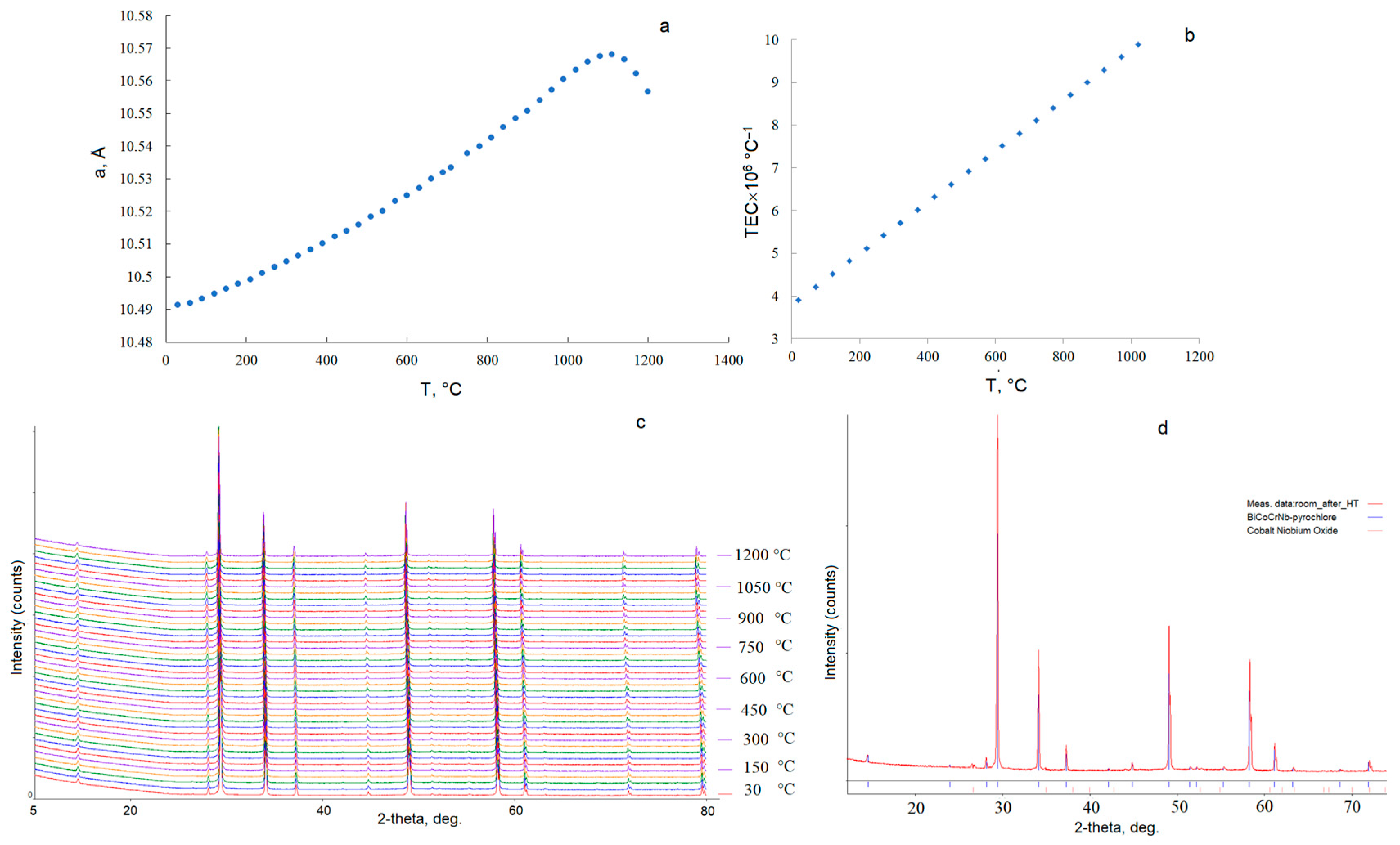
3.3. Thermal Expansion
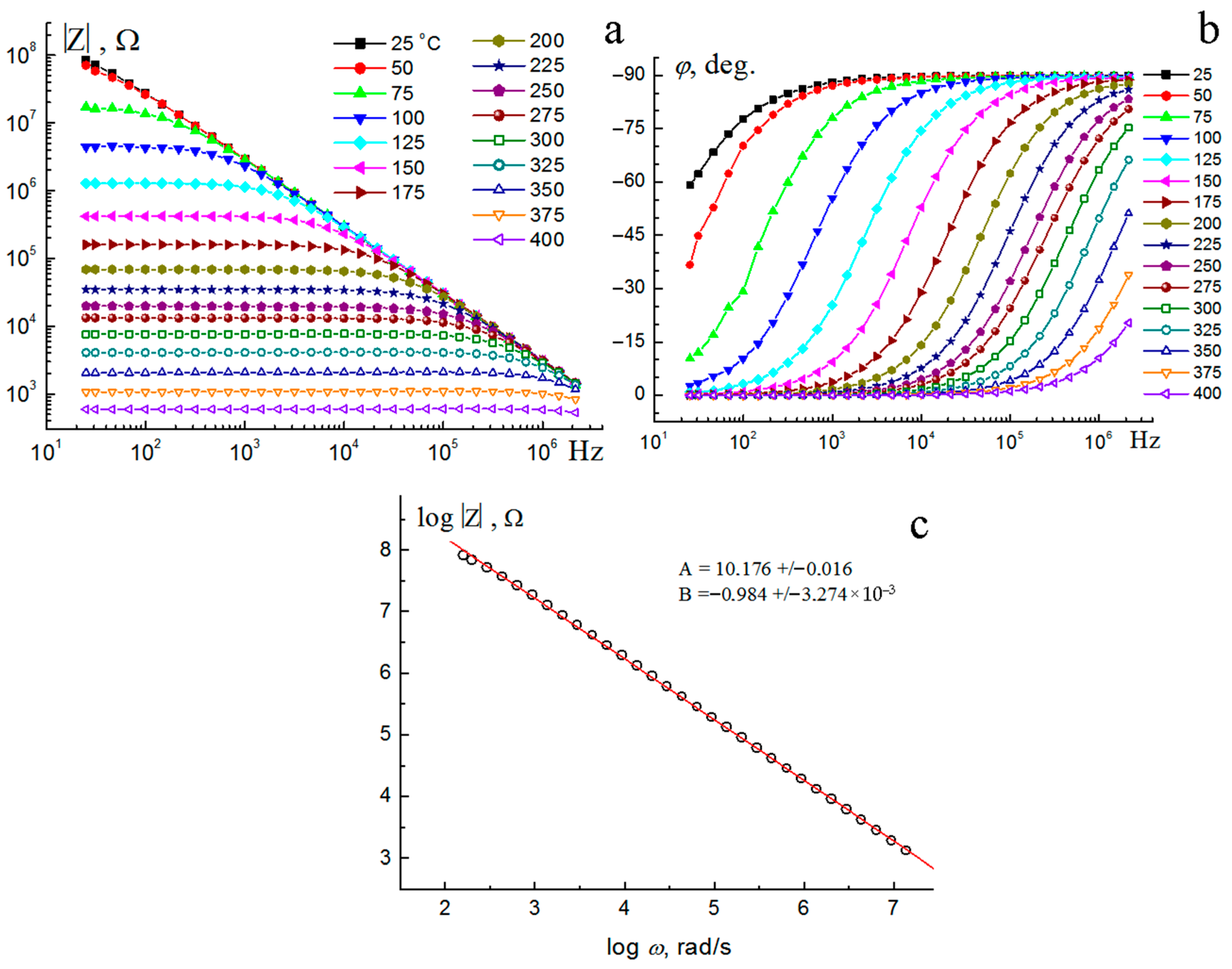
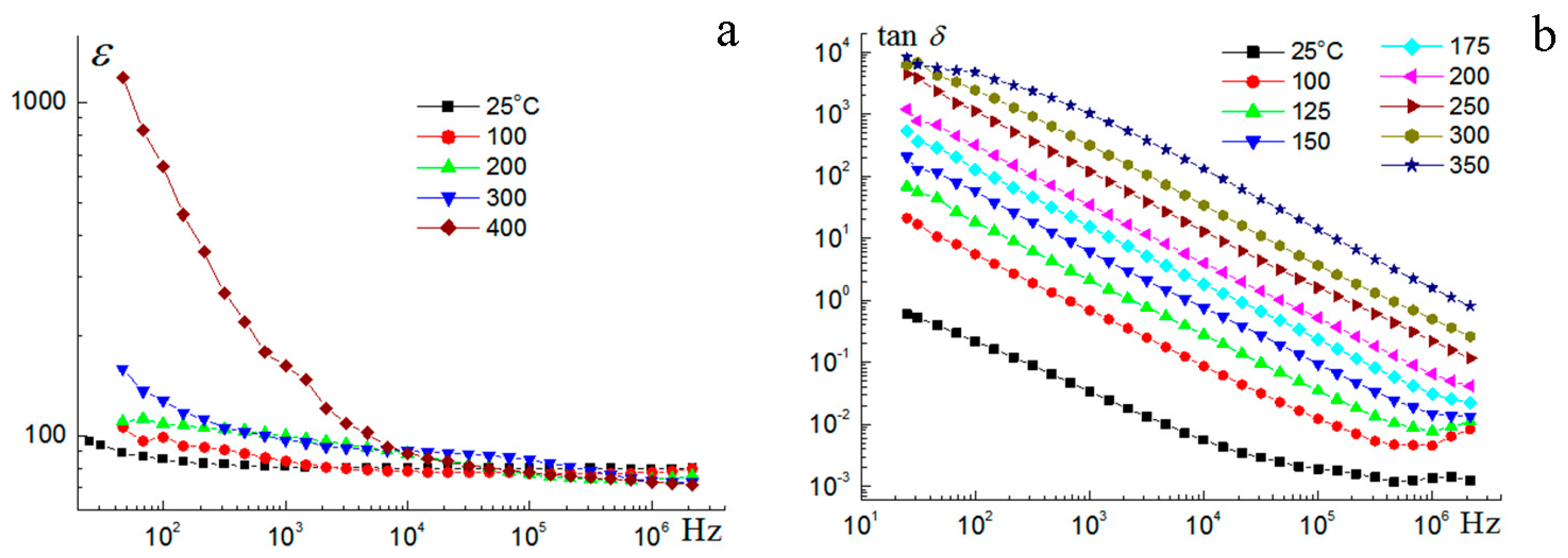
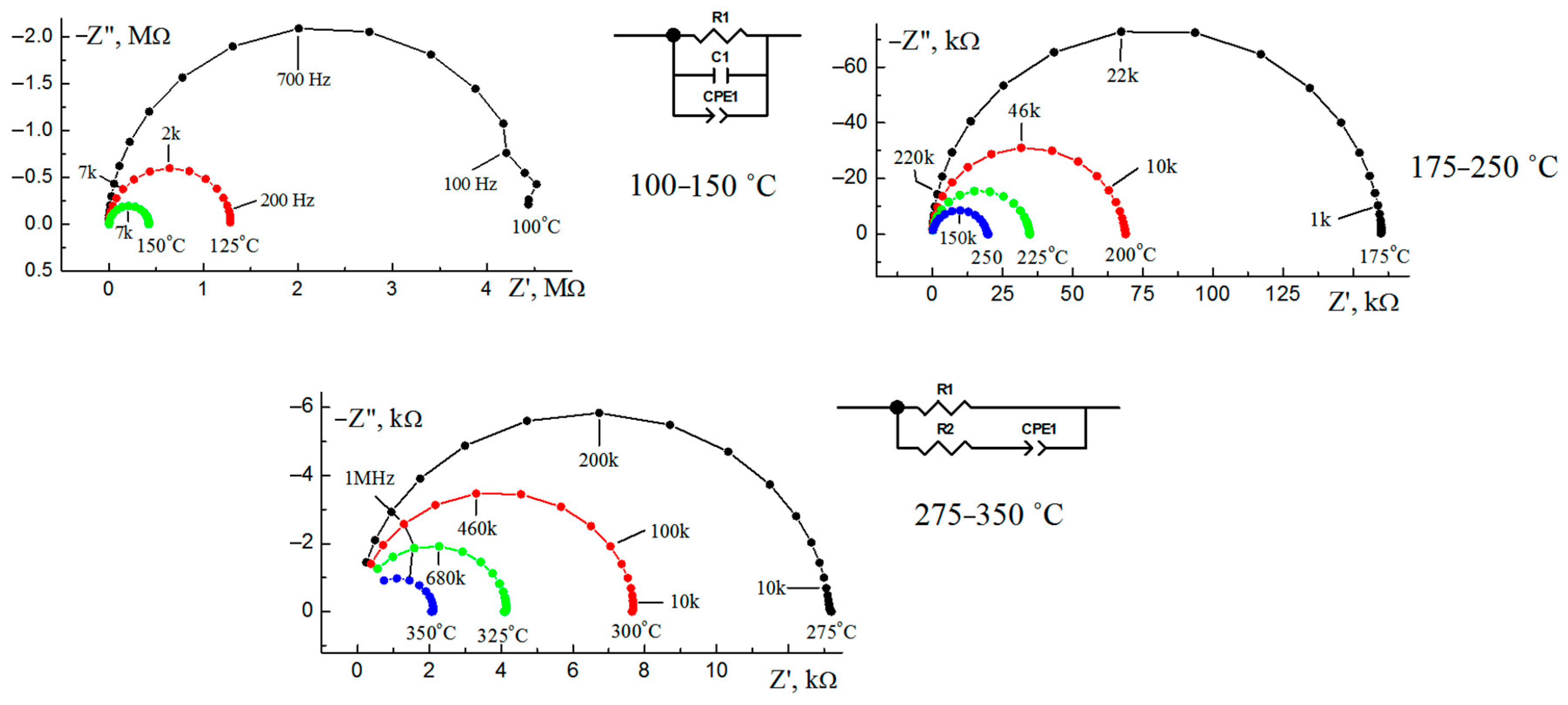
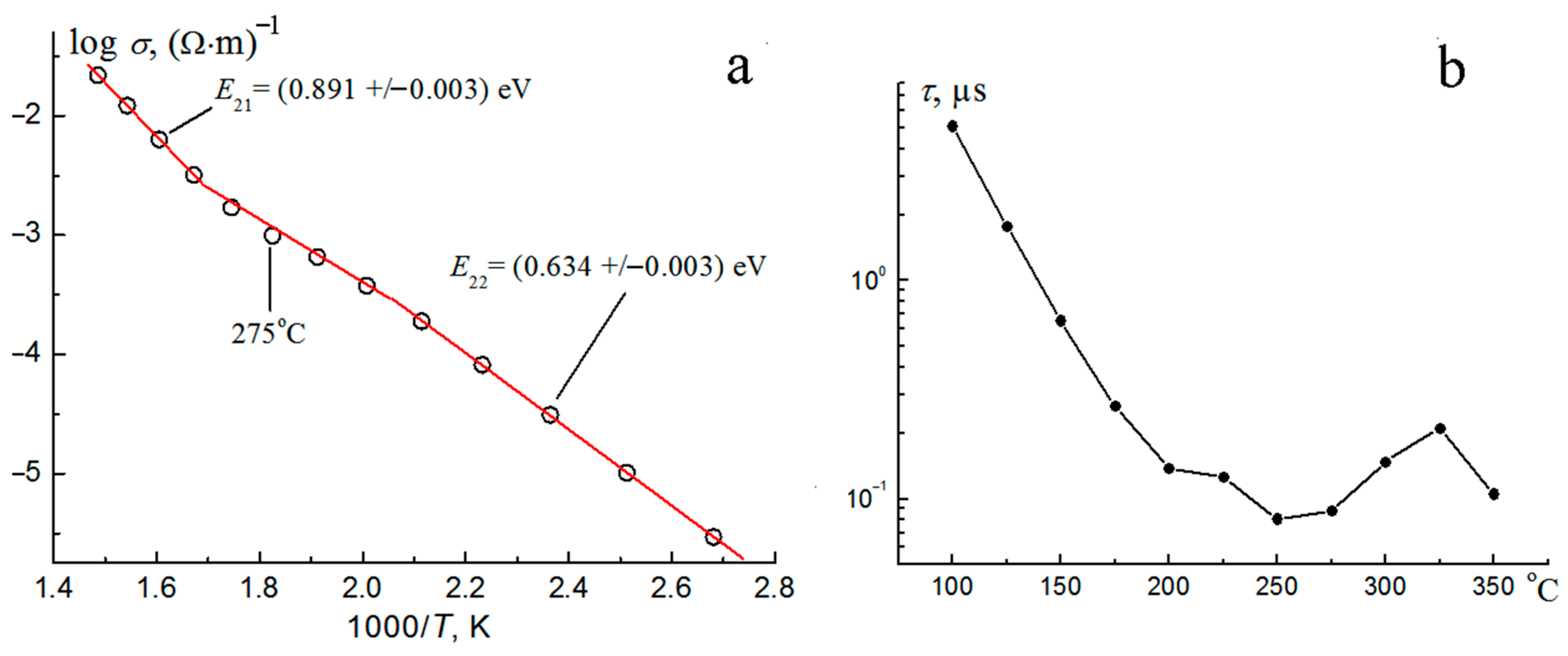
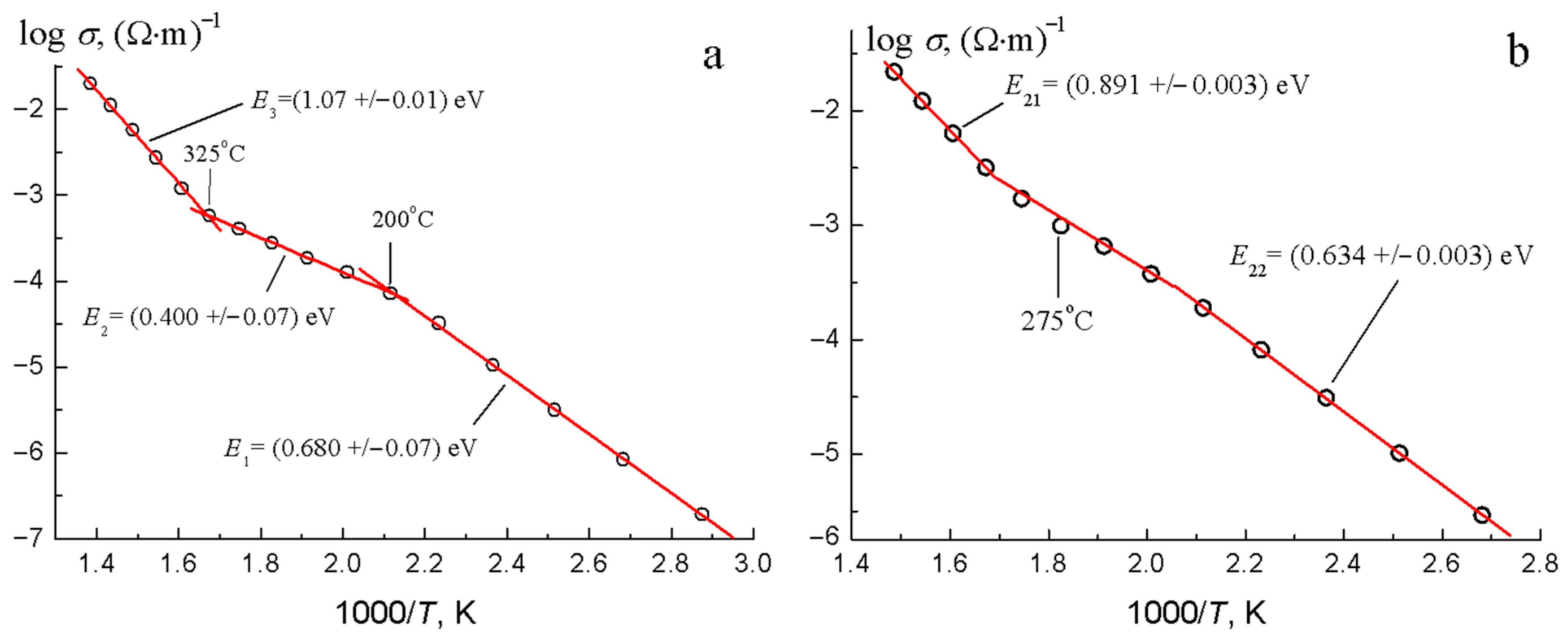
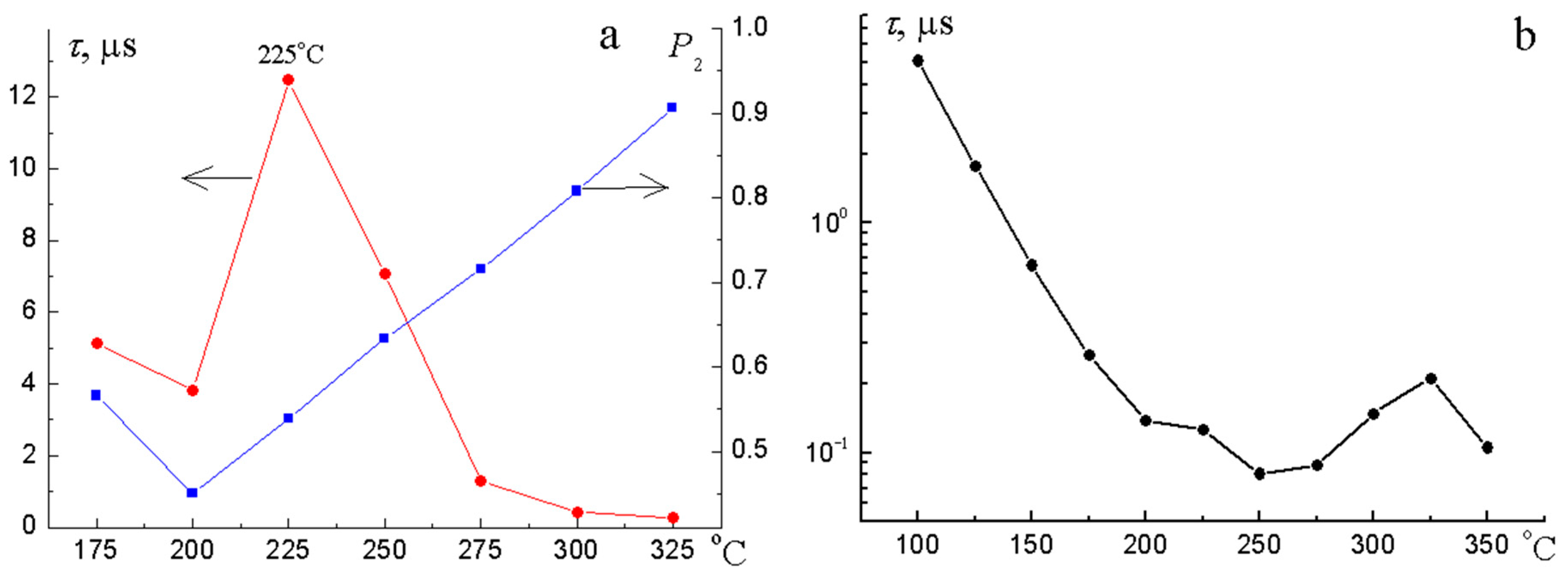
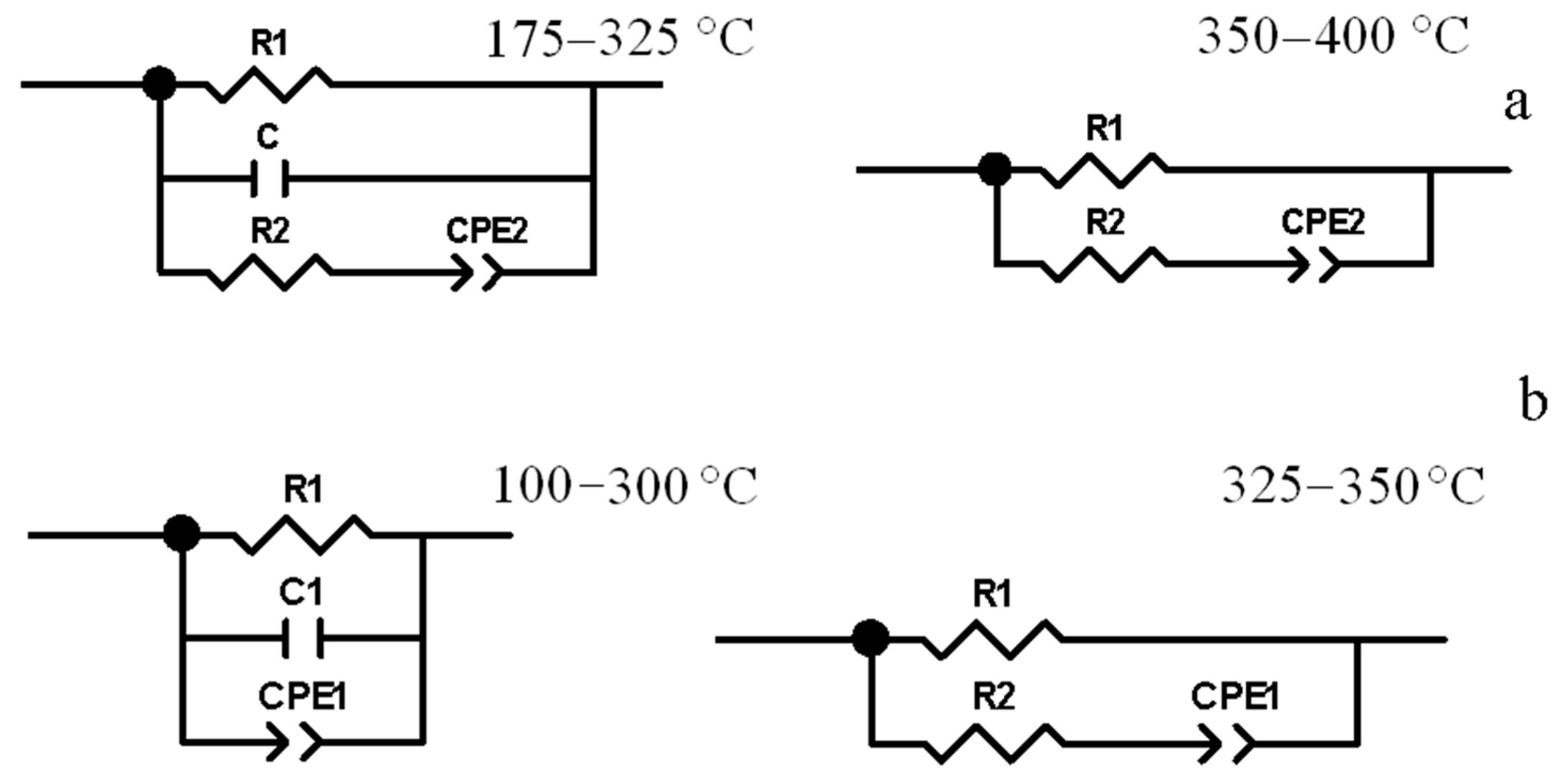
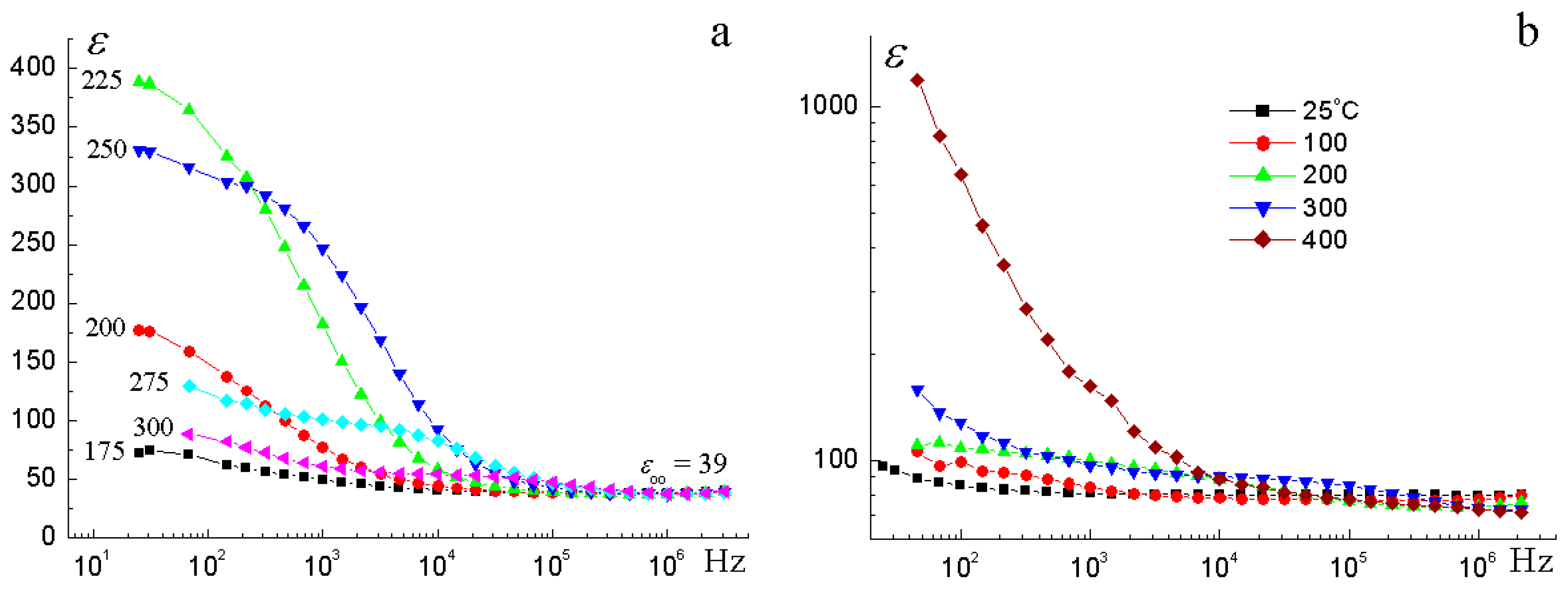
3.4. Electrical Properties
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Giampaoli, G.; Siritanon, T.; Day, B.; Li, J.; Subramanian, M.A. Temperature in-dependent low loss dielectrics based on quaternary pyrochlore oxides. Prog. Solid State Chem. 2018, 50, 16–23. [Google Scholar] [CrossRef]
- Murugesan, S.; Huda, M.N.; Yan, Y.; Al-Jassim, M.M.; Subramanian, V. Band-Engineered Bismuth Titanate Pyrochlores for Visible Light Photocatalysis. J. Phys. Chem. C 2010, 114, 10598–10605. [Google Scholar] [CrossRef]
- Du, H.; Wang, H.; Yao, X. Observations on structural evolution and dielectric properties of oxygen-deficient pyrochlores. Ceram. Int. 2004, 30, 1383–1387. [Google Scholar] [CrossRef]
- Cann, D.P.; Randall, C.A.; Shrout, T.R. Investigation of the dielectric properties of bismuth pyrochlores. Solid State Commun. 1996, 100, 529–534. [Google Scholar] [CrossRef]
- Zhuk, N.A.; Krzhizhanovskaya, M.G.; Koroleva, A.V.; Nekipelov, S.V.; Kharton, V.V.; Sekushin, N.A. Thermal Expansion, XPS Spectra, and Structural and Electrical Properties of a New Bi2NiTa2O9 Pyrochlore. Inorg. Chem. 2021, 60, 4924–4934. [Google Scholar] [CrossRef]
- McCauley, R.A. Structural Characteristics of Pyrochlore Formation. J. Appl. Phys. 1980, 51, 290–294. [Google Scholar] [CrossRef]
- Subramanian, M.A.; Aravamudan, G.; Subba Rao, G.V. Oxide pyrochlores—A review. Prog. Solid State Chem. 1983, 15, 55–143. [Google Scholar] [CrossRef]
- Yu, S.; Li, L.; Zheng, H. BMN-based transparent capacitors with high dielectric tunability. J. Alloys Compd. 2017, 699, 68–72. [Google Scholar] [CrossRef]
- Guo, Q.; Li, L.; Yu, S.; Sun, Z.; Zheng, H.; Li, J.; Luo, W. Temperature–stable dielectrics based on Cu–doped Bi2Mg2/3Nb4/3O7 pyrochlore ceramics for LTCC. Ceram. Int. 2018, 44, 333–338. [Google Scholar] [CrossRef]
- Vanderah, T.A.; Lufaso, M.W.; Adler, A.U.; Levin, I.; Nino, J.C.; Provenzano, V.; Schenck, P.K. Subsolidus phase equilibria and properties in the system Bi2O3:Mn2O3±x:Nb2O5. J. Solid State Chem. 2006, 179, 3467–3477. [Google Scholar] [CrossRef]
- Vanderah, T.A.; Siegrist, T.; Lufaso, M.W.; Yeager, M.C.; Roth, R.S.; Nino, J.C.; Yates, S. Phase Formation and Properties in the System Bi2O3:2CoO1+x:Nb2O5. Eur. J. Inorg. Chem. 2006, 2006, 4908–4914. [Google Scholar] [CrossRef]
- Valant, M.; Suvorov, D. The Bi2O3–Nb2O5–NiO Phase Diagram. J. Am. Ceram. Soc. 2005, 88, 2540–2543. [Google Scholar] [CrossRef]
- Dasin, N.A.M.; Tan, K.B.; Khaw, C.C.; Zainal, Z.; Lee, O.J.; Chen, S.K. Doping mechanisms and dielectric properties of Ca-doped bismuth magnesium niobate pyrochlores. Mater. Chem. Phys. 2019, 242, 122558. [Google Scholar] [CrossRef]
- Chon, M.P.; Tan, K.B.; Zainal, Z.; Taufiq-Yap, Y.H.; Tan, P.Y.; Khaw, C.C.; Chen, S.K. Synthesis and Electrical Properties of Zn-substituted Bismuth Copper Tantalate Pyrochlores. Int. J. Appl. Ceram. Technol. 2016, 13, 718–725. [Google Scholar] [CrossRef]
- Rychkova, L.V.; Sekushin, N.A.; Nekipelov, S.V.; Makeev, B.A.; Fedorova, A.V.; Korolev, R.I.; Zhuk, N.A. Dielectric and magnetic properties, NEXAFS spectroscopy of Co-doped of multicomponent bismuth niobate pyrochlore. Ceram. Int. 2021, 47, 6691–6698. [Google Scholar] [CrossRef]
- Valant, M. Dielectric Relaxations in Bi2O3–Nb2O5–NiO Cubic Pyrochlores. J. Am. Ceram. Soc. 2009, 92, 955–958. [Google Scholar] [CrossRef]
- Zhuk, N.A.; Sekushin, N.A.; Krzhizhanovskaya, M.G.; Kharton, V.V. Multiple relaxation, reversible electrical breakdown and bipolar conductivity of pyrochlore–type Bi2Cu0.5Zn0.5Ta2O9 ceramics. Solid State Ion. 2022, 377, 115868. [Google Scholar] [CrossRef]
- Zhuk, N.A.; Sekushin, N.A.; Krzhizhanovskaya, M.G.; Selutin, A.A.; Koroleva, A.V.; Badanina, K.A.; Nekipelov, S.V.; Petrova, O.V.; Sivkov, V.N. Photoelectron Spectroscopy Study of the Optical and Electrical Properties of Cr/Cu/Mn Tri-Doped Bismuth Niobate Pyrochlore. Sci 2025, 7, 1. [Google Scholar] [CrossRef]
- Zhuk, N.A.; Makeev, B.A.; Krzhizhanovskaya, M.G.; Nekipelov, S.V.; Sivkov, D.V.; Badanina, K.A. Features of the Phase Formation of Cr/Mn/Fe/Co/Ni/Cu Codoped Bismuth Niobate Pyrochlore. Crystals 2023, 13, 1202. [Google Scholar] [CrossRef]
- Zhuk, N.A.; Badanina, K.A.; Korolev, R.I.; Makeev, B.A.; Krzhizhanovskaya, M.G.; Kharton, V.V. Phase Formation of Co and Cr Co-Doped Bismuth Niobate with Pyrochlore Structure. Inorganics 2023, 11, 288. [Google Scholar] [CrossRef]
- Badanina, K.A.; Nekipelov, S.V.; Lebedev, A.M.; Zhuk, N.A.; Beznosikov, D.S. Conversion of Cr(III) and Co(III) During the Synthesis of Co/Cr Codoped Bismuth Niobate Pyrochlore According to NEXAFS Data. J. Sib. Fed. Univ. Math. Phys. 2024, 17, 559–569. [Google Scholar]
- Bruker, A.X.S. Topas, version 5.0. General Profile and Structure Analysis Software for Powder Diffraction Data; Bruker AXS: Karlsruhe, Germany, 2014.
- Bubnova, R.S.; Firsova, V.A.; Filatov, S.K. Software for determining the thermal expansion tensor and the graphic representation of its characteristic surface (Theta to Tensor-TTT). Glass Phys. Chem. 2013, 39, 347–350. [Google Scholar] [CrossRef]
- Zhuk, N.A.; Krzhizhanovskaya, M.G.; Sekushin, N.A.; Kharton, V.V.; Koroleva, A.V.; Nekipelov, S.V.; Sivkov, D.V.; Sivkov, V.N.; Makeev, B.A.; Lebedev, A.M.; et al. Novel Ni-Doped Bismuth–Magnesium Tantalate Pyrochlores: Structural and Electrical Properties, Thermal Expansion, X-ray Photoelectron Spectroscopy, and Near-Edge X-ray Absorption Fine Structure Spectra. ACS Omega 2021, 6, 23262–23273. [Google Scholar] [CrossRef]
- Da Cruz, J.A.; Volnistem, E.A.; Ferreira, R.F.; Freitas, D.B.; Sales, A.J.M.; Costa, L.C.; Graça, M.P.F. Structural characterization of Brazilian niobium pentoxide and treatment to obtain the single phase (H-Nb2O5). Therm. Sci. Eng. Prog. 2021, 25, 101015. [Google Scholar] [CrossRef]
- Grins, J.; Esmaeilzadeh, S.; Hull, S. Structure and Ionic Conductivity of Bi6Cr2O15, a New Structure Type Containing (Bi12O14)8n+n Columns and CrO42− Tetrahedra. J. Solid State Chem. 2002, 163, 144–150. [Google Scholar] [CrossRef]
- Liu, Y.H.; Li, J.B.; Lianga, J.K.; Luo, J.; Ji, L.N.; Zhang, J.Y.; Rao, G.H. Phase diagram of the Bi2O3–Cr2O3 system. Mater. Chem. Phys. 2008, 112, 239–243. [Google Scholar] [CrossRef]
- Zahid, A.H.; Han, Q. A review on the preparation, microstructure, and photocatalytic performance of Bi2O3 in polymorphs. Nanoscale 2021, 13, 17687–17724. [Google Scholar] [CrossRef] [PubMed]
- Gopalakrishnan, J.; Ramanan, A.; Rao, C.N.R.; Jefferson, D.A.; Smith, D.J. A homologous series of recurrent intergrowth structures of the type Bi4Am+n−2Bm+nO3(m+n)+6 formed by oxides of the aurivillius family. Solid State Chem. 1984, 55, 101–105. [Google Scholar] [CrossRef]
- Warda, S.A.; Pietzuch, W.; Massa, W.; Kesper, U.; Reinen, D. Color and Constitution of CrVI-Doped Bi2O3 Phases: The Structure of Bi14CrO24. J. Solid State Chem. 2000, 149, 209–217. [Google Scholar] [CrossRef]
- Zhuk, N.A.; Sekushin, N.A.; Krzhizhanovskaya, M.G.; Koroleva, A.; Reveguk, A.; Nekipelov, S.; Sivkov, D.; Lutoev, V.; Makeev, B.; Kharton, V. Cr-doped bismuth tantalate pyrochlore: Electrical and thermal properties, crystal structure and ESR, NEXAFS, XPS spectroscopy. Mater. Res. Bull. 2023, 58, 112067. [Google Scholar] [CrossRef]
- Zhuk, N.A.; Krzhizhanovskaya, M.G.; Koroleva, A.V.; Nekipelov, S.; Sivkov, D.; Sivkov, V.; Lebedev, A.; Chumakov, R.; Makeev, B.; Kharton, V. Spectroscopic characterization of cobalt doped bismuth tantalate pyrochlore. Solid State Sci. 2022, 125, 106820. [Google Scholar] [CrossRef]
- Zhuk, N.A.; Krzhizhanovskaya, M.G.; Sekushin, N.A.; Sivkov, D.V.; Abdurakhmanov, I.E. Crystal. Structure, dielectric and thermal properties of cobalt doped bismuth tantalate pyrochlore. J. Mater. Res. Technol. 2023, 22, 1791–1799. [Google Scholar] [CrossRef]
- Roth, R.S.; Waring, J.L. Synthesis and stability of bismutotantalite, stibiotantalite and chemically similar ABO4 compounds. Am. Mineral. 1963, 48, 1348–1356. [Google Scholar]
- Piir, I.V.; Prikhodko, D.A.; Ignatchenko, S.V.; Schukariov, A.V. Preparation and structural investigations of the mixed bismuth niobates, containing transition metals. Solid State Ion. 1997, 101–103, 1141–1146. [Google Scholar] [CrossRef]
- Shannon, R.D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr. A 1976, 32, 751–767. [Google Scholar] [CrossRef]
- Zhuk, N.A.; Krzhizhanovskaya, M.G.; Koroleva, A.V.; Selyutin, A.; Sekushin, N.; Nekipelov, S.; Sivkov, D.; Kharton, V. Cr and Mg codoped bismuth tantalate pyrochlores: Thermal expansion and stability, crystal structure, electrical and optical properties, NEXAFS and XPS study. J. Solid State Chem. 2023, 323, 124074. [Google Scholar] [CrossRef]
- Regan, T.J.; Ohldag, H.; Stamm, C.; Nolting, F.; Luning, J.; Stöhr, J.; Lhite, W.R. Chemical effects at metal/oxide interfaces studied by x-ray-absorption spectroscopy. Phys. Rev. B 2001, 64, 214422. [Google Scholar] [CrossRef]
- Gai, X.-M.; You, C.; Gao, Y.-Q.; Li, Z.; Liu, H.-T.; Zhao, W.; Zhu, P.-W.; Wang, X. Irreversible expansion and distortion relief of bismuth ruthenate under high temperature and high pressure. J. Appl. Phys. 2025, 138, 135901. [Google Scholar] [CrossRef]
- Zhuk, N.A.; Krzhizhanovskaya, M.G. Thermal expansion of bismuth magnesium tantalate and niobate pyrochlores. Ceram. Int. 2021, 47, 30099–30105. [Google Scholar] [CrossRef]
- Shukla, R.; Vasundhara, K.; Krishna, P.S.R.; Shinde, A.B.; Sali, S.K.; Kulkarni, N.K.; Achary, S.N.; Tyagi, A.K. High temperature structural and thermal expansion behavior of pyrochlore-type praseodymium zirconate. Int. J. Hydrogen Energy 2015, 40, 15672–15678. [Google Scholar] [CrossRef]
- Raison, P.E.; Pavel, C.C.; Jardin, R.; Suard, E.; Haire, R.G.; Popa, K. Thermal expansion behavior of Ce2Zr2O7 up to 898 K in conjunction with structural analyses by neutron diffraction. Phys. Chem. Miner. 2010, 37, 555–559. [Google Scholar] [CrossRef]
- Feng, J.; Xiao, B.; Zhou, R.; Pan, W. Thermal expansions of Ln2Zr2O7 (Ln = La, Nd, Sm, and Gd) pyrochlore. J. Appl. Phys. 2012, 111, 103535. [Google Scholar] [CrossRef]
- Qun-bo, F.; Feng, Z.; Fuchi, W.; Lu, W. Molecular dynamic scalculation of thermal expansion coefficient of a series of rareearth zirconates. Comput. Mater. Sci. 2009, 46, 716–719. [Google Scholar] [CrossRef]
- Lasia, A. Electrochemical Impedance Spectroscopy and Its Applications; Springer Science + Business Media: New York, NY, USA, 2014; 369p. [Google Scholar]
- Barsoukov, E.; Macdonald, J.R. Impedance Spectroscopy: Theory, Experiment and Application; Wiley-Interscience: Hoboken, NJ, USA, 2005; 606p. [Google Scholar]
- Zhang, Y.; Zhang, Z.; Zhu, X.; Liu, Z.; Li, Y.; Al-Kassab, T. Dielectric properties and microstructural characterization of cubic pyrochlored bismuth magnesium niobates. Appl. Phys. A 2013, 115, 661–666. [Google Scholar] [CrossRef]
- Osman, R.A.M.; Masó, N.; West, A.R. Bismuth Zinc Niobate Pyrochlore, a Relaxor-Like Non-Ferroelectric. J. Am. Ceram. Soc. 2011, 95, 296–302. [Google Scholar] [CrossRef]
- Jusoh, F.A.; Tan, K.B.; Zainal, Z.; Chen, S.K.; Khaw, C.C.; Lee, O.J. Novel pyrochlores in the Bi2O3-Fe2O3-Ta2O5 (BFT) ternary system: Synthesis, structural and electrical properties. J. Mater. Res. Technol. 2020, 9, 11022–11034. [Google Scholar] [CrossRef]
- Chon, M.P.; Tan, K.B.; Khaw, C.C.; Zainal, Z.; Taufiq-Yap, Y.H.; Chen, S.K.; Tan, P.Y. Subsolidus phase equilibria and electrical properties of pyrochlores in the Bi2O3–CuO–Ta2O5 ternary system. J. Alloys Compd. 2016, 675, 116–127. [Google Scholar] [CrossRef]
- Abdullah, A.; Wan Khalid, W.E.F.; Abdullah, S.Z. Synthesis and Characterization of Bismuth Nickel Tantalate Pyrochlore. Appl. Mech. Mater. 2015, 749, 30–35. [Google Scholar] [CrossRef]


| Peak | Energy (eV) |
|---|---|
| Bi4f7/2 | 158.81 |
| Bi4f5/2 | 164.14 |
| Nb3d5/2 | 206.43 |
| Nb3d3/2 | 209.17 |
| Co2p3/2 | 780.22 |
| Co2p1/2 | 796.01 |
| Co sat | 786.11 |
| Co sat | 801.97 |
| Cr2p3/2 | 576.25 |
| Cr2p1/2 | 586.15 |
| Atom | Wyckoff Site | x | y | z | SOF | Biso,Å2 |
|---|---|---|---|---|---|---|
| Bi | 96g | 0 | −0.02435(13) | 0.02435(13) | 0.1307(3) | 1.82(9) |
| Nb | 16b | 0.5000 | 0.5000 | 0.5000 | 0.660(6) | 1.07(6) |
| Co/Cr | 16b | 0.5000 | 0.5000 | 0.5000 | 0.167(6) | 1.07(6) |
| O1 | 48f | 0.1250 | 0.1250 | 0.4330(3) | 1 | 0.63(12) |
| O2 | 8a | 0.1250 | 0.1250 | 0.1250 | 0.706(1) | 0.63(12) |
| Parameter | |
|---|---|
| a (Å) | 10.49360(5) |
| α, β, γ (°) | 90, 90, 90 |
| V (Å3) | 1155.511(16) |
| Dcalc (g/cm3) | 6.836(9) |
| RB | 0.54 |
| Rwp | 3.54 |
| Rp | 2.70 |
| Rexp | 1.95 |
| GOF | 1.81 |
| Bond | Length (Å) |
|---|---|
| Bi1 –O1×2 | 2.3005(4) |
| –O1×2 | 2.368(3) |
| –O1×2 | 2.695(2) |
| –O2×2 | 2.985(3) |
| <Bi1VIII–O> | 2.59 |
| Nb1–O1 × 6 | 1.9836(15) |
| <Nb1VI–O> | 1.99 |
| T, °C | TECs (×106 °C−1) | T, °C | TECs (×106 °C−1) | T, °C | TECs (×106 °C−1) |
|---|---|---|---|---|---|
| 20 | 3.92 | 370 | 6.02 | 720 | 8.11 |
| 70 | 4.22 | 420 | 6.32 | 770 | 8.41 |
| 120 | 4.52 | 470 | 6.62 | 820 | 8.70 |
| 170 | 4.82 | 520 | 6.92 | 870 | 9.00 |
| 220 | 5.12 | 570 | 7.22 | 920 | 9.30 |
| 270 | 5.42 | 620 | 7.51 | 970 | 9.59 |
| 320 | 5.72 | 670 | 7.81 | 1020 | 9.89 |
| <20–1020> | 6.91 | ||||
| t, °C | R1, Ω | C1, pF | R2, Ω | TCPE1 | PCPE1 | χ2 × 104 |
|---|---|---|---|---|---|---|
| 100 | 4.60 × 106 | 51.9 | - | 4.73 × 10−10 | 0.503 | 8.5 |
| 125 | 1.31 × 106 | 50.9 | - | 5.51 × 10−10 | 0.546 | 6.3 |
| 150 | 4.25 × 105 | 49.9 | - | 6.10 × 10−10 | 0.580 | 6 |
| 175 | 1.61 × 105 | 48.9 | - | 1.06 × 10−9 | 0.573 | 5 |
| 200 | 69,220 | 47.7 | - | 1.67 × 10−9 | 0.574 | 5 |
| 225 | 34,776 | 45.7 | - | 1.12 × 10−9 | 0.639 | 6 |
| 250 | 19,680 | 44.7 | - | 2.40 × 10−9 | 0.610 | 3.3 |
| 275 | 13,242 | 42.7 | - | 1.08 × 10−9 | 0.687 | 5.3 |
| 300 | 7706 | 31 | - | 1.46 × 10−10 | 0.871 | 4 |
| 325 | 4149 | - | 33 | 9.08 × 10−11 | 0.962 | 2 |
| 350 | 2116 | - | 80 | 7.44 × 10−11 | 0.975 | 1.3 |
| 1 | |||||
| T, °C | R, Ω | C, pF | P2 | χ2 × 104 | |
| R1 | R2 | ||||
| 175 | 3.10 × 105 | 1.48 × 106 | 33.0 | 0.566 | 0.7 |
| 200 | 1.40 × 105 | 4.48 × 105 | 32.7 | 0.450 | 0.8 |
| 225 | 79,544 | 1.79 × 105 | 32.4 | 0.539 | 2 |
| 250 | 54,137 | 81,022 | 32.2 | 0.634 | 4.8 |
| 275 | 36,436 | 51,936 | 31.5 | 0.716 | 4 |
| 300 | 24,699 | 39,734 | 31.0 | 0.808 | 3.6 |
| 325 | 17,468 | 44,406 | 30.8 | 0.906 | 2.7 |
| 350 | 8308 | 63 | - | 0.993 | 4 |
| 375 | 3664 | 89 | - | 1 | 3.6 |
| 2 | |||||
| T, °C | R1, Ω | C, pF | PCPE1 | χ2 × 104 | |
| 100 | 4.60 × 106 | 51.9 | 0.503 | 8.5 | |
| 125 | 1.31 × 106 | 50.9 | 0.546 | 6.3 | |
| 150 | 4.25 × 105 | 49.9 | 0.580 | 6 | |
| 175 | 1.61 × 105 | 48.9 | 0.573 | 5 | |
| 200 | 69,220 | 47.7 | 0.574 | 5 | |
| 225 | 34,776 | 45.7 | 0.639 | 6 | |
| 250 | 19,680 | 44.7 | 0.610 | 3.3 | |
| 275 | 13,242 | 42.7 | 0.687 | 5.3 | |
| 300 | 7706 | 31 | 0.871 | 4 | |
| 325 | 4149 | - | 0.962 | 2 | |
| 350 | 2116 | - | 0.975 | 1.3 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhuk, N.A.; Sekushin, N.A.; Krzhizhanovskaya, M.G.; Kharton, V.V.; Sivkov, D.V.; Nekipelov, S.V. Features of Synthesis, Crystal Structure, Thermal and Electrical Properties, XPS/NEXAFS Study of Pyrochlore-Type Bi2Cr0.5Co0.5Nb2O9+Δ. Chemistry 2025, 7, 185. https://doi.org/10.3390/chemistry7060185
Zhuk NA, Sekushin NA, Krzhizhanovskaya MG, Kharton VV, Sivkov DV, Nekipelov SV. Features of Synthesis, Crystal Structure, Thermal and Electrical Properties, XPS/NEXAFS Study of Pyrochlore-Type Bi2Cr0.5Co0.5Nb2O9+Δ. Chemistry. 2025; 7(6):185. https://doi.org/10.3390/chemistry7060185
Chicago/Turabian StyleZhuk, Nadezhda A., Nikolay A. Sekushin, Maria G. Krzhizhanovskaya, Vladislav V. Kharton, Danil V. Sivkov, and Sergey V. Nekipelov. 2025. "Features of Synthesis, Crystal Structure, Thermal and Electrical Properties, XPS/NEXAFS Study of Pyrochlore-Type Bi2Cr0.5Co0.5Nb2O9+Δ" Chemistry 7, no. 6: 185. https://doi.org/10.3390/chemistry7060185
APA StyleZhuk, N. A., Sekushin, N. A., Krzhizhanovskaya, M. G., Kharton, V. V., Sivkov, D. V., & Nekipelov, S. V. (2025). Features of Synthesis, Crystal Structure, Thermal and Electrical Properties, XPS/NEXAFS Study of Pyrochlore-Type Bi2Cr0.5Co0.5Nb2O9+Δ. Chemistry, 7(6), 185. https://doi.org/10.3390/chemistry7060185







