Determination of the Activity Coefficients of Components in a Di-2-ethylhexylphosphoric Acid–n-Hexane Binary System Using Gas Chromatography

Abstract

The thermodynamic properties of di-2-ethylhexylphosphoric acid (D2EHPA) in organic solvents are critical for optimizing metal extraction processes in hydrometallurgy, necessitating precise determination of activity coefficients in binary systems such as D2EHPA–n-hexane. This study was devoted to the determination of n-hexane’s concentrations in the vapor phase over D2EHPA solutions at 293.0 K using gas chromatography (GC) and isopiestic (IP) methods. Comparison with literature data confirmed the superior reliability of GC measurements at low n-hexane concentrations. The experimentally determined activity coefficients of hexane, obtained via GC, served as the initial input parameters for UNIFAC modeling. The optimized interaction parameters were 1144 ± 25 (CH₂-HPO₄) and 228 ± 50 (HPO₄-CH₂), with the infinite dilution activity coefficient for D2EHPA ${\gamma }_{\infty }=22.1$. These results experimentally clarify the non-ideal behavior of D2EHPA–n-hexane mixtures, establishing a validated thermodynamic modeling framework for organophosphorus extractant systems. This work establishes a fundamental basis for investigating ternary systems, such as D2EHPA–aliphatic solvent–aromatic solvent and D2EHPA–metal complex–solvent systems, paving the way for enhanced liquid–liquid extraction efficiency.

1. Introduction

Di-2-ethylhexylphosphoric acid (D2EHPA) is a pivotal organophosphorus extractant in hydrometallurgy, widely employed for the separation of actinides [1,2,3], lanthanides [4,5,6], and other critical metals, including zinc [7,8], lithium [9,10], copper [11,12,13], lead [14,15], and vanadium [16,17,18].

In practical applications, D2EHPA is typically diluted in hydrocarbon solvents such as kerosene [19,20,21], forming complex systems comprising n-alkanes, monoarenes, D2EHPA molecules, and metal–D2EHPA complexes [22,23,24]. Quantitative modeling of these extraction systems necessitates precise thermodynamic data, particularly activity coefficients, to describe component interactions and optimize process efficiency.

Developing a comprehensive thermodynamic model begins with studying simplified binary systems, such as D2EHPA with a single n-alkane, to establish reliable measurement methodologies. Previous investigations have examined D2EHPA in volatile n-alkanes (C5–C8) and benzene [25,26,27], yet accurate activity coefficient data at low solvent concentrations—crucial for industrial dilute solutions—remain limited. These coefficients are subsequently calculated as a function of solvent mole fraction using the UNIFAC model, enabling the construction and validation of physicochemical models for solution non-ideality [28,29]. Such models are particularly valuable for analyzing ternary systems, such as D2EHPA–metal complex–solvent systems, and predicting D2EHPA behavior in diverse hydrocarbon mixtures using group contribution approaches.

Determining activity coefficients at low solvent concentrations poses significant experimental challenges, as traditional osmometric and isopiestic methods incur substantial errors due to difficulties in detecting small mass changes and low osmotic pressures [30]. Vapor-phase analysis, particularly gas chromatography (GC), offers a superior alternative by directly measuring gas-phase concentrations with high precision [31,32], provided the solvent’s equation of state is known for non-ideal vapor behavior.

This study aimed to develop a reliable experimental methodology for experimental determination of activity coefficients of n-hexane in binary D2EHPA solutions and obtain interaction parameters between CH₂-HPO₄ and HPO₄-CH₂ groups using UNIFAC modeling. The selection of n-hexane as a model system is justified by its structural homology with D2EHPA’s hydrocarbon radicals. Experimental data for this system are necessary for the description of more complex systems, including aliphatic and aromatic hydrocarbons.

2. Materials and Methods

2.1. Reagents

In this work, we used high-grade n-hexane (CAS 110-54-3) from EKOS-1 and D2EHPA (CAS 298-07-7) at 99% purity purchased from LeapChemCo. (Hangzhou, China). For IP measurements, high-grade n-dodecane (CAS 112-40-3) from EKOS-1 was used as a reference standard.

Di-2-ethylhexylphosphoric acid (D2EHPA), n-hexane, and dodecane were stored under controlled conditions in their original sealed containers in a dry, temperature-controlled warehouse. Storage facilities were maintained away from heat sources and direct sunlight, with all chemicals remaining within their validated shelf life (through September 2025).

Masses of components for calculation of molar fractions were determined on OHAUS Pioneer PR224 analytical scales (USA). All experiments were conducted at 293.0 K based on literature evidence [25,30] demonstrating the minimal temperature dependence of activity coefficients in this system. This temperature was selected for three key reasons: (1) it minimizes errors in vapor pressure determination for n-hexane, which increase significantly at elevated temperatures; (2) it approximates standard reference conditions; and (3) it simplifies thermal control requirements.

2.2. Gas Chromatography (GC) Method

The experimental setup for measuring hexane vapor concentrations above the D2EHPA–n-hexane solution is depicted in Figure 1. It comprised a 0.27 L glass container, thermostatically maintained at 293.0 ± 0.1 K using a water bath, equipped with a magnetic stirrer (500 rpm) and a 10 mL glass syringe for gas-phase sampling. The solution occupied 10% of the container’s volume (27 mL), sealed with a stopper featuring a 0.7 mm diameter venting tube to maintain atmospheric pressure. Vapor samples (0.3 mL) were withdrawn using the syringe, with volume consistency ensured by a 3 mm diameter steel bearing fixed inside. Post-sampling, atmospheric air was drawn into the syringe to a total volume of 10 mL, and the mixture was homogenized by manual shaking (10 cycles). The entire gas volume was then injected into a stainless-steel dosing loop (0.1 cm³) via a two-way valve connected to the gas chromatograph’s carrier line. This sampling technique accommodated both concentrated and dilute hexane mixtures by adjusting the dilution with air, minimizing analyte loss.

Hexane concentrations were quantified using an Agilent GC-6890 gas chromatograph (USA) fitted with a flame ionization detector (FID) and a 0.1 cm³ stainless-steel dosing loop. Separation was achieved on a Restek-QS-Bond capillary column (30 m length, 0.53 mm internal diameter, 20 μm film thickness). Operating conditions, detailed in

Table 1. Gas chromatograph operating conditions.

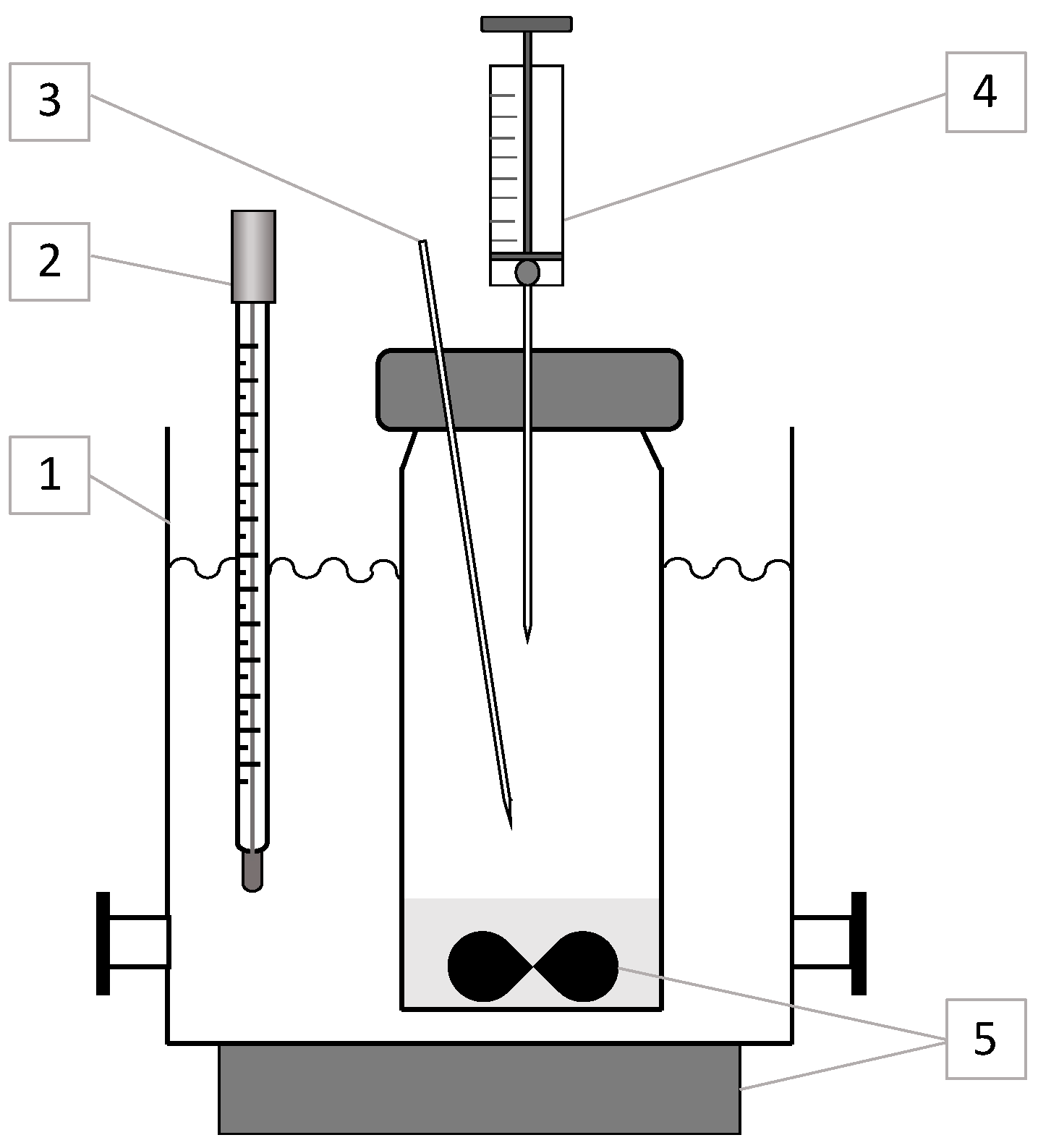
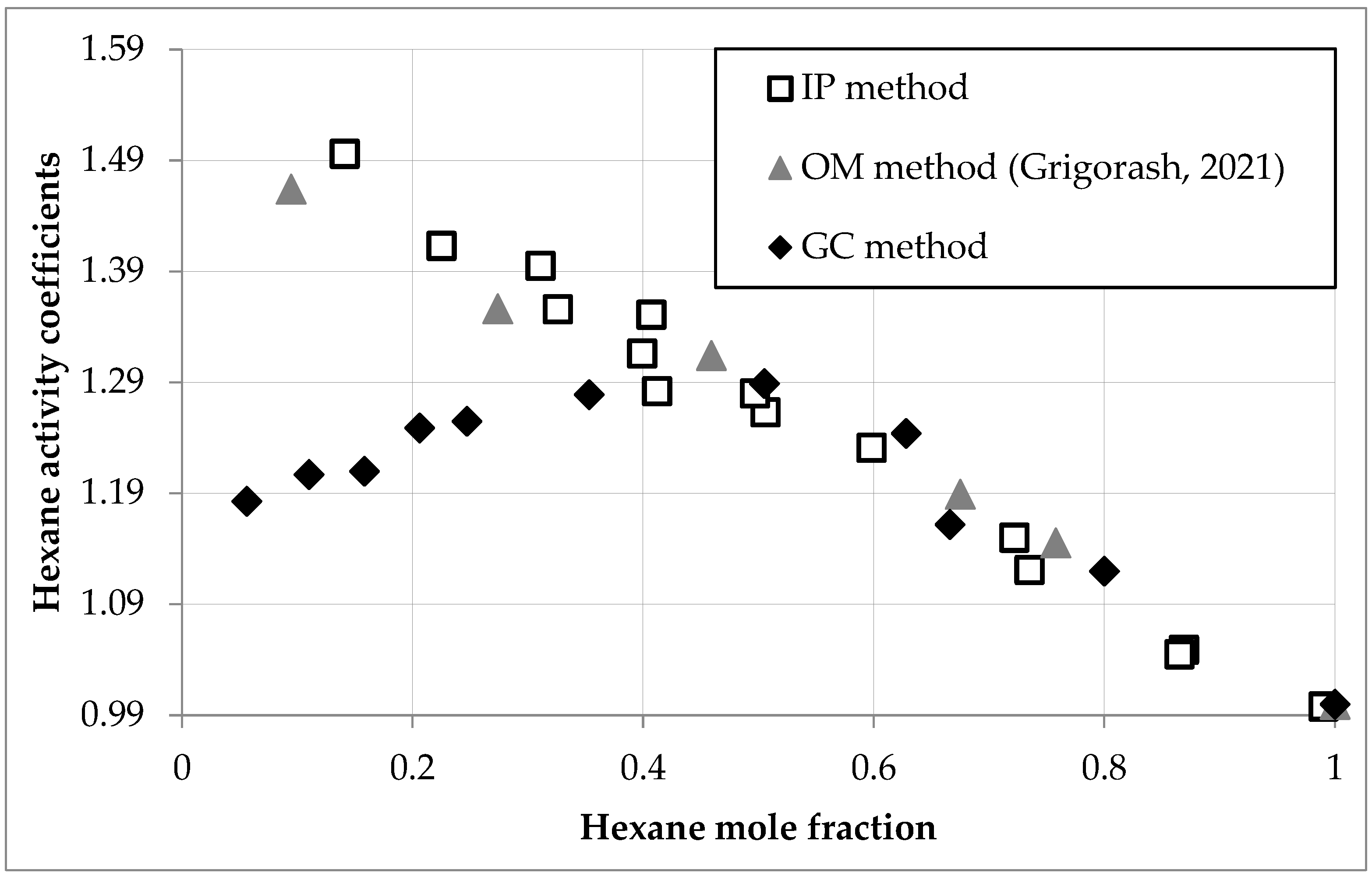
Parameter	Value
Injector temperature	473 K
Oven temperature	473 K
Detector temperature	523 K
Carrier gas, flow rate	Helium, 5.4 mL/min
Make-up gas flow rate	8 mL/min
Split ratio	1:10
H2 flow to the detector	40 mL/min
Air flow to the detector	300 mL/min
Range	3

, were optimized for hexane detection, with triplicate injections per sample yielding a relative standard deviation of ≤1.6%. The FID was calibrated daily with hexane standards (10–550 mg/L, R² = 0.998) to ensure linearity.

2.3. Calibration of Detector and Methodology for Calculating Hexane Vapor Activity

FID quantifies hexane in the injected vapor sample via peak area, necessitating a linear response across the concentration range of interest. To verify this, detector linearity was assessed prior to experiments by introducing 20 μL aliquots of liquid n-hexane (≥99.5% purity, EKOS-1) into the 0.27 L glass container, where it vaporized under magnetic stirring (500 rpm) at 293 ± 0.1 K. Peak areas were measured in triplicate, with concentrations ranging from 10 to 550 mg/L, yielding a linear calibration curve (Equation (1)):

$$\begin{array}{c}{S}_1=18.936·C-32.735,\\ R^2=0.9992,\end{array}$$

(1)

where S₁—peak area in μV∙s; C—hexane vapor concentration in mg/L.

Equation (1) was applied to determine hexane concentrations above D2EHPA–n-hexane solutions from their peak areas, with daily calibration ensuring accuracy; values were independently validated against pure hexane standards and served as inputs for thermodynamic modeling.

Hexane activity ($a_1$) was calculated as the ratio of its vapor concentration above the solution to that above pure hexane (Equation (2)):

$$a_1={\displaystyle \frac{P}{P^0}}={\displaystyle \frac{\mathrm{C}}{{\mathrm{C}}^0}},$$

(2)

where $a_1$ is the hexane activity, P and P⁰ are the vapor pressures over the solution and pure solvent (Pa), C is the hexane concentration over the D2EHPA solution (mg/L), and C⁰ is the concentration over pure hexane at 293.0 K (mg/L). Equation (2) assumes a direct proportionality between concentration and vapor pressure, valid for hexane at 293.0 K and pressures ≤ 1 atm [33].

The hexane activity coefficient (γ₁) was derived using Equation (3):

$${\gamma }_1={\displaystyle \frac{\mathrm{C}}{{\mathrm{C}}^0}}·{\displaystyle \frac{1}{x_1}},$$

(3)

where γ₁ is the activity coefficient and x₁ is the mole fraction of hexane in the liquid phase. This approach enabled precise quantification of thermodynamic properties across all compositions.

2.4. Estimation of the GC Method Errors

Weighing accuracy was assessed using an OHAUS Pioneer PR224 balance with a precision of ±0.001 g, yielding a relative error of ≤0.1% for sample masses of 1–50 g. The relative error in determining the hexane mole fraction in the D2EHPA–n-hexane solution was calculated as twice the weighing error, resulting in 0.2%, reflecting contributions from both components. To evaluate peak area precision, five consecutive 0.3 mL vapor injections were performed at 80 s intervals (retention time: 450 s), and the mean peak area (S_x) for hexane above the solution was computed. Similarly, five injections of a reference hexane vapor sample (C⁰, pure hexane at 293.0 K) were analyzed without interrupting the chromatogram, yielding the mean peak area (S₀). The relative standard deviation of individual peak areas was ≤1.6%, and the relative error of the mean peak area, at a 95% confidence level, was 1.9%, derived from standard statistical methods.

The relative error in hexane activity (a₁ = C/C⁰) was 3.8%, combining peak area errors for S_x and S₀ (1.9% each). For the activity coefficient (γ₁ = a₁/x₁), an additional 0.2% from mole fraction uncertainty was included, resulting in a total relative error of 4%. For a typical γ₁ of 1.2, this translates to an absolute error of ±0.05, deemed sufficient for UNIFAC modeling. At low hexane mole fractions (<0.05), sampling-induced vaporization altered the liquid-phase composition, necessitating correction. The adjusted hexane mass was calculated using Equation (4):

$$M^{\prime }=M-C·V,$$

(4)

where M and M′ are the initial and final hexane masses (g), C is the vapor concentration (g/L), and V is the gas-phase volume (0.27 L, container headspace). Using M′ in calculations prevented underestimation of γ₁ due to equilibrium shifts.

2.5. Isopiestic (IP) Method

The isopiestic (IP) method was employed as an alternative approach to determine the activity of volatile hexane in D2EHPA–n-hexane solutions. The IP setup consisted of a thermostatically controlled, sealed vessel (internal volume: 20 mL, maintained at 293.0 ± 0.1 K) containing two glass containers, one with the test solution (D2EHPA in n-hexane) and the other with the reference solution (dodecane in n-hexane), each with masses of 0.7–1.0 g depending on the target composition. Initial hexane mole fractions in both solutions were matched. Given that hexane activity exceeds unity in D2EHPA solutions and approximates unity in dodecane solutions, hexane vapor consistently transferred from the test to the reference solution until vapor–liquid equilibrium was achieved. Component masses were measured using an OHAUS Pioneer PR224 balance (±0.1 mg accuracy), and the containers were incubated for 56 h to reach equilibrium. Pre- and post-experiment weighing of the setup confirmed atmospheric losses below 1 mg.

Since dodecane–hexane solutions exhibit mild non-ideality, hexane activity in the reference solution was calculated using the UNIFAC model (gas–liquid equilibrium) rather than measured separately. This model accurately captures non-ideality in low-molecular-weight alkane mixtures, driven solely by configurational contributions (molecular size and shape differences), with negligible residual (energetic) effects. For hexane in dodecane at 293.0 K, the activity coefficient (γ₁) was modeled as a polynomial function of hexane mole fraction (x₁):

$${\gamma }_1=0.85441+0.16535x_1+0.08078x_1^2-0.09914x_1^3.$$

The hexane activity coefficient in the D2EHPA solution was then derived using Equation (5):

$${\gamma }_1={\displaystyle \frac{{a^{″}}_1}{{x^{\prime }}_1}}$$

(5)

where γ₁ is the activity coefficient in the D2EHPA solution (dimensionless), a₁″ is the hexane activity in the dodecane solution post-equilibrium, and x₁′ is the hexane mole fraction in the D2EHPA solution post-equilibrium.

3. Results

Hexane activity and activity coefficients in D2EHPA solutions, determined via gas chromatography (GC) and isopiestic (IP) methods, are presented in

Table 2. Hexane activity and activity coefficients in D2EHPA solutions at 293.0 K.

GC Method				IP Method
x1	C (mg/L)	a1	γ1	x1	a1	γ1
1.000	570.5	1.000	1.000	0.99	0.988	0.998
0.800	511.2	0.893	1.120	0.869	0.912	1.049
0.666	441.6	0.774	1.162	0.865	0.904	1.045
0.628	445.2	0.780	1.244	0.735	0.824	1.121
0.505	371.4	0.651	1.289	0.722	0.830	1.150
0.353	257.8	0.452	1.279	0.598	0.736	1.231
0.247	177.0	0.310	1.255	0.506	0.639	1.263
0.206	146.7	0.257	1.249	0.497	0.636	1.280
0.158	109.0	0.191	1.210	0.407	0.550	1.351
0.110	75.8	0.133	1.207	0.412	0.528	1.282
0.056	38.1	0.067	1.183	0.399	0.525	1.316
				0.326	0.442	1.356
				0.311	0.434	1.395
				0.225	0.318	1.413
				0.141	0.211	1.496

and Figure 2.

For comparative analysis, Figure 2 incorporates osmometric (OM) measurements of hexane activity coefficients from the literature [30].

Across hexane mole fractions (x₁) of 0.5–1.0, all methods yielded consistent activity coefficients (γ₁), with deviations ≤ 2% (e.g., γ₁ = 1.244–1.280 at x₁ = 0.628–0.497). Below x₁ = 0.5, discrepancies increased, reaching up to 26% at low fractions (e.g., γ₁ = 1.183 at x₁ = 0.056 (GC) vs. 1.496 at x₁ = 0.141 (IP)). The presented GC data were further used for activity coefficient calculations and modeling.

The observed divergence reflects method-specific limitations, with GC demonstrating superior reliability due to its direct measurement of hexane vapor concentrations. GC accuracy hinges on detector linearity (R² = 0.9992, Equation (1)), injection reproducibility (RSD ≤ 1.6%), and minimal deviation of hexane vapor from ideal gas behavior at 293.0 K and ≤1 atm, all validated through control experiments.

IP and OM [30] methods underestimated γ₁ at low x₁ (<0.5) due to hexane losses within the closed vessel and slow vapor transfer rates, as detailed in

Table 3. Relative mass losses of n-hexane during IP measurements at 293.0 K for x₁ = 0.8 and 0.2.

	Losses of Vessel	D2EHPA–Hexane				Dodecane–Hexane				∆m1 + ∆m2	α 3
		mD2EHPA, mg	minit 1, mg	mfinal 2, mg	∆m1, mg	mdodecane, mg	minit 1, mg	mfinal 2, mg	∆m2, mg
1	<1 mg	355.9	365.4	263.4	−102.0	238.4	480.4	563.2	82.8	–19.2	4.3
2	<1 mg	865.6	54.1	37.8	−16.3	812.2	103.7	109.6	5.9	–10.4	0.57

¹ m_init—initial mass of hexane added to vessel; ² m_final—final mass of hexane after equilibrium has been established; ³ k—ratio of transferred hexane to lost, $\mathsf{\alpha }=-{\displaystyle \frac{∆{\mathrm{m}}_2}{(∆{\mathrm{m}}_1+∆{\mathrm{m}}_2)}}$.

. For high hexane content (x₁ ≈ 1), 20% of transferred hexane was absorbed by the system (∆m₁ − ∆m₂ = 19.2 mg), increasing to 80% at low content (x₁ < 0.1, ∆m₁ − ∆m₂ = 10.4 mg). Ideally, ∆m₁ − ∆m₂ should be zero, but absorption extended equilibrium time beyond 56 h at low x₁, potentially overestimating γ₁ if equilibrium was not fully attained.

Grigorash et al. [30] reported OM errors of ≥8% at low x₁ and ≈0.8% at high x₁ using direct pressure measurements, corroborating IP’s limitations. Unlike GC, IP and OM lack selectivity, relying on mass and pressure changes driven solely by solvent evaporation. At low x₁, confounding factors—such as residual gases and slowed evaporation—amplify errors, reinforcing GC’s advantage. Precise γ₁ values below x₁ = 0.1 are critical for robust thermodynamic modeling.

4. Discussion

To model non-ideality in organic phases for solvent extraction, various frameworks express activity coefficients as functions of composition, accounting for extractant dimerization, molecular size, and intermolecular energetics [31,34,35]. The UNIFAC model, treating solutions as mixtures of functional groups, requires parameters for each group’s volume, surface area, and pairwise energy interactions. Once determined through experimental studies, these parameters can be universally applied to similar calculations across different systems. This fact is the main advantage of the UNIFAC model over alternative approaches, explaining its widespread use in thermodynamic modeling. For example, UNIFAC allows us to predict the activity coefficient of D2EHPA in mixed alkanes on the basis of a single system like D2EHPA–n-hexane. The activity coefficient (γ_i) comprises combinatorial and residual terms (Equation (6)):

$$\ln {\gamma }_i=\ln {\gamma }_i^{comb}+\ln \ln {\gamma }_i^{res}.$$

(6)

The combinatorial contribution (γ_i^comb), reflecting molecular size and shape, and residual contribution (γ_i^res), capturing energetic interactions, are given by Equations (7) and (8):

$$\ln {\gamma }_{icomb}=\ln \left({\displaystyle \frac{{\phi }_i}{x_i}}\right)+10q_i\ln {\displaystyle \frac{{\theta }_i}{{\phi }_i}}+l_i-{\displaystyle \frac{{\phi }_i}{x_i}}\sum x_i{l}_i,$$

(7)

${\phi }_i={\displaystyle \frac{r_i{x}_i}{\sum r_j{x}_j}}and {\theta }_i=q={\displaystyle \frac{q_i{x}_i}{\sum q_j{x}_j}}$ are the volume and surface fractions.

$l_i=5\left(r_i{-q}_i\right)-(r_i-1)$ is the volume factor.

$r_i=\sum n_{ik}·R_k \mathrm{a}\mathrm{n}\mathrm{d} q_i=\sum n_{ik}·Q_k$ are the Van der Waals volume and surface area of component i (relative units), n_ik is the number from group k in component i, and R_k and Q_k are group-specific parameters.

$$\ln {\gamma }_{ires}=\sum n_{is}(ln{G}_{ks}-ln{G}_{ki}),$$

(8)

where G_ks and G_ki are residual activity coefficients of group k in the solution and pure component i, calculated via Equation (9):

$$\ln G_k=Q_k\left[1-\ln \left(\sum _m{\mathsf{\theta }}_m{\mathsf{\Psi }}_{\mathrm{m}\mathrm{k}}\right)-\sum _m{\displaystyle \frac{{\mathsf{\theta }}_m{\mathsf{\Psi }}_{\mathrm{k}\mathrm{m}}}{\sum _n{\mathsf{\theta }}_n{\mathsf{\Psi }}_{\mathrm{n}\mathrm{m}}}}\right],$$

(9)

with θ_m as the surface fraction of group m, ${\mathsf{\Psi }}_{\mathrm{k}\mathrm{m}}=e^{{\displaystyle \raisebox{1ex}{$-a_{km}$}\!\left/ \!\raisebox{-1ex}{$T$}\right.}}$, and a_km as the energy interaction parameter (non-zero only for CH₂-HPO₄ interactions here).

D2EHPA–n-hexane solutions were modeled as mixtures of CH₂, CH₃, CH, and HPO₄ groups, with structural parameters listed in

Table 4. Structural parameters (r, q) of the UNIFAC model.

Group	r	q	Reference
(HA)2 1	25.88	22	[36]
CH3	0.9011	0.848	[37]
CH2	0.6744	0.540	[37]
CH	0.4469	0.228	[37]

¹ D2EHPA dimer form.

.

Energy parameters (a_km) for CH₂-HPO₄ and HPO₄-CH₂ interactions were optimized to minimize deviations between experimental and theoretical γ₁ values (Equation (10)):

$$F=\sum \left|\mathrm{l}\mathrm{n}\left({\displaystyle \frac{{\gamma }_{exp}}{{\gamma }_{teor}}}\right)\right|.$$

(10)

Figure 3 shows the lines of equal values of F as a function of the energy interaction parameters of the CH₂ group with a hypothetical pure solution of HPO₄ groups and a HPO₄ group with the same solution of CH₂ groups. The minimum is observed at 1144 ± 25 and 228 ± 50. Both values are presented in R units. The reported parameter uncertainties reflect the cumulative experimental errors in hexane’s activity coefficient measurements.

The activity coefficients for both the D2EHPA and hexane were calculated using the UNIFAC model and presented in

Table 5. UNIFAC-calculated activity coefficients of hexane (γ₁) and D2EHPA (γ₂) at 293.0 K.

x1	γ1	γ2	x1	γ1	γ2
0.01	1.202	0.99999	0.6	1.250	1.002
0.02	1.204	0.99996	0.7	1.221	1.047
0.03	1.206	0.99992	0.8	1.163	1.199
0.04	1.209	0.99985	0.9	1.088	1.861
0.05	1.211	0.99977	0.95	1.038	3.44
0.1	1.221	0.9991	0.96	1.028	4.234
0.2	1.239	0.997	0.97	1.018	5.486
0.3	1.253	0.993	0.98	1.010	7.649
0.4	1.262	0.989	0.99	1.003	11.901
0.5	1.262	0.990	1	1	22.107

. Figure 4 compares experimental γ₁ values with UNIFAC predictions at these parameters, showing strong agreement across compositions. A maximum γ₁ = 1.289 at x₁ = 0.5 aligns with GC data but diverges from IP and OM [30] trends.

Systematic adjustment of the UNIFAC energy parameters (a_km) across an extended range fails to align the isopiestic (IP) and osmometric (OM) [30] data with the observed trend, as the modeled activity coefficient (γ₁) trajectory remains insensitive to parameter variation. Notably, UNIFAC optimization using IP/OM data produces substantial deviations from experimental values (F > 0.5), while gas chromatographic (GC) data exhibit excellent agreement (F ≈ 0.1). It means, that UNIFAC predictions consistently match GC results but diverge from IP/OM measurements. In other words, the chromatographic data are consistent with the UNIFAC model over the entire range of compositions.

D2EHPA’s γ₂ remains near 1 until x₂ < 0.4, reflecting its dimerized state in concentrated solutions [38,39]. At x₂ = 0.01 (x₁ = 0.99), γ₂ reaches 11.901, rising to 22.107 as x₂ → 0, highlighting significant non-ideality in dilute industrial solutions.

5. Conclusions

The present study demonstrates the applicability of gas chromatography (GC) for determining hexane activity coefficients in a D2EHPA–n-hexane system at 293.0 K, particularly in dilute hexane solutions (x₁ < 0.05), where its precision (total error 4%) surpasses that of isopiestic (IP) and osmometric (OM) methods. Experimental data align with IP and OM results at hexane mole fractions (x₁) of 0.5–1.0 (deviations ≤ 2%) but show significant discrepancies below x₁ = 0.5, with differences up to 26% (e.g., γ₁ = 1.183 [GC] vs. 1.496 [IP] at x₁ ≈ 0.1), attributed to IP and OM’s sensitivity to hexane losses and slow vapor transfer. The GC-derived activity coefficients, peaking at γ₁ = 1.289 near x₁ = 0.5, are accurately described by the UNIFAC model, with optimized energy interaction parameters: CH₂-HPO₄ = 1144 ± 25 and HPO₄-CH₂ = 228 ± 50. The calculated parameters enable reliable calculation of activity coefficients for both components across all compositions, yielding a limiting D2EHPA activity coefficient of 22.1 as x₂ → 0.

In further studies, benzene–D2EHPA and toluene–D2EHPA systems will be considered, and the parameters of the energy interaction between the HPO₄ group and the aromatic groups CH and C-CH₃ will be determined. This will allow us to calculate the activity coefficients of solvent components and D2EHPA in any mixtures of aliphatic and aromatic hydrocarbons. Such solutions are used in the industrial extraction of valuable metals, such as rare earth elements.