Systematic Investigation on Surface Diradicals Using Theoretical Models: 2M/MgO and 2M/BaO (M = Cu, Ag, and Au)
Abstract
1. Introduction
2. Computational Procedure
2.1. Spin Contamination Error and Diradical Character
2.2. Approximate Spin Projection (AP) Method for DFT
2.3. Method
2.4. Calculated Models
3. Results and Discussion
3.1. Comparison with CAS Calculation
3.2. Spin Contamination Error
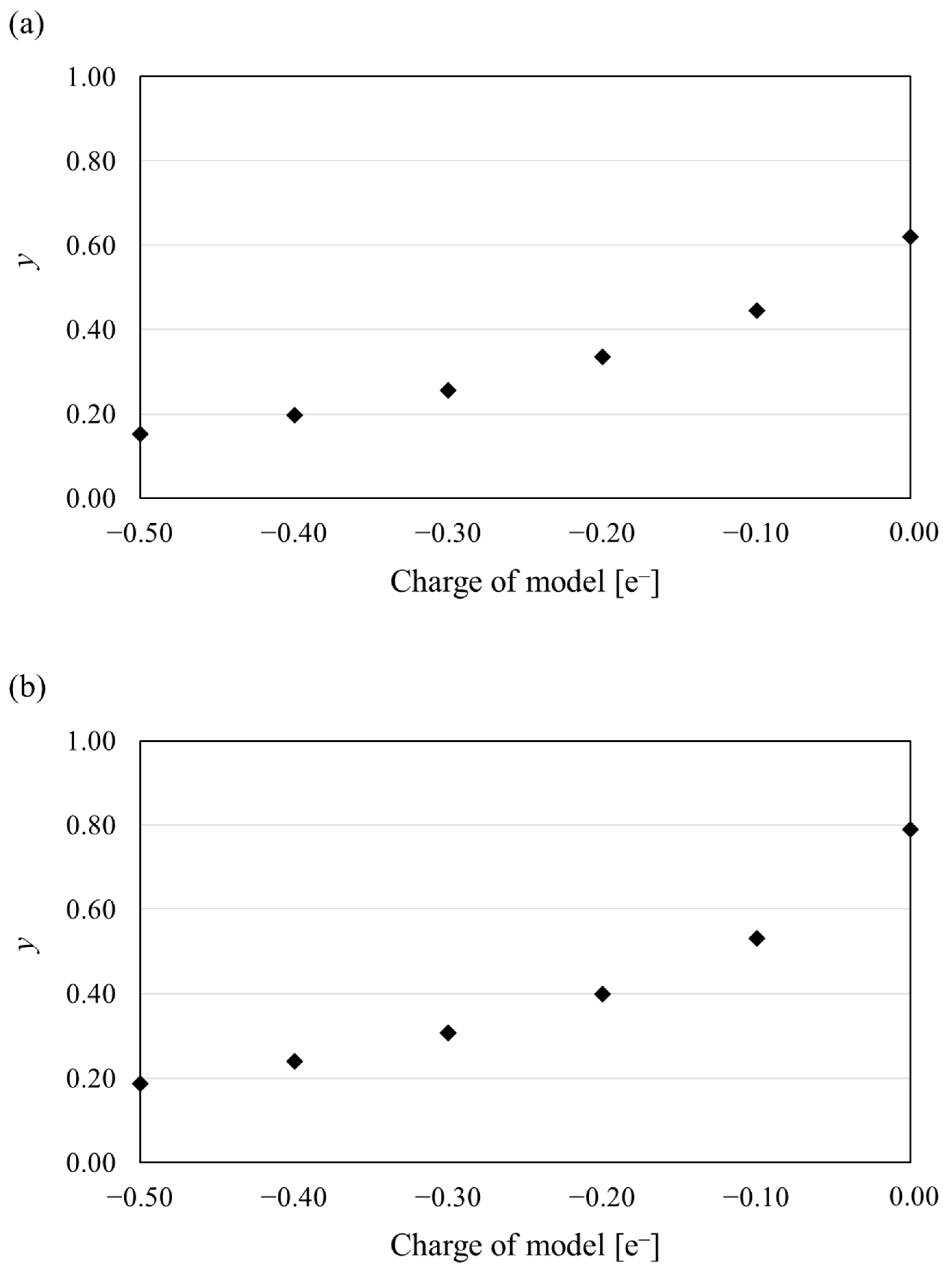
3.3. Diradical Character
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stuyver, T.; Chen, B.; Zeng, T.; Geerlings, P.; De Proft, F.; Hoffinann, R. Do Diradicals Behave Like Radicals? Chem. Rev. 2019, 119, 11291–11351. [Google Scholar] [CrossRef]
- Nishijima, M.; Mutoh, K.; Abe, J. A qualitative measure of diradical character based on radical–radical coupling reaction. Chem. Lett. 2021, 50, 1423–1427. [Google Scholar] [CrossRef]
- Noodleman, L.; Lovell, T.; Han, W.G.; Li, J.; Himo, F. Quantum chemical studies of intermediates and reaction pathways in selected enzymes and catalytic synthetic systems. Chem. Rev. 2004, 104, 459–508. [Google Scholar] [CrossRef]
- Saito, T.; Nishihara, S.; Kataoka, Y.; Nakanishi, Y.; Kitagawa, Y.; Kawakami, T.; Yamanaka, S.; Okumura, M.; Yamaguchi, K. Reinvestigation of the reaction of ethylene and singlet oxygen by the approximate spin projection method. Comparison with multireference coupled-cluster calculations. J. Phys. Chem. A 2010, 114, 7967–7974. [Google Scholar] [CrossRef]
- Saito, T.; Yasuda, N.; Kataoka, Y.; Nakanishi, Y.; Kitagawa, Y.; Kawakami, T.; Yamanaka, S.; Okumura, M.; Yamaguchi, K. Potential energy curve for ring-opening reactions: Comparison between broken-symmetry and multireference coupled cluster methods. J. Phys. Chem. A 2011, 115, 5625–5631. [Google Scholar] [CrossRef]
- Stuyver, T.; Zeng, T.; Tsuji, Y.; Geerlings, P.; de Proft, F. Diradical character as a guiding principle for the insightful design of molecular nanowires with an increasing conductance with length. Nano Lett. 2018, 18, 7298–7304. [Google Scholar] [CrossRef]
- Tada, K.; Ozaki, H.; Fujimaru, K.; Kitagawa, Y.; Kawakami, T.; Okumura, M. Can we enhance diradical character using interaction with stoichiometric surfaces of ionic oxides? A theoretical investigation using chemical indices. Phys. Chem. Chem. Phys. 2021, 23, 25024–25028. [Google Scholar] [CrossRef]
- Malrieu, J.P.; Coballol, R.; Calzado, C.J.; de Graaf, C.; Guihery, N. Magnetic interactions in molecules and highly correlated materials: Physical content, analytical derivation, and rigorous extraction of magnetic Hamiltonians. Chem. Rev. 2014, 114, 429–492. [Google Scholar] [CrossRef]
- David, G.; Wennmohs, F.; Neese, F.; Ferre, N. Chemical tuning of magnetic exchange couplings using broken-symmetry density functional theory. Inorg. Chem. 2018, 57, 12769–12776. [Google Scholar] [CrossRef]
- Kinoshita, K.; Kawakami, T.; Morita, Y.; Saito, T.; Yamanaka, S.; Okumura, M.; Yamaguchi, K. Theoretical Studies on the Magnetic and Conductive Properties of Crystals Containing Open-Shell Trioxotriangulene Radicals. Bull. Chem. Soc. Jpn. 2016, 89, 315–333. [Google Scholar] [CrossRef]
- Tada, K.; Kawakami, T.; Tanaka, S.; Okumura, M.; Yamaguchi, K. Clarification of the relationship between the magnetic and conductive properties of infinite chains in trioxotriangulene radical crystals by spin-projected DFT/plane-wave calculations. Adv. Theory Simul. 2020, 3, 2000050. [Google Scholar] [CrossRef]
- Kamada, K.; Ohta, K.; Shimizu, A.; Kubo, T.; Kishi, R.; Takahashi, H.; Botek, E.; Champagne, B.; Nakano, M. Singlet Diradical Character from Experiment. J. Phys. Chem. Lett. 2010, 1, 937–940. [Google Scholar] [CrossRef]
- Nakano, M.; Champagne, B. Theoretical Design of Open-Shell Singlet Molecular Systems for Non-linear Optics. J. Phys. Chem. Lett. 2015, 6, 3236–3256. [Google Scholar] [CrossRef]
- Muhammad, S.; Nakano, M.; Al-Sehemi, A.G.; Kitagawa, Y.; Irfan, A.; Chaudhry, A.R.; Kishi, R.; Ito, S.; Yoneda, K.; Fukuda, K. Role of a singlet diradical character in carbon nanomaterials: A novel hot spot for efficient non-linear optical materials. Nanoscale 2016, 8, 17998–18020. [Google Scholar] [CrossRef]
- Rudebusch, G.E.; Zafra, J.L.; Jorner, K.; Fukuda, K.; Marshall, J.L.; Arrechea-Marcos, I.; Espejo, G.L.; Ortiz, R.P.; Gómez-García, C.J.; Zakharov, L.N.; et al. Diindeno-fusion of an anthracene as a design strategy for stable organic biradicals. Nat. Chem. 2016, 8, 753–759. [Google Scholar] [CrossRef]
- Kubo, T. Syntheses and Properties of Open-Shell π-Conjugated Molecules. Bull. Chem. Soc. Jpn. 2021, 94, 2235–2244. [Google Scholar] [CrossRef]
- Raman, K.V.; Kamerbeek, A.M.; Mukherjee, A.; Atodiresei, N.; Sen, T.K.; Lazić, P.; Caciuc, V.; Michel, R.; Stalke, D.; Mandal, S.K.; et al. Interface-engineered templates for molecular spin memory devices. Nature 2013, 493, 509–513. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Fukui, H.; Fueno, T. Molecular-orbital (MO) theory for magnetically interacting organic-compounds-abinitio MO calculations of the effective exchange integrals for cyclophane-type carbene dimers. Chem. Lett. 1986, 15, 625–628. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Jensen, F.; Dorigo, A.; Houk, K.N. A spin correction procedure for unrestricted Hartree-Fock and Møller-Plesset wavefunctions for singlet diradicals and polyradicals. Chem. Phys. Lett. 1988, 149, 537–542. [Google Scholar] [CrossRef]
- Kitagawa, Y.; Saito, T.; Ito, M.; Shoji, M.; Koizumi, K.; Yamanaka, S.; Kawakami, T.; Okumura, M.; Yamaguchi, K. Approximately spin-projected geometry optimization method and its application to di-chromium systems. Chem. Phys. Lett. 2007, 442, 445–450. [Google Scholar] [CrossRef]
- Saito, T.; Thiel, W. Analytical gradients for density functional calculations with approximate spin projection. J. Phys. Chem. A 2012, 116, 10864–10869. [Google Scholar] [CrossRef] [PubMed]
- Yamanaka, S.; Takeda, R.; Shoji, M.; Kitagawa, Y.; Honda, H.; Yamaguchi, K. Quantum spin correction scheme for ab initio spin-unrestricted solutions: Multiple bonds case. Int. J. Quant. Chem. 2005, 105, 605–614. [Google Scholar] [CrossRef]
- Yamanaka, S.; Takeda, R.; Nakata, K.; Takada, T.; Shoji, M.; Kitagawa, Y.; Yamaguchi, K. Quantum spin correction scheme based on spin-correlation functional for Kohn–Sham spin density functional theory. J. Magn. Magn. Mater. 2007, 310, e492. [Google Scholar] [CrossRef]
- Shoji, M.; Koizumi, K.; Kitagawa, Y.; Kawakami, T.; Yamanaka, S.; Okumura, M.; Yamaguchi, K. A general algorithm for calculation of Heisenberg exchange integrals J in multispin systems. Chem. Phys. Lett. 2006, 432, 343–347. [Google Scholar] [CrossRef]
- Pokhilko, P.; Zgid, D. Broken-symmetry self-consistent GW approach: Degree of spin contamination and evaluation of effective exchange couplings in solid antiferromagnets. J. Chem. Phys. 2022, 157, 144101. [Google Scholar] [CrossRef]
- Wang, J.; Becke, A.D.; Smith, V.H. Evaluation of ⟨S2⟩ in restricted, unrestricted Hartree–Fock, and density functional based theories. J. Chem. Phys. 1995, 102, 3477–3480. [Google Scholar] [CrossRef]
- Saito, T.; Nishihara, S.; Yamanaka, S.; Kitagawa, Y.; Kawakami, T.; Yamada, S.; Isobe, H.; Okumura, M.; Yamaguchi, K. Symmetry and broken symmetry in molecular orbital description of unstable molecules IV: Comparison between single- and multi-reference computational results for antiaromtic molecules. Theor. Chem. Acc. 2011, 130, 749–763. [Google Scholar] [CrossRef]
- Cohen, A.J.; Tozer, D.J.; Handy, N.C. Evaluation of ⟨S2⟩ in density functional theory. J. Chem. Phys. 2007, 126, 214104. [Google Scholar] [CrossRef]
- Menon, A.S.; Radom, L. Consequences of spin contamination in unrestricted calculations on open-shell species: Effect of hartree−fock and møller−plesset contributions in hybrid and double-hybrid density functional theory approaches. J. Phys. Chem. A 2008, 112, 13225. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Kawakami, T.; Takano, Y.; Kitagawa, Y.; Yamashita, Y.; Fujita, H. Analytical and ab initio studies of effective exchange interactions, polyradical character, unpaired electron density, and information entropy in radical clusters (R)N: Allyl radical cluster (N = 2–10) and hydrogen radical cluster (N = 50). Int. J. Quantum Chem. 2002, 90, 370–385. [Google Scholar] [CrossRef]
- Paul, S.; Misra, A. Interpretation and Quantification of Magnetic Interaction through Spin Topology. J. Chem. Theory Comput. 2012, 8, 843–853. [Google Scholar] [CrossRef]
- Tada, K.; Koga, H.; Okumura, M.; Tanaka, S. Estimation of spin contamination error in dissociative adsorption of Au2 onto MgO(0 0 1) surface: First application of approximate spin projection (AP) method to plane wave basis. Chem. Phys. Lett. 2018, 701, 103–108. [Google Scholar] [CrossRef]
- Tada, K.; Tanaka, S.; Kawakami, T.; Kitagawa, Y.; Okumura, M.; Yamaguchi, K. Spin contamination errors on spin-polarized density functional theory/plane-wave calculations for crystals of one-dimensional materials. Appl. Phys. Express 2019, 12, 115506. [Google Scholar] [CrossRef]
- Tada, K.; Kitagawa, Y.; Kawakami, T.; Okumura, M.; Tanaka, S. Electron density-based estimation of diradical character: An easy scheme for DFT/plane-wave calculations. Chem. Lett. 2021, 50, 392–396. [Google Scholar] [CrossRef]
- Zhang, J.L.; Zhong, J.Q.; Lin, J.D.; Hu, W.P.; Wu, K.; Xu, G.Q.; Wee, A.T.S.; Chen, W. Towards single molecule switches. Chem. Soc. Rev. 2015, 44, 2998–3022. [Google Scholar] [CrossRef]
- Xiang, D.; Wang, X.; Jia, C.; Lee, T.; Guo, X. Molecular-Scale Electronics: From Concept to Function. Chem. Rev. 2016, 116, 4318–4440. [Google Scholar] [CrossRef]
- Kumar, K.S.; Ruben, M. Sublimable spin-crossover complexes: From spin-state switching to molecular devices. Angew. Chem. Int. Ed. 2021, 60, 7502–7521. [Google Scholar] [CrossRef]
- Martin, L.J.; Akhavan, B.; Bilek, M.M.M. Electric fields control the orientation of peptides irreversibly immobilized on radical-functionalized surfaces. Nat. Commun. 2018, 9, 357. [Google Scholar] [CrossRef]
- Yamashita, M. Next generation multifunctional nano-science of advanced metal complexes with quantum effect and nonlinearity. Bull. Chem. Soc. Jpn. 2021, 94, 209–264. [Google Scholar] [CrossRef]
- Kawai, S.; Silveira, O.J.; Kurki, L.; Yuan, Z.; Nishiuchi, T.; Kodama, T.; Sun, K.; Custance, O.; Lado, J.L.; Kubo, T.; et al. Local probe-induced structural isomerization in a one-dimensional molecular array. Nat. Commun. 2023, 14, 7741. [Google Scholar] [CrossRef]
- Baumann, S.; Paul, W.; Choi, T.; Lutz, C.P.; Ardavan, A.; Heinrich, A.J. Electron paramagnetic resonance of individual atoms on a surface. Science 2015, 350, 417–420. [Google Scholar] [CrossRef] [PubMed]
- Willke, P.; Bae, Y.; Yang, K.; Lado, J.L.; Ferrón, A.; Choi, T.; Ardavan, A.; Fernández-Rossier, J.; Heinrich, A.J.; Lutz, C.P. Hyperfine interaction of individual atoms on a surface. Science 2018, 362, 336–339. [Google Scholar] [CrossRef] [PubMed]
- Imada, H.; Imai-Imada, M.; Miwa, K.; Yamane, H.; Iwasa, T.; Tanaka, Y.; Toriumi, N.; Kimura, K.; Yokoshi, N.; Muranaka, A.; et al. Single-molecule laser nanospectroscopy with micro–electron volt energy resolution. Science 2021, 373, 95–98. [Google Scholar] [CrossRef] [PubMed]
- Seh, Z.W.; Kibsgaard, J.; Dickens, C.F.; Chorkendorff, I.; Nørskov, J.K.; Jaramillo, T.F. Combining theory and experiment in electrocatalysis: Insights into materials design. Science 2017, 355, 6321. [Google Scholar] [CrossRef]
- Urban, A.; Seo, D.-H.; Ceder, G. Computational understanding of Li-ion batteries. NPJ Comput. Mater. 2016, 2, 16002. [Google Scholar] [CrossRef]
- Szabo, A.; Ostlund, N.S. Modern Quantum Chemistry: Introduction to Advanced Electronic Structure Theory, 2nd ed.; Dover Publications: New York, NY, USA, 1996. [Google Scholar]
- Tada, K.; Maruyama, T.; Koga, H.; Okumura, M.; Tanaka, S. Extent of Spin Contamination Errors in DFT/Plane-wave Calculation of Surfaces: A Case of Au Atom Aggregation on a MgO Surface. Molecules 2019, 24, 505. [Google Scholar] [CrossRef]
- Fujimaru, K.; Tada, K.; Ozaki, H.; Okumura, M.; Tanaka, S. Variation in spin contamination and diradical character with distance between a singlet biradical molecule and surface. Suf. Interfaces 2022, 33, 102206. [Google Scholar] [CrossRef]
- Tada, K.; Ozaki, H.; Fujimaru, K.; Kitagawa, Y.; Kawakami, T.; Okumura, M. Diradical characters of s-indaceno [1, 2, 3-cd; 5, 6, 7-c’d’] diphenalene with and without interaction with MgO (001). e-J. Surf. Sci. Nanotech. 2022, 20, 59–67. [Google Scholar] [CrossRef]
- Tada, K.; Kawakami, T.; Hinuma, Y. Model calculations for prediction of diradical character of physisorbed molecule: P-Benzyne/MgO and p-Benzyne/SrO. Phys. Chem. Chem. Phys. 2023, 25, 29424–29436. [Google Scholar] [CrossRef]
- Sicolo, S.; Giordano, L.; Pacchioni, G. Adsorption of Late Transition Metal Atoms on MgO/Mo(100) and MgO/Ag(100) Ultrathin Films: A Comparative DFT Study. J. Phys. Chem. C 2009, 113, 16694–16701. [Google Scholar] [CrossRef]
- Giordano, L.; Baistrocchi, M.; Pacchioni, G. Bonding of Pd, Ag, and Au atoms on MgO(100) surfaces and MgO/Mo(100) ultra-thin films: A comparative DFT study. Phys. Rev. B 2005, 72, 115403. [Google Scholar] [CrossRef]
- Yulikov, M.; Sterrer, M.; Heyde, M.; Rust, H.-P.; Risse, T.; Freund, H.-J.; Pacchioni, G.; Scagnelli, A. Binding of single gold atoms on thin MgO(001) films. Phys. Rev. Lett. 2006, 96, 146804. [Google Scholar] [CrossRef] [PubMed]
- Yulikov, M.; Sterrer, M.; Risse, T.; Freund, H.-J. Gold atoms and clusters on MgO(100) films; an EPR and IRAS study. Surf. Sci. 2009, 603, 1622. [Google Scholar] [CrossRef]
- Yamaguchi, K. Self-Consistent Field: Theory and Applications; Carbo, R., Klobukowski, M., Eds.; Elsevier: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Perdew, J.P.; Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 1981, 23, 5048. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmuller, J. Efficient interactive schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmuller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Gellé, A.; Lepetit, M.-B. Fast calculation of the electrostatic potential in ionic crystals by direct summation method. J. Chem. Phys. 2008, 128, 244716. [Google Scholar] [CrossRef] [PubMed]
- Dittmer, A.; Izsák, R.; Neese, F.; Maganas, D. Accurate band gap predictions of semiconductors in the framework of the similarity transformed equation of motion coupled cluster theory. Inorg. Chem. 2019, 58, 9303. [Google Scholar] [CrossRef] [PubMed]
- Atanasov, M.; Andreici Eftimie, E.-L.; Avram, N.M.; Brik, M.G.; Neese, F. First-principles study of optical absorption energies, ligand field and spin-hamiltonian parameters of Cr3+ ions in emeralds. Inorg. Chem. 2022, 61, 178. [Google Scholar] [CrossRef] [PubMed]
- Tada, K.; Kitagawa, Y. Issues on DFT+U calculations of organic diradicals. Phys. Chem. Chem. Phys. 2023, 25, 32110–32122. [Google Scholar] [CrossRef]
- Tada, K.; Kawakami, T.; Kitagawa, Y.; Okumura, M.; Yamaguchi, K.; Tanaka, S. Comparison of Effective Exchange Integrals of H-H and H-He-H Chains vs. Single Molecules: A Theoretical Study. Chem. Lett. 2020, 49, 137–140. [Google Scholar] [CrossRef]
- Angeli, C.; Cimiraglia, R.; Evangelisti, S.; Leininger, T.; Malrieu, J.-P. Introduction of n-electron valence states for multireference perturbation theory. J. Chem. Phys. 2001, 114, 10252–10264. [Google Scholar] [CrossRef]
- Angeli, C.; Pastore, M.; Cimiraglia, R. New perspectives in multireference perturbation theory: The n-electron valence state approach. Theor. Chem. Account. 2007, 117, 743–754. [Google Scholar] [CrossRef]
- Neese, F. The ORCA program system. Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Neese, F. Software update: The ORCA program system, version 4.0. Comput. Mol. Sci. 2018, 8, e1327. [Google Scholar] [CrossRef]
- Igel-Mann, G.; Stoll, H.; Preuss, H. Pseudopotentials for main group elements (IIIa through VIIa). Mol. Phys. 1988, 65, 1321–1328. [Google Scholar] [CrossRef]
- Dolg, M.; Wedig, U.; Stoll, H.; Preuss, H. Energy-adjusted ab initio pseudopotentials for the first row transition elements. J. Chem. Phys. 1987, 86, 866–872. [Google Scholar] [CrossRef]
- Schwerdtfeger, P.; Dolg, M.; Schwarz, W.H.E.; Bowmaker, G.A.; Boyd, P.D.W. Relativistic effects in gold chemistry. I. Diatomic gold compounds. J. Chem. Phys. 1989, 91, 1762–1774. [Google Scholar] [CrossRef]
- Tada, K.; Hayashi, A.; Maruyama, T.; Koga, H.; Yamanaka, S.; Okumura, M.; Tanaka, S. Effect of surface interactions on spin contamination errors of homogeneous spin dimers, chains, and films: Model calculations of Au/MgO and Au/BaO systems. Mol. Phys. 2021, 119, e1791989. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Boguslawski, K.; Marti, K.H.; Legeza, Ö.; Reiher, M. Accurate ab Initio Spin Densities. J. Chem. Theory Comput. 2012, 8, 1970–1982. [Google Scholar] [CrossRef]
- VASP Online Manual. Available online: https://www.vasp.at/wiki/index.php/LORBIT (accessed on 30 October 2024).
- Henkelman, G.; Arnaldsson, A.; Jonsson, H. A fast and robust algorithm for Bader decomposition of charge density. Comput. Mater. Sci. 2006, 36, 354–360. [Google Scholar] [CrossRef]
- Sanville, E.; Kenny, S.D.; Smith, R.; Henkelman, G. Improved grid-based algorithm for Bader charge allocation. J. Comput. Chem. 2007, 28, 899–908. [Google Scholar] [CrossRef]
- Tang, W.; Sanville, E.; Henkelman, G. A grid-based Bader analysis algorithm without lattice bias. J. Phys. Condens. Matter 2009, 21, 084204. [Google Scholar] [CrossRef]
- Yu, M.; Trinkle, D.R. Accurate and efficient algorithm for Bader charge integration. J. Chem. Phys. 2011, 134, 064111. [Google Scholar] [CrossRef]
- VASP Online Manual. Available online: https://www.vasp.at/wiki/index.php/NELECT (accessed on 30 October 2024).
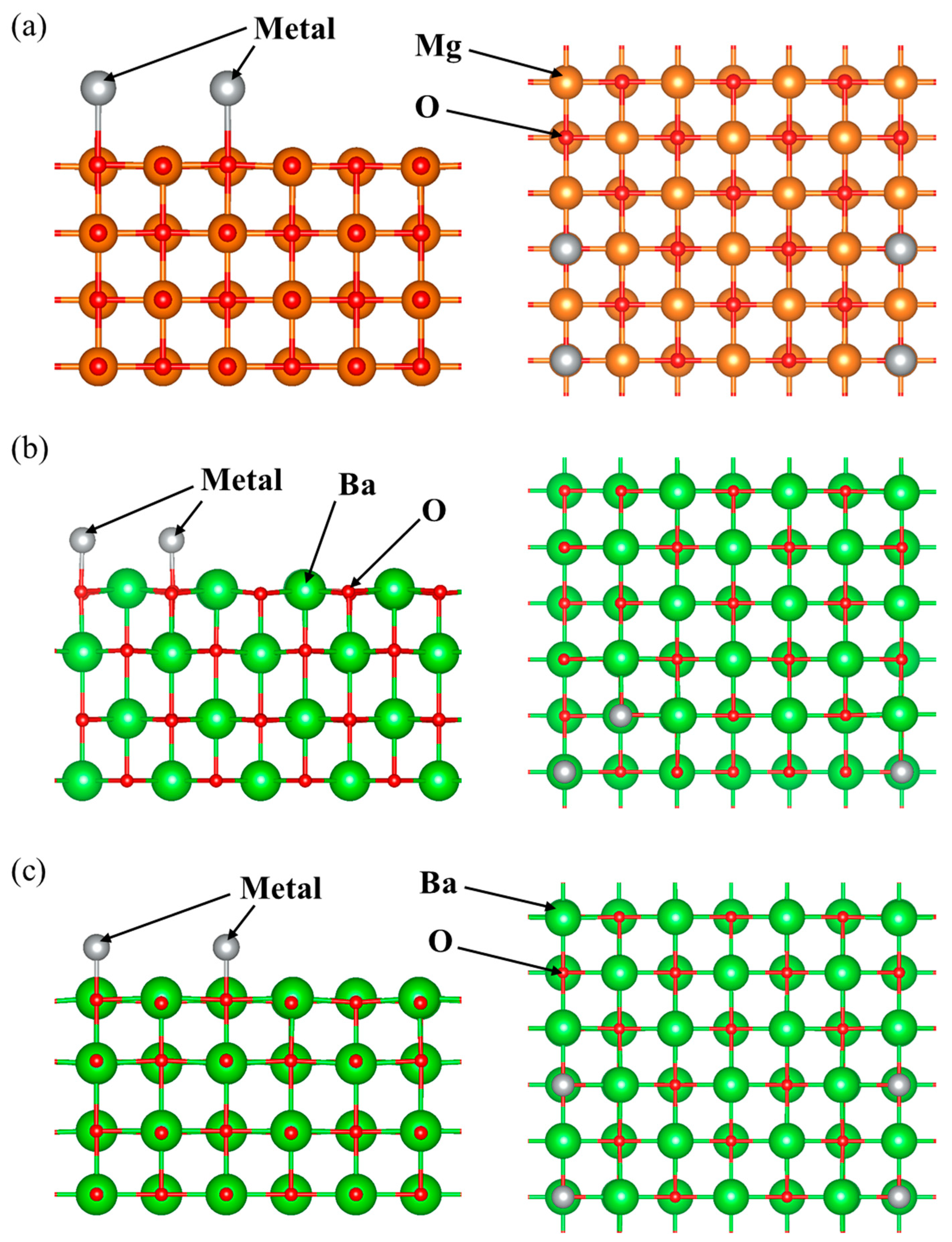

| Model A | Model B | Model C | |
|---|---|---|---|
| Surface | MgO (001) | BaO (001) | BaO (001) |
| M–M distance | 4.177 | 3.929 | 5.562 |
| Au–O distance | 2.301 | 2.209 | 2.205 |
| Ag–O distance | 2.479 | 2.257 | 2.234 |
| Cu–O distance | 1.997 | 1.883 | 1.881 |
| AP-DFT/Plane-Wave | NEVPT2 (2o, 2e) | |
|---|---|---|
| Model Agas-2Au | −0.31 | −0.12 |
| Model Bgas-2Au | −0.36 | −0.27 |
| Model Cgas-2Au | −0.02 | 0.00 |
| Model Agas-2Ag | −0.39 | −0.20 |
| Model Bgas-2Ag | −0.46 | −0.31 |
| Model Cgas-2Ag | −0.04 | −0.01 |
| Model Agas-2Cu | −0.29 | −0.16 |
| Model Bgas-2Cu | −0.40 | −0.25 |
| Model Cgas-2Cu | −0.02 | −0.01 |
| AP-DFT/Plane-Wave | CASSCF (2o, 2e) | CASSCF (12o, 22e) | |
|---|---|---|---|
| Model Agas-2Au | 0.0964 | 0.6126 | 0.6100 |
| Model Bgas-2Au | 0.0002 | 0.5127 | 0.5077 |
| Model Cgas-2Au | 0.7428 | 0.9106 | 0.9100 |
| Model Agas-2Ag | 0.0307 | 0.4771 | 0.4745 |
| Model Bgas-2Ag | 0.0000 | 0.3880 | 0.3861 |
| Model Cgas-2Ag | 0.6218 | 0.8337 | 0.8323 |
| Model Agas-2Cu | 0.2013 | 0.5173 | 0.5167 |
| Model Bgas-2Cu | 0.0906 | 0.4347 | 0.4338 |
| Model Cgas-2Cu | 0.7309 | 0.8415 | 0.8415 |
| [eV] | [eV] | [eV] | [eV] | [eV] | |
|---|---|---|---|---|---|
| Model A-2Au | −1.831 (0.045) | −1.628 (−0.058) | −0.050 (0.046) | −0.349 (0.104) | 0.145 (0.000) |
| Model B-2Au | −3.671 (0.050) | −3.606 (0.030) | 0.020 (0.051) | −0.434 (0.019) | 0.369 (0.000) |
| Model C-2Au | −3.559 (0.004) | −3.855 (−0.005) | 0.086 (0.004) | −0.018 (0.008) | 0.315 (0.000) |
| Model A-2Ag | −1.146 (0.073) | −0.769 (−0.021) | −0.317 (0.072) | −0.412 (0.094) | 0.035 (0.000) |
| Model B-2Ag | −2.294 (0.092) | −2.102 (0.092) | −0.248 (0.092) | −0.488 (0.000) | 0.296 (0.000) |
| Model C-2Ag | −1.992 (0.021) | −2.230 (0.001) | 0.040 (0.021) | −0.043 (0.020) | 0.281 (0.000) |
| Model A-2Cu | −1.968 (0.068) | −1.797 (−0.056) | −0.127 (0.069) | −0.326 (0.125) | 0.155 (0.000) |
| Model B-2Cu | −3.683 (0.080) | −3.664 (−0.056) | −0.081 (0.079) | −0.457 (0.135) | 0.439 (0.000) |
| Model C-2Cu | −3.480 (0.013) | −3.833 (0.002) | 0.074 (0.013) | −0.024 (0.011) | 0.378 (0.000) |
| Diatomic Adsorption | Mono Atom Adsorption | Difference * | |
|---|---|---|---|
| Model A-2Au | 11.254 | 11.290 | –0.036 |
| Model B-2Au | 11.352 | 11.383 | –0.031 |
| Model C-2Au | 11.358 | 11.373 | –0.015 |
| Model A-2Ag | 11.083 | 11.103 | –0.020 |
| Model B-2Ag | 11.175 | 11.211 | –0.030 |
| Model C-2Ag | 11.189 | 11.206 | –0.016 |
| Model A-2Cu | 11.091 | 11.105 | –0.013 |
| Model B-2Cu | 11.141 | 11.167 | –0.026 |
| Model C-2Cu | 11.174 | 11.189 | –0.015 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tada, K.; Masuda, K.; Kishi, R.; Kitagawa, Y. Systematic Investigation on Surface Diradicals Using Theoretical Models: 2M/MgO and 2M/BaO (M = Cu, Ag, and Au). Chemistry 2024, 6, 1572-1592. https://doi.org/10.3390/chemistry6060095
Tada K, Masuda K, Kishi R, Kitagawa Y. Systematic Investigation on Surface Diradicals Using Theoretical Models: 2M/MgO and 2M/BaO (M = Cu, Ag, and Au). Chemistry. 2024; 6(6):1572-1592. https://doi.org/10.3390/chemistry6060095
Chicago/Turabian StyleTada, Kohei, Koki Masuda, Ryohei Kishi, and Yasutaka Kitagawa. 2024. "Systematic Investigation on Surface Diradicals Using Theoretical Models: 2M/MgO and 2M/BaO (M = Cu, Ag, and Au)" Chemistry 6, no. 6: 1572-1592. https://doi.org/10.3390/chemistry6060095
APA StyleTada, K., Masuda, K., Kishi, R., & Kitagawa, Y. (2024). Systematic Investigation on Surface Diradicals Using Theoretical Models: 2M/MgO and 2M/BaO (M = Cu, Ag, and Au). Chemistry, 6(6), 1572-1592. https://doi.org/10.3390/chemistry6060095









