Next Article in Journal
8-(Pyridin-2-yl)quinolin-7-ol and Beyond: Theoretical Design of Tautomeric Molecular Switches with Pyridine as a Proton Crane Unit
Previous Article in Journal
Systematic Investigation on Surface Diradicals Using Theoretical Models: 2M/MgO and 2M/BaO (M = Cu, Ag, and Au)
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Chemistry
Volume 6
Issue 6
10.3390/chemistry6060096
chemistry-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

DFT Investigation of the Mechanism of Methoxycarbonylation of Styrene by Palladium Chloride

by
Shanti Gopal Patra
1,*,
Aritra Saha
1 and
Pratim Kumar Chattaraj
2,*
1
Department of Chemistry, National Institute of Technology Silchar, Silchar 788010, Assam, India
2
Department of Chemistry, Birla Institute of Technology, Mesra, Ranchi 835215, Jharkhand, India
*
Authors to whom correspondence should be addressed.
Chemistry 2024, 6(6), 1593-1607; https://doi.org/10.3390/chemistry6060096
Submission received: 17 October 2024 / Revised: 28 November 2024 / Accepted: 3 December 2024 / Published: 5 December 2024
(This article belongs to the Section Theoretical and Computational Chemistry)
Browse Figures
Versions Notes

Abstract

:
The alkoxycarbonylation of styrene by palladium chloride is studied employing the density functional theory (DFT). Initially, [PdCl3]– reacts with methanol to form the methoxy-bound intermediate, which undergoes β-hydride elimination to form the key intermediate [PdCl2H]–. Then, a 1,2-insertion reaction to styrene takes place to form linear and branched alkyl coordinated with the PdII. Then, CO coordination followed by a 1,1-insertion reaction leads to the formation of acyl intermediate. Next, the methanolysis leads to the formation of esters. Previous reports with other catalysts suggested the intermolecular/intramolecular transition state (TS) formation with a high activation barrier, and this step was the bottleneck. To the best of our knowledge, this is the first time we have considered a two-step mechanism for the alcoholysis of the ester formation mechanism. After coordination with the metal, the methanol undergoes oxidative addition to form the PdIV square pyramidal intermediate, followed by reductive elimination to form the ester with regeneration of the metal hydride active intermediate. Deeper insight into the nature of bonding at the TSs is obtained through energy decomposition with natural orbital for chemical valence (EDA-NOCV) and quantum theory of atoms in molecules (QTAIM).

Graphical Abstract

1. Introduction

Carbonylation reaction is the conversion of alkenes or alkynes to aldehydes, acids, esters, or lactones using carbon monoxide in a one-pot synthesis [1,2,3]. Otto Roelen, while working on the Fischer–Tropsch reaction, first reported the transition metal-catalyzed carbonylation reaction [1]. Transition metals, such as Fe, Co, Ru, Rh, Ir, etc., are utilized as catalysts for carbonylation reactions [4,5]. Along with academic development, many industrial processes are developed based on carbonylation reactions, where CO is considered the C1 feedstock [4]. One such example is the production of Monsanto acetic acid, which starts from methanol and carbon monoxide [5]. In the carbonylation reactions, the use of alkene/alkyne substrate in the presence of water, amine, and alcohol nucleophiles leads to the formation of carboxylic acid, amide, and ester, respectively [4,6]. Due to poor selectivity, the carbonylation of α-olefins leads to various products unless neighboring group participation is involved [7,8,9,10,11]. However, selectivity can be achieved by the use of different ligands [12,13,14,15,16,17,18,19], the use of other additives, and reaction conditions (temperature, CO pressure, etc.) [1,20,21,22,23].
In homogeneous catalysis involving β-hydride elimination, oxidative addition, reductive elimination, migratory insertion, and carbon–carbon bond formation, the Pd complexes are significant, as their reactivity can be tuned using various ancillary ligands [10,24,25]. One of the vital step-up reactions in organometallic chemistry is carbonylation, which can be achieved by Pd0 and PdII with region- and stereoselectivity when the complexes are decorated with suitable phosphine ligands [26,27,28,29,30,31]. Further, fine-tuning is also achieved by adding a variety of substituents to the phosphorous donor and altering the electronic and steric properties of the complexes.
Previous studies have shown that metal hydride intermediate [PdII-H] is a key intermediate for the overall transformation under acidic conditions [32,33]. Mehara et al. [34] summarized the catalytic cycle where, initially, the alkene undergoes a 1,2-insertion reaction with the [PdII-H] to form the palladium alkyl with two possibilities in the case of asymmetric alkene. Next, a 1,1-CO insertion reaction forms the acyl-palladium complexes, which have two possibilities. Finally, the alcoholysis leads to ester formation with the regeneration of the vital intermediate [PdII-H]. Various studies were performed in the past to investigate the mechanism, such as the [PdII-H] being detected through NMR [35,36,37,38]; the metal-acyl intermediate was also isolated and characterized by X-ray structures [37,39,40]. In addition, chromatography studies such as HPLC, GC-MS [37,39] and deuterium labeling [41] and theoretical studies also confirm the presence of different intermediates.
Another mechanism was proposed where the starting Pd0 catalyst is oxidized to PdII by an oxidant, which then reacts with alcohol to form the alkoxy intermediate, followed by a CO insertion reaction to form the alkoxycarbonyl-Pd intermediate [42,43]. Next, alkene undergoes a 1,2-insertion reaction followed by β-hydride elimination to form the unsaturated ester. Thus, the hydride intermediate releases proton or HCl to form the Pd0 starting compound via the reductive elimination step. In practice, the formation of the unsaturated esters is not so favorable, especially in the acidic medium where the reductive elimination step is disfavored [34]. Further, oxidizing agents (Cu(OAc)2, CuCl2) in combination with solvents (acetonitrile, DMF, DMSO) play an essential role in determining product selectivity [44].
Several modeling studies of the Pd-catalyzed alkoxycarbonylation of alkenes and alkynes were summarized in the perspective article by Ahmad et al. [45]. With bidentate diphosphine ligands, the hydride pathway is more favorable [36,39,42,46,47]. The final alcoholysis step was the most challenging, finding the most favorable path with the lowest activation energy barrier. The intramolecular alcoholysis was shown to be unsurmountable, while the intermolecular pathway could achieve a lower activation barrier [48]. Here, we have considered the catalytic methoxycarbonylation of styrene by [PdCl3]− in the presence of CO to give linear and branched esters. We have considered the hydride mechanism for the overall catalysis. The most significant change to the mechanism is the final alcoholysis step. The step consists of two sub-steps, where alcohol first undergoes coordination with the metal to form an alcohol-bound complex, which then undergoes oxidative addition to create a PdIV complex with the coordination of hydride, methoxide, and acyl. Next, it undergoes reductive elimination, where methoxide and acyl form a sigma bond to form the ester, and PdIV reduces to PdII. The free energies of different steps for the formation of branched and linear esters are compared side by side. The energy decomposition analysis with natural orbital for chemical valence (EDA-NOCV) analysis and the quantum theory of atoms in molecules (QTAIM) is carried out at the TSs to gain deeper insight into the mechanism.

2. Computational Details

The geometry optimization and frequency calculations for the intermediate and transition state structures are carried out employing the Gaussian 16 Version C1.0 [49]. The absence of any imaginary frequency in the intermediate case indicates the presence of true minima, while the presence of strong imaginary frequency implies the transition state (TS) structure. It should be noted that only one imaginary frequency was obtained in all the TSs, and the corresponding values are provided in Table S1. Intrinsic reaction coordinate (IRC) calculations for the forward and reverse direction correspond to the corresponding product and reactant, respectively. For all types of calculations, the PBE0 [50,51] functional (using the keyword PBE1PBE) was used unless otherwise specified. Optimization and frequency calculations are performed using the LanL2DZ [52] basic set for the Pd atom and 6-31+G(d,p) Pople’s basic set for the H, C, O, and Cl atoms. This combined basis is denoted as bs1. At the optimized geometry, single-point calculations are performed employing the SDD [53,54] basis set for the Pd atom and 6-311+G(d,p) Pople’s basis set for the H, C, O, and Cl atoms. This combined basis is denoted as bs2. In our recent articles on Cu [55,56] and Pd [57] complexes, reasonable results were obtained with the PBE functional and above-mentioned basis sets, and hence this level of theory is used in the current study. The solvation effect in methanol solvent was taken into consideration using the solvation molecular dynamics model (SMD) [58]. Thus, the final level of the theory of thermochemistry becomes SMD/PBE0/bs2//SMD/PBE0/bs1. To incorporate the zero-point corrections to the free energies at the SMD/PBE0/bs2, the corresponding zero-point correction is taken from the PBE0/bs1 level of theory. In the solvation process, molecules are transformed from the gas phase (1 atm) to the condensed phase (1 M), and hence, a concentration correction of ΔG0→* = 1.9 kcal mol−1 was applied to the free energy values [59,60,61]. Quantum theory of atoms in molecules (QTAIM) and electron localization function (ELF) analyses were performed using the Multiwfn Version 3.7 software [62]. In our previous studies with QTAIM, reasonable results were obtained using triple zeta bs2 Pople basis for main group and LanL2DZ/SDD basis for metal, hence the same basis set with PBE0 functional has been used in the current study [56,57,63,64]. Energy decomposition analysis (EDA) was performed at the B3LYP-D3(BJ)/def2-TZVP level of theory on the optimized geometries using the sobEDA [65] method implemented in the Multiwfn program [62]. Grimme’s dispersion correction (GD3) [66] with Becke–Johnson parameters [67] was incorporated in the EDA calculations. Extended transition state natural orbital for chemical valence (ETS-NOCV) was performed using the Multiwfn program. Good results were obtained with Ahlrich’s triple zeta basis in our earlier report [68,69,70], and hence we have utilized the Ahlrich’s triple zeta basis def2-TZVP in the EDA of the present study.

3. Results and Discussions

The general mechanistic path of the formation of ester starting from [PdCl3]− (int1), CO, styrene, and methanol proceeds through the following steps. First, methanol reacts with [PdCl3]− to form [PdCl2(OCH3)]− (int2) with the release of HCl. This step is found to be endergonic with ΔG = 14.1 kcal mol−1. Next, the hydrogen atom attached to the methyl group undergoes β-hydride elimination through the transition state TS1 (Figure 1). This forms the metal hydride intermediate [PdCl2H]− and formaldehyde. The free energy of activation is calculated to be −1.2 kcal mol−1, which is significantly less activation energy, implying the reaction’s feasibility [6]. At the TS1, the bond lengths are Pd-O—2.121, Pd-H—1.542, and C-H—1.957 Å. Here, the C-H bond is cleaved, the Pd-H bond is formed, and the C-O bond transforms from single to double. The hydride intermediate [PdCl2H]− formed is the active catalyst in the catalytic cycle. This cycle has the following steps: (i) Styrene attacks the int3 to form an alkyl-bound Pd complex. Now, in this step, the metal-bound hydride undergoes insertion into the alkene double bond in two possible ways (Scheme 1) ((a) the hydride attacks the phenyl substituted part of the alkene (cycle 1) through the formation of transition state TS2, or (b) it can attack the unsubstituted part of the alkene (cycle 2) through the formation of transition state TS2a). Here, the alkyl-bound intermediates int4 or int4a are formed. Let us first elaborate on the mechanism considering cycle 1. (ii) The CO reacts with the alkyl-bound intermediate int4 via the coordination of the CO ligand to the Pd metal to form the intermediate int5. (iii) Next, the CO insertion reaction takes place to form the intermediate int6 via the transition state formation TS3. (iv) The methanol undergoes coordination to the free site of int6 to form the methanol-bound intermediate int7. (v) The methanol-bound intermediate undergoes oxidative addition via TS4 to form the methoxide and hydride-bound PdIV complex (int8). (vi) Finally, the intermediate undergoes reductive elimination via TS5 to form the methyl ester compound and the active catalyst int3. Cycle 2 is similar to cycle 1, but the cycle starts with hydride insertion to the less substituted part of the styrene to form int4a. Thereafter, the names of the intermediates and the transition states are the same, with the addition of “a” to the names of cycle 1.
We have calculated the geometry optimization frequencies of the intermediates and transition state structures for both cycles (Scheme 1). The intermediate and TS structures of cycle 1 are shown in Figure 2 and Figure 3, respectively. For cycle 2, the respective structures of the intermediates and TSs are given in Figures S1 and S2 of the Supplementary Information File.
The free energy profile diagram of the formation of different intermediates and TSs is shown in Figure 4. In cycle 1 the hydride of int3 attacks at the phenyl-substituted part of the styrene to give the phenyl ethyl-coordinated intermediate int4. The reaction proceeds through the formation of a TS2 intermediate with an activation-free energy barrier of 2.4 kcal mol−1. The activation barrier is comparable to that in the recent report of similar reactions starting from propene using substituted phosphine-coordinated Pd complexes [16]. In cycle 2, the reaction is similar, but hydride attacks at the less-substituted part of styrene to form intermediate int4a. The reaction proceeds with the formation of TS2a with an activation energy barrier of only 0.2 kcal mol−1. Thus, the branched alkyl formation is more favorable for the hydride insertion step. In the TS2/TS2a, the bond lengths are Pd-C—2.143 (2.231), Pd-H—1.559 (1.553), C-H (1.704)—1.684 and C-C—1.421 (1.417) Å. The bond lengths are very much comparable. In the next step in cycle 1, CO gets coordinated to the vacant site to form int5. The CO coordination is found to be exergonic with ΔG = −14.3 kcal mol−1. The same reaction in cycle 2 proceeds with ΔG = −14.5 kcal mol−1 to form intermediate int5a. Then, in cycle 1, the PhCH2CH2 group undergoes an insertion reaction to the CO to form the intermediate int6. In the transition state, TS3, the PhCH2CH2 started forming a bond with the carbon atom of CO with an activation-free energy barrier of 11.5 kcal mol−1. In the case of cycle 2, in a similar reaction, the bond is formed between the carbon atom of CO and the carbon atom of the PhCH3CH group. The reaction proceeds through the formation of TS3a with an activation barrier of 11.8 kcal mol−1. It is important to note that not much difference in the activation barrier is observed in the CO insertion step. These activation barriers also correspond well with the previous report [16]. At the TS3/TS3a, the bond lengths are Pd-C—2.253 (2.321), C-C—1.938 (1.951) and C-O—1.171 (1.167) Å. The Pd-C bond length in TS3 is shorter than that of TS3a. This is because of the presence of methyl group in Ph(CH3)CH in TS3a, which increases the steric hindrance and eventually increases the barrier of CO insertion reaction of the C-C bond. However, the C-O bond length of carbonyl is shorter in TS3a, as the attack of alkyl is less close than in TS3.
Next, methanol is coordinated to the vacant site of the three coordinated intermediates int6 to form the four coordinated intermediates int7 and int7a for cycles 1 and 2, respectively. Next, methanol undergoes oxidative addition to form the PdIV intermediates int8/int8a, respectively. The reaction proceeds through the formation of transition states TS4/TS4a with an activation-free energy barrier of 40.8 and 45.7 kcal mol−1, respectively. An approximately 5 kcal mol−1 higher activation barrier for the branched acyl group suggests that linear ester formation is more favorable. At the TS4/TS4a, the bond lengths are Pd-O—2.071 (2.074), Pd-H—1.508 (1.513), O-H—1.716 (1.688) and C-O—1.201 (1.201) Å. This requires the highest activation barrier and is the rate-determining step. Next, int8/int8a, the OCH3 group, and the PhCH2CH2CO/Ph(CH3)CHCO group undergo coupling via reductive elimination to form the intermediates int9/int9a. The reactions proceed via TS5/TS5a with an activation-free energy barrier of 2.5/2.3 kcal mol−1. The difference is minimal, and the shallow activation barrier suggests the feasibility of the step. However, considering the free energy values, the linear ester is stable at 18 kcal mol−1 compared to the breached one. At TS5/TS5a, the bond lengths are Pd-O—2.139 (2.061), Pd-C—2.214 (2.041), C-O—2.006 (2.010) C-O, 1.191 (1.191) Å. The decreased C-O bond length between methoxy O and acylium C implies more substantial bond formation and feasibility. This is also supported by the increased Pd-O and Pd-C bond lengths in TS5.
The enthalpy profile of the reaction is also shown in Figure 4. The corresponding enthalpy changes in TS2 and S2a are −10.2, and −12.2 kcal/mol, respectively. For all the TSs the free energy, enthalpy and entropy change values are given in Table S2. It is found that at TS2/TS2a, the entropy term (TΔS‡) is significantly negative. In all other TSs the enthalpy changes are comparable to that of free energy change, as the corresponding entropy change is small (see Table S2).
At the methanolysis step, Walther et al. reported an activation barrier of ∼37.5 kcal mol−1. Ref. [71] carried out the methoxycarbonylation of cis-3-hexene using PdII catalysts coordinated by 1,2-bis((dimethylphosphaneyl)methyl)benzene (DMBPX) ligand at the B3LYP/TZVP/LANL2DZ//B3LYP/6-31G*/LANL2DZ level of theory. For the intramolecular methanolysis step in methoxycarbonylation of methyl 4-heptenoate with the Pd–DTBPX (where DTBPX = 1,2-bis(di-tert-butylphosphino-methyl)benzene), the overall barrier of 29.1 kcal mol−1 was reported by Roesle et al. [72] at the B3LYP/6-31G*/LANL2DZ level of theory. For the Pd–DTBPX-catalyzed methoxycarbonylation of ethane, the overall barrier was ∼42.4 kcal mol−1 at the B3PW91-D3/TZVP/LANL2DZ/SMD level of theory associated with the methanolysis step [73]. However, using 1,1′-bis(tert-butyl(pyridin-2-yl)phosphanyl)ferrocene ligand in the same study led to an activation barrier of ∼30.2 kcal mol−1. Thus, the ligand framework is crucial in decreasing the activation barrier. Jameel et al. [73] used 10-undecenoate and reported an overall barrier of ∼40.0 kcal mol−1 applying the energy span model. So, we can see that without having any better chelating ligand, we derived the barrier height of 40.9 and 45.7 kcal mol−1 for the oxidative addition of methanol. Thus, it may be speculated that better bidentate ligands may decrease the activation barrier, which is the subject of further study.
In this study, we have reported the mechanism of forming linear and branched esters starting from styrene, CO, and methanol, employing palladium chloride as a catalyst. The formation of linear esters is energetically more favorable than that of branched ones. A new mechanism is presented in the alcoholysis step with the oxidative addition of alcohol. Here, in the first step, the addition of styrene is considered, followed by the addition of CO and methanol. However, another possibility is the first formation of Pd(0)-Cl starting from [PdCl2H]– with the reductive elimination of HCl [34]. It is followed by the oxidative addition of methanol to form an alkoxy and hydride-bound intermediate. Then, a 1,1 insertion reaction of CO was used to create the acyl-bound Pd(II) intermediate. Finally, the 1,2-insertion reaction of styrene in two possible ways can also lead to the same ester formation. However, we plan to perform a comparative study of this mechanism in our future work.
Further, it is essential to note that the insertion reactions occur via a nucleophile’s insertion into the electrophilic center. For example, the hydride nucleophile undergoes 1,2 insertions into the double bond of the styrene. In the CO insertion reaction, linear and branched alkyls undergo 1,1 insertions to CO. On the other hand, ideally, the radical mechanism should be favored in oxidative addition and reductive elimination. All these steps can be better understood when calculating the local conceptual density functional theory-based descriptors such as the Fukui function, philicity, multiphilic descriptors, etc. [69]. The Fukui functions of the three types, such as the Fukui function for nucleophilic attack (f+), electrophilic attack (f–), and radical attack (f0), can predict the mechanism of a particular step. Similar descriptors with philicity, such as for nucleophilic attack (ω+), electrophilic attack (ω–), and radical attack (ω0), and multiphilic descriptors (ωk = ωk+ − ωk–) can also be used for such purposes. However, we plan to discuss this CDFT-based analysis in our future study.

3.1. Energy Decomposition Analysis (EDA) and Natural Orbital for Chemical Valence (NOCV) Analysis

Next, the energy decomposition analysis is carried out on the transition state structure of the TSs. The fragments considered for the TSs are given in Table 1. At the transition state structures, the energy decomposition analysis considers the two fragments (the details of the fragmentation scheme at different TSs are given in Table 1). The total interaction energy (ΔEtot) is dissected into electrostatic (ΔEels), exchange (ΔEx), repulsion (ΔErep), orbital (ΔEorb), DFT correlation (ΔEDFTc), and dispersion correction (ΔEdc). The values of total interaction energy and contributions from different components are given in Table 2.
In TS1, considering the [PdCl2H]− and HCHO fragments, the total interaction energy is calculated to be ∆Etot = −32.1 kcal mol−1. At this stage, the hydrogen atom transfers from the methyl group to the Pd center. The maximum contribution comes from the orbital part with ∆Eorb = −96.9 (19.1%) kcal mol−1. Other major contributing factors are ∆Eels and ∆Eex, with % contributions of 15.94 and 14.66, respectively. Further, the NOCV analysis shows that the most significant contributions come from the first two pairs (Table S3). The NOCV pair densities are shown in Tables S4 and S5. The % contributions of pairs 1 and 2 are 63.5 and 22.8, respectively. In both the orbitals, the transfer of electrons from the hydride to the metal can be seen. In TS3 and TS3a, total interaction energies are −134.10 and −114.89 kcal mol−1. In this step, the insertion of the R group (PhCH2CH2 or Ph(CH3)CH) into the CO occurs. Here, the activation energies are comparable. In this step, the maximum contribution comes from the orbital part with a percentage of ~22, as here, the R− group forms a bond with the CO moiety. A significant number of contributions also come from the electrostatic, with percentage contributions of 19.4 and 18.4, respectively. Notably, a covalent bond is formed between the R and CO moieties; hence, the orbital part is higher. At the same time, here, R is the nucleophilic type while the CO is the nucleophilic type; therefore, the interactions are of electrostatic type. Thus, the electrostatic contribution is also comparable to the orbital part. In the NOCV analysis, the contributions from pairs 1 and 2 are 74.8 and 9.7%, respectively, in TS3. Similar contribution terms can also be seen in TS3a. The first NOCV pair represents the formation of a covalent σ bond between the carbon atoms of PhCH2CH2/Ph(CH3)CH and CO, and the second one is the transfer of electrons from the formed σ bond to the metal center.
In TS4 and TS4a, the total interaction energies are −109.5 and −109.5 kcal mol−1. The maximum contributing factors here are orbital and electrostatic, with percentage contributions of ~22 and ~21 for both the TSs. It is important to note that methanol’s oxidative addition occurs at this stage. Here, PdII oxidizes to PdIV, and at the same time, 2e is transferred to methanol to form methoxide and hydride. Thus, two bonds are formed here between Pd and CH3O− and H–. Also, significant electrostatic interactions operate between positively charged PdIV and negatively charged CH3O− and H–. Although the total interaction energies are similar, the activation barrier to form TS4a is almost ~5 kcal mol−1, more than that of TS4. This is because of the steric factors that arise with the Ph(CH3)CH group in TS4a, but not the PhCH2CH2 group in TS4.

3.2. Global Electron Density Transfer (GEDT) Analysis

Global electron density transfer (GEDT) is a theoretical concept within the framework of Molecular Electron Density Theory (MEDT) [74,75]. It quantifies the net transfer of electron density between molecular fragments during a chemical reaction, particularly at the transition state (TS) structure. GEDT plays a crucial role in understanding the reactivity and mechanisms of polar organic reactions. A higher GEDT value at the TS generally corresponds to a lower activation energy, leading to a faster reaction rate. This is because the electronic stabilization of the electrophilic framework due to electron density gain outweighs the destabilization of the nucleophilic framework. In our system it can be seen (Table S2) that TS1, TS2/TS2a and TS5/TS5a have significantly low ΔG‡ within 2.5 kcal/mol, and in these TSs the GEDT values are higher, within the range of 0.812e to 1.18e. In TS3/TS3a, the ΔG‡ is ~12 kcal/mol, and the corresponding GEDT values are 0.622e and 0.520e, respectively. Only one discrepancy is observed in TS4/TS4a that may be due to the choice of fragmentation scheme. Hence the correspondence of ΔG‡ with GEDT is justified. In all the TSs, it is found that the total charge in fragment 1 is more negative compared to fragment 2. Thus, an electron density flux [74] takes place from fragment 2 to fragment 1.

3.3. Quantum Theory of Atom in Molecule (QTAIM) Analysis

The nature of the chemical bond and some quantitative aspects regarding chemical bonds is obtained through the application of quantum theory of atoms in molecules (QTAIM) [63,64,76]. The theory provides insight into a molecule’s topological distribution of electron density. A point exists between two atoms where the value of electron density is at the maximum, called the bond critical point (BCP). Some other critical points are the ring critical point (RCP) and cage critical point (CCP). From the values of different parameters such as electron density (ρ(r)), Laplacian of electron density (∇2ρ(r)), kinetic energy density (G(r)), potential energy density (V(r)), total energy density (H(r)), electron localization function (ELF), and the second eigenvalue of the Hessian matrix (λ2), the nature of chemical bonding can be understood [77,78,79].
A high value of ρ(r) with the negative sign of ∇2ρ(r) implies a strong covalent bond, while a low value of ρ(r) with the positive sign of ∇2ρ(r) implies weak interactions [77,80]. To delve deeper into the nature of bonding, the Laplacian of the electron density (∇2ρ(r)) is analyzed. This Laplacian is decomposed along the three principal axes, with λi representing the eigenvalues of the electron density Hessian matrix. The sum of these eigenvalues equals ∇2ρ(r) (Equation (1)):
∇2ρ = λ1 + λ2 + λ3 (λ1 ≤ λ2 ≤ λ3)
When two eigenvalues are negative and one is positive (λ1 < 0, λ2 < 0, λ3 > 0), this typically indicates the presence of bonded atomic pairs. A positive Laplacian suggests weaker non-covalent interactions. Negative values of λ2, particularly when accompanied by a negative Laplacian, often signify bonding interactions. Hydrogen bonding in water is a classic example. The sign of the Laplacian determines the nature of the interaction: negative denotes attraction, while positive denotes repulsion. It is important to note that the absence of a bond critical point (BCP) does not necessarily mean the absence of weak interactions. From the values and signs of different energy terms at the BCPs, the bonding is understood as covalent bonds, typically characterized by high G(r), negative V(r), V(r)/G(r) ≈ −1; ionic bonds, often associated with lower G(r), negative V(r), V(r)/G(r) ≈ −2, and weak interactions, typically characterized by lower G(r), positive V(r), V(r)/G(r) values closer to 0, and lower ρ at BCPs compared to covalent bonds [77,80].
Values of all these parameters at the TS structures of the forming and breaking bonds are summarized in Table 3. The molecular structures showing the BCP and bond paths are shown in Figures S3–S5. At TS1, the C-H bond is cleaved while the Pd-H bond is formed. Here, the values of ρ(r) are low while the ∇2ρ(r) is positive, implying weak interactions. However, the values of G(r) are positive, V(r) is positive, and −1 < V(r)/G(r) < 0, and hence it is in between covalent and weak interactions.
On the other hand, a negative value of λ2 suggests covalent characteristics. The Pd-H bond is cleaved at the TS2/TS2a, and the C-H bond is formed. Here, the trend in the values is similar, and clearly, the bonding property is between covalent and weak interaction types, i.e., a weak covalent bond. It is important to note that here, the C-C bond transforms from double to single, and is purely covalent. Thus, here, it is seen that ∇2ρ(r) is negative. In TS3/TS3a, the C-C bond is formed between CO and alkyl, and a clear indication of its covalent nature can be seen as ∇2ρ(r) is negative with a high value of ρ(r). In addition, a weak C-H∙∙∙Cl-type interaction is also observed where the C-H comes from the phenyl ring. In the TS4/TS4a, i.e., the oxidative addition step, weak interactions of the type C-H∙∙∙Cl and C-H∙∙∙O can be seen where the C-H comes from both the phenyl ring and methyl group. The Pd-H and Pd-O bonds are clearly covalent types, and their values for different parameters are not listed in Table 3. At the TS5/TS5a, the O-C bond is formed between methoxide and acyl moiety through reductive elimination. Here, the nature of the O-C bond is weakly covalent. Along with some weak interactions of the type C-H∙∙∙O (C-H from phenyl), weak H∙∙H-type interactions are also observed.

4. Conclusions

Palladium catalysts are widely utilized for the carbonylation reactions. Ester formation starts from alkene/alkyne, CO, and alcohol, and involves methoxycarbonylation. The mechanism consists of the formation of a metal hydride intermediate or alkoxy carbonyl key intermediate. An earlier report suggests the feasibility of the metal hydride intermediate. Previous studies focused on using PdII catalysts with bidentate diphosphine, NHC-type ligands. The process’s final step involves forming an intermolecular transition step at the alcoholysis step, and ultimately dictates the mechanism, as it involves a high activation energy barrier. Here is the simple starting catalyst [PdCl3]– formed in situ from PdCl2 in the presence of HCl. The alkoxy carbonylation of styrene with methanol is considered. The formations of linear ester and branched ester are taken into consideration.
Hence, two cycles are compared side by side in terms of energy. It is shown that the formation of the linear ester is energetically more favorable at the methanolysis step. The novelty of this work relates to the consideration of the alcoholysis step with an entirely new concept. It is shown through density functional theory (DFT) calculations that the alcohol coordinates to the PdII center and then undergoes oxidative addition to form hydride, methoxide, and an acyl-coordinated five-membered square pyramidal PdIV intermediate. Next, it undergoes reductive elimination to form the PdII metal hydride key intermediate and ester. The activation energies for the oxidative addition step are high, while the reductive elimination is very low. Thus, this study introduces another possibility to the alcoholysis step in the alkoxycarbonylation mechanism. The area remains open for research comparing the activation barrier when the Pd catalyst is bonded to other bidentate ancillary ligands based on diphosphine and NHC. Deeper insight into the nature of bonding of the TS structures is gained through the energy decomposition analysis with natural orbital for chemical valence (EDA-NOCV) and quantum theory of atoms in molecules (QTAIM) analysis.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/chemistry6060096/s1, Table S1: The bond lengths of various forming and breaking bonds at the transition state structures as obtained at the PBE0/bs1 level of theory, Table S2: The total charge of fragments (for fragmentation scheme see Table 1 of the main manuscript) in each TS and GEDT values in units of electrons. The Hirschfeld charges are considered in electron unit at the B3LYP/def2-TZVP//PBE0/bs1 level of theory, Table S3: NOCV Analysis at the transition state structures TS1-TS5 and TS2a-TS5a. The fragmentation scheme is given in Table 1 of the main manuscript. Values in the parenthesis represents the % orbital contribution to the total interaction energy. The calculations are performed at the B3LYP-D3(BJ)/6-311+G(d,p) level of theory. The energy values are given in kcal/mol unit, Table S4: The first two most contributing NOCV pairs of the extended transition state are natural orbital for chemical valence analysis at an isosurface value of 0.005 a.u. The green and blue isosurfaces represent the accumulation and depletion of electron density. The calculations are performed at the B3LYP-D3(BJ)/def2-TZVP//PBE0/bs1 level of theory, Table S5: The most contributing first two NOCV pairs of the extended transition state natural orbital for chemical valence analysis at an isosurface value of 0.005 a.u. The green and blue isosurfaces represents the accumulation and depletion of electron density. The calculations are performed at the B3LYP-D3(BJ)/6-311+G(d,p) level of theory, Figure S1: The intermediate structure of int3a-int8a in cycle 2. The geometry optimization is carried out at the B3LYP/bs1 level of theory. Colour code: H, white; C, grey; O, red; Cl, green; Pd, cyan, Figure S2: The transition state structure of TS2a-TS5a in cycle 2. The geometry optimization is carried out at the B3LYP/bs1 level of theory. Colour code: H, white; C, grey; O, red; Cl, green; Pd, cyan. The bond length values are given in Å unit, Figure S3: The structure of TS1 showing the bond critical point (BCP) as obtained from the QTAIM analysis, Figure S4: The structure of TS2-TS5 showing the bond critical point (BCP) as obtained from the QTAIM analysis, Figure S5: The structure of TS2a-TS5a showing the bond critical point (BCP) as obtained from the QTAIM analysis.

Author Contributions

Conceptualization, S.G.P.; methodology, S.G.P.; software, S.G.P.; validation, S.G.P. and P.K.C.; formal analysis, A.S.; investigation, S.G.P. and A.S.; resources, S.G.P. and P.K.C.; data curation, A.S.; writing—original draft preparation, S.G.P.; writing—review and editing, S.G.P. and P.K.C.; visualization, S.G.P. and A.S.; supervision, S.G.P. and P.K.C.; project administration, S.G.P. and P.K.C.; funding acquisition, P.K.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by J. C. Bose National Fellowship grant number SR/S2/JCB-09/2009.

Data Availability Statement

Data is contained within the article or Supplementary Material.

Acknowledgments

PKC would like to thank DST, New Delhi, for the J. C. Bose National Fellowship. SGP thanks the Department of Chemistry, NIT Silchar. We acknowledge the National Supercomputing Mission (NSM) for providing computing resources of “PARAM Porul” at NIT Trichy, which is implemented by C-DAC and supported by the Ministry of Electronics and Information Technology and Department of Science and Technology (DST), Government of India.

Conflicts of Interest

The authors declare that they have no conflicts of interest regarding the publication of this article, financial and/or otherwise.

References

  1. Peng, J.-B.; Geng, H.-Q.; Wu, X.-F. The Chemistry of CO: Carbonylation. Chem 2019, 5, 526–552. [Google Scholar] [CrossRef]
  2. Jurado, L.; Posada-Pérez, S.; Axet, M.R. Carbonylation Reactions Using Single-Atom Catalysts. ChemCatChem 2024, e202400543. [Google Scholar] [CrossRef]
  3. Ma, K.; Martin, B.S.; Yin, X.; Dai, M. Natural product syntheses via carbonylative cyclizations. Nat. Prod. Rep. 2019, 36, 174–219. [Google Scholar] [CrossRef] [PubMed]
  4. Wu, X.-F.; Fang, X.; Wu, L.; Jackstell, R.; Neumann, H.; Beller, M. Transition-Metal-Catalyzed Carbonylation Reactions of Olefins and Alkynes: A Personal Account. Acc. Chem. Res. 2014, 47, 1041–1053. [Google Scholar] [CrossRef] [PubMed]
  5. Beller, M.; Wu, X.-F. Transition Metal Catalyzed Carbonylation Reactions; Springer: Berlin/Heidelberg, Germany, 2013; ISBN 978-3-642-39015-9. [Google Scholar]
  6. Wei, W.-M.; Dong, F.-Q.; Zheng, R.-H.; Liu, Y.-Y.; Zhao, T.-T.; Fang, W.-J.; Qin, Y.-D. Theoretical study of the mechanism of palladium-catalyzed hydroaminocarbonylation of styrene with ammonium chloride. Comput. Theor. Chem. 2020, 1191, 113040. [Google Scholar] [CrossRef]
  7. Cernak, T.A.; Lambert, T.H. Multicatalytic Synthesis of α-Pyrrolidinyl Ketones via a Tandem Palladium(II)/Indium(III)-Catalyzed Aminochlorocarbonylation/Friedel−Crafts Acylation Reaction. J. Am. Chem. Soc. 2009, 131, 3124–3125. [Google Scholar] [CrossRef]
  8. Malkov, A.V.; Barłóg, M.; Miller-Potucká, L.; Kabeshov, M.A.; Farrugia, L.J.; Kočovský, P. Stereoselective Palladium-Catalyzed Functionalization of Homoallylic Alcohols: A Convenient Synthesis of Di- and Trisubstituted Isoxazolidines and β-Amino-δ-Hydroxy Esters. Chem.–A Eur. J. 2012, 18, 6873–6884. [Google Scholar] [CrossRef]
  9. Malkov, A.V.; Lee, D.S.; Barłóg, M.; Elsegood, M.R.J.; Kočovský, P. Palladium-Catalyzed Stereoselective Intramolecular Oxidative Amidation of Alkenes in the Synthesis of 1,3- and 1,4-Amino Alcohols and 1,3-Diamines. Chem.–A Eur. J. 2014, 20, 4901–4905. [Google Scholar] [CrossRef]
  10. Wu, X.-F.; Neumann, H.; Beller, M. Synthesis of Heterocycles via Palladium-Catalyzed Carbonylations. Chem. Rev. 2013, 113, 1–35. [Google Scholar] [CrossRef]
  11. Kočovský, P.; Bäckvall, J. The syn/anti-Dichotomy in the Palladium-Catalyzed Addition of Nucleophiles to Alkenes. Chem.–A Eur. J. 2015, 21, 36–56. [Google Scholar] [CrossRef]
  12. Shen, C.; Dong, K. Assembling Chiral Center of Heterocycles by Palladium-Catalyzed Asymmetric Hydrocarbonylation. Synlett 2022, 33, 815–821. [Google Scholar] [CrossRef]
  13. Gallarati, S.; Dingwall, P.; Fuentes, J.A.; Bühl, M.; Clarke, M.L. Understanding Catalyst Structure–Selectivity Relationships in Pd-Catalyzed Enantioselective Methoxycarbonylation of Styrene. Organometallics 2020, 39, 4544–4556. [Google Scholar] [CrossRef]
  14. Jing, T.-H.; Zhuang, Y.-Y.; Zhang, X.-X.; Qian, J.-G.; Zhao, X.-L.; Lu, Y.; Wang, H.-J.; Liu, Y. Pinwheel-like tridentate phosphines for controlling divergent regioselectivity in Pd-catalyzed alkoxycarbonylation of alkenes. J. Catal. 2024, 432, 115406. [Google Scholar] [CrossRef]
  15. Xu, T.; Sha, F.; Alper, H. Highly Ligand-Controlled Regioselective Pd-Catalyzed Aminocarbonylation of Styrenes with Aminophenols. J. Am. Chem. Soc. 2016, 138, 6629–6635. [Google Scholar] [CrossRef]
  16. Li, H.; Dong, K.; Jiao, H.; Neumann, H.; Jackstell, R.; Beller, M. The scope and mechanism of palladium-catalysed Markovnikov alkoxycarbonylation of alkenes. Nat. Chem. 2016, 8, 1159–1166. [Google Scholar] [CrossRef]
  17. Aguirre, P.A.; Lagos, C.A.; Moya, S.A.; Zúñiga, C.; Vera-Oyarce, C.; Sola, E.; Peris, G.; Bayón, J.C. Methoxycarbonylation of olefins catalyzed by palladium complexes bearing P,N-donor ligands. Dalt. Trans. 2007, 5419. [Google Scholar] [CrossRef]
  18. Dai, M.; Wang, C.; Dong, G.; Xiang, J.; Luo, T.; Liang, B.; Chen, J.; Yang, Z. Development of Thiourea-Based Ligands for the Palladium-Catalyzed Bis(methoxycarbonylation) of Terminal Olefins. Eur. J. Org. Chem. 2003, 2003, 4346–4348. [Google Scholar] [CrossRef]
  19. Fekri, S.; Mansoori, Y. Supported Bis-(NHC)-Pd(II) complex: A phosphine-free catalyst supported on magnetic mesoporous silica for the CO-free carbonylation of aryl halides. J. Organomet. Chem. 2024, 1014, 123193. [Google Scholar] [CrossRef]
  20. Klingshirn, M.A.; Rogers, R.D.; Shaughnessy, K.H. Palladium-catalyzed hydroesterification of styrene derivatives in the presence of ionic liquids. J. Organomet. Chem. 2005, 690, 3620–3626. [Google Scholar] [CrossRef]
  21. Sims, H.S.; Dai, M. Palladium-Catalyzed Carbonylations: Application in Complex Natural Product Total Synthesis and Recent Developments. J. Org. Chem. 2023, 88, 4925–4941. [Google Scholar] [CrossRef]
  22. Zhang, B.; Yuan, H.; Liu, Y.; Deng, Z.; Douthwaite, M.; Dummer, N.F.; Lewis, R.J.; Liu, X.; Luan, S.; Dong, M.; et al. Ambient-pressure alkoxycarbonylation for sustainable synthesis of ester. Nat. Commun. 2024, 15, 7837. [Google Scholar] [CrossRef] [PubMed]
  23. Schelwies, M.; Paciello, R.; Pelzer, R.; Siegel, W.; Breuer, M. Palladium-Catalyzed Low Pressure Carbonylation of Allylic Alcohols by Catalytic Anhydride Activation. Chem.–A Eur. J. 2021, 27, 9263–9266. [Google Scholar] [CrossRef] [PubMed]
  24. Fortman, G.C.; Nolan, S.P. N-Heterocyclic carbene (NHC) ligands and palladium in homogeneous cross-coupling catalysis: A perfect union. Chem. Soc. Rev. 2011, 40, 5151. [Google Scholar] [CrossRef] [PubMed]
  25. Chen, Q.-A.; Ye, Z.-S.; Duan, Y.; Zhou, Y.-G. Homogeneous palladium-catalyzed asymmetric hydrogenation. Chem. Soc. Rev. 2013, 42, 497–511. [Google Scholar] [CrossRef] [PubMed]
  26. Roberts, G.M.; Pierce, P.J.; Woo, L.K. Palladium Complexes with N-Heterocyclic Carbene Ligands As Catalysts for the Alkoxycarbonylation of Olefins. Organometallics 2013, 32, 2033–2036. [Google Scholar] [CrossRef]
  27. Demir, S.; Özdemir, İ.; Arslan, H.; VanDerveer, D. Butylene linked palladium N-heterocyclic carbene complexes: Synthesis and catalytic properties. J. Organomet. Chem. 2011, 696, 2589–2593. [Google Scholar] [CrossRef]
  28. Brennführer, A.; Neumann, H.; Beller, M. Palladium-Catalyzed Carbonylation Reactions of Aryl Halides and Related Compounds. Angew. Chemie Int. Ed. 2009, 48, 4114–4133. [Google Scholar] [CrossRef]
  29. Flahaut, A.; Roland, S.; Mangeney, P. Allylic alkylation and amination using mixed (NHC)(phosphine) palladium complexes under biphasic conditions. J. Organomet. Chem. 2007, 692, 5754–5762. [Google Scholar] [CrossRef]
  30. Hashmi, A.S.K.; Lothschütz, C.; Döpp, R.; Rudolph, M.; Ramamurthi, T.D.; Rominger, F. Gold and Palladium Combined for Cross-Coupling. Angew. Chemie Int. Ed. 2009, 48, 8243–8246. [Google Scholar] [CrossRef]
  31. Amatore, C.; Carre, E.; Jutand, A.; M’Barki, M.A. Rates and Mechanism of the Formation of Zerovalent Palladium Complexes from Mixtures of Pd(OAc)2 and Tertiary Phosphines and Their Reactivity in Oxidative Additions. Organometallics 1995, 14, 1818–1826. [Google Scholar] [CrossRef]
  32. Tooze, R.P.; Whiston, K.; Malyan, A.P.; Taylor, M.J.; Wilson, N.W. Evidence for the hydride mechanism in the methoxycarbonylation of ethene catalysed by palladium–triphenylphosphine complexes. J. Chem. Soc. Dalt. Trans. 2000, 3441–3444. [Google Scholar] [CrossRef]
  33. Nguyen, D.H.; Laurenczy, G.; Urrutigoïty, M.; Kalck, P. Hydride Route for the Palladium-Catalysed Cyclocarbonylation of Monoterpenes. Eur. J. Inorg. Chem. 2005, 2005, 4215–4225. [Google Scholar] [CrossRef]
  34. Mehara, J.; Anania, M.; Kočovský, P.; Roithová, J. Competing Mechanisms in Palladium-Catalyzed Alkoxycarbonylation of Styrene. ACS Catal. 2024, 14, 5710–5719. [Google Scholar] [CrossRef] [PubMed]
  35. Seayad, A.; Jayasree, S.; Damodaran, K.; Toniolo, L.; Chaudhari, R.V. On the mechanism of hydroesterification of styrene using an in situ-formed cationic palladium complex. J. Organomet. Chem. 2000, 601, 100–107. [Google Scholar] [CrossRef]
  36. Eastham, G.R.; Tooze, R.P.; Heaton, B.T.; Iggo, J.A.; Whyman, R.; Zacchini, S. Synthesis and spectroscopic characterisation of all the intermediates in the Pd-catalysed methoxycarbonylation of ethene. Chem. Commun. 2000, 609–610. [Google Scholar] [CrossRef]
  37. Muñoz, B.K.; Santos Garcia, E.; Godard, C.; Zangrando, E.; Bo, C.; Ruiz, A.; Claver, C. HP-NMR Study of the Pd-Catalyzed Methoxycarbonylation of Styrene Using Monodentate and Bidentate Phosphane-Modified Systems. Eur. J. Inorg. Chem. 2008, 2008, 4625–4637. [Google Scholar] [CrossRef]
  38. Bianchini, C.; Meli, A.; Oberhauser, W.; Parisel, S.; Gusev, O.V.; Kal’sin, A.M.; Vologdin, N.V.; Dolgushin, F.M. Methoxycarbonylation of styrene to methyl arylpropanoates catalyzed by palladium(II) precursors with 1,1′-bis(diphenylphosphino)metallocenes. J. Mol. Catal. A Chem. 2004, 224, 35–49. [Google Scholar] [CrossRef]
  39. Clegg, W.; Eastham, G.R.; Elsegood, M.R.J.; Heaton, B.T.; Iggo, J.A.; Tooze, R.P.; Whyman, R.; Zacchini, S. Characterization and Dynamics of [Pd(L−L)H(solv)]+, [Pd(L−L)(CH2CH3)]+, and [Pd(L−L)(C(O)Et)(THF)]+ (L−L = 1,2-(CH2PBut2)2C6H4): Key Intermediates in the Catalytic Methoxycarbonylation of Ethene to Methylpropanoate. Organometallics 2002, 21, 1832–1840. [Google Scholar] [CrossRef]
  40. Naigre, R.; Chenal, T.; Ciprés, I.; Kalck, P.; Daran, J.-C.; Vaissermann, J. Carbon monoxide as a building block in organic synthesis. Part V. Involvement of palladium-hydride species in carbonylation reactions of monoterpenes. X-ray crystal structure of [Ph3PCH2CH=CHPh]4[PdCl6][SnCl6]. J. Organomet. Chem. 1994, 480, 91–102. [Google Scholar] [CrossRef]
  41. Eastham, G.R.; Tooze, R.P.; Kilner, M.; Foster, D.F.; Cole-Hamilton, D.J. Deuterium labelling evidence for a hydride mechanism in the formation of methyl propanoate from carbon monoxide, ethene and methanol catalysed by a palladium complex. J. Chem. Soc. Dalt. Trans. 2002, 1613–1617. [Google Scholar] [CrossRef]
  42. Liu, J.; Heaton, B.T.; Iggo, J.A.; Whyman, R.; Bickley, J.F.; Steiner, A. The Mechanism of the Hydroalkoxycarbonylation of Ethene and Alkene–CO Copolymerization Catalyzed by Pd II –Diphosphine Cations. Chem.–A Eur. J. 2006, 12, 4417–4430. [Google Scholar] [CrossRef] [PubMed]
  43. Amadio, E.; Cavinato, G.; Dolmella, A.; Toniolo, L. Catalytic Properties of [Pd(COOMe)nX2−n(PPh3)2] (n = 0, 1, 2; X = Cl, NO2, ONO2, OAc and OTs) in the Oxidative Carbonylation of MeOH. Inorg. Chem. 2010, 49, 3721–3729. [Google Scholar] [CrossRef] [PubMed]
  44. Malkov, A.V.; Derrien, N.; Barłóg, M.; Kočovský, P. Palladium-Catalyzed Alkoxycarbonylation of Terminal Alkenes To Produce α,β-Unsaturated Esters: The Key Role of Acetonitrile as a Ligand. Chem.–A Eur. J. 2014, 20, 4542–4547. [Google Scholar] [CrossRef] [PubMed]
  45. Ahmad, S.; Bühl, M. Computational modelling of Pd-catalysed alkoxycarbonylation of alkenes and alkynes. Phys. Chem. Chem. Phys. 2021, 23, 15869–15880. [Google Scholar] [CrossRef]
  46. van Leeuwen, P.W.N.M.; Zuideveld, M.A.; Swennenhuis, B.H.G.; Freixa, Z.; Kamer, P.C.J.; Goubitz, K.; Fraanje, J.; Lutz, M.; Spek, A.L. Alcoholysis of Acylpalladium(II) Complexes Relevant to the Alternating Copolymerization of Ethene and Carbon Monoxide and the Alkoxycarbonylation of Alkenes: The Importance of Cis-Coordinating Phosphines. J. Am. Chem. Soc. 2003, 125, 5523–5539. [Google Scholar] [CrossRef]
  47. Clegg, W.; Eastham, G.R.; Elsegood, M.R.J.; Heaton, B.T.; Iggo, J.A.; Tooze, R.P.; Whyman, R.; Zacchini, S. Synthesis and reactivity of palladium hydrido-solvento complexes, including a key intermediate in the catalytic methoxycarbonylation of ethene to methyl propanoate. J. Chem. Soc. Dalt. Trans. 2002, 3300–3308. [Google Scholar] [CrossRef]
  48. Ahmad, S.; Crawford, L.E.; Bühl, M. Palladium-catalysed methoxycarbonylation of ethene with bidentate diphosphine ligands: A density functional theory study. Phys. Chem. Chem. Phys. 2020, 22, 24330–24336. [Google Scholar] [CrossRef]
  49. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
  50. Ernzerhof, M.; Scuseria, G.E. Assessment of the Perdew–Burke–Ernzerhof exchange-correlation functional. J. Chem. Phys. 1999, 110, 5029–5036. [Google Scholar] [CrossRef]
  51. Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
  52. Hay, P.J.; Wadt, W.R. Ab initio effective core potentials for molecular calculations. Potentials for K to Au including the outermost core orbitals. J. Chem. Phys. 1985, 82, 299–310. [Google Scholar] [CrossRef]
  53. Dolg, M.; Stoll, H.; Preuss, H.; Pitzer, R.M. Relativistic and correlation effects for element 105 (hahnium, Ha): A comparative study of M and MO (M = Nb, Ta, Ha) using energy-adjusted ab initio pseudopotentials. J. Phys. Chem. 1993, 97, 5852–5859. [Google Scholar] [CrossRef]
  54. Bergner, A.; Dolg, M.; Küchle, W.; Stoll, H.; Preuß, H. Ab initio energy-adjusted pseudopotentials for elements of groups 13–17. Mol. Phys. 1993, 80, 1431–1441. [Google Scholar] [CrossRef]
  55. Das, D.; Prakash, D.; Sarkar, P.; Sutradhar, S.; Patra, S.G.; Ghosh, B.N. Experimental and theoretical studies for instantaneous detection of l-cysteine and l-histidine using a simple Cu(II)-dppy complex. Inorganica Chim. Acta 2024, 573, 122346. [Google Scholar] [CrossRef]
  56. Sutradhar, S.; Suresh, G.K.; Sarma, S.; Das, D.; Sarkar, P.; Patra, S.G.; Ghosh, B.N. Sulphide and iodide anion recognition by a selective copper hydrogel of a chloro substituted terpyridine ligand. Inorg. Chem. Commun. 2024, 170, 113263. [Google Scholar] [CrossRef]
  57. Gogoi, B.; Borgohain, P.; Patra, S.G.; Borah, B.J.; Das, P. Pd-PEPPSI Catalyzed Dehydrogenative Oxidation of Alcohols to Carboxylic Acids: An Experimental and Theoretical Study. Organometallics 2024, 43, 2002–2015. [Google Scholar] [CrossRef]
  58. Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
  59. Martin, R.L.; Hay, P.J.; Pratt, L.R. Hydrolysis of Ferric Ion in Water and Conformational Equilibrium. J. Phys. Chem. A 1998, 102, 3565–3573. [Google Scholar] [CrossRef]
  60. Sparta, M.; Riplinger, C.; Neese, F. Mechanism of Olefin Asymmetric Hydrogenation Catalyzed by Iridium Phosphino-Oxazoline: A Pair Natural Orbital Coupled Cluster Study. J. Chem. Theory Comput. 2014, 10, 1099–1108. [Google Scholar] [CrossRef]
  61. Fantuzzi, F.; Nascimento, M.A.C.; Ginovska, B.; Bullock, R.M.; Raugei, S. Splitting of multiple hydrogen molecules by bioinspired diniobium metal complexes: A DFT study. Dalt. Trans. 2021, 50, 840–849. [Google Scholar] [CrossRef]
  62. Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
  63. Gopal Patra, S.; Kumar Chattaraj, P. Three coordinated first row-transition metal complexes, [M{N(SiMe3)2}3]−1/0: Structure, bonding, and magnetic properties. Polyhedron 2024, 256, 116990. [Google Scholar] [CrossRef]
  64. Pal, R.; Patra, S.G.; Chattaraj, P.K. Can a chemical bond be exclusively covalent or ionic? J. Chem. Sci. 2022, 134, 108. [Google Scholar] [CrossRef]
  65. Lu, T.; Chen, Q. Simple, Efficient, and Universal Energy Decomposition Analysis Method Based on Dispersion-Corrected Density Functional Theory. J. Phys. Chem. A 2023, 127, 7023–7035. [Google Scholar] [CrossRef] [PubMed]
  66. Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
  67. Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
  68. Mondal, H.; Patra, S.G.; Chattaraj, P.K. Small molecule activation and dehydrogenation of an amine–borane system using frustrated Lewis pairs. Struct. Chem. 2022, 33, 1853–1865. [Google Scholar] [CrossRef]
  69. Patra, S.G.; Jha, R.; Mondal, H.; Chattaraj, P.K. Fischer and Schrock carbene complexes in the light of global and local electrophilicity-based descriptors. J. Phys. Org. Chem. 2022, 2, e4337. [Google Scholar] [CrossRef]
  70. Mondal, H.; Patra, S.G.; Chattaraj, P.K. Unveiling novel reactivity of P/Al frustrated Lewis pair: Ring size-dependent activation of cyclic ethers/thioethers and CO2 insertion therein. J. Chem. Sci. 2022, 0123456789, 39–42. [Google Scholar] [CrossRef]
  71. Walther, G.; Knöpke, L.R.; Rabeah, J.; Chęciński, M.P.; Jiao, H.; Bentrup, U.; Brückner, A.; Martin, A.; Köckritz, A. From sunflower oil toward 1,19-diester: Mechanistic elucidation. J. Catal. 2013, 297, 44–55. [Google Scholar] [CrossRef]
  72. Roesle, P.; Caporaso, L.; Schnitte, M.; Goldbach, V.; Cavallo, L.; Mecking, S. A Comprehensive Mechanistic Picture of the Isomerizing Alkoxycarbonylation of Plant Oils. J. Am. Chem. Soc. 2014, 136, 16871–16881. [Google Scholar] [CrossRef]
  73. Dong, K.; Sang, R.; Wei, Z.; Liu, J.; Dühren, R.; Spannenberg, A.; Jiao, H.; Neumann, H.; Jackstell, R.; Franke, R.; et al. Cooperative catalytic methoxycarbonylation of alkenes: Uncovering the role of palladium complexes with hemilabile ligands. Chem. Sci. 2018, 9, 2510–2516. [Google Scholar] [CrossRef] [PubMed]
  74. Doming, L.R.; Ríos-Gutiérrez, M. A Useful Classification of Organic Reactions Based on the Flux of the Electron Density. Sci. Radices 2023, 2, 1–24. [Google Scholar] [CrossRef]
  75. Domingo, L.R. A new C–C bond formation model based on the quantum chemical topology of electron density. RSC Adv. 2014, 4, 32415–32428. [Google Scholar] [CrossRef]
  76. Patra, S.G.; Drew, M.G.B.; Datta, D. δ-Acidity of benzene in [(benzene)RuII(N-N)Cl]+. Crystal structures, nuclear magnetic resonance spectra and nucleus independent chemical shifts. Inorganica Chim. Acta 2018, 471, 228–233. [Google Scholar] [CrossRef]
  77. Bader, R.F.W. Atoms in molecules. Acc. Chem. Res. 1985, 18, 9–15. [Google Scholar] [CrossRef]
  78. Bader, R.F.W.; Essén, H. The characterization of atomic interactions. J. Chem. Phys. 1984, 80, 1943–1960. [Google Scholar] [CrossRef]
  79. Bader, R.F.W. A Bond Path: A Universal Indicator of Bonded Interactions. J. Phys. Chem. A 1998, 102, 7314–7323. [Google Scholar] [CrossRef]
  80. Bader, R.F.W. Atoms in Molecules, A Quantum Theory; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
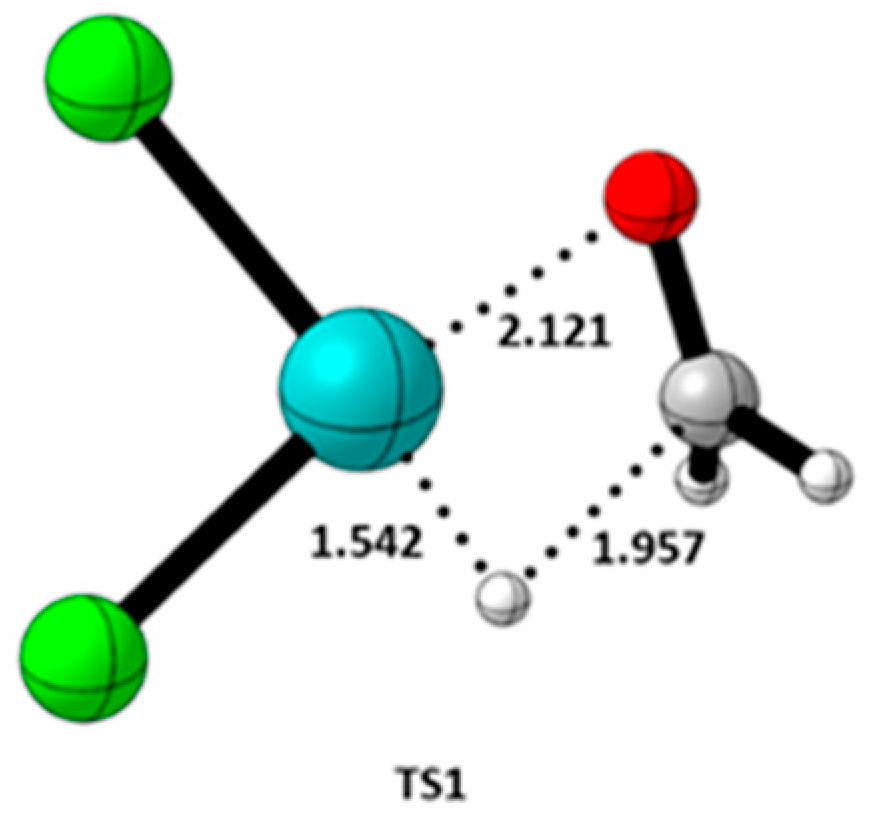
Chemistry 06 00096 g001
Figure 1. The transition state structure of TS1, i.e., β-hydride elimination step. The geometry optimization is carried out at the PBE0/bs1 level of theory. The bond length values are given in Å. Color code: H, white; C, grey; O, red; Cl, green; Pd, cyan.
Figure 1. The transition state structure of TS1, i.e., β-hydride elimination step. The geometry optimization is carried out at the PBE0/bs1 level of theory. The bond length values are given in Å. Color code: H, white; C, grey; O, red; Cl, green; Pd, cyan.
Chemistry 06 00096 g001
Chemistry 06 00096 sch001
Scheme 1. Catalytic cycles involving various transition states in intermediates for the [PdCl3]–-catalyzed alkoxycarbonylation of styrene in the presence of CO in methanol solvent.
Scheme 1. Catalytic cycles involving various transition states in intermediates for the [PdCl3]–-catalyzed alkoxycarbonylation of styrene in the presence of CO in methanol solvent.
Chemistry 06 00096 sch001
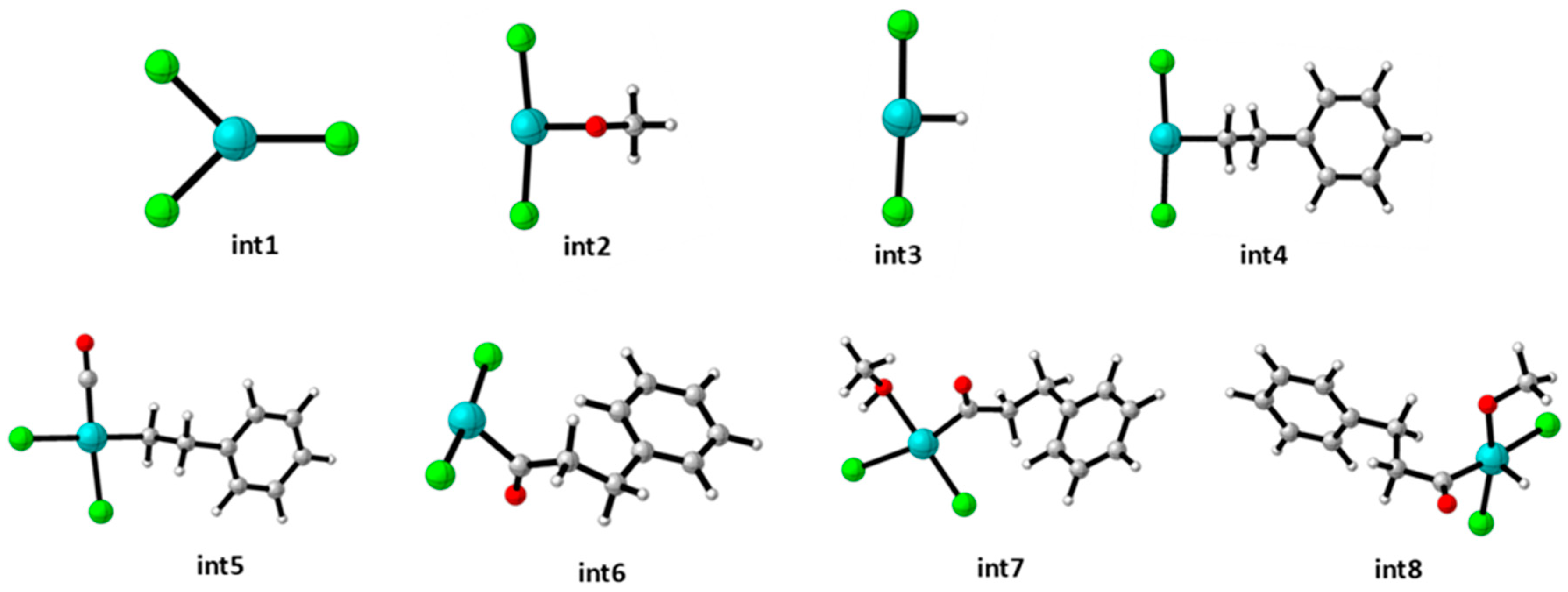
Chemistry 06 00096 g002
Figure 2. The intermediate structure of int1–int8 in cycle 1. The geometry optimization is carried out at the PBE0/bs1 level of theory. Color code: H, white; C, grey; O, red; Cl, green; Pd, cyan.
Figure 2. The intermediate structure of int1–int8 in cycle 1. The geometry optimization is carried out at the PBE0/bs1 level of theory. Color code: H, white; C, grey; O, red; Cl, green; Pd, cyan.
Chemistry 06 00096 g002
Chemistry 06 00096 g003
Figure 3. The transition state structure of TS2–TS5 in cycle 1. The geometry optimization is carried out at the PBE0/bs1 level of theory. Color code: H, white; C, grey; O, red; Cl, green; Pd, cyan. The bond length values are given in Å unit.
Figure 3. The transition state structure of TS2–TS5 in cycle 1. The geometry optimization is carried out at the PBE0/bs1 level of theory. Color code: H, white; C, grey; O, red; Cl, green; Pd, cyan. The bond length values are given in Å unit.
Chemistry 06 00096 g003
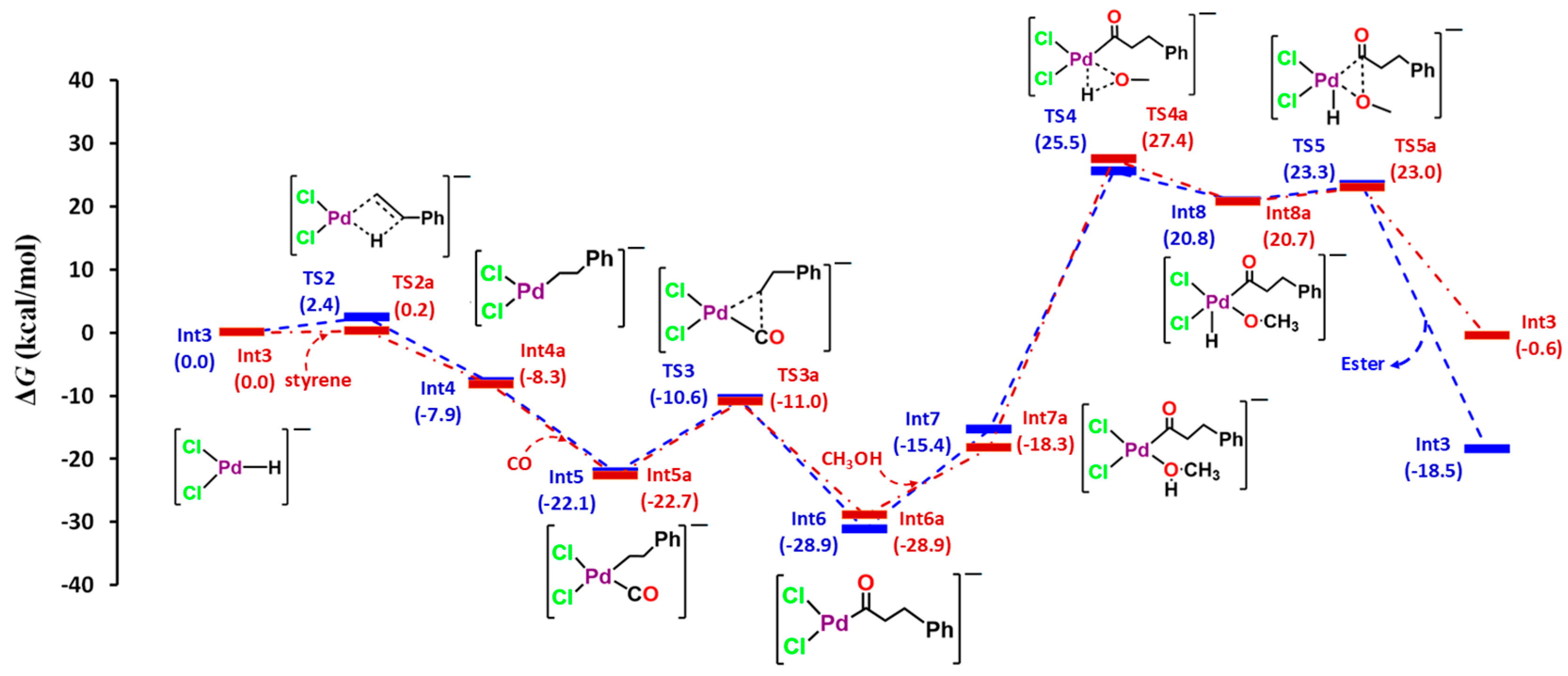
Chemistry 06 00096 g004
Figure 4. Free energy and enthalpy profile diagram of [PdCl2H]– catalyzed alkoxycarbonylation of styrene in the presence of CO in the methanol solvent. The parentheses (within first bracket) values represent the intermediates’ relative free energy values and transition states in kcal mol−1 at 298.15 K. The values within the third bracket represent the relative enthalpies. Color code: blue, free energy of cycle 1; red, free energy of cycle 2; black, enthalpy of cycle 1 and green, enthalpy of cycle 2. The calculation is carried out at the SMD/PBE0/bs2//PBE0/bs1 level of theory. The intermediates and TSs structures of cycle 1 are shown along the energy profile diagram.
Figure 4. Free energy and enthalpy profile diagram of [PdCl2H]– catalyzed alkoxycarbonylation of styrene in the presence of CO in the methanol solvent. The parentheses (within first bracket) values represent the intermediates’ relative free energy values and transition states in kcal mol−1 at 298.15 K. The values within the third bracket represent the relative enthalpies. Color code: blue, free energy of cycle 1; red, free energy of cycle 2; black, enthalpy of cycle 1 and green, enthalpy of cycle 2. The calculation is carried out at the SMD/PBE0/bs2//PBE0/bs1 level of theory. The intermediates and TSs structures of cycle 1 are shown along the energy profile diagram.
Chemistry 06 00096 g004
Table 1. The fragmentation scheme used in the energy decomposition analysis (EDA) at the different TSs of cycle 1 and cycle 2. The values in parentheses represent the charge and spin multiplicity.
Table 1. The fragmentation scheme used in the energy decomposition analysis (EDA) at the different TSs of cycle 1 and cycle 2. The values in parentheses represent the charge and spin multiplicity.
TSFragment 1 (Charge, Spin Multiplicity)Fragment 2 (Charge, Spin Multiplicity)
TS1HCHO (0, 1)[PdCl2H]– (−1, 1)
TS2styrene (0, 1)[PdCl2H]– (−1, 1)
TS2astyrene (0, 1)[PdCl2H]– (−1, 1)
TS3PhCH2CH2 (−1, 1)[PdCl2CO] (1, 1)
TS3aPhCH3CH (−1, 1)[PdCl2CO] (1, 1)
TS4CH3O (−1, 1)[PdCl2H(PhCH2CH2CO)] (−1, 1)
TS4aCH3O (−1, 1)[PdCl2H(Ph(CH3)CHCO)] (0, 1)
TS5CH3O (−1, 1)[PdCl2H(PhCH2CH2CO)] (0, 1)
TS5aCH3O (−1, 1)[PdCl2H(Ph(CH3)CHCO)] (0, 1)
Table 2. EDA analysis at the transition state TS1–TS5 and TS2a–TS5a, where the fragmentation scheme is provided in Table 1. The values in the parenthesis represent their % contribution to the total interaction energy. The calculations are performed at the B3LYP-D3(BJ)/def2-TZVP//PBE0/bs1 level of theory. The energy values are given in kcal mol−1 units.
Table 2. EDA analysis at the transition state TS1–TS5 and TS2a–TS5a, where the fragmentation scheme is provided in Table 1. The values in the parenthesis represent their % contribution to the total interaction energy. The calculations are performed at the B3LYP-D3(BJ)/def2-TZVP//PBE0/bs1 level of theory. The energy values are given in kcal mol−1 units.
Species∆Eels∆Eex∆Epauli∆Eorb∆Ecor∆Edisp∆Etot
TS1−80.6−74.2237.0−96.9−13.9−3.3−32.1
(15.9)(14.6)(46.8)(19.1)(2.7)(0.6)
TS2−114.2−110.5334.2−120.8−18.4−7.4−37.3
(16.1)(15.6)(47.3)(17.1)(2.6)(1.0)
TS2a−139.1−115.3339.2−198.1−20.9−7.6−142.0
(16.9)(14.0)(41.3)(24.1)(2.5)(0.9)
TS3−192.6−127.7428.8−217.3−17.7−7.3−134.1
(19.4)(12.8)(43.2)(21.9)(1.7)(0.7)
TS3a−150.1−104.5349.3−182.2−17.3−9.9−114.8
(18.4)(12.8)(42.9)(22.4)(2.1)(1.2)
TS4−117.1−74.3224.6−123.0−14.6−5.1−109.5
(20.9)(13.3)(40.2)(22.0)(2.6)(0.9)
TS4a−118.4−77.0232.3−125.9−15.4−5.6−110.1
(20.6)(13.4)(40.4)(21.9)(2.6)(0.9)
TS5−132.3−81.5253.0−122.4−16.5−6.0−105.8
(21.6)(13.3)(41.3)(20.0)(2.7)(0.9)
TS5a−130.0−81.3252.2−121.7−16.8−6.4−104.2
(21.3)(13.3)(41.4)(20.0)(2.7)(1.0)
Table 3. Various descriptors are obtained from the quantum theory of atoms in molecules (QTAIM) calculations in the transition state structures of the two pathways involving the bond critical point (BCPs) of the concerned non-covalent interactions. The calculations are performed at the PBE0/bs2 level of theory.
Table 3. Various descriptors are obtained from the quantum theory of atoms in molecules (QTAIM) calculations in the transition state structures of the two pathways involving the bond critical point (BCPs) of the concerned non-covalent interactions. The calculations are performed at the PBE0/bs2 level of theory.
TSDistance (Å)Bondρ(rc)∇2ρ(rc)G(rc)V(rc)H(rc)ELFλ
TS11.957C-H0.30080.12260.1235−0.2163−0.09280.6343−0.3008
TS11.542Pd-H0.13690.06990.0985−0.1795−0.08100.5295−0.1369
TS2/1.683/C-H0.3091/0.0907/0.1239−0.2253/−0.1013/0.6532/−0.3091/
TS2a1.7040.08230.04190.0359−0.0613−0.02540.6076−0.0823
TS2/1.558Pd-H0.1418/0.0625/0.1022/−0.1889/−0.8664/0.5397/−0.1418/
TS2a1.5530.14420.05130.102−0.1912−0.08920.5548−0.1442
TS2/1.421C-C0.2896/−0.74240.0984/−0.3825−0.28400.9317−0.2896
TS2a1.4170.2923−0.75600.0981−0.3855−0.28730.9341−0.2923
TS2a2.164Pd-C0.0890.2540.0862−0.1090−0.02270.2586−0.0890
TS2/2.076Pd-C0.1045/0.2010/0.0865/−0.1229/−0.0363/0.3713/−0.1045/
TS2a2.1220.09470.21430.0825−0.1114−0.02890.3197−0.0947
TS33.321Cl-H(Ph)0.04560.118130.0241−0.01870.019620.146−0.0456
TS3/1.911/C-C0.0405/−0.0663/0.1452/−0.3070/−0.1618/0.7724/−0.1102/
TS3a1.9510.1026−0.12310.1335−0.2754−0.14190.7599−0.1026
TS42.801/Cl-H(Ph)0.1091/0.0843/0.0628/−0.0482/0.0145/0.1421/−0.1091/
TS4a2.8470.0520.20010.0433−0.13450.02450.1438−0.0520
TS42.820/Cl-H(CH3)0.0377/0.1351/0.1008/−0.0777/0.0231/0.1230/−0.0377/
TS4a2.8520.11310.09870.073−0.05550.01750.1193−0.1131
TS4a2.315H-O0.03770.14130.1052−0.08080.02430.113−0.0377
TS52.343/O-H(Ph)0.04440.14880.1179−0.09930.01850.1541−0.0445
TS5a2.5610.12280.12770.0972−0.07740.01980.0893−0.1228
TS52.011H-H0.04190.13810.1063−0.08590.02040.1553−0.0419
TS5a2.0310.04290.13810.1064−0.08620.02020.167−0.0429
TS52.006/C-O0.25670.17060.1907−0.2245−0.12370.3001−0.2567
TS5a2.0110.25370.17240.1905−0.2223−0.11680.2924−0.2537
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Patra, S.G.; Saha, A.; Chattaraj, P.K. DFT Investigation of the Mechanism of Methoxycarbonylation of Styrene by Palladium Chloride. Chemistry 2024, 6, 1593-1607. https://doi.org/10.3390/chemistry6060096

AMA Style

Patra SG, Saha A, Chattaraj PK. DFT Investigation of the Mechanism of Methoxycarbonylation of Styrene by Palladium Chloride. Chemistry. 2024; 6(6):1593-1607. https://doi.org/10.3390/chemistry6060096

Chicago/Turabian Style

Patra, Shanti Gopal, Aritra Saha, and Pratim Kumar Chattaraj. 2024. "DFT Investigation of the Mechanism of Methoxycarbonylation of Styrene by Palladium Chloride" Chemistry 6, no. 6: 1593-1607. https://doi.org/10.3390/chemistry6060096

APA Style

Patra, S. G., Saha, A., & Chattaraj, P. K. (2024). DFT Investigation of the Mechanism of Methoxycarbonylation of Styrene by Palladium Chloride. Chemistry, 6(6), 1593-1607. https://doi.org/10.3390/chemistry6060096

Article Metrics

Back to TopTop