Abstract
Effects of the number of monomers (N) on the two-photon absorption (TPA) properties of π-stacked multimer models consisting of phenalenyl radicals were investigated theoretically. We conducted spectral simulations for the π-stacked N-mer models (N = 2, 4, and 6) with different stacking distances (d1) and their alternation patterns (d2/d1). Excitation energies and transition dipole moments were calculated at the extended multi-configurational quasi-degenerate second-order perturbation theory (XMC-QDPT2) level based on the complete active space self-consistent field (CASSCF) wavefunctions with the active space orbitals constructed from the singly occupied molecular orbitals (SOMOs) of monomers. The TPA cross-section value per dimer unit at the first peak, originating from the electronic transition along the stacking direction, was predicted to increase significantly as the d2/d1 approaches one, as the d1 decreases, and as the N increases from 2 to 6. These tendencies are similar to the calculation results for the static hyperpolarizabilities.
1. Introduction
Recently, stable open-shell singlet systems involving singlet diradicals and multiradicals have attracted intense attention as a novel class of functional molecular materials [,,,], although they usually exhibit high reactivity originating from partially or completely unpaired electrons. Molecular design for maintaining the high activities of unpaired electrons while increasing the kinetic and thermodynamic stabilities is indispensable for utilizing the singlet diradicals and multiradicals []. Understanding the structure–property relationships for open-shell singlet systems has been a hot topic in materials science. Diradical character (y) is a valuable chemical index characterizing the degree of open-shell in the singlet ground (S0) state [,,], taking a value from 0 (closed-shell state) to 1 (pure diradical state). Since the y of a molecular system can be easily evaluated by quantum chemical calculations, the structure–property relationships for open-shell singlet systems have been investigated in terms of y.
Nakano and coworkers theoretically predicted that the third-order nonlinear optical (NLO) properties of open-shell singlet systems can be characterized well by y [,,,,]. They derived y-dependent expressions of the static second hyperpolarizabilities (γ) for symmetric and asymmetric diradical systems. They found that these quantities are enhanced for systems with intermediate y, compared with closed-shell or complete open-shell counterparts. They also predicted a similar y-dependence for the strength of two-photon absorption (TPA) for symmetric diradicaloids [,]. TPA is a third-order nonlinear optical (NLO) process and offers various attractive applications, such as three-dimensional (3D) optical storage, 3D printing, upconverted lasers, bioimaging, and photodynamic therapy [,,,,,,,,]. Since these applications require molecular materials exhibiting the efficient TPA property at a given photon energy [,,]. Various open-shell singlet systems with a wide range of y values were designed and synthesized, and their TPA cross-section values, , were examined.
Phenalenyl 1a (PLY (R = H); Figure 1a) is a neutral π-radical system showing high thermodynamical stability due to the delocalized nature of the singly occupied molecular orbital (SOMO) []. PLY has been employed as a building block for designing open-shell conjugated systems []. values of the diphenalenyl diradical molecules called IDPL and NDPL, synthesized by Kubo and coworkers [,], were measured experimentally by Kamada and coworkers. The first TPA band was observed around 1300 nm with ~330 GM for IDPL, and around 1610 nm with ~2000 GM for NDPL (1 GM = 1 × 10−50 cm4 s photon−1) [,]. Further enhanced values could be observed when both the one-photon and two-photon resonance conditions were nearly satisfied (i.e., ) [], although the relationship between y and the increase in in this region has not been clarified sufficiently.
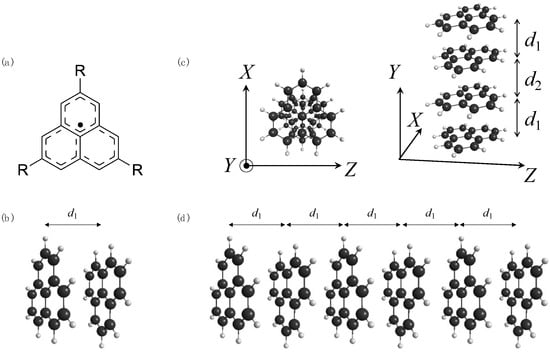
Figure 1.
Molecular structures of (a) phenalenyl radical 1a (R = H), (b) anti-type dimer model 1a2, (c) tetramer model 1a4(d2/d1), and (d) hexamer model 1a6(1.0) (d2 = d1).
Notably, several derivatives of 1a were reported to form stacked π-dimers and multimers in solution or crystalline phases [,,,]. For example, 1b (R = tBu) and 1c (R = C6H5) were reported to form anti-type π-dimers in the solid state with d~3.31 Å and ~3.02 Å, respectively. These experimental results indicate the existence of the multi-center two-electron covalent-like bonding interaction between the PLYs, known as the pancake bonding []. Furthermore, the formation of one-dimensional (1D) molecular aggregates composed of 1d (R = C6F5) with d~3.50 Å was reported [].
Yoneda and coworkers performed the density functional theory (DFT) calculations for π-dimers and tetramers of 1a (R = H) with different stacking distances d in the singlet state []. They found that y of the dimer decreases as decreasing d, and static γ per monomer takes the maximum around d = 2.9 Å, at which y is in the intermediate region. They also predicted that the static γ per monomer was further enhanced in the tetramer. Salustro and coworkers evaluated static γ per unit of infinite 1D chains of 1a [] by extending the coupled-perturbed Kohn–Sham (CPKS) analytic derivative method under the periodic boundary condition implemented in the CRYSTAL package [], which was the first direct computation of the static γ of this type of 1D chain. In a series of theoretical studies, Matsui and coworkers investigated the effects of increasing the number of monomers (N) on the γ per unit based on the 1D chains of cyclic thiazyl radicals [,]. Recently, we examined the static γ per unit of finite and infinite 1D chains of 1a with stacking distance alternations (SDAs). We proposed a y-based index to describe the electronic structures of infinite 1D chains with different SDAs []. These studies predicted that the static third-order NLO properties of closely stacked 1D chains of π-radicals are comparable to those of π-conjugated polymers.
On the other hand, there have been a few theoretical studies focusing on the TPA properties of π-stacks of open-shell molecules. In contrast to usual closed-shell systems, calculating excitation energies and transition dipole moments between the electronic states for open-shell singlet systems is still challenging because of the multi-configurational character in the ground state. In this study, we investigated the effects of the number of monomers (N) on the TPA properties of π-stacked N-mer models consisting of 1a with different primary stacking distances (1aN; see Figure 1). We attempted to apply the extended multi-configurational quasi-degenerate second-order perturbation theory (XMC-QDPT2) method [,] to evaluate the excitation energies and transition dipole moments. Although we performed calculations up to hexamer (N = 6) because of the high demands of computational resources in such calculations, the present study will provide valuable information for experimental investigations on the TPA properties of open-shell molecular assemblies.
2. Computational Details
2.1. Calculated Models and Calculation Methods
First, we optimized the geometry of monomer 1a at the UB3LYP/6-31G* level under the constraint of D3h symmetry, the same level as the previous studies [,]. Then, we constructed the anti-type π-stacked N-mer models (N = 2, 4, and 6) consisting of 1a with different stacking distances d1 (2.8 Å ≤ d1 ≤ 4.0 Å, see Figure 1b), maintaining each monomer geometry frozen. For tetramer (N = 4), we also investigated the effects of stacking distance alternation between d1 and d2, shown in Figure 1c, by changing the ratio for SDA, d2/d1, from 1.0 to 2.0. We name the N-mer model with the ratio d2/d1 1aN(d2/d1) for simplicity.
For a given N-mer system consisting of monoradicals (N = 2m; m = 1, 2, …), we can define N/2 diradical characters, yi (i = 0, 1, …, N/2–1; 1 ≥ y0 ≥ y1 ≥ … yN/2–1 ≥ 0). We evaluated the yi values of each system at the spin-projected (P)UHF/6-31G* level based on the following Yamaguchi’s formula that can efficiently remove the spin-contamination errors in the occupation numbers []:
Here, Ti is the orbital overlap between corresponding orbital pairs, and nHONO–i and nLUNO+i are the occupation numbers of UHF natural orbitals (UNOs). The averaged diradical character yav was calculated using the following formula [,]:
Note that there are N/2 radical orbital pairs in the N-mer. We also computed the standard deviation, ySD, defined by the following equation []:
These y-based indices help characterize open-shell electronic structures of N-mers []. yav is sensitive to the change in the primary stacking distance d1 but insensitive to the change in the SDA ratio. ySD can efficiently characterize the open-shell electronic structures of 1D chains of radicals with different SDA ratios. Note that and for N = 4. The occupation numbers of UNOs were calculated using the Gaussian 09 program package [].
2.2. Excited State Calculations and Spectrum Simulations
Multi-reference methods should be used to examine the ground and excited states of diradical molecules and assemblies in principle for a balanced description of both the static and dynamical electron correlations. In this study, we employed the extended (X)MC-QDPT2 method implemented in the GAMESS-US program package (ver. 2014) [] to calculate the excitation energies and transition dipole moments, although it is reported that the (multi-reference) second-order perturbation theory methods tend to overestimate the binding energy of PLY π-dimers in the S0 state []. To express the open-shell nature in the S0 state and two-photon transition of diradical systems, the two-electron and two-orbital complete active space [i.e., CAS(2,2)] is the minimal choice of the active space. For the dimer, the HOMO and LUMO constructed from the SOMOs of monomers are the minimal active orbitals. Accordingly, we performed state-averaged (SA-)CASSCF calculations based on the CAS(N, N) space, where the active orbitals are the frontier MOs constructed from the SOMOs of monomers. We solved for the low-lying three singlet states for N = 2 (all the electronic states derived from CAS(2,2) space) and for the low-lying ten singlet states with the Ag and Bu symmetries for N = 4 and 6. This symmetry constraint is expected to efficiently describe the one-photon absorption (OPA) and TPA peaks of N-mers concerning the intermonomer electronic transitions.
Although the basis sets including diffuse functions can improve the description of excitation energies and binding energies of π-dimers, we used the 6-31G* basis set since it is reported to describe the vertical excitation energies of several π-dimers with sufficient accuracy in combination with the MC-QDPT []. Then, we evaluated the excitation energies at the XMC-QDPT2 level with the intruder state avoidance parameter of 0.02. We should note that the transition dipole moments between the states were evaluated using the eigenvectors of the XMC-QDPT2 effective Hamiltonian.
The OPA cross-section, , was evaluated by the following equation []:
Here, is the speed of light in vacuum, is the angular frequency of the incident light, is the refractive index of the medium (set to 1.0 in this study). is the transition dipole moment between the states and . means the orientational average, i.e., where represents the α-axis component of the transition dipole moment . Since we solved only for the Ag and Bu states, the Z-axis component of is zero. We used the following Lorentzian function for the normalized shape function :
where and is the damping parameter. This study employed = 0.1 eV for all the damping parameters.
The TPA cross-section, , was evaluated by the following equation [,]:
Here, is the two-photon transition matrix element tensor with each component expressed as follows:
For the orientational average, , we assumed the linearly polarized incident light. For the actual calculation, we replaced in the denominator with . Again, we used the Lorentzian function for the normalized shape function :
3. Results and Discussion
3.1. Correlation Between Stacking Distances and Diradical Characters
Figure 2 shows the calculation results of yav and ySD as a function of d1 (2.8 Å ≤ d1 ≤ 4.0 Å) for each model. yav decreased monotonically as the d1 decreased, and took the intermediate values (~0.5) at d1~3.0 Å. The ratio d2/d1 did not affect the results of yav for 1a4(d2/d1). In addition, yav values of 1a2, 1a4(1.0), and 1a6(1.0) for the considered d1 were almost the same, although their open-shell characters are different. ySD can characterize such differences in the open-shell characters between the models at each d1. The calculated ySD values of 1a4(2.0) were almost zero regardless of d1, whereas those of the other models increased monotonically with decreasing d1. ySD characterizes the effective orbital interaction between the dimer units. The value of yi increases as the energy gap between the HOMO-i and LUMO+i decreases. The orbital interaction between the dimer units is weak for the tetramer when d2 >> d1. The HOMO and HOMO − 1 (LUMO and LUMO + 1) are nearly degenerated, resulting in y0~y1 (i.e., ySD~0). As the d2 approached d1 (and as the d1 became small), the orbital interaction between the dimer units resulted in the splitting of HOMO and HOMO − 1 (LUMO and LUMO + 1) and the increase in ySD. ySD of 1a6(1.0) was slightly larger than 1a4(1.0) at each d1, but it is expected to converge to a certain value as increasing N [].
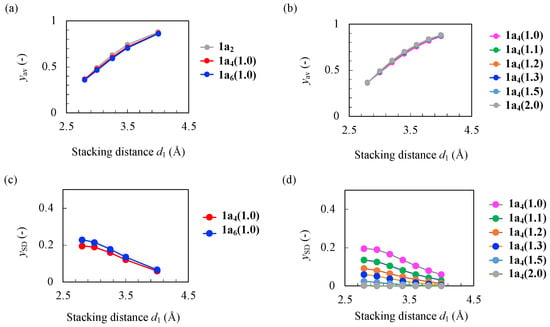
Figure 2.
Calculation results of yav (a) for the models with the uniform stacking distance d1 for 1a2, 1a4(1.0), and 1a6(1.0), (b) for 1a4(d2/d1) with different ratios d2/d1 = 1.0, 1.1, 1.2, 1.3, 1.5, and 2.0, results of ySD, (c) for 1a4(1.0) and 1a6(1.0), and (d) for 1a4(d2/d1).
3.2. One-Photon and Two-Photon Absorption Properties of Tetramers
Figure 3a shows the simulated OPA spectra for the tetramer models 1a4(d2/d1) with d1 = 3.0 Å. To compare the results with 1a2, and values per dimer unit were presented. The OPA spectra were normalized to that at the first peak of the model 1a4(1.0).
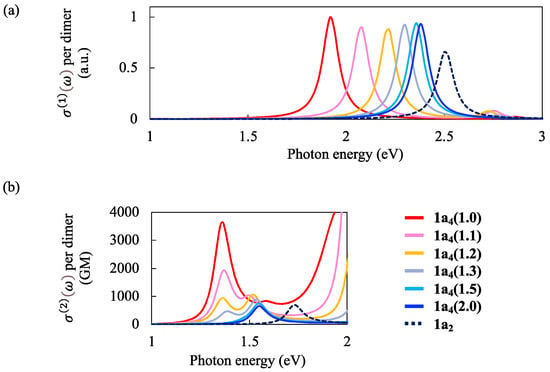
Figure 3.
Simulated (a) OPA and (b) TPA spectra of 1a2 and 1a4(d2/d1) at d1 = 3.0 Å with different ratios d2/d1 = 1.0, 1.1, 1.2, 1.3, 1.5, and 2.0. The OPA spectra were normalized to that at the first peak of the model 1a4(1.0).
The first OPA and TPA peaks were red-shifted as the d2/d1 became small (i.e., d2 approached d1) and the d1 became small. For example, the first OPA peak appeared at ~2.5 eV for 1a2, ~2.4 eV for 1a4(2.0), and ~1.9 eV for 1a4(1.0). The intensity of the first OPA peak was almost unchanged by changing the d2/d1. However, the peak intensities per dimer of 1a4(d2/d1) were stronger than that of 1a2, suggesting the delocalization of wavefunction over the dimers in the excited state.
For the TPA spectra, only a single peak appeared at ~1.7 eV for 1a2 because of the limited active space size [CAS(2,2)]. For the tetramer models 1a4(d2/d1), enhanced TPA cross-section values (per dimer) were obtained as the incident photon energy approached the excitation energy of the OPA band. This is because both the one-photon and two-photon resonance conditions were nearly satisfied in this region [,]. However, the present level of approximation for the excited state calculations would not sufficiently describe the higher-lying excited states concerning the TPA transitions in this region. In the lower-energy region of incident photon energy (<1.7 eV), we obtained a single TPA peak at ~1.6 eV for 1a4(2.0) and 1a4(1.5). As the d2/d1 decreased, this peak position was red-shifted, and another peak appeared at ~1.4 eV. The intensity of the lower-energy peak at ~1.4 eV increased drastically as the d2/d1 approached one.
In Table 1 and Table 2, we summarized the excitation energies, , and the Y-axis component of transition dipole moments, , respectively, crucial for describing these OPA and TPA peaks. The 1Ag→1Bu transition for all cases characterized the OPA peak. The value for the 1Ag→1Bu transition of the tetramer models 1a4(d2/d1) slightly increased as the d2/d1 decreased, the feature of which was reflected in the OPA peak intensities. The TPA peak at ~1.6 eV was primarily described by the virtual transition via 1Ag→1Bu→5Ag. The value for the 1Bu→5Ag transition decreased whereas the value for the 1Bu→4Ag transition increased as the d2/d1 decreased. Therefore, the virtual transition via 1Ag→1Bu→4Ag primarily described the lower-energy TPA peak at ~1.4 eV. The excitation energy of the 4Ag state was almost unchanged in the range of 1.0 ≤ d2/d1 ≤ 1.3, while the excitation energy of the 1Bu state decreased, which led to a decrease in (k: 1Bu state, f: 4Ag state) as the d2/d1 approached to one. These tendencies were attributed to the enhancement of values per dimer at ~1.4 eV.

Table 1.
Calculation results for excitation energies of 1a4(d2/d1), (in eV), at d1 = 3.0 Å with different ratios d2/d1 = 1.0, 1.1, 1.2, 1.3, 1.5, and 2.0. Results for the 1a2 are also provided for reference.

Table 2.
Calculation results for the Y-axis (stacking direction) component of transition dipole moment between the states i and j (in Debye) for 1a4(d2/d1) at d1 = 3.0 Å with different ratios d2/d1 = 1.0, 1.1, 1.2, 1.3, 1.5, and 2.0. Results for the 1a2 are also provided for reference.
In Tables S1–S4, we summarized the weights of electron configurations for these electronic states of 1a4(1.0), 1a4(1.2), 1a4(1.5), and 1a4(2.0) with d = 3.0 Å. We also plotted the HOMO-1, HOMO, LUMO, and LUMO+1 of 1a4(1.0) with d = 3.0 Å (Figure S1). Note that the bonding/anti-bonding characters of these frontier MOs were unchanged for all the considered d1 and d2 values. For all these models, the 1Ag and 1Bu states were primarily described by the ground electron configuration and the HOMO–LUMO single excitation configuration, respectively. However, the 1Ag state of 1a4(1.0) exhibited a relatively large weight for the HOMO–LUMO double excitation configuration. For 1a4(1.5) and 1a4(2.0), the 5Ag state was described by the linear combination of HOMO-1–LUMO and HOMO–LUMO+1 single excitation configurations. In contrast, the 4Ag state of these models was described by the linear combinations of the ground and several single and double excitation configurations. For 1a4(1.2), the characters of 4Ag and 5Ag were reversed from those for 1a4(1.5) and 1a4(2.0). For 1a4(1.0), the 4Ag state was described primarily by the ground and HOMO–LUMO double excitation configurations.
Next, we examined how the primary stacking distance d1 and the ratio d2/d1 affect the intensity of the first TPA peak. Figure 4 shows the values per dimer for 1a4(d2/d1) with different d1 (2.8 Å ≤ d1 ≤ 4.0 Å) as a function of the ratio d2/d1. The first TPA peak intensity increased as the d1 decreased and d2/d1 approached one. Similar tendencies were observed for the calculation results of static γ per unit of finite and infinite 1D stacks of 1a []. The results suggest that not only the static γ but also the first TPA peak value is expected to be enhanced in the uniform 1D stacks of PLYs. Such enhancements of the third-order NLO responses are expected when d1 is less than the van der Waals contact distance for the carbon atoms (3.4 Å).
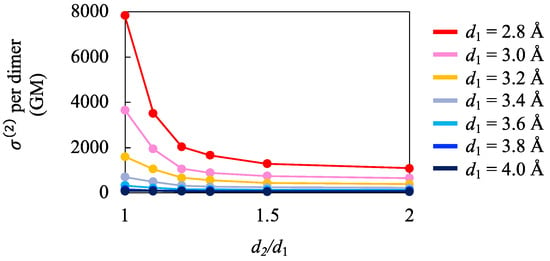
Figure 4.
Calculation results of values per dimer for 1a4(d2/d1) with different d1 (2.8 Å ≤ d1 ≤ 4.0 Å) as a function of the ratio d2/d1.
In Figure S2, we plotted variations of the excitation energies and transition dipole moments of crucial transitions for 1a4(d2/d1) with different d1 (2.8 Å ≤ d1 ≤ 4.0 Å) as a function of the ratio d2/d1. As the d1 decreased, the excitation energy for the TPA target (4Ag or 5Ag) state increased more significantly than that for the OPA target (1Bu) state. As a result, the detuning energy, , which inversely contributes to the value at the peak, became small. The magnitude of the transition dipole moment for the 1Ag→1Bu transition increased as the d1 decreased, whereas that for the 1Bu→4Ag(5Ag) transition showed somewhat complicated behaviors because the characters of 4Ag and 5Ag states exchanged at d2/d1 = 1.2–1.3.
Finally, we calculated the TPA property of the hexamer model 1a6(1.0) to examine the effects of increasing N. Figure 5 shows the calculation results of value per dimer at the first TPA peak as a function of yav for the 1a2, 1a4(1.0), and 1a6(1.0) (for the relationship between d1 and yav, see Figure 2a). The values per dimer increased as the yav decreased (i.e., as the d1 decreased) for all the models. The enhancement of values per dimer was more significant in N = 6 than in N = 4: At d0 = 3.0 Å, values per dimer of 1a4(1.0) and 1a6(1.0) were 5.1 and 8.4 times higher than that of 1a2. Further enhancement of the values per dimer unit can be expected when N approaches to ∞ (i.e., for the infinite 1D π-stacks), although the value will converge to a specific value as was observed for the calculation results of static γ per unit []. In Figure S3, we compared the excitation energies and transition dipole moments of crucial transitions for 1a2, 1a4(1.0), and 1a6(1.0) as a function of yav. As the N increased, the excitation energies for the OPA and TPA target states decreased, and the detuning energy, , became small, which is considered the main cause of enhancing values at the first peak.
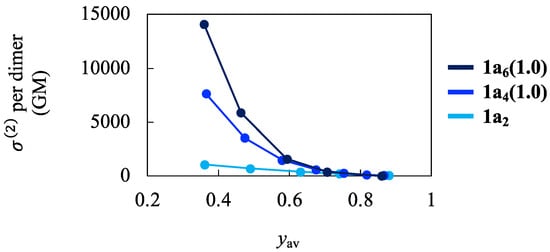
Figure 5.
Calculation results of value per dimer at the first TPA peak as a function of yav for the 1a2, 1a4(1.0), and 1a6(1.0).
4. Conclusions
In this study, we theoretically examined the low energy OPA and TPA properties of the π-stacked N-mer models, 1aN(d2/d1) (N = 2, 4, and 6), consisting of unsubstituted phenalenyl radicals with different stacking distances d1 and d2. We conducted the CASSCF(N,N) and XMC-QDPT2/6-31G* calculations for the excitation energies and transition dipole moments that were used to simulate the OPA and TPA spectra of these models. The value per dimer unit at the first peak, originating from the electronic transition along the stacking direction, was predicted to increase significantly as the d2/d1 approaches one, as the d1 decreases, and as the N increases from 2 to 6. For the 1D chains of unsubstituted phenalenyl 1a, sufficiently enhanced TPA properties are expected for d1 ≤ 3.2 Å. The appropriate d1 value and d2/d1 ratio for achieving sufficiently enhanced TPA properties would depend on the monomer species.
Calculating the y-based indices, yav, and ySD, will help specify appropriate regions for these values. Of course, it is generally challenging to characterize the electronic structures and excitation properties of 1D π-stacks with only a few indices. Calculations and analyses with sufficient accuracies are necessary for predicting the OPA and TPA properties of more realistic calculation models involving substituent groups. However, we believe the present results provide essential information for the relationship between the structural features and linear and nonlinear optical responses of actual π-stacked 1D chains of open-shell molecular species.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/chemistry6060085/s1, Figure S1: Frontier Mos involved in the active space of CASSCF calculations for 1a2, 1a4(1.0), and 1a6(1.0) with d1 = 3.0 Å, Table S1: Electron configurations describing the crucial electronic states of 1a4(1.0) with d1 = 3.0 Å, Table S2: Electron configurations describing the crucial electronic states of 1a4(1.2) with d1 = 3.0 Å, Table S3: Electron configurations describing the crucial electronic states of 1a4(1.5) with d1 = 3.0 Å, Table S4: Electron configurations describing the crucial electronic states of 1a4(2.0) with d1 = 3.0 Å, Figure S2: d2/d1 dependences of the excitation energies for OPA target state, first TPA target state, and magnitudes of the transition dipole moments (TDMs) (per dimer) for 1Ag-1Bu transition, 1Bu-TPA target (4Ag or 5Ag) state, and inverse of the detuning energy, Figure S3: yav dependences of the excitation energies for OPA target state, main TPA target state, and magnitudes of the transition dipole moments (TDMs) (per dimer) for 1Ag-1Bu transition, 1Bu-TPA target state, and inverse of the detuning energy, Table S5: Cartesian coordinates (Å) of the phenalenyl dimer model 1a2 with d = 3.0 Å where the geometry of each monomer 1a was optimized at the UB3LYP/6-31G* level under the constraint of D3h symmetry. Geometries of tetramer 1a4(d2/d1) and hexamer 1a2(1.0) models were also constructed based on this data.
Author Contributions
Conceptualization, methodology, formal analysis, investigation, M.Y. and R.K.; writing—original draft preparation, M.Y.; writing—review and editing, R.K. and Y.K.; visualization, M.Y.; supervision, Y.K.; project administration, funding acquisition, R.K. and Y.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by JSPS KAKENHI, grant numbers JP21K04995, JP22H04974, JP22H02050, and JP21H05489; International Collaborative Research Program of the Institute for Chemical Research, Kyoto University, grant numbers #2024-60 and #2024-53.
Data Availability Statement
The original contributions presented in this study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding authors.
Acknowledgments
The authors acknowledge Takashi Kubo (Osaka Univ., Japan), Kenji Kamada (AIST, Japan), and the late Masayoshi Nakano (Osaka Univ., Japan), who initiated and directed the theory-synthesis-measurement trinity approach for open-shell functional molecular design. Theoretical calculations were partly performed using the Research Center for Computational Science, Okazaki, Japan (Projects: 23-IMS-C004 and 24-IMS-C004).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Abe, M. Diradicals. Chem. Rev. 2013, 113, 7011–7088. [Google Scholar] [CrossRef] [PubMed]
- Wu, J. (Ed.) Diradicaloids, 1st ed.; Jenny Stanford Publishing: New York, NY, USA, 2022. [Google Scholar]
- Hinz, A.; Bresien, J.; Breher, F.; Schulz, A. Heteroatom-Based Diradical(Oid)s. Chem. Rev. 2023, 123, 10468–10526. [Google Scholar] [CrossRef] [PubMed]
- Ishigaki, Y.; Harimoto, T.; Shimajiri, T.; Suzuki, T. Carbon-Based Biradicals: Structural and Magnetic Switching. Chem. Rev. 2023, 123, 13952–13965. [Google Scholar] [CrossRef]
- Yamaguchi, K. The Electronic Structures of Biradicals in the Unrestricted Hartree-Fock Approximation. Chem. Phys. Lett. 1975, 33, 330–335. [Google Scholar] [CrossRef]
- Stuyver, T.; Chen, B.; Zeng, T.; Geerlings, P.; De Proft, F.; Hoffmann, R. Do Diradicals Behave Like Radicals? Chem. Rev. 2019, 119, 11291–11351. [Google Scholar] [CrossRef]
- Hayes, E.F.; Siu, A.K.Q. Electronic Structure of the Open Forms of Three-Membered Rings. J. Am. Chem. Soc. 1971, 93, 2090–2091. [Google Scholar] [CrossRef]
- Nakano, M.; Kishi, R.; Ohta, S.; Takahashi, H.; Kubo, T.; Kamada, K.; Ohta, K.; Botek, E.; Champagne, B. Relationship between Third-Order Nonlinear Optical Properties and Magnetic Interactions in Open-Shell Systems: A New Paradigm for Nonlinear Optics. Phys. Rev. Lett. 2007, 99, 033001. [Google Scholar] [CrossRef]
- Nakano, M.; Kishi, R.; Nitta, T.; Kubo, T.; Nakasuji, K.; Kamada, K.; Ohta, K.; Champagne, B.; Botek, E.; Yamaguchi, K. Second Hyperpolarizability (γ) of Singlet Diradical System: Dependence of γ on the Diradical Character. J. Phys. Chem. A 2005, 109, 885–891. [Google Scholar] [CrossRef]
- Nakano, M.; Kishi, R.; Ohta, S.; Takebe, A.; Takahashi, H.; Furukawa, S.-I.; Kubo, T.; Morita, Y.; Nakasuji, K.; Yamaguchi, K.; et al. Origin of the Enhancement of the Second Hyperpolarizability of Singlet Diradical Systems with Intermediate Diradical Character. J. Chem. Phys. 2006, 125, 074113. [Google Scholar] [CrossRef]
- Nakano, M. Open-Shell-Character-Based Molecular Design Principles: Applications to Nonlinear Optics and Singlet Fission. Chem. Rec. 2017, 17, 27–62. [Google Scholar] [CrossRef]
- Nakano, M.; Champagne, B. Nonlinear Optical Properties in Open-Shell Molecular Systems. WIREs Comput. Mol. Sci. 2016, 6, 198–210. [Google Scholar] [CrossRef] [PubMed]
- Nakano, M.; Yoneda, K.; Kishi, R.; Takahashi, H.; Kubo, T.; Kamada, K.; Ohta, K.; Champagne, B.; Botek, E. One- and Two-Photon Absorptions in Open-Shell Singlet Systems. AIP Conf. Proc. 2012, 1504, 136–142. [Google Scholar]
- Nakano, M.; Yoneda, K.; Kishi, R.; Takahashi, H.; Kubo, T.; Kamada, K.; Ohta, K.; Botek, E.; Champagne, B. Remarkable Two-Photon Absorption in Open-Shell Singlet Systems. J. Chem. Phys. 2009, 131, 114316. [Google Scholar] [CrossRef] [PubMed]
- So, P.T.C.; French, T.; Yu, W.M.; Berland, K.M.; Dong, C.Y.; Gratton, E. Time-Resolved Fluorescence Microscopy Using Two-Photon Excitation. Bioimaging 1995, 3, 49–63. [Google Scholar] [CrossRef]
- Toriumi, A.; Kawata, S.; Gu, M. Reflection Confocal Microscope Readout System for Three-Dimensional Photochromic Optical Data Storage. Opt. Lett. 1998, 23, 1924–1926. [Google Scholar] [CrossRef]
- Ehrlich, J.E.; Wu, X.L.; Lee, I.-Y.S.; Hu, Z.-Y.; Röckel, H.; Marder, S.R.; Perry, J.W. Two-Photon Absorption and Broadband Optical Limiting with Bis-Donor Stilbenes. Opt. Lett. 1997, 22, 1843–1845. [Google Scholar] [CrossRef]
- Maruo, S.; Nakamura, O.; Kawata, S. Three-Dimensional Microfabrication with Two-Photon-Absorbed Photopolymerization. Opt. Lett. 1997, 22, 132–134. [Google Scholar] [CrossRef]
- He, G.S.; Xu, C.; Prasad, P.N.; Reinhardt, B.A.; Bhatt, J.C.; McKellar, R.; Dillard, A.G. Two-Photon Absorption and Optical-Limiting Properties of Novel Organic Compounds: Erratum. Opt. Lett. 1995, 20, 1930. [Google Scholar] [CrossRef]
- Cumpston, B.H.; Ananthavel, S.P.; Barlow, S.; Dyer, D.L.; Ehrlich, J.E.; Erskine, L.L.; Heikal, A.A.; Kuebler, S.M.; Lee, I.-Y.S.; McCord-Maughon, D.; et al. Two-Photon Polymerization Initiators for Three-Dimensional Optical Data Storage and Microfabrication. Nature 1999, 398, 51–54. [Google Scholar] [CrossRef]
- Denk, W.; Strickler, J.H.; Webb, W.W. Two-Photon Laser Scanning Fluorescence Microscopy. Science 1990, 248, 73–76. [Google Scholar] [CrossRef]
- Reinhardt, B.A.; Brott, L.L.; Clarson, S.J.; Dillard, A.G.; Bhatt, J.C.; Kannan, R.; Yuan, L.; He, G.S.; Prasad, P.N. Highly Active Two-Photon Dyes: Design, Synthesis, and Characterization toward Application. Chem. Mater. 1998, 10, 1863–1874. [Google Scholar] [CrossRef]
- Dvornikov, A.S.; Walker, E.P.; Rentzepis, P.M. Two-Photon Three-Dimensional Optical Storage Memory. J. Phys. Chem. A 2009, 113, 13633–13644. [Google Scholar] [CrossRef] [PubMed]
- Pawlicki, M.; Collins, H.A.; Denning, R.G.; Anderson, H.L. Two-Photon Absorption and the Design of Two-Photon Dyes. Angew. Chem. Int. Ed. 2009, 48, 3244–32667. [Google Scholar] [CrossRef] [PubMed]
- Terenziani, F.; Katan, C.; Badaeva, E.; Tretiak, S.; Blanchard-Desce, M. Enhanced Two-Photon Absorption of Organic Chromophores: Theoretical and Experimental Assessments. Adv. Mater. 2008, 20, 4641–4678. [Google Scholar] [CrossRef]
- Albota, M.; Beljonne, D.; Brédas, J.-L.; Ehrlich, J.E.; Fu, J.-Y.; Heikal, A.A.; Hess, S.E.; Kogej, T.; Levin, M.D.; Marder, S.R.; et al. Design of Organic Molecules with Large Two-Photon Absorption Cross Sections. Science 1998, 281, 1653–1656. [Google Scholar] [CrossRef]
- Reid, D.H. The Chemistry of the Phenalenes. Q. Rev. Chem. Soc. 1965, 19, 274–302. [Google Scholar] [CrossRef]
- Kubo, T. Syntheses and Properties of Open-Shell π-Conjugated Molecules. Bull. Chem. Soc. Jpn. 2021, 94, 2235–2244. [Google Scholar] [CrossRef]
- Kubo, T.; Shimizu, A.; Sakamoto, M.; Uruichi, M.; Yakushi, K.; Nakano, M.; Shiomi, D.; Sato, K.; Takui, T.; Morita, Y.; et al. Synthesis, Intermolecular Interaction, and Semiconductive Behavior of a Delocalized Singlet Biradical Hydrocarbon. Angew. Chem. Int. Ed. 2005, 44, 6564–6568. [Google Scholar] [CrossRef]
- Kubo, T.; Shimizu, A.; Uruichi, M.; Yakushi, K.; Nakano, M.; Shiomi, D.; Sato, K.; Takui, T.; Morita, Y.; Nakasuji, K. Singlet Biradical Character of Phenalenyl-Based Kekulé Hydrocarbon with Naphthoquinoid Structure. Org. Lett. 2007, 9, 81–84. [Google Scholar] [CrossRef]
- Kamada, K.; Ohta, K.; Kubo, T.; Shimizu, A.; Morita, Y.; Nakasuji, K.; Kishi, R.; Ohta, S.; Furukawa, S.-I.; Takahashi, H.; et al. Strong Two-Photon Absorption of Singlet Diradical Hydrocarbons. Angew. Chem. Int. Ed. 2007, 46, 3544–3546. [Google Scholar] [CrossRef]
- Kamada, K.; Ohta, K.; Shimizu, A.; Kubo, T.; Kishi, R.; Takahashi, H.; Botek, E.; Champagne, B.; Nakano, M. Singlet Diradical Character from Experiment. J. Phys. Chem. Lett. 2010, 1, 937–940. [Google Scholar] [CrossRef]
- Kamada, K.; Ohta, K.; Iwase, Y.; Kondo, K. Two-Photon Absorption Properties of Symmetric Substituted Diacetylene: Drastic Enhancement of the Cross Section near the One-Photon Absorption Peak. Chem. Phys. Lett. 2003, 372, 386–393. [Google Scholar] [CrossRef]
- Goto, K.; Kubo, T.; Yamamoto, K.; Nakasuji, K.; Sato, K.; Shiomi, D.; Takui, T.; Kubota, M.; Kobayashi, T.; Yakusi, K.; et al. A Stable Neutral Hydrocarbon Radical: Synthesis, Crystal Structure, and Physical Properties of 2,5,8-Tri-Tert-Butyl-Phenalenyl. J. Am. Chem. Soc. 1999, 121, 1619–1620. [Google Scholar] [CrossRef]
- Suzuki, S.; Morita, Y.; Fukui, K.; Sato, K.; Shiomi, D.; Takui, T.; Nakasuji, K. Aromaticity on the Pancake-Bonded Dimer of Neutral Phenalenyl Radical as Studied by MS and NMR Spectroscopies and NICS Analysis. J. Am. Chem. Soc. 2006, 128, 2530–2531. [Google Scholar] [CrossRef] [PubMed]
- Mou, Z.; Uchida, K.; Kubo, T.; Kertesz, M. Evidence of σ- and π-Dimerization in a Series of Phenalenyls. J. Am. Chem. Soc. 2014, 136, 18009–18022. [Google Scholar] [CrossRef]
- Uchida, K.; Hirao, Y.; Kurata, H.; Kubo, T.; Hatano, S.; Inoue, K. Dual Association Modes of the 2,5,8-Tris(Pentafluorophenyl)Phenalenyl Radical. Chem.–Asian J. 2014, 9, 1823–1829. [Google Scholar] [CrossRef]
- Kertesz, M. Pancake Bonding: An Unusual Pi-Stacking Interaction. Chem.–Eur. J. 2019, 25, 400–416. [Google Scholar] [CrossRef]
- Yoneda, K.; Nakano, M.; Fukuda, K.; Matsui, H.; Takamuku, S.; Hirosaki, Y.; Kubo, T.; Kamada, K.; Champagne, B. Third-Order Nonlinear Optical Properties of One-Dimensional Open-Shell Molecular Aggregates Composed of Phenalenyl Radicals. Chem.–Eur. J. 2014, 20, 11129–11136. [Google Scholar] [CrossRef]
- Salustro, S.; Maschio, L.; Kirtman, B.; Rérat, M.; Dovesi, R. Third-Order Electric Field Response of Infinite Linear Chains Composed of Phenalenyl Radicals. J. Phys. Chem. C 2016, 120, 6756–6761. [Google Scholar] [CrossRef]
- Dovesi, R.; Erba, A.; Orlando, R.; Zicovich-Wilson, C.M.; Civalleri, B.; Maschio, L.; Rérat, M.; Casassa, S.; Baima, J.; Salustro, S.; et al. Quantum-Mechanical Condensed Matter Simulations with CRYSTAL. WIREs Comput. Mol. Sci. 2018, 8, e1360. [Google Scholar] [CrossRef]
- Matsui, H.; Nakano, M.; Champagne, B. Theoretical Study on the Spin State and Open-Shell Character Dependences of the Second Hyperpolarizability in Hydrogen Chain Models. Phys. Rev. A 2016, 94, 42515. [Google Scholar] [CrossRef]
- Matsui, H.; Yamane, M.; Tonami, T.; Nagami, T.; Watanabe, K.; Kishi, R.; Kitagawa, Y.; Nakano, M. Theoretical Study on the Gigantic Effect of External Static Electric Field Application on the Nonlinear Optical Properties of 1,2,3,5-Dithiadiazolyl p-Radical Dimers. Mater. Chem. Front. 2018, 2, 785–790. [Google Scholar] [CrossRef]
- Shoda, J.; Yokoyama, M.; Yoshida, W.; Matsui, H.; Sugimori, R.; Kishi, R.; Kitagawa, Y. Theoretical Study on the Correlation between Open-Shell Electronic Structures and Third-Order Nonlinear Optical Properties in One-Dimensional Chains of π-Radicals. J. Phys. Chem. A 2024, 128, 8473–8482. [Google Scholar] [CrossRef]
- Nakano, H. Quasidegenerate Perturbation Theory with Multiconfigurational Self-consistent-field Reference Functions. J. Chem. Phys. 1993, 99, 7983–7992. [Google Scholar] [CrossRef]
- Granovsky, A.A. Extended Multi-Configuration Quasi-Degenerate Perturbation Theory: The New Approach to Multi-State Multi-Reference Perturbation Theory. J. Chem. Phys. 2011, 134, 214113. [Google Scholar] [CrossRef] [PubMed]
- Nakano, M.; Takebe, A.; Kishi, R.; Ohta, S.; Nate, M.; Kubo, T.; Kamada, K.; Ohta, K.; Champagne, B.; Botek, E.; et al. Second Hyperpolarizabilities (γ) of Open-Shell Singlet One-Dimensional Systems: Intersite Interaction Effects on the Average Diradical Character and Size Dependences of γ. Chem. Phys. Lett. 2006, 432, 473–479. [Google Scholar] [CrossRef]
- Nakano, M.; Minami, T.; Fukui, H.; Kishi, R.; Shigeta, Y.; Champagne, B. Full Configuration Interaction Calculations of the Second Hyperpolarizabilities of the H4 Model Compound: Summation-over-States Analysis and Interplay with Diradical Characters. J. Chem. Phys. 2012, 136, 024315. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision D.01.; Gaussian, Inc.: Wallingford CT, USA, 2013. [Google Scholar]
- Barca, G.M.J.; Bertoni, C.; Carrington, L.; Datta, D.; De Silva, N.; Deustua, J.E.; Fedorov, D.G.; Gour, J.R.; Gunina, A.O.; Guidez, E.; et al. Recent developments in the general atomic and molecular electronic structure system. J. Chem. Phys. 2020, 152, 154102. [Google Scholar] [CrossRef]
- Cui, Z.; Lischka, H.; Beneberu, H.Z.; Kertesz, M. Rotational Barrier in Phenalenyl Neutral Radical Dimer: Separating Pancake and van Der Waals Interactions. J. Am. Chem. Soc. 2014, 136, 5539–5542. [Google Scholar] [CrossRef]
- Shirai, S.; Iwata, S.; Tani, T.; Inagaki, S. Ab Initio Studies of Aromatic Excimers Using Multiconfiguration Quasi-Degenerate Perturbation Theory. J. Phys. Chem. A 2011, 115, 7687–7699. [Google Scholar] [CrossRef]
- Ohta, K.; Yamada, S.; Kamada, K.; Slepkov, A.D.; Hegmann, F.A.; Tykwinski, R.R.; Shirtcliff, L.D.; Haley, M.M.; Sałek, P.; Gel’mukhanov, F.; et al. Two-Photon Absorption Properties of Two-Dimensional π-Conjugated Chromophores: Combined Experimental and Theoretical Study. J. Phys. Chem. A 2011, 115, 105–117. [Google Scholar] [CrossRef] [PubMed]
- Beerepoot, M.T.P.; Friese, D.H.; List, N.H.; Kongsted, J.; Ruud, K. Benchmarking Two-Photon Absorption cross Sections: Performance of CC2 and CAM-B3LYP. Phys. Chem. Chem. Phys. 2015, 17, 19306–19314. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).