Abstract
Ethylene glycol (EG) produced from biomass is a promising candidate for several new applications. In this paper, EG derivatives such as mono- and di-tert-butyl ethers are considered. However, accurate thermodynamic data are essential to optimise the technology of the direct tert-butyl ether EG synthesis reaction or reverse process isobutene release. The aim of this work is to measure the vapour pressures and combustion energies for these ethers and determine the vaporisation enthalpies and enthalpies of formation from these measurements. Methods based on the First and Second Law of Thermodynamics were combined to discover the reliable thermodynamics of ether synthesis reactions. The thermochemical data for ethylene glycol tert-butyl ethers were validated using structure–property correlations and quantum chemical calculations. The literature results of the equilibrium study of alkylation of EG with isobutene were evaluated and the thermodynamic functions of ethylene glycol tert-butyl ethers were derived. The energetics of alkylation determined according to the “First Law” and the “Second Law” methods agree very well. Some interesting aspects related to the entropy of ethylene glycol tert-butyl ethers were also revealed and discussed.
1. Introduction
Producing energy, fuels, and chemicals from renewable biomass is crucial to preventing global warming by reducing the atmospheric CO2 emissions caused by fossil fuel consumption. Cellulose, the most abundant biomass source, is currently seen as a promising alternative to fossil fuels because it is not edible and does not negatively affect the food market. The most attractive and sustainable route for the use of cellulose could be the direct conversion into platform chemicals [1]. The catalytic conversion of cellulose into ethylene glycol (EG), propylene glycol, xylitol, sorbitol, mannitol, etc. offers an alternative route to these important chemicals, which are used in the food industry as functional additives, as intermediates in the pharmaceutical industry and as monomers in the plastics industry [2]. An effective route for the one-pot production of EG from renewable cellulose using various non-expensive catalysts has attracted great interest from both academia and industry [2,3]. Compared to the petroleum-dependent multi-step process, the biomass route offers the outstanding advantages of a one-pot process and a renewable feedstock.
EG is used in the production of polyester fibres and resins (e.g., polyethylene terephthalate) and is widely applied as a component of antifreeze or coolant systems in cars and in de-icing fluids for aircraft [4]. Currently, EG is manufactured from petroleum-derived ethylene in several steps by cracking, epoxidation, and hydration [5]. The fact that EG can be derived not only from fossil resources but also from biomass [6] makes it a promising candidate for various new applications, e.g., for the synthesis of platform chemicals such as coating solvents and oxygenate additives for gasoline blends. For example, the reaction of isobutene with EG in the presence of an acid catalyst gives a mixture of mono- and di-tert-butyl ethers (see Figure 1).
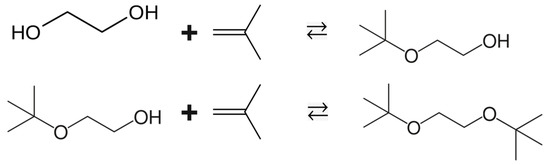
Figure 1.
Alkylation of ethylene glycol with isobutene: synthesis of ethylene glycol mono-tert-butyl ether (EGM) in the first line and the synthesis of ethylene glycol di-tert-butyl ether (EGD) in the second line.
The latter are good solvents for paints, inks, and coatings with low toxicity [7]. The tert-butyl ethers of diols are also potential oxygenate additives for motor gasoline, exhibiting high anti-knock properties [8]. Isobutene is usually produced by the steam cracking of high-boiling petroleum fractions and must be separated from the C4 mixture in an additional purification step by using either sulphuric acid extraction or molecular sieves [9]. An interesting alternative to these conventional processes is the use of EG as a very good capture agent for isobutylene from the C4 cracking fraction [10]. The tert-butyl ethers formed can then be used directly as solvents or oxygenate additives or can be readily cracked to yield very pure isobutylene, which is needed for the production of a variety of chemicals and polymers [11].
The kinetics and catalysis of the tert-butylation of EG have been intensively studied since the 1970s [10,11,12,13]. The influence of various homogeneous and heterogeneous acid catalysts and the optimisation of reaction conditions were the focus of these studies. However, the thermodynamic aspects were not of interest, although the alkylation and dealkylation of EG are reversible processes and the equilibrium of these reactions takes place under thermodynamic control. This means that the equilibrium of these reactions can be shifted towards a high yield of the desired product according to Le Chatelier’s principle. Therefore, accurate thermodynamic data (e.g., reaction enthalpies, reaction entropies, heat capacities, etc.) are indispensable to optimise the technology of the direct tert-butyl ether synthesis reaction or isobutene release in the reverse process. For the distillation of tert-butyl ethers from the reaction mixture as well as for their purification, reliable data on vapour pressures and evaporation enthalpies of the pure compounds are also needed. It has turned out that no thermodynamic data for tert-butyl ethers are available in the literature.
The aim of this work is, therefore, to measure the vapour pressures and combustion energies of tert-butyl ethers (see Figure 1) and determine the vaporisation enthalpies and enthalpies of formation from these measurements.
The focus of this study is on the thermochemical properties that are responsible for the energetics of chemical reactions, as well as for the liquid–gas phase change enthalpy. The common textbook equations relate these thermochemical properties:
where (g) is the gas phase standard molar enthalpy of formation, (liq) is the liquid state standard molar enthalpy of formation, and is the standard molar enthalpy of vaporisation. In thermochemistry, it is common to adjust all of the enthalpies involved in Equation (1) to an arbitrary but common reference temperature. In this work, we have chosen T = 298.15 K as the reference temperature. The energetics of the synthesis reactions of tert-butyl ethers according to Equations (2) and (3):
is essential for chemical-engineering calculations.
Ethylene glycole + isobutylene = EGM
EGM + isobutylene = EGD
There are two ways to derive the energetics of chemical reactions: according to the First Law of Thermodynamics or according to the Second Law of Thermodynamics [14]. If the reaction enthalpies are derived from the calorimetrically measured enthalpies of formation, they are considered to be calculated from the First Law of Thermodynamics. For thermochemistry, Hess proposed to estimate the enthalpy of reaction as the difference between the enthalpies of the formation of the reactants and products, which is also called Hess’s law. If the reaction enthalpies are derived from the temperature dependence of equilibrium constants, they are considered to be calculated from the Second Law of Thermodynamics. However, both methods complement each other. The results for a given reaction obtained by the “First Law” and “Second Law” methods can serve as a valuable test of the thermodynamic consistency and reliability of the experimental results.
In this work, we combined the methods of the “First Law” and the “Second Law” to obtain the reliable thermodynamics of the synthesis reactions of ethylene glycol tert-butyl ethers. The enthalpy of the formation of mono-tert-butyl ether was measured with high-precision combustion calorimetry and the vaporisation enthalpy was measured with transpiration and static methods. A sample of ethylene glycol di-tert-butyl ether with sufficient purity for thermochemical measurements was not available, so the thermochemical data for this ether were derived from the structure–property correlations and quantum chemical calculations. The results of the equilibrium study of Reactions (1) and (2) from the literature [15] were evaluated and the thermodynamic functions of these reactions were derived according to the “Second Law” method. The energetics of Reactions (1) and (2) determined according to the “First Law” and the “Second Law” methods agree very well. Finally, some interesting aspects related to the entropy of ethylene glycol tert-butyl ethers were revealed and discussed.
2. Experimental Methods
2.1. Materials
The sample of ethylene glycol mono-tert-butyl ether (EGM) with a purity >0.99 mass fraction was of commercial origin (TCI, # E0354). It was further purified by fractional distillation under reduced pressure. Purity was determined by capillary gas chromatography using a flame ionisation detector (FID). No impurities (greater than mass fraction 0.0004) could be detected in the sample used for the thermochemical experiments. Residual water in the sample was measured using a Mettler Toledo DL38 Karl Fischer titrator with HYDRANAL™ solvent. The mass fraction of water (865 ppm) was used for the corrections of the sample masses in the combustion calorimetry experiments.
2.2. Experimental and Theoretical Thermochemical Methods
The vapour pressures over the liquid sample of EGM were measured at different temperatures using the transpiration method [16]. About 0.5 g of the sample was used to cover the small glass beads to provide sufficient contact surface with the transporting gas and to eliminate hydraulic resistance. These covered glass spheres were loaded into the U-shaped saturator. A stream of nitrogen at a well-defined flow rate was passed through the saturator at a constant temperature (±0.1 K), and the transported material was collected in a cold trap. The amount of substance condensed in the cold trap was determined by gas chromatography and used to derive the vapour pressure according to the ideal gas law. The details of this method can be found elsewhere [16,17,18]. A brief description and the necessary details can be found in ESI.
Independently, the vapour pressures above the liquid sample of EGM were measured at different temperatures using the static method [19]. The stainless-steel cylindrical cell with the sample was kept at a constant temperature. The sample cell was connected to high-temperature capacitance manometers, which can measure vapour pressures from 0.1 to 105 Pa. The details of this method can be found elsewhere [19,20]. A brief description and the necessary details can be also found in ESI.
The experimental vapour pressure–temperature dependencies measured by either the transpiration or static method were used to derive the enthalpies of vaporisation enthalpies, , and inserted into Equation (1).
The energy of the combustion of EGM was measured with an isoperibol bomb calorimeter. The liquid sample was transferred (in the glove box) with a syringe into the polyethylene bulb (Fa. NeoLab, Heidelberg, Germany). The neck of the bulb was compressed with special tweezers and sealed by heating the neck near a glowing wire. The bulb with the liquid sample was placed in a crucible and burnt in oxygen at a pressure of 3.04 MPa, according to a procedure described in detail previously [21,22]. The combustion gases were analysed for carbon monoxide (Dräger tubes) and unburnt carbon, neither of which could be detected. To detect traces of CO in the combustion exhaust gases, they were passed through a Dräger tube (glass vial containing a chemical reagent that reacts with CO, with detection limits of 5 to 150 ppm). The energy equivalent of the calorimeter εcalor was determined with a standard reference sample of benzoic acid (sample SRM 39j, N.I.S.T.). The auxiliary quantities used for the data acquisition of combustion experiments are compiled in Table S1. For the conversion of the energy of the actual bomb process into that of the isothermal process, and the reduction to standard state, the conventional procedure was applied [23]. The necessary details can be found in ESI. The standard molar enthalpy of formation of the liquid state, (liq), was derived from their energies of combustion and inserted into Equation (1).
Quantum chemical (QC) calculations were carried out using the Gaussian 09 series software [24]. The energies of the most stable conformers were calculated using the G4 method [25]. The H298 values were finally converted to the theoretical (g, 298.15 K)theor values and discussed. Calculations were performed under the assumption of “rigid rotator”–“harmonic oscillator” and the general procedure was described elsewhere [26].
3. Results and Discussion
3.1. Absolute Vapour Pressures
The systematic vapour pressure measurements on EGM were carried out for the first time. The primary experimental vapour pressures, p, of EGM at various temperatures measured by the transpiration method are given in Table 1.

Table 1.
The absolute vapour pressures, p, and the standard vaporisation enthalpies, , and vaporisation entropies, , as determined by the transpiration method.
The primary experimental vapour pressures, p, of EGM at various temperatures measured by the static method are given in Table 2.

Table 2.
The absolute vapour pressures, p, and the standard vaporisation enthalpies, , and vaporisation entropies, , as determined by the static method.
The vapour pressures measured for EGM using the transpiration and static methods are compared in Figure S1 and are hardly distinguishable from each other. No vapour pressure measurements for mono and di-tert-butyl ethers can be found in the literature. Therefore, any additional information is valuable. Thus, we searched for individual experimental boiling temperatures at different pressures, which are sometimes given in the literature as the results of the distillation of reaction mixtures after synthesis. Since these data do not come from specific physico–chemical investigations, the temperatures are usually given in the range of a few degrees and the pressures are measured with non-calibrated manometers. However, in our previous work, we showed that reasonable trends can generally be derived even from such raw data [27]. The experimentally determined boiling temperatures for EGM at different pressures (see Figure S1) confirm this conclusion qualitatively (and quantitatively for (298.15 K) values as shown in Section 3.2). The individual experimental boiling temperatures at different pressures taken from the databases [28,29] are compiled in Table S2 and are used for the evaluation. The vapour pressure data sets given in Table 1, Table 2 and Table S2 were approximated with the following equation [16]:
In this equation, R = 8.31,446 J·K−1·mol−1; and a and b are adjustable parameters and is the difference between the molar heat capacity of the liquid and gas phases; T0 = 298.15 K was adopted in this work. The values of were estimated for the compound of interest using an empirical correlation [30] based on heat capacities (liq). The latter values were of experimental origin or were assessed using a group-contribution method [31] (see Table S3). The parameters a and b fitted to the experimental vapour pressures were used to derive the thermodynamic functions of vaporisation, as shown in the next section.
3.2. Thermodynamics of Vaporisation
The standard molar enthalpies of the vaporisation of EGM and EGD at temperature T were derived from the temperature dependence of the vapour pressures using the following equation:
The standard molar vaporisation entropies at temperature T were also derived from the temperature dependences of the vapour pressures using Equation (6):
The primary data on the vapour pressures, coefficients a and b (see Equation (4)), (T), and (T) values are compiled in Table 1, Table 2 and Table S2. The vaporisation enthalpies derived indirectly from vapour pressure measurements are usually referenced to Tav, which is defined as the average temperature of the range under study. For comparison, (Tav) values are commonly adjusted to T = 298.15 K. The temperature adjustment was performed according to Kirchhoff’s law:
A summary of the results for (298.15 K) is given in Table 3, column 5.

Table 3.
Compilation of the enthalpies of vaporisation, , derived for ethylene glycol tert-butyl ethers.
The combined uncertainties of the vaporisation enthalpies (298.15 K) from the transpiration method include the uncertainties of the experimental transpiration conditions, uncertainties of the vapour pressures, and uncertainties due to the temperature adjustment to the reference temperature T = 298.15 K, as developed elsewhere [17,18]. The combined uncertainties of the vaporisation enthalpies (298.15 K) from the static method include uncertainties from the fitting equation and uncertainties from the temperature adjustment to T = 298.15 K. Uncertainties in the temperature adjustment of vaporisation enthalpies to the reference temperature T= 298.15 K are estimated to account for 20% of the total adjustment. The combined uncertainties of the vaporisation enthalpies (298.15 K) obtained from the vapour pressure data collected in the literature (see Table S2) were calculated in the same way as for the static method.
As shown in Table 3 for EGM, our results for (298.15 K) derived from transpiration and static methods are practically indistinguishable. The (298.15 K) value estimated from the individual boiling temperatures found in the literature at different pressures also agrees with our results and is within the experimental uncertainties. No comparative data for (298.15 K) of EGD were found in the literature.
3.3. Validation of the Vaporisation Enthalpies Using Structure–Property Correlations
The absence of data on vapour pressures and vaporisation thermodynamics for tert-butyl ethers has prompted an extended validation of the enthalpies of vaporisation using structure–property correlations as follows.
3.3.1. Correlation with the Normal Boiling Temperatures Tb
A correlation of the enthalpies of vaporisation of organic molecules with their normal boiling temperatures successfully serves to mutually validate these thermal data [32]. The chemical family of alkyl ethers is thermally stable even at elevated temperatures near the boiling points, therefore, numerous reliable normal boiling temperatures for many ethers have been found in the literature (see Table 4 and Table 5).

Table 4.
Correlation of the vaporisation enthalpies (298.15 K) of ethylene glycol mono-alkyl ethers with their Tb (normal boiling temperatures).

Table 5.
Correlation of the vaporisation enthalpies (298.15 K) of di-alkyl ethers and ethylene glycol di-alkyl ethers with their Tb (normal boiling temperatures).
Numerous reliable experimental data on (298.15 K) are also available in the literature (see Table 4 and Table 5) and are ready for correlation with normal boiling temperatures.
For ethylene glycol mono-alkyl ethers R-CH2CH2OH, the following linear correlation was derived:
The uncertainty of the enthalpies of vaporisation calculated with Equation (8) is estimated to be 0.5 kJ·mol−1 (see Table 4).
For ethylene glycol di-alkyl ethers RO-CH2CH2-OR, the following linear correlation was derived:
The uncertainty of the enthalpies of vaporisation calculated with Equation (9) is estimated to be 2.0 kJ·mol−1 (see Table 5). The very high R2 correlation coefficients of Equations (8) and (9) are evidence of the consistency of the data sets on alkyl ethers included in the correlations. The “empirical” results derived from Equations (8) and (9) are listed in Table 3 and labelled Tb. These results are valuable in supporting the enthalpy of vaporisation of EGM derived from other methods, especially for EGD for which no data are available.
3.3.2. Correlation with the Enthalpies of Vaporisation of the Parent Structures
Structure–property correlations are a valuable tool to establish the consistency of experimental data in the series of parent homologues. It is evident that the ethylene glycol mono-tert-butyl ether studied in this work belongs to a general family of ethylene glycol mono-alkyl ethers, R-CH2CH2OH, which are structurally parent to the di-alkyl ethers, R-O-R. In this work, we correlated the experimental (298.15 K) values for the homologue series of R-CH2CH2OH with the experimental vaporisation enthalpies for the homologue series of di-alkyl ethers, R-O-R. The compilation of experimental data involved in this correlation is shown in Table 6.

Table 6.
Correlation of the vaporisation enthalpies, (298.15 K), of ethylene glycol mono-alkyl ethers and di-alkyl ethers (in kJ·mol−1) a.
A very good linear correlation was found for these structurally related series:
The very high R2 correlation coefficient can be taken as evidence for the general consistency of the evaluated vaporisation enthalpies of R-CH2CH2OH with the well-established set of data for d-alkyl ethers. Consequently, the enthalpy of vaporisation of ethylene glycol mono-tert-butyl ether (EGM) was derived using Equation (10) as an independent and complementary result (see Table 6).
A similar correlation was applied to EGD, as follows. The ethylene glycol di-tert-butyl ether (EGD) belongs to a general family of ethylene glycol di-alkyl ethers, RO-CH2CH2-OR, which are also structurally related to the series of di-alkyl ethers, R-O-R. Therefore, we correlated the experimental (298.15 K) values for the homologue series of RO-CH2CH2-OR with the experimental vaporisation enthalpies for the homologue series of di-alkyl ethers, R-O-R. The compilation of experimental data involved in this correlation is shown in Table 7.

Table 7.
Correlation of the vaporisation enthalpies, (298.15 K), of ethylene glycol di-alkyl ethers and di-alkyl ethers (in kJ·mol−1) a.
In this case, too, an almost perfect linear correlation (with R2 = 0.9998) was derived for these structural parent series:
The enthalpy of vaporisation of ethylene glycol di-tert-butyl ether (EGD) was, therefore, estimated according to Equation (11) and complements the results obtained in this work with other methods. The “empirical” results obtained from Equations (10) and (11) are given in Table 3 and marked SP (structure–property). These results help to ascertain the enthalpy of vaporisation of EGM and EGD determined by other methods.
As a conclusion from the validation of the vaporisation enthalpies performed in Section 3.3, completely different structure–property correlations were applied to check the data consistency for EGM and EGD (see Table 3). It was found that the experimental and empirical results agree very well for both ethers. To provide more confidence, a weighted average value was calculated for each compound (bold values in Table 3), and these values were recommended for further thermochemical calculations according to Equation (3) to derive the gas phase formation enthalpies using the (liq) values measured by combustion calorimetry, as shown in the following section.
3.4. Standard Molar Enthalpies of Formation in the Liquid Phase
The standard specific energy of combustion (liq) of liquid ethylene glycol mono-tert-butyl ether was determined from six experiments. The results of the combustion experiments are shown in Table 8.

Table 8.
The results of the combustion experiments at T = 298.15 K (p° = 0.1 MPa) for ethylene glycol mono-tert-butyl ether (EGM) a.
These (liq) values were used to calculate the experimental standard molar enthalpy of combustion, , (see Table 8) of ethylene glycol mono-tert-butyl ether, which refers to the reaction:
C6H14O2 + 9.5 O2 = 6 CO2 + 7 H2O
The standard molar enthalpy of formation, (liq), (see Table 8) was calculated based on the values of the reaction according to Equation (12) using Hess’s Law and the molar enthalpies of the formation of H2O(liq) and CO2(g) assigned by CODATA [34]. The total uncertainties of the and values were calculated according to the guidelines presented by Hubbard et al. [23] and Olofsson [35]. The uncertainty of combustion energy, (liq), was expressed as the standard deviation of the mean. According to the thermochemical practice, the uncertainties assigned to the (liq) values are twice the overall standard deviations and include the uncertainties of the calibration, the combustion energies of the auxiliary materials, and the uncertainties of the enthalpies of formation of the reaction products H2O and CO2. A summary of the thermochemical data for the ethylene tert-butyl ethers is given in Table 9.

Table 9.
Thermochemical data at T = 298.15 K for the ethylene tert-butyl ethers (p° = 0.1 MPa, in kJ·mol−1) a.
The combustion experiments with ethylene glycol mono-tert-butyl ether were carried out for the first time.
3.5. Standard Molar Enthalpies of Formation in the Gas Phase
The experimental standard molar enthalpy of formation, (liq, 298.15 K), of ethylene glycol mono-tert-butyl ether given in Table 9 was used together with the experimental vaporisation enthalpy, (298.15 K), recommended in Table 3, to derive the experimental standard molar enthalpy of formation in the gas phase, (g, 298.15 K), (see Table 9, column 4) according to Equation (3). This experimental result can now be used for comparison with the theoretical value calculated by the high-level quantum-chemical (QC) composite method G4 [25]. Nowadays, QC methods have acquired the status of a valuable tool for the mutual consistency of thermochemical results. Therefore, the agreement or disagreement between the theoretical and experimental (g, 298.15 K) values could help with the attestation of the quality of the experimental and computational procedures.
In a number of our recent studies [36], we have shown that the G4 method is capable of providing reliable gas phase enthalpies of formation (g, 298.15 K) using the atomisation procedure [26]. Therefore, in the current study, the H298 enthalpies of the most stable conformers of EGM and EGD were calculated using the G4 method and converted to the theoretical values using the atomisation procedure (see Table 9, column 5). The theoretical value (g, 298.15 K)theor = −477.2 ± 3.5 kJ·mol−1 for EGM agrees very well with the experimental result (g, 298.15 K)exp = −475.5 ± 1.7 kJ·mol−1 and this creates confidence in the calculation method. Consequently, we used the theoretical value (g, 298.15 K)theor = −553.5 ± 3.5 kJ·mol−1 for EGD and the experimental result for (298.15 K) = 52.3 ± 0.6 kJ·mol−1 to calculate the missing liquid phase enthalpy of formation (liq, 298.15 K) = −605.8 ± 3.6 kJ·mol−1 for EGD (see Table 9, column 2).
This completes the development of the data set of thermochemical values (see Table 9) required for the interpretation of the energetics of chemical reactions according to Equations (1) and (2), which represent the synthesis of platform chemicals from ethylene glycol and isobutene. These energetics are derived and discussed in the next section.
3.6. Energetics of Ethylene Glycol Alkylation Reactions from the “First Law” Method
It is well known that ether synthesis reactions from alcohols and olefins are highly exothermic [36], and accurate knowledge of the energetics of these reactions is essential for the safety of industrial processes. The liquid phase reaction enthalpies, (298.15 K), of the EGM and EGD synthesis from EG and isobutene were calculated using Hess´s Law according to the following equations:
The experimental data on (liq), required for the calculations according to Equations (13) and (14), are obtained in this work (see Table 9) or taken from the literature (see Table S4). The uncertainties of these reaction enthalpies include the uncertainties of all reactants. The enthalpies of Reactions (13) and (14) are quite similar in their experimental uncertainties. However, the reaction enthalpy of Reaction (14) is slightly more negative compared to Reaction (13), which is probably because the ethylene glycol di-tert-butyl ether is more branched and strained than the mono-tert-butyl substituted precursor. Consequently, more energy is required to form this compound. The energetics of Reactions (13) and (14) are moderate, but large enough to cause a possible reactor temperature runaway if the mixing of the reactants is disturbed. Therefore, the reliable thermodynamics of Reactions (13) and (14) evaluated in this work are useful for determining the appropriate temperature management of chemical reactors.
Another perspective for using the thermodynamic data of EGM and EGD is related to an interesting technological idea of improving the conversion of iso-olefins in the production of methyl tert-butyl ether (MTBE) or methyl tert-amyl ether (TAME). It has been found that the overall conversion of an iso-olefin can be significantly increased if the iso-olefin is first reacted with ethylene glycol at 40–70 °C and 5–7 atm over sulfonated resin catalysts and then the resulting ethylene glycol tert-alkyl ethers are reacted with methanol at an elevated temperature and 1.5–2 atm over the same catalyst [11]. The chemical reactions for the second step are shown in Figure 2.
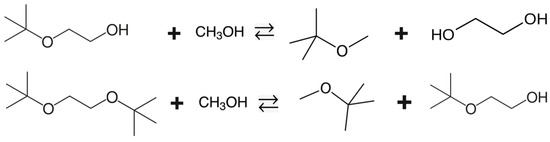
Figure 2.
The liquid phase reactions of the MTBE synthesis from EGM or EGD and methanol.
The liquid phase reactions of the MTBE synthesis from EGM or EGD and methanol are given by Equations (15) and (16):
EGM + Methanol = MTBE + Ethylene glycol
EGD + Methanol = MTBE + EGM
The liquid phase reaction enthalpies, (298.15 K), of the MTBE synthesis from EGM or EGD and methanol were calculated according to the following equations:
The experimental data on (liq) required for the calculations according to Equations (17) and (18) are obtained in this work (see Table 9) or taken from the literature (see Table S4). The uncertainties of these reaction enthalpies include the uncertainties of all reactants. It turned out that, according to our calculations, both Reactions (15) and (16) are practically thermoneutral and, therefore, technologically less demanding.
3.7. Thermodynamic Functions of Ethylene Glycol Alkylation from the “Second Law” Method
The results of the chemical equilibrium study of Reactions (1) and (2) in the presence of an acidic catalyst in the liquid phase were reported by Chang et al. [15]. The equilibrium concentrations of isobutene, EG, EGM, and EGD were measured by gas chromatography, and the concentration equilibrium constants for Reactions (1) and (2) were derived between 318 K and 393 K. The activity coefficients of the reactants were calculated with the commonly used UNIFAC method [37]. The concentration equilibrium constants were multiplied by the activity coefficients and the thermodynamic equilibrium constants Ka (1) and Ka (2) were estimated. The temperature dependences of Ka (1) and Ka (2) are shown in Figure 3.
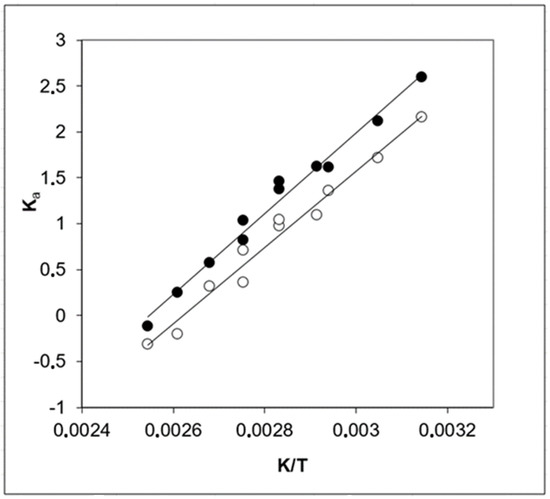
Figure 3.
Temperature dependence of the thermodynamic equilibrium constants of the tert-butylation of ethylene glycol: ○—Ka (1) for the reaction according to Equation (1) and ●—Ka (2) for the reaction according to Equation (2). Experimental data are from Chang et al. [15]. Numerical data are compiled in Table S5.
The thermodynamic functions, the reaction enthalpies, (liq), and reaction entropies, (liq), were derived from the temperature dependences of Ka (1) and Ka (2). The results are given in Table 10.

Table 10.
Thermodynamic functions and of Reactions (1) and (2) in the liquid phase and the temperature dependences ln Ka = a + b.(T/K)−1 (with correlation coefficient R2).
It turned out that the thermodynamic functions and of the synthesis of ethylene glycol mono-tert-butyl ether (Reaction 1) and the synthesis of ethylene glycol di-tert-butyl ether (Reaction 2) are hardly distinguishable within their experimental uncertainties. This finding is rather unexpected, therefore, it is now essential to compare the “First Law” reaction enthalpies, (liq, 298.15 K), for the EGM and EGD synthesis from EG and isobutene (obtained according to Equations (15) and (16)), with the “Second Law” results derived from the equilibrium study of Reactions (1) and (2).
To our satisfaction, the energetics of Reactions (1) and (2) determined according to the “First Law” and the “Second Law” methods agree well and are within their experimental uncertainties. Even the slightly larger enthalpy of reaction for Reaction (1) observed according to the “First Law” is supported by a similar trend shown by the “Second Law” (see Table 10). Such good agreement provides confidence in the reliability of all of the thermodynamic data sets evaluated in this work and used for comparison according to the “First Law” and the “Second Law”.
3.8. Entropies of Ethylene Glycol Tert-Butyl Ethers
Within the framework of this study, we were highly motivated by the practical significance of the thermodynamic functions of ethylene glycol tert-butyl ethers to optimise the technology of their production. One of the main goals was to show that, nowadays, only a reasonable combination of experimental and computational thermodynamics can reduce the costs of developing new technologies for biomass valorisation. The main focus of our thermochemical study was on the energetics of the reactions relevant to biomass valorisation. As shown in Table 10, the alkylation reactions are considerably exothermic so adequate thermal management is required to avoid the runaway of the chemical reactor. The reaction entropies (liq) of Reactions (1) and (2) derived in Table 10 should be considered as by-products in this context. Fortunately, however, these new results open up an unexpected opportunity to gain deeper insights into the structural features of ethylene glycol tert-butyl ethers, which are investigated in this work.
Indeed, according to Hess’s law, which is applied to Reactions (1) and (2), the following equations are responsible for their entropy changes:
where the (liq) values are the standard molar entropies of the corresponding reactants. Admittedly, the (liq) values for the important platform chemicals isobutene and ethylene glycol are available in the literature [38,39,40]. This opens up possibilities for estimating the unknown values (liq)(EGM) and (liq)(EGD) according to Equations (19) and (20) using the experimental reaction entropies (liq) given in Table 10. The entropies of isobutene and EG required for these calculations, as well as the results for EGM and EGD, are summarised in Table 11.

Table 11.
Experimental and estimated entropies of Reactions (1) and (2) participants (at 298.15 K in J·K−1·mol−1).
Considering that the values for (liq)(EGM) and (liq)(EGD) are new, it makes sense to use another complementary method to assess at least a possible level of these values. The correct estimation of the entropies of organic molecules is a challenging task. Various group contribution methods have been developed for this purpose, with Benson’s type [41] of increments being the most popular in the thermodynamic community. The required contributions have been analysed and revised by Domalski and Hearing [42], and we used the numerical values from this compilation for the additive calculations of the entropies of ethylene glycol tert-butyl ethers. When calculating the entropy of a molecule, it is important to consider, together with the sum of the contributions, the global symmetry number σ, which is the number of superimposable configurations that include the outer symmetry and the inner free rotors; this is described in detail by Benson [41] and helpful examples are given in [43]. The results of the additive liquid phase and gas phase entropy calculations, including the σ values, are summarised in Table 11. However, these results are rather disappointing, because, for simple molecules such as isobutene with only two inner free rotors and σ = 18 and ethylene glycol with σ = 2, the agreement with the experimental values is still acceptable for both the liquid and the gas phase. For the more complicated molecules EGM and EGD, with a considerable number of free rotors and very large symmetry numbers, the additivity did not lead to entropies comparable to the experiment (see Table 11) in either the liquid or the gas phase. This significant disagreement raised the legitimate question of whether the experimental entropies were correct. To answer this question, we calculated the gas phase entropies of EGM and EGD using the quantum chemical G4 method. The results are shown in Table 11. At first glance, it was obvious that the entropies calculated by G4 did not match the experiment either (see Table 11), but subtracting the symmetry correction (R × lnσ) from the direct G4 result brought the calculated and experimental values into agreement (see Table 11):
This very good agreement supports the reliability of the experimental liquid and gas phase entropies of EGM and EGD. At the same time, the difficulties in reconciling the experimental, additive, and quantum chemical entropies highlighted in this section provide important insights into the limitations of empirical methods and the positive experiences with quantum chemical methods. So, in this paper, the focus was not on the theory, rather, we paid attention to the practical thermodynamic aspects of biomass valorisation. Unexpectedly, however, we were confronted with theory and obtained “cashback” with theoretical aspects related to the entropy calculations of flexible molecules with a large number of free rotators.
3.9. Standard Molar Thermodynamic Functions of Ethylene Glycol Tert-Butyl Ethers
Due to the developments in “green chemistry”, EG-tert-butyl ether has been considered as a large-scale platform chemical produced from cellulose [1]. However, thermodynamic modelling and optimisation of EG-tert-butyl ether synthesis require knowledge of the fundamental thermodynamic functions of these compounds. This work has contributed by evaluating the energetic and entropic properties of EG tert-butyl ethers. Thus, we compiled the available experimental values and calculated thermodynamic formation functions for EG tert-butyl ethers, which are listed in Table 12.

Table 12.
Standard molar thermodynamic properties of ethylene glycol tert-butyl ethers at T = 298.15 K.
The entropies of formation, , were calculated based on Reactions (21) and (22):
using the following entropies of formation for Cgraphite (5.74 ± 0.13) J·K−1·mol−1, H2(g) (130.52 ± 0.02) J·K−1·mol−1, and O2(g) (205.04 ± 0.03) J·K−1·mol−1 recommended in [44]. The Gibbs function of formation, , was estimated according to Equation (23) from the values of and given Table 12:
6 Cgraphite +7 H2(g) + O2(g) = C6H14O2 (g or l)
10 Cgraphite +11 H2(g) + O2(g) = C10H22O2 (g or l)
The standard molar thermodynamic functions in the liquid and the gas phase collected in Table 12 can be used for the optimisation of EG tert-butyl ethers to be processed into further valuable biobased fuel additivities and platform chemicals.
This article was written for the Justus von Leibig’s 150 years theme issue; to build a bridge to the main topic, it is worth remembering that the “Liebig cooler” was not invented by Liebig, as is assumed, but became popular through Liebig. We have neither invented experimental thermochemical tools nor developed sophisticated quantum chemical methods. Nevertheless, through our work, we try to make “popular” the idea that the “judicious” combination of experimental, empirical, and quantum chemical methods” is the only modern way to obtain reliable practical and theoretical thermochemical results.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/chemistry5020079/s1. Table S1: Auxiliary quantities: formula, density, massic heat capacity, and expansion coefficients of the materials used in the present study [45,46]; Table S2: Compilation of data on molar heat capacities and heat capacity differences at T = 298.15 K [47]; Details on adjustment of vaporisation/sublimation enthalpies to the reference temperature T = 298.18 K; Details on transpiration method; Details on static methods; Table S3: The vapour pressures and standard vaporisation enthalpies and entropies obtained by the approximation of boiling points at different pressures available in the literature; Table S4: Thermochemical data for reference compounds [48,49]; Table S5: Experimental thermodynamic constants reported by Chang et al. [15]; Figure S1: Comparison of vapour pressures measured in this work over the liquid sample of ethylene glycol mono-tert-butyl ether.
Author Contributions
Conceptualization, methodology, validation, writing—original draft preparation, S.P.V. Investigation, validation, and writing—review and editing, A.A.Z. All authors have read and agreed to the published version of the manuscript.
Funding
S.P.V. acknowledges financial support from DFG, grant VE 265/12−1 “Glycolysis: thermodynamics and pathway predictions”. A.A.Z. is grateful to Deutsche Akademische Austausch Dienst (DAAD) for a scholarship. This paper has been supported by the Kazan Federal University Strategic Academic Leadership Program (“PRIORITY-2030”).
Data Availability Statement
All data used in this work are available from the text and supplementary materials file.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fukuoka, A.; Dhepe, P.L. Catalytic conversion of cellulose into sugar alcohols. Angew. Chem. Int. Ed. Engl. 2006, 45, 5161–5163. [Google Scholar] [CrossRef] [PubMed]
- Wang, A.; Zhang, T. One-pot conversion of cellulose to ethylene glycol with multifunctional tungsten-based catalysts. Acc. Chem. Res. 2013, 46, 1377–1386. [Google Scholar] [CrossRef] [PubMed]
- Ji, N.; Zhang, T.; Zheng, M.; Wang, A.; Wang, H.; Wang, X.; Chen, J.G. Direct Catalytic Conversion of Cellulose into Ethylene Glycol Using Nickel-Promoted Tungsten Carbide Catalysts. Angew. Chem. Int. Ed. Engl. 2008, 47, 8510–8513. [Google Scholar] [CrossRef] [PubMed]
- Yue, H.; Zhao, Y.; Ma, X.; Gong, J. Ethylene glycol: Properties, synthesis, and applications. Chem. Soc. Rev. 2012, 41, 4218–4244. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Neal, L.; Ding, D.; Wu, W.; Baroi, C.; Gaffney, A.M.; Li, F. Recent Advances in Intensified Ethylene Production—A Review. ACS Catal. 2019, 9, 8592–8621. [Google Scholar] [CrossRef]
- Kandasamy, S.; Samudrala, S.P.; Bhattacharya, S. The route towards sustainable production of ethylene glycol from a renewable resource, biodiesel waste: A review. Catal. Sci. Technol. 2019, 9, 567–577. [Google Scholar] [CrossRef]
- Smith, R.L. Review of Glycol Ether and Glycol Ether Ester Solvents Used in the Coating Industry. Environ. Health Perspect. 1984, 57, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Samoilov, V.O.; Stolonogova, T.I.; Ramazanov, D.N.; Tyurina, E.V.; Lavrent’ev, V.A.; Porukova, Y.I.; Chernysheva, E.A.; Kapustin, V.M. tert-Butyl Ethers of Renewable Diols as Oxygenated Additives for Motor Gasoline. Part I: Glycerol and Propylene Glycol. Ethers. Pet. Chem. 2023, 1–9. [Google Scholar] [CrossRef]
- Viswanadham, N.; Saxena, S.K. Etherification of glycerol for improved production of oxygenates. Fuel 2013, 103, 980–986. [Google Scholar] [CrossRef]
- Macho, V.; Kavala, M.; Kolieskova, Z. tert-Butyl ethers of polyhydric alcohols. Neftekhimiya 1979, 19, 821–827. [Google Scholar]
- Jayadeokar, S.S.; Sharma, M.M. Ion exchange resin catalysed etherification of ethylene and propylene glycols with isobutylene. React. Polym. 1993, 20, 57–67. [Google Scholar] [CrossRef]
- Klepáčová, K.; Mravec, D.; Kaszonyi, A.; Bajusl, M. Etherification of glycerol and ethylene glycol by isobutylene. Appl. Catal. A Gen. 2007, 328, 1–13. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, Z.; Tang, J.; Fei, Z.; Liu, Q.; Chen, X.; Cui, M.; Qiao, X. Quest for pore size effect on the catalytic property of defect-engineered MOF-808-SO4 in the addition reaction of isobutylene with ethylene glycol. J. Solid State Chem. 2019, 269, 9–15. [Google Scholar] [CrossRef]
- Verevkin, S.P. Gibbs Energy and Helmholtz Energy: Liquids, Solutions and Vapours; Wilhelm, E., Letcher, T.M., Eds.; Royal Society of Chemistry: Cambridge, UK, 2021; ISBN 978-1-83916-201-5. [Google Scholar]
- Chang, T.-K.; Hwang, J.-H.; Huang, H.-Y.; Su, W.-B.; Hong, C.-T. The thermodynamics properties for the liquid phase synthesis of ethylene glycol tert-butyl ether and ethylene glycol di-tert-butyl ether. Shiyou Jikan 2012, 48, 21–37. [Google Scholar]
- Verevkin, S.P.; Emel´yanenko, V.N. Transpiration method: Vapor pressures and enthalpies of vaporization of some low-boiling esters. Fluid Phase Equilibria 2008, 266, 64–75. [Google Scholar] [CrossRef]
- Verevkin, S.P.; Sazonova, A.Y.; Emel´yanenko, V.N.; Zaitsau, D.H.; Varfolomeev, M.A.; Solomonov, B.N.; Zherikova, K.V. Thermochemistry of halogen-substituted methylbenzenes. J. Chem. Eng. Data 2015, 60, 89–103. [Google Scholar] [CrossRef]
- Emel’yanenko, V.N.; Verevkin, S.P. Benchmark thermodynamic properties of 1,3-propanediol: Comprehensive experimental and theoretical study. J. Chem. Thermodyn. 2015, 85, 111–119. [Google Scholar] [CrossRef]
- Zaitsau, D.H.; Verevkin, S.P.; Sazonova, A.Y. Vapor pressures and vaporization enthalpies of 5-nonanone, linalool and 6-methyl-5-hepten-2-one. Data evaluation. Fluid Phase Equilibria 2015, 386, 140–148. [Google Scholar] [CrossRef]
- Zaitsau, D.H.; Verevkin, S.P. Vapor Pressure of Pure Methyl Oleate—The Main Componene of Biodiesel. Russ. J. Gen. Chem. 2021, 91, 2061–2068. [Google Scholar] [CrossRef]
- Verevkin, S.P.; Schick, C. Substituent effects on the benzene ring. Determination of the intramolecular interactions of substituents in tert-alkyl-substituted catechols from thermochemical measurements. J. Chem. Eng. Data 2000, 45, 946–952. [Google Scholar] [CrossRef]
- Emel´yanenko, V.N.; Verevkin, S.P.; Heintz, A. The gaseous enthalpy of formation of the ionic liquid 1-butyl-3-methylimidazolium dicyanamide from combustion calorimetry, vapor pressure measurements, and ab initio calculations. J. Am. Chem. Soc. 2007, 129, 3930–3937. [Google Scholar] [CrossRef] [PubMed]
- Hubbard, W.N.; Scott, D.W.; Waddington, G.; Rossini, F.D. Standard states and corrections for combustions in a bomb at constant volume. In Experimental Thermochemistry: Measurements of Heats of Reactions; Rossini, F.D., Ed.; Interscience: New York, NY, USA, 1956; Volume 1, pp. 75–128. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; et al. Gaussian 09, Revision A.02; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Curtiss, L.A.; Redfern, P.C.; Raghavachari, K. Gaussian-4 theory. J. Chem. Phys. 2007, 126, 84108–84112. [Google Scholar] [CrossRef]
- Verevkin, S.P.; Emel´yanenko, V.N.; Notario, R.; Roux, M.V.; Chickos, J.S.; Liebman, J.F. Rediscovering the wheel. Thermochemical analysis of energetics of the aromatic diazines. J. Phys. Chem. Lett. 2012, 3, 3454–3459. [Google Scholar] [CrossRef]
- Samarov, A.A.; Verevkin, S.P. Hydrogen storage technologies: Methyl-substituted biphenyls as an auspicious alternative to conventional liquid organic hydrogen carriers (LOHC). J. Chem. Thermodyn. 2022, 165, 106648. [Google Scholar] [CrossRef]
- SciFinder—Chemical Abstracts Service. Available online: https://scifinder.cas.org/ (accessed on 28 March 2023).
- Reaxys. Available online: https://www.reaxys.com/ (accessed on 28 March 2023).
- Chickos, J.S.; Acree, W.E. Enthalpies of sublimation of organic and organometallic compounds. 1910–2001. J. Phys. Chem. Ref. Data 2002, 31, 537–698. [Google Scholar] [CrossRef]
- Chickos, J.S.; Hosseini, S.; Hesse, D.G.; Liebman, J.F. Heat capacity corrections to a standard state: A comparison of new and some literature methods for organic liquids and solids. Struct. Chem. 1993, 4, 271–278. [Google Scholar] [CrossRef]
- Benson, S.W. Some Observations on the Structures of Liquid Alcohols and Their Heats of Vaporization. J. Am. Chem. Soc. 1996, 118, 10645–10649. [Google Scholar] [CrossRef]
- Majer, V.; Svoboda, V. Enthalpies of Vaporization of Organic Compounds: A Critical Review and Data Compilation; Blackwell Scientific Publications: Oxford, UK, 1985; pp. 1–300. [Google Scholar]
- Cox, J.D.; Wagman, D.D.; Medvedev, V.A. CODATA Key Values for Thermodynamics; Hemisphere Pub. Corp.: New York, NY, USA, 1989. [Google Scholar]
- Olofsson, G. Assignment of uncertainties, Chapter 6. In Experimental Chemical Thermodynamics. Combustion Calorimetry; Sunner, S., Mansson, M., Eds.; Pergamon Press: Oxford, UK, 1976; Volume 1, pp. 137–161. [Google Scholar]
- Verevkin, S.P.; Konnova, M.E.; Zherikova, K.V.; Pimerzin, A.A. Thermodynamics of glycerol and diols valorisation via reactive systems of acetals synthesis. Fluid Phase Equilibria 2020, 510, 112503. [Google Scholar] [CrossRef]
- Fredenslund, A.; Jones, R.L.; Prausnitz, J.M. Group-contribution estimation of activity coefficients in nonideal liquid mixtures. AIChE J. 1975, 21, 1086–1099. [Google Scholar] [CrossRef]
- Parks, G.S.; Kelley, K.K.; Huffman, H.M. Thermal data on organic compounds. V. A revision of the entropies and free energies of nineteen organic compounds. J. Am. Chem. Soc. 1929, 51, 1969–1973. [Google Scholar] [CrossRef]
- Stull, D.R.; Westrum, E.F., Jr.; Sinke, G.C. The Chemical Thermodynamics of Organic Compounds; John Wiley and Sons, Inc.: New York, NY, USA, 1969. [Google Scholar]
- Todd, S.S.; Parks, G.S. Thermal data on organic compounds. XV. Some heat capacity, entropy and free energy data for the isomeric butenes. J. Am. Chem. Soc. 1936, 58, 134–137. [Google Scholar] [CrossRef]
- Benson, S.W. Thermochemical Kinetics, 2nd ed.; Wiley-Interscience: New York, NY, USA, 1976; pp. 47–50. [Google Scholar]
- Domalski, E.S.; Hearing, E.D. Heat Capacities and Entropies of Organic Compounds in the Condensed Phase. Volume III. J. Phys. Chem. Ref. Data 1996, 25, 1. [Google Scholar] [CrossRef]
- Domalski, E.S.; Hearing, E.D. Estimation of Thermodynamic Properties of Organic Compounds in the Gas, Liquid, and Solid Phases at 298.15 K. J. Phys. Chem. Ref. Data 1988, 17, 1637. [Google Scholar] [CrossRef]
- Chase, M.W., Jr. NIST-JANAF Themochemical Tables, Fourth Edition. J. Phys. Chem. Ref. Data 1998, 9, 1–1951. [Google Scholar]
- Evans, T.W.; Edlund, K.R. Tertiary alkyl ethers, preparation and properties. Ind. Eng. Chem. 1936, 28, 1186–1188. [Google Scholar] [CrossRef]
- Verevkin, S.P.; Heintz, A. Determination of Vaporization Enthalpies of the Branched Esters from Correlation Gas Chromatography and Transpiration Methods. J. Chem. Eng. Data 1999, 44, 1240–1244. [Google Scholar] [CrossRef]
- Atake, T.; Kawaji, H.; Tojo, T.; Kawasaki, K.; Ootsuka, Y.; Katou, M.; Koga, Y. Heat Capacities of Isomeric 2-Butoxyethanols from 13 to 300 K: Fusion and Glass Transition. Bull. Chem. Soc. Jpn. 2000, 73, 1987–1991. [Google Scholar] [CrossRef]
- Pedley, J.P.; Naylor, R.D.; Kirby, S.P. Thermochemical Data of Organic Compounds, 2nd ed.; Chapman and Hall: London, UK, 1986. [Google Scholar]
- Verevkin, S.P.; Emel’yanenko, V.N.; Nell, G. 1,2-Propanediol. Comprehensive experimental and theoretical study. J. Chem. Thermodyn. 2009, 41, 1125–1131. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).