Impact of Di- and Poly-Radical Characters on the Relative
Energy of the Doubly Excited and
Abstract
1. Introduction
2. Computational Methods
3. Results
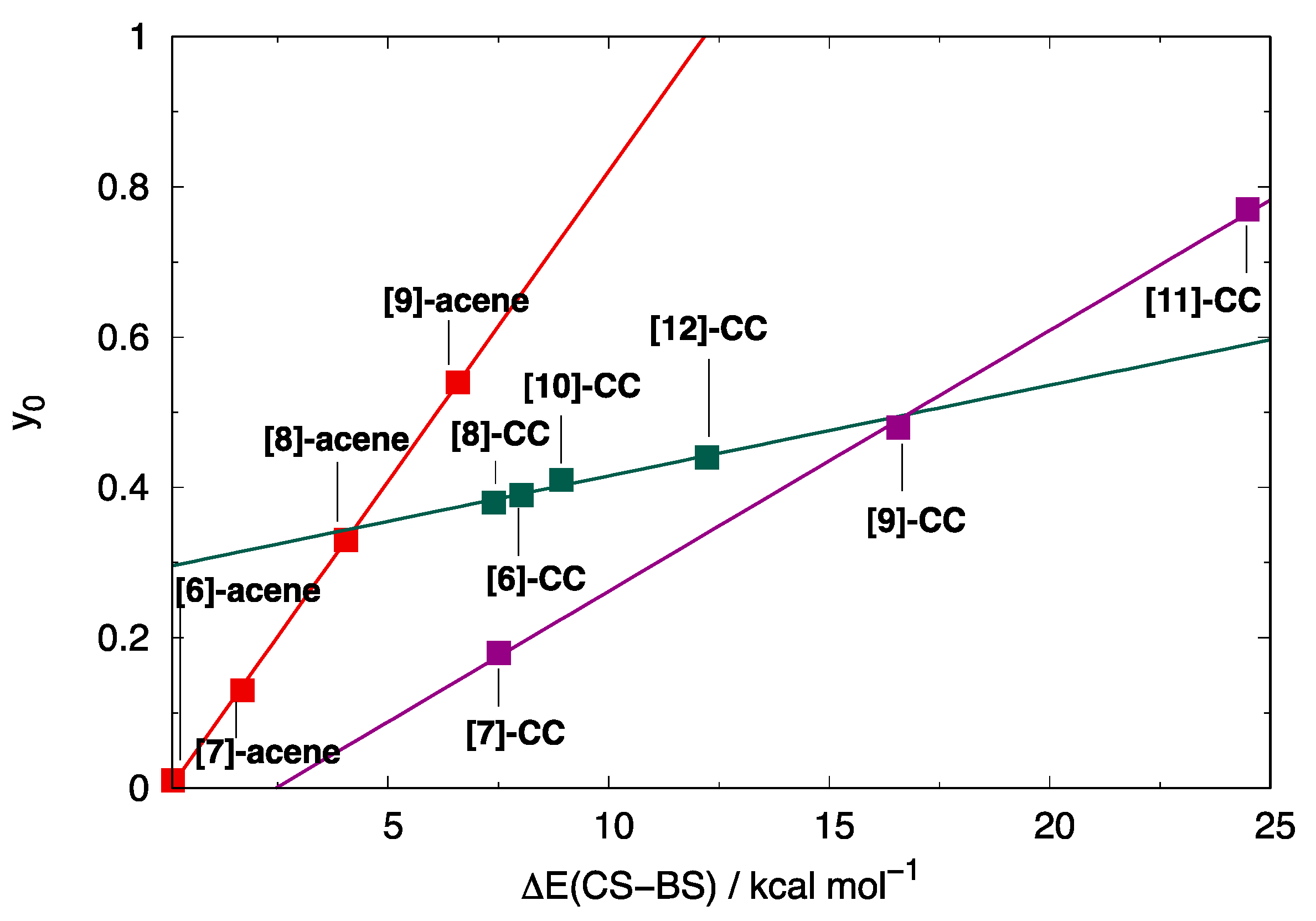
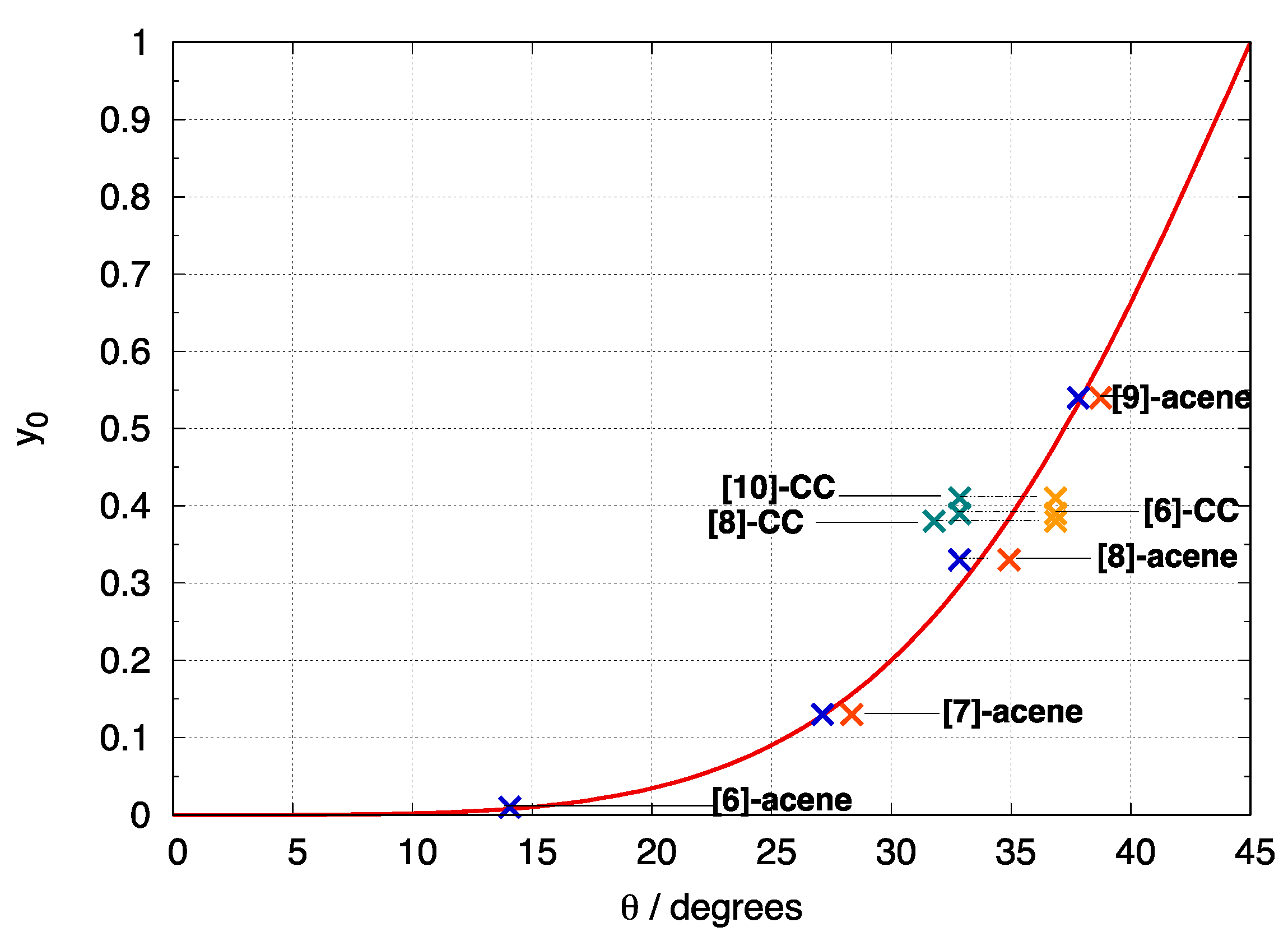
3.1. Stabilization of Open-Shell Structures
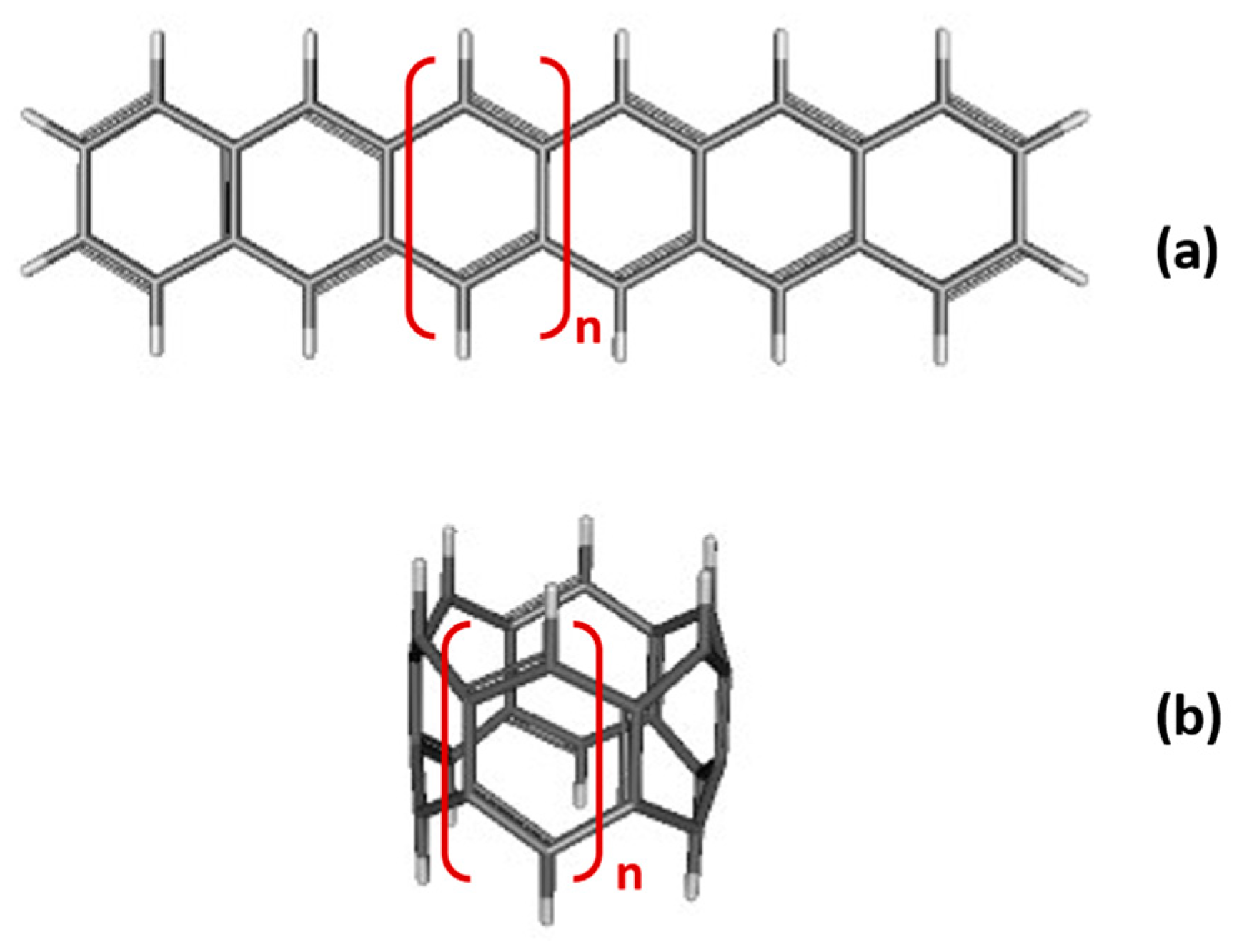
3.2. Di- and Poly-Radical Characters of [n]-acenes and [n]-CCs
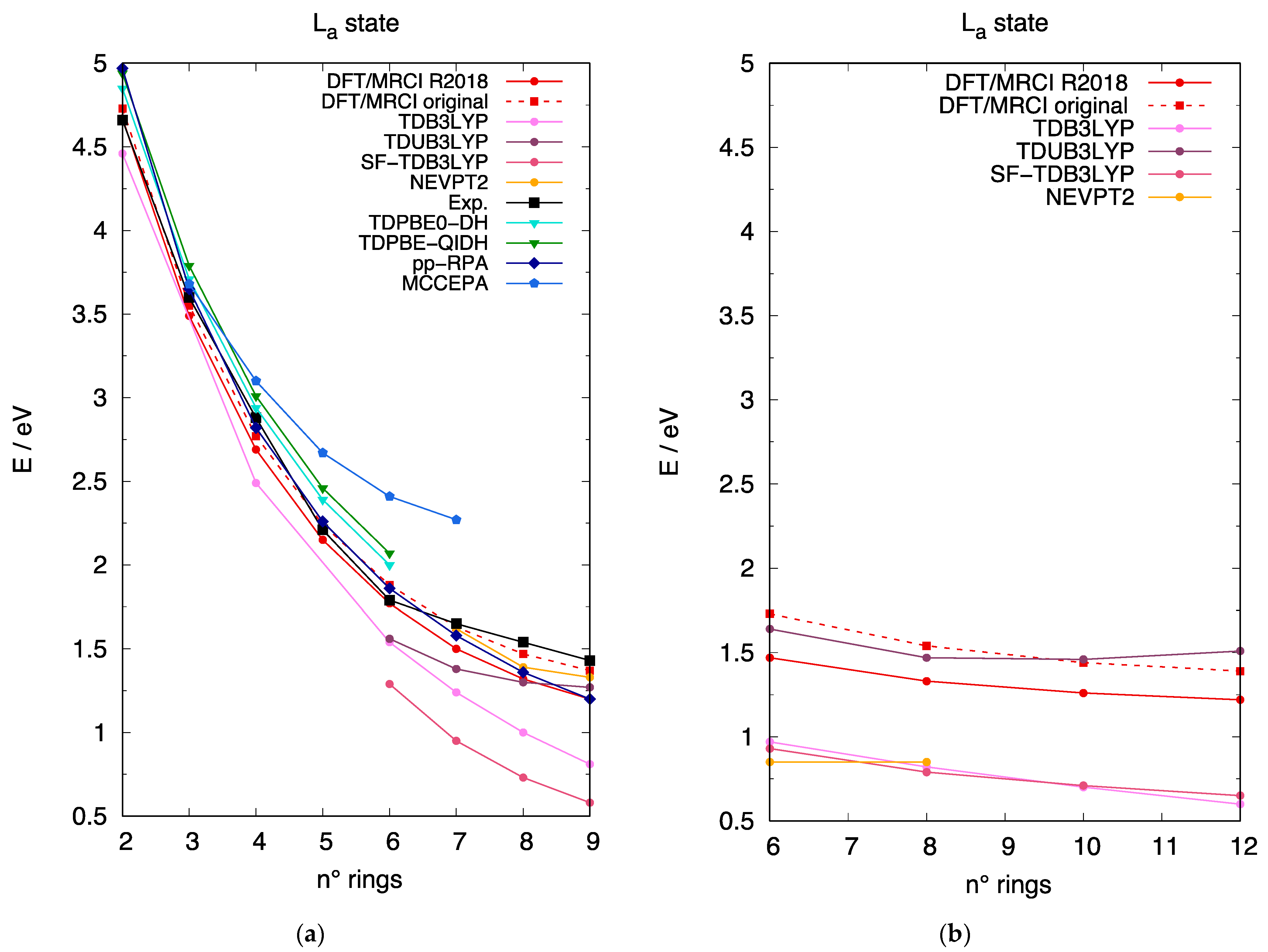
3.3. The Excited State of [n]-acenes and [n]-CCs
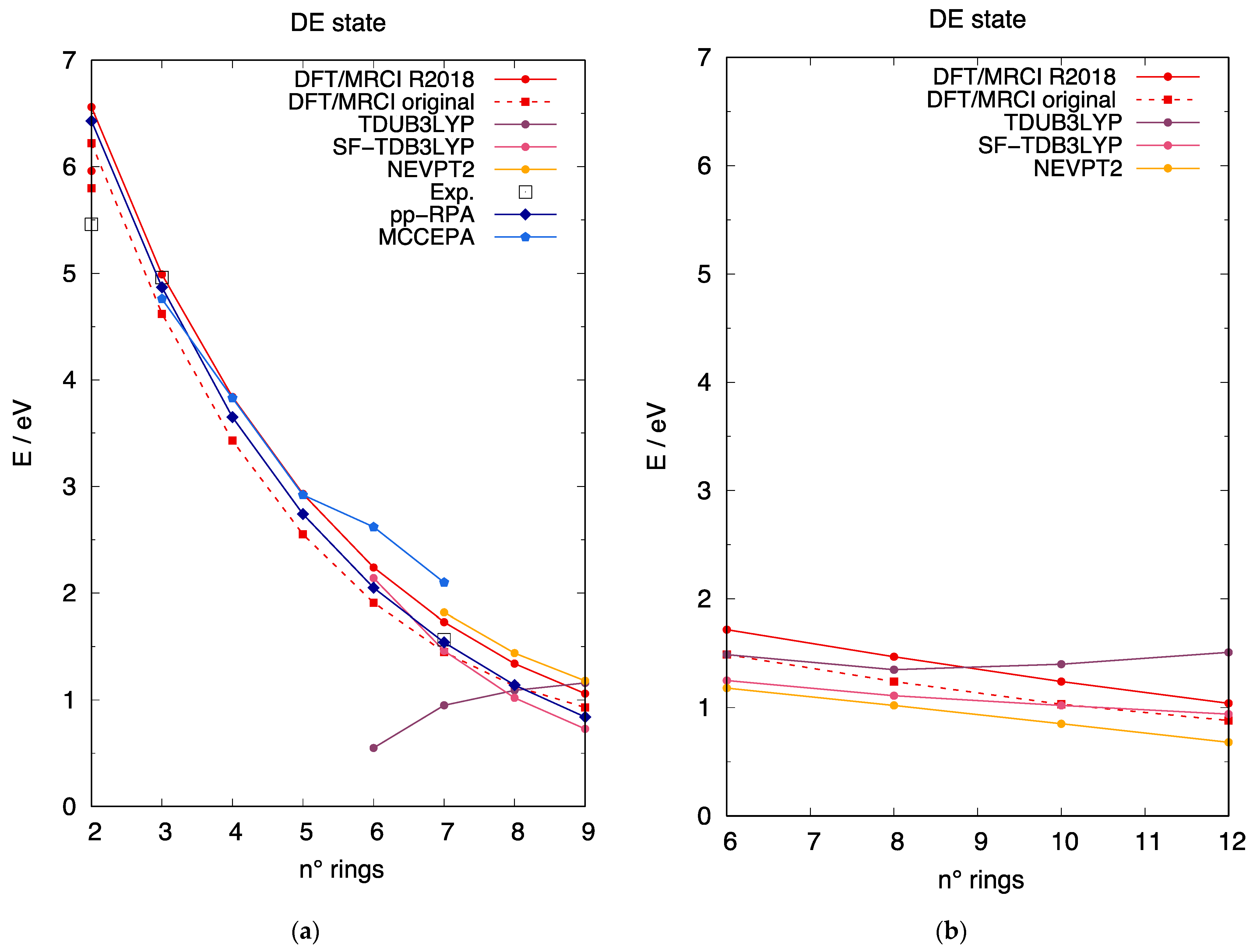
3.4. The DE Excited State of [n]-acenes and [n]-CCs
4. Discussion
4.1. Assessment of TDUDFT Results
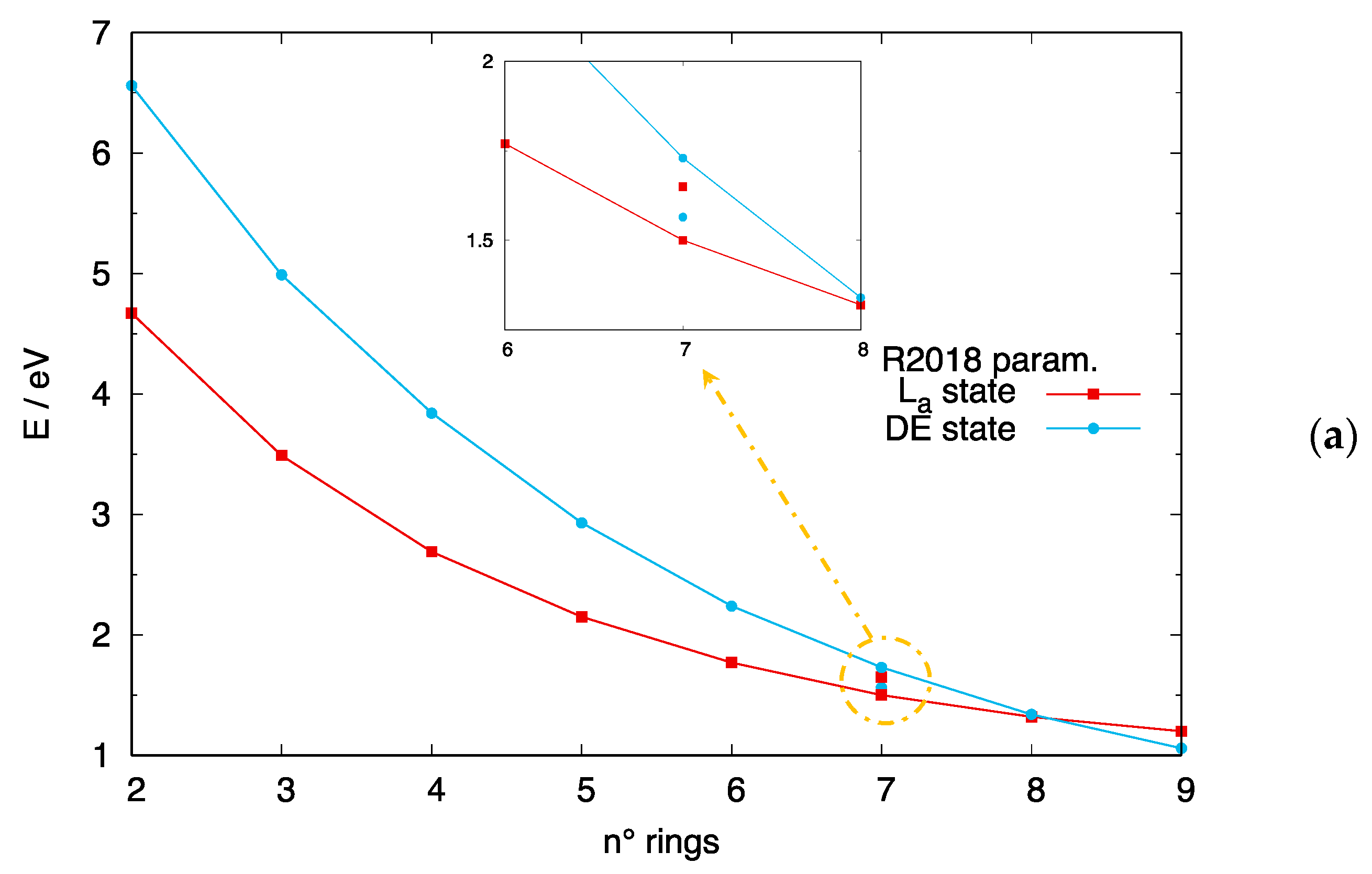
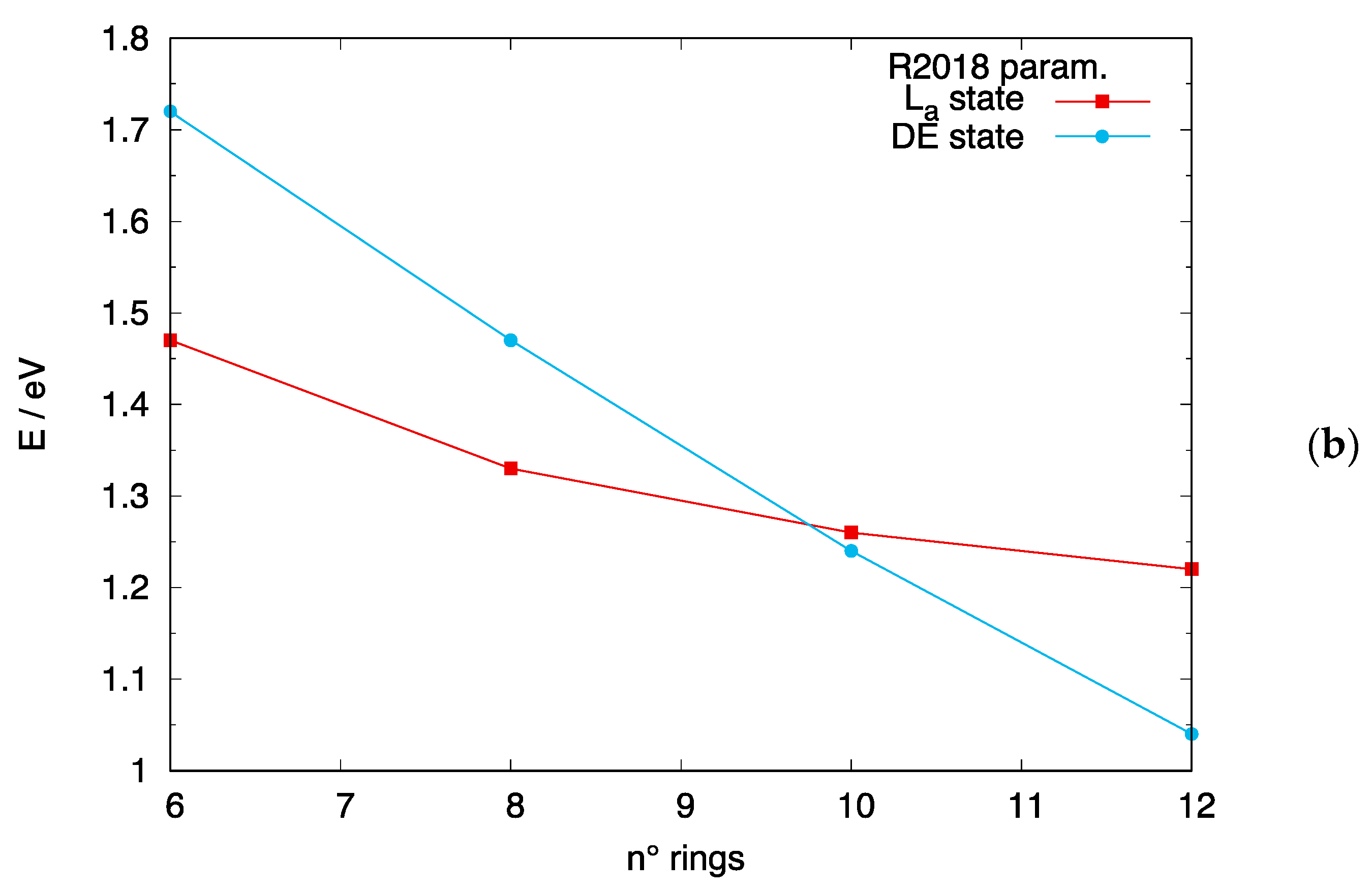
4.2. Crossing of the DE and States in [n]-acenes and [n]-CCs
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, W.; Yu, F.; Xu, Q.; Zhou, G.; Zhang, Q. Recent Progress in High Linearly Fused Polycyclic Conjugated Hydrocarbons (PCHs, n > 6) with Well-Defined Structures. Adv. Sci. 2020, 7, 1903766. [Google Scholar] [CrossRef]
- Dong, H.; Zhu, H.; Meng, Q.; Gong, X.; Hu, W. Organic photoresponse materials and devices. Chem. Soc. Rev. 2012, 41, 1754–1808. [Google Scholar] [CrossRef]
- Wang, C.; Dong, H.; Hu, W.; Liu, Y.; Zhu, D. Semiconducting π-Conjugated Systems in Field-Effect Transistors: A Material Odyssey of Organic Electronics. Chem. Rev. 2012, 112, 2208–2267. [Google Scholar] [CrossRef]
- Watanabe, M.; Chang, Y.J.; Liu, S.-W.; Chao, T.-H.; Goto, K.; Islam, M.M.; Yuan, C.-H.; Tao, Y.-T.; Shinmyozu, T.; Chow, T.J. The synthesis, crystal structure and charge-transport properties of hexacene. Nat. Chem. 2012, 4, 574–578. [Google Scholar] [CrossRef]
- Hachmann, J.; Dorando, J.J.; Aviĺs, M.; Chan, G.K.-L.L.; Avilés, M.; Chan, G.K.-L.L. The radical character of the acenes: A density matrix renormalization group study. J. Chem. Phys. 2007, 127, 134309. [Google Scholar] [CrossRef]
- Pérez-Guardiola, A.; Sandoval-Salinas, M.E.; Casanova, D.; San-Fabián, E.; Pérez-Jiménez, A.J.; Sancho-García, J.C. The role of topology in organic molecules: Origin and comparison of the radical character in linear and cyclic oligoacenes and related oligomers. Phys. Chem. Chem. Phys. 2018, 20, 7112–7124. [Google Scholar] [CrossRef]
- Trinquier, G.; David, G.; Malrieu, J.-P. Qualitative Views on the Polyradical Character of Long Acenes. J. Phys. Chem. A 2018, 122, 6926–6933. [Google Scholar] [CrossRef]
- Sun, Z.; Wu, J. Higher Order Acenes and Fused Acenes with Near-infrared Absorption and Emission. Aust. J. Chem. 2011, 64, 519. [Google Scholar] [CrossRef]
- Zuzak, R.; Dorel, R.; Krawiec, M.; Such, B.; Kolmer, M.; Szymonski, M.; Echavarren, A.M.; Godlewski, S. Nonacene Generated by On-Surface Dehydrogenation. ACS Nano 2017, 11, 9321–9329. [Google Scholar] [CrossRef]
- Zuzak, R.; Dorel, R.; Kolmer, M.; Szymonski, M.; Godlewski, S.; Echavarren, A.M. Higher Acenes by On-Surface Dehydrogenation: From Heptacene to Undecacene. Angew. Chemie Int. Ed. 2018, 57, 10500–10505. [Google Scholar] [CrossRef]
- Krüger, J.; García, F.; Eisenhut, F.; Skidin, D.; Alonso, J.M.; Guitián, E.; Pérez, D.; Cuniberti, G.; Moresco, F.; Peña, D. Decacene: On-Surface Generation. Angew. Chem. 2017, 129, 12107–12110. [Google Scholar] [CrossRef]
- Colazzo, L.; Mohammed, M.S.G.; Dorel, R.; Nita, P.; García Fernández, C.; Abufager, P.; Lorente, N.; Echavarren, A.M.; de Oteyza, D.G. On-surface synthesis of heptacene on Ag(001) from brominated and non-brominated tetrahydroheptacene precursors. Chem. Commun. 2018, 54, 10260–10263. [Google Scholar] [CrossRef]
- Urgel, J.I.; Mishra, S.; Hayashi, H.; Wilhelm, J.; Pignedoli, C.A.; Di Giovannantonio, M.; Widmer, R.; Yamashita, M.; Hieda, N.; Ruffieux, P.; et al. On-surface light-induced generation of higher acenes and elucidation of their open-shell character. Nat. Commun. 2019, 10, 861. [Google Scholar] [CrossRef] [PubMed]
- Tönshoff, C.; Bettinger, H.F. Pushing the Limits of Acene Chemistry: The Recent Surge of Large Acenes. Chem. -A Eur. J. 2021, 27, 3193–3212. [Google Scholar] [CrossRef]
- Mondai, R.; Shah, B.K.; Neckers, D.C. Photogeneration of heptacene in a polymer matrix. J. Am. Chem. Soc. 2006, 128, 9612–9613. [Google Scholar] [CrossRef]
- Mondal, R.; Tönshoff, C.; Khon, D.; Neckers, D.C.; Bettinger, H.F. Synthesis, stability, and photochemistry of pentacene, hexacene, and heptacene: A matrix isolation study. J. Am. Chem. Soc. 2009, 131, 14281–14289. [Google Scholar] [CrossRef]
- Mondal, R.; Adhikari, R.M.; Shah, B.K.; Neckers, D.C. Revisiting the Stability of Hexacenes. Org. Lett. 2007, 9, 2505–2508. [Google Scholar] [CrossRef]
- Einholz, R.; Fang, T.; Berger, R.; Grüninger, P.; Früh, A.; Chassé, T.; Fink, R.F.; Bettinger, H.F. Heptacene: Characterization in Solution, in the Solid State, and in Films. J. Am. Chem. Soc. 2017, 139, 4435–4442. [Google Scholar] [CrossRef]
- Tönshoff, C.; Bettinger, H.F. Photogeneration of octacene and nonacene. Angew. Chem. Int. Ed. 2010, 49, 4125–4128. [Google Scholar] [CrossRef]
- Shen, B.; Tatchen, J.; Sanchez-Garcia, E.; Bettinger, H.F. Evolution of the Optical Gap in the Acene Series: Undecacene. Angew. Chem. Int. Ed. 2018, 57, 10506–10509. [Google Scholar] [CrossRef] [PubMed]
- Qu, H.; Chi, C. A stable heptacene derivative substituted with electron-deficient trifluoromethylphenyl and triisopropylsilylethynyl groups. Org. Lett. 2010, 12, 3360–3363. [Google Scholar] [CrossRef]
- Krüger, J.; Eisenhut, F.; Skidin, D.; Lehmann, T.; Ryndyk, D.A.; Cuniberti, G.; García, F.; Alonso, J.M.; Guitián, E.; Pérez, D.; et al. Electronic Resonances and Gap Stabilization of Higher Acenes on a Gold Surface. ACS Nano 2018, 12, 8506–8511. [Google Scholar] [CrossRef]
- Houk, K.N.; Lee, P.S.; Nendel, M. Polyacene and cyclacene geometries and electronic structures: Bond equalization, vanishing band gaps, and triplet ground states contrast with polyacetylene. J. Org. Chem. 2001, 66, 5517–5521. [Google Scholar] [CrossRef]
- Bendikov, M.; Duong, H.M.; Starkey, K.; Houk, K.N.; Carter, E.A.; Wudl, F. Oligoacenes: Theoretical prediction of open-shell singlet diradical ground states. J. Am. Chem. Soc. 2004, 126, 7416–7417. [Google Scholar] [CrossRef]
- Jiang, D.; Dai, S. Electronic Ground State of Higher Acenes. J. Phys. Chem. A 2008, 112, 332–335. [Google Scholar] [CrossRef]
- Chai, J.-D. Density functional theory with fractional orbital occupations. J. Chem. Phys. 2012, 136, 154104. [Google Scholar] [CrossRef]
- Chai, J.-D. Thermally-assisted-occupation density functional theory with generalized-gradient approximations. J. Chem. Phys. 2014, 140, 18A521. [Google Scholar] [CrossRef]
- Wu, C.-S.; Lee, P.-Y.; Chai, J.-D. Electronic Properties of Cyclacenes from TAO-DFT. Sci. Rep. 2016, 6, 37249. [Google Scholar] [CrossRef]
- Mostafanejad, M.; DePrince, A.E. Combining Pair-Density Functional Theory and Variational Two-Electron Reduced-Density Matrix Methods. J. Chem. Theory Comput. 2019, 15, 290–302. [Google Scholar] [CrossRef]
- Yang, Y.; Davidson, E.R.; Yang, W. Nature of ground and electronic excited states of higher acenes. Proc. Natl. Acad. Sci. USA 2016, 113, E5098–E5107. [Google Scholar] [CrossRef]
- Platt, J.R. Classification of Spectra of Cata-Condensed Hydrocarbons. J. Chem. Phys. 1949, 17, 484–495. [Google Scholar] [CrossRef]
- Negri, F.; Zgierski, M.Z. Vibronic structure of the emission spectra from single vibronic levels of the S 1 manifold in naphthalene: Theoretical simulation. J. Chem. Phys. 1996, 104, 3486–3500. [Google Scholar] [CrossRef]
- Knippenberg, S.; Starcke, J.H.; Wormit, M.; Dreuw, A. The low-lying excited states of neutral polyacenes and their radical cations: A quantum chemical study employing the algebraic diagrammatic construction scheme of second order. Mol. Phys. 2010, 108, 2801–2813. [Google Scholar] [CrossRef]
- Bonačić-Koutecký, V.; Koutecký, J.; Michl, J. Neutral and Charged Biradicals, Zwitterions, Funnels in S1, and Proton Translocation: Their Role in Photochemistry, Photophysics, and Vision. Angew. Chem. Int. Ed. Engl. 1987, 26, 170–189. [Google Scholar] [CrossRef]
- Di Motta, S.; Negri, F.; Fazzi, D.; Castiglioni, C.; Canesi, E.V. Biradicaloid and Polyenic Character of Quinoidal Oligothiophenes Revealed by the Presence of a Low-Lying Double-Exciton State. J. Phys. Chem. Lett. 2010, 1, 3334–3339. [Google Scholar] [CrossRef]
- Canola, S.; Casado, J.; Negri, F. The double exciton state of conjugated chromophores with strong diradical character: Insights from TDDFT calculations. Phys. Chem. Chem. Phys. 2018, 20, 24227–24238. [Google Scholar] [CrossRef]
- González-Cano, R.C.; Di Motta, S.; Zhu, X.; López Navarrete, J.T.; Tsuji, H.; Nakamura, E.; Negri, F.; Casado, J. Carbon-Bridged Phenylene-Vinylenes: On the Common Diradicaloid Origin of Their Photonic and Chemical Properties. J. Phys. Chem. C 2017, 121, 23141–23148. [Google Scholar] [CrossRef]
- Negri, F.; Canola, S.; Dai, Y. Spectroscopy of Open-Shell Singlet Ground-State Diradicaloids: A Computational Perspective. In Diradicaloids; Wu, J., Ed.; Jenny Stanford Publishing: New York, NY, USA, 2022; pp. 145–179. ISBN 978-981-4968-08-9. [Google Scholar]
- Canola; Dai; Negri The Low Lying Double-Exciton State of Conjugated Diradicals: Assessment of TDUDFT and Spin-Flip TDDFT Predictions. Computation 2019, 7, 68. [CrossRef]
- Grimme, S.; Parac, M. Substantial errors from time-dependent density functional theory for the calculation of excited states of large π systems. ChemPhysChem 2003, 4, 292–295. [Google Scholar] [CrossRef]
- Parac, M.; Grimme, S. A TDDFT study of the lowest excitation energies of polycyclic aromatic hydrocarbons. Chem. Phys. 2003, 292, 11–21. [Google Scholar] [CrossRef]
- Wong, B.M.; Hsieh, T.H. Optoelectronic and excitonic properties of oligoacenes: Substantial improvements from range-separated time-dependent density functional theory. J. Chem. Theory Comput. 2010, 6, 3704–3712. [Google Scholar] [CrossRef]
- Richard, R.M.; Herbert, J.M. Time-Dependent Density-Functional Description of the 1 L a State in Polycyclic Aromatic Hydrocarbons: Charge-Transfer Character in Disguise? J. Chem. Theory Comput. 2011, 7, 1296–1306. [Google Scholar] [CrossRef]
- Kuritz, N.; Stein, T.; Baer, R.; Kronik, L. Charge-transfer-like π→π* excitations in time-dependent density functional theory: A conundrum and its solution. J. Chem. Theory Comput. 2011, 7, 2408–2415. [Google Scholar] [CrossRef]
- Goerigk, L.; Grimme, S. Double-hybrid density functionals provide a balanced description of excited 1La and 1Lb states in polycyclic aromatic hydrocarbons. J. Chem. Theory Comput. 2011, 7, 3272–3277. [Google Scholar] [CrossRef]
- Sandoval-Salinas, M.E.; Brémond, E.; Pérez-Jiménez, A.J.; Adamo, C.; Sancho-García, J.C. Excitation energies of polycylic aromatic hydrocarbons by double-hybrid functionals: Assessing the PBE0-DH and PBE-QIDH models and their range-separated versions. J. Chem. Phys. 2023, 158, 044105. [Google Scholar] [CrossRef]
- Brémond, E.; Ciofini, I.; Sancho-García, J.C.; Adamo, C. Nonempirical Double-Hybrid Functionals: An Effective Tool for Chemists. Acc. Chem. Res. 2016, 49, 1503–1513. [Google Scholar] [CrossRef]
- Marian, C.M.; Gilka, N. Performance of the density functional theory/multireference configuration interaction method on electronic excitation of extended π-systems. J. Chem. Theory Comput. 2008, 4, 1501–1515. [Google Scholar] [CrossRef]
- Bettinger, H.F.; Tönshoff, C.; Doerr, M.; Sanchez-Garcia, E. Electronically Excited States of Higher Acenes up to Nonacene: A Density Functional Theory/Multireference Configuration Interaction Study. J. Chem. Theory Comput. 2016, 12, 305–312. [Google Scholar] [CrossRef]
- Bettanin, F.; Ferrão, L.F.A.; Pinheiro, M.; Aquino, A.J.A.; Lischka, H.; Machado, F.B.C.; Nachtigallova, D. Singlet La and Lb Bands for N-Acenes (N = 2-7): A CASSCF/CASPT2 Study. J. Chem. Theory Comput. 2017, 13, 4297–4306. [Google Scholar] [CrossRef]
- Schulz, F.; García, F.; Kaiser, K.; Pérez, D.; Guitián, E.; Gross, L.; Peña, D. Exploring a Route to Cyclic Acenes by On-Surface Synthesis. Angew. Chemie 2019, 131, 9136–9140. [Google Scholar] [CrossRef]
- Battaglia, S.; Faginas-Lago, N.; Andrae, D.; Evangelisti, S.; Leininger, T. Increasing Radical Character of Large [n]cyclacenes Unveiled by Wave Function Theory. J. Phys. Chem. A 2017, 121, 3746–3756. [Google Scholar] [CrossRef]
- Gleiter, R.; Esser, B.; Kornmayer, S.C. Cyclacenes: Hoop-Shaped Systems Composed of Conjugated Rings. Acc. Chem. Res. 2009, 42, 1108–1116. [Google Scholar] [CrossRef]
- Guo, Q.-H.; Qiu, Y.; Wang, M.-X.; Fraser Stoddart, J. Aromatic hydrocarbon belts. Nat. Chem. 2021, 13, 402–419. [Google Scholar] [CrossRef]
- Cheung, K.Y.; Segawa, Y.; Itami, K. Synthetic Strategies of Carbon Nanobelts and Related Belt-Shaped Polycyclic Aromatic Hydrocarbons. Chemistry 2020, 26, 14791–14801. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Kono, H.; Maekawa, T.; Segawa, Y.; Yagi, A.; Itami, K. Chemical Synthesis of Carbon Nanorings and Nanobelts. Acc. Mater. Res. 2021, 2, 681–691. [Google Scholar] [CrossRef]
- Shi, T.-H.; Wang, M.-X. Zigzag Hydrocarbon Belts. CCS Chem. 2021, 3, 916–931. [Google Scholar] [CrossRef]
- Lu, X.; Wu, J. After 60 Years of Efforts: The Chemical Synthesis of a Carbon Nanobelt. Chem 2017, 2, 619–620. [Google Scholar] [CrossRef]
- Zhang, Y.; Pun, S.H.; Miao, Q. The Scholl Reaction as a Powerful Tool for Synthesis of Curved Polycyclic Aromatics. Chem. Rev. 2022, 122, 14554–14593. [Google Scholar] [CrossRef] [PubMed]
- Shi, T.; Tong, S.; Wang, M. Construction of Hydrocarbon Nanobelts. Angew. Chemie Int. Ed. 2020, 59, 7700–7705. [Google Scholar] [CrossRef] [PubMed]
- Shi, T.-H.; Guo, Q.-H.; Tong, S.; Wang, M.-X. Toward the Synthesis of a Highly Strained Hydrocarbon Belt. J. Am. Chem. Soc. 2020, 142, 4576–4580. [Google Scholar] [CrossRef] [PubMed]
- Han, Y.; Dong, S.; Shao, J.; Fan, W.; Chi, C. Synthesis of a Sidewall Fragment of a (12,0) Carbon Nanotube. Angew. Chemie Int. Ed. 2021, 60, 2658–2662. [Google Scholar] [CrossRef]
- Chen, H.; Gui, S.; Zhang, Y.; Liu, Z.; Miao, Q. Synthesis of a Hydrogenated Zigzag Carbon Nanobelt. CCS Chem. 2021, 3, 613–619. [Google Scholar] [CrossRef]
- San-Fabián, E.; Pérez-Guardiola, A.; Moral, M.; Pérez-Jiménez, A.J.; Sancho-García, J.C. Theoretical Study of Strained Carbon-based Nanobelts: Structural, Energetic, Electronic, and Magnetic Properties of [n]Cyclacenes. In Advanced Magnetic and Optical Materials; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2016; pp. 165–183. ISBN 9781119241966. [Google Scholar]
- Choi, H.S.; Kim, K.S. Structures, Magnetic Properties, and Aromaticity of Cyclacenes. Angew. Chemie Int. Ed. 1999, 38, 2256–2258. [Google Scholar] [CrossRef]
- Chen, Z.; Jiang, D.; Lu, X.; Bettinger, H.F.; Dai, S.; Schleyer, P. von R.; Houk, K.N. Open-Shell Singlet Character of Cyclacenes and Short Zigzag Nanotubes. Org. Lett. 2007, 9, 5449–5452. [Google Scholar] [CrossRef]
- Sadowsky, D.; McNeill, K.; Cramer, C.J. Electronic structures of [n]-cyclacenes (n = 6–12) and short, hydrogen-capped, carbon nanotubes. Faraday Discuss. 2010, 145, 507–521. [Google Scholar] [CrossRef]
- Pérez-Guardiola, A.; Ortiz-Cano, R.; Sandoval-Salinas, M.E.; Fernández-Rossier, J.; Casanova, D.; Pérez-Jiménez, A.J.; Sancho-García, J.C. From cyclic nanorings to single-walled carbon nanotubes: Disclosing the evolution of their electronic structure with the help of theoretical methods. Phys. Chem. Chem. Phys. 2019, 21, 2547–2557. [Google Scholar] [CrossRef]
- Ortiz, R.; Sancho-García, J.C.; Fernández-Rossier, J. Frustrated magnetic interactions in a cyclacene crystal. Phys. Rev. Mater. 2022, 6, 014406. [Google Scholar] [CrossRef]
- Casanova, D. Theoretical Modeling of Singlet Fission. Chem. Rev. 2018, 118, 7164–7207. [Google Scholar] [CrossRef]
- Zimmerman, P.M.; Zhang, Z.; Musgrave, C.B. Singlet fission in pentacene through multi-exciton quantum states. Nat. Chem. 2010, 2, 648–652. [Google Scholar] [CrossRef]
- Zimmerman, P.M.; Bell, F.; Casanova, D.; Head-Gordon, M. Mechanism for singlet fission in pentacene and tetracene: From single exciton to two triplets. J. Am. Chem. Soc. 2011, 133, 19944–19952. [Google Scholar] [CrossRef]
- Zimmerman, P.M.; Musgrave, C.B.; Head-Gordon, M. A Correlated Electron View of Singlet Fission. Acc. Chem. Res. 2013, 46, 1339–1347. [Google Scholar] [CrossRef] [PubMed]
- Zeiser, C.; Moretti, L.; Reicherter, F.; Bettinger, H.F.; Maiuri, M.; Cerullo, G.; Broch, K. Singlet Fission in Dideuterated Tetracene and Pentacene. ChemPhotoChem 2021, 5, 758–763. [Google Scholar] [CrossRef]
- Shao, Y.; Head-Gordon, M.; Krylov, A.I. The spin-flip approach within time-dependent density functional theory: Theory and applications to diradicals. J. Chem. Phys. 2003, 118, 4807–4818. [Google Scholar] [CrossRef]
- Rinkevicius, Z.; Vahtras, O.; Ågren, H. Spin-flip time dependent density functional theory applied to excited states with single, double, or mixed electron excitation character. J. Chem. Phys. 2010, 133, 114104. [Google Scholar] [CrossRef]
- Angeli, C.; Cimiraglia, R.; Evangelisti, S.; Leininger, T.; Malrieu, J.P. Introduction of n-electron valence states for multireference perturbation theory. J. Chem. Phys. 2001, 114, 10252. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.H.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S.; et al. General atomic and molecular electronic structure system. J. Comput. Chem. 1993, 14, 1347–1363. [Google Scholar] [CrossRef]
- Grimme, S.; Waletzke, M. A combination of Kohn-Sham density functional theory and multi-reference configuration interaction methods. J. Chem. Phys. 1999, 111, 5645–5655. [Google Scholar] [CrossRef]
- Marian, C.M.; Heil, A.; Kleinschmidt, M. The DFT/MRCI method. WIREs Comput. Mol. Sci. 2019, 9, 1–31. [Google Scholar] [CrossRef]
- Marian, C.M.; Heil, A.; Kleinschmidt, M. DFT/MRCI Software. Available online: https://www.theochem.hhu.de/software/dft/mrci (accessed on 15 October 2019).
- Neese, F.; Wennmohs, F.; Becker, U.; Riplinger, C. The ORCA quantum chemistry program package. J. Chem. Phys. 2020, 152, 224108. [Google Scholar] [CrossRef]
- Weigend, F. Hartree—Fock exchange fitting basis sets for H to Rn †. J. Comput. Chem. 2008, 29, 167–175. [Google Scholar] [CrossRef] [PubMed]
- Nakano, M. Open-Shell-Character-Based Molecular Design Principles: Applications to Nonlinear Optics and Singlet Fission. Chem. Rec. 2017, 17, 27–62. [Google Scholar] [CrossRef]
- Yamaguchi, K. The electronic structures of biradicals in the unrestricted Hartree-Fock approximation. Chem. Phys. Lett. 1975, 33, 330–335. [Google Scholar] [CrossRef]
- Grimme, S.; Hansen, A. A Practicable Real-Space Measure and Visualization of Static Electron-Correlation Effects. Angew. Chem. Int. Ed. 2015, 54, 12308–12313. [Google Scholar] [CrossRef]
- Bauer, C.A.; Hansen, A.; Grimme, S. The Fractional Occupation Number Weighted Density as a Versatile Analysis Tool for Molecules with a Complicated Electronic Structure. Chem. - A Eur. J. 2017, 23, 6150–6164. [Google Scholar] [CrossRef]
- Türker, L. Cyclacenes having dislocated rings. J. Mol. Struct. Theochem 2001, 536, 235–241. [Google Scholar] [CrossRef]
- Türker, L. Cryptoannulenic Behavior of Cyclacenes. Polycycl. Aromat. Compd. 1994, 4, 191–197. [Google Scholar] [CrossRef]
- Loos, P.-F.; Boggio-Pasqua, M.; Scemama, A.; Caffarel, M.; Jacquemin, D. Reference Energies for Double Excitations. J. Chem. Theory Comput. 2019, 15, 1939–1956. [Google Scholar] [CrossRef]
- Bergman, A.; Jortner, J. Two-photon spectroscopy utilizing dye lasers. Chem. Phys. Lett. 1972, 15, 309–315. [Google Scholar] [CrossRef]
- Bergman, A.; Jortner, J. Two-photon absorption spectra of crystalline naphthalene and of the naphthalene molecule in solution. Chem. Phys. Lett. 1974, 26, 323–326. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, Y.; Sancho-García, J.-C.; Negri, F.
Impact of Di- and Poly-Radical Characters on the Relative
Energy of the Doubly Excited and
Dai Y, Sancho-García J-C, Negri F.
Impact of Di- and Poly-Radical Characters on the Relative
Energy of the Doubly Excited and
Dai, Yasi, Juan-Carlos Sancho-García, and Fabrizia Negri.
2023. "Impact of Di- and Poly-Radical Characters on the Relative
Energy of the Doubly Excited and
Dai, Y., Sancho-García, J.-C., & Negri, F.
(2023). Impact of Di- and Poly-Radical Characters on the Relative
Energy of the Doubly Excited and







