Abstract
The steady-state quantum dynamics of a compound sample consisting of a semiconductor double-quantum-dot (DQD) system, non-linearly coupled with a leaking superconducting transmission line resonator, is theoretically investigated. Particularly, the transition frequency of the DQD is taken to be equal to the doubled resonator frequency, whereas the inter-dot Coulomb interaction is considered weak. As a consequence, the steady-state quantum dynamics of this complex non-linear system exhibit sudden changes in its features, occurring at a critical DQD-cavity coupling strength, suggesting perspectives for designing on-chip microwave quantum switches. Furthermore, we show that, above the threshold, the electrical current through the double-quantum dot follows the mean photon number into the microwave mode inside the resonator. This might not be the case any more below that critical coupling strength. Lastly, the photon quantum correlations vary from super-Poissonian to Poissonian photon statistics, i.e., towards single-qubit lasing phenomena at microwave frequencies.
1. Introduction
The various examples of hybrid circuit quantum electrodynamic (QED) structures exhibit a variety of quantum effects, previously achieved mainly in quantum optical setups, while presenting unquestionable advantages in the form of low-size on-chip implementation [1,2,3,4,5]. An emblematic example is the optical cavity coupling natural atoms and photons, where lasing phenomena are also achieved by additionally optically pumping the atom. A successful QED alternative system playing the role of an active medium that may induce light amplification in the resonant cavity includes artificial atoms, i.e., semiconducting double-quantum dots (DQDs) attached to normal metal leads, ensuring pumping via the applied biased voltage [6,7,8,9]. The circuit considered is driven by single-electron tunneling, leading to a population inversion in the DQD energy levels, such that, in the resonance condition with the cavity, electron transport takes place via the emission of energy quantum into the cavity [10,11,12]. In consequence, the excited microwave oscillator in the cavity may also facilitate current flow in the DQD [13,14].
The advantage of studying DQD microwave resonator systems is twofold. First, semiconducting DQDs are highly suitable candidates for qubits due to their higher degree of tunability and their experimentally attainable strong-coupling regime, as seen with the electromagnetic cavity demonstrated in Refs. [15,16,17,18]. Second, DQDs are highly efficient detectors of single-itinerant-microwave photons, which is a desirable trait of a quantum system for the realisation of quantum information processing tasks [19,20]. Thus, an electronic interface for the manipulation of photon statistics represents a promising environment for the implementation of various applications in nano-device technology [4,10,21].
DQDs coupled to a leaking resonator and immersed in various environments still show unexplored physics, fueling increasing theoretical interest and further investigations [6,14,20,22,23,24,25,26]. Also, different practical configurations may include relatively weak Coulomb interactions between charges [27,28,29,30,31], Kerr nonlinearity and a signal-driven cavity or DQD [14,32,33,34,35]. Thus, extensive theoretical inquiry is required to demonstrate the control of photon emission via transport properties in the DQD, as well as to investigate the variety of lasing resonances and their signatures in the transport current [9,27,36,37,38,39]. In addition, the Markovian master equation approach is applied in this study; this equation incorporates the dissipation and decoherence processes deteriorating the performance of a device due to its interaction with the degrees of freedom of the electronic and bosonic baths [40,41]. Further research on the creation of hybrid quantum systems and their features, involving circuit quantum electrodynamics, based on mechanical oscillators, quantum acoustodynamics via surface acoustic waves, quantum magnonics or coupling between superconducting circuits and with ensembles or single spins, can be found, for example, in Refs. [42,43,44,45].
In this study, we analyse the quantum dynamics of a complex system formed of a leaking superconducting transmission line resonator mode coupled with a semiconductor DQD qubit, while focusing on the two-photon resonance between the cavity mode and the energy separation levels of the DQD. Additionally, the interdot Coulomb interaction is considered weak enough, allowing for the simultaneous presence of two electrons in the DQD, but only one in each dot. Compared to the strong Coulomb interaction, under the two photon resonance conditions covered recently [46,47], in the current study, an additional incoherent electronic tunneling channel is established, contributing to the population of the DQD and facilitating stronger lasing effects in the resonator as a result. In the framework of open quantum systems, we employ the master equation for this system configuration and deduce the photon number characteristics and the average electronic current in the asymptotic limit of the steady state. We find a critical value for qubit-cavity coupling strengths, such that the mean number of the cavity photons is substantially enhanced or suppressed, as is the electric current through the DQD sample, demonstrating microwave quantum switching. This suggests that the electric current has a convenient mechanism of conversion into a microwave photon flux, or vice versa. Furthermore, above the threshold, the electrical current through the double-quantum dot follows the behaviours of mean photon numbers into the microwave mode inside the resonator, while this might not be the case below that critical point. Finally, the photon correlations vary from super-Poissonian to Poissonian photon statistics, that is, towards single-qubit lasing effects at microwave frequencies.
This paper is organized as follows. In Section 2, we describe the analytical approach and the system of interest, while in Section 3, we present the equations of motion characterising the considered system. Section 4 presents and analyses the obtained results. The article concludes with a summary given in Section 5.
2. Analytical Approach
We consider a hybrid setup made of a semiconducting DQD qubit which is coupled to an electromagnetic microwave resonator such as a superconducting transmission line. Furthermore, the DQD system is pumped incoherently via electron tunneling through the dots, by means of the bias voltage that is assumed to be relatively high. The Coulomb interaction is considered relatively weak, signifying that the DQD is described by the following possible states (see, e.g., Ref. [27]): the null-electron subspace or the empty-dot state, i.e., , along with the single-electron subspaces, where the electron is localized either on the left, , or the right, , dots as well as the mixed state, , denoting the situation when two electrons are simultaneously localised separately in each of the two quantum dots, with .
Assuming that the corresponding resonator and the DQD’s interactions with the photon or electronic environmental reservoirs are quite weak, in the Born–Markov approximations and with a low-temperature limit [6,27,46,47,48,49], one obtains the master equation
(with t denoting the time and ℏ the reduced Planck constant) for the reduced density matrix describing the qubit plus leaking resonator mode subsystem only, where the complete Hamiltonian, describing the investigated system, is given by
where (see, e.g., [6,27])
is the Hamiltonian of two quantum dots, forming the DQD qubit, with being their energy separation, while is the inter-dot tunnelling amplitude, whereas u denotes the inter-dot Coulomb interaction and . The Hamiltonian
describes the microwave resonator free energy and qubit–cavity interaction, with and g being the corresponding resonator frequency and coupling strength, respectively. The cavity photon creation (annihilation) operators, , obey the standard commutation relations: , . On the other hand, the qubit operators are defined as follows: , and , which obey the commutation relations for su(2) algebra, that is, and . The damping terms, entering in the right-hand side part of the master Equation (1) read
where “h.c.” stands for Hermitian conjugate, and are the corresponding electron tunneling rates and is the cavity decay rate, while [27] and . Note that the master equation’s terms given by the expressionsin the system (5) are represented in the second order in the corresponding small coupling strengths of the DQD and the cavity mode to the corresponding environmental electronic and photonic reservoirs.
Diagonalizing the first two terms of the Hamiltonian (3), using the transformation
with , and the generalized frequency , one arrives at a Hamiltonian H represented via new qubit quasispin operators, namely = , , satisfying the commutation relations: = (with the Kronecker delta), that is,
with being the inversion operator.
In what follows, it is assumed that the semiconductor DQD exchanges energy with the resonator mode when its generalized frequency is equal approximately to the doubled value of the cavity frequency . Then, in the interaction picture, given by the unitary operator with , one arrives at a time-dependent Hamiltonian, , oscillating considerably quickly in time. Its contribution to the established quantum dynamics can be obtained via the following relation:
when ; see [50,51], for example. As a result, the master Equation (1) transforms into the following:
where
Thus, due to the presence of rapidly oscillating terms in the complete Hamiltonian, arrive at an effective novel DQD-resonator Hamiltonian, , characterizing non-linear coherent two-photon effects. Here, , , , , and . The corresponding rates, entering in Equation (9), read
Notice that the master Equation (9) is obtained under the secular approximation, i.e., we considered that ; we also considered lower-temperature environments. As a result we involve parameters satisfying the adopted approximations which are also experimentally achievable [8], namely the frequency of the leaking resonator is taken of the order of GHz and the cavity decay rate is taken of the order of MHz, respectively, whereas DQD–cavity coupling strengths may reach values up to MHz.
3. The Equations of Motion
Using the master Equation (9), one obtains the exact system of equations of motion:
describing the entire sample incorporating a semiconductor DQD qubit coupled in two-photon resonance to the cavity boson mode.
The system (11) can be straghtforwardly obtained using the master Equation (9), if first one obtains the equations of motion for = , (see Refs. [52,53]), and then writing the corresponding equations for the following variables: , , , , , , , , and . The projection on the Fock states, , i.e., , with and , leads to the system (11), where . Notice that the involved analytical approach allows us to avoid decoupling the qubit–cavity correlators, when obtaining the system (11).
In general, to solve the infinite system (11), one may truncate it at a certain maximum value so that a further increase in its value, i.e., , does not modify the obtained results. As a consequence, the steady-state cavity-mode photon mean number, i.e., , is expressed as follows:
with
The current through the DQD qubit is proportional to the population in the state and , that is,
where e is the electron charge. In Equation (13), we apply the transformation (6) and the secular approximation.
The corresponding steady-state second-order cavity photon correlation function is defined commonly as [54]
Note that indicates sub-Poissonian, indicates super-Poissonian, and indicates Poissonian photon statistics.
4. Results and Discussion
Figure 1a shows the steady-state dependence of the mean cavity photon number as a function of the DQD-resonator coupling strength, near two-photon resonance, i.e., , extracted from the system of Equation (11). Particularly, the decay rates were selected within the secular approximation, that is, they were smaller than qubit frequency , in concordance with the valability of the master Equation (9). As a result, one observes a threshold transition when the mean photon number abruptly changes from lower to higher values, or, conversely, when varying to some degree the qubit–resonator coupling strength. Actually, this behaviour is typical for an externally coherently pumped and leaking cavity mode, containing a Kerr-like non-linearity [32,33], for instance. Here, however, this behaviour is due to the unilateral electronic pumping of the DQD sample, i.e., from the left to the right.
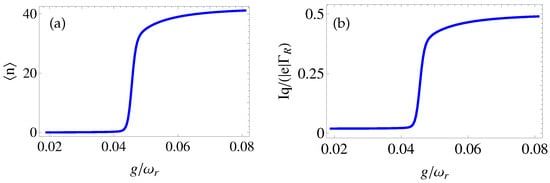
Figure 1.
The steady-state behaviour of (a) the cavity mean photon number, , and (b) the steady-state dependence of the current, , through the DQD system, as a function of . Here, , , , . See text fore details.
On the other hand, Figure 1b depicts the steady-state current through the DQD qubit, which is proportional to the populations in the state and . The current follows the same behaviour as the mean photon number: compare the behaviours by contrasting Figure 1a,b. Therefore, measuring the current through the DQD, one can estimate the photon flux leaking out from the cavity mode, or vice versa. In practice, the described process can be a practical tool with which to design on-chip microwave quantum switches, based on electric current conversion into microwave photons in hybrid DQD–resonator systems. Furthermore, the cavity photons obey the super-Poissonian statistics below the threshold, i.e., (see Figure 2), which changes to Poissonian photon statistics above the threshold, i.e., to microwave photon lasing effects, where . Around the threshold, the photon correlation evidently enhances. Actually, does not converge for , since , so one should proceed with non-zero values for DQD–cavity coupling strengths in this particular case.
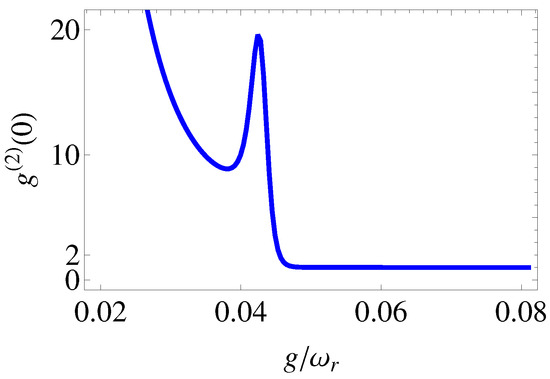
Figure 2.
The normalized steady-state second-order photon–photon correlation function versus the ratio . Other parameters as in Figure 1.
We proceed further by describing the corresponding quantum dynamics versus the experimentally controllable DQD energy separation , while all other parameters are being fixed. The resonator–DQD coupling strength g selected is below or above the threshold:see Figure 1a or Figure 1b, respectively. Thus, Figure 3a depicts the mean cavity photon number in these situations. Particularly, in the near-resonance condition, i.e., when , one observes a plateau where the mean cavity photon number does not highly vary, while the scaled energy separation is scanned around the resonance. Then, it drops to zero out of the resonance. Above the threshold, i.e., when , the current, again, follows the behaviour of the resonator mean photon number; see Figure 3b. However, this is no longer the case below the threshold, that is, when ; compare the insets in Figure 3a,b. Furthermore, within the plateau region, the photon statistics are Poissonian one since ; see Figure 4 above the threshold. On the other hand, below the threshold, the photon statistics are super-Poissonian; see the inset in Figure 4. Thus, one may observe stable single-qubit lasing effects above the critical value of the cavity–DQD coupling strength, that is, above the threshold.
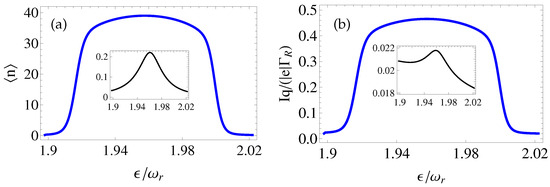
Figure 3.
The steady-state behaviours of (a) the mean cavity photon number and (b) the current through the DQD system, as a function of . Here, and , while in the insets, , i.e., below the threshold. Other parameters as in Figure 1.
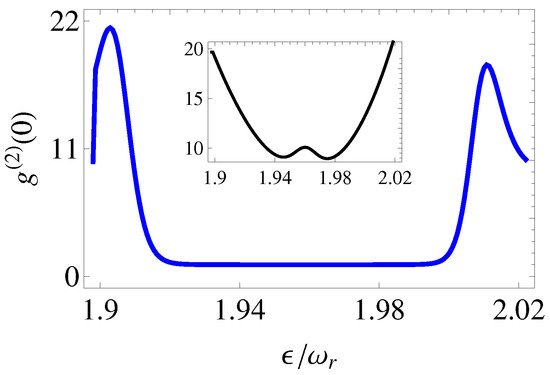
Figure 4.
The normalized steady-state second-order photon–photon correlation function versus the ratio . Other parameters as in Figure 3.
5. Summary
In summary, we have investigated a semiconducting DQD qubit coupled in two-photon resonance with a leaking microwave resonator, where the pumping of the qubit is achieved via the environmental electronic reservoirs. Particularly, the inter-dot Coulomb interaction is assumed to be weak, while the focus is on calculating the mean photon cavity number, under the secular approximation, with a corresponding accent on an obtained critical value for the qubit–resonator coupling strength, where the steady-state photon number changes abruptly. This can be practical for engineering quantum microwave switches, for instance. Moreover, the corresponding photon statistics is obtanied to vary from super-Poissonian to Poissonian photon statistics. Also, the electric current through the DQD system follows the behaviour of the cavity-mode steady-state photon number, particularly above the threshold. This way, one may achieve lasing effects in microwave-frequency domains, while having the ability to convert electric current in a photon flux. Thus, one may estimate the intensity of the photon flux, generated in cavity mode, via measuring the electric current, or vice versa.
Author Contributions
Conceptualization, M.A.M.; methodology, T.M., M.A.M. and A.I.; software, T.M. and M.A.M.; validation, M.A.M.; formal analysis, A.I.; investigation, T.M., M.A.M. and A.I.; writing—review and editing, T.M., M.A.M. and A.I.; visualization, T.M.; supervision, M.A.M. and A.I.; project administration, M.A.M. and A.I. All authors have read and agreed to the published version of the manuscript.
Funding
We highly appreciate the financial support from the Romanian Ministry of Research, Innovation and Digitization, CNCS-UEFISCDI, via the PN-IV-P8-8.3-ROMD-2023-0013 research grant, within National Plan for Research, Development and Innovation 2022–2027, PNCDI IV. M.A.M. is grateful for partial support from the Moldavian Ministry of Education and Research, through grant No. 011205.
Data Availability Statement
The original contributions presented in this study are included in the article.
Acknowledgments
This paper is dedicated to Viktor Dodonov on the occasion of his 55 years in quantum physics. M.A.M. is grateful for the nice hospitality of the Department of Theoretical Physics at the Horia Hulubei National Institute of Physics and Nuclear Engineering, Bucharest, Romania.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Bruhat, L.E.; Cubaynes, T.; Viennot, J.J.; Dartiailh, M.C.; Desjardins, M.M.; Cottet, A.; Kontos, T. Circuit QED with a quantum-dot charge qubit dressed by Cooper pairs. Phys. Rev. B 2018, 98, 155313. [Google Scholar] [CrossRef]
- Burkard, G.; Gullans, M.J.; Mi, X.; Petta, J.R. Superconductor–semiconductor hybrid-circuit quantum electrodynamics. Nat. Rev. Phys. 2020, 2, 129–140. [Google Scholar] [CrossRef]
- Haldar, S.; Barker, D.; Havir, H.; Ranni, A.; Lehmann, S.; Dick, K.A.; Maisi, V.F. Continuous microwave photon counting by semiconductor–superconductor hybrids. Phys. Rev. Lett. 2024, 133, 217001. [Google Scholar] [PubMed]
- Stanisavljević, O.; Philippe, J.-C.; Gabelli, J.; Aprili, M.; Estéve, J.; Basset, J. Efficient microwave photon-to-electron conversion in a high-Impedance quantum circuit. Phys. Rev. Lett. 2024, 133, 076302. [Google Scholar] [CrossRef]
- de Sá Neto, O.P.; de Oliveira, M.C. Signal, detection and estimation using a hybrid quantum circuit. Sci. Rep. 2024, 14, 15225. [Google Scholar] [CrossRef]
- Brandes, T. Coherent and collective quantum optical effects in mesoscopic systems. Phys. Rep. 2005, 408, 315–474. [Google Scholar] [CrossRef]
- Kulkarni, M.; Cotlet, O.; Türeci, H.E. Cavity-coupled double-quantum dot at finite bias: Analogy with lasers and beyond. Phys. Rev. B 2014, 90, 125402. [Google Scholar] [CrossRef]
- Liu, Y.-Y.; Stehlik, J.; Eichler, C.; Mi, X.; Hartke, T.R.; Gullans, M.J.; Taylor, J.M.; Petta, J.R. Threshold dynamics of a semiconductor single atom maser. Phys. Rev. Lett. 2017, 119, 097702. [Google Scholar] [CrossRef] [PubMed]
- Tabatabaei, S.M.; Neda, J. Lasing in a coupled hybrid double quantum dot-resonator system. Phys. Rev. B 2020, 101, 115135. [Google Scholar] [CrossRef]
- Gu, X.; Kockum, A.F.; Miranowicz, A.; Liu, Y.-x.; Nori, F. Microwave photonics with superconducting quantum circuits. Phys. Rep. 2017, 718–719, 1–102. [Google Scholar] [CrossRef]
- Scarlino, P.; van Woerkom, D.J.; Stockklauser, A.; Koski, J.V.; Collodo, M.C.; Gasparinetti, S.; Reichl, C.; Wegscheider, W.; Ihn, T.; Ensslin, K.; et al. All-microwave control and dispersive readout of gate-defined quantum dot qubits in circuit quantum electrodynamics. Phys. Rev. Lett. 2019, 122, 206802. [Google Scholar] [CrossRef]
- Khan, W.; Potts, P.P.; Lehmann, S.; Thelander, C.; Dick, K.A.; Samuelsson, P.; Maisi, V.F. Efficient and continuous microwave photoconversion in hybrid cavity-semiconductor nanowire double quantum dot diodes. Nat. Commun. 2021, 12, 5130. [Google Scholar] [CrossRef]
- Havir, H.; Haldar, S.; Khan, W.; Lehmann, S.; Dick, K.A.; Thelander, C.; Samuelsson, P.; Maisi, V.F. Quantum dot source-drain transport response at microwave frequencies. Phys. Rev. B 2023, 108, 205417. [Google Scholar] [CrossRef]
- Nian, L.-L.; Hu, S.; Xiong, L.; Lü, J.-T.; Zheng, B. Photon-assisted electron transport across a quantum phase transition. Phys. Rev. B 2023, 108, 085430. [Google Scholar] [CrossRef]
- Wallraff, A.; Schuster, D.I.; Blais, A.; Frunzio, L.; Huang, R.-S.; Majer, J.; Kumar, S.; Girvin, S.M.; Schoelkopf, R.J. Strong coupling of a single photon to a superconducting qubit using circuit quantum electrodynamics. Nature 2004, 431, 162–167. [Google Scholar] [CrossRef]
- Stockklauser, A.; Scarlino, P.; Koski, J.V.; Gasparinetti, S.; Andersen, C.K.; Reichl, C.; Wegscheider, W.; Ihn, T.; Ensslin, K.; Wallraff, A. Strong coupling cavity QED with gate-defined double quantum dots enabled by a high impedance resonator. Phys. Rev. X 2017, 7, 011030. [Google Scholar] [CrossRef]
- Gu, S.-S.; Kohler, S.; Xu, Y.-Q.; Wu, R.; Jiang, S.-L.; Ye, S.-K.; Lin, T.; Wang, B.-C.; Li, H.-O. Probing two driven double quantum dots strongly coupled to a cavity. Phys. Rev. Lett. 2023, 130, 233602. [Google Scholar] [CrossRef]
- Ungerer, J.H.; Pally, A.; Kononov, A.; Lehmann, S.; Ridderbos, J.; Potts, P.P.; Thelander, C.; Dick, K.A.; Maisi, V.F.; Scarlino, P.; et al. Strong coupling between a microwave photon and a singlet–triplet qubit. Nat. Commun. 2024, 15, 1068. [Google Scholar] [PubMed]
- Wong, C.H.; Vavilov, M.G. Quantum efficiency of a single microwave photon detector based on a semiconductor double quantum dot. Phys. Rev. A 2017, 95, 012325. [Google Scholar] [CrossRef]
- Ghirri, A.; Cornia, S.; Affronte, M. Microwave photon detectors based on semiconducting double quantum dots. Sensors 2020, 20, 4010. [Google Scholar] [CrossRef]
- Nian, L.-L.; Zheng, B.; Lü, J.-T. Electrically driven photon statistics engineering in quantum-dot circuit quantum electrodynamics. Phys. Rev. B 2023, 107, L241405. [Google Scholar] [CrossRef]
- Sánchez, R.; Platero, G.; Brandes, T. Resonance fluorescence in transport through quantum dots: Noise properties. Phys. Rev. Lett. 2007, 98, 146805. [Google Scholar] [CrossRef]
- Xu, C.; Vavilov, M.G. Full counting statistics of photons emitted by a double quantum dot. Phys. Rev. B 2013, 88, 195307. [Google Scholar] [CrossRef]
- Agarwalla, B.K.; Kulkarni, M.; Mukamel, S.; Segal, D. Tunable photonic cavity coupled to a voltage-biased double quantum dot system: Diagrammatic nonequilibrium Green’s function approach. Phys. Rev. B 2016, 94, 035434. [Google Scholar] [CrossRef]
- Chen, C.-C.; Stace, T.M.; Goan, H.-S. Full-polaron master equation approach to dynamical steady states of a driven two-level system beyond the weak system-environment coupling. Phys. Rev. B 2020, 102, 035306. [Google Scholar] [CrossRef]
- Hazra, S.K.; Addepalli, L.; Pathak, P.K.; Dey, T.N. Nondegenerate two-photon lasing in a single quantum dot. Phys. Rev. B 2024, 109, 155428. [Google Scholar] [CrossRef]
- Jin, J.; Marthaler, M.; Jin, P.-Q.; Golubev, D.; Schön, G. Noise spectrum of a quantum dot-resonator lasing circuit. New J. Phys. 2013, 15, 025044. [Google Scholar] [CrossRef]
- Lambert, N.; Flindt, C.; Nori, F. Photon-mediated electron transport in hybrid circuit-QED. EPL (Europhys. Lett.) 2013, 103, 17005. [Google Scholar] [CrossRef]
- Shi, P.; Hu, M.; Ying, Y.; Jin, J. Noise spectrum of quantum transport through double quantum dots: Renormalization and non-Markovian effects. AIP Adv. 2016, 6, 095002. [Google Scholar] [CrossRef]
- Karlewski, C.; Heimes, A.; Schön, G. Lasing and transport in a multilevel double quantum dot system coupled to a microwave oscillator. Phys. Rev. B 2016, 93, 045314. [Google Scholar] [CrossRef]
- Jin, J. Nonequilibirum noise spectrum and Coulomb blockade assisted Rabi interference in a double-dot Aharonov–Bohm interferometer. Phys. Rev. B 2020, 101, 235144. [Google Scholar] [CrossRef]
- Drummond, P.D.; Walls, D.F. Quantum theory of optical bistability. I. Nonlinear polarisability model. J. Phys. A 1980, 13, 725–741. [Google Scholar] [CrossRef]
- Macovei, M.A. Measuring photon-photon interactions via photon detection. Phys. Rev. A 2010, 82, 063815. [Google Scholar] [CrossRef]
- Zenelaj, D.; Potts, P.P.; Samuelsson, P. Full counting statistics of the photocurrent through a double quantum dot embedded in a driven microwave resonator. Phys. Rev. B 2022, 106, 205135. [Google Scholar] [CrossRef]
- Zenelaj, D.; Samuelsson, P.; Potts, P.P. Wigner-function formalism for the detection of single microwave pulses in a resonator-coupled double quantum dot. Phys. Rev. Res. 2025, 7, 013305. [Google Scholar] [CrossRef]
- Jin, P.-Q.; Marthaler, M.; Cole, J.H.; Shnirman, A.; Schön, G. Lasing and transport in a quantum-dot resonator circuit. Phys. Rev. B 2011, 84, 035322. [Google Scholar] [CrossRef]
- Rastelli, G.; Governale, M. Single atom laser in normal-superconductor quantum dots. Phys. Rev. B 2019, 100, 085435. [Google Scholar] [CrossRef]
- Mantovani, M.; Armour, A.D.; Belzig, W.; Rastelli, G. Dynamical multistability in a quantum-dot laser. Phys. Rev. B 2019, 99, 045442. [Google Scholar] [CrossRef]
- Agarwalla, B.K.; Kulkarni, M.; Segal, D. Photon statistics of a double quantum dot micromaser: Quantum treatment. Phys. Rev. B 2019, 100, 035412. [Google Scholar] [CrossRef]
- Stace, T.M.; Doherty, A.C.; Barrett, S.D. Population inversion of a driven two-level system in a structureless bath. Phys. Rev. Lett. 2005, 95, 106801. [Google Scholar] [CrossRef] [PubMed]
- Müller, C.; Stace, T.M. Deriving Lindblad master equations with Keldysh diagrams: Correlated gain and loss in higher order perturbation theory. Phys. Rev. A 2017, 95, 013847. [Google Scholar] [CrossRef][Green Version]
- Clerk, A.A.; Lehnert, K.W.; Bertet, P.; Petta, J.R.; Nakamura, Y. Hybrid quantum systems with circuit quantum electrodynamics. Nat. Phys. 2020, 16, 257–267. [Google Scholar] [CrossRef]
- Schegolev, A.E.; Klenov, N.V.; Bogatskaya, A.V.; Yusupov, R.D.; Popov, A.M. A pair of coupled waveguides as a classical analogue for a solid-state qubit. Sensors 2022, 22, 8286. [Google Scholar] [CrossRef] [PubMed]
- Zakharov, R.V.; Tikhonova, O.V.; Klenov, N.V.; Soloviev, I.I.; Antonov, V.N.; Yakovlev, D.S. Solid-state qubit as an on-chip controller for non-classical field states. Adv. Quantum Technol. 2024, 7, 2400141. [Google Scholar]
- Lv, W.-C.; Zhao, W.-T.; Wang, Y.; Kang, Y.-H.; Feng, W.; Zhang, G.-Q.; Yu, L.; Yang, C.-P.; Su, Q.-P. Efficient preparation of high-dimensional hybrid entangled states in circuit quantum electrodynamics. Phys. Rev. Appl. 2025, 23, 054037. [Google Scholar] [CrossRef]
- Mihaescu, T.; Isar, A.; Macovei, M.A. Two-quanta processes in coupled double-quantum-dot cavity systems. arXiv 2025, arXiv:2501.05967. [Google Scholar] [CrossRef]
- Nian, L.-L.; Wang, Y.-C.; Wang, J.-Y.; Xiong, L.; Zheng, B.; Lü, J.-T. Dissipative quantum phase transitions in electrically driven lasers. arXiv 2025, arXiv:2501.10997. [Google Scholar] [CrossRef]
- Agarwal, G.S. Quantum Statistical Theories of Spontaneous Emission and Their Relation to Other Approaches; Springer: Berlin/Heidelberg, Germany, 1974. [Google Scholar] [CrossRef]
- Kiffner, M.; Macovei, M.; Evers, J.; Keitel, C.H. Vacuum induced processes in multilevel atoms. Prog. Opt. 2010, 55, 85–197. [Google Scholar]
- James, D.F.V. Quantum computation with hot and cold ions: An assessment of proposed schemes. Fort. Phys. 2000, 48, 823–837. [Google Scholar]
- Tan, R.; Li, G.-X.; Ficek, Z. Squeezed single-atom laser in a photonic crystal. Phys. Rev. A 2008, 78, 023833. [Google Scholar] [CrossRef][Green Version]
- Quang, T.; Freedhoff, H. Atomic population inversion and enhancement of resonance fluorescence in a cavity. Phys. Rev. A 1993, 47, 2285–2292. [Google Scholar] [CrossRef] [PubMed]
- Mihaescu, T.; Cecoi, E.; Macovei, M.A.; Isar, A. Geometric discord for a driven two-qubit system. Rom. Rep. Phys. 2021, 73, 101. Available online: https://rrp.nipne.ro/2021_73_1.html (accessed on 9 October 2025).
- Glauber, R.J. The quantum theory of optical coherence. Phys. Rev. 1963, 130, 2529–2539. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).