1. Introduction
The dynamic vibration of a Segway system on an irregular stochastic road profile can be understood by combining insights from studies on vehicle dynamics, tyre models and road irregularities. A Segway is a two-wheeled self-balancing vehicle that faces unique challenges when moving over uneven terrain such as stochastic road profiles, which can affect stability and rider comfort. The use of a series elastic actuator (SEA) in Segways has been proposed to improve stability during linear and curved driving and to reduce the impact of vibrations from uneven surfaces [
1]. The dynamic response of vehicles, including Segways, to road irregularities is influenced by the tire–road interaction, where the tire’s ability to envelop short-wavelength obstacles plays a critical role in mitigating vibrations [
2]. The LuGre tire model, which considers the adhesion between the tire and road, is essential for accurately predicting the dynamic responses of the Segway system on a sinusoidal road profile [
3]. Additionally, the influence of road roughness and cross slope on dynamic loads can exacerbate the vibration experienced by the Segway, as these factors increase the dynamic wheel loads, leading to higher stresses on the vehicle’s structure [
4,
5]. The roughness resistance, a component of the resistance faced by vehicles on rough roads, is particularly relevant for Segways, as it contributes to power dissipation through vibration, affecting both performance and rider comfort [
6]. The dynamic vibration of the Segway system is further complicated by the need to navigate dynamic environments with obstacles, where velocity-based stabilizing controllers can help maintain a smooth, safe path [
7]. The interaction between the Segway’s tires and the road surface, modeled as a grid of deformable springs, allows for the efficient simulation of the vehicle’s response to varying soil properties and road profiles, providing a comprehensive understanding of the dynamic vibration phenomena [
8]. Moreover, the whole-body vibration (WBV) experienced by riders due to road irregularities, such as potholes, is a critical factor in assessing the comfort and safety of Segway systems, with vibration dose values (VDV) being a key metric for evaluating the impact of these vibrations [
9]. The accurate modeling of road irregularities using high-order filtering white noises modulated by coherent and incoherent functions ensures that the dynamic simulations of Segway systems on sinusoidal road profiles are reliable and reflective of real-world conditions [
10]. The dynamic stability of a Segway system, akin to that of other two-wheeled self-balancing robots, involves using complex control strategies to maintain balance and maneuverability, especially on uneven surfaces. The research in Ref. [
11] introduces a DNN-compensator coupled with a traditional PD-controller to enhance the stability of two-wheeled robots, demonstrating improved performance in maintaining balance and reducing pitch angle fluctuations on uneven terrains. The study [
12] of discrete-time dynamic vehicle models addresses numerical stability issues, particularly at low speeds, which are relevant for Segway systems that often operate in stop–start urban environments. The integration of such models can help in mitigating low-speed singularities, ensuring stable operation. Furthermore, the study [
13] on Autonomous Neural Dynamic Policies (ANDPs) offers a promising framework for achieving asymptotically stable behaviors in robotic systems, combining the flexibility of neural networks with the stability of dynamical systems. The performance improvement of a non-minimum phase (NMP) mini-Segway using sample and hold inputs (SHIs) is primarily explored through the discretization of continuous-time NMP systems into minimum-phase (MP) systems [
14,
15]. The implementation of this technique on a mini-Segway, equipped with a low-cost microcontroller such as Arduino demonstrates significant performance improvements, notably reducing oscillation magnitudes by over 65% compared to baseline controllers [
15]. Chunxiang Yan and Xiying Li propose a model that uses a Proportional-Integral-Derivative (PID) control algorithm to adjust vehicle parameters including attitude, speed, and acceleration, complemented by a terrain recognition algorithm based on deep learning to improve stability on complex terrains [
16]. The design and implementation of a two-wheeled self-balancing car using a fuzzy Kalman filter involves integrating advanced control algorithms to enhance stability and performance to improve the attitude estimation of the vehicle [
17].
Although some studies have advanced the modelling and control of self-balancing vehicles, limited attention has been given to the combined effects of stochastic terrain characteristics, nonlinear wheel–ground interactions, and transitions to chaotic dynamics under realistic operating conditions. Various existing approaches treat these factors in isolation, leading to gaps in predicting transitions from stable to chaotic regimes. Addressing this limitation, the present study develops a comprehensive nonlinear dynamic model of a Segway operating over the ISO 8608-classified [
18] stochastic surfaces, integrating elastic–damping effects at the contact interface with advanced analytical and numerical tools. The investigation aims to define stability boundaries, examine vibration characteristics over diverse operating scenarios, and measure the contribution of primary mechanical and control variables. The results are intended to inform the design of stability enhancement strategies that deliver reliable, efficient, and comfortable performance on a wide range of surfaces.
2. Formulation of Dynamic Equations Governing the Segway System
A simplified dynamic model of the Segway system involves a set of coupled ordinary differential equations (ODEs) that describes the evolution of the state variables over time. The equations include terms representing the dynamics of the inverted pendulum and can be represented by differential equations that relate the accelerations, velocities, positions, and forces acting on the system components.
The following assumptions are made to simplify the model and facilitate analysis during the mathematical modelling process.
- ○
When the wheels are in contact with the surface, and the system rolls without slipping, friction between the wheels and the surface varnishes.
- ○
Air resistance is often neglected in the mathematical model, assuming that the Segway moves through the air without significant aerodynamic effects.
- ○
The mass distribution of the Segway is considered constant during the dynamic analysis.
- ○
The Segway frame is assumed to have no elastic deformation, except for the tire.
Neglecting air resistance removes aerodynamic forces that grow with speed. The resistance leads to larger motions and somewhat lower onset speeds for large responses, with the difference increasing at higher speeds and in outdoor conditions. Assuming a constant mass distribution keeps the system mass properties fixed in time, no additional modulation enters the dynamics. Treating the frame as perfectly rigid makes energy storage and dissipation occur mainly in the tires through tire deformation under rider weight and at the tire-road contact.
Figure 1 presents both the physical configuration of a Segway system and the corresponding dynamic model treated as a cart-inverted pendulum system modelled as a three-degrees-of-freedom (3-DOF) system with independent coordinates
x,
y and
θ describing the motion of the system.
Figure 1a presents the actual Segway system, highlighting a structurally simple design composed of two wheels arranged on a common axis and a vertical handle used for support and steering input.
Figure 1b illustrates a schematic diagram that translates the physical system into a dynamic model in such a way that the Segway is represented as an inverted pendulum placed on a cart. The diagram captures the essential physical principles governing the Segway’s balance and motion, enabling analysis of its dynamic behavior.
The rolling dynamics of the wheels are modelled to include spring stiffness
k and damping coefficient
c, reflecting the elastic and dissipative properties that influence vibration transmission from the road to the Segway structure. The torque
τ applied to the pendulum mass and the torque
τw acting on the wheels highlight the control inputs in the dynamic model, which are fundamental for stability analysis. The vector position of mass
m and the resulting squared velocity are given by
and
respectively, where the dot on top denotes the time derivative.
A switching contact model between a Segway tire and a stochastic road profile captures the intermittent nature of tire–terrain interaction. It can be derived from
Figure 2 by distinguishing between contact and flight phases as the wheel travels across undulating surfaces.
The road is modeled as stochastic road profile
yr, the tire’s vertical position is given by
y, and
ε the contact clearance between the tire and the terrain is defined as
:The Kelvin–Voigt contact model defines the normal interaction force [
19,
20]:
where
k and
c denote the spring stiffness of wheel-ground contact and the damping coefficient in wheel-ground contact, respectively.
Accurate modelling of road surface irregularities is a critical component of analyzing the dynamic behavior of ground vehicles and self-balancing systems. The dynamic response of such systems is strongly influenced by the spectral content and amplitude of surface roughness, which act as external excitations across a range of spatial frequencies. To ensure a consistent and reproducible description of these surfaces, the ISO 8608:2016 standard [
18] introduces a statistical framework for road roughness characterization based on power spectral density (PSD) functions [
21,
22]:
where
N denotes the number of samples,
n is the spatial frequency of road profile,
n0 is the reference spatial frequency,
w is the spectral slope of road surface,
η is the roughness coefficient, and
nk is the spatial frequency index:
The surface excitation can be expressed as a function of time yr(t) = yr(vt) to allow for time-based dynamic simulations of the system under constant-speed motion.
The general form of the kinetic energy of the system is expressed to account for both translational and rotational motion of all constituent components of the Segway system. The kinetic energy comprises several terms associated with the linear motion of the wheel base along the horizontal
x and vertical
y directions, as well as the angular motion of the pendulum about its pivot point:
After substituting Equation (2) into Equation (9) and performing algebraic manipulation, the kinetic energy can be expressed in explicit form:
The system’s potential energy is given by an expression that represents the gravitational energy stored in the Segway’s inverted pendulum configuration as well as any elastic potential energy arising from road surface interactions:
where
g is the gravitation acceleration.
The system Rayleigh dissipation function represents half the total power lost through non-conservative forces, which quantifies the rate at which mechanical energy is dissipated in the Segway system due to damping forces acting in its components:
Kinetic energy
T (10) encompasses contributions from the translational motion of the cart, the rotational motion of the pendulum, and the rotation of the wheels. The potential energy
U (11) primarily arises from gravitational forces acting on the pendulum mass, elastic potential energy due to suspension elements and terrain-induced vertical displacements. The Rayleigh dissipation function
D (12) contributes as a source of energy dissipation, including viscous friction in mechanical joints, rolling resistance in the wheels, and material damping in structural components. External generalized forces
Fq represent external actions applied directly to the system, contributing mechanical work along the directions defined by the generalized coordinates
qn. The Lagrangian function serves as the foundational element in applying Lagrange’s equations of motion, which, for each generalized coordinate, are given by:
The system equation of motion governing the 3-DOF system after the implementation of the Lagragian’s function (13) can be expressed in the following form:
The mathematical model governing the system is represented by Equations (14)–(16), where Equations (15) and (16) are nonlinear. Taylor series expansion represents the value of a function in terms of its value at a specific point, the deviation from that point, and the derivatives evaluated at the same point:
For relatively small excursions of
x from
xo, higher-order terms can be neglected. The approximation leads to a linear relation between the variation in
f(
x) and the displacement from
xo. By leaving out the higher-order terms, Equation (16) takes the form
The excursions about equilibrium position are
xo = 0,
yo = 0 and
θo = 0 or π. Using Taylor series approximations:
Therefore, by applying Equation (18) to approximate the nonlinear system Equations (14)–(16) governing the Segway, the linearization relationship can be performed:
Using the expressions (20) and (21), linearized equations of motion (14), (15) and (16) only retaining linear terms can be expressed in matrix form:
where:
where ω
n is the natural frequency.
Critical speed quantifies the threshold velocity at which the Segway system transitions from stable to unstable dynamic behavior associated with the inverted pendulum component as it responds to both the gravitational restoring moment and the inertial effects induced by forward motion over the irregular stochastic road profile
The condition for stability due to Segway linear velocity can be represented by
5. Dynamic Stability of Segway System
Numerous physical and engineering systems are governed by differential equations that describe how quantities evolve under the influence of forces, constraints, and external excitations. In dynamic analysis, systems often exhibit nonlinear interactions among many degrees of freedom, which leads to coupled differential equations that can be of second or higher order. The Lorenz-like formulation is employed to recast the Equations (13)–(15) into a set of coupled first-order ODEs where each equation expresses the time derivative of a state variable as a function of the other state variables and time.
The following state variables are defined to convert the original equations into first-order form:
For systematic analysis and computational modelling, it is helpful to express the equations of motion in state-space form. Introducing appropriate state variables allows us to rewrite the system as a set of first-order differential equations, which simplifies the study of its dynamic behavior and facilitates numerical integration:
and
Equations (13)–(15) were transformed as first-order in time, forming a system of six coupled differential Equations (34)–(39), which matches the sense of Lorenz-type systems used for nonlinear dynamics.
The candidate Lyapunov function
V is the sum of the kinetic energy and potential energy:
The system is stable if for all t. If the condition holds, then the Lyapunov function demonstrates the system’s stability.
The Segway system on irregular stochastic terrain exhibits complex dynamic behavior coupled with nonlinear translational and rotational interaction motion arising under the influence of external excitations and internal restoring forces. The resulting equations of motion feature interdependencies between variables that can be exploited to reveal underlying structures similar to known chaotic systems. Reducing the governing equations to a lower-dimensional Lorenz-84 model helps retain the core nonlinear features [
28]. In the present case, the original coupled equations derived from Lagrange’s formulation, including torque balance, damping, and gravitational effects, are rewritten as a three-dimensional autonomous system. Through its dependence terms and governing parameters, the model retains its nonlinear structure. The reformulated model offers a basis for examining the geometry of phase trajectories, bifurcation responses, and chaotic tendencies.
6. Numerical Simulation
The numerical simulation of the Segway system employs specific physical and mechanical parameters characterizing the vehicle’s dynamics. The mass of the Segway body is taken as 1.2 kg, while each wheel possesses a mass of 0.2 kg. The moment of inertia of the wheel about its rotation axis is 0.02 × 10−3 kgm2, reflecting the wheel’s resistance to angular acceleration. The distance from the Segway’s center of mass to the axis of rotation, denoted as L, is set to 1 m. The radius of the wheel r is 0.032 m. The stiffness coefficient k that represents the elastic restoring force is 0.29 N/m. Additionally, damping effects, accounting for the energy dissipated due to motion, are modelled by a damping coefficient c = 0.01 Ns/m. Roughness coefficient at reference spatial frequency n0 = 0.1 m−1, spectral slope w = 2, class A: η(n0) = 16 × 10−6 m3 (highly smooth), class D: η(n0) = 256 × 10−6 m3 (average rough road) and class H: η(n0) = 4096 × 10−6 m3 (very rough).
The Runge–Kutta fourth order was employed as a discretization method for the vibration response of the Segway system generated under a specific irregular road profile. This means that the signal’s step size may be large so that the output is more widely spaced, and the interpolant is called up to produce more finely spaced results. The results of the dynamic analysis of the Segway system on an irregular stochastic road profile class H are processed using the MATLAB R2024b program. The obtained signal considers the vibrations generated by all the constituent assembly elements of the Segway system, presented in Waveform, FFT, KDE histogram, Lorenz attractor and bifurcation diagram.
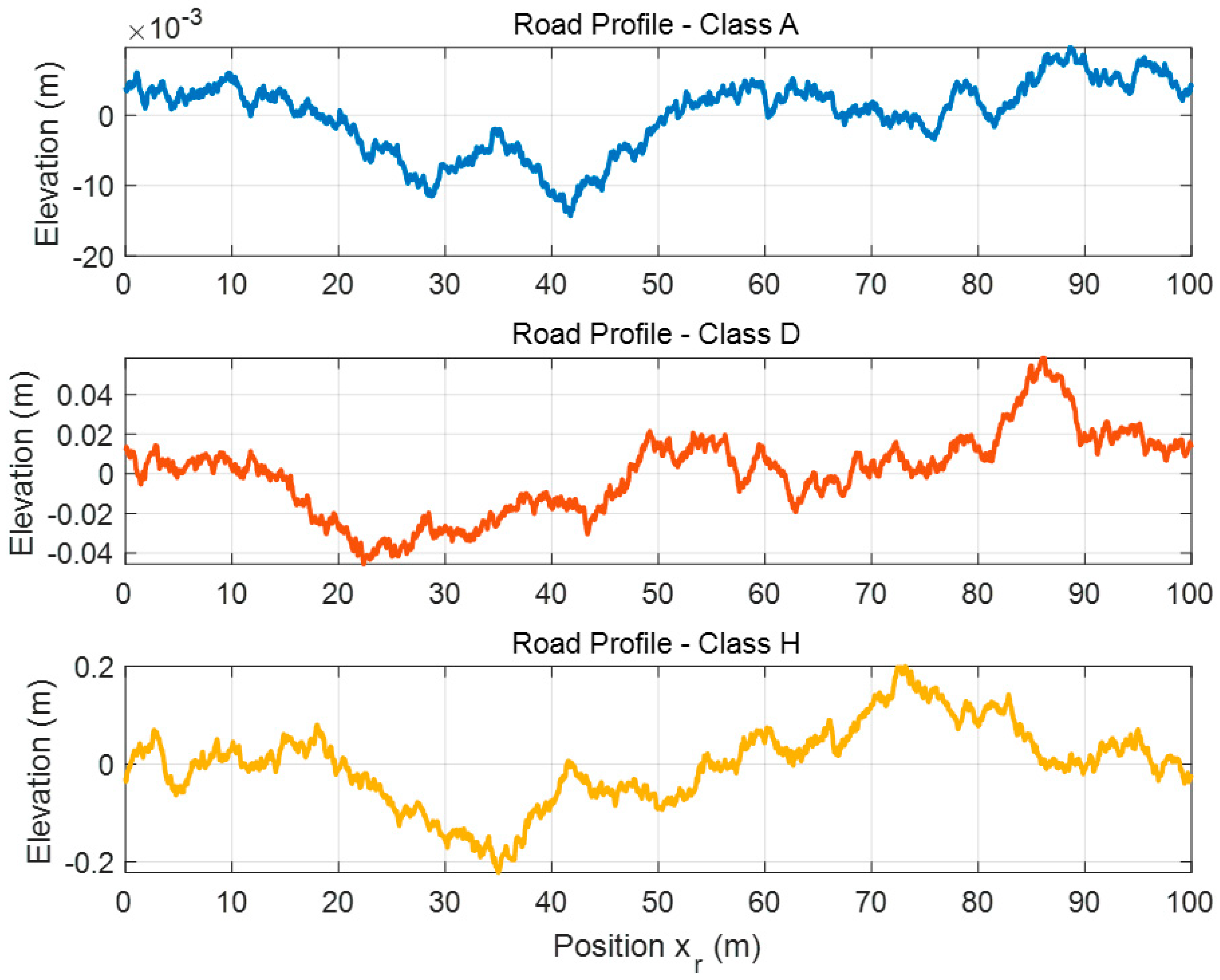
Figure 3 illustrates three representative spatial road elevation profiles generated in accordance with the ISO 8608 classification [
18], which defines surface roughness using a power spectral density. For class A, the elevation trace remains confined within the order of 10
−3 m, producing minimal high-frequency undulations. Such a profile represents near-ideal pavement conditions, where the excitation to the wheel–ground interface is dominated by low-amplitude, short-wavelength content. The class D profile displays larger-scale undulations, with elevation amplitudes approaching approximately 0.04 m representing a mid-level roughness condition, where the spatial irregularities occur over both intermediate and longer wavelengths. The class H profile exhibits the highest elevation variation, within up to 0.20 m, with quite a broad mixture of wavelengths, corresponding to highly degraded or unpaved surfaces that impart substantial vertical excitation to the Segway system.
In
Figure 4a, the initial transient response is characterized by relatively high-amplitude oscillations of 3 × 10
−3 m that quite rapidly decay within approximately the first second, indicating that the combined elastic–damping characteristics of the wheel–ground interface effectively dissipate energy from initial disturbances with the trends documented in [
29]. In both cases, once the transient phase subsides, the system transitions to a steady regime with relatively small, bounded oscillations, where variations in response magnitude arise. As time progresses, the
y-displacement converges to a small steady oscillatory regime, with magnitudes below the order of 10
−3 m. The inset zoom confirms that, at higher speeds, the oscillatory pattern becomes more pronounced in amplitude and complexity, reflecting the increased influence of inertial excitation and reduced relative dominance of damping. The differences among the velocity cases are subtle in steady state but remain measurable, with higher velocities generally showing somewhat larger amplitude variations. In
Figure 4b, the
θ-coordinate response begins with a distinct initial overshoot, where the pendulum rapidly deviates from equilibrium. The plotted curves for the different velocities show that, during the early transient phase, angular displacement is nearly identical across speeds, indicating that the initial dynamic behavior is dominated by the system’s intrinsic restoring torque and damping rather than the magnitude of forward motion. However, as shown in the zoomed insets, velocity-dependent differences emerge during the subsequent oscillations; higher speeds sustain somewhat larger angular amplitudes and reduced symmetry in the oscillation envelope, aligning with the tilt angle responses in Ref. [
30]. Both cases demonstrate that operating conditions influence the amplitude and symmetry of the oscillation envelope.
In
Figure 5a, which shows the
y-coordinate of vertical displacement spectra, several resonant peaks are evident between approximately 2 Hz and 25 Hz. The peaks correspond to the system’s natural frequencies excited by the spatial irregularities of the ISO 8608 road profile [
18] once converted into temporal frequencies. At lower velocities of 10 km/h, spectral amplitudes are relatively low and quite broadly distributed, suggesting weaker excitation of structural modes. As velocity increases, particularly at 30 and 40 km/h, the amplitudes at these resonant bands rise markedly, with the largest peaks approaching 11 × 10
−3 m. The amplification reflects stronger inertial input from faster forward motion and a higher likelihood of matching excitation frequencies with the system’s natural modes. The inset highlights the increased energy concentration in the 12–25 Hz range at higher speeds, indicating a growing susceptibility to resonant amplification in that frequency band.
Figure 5b, showing the
θ-coordinate of angular displacement spectra, reveals dominant resonant frequencies in the much lower 2–5 Hz range. The frequency band corresponds to the lower natural frequency of the inverted pendulum mode when compared with the cart’s translational mode. At lower speeds, amplitude peaks remain near 0.016 rad, but, at 30 and 40 km/h, they rise to almost 0.04 rad. The inset verifies that higher speeds increase the excitation of low-frequency rotational modes.
In
Figure 6a, at 10 km/h, the KDE analysis shows a maximum density zone emerging shortly after the transient phase and remaining concentrated around a relatively small displacement offset. The narrow density band and high peak values from the output indicate highly consistent translational motion with minimal variability. In
Figure 6b, at 20 km/h, results still display a focused maximum density zone, but the displacement spread expands to some degree, revealing a modest rise in variability associated with stronger inertial loading under the same processing method. In
Figure 6c, at 30 km/h, the KDE mapping detects multiple high-density clusters replacing the single main zone observed at lower speeds, with increased variability and quite a wider distribution of peak displacement values. The fragmentation pattern in the contour’s points to the presence of higher-frequency components and reduced predictability. In
Figure 6d, at 40 km/h, outputs show a shifted and more dispersed maximum density zone. The broader contour spread indicates that displacement states fluctuate more significantly over time, highlighting stronger nonlinear interactions between road-induced excitation and the Segway’s dynamic response.
The 3D KDE waterfall response is applied as a visualization technique to capture both the temporal evolution of displacement and the probability concentration of specific states, enabling a clearer distinction between stable and more variable operating regimes.
Figure 7a for 10 km/h shows a density surface dominated by a single, well-defined ridge with peaks labeled ‘1D’, ‘2D’ and ‘3D’. The peaks are consistently aligned along quite a narrow displacement range, and the maximum density approaches 900, indicating strong clustering of displacement values around the mean state. The regularity and compactness of the peaks indicate that the translational dynamics remain stable and predictable at this velocity. At 20 km/h,
Figure 7b depicts multiple ridges identified as ‘1D’ and ‘5D’, with density maxima falling somewhat under 900. The increased ridge count and non-uniform spacing over time suggest more variation in the displacement response. The pattern reflects a greater influence of inertial effects, causing the system to occupy a broader set of oscillatory states compared to the 10 km/h case.
Figure 7c for 30 km/h shows a density distribution retaining three main labeled ridges (‘1D’, ‘3D’ and ‘2D’) but with increased irregularity in both spacing and peak heights. Maximum densities remain around 820, but the spread of displacement values widens, marking a shift toward less predictable motion and the onset of complex oscillatory patterns.
Figure 7d for 40 km/h shows ‘1D’, ‘2D’, ‘3D’ and ‘4D’ density peaks of distributed unevenly over time and displacement. The broader spread and irregularity of the ridges reveal stronger nonlinear coupling between the translational motion and road-induced excitation, with KDE amplitude increasing periodically at this velocity.
Figure 8a displays the variation in the stability indicator across a range of velocities for three perturbation scenarios of Δ = −1, Δ = 0, and Δ = 1. All curves show a declining trend in the stability indicator as velocity increases from 0 m/s to nearly 18.5 m/s before rising again. The convergence of curves toward a singular point at approximately 18.5 m/s represents the occurrence of a saddle-node bifurcation. The system transitions from a dynamically stable to an unstable state. The system retains higher values of the stability indicator when velocities are below the bifurcation point and exhibits robust dynamic behavior capable of withstanding quite small perturbations. The stability indicator starts increasing again and suggests the emergence of new dynamic states that may become unstable, where oscillatory responses could grow instead of decay.
Figure 8b shows the Lyapunov function plotted against forward velocity with a response divided into two distinct regions by a critical threshold value indicated by a horizontal dashed line, which separates stable and unstable dynamic regions. For velocities below approximately 19.165 m/s, the Lyapunov function stays under the stability threshold and confirms that the Segway system operates in a dynamically stable regime in such a way that perturbations decrease as a function of time. With the velocities above the critical point, the Lyapunov function rises and surpasses the threshold to enter the unstable region. The behavior shows that, at higher speeds, perturbations grow instead of diminishing and cause a potential loss of balance and control. The critical velocity of 19.165 m/s aligns precisely with the saddle–node bifurcation point seen in
Figure 8a and confirms that both analytical approaches consistently identify the threshold where the system becomes unstable.
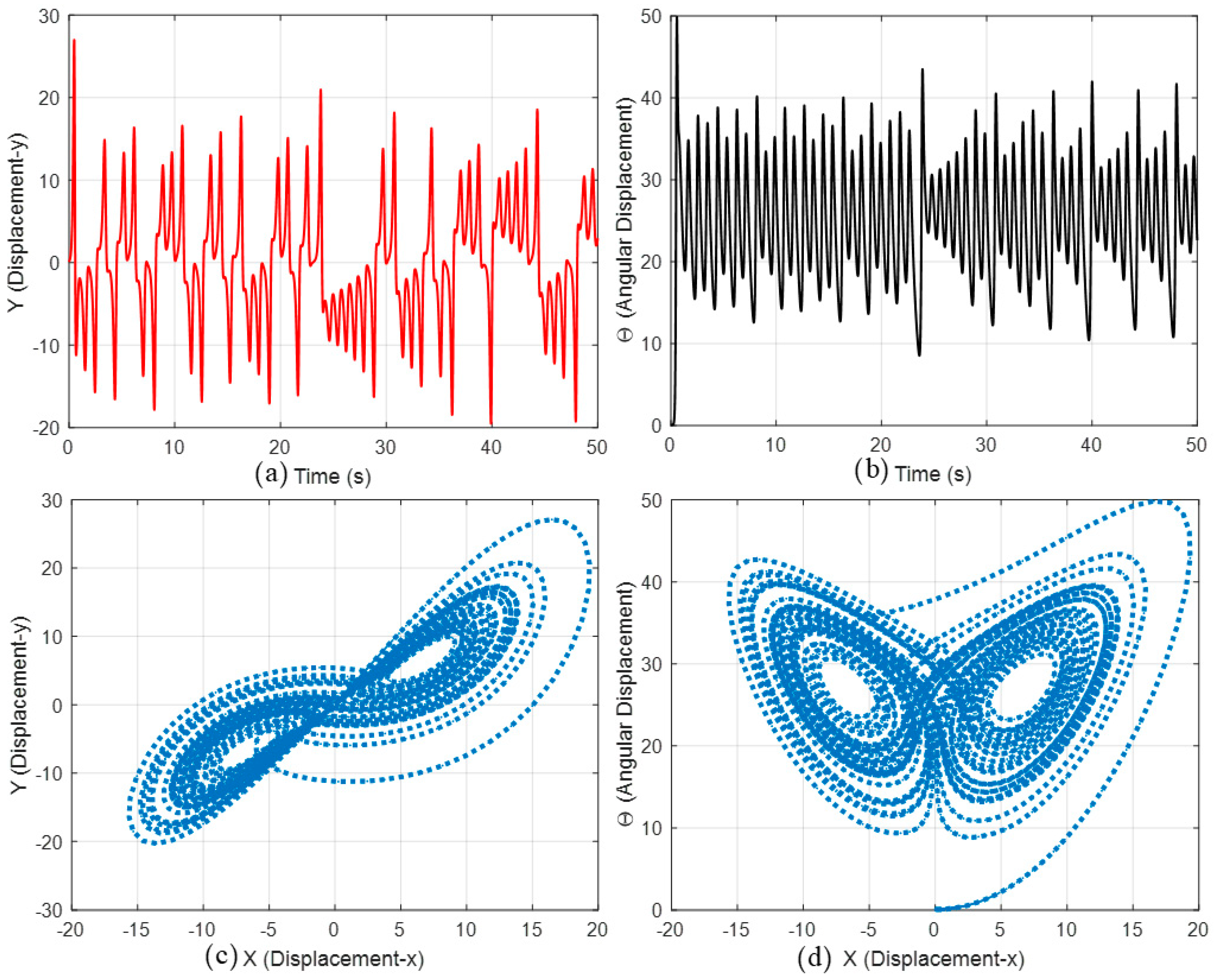
Figure 9a presents the y-coordinate of translational displacement over 50 s, displaying non-stationary oscillations with varying amplitudes. The displacement ranges from about –20 to 30, with high-amplitude bursts alternating with smaller oscillations. The variability reflects nonlinear interactions between wheel–ground excitation and pendulum dynamics, causing transitions between different oscillatory states.
Figure 9b presents the
θ-coordinate of angular displacement over the same period. Angular motion exhibits sustained oscillations with rapidly varying amplitudes, ranging from about 8 to 50. The irregular waveform indicates coupling between translational and rotational modes, with energy exchanges leading to periods of intensified angular displacement followed by more subdued motion.
Figure 9c presents the
y–x phase-space attractor with y-coordinate displacement plotted against
x-coordinate displacement. The two-lobed geometry is similar to a Lorenz attractor and indicates deterministic chaos. Trajectories circulate around two unstable equilibrium regions, intermittently transitioning between them, indicating sensitivity to initial conditions and persistent nonlinear coupling. In
Figure 9d, the
θ–x attractor displays angular displacement versus translational displacement with a double-lobe pattern that extends more along the
θ-axis than the
y–x attractor. The shape reflects the stronger influence of angular motion in the nonlinear state evolution and indicates that rotational dynamics may play a greater role in chaotic transitions than translational dynamics.
The bifurcation control parameters are defined by the influence of gravity–damping index, mass–damping coupling index, control torque ratio and normalized vertical excitation on system stability. Each parameter shows how mechanical properties and physical forces govern the conditions under which the Segway may transition between stable and unstable dynamic states. The dimensionless forms that characterize the parameters governing the dynamic behavior of the Segway system are summarized in
Table 1.
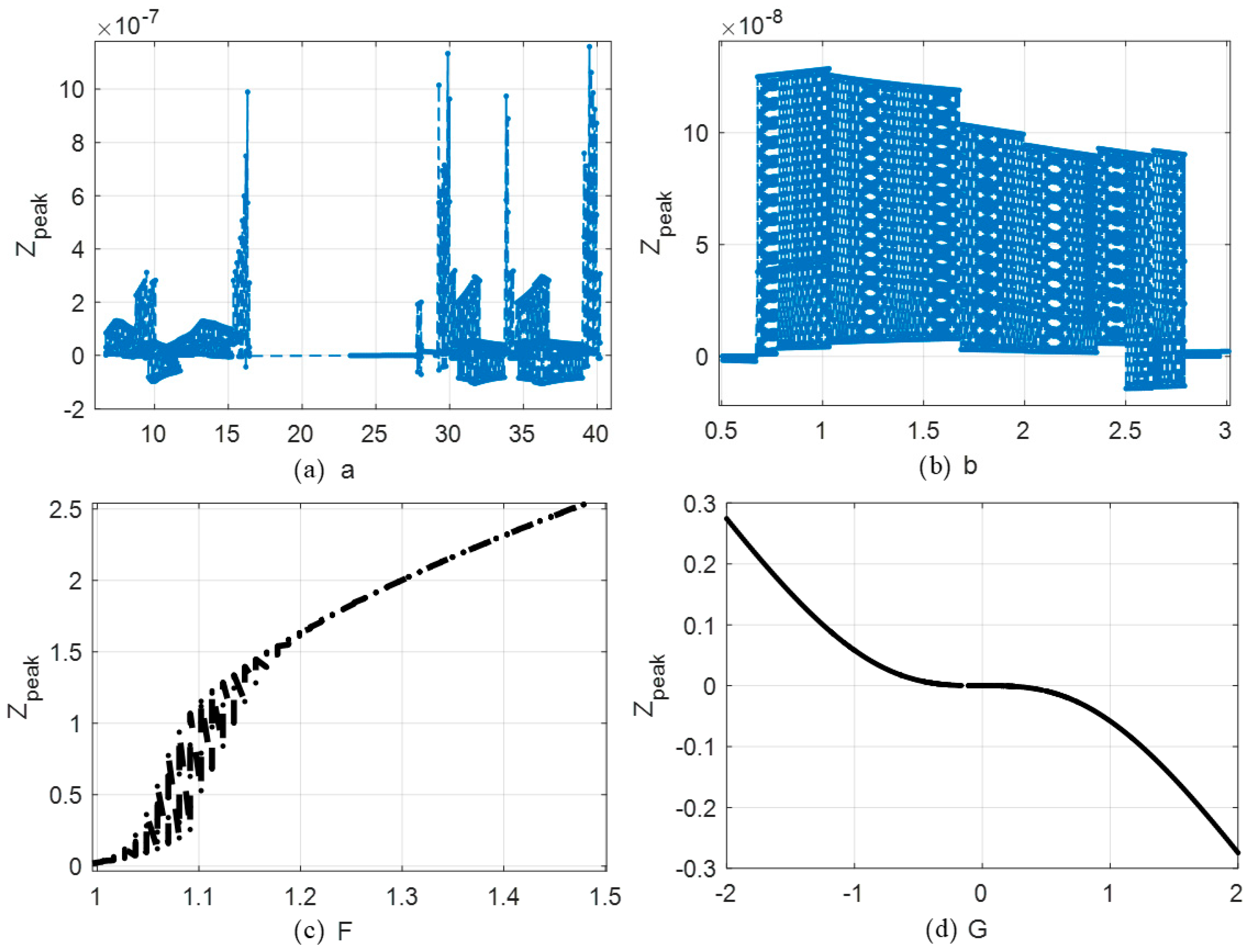
Figure 10a examines the gravity–damping index over the range 8–40, revealing distinct regions of stability and instability. Sudden transitions occur between low-amplitude states and sharply increased peaks, marking multiple bifurcation points. The clustered high-amplitude zones near specific values indicate resonance-like conditions caused by stronger nonlinear interactions in the coupled system.
Figure 10b presents the mass–damping coupling index between 0.5 and 3. Maximum peak displacement decreases gradually as
b (
Table 1) increases, yet dense vertical banding shows that oscillatory states remain complex. Multiple closely spaced bands suggest coexisting attractors and possible chaotic regions over certain parameter intervals.
Figure 10c shows the effect of the control torque ratio
F (
Table 1) from 1 to 1.5. A mostly monotonic rise in
Zpeak occurs as
F increases, with fine-scale oscillations appearing at the lower end. Scatter reduces at higher
F values, indicating convergence toward a more stable high-amplitude oscillatory regime dominated by the applied control torque.
Figure 10d illustrates the normalized vertical excitation from −2.8 to 2.8. The displacement amplitude declines steadily, crossing a near-zero plateau around
G = 0 before becoming increasingly negative. The smooth trend implies a continuous transition in dynamic states, showing that
G acts as a gradual modulator of displacement response.