Abstract
The index of success of the researchers is now mostly measured using the Hirsch index (h). Our recent precise demonstration, that statistically , where and denote, respectively, the total number of publications and total citations for the researcher, suggests that average number of citations per paper (), and hence h, are statistical numbers (Dunbar numbers) depending on the community or network to which the researcher belongs. We show here, extending our earlier observations, that the indications of success are not reflected by the total citations , rather by the inequalities among citations from publications to publications. Specifically, we show that for highly successful authors, the yearly variations in the Gini index (g, giving the average inequality of citations for the publications) and the Kolkata index (k, giving the fraction of total citations received by the top fraction of publications; corresponds to Pareto’s 80/20 law) approach each other to , signaling a precursor for the arrival of (or departure from) the self-organized critical (SOC) state of his/her publication statistics. Analyzing the citation statistics (from Google Scholar) of thirty successful scientists throughout their recorded publication history, we find that the g and k for the highly successful among them (mostly Nobel laureates, highest rank Stanford cite-scorers, and a few others) reach and hover just above (and then) below that mark, while for others they remain below that mark. We also find that all the lower (than the SOC mark 0.82) values of k and g fit a linear relationship, , with , as suggested by an approximate Landau-type expansion of the Lorenz function, and this also indicates for the (extrapolated) SOC precursor mark.
1. Introduction
Inspiring research in sociophysics (see, e.g., [1,2,3,4,5,6]) has, in years, led to intense research activities in several statistical and statistical physical models and analysis of socio-dynamical problems. For example, the social opinion formation models of Galam (see e.g., [7,8]), of Biswas-Chatterjee-Sen (see e.g., [9,10]), of Minority Games (see e.g., [11]), of Kolkata Paise Restaurant games (see, e.g., [12,13]), and others. In view of the automatically encoded wide range of the citation data of the publications by scientists and their straightforward availability on the internet, we have studied the inequality statistics from Google Scholar data. The presence of ubiquitous inequalities allowed recently the studies of various scaling, etc., properties in their statistics (see e.g., [14,15]) of the Hirsch index [16], or the universal (or limiting) self-organized critical (SOC) behavior (see e.g., [17,18,19]) and their citation inequality like the century-old Gini (g) [20] and the recently introduced Kolkata (k) [21,22] indices. It may be noted at this stage that while g values measure the overall inequality in the distributions and k gives the fraction of “mass” or of total citations coming from the fraction of avalanches or publications, these studies [17,18,19] indicated that the inequalities in the avalanche size distributions, measured by g and k, just prior to the arrival of the SOC point in several standard physical models (like the sand-pile models of Bak–Tang–Wiesenfeld (BTW) [23], Manna [24], and others), and in social contexts of citations from publications [18,19] becomes equal: . It may also be noted that corresponds to Pareto’s 80/20 law (see e.g., [21,22]). This Pareto principle asserts that 20% of the causes are responsible for 80% of the outcomes. In other words, the principle suggests that a small fraction of the factors contribute in causing a large fraction of major events, from economics to quality management and even in personal development. In business, it is often used to identify the most important areas for improvement. It may be mentioned here that our earlier studies of inequality indices g and k [17,18,19,20,21,22] corresponded to the cumulative dynamics (as the sand-pile dynamics progress and cluster distributions grow or the publications by the authors or from the institutions progress over time and the citation size distributions grow since the start of the dynamics) as the system approaches the respective SOC states. Our study here is for the same inequality indices, but for small time intervals along growth dynamical paths of individual researchers.
We study here the inequality dynamics measured by the g and k indices of several successful researchers (mostly winners of international prizes, medals, or awards like Nobel, Fields, Boltzmann, Breakthrough, highest level Stanford c-score achievers, etc.), some distinguished sociophysics researchers, along with those of a few high level (but not so high Stanford c-score, though within “top 2%”) researchers, for data up to 2022, since their recorded first publication year. We collected the citation data of the publications (from online free Google Scholar, if an individual Google Scholar page exists). We calculate the g and k indices for each year, starting their first publication, by taking the citation statistics today (collected and analyzed in July–August 2023). We extracted the values for g and k for all the recorded publications of the scientist in each overlapping five-year window (since the first publication), where the windows continuously shift by one year till the year 2022 (corresponding to the last central year 2020 of the researcher) in the following figures for each researcher. The choice of five-year window size is found to give optimal stability in statistics (a smaller three-year window size did not give stability to the citation statistics for quite a few of the scientists.)
We find that the majority of the chosen scientists crossed the mark (which we interpret here as the precursor level of the SOC point [17]) early in their life and often they hover just above or below but around that level of inequality mark. Some others just touched the precursor mark () once or even multiple times and a few remained below that mark. For other known researchers considered here, the mark occurs marginally but does not cross ever. It is to be noted that this mark of reaching the SOC state (beyond the 0.82) level of inequality is for yearly statistics (within a 5-year window which slides yearly) and not for the overall success measuring indices (in their cumulative citation statistics) studied earlier for the citation statistics of some distinguished researchers (see e.g., [14]), where the SOC mark is observed to be a little higher (.
As mentioned earlier, the Hirsch index (h) [16], which gives the highest number of publications by a researcher, each of which has received equal or more than that number of citations, does not seem give a most suitable measure [15,25] of the success of individual researchers. It has now been well demonstrated [15] (using the kinetic theoretical exchange model ideas), analyzing the Scopus citation data for the top 120,000 (within the “top 2%”) Stanford cites score achievers that statistically , where and denote, respectively, the total number of citations and total number of publications by the researcher. This suggests convincingly that the average number of citations per paper (), and hence h, are statistical numbers (given by the effective Dunbar number [26,27]) depending on the community or network in which the researcher belongs [15,18]. We show here, extending our earlier observations (see, e.g., [14,18]), that the indications of success are not reflected by the total citations , or for that matter by the Hirsch index h, rather than by the inequalities among the citations from publication to publication. Specifically, we show that for highly successful authors, the yearly variations (given by the statistics with overlapping 5-year windows) in the g index (given by the average inequality of the citations for the publications, ) and the k index (giving the fraction of total citations received by the top fraction of publications, ). In particular, achieving signals a precursor to the SOC state in the publication statistics. Analyzing the citation statistics (from the open-access Google Scholar) of thirty successful scientists throughout their recorded publication history, starting from their first recorded publication that the very successful among them (mostly Nobel laureates, higher-ranking Stanford c-scorers, and a few others) reach and hover just above and below that mark, characteristic of the SOC state ( means 82% of citations come from 18% of publications). Others remain below the (SOC) level of extreme inequality in publication statistics.
2. Socio-Statistical Inequality and Its Measures
In 1905, American economist Lorenz [2,3] developed the Lorenz curve, a graphical representation of the distribution of wealth in a society. To construct this curve (illustrated by the red curve in Figure 1), one organizes the society’s population in ascending order of their wealth and then plots the cumulative fraction of wealth, denoted as , held by the poorest p fraction of individuals. One can similarly plot the cumulative fraction of citations against the fraction of papers that attracted those many citations. As indicated in Figure 1, the Gini index is calculated from the area between the equality line and the Lorenz curve, divided by the area (1/2) below the equality line for normalization. As such, signifies perfect equality and corresponds to extreme inequality. The index k is given by the fixed point of the complementary Lorentz function . As such, k gives the fraction of citations attracted by the top cited k fraction of papers and means perfect equality, while extreme inequality corresponds to .
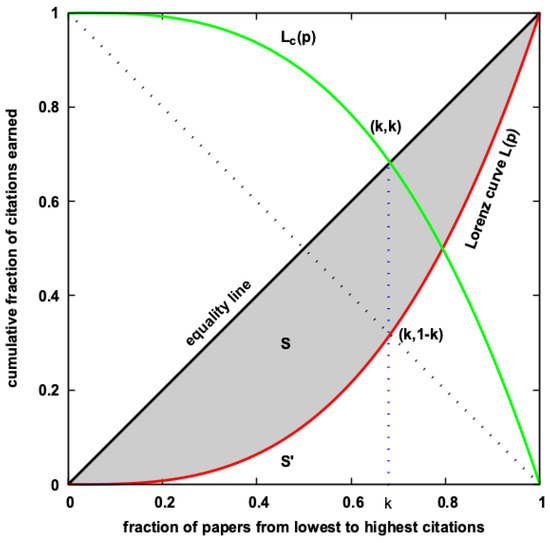
Figure 1.
The Lorenz curve, represented by (in red), denotes the cumulative proportion of total citations possessed by a fraction p of papers, when organized in ascending order of citation counts. Conversely, the black dotted line indicates perfect equality, where each paper receives an equal number of citations. The Gini index (g) is computed from the area (S) between the Lorenz curve and the equality line (the shaded region), normalized by the total area under the equality line (). The Kolkata index (k) is obtained by locating the fixed point of the complementary Lorenz function (; shown in green), defined as : . By geometry, the value of k gives the proportion of total citations owned or possessed by fraction of the top cited papers.
Landau-Like Expansion of and Approximate Relation
A minimal expansion [28] of the Lorenz function , employing a Landau-like expansion of free energy, suggests . This gives and (with B = 0, the Lorenz function can represent only the equality line in Figure 1).
One can then calculate , giving and . Since , one can obtain a quadratic equation involving g and k. An approximate solution of it, in the limit gives
where [28] suggesting that will occur at the Pareto value . We see here a little deviation in the value of the constant C in the relation (1), for all the reported observations.
3. Inequality Data Analysis from Google Scholar
We collect the citation data for all the recorded publications in each year since the first entry in the record for thirty successful researchers having individual Google Scholar page and having minimum and maximum number of total publications = 127 and 2954, minimum and maximum number of total citations = 5769 and 463,382, minimum and maximum values of h = 22 and 328, respectively, for all those selected researchers. We considered three Nobel prize winners in each of the science subjects: physics (H. Amano, B. Josephson, A. B. McDonald), chemistry (R. Henderson, J. Frank, J.-P. Sauvage), physiology and medicine (M. Houghton, G. L. Semanza, S. Yamanka), and economics (A. Banerjee, W. Nordhaus, J. Stiglitz). Two Fields medalists (mathematics; S. Smalle, E. Witten), two Boltzmann award winners (statistical physics; D. Dhar, H. E. Stanley), two Breakthrough prize winners (physics; C. Kane, A. Sen), three of the top-most cite-scorers in the Stanford Scopus c-score list (M. Graetzel, R. C. Kessler, and Z. L. Wang; considered for h-index statistics in Ref. [15]), and six known contributors in econophysics and sociophysics: W. Brian Arthur (known for “El Farol Bar Problem” of minority choice, see, e.g., [11]), B. K. Chakrabarti (one of the “fathers of econophysics” [29,30]), R. I. M. Dunbar (known for Dunbar’s number of social connectivity, see, e.g., [31]), S. Galam (considered a pioneer of sociophysics), R. Mantegna (one of the “fathers of econophysics” [29,30]), V. M. Yakovenko (pioneer of kinetic exchange models of income/wealth distributions; see, e.g., [32]). We considered three of the highest-ranked Stanford cite-scorers for 2022 (M. Graetzel, R. C. Kessler, and Z. L. Wang [33]), and, for comparison, we also considered three lower-rank holders of the same “top 2% Stanford cite-scores” (I. Fofana, U. Sennur, and N. Tomoyuki [33]).
For studying the growth of inequality in the citation statistics of each of these researchers, we select a 5-year window, starting earliest publication, and note the present-day citations of each of these publications. We then construct the Lorenz function (see Figure 1) and extract the g and k indices as described in Section 4. We associate the g and k values with the middle year of the respective 5-year window and shift the window by one year and get the values of the inequality indices for each of the successive years up to 2020 (considering data up to 2022). These are shown in the following Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6.
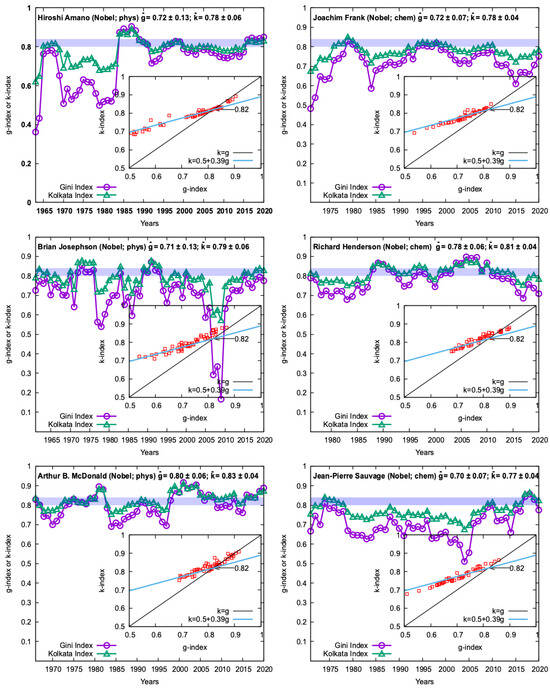
Figure 2.
Yearly variations of the citation inequality indices, Gini (g) and Kolkata (k), for three Nobel prize winners in physics and three in chemistry. The indices are calculated using the present citation data for the publications within a 5-year window, starting from first recorded one in Google Scholar, and the window sliding by one year. The corresponding year shown is mid mid-year of the window until 2022 (shown for year 2020 for the last 5-year window). The g value crossing above (and coming down) the k value marks the precursor of onset (leaving) the SOC state with time. The inset shows k versus g (in red) over the entire career of the scientist. It fits well with the linear (Landau-like) relationship, , suggesting a crossing SOC precursor point at .
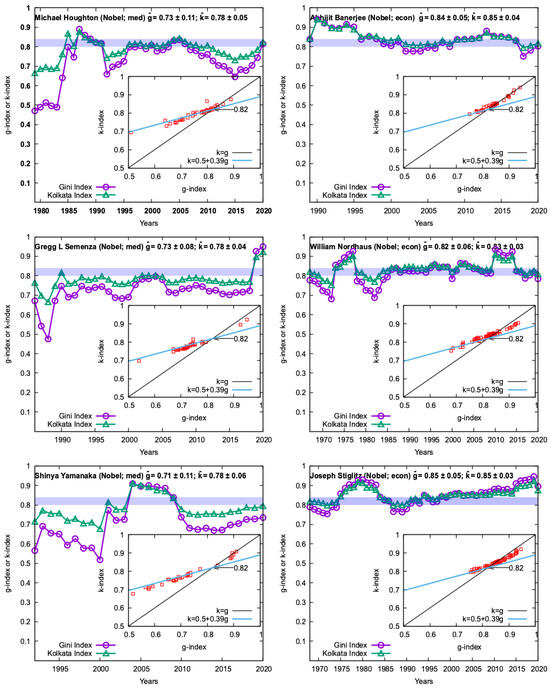
Figure 3.
Yearly variations of the citation inequality indices, Gini (g) and Kolkata (k), for three Nobel prize winners in physiology-medicine and three in economics. The indices are calculated using the present citation data for the publications within a 5-year window, starting from the first recorded one in Google Scholar, and the window sliding by one year. The corresponding year shown is mid-year of the window until 2022 (shown for the year 2020 for the last 5-year window). The g value crossing above (and coming down) the k value marks the precursor of onset (leaving) the SOC state with time. The inset shows k versus g (in red) over the entire career of the scientist. It fits well with the linear (Landau-like) relationship, , suggesting a crossing SOC precursor point at .
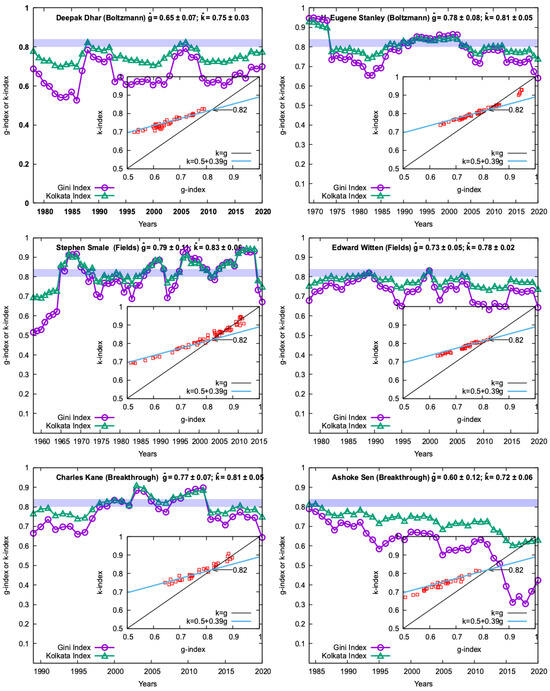
Figure 4.
Yearly variations of the citation inequality indices, Gini (g) and Kolkata (k), for two winners each of Fields medal (mathematics), Boltzmann prize (statistical physics) and Breakthrough prize (physics). The indices are calculated using the present citation data for the publications within a 5-year window, starting from first recorded one in Google Scholar, and the window sliding by one year. The corresponding year shown is mid year of the window until 2022 (shown for year 2020 for the last 5-year window). The g value crossing above (and coming down) the k value marks the precursor of onset (leaving) the SOC state with time. The inset shows k versus g (in red) over the entire career of the scientist. It fits well with the linear (Landau-like) relationship, , suggesting a crossing SOC precursor point at .
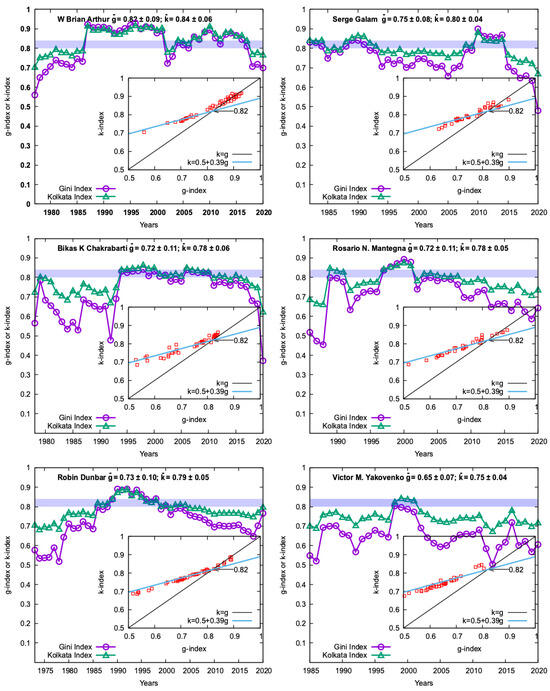
Figure 5.
Yearly variations of the citation inequality indices, Gini (g) and Kolkata (k), for six distinguished researchers in econophysics and sociophysics. The indices are calculated using the present citation data for the publications within a 5-year window, starting from the first recorded one in Google Scholar, and the window sliding by one year. The corresponding year shown is mid-year of the window until 2022 (shown for year 2020 for the last 5-year window). The g value crossing above (and coming down) the k value marks the precursor of onset (leaving) the SOC state with time. The inset shows k versus g (in red) over the entire career of the scientist. It fits well with the linear (Landau-like) relationship, , suggesting a crossing SOC precursor point at .
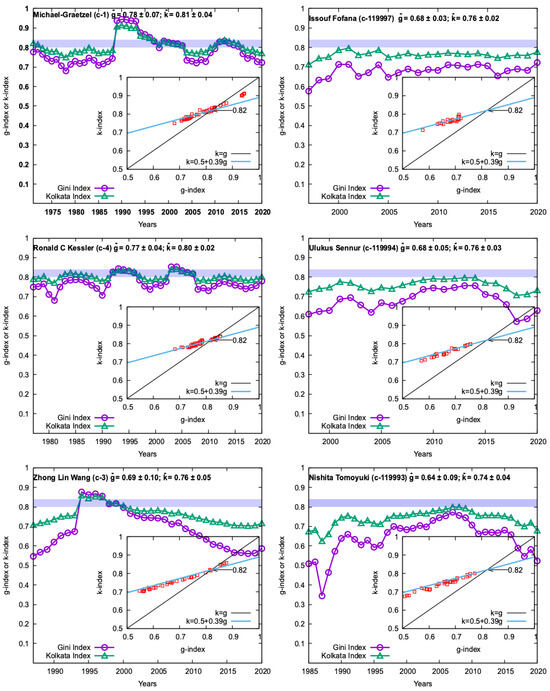
Figure 6.
Yearly variations of the citation inequality indices, Gini (g) and Kolkata (k), for three top-most Stanford cite-scores and three lower rank entries from the “top 2% Stanford cite-scores” [15,33]. The indices are calculated using the present citation data for the publications within a 5-year window, starting from first recorded one in Google Scholar, and the window sliding by one year. The corresponding year shown is mid mid-year of the window until 2022 (shown for year 2020 for the last 5-year window). The g value crossing above (and coming down) the k value marks the precursor of onset (leaving) the SOC state with time. The inset shows k versus g (in red) over the entire career of the scientist. It fits well with the linear (Landau-like) relationship, , suggesting a crossing SOC precursor point at .
One can see from Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6, for all the above-mentioned thirty scientists that for many of them (mostly Nobel prize winners and highest rank c-scorers), the g-index value goes over the k-index value in one (or multiple years) by crossing the line (see the corresponding insets). These crossings of the indices (at values above 0.80 value) preciously indicates large inequalities and entry into the SOC state [17] of the citation statistics of these scientists (see Table 1 for consolidated results of g and k).

Table 1.
Consolidated inequality index () results for the citation statistics (from Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6) of the thirty chosen scientists (including twelve Nobel prize winners, two Fields medalists, two Boltzmann award winners, two Breakthrough prize winners, six distinguished sociophysics and econophysics researchers, three from the top and three from the bottom of the “top 2% Stanford cite-score scientists” (2022 list). NP(P) stands for Nobel Prize in physics, NP(C) stands for Nobel Prize in chemistry, NP(M) stands for Nobel Prize in physiology or medicine and NP(E) stands for Nobel Prize in economics, FM stands for Fields Medal in mathematics, BA stands for Boltzmann Award in statistical physics, BP(P) stands for Breakthrough Prize in physics, FEP stands for “fathers of econoophysics” [29,30], EFBP stands for “El Farol Bar problem” (see, e.g., [11]), DN stands for “Dunbar Number” (see, e.g., [31]), FSP stands for “father of sociophysics”, PKEM stands for pioneer in kinetic exchange modeling of Wealth distribution [32], SCS-x stands for Stanford Cite Score rank (‘x’ denoting the rank) among the “top 2%” scientists in 2022 [33], and “yearly-av.” stands for yearly-averaged publication in 5-year window; see text for more details.
Although the study of the time variations of the g and k indices (as shown in Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6) and checking if g value ever goes over the k value by crossing the k versus g line (as shown in the insets) is indispensable for detecting if the SOC state has arrived or not, one can also have a straightforward (but only approximate) indication of the SOC state by looking at the ratio R of the citation number of the highest cited paper and the effective Dunbar number D given by the average citation of the researcher. In Table 2, we compare these values (where ) and see how its higher values compare with the observation of SOC (when k versus g line is crossed affirmatively). We find, for , more than of cases correspond to the SOC level.

Table 2.
An approximate indicator, , where the effective Dunbar number ( denotes the total number of citations for papers by the researcher) and denotes the citation of the most-cited paper by the researcher, to check if the researcher has achieved the SOC level or not. We find, for , the corresponding researchers certainly belong to the SOC level ( success rate).
4. Summary and Discussion
Our earlier analysis [15] of the Scopus citation data for the 120,000 top Stanford cite-score scientists showed that the Hirsch index , where and denote, respectively, the total number of citations and the total number of publications by the researcher. This, in turn, says that the average number of citations per paper (, and hence h, are statistical numbers (determined by the effective Dunbar number [26,31]) of the community or network (coauthors and followers) in which the researcher belongs [15,18]. Indeed, the anticipated increase in research impacts through collaboration (by increasing the number of coauthors) has been studied in Ref. [34], by looking at the average value of the community Dunbar number or . Also, a detailed study from Google Scholar data on the relation between the Hirsch index of individual scientists with their average number of co-authors per paper has been reported in Ref. [35]. Our study here shows that the Hirsch index can not be a suitable measure of success for the researchers (even in Table 1; the highest does not correspond to a Nobel Prize winner, while the least one with do).
In an earlier study [18], we proposed that the citation inequality indices Gini and Kolkata to give better measures of success of the scientist (not or h) and g and k both expected to approach equality at for successful researchers. It may be mentioned here that we used the entire citation data (over all the years) to get the Lorenz curve and the overall values of g and k of the researcher, and this gave a little higher value of point. Indeed, our numerical study [17] of the overall or cumulative inequality statistics of the avalanches or cluster sizes in some mostly studied and mstly established SOC models also suggested the arrival of the equality point of the avalanche size inequality indices () just appears as a precursor of the SOC point of the respective sand-pile or SOC models. In other words, as mentioned already, the SOC points in sandpile models (like BTW [23], Manna [24], and other models) of physics signifies a critical state where sand grain avalanches of all sizes occur following a power law distribution. As shown in Ref. [17], even in these physics SOC models, the inequality statistics (Gini and Kolkata indices) corresponding to the avalanche size statistics reach similar values for the inequality indices of the unequal citations (considered here equivalent to the sand mass avalanches in sand piles).
We analyzed the citation data for all the recorded publications in each year since the first entry in the record for the chosen thirtky successful scientists, each having an individual Google Scholar page. They have the minimum and maximum number of total publications = 127 and 2954, and minimum and maximum number of total citations, = 5769 and 463,382, respectively. For studying the growth of inequality in the citation statistics of each of these scientists, we select 5-year windows, where the central year of each window moves every year. We construct the Lorenz functions for each of these windows (see Figure 1) and extract the yearly values (corresponding to the central year of the window) of g and k indices. We have plotted these yearly g and k values for all the working years, starting the recorded first year and for the third year from there and continued for successive years up to 2022 (by considering data up to 2022) for each of these chosen thirty scientists. These are then shown in Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6. The insets in each Figure show the corresponding plot of k versus g (disregarding the yearly sequence). These plots in all thirty cases of the researchers show quite a good linear fit to (cf. Equation (1)), as obtained approximately using a (Landau-like) minimal polynomial expansion of the Lorenz function (see Section 2). The insets also show the actual or extrapolated (precursor of sand-pile SOC) point at . As we can see from Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6, for ten of the twelve Nobel prize winners, several of the other international prize winners are considered here, known sociophysicists, econophysicists, and all three of the highest rank Stanford cite-scorers, the crossing(s) of k versus g (often at multiple years), do take place convincingly. The same is also true (often marginally), for several others. The three lower rank (yet from the “top 2%”) Stanford cite-scorers did not come up to point. There are certainly a few notable anomalies in this analysis of the data set; e.g., B. Josephson, J. Frank (both Nobel laureates), D. Dhar (Boltzmann award winner), and A. Sen (Breakthrough prize winner) do not fit this picture of indeed reaching the SOC point. These anomalies may indicate some shortcomings of this kind of analysis. On the other hand, noting that out of twenty seven of the researchers have chosen here (neglecting the three lower rank, though from the “top 2%” Stanford cite-scorers), the visible evidence of SOC are seen for nineteen (neglecting the “no” and “marginal” entries in the last column of Table 1 for these twenty seven researchers), indicating a success rate more than 70% for identifying the outstanding researchers. In Table 2, we give quite a simple (though approximate) indicator (where denotes the maximum citation of any paper and D the effective Dunbar number of the researcher) to check if the researcher has achieved the SOC level or not. We see that the SOC level is achieved for , with a more than 94% coincidence rate.
In summary, as the Hirsch index h of a prolific researcher grows with the total citations as [15] and grows linearly with the total number of publications by the researcher, (see [15,18]), where the effective Dunbar number D (∼75 [15]) of the network community in which the scientist belongs, h and can only give some average measures of success. In fact, most appreciated members of the community can in principle have uniformly high citations of order D for each of their publications and hence 75. Though such uniformly appreciated or cited scientists will have significantly low values of Gini and Kolkata indices, 0 and . Our study here shows, notwithstanding some anomalies, most successful researchers have large fluctuations in the citations of one or more of their publications (presumably due to uneven but accurate appreciations from the usual Dunbar network or community and also possibly from outside the usual Dunbar community), which do not increase directly the D or h values, but lead to larger values of their inequality indices g and k, which may then hover around the SOC level value , a little above the Pareto value (k = 0.80).
Author Contributions
Conceptualization, A.G. and B.K.C.; methodology, A.G. and B.K.C.; software, A.G.; formal analysis, A.G.; investigation, A.G.; writing—original draft, B.K.C.; writing—review and editing, A.G.; supervision, B.K.C. Chakrabarti. All authors have read and agreed to the published version of the manuscript.
Funding
B.K.C. is grateful to the Indian National Science Academy for their Senior Scientist Research Grant.
Data Availability Statement
The data that support the findings of this study are available on request from the corresponding author.
Acknowledgments
We are thankful to Soumyajyoti Biswas, Arnab Chatterjee, and Arnab Das for careful readings of the manuscript and useful criticisms and suggestions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- de Oliveira, S.M.; de Oliveira, P.M.C.; Stauffer, D. Evolution, Money, War and Computers. Non-Traditional Applications of Computational Statistical Physics; B. G. Teubner Stuttgart: Leipzig, Germany; Springer Fachmedien Wiesbaden GmbH: Wiesbaden, Germany, 1999. [Google Scholar] [CrossRef]
- Chakrabarti, B.K.; Chakraborti, A.; Chatterjee, A. (Eds.) Econophysics and Sociophysics: Trends and Perspectives; Wiley-VCH Verlag GmbH and Co. KGaA: Weinheim, Germany, 2006. [Google Scholar] [CrossRef]
- Castelano, C.; Fortunato, S.; Loreto, V. Statistical physics of social dynamics. Rev. Mod. Phys. 2009, 81, 591–646. [Google Scholar] [CrossRef]
- Helbing, D. Quantitative Sociodynamics: Stochastic Methods & Models of Social Interaction Processes; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- Galam, S. Sociophysics: A Physicist’s Modeling of Psycho-Political Phenomena; Springer Science+Business Media, LLC: New York, NY, USA, 2012. [Google Scholar] [CrossRef]
- Sen, P.; Chakrabarti, B.K. Sociophysics: An Introduction; Oxford University Press: Oxford, UK, 2014; Available online: https://archive.org/details/sociophysicsintr0000senp (accessed on 2 December 2023).
- Galam, S. Sociophysics: A review of Galam models. Int. J. Mod. Phys. C 2008, 19, 409–440. [Google Scholar] [CrossRef]
- Galam, S.; Cheon, T. Tipping points in opinion dynamics: A universal formula in five dimensions. Front. Phys. 2020, 8, 566580. [Google Scholar] [CrossRef]
- Biswas, S.; Chatterjee, A.; Sen, P.; Mukherjee, S.; Chakrabarti, B.K. Social dynamics through kinetic exchange: The BChS model. Front. Phys. 2023, 11, 1196745. [Google Scholar] [CrossRef]
- Filho, E.A.; Lima, F.W.; Alves, T.A.; Alves, G.A.; Plascak, J.A. Opinion dynamics systems via Biswas–Chatterjee–Sen model on Solomon networks. Physics 2023, 5, 873–882. [Google Scholar] [CrossRef]
- Challet, D.; Marsili, M.; Zhang, Y.-C. Minority Games. Interacting Agents in Financial Markets; Oxford University Press: Oxford, UK, 2005. [Google Scholar]
- Martin, L. Extending Kolkata Paise Restaurant problem to dynamic matching in mobility markets. Jr. Manag. Sci. 2019, 4, 1–34. [Google Scholar] [CrossRef]
- Harlalka, A.; Belmonte, A.; Griffin, C. Stability of dining clubs in the Kolkata Paise Restaurant Problem with and without cheating. Phys. A Stat. Mech. Appl. 2023, 620, 128767. [Google Scholar] [CrossRef]
- Ghosh, A.; Chakrabarti, B.K.; Ram, D.R.S.; Mitra, M.; Maiti, R.; Biswas, S.; Banerjee, S. Scaling behavior of the Hirsch index for failure avalanches, percolation clusters, and paper citations. Front. Phys. 2022, 10, 1019744. [Google Scholar] [CrossRef]
- Ghosh, A.; Chakrabarti, B.K. Scaling and kinetic exchange like behavior of Hirsch index and total citation distributions: Scopus-CiteScore data analysis. Phys. A Stat. Mech. Appl. 2023, 626, 129061. [Google Scholar] [CrossRef]
- Hirsch, J.E. An index to quantify an individual’s scientific research output. Proc. Natl. Acad. Sci. USA 2005, 102, 16569–16572. [Google Scholar] [CrossRef] [PubMed]
- Manna, S.S.; Biswas, S.; Chakrabarti, B.K. Near universal values of social inequality indices in self-organized critical models. Phys. A Stat. Mech. Appl. 2022, 596, 127121. [Google Scholar] [CrossRef]
- Ghosh, A.; Chakrabarti, B.K. Limiting value of the Kolkata index for social inequality and a possible social constant. Phys. A Stat. Appl. 2021, 573, 125944. [Google Scholar] [CrossRef]
- Banerjee, S.; Biswas, S.; Chakrabarti, B.K.; Challagundla, S.K.; Ghosh, A.; Guntaka, S.R.; Koganti, H.; Kondapalli, A.R.; Maiti, R.; Mitra, M.; et al. Evolutionary dynamics of social inequality and coincidence of Gini and Kolkata indices under unrestricted competition. Int. J. Mod. Phys. C 2023, 34, 2350048. [Google Scholar] [CrossRef]
- Gini, C. Measurement of inequality of incomes. Econ. J. 1921, 31, 124–126. [Google Scholar] [CrossRef]
- Ghosh, A.; Chattopadhyay, N.; Chakrabarti, B.K. Inequality in societies, academic institutions and science journals: Gini and k-indices. Phys. A Stat. Mech. Appl. 2014, 410, 30–34. [Google Scholar] [CrossRef]
- Banerjee, S.; Chakrabarti, B.K.; Mitra, M.; Mutuswami, S. Social inequality measures: The Kolkata index in comparison with other measures. Front. Phys. 2020, 8, 562182. [Google Scholar] [CrossRef]
- Bak, P.; Tang, C.; Wiesenfeld, K. Self-organized criticality: An explanation of the 1/f noise. Phys. Rev. Lett. 1987, 59, 381–384. [Google Scholar] [CrossRef]
- Manna, S.S. Two-state model of self-organized criticality. J. Phys. A Math. Gen. 1991, 24, L363–L370. [Google Scholar] [CrossRef]
- Yong, A. A critique of hirsch’s citation index: A combinatorial fermi problem. Not. Am. Math. Soc. 2014, 61, 1040–1050. [Google Scholar] [CrossRef]
- Dunbar, R.I.M. Neocortex size as a constraint on group size in primates. J. Hum. Evol. 1992, 22, 469–493. [Google Scholar] [CrossRef]
- Dunbar, R. How Many Friends Does One Person Need? Dunbar’s Number and Other Evolutionary Quirks; Faber and Faber Limited: London, UK, 2010; Available online: https://archive.org/details/howmanyfriendsdo0000dunb (accessed on 2 December 2023).
- Joseph, B.; Chakrabarti, B.K. Variation of Gini and Kolkata indices with saving propensity in the Kinetic Exchange model of wealth distribution: An analytical study. Phys. A Stat. Mech. Appl. 2022, 594, 127051. [Google Scholar] [CrossRef]
- Jovanovic, F.; Schinckus, C. Econophysics and Financial Economics: An Emerging Dialogue; Oxford University Press: Oxford, UK, 2017; p. 178. [Google Scholar] [CrossRef]
- Schinckus, C. When Physics Became Undisciplined: An Essay on Econophysics. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2018; pp. 15–16. [Google Scholar] [CrossRef]
- Dunbar, R.I.M. Coevolution of neocortical size, group size and language in humans. Behav. Brain Sci. 1993, 16, 681–735. [Google Scholar] [CrossRef]
- Yakovenko, V.M.; Rosser, J.B. Statistical mechanics of money, wealth, and income. Rev. Mod. Phys. 2009, 81, 1703–1725. [Google Scholar] [CrossRef]
- Ioannidis, J.P.A. September 2022 Data-Update for “Updated Science-Wide Author Databases of Standardized Citation Indicators”. Version 5; Elsevier Data Repository, Elsevier Inc.: New York, NY, USA, 2022. [Google Scholar] [CrossRef]
- Katz, J.S.; Hicks, D. How much is a collaboration worth? A calibrated bibliometric model. Sociometrics 1997, 40, 541–554. [Google Scholar] [CrossRef]
- Arnaboldi, V.; Dunbar, R.I.M.; Passarella, A.; Conti, M. Analysis of co-authorship ego networks. In Advances in Network Science. Proceedings of the 12th International Conference and School, NetSci-X 2016, Wroclaw, Poland, 11–13 January 2016; Wierzbicki, A., Brandes, U., Schweitzer, F., Pedreschi, D., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 82–96. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).