On Possible Minimal Length Deformation of Metric Tensor, Levi-Civita Connection, and the Riemann Curvature Tensor

Abstract

The minimal length conjecture is merged with a generalized quantum uncertainty formula, where we identify the minimal uncertainty in a particle’s position as the minimal measurable length scale. Thus, we obtain a quantum-induced deformation parameter that directly depends on the chosen minimal length scale. This quantum-induced deformation is conjectured to require the generalization of Riemannian spacetime geometry underlying the classical theory of general relativity to an eight-dimensional spacetime fiber bundle, which dictates the deformation of the line element, metric tensor, Levi-Civita connection, Riemann curvature tensor, etc. We calculate the deformation thus produced in the Levi-Civita connection and find it to explicitly and exclusively depend on the product of the minimum measurable length and the particle’s spacelike four-acceleration vector, $L^2{\ddot{x}}^2$. We find that the deformed Levi-Civita connection preserves all properties of its undeformed counterpart, such as torsion freedom and metric compatibility. Accordingly, we have constructed a deformed version of the Riemann curvature tensor whose expression can be factorized in all its terms with different functions of $L^2{\ddot{x}}^2$. We also show that the classical four-manifold status of being Riemannian is preserved when the quantum-induced deformation is negligible. We study the dependence of a parallel-transported tangent vector on the spacelike four-acceleration. We illustrate the impact of the minimal-length-induced quantum deformation on the classical geometrical objects of the general theory of relativity using the unit radius two-sphere example. We conclude that the minimal length deformation implies a correction to the spacetime curvature and its contractions, which is manifest in the additional curvature terms of the corrected Riemann tensor. Accordingly, quantum-induced effects endow an additional spacetime curvature and geometrical structure.

1. Introduction

1.1. Generalized Uncertainty Principle

The Heisenberg uncertainty principle (HUP) is one major aspect of the conceptual difference between classical and quantum physics. Certainly, it arises from pure quantum mechanical effects stemming from the wave–particle duality, which tells us that there is an inherent fuzziness in nature at some microscopic length scale. It is intuitively expected that if gravitational effects are taken into consideration near the proper fundamental length scale, the added fuzziness and its implications should be taken into account by deforming (modifying) HUP into an extended or generalized version commonly dubbed as the ‘generalized uncertainty principle’ (GUP), or equivalently the modified dispersion relations’ [1,2,3,4,5,6,7,8,9,10,11,12,13], which has been used extensively in attempts to explain the origin of the gravitational field and how a particle behaves in it near fundamental length scales. Before we proceed further with the GUP, it might be instructive to mention that there exist other approaches that endeavor to modify quantum mechanics (QM) at subatomic scales by assuming, for example, that Planck’s constant is not universal but rather runs with a particle’s interaction cross sections [14] or with the interaction energy [15].

The GUP is a modified Heisenberg uncertainty relation that predicts a deformed canonical commutator. Given the geometrical nature of the classical theory of general relativity (GR), it is natural to expect that the endeavor of modifying HUP to GUP should be accompanied by a program for modifying the underlying geometrical framework.

There are three main approaches to a GUP, which are reviewed here [16,17]. For example, the GUP model we are adopting in the present paper is a generalized uncertainty relation that characterizes the minimal length as a (nontrivial) minimal uncertainty in position measurements (see, for example, Equation (1) in Ref. [6]). This model was originally constructed by Michele Maggiore [7] mainly using string theoretic arguments and independently by Achim Kempf [18] using formal nonrelativistic quantum mechanical and group theoretical arguments.

We have already used this GUP model in a recent paper [19] to study the possible implications on the geodesic equation, while in the present study, we implement the same GUP model, within the same geometrical embedding (but in a slightly different exposition), to study its impact on the metric tensor, Levi-Civita connection, parallel transport, and symmetries of the Levi-Civita connection, which is elaborated in Section 3 and Section 4.

1.2. Motivating the Minimal Length Scale Scenario

Over the past few decades, much effort has gone towards creating a unified formalism combining QM and GR, or alternatively accounting for their main effects and consequences in a consistent fashion, which has resulted in the creation of a number of potential candidate theories (models). To name a few, string theory (ST), loop quantum gravity (LQG), and doubly (deformed) special relativity (DSR) are typical examples of available roads to a theory of quantum gravity (QG) [20]. To be precise, DSR has been argued to provide an effective limit of quantum gravity in an almost-flat regime.

Due to long-standing unresolved challenges, it is predicted that a definitive solution is still far away despite these and other attempts. (an extensive though incomprehensive survey can be found in Ref. [21]). Consequently, it can be inferred that there is a need to approach QG differently.

In this quest, one viable track might be the modification of the underlying spacetime geometry at fundamental scales to incorporate quantum effects within the framework of a GUP model. This is the track to QG we are exploiting in Section 2 here.

Generally, ST, LQG, DSR, and various gedanken experiments suggest the inevitability of the existence of a fundamental physical minimum length (scale) and/or a modification of the HUP near the Planck scale to the GUP in a way that prevents the length (energy/momentum) uncertainty from being arbitrarily small (large) [7,20,22].We are not here in a position to formally compare different QG theories/models incorporating the concept of minimal length scale. However, it might be illuminating to highlight that, for example, in ST [20], it has been discovered that there is such an uncertainty that is believed to be generally a spacetime uncertainty that implies a bound determined by the string scale, which may not be the same as the Planck scale. In LQG [20], the area and volume operator’s eigenvalues are constrained, while the early universe’s curvature is constrained to a Planckian value in the simplified model of loop quantum cosmology. In DSR [20,23,24], the minimal length scale is an invariant of the theory that is consistently set to be a Planck length scale; it is an observer-independent scale.

As a result of these several limitations, it might be inaccurate to refer to a “minimal length”, as there is always no bound on the length itself, only on the powers of spatiotemporal distances. In order to avoid confusion, it is best to refer to a “minimal length scale" in a more generic sense while leaving the specifics of how this scale is used to measure physical quantities up for debate. Finally, it is important to emphasize here that this is not the case in the GUP approach we are adopting in the present paper [6,18], where we have the choice of identifying the length uncertainty as the minimal measurable length. More interestingly, we also have the choice of fixing the scale of minimal length to Planck length or else. So far, and as far as we know, there is no theoretical or empirical compelling reason to fix the minimal length scale to a specific value. This argument is formally elaborated using Equations (1)–(4) in Section 2.

The present study manifestly introduces a minimal length approach. However, it might be even more more illuminating to shed some light on the possible connection between the concept of minimal length scale and that of maximal acceleration scale.

1.3. Maximal Acceleration

The possibility of the existence of a maximal acceleration limit was originally suggested by Eduardo Caianiello [25] as a by-product of his endeavor to ‘geometrize QM’ through the identification of the physical spacetime of a quantum particle as a four-dimensional hypersurface locally embedded in eight-dimensional phase space, leading to the reformulation of the mechanics of physical objects being limited not only by maximal velocity but also by maximal acceleration.

Based on energy–time HUP, Caianiello [26] also suggested later a maximal acceleration, $A_{\max }$, such that $A_{\max }=2m{c}^3/\hslash =c^2/R$, where m denotes the mass of a massive particle, c denotes the speed of light, ℏ denotes the reduced Planck’s constant, and R was interestingly enough interpreted by Caianiello to be some radius of particle rotation or generally a length scale of the order of the ‘linear dimension’ of the particle, which cannot exceed the limit set by $(\sim c^2/R)$, i.e., a minimal length scale. The connection between minimum length and maximal acceleration is hereby clear enough.

More recently, Ricardo Torromé [27] reformulated Caianiello’s maximal acceleration formula in a covariant form and introduced a couple of possible interpretations for the mass scale (m) as either the rest mass of the accelerated particle, of the order of the lightest neutrino mass scale, or some universal mass scale of the order of the Planck mass. The latter is the most common choice within the framework of ST-inspired models [28]. Torromé also emphasized that the maximal acceleration, in his model, is invariant under arbitrary local coordinate changes. This feature is certainly in contrast to Caianiello’s original approach.

Using a totally different approach based on black hole thermodynamics, Howard Brandt [29] derived equations clearly suggesting the possibility of the existence of a maximal acceleration scale as a direct result of the existence of a maximum temperature limit for black holes by studying their radiation and thermal equilibrium. More interestingly, Brandt also showed that such a maximal acceleration limit is directly related to the existence of a minimal black hole radius, a minimal length scale of the order of the Planck length. Finally, we have to highlight that Brandt’s model uses an invariant metric, and thereby, the metric is observer independent. It also depends on some universal mass scale near the Planck mass scale, but does not depend on the particle mass.

Moreover, it is quite relevant and worth mentioning in this context that Frederic Schuller [28] managed to encode dynamical symmetries of Born–Infeld theory in a pseudo-complex geometry on the tangent bundle of generally curved spacetime manifolds. Schuller obtained a ‘dynamically lifted’ new ‘kinematised’ version of Einstein field equations that suggest not only the existence of a maximal acceleration limit for particles but also the emergence of anticommutation relations that might be valid for a ‘first quantization’ of general relativity.

To this point, we conclude this short discussion on maximal acceleration by the following remarks:

• Maximal acceleration and minimal length scales seem to be naturally intertwined in different physical contexts.
• Maximal acceleration and minimal length can, in principle, be formulated in either observer-dependent or observer-independent geometrical frameworks.
• Some of the prominent maximal acceleration approaches may evolve to be promising candidates in the quest of the quantisation of GR.

In Section 2, we develop a formal though simple relationship between the minimal measurable length and the maximal acceleration. However, we emphasize that our formal analysis thereafter makes almost exclusive explicit reference to the minimal length.

1.4. Finsler Geometry

Finsler geometry is considered to be a natural generalization to the Riemannian geometry whenever the metric depends on the particle’s velocity (momentum), and thereby, an analysis on the (co-)tangent bundle (phase space) is in order. Thus, and without delving into unnecessary technical details, Finsler geometry is viewed to share significantly similar features with the geometrical embedding scenario we assume in the present study, which is adapted based on Caianiello’s fiber bundle eight-manifold [30]. We assume such an eight-manifold to host the quantum effects of gravitational fields and embed them in the fabric of classical spacetime geometry, which is formally elaborated in our technical analysis developed in Section 3.

The implementation of Finsler geometry in the context of ‘geometrizing’ quantum mechanics and quantum field theory has been the quest of some authors for a couple of decades or so.

In connection with the main scope of the present study, we find it more convenient to highlight the following relevant contributions:

• Brandt [31] investigated Finsler fields in the arena of the maximal acceleration invariant spacetime tangent bundle.
• Torromé [27] developed a covariant version of Caianiello’s model, which is a typical example where diverse types of structures including Finsler’s appear in a natural way.
• Giovanni Amelino-Camelia and collaborators [32] established a link between Finsler geometry, models with curved momentum space and DSR symmetries that have been recently of interest in the QG literature.
• Florian Girelli and collaborators [33] proposed that QG phenomenology may be associated with an energy-dependent geometry (modified dispersion relations) that corresponds to a Finsler geometry. The symmetries arising in this context have a role in other QG alternative scenarios, such as DSR and emergent spacetime-like models.
• One of the authors of the present paper (A.T.), in his recent paper [34], introduced an approach to ‘quantize’ the fundamental tensor (metric tensor) and first fundamental form (line element) by extending the four-dimensional Riemann manifold to the eight-dimensional Finsler manifold, in which the quadratic restriction on the length measure is relaxed. A.T. emphasizes that these results represent “quantum-induced corrections but not a full quantization”.

Apart from the wide range of similar features shared by Finsler’s and Caianiello’s manifolds, we choose to limit our analysis reported in the present paper to the geometrical framework of Caianiello’s fiber bundle setup [30] and save the direct exposition to Finsler-type manifolds to a future project. We believe that the implementation of Finsler manifolds might generally deepen and strengthen the conceptual and formal background from a geometrical point of view. However, per the assumed scope of the present paper, we do not expect it to result in any notable impact on the results of the calculations supporting the main conclusions thus reached.

1.5. Relative Locality

Now let us briefly discuss the observer-dependent property of the particle metric and trajectories in momentum space, which goes in the literature as “relative (non-)locality” or the “principle of relative locality” [35].

The relevance to the geometrical setup we implement in the formal analysis presented in the next Sections is because we choose to follow the main ideas underlying Caianiello’s original geometrical construction [30,36,37]. This geometrical framework is formally motivated and developed in Section 3.

In this framework, the physical picture leading to the property of observer dependence (or relative locality) may be simplified as follows: particles live in a four-spacetime manifold embedded, at fundamental microscopic levels, in an eight-dimensional phase space. As a consequence, a particle subject to different interactions has different trajectories (different velocities) in momentum space and is thereby naturally seen by different observers to live in different observer-dependent four-dimensional geometries.

This perspective of relative locality is believed to be compatible with a conjecture according to Gary Gibbons and Stephen Hawking [38] that reads “in a typical quantum theory of gravity, the spacetime metric should be observer-dependent”.

In this vein, more recently and also more relevant to the formal geometrical construction adopted in the present study, Amelino-Camelia and collaborators [35] proposed a deepening of the relativity principle according to which the invariant arena for non–quantum physics is phase space rather than spacetime. In this framework, absolute locality is replaced by ‘relative locality’, which (interestingly enough) results from deforming momentum space.

Moreover, it is remarkable that the aspects of relative locality are seen naturally intertwined with any formal procedures involving deformed (curved) momentum space and/or non–commutative geometry. In addition to Amelino-Camelia’s version of relative locality [35], typical examples include but are not limited to Alain Connes’s non–commutative geometry [39], both the two main formulations of DSR [23,40], and not to mention the formal procedure adopted in the present study.

1.6. Phenomenology

Making contact with phenomenology is the most important part of any model. Minimal-length-scale-inspired models have grown to become one of the most well-developed and highly motivated fields in the phenomenology of quantum gravity. Consequently, before we terminate our introduction, we are in order to address some of the expected phenomenological consequences of the existence of a minimal measurable length and the resulting modification of the metric tensor and other geometrical structures. In this vein, it is important to comprehend the numerous efforts made to constrain the GUP deformation parameter (β), motivated in Section 4, by optomechanical/interferometry studies, on the one hand, and gravitational/cosmological data, on the other (see, e.g., Refs. [20,41] for a review).

Moreover, one notable recent development, which is especially relevant to the question of a minimal length scale, is the possibility that direct evidence for the discrete nature of spacetime may be found in the emission spectra of primordial black holes, if such black holes exist and can be observed [42,43].

An interesting though outdated account of some possible phenomenological consequences of the original version of Caianiello’s model involving different particle mass scales and thereby different maximal acceleration limits is reported in [36].

Even more interestingly, GUP can lead to some phenomenological quantum gravitational models that can, in principle, be probed at relatively low energies [16,44].

Finally, and in the interest of being more concrete about the plausibility of measuring (at least) the bounds of the GUP β, let us brief on a recipe recently suggested by Zhong-Wen Feng and collaborators [45] to constrain the GUP by exploiting the first detected gravitational wave (GW150914) data to set bounds on β without violating the equivalence principle. In this endeavor, the authors of Ref. [45]:

• obtain the GUP-deformed commutator (similar to Equation (2) in Section 2 in the present paper);
• decide the deformed dispersion relation (to the first order in β) from the deformed commutator;
• calculate the deformed group speed of gravitons assuming them to be massless;
• calculate the difference between the deformed speed of massless gravitons and that of light;
• calculate the upper bound of the group velocity at the measured beak frequency and finally,
• calculate the upper bound of β.

The present paper is organized as follows. In Section 2, GUP-inspired expressions for the minimal measurable length and the corresponding maximal acceleration are derived. Extending the four-dimensional manifold, M, to an eight-dimensional spacetime tangent bundle, $TM$, and the possible quantum-induced deformation of the metric tensor is introduced in Section 3. The possible deformation of the Levi-Civita connection on the Riemannian manifold is discussed in Section 4. The parallel transport of a vector on the Riemannian manifold is elaborated in Section 5. The deformed Riemann curvature tensor is developed in Section 6. Section 7 is dedicated to a general summary and conclusion.

2. Minimal Measurable Length

As discussed in Section 1.3, the concept of minimal length L emerges from the point that a minimal measurable length uncertainty is predicted in various theories of QG, as a consequence of the expected added fuzziness of the spacetime structure due to gravitational impacts near the fundamental scales of sufficiently high energy necessary to resolve a fundamentally small distance. We choose to adopt Kempf’s version of GUP [6], which suggests

$$\begin{array}{c}\hfill \Delta x\Delta p\ge \frac{\hslash }{2}\left[1+\mathit{\beta }{\left(\Delta p\right)}^2+\mathit{\beta }{\langle p\rangle }^2\right],\end{array}$$

(1)

where $\langle p\rangle$ is the momentum expectation value and, $\Delta x$ and $\Delta p$ represent the length and momentum uncertainties, respectively. The GUP parameter $\mathit{\beta }={\mathit{\beta }}_{0}G/(c^3\hslash )$, with G the gravitational constant and ${\mathit{\beta }}_0$ being a dimensionless parameter that conveys the impacts of gravity on HUP, which is one of the main principles of QM, and shapes the transition to GUP. ${\mathit{\beta }}_0$ is of the order of 1 according to different independent theoretical estimations [41], while the available empirical bounds from recent cosmological observations of gravitational and non–gravitational origin still need much improvement [41,46]. We assume here that ${\mathit{\beta }}_0$ is left to be determined empirically (see Section 1.6).

The known commutation relation between length and momentum operators now reads:

$$\begin{array}{ccc}\hfill \left[\widehat{x},\widehat{p}\right]& =& i\hslash \left(1+\mathit{\beta }{\widehat{p}}^2\right).\hfill \end{array}$$

(2)

The minimum uncertainty of position $\Delta x_{\min }$ for all values of $\langle p\rangle$ is

$$\begin{array}{c}\hfill \Delta x_{\min }\left(\langle p\rangle \right)=\hslash \sqrt{\mathit{\beta }}\sqrt{1+\mathit{\beta }{\langle p\rangle }^2}.\end{array}$$

(3)

When ${\langle p\rangle }^2=0$, the absolute minimum uncertainty of position becomes

$$\begin{array}{c}\hfill \Delta x_0=\hslash \sqrt{\mathit{\beta }}.\end{array}$$

(4)

One can identify the minimum uncertainty of position, $\Delta x_0$, as the minimal measurable length scale, which indicates the distance where quantum effects of the gravitational interaction are expected to become significant; then the minimal measurable length becomes

$$\begin{array}{cc}\hfill L& =\Delta x_0=\hslash \sqrt{\mathit{\beta }}.\hfill \end{array}$$

(5)

The minimal length may be assumed as a fundamental physical quantity obtained from a combination of fundamental physical quantities such as G from gravity, ℏ from quantum mechanics and c from special relativity [47]. That is,

$$\begin{array}{cc}\hfill L& =l_{\mathrm{P}}=\sqrt{{\displaystyle \frac{\hslash G}{c^3}}},\hfill \end{array}$$

(6)

where $l_{\mathrm{P}}$ denotes Planck length.

As we tried to motivate in Section 1.4, the concept of maximal acceleration can be directly related to the concept of minimal length. In this context, if we choose to follow Brandt [48], we may directly identify $L=l_{\mathrm{P}}$. Thus, the maximal acceleration $A_{\max }$ can be expressed as

$$\begin{array}{c}\hfill A_{\max }={\displaystyle \frac{c^2}{l_{\mathrm{P}}}}=\sqrt{{\displaystyle \frac{c^7}{\hslash G}}}.\end{array}$$

(7)

In this choice, the maximal acceleration is defined by the known physical constants.

However, we choose to follow Caianiello [26] and let the length parameter L be arbitrary. In our perspective, this choice is not just to preserve the dimensionality of the length required for the consistency of the following equations. There is an added value for this choice that stems from a phenomenological point of view; L should be taken as a free parameter, which may be constrained later using the available empirical data. This is left for a future study.

For arbitrary L, the maximal acceleration is thus

$$\begin{array}{cc}\hfill A_{\max }& ={\displaystyle \frac{c^2}{L}}.\hfill \end{array}$$

(8)

From Equations (5) and (8), one obtains:

$$\begin{array}{c}\hfill A_{\max }=\sqrt{{\displaystyle \frac{c^4}{{\hslash }^2\mathit{\beta }}}},\end{array}$$

(9)

which is an expression for $A_{\max }$ in terms of the GUP $\mathit{\beta }$ exclusively.

Following this choice, we have obtained expressions for both L and $A_{\max }$ explicitly in terms of the GUP $\mathit{\beta }$ and a couple of physical constants. It also has to be highlighted here that, unlike some treatments of Caianiello’s model [26], we choose here not to consider any scenarios involving explicit dependence of the maximal acceleration on the mass in general. Finally, our consideration in the next Sections dictates that our formal analysis makes (almost) exclusively explicit reference to the minimal length rather than the maximal acceleration.

3. The Deformation of Metric Tensor

To include quantum effects of the gravitational interaction on the spacetime geometry near the fundamental scale at which such effects are expected to become important, we follow the main ideas of Caianiello’s original model [30,36,37], which suggests that the classical GR and thereby the classical spacetime geometry can be described by a four-dimensional spacetime embedded as a hypersurface in an eight-dimensional manifold, $M_8$. The four-velocity space is assumed to include the quantum regime, where one expects to see the quantum (GUP)-induced effects at a minimal length scale. The extended dimensions, the eight dimensions $x^A$, in the manifold $M_8$ are

$$\begin{array}{c}\hfill x^A=(x^{\mathit{\mu }},(L/c){\dot{x}}^{\mathit{\mu }}),\end{array}$$

(10)

where $x^{\mathit{\mu }}$ is the four spacetime dimensions (four-dimensional submanifold of the manifold $M_8$), ${\dot{x}}^{\mathit{\mu }}={\displaystyle \frac{d{x}^{\mathit{\mu }}}{ds}}$ is the four-velocity, and $A=0,\dots ,7$, $\mathit{\mu }=0,\dots ,3$, L is the minimal length. Here, as explained above in Section 2, L may be defined according to Kempf’s GUP model as a minimal uncertainty of position (5), $L=\Delta x_0=\hslash \sqrt{\mathit{\beta }}$ [6]; or one can assume the value of minimal length to be the Planck length, (6), L $=l_p$$=\sqrt{(\hslash G/c^3)}$.

In light of the main purpose of this paper, the geometrical embedding described above is regarded only as a formal procedure to generate, from a given metric $g_{\mathit{\mu }\mathit{\nu }}$, a new metric ${\tilde{g}}_{\mathit{\mu }\mathit{\nu }}$, which differs from $g_{\mathit{\mu }\mathit{\nu }}$ by a correction (deformation) factor, which is determined just below.

The deformed line element $\left(d{\tilde{s}}^2\right)$ with metric, $g_{AB}$, in the eight-dimensional manifold $M_8$ [29,49] is thereby given by

$$\begin{array}{c}\hfill d{\tilde{s}}^2=g_{AB}d{x}^{A}d{x}^B,\end{array}$$

(11)

where $g_{AB}$ is a result of an outer product as the following $g_{AB}=g_{\mathit{\mu }\mathit{\nu }}\otimes g_{\mathit{\mu }\mathit{\nu }}$.

In Equation (11), we substitute for $d{x}^A$ and $d{x}^B$ by the differential form of Equaiton (10):

$$\begin{array}{c}\hfill d{\tilde{s}}^2=\left(1+L{g}_{\mathit{\mu }\mathit{\nu }}{\displaystyle \frac{d{x}^{\mathit{\mu }}}{ds}}{\displaystyle \frac{d{\dot{x}}^{\mathit{\nu }}}{ds}}+L{g}_{\mathit{\mu }\mathit{\nu }}{\displaystyle \frac{d{\dot{x}}^{\mathit{\mu }}}{ds}}{\displaystyle \frac{d{x}^{\mathit{\nu }}}{ds}}+L^2{g}_{\mathit{\mu }\mathit{\nu }}{\displaystyle \frac{d{\dot{x}}^{\mathit{\mu }}}{ds}}{\displaystyle \frac{d{\dot{x}}^{\mathit{\nu }}}{ds}}\right)d{s}^2,\end{array}$$

(12)

where $c=1$, $d{s}^2=g_{\mathit{\mu }\mathit{\nu }}d{x}^{\mathit{\mu }}d{x}^{\mathit{\nu }}$ is the classical line element,

$$\begin{array}{c}\hfill d{\tilde{s}}^2=d{s}^2+L^2{g}_{\mathit{\mu }\mathit{\nu }}{\ddot{x}}^{\mathit{\mu }}{\ddot{x}}^{\mathit{\nu }}d{s}^2\end{array}$$

(13)

where ${\ddot{x}}^{\mathit{\mu }}={\displaystyle \frac{d{\dot{x}}^{\mathit{\mu }}}{ds}}$ is the acceleration of the particle, $\mathit{\mu }$ and $\mathit{\nu }$ are dummy indices, and $\overrightarrow{\dot{x}}·\overrightarrow{\dot{x}}=-1$; then $\overrightarrow{\dot{x}}·\overrightarrow{\ddot{x}}=0$,

$$\begin{array}{c}\hfill d{\tilde{s}}^2=(1+L^2{\ddot{x}}^2)d{s}^2\end{array}$$

(14)

where ${\ddot{x}}^2=g_{\mathit{\mu }\mathit{\nu }}{\ddot{x}}^{\mathit{\mu }}{\ddot{x}}^{\mathit{\nu }}$. The deformed line element in four-dimension spacetime, as a projection from eight dimensions into four dimensions, is

$$\begin{array}{c}\hfill d{\tilde{s}}^2={\tilde{g}}_{\mathit{\mu }\mathit{\nu }}d{x}^{\mathit{\mu }}d{x}^{\mathit{\nu }},\end{array}$$

(15)

where ${\tilde{g}}_{\mathit{\mu }\mathit{\nu }}$ is the deformed (modified) metric tensor.

The deformed metric tensor ${\tilde{g}}_{\mathit{\mu }\mathit{\nu }}$ is the quantum-induced metric of the spacetime hypersurface, which is embedded in the extended manifold $M_8$. The relation between the deformed metric tensor and the classical metric tensor is obtained by equating Equations (14) and (15),

$$\begin{array}{c}\hfill {\tilde{g}}_{\mathit{\mu }\mathit{\nu }}=(1+L^2{\ddot{x}}^2)g_{\mathit{\mu }\mathit{\nu }},\end{array}$$

(16)

where ${\ddot{x}}^2=g_{\mathit{\alpha }\mathit{\gamma }}{\ddot{x}}^{\mathit{\alpha }}{\ddot{x}}^{\mathit{\gamma }}$, $\mathit{\gamma }$, and $\mathit{\alpha }$ are dummy indices, and $\mathit{\mu }$ and $\mathit{\nu }$ are free indices. For flat spacetime,

$$\begin{array}{c}\hfill {\tilde{\mathit{\eta }}}_{\mathit{\mu }\mathit{\nu }}=(1+L^2{\ddot{x}}^2){\mathit{\eta }}_{\mathit{\mu }\mathit{\nu }},\end{array}$$

(17)

where ${\mathit{\eta }}_{\mathit{\mu }\mathit{\nu }}$ defines the Minkowski metric.

The relation between the correction factor $(1+L^2{\ddot{x}}^2)$ and GUP can be derived by substituting for L from Equation (16) by Equation (5),

$$\begin{array}{c}\hfill {\tilde{g}}_{\mathit{\mu }\mathit{\nu }}=(1+{\hslash }^2\mathit{\beta }{\ddot{x}}^2)g_{\mathit{\mu }\mathit{\nu }}.\end{array}$$

(18)

The correction factor of the deformed metric tensor can also be reformulated in terms of the maximal acceleration $A_{\max }$. This can be performed by substituting for L in Equation (16) from Equation (7); the deformed metric tensor is

$$\begin{array}{c}\hfill {\tilde{g}}_{\mathit{\mu }\mathit{\nu }}=\left(1+{\displaystyle \frac{1}{A_{\max }^2}}{\ddot{x}}^2\right)g_{\mathit{\mu }\mathit{\nu }},\end{array}$$

(19)

where $c=1$ is set and the GUP definition of maximal acceleration from Equation (9), $A_{\max }={\displaystyle \frac{1}{\hslash \sqrt{\mathit{\beta }}}}$, is used.

4. The Deformation of Levi-Civita Connection in Riemannian Manifold

A “connection” is defined as a geometric object on a smooth manifold connecting nearby tangent spaces. The tangent vector fields are covariant derivatives on that manifold. When covariant derivatives reduce to the ordinary partial derivatives, the connection is called Levi-Civita connection or Christoffel symbol, which dictates how to perform the parallel transport of tangent vectors on a manifold. In classical GR, the connection plays the role of the gravitational force field, where the metric tensor is the corresponding gravitational potential.

The minimal length approach suggests the deformation of the metric tensor as follows.

• For curved space,

  $$\begin{array}{ccc}\hfill {\tilde{g}}_{\mathit{\mu }\mathit{\nu }}& =& g_{\mathit{\mu }\mathit{\nu }}+L^2{\ddot{x}}^2{g}_{\mathit{\mu }\mathit{\nu }}=g_{\mathit{\mu }\mathit{\nu }}+q_{\mathit{\mu }\mathit{\nu }}.\hfill \end{array}$$

  (20)
  With Equation (5), $q_{\mathit{\mu }\mathit{\nu }}$ can be suggested as a GUP-contributed part, which reads

  $$\begin{array}{ccc}\hfill q_{\mathit{\mu }\mathit{\nu }}& =& \mathit{\beta }{\hslash }^2{\ddot{x}}^2{g}_{\mathit{\mu }\mathit{\nu }}.\hfill \end{array}$$

  (21)
• For flat space,

  $$\begin{array}{ccc}\hfill {\tilde{\mathit{\eta }}}_{\mathit{\mu }\mathit{\nu }}& =& {\mathit{\eta }}_{\mathit{\mu }\mathit{\nu }}+\mathit{\beta }{\hslash }^2{\ddot{x}}^2{\mathit{\eta }}_{\mathit{\mu }\mathit{\nu }}={\mathit{\eta }}_{\mathit{\mu }\mathit{\nu }}+h_{\mathit{\mu }\mathit{\nu }},\hfill \end{array}$$

  (22)

  where $h_{\mathit{\mu }\mathit{\nu }}=\mathit{\beta }{\hslash }^2{\ddot{x}}^2{\mathit{\eta }}_{\mathit{\mu }\mathit{\nu }}$.

Both $g_{\mathit{\mu }\mathit{\nu }}$ and ${\tilde{g}}_{\mathit{\mu }\mathit{\nu }}$ share common properties. They turn the covariant tensor into a contravariant tensor and vice versa. The symmetry property of a deformed metric tensor is

$${\tilde{g}}_{\mathit{\mu }\mathit{\nu }}={\displaystyle \frac{1}{2}}({\tilde{g}}_{\mathit{\mu }\mathit{\nu }}+{\tilde{g}}_{\mathit{\nu }\mathit{\mu }}),$$

(23)

and the left-hand side (lhs) of Equation (23) is

$${\tilde{g}}_{\mathit{\mu }\mathit{\nu }}=g_{\mathit{\mu }\mathit{\nu }}+L^2{\ddot{x}}^2{g}_{\mathit{\mu }\mathit{\nu }},$$

(24)

and the right-hand side (rhs) of Equation (23) is

$${\displaystyle \frac{1}{2}}({\tilde{g}}_{\mathit{\mu }\mathit{\nu }}+{\tilde{g}}_{\mathit{\nu }\mathit{\mu }})={\displaystyle \frac{1}{2}}(g_{\mathit{\mu }\mathit{\nu }}+L^2{\ddot{x}}^2{g}_{\mathit{\mu }\mathit{\nu }}+g_{\mathit{\nu }\mathit{\mu }}+L^2{\ddot{x}}^2{g}_{\mathit{\nu }\mathit{\mu }}).$$

(25)

It is known (see, e.g., Section 7.3.4 in Ref. [50]) that $g_{\mathit{\mu }\mathit{\nu }}$ in classical GR is symmetric in its indices; then, in third and fourth terms of Equation (25), $g_{\mathit{\nu }\mathit{\mu }}$ is replaced by $g_{\mathit{\mu }\mathit{\nu }}$. Following this by performing some straightforward algebraic manipulations, one obtains:

$${\displaystyle \frac{1}{2}}({\tilde{g}}_{\mathit{\mu }\mathit{\nu }}+{\tilde{g}}_{\mathit{\nu }\mathit{\mu }})=g_{\mathit{\mu }\mathit{\nu }}+L^2{\ddot{x}}^2{g}_{\mathit{\mu }\mathit{\nu }}$$

(26)

One can see that Equations (24) and (26) are the same; then the rhs of Equation (23) is the same as the rhs of this equation. The deformed metric tensor is symmetric under the interchange of its indices $\mathit{\mu }$ and $\mathit{\nu }$.

For the deformed Levi-Civita connection, let us replace $g_{\mathit{\mu }\mathit{\nu }}$ in Equation (A14) with the deformed metric tensor ${\tilde{g}}_{\mathit{\mu }\mathit{\nu }}$ (20), where the partial derivatives are obviously commutative as well. The deformed metric tensor is compatible; see Appendix B. Thus, the deformation of the Levi-Civita connection (A14) can be expressed as

$${\tilde{\mathrm{\Gamma }}}_{\mathit{\beta }\mathit{\mu }}^{\mathit{\gamma }}={\displaystyle \frac{1}{2}}{\tilde{g}}^{\mathit{\alpha }\mathit{\gamma }}({\tilde{g}}_{\mathit{\alpha }\mathit{\beta },\mathit{\mu }}+{\tilde{g}}_{\mathit{\alpha }\mathit{\mu },\mathit{\beta }}-{\tilde{g}}_{\mathit{\beta }\mathit{\mu },\mathit{\alpha }}).$$

(27)

For curved space, by substituting Equations (20) and (A9) into Equation (27), one obtains:

$$\begin{array}{ccc}\hfill {\tilde{\Gamma }}_{\mathit{\beta }\mathit{\mu }}^{\mathit{\gamma }}& =& \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}\frac{1}{2}{g}^{\mathit{\alpha }\mathit{\gamma }}\left(g_{\mathit{\alpha }\mathit{\beta },\mathit{\mu }}+g_{\mathit{\alpha }\mathit{\mu },\mathit{\beta }}-g_{\mathit{\beta }\mathit{\mu },\mathit{\alpha }}\right)={\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}{\Gamma }_{\mathit{\beta }\mathit{\mu }}^{\mathit{\gamma }},\hfill \end{array}$$

(28)

where ${\tilde{g}}^{\mathit{\alpha }\mathit{\gamma }}={\displaystyle \frac{g^{\mathit{\alpha }\mathit{\gamma }}}{(1+L^2{\ddot{x}}^2)}}$.

One can immediately see that vanishing $L^2{\ddot{x}}^2$ straightforwardly retrieves the undeformed Levi-Civita connection, ${\Gamma }_{\mathit{\beta }\mathit{\mu }}^{\mathit{\gamma }}$. This is also the case, at vanishing $L^2$ (no minimal length scale) and/or at vanishing ${\ddot{x}}^2$ (the test particle is not accelerating). In other words, in this case, there is no GUP-induced deformation of GR. It was shown for Equation (20) that both deformation ingredients are interdependent. The parameterization of the four coordinates on M in eight coordinates on $TM$ emerges as spacelike four-acceleration ${\ddot{x}}^2$ and creates an additional geometric structure. Equation (28) reveals that the deformation of the Levi-Civita connection is exclusively localized in its coefficient, while the undeformed connection ${\Gamma }_{\mathit{\beta }\mathit{\mu }}^{\mathit{\gamma }}$ possesses unity as a coefficient. The deformed connection obtains the coefficient $(1+2L^2{\ddot{x}}^2)/(1+L^2{\ddot{x}}^2)$. This means that the Levi-Civita connection preserves, on the one hand, its geometric nature as in classical GR, for instance, and, on the other hand, the deformation via additional curvature on the eight-dimensional manifold, especially at the energy scale in which $L^2{\ddot{x}}^2$ becomes significant.

5. Parallel Transport on Riemannian Manifold

It is known that in flat space, one may choose a coordinate system, such as the Minkowskian in which the covariant derivatives are just equal to ordinary derivatives. However, one may also choose curvilinear (e.g., spherical) coordinates where the Christoffel symbol is not vanishing even in flat space. In curved space, however, the differentiation of the basis vectors can be expressed by the Levi-Civita connection. In both the flat and curved spaces, the covariant derivatives can be defined as the rates of change of the tangent vector fields (ordinary derivatives, for instance) with the normal component subtracted, i.e., parallel transport. Vanishing covariant derivatives of a vector $\overrightarrow{v}=v^{\mathit{\alpha }}{e}_{\mathit{\alpha }}$ means that $\overrightarrow{v}$ is parallel-transported, i.e., keeping $\overrightarrow{v}$ a constant as possible,

$$\begin{array}{c}\hfill {\displaystyle \frac{d}{d\mathit{\lambda }}}{v}^{\mathit{\alpha }}+{\Gamma }_{\mathit{\sigma }\mathit{\rho }}^{\mathit{\alpha }}{\displaystyle \frac{d{x}^{\mathit{\sigma }}}{d\mathit{\lambda }}}{v}^{\mathit{\rho }}=0,\end{array}$$

(29)

where $\mathit{\lambda }$ is a parameter along the parallel-transport curve and the dependence of the parallel transport on the connection ${\Gamma }_{\mathit{\sigma }\mathit{\rho }}^{\mathit{\alpha }}$ is known. With the deformation, ${\Gamma }_{\mathit{\sigma }\mathit{\rho }}^{\mathit{\alpha }}$ is to be replaced by ${\tilde{\Gamma }}_{\mathit{\sigma }\mathit{\rho }}^{\mathit{\alpha }}$ (28), i.e., Equation (29) can then be rewritten as

$${\displaystyle \frac{d}{d\mathit{\lambda }}}{v}^{\mathit{\alpha }}+{\displaystyle \frac{(1+2L^2{\ddot{x}}^2)}{(1+L^2{\ddot{x}}^2)}}{\Gamma }_{\mathit{\sigma }\mathit{\rho }}^{\mathit{\alpha }}{\displaystyle \frac{d{x}^{\mathit{\sigma }}}{d\mathit{\lambda }}}{v}^{\mathit{\rho }}=0,$$

(30)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d}{d\mathit{\lambda }}}{v}^{\mathit{\alpha }}& =& -{\displaystyle \frac{1}{1+L^2{\ddot{x}}^2}}{\Gamma }_{\mathit{\sigma }\mathit{\rho }}^{\mathit{\alpha }}{\displaystyle \frac{d{x}^{\mathit{\sigma }}}{d\mathit{\lambda }}}{v}^{\mathit{\rho }}-\frac{2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}{\Gamma }_{\mathit{\sigma }\mathit{\rho }}^{\mathit{\alpha }}{\displaystyle \frac{d{x}^{\mathit{\sigma }}}{d\mathit{\lambda }}}{v}^{\mathit{\rho }}.\hfill \end{array}$$

(31)

Figure 1 shows the Levi-Civita connection between the vector $\overrightarrow{v}$ parameterized in $\mathit{\lambda }$$\overrightarrow{v}(\mathit{\lambda })$ and its parallel-transported counterpart at $\mathit{\lambda }+d\mathit{\lambda }$; $\overrightarrow{v}(\mathit{\lambda }+d\mathit{\lambda })$.

The parallel transport can define the curvature of a manifold by taking the parallel transport of a vector over a closed loop; then a definition of curvature tensor may be obtained.

The equation of the parallel transport of the vector $v^{\mathit{\alpha }}$ around a loop with a deformed connection is

$$\mathit{\delta }{v}^{\mathit{\alpha }}=\mathit{\delta }a\mathit{\delta }b[{\tilde{\Gamma }}_{\mathit{\mu }\mathit{\sigma },\mathit{\lambda }}^{\mathit{\alpha }}-{\tilde{\Gamma }}_{\mathit{\mu }\mathit{\lambda },\mathit{\sigma }}^{\mathit{\alpha }}+{\tilde{\Gamma }}_{\mathit{\nu }\mathit{\lambda }}^{\mathit{\alpha }}{\tilde{\Gamma }}_{\mathit{\mu }\mathit{\sigma }}^{\mathit{\nu }}-{\tilde{\Gamma }}_{\mathit{\nu }\mathit{\sigma }}^{\mathit{\alpha }}{\tilde{\Gamma }}_{\mathit{\mu }\mathit{\lambda }}^{\mathit{\nu }}]v^{\mathit{\mu }},$$

(32)

where $\mathit{\delta }{v}^{\mathit{\alpha }}$ is the changing of $v^{\mathit{\alpha }}$ by the transport around the loop, and $\mathit{\delta }a\mathit{\delta }b$ is the area of the loop.

6. Deformed Riemann Curvature Tensor

In GR, the components of the Riemann curvature tensor, $R_{\mathit{\beta }\mathit{\mu }\mathit{\nu }}^{\mathit{\gamma }}$, can be constructed from the Levi-Civita connection [51],

$$\begin{array}{ccc}\hfill R_{\mathit{\beta }\mathit{\mu }\mathit{\nu }}^{\mathit{\gamma }}& =& {\Gamma }_{\mathit{\beta }\mathit{\nu },\mathit{\mu }}^{\mathit{\gamma }}-{\Gamma }_{\mathit{\beta }\mathit{\mu },\mathit{\nu }}^{\mathit{\gamma }}+{\Gamma }_{\mathit{\sigma }\mathit{\mu }}^{\mathit{\gamma }}{\Gamma }_{\mathit{\beta }\mathit{\nu }}^{\mathit{\sigma }}-{\Gamma }_{\mathit{\sigma }\mathit{\nu }}^{\mathit{\gamma }}{\Gamma }_{\mathit{\beta }\mathit{\mu }}^{\mathit{\sigma }}.\hfill \end{array}$$

(33)

This expression holds for all connections regardless of their metric compatibility or torsion freedom property. Accordingly, the deformed Riemann tensor can be expressed in terms of the deformed Levi-Civita connections and their derivatives as follows:

$$\begin{array}{ccc}\hfill {\tilde{R}}_{\mathit{\beta }\mathit{\mu }\mathit{\nu }}^{\mathit{\gamma }}& =& {\tilde{\Gamma }}_{\mathit{\beta }\mathit{\nu },\mathit{\mu }}^{\mathit{\gamma }}-{\tilde{\Gamma }}_{\mathit{\beta }\mathit{\mu },\mathit{\nu }}^{\mathit{\gamma }}+{\tilde{\Gamma }}_{\mathit{\sigma }\mathit{\mu }}^{\mathit{\gamma }}{\tilde{\Gamma }}_{\mathit{\beta }\mathit{\nu }}^{\mathit{\sigma }}-{\tilde{\Gamma }}_{\mathit{\sigma }\mathit{\nu }}^{\mathit{\gamma }}{\tilde{\Gamma }}_{\mathit{\beta }\mathit{\mu }}^{\mathit{\sigma }}.\hfill \end{array}$$

(34)

One substitutes Equation (28) into Equation (34) for the deformed Levi-Civita connection in terms of the classical one,

$$\begin{array}{ccc}\hfill {\tilde{\Gamma }}_{\mathit{\sigma }\mathit{\mu }}^{\mathit{\gamma }}& =& {\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}\frac{g^{\mathit{\gamma }\mathit{\alpha }}}{2}\left(g_{\mathit{\mu }\mathit{\alpha },\mathit{\sigma }}+g_{\mathit{\sigma }\mathit{\alpha },\mathit{\mu }}-g_{\mathit{\sigma }\mathit{\mu },\mathit{\alpha }}\right)={\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}{\Gamma }_{\mathit{\sigma }\mathit{\mu }}^{\mathit{\gamma }},\hfill \end{array}$$

(35)

$$\begin{array}{ccc}\hfill {\tilde{\Gamma }}_{\mathit{\sigma }\mathit{\nu }}^{\mathit{\gamma }}& =& {\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}\frac{g^{\mathit{\gamma }\mathit{\alpha }}}{2}\left(g_{\mathit{\nu }\mathit{\alpha },\mathit{\sigma }}+g_{\mathit{\sigma }\mathit{\alpha },\mathit{\nu }}-g_{\mathit{\sigma }\mathit{\nu },\mathit{\alpha }}\right)={\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}{\Gamma }_{\mathit{\sigma }\mathit{\nu }}^{\mathit{\gamma }},\hfill \end{array}$$

(36)

$$\begin{array}{ccc}\hfill {\tilde{\Gamma }}_{\mathit{\beta }\mathit{\mu }}^{\mathit{\sigma }}& =& {\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}\frac{g^{\mathit{\sigma }\mathit{\alpha }}}{2}\left(g_{\mathit{\mu }\mathit{\alpha },\mathit{\beta }}+g_{\mathit{\beta }\mathit{\alpha },\mathit{\mu }}-g_{\mathit{\beta }\mathit{\mu },\mathit{\alpha }}\right)={\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}{\Gamma }_{\mathit{\beta }\mathit{\mu }}^{\mathit{\sigma }},\hfill \end{array}$$

(37)

$$\begin{array}{ccc}\hfill {\tilde{\Gamma }}_{\mathit{\beta }\mathit{\nu }}^{\mathit{\sigma }}& =& {\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}\frac{g^{\mathit{\sigma }\mathit{\alpha }}}{2}\left(g_{\mathit{\nu }\mathit{\alpha },\mathit{\beta }}+g_{\mathit{\beta }\mathit{\alpha },\mathit{\nu }}-g_{\mathit{\beta }\mathit{\nu },\mathit{\alpha }}\right)={\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}{\Gamma }_{\mathit{\beta }\mathit{\nu }}^{\mathit{\sigma }}\hfill \end{array}$$

(38)

Thus, the derivative of the deformed Levi-Civita connection is straightforwardly derived:

$$\begin{array}{ccc}\hfill {\tilde{\Gamma }}_{\mathit{\beta }\mathit{\mu },\mathit{\nu }}^{\mathit{\gamma }}& =& {\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}\left[\frac{g_{,\mathit{\nu }}^{\mathit{\gamma }\mathit{\alpha }}}{2}\left(g_{\mathit{\mu }\mathit{\alpha },\mathit{\beta }}+g_{\mathit{\beta }\mathit{\alpha },\mathit{\mu }}-g_{\mathit{\beta }\mathit{\mu },\mathit{\alpha }}\right)+\frac{g^{\mathit{\gamma }\mathit{\alpha }}}{2}\left(g_{\mathit{\mu }\mathit{\alpha },\mathit{\beta },\mathit{\nu }}+g_{\mathit{\beta }\mathit{\alpha },\mathit{\mu },\mathit{\nu }}-g_{\mathit{\beta }\mathit{\mu },\mathit{\alpha },\mathit{\nu }}\right)\right]\hfill \\ & +& \frac{2\left(1+L^2{\ddot{x}}^2\right)-\left(1+2L^2{\ddot{x}}^2\right)}{{\left(1+L^2{\ddot{x}}^2\right)}^2}{L}^2{\left(g_{\mathit{\xi }\mathit{\zeta }}{\ddot{x}}^{\mathit{\xi }}{\ddot{x}}^{\mathit{\zeta }}\right)}_{,\mathit{\nu }}{\Gamma }_{\mathit{\beta }\mathit{\mu }}^{\mathit{\gamma }}\hfill \\ & =& \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}{\Gamma }_{\mathit{\beta }\mathit{\mu },\mathit{\nu }}^{\mathit{\gamma }}+\frac{L^2{g}_{\mathit{\xi }\mathit{\zeta },\mathit{\nu }}{\ddot{x}}^{\mathit{\xi }}{\ddot{x}}^{\mathit{\zeta }}}{{\left(1+L^2{\ddot{x}}^2\right)}^2}{\Gamma }_{\mathit{\beta }\mathit{\mu }}^{\mathit{\gamma }},\hfill \end{array}$$

(39)

where $\mathit{\xi }$ and $\mathit{\zeta }$ are dummy indices, ${\ddot{x}}_{,\mathit{\nu }}^{\mathit{\xi }}=0$, and ${\ddot{x}}_{,\mathit{\nu }}^{\mathit{\zeta }}=0$, as elaborated in Appendix A. Similarly,

$$\begin{array}{ccc}\hfill {\tilde{\Gamma }}_{\mathit{\beta }\mathit{\nu },\mathit{\mu }}^{\mathit{\gamma }}& =& \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}\left[\frac{g_{,\mathit{\mu }}^{\mathit{\gamma }\mathit{\alpha }}}{2}\left(g_{\mathit{\nu }\mathit{\alpha },\mathit{\beta }}+g_{\mathit{\beta }\mathit{\alpha },\mathit{\nu }}-g_{\mathit{\beta }\mathit{\nu },\mathit{\alpha }}\right)+\frac{g^{\mathit{\gamma }\mathit{\alpha }}}{2}\left(g_{\mathit{\nu }\mathit{\alpha },\mathit{\beta },\mathit{\mu }}+g_{\mathit{\beta }\mathit{\alpha },\mathit{\nu },\mathit{\mu }}-g_{\mathit{\beta }\mathit{\nu },\mathit{\alpha },\mathit{\mu }}\right)\right]\hfill \\ & +& \frac{2\left(1+L^2{\ddot{x}}^2\right)-\left(1+2L^2{\ddot{x}}^2\right)}{{\left(1+L^2{\ddot{x}}^2\right)}^2}{L}^2{\left(g_{\mathit{\xi }\mathit{\zeta }}{\ddot{x}}^{\mathit{\xi }}{\ddot{x}}^{\mathit{\zeta }}\right)}_{,\mathit{\mu }}{\Gamma }_{\mathit{\beta }\mathit{\nu }}^{\mathit{\gamma }}\hfill \\ & =& \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}{\Gamma }_{\mathit{\beta }\mathit{\nu },\mathit{\mu }}^{\mathit{\gamma }}+\frac{L^2{g}_{\mathit{\xi }\mathit{\zeta },\mathit{\mu }}{\ddot{x}}^{\mathit{\xi }}{\ddot{x}}^{\mathit{\zeta }}}{{\left(1+L^2{\ddot{x}}^2\right)}^2}{\Gamma }_{\mathit{\beta }\mathit{\nu }}^{\mathit{\gamma }}.\hfill \end{array}$$

(40)

With $g_{\mathit{\xi }\mathit{\zeta }}{g}^{\mathit{\xi }\mathit{\zeta }}=1$, we replace $g_{\mathit{\xi }\mathit{\zeta },\mathit{\nu }}{\ddot{x}}^{\mathit{\xi }}{\ddot{x}}^{\mathit{\zeta }}$ by ${\ddot{x}}^2{g}_{\mathit{\xi }\mathit{\zeta },\mathit{\nu }}{g}^{\mathit{\xi }\mathit{\zeta }}$ in Equations (39) and (40). By substituting into Equation (34), the minimal length-induced correction to the Riemann curvature tensor is

$$\begin{array}{cc}{\tilde{R}}_{\mathit{\beta }\mathit{\mu }\mathit{\nu }}^{\mathit{\gamma }}\hfill & ={\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}{\Gamma }_{\mathit{\beta }\mathit{\nu },\mathit{\mu }}^{\mathit{\gamma }}+{\displaystyle \frac{L^2{\ddot{x}}^2}{{(1+L^2{\ddot{x}}^2)}^2}}{g}_{\mathit{\eta }\mathit{\zeta },\mathit{\mu }}{g}^{\mathit{\eta }\mathit{\zeta }}{\Gamma }_{\mathit{\beta }\mathit{\nu }}^{\mathit{\gamma }}-{\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}{\Gamma }_{\mathit{\beta }\mathit{\mu },\mathit{\nu }}^{\mathit{\gamma }}\hfill \\ & -{\displaystyle \frac{L^2{\ddot{x}}^2}{{(1+L^2{\ddot{x}}^2)}^2}}{g}_{\mathit{\eta }\mathit{\zeta },\mathit{\nu }}{g}^{\mathit{\eta }\mathit{\zeta }}{\Gamma }_{\mathit{\beta }\mathit{\mu }}^{\mathit{\gamma }}+{\displaystyle \frac{{(1+2L^2{\ddot{x}}^2)}^2}{{(1+L^2{\ddot{x}}^2)}^2}}{\Gamma }_{\mathit{\sigma }\mathit{\mu }}^{\mathit{\gamma }}{\Gamma }_{\mathit{\beta }\mathit{\nu }}^{\mathit{\sigma }}-{\displaystyle \frac{{(1+2L^2{\ddot{x}}^2)}^2}{{(1+L^2{\ddot{x}}^2)}^2}}{\Gamma }_{\mathit{\sigma }\mathit{\nu }}^{\mathit{\gamma }}{\Gamma }_{\mathit{\beta }\mathit{\mu }}^{\mathit{\sigma }}.\hfill \end{array}$$

(41)

Taking common factors and rearranging, one obtains:

$$\begin{array}{cc}{\tilde{R}}_{\mathit{\beta }\mathit{\mu }\mathit{\nu }}^{\mathit{\gamma }}\hfill & ={\displaystyle \frac{{(1+2L^2{\ddot{x}}^2)}^2}{{(1+L^2{\ddot{x}}^2)}^2}}\left({\Gamma }_{\mathit{\sigma }\mathit{\mu }}^{\mathit{\gamma }}{\Gamma }_{\mathit{\beta }\mathit{\nu }}^{\mathit{\sigma }}-{\Gamma }_{\mathit{\sigma }\mathit{\nu }}^{\mathit{\gamma }}{\Gamma }_{\mathit{\beta }\mathit{\mu }}^{\mathit{\sigma }}\right)+{\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}\left({\Gamma }_{\mathit{\beta }\mathit{\nu },\mathit{\mu }}^{\mathit{\gamma }}-{\Gamma }_{\mathit{\beta }\mathit{\mu },\mathit{\nu }}^{\mathit{\gamma }}\right)\hfill \\ & +{\displaystyle \frac{L^2{\ddot{x}}^2}{{(1+L^2{\ddot{x}}^2)}^2}}\left(g_{\mathit{\eta }\mathit{\zeta },\mathit{\mu }}{g}^{\mathit{\eta }\mathit{\zeta }}{\Gamma }_{\mathit{\beta }\mathit{\nu }}^{\mathit{\gamma }}-g_{\mathit{\eta }\mathit{\zeta },\mathit{\nu }}{g}^{\mathit{\eta }\mathit{\zeta }}{\Gamma }_{\mathit{\beta }\mathit{\mu }}^{\mathit{\gamma }}\right).\hfill \end{array}$$

(42)

In Equation (42), the partial derivatives of all metric tensors $g_{\mathit{\eta }\mathit{\zeta },\mathit{\mu }}$ and $g_{\mathit{\eta }\mathit{\zeta },\mathit{\nu }}$ can respectively be replaced by metric tensors and Levi-Civita connections as follows:

$$\begin{array}{ccc}\hfill g_{\mathit{\xi }\mathit{\zeta },\mathit{\mu }}& =& g_{\mathit{\zeta }\mathit{\lambda }}{\Gamma }_{\mathit{\xi }\mathit{\mu }}^{\mathit{\lambda }}+g_{\mathit{\xi }\mathit{\lambda }}{\Gamma }_{\mathit{\zeta }\mathit{\mu }}^{\mathit{\lambda }},\hfill \end{array}$$

(43)

$$\begin{array}{ccc}\hfill g_{\mathit{\xi }\mathit{\zeta },\mathit{\nu }}& =& g_{\mathit{\zeta }\mathit{\lambda }}{\Gamma }_{\mathit{\xi }\mathit{\nu }}^{\mathit{\lambda }}+g_{\mathit{\xi }\mathit{\lambda }}{\Gamma }_{\mathit{\zeta }\mathit{\nu }}^{\mathit{\lambda }},\hfill \end{array}$$

(44)

$$\begin{array}{cc}\hfill {\tilde{R}}_{\mathit{\beta }\mathit{\mu }\mathit{\nu }}^{\mathit{\gamma }}& ={\displaystyle \frac{{(1+2L^2{\ddot{x}}^2)}^2}{{(1+L^2{\ddot{x}}^2)}^2}}\left({\Gamma }_{\mathit{\sigma }\mathit{\mu }}^{\mathit{\gamma }}{\Gamma }_{\mathit{\beta }\mathit{\nu }}^{\mathit{\sigma }}-{\Gamma }_{\mathit{\sigma }\mathit{\nu }}^{\mathit{\gamma }}{\Gamma }_{\mathit{\beta }\mathit{\mu }}^{\mathit{\sigma }}\right)+{\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}\left({\Gamma }_{\mathit{\beta }\mathit{\nu },\mathit{\mu }}^{\mathit{\gamma }}-{\Gamma }_{\mathit{\beta }\mathit{\mu },\mathit{\nu }}^{\mathit{\gamma }}\right)\hfill \\ & +{\displaystyle \frac{L^2{\ddot{x}}^2}{{(1+L^2{\ddot{x}}^2)}^2}}\left[\left({\mathit{\delta }}_{\mathit{\lambda }}^{\mathit{\xi }}{\Gamma }_{\mathit{\xi }\mathit{\mu }}^{\mathit{\lambda }}+{\mathit{\delta }}_{\mathit{\lambda }}^{\mathit{\zeta }}{\Gamma }_{\mathit{\zeta }\mathit{\mu }}^{\mathit{\lambda }}\right){\Gamma }_{\mathit{\beta }\mathit{\nu }}^{\mathit{\gamma }}-\left({\mathit{\delta }}_{\mathit{\lambda }}^{\mathit{\xi }}{\Gamma }_{\mathit{\xi }\mathit{\nu }}^{\mathit{\lambda }}+{\mathit{\delta }}_{\mathit{\lambda }}^{\mathit{\zeta }}{\Gamma }_{\mathit{\zeta }\mathit{\nu }}^{\mathit{\lambda }}\right){\Gamma }_{\mathit{\beta }\mathit{\mu }}^{\mathit{\gamma }}\right].\hfill \end{array}$$

(45)

Using a delta tensor to transform the dummy indices, Equation (45) is re-expressed as

$$\begin{array}{cc}\hfill {\tilde{R}}_{\mathit{\beta }\mathit{\mu }\mathit{\nu }}^{\mathit{\gamma }}=& {\displaystyle \frac{{(1+2L^2{\ddot{x}}^2)}^2}{{(1+L^2{\ddot{x}}^2)}^2}}\left({\Gamma }_{\mathit{\sigma }\mathit{\mu }}^{\mathit{\gamma }}{\Gamma }_{\mathit{\beta }\mathit{\nu }}^{\mathit{\sigma }}-{\Gamma }_{\mathit{\sigma }\mathit{\nu }}^{\mathit{\gamma }}{\Gamma }_{\mathit{\beta }\mathit{\mu }}^{\mathit{\sigma }}\right)+{\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}\left({\Gamma }_{\mathit{\beta }\mathit{\nu },\mathit{\mu }}^{\mathit{\gamma }}-{\Gamma }_{\mathit{\beta }\mathit{\mu },\mathit{\nu }}^{\mathit{\gamma }}\right)\hfill \\ & +{\displaystyle \frac{2L^2{\ddot{x}}^2}{{(1+L^2{\ddot{x}}^2)}^2}}\left[{\Gamma }_{\mathit{\lambda }\mathit{\mu }}^{\mathit{\lambda }}{\Gamma }_{\mathit{\beta }\mathit{\nu }}^{\mathit{\gamma }}-{\Gamma }_{\mathit{\lambda }\mathit{\nu }}^{\mathit{\lambda }}{\Gamma }_{\mathit{\beta }\mathit{\mu }}^{\mathit{\gamma }}\right],\hfill \end{array}$$

(46)

substitute Equation (33) into Equation (46) for $\left({\Gamma }_{\mathit{\beta }\mathit{\nu },\mathit{\mu }}^{\mathit{\gamma }}-{\Gamma }_{\mathit{\beta }\mathit{\mu },\mathit{\nu }}^{\mathit{\gamma }}\right)$,

$$\begin{array}{cc}{\tilde{R}}_{\mathit{\beta }\mathit{\mu }\mathit{\nu }}^{\mathit{\gamma }}=\hfill & {\displaystyle \frac{{(1+2L^2{\ddot{x}}^2)}^2}{{(1+L^2{\ddot{x}}^2)}^2}}\left({\Gamma }_{\mathit{\sigma }\mathit{\mu }}^{\mathit{\gamma }}{\Gamma }_{\mathit{\beta }\mathit{\nu }}^{\mathit{\sigma }}-{\Gamma }_{\mathit{\sigma }\mathit{\nu }}^{\mathit{\gamma }}{\Gamma }_{\mathit{\beta }\mathit{\mu }}^{\mathit{\sigma }}\right)+{\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}\left(R_{\mathit{\beta }\mathit{\mu }\mathit{\nu }}^{\mathit{\gamma }}+{\Gamma }_{\mathit{\sigma }\mathit{\nu }}^{\mathit{\gamma }}{\Gamma }_{\mathit{\beta }\mathit{\mu }}^{\mathit{\sigma }}-{\Gamma }_{\mathit{\sigma }\mathit{\mu }}^{\mathit{\gamma }}{\Gamma }_{\mathit{\beta }\mathit{\nu }}^{\mathit{\sigma }}\right)\hfill \\ & +{\displaystyle \frac{2L^2{\ddot{x}}^2}{{(1+L^2{\ddot{x}}^2)}^2}}\left[{\Gamma }_{\mathit{\lambda }\mathit{\mu }}^{\mathit{\lambda }}{\Gamma }_{\mathit{\beta }\mathit{\nu }}^{\mathit{\gamma }}-{\Gamma }_{\mathit{\lambda }\mathit{\nu }}^{\mathit{\lambda }}{\Gamma }_{\mathit{\beta }\mathit{\mu }}^{\mathit{\gamma }}\right],\hfill \end{array}$$

(47)

take $\left({\Gamma }_{\mathit{\sigma }\mathit{\mu }}^{\mathit{\gamma }}{\Gamma }_{\mathit{\beta }\mathit{\nu }}^{\mathit{\sigma }}-{\Gamma }_{\mathit{\sigma }\mathit{\nu }}^{\mathit{\gamma }}{\Gamma }_{\mathit{\beta }\mathit{\mu }}^{\mathit{\sigma }}\right)$ as a common factor,

$$\begin{array}{cc}{\tilde{R}}_{\mathit{\beta }\mathit{\mu }\mathit{\nu }}^{\mathit{\gamma }}=\hfill & {\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}{R}_{\mathit{\beta }\mathit{\mu }\mathit{\nu }}^{\mathit{\gamma }}+{\displaystyle \frac{{(1+2L^2{\ddot{x}}^2)}^2-(1+L^2{\ddot{x}}^2)(1+2L^2{\ddot{x}}^2)}{{(1+L^2{\ddot{x}}^2)}^2}}\left({\Gamma }_{\mathit{\sigma }\mathit{\mu }}^{\mathit{\gamma }}{\Gamma }_{\mathit{\beta }\mathit{\nu }}^{\mathit{\sigma }}-{\Gamma }_{\mathit{\sigma }\mathit{\nu }}^{\mathit{\gamma }}{\Gamma }_{\mathit{\beta }\mathit{\mu }}^{\mathit{\sigma }}\right)\hfill \\ & +{\displaystyle \frac{2L^2{\ddot{x}}^2}{{(1+L^2{\ddot{x}}^2)}^2}}\left[{\Gamma }_{\mathit{\lambda }\mathit{\mu }}^{\mathit{\lambda }}{\Gamma }_{\mathit{\beta }\mathit{\nu }}^{\mathit{\gamma }}-{\Gamma }_{\mathit{\lambda }\mathit{\nu }}^{\mathit{\lambda }}{\Gamma }_{\mathit{\beta }\mathit{\mu }}^{\mathit{\gamma }}\right],\hfill \end{array}$$

(48)

and simplify the second term of Equation (48):

$$\begin{array}{cc}\hfill {\tilde{R}}_{\mathit{\beta }\mathit{\mu }\mathit{\nu }}^{\mathit{\gamma }}=& {\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}{R}_{\mathit{\beta }\mathit{\mu }\mathit{\nu }}^{\mathit{\gamma }}+{\displaystyle \frac{(1+2L^2{\ddot{x}}^2)L^2{\ddot{x}}^2}{{(1+L^2{\ddot{x}}^2)}^2}}\left({\Gamma }_{\mathit{\sigma }\mathit{\mu }}^{\mathit{\gamma }}{\Gamma }_{\mathit{\beta }\mathit{\nu }}^{\mathit{\sigma }}-{\Gamma }_{\mathit{\sigma }\mathit{\nu }}^{\mathit{\gamma }}{\Gamma }_{\mathit{\beta }\mathit{\mu }}^{\mathit{\sigma }}\right)+{\displaystyle \frac{2L^2{\ddot{x}}^2}{{(1+L^2{\ddot{x}}^2)}^2}}\left[{\Gamma }_{\mathit{\lambda }\mathit{\mu }}^{\mathit{\lambda }}{\Gamma }_{\mathit{\beta }\mathit{\nu }}^{\mathit{\gamma }}-{\Gamma }_{\mathit{\lambda }\mathit{\nu }}^{\mathit{\lambda }}{\Gamma }_{\mathit{\beta }\mathit{\mu }}^{\mathit{\gamma }}\right].\hfill \end{array}$$

(49)

Equation (49) generalizes the Riemann curvature tensor by introducing the effect of minimal length or GUP-quantum-induced deformation. At vanishing $L^2$ and/or ${\ddot{x}}^2$, the undeformed Riemann curvature tensor $R_{\mathit{\beta }\mathit{\mu }\mathit{\nu }}^{\mathit{\gamma }}$ can be retrieved entirely.

The eminent ingredients added by the correction $L^2{\ddot{x}}^2$ can be illustrated in an example of a sphere surface (two-dimensional manifold) with the radius $r=1$. Compared with the undeformed case, the deformed Reimann curvature tensor has additional geometric structure that likely reveals supplementary insights to be discovered. The Cartesian coordinates can be expressed by polar coordinates: radius r, inclination $u^1$, and azimuth $u^2$ as $x=cos\left(u^2\right)sin\left(u^1\right)$, $y=sin\left(u^2\right)sin\left(u^1\right)$, and $z=cos\left(u^1\right)$.

As shown in Equations (35)–(38), the minimal-length-induced corrections originated in $L^2{\ddot{x}}^2$ are combined in the deformed metric tensor and the connection. Therefore, one needs just to determine the components of the classical metric tensor on a two-sphere,

$$\begin{array}{ccc}\hfill g_{ij}& =& \left[\begin{array}{cc}\hfill 1& 0\\ \hfill 0& {(sin\left(u^1\right))}^2\end{array}\right],\hfill \end{array}$$

and coefficients of the classical connections

$$\begin{array}{ccc}\hfill {\Gamma }_{11}^1=0,& & {\Gamma }_{11}^2=0,\hfill \\ \hfill {\Gamma }_{12}^1=0,& & {\Gamma }_{12}^2=cot\left(u^1\right),\hfill \\ \hfill {\Gamma }_{21}^1=0,& & {\Gamma }_{21}^2=cot\left(u^1\right),\hfill \\ \hfill {\Gamma }_{22}^1=\frac{1}{2}sin\left(2u^1\right),& & {\Gamma }_{22}^2=0.\hfill \end{array}$$

Then, the corresponding coefficients of a deformed Riemann curvature tensor are given as

$$\begin{array}{ccc}\hfill {\tilde{R}}_{212}^1& =& \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}{\left[sin\left(u^1\right)\right]}^2+\frac{\left(2L^2{\ddot{x}}^2-1\right)L^2{\ddot{x}}^2}{{\left(1+L^2{\ddot{x}}^2\right)}^2}{\left[cos\left(u^1\right)\right]}^2,\hfill \end{array}$$

(50)

which means that at the poles, where $u^1=\{0,\pi \}$, ${\tilde{R}}_{212}^1=(2L^2{\ddot{x}}^2-1)L^2{\ddot{x}}^2/{(1+L^2{\ddot{x}}^2)}^2$, i.e., is finite, as well as at the equator, where $u^1=\pi /2$, ${\tilde{R}}_{212}^1=(1+2L^2{\ddot{x}}^2)/(1+L^2{\ddot{x}}^2)$, i.e., is finite as well. These two examples highlight the significance of the minimal length contributions encoded in $L^2{\ddot{x}}^2$. In the classical limit, i.e., vanishing $L^2$ and/or ${\ddot{x}}^2$, only finite $R_{212}^1$ signals curved spaces, as this exclusively depends on the inclination. For instance, at the poles, the space is flat! With this correction, this is not necessarily the case everywhere. The only exception might be ${\ddot{x}}^2=0.5$ in units of $1/L^2$. Here, both classical and deformed coefficients $R_{212}^1$ indeed vanish, at $u^1=\{0,\pi \}$, while their values, at $u^1=\pi /2$, are also coincident and positive.

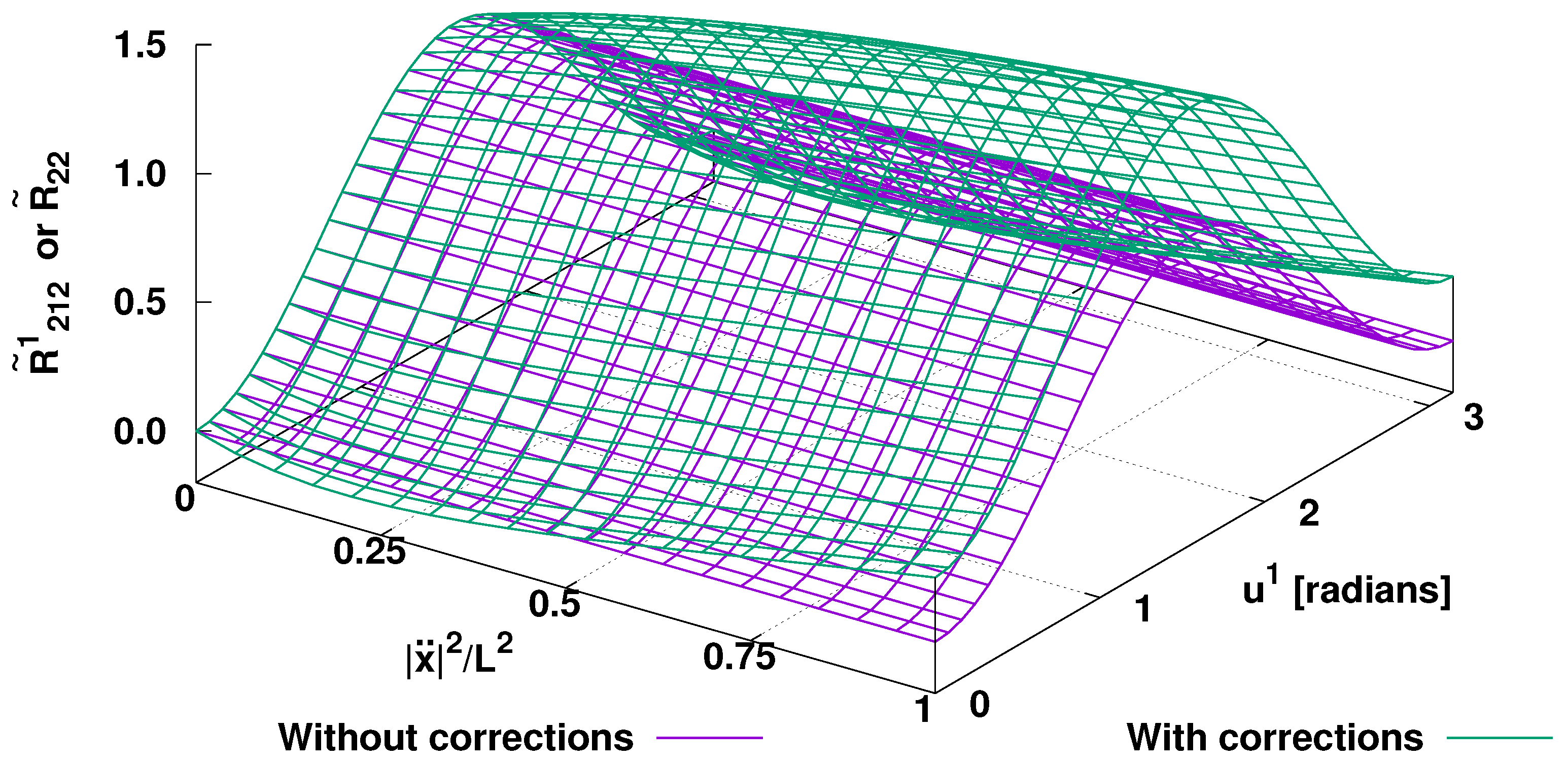
Figure 2 shows the coefficients of Riemann and Ricci curvature tensors in a sphere surface (two-dimensional manifold) with the radius $r=1$, Equation (50). For the sake of simplicity, we assume that the squared spacelike acceleration ${\ddot{x}}^2$ is given in units of $1/L^2$. This assures correct dimensions and sets an upper bound on ${\ddot{x}}^2$ in units of $1/L^2$.

Figure 2 depicts the dependence of ${\tilde{R}}_{212}^1$ and ${\tilde{R}}_{22}$ on both $u^1$ and ${\ddot{x}}^2$. It is apparent that the minimal length contributions are significant everywhere. the second term in Equation (50), which is the same for Riemann and Ricci tensors, may reveal additional geometrical structures and curvatures in a future study.

7. Summary and Conclusions

The minimal length scale scenario emerging from many quantum gravity approaches is conjectured to integrate gravity in quantum mechanics through the generalization of the Heisenberg uncertainty principle to a generalized uncertainty principle (GUP). GUP can be used to help incorporate the quantum effects of the gravitational interaction on the spacetime geometry near the minimal scale of the length at which such effects are expected to become important. Eventually, it is expected that the key geometrical objects involved in the classical description of spacetime geometry within the framework of the classical theory of general relativity (GR) will be deformed (modified).

To achieve the quantum-induced deformation of geometrical structures on spacetime manifold M, we have identified the minimum uncertainty of distance $\Delta x_0$ in Kempf’s GUP model as the minimal measurable length scale L. Then we have followed the main ideas and formal procedure (recipe) for the calculation of the quantum-induced curvature in a relativistic eight-dimensional spacetime tangent bundle (phase space) $TM$ in the Riemannian manifold first suggested by Caianiello [25] and further developed later by Brandt [29]. The local coordinates $x^{\mathit{\mu }}$ on M are combined with the tangent vectors ${\dot{x}}^{\mathit{\mu }}=d{x}^{\mathit{\mu }}/ds$ on $TM$.

It has to be emphasized that the adapted recipe (following Caianiello [30]) we are adopting in the present study in the interest of eventually calculating the expected deformations in the main geometrical structures of the classical GR, such as the metric tensor, connection, and Riemann curvature tensor, has the following features.

• Unlike Caianiello’s approach [26], our approach is explicitly independent of any particle mass scale.
• It explicitly manifests a minimal length scale that can naturally be related to a maximal acceleration scale via some quantum deformation parameter and/or some fundamental physical constants depending on the minimal length scale chosen.
• Unlike Brandt’s approach [29], in our approach, the metric and other geometrical objects are observer dependent.
• Again, unlike Brandt’s approach [29], there is no universal length scale (or mass scale) strictly required to define the minimal length (or maximal acceleration). We do not have or need to identify the minimal length scale to be exactly Planck scale (unless phenomenological constraints are imposed, which is left for a future project).
• No formal ’quantisation’ scheme is assumed (at least for the scope of the present paper). However, one may safely assume a semiclassical or effective quantization scheme.

To the best of our knowledge, what we consider as a novel contribution in the present study might include the following:

• Exploitation of Kempf’s GUP-inspired minimal length uncertainty as the minimal measurable length scale in the context of studying the quantum effects of gravitational interaction.
• Use of the above summarized Caianiello’s recipe [26,30] to derive the possible deformation (modification) factor of the Levi-Civita connection (see Equation (28)), which is found to exclusively depend on the product of the minimal length scale and the particle’s proper four-acceleration. This result has not been published before.
• Discussion of the properties of the GUP-deformed Levi-Civita connection justifying its preservation of the embedded four-manifold nature of being Riemannian.
• Derivation of the dependence of a normalized parallel-transported vector on the spacelike four-acceleration. This study manifests that the minimal length uncertainty and the deformation recipe are significant, especially at the energy scale in which $L^2{\ddot{x}}^2$ becomes significant.
• Calculation of the deformed Riemann curvature tensor, which well illustrates that GUP-induced deformation may be another significant source of curvature, especially in the limit where $L^2{\ddot{x}}^2$ is significant.

We conclude that the correction of the Levi-Civita connection is exclusively factorized in the coefficient $(1+2L^2{\ddot{x}}^2)/(1+L^2{\ddot{x}}^2)$ (see Equation (28)), which combines minimal length uncertainty (GUP effect), geometric structural, non–commutative algebraic, and gravitational ingredients. On the one hand, this means that the deformed Levi-Civita connection preserves all properties of its undeformed counterpart, such as torsion freedom and metric compatibility. On the other hand, its geometric nature as connecting nearby tangent spaces on a smooth manifold is also preserved on discrete spaces. Moreover, we have derived how the deformed Levi-Civita connection shapes the parallel transport of a tangent vector on a Riemannian manifold.

We also conclude that the deformation via an additional quantum-induced curvature on an eight-dimensional manifold likely reveals a fine geometric structure. This is well understood from the results of the calculation of the GUP-induced deformed Riemann curvature tensor here (see Equation (49)). The quite simple example of the two-sphere of the unit radius discussed in Section 6 and visualized graphically in Figure 2 should be helpful in grasping the geometrical impact of our suggested quantum-induced deformation on such geometrical objects as the Riemann curvature and its contraction. In the expression for the deformed Riemann curvature (see Equation (49)), all terms are factorized by different polynomial functions of $L^2{\ddot{x}}^2$ in such a way that the classical Riemann curvature is retrieved in the limit when $L^2{\ddot{x}}^2$ becomes negligible.

At the macroscopic level, where $\hslash \to 0$, the modification (deformation) of the metric tensor, Levi-Civita connection, Riemann curvature tensor, etc., vanishes, and their classical GR forms are restored. This ensures that such modifications have a quantum origin that manifests exclusively at the appropriate fundamental scales where $L^2{\ddot{x}}^2$ becomes significant. The extra curvature of the deformed manifold exists if and only if $d{\dot{x}}^{\mathit{\mu }}\ne 0$, and it is entirely due to the proper acceleration of the test particle rather than any other matter or energy–momentum sources.