1. Introduction
The study of natural or mixed convection flows either in fluids or in fluid-saturated porous media is, with a limited number of exceptions, modelled theoretically by claiming the validity of the Oberbeck–Boussinesq approximation. There are several thorough and comprehensive analyses of how this approximation can be established starting from a general formulation of the local balance equations of mass, momentum and energy for a fluid. Beyond the many textbooks of fluid dynamics and convection heat transfer, we mention the analyses of this topic presented in Chapter 8 of the book by Zeytounian [
1], as well as in the papers by Rajagopal, Ruzicka, and Srinivasa [
2] and by Zeytounian [
3]. Such discussions on the origin and on the range of applicability of the Oberbeck–Boussinesq approximation stem from pioneering papers such as those by Spiegel and Veronis [
4], by Gray and Giorgini [
5] and by Hills and Roberts [
6]. On the other hand, further papers offer interesting perspectives on possible extended forms of the Oberbeck–Boussinesq approximation [
7,
8,
9,
10,
11,
12].
The aim of this short paper is neither a comprehensive analysis of the Oberbeck–Boussinesq approximation nor a novel deduction of the approximate mathematical model. For the former purpose, we refer to the extremely large body of literature on the topic, where the few references cited above are just a definitely limited sample, while the books by Gebhart, Jaluria, Mahajan, and Sammakia [[
13] and by Straughan [
14] provide comprehensive surveys. For the latter purpose, we mention the recent paper by Barletta [
15]. In fact, the objective of this paper is to highlight an aspect of the Oberbeck–Boussinesq approximation that may be the source of pitfalls, i.e., the duality of variable fluid density and constant fluid density. If it is recognised that the approximation scheme predicates a variable density which is pressure independent and varying with the temperature, in some instances one may forget that such variable density serves only to define the buoyancy force within the local momentum balance equation. Utilising the variable density outside this very specific context may lead to unphysical predictions and, hence, to incorrect conclusions. Such conclusions are incorrect as they usually conflict with the principle of mass conservation. A final discussion about the interpretation of the Oberbeck–Boussinesq approximation as a limiting case of the general local balance equations of mass, momentum and energy is presented.
3. The Rectangular Cavity with Side Heating
Let us consider the classical problem of two–dimensional natural convection in a rectangular cavity with rigid and impermeable side boundaries kept at uniform, but different, temperatures,
and
, while the upper and lower sides are kept adiabatic. It is not restrictive to assume
. A sketch of the system is provided in
Figure 1.
It is well–known that, with sufficiently small differences −, a steady-state natural convection flow occurs in the cavity. In non-dimensional terms, this restriction is equivalent to a sufficiently small Rayleigh number. The steady-state flow is cellular in character, with one or more convective cells. For a given fluid, the number of stationary convective cells depends on the aspect ratio, , where H and L are the half–height and half–width of the cavity, and on the Rayleigh number.
We denote with
S the horizontal midplane surface with
and
. Since the flow system is modelled as two-dimensional in the
xy plane,
S is considered with unit depth in the
z direction. Then, we can immediately conclude that
as a straightforward consequence of Equation (
1). In fact, one can just integrate Equation (
1) over the upper half-domain
and then employ Gauss’ theorem by recalling that
S is the only permeable boundary of such a domain. Here,
v is the
y component of
u. Then, we may wonder how we could evaluate the mass flow rate,
, across
S. There is a correct way and an incorrect way. The correct way is by applying the principle that the fluid density is to be considered constant and equal to
, so that Equation (
12) yields
The incorrect way is by employing the variable density given by Equation (
4), so that Equation (
12) yields
The difference between the correct method expressed by Equation (
13) and the incorrect method expressed by Equation (
14) is that, in the former, we employ the reference density,
, while, in the latter, we employ the variable density,
. The reason why Equation (
14) yields
is that, at least with a sufficiently small temperature difference,
, both
v and
are odd functions of
x with
, positive for
and negative for
(see, for instance, de Vahl Davis [
16]). Thus, their product,
, is an even and positive function of
x throughout the domain of integration
, so that Equation (
14) leads to the conclusion that
. The numerical solution discussed by de Vahl Davis [
16] is complemented by a straightforward analytical solution, which predicts the same symmetry for
v and
and which holds for a very tall cavity,
. Such an asymptotic solution is briefly outlined in
Appendix A with an explicit, though incorrect, evaluation of the mass flow rate based on the formula given by Equation (
14).
We mention that Equation (
12) holds also for any other
plane
S, as a consequence of Equation (
1). We also note that, here, our arguments are strictly relative to the example examined in this section. Certainly, there are situations where the mass flow rate, evaluated coherently with the Oberbeck–Boussinesq approximation, is nonzero. For instance, this is the case for the flow system to be discussed in
Section 4.
We said that Equation (
14) expresses the incorrect way to evaluate
, since the conclusion
is an evident violation of the mass conservation within the upper half–domain
or in the lower half–domain,
. In fact, both for the upper and the lower half–domains,
S would be the only permeable boundary and it would be crossed by a net mass flow rate. Such a situation, in a stationary regime, yields a violation of the principle of mass conservation.
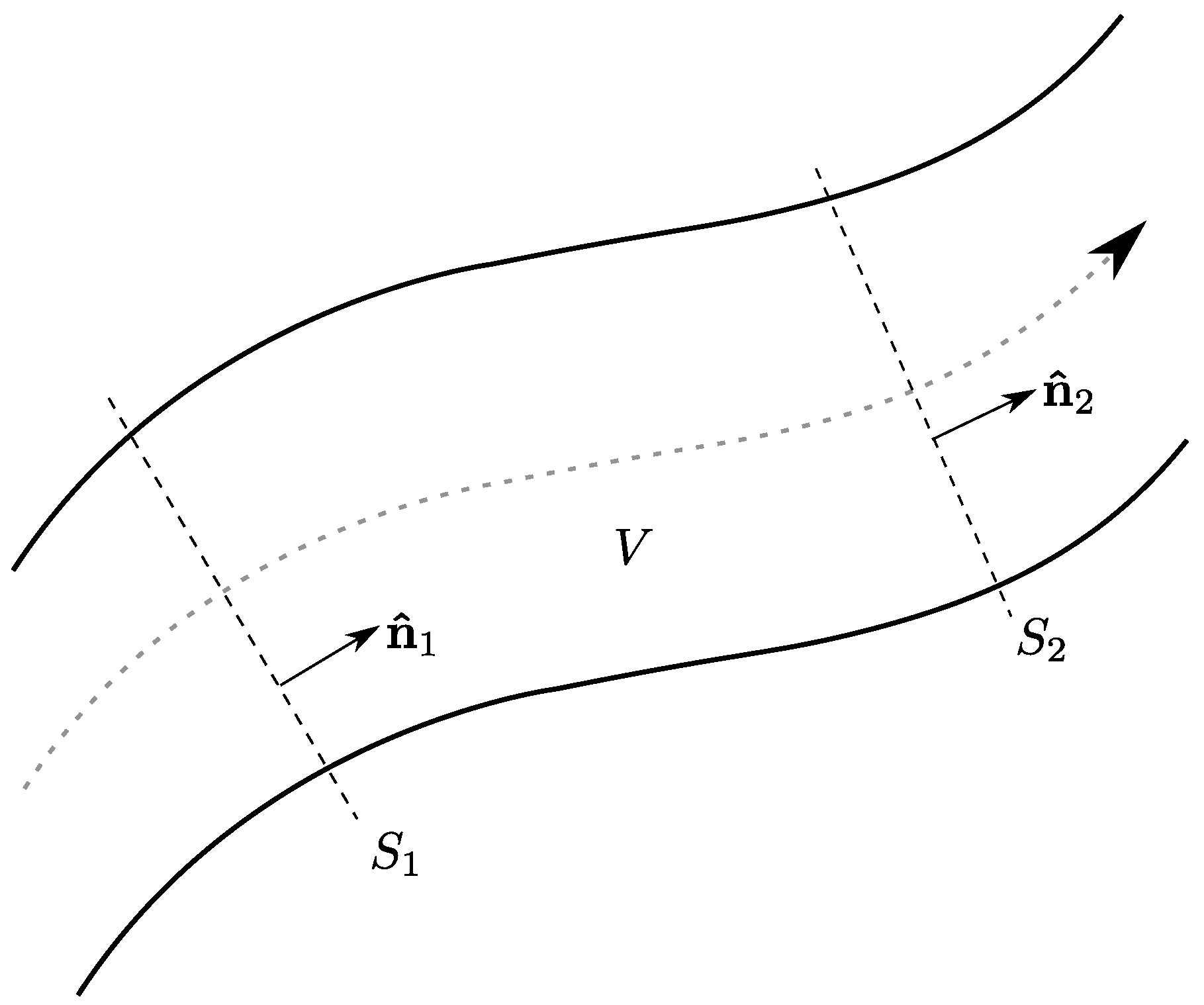
4. Mixed Convection Duct Flow
Let us consider the internal mixed convection in a duct with an impermeable wall having an increasing temperature along the streamwise direction. Such a behaviour is observed, for instance, when the duct wall is subject to an incoming uniform heat flux. We consider the case of stationary flow.
As sketched in
Figure 2, we consider the region
V delimited by the cross–sections,
and
. Since, the fluid is heated in the streamwise direction, we have an average temperature evaluated at the cross–section
, denoted by
, smaller than the average temperature evaluated at the cross–section
, denoted by
. Then, a judicious choice of the reference temperature,
, for the Oberbeck–Boussinesq approximation in the domain
V is the volume-averaged temperature,
Such a volume–averaged temperature value,
, is larger than
and smaller than
. Let us evaluate the average velocities across
and
,
where
and
are the unit vectors of the surfaces
and
, oriented in the streamwise direction as shown in
Figure 2. Equation (
1), after an integration over
V and use of Gauss’ theorem, yields the equality
. One can wonder how one can evaluate the mass flow rates across
and
, i.e.,
and
, respectively. The right way is by assuming that the fluid density is to be considered constant and equal to
all over
V, so that
Since
, Equations (
16) and (
17) allow one to conclude that
, which is in perfect agreement with the principle of mass conservation.
The incorrect way to evaluate
and
is by employing the variable density,
, defined by Equation (
4). In this case, one would write
From Equation (
18) and from the equality
, one has
By employing again the equality and by recalling that the average temperature over is smaller than the average temperature over , one can immediately conclude that , i.e., the mass rate flowing through is larger than the mass rate flowing through which, in a stationary regime, means a violation of the principle of mass conservation.
5. A Vertical Porous Slab Separating Two Fluid Reservoirs
Let us consider an infinitely wide wall separating two fluid reservoirs kept at different temperatures,
and
. As shown in
Figure 3, the wall has a porous insertion bounded by two planes
and
. The fluid in the left-hand reservoir is the same as that in the right-hand reservoir and they are both in a rest state. The same fluid saturates the porous slab. The Oberbeck–Boussinesq approximation can be applied by assuming the reference temperature,
.
One can evaluate the pressure distribution on the boundaries
and
as the hydrostatic pressure. By employing Equation (
9), the pressure distribution on the plane
is given by
while, on
, we have
Equations (
20) and (
21) have been used to formulate the pressure conditions at the porous slab boundaries in Refs. [
17,
18,
19,
20]. The pressurisation constants,
and
, can be equal or not depending on the conditions externally imposed on the two reservoirs. For instance, one may have a situation where the reservoir at temperature
is compressed on its top, while the reservoir at temperature
is open to the atmospheric pressure. In such a situation, one has
. Equations (
20) and (
21) reveal that the pressure distribution on
and
is
y–dependent, but the pressure difference across the porous slab is a constant,
If none of the two reservoirs is pressurised, then
. If
, one may have a seepage throughflow across the porous slab [
18].
As sketched in
Figure 3, the porous insertion is bounded above and below by an impermeable material, so that application of Equation (
1) yields
where
U is the
x component of the seepage velocity,
U, across the porous material. By recalling that the fluid density is to be intended as uniform with the value
, Equation (
23) implies that the mass flow rates across
and
are equal as required by mass conservation,
This is the correct and consistent application of the Oberbeck–Boussinesq scheme to this sample case.
There is always the possibility of introducing errors, as in the previous examples. One may enforce the validity of Equation (
4) in the evaluation of the hydrostatic pressures in the two reservoirs so that Equations (
20) and (
21) are replaced by
and
where
Equations (
25) and (
26) yield an
y–dependent pressure difference across the porous layer,
Even in the absence of pressurisation in one of the two reservoirs
, Equation (
28) entails a pressure difference across the porous layer which, in turn, leads to the prediction of a horizontal throughflow across the porous layer [
21]. Such a stationary throughflow is unphysical as it would lead to a violation of mass conservation. In fact, consistently with the assumption of a variable density, as given by Equation (
4), the mass flow rate across
is expressed as
while the mass flow rate across
is given by
The violation of mass conservation is quantified by a relative error,
where Equations (
23), (
29) and (
30) have been employed. Interestingly enough, should
be considered as negligible,
, then the pressure distributions given by Equations (
25) and (
26), and employed in the study carried out by Vynnycky and Mitchell [
21], would turn out to match perfectly the correct pressure distributions expressed by Equations (
20) and (
21). More precisely, the corrective terms introduced in Equations (
25) and (
26), i.e.,
, can be taken into account consistently only if the solenoidal constraint for the velocity,
, is replaced by the variable-density local mass balance equation,
. An intermediate approximation, such as that used in Ref. [
21], where Equations (
25) and (
26) are employed in combination with
, would be flawed as it leads to a violation of the principle of mass conservation.
6. The Froude Number and the Rayleigh Number
Let us reconsider Equations (
8)–(
10). The pressure gradient and gravitational force contributions to the local momentum balance are given by the force per unit volume,
where we are assuming that the
y–axis is vertical and orientated upward. The unit vector along the
y–axis is denoted by
. We can rescale
F in order to obtain a dimensionless formulation of the local momentum balance equation. The dimensionless
F denoted with an asterisk is given by
where the constant
is a reference pressure difference and the constant
L is a reference length. One can also define the dimensionless coordinates pressure and temperature as
where
is a reference temperature difference. On account of Equations (
33) and (
34), Equation (
32) yields
where the Froude number is defined as
and
is given by
It is noteworthy that the usual definition is
(see, for instance, the paper by Mayeli and Sheard [
10]), where
is a reference velocity. In fact, Equation (
36) matches perfectly the usual definition provided that one chooses
. One may also mention that, according to other authors (e.g., Zeytounian [
1]),
should be defined as a velocity ratio, so that it is given by the square root of the quantity identified by Mayeli and Sheard [
10] as the Froude number. In our discussion, we will rely on the definition given by Equation (
36).
It is quite evident that one can, legitimately, set the reference pressure difference
. This choice, from Equation (
36), would yield
. In this case, assuming
would justify an assumption of constant density in the mass balance equation, but it would also unavoidably imply a negligible buoyancy contribution to
as given by Equation (
35). Indeed, in this case, the limit
yields
In Equation (
38), there is no buoyancy force, so that the dynamics predicted is that of a perfectly incompressible fluid. Thus, in order to preserve the contribution of the buoyancy force, one cannot set neither
nor
. Indeed, a possibility is that the Oberbeck–Boussinesq approximate governing Equations (
1)–(
3) are a limiting case of the local balance equations for a fully compressible (variable density) flow when
The double limit defined by Equation (
39) is stated, although in slightly different terms, by Hills and Roberts [
6] and reported also by other authors [
3,
22]. It is also implicitly employed in the analysis carried out by Rajagopal, Ruzicka, and Srinivasa [
2].
In the case of natural convection, where buoyancy alone causes the flow, a typical choice of
is
Thus, the ratio
coincides with the Rayleigh number,
The approach based on the limit defined by Equation (
39) leads to a singular behaviour of
, as one can immediately infer from Equation (
35), since
tends to infinity in the limit. Stated in these terms, the singular nature of the Oberbeck–Boussinesq limit of
seems unavoidable, if one aims to keep a finite contribution of the buoyancy force. Actually, there is just one way to avoid a singular behaviour for
in the limit defined by Equation (
39). One should constrain
∇P to be equal to
whenever the Oberbeck–Boussinesq approximation is used. More precisely, one must have
or, equivalently, by employing Equation (
39),
This result can be reformulated by defining a dimensionless scalar field,
, such that, when the limit (
39) is to be taken, one may write
Thus, Equation (
35) yields
so that the limit (
39) leads to a finite result. It must be pointed out that, from a physical viewpoint, the meaning of the term
has no connection with the difference between the pressure gradient and the hydrostatic pressure gradient, as this difference tends to zero in the limit (
39).
Interestingly enough, the derivation of the Oberbeck–Boussinesq approximation presented by Rajagopal, Ruzicka, and Srinivasa [
2], recently reformulated within a simplified framework by Barletta [
15], leads to the same conclusion drawn above, namely that the pressure gradient must always coincide with the hydrostatic pressure gradient. We mention that the treatment presented by Rajagopal, Ruzicka, and Srinivasa [
2] is based on a dimensionless scaling of the governing balance equations where the reference length is
and the reference velocity is
, where
is the perturbation parameter. The Oberbeck–Boussinesq approximation is defined as the asymptotic case where
. Thus, the dimensionless scaling is singular in this limit. Incidentally,
is proportional to
, with
given by Equation (
37). The study reported by Rajagopal,
Ruzicka, and Srinivasa [
2] discusses in detail the serious drawbacks of the previous theoretical studies that define the Oberbeck–Boussinesq approximation as a limiting case obtained by letting one or more perturbation parameters to zero. Examples are the papers by Spiegel and Veronis [
4], by Gray and Giorgini [
5] and by Hills and Roberts [
6]. As a consequence, one can say that an asymptotic theory, based on a suitable perturbation scheme, which is aimed at a completely rigorous and physically convincing deduction of the Oberbeck–Boussinesq set of governing Equations (
1)–(
3) is based on the ideas conveyed in the paper by Rajagopal, Ruzicka, and Srinivasa [
2] under the restatement provided by Barletta [
15].