Introducing Quantum Technologies at Secondary School Level: Challenges and Potential Impact of an Online Extracurricular Course
Abstract
:1. Introduction
1.1. The Use of Quantum Technologies to Introduce Quantum Mechanics
1.2. The Educational Path to Quantum Technologies
1.3. Aims of the Study
2. Methods and Tools
2.1. Instructional Context
2.2. Sample
2.3. Instruments
2.3.1. Quantum Technologies Inventory (QTI)
2.3.2. Views about Quantum Technologies (VAQT)
- Assuming to use ideal measuring instruments, in physics I must describe the results of measurements probabilistically only if I have incomplete information about the system;
- It is possible for physicists to carefully perform the same experiment and get two very different results that are both correct;
- Quantum computers will never work, because it is impossible to build an hardware that is accurate enough;
- Scientists say that quantum communication makes it possible to teleport a particle from one place to another;
- Scientists say that quantum communication does not make possible the teleportation of a particle from one place to another, but only the transfer of its characteristics.
2.4. Data Analysis
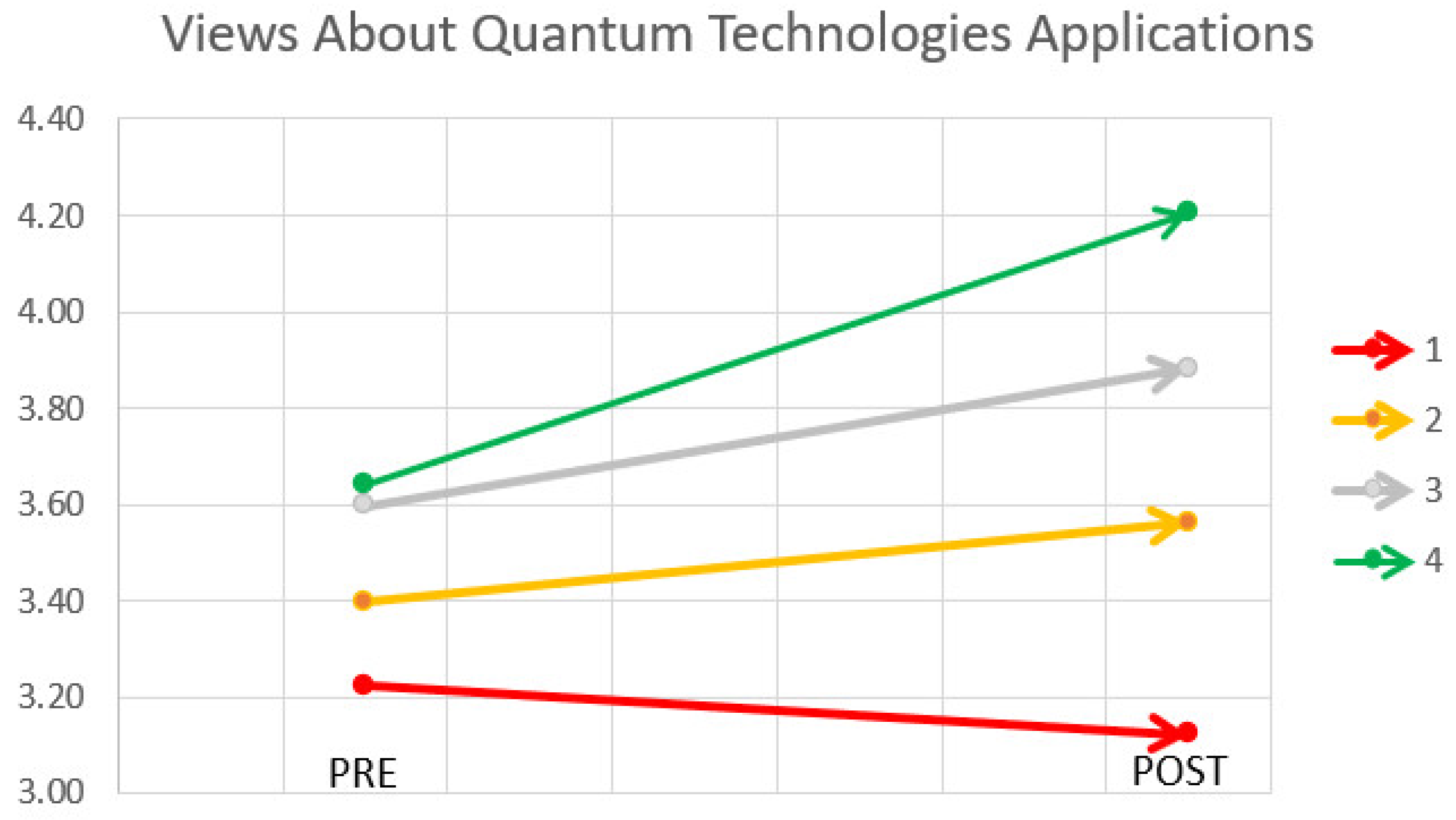
3. Results
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Path Description
Appendix A.1. Plenary Introductory Lectures
- Lecture 1Objective: quantum state, superposition stateContent: qubits, Dirac representation, role of probability in quantum mechanics
- 1.
- Classical and quantum coin-flipping game
- 2.
- How to describe a quantum coin: bits and qubits
- Dirac notation
- Superposition states
- Visual representation of qubits (Bloch sphere)
- 3.
- Operations on quantum coin: single qubit quantum logic gates
- I, NOT, Z, H
- 4.
- Physical examples of qubits
- Single photon after a beam splitter (QuVis, MILQ [33])
- Electronic spin
- Cavity atom
- Superconducting circuits
- Lecture 2Objective: measurementContent: representation of quantum measures, role of probability, non-compatible measurements
- 1.
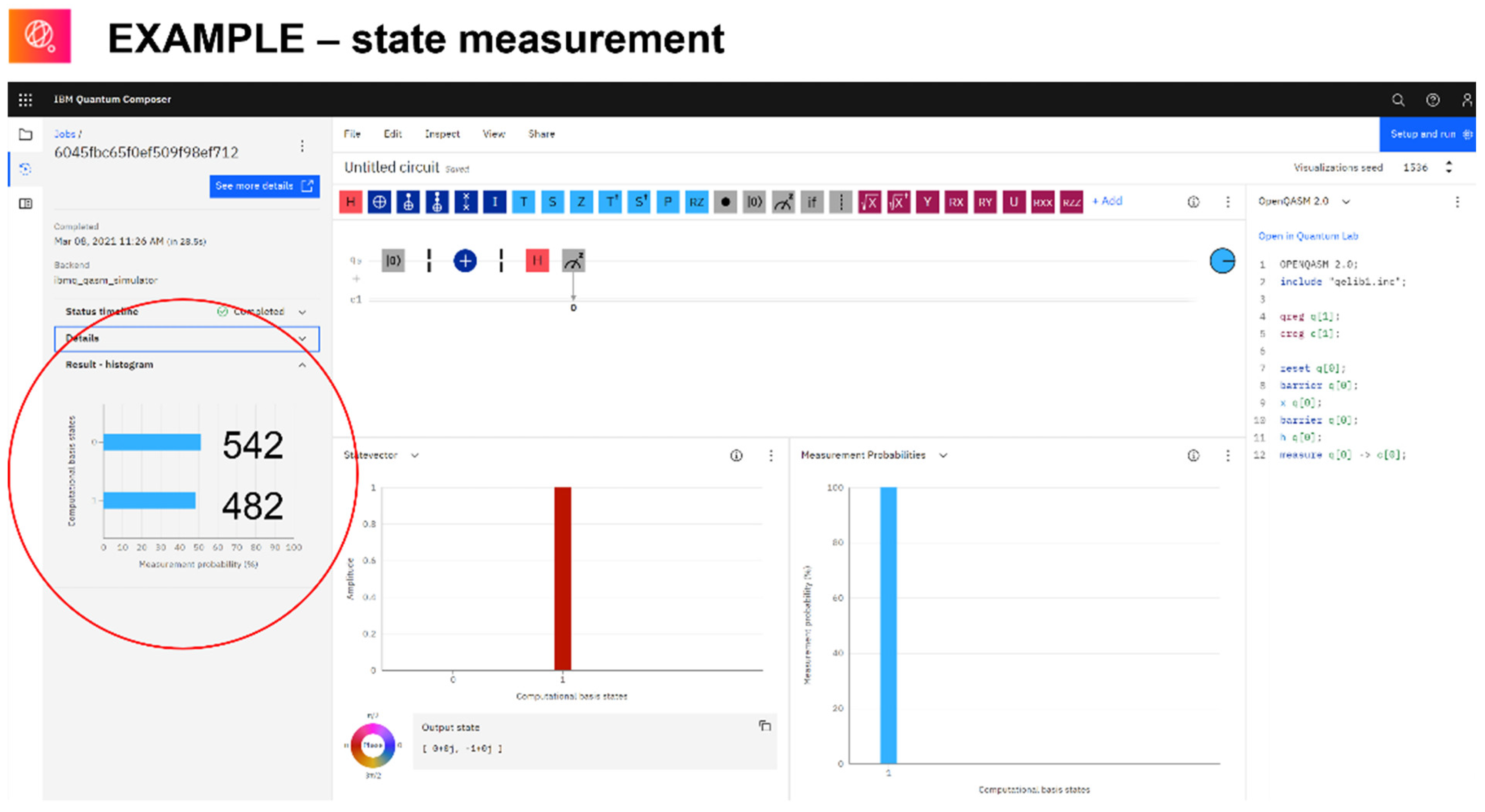
- Introduction to IBM Quantum experience
- again on the logic of H, NOT, Z, X, and exercises on IBMQ
- definition of coefficients of superposition states (probability amplitude), probability, and measurement
- 2.
- Stern–Gerlach experiment
- simulated experiments for sequences of Stern-Gerlach apparatuses performed using QuVis
- discussion on the logical necessity of describing the spin state of the electron as a superposition state
- 3.
- Experiments with QuVis
- difference between mixtures and superposition states
- sequence of three Stern–Gerlach apparatuses
- Lecture 3Objective: entanglementContent: separable and entangled states, correlated measurements
- 1.
- Introduction
- two-qubit states (basis elements, normalization)
- difference between entangled state and separable state
- measurement of single qubits in many-qubit states
- Bell states: invariance upon basis rotation
- reprise of Stern–Gerlach experiments to discuss the value of reality to be attributed to the variables
- 2.
- IBMQ interlude
- quantum circuit to generate entangled states
- 3.
- Application of entanglement
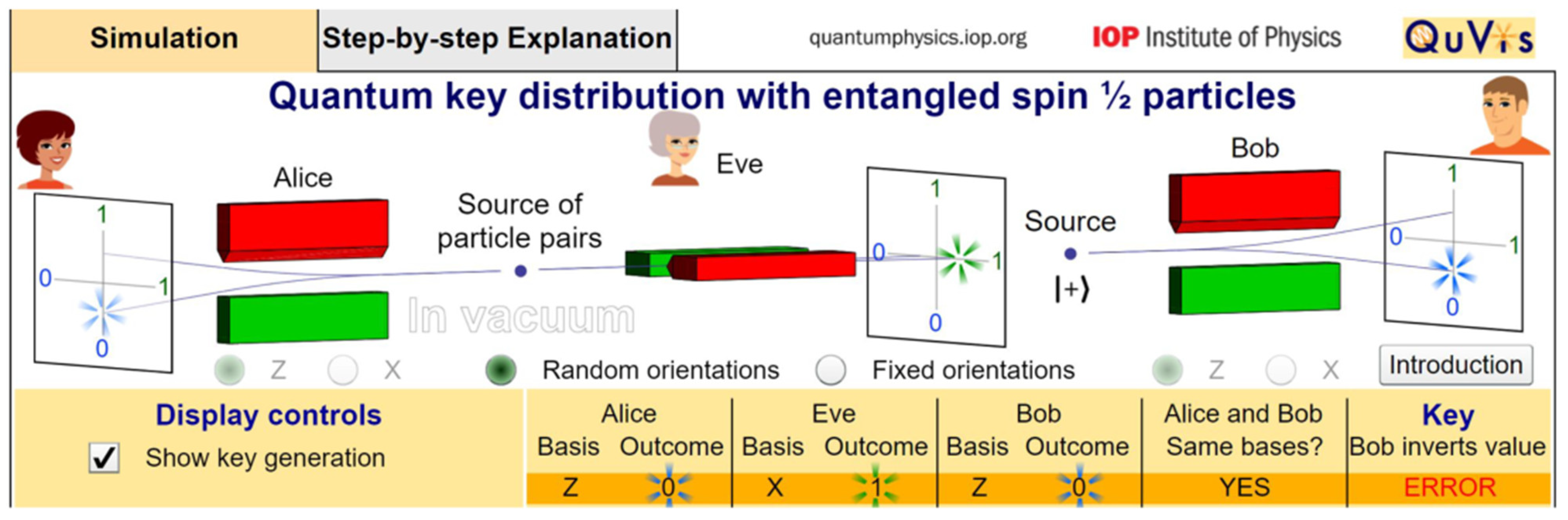
- QuVis: cryptographic protocol BBM92
- 4.
- Historical contextualization
- Einstein-Podolsky-Rosen (EPR) paradox (Schrödinger’s cat): locality and realism
- Bell’s inequalities: classical correlations vs entanglement
- QuVis: cryptographic protocol BBM92
- Lecture 4Objective: synthesis of concepts and formalismContent: axiomatic conceptual framework of quantum mechanics, interpretative problems
- 1.
- Summary of the concepts discussed in the previous lectures
- highlight the connections among the concepts
- introduce concepts intentionally not mentioned in the lectures but that the students will encounter in their course of study: uncertainty principle, wave function, dualism
- 2.
- Interpretative problems in quantum mechanics
- EPR paradox
- Bell’s inequalities
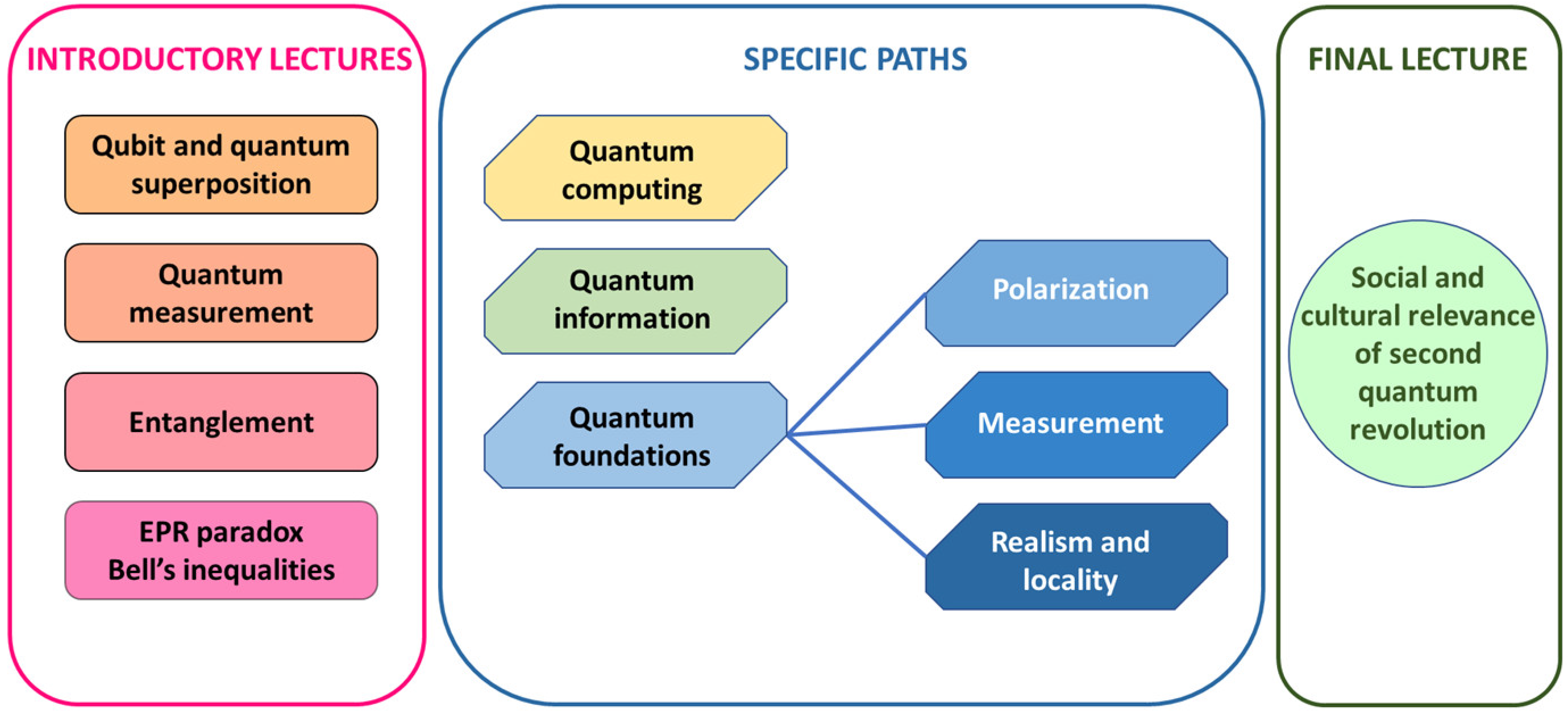
Appendix A.2. Specific Paths
- Quantum computing (Figure A1)
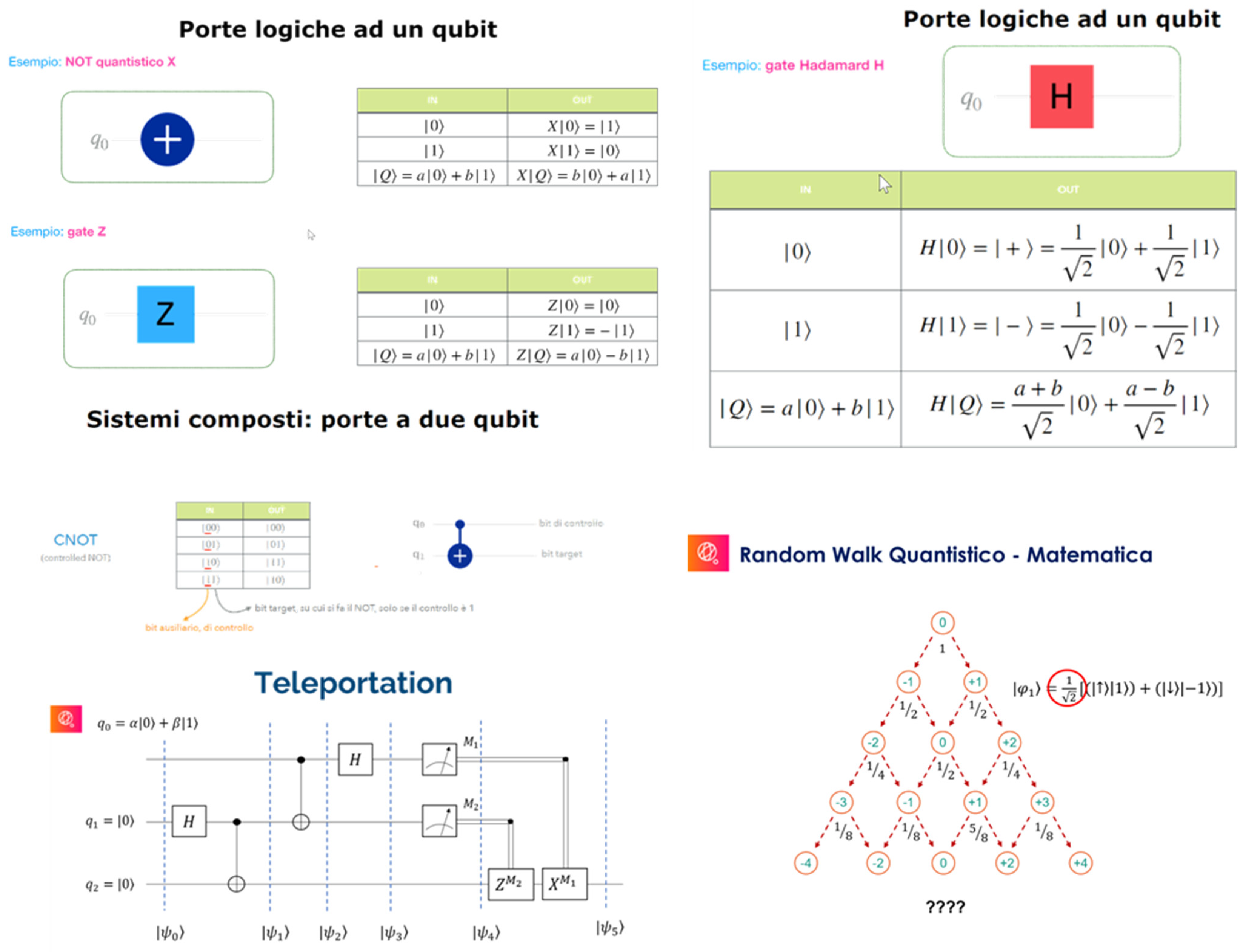
- Quantum information (Figure A2)

- Fundamentals: Polarization (Figure A3)

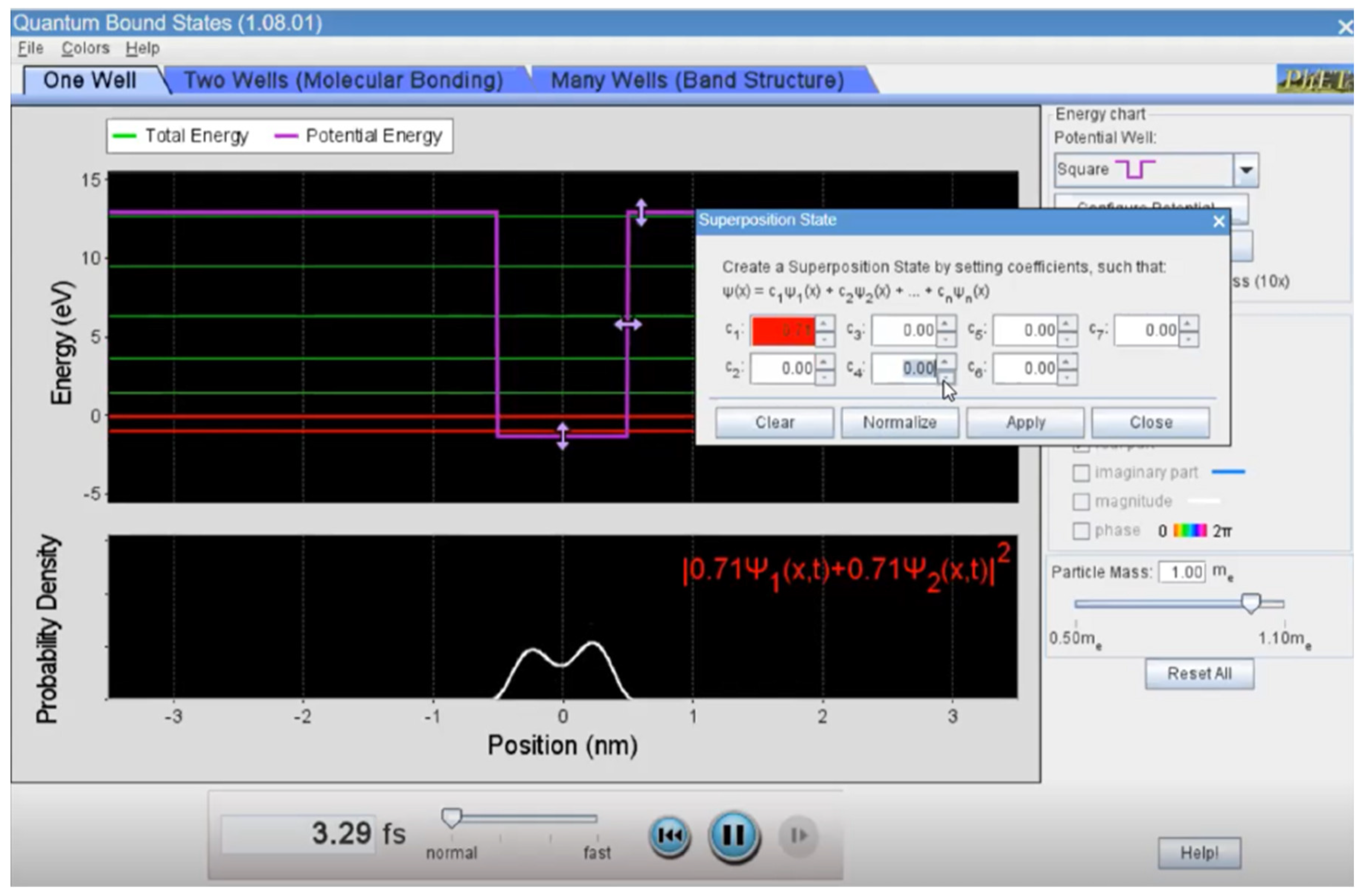
- Fundamentals: Measurement Paradox (Figure A4)
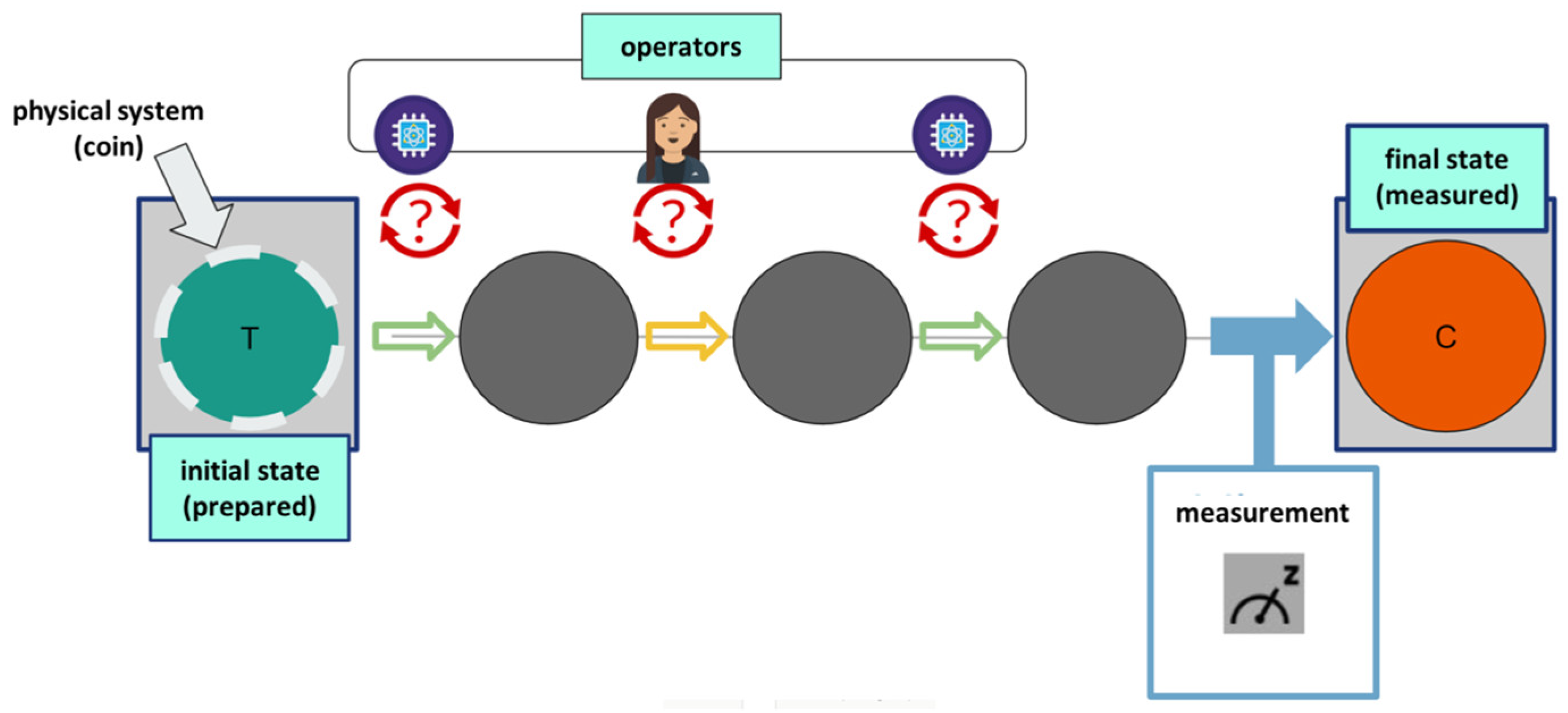
- Fundamentals: Realism and Locality (Figure A5)

Appendix A.3. Final Lecture (Figure A6)

Appendix B. Quantum-Technologies (QT) Questionnaire
- (a)
- Yes. Knowing how the transformation changes the initial state, the final state is uniquely determined (20%)
- (b)
- No. You could get different states because the transformation might not end up on a well-defined state |0〉 or |1〉 but on an intermediate state (36%)
- (c)
- No, because I can obtain states with different probability defined by the superposition coefficients (39%)
- (d)
- Yes, the state remains the same regardless the transformation (3%)
- (a)
- the outcome of any measure on the system with certainty (7%)
- (b)
- the outcome of a single measurement of any observable within the limits set by the uncertainty principle (30%)
- (c)
- the probability of different outcomes of any given measure on the system (53%)
- (d)
- the state a system after any measurement process with certainty (9%)
- (a)
- The state of the single qubit |Q〉 is |0〉 with probability p0 = |a|2 or |1〉 with probability p1 = |b|2 (52%)
- (b)
- The state of the single qubit |Q〉 is different from both |0〉 and |1〉 (15%)
- (c)
- The state of the single qubit |Q〉 is both |0〉 and |1〉 (18%)
- (d)
- The state of the single qubit |Q〉 oscillates between |0〉 and |1〉 (13%)
- (a)
- |Ψ1〉 is separable (can be factorized), |Ψ2〉 is entangled (17%)
- (b)
- |Ψ2〉 is separable (can be factorized), |Ψ1〉 is entangled (40%)
- (c)
- Both states are separable (can be factorized) (16%)
- (d)
- Both states are entangled states (22%)
- (a)
- The same measurement made on system B gives the same result (14%)
- (b)
- The same measurement made on system B gives the opposite result (19%)
- (c)
- We will be able to predict with certainty the outcome of any measurement made on system B (15%)
- (d)
- We will be able to predict with certainty the outcome of the same measurement made on system B (51%)
- (a)
- In prediction (1), we do not know the initial conditions precisely enough. In prediction (2) even if the initial conditions are known, the outcome of the interaction is inherently uncertain. (31%)
- (b)
- In both predictions, we do not know the initial conditions precisely enough (10%)
- (c)
- In prediction (1), we do not know the initial conditions precisely enough. In prediction (2) even if the initial conditions are known, we do not know how the interaction works precisely enough (23%)
- (d)
- To be able to make non-probabilistic predictions, in both cases we would need to have perfect control of the experiment, which is not currently possible (33%)
- (a)
- it had no defined value (38%)
- (b)
- it was ↑ already, but the experimenter didn’t know (22%)
- (c)
- it was zero (11%)
- (d)
- it was ↓ the 50% of the time and ↑ the 50% of the time (27%)
- (a)
- the outcome of a measurement is always unpredictable (9%)
- (b)
- the outcome of a measurement is always predictable (5%)
- (c)
- the outcome of a measurement is predictable with certainty when the process of preparation and of measure are related to the same observable of the system (32%)
- (d)
- the outcome of the measurement process is always predictable only in terms of the probability of outcomes and never with certainty (54%)
References
- Fox, M.F.; Zwickl, B.M.; Lewandowski, H.J. Preparing for the quantum revolution: What is the role of higher education? Phys. Rev. Phys. Educ. Res. 2020, 16, 020131. [Google Scholar] [CrossRef]
- H.R.6227―National Quantum Initiative Act. Available online: https://www.congress.gov/bill/115th-congress/house-bill/6227 (accessed on 1 September 2022).
- Raymer, M.G.; Monroe, C. The US National Quantum Initiative. Quant. Sci. Technol. 2019, 4, 020504. [Google Scholar] [CrossRef]
- Riedel, M.; Kovacs, M.; Zoller, P.; Mlynek, J.; Calarco, T. Europe’s Quantum Flagship Initiative. Quant. Sci. Technol. 2019, 4, 020501. [Google Scholar] [CrossRef]
- Ayene, M.; Kriek, J.; Damtie, B. Wave-particle duality and uncertainty principle: Phenomenographic categories of description of tertiary physics students’ depictions. Phys. Rev. ST-PER 2011, 7, 020113. [Google Scholar] [CrossRef]
- Ke, J.-L.; Monk, M.; Duschl, R. Learning introductory quantum physics: Sensori-motor experiences and mental models. Int. J. Sci. Educ. 2005, 27, 1571–1594. [Google Scholar] [CrossRef]
- Johnston, I.D.; Crawford, K.; Fletcher, P.R. Student difficulties in learning quantum mechanics. Int. J. Sci. Educ. 1998, 20, 427–446. [Google Scholar] [CrossRef]
- Manilla, K.; Koponen, I.T.; Niskanen, J.A. Building a picture of students’ conceptions of wave- and particle-like properties of quantum entities. Eur. J. Phys. 2002, 23, 45–53. [Google Scholar] [CrossRef]
- Tsaparlis, G.; Papaphotis, G. Quantum-chemical concepts: Are they suitable for secondary students? High-school students’ conceptual difficulties and attempts at conceptual change: The case of basic quantum chemical concepts. Chem. Educ. Res. Pract. Eur. 2002, 3, 129–144. [Google Scholar] [CrossRef]
- Tsaparlis, G.; Papaphotis, G. High-school students’ conceptual difficulties and attempts at conceptual change: The case of basic quantum chemical concepts. Int. J. Sci. Educ. 2009, 31, 895–930. [Google Scholar] [CrossRef]
- Marshman, E.; Singh, C. Framework for understanding the patterns of student difficulties in quantum mechanics. Phys. Rev. ST Phys. Educ. Res. 2015, 11, 020119. [Google Scholar] [CrossRef] [Green Version]
- Krijtenburg-Lewerissa, K.; Pol, H.J.; Brinkman, A.; van Joolingen, W.R. Insights into teaching quantum mechanics in secondary and lower undergraduate education. Phys. Rev. Phys. Educ. Res. 2017, 13, 010109. [Google Scholar] [CrossRef]
- Singh, C.; Marshman, E. Review of student difficulties in upper-level quantum. Phys. Rev. ST Phys. Educ. Res. 2015, 11, 020117. [Google Scholar] [CrossRef]
- Kalkanis, G.; Hadzidaki, P.; Stavrou, D. An instructional model for a radical conceptual change towards quantum mechanics concepts. Sci. Educ. 2003, 87, 257–280. [Google Scholar] [CrossRef]
- Bouchée, T.; de Putter-Smits, L.; Thurlings, M.; Pepin, B. Towards a better understanding of conceptual difficulties in introductory quantum physics courses. Stud. Sci. Educ. 2022, 58, 183–202. [Google Scholar] [CrossRef]
- Stefani, C.; Tsaparlis, G. Students’ levels of explanations, models, and misconceptions in basic quantum chemistry: A phenomenographic study. J. Res. Sci. Teach. 2009, 46, 520–536. [Google Scholar] [CrossRef]
- Satanassi, S. The challenge of Quantum Manifesto for science education: Designing a teaching module on quantum computers for secondary school students. II Nuovo Cim. 2020, 43, 130. [Google Scholar] [CrossRef]
- Mermin, N.D. Quantum Computer Science—An Introduction; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar] [CrossRef]
- Satanassi, S.; Fantini, P.; Spada, R.; Levrini, O. Quantum Computing for high school: An approach to interdisciplinary in STEM for teaching. J. Phys. Conf. Ser. 2019, 1929, 012053. [Google Scholar] [CrossRef]
- Satanassi, S.; Ercolessi, E.; Levrini, O. Designing and implementing materials on quantum computing for secondary school students: The case of teleportation. Phys. Rev. Phys. Educ. Res. 2022, 18, 010122. [Google Scholar] [CrossRef]
- IBM Quantum. Available online: https://quantum-computing.ibm.com/ (accessed on 1 September 2022).
- Sakurai, J.-J.; Napolitano, J. Modern Quantum Mechanics; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar] [CrossRef]
- Uncertainty of Spin Measurement Outcomes. Available online: https://www.st-andrews.ac.uk/physics/quvis/simulations_html5/sims/MeasurementUncertainty/measurement-outcome-uncertainty.html (accessed on 1 September 2020).
- Bell, J.S. Speakable and Unspeakable in Quantum Mechanics; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar] [CrossRef]
- La Seconda Rivoluzione Quantistica: Presente e Futuro Delle Tecnologie Quantistiche. Available online: https://www.youtube.com/watch?v=_LoWS0MBTu8&t=448s (accessed on 1 September 2022).
- Michelini, M.; Zuccarini, G. University students’ reasoning on physical information encoded in quantum state at a point in time. In Proceedings of the 2014 Physics Education Research Conference, Minneapolis, MN, USA, 30–31 July 2014; pp. 187–190. [Google Scholar] [CrossRef]
- Michelini, M.; Stefanel, A. A path to build basic Quantum Mechanics ideas in the context of light polarization and learning outcomes of secondary students. J. Phys. Conf. Ser. 2021, 1929, 012052. [Google Scholar] [CrossRef]
- Scotti di Uccio, U.; Colantonio, A.; Galano, S.; Marzoli, I.; Trani, F.; Testa, I. Design and validation of a two-tier questionnaire on basic aspects in quantum mechanics. Phys. Rev. Phys. Educ. Res. 2019, 15, 010137. [Google Scholar] [CrossRef]
- Zuccarini, G. Analyzing the structure of basic quantum knowledge for instruction. Am. J. Phys. 2020, 88, 385–394. [Google Scholar] [CrossRef]
- Chiou, G.-L.; Lee, M.-H.; Tsai, C.-C. High school students’ approaches to learning physics with relationship to epistemic views on physics and conceptions of learning physics. Res. Sci. Technol. Ed. 2013, 31, 1–15. [Google Scholar] [CrossRef]
- Field, A. Discovering Stastitics Using IBM SPSS Statistics; SAGE Publications: London, UK, 2013. [Google Scholar]
- Italian Quantum Weeks. Available online: https://www.quantumweeks.it/ (accessed on 1 September 2022).
- MILQ―Teaching Quantum Physics. Available online: https://www.milq.info/en/ (accessed on 1 September 2022).


| Concept | Sub-Topic | Item |
|---|---|---|
| State | Bra-Ket Formalism | Q3 Q4 Q7 |
| State and eigenstate in quantum physics | Q1 Q2 Q3 | |
| Logical gate | Q1 | |
| Qubit | Q3 | |
| Superposition | Q1 Q7 | |
| Measurement | Statistical nature of the measurement | Q2 Q6 Q8 |
| Wave function collapse | Q7 | |
| Entanglement | Formalism | Q4 |
| measurement on entangled states | Q5 |
| Answer Choice | Q1 | Q2 | Q3 | Q4 | Q5 | Q6 | Q7 | Q8 |
|---|---|---|---|---|---|---|---|---|
| A | 20% | 7% | 52% | 17% | 14% | 31% | 38% | 9% |
| B | 36% | 30% | 15% | 40% | 18% | 10% | 22% | 5% |
| C | 39% | 53% | 18% | 16% | 15% | 23% | 11% | 32% |
| D | 3% | 9% | 13% | 22% | 51% | 33% | 27% | 55% |
| No answer | 1% | 1% | 2% | 4% | 3% | 3% | 2% | 1% |
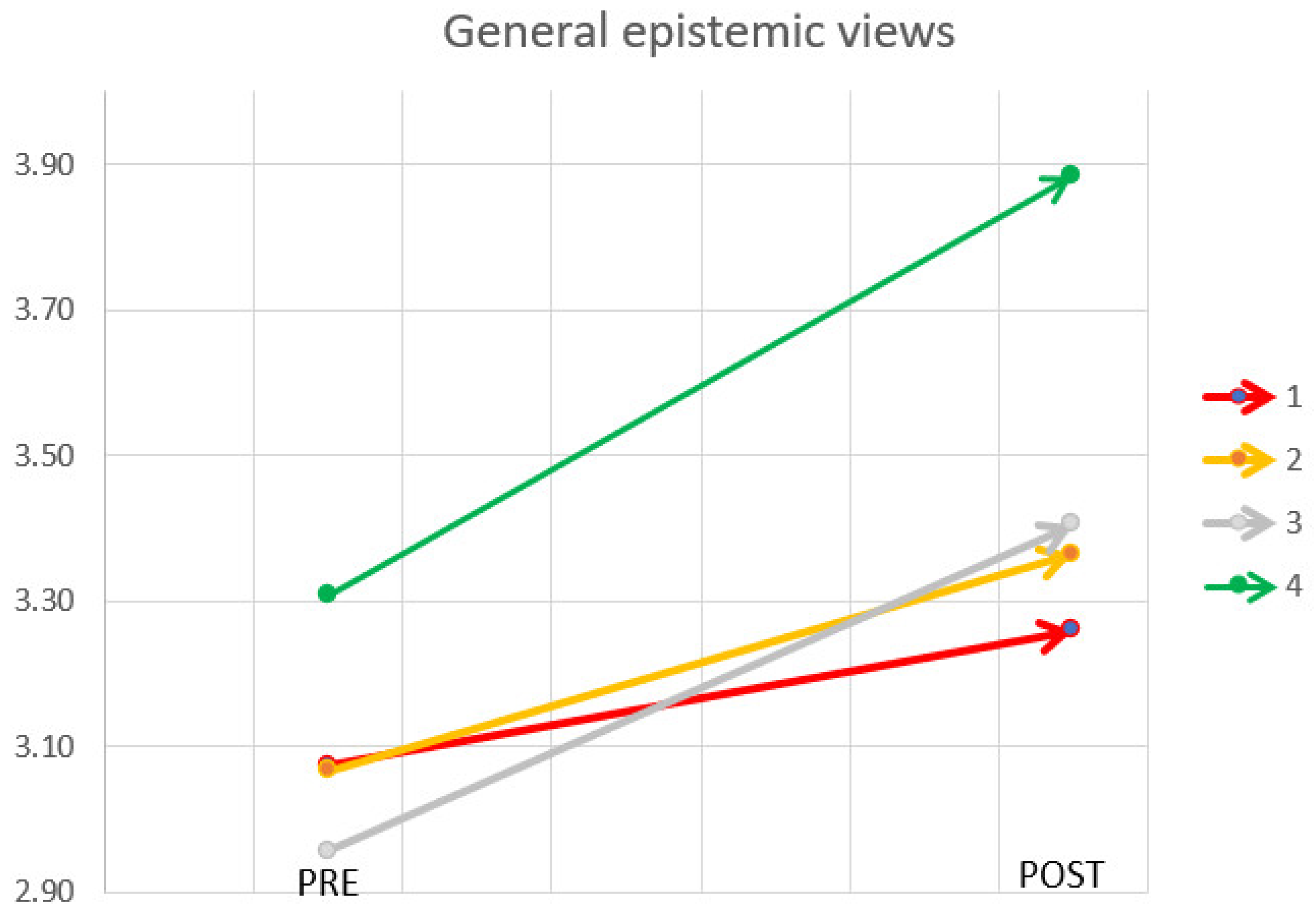
| Group | QTI Score | Number of Students (N = 162) | Cohen’s d | |
|---|---|---|---|---|
| General epistemic views | QT applications | |||
| G1 | 0–3 | 25 | 0.23 | −0.14 |
| G2 | 4–5 | 71 | 0.36 | 0.22 |
| G3 | 6–7 | 56 | 0.49 | 0.38 |
| G4 | 8–10 | 10 | 0.54 | 0.96 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bondani, M.; Chiofalo, M.L.; Ercolessi, E.; Macchiavello, C.; Malgieri, M.; Michelini, M.; Mishina, O.; Onorato, P.; Pallotta, F.; Satanassi, S.; et al. Introducing Quantum Technologies at Secondary School Level: Challenges and Potential Impact of an Online Extracurricular Course. Physics 2022, 4, 1150-1167. https://doi.org/10.3390/physics4040075
Bondani M, Chiofalo ML, Ercolessi E, Macchiavello C, Malgieri M, Michelini M, Mishina O, Onorato P, Pallotta F, Satanassi S, et al. Introducing Quantum Technologies at Secondary School Level: Challenges and Potential Impact of an Online Extracurricular Course. Physics. 2022; 4(4):1150-1167. https://doi.org/10.3390/physics4040075
Chicago/Turabian StyleBondani, Maria, Maria Luisa Chiofalo, Elisa Ercolessi, Chiara Macchiavello, Massimiliano Malgieri, Marisa Michelini, Oxana Mishina, Pasquale Onorato, Filippo Pallotta, Sara Satanassi, and et al. 2022. "Introducing Quantum Technologies at Secondary School Level: Challenges and Potential Impact of an Online Extracurricular Course" Physics 4, no. 4: 1150-1167. https://doi.org/10.3390/physics4040075
APA StyleBondani, M., Chiofalo, M. L., Ercolessi, E., Macchiavello, C., Malgieri, M., Michelini, M., Mishina, O., Onorato, P., Pallotta, F., Satanassi, S., Stefanel, A., Sutrini, C., Testa, I., & Zuccarini, G. (2022). Introducing Quantum Technologies at Secondary School Level: Challenges and Potential Impact of an Online Extracurricular Course. Physics, 4(4), 1150-1167. https://doi.org/10.3390/physics4040075










