Abstract
Quantum technologies have outgrown mere fundamental research in laboratories over recent years, and will facilitate more and more potentially disruptive applications in a wide range of fields in the future. In foresight, qualification opportunities need to be implemented in order to train qualified specialists, referred to as the future quantum workforce, in various fields. Universities world-wide have launched qualification programmes for engineers focusing on quantum optics and photonics. In many of these programmes, students attend courses on quantum physics contextualized via quantum optics experiments with heralded photons, because: (1) their experimental and physical foundations may be directly leveraged to teaching a number of quantum technology applications, and (2) physics education research has provided empirical evidence, according to which such quantum optics-based approaches are conducive to learning about quantum concepts. While many teachers are confident about the effectiveness of their concepts, there is little empirical evidence due to the lack of content-area-specific research tools. We present a 16-item concept inventory to assess students’ conceptual understanding of quantum optics concepts in the context of experiments with heralded photons adopted from a test instrument published in the literature. We have administered this Quantum Optics Concept Inventory as a post-test to students after instruction on quantum optics as part of an undergraduate engineering course. We evaluated the instruments’ psychometric quality, both in terms of classical test theory, and using a Rasch scaling approach. The Quantum Optics Concept Inventory enables a reliable measure (), and the data gathered show a good fit to the Rasch model. The students’ scores suggest that fundamental quantum effects pose striking learning hurdles to the engineering students. In contrast, most of the students are able to cope with the experimental and technical foundations of quantum optics experiments with heralded photons and their underlying principles, such as the coincidence technique used for the preparation of single-photon states. These findings are in accordance with prior research, and hence, the Quantum Optics Concept Inventory may serve as a fruitful starting point for future empirical research with regard to the education of the future quantum workforce.
1. Introduction
Quantum technologies have evolved dynamically in recent years [1]: From purely fundamental research in laboratories, they have increasingly moved toward potential disruptive applications in a wide range of fields until today [2,3]. To establish quantum technologies in future industry sustainably, it becomes necessary to train qualified specialists—the future quantum workforce [4], e.g., quantum engineers, since an increase in the “engineering talent flow [...] could vastly accelerate the development of quantum technologies” [5] (p. 3). According to [5] the term “quantum engineering” refers to the “application of engineering methods and principles to quantum information systems and problems” [5] (p. 3). Hence, qualification opportunities need to be implemented for this target group, both in terms of training at universities and in terms of training for professionals.
1.1. Educating the Future Quantum Workforce
Many initiatives have been implemented that aim at boosting the development of quantum ecosystems, and addressing the industry’s request for a quantum-literate workforce. A topical overview of the quantum workforce landscape is provided in Ref. [6]. For example, in the US, the Quantum Information Science and Technology Workforce Development National Strategic Plan [7] was set up, and with the National Q-12 Education Partnership, a consortium has been established with the aim of preparing “America’s next generation workforce with the tools to succeed in the industries of the future” [8]; see [9] for a comprehensive overview of Quantum Information Science courses at US institutions. In Europe, the Quantum Flagship [10] is flanked by the Coordination and Support Action for Quantum Technology Education (QTEdu CSA) [11], which aims at “bringing together quantum professionals from different walks of quantum education, research, and industry to help define the future of Europe’s quantum workforce as the second quantum revolution unfolds” [11]. With Canada’s National Quantum Strategy [12], the Sydney Quantum Academy in Australia [13], India’s National Mission on Quantum Technologies and Applications [14], or Singapore’s Quantum Engineering Program [15], similar efforts aimed at educating the future quantum workforce have been launched in other parts of the world.
In prior research, the industry needs for the future quantum workforce have been explored in different studies [16,17,18]. The results of such studies are essential for future efforts, since they may serve as a starting point for the development of target-group-specific educational programmes on quantum technologies, as has recently been shown with the development of a quantum engineering (undergraduate) programme presented in Ref. [5]. In the European context, a comprehensive Delphi study has been conducted within the QTEdu CSA, in order to collect quantum-specific competences that experts from academia and industry demand for the future quantum workforce [19,20]. The Delphi study results contributed to the development of the European Competence Framework for Quantum Technologies [21]. One prominent competence domain highlighted by the Competence Framework refers to quantum optics as a basis for quantum technologies, and closely related, its application in quantum photonics [21].
Quantum photonics and the underlying quantum optics fundamentals are highly relevant for almost all applications of quantum technologies, either as a core component of the application, e.g., in quantum imaging or quantum communication, or as an enabling technology [22]. Thus, quantum photonics are not limited to a specific application field. On the other hand, quantum photonics are the technology on the basis of which commercial applications can already be expected in the near future [2,22], e.g., in quantum sensor technology. For this reason, we believe that strengthening education in the field of quantum optics in (undergraduate) engineering programmes might have an impact on boosting developments in the field.
Different universities world-wide have already launched qualification programmes for engineering studies focusing on quantum optics and photonics [23,24,25,26]. Common are programmes that introduce students to the essential content domains of quantum physics via quantum optics fundamentals, most often starting from experiments with heralded photons (see [27]) for two main reasons:
- (1)
- The experimental and physical foundations of experiments with heralded photons may directly be leveraged to quantum technology applications within teaching scenarios, e.g., with regard to quantum computing [28], quantum metrology [29], or quantum information [30,31]. This content-specific argument is especially important with regard to undergraduate courses within study programmes for prospective quantum engineers.
- (2)
- Such experiments “provide the simplest method to date for demonstrating the essential mystery of quantum physics” [32] (p. 1), and “elegantly illustrate the fundamental concepts of quantum mechanics such as the wave-particle duality of a single photon, single-photon interference, and the probabilistic nature of quantum measurement” [33] (p. 1). Hence, such quantum optics-based approaches are likely to be conducive to circumvent widespread learning difficulties regarding quantum concepts, as has already been indicated by empirical results presented in Ref. [34].
1.2. Aim of This Study
Despite the above-mentioned advantages that potentially emerge from the integration of quantum optics courses with a focus on experiments with heralded photons into quantum engineering study programmes, no empirical results regarding the evaluation of such study programmes have been published in the literature so far. Not least, this is due to a lack of target-group- and content-domain-specific concept inventories that allow for the investigation of students’ learning progression. Therefore, the development of a concept inventory that can be used to inform instructors about engineering students’ mastery of quantum optics concepts constitutes a research desideratum to date. This is where this project comes in: We present a 16-item concept inventory to assess students’ conceptual understanding of quantum optics, with a focus on experiments with heralded photons on a qualitative level. We administered this Quantum Optics Concept Inventory as a post-test to students in the end of a four-week programme on quantum optics that is embedded into an undergraduate engineering course leading students from the basics of heralded photons experiments to the first insights into quantum technologies applications. Consequently, the objectives of the study presented in this paper are twofold: From a Rasch scaling approach, we
- (1)
- investigate as to how our concept inventory psychometrically functions on a sample of engineering students,
- (2)
- establish a difficulty scale regarding concepts covered by quantum optics experiments with heralded photons suggested by students’ scores on the concept inventory.
In Section 2, we provide insights into the research background regarding learning about quantum optics content domains, before the development of the Quantum Optics Concept Inventory for engineering students is sketched in Section 3. The research questions are formulated in Section 4, and, in Section 5, we outline the methodology employed in our study. The results obtained with regard to the research questions are given in Section 6, and finally, we discuss our findings against the backdrop of the literature in Section 7.
2. Research Background
In recent years, there has been an increase in the number of research projects aimed at introducing students of different levels and target groups to quantum physics, starting from a quantum optical perspective [32,35,36,37,38,39]. Although empirical research on teaching and learning quantum physics is gaining pace in general [40], there have been no empirical studies examining engineering students’ learning in such quantum optics courses to date. Contributing to closing this gap is a major goal of this study. In the next two Subsections, we present some results of research on the teaching and learning of quantum optics in secondary and undergraduate physics courses, in order to situate the study presented in this paper against the backdrop of the existing literature.
2.1. Assessment of Students’ Conceptual Understanding of Quantum Optics
Various concept inventories that allow for the assessment of students’ conceptual understanding of quantum physics have been published so far; a detailed overview of these concept tests aimed at the secondary school level or at the undergraduate physics level is given in Ref. [41]. These instruments either cover basic content domains of quantum physics (see [42,43,44,45]) or address aspects of the quantum formalism (see [46,47,48]).
The only test instrument on the introductory aspects of quantum optics is presented in Ref. [49]. This instrument consists of single-choice items, and has been developed in an iterative process, including different rounds of piloting. In terms of content, it covers both theoretical and experimental aspects of experiments with heralded photons. The content validity of the instrument has been ensured by means of an expert survey, and the tests’ psycometric properties have been analyzed in terms of classical test theory, based on data from undergraduate engineering students after instruction in introductory quantum optics. The test was found to enable a reliable measure (), and has good item statistics. This instrument serves as a starting point for the project presented in this paper: In Section 3, we describe how we adapted it for use on a sample of engineering students.
2.2. Students’ Conceptions on Quantum Optics Aspects
Two reviews provide a comprehensive overview of learning difficulties that students may encounter in quantum physics: one review focusing on secondary and lower elementary levels [41], and another one focusing on upper-level undergraduate students [50]. Currently, only a few studies with relatively small samples have been published exploring obstacles that students encounter with regards to quantum optics [33,51,52,53,54]. An exploratory interview study identifying students’ difficulties regarding different quantum optics content domains is reported in Ref. [55]. In [55], it was shown that (a) students are predominantly unprejudiced towards the experimental and technical foundations of quantum optics experiments, e.g., with regard to the preparation of single-photon states in experiments with heralded photons via coincident events on binary detectors, and that (b) most of the students can cope with the underlying principles [55]. These indications are also supported in further studies, e.g., exploiting the technique of probing acceptance [51]. In contrast, students specifically showed learning difficulties with regard to quantum effects and photons, which are in accordance with the findings from earlier studies into students’ difficulties with aspects of quantum physics (see, e.g., [56,57]), for example:
- a part of the learners interpret single-photon interference via photons that divide and then overlap with themselves [55] (p. 216);
- a part of the respondents equate photons with waves and conclude from this the necessity of observing interference phenomena [55] (p. 221);
- some learners claim that the photons’ localization would fail due to the small size of the photons [55] (p. 227);
- furthermore, a part of the participants believe that quantum anticorrelation at a beam splitter cube would be caused by photons behaving like haptical particles, being either reflected or transmitted [55] (p. 232).
With respect to the technical basics of quantum optics, learning difficulties regarding the detection of photons have been reported in the literature [51,58]: for example, a widespread misconception is that a pulse or click of a single-photon detector proves the detection of a single photon, but “this is not in agreement with the theory. A photo multiplier tube (PMT) or avalanche photo diode (APD) sends clicks, because engineers designed them to do so” [51] (p. 2).
For the development of the Quantum Optics Concept Inventory presented in this paper (see Section 3), we particularly referred to difficulties that students encounter with aspects of quantum optics that are documented in the literature, as presented in this subsection.
3. The Quantum Optics Concept Inventory for Engineering Students
We used the instrument described in Ref. [49], which is the result of a comprehensive process of development and piloting (described in Section 2), as a starting point for the development of our Quantum Optics Concept Inventory, focusing on qualitative aspects of experiments with heralded photons. We adopted the instrument for use in the primary target group of engineering students. Namely, we took two steps for the development:
- (1)
- we updated the existing items (and the corresponding distractors) from Ref. [49], in terms of language, and
- (2)
- beyond the content domains covered in the test of Ref. [49], namely (a) the theoretical and (b) the experimental basics of quantum optics, we developed new items to incorporate the thematic area of the technical basics of quantum optics experiments into the instrument, since we believe this content domain to be relevant to future quantum engineers.
In total, the Quantum Optics Concept Inventory consists of 16 single-choice items. In tier one, the participants are asked to select exactly one out of three answer options. In tier two, the participants are asked to rate their answer confidence on a five-point rating scale (1 stays for “I guessed”, 2 for “not sure”, 3 for “undecided”, 4 for “sure”, and 5 for “very sure”). A point is assigned if and only if the correct answer option was chosen in tier one, plus the respondent was at least sure with the response, meaning that a minimum of 4 was chosen on the confidence scale in tier two. Comparable confidence scales have previously been used for concept inventories, and they lead to the combination of two fundamental advantages [49,59,60,61]: On the one hand, the confidence scale
- (1)
- helps to minimize the effect of guessing, and hence, is “useful for gauging the quality of students’ understanding” [59] (p. 3); on the other hand,
- (2)
- it allows for the exploration of learning difficulties regarding the content area under investigation, namely by analyzing incorrect answers that were given confidently [62]. This point is postponed for the future research.
From a content-specific perspective, the Quantum Optics Concept Inventory aimed at engineering students is developed to test three content domains regarding quantum optics with heralded photons: technical-experimental foundations (domain 1), preparation of single-photon states (domain 2), and quantum effects (domain 3). Each domain is addressed by at least five items. An overview of the three content areas and the topics covered are given in Table 1.

Table 1.
Overview of the content domains covered in the Quantum Optics Concept Inventory, and the topics addressed with the related items. For a didactically prepared overview of the subject-specific topics represented in the test, e.g., the anticorrelation of single-photon states (see [18,51]). The list of items is given in Appendix A.
The content validity of the Quantum Optics Concept Inventory addressing the context of experiments with heralded photons was checked by means of an expert survey with faculty members [63]. For the investigation of further aspects of validity, in particular with regards to construct validity, we checked the fit of the data gathered in our study to a one-dimensional Rasch model. Therefore, we refer the reader to our methods and results in Section 5 and Section 6. Beyond that, we also describe reliablity issues in the results in Section 6.
4. Research Questions
The psychometric characterization of the Quantum Optics Concept Inventory (see Section 3) with respect to the primary target group of engineering students is the main goal of this study. Hence, the first research question (RQ1) to be addressed is:
- RQ1:
- How does the Quantum Optics Concept Inventory function on a sample of engineering students?
In the literature, qualitative approaches have been taken so far to explore difficulties that students encounter with quantum optics concepts (see Section 2). We have outlined findings from prior studies according to which students seem to be unprejudiced towards experiments with heralded photons, in particular, regarding the preparation of single-photon states, and most of the students can cope with the underlying principles. Conversely, quantum physical effects pose more difficulties to learners. Hence, to draw on earlier studies, and to shed new light on the difficulties that engineering students encounter with certain content aspects of quantum optics experiments with heralded photons using our concept inventory, we approach a clarification of the following second research question (RQ2) in this paper:
- RQ2:
- What difficulty scale of quantum optics content aspects is suggested by students’ scores on the concept inventory?
5. Methods
5.1. Test Administration and Sample
The Quantum Optics Concept Inventory used was administered to second-year engineering students (144 males, 68 females, 4 not specified) as a post-test after the students had participated in a four-week program about quantum optics with heralded photons. This four-week program was integrated in a regular introductory physics lecture for future engineers. In Section 5.2, a brief overview of the four-week intervention is given while in Appendix B, we provide an in-depth description of the educational pathway and the content aspects covered. None of the participants had any prior instruction in quantum physics beyond school physics.
The participation in our study was voluntary, and was not financially recompensed. In addition, the students were informed about anonymity, as well as about processing of their data, and were asked to give their consent to participate.
5.2. Intervention
The educational pathway of the four-week program was based on an introductory quantum optics course originally developed for the secondary school level as well as for the lower undergraduate levels, and is described in detail in [51]. For the purpose of this study, this concept was adapted in terms of content and depth—specifically, two important modifications dedicated to future engineers have been made to the original version [51] for the four-week program. Namely,
- (1)
- while the original teaching concept exclusively covered aspects of experiments with heralded photons qualitatively to make quantum effects accessible [51], during the course implemented in this study, the same topics were also covered on a formal level, as proposed in [64];
- (2)
- to conclude, the course implemented in this study provided future engineers with an outlook on quantum technologies, namely by dealing with quantum cryptography, e.g., the BB84 protocol with single-photons [65,66].
The four-week program was divided into two consecutive parts, and culminated in the discussion of the 1986 paper by Grangier et al. [67]. Hence, from a theoretical point of view, the program was based on the theory of optical coherence, which “investigates the properties of light in terms of correlation functions between two distinct fields or of a single field at different points in time and space” [68] (p. 144).
It is noteworthy that the development of a well-grounded proposal for educating the future quantum workforce is beyond the scope of this paper. However, to provide a deeper background of the intervention implemented in this study, we sketch the essential topics that were covered in the four-week quantum optics course, in Appendix B. We reflect on the role of the educational path for the results of this study in the limitation (see Section 8.1).
5.3. Data Analysis
In the following, we present the analysis tools incorporated into our research, bundled for each research question.
5.3.1. Analysis Carried out to Answer RQ1
In a first step, we provide a characterization of the instrument in the sense of classical test theory; i.e., Cronbach’s , as well as the items’ point-biserial coefficents and items difficulties are presented. Here, we refer to the accepted ranges of to for the item difficulty [69] and values 0.20 for the point-biserials [70]. For Cronbach’s , values above are considered as acceptable [71].
In a further step, the goal is to divorce statements regarding the concept inventory from the sample it was piloted with. This is enabled via dichotomous Rasch scaling. To justify this analysis, we investigated the pre-conditions of Rasch scaling (see [72]) by verifying that:
- the skewness and kurtosis of the items do not exceed the range of to ,
- the items are locally independent, and
- the uni-dimensionality of the construct can be assumed.
It is noteworthy that a verification of our instrument’s uni-dimensionality also supports construct validity [60].
After the pre-conditions of Rasch Scaling are met, the participants’ ability levels and the items’ difficulties are estimated. The goodness-of-fit parameters, Outfit mean-square (MNSQ) and Infit MNSQ, further describe how well the items fit the model—their expected value is 1; values below this indicate unmodeled noise, and values above this indicate redundancy, meaning that the respective item does not contribute much to estimating the participants’ latent trait levels [73]. The accepted ranges for these fit statistics are between and [74]. All parameters were calculated using the software R (Version 4.1.2) and its packages ltm (1.0-2) [75], TAM 4.0-16 [76], and eRm (1.0-2) [77].
5.3.2. Analysis Carried out to Answer RQ2
In our concept test, three quantum optics content domains are addressed with at least five items each (see Table 1). To compare the difficulties of the items related to each of these content domains, we calculated their average values, (in logits), and their uncertainties in terms of standard errors (SEs), as has been performed in prior studies [78].
Since the average difficulty of all items is set to zero in the Rasch modeling approach, item groups with negative average item difficulties are easier to solve for the sample students than the test average, whereas item groups with positive average item difficulties are more difficult than the test average.
6. Results
6.1. Psychometric Characterization
First, a distractor analysis was conducted, which revealed that for most of the items of our concept inventory, each answer option was selected by at least of the participants, which constitutes a widely used criterion in test development (see [49,60]). Next, we analyzed item difficulties and point-biserial coefficents in the sense of classical test theory (see Table 2). It can be observed that Cronbach’s increases only slightly when item 10 is omitted. The item difficulties and the point biserials show a reasonable range, overall.

Table 2.
Each item’s difficulty and point-biserial-coefficent, as well as the adjusted Cronbach’s if the respective item is dropped. See text for details.
A dichotomous Rasch model was justified by the data. Values of skewness and kurtosis are given in Table 3. Item 4 does not meet the criterion mentioned in Section 5; however, it was retained for content reasons, as we elaborate on in Section 7. Local independence was verified by checking the correlation matrix for values above [79,80]. Uni-dimensionality was confirmed using the R-package sirt (version 3.9-4), finding weighted indices (<0.20), (<0.25), and (<0.36) [81]. In summary, the pre-conditions of Rasch scaling were met.

Table 3.
Overview of the relevant parameters for a dichotomous Rasch Model; “SE” stands for the standard error of item difficulty. See text for details.
The “expected a posteriori/plausible value” (EAP/PV) reliability was found to be , and the “weighted likelihood estimates” (WLE) reliability was , exceeding the lower threshold of according to [74]. An overview of all the estimated parameters by the Rasch model is presented in Table 3. The values of the Infit MNSQ and Outfit MNSQ all lie in the accepted range indicating a good Rasch homogeneity. The Infit statistic varies between (item 3) and (item 10), with a mean value of . The Outfit statistic varies between (item 3) and (item 10), with a mean value of . A graphical representation of the findings is given in Figure 1.
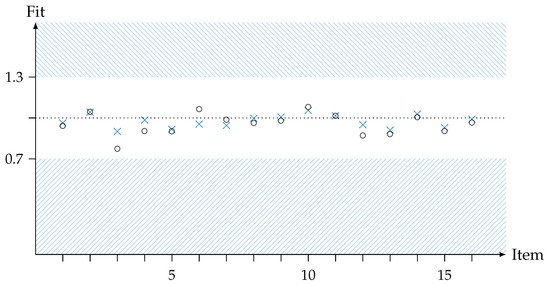
Figure 1.
Infit MNSQ (crosses) and Outfit MNSQ (circles) for all items of the concept inventory. See text for details.
The item difficulties may be investigated by visualizing their relationship to the solving probability. In this regard, each item can be described by a logit function, where the solving probability is plotted against the latent trait level on a continuous scale. The resulting graph of this function is characteristic for the item, and is thus called the item characteristic curve [74]. The curves are shown in Figure 2.
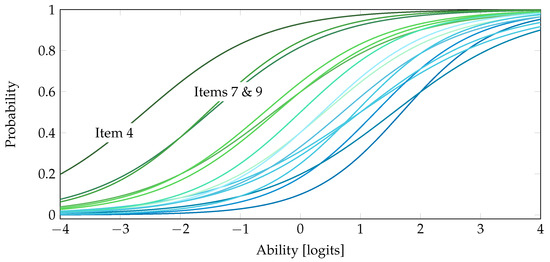
Figure 2.
Item characteristic curves (ICC) for all items of the concept inventory. While the blue, light-blue, and light-green curves correspond to items that show good fit to the Rasch model, the outliers, namely items 4, 7, and 9, can also be identified. This observation is further substantiated analyzing the Wright Map presented in Figure 3.
The item difficulty ranges from logits (item 4) to logits (item 1). More important, however, is how the items correspond to the latent trait levels within the sample. This connection is investigated in Figure 3 using a Wright Map. The Wright Map shows the distribution of item difficulty and respondent latent trait level on a common scale, and thus enables an assessment of how well the instrument is suited to measuring different areas of ability. For example, Figure 3 shows that in densely populated areas, the item density reacts accordingly, but in the upper end of the ability scale (≥2 logits), no item corresponds, meaning that our concept inventory is not suited to distinguishing between participants with very high trait levels. In other words, in the future, this concept inventory may be refined by developing at least one more difficult item.
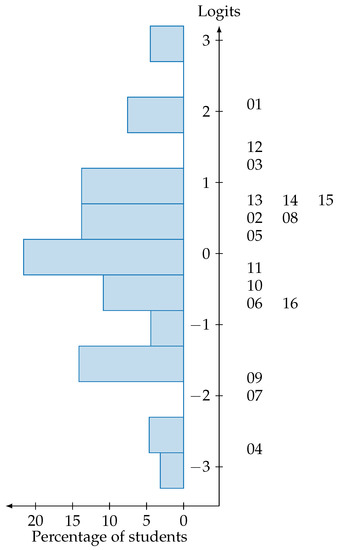
Figure 3.
Wright Map of our concept inventory. The left-hand side represent the frequency of respondents’ latent trait levels within the sample. The right-hand side represents a hierarchical order of all items along the logit scale.
In summary, the results presented in this Subsection may contribute to a clarification of the research question RQ1. We judge the overall psychometric quality of the Quantum Optics Concept Inventory and its functioning on our sample of engineering students in Section 7 below referring to the literature on concept inventories.
6.2. Difficulty Scale of Quantum Optics Concepts
The Rasch scaling of our concept inventory was further leveraged to investigate the mean difficulty of the different content domains covered in our diagnostic tool (see Table 1), as has been performed in prior research using concept inventories (see [82]).
The most difficult content domain appears to be domain 3 (quantum effects), with an average item difficulty of (, ), as is graphically shown in Figure 4. The next content domain according to difficulty is the domain 1 on technical and experimental foundations of quantum optics experiments with heralded photons (, ). This content domain, in total, appears to be slightly more difficult than the average. In contrast, the content domain 2 on the preparation of single-photon states (, ) lays well below the average difficulty, and hence, the corresponding items did not pose a problem for a majority of the students. In summary, these results allow for the establishment of a difficulty scale of quantum optics concepts with respect to experiments with heralded photons, and hence, they contribute to a clarification of research question RQ2.
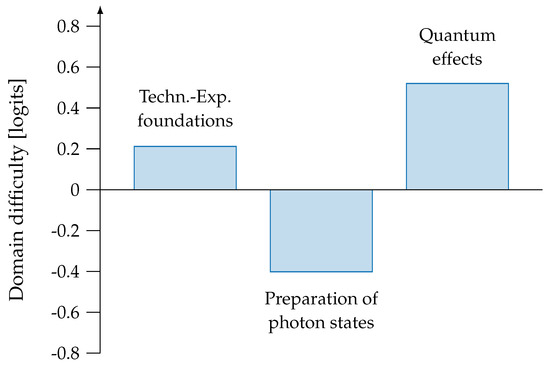
Figure 4.
Average difficulties of the quantum optics concepts, evaluated by our concept inventory, measured in logits.
In Section 7 just below, we discuss the observed differences between the three content domains covered in our concept inventory with regard to their average item difficulties. There, we provide evidence that the findings of our study are consistent with prior research, and derive implications for the future. Based on the results obtained, it is not possible to resolve statistically significant differences regarding the mean item difficulties on a level. This problem can be addressed by adding further items to the concept inventory covering the three content domains, respectively. This point is addressed in Section 8.1.
7. Discussion
7.1. Discussion of RQ1
From the standpoint of classical test theory, the item difficulties and point-biserials lie in the desired range for all items (except for item 4) and constitute a scale with good internal consistency expressed by Cronbach’s .
The Rasch analysis of the concept inventory showed a good degree of functioning for almost all test items. Only item 4 may be revisited due to its skewness and kurtosis values, even though it shows good fit statistics. The Wright Map (see Figure 3) illustrates how well the items can be ordered along the logit scale; they measure a conceptual understanding of quantum optics on different trait levels, and most items measure around the 0 logit area, which is most densely populated. We conclude that the test is well designed for the population that it is intended to be applied on. Merely for very high trait levels, at least one further item should be developed in the future. Additionally, one could make a case for also developing items in the region of about logits and about logits, as visual gaps can be observed both in the Wright Map, as well as in the overview of the item characteristic curves (see Figure 2). Further refinement to close this gap, and thus, to contribute to an overall continuous item difficulty distribution may result in a further refined concept inventory for quantum optics in engineering curricula.
In essence, only item 4 turned out to be problematic. It seemed too easy for our sample, from the perspective of classical test theory (item difficulty ). In addition, its high skewness and kurtosis suggest a deviation from the normal distribution. However, the Wright Map substantiates that items of such difficulty ( logits from the Rasch perspective) are in fact necessary, and no other item measures similarly at the lower end of the scale. Furthermore, item 4 is important for content reasons, since it is the only item of the instrument that asks for a differentiation between single-photon from further types of quanta, e.g., single electrons, in this case. The mix-up of photons and electrons, however, has been proven to be a learning obstacle to students in [83,84]. To this end, this item is to be retained in order to ensure content validity. Additionally, such outlier items are considered in a categorial judgement scheme provided in [70]. We use this judgement scheme to summarize the above discussed observations, allowing for a holistic judgement regarding all relevant concept inventory characteristics. In this regard, we follow Ref. [60], where this judgement scheme has been expanded to Rasch scaling parameters. The overall quality of our concept inventory is summarized in Table 4.

Table 4.
Categorial judgment scheme and assignment rules for evaluating a concept inventory according to [70]. Values in parenthesis indicate the number of items that can fall outside of this recommendation. The judgement of our concept inventory is presented in the last column labeled QOCI.
7.2. Discussion of RQ2
The Quantum Optics Concept Inventory is developed to test students’ conceptual understanding of quantum optics basics, with a focus on experiments with heralded photons focusing on three content domains, namely technical-experimental foundations (domain 1), the preparation of single-photon states (domain 2), and quantum effects (domain 3).
The data analysis presented in Section 6 revealed that the content domain 3 addressing quantum effects was the most challenging one for the study participants (average item difficulty, ). The content domain was covered by six items, three of which address single-photon interference (items 11, 12, and 13), and two of which focus on single-photons and the anticorrelation effect (items 14 and 16). Analyzing these items in more detail, two observations become striking.
- (1)
- The item difficulties of the items 12 ( logits), and 13 ( logits) both lay well above average—hence, single-photon interference obviously poses conceptual difficulties to the study participants. This observation is in accordance with prior research, and can be enriched by findings from various qualitative studies exploring student difficulties on the interference of single quanta [33,55].
- (2)
- Item 14, focusing on the anticorrelation effect of single-photon states at an optical beam splitter cube, has an item difficulty of logits. Hence, the concept that photons are either transmitted or reflected at a beam splitter cube seems to be difficult for students. This observation fits well with results presented in an earlier contribution [51], where the authors used a micro-intervention to explore students’ understanding of single-photons’ anticorrelation, using the technique of probing acceptance. Beyond that, this observation is particularly striking against the background of the finding described above regarding single-photon interference: while items 12 and 13 address the wave nature of photons, item 14 can be associated with a particle nature of photons. Hence, the three items represent one of the fundamental issues of quantum physics: wave-particle duality.
Taken together, the observations fit well with previous studies into students’ conceptual hurdles regarding the wave-particle duality of quantum entities (see [55,85,86]; for a review of studies on this topic, see [41]). In summary, it is not a surprise that in Ref. [87], the authors demand “a radical reconstruction” (p. 257) of learners’ initial knowledge when it comes to learning about quantum physics.
The items related to the content domain 1 on technical-experimental foundations had an average item difficulty of . The content domain is covered by five items of the concept inventory, which cover the whole logit scale regarding item difficulties, ranging from logits (item 4) at the lower end of the difficulty scale, to logits (item 1) at the upper end. While the more difficult items of this content domain (item 1, with logits, and item 2, with logits) cover experimental aspects, e.g., the use of beam splitter cubes (item 1) or the adjustment of optical experiments (item 2), the other items covering technical aspects appear to have low-to-average item difficulties ( logits for item 4, logits for item 5, and logits for item 8).
Finally, the items related to the content domain 2 on the preparation of single-photon states had an average item difficulty of , and hence, were easier than average. This observation is in accordance to the results of prior (qualitative) studies, which revealed that students can predominantly cope well with the basic ideas underlying the preparation of single-photon states in experiments with heralded photons via coincident events on binary detectors [51,55]. To this end, we believe that the results obtained provide a further argument in favor of using the experimental setting of heralded photons as a gateway towards quantum effects in teaching quantum physics. The easiest items related to this content domain were items 6 ( logits) and 7 ( logits), addressing the concept of energy levels and energy conservation in the context of nonlinear optics. In contrast, the most difficult, item 3 ( logits), referred to parametric downconversion (PDC), a nonlinear effect leading to the emission of photon pairs from a nonlinear crystal irradiated by a laser at a certain wavelength. An in-depth analysis of the students’ response behavior on the answer options of item 3 shows that the students tend to conceptually mess up PDC with reflection and diffraction from geometrical optics.
8. Conclusions
We presented a 16-item Quantum Optics Concept Inventory aimed at assessing engineering students’ conceptual understandings of the fundamental aspects of quantum optics experiments with heralded photons. This tool has been adopted from an instrument previously published elsewhere [49]. We added items related to the technical aspects of single-photon experiments, e.g., addressing single-photon detection, making it a valuable tool for evaluating teaching-learning scenarios.
- aimed at engineering university students, and
- designed to introduce these students to quantum physics and modern quantum technologies via quantum optics experiments with heralded photons.
8.1. Limitations
There are some limitations of our study that may serve as a springboard for future research. These limitations either stem from the study design itself (Section 8.1.1), or are related to the concept inventory evaluated in this study (Section 8.1.2).
8.1.1. Limitations of this Study
Without a doubt, the evaluation of the Quantum Optics Concept Inventory presented in this paper is—at least to some extent—dependent on the quantum optics instruction that the study participants had received prior to test administration. This a known concern in educational research in general [88]—especially when it comes to piloting novel assessment tools. However, in the current study, this issue was mitigated by means of Rasch scaling utilized for the psychometric characterization of the Quantum Optics Concept Inventory, since the Rasch model permits the separation of person and item parameters [89].
Against the backdrop of the above argumentation, it becomes apparent that the difficulty scale of quantum optics concepts established on the basis of the participants’ test results (see Section 6.2) should not be confused with statements about the perceived difficulty of quantum optics topics. Rather, this difficulty scale should be understood to shed more light on (a) the items of the Quantum Optics Concept Inventory, and (b) on possible learning difficulties that might pose obstacles to student learning in the context of introductory quantum optics (see Section 7.2). Taken together, the results presented in this study may not only lead to a revision of the Quantum Optics Concept Inventory, but they might also initiate the refinement of the four-week program implemented in a lecture for future engineers in the course of this study.
8.1.2. Limitations Related to the Quantum Optics Concept Inventory
We merged the viewpoints of classical test theory with those of probabilistic test theory to provide a psychometric characterization of the Quantum Optics Concept Inventory. Based on the data gathered from engineering students who took the Quantum Optics Concept Inventory as a post-test after instruction, we found our instrument to exhibit average-to-excellent psychometric properties following the categorical judgment scheme for evaluating a concept inventory of Ref. [70]. In particular, the Rasch analysis results revealed that the items discriminate well among students from lower to medium–high competence levels (see Figure 3). However, the items do not manage to discriminate well between students at the upper end of the ability scale. Hence, in order to refine our instrument accordingly, items with a higher difficulty should be added.
Analyzing the data in more detail with respect to the content domains covered in our inventory (see Table 1), findings from prior research could be replicated, adding further evidence for the functioning of our concept inventory: The average item difficulty for the items related to the content domain 3 on quantum effects lies well above the average. Specifically, we found that items addressing different aspects of wave-particle duality, i.e., items 12, 13, and 14, covering single-photon interference and the anticorrelation of single-photon states, were found at the upper end of the difficulty scale. This is consistent with the wave-particle duality posing several conceptual hurdles to learners from different target groups, as is well documented in the literature [41]. However, more differentiated statements on student conceptions, especially regarding quantum optics concepts, are difficult to make with the current version of our concept inventory: since for now, all topics are covered with only two or three items each, further items would be required in order to allow for a more comprehensive insight into students’ conceptions regarding the respective isolated topics. In contrast, the brevity of our concept inventory allows for economic practical use aimed at the evaluation of teaching–learning environments. Against this backdrop, the creation of additional items is always to be considered carefully, in order to maintain the practical applicability of the instrument.
Finally, at the qualitative level, an important limitation must be considered, which stems from the fact that the items of the Quantum Optics Concept Inventory represent a compromise of the following criteria:
- (i)
- intelligible wording,
- (ii)
- coverage of overarching concepts of quantum optics in the heralded photon realm, rather than addressing all the details of a topic,
- (iii)
- subject-specific correctness.
Item 7 of the Quantum Optics Concept Inventory (see Appendix A), which deals with PDC, may serve as a prime example of this tradeoff: While PDC photons in general have different frequencies, in this item, we focus on the particular situation where the two PDC photons have equal frequencies. Hence, this item is intended to evaluate whether students have understood that energy is conserved in the PDC process. In contrast, assessing students’ conceptual understanding of details of phasematching conditions is outside the scope of this item (see bullet 2 in the above list). Again, developing additional items that cover further topics and aspects related to quantum optics experiments with heralded photons could help alleviate the constraints imposed by the aforementioned compromise.
8.2. Outlook
In the future, standardized feedback formats need to be established, such that outcomes can easily be communicated to various stakeholders, e.g., to teachers or to their students [90]. For this purpose, instead of presenting statistics based on raw test values, feedback formats that map the distribution of student performance on categorically graded levels of proficiency are required. Future studies may draw on the determination of such levels of proficiency with respect to the content area under investigation, in order to describe (and predict) students’ learning progressions [91].
The number of proficiency levels regarding quantum optics experiments with heralded photons that can be empirically separated using our concept inventory depends on the person separation reliability of our concept inventory. According to [92], the person seperation reliability, s, can be used to calculate the G-value,
which allows for the determination of the number of empirically separable proficiency levels via
Here, is the closest integer; for details, see [74]. For the Quantum Optics Concept Inventory under investigation, we obtained , and hence, , meaning that it allows us to differentiate between
proficiency levels among engineering students. After a revision of our instrument to tackle the above-mentioned weaknesses, future research will address the definition of the proficiency levels regarding quantum optics experiments with heralded photons based on data from larger samples.
Author Contributions
Conceptualization, all authors; methodology, all authors; formal analysis, all authors; investigation, all authors; writing—original draft preparation, all authors; writing—review and editing, all authors; visualization, all authors. All authors have read and agreed to the published version of the manuscript.
Funding
We acknowledge financial support by Deutsche Forschungsgemeinschaft and Friedrich-Alexander-Universität Erlangen-Nürnberg within the funding programme “Open Access Publication Funding”.
Institutional Review Board Statement
Ethical review and approval were waived for this study, due to the fact that the study was in accordance with the Local Legislation and Institutional Requirements: Research Funding Principles (https://www.dfg.de/en/research_funding/principles_dfg_funding/research_data/index.html, (accessed on 15 September 2022)), and General Data Protection Regulation (https://www.datenschutz-grundverordnung.eu/wp-content/uploads/2016/04/CONSIL_ST_5419_2016_INIT_EN_TXT.pdf (accessed on 15 September 2022)).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study to publish this paper.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. The Quantum Optics Concept Inventory
(The correct answer option is marked by an asterisk.)
Item 1. A beam splitter
- (a)
- is employed in the Michelson interferometer, because it can be used to split an incident ray of light into two partial beams.
- (b)
- is made out of two merged prisms, where one of them is responsible for the transmitted beam and one for the reflected beam.
- *(c)
- separates incident rays of light or superimposes two rays of light.
Item 2. To precisely adjust a laser beam along a specific straight line on a breadboard in a quantum optics experiment,
- (a)
- two mirrors can be used to deflect the laser on this line.
- *(b)
- two apertures can be used to define two points laying on this line.
- (c)
- two lenses can be used to focus the laser beam on this line.
Item 3. If a non-linear crystal is irradiated by laser light, then,
- *(a)
- light is emitted by the crystal.
- (b)
- the laser beam is divided in two beams.
- (c)
- diffraction leads to laser light forming a cone after passing the crystal.
Item 4. Experiments with heralded photons differ from experiments with single electrons, because:
- (a)
- electrons are bigger than photons, leading to technical difficulties.
- (b)
- conducting the double-slit experiment one after the other with single electrons does not lead to an interference pattern.
- *(c)
- experiments with single electrons require a vacuum.
Item 5. The human eye may not be used as a detector for single photons, because:
- *(a)
- the intensity of the light falling on the eye in the single-photon regime ist too low.
- (b)
- the eye can only perceive light at specific wavelengths, but not those of single photons.
- (c)
- the photons are too small to be resolved with human eyes.
Item 6. If an electron transitions from an energy state to an energy state , light is emitted. The bigger the energy difference, , (adopted from [43])
- (a)
- the more photons are emitted.
- (b)
- the longer the wavelength of the emitted light.
- *(c)
- the shorter the wavelength of the emitted light.
Item 7. When irradiated with laser light at a certain wavelength, parametric downconversion can be driven in a nonlinear crystal. This process leads to the emission of photon pairs. Both photons have
- (a)
- half the wavelength of the incident laser light.
- (b)
- the same wavelength of the incident light of the laser.
- *(c)
- double the wavelength of the incident light of the laser.
Item 8. Avalanche photodiodes used for single-photon detection
- (a)
- count the number of registered photons within a certain time interval.
- *(b)
- lead to electron avalanches when some kind of energy portion is registered.
- (c)
- point to the detection of a single-photon with each click.
Item 9. Coincident events measured at avalanche photodiodes in experiments with heralded photons
- *(a)
- mark simultaneous clicks at two or more detectors.
- (b)
- represent a measure of the detectors’ dark count rate.
- (c)
- can each be associated with the detection of a single-photon state.
Item 10. The coincidence technique is used in experiments with heralded photons
- (a)
- to show that photons are physical entities with finite size.
- (b)
- in order to experiment with two single-photons simultaneously.
- *(c)
- for single-photon detections.
Item 11. When the double-slit experiment is repeatedly performed with only one single-photon in the apparatus at a time,
- *(a)
- an interference pattern with minima and maxima can be observed.
- (b)
- two well-defined detection zones can be observed.
- (c)
- two well-defined detection zones and a zero-order maximum can be observed.
Item 12. In the Michelson interferometer, (answer options adopted from [34,45])
- (a)
- the single-photon follows a specific path, regardless of whether I observe this path or not.
- (b)
- the current position of a photon between source and detector is not indeterminate in principle, but unknown to the experimenter.
- *(c)
- the photon behaves like a particle and like a wave. It is none of them.
Item 13. Which statement about the behavior of a single-photon state in an interferometer is correct? (answer options adopted from [34,45])
- *(a)
- No one can say with certainty at which output port of the beam splitter cube a single-photon will be detected.
- (b)
- A single-photon state is divided at the beam splitter cube.
- (c)
- In the interferometer, the single-photon state is found in a superposition state of both, particle and wave.
Item 14. Anticorrelation of single-photon states can be observed at the outputs of a beam splitter cube because
- (a)
- more coincident events are detected between the outputs of the beam splitter than can be expected at random.
- *(b)
- a single-photon may only be detected once.
- (c)
- a single photon can be in both states, ’reflected’ and ’transmitted’, at the same time.
Item 15. For the preparation of single-photon states in experiments with heralded photons, one needs
- *(a)
- exactly two single-photon detectors.
- (b)
- at least one single-photon detector.
- (c)
- at least three single-photon detectors.
Item 16. Single-photons can be regarded as
- (a)
- spherical entities moving along a wavy path with the speed of light.
- (b)
- elementary energy portions of light surrounded by a wave that is responsible for interference.
- *(c)
- indivisible energy portions of light that are never detected on both output ports of a beam splitter cube simultaneously.
Appendix B. Overview of the Four-Week Program on Introductory Quantum Optics
Appendix B.1. Part I: Foundations of Quantum Optics Experiments with Heralded Photons
The course’s first part covered technical and experimental key ideas regarding experiments with heralded photons in order to help the students to make sense out of the experimental results in the later stage of the course:
- First, optical components widely used in quantum optics labs were introduced: For example, the role of mirrors for the adjustment of quantum optics experiments or the action of a beam splitter on incident light (see, e.g., [93,94]) were described.
- Second, the study participants were introduced to the properties of avalanche photodiodes operating above their breakdown voltage—also referred to as single-photon avalanche diode (SPAD) [95,96]: For example, quantum efficiency, dark count rate, and dead time [68] were covered. SPADs are binary detectors, which means that the “outcome of these APD’s is either ‘off’ (no photons detected) or ‘on,’ i.e., a ‘click,’ indicating the detection of one or more photons” [97] (p. 1).
- Third, the students were introduced to spontaneous parametric downconversion (PDC) [98], a quantum electrodynamic process in which “an incoming pump photon decays, under energy and momentum conservation, into a photon-pair” [99] (p. 351). Here, the students learned that a) PDC is driven by irradiating a nonlinear crystal (e.g., -barium borate) with a pump beam, most often emitted by a laser, and that b) the “spectral properties of PDC states are governed by the phasematching properties of the nonlinear material, and this determines the frequencies of the downconverted photons” [100] (p. 3442). For an comprehensive overview of parametric downconversion, we refer the reader to [101].
Appendix B.2. Part II: Experiments with Heralded Photons
The course’s second part made use of the foundation that was laid in the first part: On the one hand, the students were introduced to the preparation of single-photon Fock states. On the other hand, they got in touch with quantum effects that indeed require the quantization of the electromagnetic field. To provide engineering students with insights into real quantum laboratories, interactive screen experiments of heralded photon experiments previously developed by Bronner et al. [37] were shown throughout the lectures.
- First, the students learned about heralded single-photon state preparation, which is widely used in quantum optics research [102,103,104,105]). That is, one of the PDC photons is detected and heralds the second photon at a spatially separated detector—hence, simultaneous clicks at two detectors, also referred to as a coincident events, are “taken as preparation and detection of a single photon state” [37] (p. 348).
- Second, heralded single-photon states incident on a 50:50 beam splitter were investigated. In this experiment, the lack of coincident events at the output ports of the beam splitter, i.e., photon antibunching [106], was discussed. This anticorrelation effect is irreconcilable with any classical description of light: “A single photon can only be detected once” [67] (p. 173). These observations were further substantiated on a formal level a) by means of the second-order correlation function , which allows for a judgement of the purity of single-photon states [94], and b) by highlighting the ideas of quantum superposition and quantum random, as has been achieved in [31].
- The investigation and quantum description of Grangier et al.’s experiment from 1986 [67] represents the last step of the course. In this experiment, the students realized that by using only one single-photon state, the anticorrelation at a 50:50 beam splitter appeared simultaneously to the single-photon interference observed in a spatially separated interferometer (e.g., a Michelson interferometer) using the same single-photon state in the same experimental set-up. The students experienced that the “quantum interference phenomenon shown experimentally is a consequence of the interplay of superposition and nonlocality” [64] (p. 17), while the idea of the photon as a localizable particle is not valid. Instead, in this course, the photon was introduced as an elementary field mode excitation in the sense of quantum electrodynamics [83,84,107,108].
- In the outlook, the engineering students were given first insights into quantum technologies 2.0, namely by applying an understanding of heralded photons experiments to the context of quantum cryptography.
References
- Dowling, J.P.; Milburn, G.J. Quantum technology: The second quantum revolution. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2003, 361, 1655–1674. [Google Scholar] [CrossRef] [PubMed]
- Acín, A.; Bloch, I.; Buhrman, H.; Calarco, T.; Eichler, C.; Eisert, J.; Esteve, D.; Gisin, N.; Glaser, S.J.; Jelezko, F.; et al. The quantum technologies roadmap: A European community view. New J. Phys. 2018, 20, 080201. [Google Scholar] [CrossRef]
- Foti, C.; Anttila, D.; Maniscalco, S.; Chiofalo, M. Quantum physics literacy aimed at K12 and the general public. Universe 2021, 7, 86. [Google Scholar] [CrossRef]
- Venegas-Gomez, A. The quantum ecosystem and its future workforce: A journey through the funding, the hype, the opportunities, and the risks related to the emerging field of quantum technologies. PhotonicsViews 2020, 17, 34–38. [Google Scholar] [CrossRef]
- Asfaw, A.; Blais, A.; Brown, K.R.; Candelaria, J.; Cantwell, C.; Lincoln, D.C.; Combes, J.; Debroy, D.M.; Donohue, J.M.; Economou, S.E.; et al. Building a quantum engineering undergraduate program. IEEE Trans. Educ. 2022, 65, 220–242. [Google Scholar] [CrossRef]
- Kaur, M.; Venegas-Gomez, A. Defining the quantum workforce landscape: A review of global quantum education initiatives. Opt. Eng. 2022, 61, 081806. [Google Scholar] [CrossRef]
- Stephen Binkley, J. et al. [Subcommittee on Quantum Information Science]; Collins, F. et al. [Committee on Science]; Lander, E. et al. [National Science & Technology Council] Quantum Information Science and Technology Workforce Development National Strategic Plan; Technical Report; United States Government: Washington, DC, USA, 2022. Available online: https://www.quantum.gov/scqis-releases-strategic-plan-for-qist-workforce/ (accessed on 15 September 2022).
- National Q-12 Education Partnership. Growing the Quantum Workforce. Available online: https://q12education.org/ (accessed on 15 September 2022).
- Cervantes, B.; Passante, G.; Wilcox, B.R.; Pollock, S.J. An overview of Quantum Information Science courses at US institutions. In Proceedings of the Physics Education Research Conference 2021: 2021 PERC, Virtual, 4–5 August 2021; Bennett, M.B., Frank, B.W., Vieyra, R., Eds.; American Association of Physics Teachers: College Park, MD, USA, 2021; pp. 93–98. [Google Scholar] [CrossRef]
- Quantum Flagship. The Future Is Quantum. Available online: https://qt.eu/ (accessed on 15 September 2022).
- Quantum Technology Education. European Open Portal: Community and Resources. Available online: https://qtedu.eu/ (accessed on 15 September 2022).
- National Quantum Strategy. Available online: https://ised-isde.canada.ca/site/national-quantum-strategy/en (accessed on 15 September 2022).
- Sydney Quantum Academy. Available online: https://www.sydneyquantum.org/ (accessed on 15 September 2022).
- Quantum Technologies. Available online: https://www.psa.gov.in/technology-frontiers/quantum-technologies/346 (accessed on 15 September 2022).
- QEP: The Quantum Engineering Program. 2022. Available online: https://qepsg.org/ (accessed on 15 September 2022).
- Hughes, C.; Finke, D.; German, D.A.; Merzbacher, C.; Vora, P.M.; Lewandowski, H.J. Assessing the needs of the quantum industry. IEEE Trans. Educ. 2022. [Google Scholar] [CrossRef]
- Aiello, C.D.; Awschalom, D.D.; Bernien, H.; Brower, T.; Brown, K.R.; Brun, T.A.; Caram, J.R.; Chitambar, E.; Felice, R.D.; Edmonds, K.M.; et al. Achieving a quantum smart workforce. Quant. Sci. Technol. 2021, 6, 030501. [Google Scholar] [CrossRef]
- Fox, M.F.J.; Zwickl, B.M.; Lewandowski, H.J. Preparing for the quantum revolution: What is the role of higher education? Phys. Rev. Phys. Educ. Res. 2020, 16, 020131. [Google Scholar] [CrossRef]
- Gerke, F.; Müller, R.; Bitzenbauer, P.; Ubben, M.; Weber, K.A. Requirements for future quantum workforce—A Delphi study. J. Phys. Conf. Ser. 2022, 2297, 012017. [Google Scholar] [CrossRef]
- Greinert, F.; Müller, R.; Bitzenbauer, P.; Ubben, M.S.; Weber, K.A. The future quantum workforce: Competences, requirements and forecasts. arXiv 2022, arXiv:2208.08249. [Google Scholar] [CrossRef]
- Greinert, F.; Müller, R. Competence Framework for Quantum Technologies: Methodology and Version History; European Commission: Brussels, Belgium, 2021. [Google Scholar] [CrossRef]
- Moody, G.; Sorger, V.J.; Blumenthal, D.J.; Juodawlkis, P.W.; Loh, W.; Sorace-Agaskar, C.; Jones, A.E.; Balram, K.C.; Matthews, J.C.F.; Laing, A.; et al. 2022 Roadmap on integrated quantum photonics. J. Phys. Photonics 2022, 4, 012501. [Google Scholar] [CrossRef]
- Leibniz Universität Hannover. Quantum Engineering (Master of Science). Available online: https://tinyurl.com/bdftkpec (accessed on 15 September 2022).
- Rainò, G.; Novotny, L.; Frimmer, M. Quantum engineers in high demand. Nat. Mater. 2021, 20, 1449. [Google Scholar] [CrossRef]
- Universität Stuttgart. Photonic Engineering. Master of Science. Available online: https://www.uni-stuttgart.de/en/study/study-programs/Photonic-Engineering-M.Sc-00001./ (accessed on 15 September 2022).
- Princeton UniversityElectrical and Computer Engineering. Redesigned Quantum Optics Course Brings Applications to the Heart of the Experience. Available online: https://tinyurl.com/4uw4j7nn (accessed on 15 September 2022).
- Duarte, F. Quantum Optics for Engineers; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar] [CrossRef]
- O’Brien, J.L. Optical Quantum Computing. Science 2007, 318, 1567–1570. [Google Scholar] [CrossRef] [PubMed]
- von Helversen, M.; Böhm, J.; Schmidt, M.; Gschrey, M.; Schulze, J.H.; Strittmatter, A.; Rodt, S.; Beyer, J.; Heindel, T.; Reitzenstein, S. Quantum metrology of solid-state single-photon sources using photon-number-resolving detectors. New J. Phys. 2019, 21, 035007. [Google Scholar] [CrossRef]
- Förtsch, M.; Fürst, J.U.; Wittmann, C.; Strekalov, D.; Aiello, A.; Chekhova, M.V.; Silberhorn, C.; Leuchs, G.; Marquardt, C. A versatile source of single photons for quantum information processing. Nat. Commun. 2013, 4, 1818. [Google Scholar] [CrossRef] [PubMed]
- Bronner, P.; Strunz, A.; Silberhorn, C.; Meyn, J.P. Demonstrating quantum random with single photons. Eur. J. Phys. 2009, 30, 1189–1200. [Google Scholar] [CrossRef]
- Pearson, B.J.; Jackson, D.P. A hands-on introduction to single photons and quantum mechanics for undergraduates. Am. J. Phys. 2010, 78, 1422. [Google Scholar] [CrossRef]
- Marshman, E.; Singh, C. Investigating and improving student understanding of quantum mechanics in the context of single photon interference. Phys. Rev. Phys. Educ. Res. 2017, 13, 010117. [Google Scholar] [CrossRef]
- Bitzenbauer, P. Effect of an introductory quantum physics course using experiments with heralded photons on preuniversity students’ conceptions about quantum physics. Phys. Rev. Phys. Educ. Res. 2021, 17, 020103. [Google Scholar] [CrossRef]
- Galvez, E.J.; Holbrow, C.H.; Pysher, M.J.; Martin, J.W.; Courtemanche, N.; Heilig, L.; Spencer, J. Interference with correlated photons: Five quantum mechanics experiments for undergraduates. Am. J. Phys. 2005, 73, 127–140. [Google Scholar] [CrossRef]
- Thorn, J.J.; Neel, M.S.; Donato, V.W.; Bergreen, G.S.; Davies, R.E.; Beck, M. Observing the quantum behavior of light in an undergraduate laboratory. Am. J. Phys. 2004, 72, 1210–1219. [Google Scholar] [CrossRef]
- Bronner, P.; Strunz, A.; Silberhorn, C.; Meyn, J.P. Interactive screen experiments with single photons. Eur. J. Phys. 2009, 30, 345–353. [Google Scholar] [CrossRef]
- Bitzenbauer, P. Practitioners’ views on new teaching material for introducing quantum optics in secondary schools. Phys. Educ. 2021, 56, 055008. [Google Scholar] [CrossRef]
- Scholz, R.; Friege, G.; Weber, K.A. Undergraduate quantum optics: Experimental steps to quantum physics. Eur. J. Phys. 2018, 39, 055301. [Google Scholar] [CrossRef]
- Bitzenbauer, P. Quantum physics education research over the last two decades: A bibliometric analysis. Educ. Sci. 2021, 11, 699. [Google Scholar] [CrossRef]
- Krijtenburg-Lewerissa, K.; Pol, H.; Brinkman, A.; van Joolingen, W. Insights into teaching quantum mechanics in secondary and lower undergraduate education. Phys. Rev. Phys. Educ. Res. 2017, 13, 010109. [Google Scholar] [CrossRef]
- Wuttiprom, S.; Sharma, M.D.; Johnston, I.D.; Chitaree, R.; Soankwan, C. Development and use of a conceptual survey in introductory quantum physics. Int. J. Sci. Educ. 2009, 31, 631–654. [Google Scholar] [CrossRef]
- McKagan, S.B.; Perkins, K.K.; Wieman, C.E. Design and validation of the Quantum Mechanics Conceptual Survey. Phys. Rev. Phys. Educ. Res. 2010, 6, 020121. [Google Scholar] [CrossRef]
- di Uccio, U.S.; Colantonio, A.; Galano, S.; Marzoli, I.; Trani, F.; Testa, I. Design and validation of a two-tier questionnaire on basic aspects in quantum mechanics. Phys. Rev. Phys. Educ. Res. 2019, 15, 010137. [Google Scholar] [CrossRef]
- Müller, R.; Wiesner, H. Teaching quantum mechanics on an introductory level. Am. J. Phys. 2002, 70, 200–209. [Google Scholar] [CrossRef]
- Cataloglu, E.; Robinett, R.W. Testing the development of student conceptual and visualization understanding in quantum mechanics through the undergraduate career. Am. J. Phys. 2002, 70, 238–251. [Google Scholar] [CrossRef]
- Goldhaber, S.; Pollock, S.; Dubson, M.; Beale, P.; Perkins, K.; Sabella, M.; Henderson, C.; Singh, C. Transforming upper-division quantum mechanics: Learning goals and assessment. AIP Conf. Proc. 2009, 1179, 145–148. [Google Scholar] [CrossRef]
- Marshman, E.; Singh, C. Validation and administration of a conceptual survey on the formalism and postulates of quantum mechanics. Phys. Rev. Phys. Educ. Res. 2019, 15, 020128. [Google Scholar] [CrossRef]
- Bitzenbauer, P. Development of a test instrument to investigate secondary school students’ declarative knowledge of quantum optics. Eur. J. Sci. Math. Educ. 2021, 9, 57–79. [Google Scholar] [CrossRef]
- Singh, C.; Marshman, E. Review of student difficulties in upper-level quantum mechanics. Phys. Rev. Phys. Educ. Res. 2015, 11, 020117. [Google Scholar] [CrossRef]
- Bitzenbauer, P.; Meyn, J.P. A new teaching concept on quantum physics in secondary schools. Phys. Educ. 2020, 55, 055031. [Google Scholar] [CrossRef]
- Bitzenbauer, P.; Meyn, J.P. Fostering students’ conceptions about the quantum world—Results of an interview study. Prog. Sci. Educ. 2021, 4, 40–51. [Google Scholar] [CrossRef]
- Ubben, M.S.; Bitzenbauer, P. Two cognitive dimensions of students’ mental models in science: Fidelity of gestalt and functional fidelity. Educ. Sci. 2022, 12, 163. [Google Scholar] [CrossRef]
- Waitzmann, M.; Scholz, R.; Weßnigk, S. Wirkung eines Realexperiments auf quantenphysikalische Argumentation. Unsicherheit als Element von naturwissenschaftsbezogenen Bildungsprozessen. In Proceedings of the Jahrestagung der Gesellschaft für Didaktik der Chemie und Physik, Online, 13–16 September 2021; Universität Duisburg-Essen: Duisburg, Germany, 2022; p. 42. [Google Scholar]
- Bitzenbauer, P. Quantenoptik an Schulen. Studie im Mixed-Methods Design zur Evaluation des Erlanger Unterrichtskonzepts zur Quantenoptik; Logos Verlag: Berlin, Germany, 2020. [Google Scholar] [CrossRef]
- Ireson, G. The quantum understanding of pre-university physics students. Phys. Educ. 2000, 35, 15–21. [Google Scholar] [CrossRef]
- Ireson, G. A multivariate analysis of undergraduate physics students’ conceptions of quantum phenomena. Eur. J. Phys. 1999, 20, 193–199. [Google Scholar] [CrossRef]
- Donhauser, A.; Bitzenbauer, P.; Meyn, J.P. Von Schnee- und Elektronenlawinen: Entwicklung eines Erklärvideos zu Einzelphotonendetektoren. PhyDid B—Didaktik der Physik—Beiträge zur DPG-Frühjahrstagung 2020, Bonn, 235–240. Available online: https://ojs.dpg-physik.de/index.php/phydid-b/article/view/1021 (accessed on 15 September 2022).
- Aslanides, J.S.; Savage, C.M. Relativity concept inventory: Development, analysis, and results. Phys. Rev. Phys. Educ. Res. 2013, 9, 010118. [Google Scholar] [CrossRef]
- Veith, J.M.; Bitzenbauer, P.; Girnat, B. Assessing learners’ conceptual understanding of introductory group theory using the CI2GT: Development and analysis of a concept inventory. Educ. Sci. 2022, 12, 376. [Google Scholar] [CrossRef]
- Urlacher, M.A.; Brown, S.A.; Steif, P.S.; Bornasal, F.B. Practicing civil engineers’ understanding of statics concept inventory questions. In Proceedings of the 2015 ASEE Annual Conference and Exposition, Seattle, WA, USA, 14–17 June 2015; pp. 26.1236.1–26.1236.12. [Google Scholar] [CrossRef]
- Hasan, S.; Bagayoko, D.; Kelley, E.L. Misconceptions and the Certainty of Response Index (CRI). Phys. Educ. 1999, 34, 294–299. [Google Scholar] [CrossRef]
- Bitzenbauer, P.; Meyn, J.P. Inhaltsvalidität eines Testinstruments zur Erfassung deklarativen Wissens zur Quantenoptik. PhyDid B—Didaktik der Physik—Beiträge zur DPG-Frühjahrstagung 2020, Bonn, 149–156. Available online: https://ojs.dpg-physik.de/index.php/phydid-b/article/view/1022 (accessed on 15 September 2022).
- Scholz, R.; Wessnigk, S.; Weber, K.A. A classical to quantum transition via key experiments. Eur. J. Phys. 2020, 41, 055304. [Google Scholar] [CrossRef]
- Kohnle, A.; Rizzoli, A. Interactive simulations for quantum key distribution. Eur. J. Phys. 2017, 38, 035403. [Google Scholar] [CrossRef]
- Bloom, Y.; Fields, I.; Maslennikov, A.; Rozenman, G.G. Quantum cryptography—A simplified undergraduate experiment and simulation. Physics 2022, 4, 104–123. [Google Scholar] [CrossRef]
- Grangier, P.; Roger, G.; Aspect, A. Experimental evidence for a photon anticorrelation effect on a beam splitter: A new light on single-photon interferences. Europhys. Lett. 1986, 1, 173–179. [Google Scholar] [CrossRef]
- Silberhorn, C. Detecting quantum light. Contemp. Phys. 2007, 48, 143–156. [Google Scholar] [CrossRef]
- Kline, T. Psychological Testing: A Practical Approach to Design and Evaluation; SAGE Publications, Inc.: Thousand Oaks, CA, USA, 2005. [Google Scholar]
- Jorion, N.; Gane, B.D.; James, K.; Schroeder, L.; DiBello, L.V.; Pellegrino, J.W. An analytic framework for evaluating the validity of concept inventory claims. J. Eng. Educ. 2015, 104, 454–496. [Google Scholar] [CrossRef]
- Taber, K.S. The Use of Cronbach’s alpha when developing and reporting research instruments in science education. Res. Sci. Educ. 2018, 48, 1273–1296. [Google Scholar] [CrossRef]
- Cantó-Cerdán, M.; Cacho-Martínez, P.; Lara-Lacárcel, F.; García-Muñoz, Á. Rasch analysis for development and reduction of Symptom Questionnaire for Visual Dysfunctions (SQVD). Sci. Rep. 2021, 11, 14855. [Google Scholar] [CrossRef] [PubMed]
- Winter-Hölzl, A.; Wäschle, K.; Wittwer, J.; Watermann, R.; Nückles, M. Entwicklung und Validierung eines Tests zur Erfassung des Genrewissens Studierender und Promovierender der Bildungswissenschaften. Zeit. Pädag. 2015, 61, 185–202. [Google Scholar] [CrossRef]
- Planinic, M.; Boone, W.J.; Susac, A.; Ivanjek, L. Rasch analysis in physics education research: Why measurement matters. Phys. Rev. Phys. Educ. Res. 2019, 15, 020111. [Google Scholar] [CrossRef]
- Rizopoulos, D. Package ’ltm’. 18 February 2022. Available online: https://cran.r-project.org/web/packages/ltm/ltm.pdf (accessed on 15 September 2022).
- Robitzsch, A.; Kiefer, A.; Wu, M. Package ’TAM’. 28 August 2022. Available online: https://cran.r-project.org/web/packages/TAM/TAM.pdf (accessed on 15 September 2022).
- Mair, P.; Hatzinger, R.; Maier, M.J.; Rusch, T.; Debelak, R. Package ’eRm’. 15 February 2022. Available online: https://cran.r-project.org/web/packages/eRm/eRm.pdf (accessed on 15 September 2022).
- Matejak Cvenic, K.; Planinic, M.; Susac, A.; Ivanjek, L.; Jelicic, K.; Hopf, M. Development and validation of the Conceptual Survey on Wave Optics. Phys. Rev. Phys. Educ. Res. 2022, 18, 010103. [Google Scholar] [CrossRef]
- Chen, W.-H.; Thissen, D. Local Dependence indexes for item pairs using item response theory. J. Educ. Behav. Stat. 1997, 22, 265–289. [Google Scholar] [CrossRef]
- Christensen, K.B.; Makransky, G.; Horton, M. Critical values for Yen’s Q3: Identification of local dependence in the Rasch model using residual correlations. App. Psych. Meas. 2017, 41, 178–194. [Google Scholar] [CrossRef]
- Jang, E.E.; Roussos, L. An Investigation into the dimensionality of TOEFL using conditional covariance-based nonparametric approach. J. Educ. Meas. 2007, 44, 1–21. [Google Scholar] [CrossRef]
- Susac, A.; Planinic, M.; Klemencic, D.; Milin Sipus, Z. Using the Rasch model to analyze the test of understanding of vectors. Phys. Rev. Phys. Educ. Res. 2018, 14, 023101. [Google Scholar] [CrossRef]
- Jones, D.G.C. Teaching modern physics-misconceptions of the photon that can damage understanding. Phys. Educ. 1991, 26, 93–98. [Google Scholar] [CrossRef]
- Kidd, R.; Ardini, J.; Anton, A. Evolution of the modern photon. Am. J. Phys. 1989, 57, 27–35. [Google Scholar] [CrossRef]
- Nousiainen, M.; Koponen, I.T. Pre-service teachers’ declarative knowledge of wave-particle dualism of electrons and photons: Finding lexicons by using network analysis. Educ. Sci. 2020, 10, 76. [Google Scholar] [CrossRef]
- Hoehn, J.R.; Gifford, J.D.; Finkelstein, N.D. Investigating the dynamics of ontological reasoning across contexts in quantum physics. Phys. Rev. Phys. Educ. Res. 2019, 15, 010124. [Google Scholar] [CrossRef]
- Kalkanis, G.; Hadzidaki, P.; Stavrou, D. An instructional model for a radical conceptual change towards quantum mechanics concepts. Sci. Educ. 2003, 87, 257–280. [Google Scholar] [CrossRef]
- Veith, J.M.; Girnat, B.; Bitzenbauer, P. The role of affective learner characteristics for learning about abstract algebra: A multiple linear regression analysis. EURASIA J. Math. Sci. Technol. Educ. 2022, 18, em2157. [Google Scholar] [CrossRef]
- Rasch, G. On general laws and the meaning of measurement in psychology. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability. Volume 4: Contributions to Biology and Problems of Medicine, Berkeley, CA, USA, 20 June–30 July 1960; Neyman, J., Ed.; University of California Press: Berkeley/Los Angeles, CA, USA, 1961; pp. 321–333. Available online: https://projecteuclid.org/Proceedings/berkeley-symposium-on-mathematical-statistics-and-probability/proceedings-of-the-fourth-berkeley-symposium-on-mathematical-statistics-and/toc/bsmsp/1200512872 (accessed on 15 September 2022).
- Pant, H.A.; Tiffin-Richards, S.P.; Köller, O. Standard-Setting für Kompetenztests im Large-Scale-Assessment. Projekt Standardsetting. Zeit. Pädag. 2010, 56, 175–188. [Google Scholar] [CrossRef]
- Duncan, R.G.; Hmelo-Silver, C.E. Learning progressions: Aligning curriculum, instruction, and assessment. J. Res. Sci. Teach. 2009, 46, 606–609. [Google Scholar] [CrossRef]
- Wright, B.D.; Masters, G.N. Rating Scale Analysis; MESA Press: Chicago, IL, USA, 1982. [Google Scholar]
- Prasad, S.; Scully, M.O.; Martienssen, W. A quantum description of the beam splitter. Opt. Comm. 1987, 62, 139–145. [Google Scholar] [CrossRef]
- Loudon, R. The Quantum Theory of Light; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Cova, S.; Longoni, A.; Andreoni, A. Towards picosecond resolution with single-photon avalanche diodes. Rev. Sci. Instr. 1981, 52, 408–412. [Google Scholar] [CrossRef]
- Cova, S.; Ghioni, M.; Lacaita, A.; Samori, C.; Zappa, F. Avalanche photodiodes and quenching circuits for single-photon detection. Appl. Opt. 1996, 35, 1956–1976. [Google Scholar] [CrossRef] [PubMed]
- Zambra, G.; Andreoni, A.; Bondani, M.; Gramegna, M.; Genovese, M.; Brida, G.; Rossi, A.; Paris, M.G.A. Experimental reconstruction of photon statistics without photon counting. Phys. Rev. Lett. 2005, 95, 063602. [Google Scholar] [CrossRef] [PubMed]
- Hong, C.K.; Mandel, L. Theory of parametric frequency down conversion of light. Phys. Rev. A 1985, 31, 2409–2418. [Google Scholar] [CrossRef] [PubMed]
- Christ, A.; Fedrizzi, A.; Hüel, H.; Jennewein, T.; Silberhorn, C. Parametric down-conversion. In Single-Photon Generation and Detection. Physics and Applications; Migdall, A., Polyakov, S.V., Fan, J., Bienfang, J.C., Eds.; Elsevier: Amsterdam, The Netherlands, 2013; pp. 351–410. [Google Scholar] [CrossRef]
- Christ, A.; Eckstein, A.; Mosley, P.J.; Silberhorn, C. Pure single photon generation by type-I PDC with backward-wave amplification. In Proceedings of the European Conference on Lasers and Electro-Optics and the European Quantum Electronics Conference: CLEO Europe/EQEC 2009 (Abstracts), Munich, Germany, 14–19 June 2009; IEEE: Piscataway, NJ, USA, 2009; p. 917. [Google Scholar] [CrossRef]
- Couteau, C. Spontaneous parametric down-conversion. Contemp. Phys. 2018, 59, 291–304. [Google Scholar] [CrossRef]
- Brida, G.; Degiovanni, I.P.; Genovese, M.; Migdall, A.; Piacentini, F.; Polyakov, S.V.; Ruo Berchera, I. Experimental realization of a low-noise heralded single-photon source. Opt. Express 2011, 19, 1484–1492. [Google Scholar] [CrossRef] [PubMed]
- Lounis, B.; Orrit, M. Single-photon sources. Rep. Prog. Phys. 2005, 68, 1129–1179. [Google Scholar] [CrossRef]
- Krapick, S.; Herrmann, H.; Quiring, V.; Brecht, B.; Suche, H.; Silberhorn, C. An efficient integrated two-color source for heralded single photons. New J. Phys. 2013, 15, 033010. [Google Scholar] [CrossRef]
- Genovese, M.; Gramegna, M.; Brida, G.; Bondani, M.; Zambra, G.; Andreoni, A.; Rossi, A.R.; Paris, M.G.A. Measuring the photon distribution with ON/OFF photodetectors. Laser Phys. 2006, 16, 385–392. [Google Scholar] [CrossRef]
- Kimble, H.J.; Dagenais, M.; Mandel, L. Photon antibunching in resonance fluorescence. Phys. Rev. Lett. 1977, 39, 691–695. [Google Scholar] [CrossRef]
- Hobson, A. There are no particles, there are only fields. Am. J. Phys. 2013, 81, 211–223. [Google Scholar] [CrossRef]
- Strnad, J. Photons in introductory quantum physics. Am. J. Phys. 1986, 54, 650–652. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).