Recent Progress of Shell-Model Calculations, Monte Carlo Shell Model, and Quasi-Particle Vacua Shell Model
Abstract
1. Introduction
2. Conventional Diagonalization Method for Shell-Model Calculations
2.1. Shell-Model Hamiltonian Matrix and Its Dimension
2.2. Lanczos Method
2.3. Block Lanczos Method
3. Approximation Methods to Exact Diagonalization
3.1. Monte Carlo Shell Model
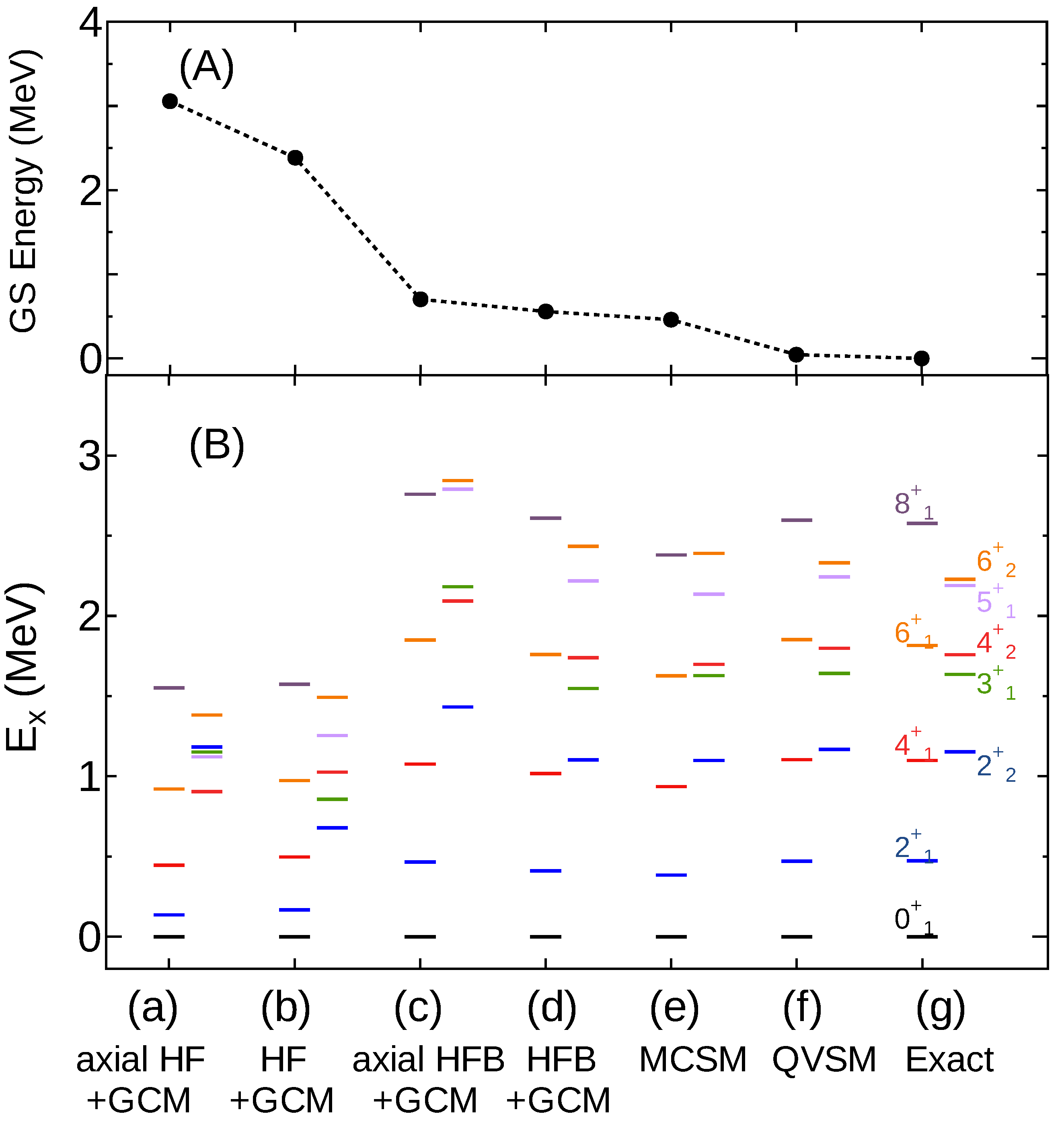
3.2. Quasiparticle Vacua Shell Model
4. Summary
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Caurier, E.; Martinez-Pinedo, G.; Nowacki, F.; Poves, A.; Zuker, A.P. The shell model as unified view of nuclear structure. Rev. Mod. Phys. 2005, 77, 427–488. [Google Scholar] [CrossRef]
- Otsuka, T.; Gade, A.; Sorlin, O.; Suzuki, T.; Utsuno, Y. Evolution of shell structure in exotic nuclei. Rev. Mod. Phys. 2020, 92, 015002. [Google Scholar] [CrossRef]
- Martínez-Pinedo, G.; Langanke, K. Shell model applications in nuclear astrophysics. Physics 2022, 4, 677–689. [Google Scholar] [CrossRef]
- Shimizu, N.; Togashi, T.; Utsuno, Y. Gamow-Teller transitions of neutron-rich N=82, 81 nuclei by shell-model calculations. Prog. Theor. Exp. Phys. 2021, 2021, 033D01. [Google Scholar] [CrossRef]
- Menéndez, J.; Poves, A.; Caurier, E.; Nowacki, F. Disassembling the nuclear matrix elements of the neutrinoless ββ decay. Nucl. Phys. A 2009, 818, 139–151. [Google Scholar] [CrossRef]
- Coraggio, L.; Gargano, A.; Itaco, N.; Mancino, R.; Nowacki, F. Calculation of the neutrinoless double-β decay matrix element within the realistic shell model. Phys. Rev. C 2020, 101, 044315. [Google Scholar] [CrossRef]
- Shimizu, N.; Menéndez, J.; Yako, K. Double Gamow-Teller transitions and its relation to neutrinoless ββ decay. Phys. Rev. Lett. 2018, 120, 142502. [Google Scholar] [CrossRef]
- Yanase, K.; Shimizu, N. Large-scale shell-model calculations of nuclear Schiff moments of 129Xe and 199Hg. Phys. Rev. C 2020, 102, 065502. [Google Scholar] [CrossRef]
- Cohen, S.; Kurath, D. Effective interactions for the 1p shell. Nucl. Phys. 1965, 73, 1–24. [Google Scholar] [CrossRef]
- Brown, B.A.; Richter, W. New “USD” Hamiltonians for the sd shell. Phys. Rev. C 2006, 74, 034315. [Google Scholar] [CrossRef]
- Honma, M.; Otsuka, T.; Brown, B.A.; Mizusaki, T. New effective interaction for pf shell nuclei and its implications for the stability of the N=Z=28 closed core. Phys. Rev. C 2004, 69, 034335. [Google Scholar] [CrossRef]
- Richter, W.A.; Van Der Merwe, M.G.; Julies, R.E.; Brown, B.A. New effective interactions for the 0f1p shell. Nucl. Phys. A 1991, 523, 325–353. [Google Scholar] [CrossRef]
- Honma, M.; Otsuka, T.; Mizusaki, T.; Hjorth-Jensen, M. New effective interaction for f5pg9-shell nuclei. Phys. Rev. C 2009, 80, 064323. [Google Scholar] [CrossRef]
- Hjorth-Jensen, M.; Kuo, T.T.S.; Osnes, E. Realistic effective interactions for nuclear systems. Phys. Rep. 1995, 261, 125–270. [Google Scholar] [CrossRef]
- Stroberg, S.R.; Henderson, J.; Hackman, G.; Ruotsalainen, P.; Hagen, G.; Holt, J.D. Systematics of E2 strength in the sd shell with the valence-space in-medium similarity renormalization group. Phys. Rev. C 2022, 105, 034333. [Google Scholar] [CrossRef]
- Jansen, G.R.; Engel, J.; Hagen, G.; Navratil, P.; Signoracci, A. Ab-initio coupled-cluster effective interactions for the shell model: Application to neutron-rich oxygen and carbon isotopes. Phys. Rev. Lett. 2014, 113, 142502. [Google Scholar] [CrossRef] [PubMed]
- Coraggio, L.; De Gregorio, G.; Gargano, A.; Itaco, N.; Fukui, T.; Ma, Y.Z.; Xu, F.R. Shell-model study of calcium isotopes toward their drip line. Phys. Rev. C 2020, 102, 054326. [Google Scholar] [CrossRef]
- Tsunoda, N.; Otsuka, T.; Shimizu, N.; Hjorth-Jensen, M.; Takayanagi, K.; Suzuki, T. Exotic neutron-rich medium-mass nuclei with realistic nuclear forces. Phys. Rev. C 2017, 95, 021304. [Google Scholar] [CrossRef]
- Smirnova, N.A.; Barrett, B.R.; Kim, Y.; Shin, I.J.; Shirokov, A.M.; Dikmen, E.; Maris, P.; Vary, J.P. Effective interactions in the sd shell. Phys. Rev. C 2019, 100, 054329. [Google Scholar] [CrossRef]
- Miyagi, T.; Stroberg, S.R.; Holt, J.D.; Shimizu, N. Ab initio multishell valence-space Hamiltonians and the island of inversion. Phys. Rev. C 2020, 102, 034320. [Google Scholar] [CrossRef]
- Tsunoda, N.; Otsuka, T.; Takayanagi, K.; Shimizu, N.; Suzuki, T.; Utsuno, Y.; Yoshida, S.; Ueno, H. The impact of nuclear shape on the emergence of the neutron dripline. Nature 2020, 587, 66–71. [Google Scholar] [CrossRef] [PubMed]
- Otsuka, T.; Honma, M.; Mizusaki, T.; Shimizu, N.; Utsuno, Y. Monte Carlo shell model for atomic nuclei. Prog. Part. Nucl. Phys. 2001, 47, 319–400. [Google Scholar] [CrossRef]
- Shimizu, N.; Abe, T.; Honma, M.; Otsuka, T.; Togashi, T.; Tsunoda, Y.; Utsuno, Y.; Yoshida, T. Monte Carlo shell model studies with massively parallel supercomputers. Phys. Scr. 2017, 92, 063001. [Google Scholar] [CrossRef]
- Shimizu, N.; Tsunoda, Y.; Utsuno, Y.; Otsuka, T. Variational approach with the superposition of the symmetry-restored quasiparticle vacua for nuclear shell-model calculations. Phys. Rev. C 2021, 103, 014312. [Google Scholar] [CrossRef]
- Brown, B.A.; Etchegoyen, A.; Rae, W.D.M.; Godwin, N.S. The Computer Code OXBASH; MSU-NSCL Report 524; National Superconducting Cyclotron Laboratory: East Lansing, MI, USA, 1988. [Google Scholar]
- Brown, B.A.; Etchegoyen, A.; Godwin, N.S.; Rae, W.D.M.; Richter, W.A.; Ormand, W.E.; Warburton, E.K.; Winfield, J.S.; Zhao, L.; Zimmerman, C.H. Oxbash for Windows PC; MSU-NSCL Report 1289; National Superconducting Cyclotron Laboratory: East Lansing, MI, USA, 2004. [Google Scholar]
- Brown, B.A.; Rae, W.D.M. The shell-model code NuShellX@ MSU. Nucl. Data Sheets 2014, 120, 115–118. [Google Scholar] [CrossRef]
- Caurier, E. Computer Code ANTOINE; Centre de Recherches Nucléaires: Strasbourg, France, 1989. [Google Scholar]
- Caurier, E.; Nowacki, F. Coupled Code NATHAN; Centre de Recherches Nucléaires: Strasbourg, France, 1995. [Google Scholar]
- Mizusaki, T. Development of a new code for large-scale shell-model calculations using a parallel computer. RIKEN Accel. Prog. Rep. 1999, 33, 14. Available online: https://www.nishina.riken.jp/researcher/APR/Document/ProgressReport_vol_33.pdf (accessed on 24 August 2020).
- Mizusaki, T.; Shimizu, N.; Utsuno, Y.; Honma, M. The MSHELL64 code. 2013; unpublished. [Google Scholar]
- Shao, M.; Aktulga, H.M.; Yang, C.; Ng, E.G.; Maris, P.; Vary, J.P. Accelerating nuclear configuration interaction calculations through a preconditioned block iterative eigensolver. Comput. Phys. Commun. 2018, 222, 1–13. [Google Scholar] [CrossRef]
- Johnson, C.W.; Ormand, W.E.; Krastev, P.G. Factorization in large-scale many-body calculations. Comput. Phys. Commun. 2013, 184, 2761–2774. [Google Scholar] [CrossRef]
- Shimizu, N.; Mizusaki, T.; Utsuno, Y.; Tsunoda, Y. Thick-restart block Lanczos method for large-scale shell-model calculations. Comput. Phys. Commun. 2019, 244, 372–384. [Google Scholar] [CrossRef]
- Lanczos, C. An iteration method for the solution of the eigenvalue problem of linear differential and integral operators. J. Res. Nat. Bur. Standards 1950, 45, 255–282. [Google Scholar] [CrossRef]
- Shimizu, N.; Utsuno, Y.; Futamura, Y.; Sakurai, T.; Mizusaki, T.; Otsuka, T. Stochastic estimation of level density in nuclear shell-model calculations. EPJ Web Conf. 2016, 122, 02003. [Google Scholar] [CrossRef]
- Wu, K.; Simon, H. Thick-restart Lanczos method for large symmetric eigenvalue problems. SIAM J. Matrix Anal. Appl. 2000, 22, 602–616. [Google Scholar] [CrossRef]
- Aktulga, H.M.; Afibuzzaman, M.; Williams, S.; Buluç, A.; Shao, M.; Yang, C.; Ng, E.G.; Maris, P.; Vary, J.P. A high performance block eigensolver for nuclear configuration interaction calculations. IEEE Trans. Parallel Distrib. Syst. 2017, 28, 1550–1563. [Google Scholar] [CrossRef]
- Mizusaki, T.; Kaneko, K.; Honma, M.; Sakurai, T. Filter diagonalization of shell-model calculations. Phys. Rev. C 2010, 82, 024310. [Google Scholar] [CrossRef]
- Ikegami, T.; Sakurai, T.; Nagashima, U. A filter diagonalization for generalized eigenvalue problems based on the Sakurai—Sugiura projection method. J. Comput. Appl. Math 2010, 233, 1927–1936. [Google Scholar] [CrossRef]
- Shimizu, N.; Utsuno, Y.; Futamura, Y.; Sakurai, T.; Mizusaki, T.; Otsuka, T. Stochastic estimation of nuclear level density in the nuclear shell model: An application to parity-dependent level density in 58Ni. Phys. Lett. B 2016, 753, 13–17. [Google Scholar] [CrossRef]
- Michel, N.; Aktulga, H.M.; Jaganathen, Y. Toward scalable many-body calculations for nuclear open quantum systems using the Gamow Shell Model. Comput. Phys. Commun. 2020, 247, 106978. [Google Scholar] [CrossRef]
- Mizusaki, T.; Myo, T.; Katō, K. A new approach for many-body resonance spectroscopy with the complex scaling method. Prog. Theor. Exp. Phys. 2014, 2014, 091D01. [Google Scholar] [CrossRef][Green Version]
- Koonin, S.E.; Dean, D.J.; Langanke, K. Shell model Monte Carlo methods. Phys. Rep. 1997, 278, 1–77. [Google Scholar] [CrossRef]
- Adami, C.; Koonin, S.E. Complex Langevin equation and the many fermion problem. Phys. Rev. C 2001, 63, 034319. [Google Scholar] [CrossRef]
- Bonnard, J.; Juillet, O. Constrained-path quantum Monte Carlo approach for the nuclear shell model. Phys. Rev. Lett. 2013, 111, 012502. [Google Scholar] [CrossRef] [PubMed]
- Alhassid, Y.; Bonett-Matiz, M.; Liu, S.; Nakada, H. Direct microscopic calculation of nuclear level densities in the shell model Monte Carlo approach. Phys. Rev. C 2015, 92, 024307. [Google Scholar] [CrossRef]
- Dukelsky, J.; Pittel, S.; Dimitrova, S.; Stoitsov, M. Density matrix renormalization group method and large-scale nuclear shell-model calculations. Phys. Rev. C 2002, 65, 054319. [Google Scholar] [CrossRef]
- Pittel, S.; Sandulescu, N. Density matrix renormalization group and the nuclear shell model. Phys. Rev. C 2006, 73, 014301. [Google Scholar] [CrossRef]
- Legeza, Ö.; Veis, L.; Poves, A.; Dukelsky, J. Advanced density matrix renormalization group method for nuclear structure calculations. Phys. Rev. C 2015, 92, 051303. [Google Scholar] [CrossRef]
- Hara, K.; Sun, Y. Projected shell model and high-spin spectroscopy. Int. J. Mod. Phys. E 1995, 4, 637–785. [Google Scholar] [CrossRef]
- Gao, Z.-C.; Horoi, M. Angular momentum projected configuration interaction with realistic Hamiltonians. Phys. Rev. C 2009, 79, 014311. [Google Scholar] [CrossRef]
- Jiao, L.F.; Sun, Z.H.; Xu, Z.X.; Xu, F.R.; Qi, C. Correlated-basis method for shell-model calculations. Phys. Rev. C 2014, 90, 024306. [Google Scholar] [CrossRef]
- Mizusaki, T.; Shimizu, N. New variational Monte Carlo method with an energy variance extrapolation for large-scale shell-model calculations. Phys. Rev. C 2012, 85, 021301. [Google Scholar] [CrossRef]
- Shimizu, N.; Mizusaki, T. Variational Monte Carlo method for shell-model calculations in odd-mass nuclei and restoration of symmetry. Phys. Rev. C 2018, 98, 054309. [Google Scholar] [CrossRef]
- Yoshinaga, N.; Higashiyama, K. Systematic studies of nuclei around mass 130 in the pair-truncated shell model. Phys. Rev. C 2004, 69, 054309. [Google Scholar] [CrossRef]
- Zhao, Y.M.; Arima, A. Nucleon-pair approximation to the nuclear shell model. Phys. Rep. 2014, 545, 1–45. [Google Scholar] [CrossRef]
- Shimizu, N.; Mizusaki, T.; Kaneko, K.; Tsunoda, Y. Generator-coordinate methods with symmetry-restored Hartree-Fock-Bogoliubov wave functions for large-scale shell-model calculations. Phys. Rev. C 2021, 103, 064302. [Google Scholar] [CrossRef]
- Schmid, K.W. On the use of general symmetry-projected Hartree–Fock–Bogoliubov configurations in variational approaches to the nuclear many-body problem. Prog. Part. Nucl. Phys. 2004, 52, 565–633. [Google Scholar] [CrossRef]
- Schmid, K.W.; Grümmer, F.; Kyotoku, M.; Faessler, A. Selfconsistent description of non-yrast states in nuclei: The excited VAMPIR approach. Nucl. Phys. A 1986, 452, 493–512. [Google Scholar] [CrossRef]
- Puddu, G. Hybrid schemes for the calculation of low-energy levels of shell model Hamiltonians. J. Phys. G Nucl. Part. Phys. 2006, 32, 321–331. [Google Scholar] [CrossRef]
- Puddu, G. Calculation of energy levels with the hybrid multi-determinant method in the fp region. Eur. Phys. J. A 2007, 34, 413–415. [Google Scholar] [CrossRef]
- Puddu, G. A study of open shell nuclei using chiral two-body interactions. J. Phys. G Nucl. Part. Phys. 2021, 48, 045105. [Google Scholar] [CrossRef]
- Horoi, M.; Brown, B.A.; Zelevinsky, V. Exponential convergence method: Nonyrast states, occupation numbers, and a shell-model description of the superdeformed band in 56Ni. Phys. Rev. C 2003, 67, 034303. [Google Scholar] [CrossRef]
- Mizusaki, T.; Imada, M. Extrapolation method for shell model calculations. Phys. Rev. C 2002, 65, 064319. [Google Scholar] [CrossRef]
- Zhan, H.; Nogga, A.; Barrett, B.R.; Vary, J.P.; Navratil, P. Extrapolation method for the no-core shell model. Phys. Rev. C 2004, 69, 034302. [Google Scholar] [CrossRef]
- Shimizu, N.; Utsuno, Y.; Mizusaki, T.; Otsuka, T.; Abe, T.; Honma, M. Novel extrapolation method in the Monte Carlo shell model. Phys. Rev. C 2010, 82, 061305. [Google Scholar] [CrossRef]
- Puddu, G. An efficient method to evaluate energy variances for extrapolation methods. J. Phys. G Nucl. Part. Phys. 2012, 39, 085108. [Google Scholar] [CrossRef][Green Version]
- Stumpf, C.; Braun, J.; Roth, R. Importance-truncated large-scale shell model. Phys. Rev. C 2016, 93, 021301(R). [Google Scholar] [CrossRef]
- Roth, R.; Navrátil, P. Ab initio study of 40Ca with an importance-truncated no-core shell model. Phys. Rev. Lett. 2007, 99, 092501. [Google Scholar] [CrossRef]
- Honma, M.; Mizusaki, T.; Otsuka, T. Diagonalization of Hamiltonians for many-body systems by auxiliary field quantum Monte Carlo technique. Phys Rev. Lett. 1995, 75, 1284–1287. [Google Scholar] [CrossRef]
- Honma, M.; Mizusaki, T.; Otsuka, T. Nuclear shell model by the quantum Monte Carlo diagonalization method. Phys Rev. Lett. 1996, 77, 3315–3318. [Google Scholar] [CrossRef]
- Shimizu, N.; Abe, T.; Tsunoda, Y.; Utsuno, Y.; Yoshida, T.; Mizusaki, T.; Honma, M.; Otsuka, T. New-generation Monte Carlo shell model for the K computer era. Prog. Theor. Exp. Phys. 2012, 2012, 01A205. [Google Scholar] [CrossRef]
- Shimizu, N.; Tsunoda, Y. SO(3) quadratures in angular-momentum projection. arXiv 2022, arXiv:2205.04119. [Google Scholar]
- Utsuno, Y.; Shimizu, N.; Otsuka, T.; Abe, T. Efficient computation of Hamiltonian matrix elements between non-orthogonal Slater determinants. Comput. Phys. Commun. 2013, 184, 102–108. [Google Scholar] [CrossRef][Green Version]
- Horoi, M.; Brown, B.A.; Otsuka, T.; Honma, M.; Mizusaki, T. Shell model analysis of the 56Ni spectrum in the full pf model space. Phys. Rev. C 2006, 73, 061305(R). [Google Scholar] [CrossRef]
- Otsuka, T.; Honma, M.; Mizusaki, T. Structure of the N=Z=28 closed shell studied by Monte Carlo shell model calculation. Phys. Rev. Lett. 1998, 81, 1588–1591. [Google Scholar] [CrossRef]
- Ring, P.; Schuck, P. The Nuclear Many-Body Problem; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Brown, B.A.; Stone, N.J.; Stone, J.R.; Towner, I.S.; Hjorth-Jensen, M. Magnetic moments of the states around 132Sn. Phys. Rev. C 2005, 71, 044317. [Google Scholar] [CrossRef]
- Morris, T.D.; Simonis, J.; Stroberg, S.R.; Stumpf, C.; Hagen, G.; Holt, J.D.; Jansen, G.R.; Papenbrock, T.; Roth, R.; Schwenk, A. Structure of the lightest tin isotopes. Phys. Rev. Lett. 2018, 120, 152503. [Google Scholar] [CrossRef] [PubMed]
- Hebeler, K.; Bogner, S.; Furnstahl, R.J.; Nogga, A.; Schwenk, A. Improved nuclear matter calculations from chiral low-momentum interactions. Phys. Rev. C 2011, 83, 031301(R). [Google Scholar] [CrossRef]
- Togashi, T.; Otsuka, T.; Shimizu, N.; Utsuno, Y. E1 strength function in the Monte Carlo shell model. JPS Conf. Proc. 2018, 23, 012031. [Google Scholar] [CrossRef]



| Nuclide | Model Space | M-Scheme Dim | J-Scheme Dim |
|---|---|---|---|
| C | (p shell) | 51 | 9 |
| Si | ( shell) | 93,710 | 3372 |
| Ni | ( shell) | ||
| Y | (, ) | ||
| Sm | () | ||
| Dy | , | ||
| () |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shimizu, N. Recent Progress of Shell-Model Calculations, Monte Carlo Shell Model, and Quasi-Particle Vacua Shell Model. Physics 2022, 4, 1081-1093. https://doi.org/10.3390/physics4030071
Shimizu N. Recent Progress of Shell-Model Calculations, Monte Carlo Shell Model, and Quasi-Particle Vacua Shell Model. Physics. 2022; 4(3):1081-1093. https://doi.org/10.3390/physics4030071
Chicago/Turabian StyleShimizu, Noritaka. 2022. "Recent Progress of Shell-Model Calculations, Monte Carlo Shell Model, and Quasi-Particle Vacua Shell Model" Physics 4, no. 3: 1081-1093. https://doi.org/10.3390/physics4030071
APA StyleShimizu, N. (2022). Recent Progress of Shell-Model Calculations, Monte Carlo Shell Model, and Quasi-Particle Vacua Shell Model. Physics, 4(3), 1081-1093. https://doi.org/10.3390/physics4030071





