Abstract
A review of recent advances in the study of the energy splitting between excited isobaric analogue states is presented. Some of the experimental developments, and new approaches, associated with spectroscopy of the most proton-rich members of isobaric multiplets, are discussed. The review focuses on the immense impact of the shell-model in the analysis of energy differences and their interpretation in terms of nuclear structure phenomena.
1. Introduction
The approximate charge symmetry and charge independence of the nucleon-nucleon (NN) interaction [1] results in elegant symmetries in the behaviour of the otherwise exceptionally complex nuclear system. Examining and exploiting these isospin-related symmetries, and determining the extent to which they are broken, has become a rich field of nuclear structure physics over the last 30 years. When the symmetries are slightly broken, this provides an opportunity to observe nuclear behaviour through the lens of the well-understood electromagnetic interaction, providing a probe of nuclear structure phenomena such as pairing, particle alignments, shape changes and radii. It may even be possible to learn about the charge-dependent components of the nuclear interaction itself. Moreover, it is possible to exploit the often near-perfect isospin symmetry between pairs of analogue states to extract information other phenomena; in this review such an example is provided in the study of neutron skins.
Wigner’s isospin concept [2] provided the conceptual and mathematical foundation for describing these symmetries. All states are assigned an isospin,, quantum number, T, with a projection defined by , where N denotes the number of neutrons and Z the number of protons in a nucleus. In this formalism, the nucleon is treated as two states of the same particle with quantum number t and projection for the proton/neutron respectively. With the concept of isospin established, we now have a powerful isospin classification scheme, which enables us to map out, in isospin space, the resulting symmetries—visualised in Figure 1. Crucially, the mathematical formalism of isospin enables the treatment of the two types of fermion in the same system, allowing predictions based on the assumption of pure isospin symmetry, and the tools to model the observed deviations from that symmetry.
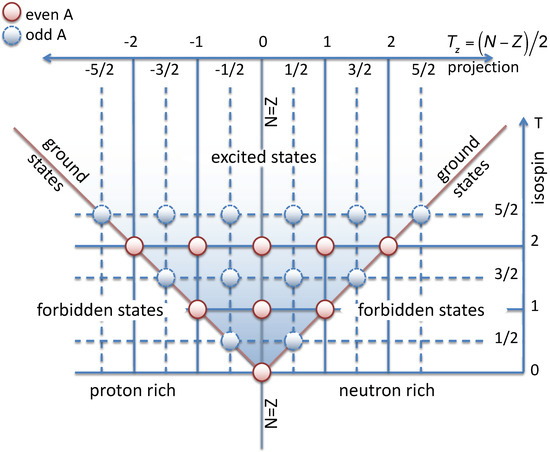
Figure 1.
A schematic visualisation of the classification of nuclear states according to the total isospin quantum numbers . Each circle represents a set of states, of given isospin, which are allowed by the Pauli principle. Note that the diagram assumes that the lowest-energy set of states in any nucleus have the lowest allowed value of isospin. This is usually, but not always, true, e.g., odd-odd nuclei (equal and odd numbers of neutrons, , and protons, ).
This short review focuses on the energy differences between excited isobaric analogue states—i.e., analogue states of the same isospin T in different members of an isobaric multiplet (different ). With perfect isospin symmetry, and in the absence of electromagnetic effects, the excitation energies would be identical. In reality the electromagnetic effects, and any other isospin-non conserving interactions, such as charge-dependent nuclear forces, lift the degeneracy. The study, and modelling, of these differences is discussed here. Two types of energy difference are usually measured: mirror energy differences (MED) for mirror nuclei () or triplet energy differences (TED) for isobaric triplets (, ). MED and TED, the differences in excitation energy, , are defined by:
respectively, with J the total angular momentum quantum number.
Developments of experimental technique, especially in the -ray spectroscopy of excited states in proton-rich nuclei, have led to a wealth of new data in recent years, allowing for experimental measurements of MED, e.g., [3,4,5,6,7,8,9,10,11], and TED, e.g., [12,13,14,15]. It is, however, the interpretation of these observations through shell-model analysis that has energised this field of study (e.g., [16,17,18,19,20,21]). This has allowed detailed nuclear structure phenomena, and especially their evolution with angular momentum and excitation along the yrast line, to be investigated in detail. This review outlines some experimental advances in Section 2 including specific case studies. The shell-model approach is outlined in Section 3 and some recent advances, made through shell-model interpretation, are discussed in Section 4.
2. Advances in Experimental Techniques and Selected Case Studies
The key challenge, in experimental measurements of energy differences between excited states of isobaric multiplets, is the typically low cross sections for, or low production rates of, the required proton-rich (i.e., , ) nuclei. Two reaction mechanisms are generally employed: fusion-evaporation reactions with stable beams at near Coulomb-barrier energies and knockout reactions from relativistic radioactive beams. For fusion-evaporation reactions, the major difficultly is the low production cross section of the neutron-evaporation channels that lead to the required proton-rich systems, leading to cross sections often less than 1 b—i.e., representing a fraction of < of the total reaction cross section. The experimental challenge is therefore the clean selection of the reaction channel to remove the huge background from proton-emission channels. In the second method, knockout from fast radioactive beams, the knockout cross sections are reasonable (∼few mb) and the identification of the desired proton-rich fragment is straightforwardly achieved with post-target magnetic spectrometers. However, here the experimental challenge comes from the potentially low secondary beam rates and from performing high-resolution -ray spectroscopy at high beam velocities, v (v/0.35–0.55, where c is the speed of light), with the associated Doppler-broadening issues. Since the last reviews of this topic, e.g., [3,4], progress has been made in addressing these two sets of challenges, which have in turn led to advances in our understanding of MED and TED.
In the following Section 2.1, Section 2.2 and Section 2.3, three example cases studies are presented which highlight the recent experimental advances. The impact of these case studies on our shell-model based interpretation of isospin-symmetry breaking, in mirror nuclei and isobaric triplets, is discussed in Section 4.
2.1. Prompt Tagging of Fusion-Evaporation Channels and a Case Study: The A = 23, Mirror Nuclei
In fusion-evaporation reactions, the required proton-rich nuclei are populated with low cross sections and, following the evaporation of at least one prompt neutron, often at the same time as evaporated charged particles. One method of selection of the desired reaction channel is to surround the target with high-efficiency neutron- and charged-particle detectors, in addition to the high-resolution -ray array. As a case study, we use the example of the mass number mirror nuclei Mg/Na [11]. This mirror pair was studied at GANIL (Grand Accélérateur National d’Ions Lourds), Caen, France, using an O beam on C target with the nuclei of interest populated through the and reaction channels, respectively. The prompt rays were detected with the EXOGAM array [22]. The prompt evaporated neutrons were detected with the Neutron Wall [23], an array of 50 liquid scintillator detectors. The proton and alpha particles were detected with DIAMANT [24], an array of 80 CsI scintillators. These highly-efficient detectors enabled a clean channel selection through the full identification of all emitted particles, allowing for the event-by-event tagging of the rays from the nuclei of interest. In this case study, the cleanliness of the channel selection allowed for the confident assignment of states in proton-rich Mg up to angular momentum/parity of , through a – coincidence analysis and using comparisons with the mirror nucleus, on which an identical analysis was performed. The identification of these states enabled MED to be determined up to high spin, and this proved crucial in the subsequent shell-model analysis. The impact of this measurement, and of the resulting shell-model analysis, connected to radii and neutron skins, is discussed in Section 4.2.
For the study of heavier proton-rich or nuclei, and especially where beam/target combinations are not possible, prompt particle tagging of the nuclei of interest becomes more challenging due to very low production cross sections and the need to identify more than one evaporated neutron. The development of more efficient, highly modular, neutron detector arrays such as NEDA [25], coupled to the improvements in high-resolution and high-efficiency -ray measurement afforded by the AGATA -ray array [26], provide exciting possibilities (e.g., [27]). The recent in-beam spectroscopy of Ru [28] through a evaporation channel, using the AGATA, DIAMANT, Neutron Wall and NEDA arrays, provides a characteristic example.
2.2. Decay Tagging of Fusion-Evaporation Channels and a Case Study: The Nucleus Se
Instead of tagging the prompt emitted rays by the prompt evaporated particles, an alternative approach to select the low cross-section neutron-evaporation channel of interest is to tag the rays by the ground-state decay emissions characteristic of the nucleus of interest. For spectroscopy of nuclei, a highly effective technique is recoil-beta tagging (RBT) [29,30], which takes advantage of cases where the ground state of the nucleus of interest () -decays to its isobaric analogue state in the neighbour. Such decays are characterised by fast, superallowed, -decays, with high end-point energy.
In the RBT approach, outlined in Figure 2, a triggerless data acquisition system is used to enable temporal correlation between prompt -ray emission at the target and the subsequent decays of the residual nuclear ground state. The recoiling nuclei are separated using a magnetic spectrometer and implanted in a highly pixellated double-sided silicon strip detector (DSSSD). The subsequent decay of the ground state of the implanted nucleus is detected in the same position as the implantation within the DSSSD and a second detector (a planar Ge detector or plastic scintillator) is used to measure the remaining energy of the -decay A correlation in time of the three events (prompt emission, implantation and -decay) and in position using the pixellated DSSSD, allows the selection of the proton-rich nucleus when a short correlation time (few 10 s of ms, typically) is required as well as a high-energy -decay
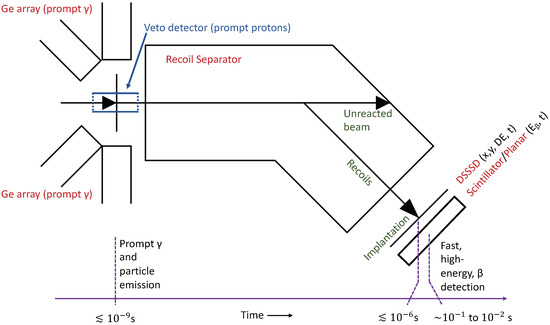
Figure 2.
A schematic diagram summarising the recoil-beta-tagging technique, [29] used for identifying prompt decays, emitted from proton-rich nuclei through tagging with the characteristic superallowed -decay of the residue ground state. See text for details.
The example of spectroscopy of Se [12] is chosen as the case study for this technique. The experiment was performed at the at the University of Jyväskylä (JYFL) using the JUROGAMII -ray array and the RITU gas filled separator [31,32], in which Se was populated through a evaporation channel. The fusion products were implanted in the DSSSD, which was followed by a planar Ge detector for detection of the high-energy positrons from the fast superallowed -decay. A key component of this experiment was the inclusion of a high-efficiency veto detector to measure prompt charged particles—the UoYTube [33] detector. This is essential to help identify, and remove, contamination in the final spectrum coming from reaction channels with evaporation of one or more charged particles. The resulting clean spectrum identified decays from states with , and , which in turn enabled the completion of the full set of isobaric analogue states up to in the triplet, allowing the TED to be extracted. The impact of this result on the understanding of isotensor isospin non-conserving interactions, within the shell model description of TED, is discussed in Section 4.1.
Since the work on Se, the same RBT approach, including charged-particle vetoing, has been applied successfully at JYFL to identify the excited states in the nuclei Kr [13] and Sr [15], and a programme using the same methodology is underway using the new MARA spectrometer [34], which additionally allows for mass selection and identification.
2.3. Knockout Reactions at Intermediate Energies and a Case Study: The Nuclei Fe and Zn
Spectroscopy of the most proton-rich systems (i.e., ) presents significant challenges for fusion reactions, since evaporation of at least three neutrons will be required to access the nuclei of interest. Indeed the majority of the recent in-beam -ray spectroscopic studies of nuclei have been performed with one- (or two-) neutron knockout reactions from relativistic fragmentation beams. The knockout reaction, being a direct process, will populate specific, usually low-lying, states, those bound states for which there is a large spectroscopic overlap between the ground-state configuration of the beam and the final state of the residue, with respect to neutron removal from a specific orbital. Whilst the range of final states can be rather limited, compared with fusion reactions, the reactions (and final spectra) can be easier to interpret, especially when combined with cross-section calculations based on a reaction model using shell-model spectroscopic factors. This, in turn, helps give confidence to the assignment of the observed states, when comparing with the analogue states in the mirror nucleus. Moreover, population of high-J states in proton-rich systems is possible in specific conditions, e.g., through knockout from isomeric states (e.g., [7]) or through two-neutron removal from a beam species with a ground state (e.g., [5]).
The case studies discussed here are the very recent works related to the observation of excited states in nuclei Zn [9] and Fe [8]. These studies have enabled the examination of , , mirror pairs, providing stringent tests of the shell-model prescription for “distant” mirror pairs (large difference in ). In both of these examples, one-neutron knockout reactions were performed on odd-A relativistic fragmentation beams. For Zn [9], the experiment was performed at the RIBF facility (Radioactive Isotope Beam Factory), at the RIKEN Nishina Center, Japan. Fragmentation of a beam of Kr at 345MeV/u produced a secondary beam of Zn fragments, separated and identified using the BigRIPS spectrometer [35]. The Be reaction target was surrounded by the DALI2+ NaI -ray array [36] and the final knockout residues identified by the Zero Degree Spectrometer [35]. For Fe [8], the experiment was performed at NCSL (National Superconducting Cyclotron Laboratory, East Lansing, MI, USA). A primary beam of Ni at 160 MeV/u was used to create a Fe fragment beam, separated using the A1900 spectrometer [37]. The reaction target was surrounded by the GRETINA Ge -ray tracking array [38] and the final knockout residues identified by the S800 Spectrograph [39].
In both the above reactions, the ground-state of the beam species was , where the Fermi-level for the odd, unpaired, neutron was in the shell. In both cases, excited states of , , and were observed ( is the highest-J state that can be populated directly). The predicted spectroscopic factors for both reactions suggest that the yrast and yrare states of , , and are expected to be directly populated, with strong populations of states, which matched the experimental observations [8,9]. It was not possible to identify decays from the yrare states in Zn, but the higher resolution of the -ray array in the Fe study enabled the yrare state decays to be tentatively identified.
In the Fe case, the experiment also used the “mirrored knockout” technique, which has proven to be especially powerful for the observation and assignment of analogue states in mirror pairs. In this approach, as well as using the Fe reaction, the mirror partner to Fe, Ti, was studied through a V reaction (this required a separate setting of the A1900 spectrometer). Since the two beam species, Fe and V, are also mirror nuclei, these reactions comprise a complete pair of “analogue” knockout reactions—i.e., reflected around the line. Isospin symmetry also implies that the spectroscopic factor for each specific knockout path (removal from a specific orbital to a specific final state) should be essentially identical in both mirror nuclei, and this should, in turn, lead to very similar distributions of knockout strength when the mirror nuclei are studied in the same experimental conditions. Since the scheme of Ti is known, this helps considerably in the assignment of their analogue states in Fe. The mirrored knockout approach was first demonstrated in [6] and has been employed in a number of other cases [10,14,40].
The spectra in Figure 3 show the resulting -ray spectra for this mirrored reaction: Figure 3a shows the V Ti reaction and Figure 3b the mirrored Fe Fe reaction. One can see very similar population distribution from the spectra. The spectra, as expected, are dominated by the decays from the states (labelled with blue squares), the states (green diamonds) and the states (red stars) [8,41]. The spectra also show the clear benefit of using a Ge -ray tracking array (i.e., GRETINA) for in-beam spectroscopy with relativistic beams. The position-sensitivity afforded by the pulse-shape-analysis approach allowed for accurate Doppler reconstruction (e.g., [38]), reducing the otherwise huge impact of Doppler broadening at these high fragment velocities.
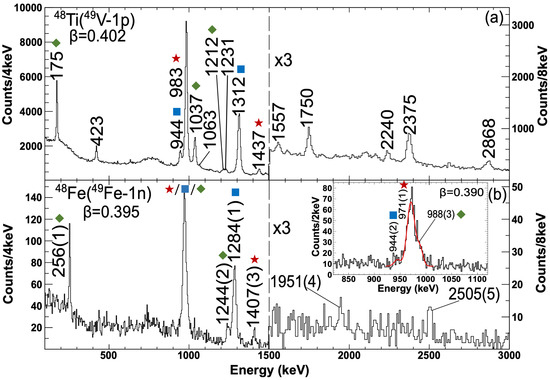
Figure 3.
The -ray spectra observed in the case study [8]. The spectra are measured with the GRETINA array following the identification and selection of the relevant incoming and outgoing fragment beams. Panel (a) shows the V Ti reaction and (b) the mirrored Fe Fe reaction. The peaks are labelled by the -ray energy and the symbols refer to the angular momentum/parity, , of the states from which these decays proceed. Decays from the states are labelled with blue squares, the states with green diamonds and the states with red stars. The insert in (b) shows how the peak around 970 keV comprises three rays. Adapted from [41].
The use of knockout reactions, and the mirrored-knockout technique, has provided a wealth of data on MED in the upper region which has, in turn, helped shed light on the role of isospin-non-conserving interactions in the shell-model analysis; see Section 4.1. The Zn case has also yielded information on how occupation of specific shell-model orbitals have a shape-driving effect; see Section 4.2.
3. Shell Model Approach for Energy Differences between Excited Analogue States
Without a reliable model to describe MED and TED as a function of J, the experimental observations of the variation of MED and TED with J cannot be interpreted in any physically meaningful sense. The shell-model approach to modelling MED and TED has transformed this field of research, allowing interpretation in terms of detailed nuclear structure phenomena including particle alignments and changes in nuclear shape/radii. Indeed, the happy coincidence that occurred around 20 years ago was that exceptionally powerful large-scale shell-model calculations were becoming available (e.g., [42,43]) in exactly the region where major experimental advances in the spectroscopy of mirror nuclei were taking place—i.e., the lower part of the shell.
If perfect isospin symmetry between analogue states is assumed, and that the contributions to MED and TED are entirely related to electromagnetic effects, there are a number of effects that can contribute to MED/TED, and their variation with excitation energy/J, which can in principle be calculated in the shell-model approach. The key factor is the multipole effect of re-coupling the angular momentum of pairs of protons, resulting in a decrease in spatial overlap of the protons, with increasing coupled J, and hence a reduction in the Coulomb energy. This is straightforward to model in large-scale shell-model calculations through the application of Coulomb matrix elements, calculated in the usual harmonic oscillator (HO) basis, in addition to the nuclear effective interaction. Initial attempts to model MED, using just this approach, were only partially successful (e.g., [44,45]) and it was concluded from that analysis that additional ingredients (including of multipole origin) were missing in the model. Indeed, better agreement was obtained using “empirical” effective Coulomb matrix elements, extracted from the mirror nuclei (e.g., [46]) or sets of ad hoc Coulomb matrix elements derived from fits to the data in the centre of the shell [44].
It was clearly important to develop a consistent shell-model approach for prediction of MED and rooted correctly in the physics. The breakthrough came with the seminal work of Zuker et al. [16], in which multipole and monopole effects were treated together in the same shell-model prescription. The model was developed and tested using MED measured in the centre of the shell, with shell-model calculations performed with the ANTOINE code [42,43] in the full space, using the mass-dependent effective interaction for the -shell, KB3G [47]. This model has formed the basis of the large-scale shell-model approach to MED and TED ever since; see, e.g., [3] for an earlier review. In this approach, the energy differences between analogue states within the shell model can be separated into four components, which can be calculated individually, so that the impact of each can be evaluated.
The first and last terms below are multipole terms. These can be calculated by determining the appropriate matrix elements of the interactions and calculating expectation values through first-order perturbation theory using a set of wave functions calculated in an isoscalar basis. The remaining two components are monopole terms, associated with bulk Coulomb effects and EM-induced shifts in single-particle energies. The four components are as follows.
3.1. Coulomb Multipole Interaction:
This multipole term accounts for the contribution of the two-body Coulomb interaction to the MED. The contribution to the MED or TED arises due to protons re-coupling angular momentum, with the resulting change in Coulomb energy, and the different numbers of active pairs between the isospin-symmetric configurations of the isobaric analogue states. It is accounted for in the shell-model simply through the application of Coulomb matrix elements, calculated in a HO basis.
3.2. Single-Particle Contributions: and
It was recognised by Zuker et al. [16] that the single-particle splitting between neutron and proton orbitals, induced by the Coulomb interaction, should be accounted for. In the shell model, this can be achieved through introducing shifts between the neutron and proton single particle levels before diagonalisation. The required Coulomb shifts () can be determined through the formalism derived by Duflo and Zuker [48]. Since MED are normalised to the ground state, this term will only become significant where configurations change along the yrast line, and where there are different orbital occupancies between protons and neutrons. This term was eventually neglected by Zuker et al. [16], since they showed that other monopole effects (see Section 3.3) dominate in the specific region being tested. However, this will not always be the case, and the term is routinely included in MED calculations.
A second single particle term, not originally included by Zuker et al. [16], is the electromagnetic spin-orbit effect (. This is a purely electromagnetic effect, affecting both proton and neutron levels, associated with the spin magnetic moment of the nucleon interacting with the Coulomb field of the nucleus. The formalism was introduced by Nolen and Schiffer [49] in their description of Coulomb displacement energies. This effect, which has opposite signs for protons and neutrons, can be significant for MED, especially where occupancy of orbitals with and (where j, l and s are the total, orbital and spin angular momentum quantum numbers) are both changing (e.g., [50]).
In calculations of MED, both these effects are routinely included. Generally, however, these contributions are expected to cancel in TED calculations, due to the double-difference method of determining TED.
3.3. Radial Contribution:
A major innovation, introduced by Lenzi et al. [51], and included in the prescription of Ref. [16], is the recognition that the nuclear radius may change along the yrast line with increasing excitation energy, resulting in a change in the bulk Coulomb energy. This, in turn, will contribute to the MED through the difference in Z between the mirror pair. It was recognised [16,51] that orbital radii depend on l and that, in the region, it was the changing occupancy of the low-l orbitals and which would drive the nucleus to larger radii.
Unlike the and terms above, for which the MED will depend on the difference between proton and neutron orbital occupancies, the term will depend on the average (proton plus neutron) occupancy of the two p orbits. The MED contribution due to the term is then calculated using
where is the total occupancy of the and orbitals for neutrons () and protons (), and accounts for the difference in Z between the mirror nuclei. The coefficient was estimated in Ref. [3] as 200 keV, based on the mirror nuclei, and this number has been used extensively in the region. In the region, the occupancy of is often negligibly small, and so is neglected in the MED calculation. However, above it should be included (e.g., [9]). In the -shell the same formalism has been used (e.g., [11,52,53]), but instead tracking the occupancy of the orbital.
Again, as with the previous term, this effect cancels in the calculation of TED.
3.4. Isospin Non-Conserving (INC) Interaction:
Zuker et al. [16] recognised that an additional multipole component is required, in the model, to account for the experimental MED and TED observed in the region (the inclusion of the HO Coulomb matrix elements were shown to be insufficient). Zuker et al. [16] extracted an additional effective INC interaction through comparing the HO Coulomb matrix elements with the MED and TED for the isospin triplet. An isovector matrix element, was derived for orbital the from the , mirror nuclei and an isotensor matrix element extracted from the TED for triplet. These matrix elements were derived as a function of angular-momentum coupling J, and it was observed that the dominant components appeared to be at for and for and both of the order of +100 keV. It was observed [16] that these additional interactions, when included in the shell-model calculations, along with the first and third terms above, allowed for a very good description of the data available at the time. It was later noted [17], once more data became available, that an isovector INC matrix element of the order of −100 keV at gives essentially very similar results to the original value of +100 keV at .
Whatever the origin of this effect, the inclusion of these additional effective isovector and isotensor interactions appeared to be an essential inclusion in the modelling of MED and TED, respectively, at least in the region. The importance of inclusion of such INC isovector and/or isotensor interactions has also been investigated in the shell [11,52] and in the upper shell (e.g., [18,21]).
4. Recent Advances Based on Shell-Model Analysis
The shell-model approach described in Section 3 has formed the backbone of this field of study over the last two decades. The strength of the shell-model prescription is the simultaneous inclusion of the multipole and monopole effects, since the relative scale of the contributions of the four components described in Section 3 changes from case to case. Examples of this are the and mirror nuclei with [8,54], one of which is a case study in Section 2.3. Each of these pairs of mirror nuclei, which lie in the exact centre of the shell, would also be “cross conjugate” nuclei in the assumption of a single isolated shell. In this extreme assumption, which is not bad for the shell, all multipole MED would be zero since the number of protons in one nucleus is the same as the number of proton holes in the mirror partner. In the case of the , mirrors [54] this appears to be the case, and the experimental MED is largely accounted for by the monopole term. This nicely demonstrates the power of the approach in accounting for a range of phenomena.
In this Section, some of the latest developments in this field, specifically relating to shell-model analysis, are discussed, focussing in particular on the results from the case studies presented in Section 2.
4.1. Isospin-Non-Conserving Interactions
One of the key areas of study has been to map out the influence of the additional effective INC interactions (see Section 3.4). In the shell, a large amount of data have become available which has enabled a more complete numerical evaluation of the influence of these INC effects. In Refs. [17,18], all available MED and TED data in the shell (at that time) were gathered and modelled using a consistent shell-model approach. The shell-model MED and TED were then fitted to the experimental data, allowing the magnitude of the J-dependent INC terms and to vary freely; the former (isovector) term was derived from the MED and the latter (isotensor) term from the TED. The key results are shown in Table 1. The results of two types of fit are presented: one where a single matrix element is considered (at a coupling of ) and the second where all four matrix elements were allowed to be non-zero. Only matrix elements were considered. See Refs. [17,18] for a full discussion of the analysis.

Table 1.
Data collected from Refs. [17,18]. The isovector and isotensor INC matrix elements, for pairs, extracted from fits across the whole shell (see text for details). For the full fits, a monopole centroid has been subtracted as part of the fitting process to allow the J-dependence to be fully evaluated. The numbers in the parentheses are the errors on the fitted values.
Two key results emerged from the analysis. Firstly, for the purpose of MED and TED, it is having the correct J-dependence of these matrix elements that is crucial in the determination of the theoretical MED and TED; the extracted results do indeed have a strong J-dependence. Secondly, it was shown that a single matrix element at gives, essentially, as good a fit as allowing all four matrix elements to vary. Hence a prescription in which a single INC matrix element ( or ) is included is now the commonly used approach for modelling MED and TED (e.g., [8,9,10,11,18,52]). The results in Table 1 suggest that an isovector matrix element of the order of keV is required for MED and an isotensor matrix element of the order of keV is required for TED. These conclusions are essentially consistent with the original study of Zuker et al. [16]. Indeed, the fits in Ref. [17] indicates that a positive isovector matrix element at (as was originally extracted in [16]) has a similar effect as a negative matrix element at . Again, the key contributor is the J-dependence, not the absolute magnitude, of these matrix elements.
Figure 4 shows experimental and shell-model MED in the shell. The solid blue lines contain the full shell-model calculation, performed exactly as described in Section 3, with a single isovector matrix element of keV, the figure extracted from the fits [17] (see Table 1). The red dashed lines show the calculations without included. It is clear from data like these the crucial role that this effective INC interaction has, especially at low J, in the description of MED in the region.
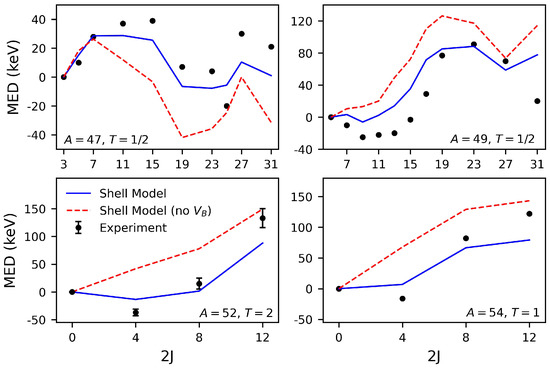
Figure 4.
Experimental and shell-model MED in the shell. The solid blue lines contain the full shell-model calculation, including a single isovector INC matrix element of keV. See text for details. The red dashed lines show the calculations without included. Data for “Shell Model (no )” originally presented in Ref. [17]. Where error bars are not visible, they are smaller than the data markers.
It is certainly of interest to understand the importance of this effect in other mass regions. In general, this is more challenging in regions where there are more orbitals in play and where the influence of the monopole contributions may be large. In the shell, inclusion of the INC term also appears to be necessary, with matrix elements of the same order as described above [11,52]. In the upper shell, it has been challenging to find a consistent picture for MED, and this remains an open question, e.g., [21]. However, a very recent analysis of the , mirror nuclei has been performed [9], using the same modelling as that presented for the , mirrors later in Section 4.2. In the mirror nuclei, the shell is expected to be almost fully filled and so the MED will be insensitive to the inclusion of in the orbital, but will be sensitive to its inclusion in the other orbitals. The analysis indicated that a much better match to the experimental MED was obtained when a negative matrix element for was included for all the orbitals.
The physical origin of the isovector INC interaction in the modelling of MED remains unclear, and the analysis presented in Reference [17] suggests that the matrix elements and their J dependence (see Table 1) cannot be reconciled easily with the properties of known nuclear charge-symmetry breaking interaction. This therefore points to other electromagnetic contributions missing in the model; see Ref. [17] for a discussion.
Turning to TED, and the impact of the isotensor INC interaction , the case study of Se (Section 2) and the , isobaric triplet provides a practical example. The successful spectroscopy of Se [12] up to completed the isobaric triplet and allowed for TED to be determined to . The experimental data are presented in Figure 5. The large negative TED observed are typical of all triplets; see, e.g., [18]. Figure 5 also contains the result of the shell-model calculation performed following the prescription in Section 3 and using the JUN45 interaction [55]; see black line. The calculations were originally performed in Ref. [18], and updated for this review. The shell-model calculation does not contain calculations related to the two monopole components ( and ) since these effectively cancel to zero due to the double-difference method of calculating the TED. Hence, only the two multipole interactions, (Coulomb) and (INC), are relevant for this calculation. The shell-model results are plotted in Figure 5, for different strengths of the INC parameter , for couplings. The blue dotted line shows (i.e., just contributes), the black solid line has keV and the red dashed line shows keV. The calculation with keV (black line) is consistent with the prescription in [16] and with the data in Table 1. The interaction was applied equally to all orbits in the valence space although, in this case, it is the contribution from the that dominates [18].
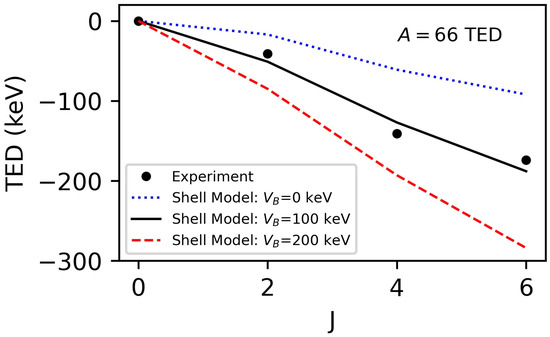
Figure 5.
Experimental and shell-model TED for the , isobaric triplet. The black line shows the full shell-model calculation, including a single isotensor INC matrix element of keV in all orbitals in the valence space. The other lines show the shell-model results using different strengths of the INC parameter, . See text for details. The calculations presented are based on the approach of Ref. [18]. The error bars on the data points are smaller than the data markers.
Two conclusions can be drawn from the comparison with the shell-model results when keV is applied. The first is that the agreement with experimental TED would fail badly without the inclusion of this additional effective isotensor INC term. Secondly, it can be shown from this analysis [18] that the two components, (Coulomb) and (INC), have approximately the same magnitude when is applied. This is not that surprising since, as noted above, it is the J-dependence of the matrix elements that influences the TED, and the Coulomb matrix elements generally vary by around 100 keV from to . The key point is that the contribution of the isotensor INC term, to the TED, is as large as that of the Coulomb two-body interaction.
Lenzi et al. [18] performed a similar analysis for all triplets between and , using four different interactions, as appropriate to the valence space being used, and applying an isotensor matrix element of keV in all orbitals. A remarkably consistent picture emerged, with observations very similar to that for ; i.e., that the contribution is significant, and required, across the full range of triplets studied. An important point to note is that, for TED, we have seen that the monopole terms of the shell-model prescription do not contribute significantly. Therefore, the TED is essentially only sensitive to multipole effects and thus represents an observable that can shed light on the nature of effective isospin-non conserving interactions. Since the size of the required interaction appears to be largely independent of mass region, orbital or shell-model interaction, it is natural to examine whether or not the true charge dependence of the nuclear interaction [1] could be the origin. It was shown by Ormand and Brown [56] that nucleon scattering data suggests that the nuclear interaction is approximately 2–3% stronger than the and interactions. The analysis of Reference [18] indeed indicated that the scale, and sign, of the effective isotensor interaction interaction appear to be approximately consistent with that estimate for the charge-dependence of the NN interaction. This indeed highlights the power of using energy differences, coupled to a reliable shell-model calculation, to probe effective nucleon interactions.
4.2. Nuclear Radii and Neutron Skins
In Section 3, it was demonstrated how occupation of low-l orbitals can contribute to MED and that this can be accounted for in the shell model through tracking of the total (proton plus neutron) occupation of low-l orbits: in the region this would be the occupancy of the orbitals. This provides the first indication that MED can yield real physical insight into changes in nuclear radii.
Recently, Bonnard et al. [19] have investigated the role of the occupation of low-l “halo” orbitals in driving radii and on their influence in the development of neutron skins. They have been able to show that the effect on the total radius of occupation of one of the low-l orbitals is strongly dependent on the extent of the occupation of that orbital. For example, in the shell, the occupancy of the p orbits is generally expected to be low (the shell-model occupancies are ≪ 1). Moreover, the parameterisation of the term (see Section 3) has been optimised for that region. However, in heavier nuclei, once the shell is full, the occupancies of the p orbits will increase significantly, and the work of Bonnard et al. [19] suggests that the radial-driving effect of the p orbit will be significantly smaller in this circumstance.
This has been investigated in the , mirror nuclei following the spectroscopy of Zn [9], discussed as a case study in Section 2.3. Figure 6 shows the experimental MED compared with the shell-model calculations. These calculations have been performed with a modified KB3G interaction, KB3GR (Caurier, E.; Poves, A. Unpublished work) which has been optimised for this region. The calculation using the standard parameterisation for the radial term ( keV, see Equation (3)) is shown by the red dashed line. However, in this case, protons in Zn (and neutrons in its mirror, Fe) are already occupying the orbital, and the results of Reference [19] therefore imply that the radial term is likely to be overestimated. Therefore, in the analysis of the mirrors, Fernández et al. [9] reduced the parameter (see Equation (3)) for the occupancies, from the standard value of 200 keV. The parameter for the , which remains largely unoccupied, was left unchanged. The results can be seen in Figure 6 where a smaller value of keV is applied for the orbital; see solid blue line. This gives a much better description, in qualitative agreement with the results of Bonnard et al. [19]. It is also noteworthy that the multipole contributions to the MED for this mirror pair turn out to be small, due to particle-hole symmetry; both nuclei have two particles and two holes with respect to Ni. This makes this mirror pair sensitive to the remaining significant monopole contribution, , making this an ideal test case to examine radial effects.
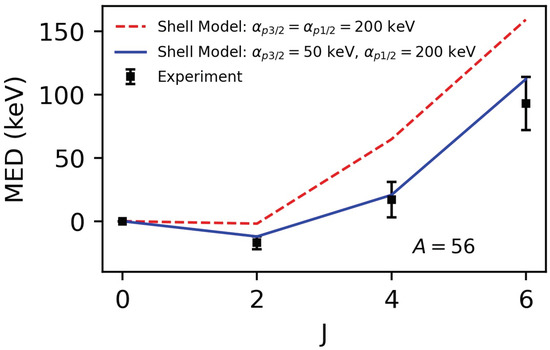
Figure 6.
Results from [9]. The experimental MED for the , mirror nuclei compared with the results of shell-model calculations performed with the KB3GR interaction. The model uses the standard parameterisation, but with a varying value of the scaling parameter, (Equation (3)), used in the determination of the radial contribution to the MED due to the occupation of the orbital. See text for details.
As well as the total nuclear radius having an impact on the Coulomb energy, and hence MED, for a mirror pair, any difference between the neutron and proton radii (i.e., neutron skin) could also have an effect on MED if, as isospin symmetry would suggest, the neutron radius of one member of a mirror pair is equal to the proton radius of the other. This idea, also inspired by the study in Ref. [19], was pursued in the analysis of the mirror nuclei by Boso et al. [11], work that was made possible by the spectroscopy of Mg, our remaining case study (see Section 2.1). The analysis was undertaken using a no-core shell-model approach based on the monopole-corrected interaction (MCI) [57], which contains all the necessary Coulomb and charge-symmetry breaking terms. The MCI matrix elements were computed using different size parameters for neutrons and protons (i.e., allowing for the possibility of different neutron and proton radii). Whilst the proton radius of Na is experimentally known, its neutron radius is not. The neutron radius (and hence neutron skin) was then determined following the method of Duflo and Zuker [48] by adjusting the neutron radius until the experimental ground state mirror displacement energy (MDE) is reproduced by the model. The method was then repeated state by state, in order to reproduce the MED, allowing for the variation of the skin thickness as a function of J for the excited states.
Full details can be found in Ref. [11] but the key results are shown in Figure 7. The neutron skin thickness parameter, , is plotted using the blue circles. , in the paramaterisation of Duflo and Zuker [48], is proportional to difference between the neutron and proton rms (root mean square) radii and is defined as , where the exponential factor is a correction term, applied for light nuclei [48]. These results show that the neutron skin, as derived from the MED, varies significantly from state to state. This, in turn, implies neutron skin sizes, and their variation with excitation energy/J, can influence the MED and, if so, it is an effect currently not included in the MED models. Another key observation is that the skin thickness, has a correlation with the difference between the neutron and proton occupancies of the orbit. This difference is plotted as in Figure 7 (red squares). This analysis was repeated for a range of other odd-A mirror nuclei in the shell, and similar variations of neutron-skin thickness with J were suggested by that analysis; see Ref. [11] for the full results and discussion. Inclusion of effects of this kind in the calculation of MED is clearly an exciting future topic for investigation.
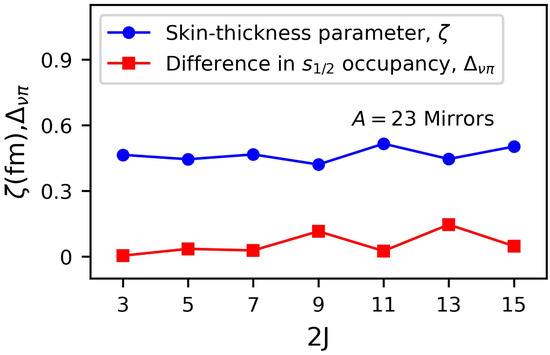
Figure 7.
Data from Ref. [11]. Blue circles: the neutron skin thickness parameter, , defined in Ref. [48], which is proportional to difference between the neutron and proton rms radii. This parameter has been extracted through fitting to the measured MED. Red squares: , the difference between the neutron and proton occupancies of the orbit, for each state. See text and Ref. [11] for details.
5. Summary and Outlook
In this short review, some of the latest experimental advances have been presented. The advent of the new radioactive beam facilities will allow some of these techniques to be applied to allow spectroscopy of the most exotic proton-rich systems, or to perform high precision tests of the predictions that come from the isospin formalism. The high-intensity intermediate-energy fragmentation beams available at the upcoming FRIB (Facility for Rare Isotope Beams, East Lansing, MI, USA) and FAIR (Facility for Antiproton and Ion Research, Darmstadt, Germany) facilities are expected to have particular impact. Techniques such as those described Section 2.3, can be applied to access nuclei with large proton excess and pursue spectroscopy of mirror nuclei in the upper half of the region. The high-velocity beams also allow for a range of lifetime-measurement techniques to be applied, allowing for precision tests of the isospin-dependence of transition strengths. From a theoretical perspective, it will be especially important to develop a better understanding of the origin of the effective isovector isospin non-conserving (INC) interactions (see Section 4.1). Moreover, the link between mirror energy differences (MED) and radii/neutron skin is especially exciting and should be developed further in future shell-model work. As the study of energy splitting between isobaric multiplets develops in the future, the exciting developments in the shell-model, some of which have been discussed, will have crucial role to play.
Funding
This research was funded by the UKRI (UK Research and Innovation) Science and Technology Facilities Council under grant number ST/V001108/1.
Data Availability Statement
No new data are presented in this work. The data used can be found in the corresponding references.
Conflicts of Interest
The author declares no conflict of interest.
References
- Machleidt, R.; Slaus, I. The nucleon-nucleon interaction. J. Phys. Nucl. G Part. Phys. 2001, 27, R69–R108. [Google Scholar] [CrossRef]
- Wigner, E. On the consequences of the symmetry of the nuclear Hamiltonian on the spectroscopy of nuclei. Phys. Rev. 1937, 51, 106–119. [Google Scholar] [CrossRef]
- Bentley, M.A.; Lenzi, S.M. Coulomb energy differences between high-spin states in isobaric multiplets. Prog. Part. Nucl. Phys. 2007, 59, 497–561. [Google Scholar] [CrossRef]
- Ekman, J.; Fahlander, C.; Rudolph, D. Mirror symmetry in the upper fp shell. Mod. Phys. Lett. A 2005, 20, 2977–2992. [Google Scholar] [CrossRef]
- Davies, P.J.; Bentley, M.A.; Henry, T.W.; Simpson, E.C.; Gade, A.; Lenzi, S.M.; Baugher, T.; Bazin, D.; Berryman, J.S.; Bruce, A.M.; et al. Mirror energy differences at large isospin studied through direct two-nucleon knockout. Phys. Rev. Lett. 2013, 111, 072501. [Google Scholar] [CrossRef]
- Milne, S.A.; Bentley, M.A.; Simpson, E.C.; Dodsworth, P.; Baugher, T.; Bazin, D.; Berryman, J.S.; Bruce, A.M.; Davies, P.J.; Diget, C.A.; et al. Mirrored one-nucleon knockout reactions to the Tz = ±A=53 mirror nuclei. Phys. Rev. C 2016, 93, 024318. [Google Scholar] [CrossRef]
- Milne, S.A.; Bentley, M.A.; Simpson, E.C.; Baugher, T.; Bazin, D.; Berryman, J.S.; Bruce, A.M.; Davies, P.J.; Diget, C.A.; Gade, A.; et al. Isospin symmetry at high spin studied via nucleon knockout from isomeric states. Phys. Rev. Lett. 2016, 117, 082502. [Google Scholar] [CrossRef]
- Yajzey, R.; Bentley, M.A.; Simpson, E.C.; Haylett, T.; Uthayakumaar, S.; Bazin, D.; Belarge, J.; Bender, P.C.; Davies, P.J.; Elman, B.; et al. Spectroscopy of the Tz = ±2 mirror nuclei 48Fe/48Ti using mirrored knockout reactions. Phys. Lett. B 2021, 823, 136757. [Google Scholar] [CrossRef]
- Fernández, A.; Jungclaus, A.; Doornenbal, P.; Bentley, M.A.; Lenzi, S.M.; Rudolph, D.; Browne, F.; Cortés, M.L.; Koiwai, T.; Taniuchi, R.; et al. Mirror energy differences above the 0f7/2 shell: First γ-ray spectroscopy of the Tz = −2 nucleus 56Zn. Phys. Lett. B 2021, 823, 136784. [Google Scholar] [CrossRef]
- Uthayakumaar, S.; Bentley, M.A.; Simpson, E.C.; Haylett, T.; Yajzey, R.; Lenzi, S.M.; Satuła, W.; Bazin, D.; Belarge, J.; Bender, P.C.; et al. Spectroscopy of the T = A = 47 and A = 45 mirror nuclei via one- and two-nucleon knockout reactions. Phys. Rev. C 2022, 106, 024327. [Google Scholar] [CrossRef]
- Boso, A.; Lenzi, S.M.; Recchia, F.; Bonnard, J.; Zuker, A.P.; Aydin, S.; Bentley, M.A.; Cederwall, B.; Clement, E.; de France, G.; et al. Neutron skin effects in mirror energy differences: The case of 23Mg−23Na. Phys. Rev. Lett. 2018, 121, 032502. [Google Scholar] [CrossRef]
- Ruotsalainen, P.; Jenkins, D.G.; Bentley, M.A.; Wadsworth, R.; Scholey, C.; Auranen, K.; Davies, P.J.; Grahn, T.; Greenlees, P.T.; Henderson, J.; et al. Spectroscopy of proton-rich 66Se up to Jπ = 6+: Isospin-breaking effect in the A = 66 isobaric triplet. Phys. Rev. C 2013, 88, 041308. [Google Scholar] [CrossRef]
- Debenham, D.M.; Bentley, M.A.; Davies, P.J.; Haylett, T.; Jenkins, D.G.; Joshi, P.; Sinclair, L.F.; Wadsworth, R.; Ruotsalainen, P.; Henderson, J.; et al. Spectroscopy of 70Kr and isospin symmetry in the T = 1fpg shell nuclei. Phys. Rev. C 2016, 94, 054311. [Google Scholar] [CrossRef]
- Wimmer, K.; Korten, W.; Arici, T.; Doornenbal, P.; Aguilera, P.; Algora, A.; Ando, T.; Baba, H.; Blank, B.; Boso, A.; et al. Shape coexistence and isospin symmetry in A = 70 nuclei: Spectroscopy of the Tz = −1 nucleus 70Kr. Phys. Lett. B 2018, 785, 441–446. [Google Scholar] [CrossRef]
- Henderson, J.; Jenkins, D.G.; Kaneko, K.; Ruotsalainen, P.; Sarriguren, P.; Auranen, K.; Bentley, M.A.; Davies, P.J.; Görgen, A.; Grahn, T.; et al. Spectroscopy on the proton drip-line: Probing the structure dependence of isospin nonconserving interactions. Phys. Rev. C 2014, 90, 051303. [Google Scholar] [CrossRef]
- Zuker, A.P.; Lenzi, S.M.; Martínez-Pinedo, G.; Poves, A. Isobaric multiplet yrast energies and isospin nonconserving forces. Phys. Rev. Lett. 2002, 89, 142502. [Google Scholar] [CrossRef]
- Bentley, M.A.; Lenzi, S.M.; Simpson, S.A.; Diget, C.A. Isospin-breaking interactions studied through mirror energy differences. Phys. Rev. C. 2015, 92, 024310. [Google Scholar] [CrossRef]
- Lenzi, S.M.; Bentley, M.A.; Lau, R.; Diget, C.A. Isospin-symmetry breaking corrections for the description of triplet energy differences. Phys. Rev. C. 2018, 98, 054322. [Google Scholar] [CrossRef]
- Bonnard, J.; Lenzi, S.M.; Zuker, A.P. Neutron skins and halo orbits in the sd and pf shells. Phys. Rev. Lett. 2016, 116, 212501. [Google Scholar] [CrossRef]
- Kaneko, K.; Sun, Y.; Mizusaki, T.; Tazaki, S. Variation in displacement energies Due to isospin-nonconserving forces. Phys. Rev. Lett. 2013, 110, 172505. [Google Scholar] [CrossRef] [Green Version]
- Kaneko, K.; Sun, Y.; Mizusaki, T.; Tazaki, S. Isospin nonconserving interaction in the T = 1 analogue states of the mass-70 region. Phys. Rev. C 2014, 89, 031302. [Google Scholar] [CrossRef]
- Azaiez, F. EXOGAM: A γ-ray spectrometer for radioactive beams. Nucl. Phys. A 1999, 654, 1003c–1008c. [Google Scholar] [CrossRef]
- Skeppstedt, O.; Roth, H.A.; Lindström, L.; Wadsworth, R.; Hibbert, I.; Kelsall, N.; Jenkins, D.G.; Grawe, H.; Górska, M.; Moszyński, M.; et al. The EUROBALL neutron wall–design and performance tests of neutron detectors. Nucl. Instrum. Meth. Phys. Res. A 1999, 421, 531–541. [Google Scholar] [CrossRef]
- Scheurer, J.N.; Aiche, M.; Aleonard, M.M.; Barreau, G.; Bourgine, F.; Boivin, D.; Cabaussel, D.; Chemin, J.F.; Doan, T.P.; Goudour, J.P.; et al. Improvements in the in-beam γ-ray spectroscopy provided by an ancillary detector coupled to a Ge γ-spectrometer: The DIAMANT-EUROGAM II example. Nucl. Instrum. Meth. Phys. Res. A 1997, 385, 501–510. [Google Scholar] [CrossRef]
- Valiente-Dobón, J.J.; Jaworski, G.; Goasduff, A.; Egea, F.J.; Modamio, V.; Hüyük, T.; Triossi, A.; Jastrząb, M.; Söderström, P.A.; Di Nitto, A.; et al. NEDA—NEutron Detector Array. Nucl. Instrum. Meth. Phys. Res. A 2019, 927, 81–86. [Google Scholar] [CrossRef]
- Akkoyun, S.; Algora, A.; Alikhani, B.; Ameil, F.; de Angelis, G.; Arnold, L.; Astier, A.; Ataç, A.; Aubert, Y.; Aufranc, C.; et al. AGATA—Advanced GAmma Tracking Array. Nucl. Instrum. Meth. Phys. Res. A 2012, 668, 26–58. [Google Scholar] [CrossRef]
- Korten, W.; Atac, A.; Beaumel, D.; Bednarczyk, P.; Bentley, M.A.; Benzoni, G.; Boston, A.; Bracco, A.; Cederkäll, J.; Cederwall, B.; et al. Physics opportunities with the Advanced Gamma Tracking Array: AGATA. Eur. Phys. J. A 2020, 56, 137. [Google Scholar] [CrossRef]
- Cederwall, B.; Liu, X.; Aktas, O.; Ertoprak, A.; Zhang, W.; Qi, C.; Clément, E.; de France, G.; Ralet, D.; Gadea, A.; et al. Isospin Properties of Nuclear Pair Correlations from the Level Structure of the Self-Conjugate Nucleus 88Ru. Phys. Rev. Lett. 2020, 124, 062501. [Google Scholar] [CrossRef]
- Steer, A.; Jenkins, D.; Glover, R.; Bondili, S.N.; Pattabiraman, N.; Wadsworth, R.; Eeckhaudt, S.; Grahn, T.; Greenlees, P.; Jones, P.; et al. Recoil-beta tagging: A novel technique for studying proton-drip-line nuclei. Nucl. Instrum. Meth. Phys. Res. A 2006, 565, 630–636. [Google Scholar] [CrossRef]
- Nara Singh, B.S.; Steer, A.N.; Jenkins, D.G.; Wadsworth, R.; Bentley, M.A.; Davies, P.J.; Glover, R.; Pattabiraman, N.S.; Lister, C.J.; Grahn, T.; et al. Coulomb shifts and shape changes in the mass 70 region. Phys. Rev. C 2007, 75, 061301. [Google Scholar] [CrossRef] [Green Version]
- Leino, M.; Äystö, J.; Enqvist, T.; Heikkinen, P.; Jokinen, A.; Nurmia, M.; Ostrowski, A.; Trzaska, W.; Uusitalo, J.; Eskola, K.; et al. Gas-filled recoil separator for studies of heavy elements. Nucl. Instrum. Meth. Phys. Res. B 1995, 99, 653–656. [Google Scholar] [CrossRef]
- Sarén, J.; Uusitalo, J.; Leino, M.; Sorri, J. Absolute transmission and separation properties of the gas-filled recoil separator RITU. Nucl. Instrum. Meth. Phys. Res. A 2011, 654, 508–521. [Google Scholar] [CrossRef]
- Henderson, J.; Ruotsalainen, P.; Jenkins, D.G.; Scholey, C.; Auranen, K.; Davies, P.J.; Grahn, T.; Greenlees, P.T.; Henry, T.W.; Herzáň, A.; et al. Enhancing the sensitivity of recoil-beta tagging. J. Instrum. 2013, 8, P04025. [Google Scholar] [CrossRef]
- Sarén, J.; Uusitalo, J.; Leino, M.; Greenlees, P.; Jakobsson, U.; Jones, P.; Julin, R.; Juutinen, S.; Ketelhut, S.; Nyman, M.; et al. The new vacuum-mode recoil separator MARA at JYFL. Nucl. Instrum. Meth. Phys. Res. B 2008, 266, 4196–4200. [Google Scholar] [CrossRef]
- Kubo, T.; Kameda, D.; Suzuki, H.; Fukuda, N.; Takeda, H.; Yanagisawa, Y.; Ohtake, M.; Kusaka, K.; Yoshida, K.; Inabe, N.; et al. BigRIPS separator and ZeroDegree spectrometer at RIKEN RI Beam Factory. Prog. Theor. Exp. Phys. 2012, 2012. [Google Scholar] [CrossRef]
- Takeuchi, S.; Motobayashi, T.; Togano, Y.; Matsushita, M.; Aoi, N.; Demichi, K.; Hasegawa, H.; Murakami, H. DALI2: A NaI(Tl) detector array for measurements of γ rays from fast nuclei. Nucl. Instrum. Meth. Phys. Res. A 2014, 763, 596–603. [Google Scholar] [CrossRef]
- Morrissey, D.J.; Sherrill, B.M.; Steiner, M.; Stolz, A.; Wiedenhoever, I. Commissioning the A1900 projectile fragment separator. Nucl. Instrum. Meth. Phys. Res. B 2003, 204, 90–96. [Google Scholar] [CrossRef]
- Weisshaar, D.; Bazin, D.; Bender, P.C.; Campbell, C.M.; Recchia, F.; Bader, V.; Baugher, T.; Belarge, J.; Carpenter, M.P.; Crawford, H.L.; et al. The performance of the γ-ray tracking array GRETINA for γ-ray spectroscopy with fast beams of rare isotopes. Nucl. Instrum. Meth. Phys. Res. A 2017, 847, 187–198. [Google Scholar] [CrossRef]
- Bazin, D.; Caggiano, J.A.; Sherrill, B.M.; Yurkon, J.; Zeller, A. The S800 spectrograph. Nucl. Instrum. Meth. Phys. Res. B 2003, 204, 629–633. [Google Scholar] [CrossRef]
- Spieker, M.; Gade, A.; Weisshaar, D.; Brown, B.A.; Tostevin, J.A.; Longfellow, B.; Adrich, P.; Bazin, D.; Bentley, M.A.; Brown, J.R.; et al. One-proton and one-neutron knockout reactions from N=Z = 2856Ni to the A = 55 mirror pair 55Co and 55Ni. Phys. Rev. C 2019, 99, 051304. [Google Scholar] [CrossRef] [Green Version]
- Yajzey, R. The Isospin Symmetry of the A = 48, T = 2 Mirror Nuclei Studied Through the Mirrored Knockout Technique. Ph.D. Thesis, University of York, York, UK, 2022. Available online: https://etheses.whiterose.ac.uk/30822/ (accessed on 6 July 2022).
- Caurier, E.; Nowacki, F. Present Status of Shell Model Techniques. Acta Phys. Pol. B 1999, 30, 705–714. Available online: https://www.actaphys.uj.edu.pl/R/30/3/705 (accessed on 3 August 2022).
- Caurier, E.; Martínez-Pinedo, G.; Nowacki, F.; Poves, A.; Zuker, A.P. The shell model as a unified view of nuclear structure. Rev. Mod. Phys. 2005, 77, 427–488. [Google Scholar] [CrossRef]
- Bentley, M.A.; O’Leary, C.D.; Poves, A.; Martinez-Pinedo, G.; Appelbe, D.E.; Bark, R.A.; Cullen, D.M.; Ertürk, S.; Maj, A. Mirror and valence symmetries at the centre of the f7/2 shell. Phys. Lett. B 1998, 437, 243–248. [Google Scholar] [CrossRef]
- Williams, S.J.; Bentley, M.A.; Warner, D.D.; Bruce, A.M.; Cameron, J.A.; Carpenter, M.P.; Fallon, P.; Frankland, L.; Gelletly, W.; Janssens, R.V.F.; et al. Anomalous Coulomb matrix elements in the f7/2 shell. Phys. Rev. C 2003, 68, 011301. [Google Scholar] [CrossRef]
- Bentley, M.A.; Williams, S.J.; Joss, D.T.; O’Leary, C.D.; Bruce, A.M.; Cameron, J.A.; Carpenter, M.P.; Fallon, P.; Frankland, L.; Gelletly, W.; et al. Mirror symmetry at high spin in 51Fe and 51Mn. Phys. Rev. C 2000, 62, 051303. [Google Scholar] [CrossRef]
- Poves, A.; Sánchez-Solano, J.; Caurier, E.; Nowacki, F. Shell model study of the isobaric chains A=50, A = 51 and A = 52. Nucl. Phys. A 2001, 694, 157–198. [Google Scholar] [CrossRef]
- Duflo, J.; Zuker, A.P. Mirror displacement energies and neutron skins. Phys. Rev. C 2002, 66, 051304. [Google Scholar] [CrossRef]
- Nolen, J.A.; Schiffer, J.P. Coulomb Energies. Annu. Rev. Nucl. Sci. 1969, 19, 471–526. [Google Scholar] [CrossRef]
- Ekman, J.; Rudolph, D.; Fahlander, C.; Zuker, A.P.; Bentley, M.A.; Lenzi, S.M.; Andreoiu, C.; Axiotis, M.; de Angelis, G.; Farnea, E.; et al. Unusual isospin-breaking and isospin-mixing effects in the A = 35 mirror nuclei. Phys. Rev. Lett. 2004, 92, 132502. [Google Scholar] [CrossRef]
- Lenzi, S.M.; Mărginean, N.; Napoli, D.R.; Ur, C.A.; Zuker, A.P.; de Angelis, G.; Algora, A.; Axiotis, M.; Bazzacco, D.; Belcari, N.; et al. Coulomb energy differences in T = 1 mirror rotational bands in 50Fe and 50Cr. Phys. Rev. Lett. 2001, 87, 122501. [Google Scholar] [CrossRef]
- Lenzi, S.M.; Lau, R. A systematic study of mirror and triplet energy differences. J. Phys. Conf. Ser. 2015, 580, 012028. [Google Scholar] [CrossRef]
- Testov, D.A.; Boso, A.; Lenzi, S.M.; Nowacki, F.; Recchia, F.; de Angelis, G.; Bazzacco, D.; Colucci, G.; Cottini, M.; Galtarossa, F.; et al. High-spin intruder states in the mirror nuclei 31S and 31P. Phys. Rev. C 2021, 104, 024309. [Google Scholar] [CrossRef]
- Bentley, M.A.; Chandler, C.; Taylor, M.J.; Brown, J.R.; Carpenter, M.P.; Davids, C.; Ekman, J.; Freeman, S.J.; Garrett, P.E.; Hammond, G.; et al. Isospin symmetry of odd-odd mirror nuclei: Identification of excited states in N = Z−248Mn. Phys. Rev. Lett. 2006, 97, 132501. [Google Scholar] [CrossRef] [PubMed]
- Honma, M.; Otsuka, T.; Mizusaki, T.; Hjorth-Jensen, M. New effective interaction for f5pg9-shell nuclei. Phys. Rev. C 2009, 80, 064323. [Google Scholar] [CrossRef]
- Ormand, W.E.; Brown, B.A. Empirical isospin-nonconserving hamiltonians for shell-model calculations. Nucl. Phys. A 1989, 491, 1–23. [Google Scholar] [CrossRef]
- Bonnard, J.; Zuker, A.P. Radii in the sd shell and the 1s1/2 “halo” orbit: A game changer. J. Phys. Conf. Ser. 2018, 1023, 012016. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).