Nonextensive Statistics in High Energy Collisions
Abstract
1. Introduction
2. Momentum Distributions
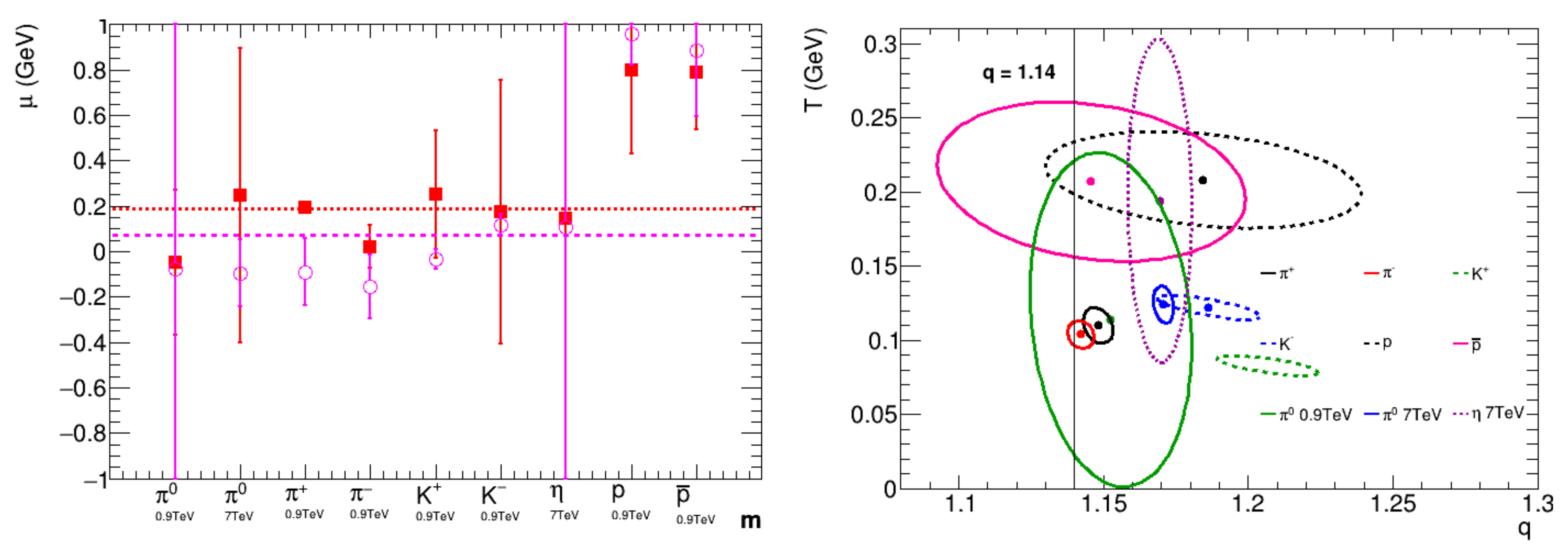
3. Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wilk, G.; Włodarczyk, W. Quasi-power laws in multiparticle production processes. Chaos Solit. Fract. 2015, 81, 487–496. [Google Scholar] [CrossRef]
- Cleymans, J.; Hippolyte, B.; Paradza, M.W.; Sharma, N. Hadron resonance gas model and high multiplicities in p-p, p-Pb and Pb-Pb collisions at the LHC. Int. J. Mod. Phys. 2019, 28, 1940002. [Google Scholar] [CrossRef]
- Oeschler, H.; Cleymans, J.; Hippolyte, B.; Redlich, K.; Sharma, N. Ratios of strange hadrons to pions in collisions of large and small nuclei. Eur. Phys. J. 2017, 77, 584. [Google Scholar] [CrossRef][Green Version]
- Tsallis, C. Possible Generalization of the Boltzmann-Gibbs Statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Cleymans, J.; Worku, D. The Tsallis distribution in proton-proton collisions at root s = 0.9 TeV at the LHC. J. Phys.-Nucl. Part. Phys. 2012, 39, 025006. [Google Scholar] [CrossRef]
- Cleymans, J.; Paradza, M.W. Tsallis statistics in high energy physics: Chemical and thermal freeze-outs. Physics 2020, 2, 654–664. [Google Scholar] [CrossRef]
- Rath, R.; Khuntia, A.; Sahoo, R.; Cleymans, J. Event multiplicity, transverse momentum and energy dependence of charged particle production, and system thermodynamics in pp collisions at the large hadron collider. J. Phys. G Nucl. Part. Phys. 2020, 47, 055111. [Google Scholar] [CrossRef]
- Khuntia, A.; Sharma, H.; Tiwari, S.K.; Sahoo, R.; Cleymans, J. Radial flow and differential freeze-out in proton-proton collisions at √s=7 TeV at the LHC. Eur. Phys. J. A 2019, 55, 3. [Google Scholar] [CrossRef]
- Bhattacharyya, T.; Cleymans, J.; Marques, L.; Mogliacci, S.; Paradza, M.W. On the precise determination of the Tsallis parameters in proton–proton collisions at LHC energies. J. Phys. G 2018, 45, 055001. [Google Scholar] [CrossRef]
- Cleymans, J.; Man Lo, P.; Redlich, K.; Sharma, N. Multiplicity dependence of (multi)strange baryons in the canonical ensemble with phase shift corrections. Phys. Rev. C 2021, 103, 014904. [Google Scholar] [CrossRef]
- Sharma, N.; Cleymans, J.; Hippolyte, B. Thermodynamic limit in high-multiplicity proton-proton collisions at √s=7 TeV. Adv. High Energy Phys. 2019, 2019, 5367349. [Google Scholar] [CrossRef]
- Bugaev, K.; Sagun, V.; Ivanytskyi, A.; Nikonov, E.; Cleymans, J.; Mishustin, I.; Zinovjev, G.; Bravina, L.V.; Zabrodin, E.E. Separate freeze-out of strange particles and the quark-hadron phase transition. EPJ Web Conf. 2018, 182, 02057. [Google Scholar] [CrossRef][Green Version]
- Azmi, M.D.; Bhattacharyya, T.; Cleymans, J.; Paradza, M. Energy density at kinetic freeze-out in Pb-Pb collisions at the LHC using the Tsallis distribution. J. Phys. G Nucl. Part. Phys. 2020, 47, 045001. [Google Scholar] [CrossRef]
- Deppman, A.; Megias, E.; Menezes, D.P. Fractals, nonextensive statistics, and QCD. Phys. Rev. 2020, 101, 034019. [Google Scholar] [CrossRef]
- Sena, I.; Deppman, A. Systematic analysis of p(T)-distributions in p plus p collisions. Eur. Phys. J. A 2013, 49, 17. [Google Scholar] [CrossRef]
- Liu, F.H.; Gao, Y.Q.; Li, B.C. Comparing two-Boltzmann distribution and Tsallis statistics of particle transverse momentums in collisions at LHC energies. Eur. Phys. J. A 2014, 50, 123. [Google Scholar] [CrossRef]
- Khandai, P.K.; Sett, P.; Shukla, P.; Singh, V. System size dependence of hadron pT spectra in p+p and Au+Au collisions at √sNN = 200 GeV. J. Phys. G Nucl. Part Phys. 2014, 41, 025105. [Google Scholar] [CrossRef]
- Wong, C.Y.; Wilk, G. Tsallis fits to pT spectra and multiple hard scattering in pp collisions at the LHC. Phys. Rev. D 2013, 87, 114007. [Google Scholar] [CrossRef]
- Marques, L.; Andrade, E.; Deppman, A. Nonextensivity of hadronic systems. Phys. Rev. D 2013, 87, 114022. [Google Scholar] [CrossRef]
- Cleymans, J.; Lykasov, G.I.; Parvan, A.S.; Sorin, A.S.; Teryaev, O.V.; Worku, D. Systematic properties of the Tsallis Distribution: Energy Dependence of Parameters in High-Energy p-p Collisions. Phys. Lett. B 2013, 723, 351–354. [Google Scholar] [CrossRef]
- Azmi, M.D.; Cleymans, J. Transverse momentum distributions in proton–proton collisions at LHC energies and tsallis thermodynamics. J. Phys. G Nucl. Part. Phys. 2014, 41, 065001. [Google Scholar] [CrossRef]
- Rybczynski, M.; Wlodarczyk, Z. Tsallis statistics approach to the transverse momentum distributions in p-p collisions. Eur. Phys. J. C 2014, 74, 2785. [Google Scholar] [CrossRef]
- Marques, L.; Cleymans, J.; Deppman, A. Description of high-energy pp collisions using Tsallis thermodynamics: Transverse momentum and rapidity distributions. Phys. Rev. D 2015, 91, 054025. [Google Scholar] [CrossRef]
- Bíró, G.; Barnaföldi, G.G.; Biró, T.S. Tsallis-thermometer: A QGP indicator for large and small collisional systems. J. Phys. G Nucl. Part. Phys. 2020, 47, 105002. [Google Scholar] [CrossRef]
- Shen, K.; Barnafoldi, G.G.; Biro, T.S. Hadronization within the non-extensive approach and the evolution of the parameters. Eur. Phys. J. A 2019, 55, 126. [Google Scholar]
- Zheng, H.; Zhu, L.; Bonasera, A. Systematic analysis of hadron spectra in p+p collisions using tsallis distributions. Phys. Rev. D 2015, 92, 074009. [Google Scholar] [CrossRef]
- ALICE Collaboration. Neutral pion and η meson production in proton–proton collisions at √s = 0.9 TeV and √s = 7 TeV. Phys. Lett. B 2012, 717, 162–172. [Google Scholar] [CrossRef]
- ALICE Collaboration. Production of pions, kaons and protons in pp collisions at √s = 900 GeV with ALICE at the LHC. Eur. Phys. J. C 2011, 71, 1655. [Google Scholar] [CrossRef]
- Griffiths, D.J. Introduction to Elementary Particles; John Wiley & Sons, Inc.: New York, NY, USA, 1987; Available online: http://nuclphys.sinp.msu.ru/books/b/Griffiths.pdf (accessed on 25 May 2022).
- Deppman, A. Self-consistency in non-extensive thermodynamics of highly excited hadronic states. Physica A 2012, 391, 6380–6385. [Google Scholar] [CrossRef]
- Wilk, G.; Włodarczyk, W. Some intriguing aspects of multiparticle production processes. Int. J. Mod. Phys. A 2018, 33, 1830008. [Google Scholar] [CrossRef]
- Wilk, G.; Wlodarczyk, Z. The imprints of nonextensive statistical mechanics in high-energy collisions. Chaos Solit. Fract. 2002, 13, 581–594. [Google Scholar] [CrossRef]
- Hanel, R.; Thurner, S.; Gell-Mann, M. Generalized entropies and the transformation group of superstatistics. Proc. Nat. Acad. Sci. USA 2011, 108, 6390–6394. [Google Scholar] [CrossRef]
- Megias, E.; Lima, J.A.S.; Deppman, A. Transport equation for small systems and the nonadditive entropy. Mathematics 2022, 20, 1625. [Google Scholar] [CrossRef]
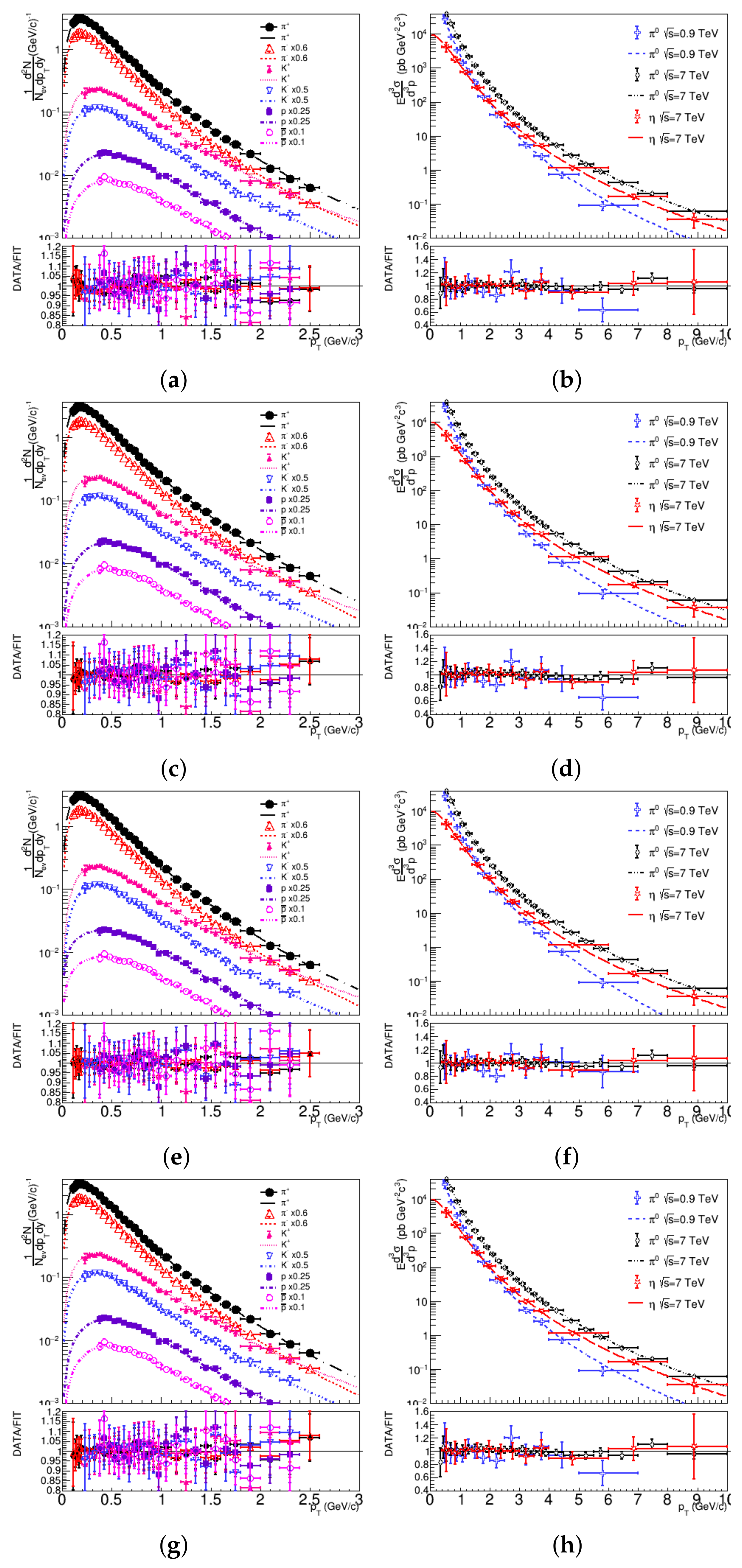
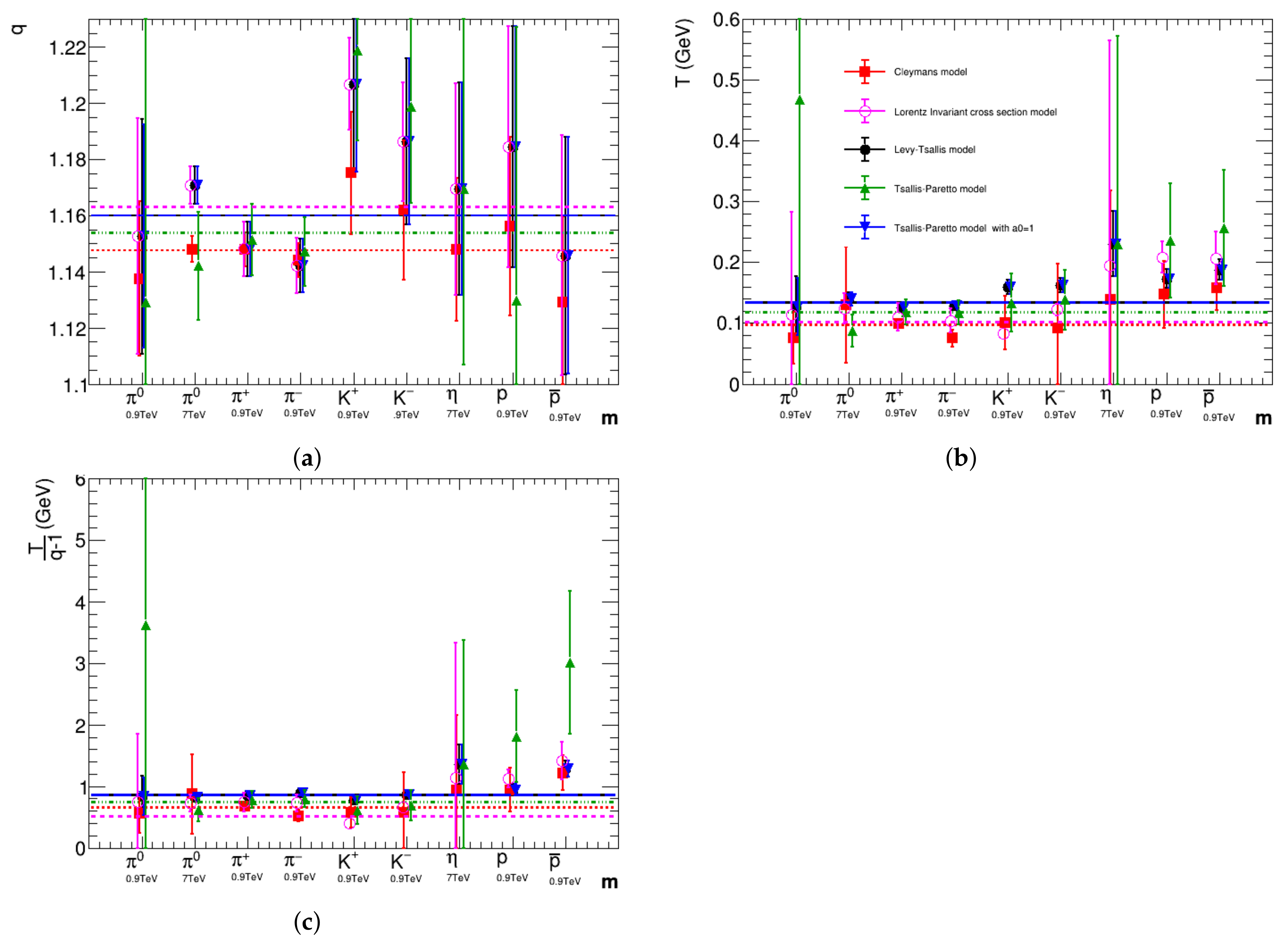
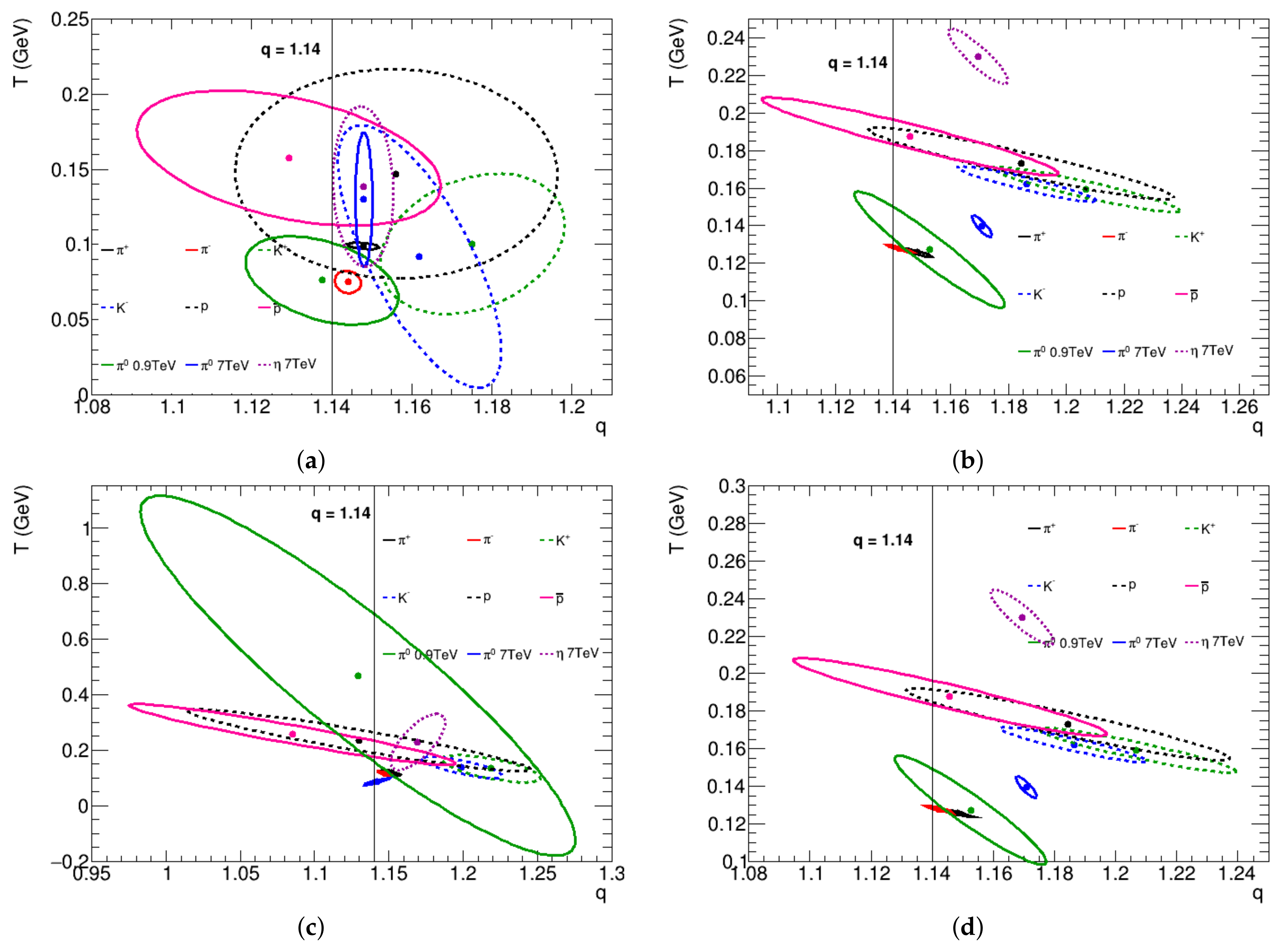
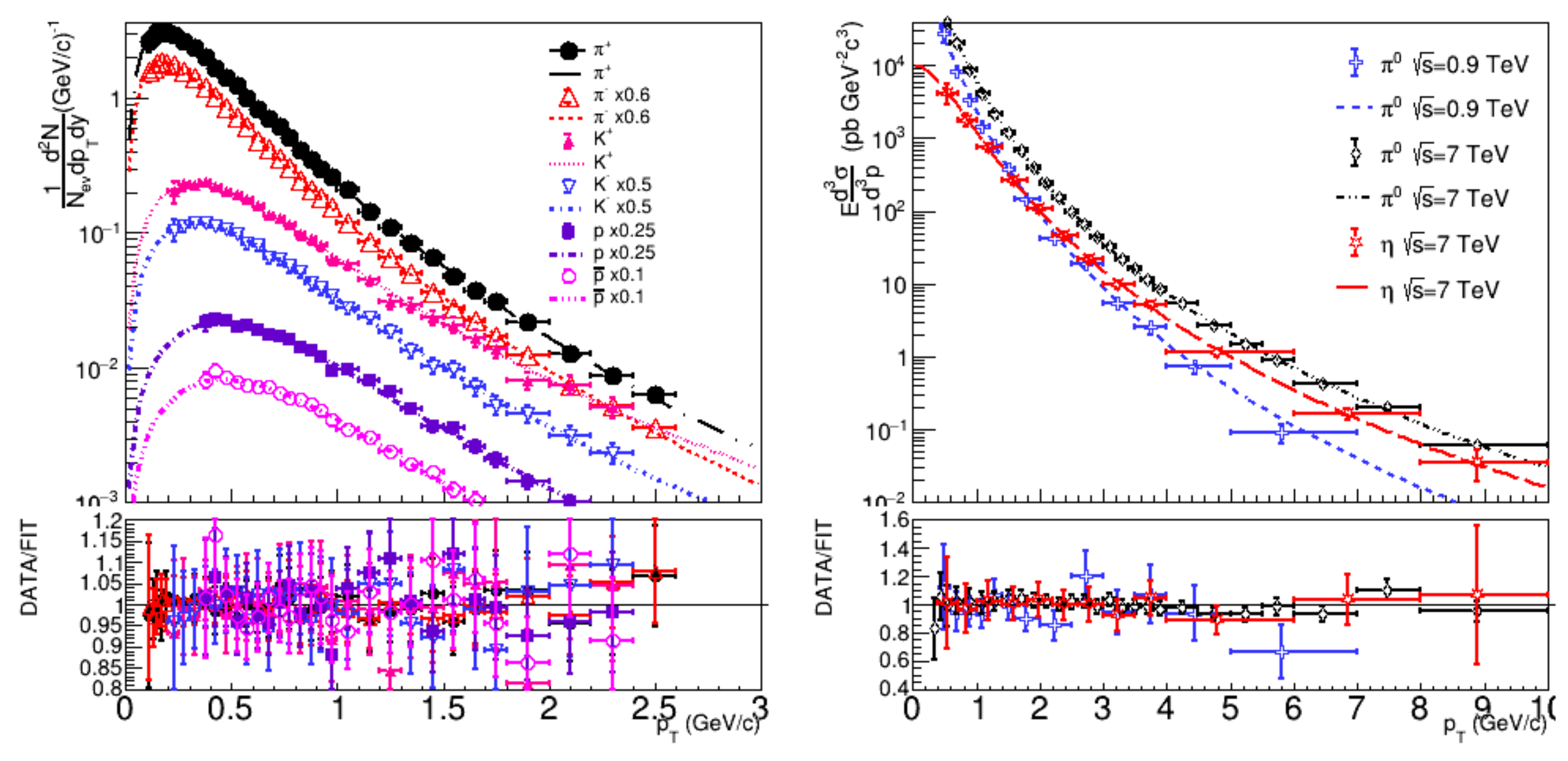
| (TeV) | Particle | q | T (GeV) | (GeV/) | (fm) | (GeV) | |
|---|---|---|---|---|---|---|---|
| 0.9 | 1.148 ± 0.005 | 0.091 ± 0.001 | 0.139570 | 0.141 ± 0.002 | 3.67/29 | ||
| 0.9 | 1.145 ± 0.005 | 0.076 ± 0.002 | 0.139570 | 0.031 ± 0.004 | 2.19/29 | ||
| 0.9 | 1.176 ± 0.015 | 0.092 ± 0.005 | 0.49368 | 0.20 ± 0.02 | 5.34/23 | ||
| 0.9 | 1.16 ± 0.01 | 0.084 ± 0.006 | 0.49368 | 0.129 ± 0.026 | 3.50/23 | ||
| 0.9 | p | 1.16 ± 0.02 | 0.09 ± 0.01 | 0.938272 | 774 ± 16 | 0.44 ± 0.05 | 7.43/21 |
| 0.9 | 1.13 ± 0.02 | 0.10 ± 0.01 | 0.938272 | 730 ± 20 | 0.36 ± 0.06 | 7.78/20 | |
| 0.9 | 1.14 ± 0.03 | 0.08 ± 0.04 | 0.134977 | (1 ± 4) × | −0.05 ± 0.32 | 0.51/9 | |
| 7 | 1.148 ± 0.005 | 0.13 ± 0.10 | 0.134977 | (0.5 ± 2.7) | 0.2 ± 0.6 | 0.94/29 | |
| 7 | 1.15 ± 0.03 | 0.1 ± 0.2 | 0.54751 | (0.2 ± 1.8) × | 0.1 ± 1.2 | 0.09/9 |
| (TeV) | Particle | q | T (GeV) | (GeV/) | /ndf | |
|---|---|---|---|---|---|---|
| 0.9 | 1.148 ± 0.008 | 0.126 ± 0.003 | 0.139570 | 1.49 ± 0.02 | 3.07/30 | |
| 0.9 | 1.142 ± 0.008 | 0.128 ± 0.003 | 0.139570 | 1.48 ± 0.02 | 1.84/30 | |
| 0.9 | 1.21 ± 0.02 | 0.159 ± 0.009 | 0.49368 | 0.184 ± 0.004 | 5.41/24 | |
| 0.9 | 1.19 ± 0.02 | 0.162 ± 0.009 | 0.49368 | 0.182 ± 0.004 | 3.59/24 | |
| 0.9 | p | 1.19 ± 0.03 | 0.17 ± 0.01 | 0.938272 | 0.083 ± 0.002 | 7.43/21 |
| 0.9 | 1.14 ± 0.03 | 0.19 ± 0.01 | 0.938272 | 0.079 ± 0.002 | 7.75/21 | |
| 0.9 | 1.15 ± 0.04 | 0.13 ± 0.05 | 0.134977 | (9 ± 5) × | 0.47/10 | |
| 7 | 1.171 ± 0.007 | 0.14 ± 0.01 | 0.134977 | (17 ± 3) × | 1.17/30 | |
| 7 | 1.17 ± 0.04 | 0.23 ± 0.05 | 0.54751 | (15 ± 5) × | 0.09/10 |
| (TeV) | Particle | q | T (GeV) | (GeV/) | C [(GeV/] | /ndf | |
|---|---|---|---|---|---|---|---|
| 0.9 | 1.15 ± 0.01 | 0.12 ± 0.02 | 0.139570 | 43 ± 18 | 1.1 ± 0.2 | 2.69/29 | |
| 0.9 | 1.148 ± 0.009 | 0.12 ± 0.01 | 0.139570 | 43 ± 17 | 1.1 ± 0.2 | 1.18 /29 | |
| 0.9 | 1.22 ± 0.03 | 0.13 ± 0.04 | 0.49368 | 2 ± 1 | 1.2 ± 0.4 | 5.02/23 | |
| 0.9 | 1.20 ± 0.03 | 0.14 ± 0.04 | 0.49368 | 1.94 ± 1.20 | 1.3 ± 0.4 | 3.12/23 | |
| 0.9 | p | 1.13 ± 0.07 | 0.23 ± 0.07 | 0.938272 | 0.24 ± 0.08 | 0.6 ± 0.4 | 6.48/20 |
| 0.9 | 1.08 ± 0.07 | 0.27 ± 0.07 | 0.938272 | 0.19 ± 0.06 | 0.6 ± 0.3 | 6.27/20 | |
| 0.9 | 1.1 ± 0.3 | 0.5 ± 1.1 | 0.134977 | (0.8 ± 2.7) × | −1 ± 3 | 0.34/9 | |
| 7 | 1.14 ± 0.02 | 0.09 ± 0.03 | 0.134977 | (3± 4) × | 2 ± 1 | 0.90/29 | |
| 7 | 1.17 ± 0.06 | 0.2 ± 0.3 | 0.54751 | (0.7 ± 2.0) × | 1 ± 3 | 0.09/9 |
| G (TeV) | Particle | q | T (GeV) | (GeV/) | C [(GeV/] | /ndf |
|---|---|---|---|---|---|---|
| 0.9 | 1.148 ± 0.008 | 0.126 ± 0.003 | 0.139570 | 33.4 ± 0.8 | 3.07/30 | |
| 0.9 | 1.142 ± 0.008 | 0.128 ± 0.003 | 0.139570 | 32.7 ± 0.7 | 1.84/30 | |
| 0.9 | 1.21 ± 0.02 | 0.159 ± 0.009 | 0.49368 | 1.30 ± 0.07 | 5.41/24 | |
| 0.9 | 1.19 ± 0.02 | 0.162 ± 0.009 | 0.49368 | 1.30 ± 0.06 | 3.59/24 | |
| 0.9 | p | 1.19 ± 0.03 | 0.17 ± 0.01 | 0.938272 | 0.34 ± 0.02 | 7.43/21 |
| 0.9 | 1.14 ± 0.03 | 0.19 ± 0.01 | 0.938272 | 0.31 ± 0.02 | 7.75/21 | |
| 0.9 | 1.15 ± 0.04 | 0.13 ± 0.05 | 0.134977 | (2 ± 2) × | 0.47/10 | |
| 7 | 1.171 ± 0.007 | 0.14 ± 0.01 | 0.134977 | (31 ± 9) × | 1.17/30 | |
| 7 | 1.17 ± 0.04 | 0.23 ± 0.05 | 0.54751 | (7 ± 4) × | 0.09/10 |
| (TeV) | Particle | q | T (GeV) | (GeV/) | (fm) | (GeV) | /ndf |
|---|---|---|---|---|---|---|---|
| 0.9 | 1.148 ± 0.008 | 0.115 ± 0.003 | 0.139570 | −0.062 ± 0.009 | 3.07/29 | ||
| 0.9 | 1.142 ± 0.008 | 0.124 ± 0.003 | 0.139570 | −0.017 ± 0.007 | 1.84/29 | ||
| 0.9 | 1.21 ± 0.02 | 0.107 ± 0.009 | 0.49368 | 789 ± 20 | 0.08 ± 0.04 | 5.41/23 | |
| 0.9 | 1.19 ± 0.02 | 0.111 ± 0.009 | 0.49368 | 825 ± 20 | 0.06 ± 0.04 | 3.60/23 | |
| 0.9 | p | 1.19 ± 0.03 | 0.10 ± 0.01 | 0.938272 | 442 ± 8 | 0.41 ± 0.06 | 7.43/20 |
| 0.9 | 1.14 ± 0.03 | 0.11 ± 0.02 | 0.938272 | 0.23 ± 0.08 | 7.75/20 | ||
| 0.9 | 1.15 ± 0.04 | 0.1 ± 0.2 | 0.134977 | (0.1 ± 1.4) × | −0.08 ± 1.12 | 0.47/9 | |
| 7 | 1.171 ± 0.007 | 0.12 ± 0.02 | 0.134977 | (2 ± 3) × | −0.10 ± 0.15 | 1.17/29 | |
| 7 | 1.17 ± 0.04 | 0.2 ± 0.4 | 0.54751 | (0.6 ± 8.4) × | 0.1 ± 2.2 | 0.09/9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rocha, L.Q.; Megías, E.; Trevisan, L.A.; Olimov, K.K.; Liu, F.; Deppman, A. Nonextensive Statistics in High Energy Collisions. Physics 2022, 4, 659-671. https://doi.org/10.3390/physics4020044
Rocha LQ, Megías E, Trevisan LA, Olimov KK, Liu F, Deppman A. Nonextensive Statistics in High Energy Collisions. Physics. 2022; 4(2):659-671. https://doi.org/10.3390/physics4020044
Chicago/Turabian StyleRocha, Lucas Q., Eugenio Megías, Luis A. Trevisan, Khusniddin K. Olimov, Fuhu Liu, and Airton Deppman. 2022. "Nonextensive Statistics in High Energy Collisions" Physics 4, no. 2: 659-671. https://doi.org/10.3390/physics4020044
APA StyleRocha, L. Q., Megías, E., Trevisan, L. A., Olimov, K. K., Liu, F., & Deppman, A. (2022). Nonextensive Statistics in High Energy Collisions. Physics, 4(2), 659-671. https://doi.org/10.3390/physics4020044








