Critical Angle Refractometry for Lossy Media with a Priori Known Extinction Coefficient

Abstract

Critical angle refractometry is an established technique for determining the refractive index of liquids and solids. For transparent samples, the critical angle refractometry precision is limited by incidence angle resolution. For lossy samples, the precision is also affected by reflectance measurement error. In the present study, it is demonstarted that reflectance error can be practically eliminated, provided that the sample’s extinction coefficient is a priori known with sufficient accuracy (typically, better than $5\%$) through an independent measurement. Then, critical angle refractometry can be as precise with lossy media as with transparent ones.

1. Introduction

Critical angle refractometry is the standard for determining the refractive index of transparent media [1,2,3,4,5,6]. The method relies on measurements of the reflectance, $R\left(\theta \right)$, of the interface, formed by a transparent front medium (which is commonly a prism) of known refractive index, $n_o$, and the sample of unknown index, n, for a range of incidence angles, $\theta$, that includes the critical angle, ${\theta }_c$, of total internal reflection (TIR) [7,8,9].

As it is shown in Figure 1, the critical angle is located at a sharp discontinuity of the $\theta$-derivative, $R^{\prime }\left(\theta \right)$; the refractive index of the sample is obtained from the TIR condition:

$$n/n_o=sin{\theta }_c,$$

(1)

with the corresponding relative error:

$$\delta n/n=\delta {\theta }_c/tan{\theta }_c.$$

(2)

In determining the TIR critical angle, the error, $\delta {\theta }_c$, is mainly regulated by the angular resolution of the experimental setup, which is typically between 20 $\mathsf{\mu }$rad and 100 $\mathsf{\mu }$rad for state-of-the-art refractometers [10].

Critical angle refractometry has also been used with lossy media where the refractive index turns into the complex number, $n=n_r+i{n}_i$, the imaginary part of which (imaginary index) incorporates loss effects, namely, absorption and/or scattering. The reflectance profile, $R\left(\theta \right)$, becomes smoother, and the critical angle, ${\theta }_c$, is located at the maximum of $R^{\prime }\left(\theta \right)$, which now marks the gradual transition from the attenuated TIR (a-TIR) to the partial reflection regime; see Figure 1. The underlying assumption is that Equation (1) is still valid (at least approximately) and that it can be used to obtain an estimate of the real index of the lossy sample [11,12]. This assumption introduces systematic errors that have been the subject of extensive discussion; see, e.g., [13,14,15] Let us note that fitting the reflectance profile, $R\left(\theta \right)$, to Fresnel equations is another way to compute the complex optical constants [16,17,18]. However, bearing its own strengths and weaknesses, data regression is not a point method and, thus, cannot be taken as a “critical angle” refractometry approach in itself.

Recently, the universal condition of a-TIR,

$$n_r/n_o=g_1({\theta }_c,R_c)\mathrm{and}{n}_i/n_o=g_2({\theta }_c,R_c),$$

(3)

was proposed, where $R_c$ is the critical reflectance at ${\theta }_c$, and functions $g_1$ and $g_2$ are derived from the Fresnel equations [19]. In the case of the s-polarisation, which is the main foucus of the present study, these equations are given in Section 2. Using Equation (3), the complex refractive index can be determined by ${\theta }_c$ and $R_c$.

Then, the relative error of the real index, $\delta n_r/n_r$, depends on both $\delta {\theta }_c$ and $\delta R_c$:

$$\frac{\delta n_r}{n_r}=\frac{1}{g_1}·\sqrt{{\left(\frac{\partial g_1}{\partial {\theta }_c}·\delta {\theta }_c\right)}^2+{\left(\frac{\partial g_1}{\partial R_c}·\delta R_c\right)}^2}.$$

(4)

In determining the critical reflectance, the error $\delta R_c$ is mainly due to intensity fluctuations of the laser sources and, therefore, to be of the order of ${10}^{-2}$, which is at least two orders of magnitude larger than $\delta {\theta }_c$. As a result, critical angle refractometry is less precise with lossy media than it is with transparent ones.

In this paper, it is demonstrated that the critical reflectance can be numerically computed with higher accuracy than it can be experimentally obtained, provided that the extinction coefficient of the sample is a priori known with sufficient accuracy (<5%, typically). Then, the real index relative error for lossy samples (being $\delta {\theta }_c$ and $\delta R_c$ dependent; see Equation (4)) can become equal to the relative error for transparent samples (which is only $\delta {\theta }_c$ dependent; see Equation (2)). This is a significant advancement in the field of optical characterisation of absorbing and/or scattering media, which include, among others, various forms of biological matter, non-transparent liquids, colloids and food products.

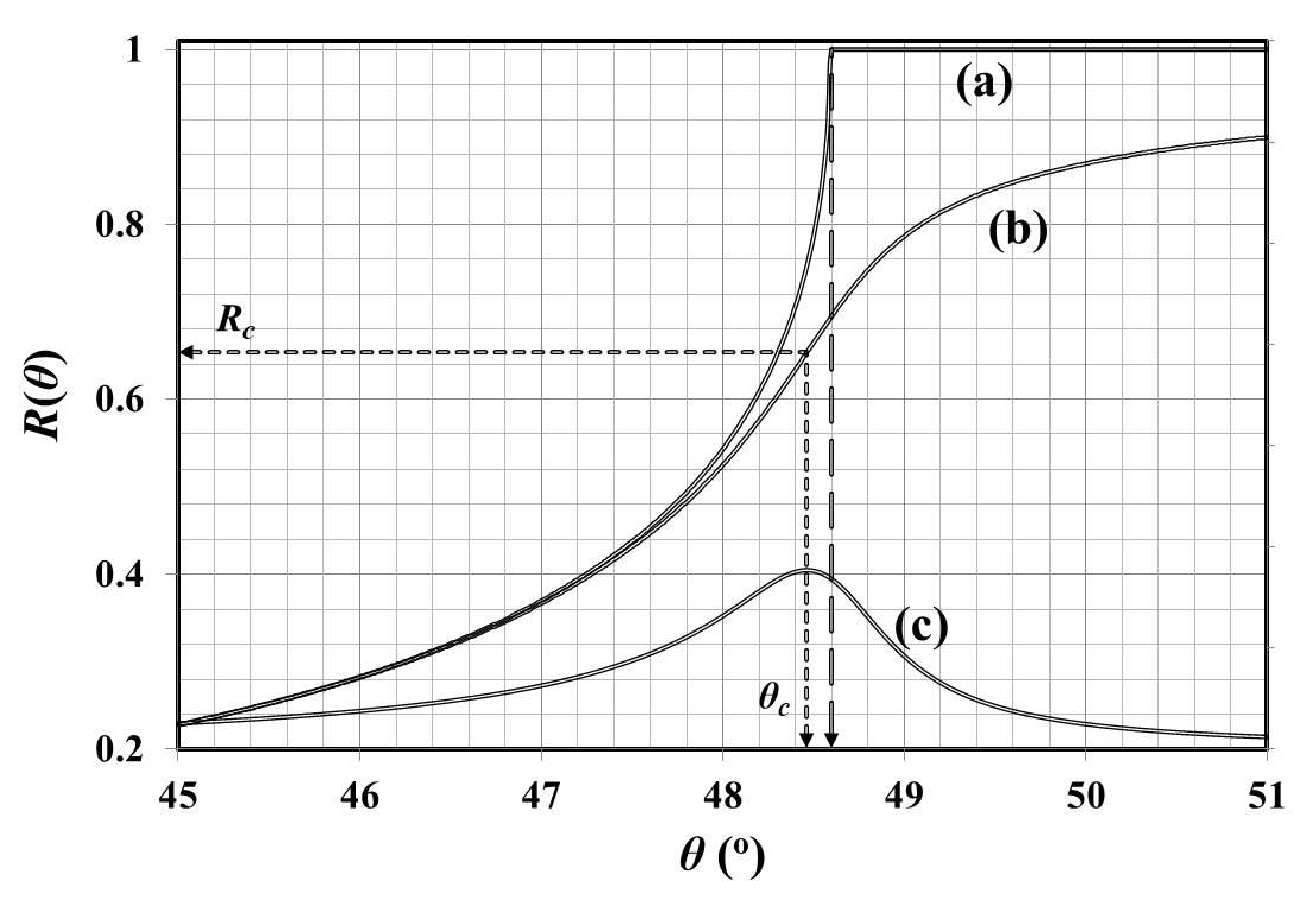
2. Background Theory and Initial Observations

The functions $g_1$ and $g_2$ [19] are compactly expressed in terms of the sample’s complex dielectric constant, ${ϵ}_r+i·{ϵ}_i={(n_r+i·n_i)}^2$, and the prism’s dielectric constant, ${ϵ}_o=n_p^2$:

$$g_1={\left[\frac{\sqrt{{ϵ}_r^2+{ϵ}_i^2}}{2{ϵ}_o}+\frac{{ϵ}_r}{2{ϵ}_o}\right]}^{1/2}\mathrm{and}{g}_2={\left[\frac{\sqrt{{ϵ}_r^2+{ϵ}_i^2}}{2{ϵ}_o}-\frac{{ϵ}_r}{2{ϵ}_o}\right]}^{1/2},$$

(5)

where

$$\frac{{ϵ}_r}{{ϵ}_o}=\frac{\alpha +t^2}{1+t^2}\mathrm{and}\frac{{ϵ}_i}{{ϵ}_o}=\frac{\sqrt{{\gamma }^2-{\alpha }^2}}{1+t^2},$$

(6)

with

$$\alpha =\frac{{(1+\gamma )}^2}{2{\rho }^2}-\gamma ,\gamma =\frac{2t}{(3{\rho }^2-2\rho -2)t+\rho \sqrt{(9{\rho }^2-12\rho -8)t^2-4}},$$

(7)

and

$$t=tan{\theta }_c,\rho =\frac{1+R_c}{1-R_c}.$$

(8)

As it is described in [19], the preceding formalism, which is valid for s-polarisation, calculates output values $(n_r,n_i)$ from refractometric input pairs $({\theta }_c,R_c)$ by successive algebraic substitutions into Equations (5)–(8). Let us remark that Equations (5) and (6) are also valid for p-polarised light, in which case however, there exist no explicit solutions for $\alpha$ and $\gamma$ such as those provided by Equation (7). Instead, these parameters can be calculated as solutions to two algebraic equations, as is analytically shown in [19]. In that sense, the forthcoming analysis may be replicated for p-polarisation. Despite some more complication in the calculations, the results, reported here for s-polarisation, are qualitatively similar to those of p-polarisation.

Figure 2 gives a graphical insight by the isoangular curve which consists of pairs $(n_r/n_o,n_i/n_o)$, computed by keeping ${\theta }_c$ constant (${\theta }_c=\pi /4$ in this example), while letting $R_c$ to vary. There is no loss of generality, associated with the specific choice of ${\theta }_c$, because larger (smaller) critical angles simply shift the curve to the right (left). An indicative measurement (with ${\theta }_c=\pi /4,R_c$ varying) defines a single point in the $(n_r/n_o,n_i/n_o)$-plane, whose coordinates uniquely determine the complex refractive index.

In Figure 2, one can observe quite wide range, spanned by the imaginary index as the critical reflectance varies, especially compared to the relatively modest shift for the real index, which is nevertheless non-negligible. The vertical dashed line in Figure 2 marks the transparency limit $n_r/n_o=sin(\pi /4)\approx 0.707$, which is the estimate of the TIR-condition (Equation (1)) for each point of the isoangular curve. Unsurprisingly, this estimate practically coincides with the exact result for small $n_i/n_o$, e.g., $n_i/n_o\ll {10}^{-4}$, a range that includes, for example, most liquids at wavelengths far from their ultraviolet or infrared resonances, but excludes most forms of biological matter, even in the therapeutic optical window. The most interesting feature in Figure 2 is the turning point of the isoangular curve, which vividly demonstrates that the systematic error, introduced by use of Equation (1) with lossy media, does not increase monotonically with attenuation but decreases above the turning point, and even becomes zero when the isoangular curve crosses the transparency limit marked by the dashed vertical line. This behaviour, which now emerges as a natural consequence of the universal a-TIR condition, had been previously observed [13,20] and labeled as inexplicable by other authors [14].

3. Method’s Application with a Priori Known Extinction Coefficient

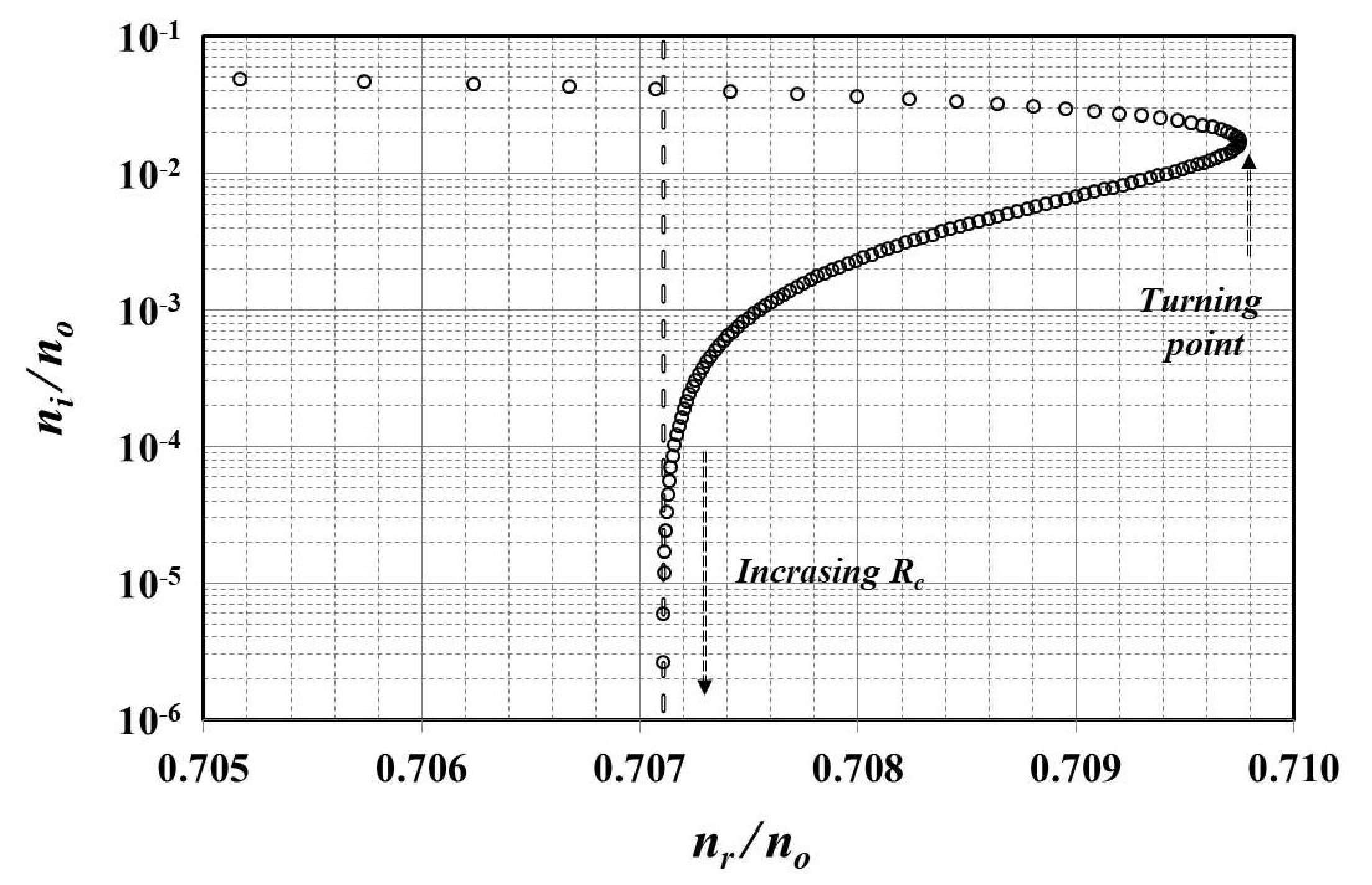
3.1. Main Concept

The sample’s extinction coefficient, $\mu$, i.e., the sum of the absorption coefficient, ${\mu }_a$, and the scattering coefficient, ${\mu }_s$, can be a priori known via an independent experimental method such as absorption spectroscopy or collimated transmittance spectroscopy. This type of independent extinction coefficient measurement has been reported earlier for pure water [21], various emulsions [22], bioliquids [23], oils [24] and semiconductors [25]; typically, the relative error, ${\sigma }_{\mu }=\delta \mu /\mu$, in the measurement of the extinction coefficient is of $0.1\%$ to $10\%$ [26,27,28,29,30].

The formalism, described in Section 2, can be used to calculate the real part of the refractive index (real index) from the value of the critical angle alone. The direct measurement of critical reflectance is no longer needed, since $R_c$ can be determined from the value of the extinction coefficient, which is related to the imaginary index [31]:

$$\mu =\frac{4\pi n_i}{\lambda },$$

(9)

so that the following equation holds true ($\lambda$ is the light wavelength):

$$g_2({\theta }_c,R_c)=\frac{n_i}{n_o}=\frac{\mu \lambda }{4\pi n_o}.$$

(10)

Solving Equation (10) for $R_c$ (the only unknown variable) is a simple task for iterative computing software such as Mathematica’s FindRoot or Mathcad’s Find. As long as the initial guess root is kept within its physically meaningful range, $0<R_c<1$, the solution is always unique and unambiguous. Substituting the measured value of ${\theta }_c$ and the numerically retrieved value of $R_c$ in $g_1({\theta }_c,R_c)$ yields the real index of the lossy sample.

The procedure described has a straightforward graphical interpretation. Let us consider the measurement of a critical angle, for example, ${\theta }_c=\pi /4$, so that one can refer to Figure 2. An a priori known value of the extinction coefficient (equivalently, $n_i$) defines a unique horizontal line that crosses the isoangular curve at a single point; locating its position is equivalent to numerically computing the value of $R_c$. The abscissa of that point is the real index of the lossy medium.

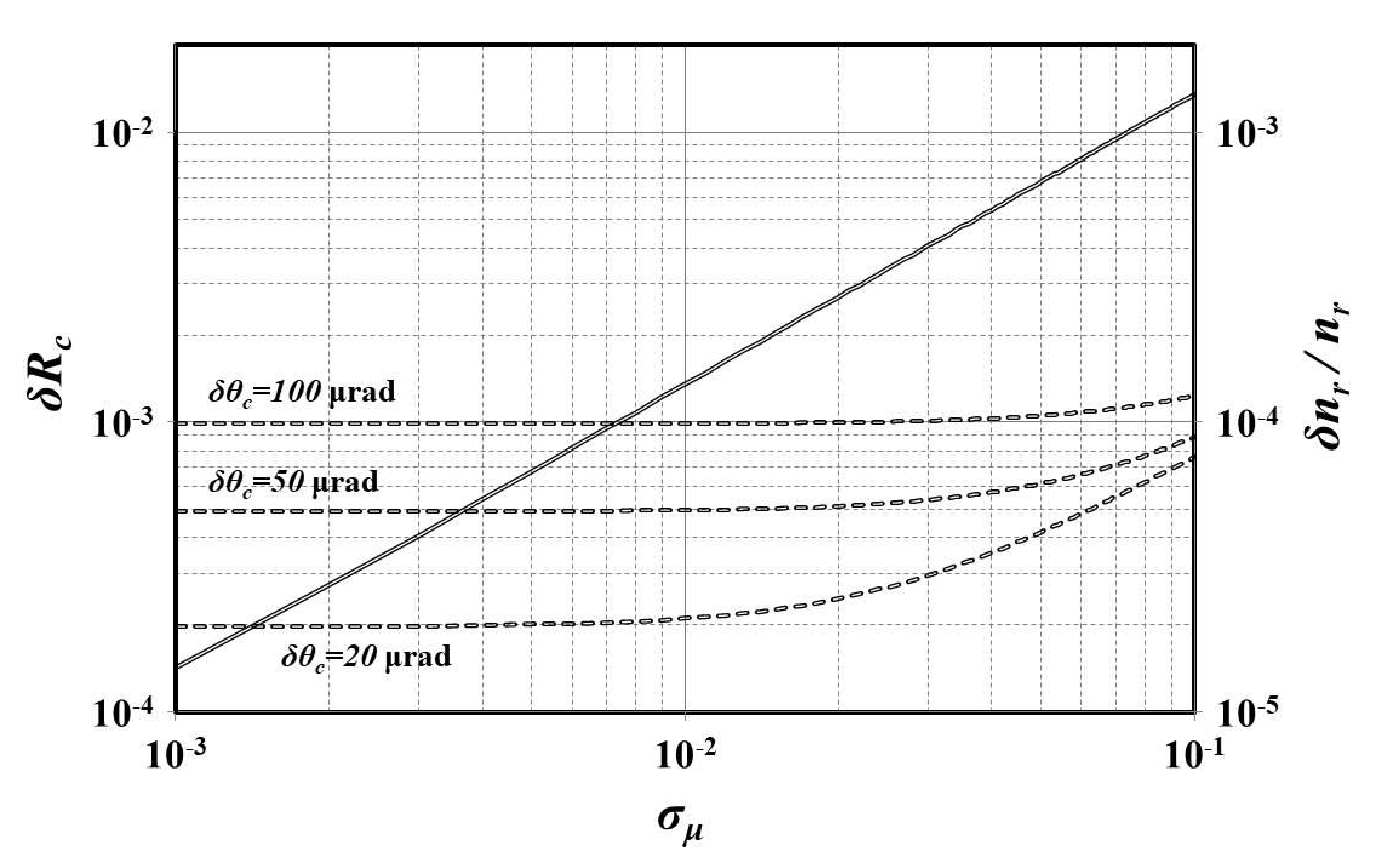
3.2. Critical Reflectance Error

The formalism of Section 2 enables the calculation of $n_r$ from the values of ${\theta }_c$ and $R_c$. The method, introduced in Section 3.1, retrieves the numerical value of $R_c$ from the extinction coefficient (when the extinction coefficient is already known) instead of its direct measurement. To better appreciate the advantage of the proposed method, one has to remember that the experimental error of a direct reflectance measurement is typically greater than ${10}^{-2}$. Breaking this threshold does not seem possible with standard unstabilized laser sources of moderate cost, such as those used in common refractometers.

Let us now show that the propagated error, $\delta R_c$, of the numerically retrieved $R_c$ can be kept below the ${10}^{-2}$ threshold. To this end, one accounts for the fact that $R_c$ is numerically computed from input values of ${\theta }_c$ and $\mu$, or equivalently, ${\theta }_c$ and $n_i$, which are assumed to be independent variables, so that the covariance between them can be taken to be zero. Therefore, propagated error $\delta R_c$ conveys corresponding experimental errors $\delta {\theta }_c$ and $\delta n_i$:

$$\delta R_c=\sqrt{{\left(\frac{\partial R_c}{\partial {\theta }_c}·\delta {\theta }_c\right)}^2+{\left(\frac{\partial R_c}{\partial n_i}·\delta n_i\right)}^2}.$$

(11)

Critical reflectance, $R_c$, is not expressed explicitly as a function of ${\theta }_c$ and $n_i$. Instead, Equation (10) can be restated in the implicit form: $F({\theta }_c,R_c,n_i)=F(g_2({\theta }_c,R_c),n_i)=g_2({\theta }_c,R_c)-n_i/n_o=0$. Then, the derivatives in Equation (11) can be obtained using the implicit function theorem:

$$\frac{\partial R_c}{\partial {\theta }_c}=-\left(\frac{\partial F}{\partial {\theta }_c}\right)/\left(\frac{\partial F}{\partial R_c}\right)=-\left(\frac{\partial g_2}{\partial {\theta }_c}\right)/\left(\frac{\partial g_2}{\partial R_c}\right),$$

(12)

and

$$\frac{\partial R_c}{\partial n_i}=-\left(\frac{\partial F}{\partial n_i}\right)/\left(\frac{\partial F}{\partial R_c}\right)=\frac{1}{n_o}/\left(\frac{\partial g_2}{\partial R_c}\right).$$

(13)

Moreover, one can introduce the relative error, ${\sigma }_{\mu }$, which is related to $\delta n_i$ and $\delta \mu$:

$${\sigma }_{\mu }=\frac{\delta \mu }{\mu }=\frac{\delta n_i}{n_i}=\frac{\delta n_i}{g_2·n_o}.$$

(14)

Substituting Equations (12)–(14) into Equation (11) yields:

$$\delta R_c=|\frac{\partial g_2}{\partial R_c}{|}^{-1}\sqrt{{\left(\frac{\partial g_2}{\partial {\theta }_c}·\delta {\theta }_c\right)}^2+{({\sigma }_{\mu }·g_2)}^2}.$$

(15)

Values of $g_2$ and its two partial derivatives that appear in Equation (15) can be easily computed for any pair $({\theta }_c,R_c)$. Therefore, error $\delta R_c$ can be estimated as a function of the variables ${\theta }_c,R_c,\delta {\theta }_c$, and ${\sigma }_{\mu }$. Numerical investigation reveals that $\delta R_c$ is practically independent of $\delta {\theta }_c$, at least when this parameter is kept within its reasonable range, 20 $\mathsf{\mu }$rad $\le \delta {\theta }_c\le$ 100 $\mathsf{\mu }$rad. This observation reflects the easily verifiable fact that

$$\frac{\partial g_2}{\partial {\theta }_c}·\delta {\theta }_c\ll {\sigma }_{\mu }·g_2,$$

(16)

which reduces Equation (15) to the approximate form:

$$\delta R_c\approx |\frac{\partial g_2}{\partial R_c}{|}^{-1}·{\sigma }_{\mu }·g_2,$$

(17)

and narrows $\delta R_c$ down to a function of only three variables, namely, of ${\theta }_c,R_c,$ and ${\sigma }_{\mu }$.

Figure 3 shows the results of calculations of $\delta R_c$ versus ${\sigma }_{\mu }$ for indicative values ${\theta }_c=\pi /4$ and $R_c=0.5$: the solid line, produced via the exact Equation (15). In agreement with the approximate Equation (17), $\delta R_c$ is not affected by $\delta {\theta }_c$ and increases linearly with ${\sigma }_{\mu }$, which is taken within the range $0.1\%\le {\sigma }_{\mu }\le 10\%$. One can observe that $\delta R_c\approx {10}^{-4}$ (or ${10}^{-3}$) when ${\sigma }_{\mu }\approx 0.1\%$ ($1\%$), indicating that critical reflectance error can be two (one) orders of magnitude smaller than the ${10}^{-2}$ threshold, when $R_c$ is numerically retrieved from the a priori known extinction coefficient.

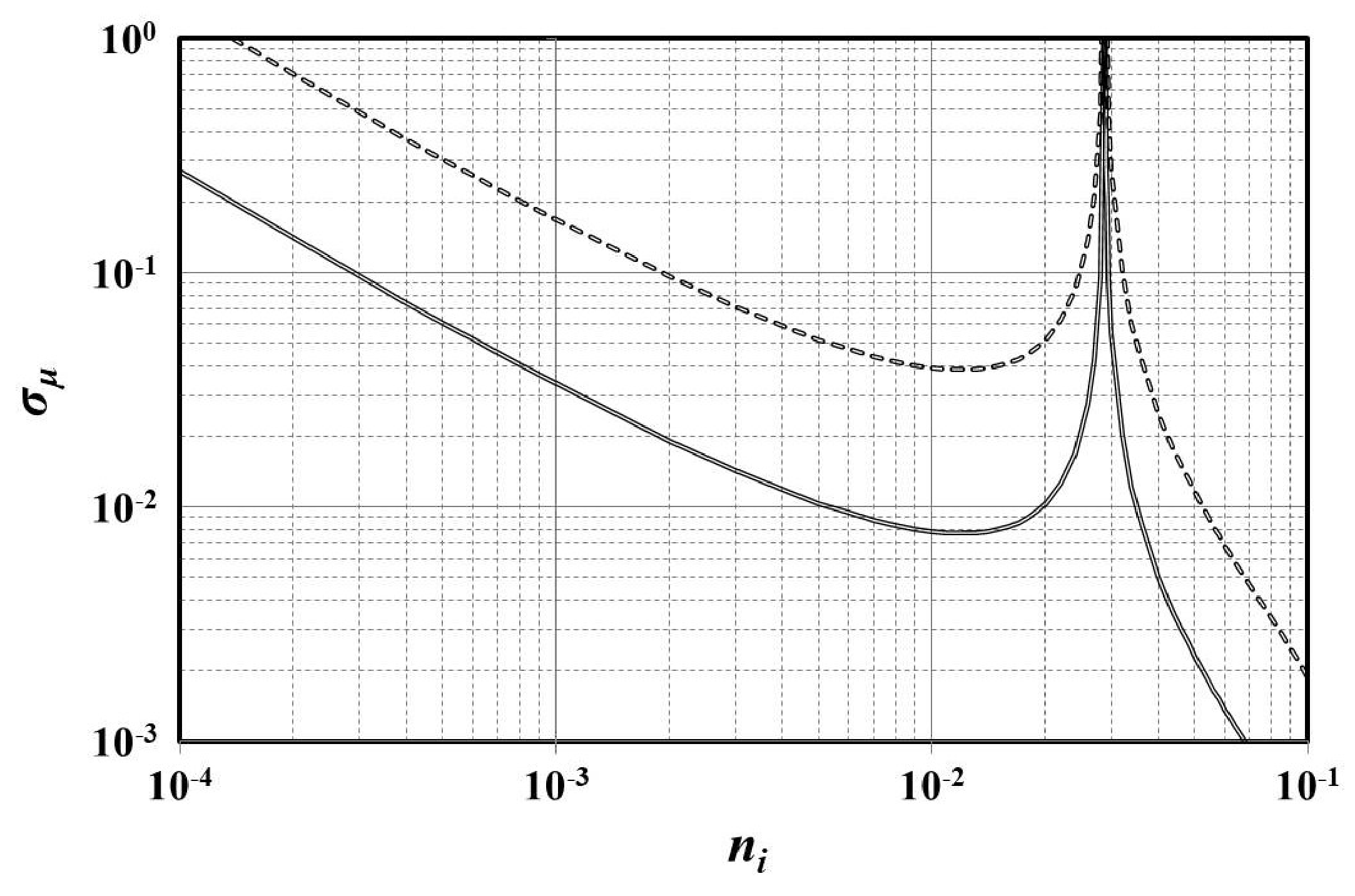
3.3. Real Index Error

The relative error, $\delta n_r/n_r$, can be computed as a function of the variables ${\theta }_c,R_c,\delta {\theta }_c$, and ${\sigma }_{\mu }$ by substituting Equation (15) into Equation (4).

Figure 3 shows $\delta n_r/n_r$ versus ${\sigma }_{\mu }$ for ${\theta }_c=\pi /4$ and $R_c=0.5$: the dashed lines correspond to $\delta {\theta }_c=100,50$ and 20 $\mathsf{\mu }$rad, as indicated. The error lines become horizontal for small ${\sigma }_{\mu }$ at a constant value $\delta n_r/n_r\approx \delta {\theta }_c/tan{\theta }_c$ (in this example, $tan{\theta }_c=1$). In the horizontal region, the relative real index error is practically equal to that of a transparent sample (cf. Equation (2)). This observation alone proves that refractometry with lossy media can be as precise as the refractometry with transparent ones, provided that the extinction coefficient is a priori known with sufficient accuracy. The horizontal regions terminate at a maximum permissible ${\sigma }_{\mu }$, above which $\delta n_r/n_r$ continues to increase beyond the transparency limit. In the example considered, this transition occurs in the vicinity of ${\sigma }_{\mu }\approx 1\%$ when $\delta {\theta }_c=20$ $\mathsf{\mu }$rad, at ${\sigma }_{\mu }\approx 2\%$ when $\delta {\theta }_c=50$ $\mathsf{\mu }$rad, and at ${\sigma }_{\mu }\approx 4\%$ when $\delta {\theta }_c=100$ $\mathsf{\mu }$rad.

Note that the upper and lower dashed lines in Figure 3 flatten out at $\delta n_r/n_r\approx {10}^{-4}$ (when $\delta {\theta }_c=100$ $\mathsf{\mu }$rad) and $\delta n_r/n_r\approx 2\times {10}^{-5}$ (when $\delta {\theta }_c=20$ $\mathsf{\mu }$rad). These levels match the specifications of modern refractometers operating with transparent samples, which typically prescribe an error $\delta n/n$ between ∼${10}^{-4}$ (standard precision) and ∼$2\times {10}^{-5}$ (ultimate precision) [32].

As a final exercise, let us consider the refractometric measurement of a lossy sample with $n_r=1.5$ by use of a reference front medium with $n_o=2$, so that $n_r/n_o=0.75$. With these assumptions, as given, it is straightforward to calculate the magnitude of ${\sigma }_{\mu }$ that is required to reach (i) the ultimate precision $\delta n_r/n_r\approx 2\times {10}^{-5}$, assuming that the refractometer measures critical angles with an ultrahigh accuracy $\delta {\theta }_c=20$ $\mathsf{\mu }$rad, and (ii) a standard precision $\delta n_r/n_r\approx {10}^{-4}$, with a more tolerant $\delta {\theta }_c=100$ $\mathsf{\mu }$rad. The calculations are shown in Figure 4 by solid and dashed lines, respectively.

Therein, one observes a general trend: the maximum permissible ${\sigma }_{\mu }$ decreases with increasing $n_i$. This trend clearly indicates that the need for accurate measurements of the extinction coefficient is more acute when optical loss is growing. There is one exception to this, which manifests itself as a characteristic sharp peak at larger $n_i$. This peak reflects the vertical slope of the isoangular curve at the turning point, see Figure 2. Quite naturally, ${\sigma }_{\mu }$ is found increasing again at the transparent limit, where the slope of the isoangular curve is again nearly vertical. Likewise, ${\sigma }_{\mu }$ decreases rapidly for larger $n_i$ after the peak because the slope of isoangular curve above there is zero

To better understand the interpretation made, let us point that a vertical slope in Figure 2 suggests that small enough change in the imaginary index causes zero shift to the real index. Similarly, a horizontal slope suggests that small change in the imaginary index causes a maximum shift in the real index. Hence, the real index error minimizes (and the maximum permissible ${\sigma }_{\mu }$ maximizes) as soon as the slope turns vertical, and vice versa.

Meantime, the most important observation in Figure 4 is that the real index of the sample can be measured with an extreme precision, $\delta n_r/n_r\approx 2\times {10}^{-5}$, as long as $n_i<{10}^{-1}$ and ${\sigma }_{\mu }\approx 0.1\%$ (solid line). Note that although being strict, this situation is indeed realistic. For example, the extinction coefficient of water has been measured with a relative error even less than $0.1\%$ near its infrared absorption peak (at $\lambda =1410$ nm), where $n_i=2.3675\times {10}^{-4}$ [21]; see discussion in Section 3.4 below. This is also possible with a much more lax ${\sigma }_{\mu }\approx 1\%$ for all $n_i<{10}^{-2}$. An adequate for many applications error $\delta n_r/n_r\approx {10}^{-4}$ is reached with ${\sigma }_{\mu }\approx 4\%$ for all $n_i<4\times {10}^{-2}$ (dashed line). These observations illustrate the functionality of the proposed method with all but the most extremely attenuating media.

3.4. Comments on Implementation Issues

The proposed method involves the tandem use of two instruments. The first determines the reflectance profile at the sample’s interface with a prism; prism coupling refractometers operate routinely in various laboratories and they are also commercially available; see, e.g. Metricons’s 2010/M model. The second measures the sample’s extinction coefficient. Collimated transmittance setups (typically, homemade) suit ideally this purpose; see, e.g., [21,26,27]. The corresponding operating principle is straightforward. The transmitted portion of a collimated light beam, travelling through sample sections of variable length, is monitored; the extinction coefficient is then deduced by fitting experimental results to the known Lambert-Beer law. This technique is commonly used for fluids where liquid cells of different sizes facilitate tuning of the path length. The technique is also applicable for solid samples, provided that slices of variable thickness can be cut.

This tandem measurement is actually known. In [21], the (real) refractive index and the extinction coefficient of several types of liquids, including water, were measured by the combined use of critical angle refractometetry and collimated transmittance spectroscopy. Unaware of the attenuated-TIR condition (Equation (3)) at that time, the standard TIR law of transparent media (Equation (1)) was exploited in [21] to determine the real index. Let us see, through a didactic example, how the method, proposed in this paper, adjusts those results.

Let us start by selecting the reported data for water at a wavelength $\lambda =1410$ nm, where the extinction coefficient, $\mu =21.1$ cm${}^{-1}$, was measured [21] translating via Equation (9) into the imaginary index, $n_i=2.3675\times {10}^{-4}$. The relative error in this measurement was as small as ${\sigma }_{\mu }=0.05\%$. Using an SF13 glass prism with $n_o=1.7068$, the real index was approximated by the standard TIR condition, leading to the value $n_r=1.3183$, which, given the index of the prism, corresponds to the critical angle ${\theta }_c={50.568}^{\circ }$.

Using the required input pair (${\theta }_c={50.568}^{\circ },\mu =21.1$ cm${}^{-1}$), the method, proposed in the current paper, yields, first, the critical reflectance $R_c=91.99\%$ and, then, the real index of water, corrected to a new value, $n_r=1.31842$. The correction from the previous estimate ($n_r=1.3183$) is relatively modest, while non negligible for applications requiring high accuracy. The modest correction effect is expected (cf. Figure 2), since the imaginary index in our example just exceeds ${10}^{-4}$; it would have been much stronger, had the sample been more attenuating.

Using Equation (15), the prescribed ${\sigma }_{\mu }=0.05\%$ value, combined with an assumed error in the measurement of critical angle, 20 $\mathsf{\mu }$rad $\le \delta {\theta }_c\le 100$ $\mathsf{\mu }$rad, leads to a propagated error in the numerical estimation of the critical reflectance within $\delta R_c\approx 0.002\%$. Such an accuracy is surely orders of magnitude higher than the ∼$1\%$ uncertainty with which critical reflectance can be directly measured. This finding manifests the main advantage of the method here described. Then, within the same $\delta {\theta }_c$ range, this method yields the real index with an error of $2\times {10}^{-5}\le \delta n_r\le 1\times {10}^{-4}$, the latter calculated as it is described in Section 3.3. It is worth noticing the compliance of this result with Figure 3.

4. Conclusions

In this paper, the universal attenuated total internal reflection (a-TIR) condition is exploited in order to accurately determine the real part of the refractive index (real index), n_r, of lossy media from the critical incidence angle, ${\theta }_c$, at s-polarisation given the extinction coefficient, $\mu$. This is accomplished in a two-step procedure. First, the critical reflectance, $R_c$, is numerically retrieved from the pair $({\theta }_c,\mu )$. Then, the real index is calculated from ${\theta }_c$ and $R_c$.

Numerical investigation reveals that $R_c$ can be recovered (in the first step) more accurately than it can be directly measured. As a consequence the determination of the real index (in the second step) becomes more precise. The relative error, $\delta n_r/n_r$, can be reduced down to $2\times {10}^{-5}$ when the respective error in the independent measurement of $\mu$ is in the range of $0.1\%$ to $1\%$.

The results, obtained here, demonstrate that refractometry of lossy media can be as precise as with transparent media, a development that is of interest to various applications in biomedical optics, material characterisation, analytical chemistry and quality control.