Up to this point, we discussed the formal proofs of variance inequalities, and illustrated their effects in
Figure 1. In the following, we will show the direct connections of the variance inequalities to the line-shapes of
Figure 1 and to the corresponding figures of [
4,
8]. To simplify the notations, we will take
and
equal to zero (as in the simulations). It must be recalled that the illustrated simulations deal with a large number of tracks with different successions of hit quality (
). For each succession of
, extracted from the allowed set of
, we have a definite form of the estimators
and
(weighted least-squares). Instead,
and
(standard least-squares) are formally invariant. The studied estimator is the track direction
, thus
and
are the selected estimators. These demonstrations can be easily extended to other estimators.
5.1. The Line-Shapes of the Estimators and
For any set of observations
, the estimator
gives a definite value
. The set of all possible
has the probability distribution
(with the method of [
5,
7]):
Due to the linearity of
in the observations
, this integral gives a weighted convolution of the functions
. For the convolution theorems [
12], the variance of
is given by the
of Equation (
12) with the corresponding
:
In the case of [
4,
8], the convolution of Gaussian PDFs gives another Gaussian function with the variance
, therefore
becomes:
The mean value of is zero, as it must be for the unbiasedness of the estimator, and its maximum is .
A similar procedure of Equations (
45)–(
47) can be extended to the standard least-squares with the due differences
,
and
(
is the variance-covariance matrix of the standard fit). In this case the variance of the convolution is defined:
and, for Gaussian PDFs, the probability
is the function:
The maximum of
is
. For the inequality (
18), it is:
The equality is true if, and only if, all the
of the track are identical. Now this condition must be inserted for the randomization of the
. In the weighted fits, the law of large numbers determines the convergence of the line-shape toward the function:
Analogously for the standard fits:
The probability of the sequence of hit quality is
. The law of large numbers gives even an easier way for an analytical calculation of the maximums of the two distributions:
where the index
k indicates a track of a large number of simulated tracks,
is the corresponding variance calculated as in the definition of
and
with the expression
. The inequality (
50) assures that
. For our 150,000 tracks the convergence of the maximums of the empirical PDFs to Equation (
53) is excellent for Gaussian PDFs. For the rectangular PDFs of
Figure 1, the results of Equation (
53) are good for the standard fit but slightly higher for weighted fits (3∼4%). The strong similarity of the line-shapes of the rectangular PDFs with the Gaussian PDFs is due to the convolutions among various functions
that rapidly tend to approximate Gaussian functions (Central Limit Theorem). The weighted convolutions of Equation (
45) has higher weights for the PDFs of good hits. These contribute mostly to the maximum of the line-shape. Unfortunately, the good hits have a lower probability and the lower number of the convolved PDFs produce the worst approximation to a Gaussian than in the case of standard fit. In fact, in the probability
of the standard fit, the weights of the convolved functions are identical and the convergence to a Gaussian is better (for N not too small). Better line-shapes, for non-Gaussian PDFs, can be obtained with the approximations of [
13] for doing convolutions.
5.2. Resolution of Estimators
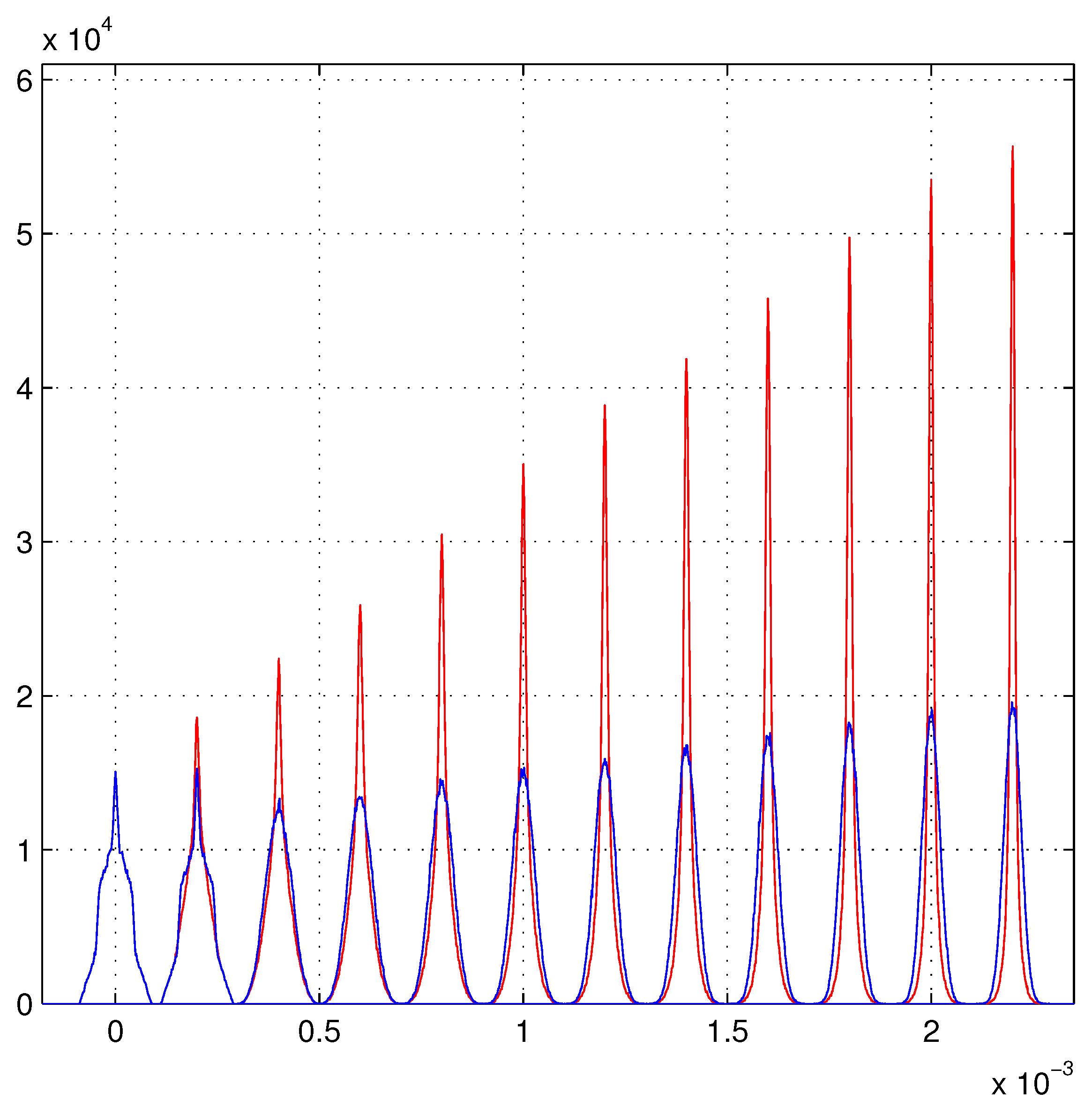
Figure 1 evidences the large differences of the
-PDFs of the weighted least-squares fits compared to the
-PDFs of the standard fits. For
the PDFs of the standard fits are very similar to Gaussian. Instead, the PDFs of the weighted fits are surely non-Gaussian. The definition of resolution becomes very complicated in these cases. In our previous papers, we always used the maximums of the PDFs to compare the resolution of different algorithms. Our convention may be criticized on the ground of the usual definition as the standard deviation of all the data. The weakness of this position is evident for non-Gaussian distributions. In fact, the standard deviation (as the variance), for non-Gaussian PDF, is mainly controlled by the tails of the distributions. Instead, the maximums are not directly affected by the tails and they are true points of the PDFs. We have to recall that the preference of the standard deviation is inherited from the low-statistics of the pre-computer era (when the maximums of data distributions were impossible to obtain). The long demonstrations about the Bessel correction (
in place of
) were relevant for the low-statistics, but absolutely irrelevant for our large numbers of data. In addition to this, a decreasing resolution, when the resolving power of the algorithm/detector increases, easily creates contradictory statements.
Let us justify our preference. The resolution indicates a property of an algorithm/instrument to discriminate near values of the calculated/measured parameters (for example two near tracks). Clearly, the maximum resolving power is obtained if the response of the algorithm/instrument is a Dirac
-function. In this case, the parameters (the two near tracks) are not resolved if, and only if, they coincide. Therefore, the algorithm with the best resolution is the one with the better approximation of a Dirac
-function. Among a set of responses, it is evident that the response with the highest maximum is the better approximation of a Dirac
-function and thus that with the largest resolution. This is the reason for our selection. However, our preference is a “conservative” position. In fact, in recent years it is easy to find, in literature, other “extremist” conventions. A frequent practice (as in [
14] or in Figure 18 of [
15]) is to fit the central part (the core) of the distribution with a piece of Gaussian and to take the standard deviation of this Gaussian as the measure of the resolution.
The Gaussian toy model allows us to calculate the variance of a Gaussian fitted to the core of the PDFs. A method to fit a Gaussian is to fit a parabola to the logarithm of the set of data. The second derivative of the parabola, at the maximum of the distribution, is the inverse of the variance of the Gaussian. This variance can be obtained by the function
of Equations (
51) and (
53):
The common factors are eliminated in the last fraction. Gaussian functions, with standard deviations
, reproduce well the core of
even if the Gaussian rapidly deviates from
. Instead, the Gaussian functions, with the height coinciding with
, are outside the core of
, their full width at half maximum is always larger.
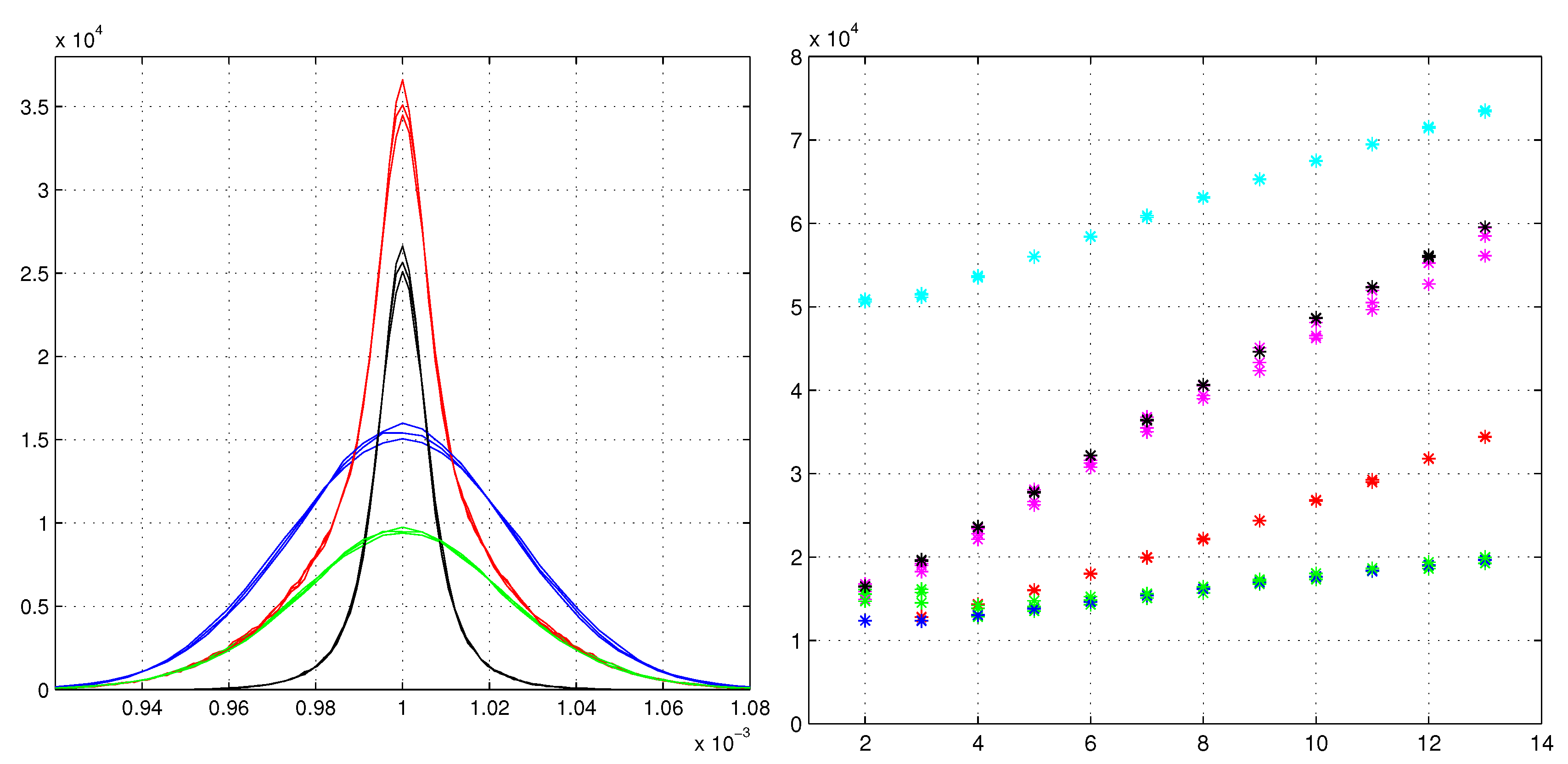
Figure 2 illustrates a few of these aspects for three different toy models.
The left side of
Figure 2 reports the line-shapes for N = 7 layers of the three toy models: the Gaussian of [
4,
8], the rectangular of
Figure 1 and a toy model with triangular PDFs. These three types of PDFs are those considered by Gauss in his paper of 1823 [
11] on the least-squares method. The line-shapes are almost identical with small differences in their maximums. The red line-shapes are formed by the sums of the black and the green lines, respectively the fraction of the red ones given by the tracks with two or more good hits, and the fraction given by tracks with less than two good hits. The heights of the red lines have essential contributions from the black distributions. The line-shapes with the lowest maximums are those of the rectangular toy model and the highest maximums are those of the Gaussian toy model.
The right side of
Figure 2 compares the various parameters as effective heights
(like Gaussian PDFs with variance
) and the maximums of the real empirical PDFs. For the standard fits, only the
corresponding to the variances are reported (blue asterisks). The green asterisks are the maximums of the blue lines of
Figure 1. Excluding the cases N = 2 and N = 3, the two heights are almost coincident. The case N = 2 is dealt with in
Section 2.2. For N = 3, the standard fit tends to have very similar estimators to those of N = 2, this is due to
that suppresses the central observations. Instead for the heteroscedastic fit, the reported heights
are largely different. The red asterisks have
as the variance of the three simulated distributions, the magenta asterisks are the maximums of the three histograms. The black asterisks are the
of Equation (
53). The highest (cyan) asterisks are the
from Equation (
54). Equation (
54) has the form of weighted mean of the inverse of the variance of
, with a weight proportional to the maximum of its
. This form allows its extension to rectangular and triangular toy models even if their derivatives could be problematic. However, these fitted Gaussian PDFs are slightly too narrow for the non-Gaussian toy models, so we applied a small reduction (0.87) to the cyan heights to have a better fit with the rectangular toy models with N ≥ 7. We calculated
of Equation (
54) even for the standard fit (not reported in
Figure 2). The cases with N = 2 and N = 3 are identical to the case of the Gaussian toy model, but these heights drop rapidly converging to the green asterisks of
Figure 2 for N ≥ 6. Hence, coming back to the resolution, the gain in resolution, with respects to the homoscedastic fit, has values: 1.34, 2.4 and 4.1, for the model with seven detecting layers. Waiting for a general convention to define the resolution in these non-Gaussian distributions, our preferred value is 2.4 times the result of the standard fit. However, it is better to correlate the obtained line-shapes to physical parameters of the problem. In [
7], we used the magnetic field and the signal-to-noise ratio to measure the fitting improvements.
Lastly, we have to remember that the non-Gaussian models allow a further increase in resolution with the maximum-likelihood search. Authors in [
6,
7] show the amplitude of the increase in resolution due to the maximum-likelihood search. If the triangular and rectangular toy models had similar improvements, the Gaussian-model would be the worst of all.