Abstract
Since the pioneering works of Newton (1643–1727), mechanics has been constantly reinventing itself: reformulated in particular by Lagrange (1736–1813) then Hamilton (1805–1865), it now offers powerful conceptual and mathematical tools for the exploration of dynamical systems, essentially via the action-angle variables formulation and more generally through the theory of canonical transformations. We propose to the (graduate) reader an overview of these different formulations through the well-known example of Foucault’s pendulum, a device created by Foucault (1819–1868) and first installed in the Panthéon (Paris, France) in 1851 to display the Earth’s rotation. The apparent simplicity of Foucault’s pendulum is indeed an open door to the most contemporary ramifications of classical mechanics. We stress that adopting the formalism of action-angle variables is not necessary to understand the dynamics of Foucault’s pendulum. The latter is simply taken as well-known and simple dynamical system used to exemplify and illustrate modern concepts that are crucial in order to understand more complicated dynamical systems. The Foucault’s pendulum first installed in 2005 in the collegiate church of Sainte-Waudru (Mons, Belgium) will allow us to numerically estimate the different quantities introduced.
1. Introduction: Sainte-Waudru’s Pendulum
The simple pendulum consists of a bob of mass attached at one end of a rigid cable of length l whose mass is negligible compared to . The other end of the cable is attached at the vertical, thereby suspending the bob of the pendulum. It can therefore be considered that the dynamics of the bob is governed by Newton’s equations , and being the weight of the bob and the tension of the cable, respectively, and the acceleration of the bob where denotes the time derivative of the dynamical variable . A schematic representation of a simple pendulum is given in Figure 1, particularized to the pendulum installed in the collegiate church of Sainte-Waudru (Mons, Belgium). This Foucault’s pendulum (FP) was installed for the first time by the University of Mons (UMONS) in 2005 and has regularly been exhibited since then [1,2]. As shown in any textbook on classical mechanics, see for example [3,4,5,6], the resolution of Newton’s equation reveals that the simple pendulum, once slightly set out of its equilibrium position (, performs a periodic swing with period , where and g is gravitational acceleration. For small oscillations, the period is independent of both the mass of the bob and of the amplitude of the swing. For some original references, see e.g., [7,8,9]. Detailed explanations including a discussion of the special case of the motion at the equator can be found in [10]. For other relevant references, see e.g., [11,12]. A precise historical account of Foucault’s experiment together with references to the various attempts at a theoretical understanding can be found in the recent review [13].
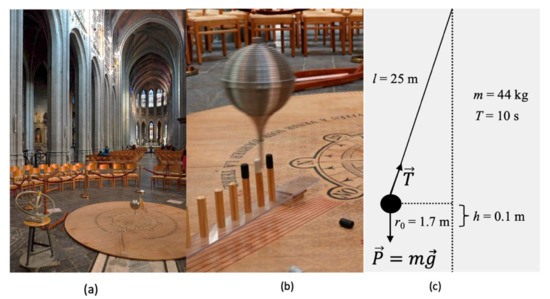
Figure 1.
(a) Foucault’s pendulum installed in the nave of Sainte-Waudru’s collegiate church. (b) Zoom on the bob. The rotation of the pendulum’s plane of swing is exemplified by the successive fall of the neighbouring corks. (c) Schematic view of the latter pendulum at release. The constant is the pendulum length. The amplitude is , causing a vertical displacement with respect to the equilibrium position. The oscillation period is . The vectors and are the weight of the bob and the tension of the cable, respectively.
The amplitude sets the total energy of the pendulum, E, which can be expressed as the potential energy of the bob at release with zero initial velocity: . For Saint Waudru’s FP one has , , and . Numerical quantities will be given with three significant digits. Strictly speaking, frictional forces must be added to the model. They will be neglected here. Friction dissipates the energy of the system: it does not influence the period and only causes a progressive decrease of the amplitude. However, only the periodic behaviour of pendular dynamics is relevant for our purpose.
In spite of the damping due to friction forces, a FP can oscillate for more than enough time to prove that the Earth is rotating. The Earth surface rotates with an angular velocity of lap/day, 1 lap = 2π rad, with respect to an imaginary inertial sphere of same radius and centre as that of the Earth. With respect to however, the normal to the instantaneous plane of oscillation of the FP defines an inertial direction: as Newton’s mechanics shows, it is a consequence of the fact that the force undergone by the bob of mass is always directed towards the center of the Earth. There is no sideways force on the bob as viewed from ; see for example the extensive discussion in [10]. The invariance of the oscillation plane’s orientation in the reference frame causes an apparent rotation of the oscillation plane in the local reference frame that goes in the direction opposite to the one of the Earth, see Figure 2. Only the vertical component of (whose norm is ) in the local frame causes this rotation. In our case, FP’s latitude is φ = 50.5° and .
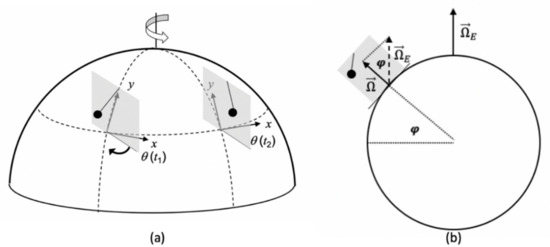
Figure 2.
(a) Foucault’s pendulum in the inertial reference frame—the northern hemisphere is shown. Changes in the angle θ between the oscillation plane and the x axis of local frame are shown at times and . Curved arrows show the counterclockwise and clockwise rotations of the Earth and of the oscillation plane viewed from the local frame, respectively, (b) Sectional view of the Earth and Foucault’s pendulum. Pendulum’s latitude, φ, is shown as well as the Earth angular velocity () and the oscillation plane’s angular velocity ().
Newton’s equation leads, after calculations, to the radial trajectory
The angle may be obtained from to get the trajectory (r(t), in polar coordinates, see Figure 3 and e.g., [9]. The trajectory in the horizontal plane is a hypocycloid (Figure 3). It can be computed from (1) that the FP never turns back to its equilibrium position (): there is a minimal radius , whose origin is the Earth rotation. However, observing this minimum radius is not easy: in Sainte-Waudru it is only 0.153 mm! Another way is more promising: it appears that is shifted by
during one period [8], that is 0.0322° in our example. This remains very small, but just wait 10 min in Saint-Waudru’s nave and the angle of deviation will be 1.93°, which corresponds to a perfectly observable displacement of 5.73 cm on a circle of 1.7 m radius. This displacement is made visible in Sainte-Waudru by the successive falls of the regularly spaced corks (see Figure 1).
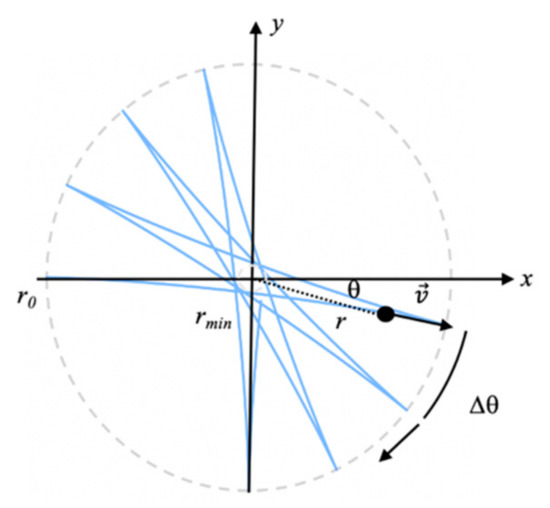
Figure 3.
Typical trajectory of the FP in the horizontal plane (the pendulum is thus seen from above). The position of the bob is expressed in polar coordinates since the bob’s vertical motion is negligible. The shift and the instantaneous horizontal velocity of the bob are displayed. The arrow outside of the circle indicates the direction of the oscillation plane’s rotation viewed from the local frame. Conventions of Figure 2 are kept.
2. Parallel Transport along a Sphere
The FP illustrates an important geometric concept called parallel transport. In this very context, see [14]. The velocity of the bob in the plane tangent to the Earth is a vector. Like any velocity it represents an instantaneous displacement along a curve which traces the trajectory. The apparent rotation of the oscillation plane can be thought of equivalently as a change in the direction of the velocity vector of the bob. This picture hides an unsuspected difficulty. If it is true that in the Euclidean space of Newtonian mechanics one can compare two vectors at different points by dragging them parallel to themselves so as to bring their origin to the same point, it is however not possible, in a more general space, to compare vectors at different points. The space to which the plane coordinatized by is tangent is nothing else than the surface of the Earth, i.e., a sphere. As can be seen from Figure 2, the local plane tangent to the Earth at instant is not the one at : both planes are tangent to , albeit not at the same points.
How can one compare vectors at different points on a sphere? Levi-Civita came up with a method valid for general surfaces, that we summarize along the lines of [15,16]. To transport a vector from a point P to another nearby point Q of , Levi-Civita proposed to embed the sphere into the three-dimensional Euclidean space and to move the vector from its initial point P to the neighbouring point Q using the Euclidean notion of parallel displacement, the very notion of “sliding” used by our schoolchildren who learn Newtonian mechanics. The resulting vector, , is generally not tangent to the sphere It has then to be projected onto the surface of the sphere, thereby obtaining a vector in Q denoted . Starting from this new vector and proceeding in a similar way, step by step for all the points along a curve passing through P and Q, a whole family of vectors tangent to the sphere can be constructed along the latter curve. This construction is illustrated in Figure 4.
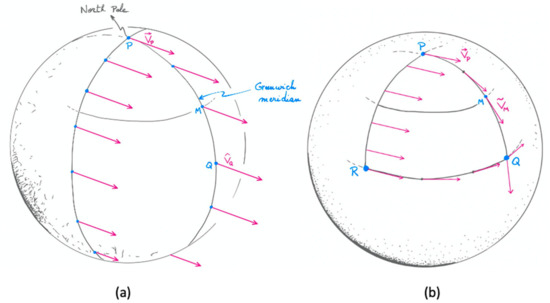
Figure 4.
(a) Parallel transport of vector along two meridians computed in the three-dimensional Euclidean space. (b) Right: Parallel transport of vector computed with Levi-Civita’s method for the curves PRQ and PQ.
Without any specification of a particular curve, the parallel transport operation is ambiguous. It is interesting to see what happens for two different curves that connect points P and Q on the Earth’s surface. Taking the curves PQ and PRQ in Figure 4, depending on whether one follows the first or the second curve, the vector obtained by parallel transport will point to the south or will be tangent to the equator. Two different orthogonal vectors are thus obtained. Parallel transport of a vector along all the curves that start from a point on the sphere and return to the same point gives vectors at that point that actually differ from the initial vector by a rotation by an arbitrary angle. In the case of the Foucault’s pendulum, the relevant curve is the parallel passing through the vertical of its equilibrium position (the parallel of latitude 50.5° in our example). The parallel transport of the bob velocity vector along that parallel generates an apparent rotation of its direction for a local observer. This rotation is measurable through the displacement of the oscillation plane of the pendulum. An explicit calculation of bob velocity’s parallel transport based on spherical trigonometry leads to Equation (2) [17].
3. Lagrange
Lagrange elaborated a formulation of mechanics that makes it possible to free oneself from the complicated drawings asked to our high school students (Figure 1) in order to solve a problem in mechanics by identifying the different forces at play, finding their resultant, and then solving Newton’s equations [18]. Unlike Newton who strove to present his results in the most ancient formalism possible, the way Euclid (around 300 ACN) would have done, Lagrange understood the importance of no longer having to make “inspired drawings” to have a chance of solving a problem of mechanics. Moreover, if Newton’s equations are simple in Cartesian coordinates, they become much more complicated in other coordinate systems better suited to the geometry of the system under study, such as polar coordinates in the FP case.
By invoking a “principle of least action”, Lagrange replaced Newton’s technical arsenal by the search for a single function, named after him Lagrangian and denoted L. Typically, , which is the difference between the kinetic and potential energies of the system. Lagrange’s postulate is that the system, during its temporal evolution between two instants and , will always minimize the action, . The Lagrangian can be written in any coordinate system and the real number it provides for a given state of the system will always be the same, regardless of the coordinates used. For example the FP Lagrangian is , where are the rates of changes of [19]. The space parameterized by the Lagrange variables is called configuration space.
From the principle of least action, equations of motion―called Euler-Lagrange equations―can be deduced which take the same form in all coordinate systems and are, in the present case of the FP, equivalent to Newton’s equation. The Euler-Lagrange equations read = 0, with the position coordinates, and the subscript runs from 1 to the number of degrees of freedom of the system under study. The symbols d and denote the total and partial derivatives, respectively. But that is not all. Lagrange’s analytical formalism also makes it possible to ignore the vast majority of forces at play, such as the tension in the cable of the FP. It is therefore of little importance to know the tensions and constraints imposed on the solid body whose motion is being studied. All that matters is to know that the body remains solid, with a constant shape and subject to external forces and constraints such as the weight and the constancy of the length of the cable suspending the bob.
A detailed discussion of the FP in the Lagrangian formalism can be found in [19]. In the rest of this article, we will take inspiration from this book, extracting the key concepts while limiting the associated mathematical developments.
4. From Configuration Space to Phase Space
The choice of a “good” coordinate system reflects the symmetries of the system under study. Hamilton sought for even more symmetry by not limiting the visualization of a system to position variables only. In his formalism he introduced from the very beginning the following fundamental idea: the variables of position and velocity are independent. They can be chosen independently at any moment and the dynamical equations will “propagate” these initial conditions into the future. Hamilton defined variables named “momenta” generalizing the velocities (one momentum variable for each position coordinate ) and then constructed, for any Lagrangian L having a regular Hessian matrix of components , a new function H named Hamiltonian. The function H depends on the position and momentum variables only, once one expresses the velocities in terms of the positions and momenta by inverting the relations The space parametrized by the independent position and momentum variables is called phase space. Using the principle of least action extended to phase space, Hamilton obtained first-order differential equations, and , quite differently from Newton’s and Lagrange’s equations which are of the second order in the time-derivatives. The number of these first-order differential equations is equal to the dimension of phase space. One half of Hamilton’s equations allows to express the momenta as functions of the velocities while the other half gives equations which, combined with the first half, reduce to the Euler-Lagrange equations.
The Hamiltonian for the FP is of the form + , i.e., a function of the position and momentum variables. The space is the FP phase space. Hamilton’s equations yield
They reveal the existence of a constant of motion, . In the case of Sainte-Waudru’s FP, it takes the value . Moreover, Hamilton’s equations lead to and finally to the radial trajectory given by Equation (1).
The dynamics of the FP can be visualized via the pairs of variables and , each describing a plane in which the dynamics will draw curves. The phase space provides a succinct geometrical representation of the dynamical evolution of the pendulum, illustrated in Figure 5. In the plane , is constant during the complete oscillation. Let us now go through the pendulum’s oscillation cycle in the plane , clockwise from point A. This point corresponds to FP’s release: the amplitude is at its maximum and the velocity is null. Then the bob falls down, its radial velocity decreasing ( until its absolute value reaches a maximum in B. The radial position of bob reaches a minimal value at C where the radial velocity goes back to zero. Then, the radial coordinate r of the bob increases until reaches a maximal value at D. The pendulum finally returns to point A, from where it starts a new oscillation cycle.
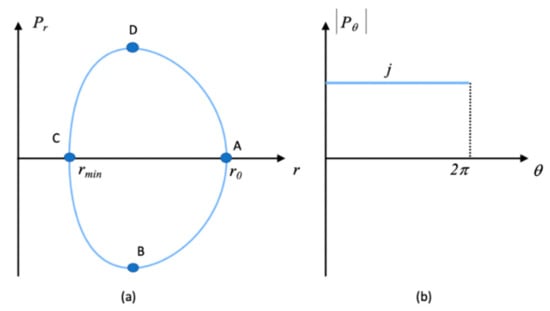
Figure 5.
(a) Foucault’s pendulum trajectory in the plane of phase space, computed with Equations (1) and (3). (b) Same for the plane .
Why introducing this apparent complication created by the doubling of variables between the configuration space and the phase space, if at the end of the day one recovers Lagrange’s equations? The reason is that phase space has a remarkable geometrical structure that allows for canonical transformations: transformations of the phase space coordinates that preserve the expression of Hamilton’s equations of motion and mix the position and momentum variables among them, rendering such a distinction actually artificial. The phase space variables can indeed mix and give rise to new canonical variables that not only preserve the simple expression of Hamilton’s equations but can also offer an immediate resolution of these equations of motion, as we will now explain.
5. Motion on a Torus
For a bounded motion such as that of the FP, a canonical transformation always exists that starts from and leads to new phase space coordinates called action-angle variables . A remarkable property is that the action variables are invariant over time for given initial conditions. For the FP, calculations show that and . Numerically, the latter takes the value 20 J·s in our example. These two action variables are proportional, respectively, to the area of the rectangle shown to the right of Figure 5 and to the area inside the curve shown to the left of the same figure. Each of the angle variables range from 0 to 2π and give the position of the dynamical system in the corresponding cycle of the periodic motion. As shown in Figure 6, the dynamical evolution of the FP in phase space can be seen as the displacement of a particle on a torus—a doughnut. The surfaces of the two sections of the doughnut are equal to and while the two angles that describe the circulation of the particle on the torus are the angle variables .
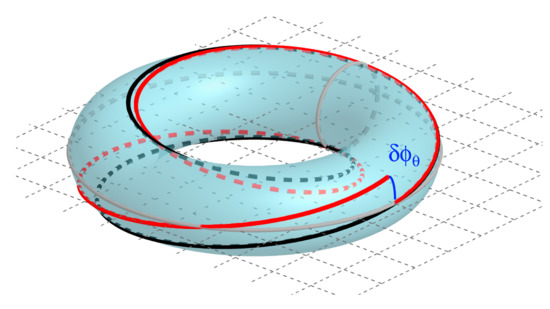
Figure 6.
Representation of the phase space of the Foucault’s pendulum in terms of the angle-action variables [20]. The two sections of the torus (sections limited by the two grey circles) are of dimensions and . The two curves on the surface of the torus correspond to the trajectory of the pendulum neglecting the rotation of the Earth (in black) or including it (in red). A point of a curve on the torus corresponds to a given value of the couple of angle variables . The infinitesimal Berry-Hannay angle, δ, is shown in blue font.
More generally, for a dynamical evolution which occurs in a compact volume of phase space, a transformation exists which allows to see any such dynamical evolution as the displacement of a particle on a torus of dimension n, if n is the number of independent position variables. The surfaces of the different sections of the torus are the action variables while the n angles that describe the circulation of the particle on the torus are the angle variables.
Let us come back to FP. The Hamiltonian takes a simple form in action-angle coordinates: . Hamilton’s equations of motion lead to and . Would the Earth not rotate, one would have and the angle variable would increase exactly two times faster than : in the representation proposed in Figure 6, the complete trajectory of the FP would draw a closed curve (in black). However, the Earth rotates and therefore Ω is different from zero: it causes a perturbation in the evolution of and as a result, the red curve that corresponds to the actual situation is not closed. There is a discrepancy between the red and black curves and the resulting angular deviation is the infinitesimal Berry-Hannay angle corresponding to one period of the pendulum. The cumulated angular deviation after 1 day is called the Berry-Hannay angle [21,22] for the FP. It is equal to and corresponds to the angular displacement of the oscillation plane over one day.
The geometric notion underlying the Barry-Hannay angle is that of holonomy. For extensive discussions on this crucial concept in Physics and for more references, see the book [23] and the original papers reprinted in [24]. As it can be read in [23,24], the appearance of a Berry-Hannay angle is observed in many other systems than the FP. As first shown by Foucault by using a gyroscope in 1852 and later exemplified by Bryan [25], vibrating bodies also define inertial directions and are therefore subject to FP-like precession. Bryan’s effect more specifically concerns standing waves in rotating solids of revolution. This effect has since then been shown to occur in vibrating gyroscopes and is related to the concept of holonomy [26]; it can even be used to design angle measuring MEMS (microelectromechanical systems) gyroscopes [27].
6. Conclusions
The path that we have made through the different formulations of mechanics starts from a formulation where the fundamental observables are the positions of the rigid body as well as its velocities and accelerations, obtained by successive time derivatives of the positions. At the end of our journey, the problem is represented in phase space in terms of the invariants of motion (the action variables) and of the positioning of the moving body on the different cycles constituting this motion (the angle variables). The evolution of mechanics thus tends to abstract itself from the particularities of each problem in order to evolve towards a general formalism where any dynamical system with (quasi-)periodic motion can be characterized by universal concepts. The Berry-Hannay angle is such a concept. In the case of Foucault’s pendulum, it gives a measure of the rotation of the oscillation plane after one day, through the non-closed trajectory of the bob in phase space coordinatized by the action-angle variables.
The particular behavior of the Foucault’s pendulum can also be interpreted in terms of the parallel transport of the velocity vector of the bob. This notion has become central in modern Physics through the concept of connection; here, the Levi-Civita connection on the sphere, which expresses how the tangent vectors to the sphere are transported parallel to themselves along any given curve on the sphere. The same Levi-Civita concept of parallel transport allowed Einstein (1879–1955), with the help of Marcel Grossmann (1878–1936), to better understand Gravitation. Indeed, the mathematics of General Relativity in its original formulation is entirely based on Levi-Civita’s notion of parallel transport on a curved manifold representing our space-time populated with matter and radiation.
The Hamiltonian formalism of mechanics makes it possible to completely solve many problems that cannot be solved otherwise, such as the problem of a massive particle attracted by two centers (for example the Earth subject to the combined gravitational attractions of the Sun and Jupiter), see e.g., [19]. Hamilton’s approach is instrumental for controlling the position of a satellite or space probe, or for understanding the general dynamics of chaotic systems [5]. For more references on the wide variety of applications of Hamilton’s formulation of classical mechanics, see e.g., the Introduction of the book [23]. Finally, we recall that Nature is quantum at its most fundamental level. Here as well, the Hamiltonian formalism plays a crucial role in quantum mechanics and quantum field theory, see e.g., [28,29] and references therein.
Author Contributions
Conceptualization, N.B., F.B.; writing—original draft preparation, N.B., F.B.; writing—review and editing, N.B., F.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
We thank Francesco Lo Bue for the successful installation of Foucault’s pendulum at Saint Waudru’s collegiate church and for fruitful discussions at early stages of this manuscript. We thank Tracy Gittins for his advice on English.
Conflicts of Interest
The authors declare no conflict of interest.
References
- MUMONS. Available online: https://mumons.be/ (accessed on 31 August 2020).
- Vous Étes Invitès À Voir Tourner La Terre; Collegiale Ste Waudrau; UMONS: Mons, Belgium, 2018; Available online: https://mumons.be/wp-content/uploads/2019/08/Pendules_livret.pdf (accessed on 31 August 2020).
- Kibble, T.W.B.; Berkshire, F.J. Classical Mechanics; Imperial College Press: London, UK, 2004; pp. 117–119. [Google Scholar]
- Landau, L.; Lifchitz, E. Physique Théorique. Tome 1: Mécanique; Mir: Moscou, URSS, 1981; pp. 154–159. [Google Scholar]
- Arnold, V. Méthodes Mathématiques de la Mécanique Classique; Mir: Moscou, URSS, 1976; pp. 135–136. [Google Scholar]
- Spindel, P.H. Mécanique: Mécanique Newtonienne; Edition Scientifiques; GB Contemporary Publishing International: Paris, France, 2004; Volume 1, pp. 116–120. [Google Scholar]
- Chessin, A.S. On Foucault’s pendulum. Am. J. Math. 1985, 1, 81–88. [Google Scholar] [CrossRef]
- Mac Millan, W.D. On Foucault’s pendulum. Am. J. Math. 1915, 37, 95–106. [Google Scholar] [CrossRef][Green Version]
- Noble, W.J. A Direct treatment of the Foucault pendulum. Am. J. Phys. 1952, 20, 334–336. [Google Scholar] [CrossRef]
- Somerville, W.B. The description of Foucault’s pendulum. Q. J. R. Astron. Soc. 1972, 13, 40–62. [Google Scholar]
- Hart, J.B.; Miller, R.E.; Mills, R.L. A simple geometric model for visualizing the motion of a Foucault pendulum. Am. J. Phys. 1987, 55, 67–70. [Google Scholar] [CrossRef]
- Phillips, N. What makes the Foucault pendulum move among the stars? Sci. Educ. 2004, 13, 653–661. [Google Scholar] [CrossRef]
- Sommeria, J. Foucault and the rotation of the Earth. Comptes Rendus Phys. 2017, 18, 520–525. [Google Scholar] [CrossRef]
- Oprea, J. Geometry and the Foucault pendulum. Amer. Math. Mon. 1995, 102, 515–522. [Google Scholar] [CrossRef]
- Penrose, R. The Road to Reality: A Complete Guide to The Laws of The Universe; Vintage: London, UK, 2007; pp. 292–321. [Google Scholar]
- Levi-Civita, T. Nozione di parallelismo in una varietà qualunque e conseguente specificazione geometrica della curvatura riemanniana. Rend. Circ. Mat. Palermo 1917, 42, 173–215. Available online: https://www.semanticscholar.org/paper/Nozione-di-parallelismo-in-una-varietà-qualunque-e-Levi-Civita/250799430621d438ce3dfb6deb139ba6db2565b9 (accessed on 31 August 2020). [CrossRef]
- Von Bergmann, J.; Von Bergmann, H.C. Foucault pendulum through basic geometry. Am. J. Phys. 2007, 75, 888–892. [Google Scholar] [CrossRef]
- Lagrange, J.L. Méchanique Analitique, 1st ed.; La Veuve Desaint: Paris, France, 1788; p. 189. Available online: https://gallica.bnf.fr/ark:/12148/bpt6k862625.image (accessed on 31 August 2020).
- José, J.V.; Saletan, E.J. Classical Dynamics: A Contemporary Approach; Cambridge University Press: Cambridge, UK, 1998; pp. 367–371. [Google Scholar]
- The Plot Has Been Made With the Free Software GeoGebra Classic 6. Available online: https://www.geogebra.org/m/hsjeyjcd (accessed on 20 April 2020).
- Hannay, J.H. Angle variable holonomy in adiabatic excursion of an integrable Hamiltonian. J. Phys. A Math. Gen. 1985, 18, 221–230. [Google Scholar] [CrossRef]
- Berry, M. Classical adiabatic angles and quantal adiabatic phase. J. Phys. A. Math. Gen. 1985, 18, 15–27. [Google Scholar] [CrossRef]
- Marsden, J.E.; Ratiu, T.S. Introduction to Mechanics and Symmetry; Springer: NY, USA, 1999; pp. 1–59. [Google Scholar]
- Wilczek, F.; Shapere, A. Geometric Phases in Physics; World Scientific: Singapore, 1989; p. 528. [Google Scholar]
- Bryan, G.H. On the beats in the vibrations of a revolving cylinder or bell. Proc. Camb. Philos. Soc. Math. Phys. Sci. 1890, 7, 101–114. [Google Scholar]
- Andersson, S.B.; Krishaprasad, P.S. The Hannay-Berry Phase of the Vibrating Ring Gyroscope; Technical Research Report no. CDCSS TR 2004-2; University of Maryland: College Park, MD, USA, 2004; p. 26. [Google Scholar]
- Prikhodko, I.P.; Zotov, S.A.; Trusov, A.A.; Shkel, A.M. Foucault pendulum on a chip: Angle measuring silicon MEMS gyroscope. In Proceedings of the 2011 IEEE 24th International Conference on Micro Electro Mechanical Systems, Cancun, Mexico, 23–27 January 2011; pp. 161–164. [Google Scholar]
- Weinberg, S. The Quantum Theory of Fields; Cambridge University Press: Cambridge, UK, 1995; pp. 378–383. [Google Scholar]
- Srednicki, M. Quantum Field Theory; Cambridge University Press: Cambridge, UK, 2007; pp. 43–48. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).