Electron Beam Transport in Plasma-Accelerator-Driven Free-Electron Lasers in the Presence of Coherent Synchrotron Radiation and Microbunching Instability
Abstract
1. Introduction
2. Model of Microbunching Instability
2.1. Electron Beam Delivery System
2.2. Spectral Gain and Slice Energy Spread
2.3. Switchyard Optics Design
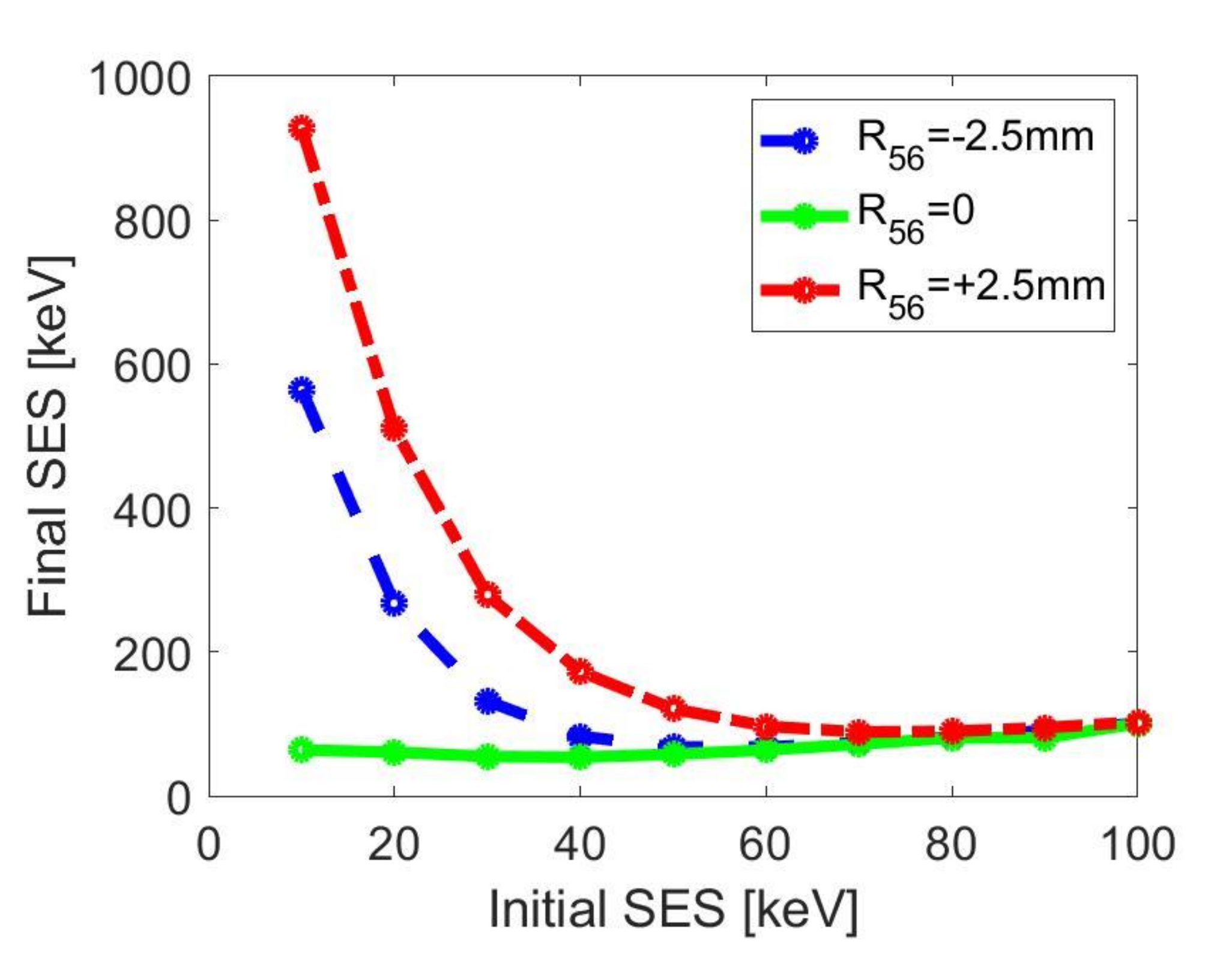
3. Results
3.1. Microbunching Instability
3.2. Coherent Synchrotron Radiation
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Huang, Z.; Stupakov, G. Control and application of beam microbunching in high brightness linac-driven free electron lasers. Nucl. Instrum. Phys. Res. A 2018, 907, 182. [Google Scholar] [CrossRef]
- Di Mitri, S. Coherent Synchrotron Radiation and Microbunching Instability. In Proceedings of the CERN Accelerator School: Free Electron Lasers and Energy Recovery Linacs, Hamburg, Germany, 31 May–10 June 2016. [Google Scholar]
- Saldin, E.L.; Schneidmiller, E.A.; Yurkov, M.V. Klystron instability of a relativistic electron beam in a bunch compressor. Nucl. Instrum. Phys. Res. A 2002, 490, 1. [Google Scholar] [CrossRef]
- Heifets, S.; Stupakov, G.; Krinsky, S. Coherent synchrotron radiation instability in a bunch compressor. Phys. Rev. Special Topics Accel. Beams 2002, 5, 064401. [Google Scholar] [CrossRef]
- Huang, Z.; Kim, K.-J. Formulas for coherent synchrotron radiation microbunching in a bunch compressor chicane. Phys. Rev. Special Topics Accel. Beams 2002, 5, 074401. [Google Scholar] [CrossRef]
- Marcus, G.; Fawley, W.M.; Bohler, D.; Ding, Y.; Feng, Y.; Hemsing, E.; Huang, Z.; Krzywinski, J.; Lutman, A.; Ratner, D. Experimental observations of seed growth and accompanying pedestal contamination in a self-seeded, soft x-ray free-electron laser. Phys. Rev. Accel. Beams 2019, 22, 080702. [Google Scholar] [CrossRef]
- Ratner, D.; Behrens, C.; Ding, Y.; Huang, Z.; Marinelli, A.; Maxwell, T.; Zhou, F. Time-resolved imaging of the microbunching instability and energy spread at the Linac Coherent Light Source. Phys. Rev. ST Accel. Beams 2015, 18, 030704. [Google Scholar] [CrossRef]
- Lu, H.; Liu, M.; Wang, W.; Wang, C.; Liu, J.; Deng, A.; Xu, J.; Xia, C.; Li, W.; Zhang, H.; et al. Laser wakefield acceleration of electron beams beyond 1 GeV from an ablative capillary discharge waveguide. Appl. Phys. Lett. 2011, 99, 091502. [Google Scholar] [CrossRef]
- Wang, W.; Zgadzaj, R.; Fazel, N.; Li, Z.; Yi, S.A.; Zhang, X.; Henderson, W.; Chang, Y.-Y.; Korzekwa, R.; Tsai, H.-E.; et al. Quasi-monoenergetic laser-plasma acceleration of electrons to 2 GeV. Nat. Commun. 2013, 4, 1988. [Google Scholar] [CrossRef]
- Kim, H.T.; Pae, K.H.; Cha, H.J.; Kim, I.J.; Yu, T.J.; Sung, J.H.; Lee, S.K.; Jeong, T.M.; Lee, J. Enhancement of electron energy to the multi-GeV regime by a dual-stage laser-wakefield accelerator pumped by petawatt laser pulses. Phys. Rev. Lett. 2013, 111, 165002. [Google Scholar] [CrossRef]
- Leemans, W.P.; Gonsalves, A.J.; Mao, H.S.; Nakamura, K.; Benedetti, C.; Schroeder, C.B.; Tóth, C.; Daniels, J.; Mittelberger, D.E.; Bulanov, S.S.; et al. Multi-GeV electron beams from capillary-discharge-guided subpetawatt laser pulses in the self-trapping regime. Phys. Rev. Lett. 2014, 113, 245002. [Google Scholar] [CrossRef]
- Maier, A.R.; Meseck, A.; Reiche, S.; Schroeder, C.B.; Seggebrock, T.; Gruner, F. Demonstration scheme for a laser-plasma-driven free-electron laser. Phys. Rev. X 2012, 2, 031019. [Google Scholar] [CrossRef]
- Labat, M.; Loulergue, A.; Andre, T.; Andriyash, I.A.; Ghaith, A.; Khojoyan, M.; Marteau, F.; Valléau, M.; Briquez, F.; Benabderrahmane, C.; et al. Robustness of a plasma acceleration based free electron laser. Phys. Rev. Accel. Beams 2018, 21, 114802. [Google Scholar] [CrossRef]
- André, T.; Andriyash, I.A.; Loulergue, A.; Labat, M.; Roussel, E.; Ghaith, A.; Khojoyan, M.; Thaury, C.; Valléau, M.; Briquez, F.; et al. Control of laser plasma accelerated electrons for light sources. Nat. Commun. 2018, 9, 1334. [Google Scholar] [CrossRef]
- Decking, W.; Obier, F. Layout of the Beam Switchyard at the European XFEL, WEPC073. In Proceedings of the 11th European Particle Accelerator Conference, Genoa, Italy, 23–27 June 2008. [Google Scholar]
- Milas, N.; Gough, C. Design of the SwissFEL Switchyard, WEPB16. In Proceedings of the 32nd International Free Electron Laser Conference, Malmö, Sweden, 23–27 August 2010. [Google Scholar]
- Placidi, M.; Jung, J.-Y.; Ratti, A.; Sun, C. Compact switchyard schemes. Nucl. Instr. Meth. Phys. Res. A 2014, 768, 14–19. [Google Scholar] [CrossRef]
- Faatz, B.; Plönjes, E.; Ackermann, S.; Agababyan, A.; Asgekar, V.; Ayvazyan, V.; Baark, S.; Baboi, N.; Balandin, V.; Von Bargen, N.; et al. Simultaneous operation of two soft x-ray free-electron lasers driven by one linear accelerator. New J. Phys. 2016, 18, 062002. [Google Scholar] [CrossRef]
- Hara, T.; Fukami, K.; Inagaki, T.; Kawaguchi, H.; Kinjo, R.; Kondo, C.; Otake, Y.; Tajiri, Y.; Takebe, H.; Togawa, K.; et al. Pulse-by-pulse multi-beam-line operation for x-ray free-electron lasers. Phys. Rev. Accel. Beams 2016, 19, 020703. [Google Scholar] [CrossRef]
- Alotaibi, B.M.; Khalil1, S.M.; McNeil, B.W.J.; Traczykowski, P. Modelling a laser plasma accelerator driven free electron laser. J. Phys. Commun. 2019, 3, 6. [Google Scholar] [CrossRef]
- Di Mitri, S.; Cornacchia, M. Electron beam brightness in linac drivers for free-electron-lasers. Phys. Rep. 2014, 539, 1–48. [Google Scholar] [CrossRef]
- Wiggins, S.M.; Issac, R.C.; Welsh, G.H.; Brunetti, E.; Shanks, R.P.; Anania, M.P.; Cipiccia, S.; Manahan, G.G.; Aniculaesei, C.; Ersfeld, B.; et al. High quality electron beams from a laser wakefield accelerator. Plasma Phys. Contr. Fusion 2010, 52, 12. [Google Scholar] [CrossRef][Green Version]
- Huang, Z.; Ding, Y.; Schroeder, C.B. Compact X-ray free-electron laser from a laser-plasma accelerator using a transverse-gradient undulator. Phys. Rev. Lett. 2012, 109, 204891. [Google Scholar] [CrossRef]
- Samant, S.A.; Upadhyay, A.K.; Krishnagopal, S. High brightness electron beams from density transition laser wakefield acceleration for short-wavelength free-electron lasers. Plasma Phys. Contr. Fusion 2014, 56, 9. [Google Scholar] [CrossRef]
- Pousa, A.F.; de la Ossa, A.M.; Assmann, R. Intrinsic energy spread and bunch length growth in plasma-based accelerators due to betatron motion. Sci. Rep. 2019, 9, 17690. [Google Scholar] [CrossRef] [PubMed]
- Couprie, M.E.; Loulergue, A.; Labat, M.; Lehe, R.; Malka, V. Towards a free electron laser based on laser plasma accelerators. J. Phys. B 2014, 47, 23. [Google Scholar] [CrossRef]
- Brinkmann, R.; Delbos, N.; Dornmair, I.; Kirchen, M.; Assmann, R.; Behrens, C.; Floettmann, K.; Grebenyuk, J.; Gross, M.; Jalas, S.; et al. Chirp mitigation of plasma-accelerated beams by a modulated plasma density. Phys. Rev. Lett. 2017, 118, 214801. [Google Scholar] [CrossRef] [PubMed]
- Pousa, A.F.; de la Ossa, A.M.; Brinkmann, R.; Assmann, R. Compact multistage plasma-based accelerator design for correlated energy spread compensation. Phys. Rev. Lett. 2019, 123, 054801. [Google Scholar] [CrossRef] [PubMed]
- Loulergue, A.; Labat, M.; Evain, C.; Benabderrahmane, C.; Malka, V.; Couprie, M.E. Beam manipulation for compact laser wakefield accelerator based free-electron lasers. New J. Phys. 2015, 17. [Google Scholar] [CrossRef]
- Nghiem, P.A.P.; Assmann, R.; Beck, A.; Chancé, A.; Chiadroni, E.; Cros, B.; Ferrario, M.; Pousa, A.F.; Giribono, A.; Gizzi, L.A.; et al. Toward a plasma-based accelerator at high beam energy with high beam charge and high beam quality. Phys. Rev. Accel. Beams 2020, 23, 031301. [Google Scholar] [CrossRef]
- Bosch, R.A.; Klemann, K.J.; Wu, J. Modeling two-stage bunch compression with wakefields: Macroscopic properties and microbunching instability. Phys. Rev. ST Accel. Beams 2008, 11, 090702. [Google Scholar] [CrossRef]
- Di Mitri, S.; Perosa, G.; Brynes, A.D.; Setija, I.; Spampinati, S.; Williams, P.; Wolski, A.; Allaria, E.; Brussaard, S.; Gianessi, L.; et al. Experimental evidence of intrabeam scattering in a free-electron laser driver. New J. Phys. 2020. [Google Scholar] [CrossRef]
- EUPRAXIA Conceptual Design Report. Available online: http://www.lnf.infn.it/sis/preprint/pdf/getfile.php?filename=INFN-18-03-LNF.pdf (accessed on 26 August 2020).
- Bonifacio, R.; Pellegrini, C.; Narducci, L. Collective instabilities and high-gain regime in a free electron laser. Opt. Commun. 1984, 50, 373–378. [Google Scholar] [CrossRef]
- Venturini, M. Models of longitudinal space-charge impedance for microbunching instability. Phys. Rev. Spec. Top. Accel. Beams 2008, 11, 034401. [Google Scholar] [CrossRef]
- Huang, Z.; Borland, M.; Emma, P.; Wu, J.; Limborg, C.; Stupakov, G.; Welch, J. Suppression of microbunching instability in the linac coherent light source. Phys. Rev. Spec. Top. Accel. Beams 2004, 7, 074401. [Google Scholar] [CrossRef]
- Tsai, C.-Y.; Di Mitri, S.; Douglas, D.; Li, R.; Tennant, C. Conditions for coherent-synchrotron-radiation-induced microbunching suppression in multibend beam transport or recirculation arcs. Phys. Rev. Accel. Beams 2017, 20, 024401. [Google Scholar] [CrossRef]
- Di Mitri, S.; Spampinati, S. Microbunching instability study in a linac-driven free electron laser switchyard beam line. Phys. Rev. Accel. Beams 2017, 20, 120701. [Google Scholar] [CrossRef]
- Perosa, G.; Allaria, E.M.; Badano, L.; Bruchon, N.; Cinquegrana, P.; Danailov, M.B.; Demidovich, A.; De Ninno, G.; Giannessi, L.; Mirian, N.; et al. Linear optics control of sideband instability for improved free-electron laser spectral brightness. Phys. Rev. 2020, in press. [Google Scholar]
- Di Mitri, S.; Spampinati, S. Microbunching instability suppression via electron-magnetic-phase mixing. Phys. Rev. Lett. 2014, 112, 134802. [Google Scholar] [CrossRef]
- Derbenev, Y.S.; Rossbach, J.; Saldin, E.L.; Shiltsev, V.D. Microbunch Radiative Tail—Head Interaction, TESLA-FEL 95-05; DESY: Hamburg, Germany, 1995. [Google Scholar]
- Di Mitri, S.; Cornacchia, M.; Spampinati, S. Cancellation of coherent synchrotron radiation kicks with optics balance. Phys. Rev. Lett. 2013, 110, 014801. [Google Scholar] [CrossRef]


| Parameter | Value |
|---|---|
| Energy | 1, 5 GeV |
| Charge | 30 pC |
| Peak current | 3 kA |
| Duration, RMS | 4 fs |
| Slice energy spread, RMS | 10–300 keV |
| Normalized emittance, RMS | 0.3 μm rad |
| Transverse size, RMS | <40 μm |
| Parameter | Value |
|---|---|
| Energy | 1, 5 GeV |
| Dipole length | 0.5 m |
| Dipole bending angle | 5, 3 deg |
| Drift length in each cell | 5 m |
| Drift length between cells | 10 m |
| || | <3 mm |
| Maximum dispersion function | 30 mm |
| Average betatron function | 10 m |
| Peak Gain | ||
|---|---|---|
| +2.5 | 407 | 928 |
| 0 | 38 | 64 |
| −2.5 | 281 | 565 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Mitri, S.; Perosa, G. Electron Beam Transport in Plasma-Accelerator-Driven Free-Electron Lasers in the Presence of Coherent Synchrotron Radiation and Microbunching Instability. Physics 2020, 2, 521-530. https://doi.org/10.3390/physics2040029
Di Mitri S, Perosa G. Electron Beam Transport in Plasma-Accelerator-Driven Free-Electron Lasers in the Presence of Coherent Synchrotron Radiation and Microbunching Instability. Physics. 2020; 2(4):521-530. https://doi.org/10.3390/physics2040029
Chicago/Turabian StyleDi Mitri, Simone, and Giovanni Perosa. 2020. "Electron Beam Transport in Plasma-Accelerator-Driven Free-Electron Lasers in the Presence of Coherent Synchrotron Radiation and Microbunching Instability" Physics 2, no. 4: 521-530. https://doi.org/10.3390/physics2040029
APA StyleDi Mitri, S., & Perosa, G. (2020). Electron Beam Transport in Plasma-Accelerator-Driven Free-Electron Lasers in the Presence of Coherent Synchrotron Radiation and Microbunching Instability. Physics, 2(4), 521-530. https://doi.org/10.3390/physics2040029






