Basis and Prospects of Combining Electroadsorption Modeling Approaches for Capacitive Deionization
Abstract
:1. Introduction
2. Materials and Methods
2.1. Theory
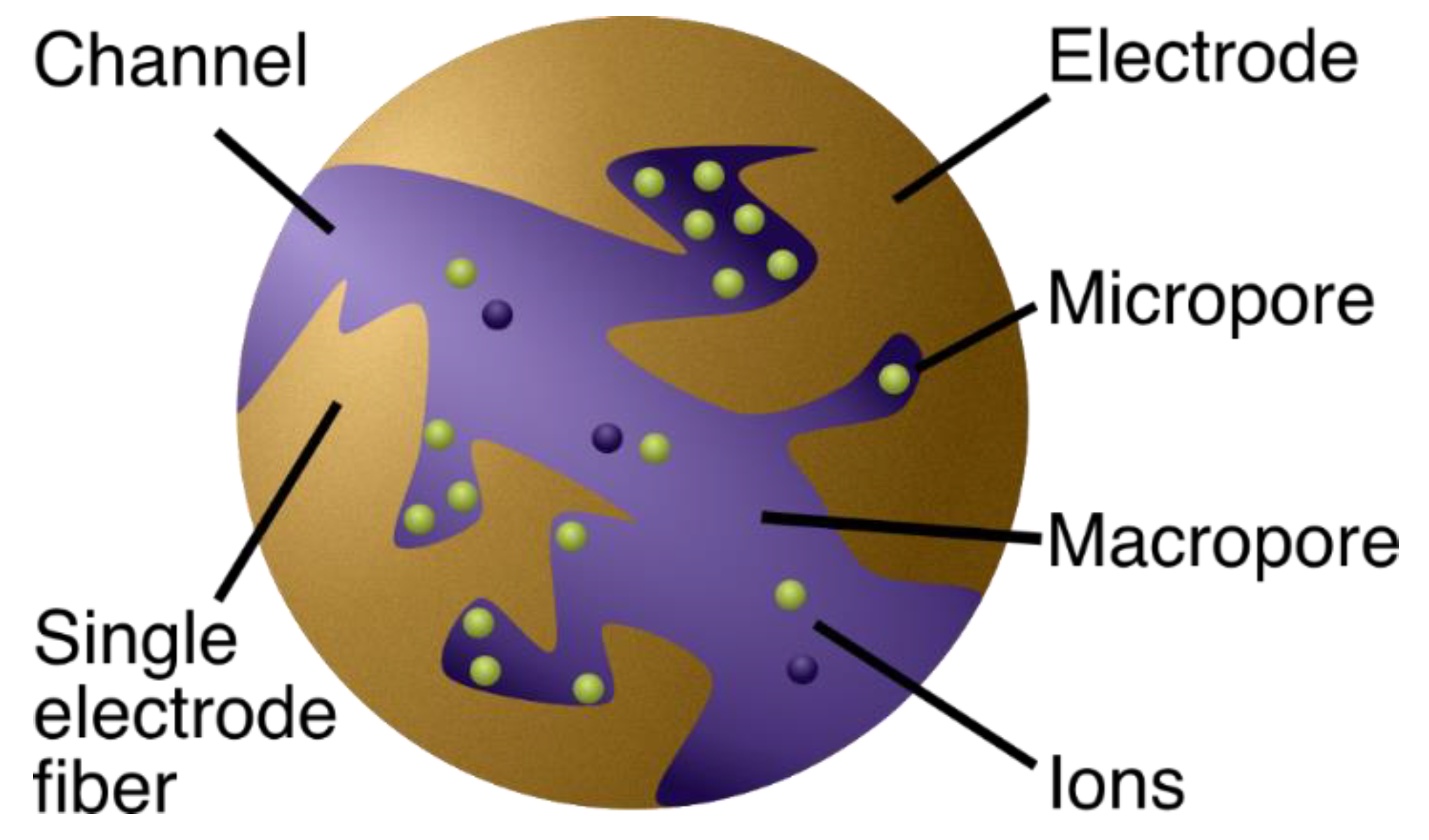
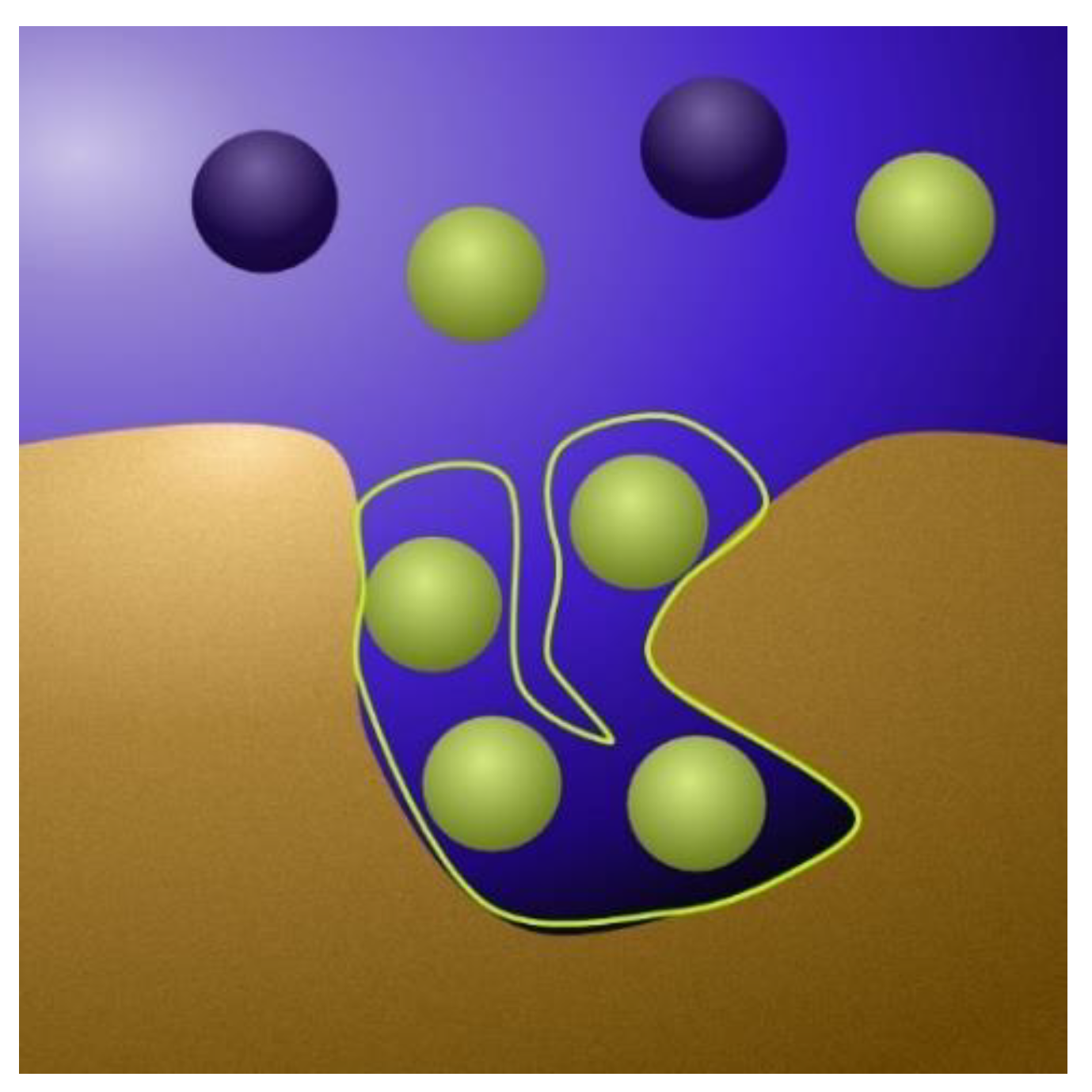
2.1.1. The Physics Behind the Models
2.1.2. From Physics to Model
2.1.3. Dynamic Langmuir Model
2.1.4. Ion Transport
2.1.5. Implementing a Model
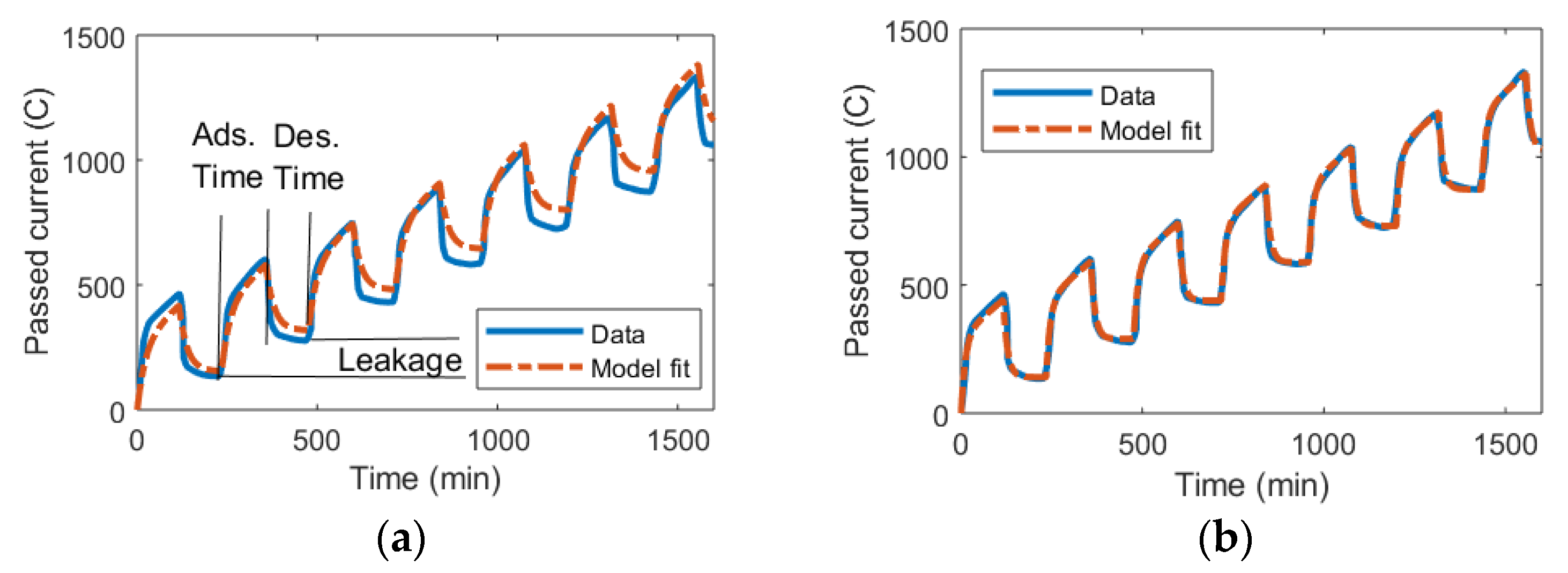
2.2. Data for Model Validation
3. Results
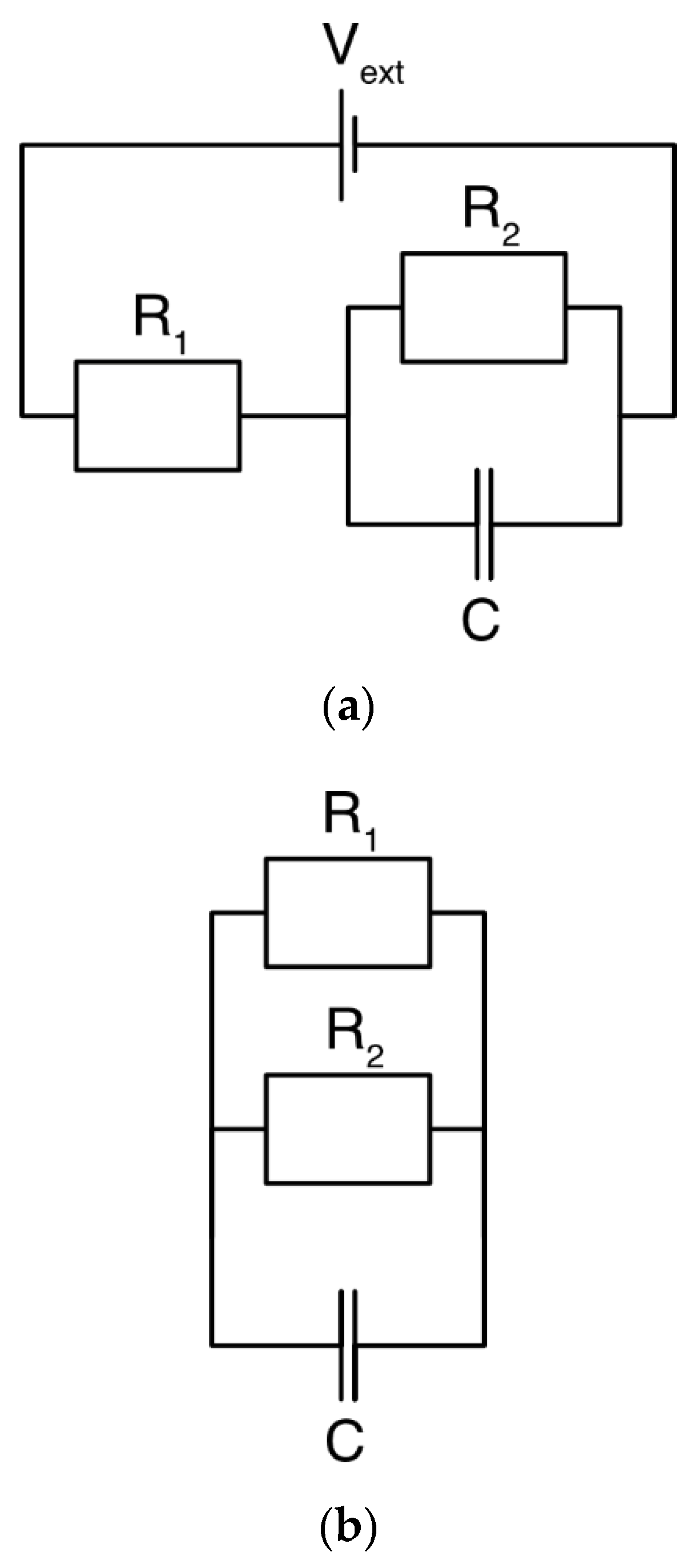
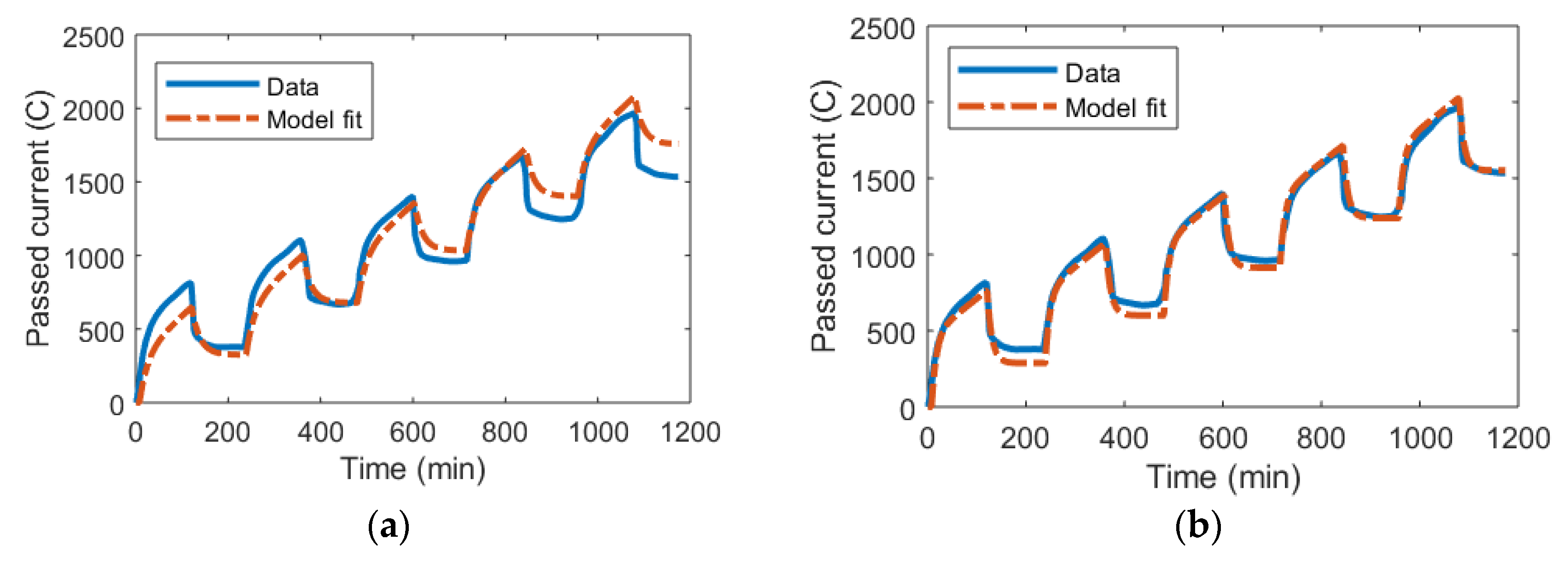
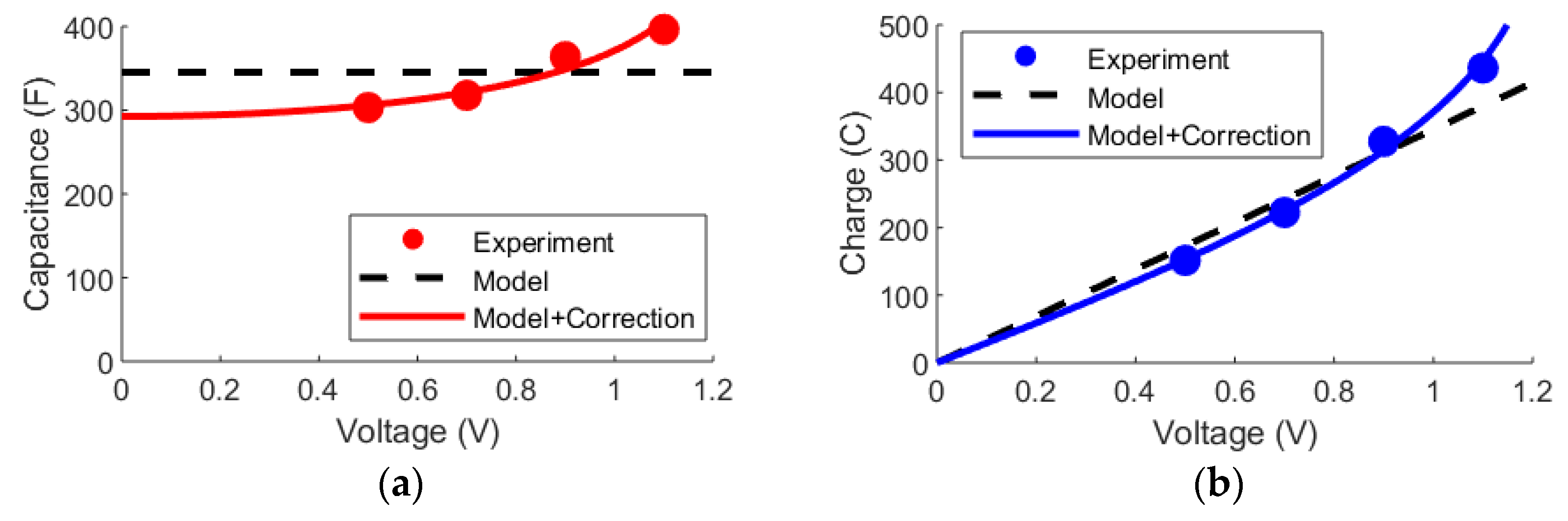
3.1. DL Model and the Randles Circuit
3.2. mD Model and the Randles Circuit
3.3. DL and mD Models
3.4. Outlook
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- The Sustainable Development Goals Report; UN: New York. NY, USA, 2018.
- González, A.; Goikolea, E.; Barrena, J.A.; Mysyk, R. Review on Supercapacitors: Technologies and Materials. Renew. Sustain. Energy Rev. 2016, 58, 1189–1206. [Google Scholar] [CrossRef]
- Zhong, C.; Deng, Y.; Hu, W.; Qiao, J.; Zhang, L.; Zhang, J. A Review of Electrolyte Materials and Compositions for Electrochemical Supercapacitors. Chem. Soc. Rev. 2015, 44, 7484–7539. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Zhang, L.; Zhang, J. A Review of Electrode Materials for Electrochemical Supercapacitors. Chem. Soc. Rev. 2012, 41, 797–828. [Google Scholar] [CrossRef] [Green Version]
- Gan, L.; Wu, Y.; Song, H.; Zhang, S.; Lu, C.; Yang, S.; Wang, Z.; Jiang, B.; Wang, C.; Li, A. Selective Removal of Nitrate Ion Using a Novel Activated Carbon Composite Carbon Electrode in Capacitive Deionization. Sep. Purif. Technol. 2019, 212, 728–736. [Google Scholar] [CrossRef]
- Qu, Y.; Campbell, P.G.; Hemmatifar, A.; Knipe, J.M.; Loeb, C.K.; Reidy, J.J.; Hubert, M.A.; Stadermann, M.; Santiago, J.G. Charging and Transport Dynamics of a Flow-Through Electrode Capacitive Deionization System. J. Phys. Chem. B 2018, 122, 240–249. [Google Scholar] [CrossRef] [PubMed]
- Hemmatifar, A.; Stadermann, M.; Santiago, J.G. Two-Dimensional Porous Electrode Model for Capacitive Deionization. J. Phys. Chem. C 2015, 119, 24681–24694. [Google Scholar] [CrossRef]
- Porada, S.; Zhao, R.; Van Der Wal, A.; Presser, V.; Biesheuvel, P.M. Review on the Science and Technology of Water Desalination by Capacitive Deionization. Prog. Mater. Sci. 2013, 58, 1388–1442. [Google Scholar] [CrossRef] [Green Version]
- Suss, M.E.; Porada, S.; Sun, X.; Biesheuvel, P.M.; Yoon, J.; Presser, V. Water Desalination via Capacitive Deionization: What Is It and What Can We Expect from It? Energy Environ. Sci. 2015, 8, 2296–2319. [Google Scholar] [CrossRef] [Green Version]
- Ahualli, S.; Iglesias, G.R. Principles and Theoretical Models of CDI: Experimental Approaches. Interface Sci. Technol. 2018, 24, 169–192. [Google Scholar] [CrossRef]
- Anderson, M.A.; Cudero, A.L.; Palma, J. Capacitive Deionization as an Electrochemical Means of Saving Energy and Delivering Clean Water. Comparison to Present Desalination Practices: Will It Compete? Electrochim. Acta 2010, 55, 3845–3856. [Google Scholar] [CrossRef]
- Qin, M.; Deshmukh, A.; Epsztein, R.; Patel, S.K. Comparison of Energy Consumption in Desalination by Capacitive Deionization and Reverse Osmosis. Desalination 2019, 455, 100–114. [Google Scholar] [CrossRef]
- Nordstrand, J.; Dutta, J. Dynamic Langmuir Model: A Simpler Approach to Modeling Capacitive Deionization. J. Phys. Chem. C 2019, 123, 16479–16485. [Google Scholar] [CrossRef] [Green Version]
- Dykstra, J.E.; Zhao, R.; Biesheuvel, P.M.; Wal, A.V.D. Resistance Identification and Rational Process Design in Capacitive Deionization. Water Res. 2016, 88, 358–370. [Google Scholar] [CrossRef] [PubMed]
- Jande, Y.A.C.; Kim, W.S. Predicting the Lowest Effluent Concentration in Capacitive Deionization. Sep. Purif. Technol. 2013, 224–230. [Google Scholar] [CrossRef]
- Biesheuvel, P.M.; Fu, Y.; Bazant, M.Z. Diffuse Charge and Faradaic Reactions in Porous Electrodes. Phys. Rev. E 2011, 83. [Google Scholar] [CrossRef] [Green Version]
- Suss, M.E.; Biesheuvel, P.M.; Baumann, T.F.; Stadermann, M.; Santiago, J.G. In Situ Spatially and Temporally Resolved Measurements of Salt Concentration between Charging Porous Electrodes for Desalination by Capacitive Deionization. Environ. Sci. Technol. 2014, 48, 2008–2015. [Google Scholar] [CrossRef]
- Guyes, E.N.; Shocron, A.N.; Simanovski, A.; Biesheuvel, P.M.; Suss, M.E. A One-Dimensional Model for Water Desalination by Flow-through Electrode Capacitive Deionization. Desalination 2017, 415, 8–13. [Google Scholar] [CrossRef] [Green Version]
- Nordstrand, J.; Laxman, K.; Myint, M.T.Z.; Dutta, J. An Easy-to-Use Tool for Modeling the Dynamics of Capacitive Deionization. J. Phys. Chem. A 2019, 123, 6628–6634. [Google Scholar] [CrossRef] [Green Version]
- Nordstrand, J.; Dutta, J. Simplified Prediction of Ion Removal in Capacitive Deionization of Multi-Ion Solutions. Langmuir 2020. [Google Scholar] [CrossRef] [Green Version]
- Laxman, K.; Husain, A.; Nasser, A.; Al, M.; Dutta, J. Tailoring the Pressure Drop and Fluid Distribution of a Capacitive Deionization Device. Desalination 2019, 449, 111–117. [Google Scholar] [CrossRef]
- Laxman, K.; Myint, M.T.Z.; Khan, R.; Pervez, T.; Dutta, J. Improved Desalination by Zinc Oxide Nanorod Induced Electric Field Enhancement in Capacitive Deionization of Brackish Water. Desalination 2015, 359, 64–70. [Google Scholar] [CrossRef]
- Myint, M.T.Z.; Al-Harthi, S.H.; Dutta, J. Brackish Water Desalination by Capacitive Deionization Using Zinc Oxide Micro/Nanostructures Grafted on Activated Carbon Cloth Electrodes. Desalination 2014, 344, 236–242. [Google Scholar] [CrossRef]
- Maddah, H.A.; Shihon, M.A. Activated Carbon Cloth for Desalination of Brackish Water Using Capacitive Deionization. In Desalination and Water Treatment; BoD—Books on Demand: Norderstedt, Germany, 2018. [Google Scholar] [CrossRef] [Green Version]
- Myint, M.T.Z.; Dutta, J. Fabrication of Zinc Oxide Nanorods Modified Activated Carbon Cloth Electrode for Desalination of Brackish Water Using Capacitive Deionization Approach. Desalination 2012, 305, 24–30. [Google Scholar] [CrossRef]
- Sefara, M. Pore Classification in the Characterization of Porous Materials: A Perspective. Cent. Eur. J. Chem. 2007, 5, 385–395. [Google Scholar] [CrossRef]
- Porada, S.; Borchardt, L.; Oschatz, M.; Bryjak, M.; Atchison, J.S.; Keesman, K.J.; Kaskel, S.; Biesheuvel, P.M.; Presser, V. Direct Prediction of the Desalination Performance of Porous Carbon Electrodes for Capacitive Deionization. Energy Environ. Sci. 2013, 6, 3700–3712. [Google Scholar] [CrossRef] [Green Version]
- Railsback, B. Variation in Hydrated Radius of Ions. 2019. Available online: http://www.gly.uga.edu/railsback/Fundamentals/815HydratedCationRadii04LS.pdf (accessed on 11 March 2019).
- Laxman, K.; Al Gharibi, L.; Dutta, J. Capacitive Deionization with Asymmetric Electrodes: Electrode Capacitance vs. Electrode Surface Area. Electrochim. Acta 2015, 176, 420–425. [Google Scholar] [CrossRef]
- Laxman, K.; Tay, M.; Myint, Z.; Bourdoucen, H.; Dutta, J. Enhancement in Ion Adsorption Rate and Desalination Efficiency in a Capacitive Deionization Cell through Improved Electric Field Distribution Using Electrodes Composed of Activated Carbon Cloth Coated with Zinc Oxide Nanorods. Appl. Mater. Interfaces 2014, 6, 10113–10120. [Google Scholar] [CrossRef]
- Wang, G.; Ling, Y.; Qian, F.; Yang, X.; Liu, X.X.; Li, Y. Enhanced Capacitance in Partially Exfoliated Multi-Walled Carbon Nanotubes. J. Power Sources 2011, 196, 5209–5214. [Google Scholar] [CrossRef]
- Keneko, K.; Ishii, C.; Ruike, M.; Kuwabara, H. Origin of Superhigh Surface Area and Microcrystalline Structures of Activated Carbons. Carbon 1992, 30, 1075–1088. [Google Scholar] [CrossRef]
- Zhao, R.; Biesheuvel, P.M.; Miedema, H.; Bruning, H.; Wal, A.V.D. Charge Efficiency: A Functional Tool to Probe the Double-Layer Structure Inside of Porous Electrodes and Application in the Modeling of Capacitive Deionization. J. Phys. Chem. Lett. 2010, 205–210. [Google Scholar] [CrossRef]
- Gallagher, K.G.; Fuller, T.F. Kinetic Model of the Electrochemical Oxidation of Graphitic Carbon in Acidic Environments. Phys. Chem. Chem. Phys. 2009, 11, 11557–11567. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Liang, P.; Bian, Y.; Sun, X.; Ma, J.; Jiang, Y.; Huang, X. Enhancement of Salt Removal in Capacitive Deionization Cell through PeriodicallySeparation and Purification Techn Alternated Oxidation of Electrodes. Sep. Purif. Technol. 2018, 194, 451–456. [Google Scholar] [CrossRef]
- Gao, X.; Omosebi, A.; Landon, J.; Liu, K. Enhancement of Charge Efficiency for a Capacitive Deionization Cell Using Carbon Xerogel with Modified Potential of Zero Charge. Electrochem. Commun. 2014, 39, 22–25. [Google Scholar] [CrossRef]
- Li, H.; Zaviska, F.; Liang, S.; Li, J.; He, L.; Yang, H.Y. A High Charge Efficiency Electrode by Self—Assembling Sulphonated Reduced Graphene Oxide onto Carbon Fibre: Towards Enhanced Capacitive Deionization. J. Mater. Chem. A 2014, 3484–3491. [Google Scholar] [CrossRef]
- Kim, T.; Dykstra, J.E.; Porada, S.; van der Wal, A.; Yoon, J.; Biesheuvel, P.M. Enhanced Charge Efficiency and Reduced Energy Use in Capacitive Deionization by Increasing the Discharge Voltage. J. Colloid Interface Sci. 2015, 446, 317–326. [Google Scholar] [CrossRef]
- Box, G.E.P. Robustness in the Strategy of Scientific Model Building. In Robustness in Statistics; Academic press Inc.: Waltham, MA, USA, 1979. [Google Scholar] [CrossRef]
- Fiorenti, S.; Guanetti, J.; Guezennec, Y.; Onori, S. Modeling and Experimental Validation of a Hybridized Energy Storage System for Automotive Applications. J. Power Sources 2013, 241, 112–120. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, Z.; Hu, X.; Sun, F.; Dorrell, D.G. A Comparative Study of Equivalent Circuit Models of Ultracapacitors for Electric Vehicles. J. Power Sources 2015, 274, 899–906. [Google Scholar] [CrossRef]
- Masarapu, C.; Zeng, H.F.; Hung, K.H.; Wei, B. Effect of Temperature on the Capacitance of Carbon Nanotube Supercapacitors. ACS Nano 2009, 3, 2199–2206. [Google Scholar] [CrossRef]
- Dongowski, G.; Neubert, R.H.H.; Heinevetter, L. Permeation of Bile Acids across Artificial Lipid Membranes and Caco-2 Monolayers. Pharmazie 1999, 54, 517–520. [Google Scholar] [CrossRef]
- Brug, G.J.; van den Eeden, A.L.G.; Sluyters-Rehbach, M.; Sluyters, J.H. The Analysis of Electrode Impedances Complicated by the Presence of a Constant Phase Element. J. Electroanal. Chem. 1984, 176, 275–295. [Google Scholar] [CrossRef]
- Suss, M.E.; Baumann, T.F.; Worsley, M.A.; Rose, K.A.; Jaramillo, T.F.; Stadermann, M.; Santiago, J.G. Impedance-Based Study of Capacitive Porous Carbon Electrodes with Hierarchical and Bimodal Porosity. J. Power Sources 2013, 241, 266–273. [Google Scholar] [CrossRef]
- Brogioli, D.; La Mantia, F. Capacitive Energy Extraction from Double Layer Expansion (CDLE). In Fundamentals of the Method, 1st ed.; Elsevier Ltd.: Amsterdam, The Netherlands, 2018; Volume 24. [Google Scholar] [CrossRef]
- Gongadze, E.; Petersen, S.; Beck, U.; Van Rienen, U. Classical Models of the Interface between an Electrode and an Electrolyte. In Proceedings of the COMSOL Conference, Boston, MA, USA, 8–10 October 2009. [Google Scholar]
- Delgado, Á.V.; Ahualli, S.; Fernándex, M.M.; Iglesias, G.R.; Jiménez, M.L. Charge and Potential Distribution in the Electrical Double Layer of Porous Materials: Models. Interface Sci. Technol. 2018, 24, 3–18. [Google Scholar] [CrossRef]
- Biesheuvel, P.M.; Porada, S.; Levi, M.; Bazant, M.Z. Attractive Forces in Microporous Carbon Electrodes for Capacitive Deionization. J. Solid State Electrochem. 2014, 18, 1365–1376. [Google Scholar] [CrossRef] [Green Version]
- Porada, S.; Bryjak, M.; Van Der Wal, A.; Biesheuvel, P.M. Effect of Electrode Thickness Variation on Operation of Capacitive Deionization. Electrochim. Acta 2012, 75, 148–156. [Google Scholar] [CrossRef] [Green Version]
- Biesheuvel, P.M.; Fu, Y.; Bazant, M.Z. Electrochemistry and Capacitive Charging of Porous Electrodes in Asymmetric Multicomponent Electrolytes. Russ. J. Electrochem. 2012, 48, 580–592. [Google Scholar] [CrossRef] [Green Version]
- Biesheuvel, P.M. Activated Carbon Is an Electron-Conducting Amphoteric Ion Adsorbent. arXiv 2015, arXiv:1509.06354. [Google Scholar]
- Zhao, R.; Satpradit, O.; Rijnaarts, H.H.M.; Biesheuvel, P.M.; van der Wal, A. Optimization of Salt Adsorption Rate in Membrane Capacitive Deionization. Water Res. 2013, 47, 1941–1952. [Google Scholar] [CrossRef]
- Langmuir, I. The Adsorption of Gases on Plane Surfaces of Glass, Mica and Platinum. J. Am. Chem. Soc. 1918, 40, 1361–1403. [Google Scholar] [CrossRef] [Green Version]
- Azizian, S.; Eris, S.; Wilson, L.D. Re-Evaluation of the Century-Old Langmuir Isotherm for Modeling Adsorption Phenomena in Solution. Chem. Phys. 2018, 513, 99–104. [Google Scholar] [CrossRef]
- Li, H.; Pan, L.; Lu, T.; Zhan, Y.; Nie, C.; Sun, Z. A Comparative Study on Electrosorptive Behavior of Carbon Nanotubes and Graphene for Capacitive Deionization. J. Electroanal. Chem. 2011, 653, 40–44. [Google Scholar] [CrossRef]
- Ryoo, M.W.; Kim, J.H.; Seo, G. Role of Titania Incorporated on Activated Carbon Cloth for Capacitive Deionization of NaCl Solution. J. Colloid Interface Sci. 2003, 264, 414–419. [Google Scholar] [CrossRef]
- Gabelich, C.J.; Tran, T.D.; Suffet, I.H. “Mel.” Electrosorption of Inorganic Salts from Aqueous Solution Using Carbon Aerogels. Environ. Sci. Technol. 2002, 36, 3010–3019. [Google Scholar] [CrossRef]
- Wang, G.; Qian, B.; Dong, Q.; Yang, J.; Zhao, Z.; Qiu, J. Highly Mesoporous Activated Carbon Electrode for Capacitive Deionization. Sep. Purif. Technol. 2013, 103, 216–221. [Google Scholar] [CrossRef]
- Li, H.; Lu, T.; Pan, L.; Zhang, Y.; Sun, Z. Electrosorption Behavior of Graphene in NaCl Solutions. J. Mater. Chem. 2009, 19, 6773–6779. [Google Scholar] [CrossRef]
- Rudzinski, W.; Lee, S.L.; Panczyk, T.; Yan, C.C.S. A Fractal Approach to Adsorption on Heterogeneous Solids Surfaces. 2. Thermodynamic Analysis of Experimental Adsorption Data. J. Phys. Chem. B 2001, 105, 10857–10866. [Google Scholar] [CrossRef]
- Kowanga, K.D.; Gatebe, E.; Mauti, G.O.; Mauti, E.M. Kinetic, Sorption Isotherms, Pseudo-First-Order Model and Pseudo-Second-Order Model Studies of Cu (II) and Pb (II) Using Defatted Moringa Oleifera Seed Powder. J. Phytopharm. 2016, 5, 71–78. [Google Scholar]
- Wang, L.; Wang, M.; Huang, Z.-H.; Cui, T.; Gui, X.; Kang, F.; Wang, K.; Wu, D. Capacitive Deionization of NaCl Solutions Using Carbon Nanotube Sponge Electrodes. J. Mater. Chem. 2011, 21, 18295. [Google Scholar] [CrossRef]
- Li, H.; Pan, L.; Zhang, Y.; Zou, L.; Sun, C.; Zhan, Y.; Sun, Z. Kinetics and Thermodynamics Study for Electrosorption of NaCl onto Carbon Nanotubes and Carbon Nanofibers Electrodes. Chem. Phys. Lett. 2010, 485, 161–166. [Google Scholar] [CrossRef]
- Rudzinski, W.; Plazinski, W. Kinetics of Solute Adsorption at Solid/Solution Interfaces: A Theoretical Development of the Empirical Pseudo-First and Pseudo-Second Order Kinetic Rate Equations, Based on Applying the Statistical Rate Theory of Interfacial Transport. J. Phys. Chem. B 2006, 16514–16525. [Google Scholar] [CrossRef]
- Li, H.; Zou, L.; Pan, L.; Sun, Z. Using Graphene Nano-Flakes as Electrodes to Remove Ferric Ions by Capacitive Deionization. Sep. Purif. Technol. 2010, 75, 8–14. [Google Scholar] [CrossRef]
- Li, H.; Zou, L. Ion-Exchange Membrane Capacitive Deionization: A New Strategy for Brackish Water Desalination. Desalination 2011, 275, 62–66. [Google Scholar] [CrossRef]
- Ljung, L. ODE Parameter Estimation (Grey-Box Modeling). In System Identification Toolbox; TM User’s Guide; MathWorks: Natick, MA, USA, 2014. [Google Scholar]
- Rohatgi, A. WebPlotDigitizer. 2019. Available online: https://automeris.io/WebPlotDigitizer (accessed on 11 March 2019).
- Bouhadana, Y.; Ben-Tzion, M.; Soffer, A.; Aurbach, D. A Control System for Operating and Investigating Reactors: The Demonstration of Parasitic Reactions in the Water Desalination by Capacitive de-Ionization. Desalination 2011, 268, 253–261. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nordstrand, J.; Dutta, J. Basis and Prospects of Combining Electroadsorption Modeling Approaches for Capacitive Deionization. Physics 2020, 2, 309-324. https://doi.org/10.3390/physics2020016
Nordstrand J, Dutta J. Basis and Prospects of Combining Electroadsorption Modeling Approaches for Capacitive Deionization. Physics. 2020; 2(2):309-324. https://doi.org/10.3390/physics2020016
Chicago/Turabian StyleNordstrand, Johan, and Joydeep Dutta. 2020. "Basis and Prospects of Combining Electroadsorption Modeling Approaches for Capacitive Deionization" Physics 2, no. 2: 309-324. https://doi.org/10.3390/physics2020016
APA StyleNordstrand, J., & Dutta, J. (2020). Basis and Prospects of Combining Electroadsorption Modeling Approaches for Capacitive Deionization. Physics, 2(2), 309-324. https://doi.org/10.3390/physics2020016





