Kinetic Freeze-Out Properties from Transverse Momentum Spectra of Pions in High Energy Proton-Proton Collisions

Abstract

Transverse momentum spectra of negative and positive pions produced at mid-(pseudo)rapidity in inelastic or non-single-diffractive proton-proton collisions over a center-of-mass energy, $\sqrt{s}$, range from a few GeV to above 10 TeV are analyzed by the blast-wave fit with Boltzmann (Tsallis) distribution. The blast-wave fit results are well fitting to the experimental data measured by several collaborations. In a particular superposition with Hagedorn function, both the excitation functions of kinetic freeze-out temperature ($T_0$) of emission source and transverse flow velocity (${\beta }_T$) of produced particles obtained from a given selection in the blast-wave fit with Boltzmann distribution have a hill at $\sqrt{s}\approx 10$ GeV, a drop at dozens of GeV, and then an increase from dozens of GeV to above 10 TeV. However, both the excitation functions of $T_0$ and ${\beta }_T$ obtained in the blast-wave fit with Tsallis distribution do not show such a complex structure, but a very low hill. In another selection for the parameters or in the superposition with the usual step function, $T_0$ and ${\beta }_T$ increase generally quickly from a few GeV to about 10 GeV and then slightly at above 10 GeV, there is no such the complex structure, when also studying nucleus-nucleus collisions.

1. Introduction

Chemical and thermal or kinetic freeze-outs are two of important stages of system evolution in high energy collisions. The excitation degrees of interacting system at the two stages are possibly different from each other. To describe different excitation degrees of interacting system at the two stages, one can use chemical and kinetic freeze-out temperatures respectively. Generally, at the stage of chemical freeze-out, the ratios of different types of particles are no longer changed, and the chemical freeze-out temperature can be obtained from the ratios of different particles in the framework of thermal model [1,2,3]. At the stage of kinetic freeze-out, the transverse momentum spectra of different particles are no longer changed, and the dissociation temperature [4] or kinetic freeze-out temperature can be obtained from the transverse momentum spectra according to the hydrodynamical model [4] and the subsequent blast-wave fit with Boltzmann distribution [5,6,7] or with Tsallis distribution [8,9,10].

It should be pointed out that the transverse momentum spectra even though in narrow range contain both the contributions of random thermal motion and transverse flow of particles. The random thermal motion and transverse flow reflect the excitation and expansion degrees of the interacting system (or emission source) respectively. To extract the kinetic freeze-out temperature from transverse momentum spectra, we have to exclude the contribution of transverse flow, that is, we have to disengage the random thermal motion and transverse flow. There are more than one methods to disengage the two issues [4]. The simplest and easiest method is to use the blast-wave fit with Boltzmann distribution [5,6,7] and with Tsallis distribution [8,9,10] to analyze the transverse momentum spectra, though other method such as the alternative method [6,11,12,13,14,15,16,17] can obtain similar results [18].

The early blast-wave fit is based on the Boltzmann distribution [5,6,7]. An alternative blast-wave fit is used due to the Tsallis distribution [8,9,10]. Both types of blast-wave fit can be used to disengage the random thermal motion and transverse flow. Then, the kinetic freeze-out temperature of interacting system and transverse flow velocity of light flavor particles can be extracted. Most of light flavor particles are produced in soft excitation process and have narrow transverse momentum range up to 2∼3 GeV/c. A few part of light flavor particles are produced in hard scattering process and have higher transverse momenta. Generally, heavy flavor particles are produced via hard scattering process. From the point of view of disengaging or extraction, particles produced in hard scattering process are not needed to consider by us.

The excitation function of kinetic freeze-out temperature, that is, the dependence of kinetic freeze-out temperature on collision energy, is very interesting for us to study the properties of high energy collisions. We think that the particular change of excitation functions of kinetic freeze-out temperature and other parameters are related to the critical-end-point (CEP) of phase transition from hadronic matter to quark-gluon plasma (QGP or quark matter) happened in central nucleus-nucleus ($AA$ or A-A) collisions, where the particular change means the appearances of saturation, minimum, maximum, knee point, asymptotical line, etc. For high multiplicity proton–proton ($pp$ or p-p) collisions, even for minimum-bias $pp$ collisions, the particular change of excitation functions of some parameters are expected to compare with those in $AA$ collisions, where the quark degree of freedom in minimum-bias $pp$ collisions is expected to play initially a main role at the energy of particular change, though QGP is not expected to form in minimum-bias $pp$ collisions due to small system and products. The minimum of excitation function is also related to the soft point of equation of state (EOS) of hadronic matter or QGP, which is also related to the phase transition.

Although there are many studies on the excitation functions of kinetic freeze-out temperature and other parameters, the results seem to be inconsistent. For example, over a center-of-mass energy per nucleon pair, $\sqrt{s_{NN}}$, range from a few GeV to a few TeV, the excitation function of kinetic freeze-out temperature in gold-gold (Au-Au) and lead-lead (Pb-Pb) collisions initially increases and then inconsistently saturates [19,20], increases [21], or decreases [22,23] with the increase of collision energy. On the contrary, the excitation function of the chemical freeze-out temperature shows initially increases and then consistently saturates with collision energy [1,2,3,4]. Comparatively, as the basic processes in $AA$ collisions, $pp$ collisions are very important in the study of the mentioned excitation functions. However, the excitation functions in $pp$ collisions are short of studies. We hope to study the particular changes of excitation functions in $pp$ collisions due to they being also related to quark degree of freedom, but not QGP. Indeed, it is worth to study the excitation functions of kinetic freeze-out temperature and other parameters in $pp$ collisions and to judge their tendencies over an energy range from GeV to TeV.

In this paper, by using the blast-wave fit with Boltzmann distribution [5,6,7] and with Tsallis distribution [8,9,10], we study the excitation functions of some concerned quantities in inelastic (INEL) or non-single-diffractive (NSD) $pp$ collisions which are closer to peripheral nuclear collisions comparing with central ones. The experimental transverse momentum spectra of negative and positive pions (${\pi }^{-}$ and ${\pi }^{+}$) measured mainly at the mid-rapidity by the NA61/SHINE Collaboration [24] at the the Super Proton Synchrotron (SPS) and its beam energy scan (BES) program, the PHENIX [25] and STAR [6] Collaborations at the Relativistic Heavy Ion Collider (RHIC), as well as the ALICE [26] and CMS [27,28] Collaborations at the Large Hadron Collider (LHC) are analyzed, while the data in the forward and backward rapidity regions are not available in most cases.

The remainder of this paper is structured as follows. The formalism and method are shortly described in Section 2. Results and discussion are given in Section 3. In Section 3.1, we summarize our main observations and conclusions.

2. Formalism and Method

There are two main processes of particle productions, namely the soft excitation process and the hard scattering process, in high energy collisions. For the soft excitation process, the method used in the present work is the blast-wave fit [5,6,7,8,9,10] that has wide applications in particle productions. The blast-wave fit is based on two types of distributions. One is the Boltzmann distribution [5,6,7] and another one is the Tsallis distribution [8,9,10]. As an application of the blast-wave fit, we present directly its formalisms in the following. Although the blast-wave fit has abundant connotations, we focus only our attention on the formalism of transverse momentum ($p_T$) distribution in which the kinetic freeze-out temperature ($T_0$) and mean transverse flow velocity (${\beta }_T$) are included.

We are interested in the blast-wave fit with Boltzmann distribution in its original form. According to [5,6,7], the blast-wave fit with Boltzmann distribution results in the probability density distribution of $p_T$ to be

$$\begin{array}{cc}\hfill f_1\left(p_T\right)=& \frac{1}{N}\frac{dN}{d{p}_T}=C_1{p}_T{m}_T{\int }_0^{R}rdr\times \hfill \\ \hfill & I_0\left[\frac{p_{T}sinh\left(\rho \right)}{T_0}\right]K_1\left[\frac{m_{T}cosh\left(\rho \right)}{T_0}\right],\hfill \end{array}$$

(1)

where $C_1$ is the normalized constant, $m_T=\sqrt{p_T^2+m_0^2}$ is the transverse mass, $m_0$ is the rest mass, r is the radial coordinate in the thermal source, R is the maximum r which can be regarded as the transverse size of source in the case of neglecting the expansion, $r/R$ is the relative radial position which has in fact more meanings than r and R themselves, $I_0$ and $K_1$ are the modified Bessel functions of the first and second kinds respectively, $\rho ={tanh}^{-1}\left[\beta \left(r\right)\right]$ is the boost angle, $\beta \left(r\right)={\beta }_S{(r/R)}^{n_0}$ is a self-similar flow profile, ${\beta }_S$ is the flow velocity on the surface, and $n_0=2$ is used in the original form [5]. There is the relation between ${\beta }_T$ and $\beta \left(r\right)$. As a mean of $\beta \left(r\right)$, ${\beta }_T=(2/R^2){\int }_0^{R}r\beta \left(r\right)dr=2{\beta }_S/(n_0+2)$.

We are also interested in the blast-wave fit with Tsallis distribution in its original form. According to [8,9,10], the blast-wave fit with Tsallis distribution results in the $p_T$ distribution to be

$$\begin{array}{cc}\hfill f_2\left(p_T\right)=& \frac{1}{N}\frac{dN}{d{p}_T}=C_2{p}_T{m}_T{\int }_{-\pi }^{\pi }d\varphi {\int }_0^{R}rdr\{1+\hfill \\ \hfill & \frac{q-1}{T_0}\left[m_{T}cosh\left(\rho \right)-p_{T}sinh\left(\rho \right)cos\left(\varphi \right)\right]{\}}^{-1/(q-1)},\hfill \end{array}$$

(2)

where $C_2$ is the normalized constant, q is an entropy index that characterizes the degree of non-equilibrium, $\varphi$ denotes the azimuthal angle, and $n_0=1$ is used in the original form [8]. Because of $n_0$ being an insensitive quantity, the results corresponding to $n_0=1$ and 2 for the blast-wave fit with Boltzmann or Tsallis distribution are harmonious [18]. In fact, in some literature [29], $n_0$ is regarded as a free parameter which changes largely by several times and increases 1 in the number of free parameter, which is not our expectation in the present work. In addition, the index $-1/(q-1)$ used in Equation (2) can be replaced by $-q/(q-1)$ due to q being very close to 1. This substitution results in a small and negligible difference in the Tsallis distribution [30,31].

For a not too wide $p_T$ spectrum, the above two equations can be used to describe the $p_T$ spectrum and to extract $T_0$ and ${\beta }_T$. For a wide $p_T$ spectrum, we have to consider the contribution of hard scattering process. According to the quantum chromodynamics (QCD) calculus [32,33,34], the contribution of hard scattering process is parameterized to be an inverse power-law

$$\begin{array}{c}\hfill f_H\left(p_T\right)=\frac{1}{N}\frac{dN}{d{p}_T}=A{p}_T{\left(1+\frac{p_T}{p_0}\right)}^{-n}\end{array}$$

(3)

which is the Hagedorn function [35,36], where $p_0$ and n are free parameters, and A is the normalization constant related to the free parameters. In literature [37,38,39,40,41,42,43], there are respectively modified Hagedorn functions

$$\begin{array}{c}\hfill f_H\left(p_T\right)=\frac{1}{N}\frac{dN}{d{p}_T}=A\frac{p_T^2}{m_T}{\left(1+\frac{p_T}{p_0}\right)}^{-n},\end{array}$$

(4)

$$\begin{array}{c}\hfill f_H\left(p_T\right)=\frac{1}{N}\frac{dN}{d{p}_T}=A{p}_T{\left(1+\frac{p_T^2}{p_0^2}\right)}^{-n},\end{array}$$

(5)

and

$$\begin{array}{c}\hfill f_H\left(p_T\right)=\frac{1}{N}\frac{dN}{d{p}_T}=A{\left(1+\frac{p_T^2}{p_0^2}\right)}^{-n},\end{array}$$

(6)

where the three normalization constants A, free parameters $p_0$, and free parameters n are severally different, though the same symbols are used to avoid trivial expression.

The experimental $p_T$ spectrum distributed in a wide range can be described by a superposition of the contributions of the soft excitation and hard scattering processes. If one of Equations (1) and (2) describes the contribution of the soft excitation process, one of Equations (3)–(6) describes the contribution of the hard scattering process. To describe the spectrum in a wide $p_T$ range, we can superpose a two-component superposition like this

$$\begin{array}{c}\hfill f_0\left(p_T\right)=k{f}_S\left(p_T\right)+(1-k)f_H\left(p_T\right),\end{array}$$

(7)

where k ($1-k$) denotes the contribution fraction of the soft excitation (hard scattering) process, and $f_S\left(p_T\right)$ denotes one of Equations (1) and (2). As for the four $f_H\left(p_T\right)$, we are inclined to the first one due to its more applications. Naturally, we have the normalization condition ${\int }_0^{p_{Tmax}}{f}_0\left(p_T\right)d{p}_T=1$, where $p_{Tmax}$ denotes the maximum $p_T$. In Equation (7), the soft component contributes in low $p_T$ region and the hard component contributes in whole $p_T$ range. The two contributions overlap each other in low $p_T$ region.

According to Hagedorn’s model [35], we may also use the usual step function to superpose the two functions. That is

$$\begin{array}{c}\hfill f_0\left(p_T\right)=A_1\theta (p_1-p_T)f_S\left(p_T\right)+A_2\theta (p_T-p_1)f_H\left(p_T\right),\end{array}$$

(8)

where $A_1$ and $A_2$ are constants which result in the two components to be equal to each other at $p_T=p_1\approx 2\sim 3$ GeV/c. The contribution fraction of the soft excitation (hard excitation) process in Equation (8) is $k={\int }_0^{p_1}{A}_1{f}_S\left(p_T\right)d{p}_T$ [$1-k={\int }_{p_1}^{p_{Tmax}}{A}_2{f}_H\left(p_T\right)d{p}_T$] due to ${\int }_0^{p_{Tmax}}{f}_0\left(p_T\right)d{p}_T=1$. In Equation (8), the soft component contributes in low $p_T$ region and the hard component contributes in high $p_T$ region. The two contributions link with each other at $p_T=p_1$.

In some cases, the contribution of resonance production for pions in very-low $p_T$ range has to be considered. We can use a very-soft component for the $p_T$ range from 0 to 0.2∼0.3 GeV/c which covers the contribution of resonance production. Let $k_{VS}$ and $k_S$ denote the contribution fractions of the very-soft and soft processes respectively. Equation (7) is revised to

$$\begin{array}{cc}\hfill f_0\left(p_T\right)=& k_{VS}{f}_{VS}\left(p_T\right)+k_S{f}_S\left(p_T\right)\hfill \\ \hfill & +(1-k_{VS}-k_S)f_H\left(p_T\right),\hfill \end{array}$$

(9)

where $f_{VS}\left(p_T\right)$ denotes one of Equations (1) and (2) as $f_S\left(p_T\right)$, but having smaller parameter values comparing with $f_S\left(p_T\right)$. Anyhow, both the very-soft and soft processes are belong to the soft process. Correspondingly, Equation (8) is revised to

$$\begin{array}{cc}\hfill f_0\left(p_T\right)=& A_1\theta (p_1-p_T)f_{VS}\left(p_T\right)\hfill \\ \hfill & +A_2\theta (p_T-p_1)\theta (p_2-p_T)f_S\left(p_T\right)\hfill \\ \hfill & +A_3\theta (p_T-p_2)f_H\left(p_T\right),\hfill \end{array}$$

(10)

where $A_1$, $A_2$, and $A_3$ are constants which result in the two contiguous components to be equal to each other at $p_T=p_1$ and $p_T=p_2$.

The above two types of superpositions [Equations (7) and (8)] treat the soft and hard components by different ways in the whole $p_T$ range. Equation (7) means that the soft component contributes in a range from 0 up to 2∼3 GeV/c or a little more. The hard component contributes in the whole $p_T$ range, though the main contributor in the low $p_T$ region is the soft component and the sole contributor in the high $p_T$ region is the hard component. Equation (8) shows that the soft component contributes in a range from 0 up to $p_1$, and the hard component contributes in a range from $p_1$ up to the maximum. The boundary of the contributions of soft and hard components is $p_1$. There is no mixed region for the two components in Equation (8).

In the case of including only the soft component, Equations (7) and (8) are the same. In the case of including both the soft and hard components, their common parameters such as $T_0$, ${\beta }_T$, $p_0$, and n should be severally to have small differences from each other. To avoid large differences, we should select the experimental data in a narrow $p_T$ range. In addition, the very-soft component in Equations (9) and (10) does not need to consider in some cases due to the fact that the spectrum in very-low $p_T$ range are possibly not available in experiment. Then, Equations (9) and (10) are degenerated to Equations (7) and (8) respectively in some cases.

In the fit process, firstly, we use Equation (7) to extract the related parameters, where $f_S\left(p_T\right)$ and $f_H\left(p_T\right)$ are exactly Equations (1) or (2) and (3) respectively. Regardless of Equation (1) or (2) is regarded as $f_S\left(p_T\right)$, the situation is similar due to Equations (1) and (2) being harmonious in trends of parameters [18], though one more parameter (the entropy index q) is needed in Equation (2). Secondly, we use Equation (8) to extract the related parameters as comparisons with those from Equations (7). In the case of Equations (7) and (8) being not suitable, Equations (9) and (10) can be used due to the very-low component from resonance decays being included in the first items of the two fits. Meanwhile, the contribution of resonance decays in the low component is naturally included in the second items of Equations (9) and (10) or in the first items of Equations (7) and (8). Thus, the contribution of resonance decays which is available in the very-low or low component in experiment is naturally considered by us.

It should be pointed out that although Equations (9) and (10) are not used in the final fits in the present work, we hope to keep them here due to the fact that we need them to give further explanations. From theses explanations, one can see the relations between Equations (9)/(10) and (7)/(8), as well as possible applications of Equations (9) and (10).

3. Results and Discussion

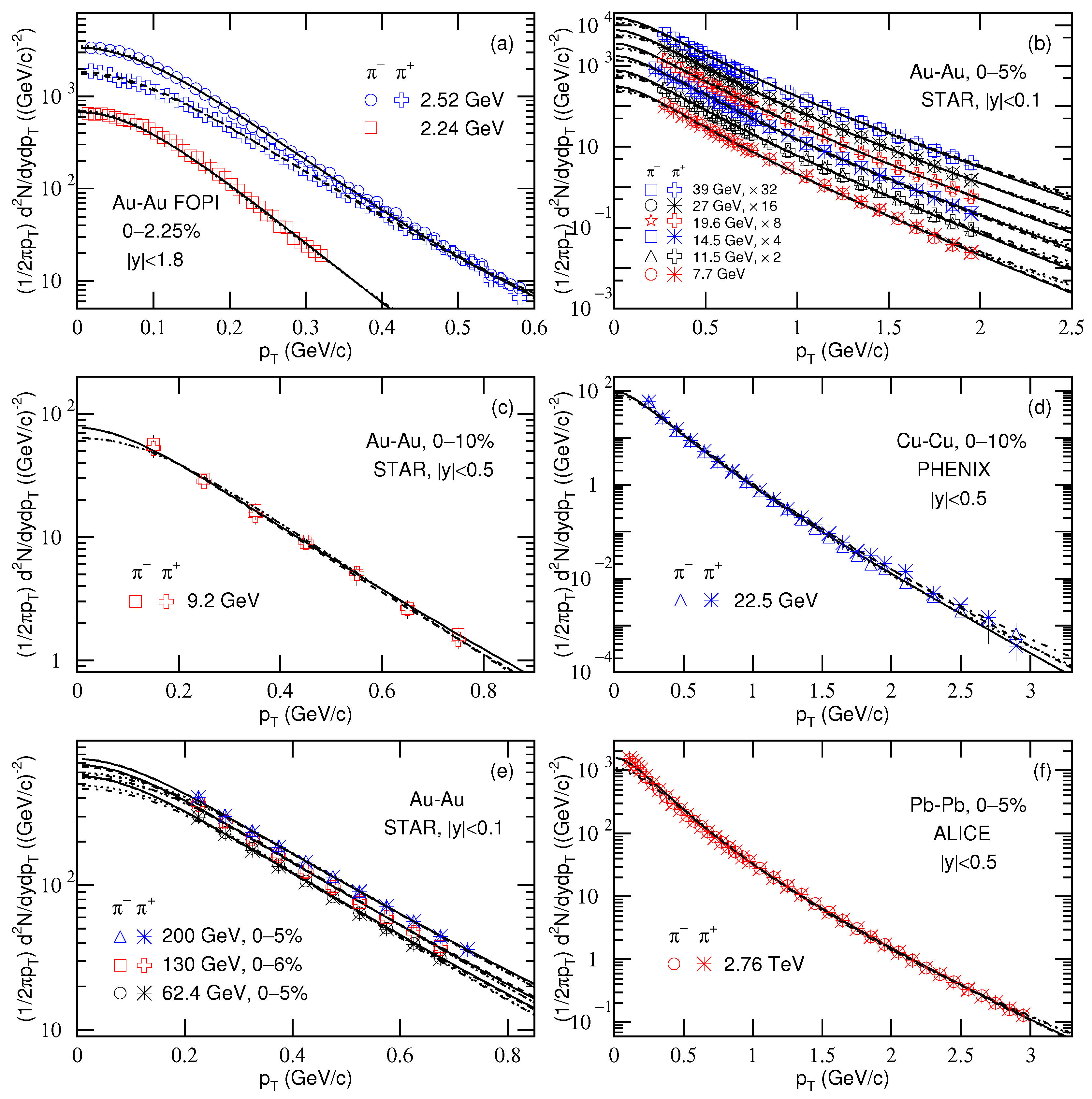
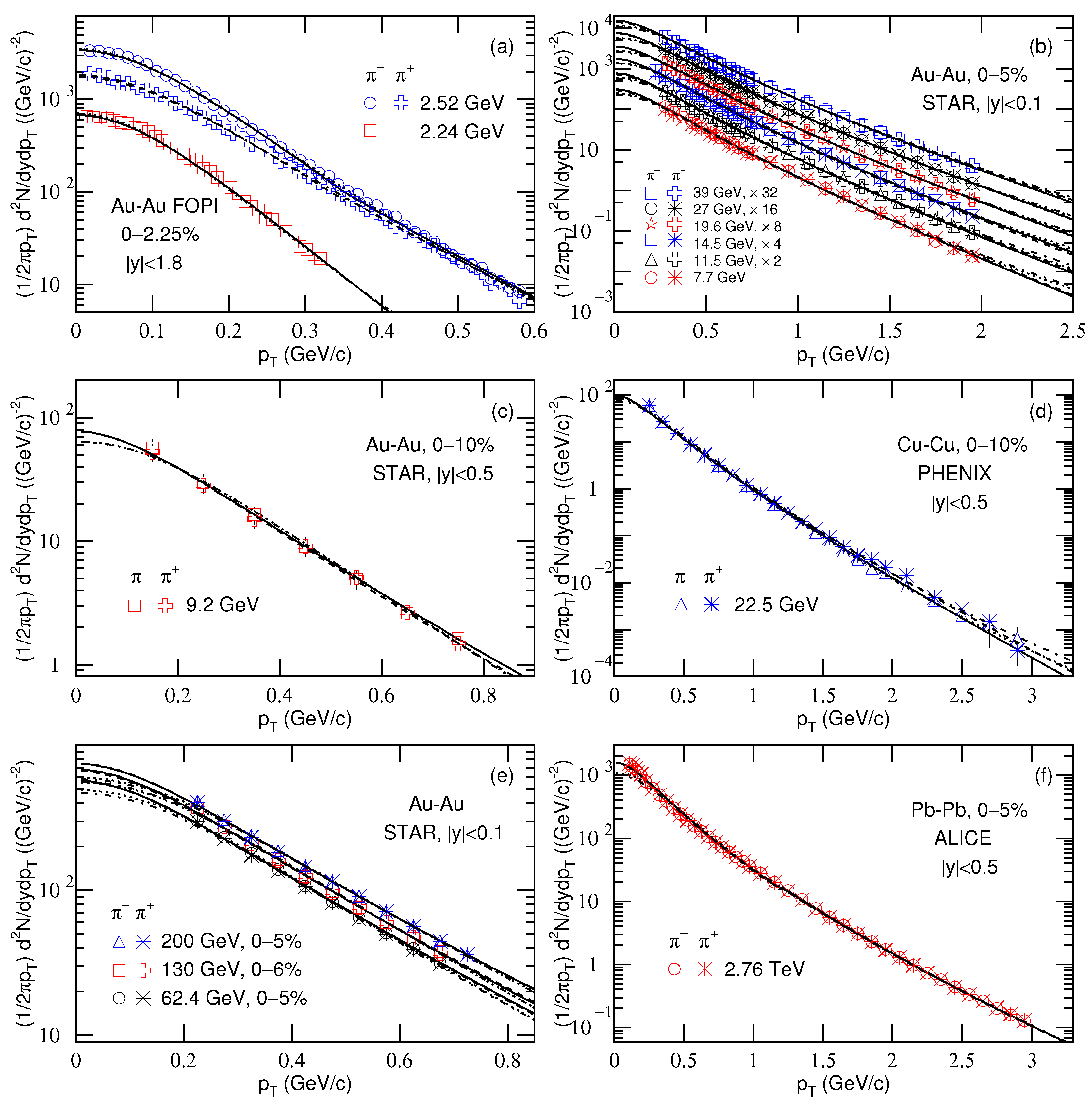
3.1. Comparison with Data by Equation (7)

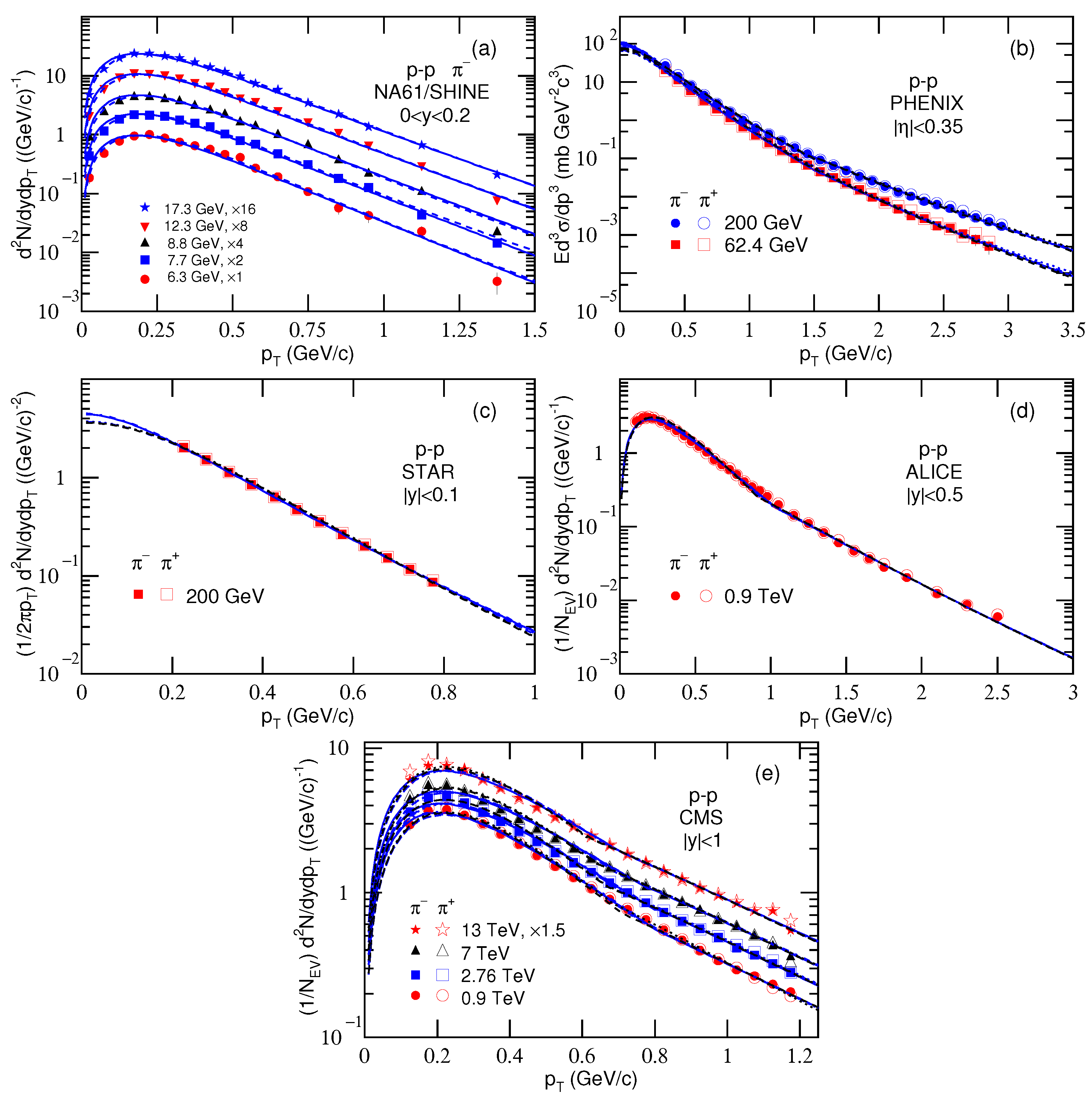
Figure 1 shows the transverse momentum spectra of ${\pi }^{-}$ and ${\pi }^{+}$ produced at mid-(pseudo)rapidity in $pp$ collisions at high center-of-mass energies, where different mid-(pseudo)rapidity (y or $\eta$) intervals and energies ($\sqrt{s}$) are marked in the panels. Different forms of the spectra are used due to different Collaborations, where N, E, p, $\sigma$, and $N_{EV}$ denote the particle number, energy, momentum, cross-section, and event number, respectively. The closed and open symbols presented in panels (a)–(e) represent the data of ${\pi }^{-}$ and ${\pi }^{+}$ measured by the NA61/SHINE [24], PHENIX [25], STAR [6], ALICE [26], and CMS [27,28] Collaborations, respectively, where in panel (a) only the spectra of ${\pi }^{-}$ are available, and panel (c) is for NSD events and other panels are for INEL events. Although the $pp$ collisions are divided on the multiplicity classes in experiments on the LHC, we have used the minimum-bias INEL events [26,27,28] which can be regarded as the combination of the events in different multiplicity classes with different yields. We regret not using the ATLAS Collaboration results [44,45,46,47,48] given no data on the $p_T$ spectra of ${\pi }^{-}$ and ${\pi }^{+}$. These data show wider $p_T$ spectra of charged particles to be used in our foreseen studies. In some cases, different amounts marked in the panels are used to scale the data for clarity. We have fitted the data by two sets of parameter values in Equation (7) so that we can see the fluctuations of parameter values. The blue solid (dotted) curves are our results for ${\pi }^{-}$ (${\pi }^{+}$) spectra fitted by Equation (7) through Equations (1) and (3), and the blue dashed (dot-dashed) curves are our results for ${\pi }^{-}$ (${\pi }^{+}$) spectra fitted by Equation (7) through Equations (2) and (3), by the first set of parameter values, in which k is taken to close to 0.5 as much as possible. The black curves are our results fitted by the second set of parameter values for comparison, in which k is taken to close to 1 as much as possible. The values of free parameters ($T_0$, ${\beta }_T$, q if available, k, $p_0$, and n), normalization constant ($N_0$), ${\chi }^2$, and number of degrees of freedom (ndof) corresponding to the curves in Figure 1 are listed in

Table 1. Values of free parameters ($T_0$, ${\beta }_T$, k, $p_0$, and n), normalization constant ($N_0$), ${\chi }^2$, and ndof corresponding to the solid (dotted) curves for ${\pi }^{-}$ (${\pi }^{+}$) spectra in Figure 1 in which different data are measured in different mid-(pseudo)rapidity intervals at different energies by different Collaborations. The values presented in terms of value${}_1$/value${}_2$ denote respectively the first and second sets of parameter values in Equation (7) through Equations (1) and (3) in which $k\ne 1$.

Collab.	$\sqrt{\mathit{s}}$ (GeV)	Part.	${\mathit{T}}_0$ (MeV)	${\mathit{\beta }}_{\mathit{T}}$ (c)	k	${\mathit{p}}_0$ (GeV/c)	n	${\mathit{N}}_0$	${\mathit{\chi }}^2$	ndof
NA61/	6.3	${\pi }^{-}$	$108\pm 5$	$0.30\pm 0.02$	1	−	−	$0.08\pm 0.01$	21	15
SHINE	7.7	${\pi }^{-}$	$109\pm 5$	$0.31\pm 0.02$	1	−	−	$0.10\pm 0.01$	34	15
INEL	8.8	${\pi }^{-}$	$110\pm 5$	$0.31\pm 0.02$	1	−	−	$0.10\pm 0.01$	73	15
	12.3	${\pi }^{-}$	$111\pm 6$	$0.32\pm 0.02$	1	−	−	$0.12\pm 0.01$	59	15
	17.3	${\pi }^{-}$	$112\pm 6$	$0.33\pm 0.02$	1	−	−	$0.13\pm 0.01$	26	15
PHENIX	62.4	${\pi }^{-}$	$96\pm 5/114\pm 6$	$0.27\pm 0.01/0.34\pm 0.02$	$0.66\pm 0.01/0.98\pm 0.01$	$3.60\pm 0.18/6.06\pm 0.30$	$19.23\pm 0.96/18.63\pm 0.93$	$21.55\pm 1.08/18.96\pm 0.95$	7/28	20
INEL		${\pi }^{+}$	$96\pm 5/114\pm 6$	$0.27\pm 0.01/0.34\pm 0.02$	$0.66\pm 0.01/0.98\pm 0.01$	$3.63\pm 0.18/6.07\pm 0.30$	$19.03\pm 0.95/18.63\pm 0.93$	$20.81\pm 1.04/18.57\pm 0.93$	11/11	20
	200	${\pi }^{-}$	$100\pm 5/116\pm 5$	$0.30\pm 0.02/0.36\pm 0.02$	$0.62\pm 0.01/0.96\pm 0.02$	$4.19\pm 0.21/6.45\pm 0.32$	$19.01\pm 0.95/18.01\pm 0.90$	$23.98\pm 1.20/22.77\pm 1.14$	26/21	21
		${\pi }^{+}$	$100\pm 5/115\pm 5$	$0.30\pm 0.02/0.35\pm 0.02$	$0.62\pm 0.01/0.96\pm 0.02$	$4.21\pm 0.21/6.46\pm 0.32$	$19.01\pm 0.95/18.00\pm 0.90$	$24.41\pm 1.22/24.41\pm 1.22$	54/26	21
STAR	200	${\pi }^{-}$	$98\pm 6/112\pm 5$	$0.29\pm 0.02/0.34\pm 0.02$	$0.61\pm 0.03/0.98\pm 0.02$	$4.01\pm 0.20/6.00\pm 0.30$	$19.21\pm 0.96/18.61\pm 0.93$	$0.27\pm 0.01/0.92\pm 0.05$	76/3	6
NSD		${\pi }^{+}$	$99\pm 6/112\pm 5$	$0.29\pm 0.02/0.34\pm 0.02$	$0.60\pm 0.03/0.98\pm 0.02$	$4.01\pm 0.20/6.00\pm 0.30$	$19.21\pm 0.96/18.61\pm 0.93$	$0.27\pm 0.01/0.27\pm 0.01$	96/4	6
ALICE	900	${\pi }^{-}$	$101\pm 5/116\pm 6$	$0.31\pm 0.02/0.36\pm 0.02$	$0.63\pm 0.02/0.94\pm 0.02$	$4.39\pm 0.22/6.81\pm 0.34$	$18.89\pm 0.94/17.35\pm 0.87$	$1.47\pm 0.07/1.47\pm 0.07$	38/126	27
INEL		${\pi }^{+}$	$101\pm 5/116\pm 6$	$0.31\pm 0.02/0.35\pm 0.02$	$0.63\pm 0.02/0.95\pm 0.02$	$4.42\pm 0.22/6.96\pm 0.35$	$18.81\pm 0.94/17.35\pm 0.87$	$1.47\pm 0.07/1.47\pm 0.07$	49/137	27
CMS	900	${\pi }^{-}$	$101\pm 5/115\pm 6$	$0.31\pm 0.02/0.35\pm 0.02$	$0.63\pm 0.03/0.91\pm 0.02$	$4.43\pm 0.22/7.08\pm 0.35$	$18.71\pm 0.93/17.13\pm 0.87$	$3.65\pm 0.18/3.49\pm 0.17$	24/62	16
INEL		${\pi }^{+}$	$101\pm 5/115\pm 5$	$0.31\pm 0.02/0.35\pm 0.02$	$0.63\pm 0.03/0.92\pm 0.02$	$4.43\pm 0.22/7.04\pm 0.35$	$18.71\pm 0.93/17.16\pm 0.86$	$3.70\pm 0.19/3.55\pm 0.18$	16/59	16
	2760	${\pi }^{-}$	$103\pm 6/116\pm 4$	$0.33\pm 0.02/0.36\pm 0.02$	$0.63\pm 0.03/0.90\pm 0.02$	$4.68\pm 0.23/7.80\pm 0.39$	$18.41\pm 0.92/16.45\pm 0.82$	$4.47\pm 0.22/4.31\pm 0.22$	34/70	16
		${\pi }^{+}$	$102\pm 6/116\pm 5$	$0.33\pm 0.02/0.36\pm 0.02$	$0.63\pm 0.04/0.91\pm 0.02$	$4.69\pm 0.23/7.90\pm 0.39$	$18.39\pm 0.92/16.35\pm 0.82$	$4.55\pm 0.23/4.43\pm 0.22$	35/74	16
	7000	${\pi }^{-}$	$104\pm 5/117\pm 6$	$0.34\pm 0.02/0.37\pm 0.02$	$0.62\pm 0.03/0.89\pm 0.02$	$4.79\pm 0.24/8.00\pm 0.40$	$18.21\pm 0.91/16.13\pm 0.81$	$5.50\pm 0.27/5.49\pm 0.27$	48/67	16
		${\pi }^{+}$	$103\pm 5/116\pm 4$	$0.34\pm 0.02/0.36\pm 0.02$	$0.61\pm 0.04/0.89\pm 0.02$	$4.80\pm 0.24/8.20\pm 0.41$	$18.21\pm 0.91/16.00\pm 0.80$	$5.54\pm 0.28/5.52\pm 0.28$	55/70	16
	13000	${\pi }^{-}$	$105\pm 5/117\pm 5$	$0.35\pm 0.02/0.37\pm 0.02$	$0.61\pm 0.03/0.89\pm 0.02$	$4.90\pm 0.24/8.30\pm 0.41$	$18.11\pm 0.90/15.99\pm 0.80$	$5.07\pm 0.25/5.07\pm 0.25$	30/28	16
		${\pi }^{+}$	$104\pm 5/117\pm 5$	$0.34\pm 0.02/0.36\pm 0.02$	$0.64\pm 0.04/0.88\pm 0.02$	$5.00\pm 0.25/8.99\pm 0.43$	$18.00\pm 0.90/15.59\pm 0.78$	$5.12\pm 0.26/5.15\pm 0.26$	36/42	16

and

Table 2. Values of free parameters ($T_0$, ${\beta }_T$, qk, $p_0$, and n), normalization constant ($N_0$), ${\chi }^2$, and ndof corresponding to the dashed (dot-dashed) curves for ${\pi }^{-}$ (${\pi }^{+}$) spectra in Figure 1 in which different data are measured in different mid-(pseudo)rapidity intervals at different energies by different Collaborations. The values presented in terms of value${}_1$/value${}_2$ denote respectively the first and second sets of parameter values in Equation (7) through Equations (2) and (3) in which $k\ne 1$.

Collab.	$\sqrt{\mathit{s}}$ (GeV)	Part.	${\mathit{T}}_0$ (MeV)	${\mathit{\beta }}_{\mathit{T}}$ (c)	q	${\mathit{p}}_0$ (GeV/c)	n	${\mathit{N}}_0$	${\mathit{\chi }}^2$	ndof
NA61/	6.3	${\pi }^{-}$	$81\pm 4$	$0.19\pm 0.01$	$1.05\pm 0.002$	1	−	−	$0.08\pm 0.01$	12	14
SHINE	7.7	${\pi }^{-}$	$81\pm 4$	$0.20\pm 0.01$	$1.06\pm 0.002$	1	−	−	$0.10\pm 0.01$	13	14
INEL	8.8	${\pi }^{-}$	$83\pm 4$	$0.20\pm 0.01$	$1.05\pm 0.002$	1	−	−	$0.10\pm 0.01$	24	14
	12.3	${\pi }^{-}$	$84\pm 4$	$0.21\pm 0.01$	$1.06\pm 0.002$	1	−	−	$0.12\pm 0.01$	14	14
	17.3	${\pi }^{-}$	$85\pm 4$	$0.21\pm 0.01$	$1.06\pm 0.002$	1	−	−	$0.13\pm 0.01$	5	14
PHENIX	62.4	${\pi }^{-}$	$78\pm 4/86\pm 4$	$0.18\pm 0.01/0.21\pm 0.01$	$1.04\pm 0.01/1.06\pm 0.01$	$0.63\pm 0.03/0.98\pm 0.05$	$3.02\pm 0.15/5.36\pm 0.27$	$16.99\pm 0.85/18.73\pm 0.94$	$19.53\pm 0.98/18.26\pm 0.91$	16/18	19
INEL		${\pi }^{+}$	$79\pm 5/85\pm 4$	$0.18\pm 0.01/0.21\pm 0.01$	$1.04\pm 0.01/1.06\pm 0.01$	$0.63\pm 0.02/0.97\pm 0.05$	$3.10\pm 0.15/5.36\pm 0.27$	$16.99\pm 0.85/18.73\pm 0.94$	$18.42\pm 0.92/18.26\pm 0.91$	30/23	19
	200	${\pi }^{-}$	$80\pm 5/86\pm 4$	$0.19\pm 0.01/0.23\pm 0.01$	$1.02\pm 0.01/1.06\pm 0.01$	$0.59\pm 0.02/0.95\pm 0.05$	$3.53\pm 0.17/5.99\pm 0.30$	$16.68\pm 0.84/18.23\pm 0.91$	$24.48\pm 1.22/23.86\pm 1.19$	39/24	20
		${\pi }^{+}$	$80\pm 5/86\pm 4$	$0.19\pm 0.01/0.23\pm 0.01$	$1.02\pm 0.01/1.06\pm 0.01$	$0.59\pm 0.03/0.95\pm 0.05$	$3.53\pm 0.17/6.09\pm 0.30$	$16.68\pm 0.84/18.23\pm 0.91$	$25.07\pm 1.25/24.49\pm 1.22$	45/68	20
STAR	200	${\pi }^{-}$	$79\pm 5/85\pm 4$	$0.19\pm 0.01/0.23\pm 0.01$	$1.04\pm 0.01/1.05\pm 0.01$	$0.62\pm 0.03/0.95\pm 0.05$	$3.70\pm 0.18/5.89\pm 0.29$	$16.68\pm 0.82/18.43\pm 0.92$	$0.26\pm 0.01/0.26\pm 0.01$	22/39	5
NSD		${\pi }^{+}$	$79\pm 4/85\pm 4$	$0.19\pm 0.01/0.23\pm 0.01$	$1.04\pm 0.01/1.05\pm 0.01$	$0.62\pm 0.02/0.95\pm 0.05$	$3.70\pm 0.18/5.89\pm 0.29$	$16.68\pm 0.82/18.43\pm 0.92$	$0.27\pm 0.01/0.26\pm 0.01$	15/28	5
ALICE	900	${\pi }^{-}$	$81\pm 5/86\pm 4$	$0.20\pm 0.01/0.25\pm 0.01$	$1.03\pm 0.01/1.06\pm 0.01$	$0.53\pm 0.02/0.93\pm 0.05$	$3.63\pm 0.19/6.39\pm 0.32$	$16.68\pm 0.81/18.03\pm 0.90$	$1.47\pm 0.07/1.47\pm 0.07$	34/419	26
INEL		${\pi }^{+}$	$80\pm 3/86\pm 4$	$0.20\pm 0.01/0.25\pm 0.01$	$1.03\pm 0.01/1.06\pm 0.01$	$0.53\pm 0.03/0.93\pm 0.05$	$3.64\pm 0.19/6.39\pm 0.32$	$16.68\pm 0.81/18.03\pm 0.90$	$1.50\pm 0.08/1.50\pm 0.08$	51/558	26
CMS	900	${\pi }^{-}$	$81\pm 3/87\pm 4$	$0.19\pm 0.01/0.25\pm 0.01$	$1.02\pm 0.01/1.05\pm 0.01$	$0.51\pm 0.03/0.89\pm 0.05$	$3.74\pm 0.19/6.79\pm 0.34$	$16.68\pm 0.80/17.83\pm 0.89$	$3.67\pm 0.18/3.45\pm 0.17$	8/124	15
INEL		${\pi }^{+}$	$80\pm 4/87\pm 4$	$0.19\pm 0.01/0.25\pm 0.01$	$1.02\pm 0.01/1.05\pm 0.01$	$0.51\pm 0.02/0.89\pm 0.05$	$3.72\pm 0.19/6.79\pm 0.34$	$16.68\pm 0.80/17.83\pm 0.89$	$3.74\pm 0.19/3.59\pm 0.18$	6/121	15
	2760	${\pi }^{-}$	$81\pm 5/88\pm 4$	$0.21\pm 0.01/0.26\pm 0.01$	$1.02\pm 0.01/1.05\pm 0.01$	$0.49\pm 0.02/0.86\pm 0.05$	$3.96\pm 0.20/7.49\pm 0.37$	$16.56\pm 0.80/17.47\pm 0.87$	$4.46\pm 0.22/4.24\pm 0.21$	15/114	15
		${\pi }^{+}$	$81\pm 5/88\pm 4$	$0.21\pm 0.01/0.26\pm 0.01$	$1.02\pm 0.01/1.05\pm 0.01$	$0.49\pm 0.03/0.86\pm 0.05$	$3.92\pm 0.20/7.49\pm 0.37$	$16.55\pm 0.80/17.47\pm 0.87$	$4.56\pm 0.23/4.44\pm 0.22$	15/115	15
	7000	${\pi }^{-}$	$83\pm 4/89\pm 4$	$0.21\pm 0.01/0.27\pm 0.01$	$1.02\pm 0.01/1.05\pm 0.01$	$0.47\pm 0.02/0.84\pm 0.05$	$3.98\pm 0.19/7.69\pm 0.38$	$16.30\pm 0.81/17.37\pm 0.87$	$5.55\pm 0.28/5.41\pm 0.27$	23/129	15
		${\pi }^{+}$	$82\pm 4/87\pm 4$	$0.21\pm 0.01/0.26\pm 0.01$	$1.02\pm 0.01/1.05\pm 0.01$	$0.47\pm 0.03/0.84\pm 0.05$	$3.99\pm 0.19/7.59\pm 0.38$	$16.37\pm 0.81/17.37\pm 0.87$	$5.60\pm 0.28/5.60\pm 0.28$	31/171	15
	13000	${\pi }^{-}$	$83\pm 5/88\pm 4$	$0.22\pm 0.01/0.27\pm 0.01$	$1.02\pm 0.01/1.05\pm 0.01$	$0.46\pm 0.02/0.82\pm 0.05$	$4.05\pm 0.20/7.89\pm 0.39$	$16.31\pm 0.82/17.27\pm 0.86$	$5.20\pm 0.26/5.10\pm 0.26$	13/50	15
		${\pi }^{+}$	$84\pm 5/86\pm 4$	$0.23\pm 0.01/0.27\pm 0.01$	$1.02\pm 0.01/1.05\pm 0.01$	$0.47\pm 0.03/0.80\pm 0.05$	$4.09\pm 0.20/7.99\pm 0.40$	$16.28\pm 0.82/17.07\pm 0.85$	$5.20\pm 0.26/5.10\pm 0.26$	27/74	15

, where the errors of fit parameters are obtained by the statistical simulation method [49], no matter what ${\chi }^2$/ndof is. The parameter values presented in terms of value${}_1$/value${}_2$ denote respectively the first and second sets of parameter values in Equation (7) through Equations (1)–(3) in which $k\ne 1$. One can see that Equation (7) with two sets of parameter values describes the $p_T$ spectra at mid-(pseudo)rapidity in $pp$ collisions over an energy range from a few GeV to above 10 TeV. The blast-wave fit with Boltzmann distribution and with Tsallis distribution presents similar results. The free parameters show some laws in the considered energy range. For a given parameter, its fluctuation at given energy is obvious in some cases. Because of the data being not available in very-low $p_T$ range, Equation (9) is not used in the fit.

It should be noted that, from the fit process we know that, the Tsallis expression, Equation (2), having a polynomial behavior at large $p_T$ could be a better description for the spectra at large values of $p_T$, where the Boltzmann expression, Equation (1) does not work possibly at large $p_T$ if we use the same parameters $T_0$ and ${\beta }_T$. In some cases, for the spectra in a wide $p_T$ range, a single Tsallis expression is suitable, and two- or three-component Boltzmann expression is needed. Our previous work [50] studied both the Tsallis and Boltzmann distributions without flow effect and also confirms this issue. Indeed, the Tsallis description is better than the Boltzmann one, though the former has one more parameter q. In fact, the introduction of the entropy index q in the Tsallis description has the meaning of reality. As discussed in Section 2, q characterizes the degree of non-equilibrium. In addition, when $q\to 1$, the Tsallis description degenerates to the Boltzmann one.

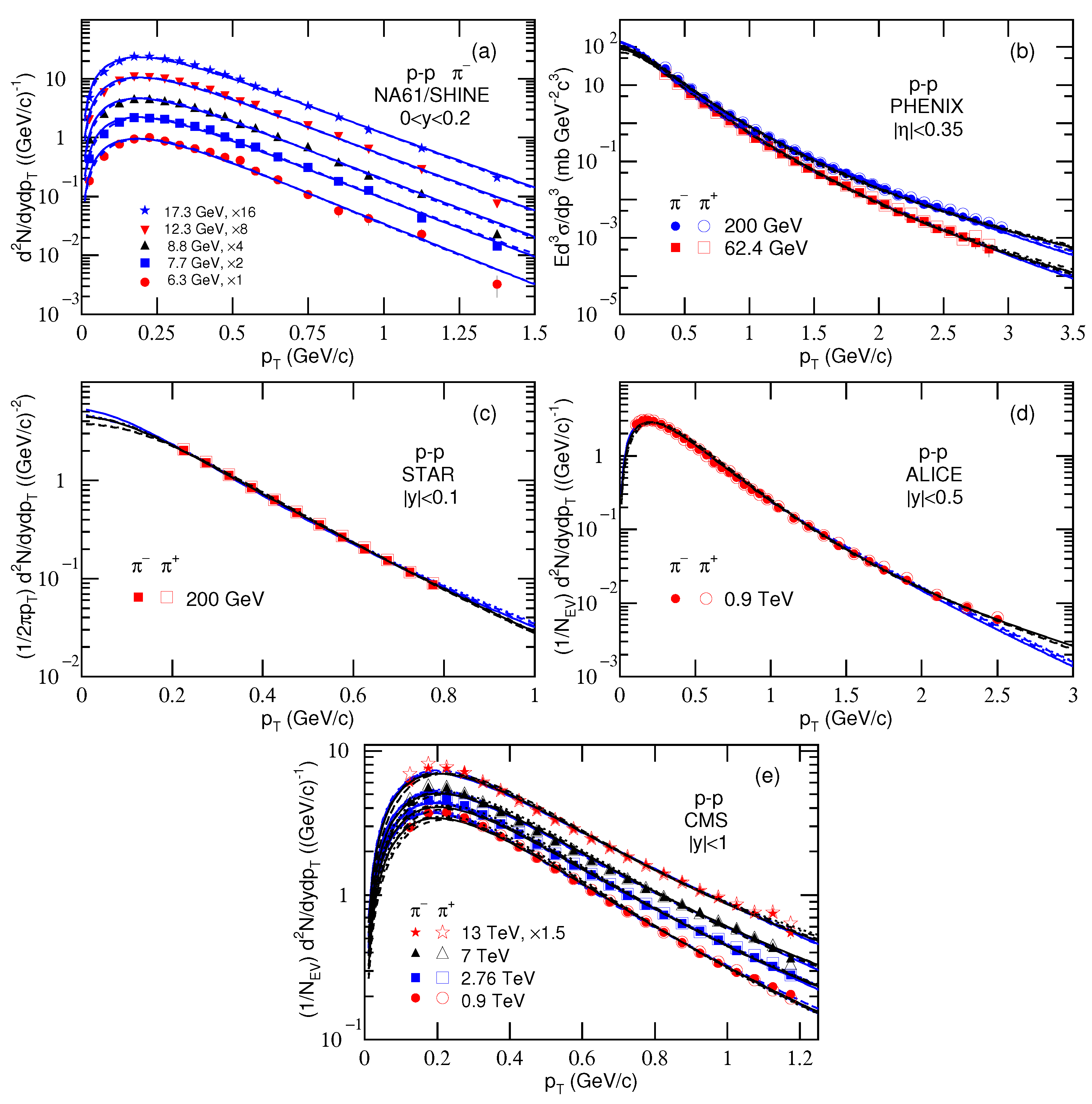
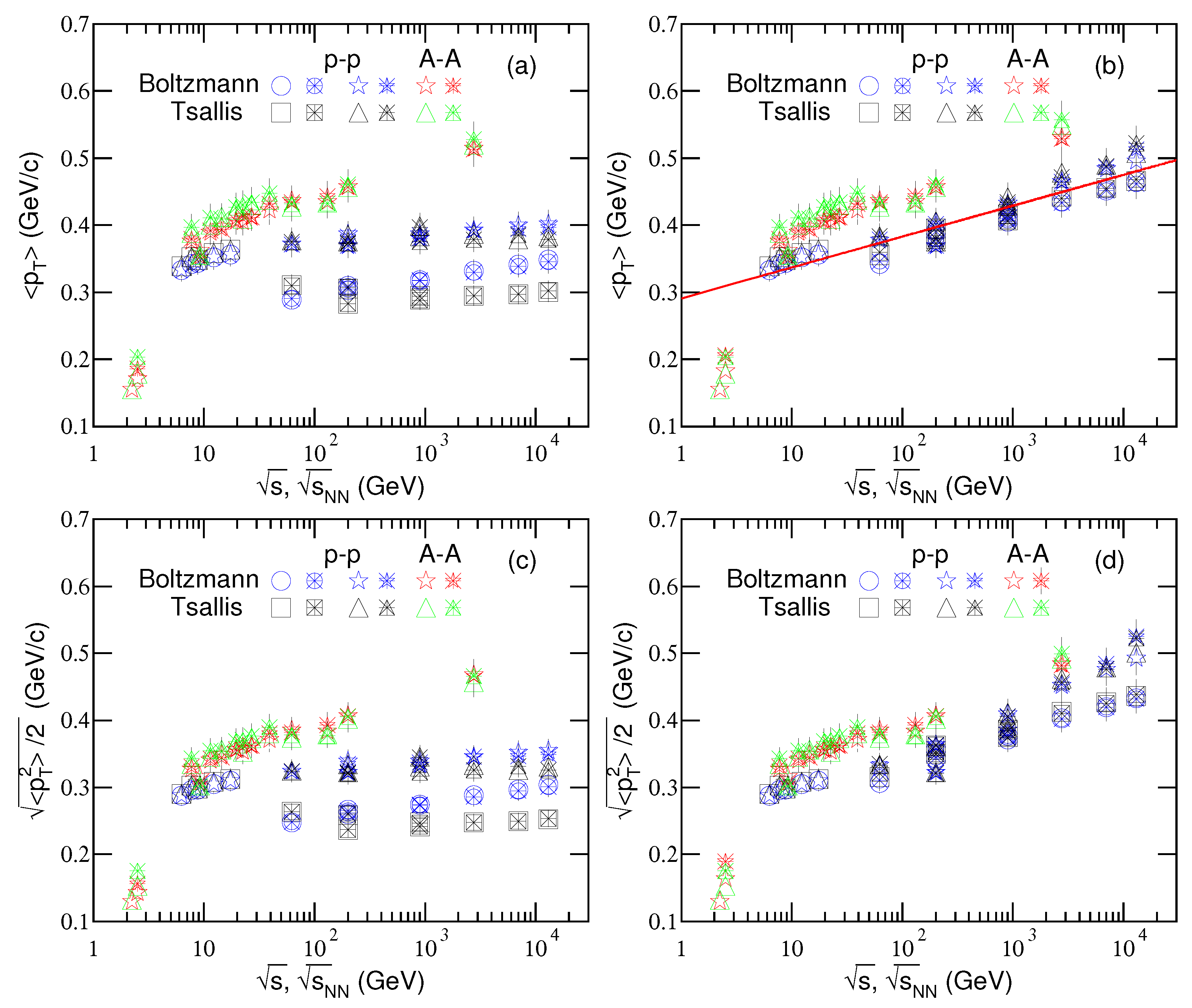
To see clearly the excitation functions of free parameters, Figure 2a–e show the dependences of $T_0$, ${\beta }_T$, $p_0$, n, and k on $\sqrt{s}$, respectively. The blue and black closed and open symbols represent the parameter values corresponding to ${\pi }^{-}$ and ${\pi }^{+}$ respectively, which are listed in Table 1 and Table 2. The blue circles (black squares) represent the first set of parameter values obtained from Equation (7) through Equations (1)–(3). The blue asterisks (black triangles) represent the second set of parameter values obtained from Equation (7) through Equations (1)–(3). One can see that the difference between the results of ${\pi }^{-}$ and ${\pi }^{+}$ is not obvious. In the excitation functions of the first set of $T_0$ and ${\beta }_T$ obtained from the blast-wave fit with Boltzmann distribution, there are a hill at $\sqrt{s}\approx 10$ GeV, a drop at dozens of GeV, and then an increase from dozens of GeV to above 10 TeV. In the excitation functions of the first set of $T_0$ and ${\beta }_T$ obtained from the blast-wave fit with Tsallis distribution, there is no the complex structure, but a very low hill. In the excitation functions of the second set of $T_0$ and ${\beta }_T$, there is a slight increase from about 10 GeV to above 10 TeV. In Equation (7) contained the blast-wave fit with both distributions, in the excitation functions of $p_0$ and n, there are a slight decrease and increase respectively in the case of the hard component being available. The excitation function of k shows that the contribution ($1-k$) of hard component slightly increases from dozens of GeV to above 10 TeV, and it has no contribution at around 10 GeV. At given energies, the fluctuations in a given parameter result in different excitation functions due to different selections. As a comparison, the red asterisks (green triangles) in Figure 2 represent the results from $AA$ collisions which are discussed in detail in the Appendix A. One can see that the results from $AA$ collisions approach to those from $pp$ collisions with the second set of parameters, though only the soft component is used in most cases.

Indeed, $\sqrt{s_{NN}}\approx 10$ GeV is a special energy for $AA$ collisions as indicated by Cleymans [51]. The present work shows that $\sqrt{s}\approx 10$ GeV is also a special energy for $pp$ collisions. In particular, there is a hill in the excitation functions of $T_0$ and ${\beta }_T$ in $pp$ collisions due to a given selection of the parameters. At this energy (11 GeV more specifically [51]), the final state has the highest net baryon density, a transition from a baryon-dominated to a meson-dominated final state takes place, and the ratios of strange particles to mesons show clear and pronounced maximums [51]. These properties result in this special energy.

At 11 GeV, the chemical freeze-out temperature in $AA$ collisions is about 151 MeV [51], and the present work shows that the kinetic freeze-out temperature in $pp$ collisions is about 105 MeV, extracted from the blast-wave fit with Boltzmann distribution. If we do not consider the difference between $AA$ and $pp$ collisions, though cold nuclear effect exists in $AA$ collisions, the chemical freeze-out happens obviously earlier than the kinetic one. According to an ideal fluid consideration, the time evolution of temperature follows $T_f=T_i{({\tau }_i/{\tau }_f)}^{1/3}$, where $T_i$ (=300 MeV) and ${\tau }_i$ (=1 fm) are the initial temperature and proper time respectively [52,53], and $T_f$ and ${\tau }_f$ denote the final temperature and time respectively, the chemical and kinetic freeze-outs happen at 7.8 and 23.3 fm respectively. It should be noted that in the calculation of ${\tau }_f$, the Lorentz factor is not considered. If we consider the mean Lorentz factor ($\overline{\gamma }\approx 5$–6) of charged pions in the rest frame of emission source [15,16,17,18], the value of freeze-out time will be smaller.

Strictly, $T_0$ (${\beta }_T$) obtained from the pion spectra in the present work is less than that averaged by weighting the yields of pions, kaons, protons, and other light particles. Fortunately, the fraction of the pion yield in high energy collisions are major (≈85%). The parameters and their tendencies obtained from the pion spectra are similar to those obtained from the spectra of all light particles. To study the excitation functions of $T_0$ and ${\beta }_T$, it does not matter if we use the spectra of pions instead of all light particles.

It should be noted that the main parameters $T_0$ and ${\beta }_T$ are correlated in some way. Although the excitation functions of $T_0$ (${\beta }_T$) which are acceptable in the fit process are not sole, their tendencies are harmonious in most cases, in particular in the energy range from the RHIC to LHC. Combining with our previous work [18], we could say that there is a slight (≈10%) increase in the excitation function of $T_0$ and an obvious (≈35%) increase in the excitation function of ${\beta }_T$ from the RHIC to LHC. At least, the excitation functions of $T_0$ and ${\beta }_T$ do not decrease from the RHIC to LHC.

However, the excitation function of $T_0$ from low to high energies is not always incremental or invariant, though the excitation function of ${\beta }_T$ has the trend of increase in general. For example, In [4], $T_0$ slowly decreases as $\sqrt{s}$ increases from 23 GeV to 1.8 TeV, and ${\beta }_T$ slowly increases with $\sqrt{s}$. In [19,20], $T_0$ has no obvious change and ${\beta }_T$ has a slight (≈10%) increase from the RHIC to LHC. In [21], $T_0$ has a slight (≈9%) increase and ${\beta }_T$ has a large (≈65%) increase from the RHIC to LHC. In [22,23], $T_0$ has a slight (≈5%) decrease from the RHIC to LHC and ${\beta }_T$ increases by ≈20% from 39 to 200 GeV. It is convinced that ${\beta }_T$ increases from the RHIC to LHC, though the situation of $T_0$ is doubtful.

Although some works [54,55,56,57] reported a decrease of $T_0$ and an increase of ${\beta }_T$ from the RHIC to LHC, our re-scans on their plots show a different situation of $T_0$. For example, in [54], our re-scans show that $T_0$ has no obvious change and ${\beta }_T$ has a slight (≈9%) increase from the top RHIC to LHC, though there is an obvious hill or there is an increase by ≈30% in $T_0$ in 5–40 GeV comparting with that at the RHIC. Authors in [55] shows similar results to [54] with the almost invariant $T_0$ from the top RHIC to LHC, an increase by ≈28% in $T_0$ in 7–40 GeV comparing with that at the top RHIC, and an increase by ≈8% in ${\beta }_T$ comparing with that at the top RHIC. Authors in [56,57] shows similar result to [54,55] on $T_0$, though the excitation function of ${\beta }_T$ is not available.

In some cases, the correlation between $T_0$ and ${\beta }_T$ are not negative, though some works [54,55] show negative correlation over a wide energy range. For a give $p_T$ spectrum, it seems that a larger $T_0$ corresponds to a smaller ${\beta }_T$, which shows a negative correlation. However, this negative correlation is not sole case. In fact, a couple of suitable $T_0$ and ${\beta }_T$ can fit a given $p_T$ spectrum. A series of $p_T$ spectra at different energies possibly show a positive correlation between $T_0$ and ${\beta }_T$, or independent of $T_0$ on ${\beta }_T$, in a narrow energy range. Very recently, authors in [58] shows approximately independent of $T_0$ on ${\beta }_T$ in $pp$ collisions at $\sqrt{s}=7$ TeV, and negative correlations in p-Pb collisions at $\sqrt{s_{NN}}=5.02$ TeV and in Pb-Pb collisions at $\sqrt{s_{NN}}=2.76$ TeV, for different average charged-particle multiplicity densities, i.e., for different centrality classes. These results are partly in agreement with our results. It seems that the correlation between $T_0$ and ${\beta }_T$ is an open question at present, though some researchers think that there is a negative correlation between $T_0$ and ${\beta }_T$. In our opinion, the type of correlation between $T_0$ and ${\beta }_T$ depends on three factors, that is the choices of fitted region in low and medium $p_T$ range, fixed or changeable $n_0$, sensitivity of ${\beta }_T$ on centrality. Indeed, more studies are needed in the near future.

To study further the behaviors of parameters, Figure 3 shows the excitation functions of (a)(b) mean $p_T$ ($\langle p_T\rangle$) and (c)(d) ratio of root-mean-square $p_T$ ($\sqrt{\langle p_T^2\rangle }$) to $\sqrt{2}$, where the left panel [(a)(c)] corresponds to the results of the first component [Equation (1) or (2)] and the right panel [(b)(d)] corresponds to the results of the two components [Equation (7)]. The open symbols (open symbols with asterisks) represent the values corresponding to ${\pi }^{-}$ (${\pi }^{+}$) spectra. The blue circles (black squares) represent the values obtained indirectly from Equations (1) and (2) for the left panel or Equation (7) through Equations (1)–(3) for the right panel, by the first set of parameter values. The results by the second set of parameter values are presented by the blue asterisks (black triangles). These values are indirectly obtained from the equations according to the parameters listed in Table 1 and Table 2 over a $p_T$ range from 0 to 5 GeV/c which is beyond the available range of the data. If the initial temperature of interacting system is approximately presented by $T_i=\sqrt{\langle p_T^2\rangle /2}$ [59,60,61], the lower panel shows the excitation function of initial temperature. Because of excluding different contribution fractions of the second component, the left panel [(a)(c)] shows some differences in the case of using two sets of parameter values. It should be noted that the root-mean square momentum component of particles in the rest frame of isotropic emission source is regarded as the initial temperature, or at the least it is a reflection of the initial temperature. The relations in the left panel are complex and multiple due to different sets of parameter values. The line in Figure 3b is fitted to various symbols by linear function

$$\begin{array}{c}\hfill \langle p_T\rangle =(0.291\pm 0.006)+(0.020\pm 0.001)ln\sqrt{s}\end{array}$$

(11)

with ${\chi }^2$/ndof = 54/82. From the line one can see that the behavior of $\langle p_T\rangle$. In particular, with the increase of $ln\sqrt{s}$ and including the contribution of second component, $\langle p_T\rangle$ increases approximately linearly. As a comparison, the red asterisks (green triangles) in Figure 3 represent the results for $AA$ collisions, which are indirectly obtained according to the parameter values listed in

Table A1. Values of $T_0$, ${\beta }_T$, k, $p_0$, n, $N_0$, ${\chi }^2$, and ndof corresponding to the solid (dotted) curves for ${\pi }^{-}$ (${\pi }^{+}$) spectra in Figure A1.

Collab.	$\sqrt{{\mathit{s}}_{\mathbf{NN}}}$ (GeV)	Part.	${\mathit{T}}_0$ (MeV)	${\mathit{\beta }}_{\mathit{T}}$ (c)	k	${\mathit{p}}_0$ (GeV/c)	n	${\mathit{N}}_0$	${\mathit{\chi }}^2$	ndof
FOPI Au-Au	2.24	${\pi }^{-}$	$43\pm 2$	$0.27\pm 0.02$	1	−	−	$1734.50\pm 16.33$	38	33
0–2.25%	2.52	${\pi }^{-}$	$54\pm 3$	$0.21\pm 0.02$	$0.96\pm 0.01$	$3.81\pm 0.23$	$19.00\pm 0.9$	$2180.50\pm 18.31$	11	40
		${\pi }^{+}$	$59\pm 6$	$0.23\pm 0.02$	$0.94\pm 0.01$	$3.91\pm 0.31$	$18.00\pm 0.5$	$1385.40\pm 13.01$	16	40
STAR Au-Au	7.7	${\pi }^{-}$	$118\pm 6$	$0.33\pm 0.01$	1	−	−	$20.08\pm 1.08$	17	23
0–5%		${\pi }^{+}$	$118\pm 6$	$0.34\pm 0.01$	1	−	−	$19.03\pm 0.64$	27	23
0–10%	9.2	${\pi }^{-}$	$111\pm 6$	$0.34\pm 0.02$	1	−	−	$21.18\pm 1.00$	1	4
		${\pi }^{+}$	$110\pm 6$	$0.30\pm 0.02$	1	−	−	$21.68\pm 1.62$	1	4
0–5%	11.5	${\pi }^{-}$	$119\pm 6$	$0.35\pm 0.02$	1	−	−	$25.76\pm 1.80$	4	23
		${\pi }^{+}$	$120\pm 6$	$0.35\pm 0.02$	1	−	−	$24.39\pm 1.32$	8	23
	14.5	${\pi }^{-}$	$121\pm 6$	$0.35\pm 0.02$	1	−	−	$30.22\pm 1.60$	1	25
		${\pi }^{+}$	$120\pm 7$	$0.35\pm 0.02$	1	−	−	$29.47\pm 1.62$	1	25
	19.6	${\pi }^{-}$	$123\pm 7$	$0.36\pm 0.02$	1	−	−	$31.62\pm 1.50$	3	23
		${\pi }^{+}$	$124\pm 7$	$0.36\pm 0.02$	1	−	−	$31.10\pm 1.52$	3	23
	27	${\pi }^{-}$	$124\pm 6$	$0.36\pm 0.02$	1	−	−	$34.95\pm 1.40$	3	23
		${\pi }^{+}$	$124\pm 5$	$0.36\pm 0.02$	1	−	−	$34.31\pm 1.22$	3	23
	39	${\pi }^{-}$	$128\pm 5$	$0.36\pm 0.02$	1	−	−	$37.09\pm 2.12$	4	23
		${\pi }^{+}$	$129\pm 5$	$0.37\pm 0.02$	1	−	−	$35.06\pm 2.42$	2	23
	62.4	${\pi }^{-}$	$131\pm 6$	$0.37\pm 0.02$	1	−	−	$42.60\pm 2.20$	9	4
		${\pi }^{+}$	$130\pm 6$	$0.36\pm 0.02$	1	−	−	$42.16\pm 2.36$	9	4
0–6%	130	${\pi }^{-}$	$129\pm 5$	$0.37\pm 0.02$	1	−	−	$50.22\pm 1.55$	25	4
		${\pi }^{+}$	$130\pm 6$	$0.38\pm 0.02$	1	−	−	$48.88\pm 1.09$	21	4
0–5%	200	${\pi }^{-}$	$132\pm 6$	$0.39\pm 0.02$	1	−	−	$57.94\pm 1.67$	6	5
		${\pi }^{+}$	$131\pm 5$	$0.39\pm 0.02$	1	−	−	$57.81\pm 1.54$	9	5
PHENIX Cu-Cu	22.5	${\pi }^{-}$	$127\pm 6$	$0.34\pm 0.02$	1	−	−	$35.06\pm 1.85$	10	20
0–10%		${\pi }^{+}$	$126\pm 6$	$0.35\pm 0.02$	1	−	−	$34.93\pm 2.21$	13	20
ALICE Pb-Pb	2760	${\pi }^{-}$	$133\pm 5$	$0.42\pm 0.02$	$0.94\pm 0.02$	$5.81\pm 0.34$	$18.00\pm 0.87$	$759.82\pm 12.22$	37	35
0–5%		${\pi }^{+}$	$133\pm 6$	$0.43\pm 0.02$	$0.84\pm 0.02$	$5.79\pm 0.35$	$18.00\pm 0.87$	$754.17\pm 21.00$	37	35

and

Table A2. Values of $T_0$, ${\beta }_T$, q, k, $p_0$, n, $N_0$, ${\chi }^2$, and ndof corresponding to the dashed (dot-dashed) curves for ${\pi }^{-}$ (${\pi }^{+}$) spectra in Figure A1.

Collab.	$\sqrt{{\mathit{s}}_{\mathit{N}\mathit{N}}}$ (GeV)	Part.	${\mathit{T}}_0$ (MeV)	${\mathit{\beta }}_{\mathit{T}}$ (c)	q	k	${\mathit{p}}_0$ (GeV/c)	n	${\mathit{N}}_0$	${\mathit{\chi }}^2$	ndof
FOPI Au-Au	2.24	${\pi }^{-}$	$28\pm 2$	$0.10\pm 0.02$	$1.07\pm 0.01$	1	−	−	$1734.50\pm 15.01$	42	32
0–2.25%	2.52	${\pi }^{-}$	$33\pm 2$	$0.11\pm 0.02$	$1.08\pm 0.01$	1	−	−	$2205.40\pm 18.01$	5	42
		${\pi }^{+}$	$39\pm 3$	$0.12\pm 0.02$	$1.08\pm 0.01$	1	−	−	$1362.80\pm 12.01$	13	42
STAR Au-Au	7.7	${\pi }^{-}$	$88\pm 6$	$0.23\pm 0.01$	$1.06\pm 0.01$	1	−	−	$19.45\pm 1.08$	31	22
0–5%		${\pi }^{+}$	$90\pm 6$	$0.24\pm 0.01$	$1.06\pm 0.01$	1	−	−	$18.64\pm 0.64$	35	22
0–10%	9.2	${\pi }^{-}$	$89\pm 6$	$0.23\pm 0.02$	$1.04\pm 0.01$	1	−	−	$21.99\pm 1.00$	2	3
		${\pi }^{+}$	$88\pm 6$	$0.23\pm 0.02$	$1.04\pm 0.01$	1	−	−	$21.93\pm 1.62$	2	3
0–5%	11.5	${\pi }^{-}$	$92\pm 6$	$0.22\pm 0.02$	$1.06\pm 0.01$	1	−	−	$25.13\pm 1.80$	18	22
		${\pi }^{+}$	$94\pm 5$	$0.22\pm 0.02$	$1.06\pm 0.02$	1	−	−	$24.27\pm 1.22$	21	22
	14.5	${\pi }^{-}$	$93\pm 5$	$0.23\pm 0.02$	$1.06\pm 0.02$	1	−	−	$30.47\pm 1.20$	3	24
		${\pi }^{+}$	$93\pm 5$	$0.23\pm 0.02$	$1.06\pm 0.01$	1	−	−	$29.47\pm 2.22$	3	24
	19.6	${\pi }^{-}$	$96\pm 6$	$0.24\pm 0.02$	$1.06\pm 0.01$	1	−	−	$32.12\pm 1.30$	26	22
		${\pi }^{+}$	$96\pm 5$	$0.24\pm 0.02$	$1.06\pm 0.01$	1	−	−	$30.47\pm 1.22$	10	22
	27	${\pi }^{-}$	$96\pm 6$	$0.24\pm 0.02$	$1.06\pm 0.02$	1	−	−	$34.32\pm 2.10$	17	22
		${\pi }^{+}$	$97\pm 5$	$0.25\pm 0.02$	$1.06\pm 0.01$	1	−	−	$32.79\pm 1.52$	9	22
	39	${\pi }^{-}$	$96\pm 5$	$0.25\pm 0.02$	$1.06\pm 0.02$	1	−	−	$35.59\pm 1.42$	15	22
		${\pi }^{+}$	$97\pm 5$	$0.25\pm 0.02$	$1.07\pm 0.02$	1	−	−	$34.18\pm 1.22$	8	22
	62.4	${\pi }^{-}$	$89\pm 7$	$0.25\pm 0.02$	$1.07\pm 0.01$	1	−	−	$41.66\pm 1.20$	16	3
		${\pi }^{+}$	$90\pm 7$	$0.25\pm 0.02$	$1.07\pm 0.02$	1	−	−	$40.28\pm 1.62$	14	3
0–6%	130	${\pi }^{-}$	$91\pm 7$	$0.25\pm 0.02$	$1.07\pm 0.01$	1	−	−	$48.57\pm 1.90$	57	3
		${\pi }^{+}$	$91\pm 5$	$0.25\pm 0.02$	$1.07\pm 0.01$	1	−	−	$49.00\pm 1.02$	49	3
0–5%	200	${\pi }^{-}$	$93\pm 7$	$0.26\pm 0.02$	$1.08\pm 0.01$	1	−	−	$55.93\pm 1.60$	20	4
		${\pi }^{+}$	$93\pm 5$	$0.26\pm 0.02$	$1.08\pm 0.01$	1	−	−	$55.10\pm 1.52$	18	4
PHENIX Cu-Cu	22.5	${\pi }^{-}$	$94\pm 6$	$0.25\pm 0.02$	$1.05\pm 0.01$	1	−	−	$36.63\pm 2.62$	8	19
0–10%		${\pi }^{+}$	$99\pm 6$	$0.25\pm 0.02$	$1.06\pm 0.01$	1	−	−	$35.94\pm 3.65$	21	19
ALICE Pb-Pb	2760	${\pi }^{-}$	$101\pm 5$	$0.33\pm 0.02$	$1.07\pm 0.02$	$0.90\pm 0.02$	$6.16\pm 0.34$	$17.93\pm 0.87$	$715.84\pm 21.33$	88	34
0–5%		${\pi }^{+}$	$102\pm 6$	$0.33\pm 0.02$	$1.07\pm 0.02$	$0.91\pm 0.02$	$6.26\pm 0.35$	$17.63\pm 0.87$	$671.86\pm 13.56$	73	34

. One can see that the results for $AA$ collisions are greater than those for $pp$ collisions at around 10 GeV and above.

The quantities $\langle p_T\rangle$ and $T_i$ are very important to understand the excitation degree of interacting system. As for the right panel in Figure 3 which is for the two-component, the incremental trend for $\langle p_T\rangle$ and $T_i$ with the increase of $\sqrt{s}$ ($\sqrt{s_{NN}}$) is a natural result due to more energy deposition at higher energy. Although $\langle p_T\rangle$ and $T_i$ are obtained from the parameter values listed in Table 1 and Table 2 (A1 and A2), they are independent of fits or models. More investigations on the excitation functions of $\langle p_T\rangle$ and $T_i$ are needed due to their importance.

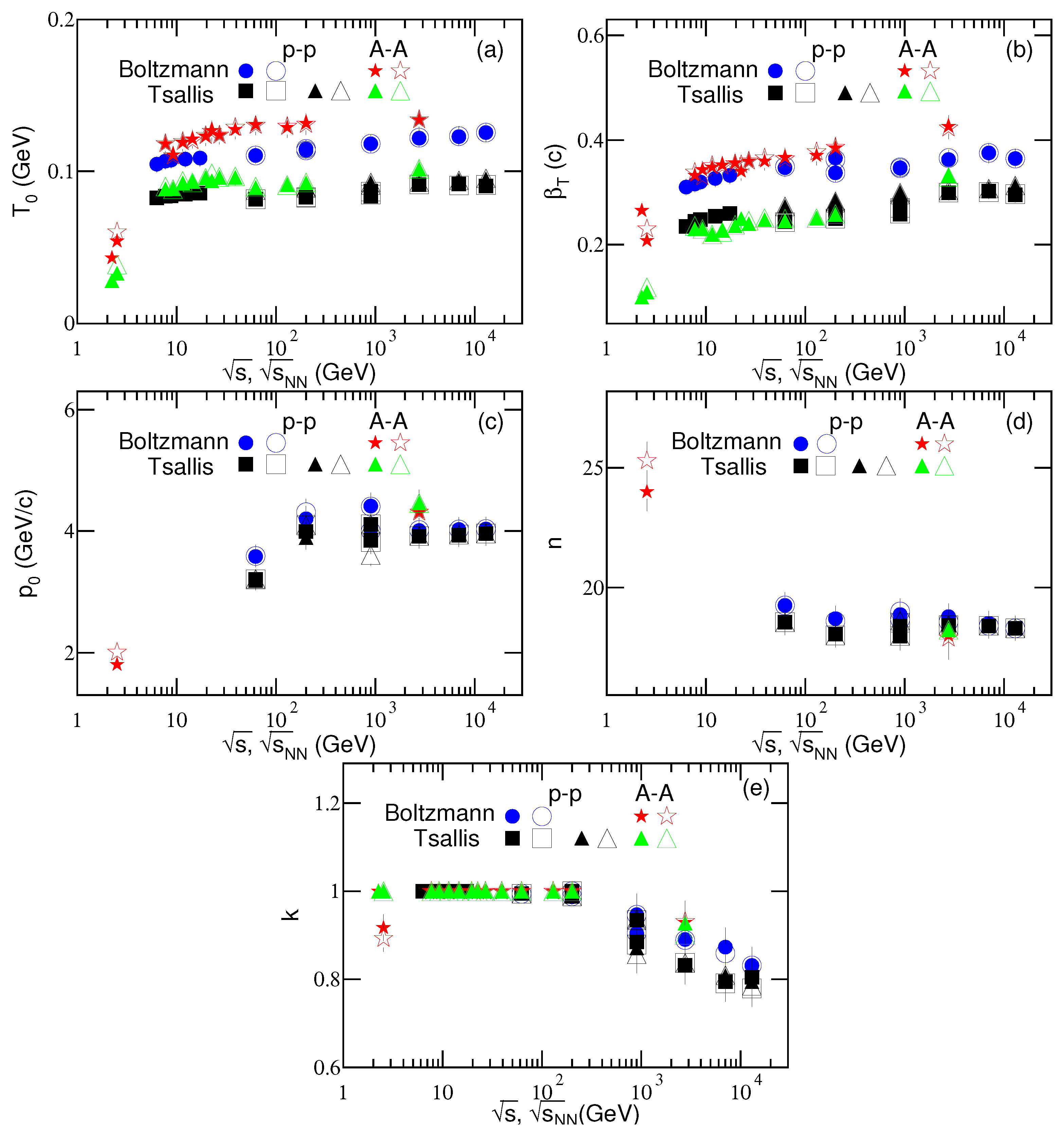
3.2. Comparison with Data by Equation (8)

To discuss further, for comparisons with the results from Equation (7), we reanalyze the spectra by Equation (8) and study the trends of new parameters. Figure 4 is the same as Figure 1, but showing the results fitted by Equation (8) through Equations (1) and (3) and through Equations (2) and (3) respectively. For Equation (8) through Equations (1) and (3), only one set of parameter values are used due to the fact that there is no correlation in the extraction of parameters in the two-component fit. For Equation (8) through Equations (2) and (3), two sets of parameter values are used to see the insensitivity of main parameters. The first set of parameter values are obtained by the method of least squares. The second set of parameter values are obtained by increasing or decreasing main parameters ($T_0$, ${\beta }_T$, q, and k) by a few percent, and limits the increase of ${\chi }^2$ by a few percent. The values of related parameters are listed in

Table 3. Values of $T_0$, ${\beta }_T$, k, $p_0$, n, $N_0$, ${\chi }^2$, and ndof corresponding to the solid (dotted) curves for ${\pi }^{-}$ (${\pi }^{+}$) spectra in Figure 4, where Equation (8) through Equations (1) and (3) is used.

Collab.	$\sqrt{\mathit{s}}$ (GeV)	Part.	${\mathit{T}}_0$ (MeV)	${\mathit{\beta }}_{\mathit{T}}$ (c)	k	${\mathit{p}}_0$ (GeV/c)	n	${\mathit{N}}_0$	${\mathit{\chi }}^2$	ndof
NA61/	6.3	${\pi }^{-}$	$105\pm 5$	$0.31\pm 0.02$	1	−	−	$0.08\pm 0.01$	24	15
SHINE	7.7	${\pi }^{-}$	$106\pm 5$	$0.32\pm 0.02$	1	−	−	$0.10\pm 0.01$	44	15
INEL	8.8	${\pi }^{-}$	$107\pm 5$	$0.32\pm 0.02$	1	−	−	$0.10\pm 0.01$	86	15
	12.3	${\pi }^{-}$	$108\pm 5$	$0.33\pm 0.02$	1	−	−	$0.12\pm 0.01$	78	15
	17.3	${\pi }^{-}$	$109\pm 5$	$0.33\pm 0.02$	1	−	−	$0.13\pm 0.01$	34	15
PHENIX	62.4	${\pi }^{-}$	$111\pm 5$	$0.35\pm 0.02$	$0.99\pm 0.01$	$3.58\pm 0.18$	$19.26\pm 0.56$	$19.48\pm 0.97$	9	20
INEL		${\pi }^{+}$	$111\pm 5$	$0.35\pm 0.02$	$0.99\pm 0.01$	$3.59\pm 0.18$	$19.26\pm 0.56$	$19.54\pm 0.97$	18	20
	200	${\pi }^{-}$	$115\pm 6$	$0.37\pm 0.02$	$0.99\pm 0.02$	$4.20\pm 0.21$	$18.71\pm 0.54$	$24.11\pm 1.20$	16	21
		${\pi }^{+}$	$115\pm 6$	$0.36\pm 0.02$	$0.99\pm 0.02$	$4.31\pm 0.22$	$18.61\pm 0.53$	$24.96\pm 1.22$	26	21
STAR	200	${\pi }^{-}$	$114\pm 6$	$0.34\pm 0.02$	1	−	−	$0.26\pm 0.01$	2	6
NSD		${\pi }^{+}$	$114\pm 6$	$0.34\pm 0.02$	1	−	−	$0.27\pm 0.01$	6	6
ALICE	900	${\pi }^{-}$	$118\pm 5$	$0.35\pm 0.02$	$0.95\pm 0.02$	$4.41\pm 0.22$	$18.67\pm 0.53$	$3.70\pm 0.18$	101	27
INEL		${\pi }^{+}$	$118\pm 5$	$0.35\pm 0.02$	$0.95\pm 0.02$	$4.40\pm 0.22$	$18.67\pm 0.53$	$3.69\pm 0.18$	131	27
CMS	900	${\pi }^{-}$	$118\pm 6$	$0.35\pm 0.02$	$0.91\pm 0.02$	$4.03\pm 0.20$	$18.87\pm 0.54$	$8.90\pm 0.44$	47	16
INEL		${\pi }^{+}$	$118\pm 5$	$0.35\pm 0.02$	$0.91\pm 0.02$	$4.00\pm 0.20$	$18.67\pm 0.55$	$9.03\pm 0.45$	43	16
	2760	${\pi }^{-}$	$122\pm 6$	$0.36\pm 0.02$	$0.89\pm 0.02$	$4.01\pm 0.18$	$18.80\pm 0.54$	$11.34\pm 0.57$	57	16
		${\pi }^{+}$	$122\pm 6$	$0.37\pm 0.02$	$0.89\pm 0.02$	$4.02\pm 0.18$	$18.57\pm 0.53$	$11.54\pm 0.58$	76	16
	7000	${\pi }^{-}$	$123\pm 6$	$0.38\pm 0.02$	$0.87\pm 0.02$	$4.03\pm 0.18$	$18.50\pm 0.52$	$14.50\pm 0.73$	73	16
		${\pi }^{+}$	$123\pm 6$	$0.38\pm 0.02$	$0.86\pm 0.02$	$4.03\pm 0.18$	$18.40\pm 0.52$	$14.66\pm 0.73$	90	16
	13000	${\pi }^{-}$	$126\pm 6$	$0.37\pm 0.02$	$0.83\pm 0.02$	$4.04\pm 0.19$	$18.30\pm 0.51$	$13.62\pm 0.68$	31	16
		${\pi }^{+}$	$126\pm 6$	$0.37\pm 0.02$	$0.83\pm 0.02$	$4.04\pm 0.19$	$18.30\pm 0.51$	$13.84\pm 0.69$	57	16

and

Table 4. Values of $T_0$, ${\beta }_T$, q, k, $p_0$, n, $N_0$, ${\chi }^2$, and ndof corresponding to the dashed (dot-dashed) curves for ${\pi }^{-}$ (${\pi }^{+}$) spectra in Figure 4, where Equation (8) through Equations (2) and (3) is used.

Collab.	$\sqrt{\mathit{s}}$ (GeV)	Part.	${\mathit{T}}_0$ (MeV)	${\mathit{\beta }}_{\mathit{T}}$ (c)	q	k	${\mathit{p}}_0$ (GeV/c)	n	${\mathit{N}}_0$	${\mathit{\chi }}^2$	ndof
NA61/	6.3	${\pi }^{-}$	$83\pm 5$	$0.24\pm 0.01$	$1.04\pm 0.01$	1	−	−	$0.09\pm 0.01$	11	14
SHINE	7.7	${\pi }^{-}$	$84\pm 5$	$0.25\pm 0.02$	$1.04\pm 0.01$	1	−	−	$0.10\pm 0.01$	8	14
INEL	8.8	${\pi }^{-}$	$84\pm 5$	$0.25\pm 0.01$	$1.04\pm 0.01$	1	−	−	$0.10\pm 0.01$	23	14
	12.3	${\pi }^{-}$	$85\pm 5$	$0.26\pm 0.01$	$1.05\pm 0.01$	1	−	−	$0.12\pm 0.01$	11	14
	17.3	${\pi }^{-}$	$86\pm 5$	$0.26\pm 0.01$	$1.05\pm 0.01$	1	−	−	$0.13\pm 0.01$	4	14
PHENIX	62.4	${\pi }^{-}$	$82\pm 4/88\pm 4$	$0.24\pm 0.01/0.27\pm 0.01$	$1.07\pm 0.01/1.05\pm 0.01$	$0.99\pm 0.01/0.99\pm 0.01$	$3.20\pm 0.19/3.19\pm 0.18$	$18.56\pm 0.51/18.56\pm 0.51$	$18.27\pm 0.91/19.18\pm 0.93$	33/39	18
INEL		${\pi }^{+}$	$82\pm 5/88\pm 4$	$0.24\pm 0.01/0.27\pm 0.01$	$1.07\pm 0.01/1.06\pm 0.01$	$0.99\pm 0.01/0.99\pm 0.01$	$3.20\pm 0.19/3.21\pm 0.18$	$18.56\pm 0.51/18.56\pm 0.51$	$17.19\pm 0.89/17.36\pm 0.90$	15/15	18
	200	${\pi }^{-}$	$83\pm 5/90\pm 4$	$0.25\pm 0.02/0.28\pm 0.01$	$1.07\pm 0.01/1.06\pm 0.01$	$0.99\pm 0.01/0.99\pm 0.01$	$3.99\pm 0.19/3.89\pm 0.19$	$18.06\pm 0.51/18.06\pm 0.51$	$23.21\pm 1.15/22.40\pm 1.10$	16/31	19
		${\pi }^{+}$	$83\pm 5/90\pm 4$	$0.25\pm 0.02/0.28\pm 0.01$	$1.07\pm 0.01/1.06\pm 0.01$	$0.99\pm 0.01/0.99\pm 0.01$	$4.09\pm 0.20/4.09\pm 0.20$	$18.01\pm 0.50/18.01\pm 0.51$	$23.00\pm 1.16/22.40\pm 1.14$	26/32	19
STAR	200	${\pi }^{-}$	$83\pm 5/89\pm 4$	$0.25\pm 0.01/0.28\pm 0.01$	$1.06\pm 0.01/1.04\pm 0.01$	1	−	−	$0.26\pm 0.01$	34	5
NSD		${\pi }^{+}$	$83\pm 5/89\pm 4$	$0.25\pm 0.01/0.28\pm 0.01$	$1.06\pm 0.01/1.04\pm 0.01$	1	−	−	$0.26\pm 0.01$	38	5
ALICE	900	${\pi }^{-}$	$84\pm 5/91\pm 4$	$0.26\pm 0.01/0.30\pm 0.01$	$1.06\pm 0.01/1.03\pm 0.01$	$0.94\pm 0.02/0.94\pm 0.02$	$4.11\pm 0.19/4.11\pm 0.19$	$17.99\pm 0.50/17.99\pm 0.50$	$0.59\pm 0.02/0.58\pm 0.02$	187/287	25
INEL		${\pi }^{+}$	$85\pm 4/91\pm 4$	$0.26\pm 0.01/0.30\pm 0.01$	$1.06\pm 0.01/1.03\pm 0.01$	$0.94\pm 0.02/0.94\pm 0.02$	$4.11\pm 0.20/4.11\pm 0.20$	$17.99\pm 0.40/17.99\pm 0.40$	$0.59\pm 0.02/0.58\pm 0.02$	232/333	25
CMS	900	${\pi }^{-}$	$87\pm 4/92\pm 4$	$0.27\pm 0.01/0.30\pm 0.01$	$1.05\pm 0.01/1.03\pm 0.01$	$0.88\pm 0.02/0.87\pm 0.02$	$3.85\pm 0.19/3.85\pm 0.19$	$18.40\pm 0.51/18.40\pm 0.51$	$1.43\pm 0.26/1.42\pm 0.27$	79/95	14
INEL		${\pi }^{+}$	$87\pm 4/93\pm 4$	$0.27\pm 0.01/0.30\pm 0.01$	$1.05\pm 0.01/1.03\pm 0.01$	$0.88\pm 0.02/0.86\pm 0.02$	$3.82\pm 0.19/3.82\pm 0.19$	$18.53\pm 0.51/18.53\pm 0.51$	$1.42\pm 0.25/1.42\pm 0.24$	70/72	14
	2760	${\pi }^{-}$	$91\pm 5/93\pm 5$	$0.30\pm 0.01/0.30\pm 0.02$	$1.04\pm 0.01/1.03\pm 0.01$	$0.83\pm 0.02/0.83\pm 0.02$	$3.92\pm 0.20/3.92\pm 0.20$	$18.43\pm 0.52/18.43\pm 0.52$	$1.67\pm 0.27/1.81\pm 0.27$	70/72	14
		${\pi }^{+}$	$92\pm 5/93\pm 5$	$0.30\pm 0.02/0.30\pm 0.02$	$1.04\pm 0.01/1.03\pm 0.01$	$0.84\pm 0.02/0.84\pm 0.02$	$3.92\pm 0.20/3.92\pm 0.20$	$18.43\pm 0.51/18.43\pm 0.51$	$1.83\pm 0.27/1.82\pm 0.26$	87/88	14
	7000	${\pi }^{-}$	$92\pm 4/94\pm 5$	$0.30\pm 0.02/0.31\pm 0.02$	$1.04\pm 0.01/1.03\pm 0.01$	$0.79\pm 0.02/0.81\pm 0.02$	$3.94\pm 0.19/3.94\pm 0.19$	$18.41\pm 0.50/18.41\pm 0.50$	$2.30\pm 0.32/2.30\pm 0.33$	68/69	14
		${\pi }^{+}$	$91\pm 4/94\pm 5$	$0.30\pm 0.01/0.31\pm 0.02$	$1.03\pm 0.01/1.03\pm 0.01$	$0.79\pm 0.02/0.81\pm 0.02$	$3.95\pm 0.20/3.95\pm 0.20$	$18.41\pm 0.50/18.41\pm 0.50$	$2.31\pm 0.33/2.30\pm 0.32$	87/92	14
	13000	${\pi }^{-}$	$91\pm 5/95\pm 5$	$0.30\pm 0.01/0.31\pm 0.02$	$1.04\pm 0.01/1.02\pm 0.01$	$0.81\pm 0.02/0.80\pm 0.02$	$3.96\pm 0.19/3.96\pm 0.19$	$18.31\pm 0.41/18.31\pm 0.41$	$2.19\pm 0.39/2.17\pm 0.38$	34/39	14
		${\pi }^{+}$	$91\pm 5/95\pm 5$	$0.30\pm 0.01/0.31\pm 0.02$	$1.03\pm 0.01/1.02\pm 0.01$	$0.78\pm 0.02/0.79\pm 0.02$	$3.96\pm 0.19/3.96\pm 0.19$	$18.31\pm 0.41/18.31\pm 0.41$	$2.18\pm 0.38/2.17\pm 0.36$	56/59	14

which are the same as Table 1 and Table 2 respectively, and with only one set of parameter values in Table 3. The related parameters are shown in Figure 5 and the leading-out parameters are shown in Figure 6, which are the same as Figure 2 and Figure 3 respectively, and with only one set of parameter values for Equation (8) through Equations (1) and (3). In particular, k in Figure 5 is obtained by $k={\int }_0^{p_1}{A}_1{f}_S\left(p_T\right)d{p}_T$ due to $f_0\left(p_T\right)$ is normalized to 1, as discussed following Equation (8). The lines in Figure 6a,b are fitted by linear functions

$$\begin{array}{c}\hfill \langle p_T\rangle =(0.318\pm 0.004)+(0.010\pm 0.001)ln\sqrt{s}\end{array}$$

(12)

and

$$\begin{array}{c}\hfill \langle p_T\rangle =(0.307\pm 0.005)+(0.017\pm 0.001)ln\sqrt{s}\end{array}$$

(13)

with ${\chi }^2$/ndof = 55/61 and 28/61 respectively, though the linear relationships between the parameters and $ln\sqrt{s}$ may be not the best fitting functions. Similar to Figure 2 and Figure 3, the results for $AA$ collisions from Equation (8) are also presented in Figure 5 and Figure 6 for comparisons. One can see the similarity in both $pp$ and $AA$ collisions in the considered energy range.

From Figure 4 one can see that Equation (8) fits similarly good the data as Equation (7). Because of the data being not available in very-low $p_T$ range, Equation (10) is not used in the fit. $T_0$ and ${\beta }_T$ in Figure 5 increase slightly from a few GeV to above 10 TeV with some fluctuations in some cases, which is partly similar to those in Figure 2. Other parameters in Figure 5 show somehow similar trends toFigure 2 with some differences. The left panels in Figure 3 and Figure 6 are different due to the first component being in different superpositions. The right panels in Figure 3 and Figure 6 are very similar to each other due to the same data sets being fitted. We would like to point out that Figure 1 and Figure 4 present various cases which are displayed together and result in Figure 2 and Figure 3 as well as Figure 5 and Figure 6 depicting much more data in which some energy points are taken from Figure A1 and Figure A2 in the Appendix A.

Before continuing this work, we would like to point out the justification and correctness for the comparisons of $pp$ and central $AA$ collisions in Figure 2, Figure 3, Figure 5 and Figure 6. No matter peripheral or central $AA$ collisions, a set of nucleon-nucleon collisions in participant region are similar to the minimum-bias $pp$ collisions. Peripheral $AA$ collisions are similar to central collisions with smaller projectile and target nuclei, while central $AA$ collisions are just central collisions with large nuclei. Because of collision energies considered in this work are high, the nucleon-nucleon correlation, cluster structure, medium effect, and other nuclear effects in participant region can be neglected. Meanwhile, the cold nuclear or spectator effect in non-central $AA$ collisions can be neglected, too. In our opinion, we may compare the minimum-bias $pp$ collisions with the $AA$ collisions in any centrality class.

Combining with our recent work [62], it is shown the similarity in $pp$ and $AA$ collisions, though $AA$ collisions appear larger $T_0$, ${\beta }_T$, $\langle p_T\rangle$, and $T_i$ in most cases. Moreover, it is well seen that Tsallis does not distinguish well between the data in $pp$ and $AA$ collisions [63,64,65]. Indeed, at high energy, both $pp$ and $AA$ collisions produce many particles and obey statistical law. In addition, $pp$ collisions are the basic sub-process in $AA$ collisions. It is natural that $pp$ and $AA$ collisions show similar law. However, concerning around 10–20 GeV change, this is expected as soon as QCD effects/calculations may not be directly applicable below this point, plus seem to be smoothed away by other processes in $AA$ collisions. This is well visible as a clear difference as shown in [63,64,65], where the data in $pp$ collisions goes well with the data in electron-positron collisions, while the data in $AA$ collisions are different.

The differences between Equations (7) and (8) are obviously, though the similar components are used in them. In our recent works [18,66], Equations (7) and (8) are used respectively. Although there is correlation in the extraction of parameters, a smooth curve can be easily obtained by Equation (7). Although it is not easy to obtain a smooth curve at the point of junction, there is no or less correlation in the extraction of parameters by Equation (8). In consideration of obtaining a set of parameters with least correlation, we are inclined to use Equation (8) to extract the related parameters. This inclining results in Equation (8) to separate determinedly the contributions of soft and hard processes.

It should be noted that the system of $pp$ collisions at low energy is probably not in thermal equilibrium or local thermal equilibriums due to low multiplicity, which is not the case of the present work. In fact, the present work treats $pp$ collisions at high energies in which the multiplicities in most cases are not too low. In addition, related review work [67] shows that small system also appears similar collective behavior to $AA$ collisions. This renders that the idea of local thermal equilibrium is suitable to high energy $pp$ collisions for which the blast-wave fit can be used, though QGP is not expected to form in minimum-bias events.

Although we have used the blast-wave fit in the superposition function with two components in which the second component is an inverse power-law, the blast-wave part is not necessary for fitting process itself. In fact, the superposition of (two-)Boltzmann (or Tsallis) distribution and inverse power-law can fit the data in most cases [30,31,65]. In particular, in our very recent work [68], we used the Tsallis–Pareto-type function [28,69,70] to fit $p_T$ spectra in a wide range, in which there is no boosted part. The merits of the boosted part are that some additional quantities such as $T_0$ and ${\beta }_T$ can be obtained and physics picture is more abundant.

To avoid the dependences of $T_0$ and ${\beta }_T$ on fits or models, one can use $\langle p_T\rangle$ to describe synchronously $T_0$ and ${\beta }_T$. Generally, $\langle p_T\rangle$ is independent of fits or models, though it can be calculated from fits or models. Averagely, the contribution of one participant in each binary collisions is $\langle p_T\rangle /2$ which is resulted from both the thermal motion and flow effect. Let $k_0$ denote the contribution fraction of thermal motion. The contribution fraction of flow effect is naturally $1-k_0$. Thus, we define $T_0=k_0\langle p_T\rangle /2$ and ${\beta }_T=(1-k_0)\langle p_T\rangle /2m_0\overline{\gamma }$. As a free parameter, $k_0$ depends on collision energy, which is needed to study further.

3.3. More Discussions

Before summary and conclusions, we would like to underline the preponderance of the present work. Comparing with PYTHIA or other perturbative QCD simulation tools [71,72,73,74], the present work is simpler and more applicative in obtaining the excitation functions of $T_0$ and ${\beta }_T$, though the usual fitting method is used. In a recent work [75], it was pointed out that the PYTHIA Monte Carlo [71,72] disagrees with some data, and the two-component (soft+hard) model describes the data accurately and comprehensively, though the two-component model used in [75] is different from the fit used in the present work. In addition, the present work is a data-driven reanalysis based on some physics considerations, but not a simple fit to the data. From the data-driven reanalysis, the excitation functions of some quantities have been obtained.

From the excitation functions, one can see some complex structures which are useful to study the properties of particle production and system evolution at different energies. In particular, in the energy range around 10 GeV, the excitation functions have transition which implies the phase of interaction matter had changed. In addition, by using the two-component fit, the present work also presents a new method to extract the contribution fraction of hard component. One can see that this contribution fraction is 0 in the energy range around 10 GeV. This implies that the interactions in the energy range around 10 GeV have only soft component, and that above 10 GeV have both soft and hard components. The interaction mechanisms in the two energy ranges are different.

We would like to emphasize that the aim of the present work is to look for possible signatures of a transition from baryon-dominated to meson-dominated hadron production mechanism by fitting pion $p_T$ spectra at mid-(pseudo)rapidity in $pp$ collisions which also show collective phenomenon [67]. The main conclusion regards a possible indication of such an effect at about 10–20 GeV visible in a drop of the temperature extracted using a blast-wave model with Boltzmann distribution to model the soft excitation mode. Such a conclusion seems not straightforward since the results are strongly biased by different $p_{Tmax}$ used to fit data at different energies. In fact, the results are less affected by $p_{Tmax}$ due to the fact that the parameters are mainly determined by the spectra in low and intermediate $p_T$ regions. Larger $p_{Tmax}$ does not change the trend of inverse power-law, which does not affect obviously the parameters. Although $p_{Tmax}$ has no obvious influence on the parameters, we have used $p_{Tmax}=5$ Gev/c in our calculation.

It should be noted that the blast-wave analysis is known to be sensitive to the selected $p_T$ range in the case of using a not too wide and local one such as 1–2 GeV/c. To avoid this dependence, we have used a wide enough $p_T$ range from 0 to a large value, but not a narrow and local one. In addition, looking at the fit results when using a Tsallis function to describe soft excitation processes such a drop in the k-parameter is no longer visible which seems to mean that the fit is less sensitive to the hard component and also less sensitive to $p_{Tmax}$. Using the Tsallis function assumption also the drop in the temperature is no longer visible which means that the effect on the temperature seen with the Boltzmann assumption seems to be model dependent. In fact, the parameters discussed in the present work are indeed model dependent. We hope to extract model independent parameters in the near future. Our definition $T_0=k_0\langle p_T\rangle /2$ and ${\beta }_T=(1-k_0)\langle p_T\rangle /2m_0\overline{\gamma }$ are a possible choice for the model independent parameters.

On the other hand, although comparing Boltzmann with Tsallis is an interesting physical problem, which could not be understood without another comparison with the generic super-statistics, as the one implemented in particle productions [76,77,78,79]. The latter—in contrary to Boltzmann and Tsallis—lets the system alone judge about its statistical nature, whether extensive or non-extensive (equilibrium or non-equilibrium). As pointed out in [76,77,78,79], the particle production at BES energies is likely a non-extensive process but not necessarily Boltzmann or Tsallis type. Indeed, further study on particle production in high energy collisions is needed in the future.

In particular, larger $T_0$ means higher excitation degree and shorter lifetime of the fireball formed in high energy collisions. At the LHC energy, the fireball should have higher excitation degree comparing with that at the top RHIC energy, though longer lifetime is possible at the LHC energy [55,80]. As a result of competition between excitation degree and lifetime, $T_0$ shows the trend of increase with energy in the present work. Meanwhile, our result on larger ${\beta }_T$ means quicker expansion at the LHC energy. These trends are harmonious with those of $\langle p_T\rangle$ and $T_i$ as well as other method such as the alternative method [16,18,66] by which $T_0$ and ${\beta }_T$ are also obtained.

4. Summary and Conclusions

The transverse momentum spectra of ${\pi }^{-}$ and ${\pi }^{+}$ produced at mid-(pseudo)rapidity in $pp$ collisions over an energy range from a few GeV to above 10 TeV have been analyzed by the superposition of the blast-wave fit with Boltzmann distribution or with Tsallis distribution and the inverse power-law (Hagedorn function). The fit results are well fitting to the experimental data of NA61/SHINE, PHENIX, STAR, ALICE, and CMS Collaborations. The values of related parameters are extracted from the fit process and the excitation functions of parameters are obtained.

In the particular superposition Equation (7) and with a given selection, both excitation functions of $T_0$ and ${\beta }_T$ obtained from the blast-wave fit with Boltzmann distribution show a hill at $\sqrt{s}\approx 10$ GeV, a drop at dozens of GeV, and an increase from dozens of GeV to above 10 TeV. The mentioned two excitation functions obtained from the blast-wave fit with Tsallis distribution does not show such a complex structure, but a very low hill. In another selection for the parameters in Equation (7) or in the superposition Equation (8), $T_0$ and ${\beta }_T$ increase generally quickly from a few GeV to about 10 GeV and then slightly at above 10 GeV. There is no the complex structure, too. In both superpositions, the excitation function of $p_0$ (n) shows a slight decrease (increase) in the case of the hard component being available. From the RHIC to LHC, there is a positive (negative) correlation between $T_0$ and ${\beta }_T$ ($p_0$ and n). The contribution of hard component slightly increases from dozens of GeV to above 10 TeV, and it has no contribution at around 10 GeV.

In the case of considering the two components together, the mean transverse momentum and the initial temperature increase obviously with the increase of logarithmic collision energy in the considered energy range. From a few GeV to above 10 TeV, the collision system takes place possibly a transition at around 10 GeV, where the transition from a baryon-dominated to a meson-dominated final state takes place. No matter what a structure appears, the energy range around 10 GeV is a special one due to the slope of $T_0$ excitation function having large variation. Indeed, the mentioned energy range is needed further study in the future.