Hypothesis about Enrichment of Solar System
Abstract
:1. Introduction
2. Problem Definition and Proposed Solution
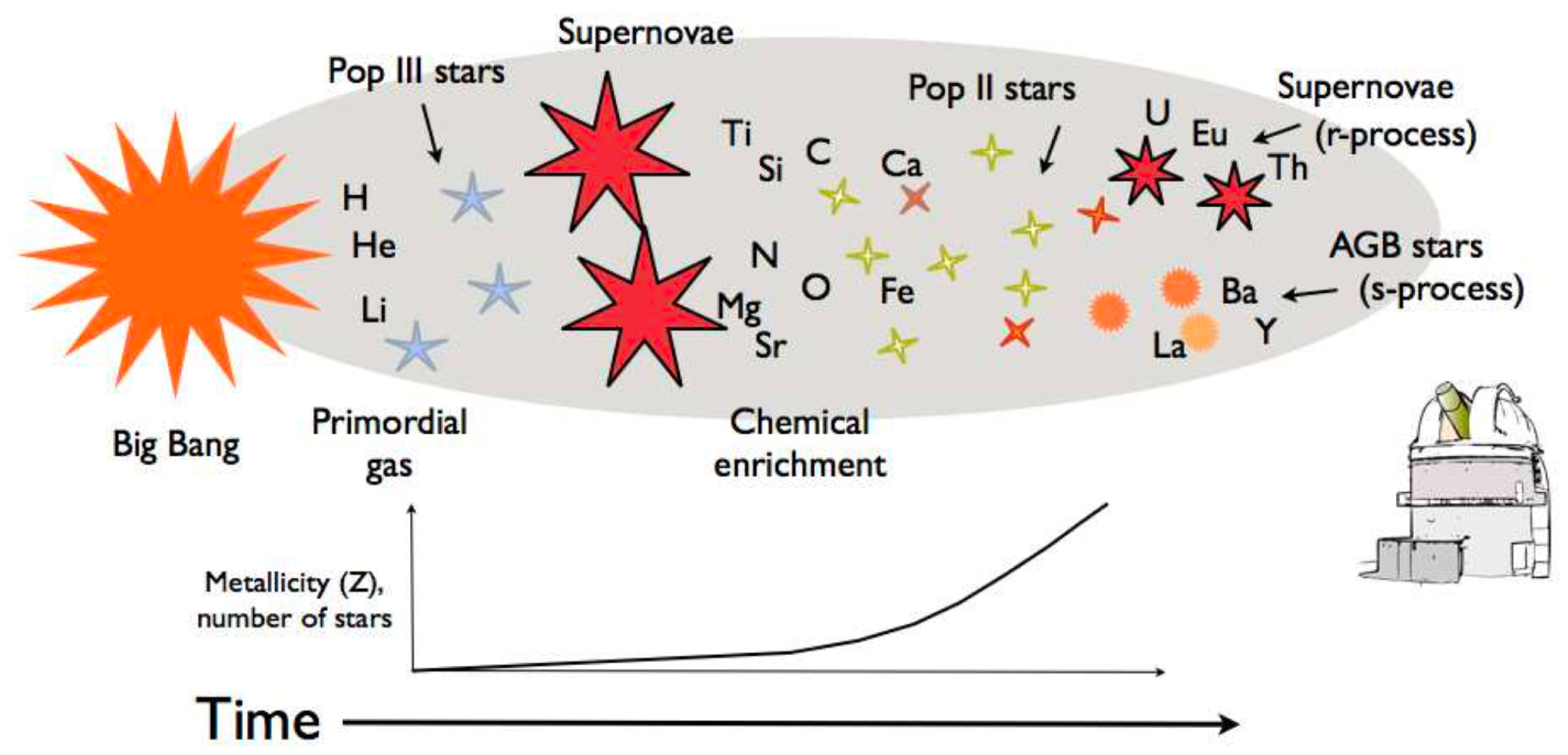
2.1. Galactic Nucleogenesis
2.2. Challenges in Understanding of Origins of Solar System Isotopes
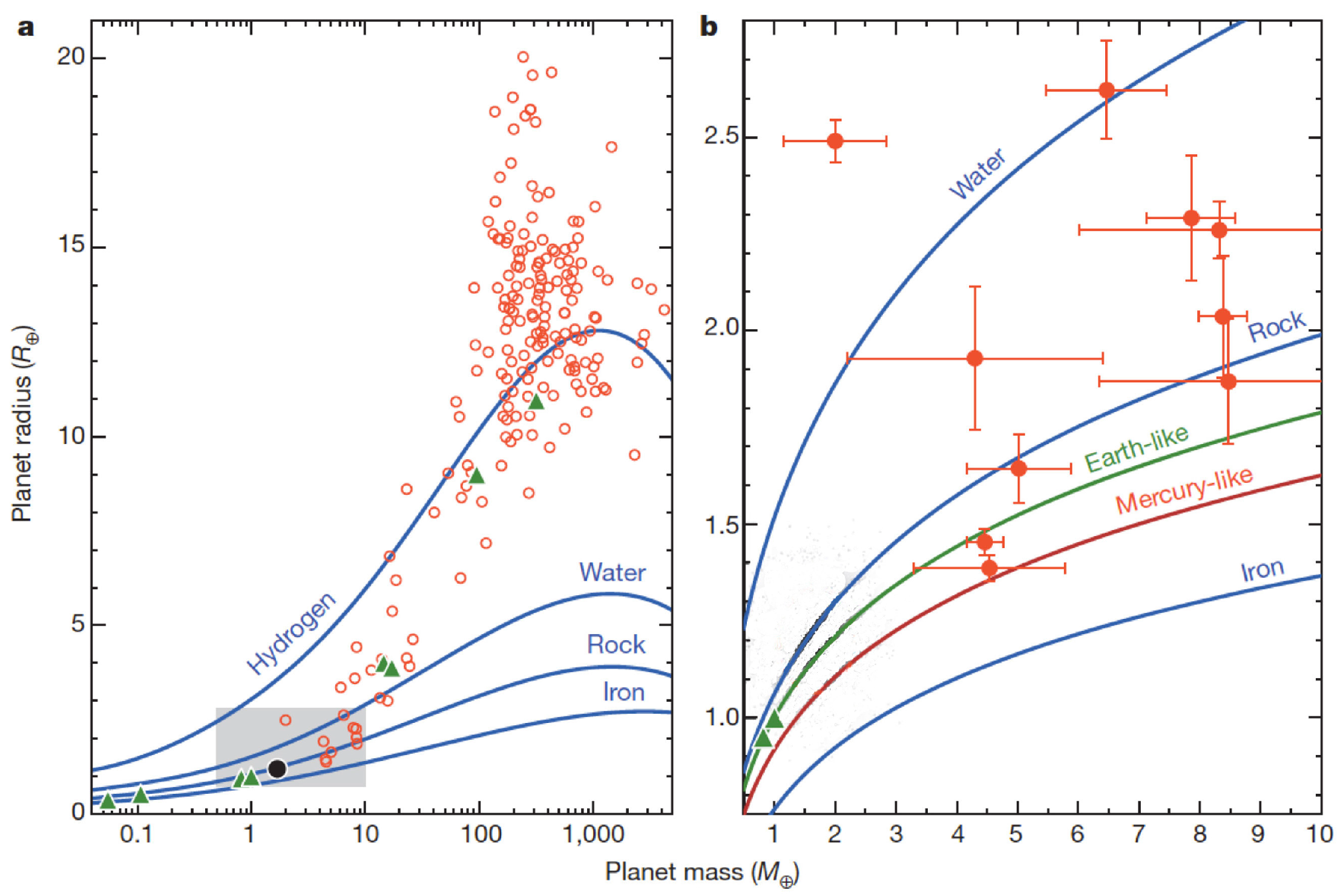
2.3. Challenges in Understanding of Planetary Structure of Solar System
2.4. Summary of Proposed Hypothesis (Nuclear-Fission “Event” within Solar System)
3. Key Physical Processes
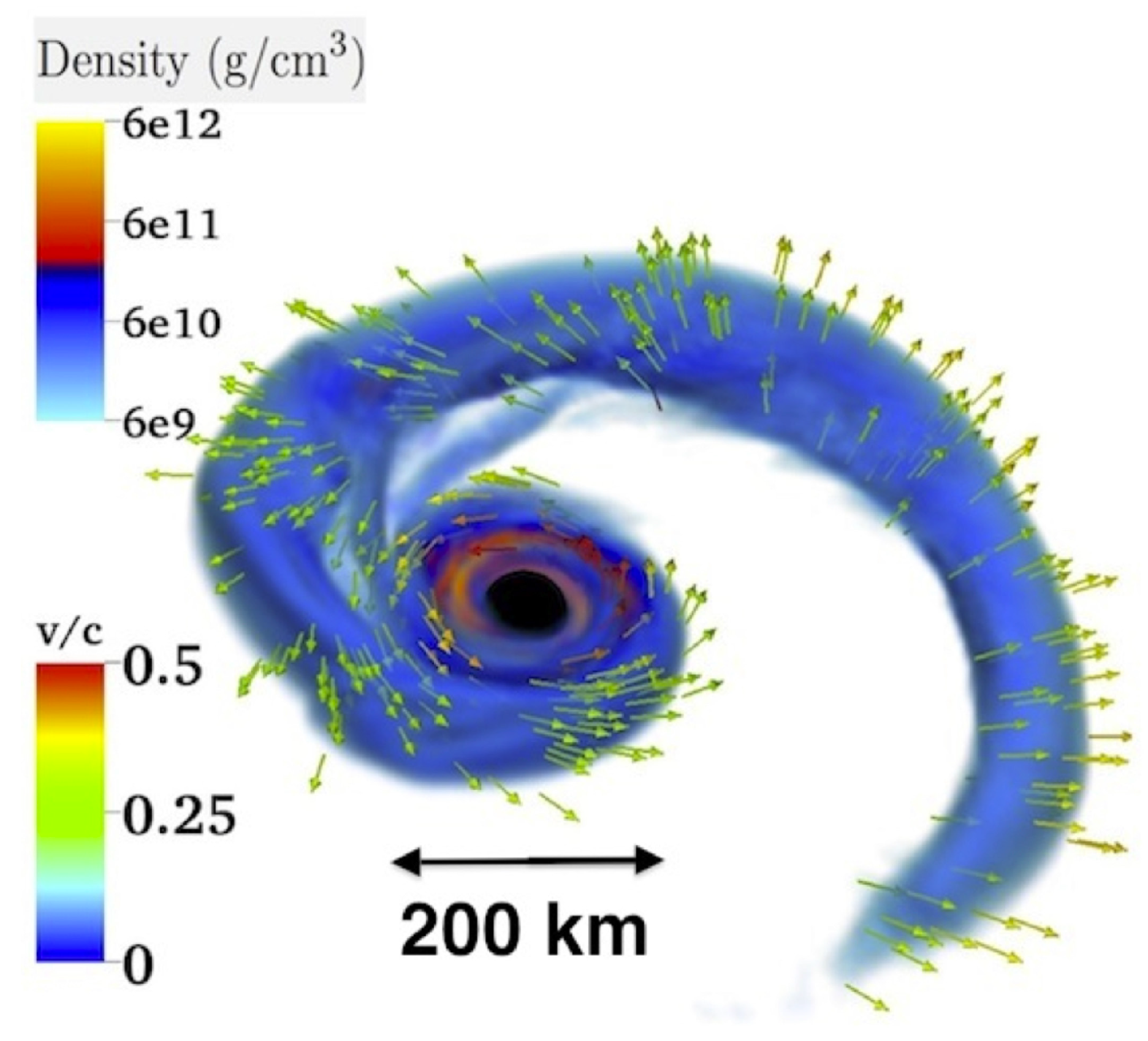
3.1. Nuclear-Fission-Capable Object of Galactic Origin
3.1.1. Compact Super-Dense Stellar Fragment
3.1.2. Instability of Nuclear Matter: Nuclear Fog
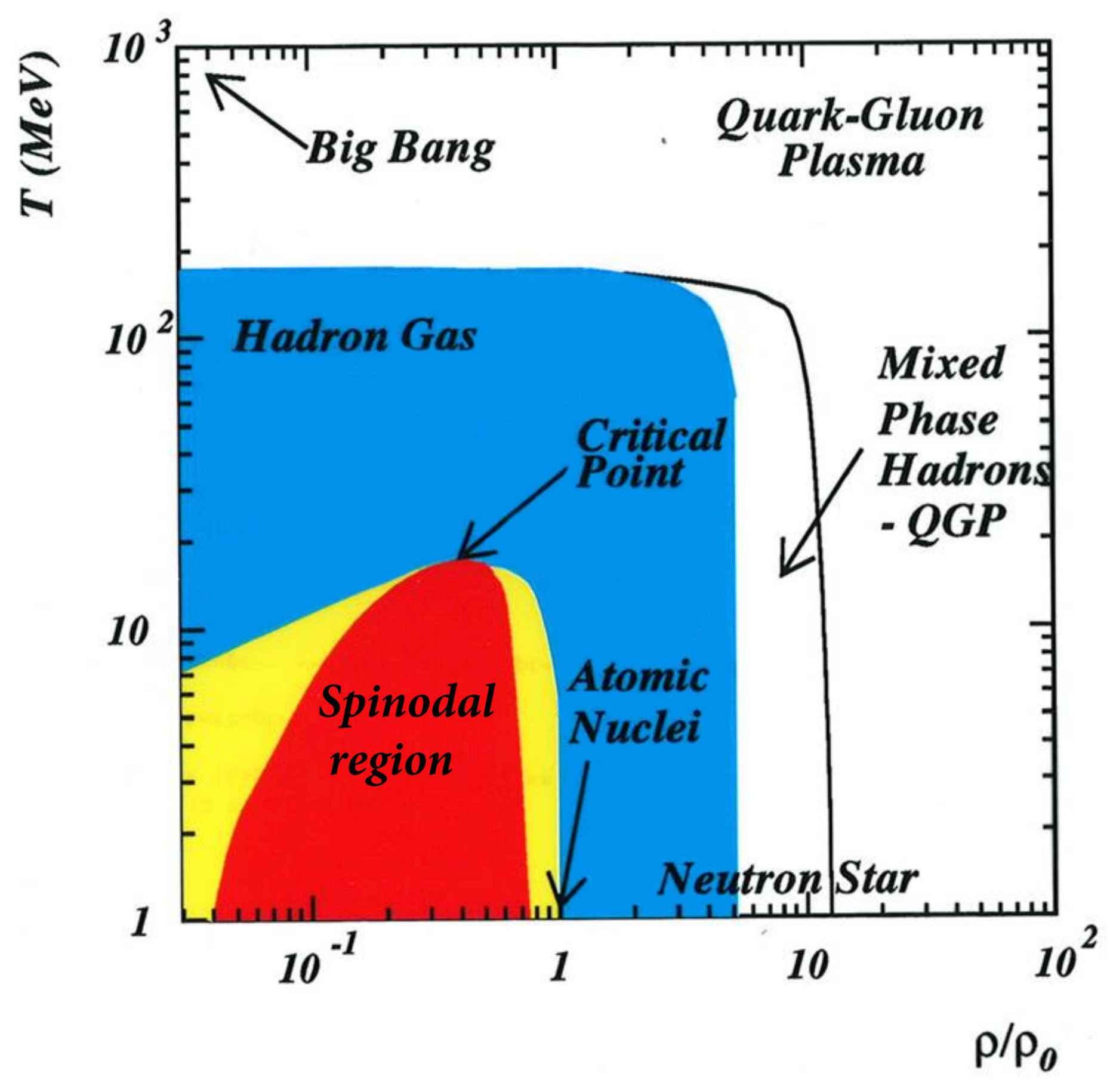
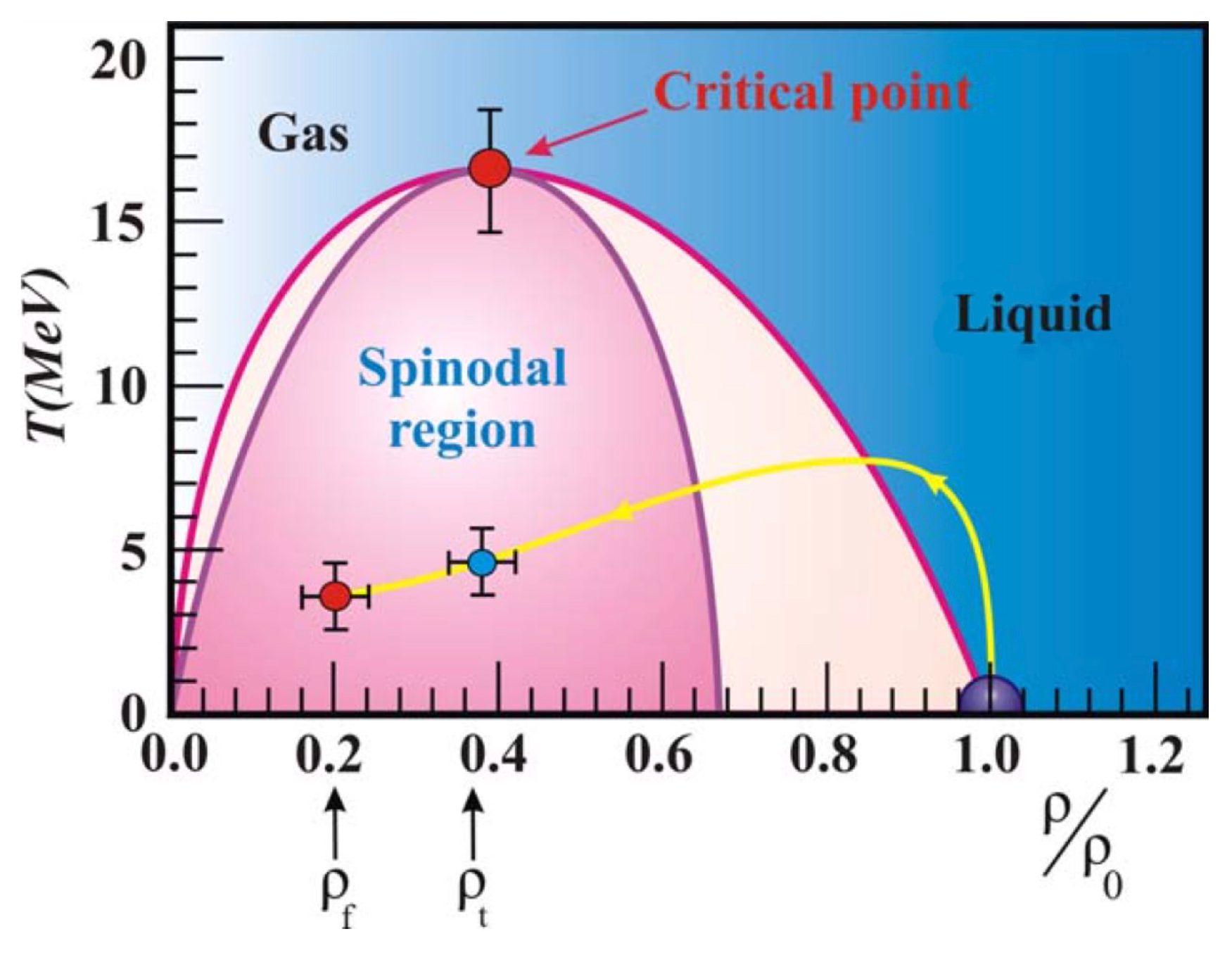
Mixed-Phase (Nuclear Fog) and Spinodal Zones
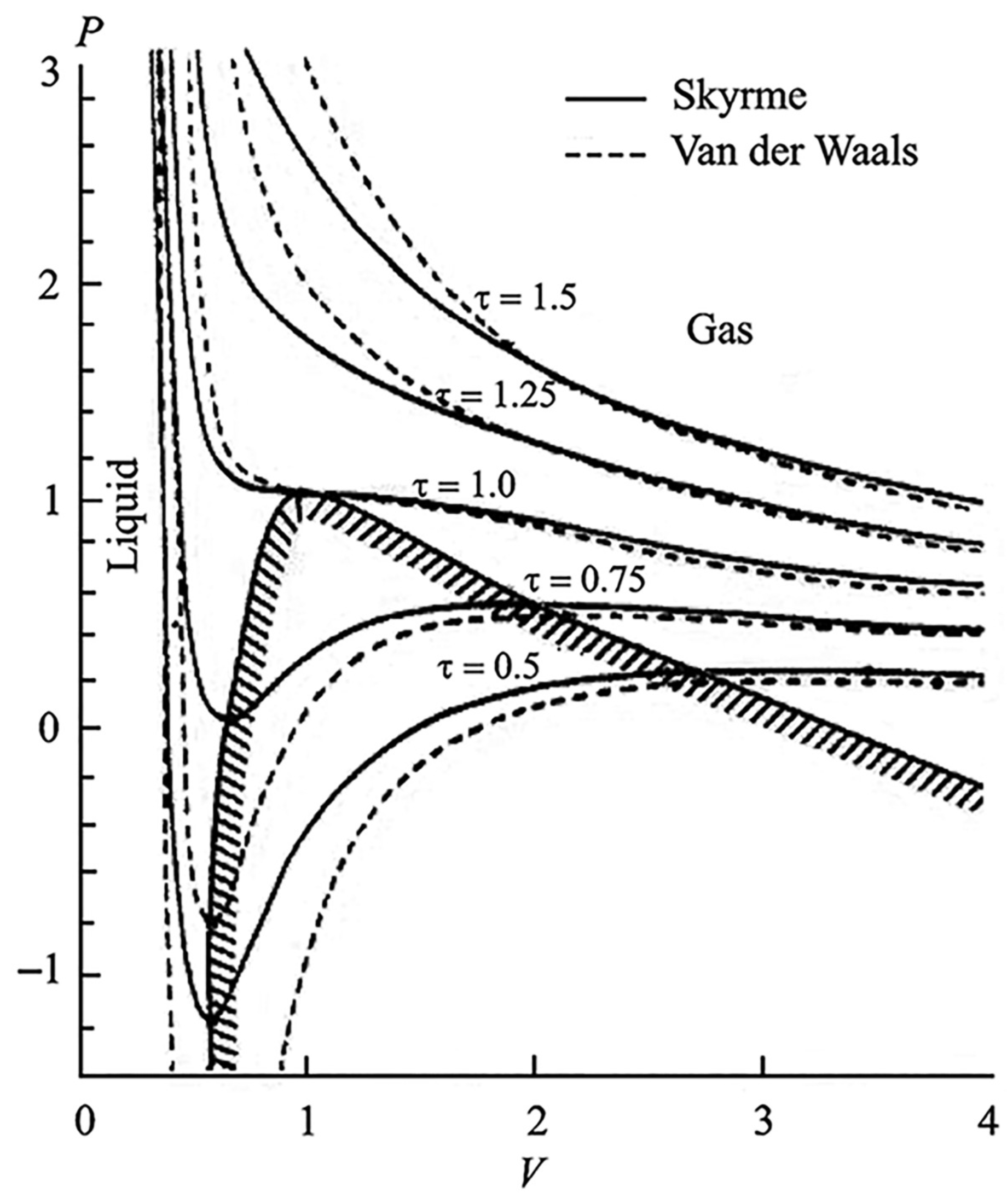
EOS for Nuclear Matter Permitting Nuclear Fog
Decompression of Nuclear Matter
3.2. Nuclear-Fission-Trigger (Perturbation Due to Encounter with “Obstacle”)
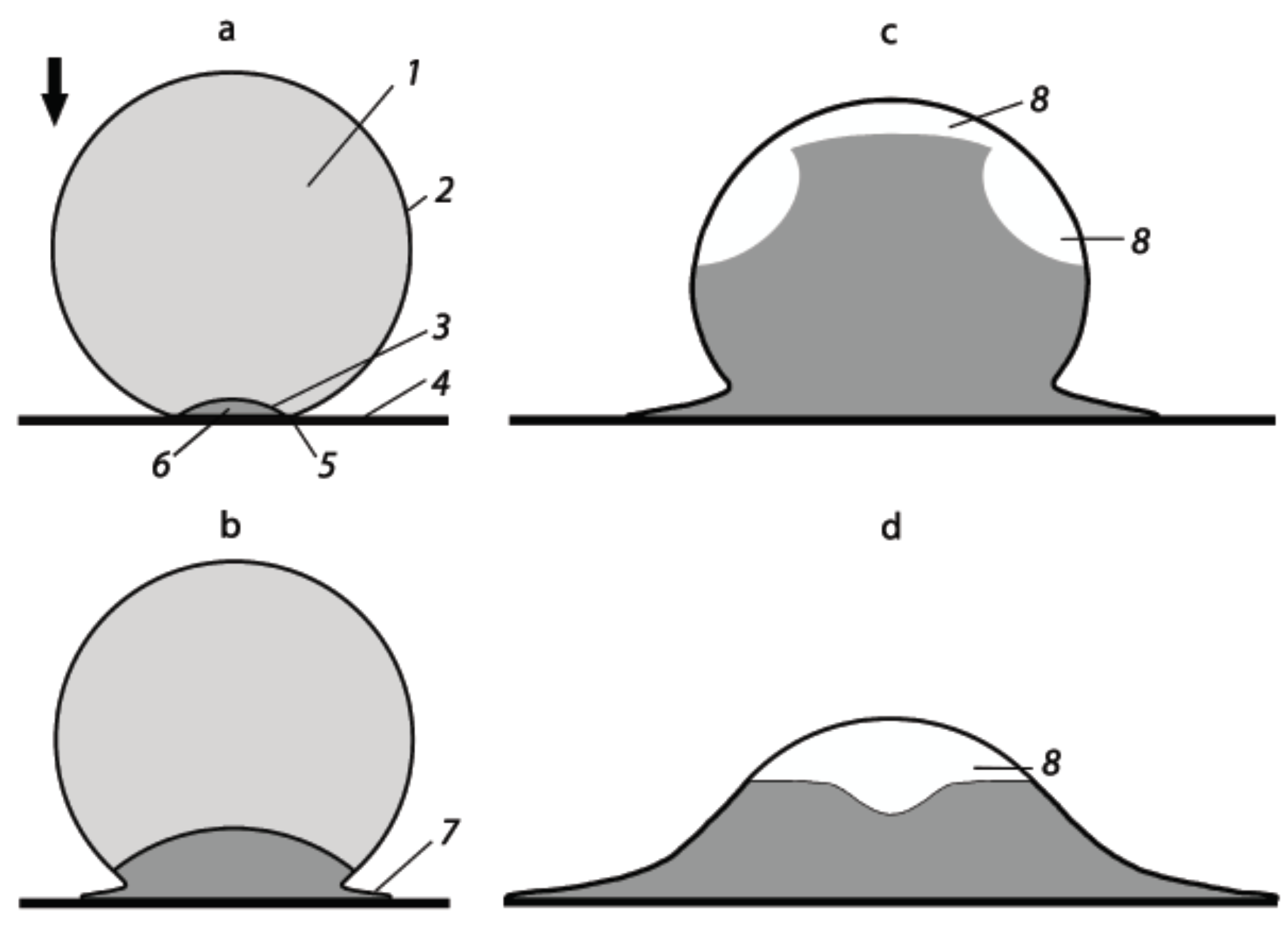
3.2.1. Effect of Deceleration
3.2.2. Compression/Decompression
3.3. Nuclear-Fission-Driven Nucleogenesis
3.3.1. Evolution Equations
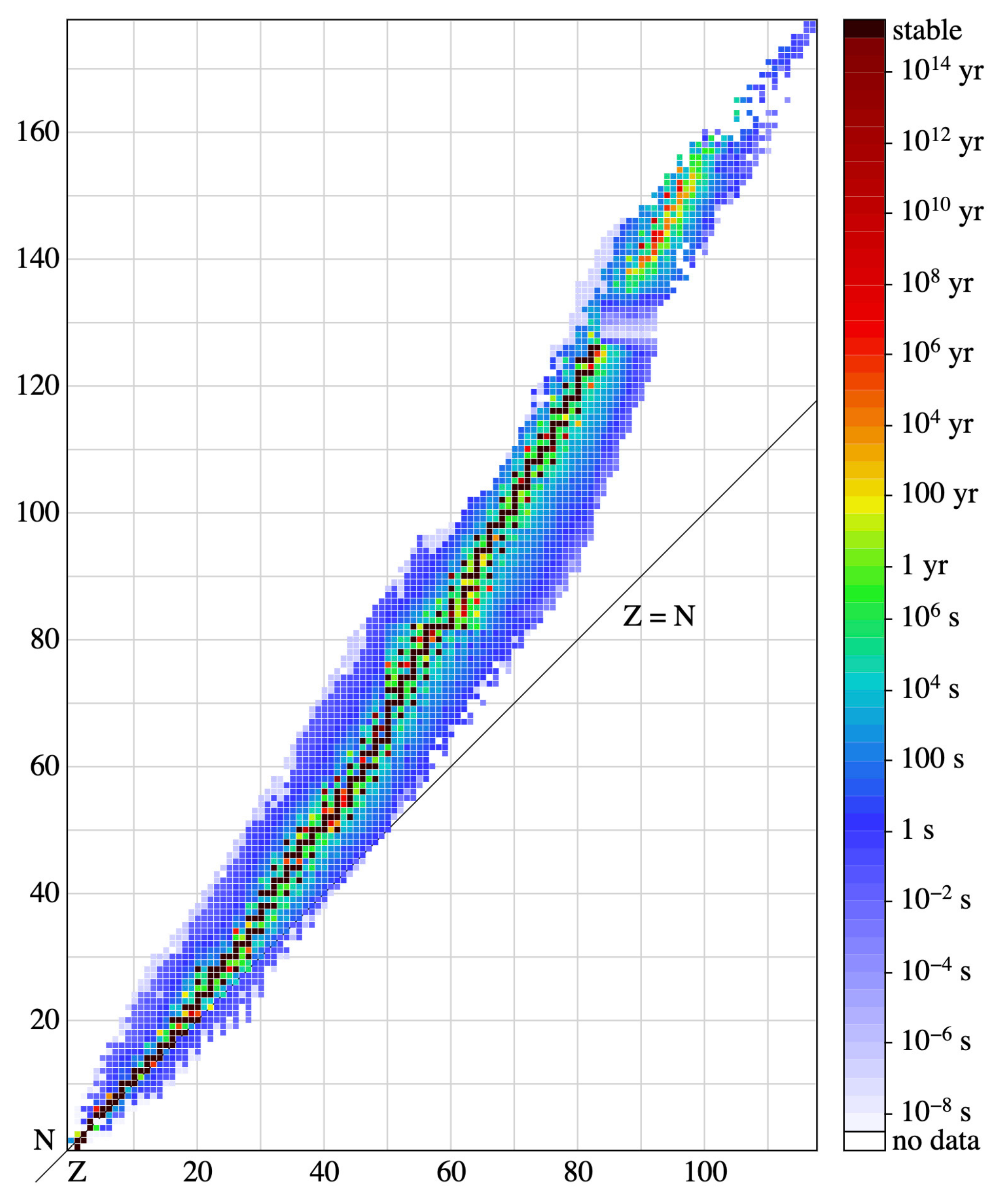
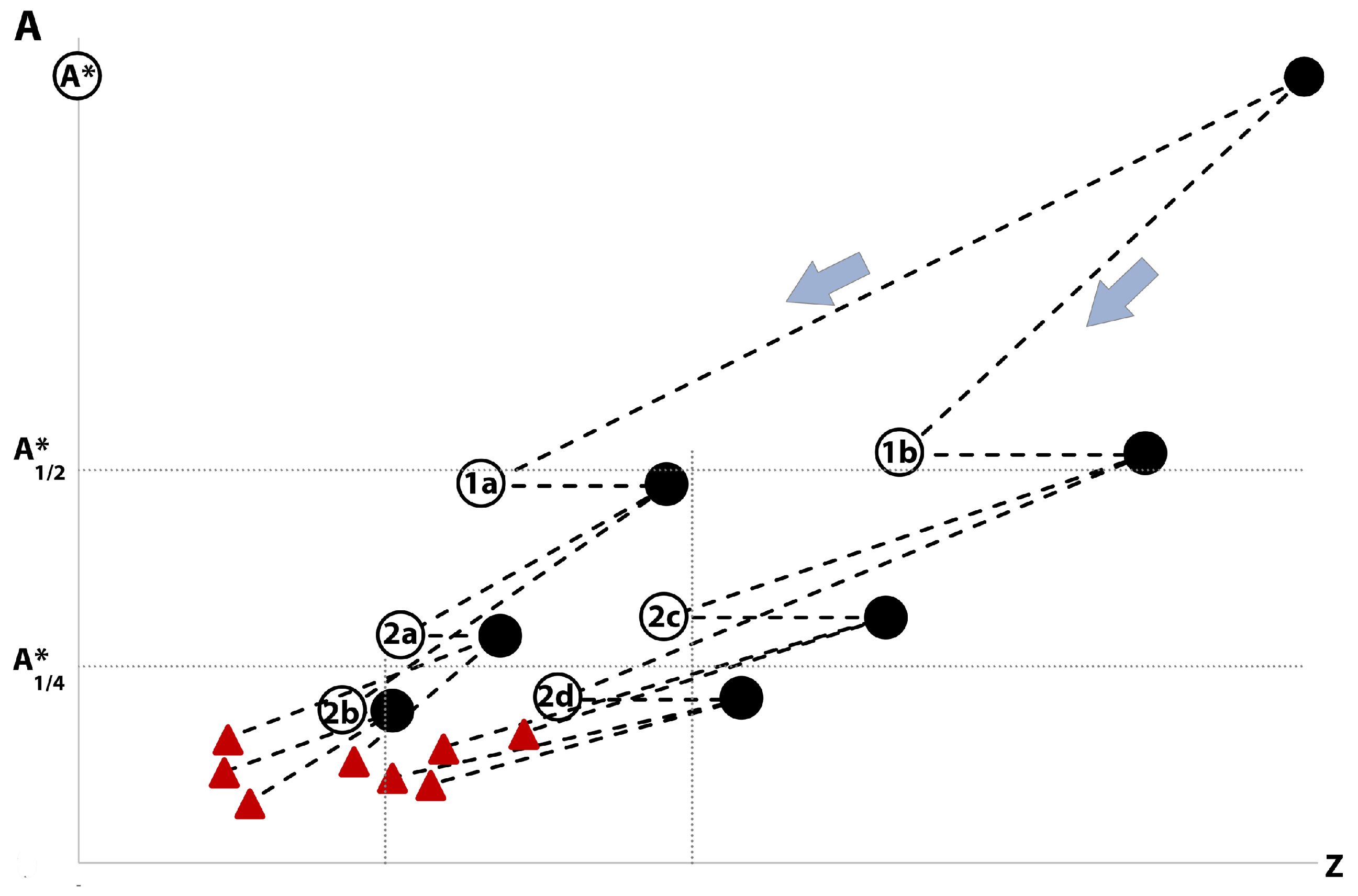
3.3.2. Fission of Super-Heavy Nuclei
3.3.3. Nucleogenetic Cascades
- The (quasi-stable) compact stellar object (a giant-nuclear-drop) (outlined in Section 3.1 and modeled below in Section 4.1) becomes thermodynamically destabilized and thus localized decompression takes place in its interior.
- As the result of decompression, the matter enters the state of nuclear-fog (i.e., charged nuclear-fog-droplets form).
- As known from experiments on heavy-nuclei collisions, the nuclear-fog-droplets fragment further into multiple mini-droplets (mega-nuclei):«The classical fog is unstable substance, which transforms finally into liquid “sea” with “atmosphere” of the saturated vapor. The nuclear, charged fog is stable in respect to such fortune. But it “explodes” because of the Coulomb repulsion. This event is detected as multifragmentation.»[90]It is the evolution of these unstable, short-living, mega-nuclei which is discussed in this section. This evolution eventually leads to nucleogenesis of various unstable and finally stable nuclides (isotopes of chemical elements).
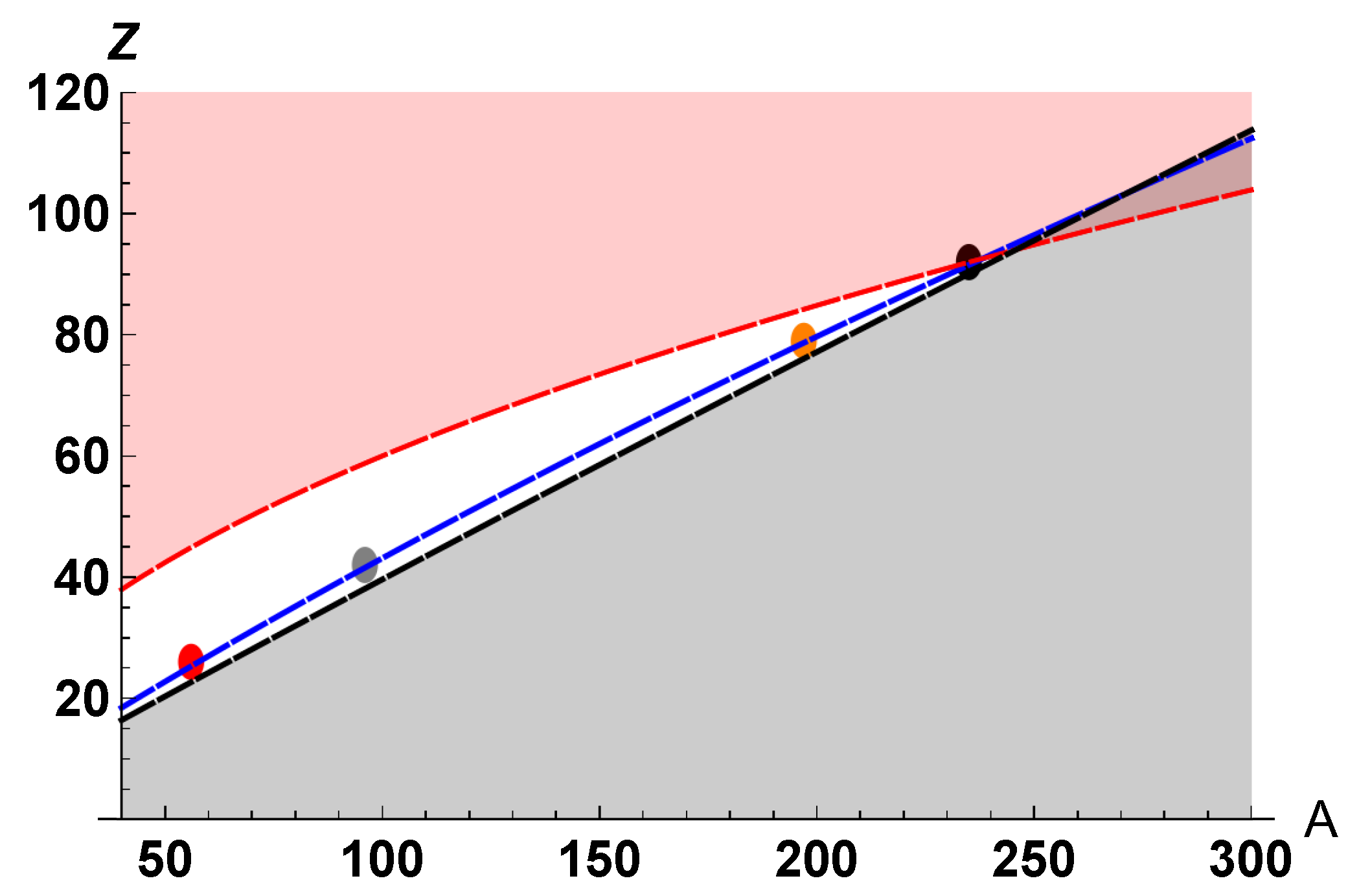
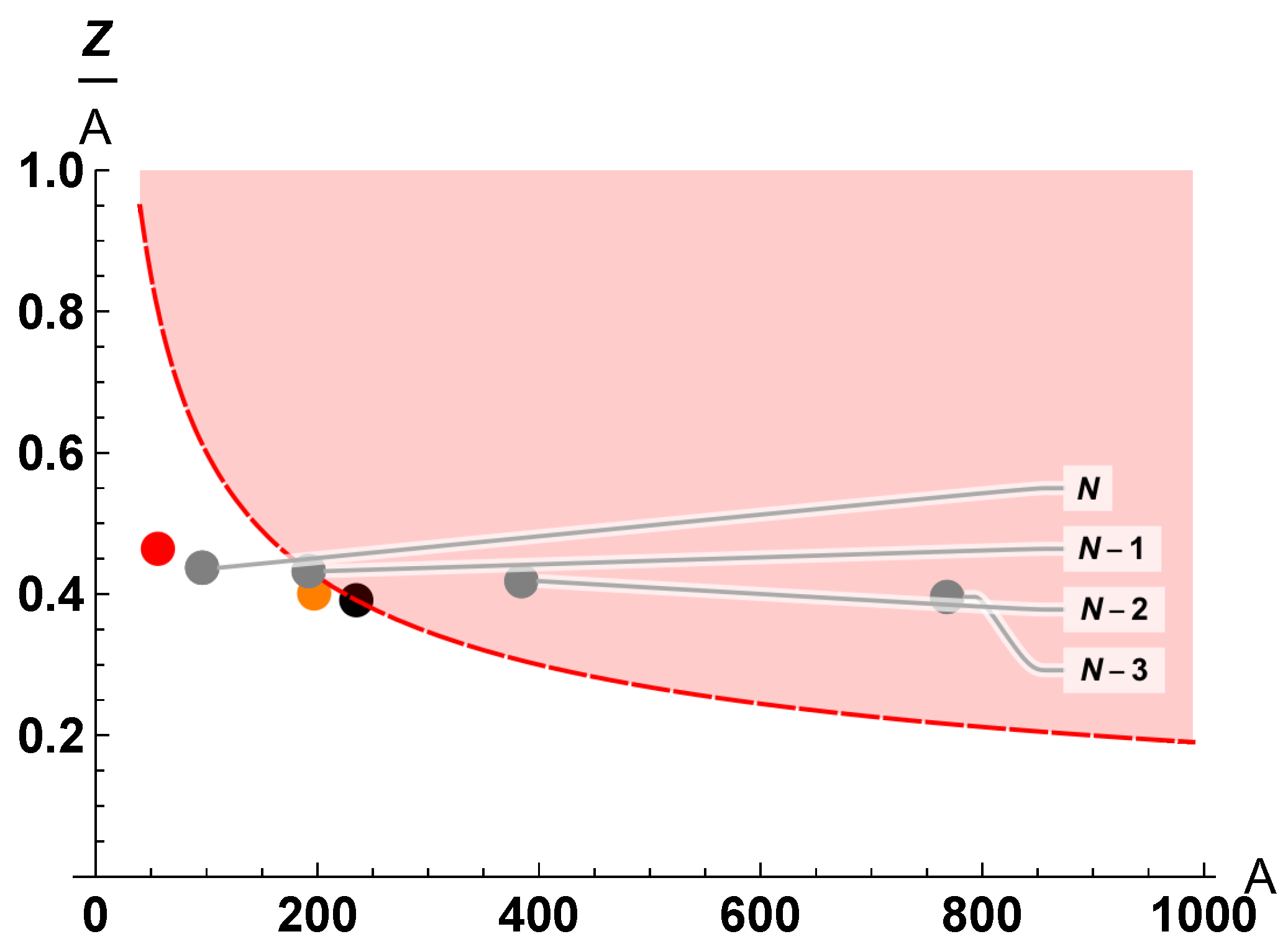
- As reminded earlier, in the framework of the proposed hypothesis, the giant-nuclear-drop (stellar object) became thermodynamically destabilized, experienced localized decompression, where (charged) nuclear-fog-droplets (“nfd”) formed. These droplets underwent multi-fragmentation (each ) into (charged) initial mega-nuclei whose size-distribution is broad and unpredictable. For these mega-nuclei ∼0 but . No initial are pictured in Figure 11.
- For these initial mega-nuclei (which could be depicted below n-line and -line, close to A-axis) n- and -decays are permitted. Therefore, below red f-line each mega-nucleus sheds neutrons and electrons—its rises—such evolution follows some seemingly-smooth (in log-scale) non-jumping line (not plotted). If red f-line is never reached, the nucleus evolves within the purple zone until it reaches the valley-of-stability (its neutron-rich “lower ” side).
- When increase is sufficient to reach red f-line, then fission-process starts (see the start of the lower dotted path, for example; only one daughter-nucleus of each generation is depicted as one gray dot). During the fission process, the system transitions from state k to state according to its evolution equation, the general form of which may be written as:Generally speaking, the structure of multiplication factor for mega A is unknown, but obviously the function is stochastic and it conforms to certain internal symmetries. In our scenario, this function can be written asIt is determined by the amounts of emitted neutrons and emitted electrons , which follows from the obvious definition: . The physical meaning lies not in the absolute values of quantities and , which are obviously positive, but in the ratios and the combination. Functions and are random. For example, as mentioned, experimentally-measured in one fission event of may vary from 1 to 8, yielding the multi-event average of 2.2. Therefore, due to this randomness, the system (from a state located on the red f-line) may jump into the red zone, slide along the red f-line, or return into the no-fission zone (below red f-line). The final decisive judgment about these paths and their choice, belongs to experimental studies. Figure 11 shows 3 possibilities where the system continues within the red zone once fission starts. The upper jump-path is for the case when the system evolves in the fission-zone. The middle jump-path is when the system can also have intensive neutron-losses. The lower jump-path is when an additional channel opens—beta-emission. The idea of the evolution equation in the form Equation (12) originated historically in exploration of processes of neutron-multiplication in nuclear-reactors and related applications.
4. Model and Results
4.1. Model of Fission-Capable Stellar Fragment
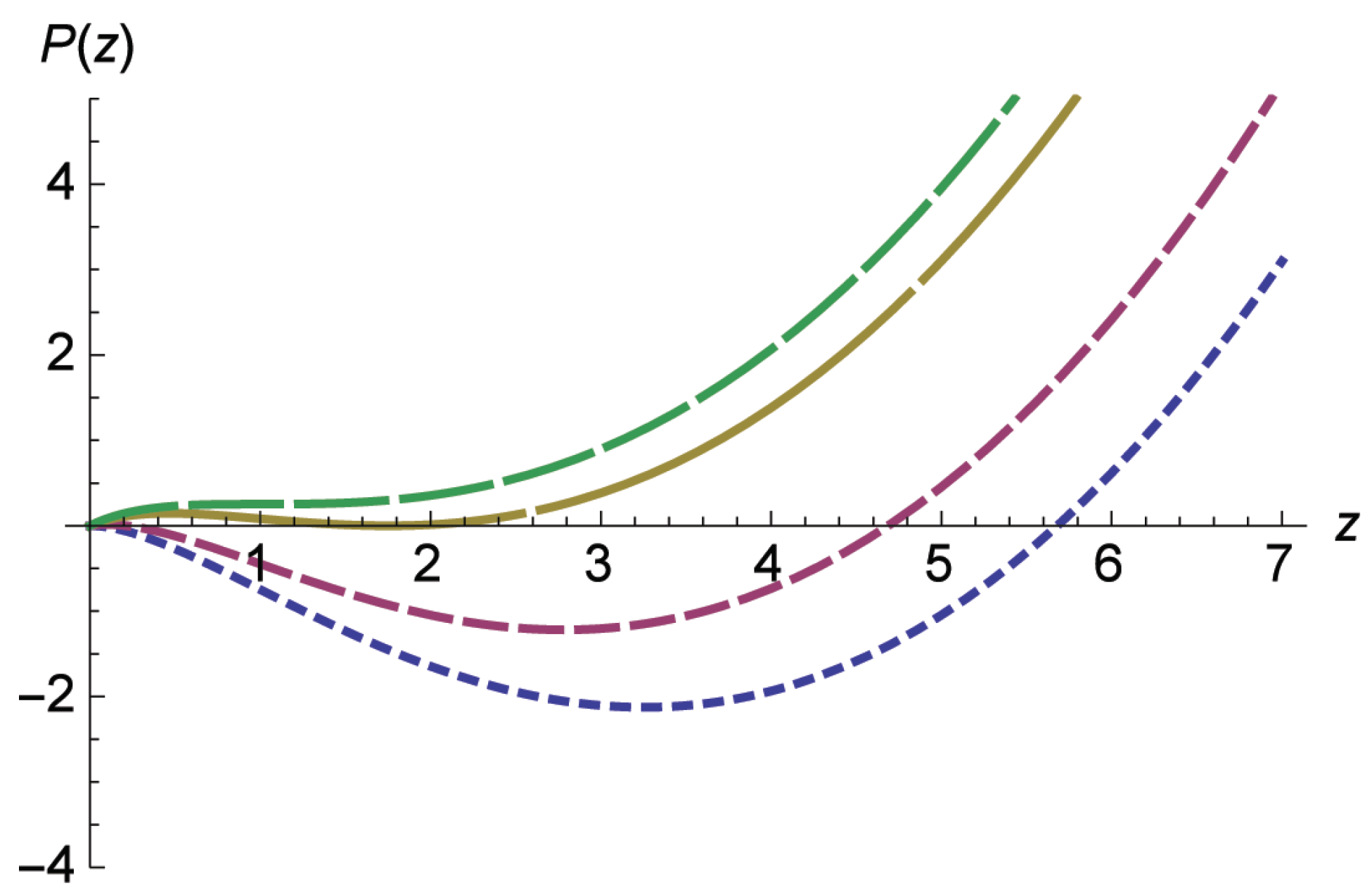
4.1.1. EOS with Nuclear Fog Interpolation
- The expression for f must obviously contain a term that determines the rest mass of nucleon (term with ). This expression should contain the term associated with “repulsion” due to the hard core inside the nucleons (term∼, where z is dimensionless density). This is a “universal” term in the sense that it provides “non–violation” of the principle of causality: the “adiabatic speed” of propagation of elastic perturbations in a medium should not exceed the speed of light.
- The free energy f must contain a “thermal term” that depends on the temperature of the medium. This positive correcting term can be “quadratic” in the temperature ∼ when the temperature of the Fermi system is smaller than the degeneracy temperature , or it has the dependence ∼ when the temperature is greater than .
- In the intermediate range of temperatures, the temperature dependence is obviously more complex. But this is not important at this stage of consideration since its role is to “make a small correction” to the density value for which the pressure becomes equal to zero.
- Finally, a term assuring transition from the domain where the medium has net traits of “fluid” to the domain where the medium is more similar to “gas” must be present in the free energy f. This term must have a less steep dependence on density z than a linear one, to not violate the causality principle in the domain of high densities.
4.1.2. Structural Stability of “Small” Super-Dense Compact Objects
4.2. Results
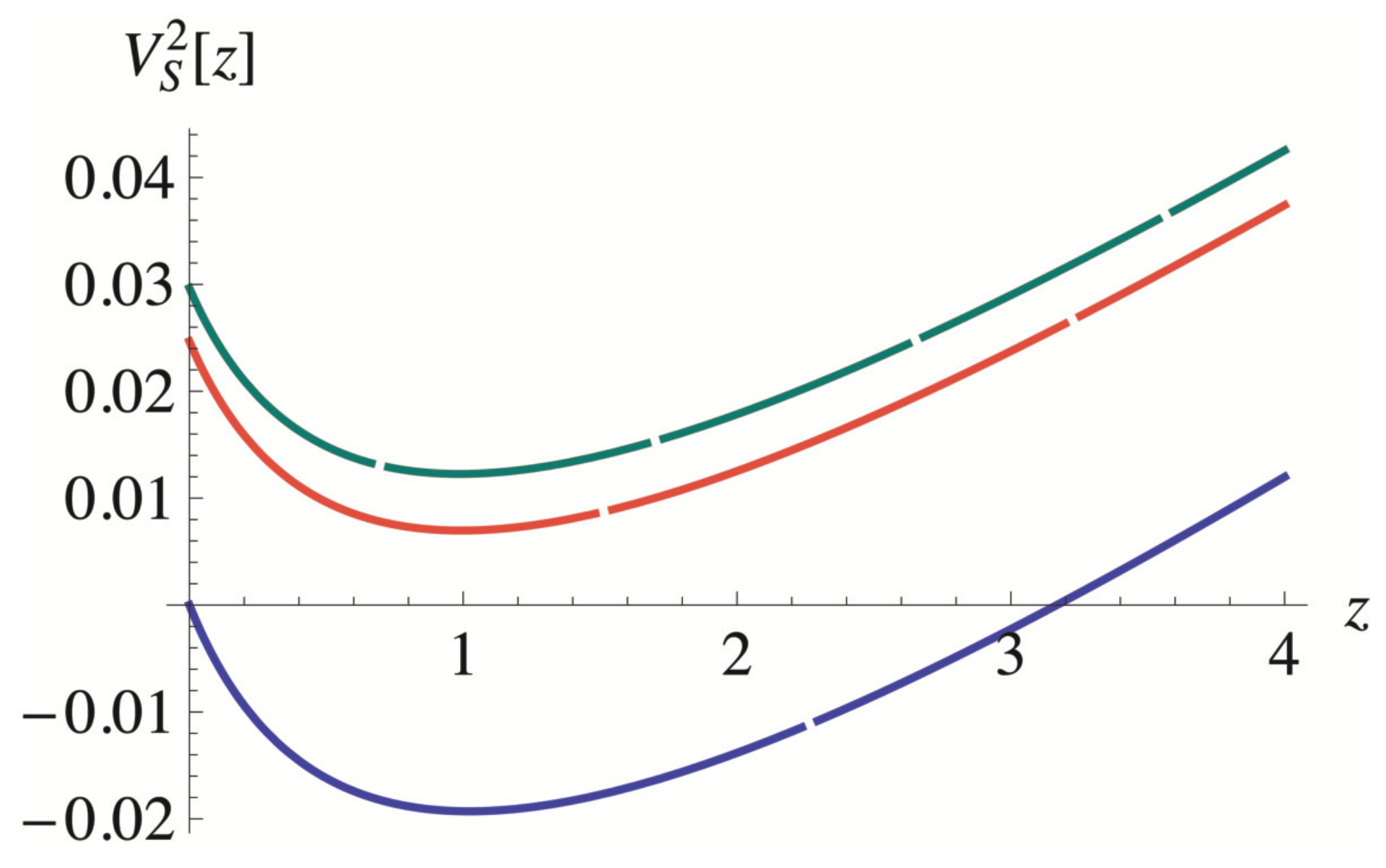
4.2.1. Thermodynamical Criteria of Instability
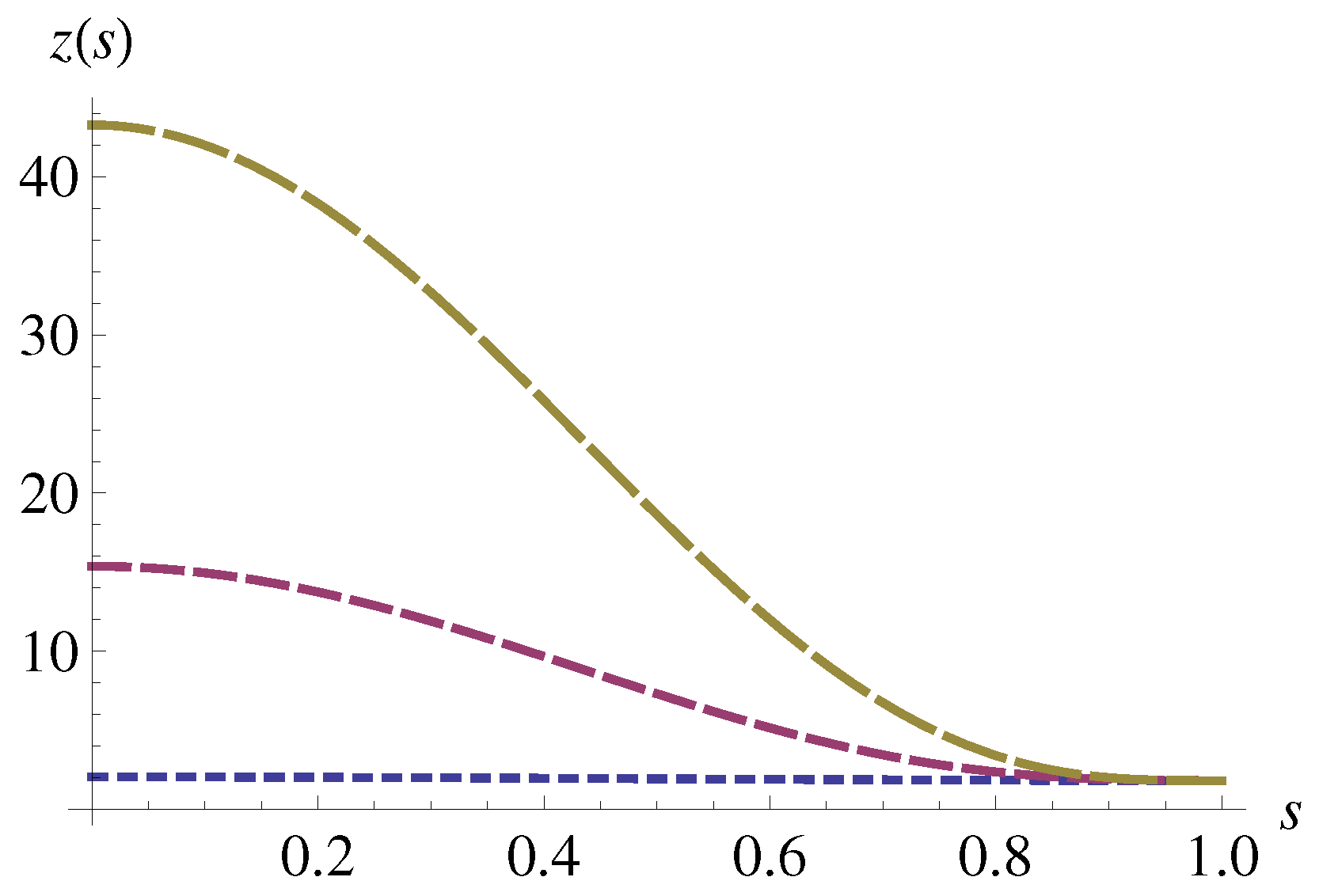
4.2.2. Mass and Radius of Stellar Fragment
5. Discussion
5.1. Structural Disintegration of Compact Super-Dense Stellar Fragment
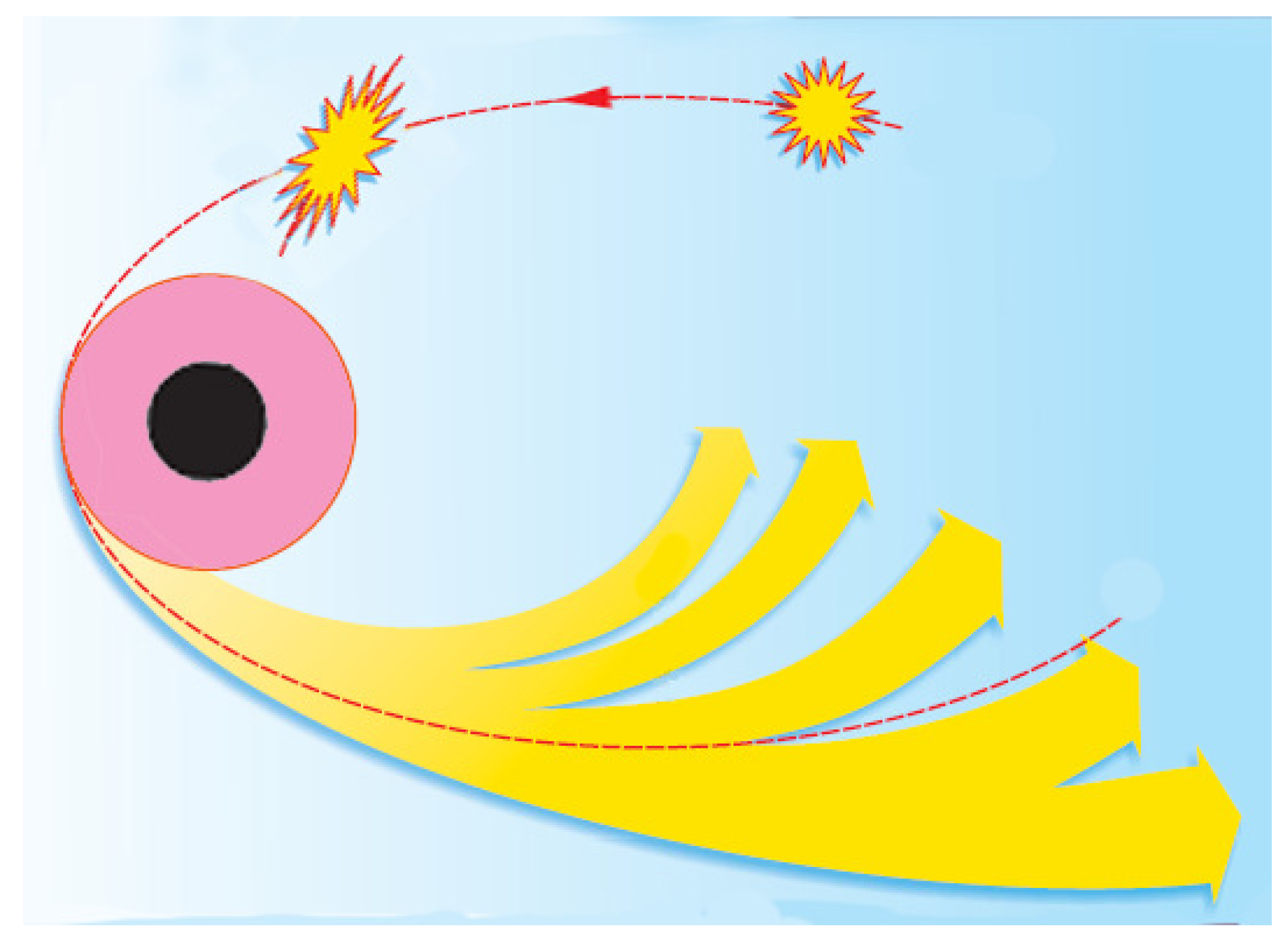
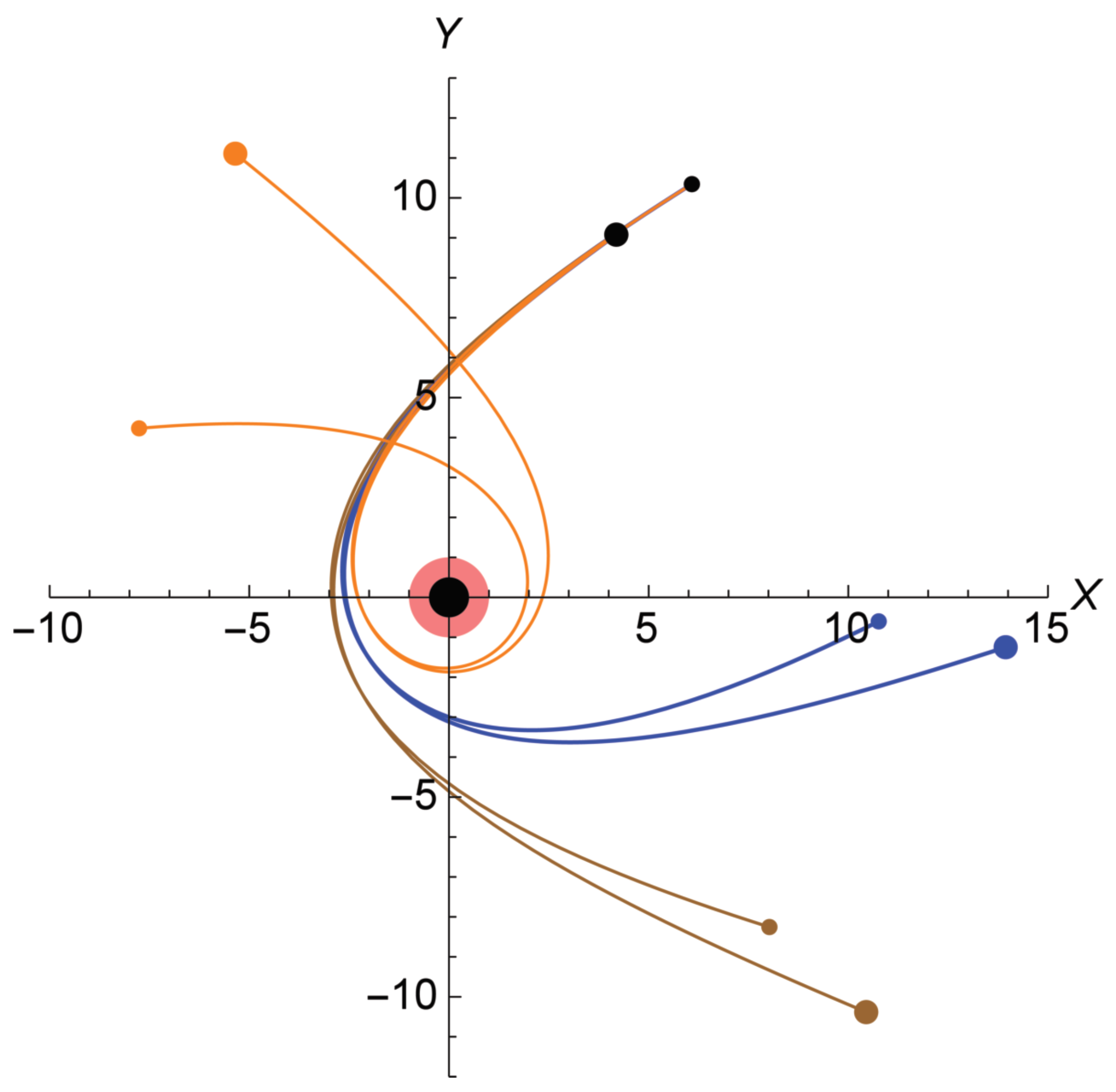
5.2. Likelihood of Stellar Encounter
5.2.1. The Concepts of Likelihood
5.2.2. The Meaning of Numbers
5.2.3. The Fate of Other Stellar Fragments
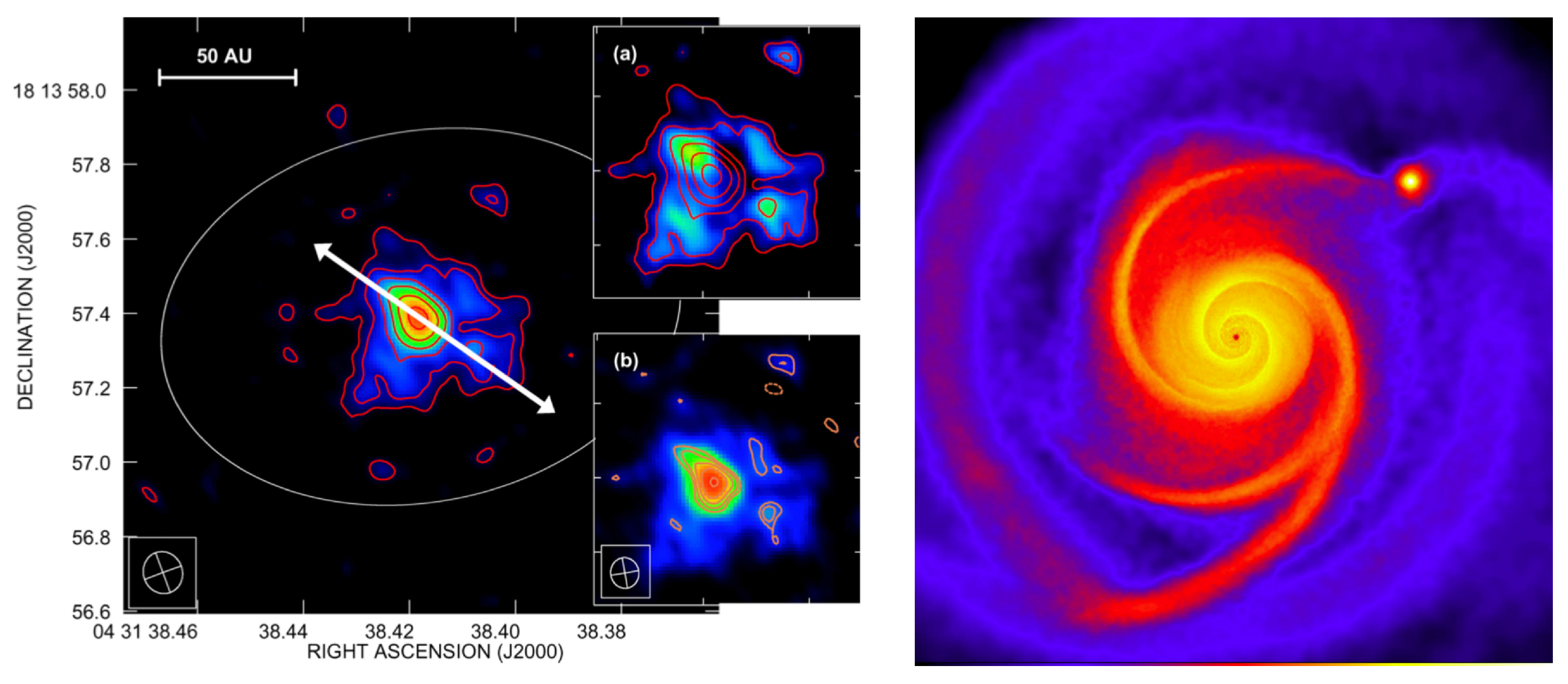
5.3. Implications for Formation of Sun and Planets
5.3.1. Protonebula
5.3.2. Pre-Event Formation of Gaseous Solar System
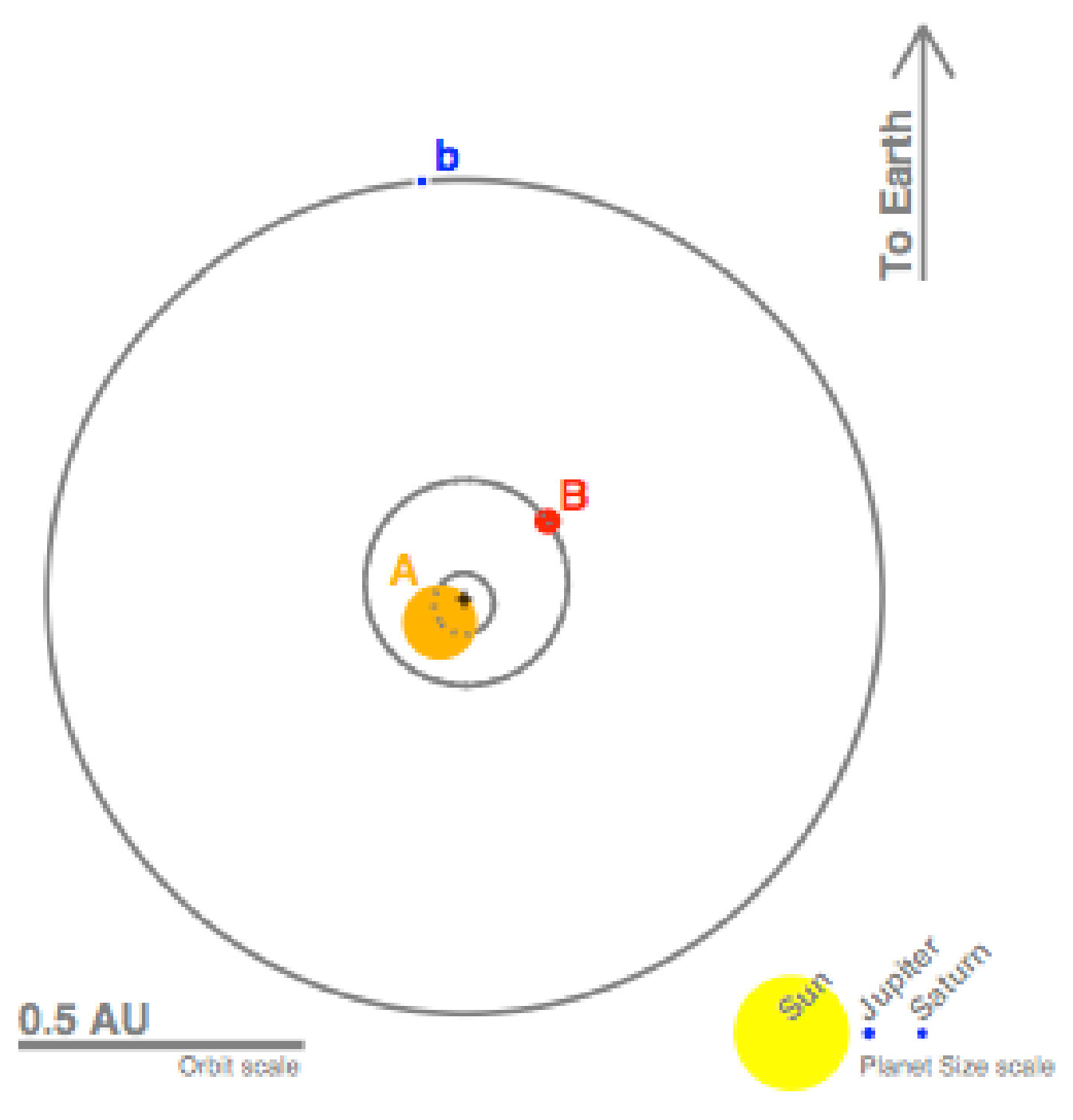
A. Binary Companion
B. “Inner”-Jupiter
- Disk instability can produce self-gravitating protoplanets with cores in about 1000 years, so there is no problem with forming gas giant planets in even the shortest-lived protoplanetary disks.
- Disk instability is enhanced in increasingly massive disks, and so it should be able to form planets at least as massive as Jupiter, given that Jupiter-mass clumps form even in disks with masses of about 0.1 the Sun’s mass.
- Disk instability sidesteps any problem with Type I orbital migration, and with gap-limited mass accretion, because the clumps form directly from the gas without requiring the prior existence of a solid core subject to Type I drift that can disappear before opening a gap. Once they are formed, the clumps quickly open a disk gap, preventing Type I motion with respect to the gas, but only after most of the protoplanet’s mass has already been captured. Thereafter the protoplanet migrates with the disk; in the case of the solar system, little orbital migration appears to be necessary, implying a short lifetime for the solar nebula.
5.3.3. Post-Event Dispersion and Accretion of Debris (into “Rocks”, Later Planets)
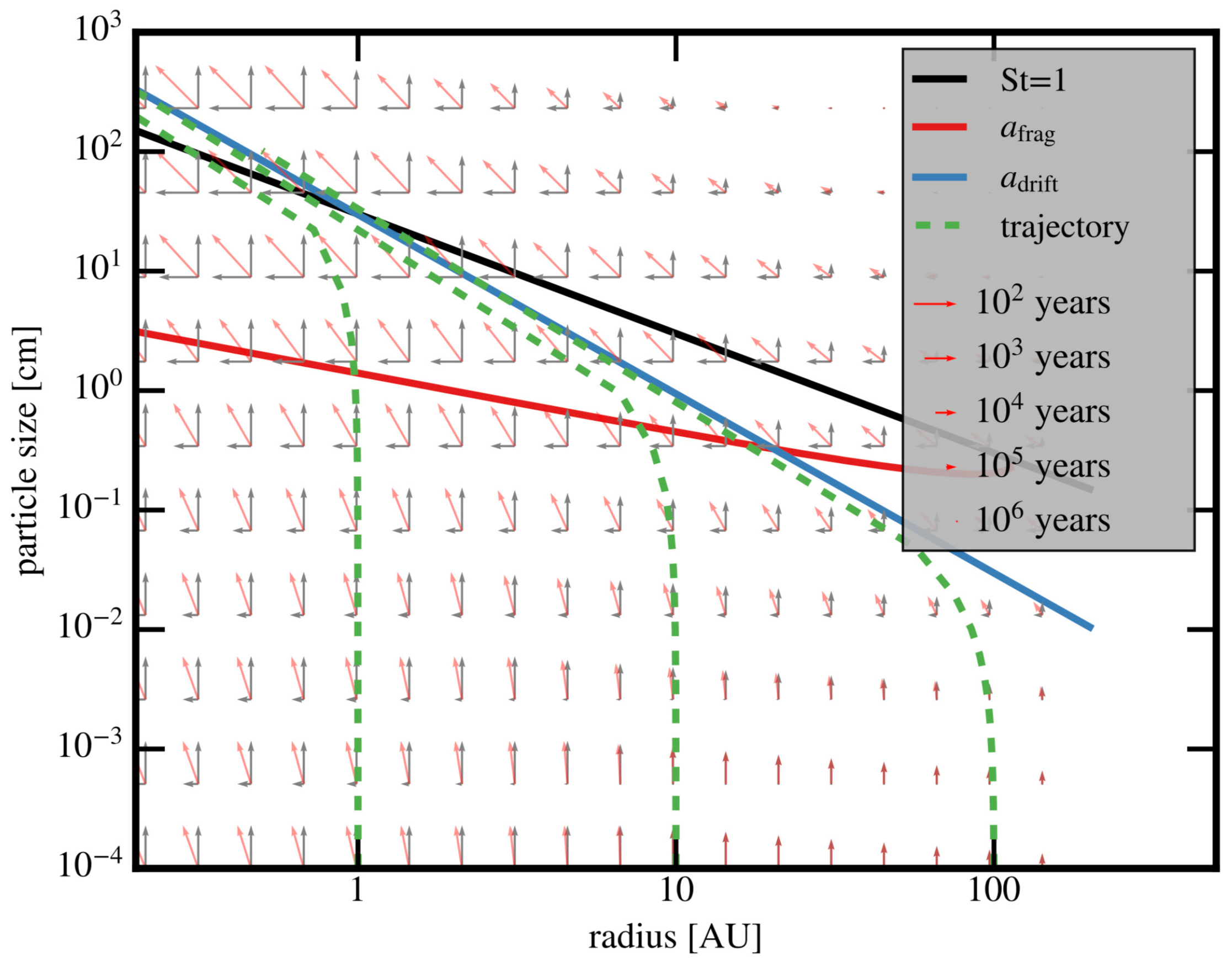
First Planetesimals: «Meter-Size Barrier» Problem in Accretion Model
Meteoritic Data
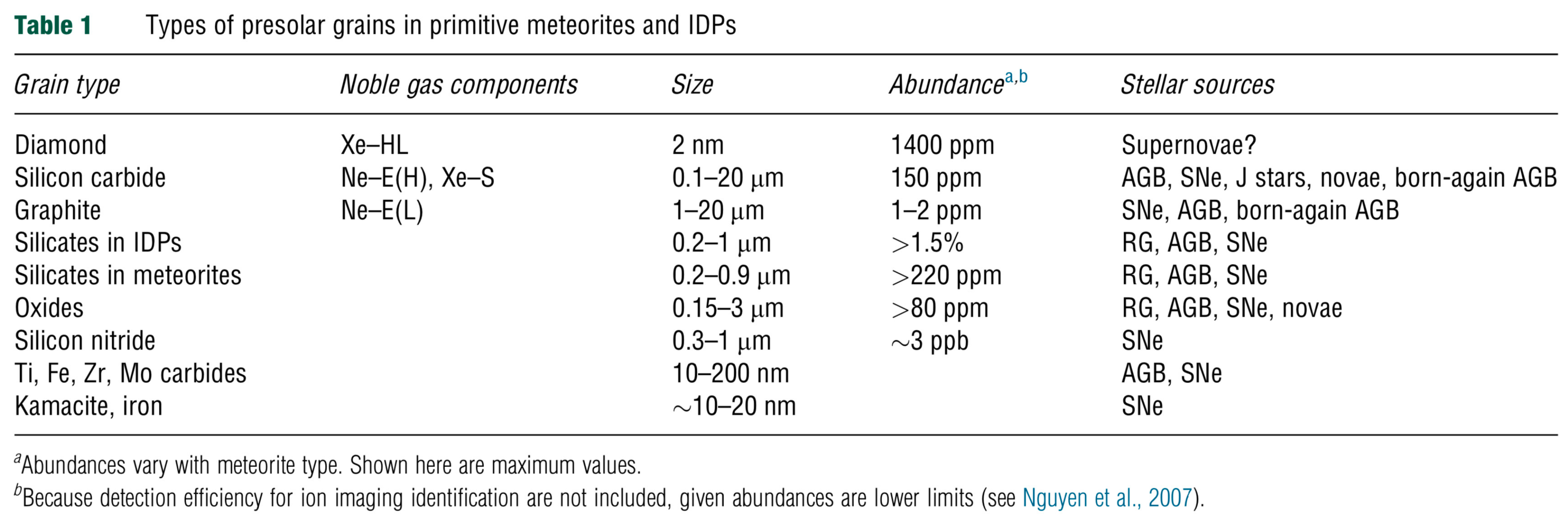
p-Elements
Bimodal Planetary Structure
The «Solar Modeling Problem»
Enrichment of Gaseous Giants
«The proposal to enrich the atmospheres through impacts by small bodies (Boss 1998) is no longer viable, as there are no small bodies we know of that exhibit solar ratios of noble gases, nitrogen, carbon and sulfur. [...] the comets we know could not have delivered the nitrogen we now find on Jupiter. Thus the GPMS results effectively rule out the gravitational disk instability models for forming Jupiter.»[174] (emphasis added)
«If Jupiter’s atmosphere is indeed representative of the bulk composition of the planet, this three-fold enrichment implies the addition of at least 12 Earth masses of these solar composition icy planetesimals (SCIPs) to the complement of heavy elements contributed by the nebular gas itself. If this material has also enriched the other giant planets, it must have been the most abundant solid in the early solar system (Owen and Encrenaz 2003). The resulting total of 18 Earth masses of heavy elements is well within the range of 10–43 Earth masses derived from interior models. The origin of these unusual planetesimals is difficult to understand.»[174] (emphasis added)
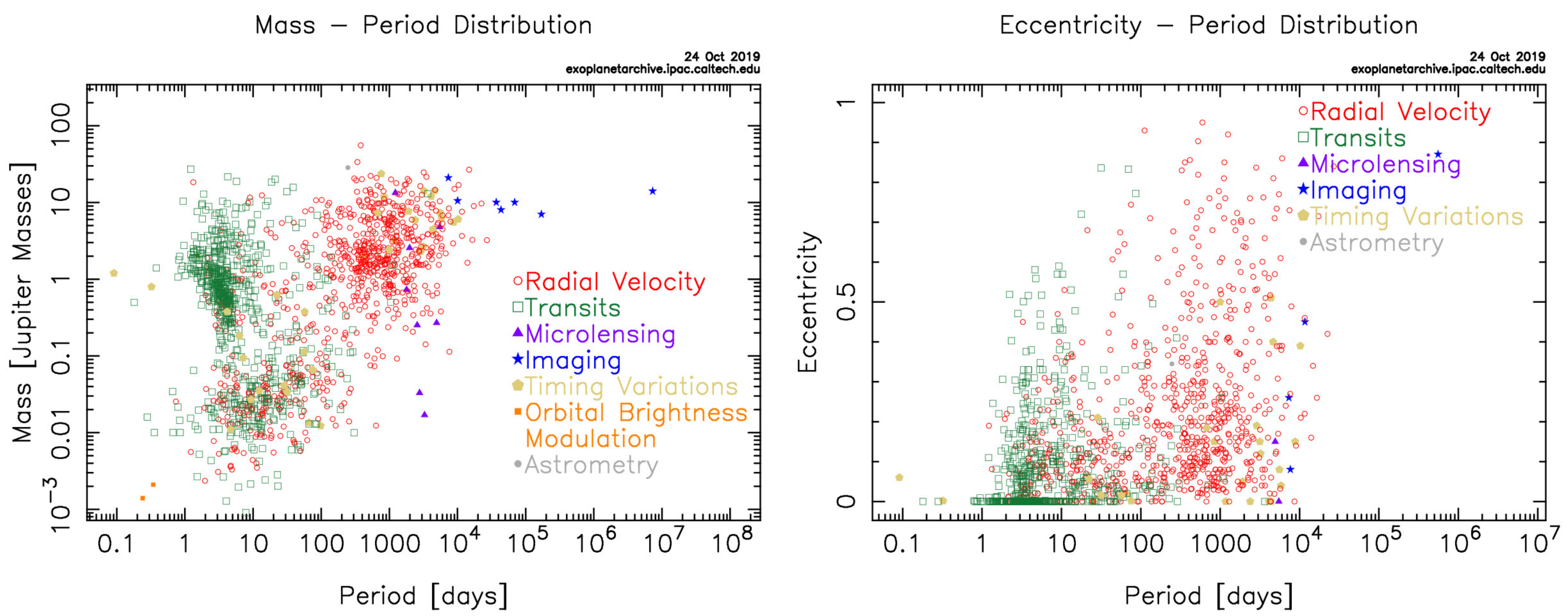
5.4. Exoplanetary Systems Comparison
6. Final Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Jacobson, H.R.; Frebel, A. Observational nuclear astrophysics: Neutron-capture element abundances in old, metal-poor stars. J. Phys. G Nucl. Part. Phys. 2014, 41, 044001. [Google Scholar] [CrossRef] [Green Version]
- Gallino, R.; Arlandini, C.; Busso, M.; Lugaro, M.; Travaglio, C.; Straniero, O.; Chieffi, A.; Limongi, M. Evolution and Nucleosynthesis in Low-Mass Asymptotic Giant Branch Stars. II. Neutron Capture and thes-Process. Astrophys. J. 1998, 497, 388–403. [Google Scholar] [CrossRef]
- Arlandini, C.; Kappeler, F.; Wisshak, K.; Gallino, R.; Lugaro, M.; Busso, M.; Straniero, O. Neutron Capture in Low-Mass Asymptotic Giant Branch Stars: Cross Sections and Abundance Signatures. Astrophys. J. 1999, 525, 886–900. [Google Scholar] [CrossRef] [Green Version]
- Busso, M.; Gallino, R.; Wasserburg, G.J. Nucleosynthesis in Asymptotic Giant Branch Stars: Relevance for Galactic Enrichment and Solar System Formation. Annu. Rev. Astron. Astrophys. 1999, 37, 239–309. [Google Scholar] [CrossRef] [Green Version]
- Burbidge, E.M.; Burbidge, G.R.; Fowler, W.A.; Hoyle, F. Synthesis of the Elements in Stars. Rev. Mod. Phys. 1957, 29, 547–650. [Google Scholar] [CrossRef] [Green Version]
- Cameron, A. Stellar Evolution, Nuclear Astrophysics, and Nucleogenesis, 2nd ed.; Atomic Energy of Canada Ltd.: Chalk River, ON, Canada, 1957. [Google Scholar]
- Arnould, M.; Goriely, S.; Takahashi, K. The r-process of stellar nucleosynthesis: Astrophysics and nuclear physics achievements and mysteries. Phys. Rep. 2007, 450, 97–213. [Google Scholar] [CrossRef] [Green Version]
- Woosley, S.E.; Wilson, J.R.; Mathews, G.J.; Hoffman, R.D.; Meyer, B.S. The r-Process and Neutrino-heated Supernova Ejecta. Astrophys. J. 1994, 433, 229. [Google Scholar] [CrossRef]
- Janka, H.T. Explosion Mechanisms of Core-Collapse Supernovae. Annu. Rev. Nucl. Part. Sci. 2012, 62, 407–451. [Google Scholar] [CrossRef] [Green Version]
- Lattimer, J.M.; Schramm, D.N. Black-Hole-Neutron-Star Collisions. Astrophys. J. 1974, 192, L145–L147. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Schramm, D.N. The tidal disruption of neutron stars by black holes in close binaries. Astrophys. J. 1976, 210, 549–567. [Google Scholar] [CrossRef] [Green Version]
- Symbalisty, E.; Schramm, D.N. Neutron Star Collisions and the r-Process. Astrophys. Lett. 1982, 22, 143. [Google Scholar]
- Cowan, J.J.; Sneden, C.; Lawler, J.E.; Aprahamian, A.; Wiescher, M.; Langanke, K.; Martínez-Pinedo, G.; Thielemann, F.K. Making the Heaviest Elements in the Universe: A Review of the Rapid Neutron Capture Process. arXiv 2019, arXiv:1901.01410. [Google Scholar]
- Sneden, C. Genesis of the Heaviest Elements in the Milky Way Galaxy. Science 2003, 299, 70–75. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cameron, A.G.W. Some Nucleosynthesis Effects Associated with r-Process Jets. Astrophys. J. 2003, 587, 327–340. [Google Scholar] [CrossRef] [Green Version]
- Winteler, C.; Käppeli, R.; Perego, A.; Arcones, A.; Vasset, N.; Nishimura, N.; Liebendörfer, M.; Thielemann, F.K. Magnetorotationally Driven Supernovae as the Origin of Early Galaxy r-process Elements? Astrophys. J. 2012, 750, L22. [Google Scholar] [CrossRef] [Green Version]
- Nishimura, N.; Takiwaki, T.; Thielemann, F.K. The r-process Nucleosynthesis in the Various Jet-like Explosions of Magnetorotational Core-collapse Supernovae. Astrophys. J. 2015, 810, 109. [Google Scholar] [CrossRef] [Green Version]
- Mösta, P.; Roberts, L.F.; Halevi, G.; Ott, C.D.; Lippuner, J.; Haas, R.; Schnetter, E. r-process Nucleosynthesis from Three-dimensional Magnetorotational Core-collapse Supernovae. Astrophys. J. 2018, 864, 171. [Google Scholar] [CrossRef] [Green Version]
- Fernández, R.; Metzger, B.D. Delayed outflows from black hole accretion tori following neutron star binary coalescence. Mon. Not. R. Astron. Soc. 2013, 435, 502–517. [Google Scholar] [CrossRef] [Green Version]
- Bauswein, A.; Goriely, S.; Janka, H.T. Systematics of Dynamical Mass Ejection, Nucleosynthesis, and Radioactively Powered Electromagnetic Signals from Neutron-star Mergers. Astrophys. J. 2013, 773, 78. [Google Scholar] [CrossRef] [Green Version]
- Korobkin, O.; Rosswog, S.; Arcones, A.; Winteler, C. On the astrophysical robustness of the neutron star merger r-process. Mon. Not. R. Astron. Soc. 2012, 426, 1940–1949. [Google Scholar] [CrossRef] [Green Version]
- Foucart, F.; Deaton, M.B.; Duez, M.D.; O’Connor, E.; Ott, C.D.; Haas, R.; Kidder, L.E.; Pfeiffer, H.P.; Scheel, M.A.; Szilagyi, B. Neutron star-black hole mergers with a nuclear equation of state and neutrino cooling: Dependence in the binary parameters. Phys. Rev. D 2014, 90. [Google Scholar] [CrossRef] [Green Version]
- Mennekens, N.; Vanbeveren, D. Massive double compact object mergers: Gravitational wave sources and r-process element production sites. Astron. Astrophys. 2014, 564, A134. [Google Scholar] [CrossRef] [Green Version]
- Kyutoku, K.; Ioka, K.; Okawa, H.; Shibata, M.; Taniguchi, K. Dynamical mass ejection from black hole-neutron star binaries. Phys. Rev. D 2015, 92. [Google Scholar] [CrossRef] [Green Version]
- Roberts, L.F.; Lippuner, J.; Duez, M.D.; Faber, J.A.; Foucart, F.; Lombardi, J.C.; Ning, S.; Ott, C.D.; Ponce, M. The influence of neutrinos on r-process nucleosynthesis in the ejecta of black hole–neutron star mergers. Mon. Not. R. Astron. Soc. 2016, 464, 3907–3919. [Google Scholar] [CrossRef] [Green Version]
- Rosswog, S.; Piran, T.; Nakar, E. The multimessenger picture of compact object encounters: Binary mergers versus dynamical collisions. Mon. Not. R. Astron. Soc. 2013, 430, 2585–2604. [Google Scholar] [CrossRef] [Green Version]
- Perego, A.; Rosswog, S.; Cabezon, R.M.; Korobkin, O.; Kappeli, R.; Arcones, A.; Liebendorfer, M. Neutrino-driven winds from neutron star merger remnants. Mon. Not. R. Astron. Soc. 2014, 443, 3134–3156. [Google Scholar] [CrossRef]
- Martin, D.; Perego, A.; Arcones, A.; Thielemann, F.K.; Korobkin, O.; Rosswog, S. Neutrino-driven Winds in the Aftermath of a Neutron Star Merger: Nucleosynthesis and Electromagnetic Transients. Astrophys. J. 2015, 813, 2. [Google Scholar] [CrossRef] [Green Version]
- Sekiguchi, Y.; Kiuchi, K.; Kyutoku, K.; Shibata, M.; Taniguchi, K. Dynamical mass ejection from the merger of asymmetric binary neutron stars: Radiation-hydrodynamics study in general relativity. Phys. Rev. D 2016, 93. [Google Scholar] [CrossRef] [Green Version]
- Radice, D.; Galeazzi, F.; Lippuner, J.; Roberts, L.F.; Ott, C.D.; Rezzolla, L. Dynamical mass ejection from binary neutron star mergers. Mon. Not. R. Astron. Soc. 2016, 460, 3255–3271. [Google Scholar] [CrossRef]
- Wu, M.R.; Fernández, R.; Martínez-Pinedo, G.; Metzger, B.D. Production of the entire range of r-process nuclides by black hole accretion disc outflows from neutron star mergers. Mon. Not. R. Astron. Soc. 2016, 463, 2323–2334. [Google Scholar] [CrossRef] [Green Version]
- Paulucci, L.; Horvath, J.E.; Benvenuto, O. Nucleosynthesis in Strange Star Mergers. Int. J. Mod. Phys. Conf. Ser. 2017, 45, 1760042. [Google Scholar] [CrossRef] [Green Version]
- Pruet, J.; Thompson, T.A.; Hoffman, R.D. Nucleosynthesis in Outflows from the Inner Regions of Collapsars. Astrophys. J. 2004, 606, 1006–1018. [Google Scholar] [CrossRef] [Green Version]
- Siegel, D.M.; Barnes, J.; Metzger, B.D. Collapsars as a major source of r-process elements. Nature 2019, 569, 241–244. [Google Scholar] [CrossRef] [Green Version]
- Bramante, J.; Linden, T. On the r-process Enrichment of Dwarf Spheroidal Galaxies. Astrophys. J. 2016, 826, 57. [Google Scholar] [CrossRef] [Green Version]
- Fuller, G.M.; Kusenko, A.; Takhistov, V. Primordial Black Holes and r-Process Nucleosynthesis. Phys. Rev. Lett. 2017, 119. [Google Scholar] [CrossRef] [Green Version]
- Meyer, B.S. The r-, s-, and p-Processes in Nucleosynthesis. Annu. Rev. Astron. Astrophys. 1994, 32, 153–190. [Google Scholar] [CrossRef]
- Rauscher, T.; Dauphas, N.; Dillmann, I.; Fröhlich, C.; Fülöp, Z.; Gyürky, G. Constraining the astrophysical origin of the p-nuclei through nuclear physics and meteoritic data. Rep. Prog. Phys. 2013, 76, 066201. [Google Scholar] [CrossRef] [Green Version]
- Dauphas, N.; Schauble, E.A. Mass Fractionation Laws, Mass-Independent Effects, and Isotopic Anomalies. Annu. Rev. Earth Planet. Sci. 2016, 44, 709–783. [Google Scholar] [CrossRef] [Green Version]
- Qin, L.; Carlson, R.W. Nucleosynthetic isotope anomalies and their cosmochemical significance. Geochem. J. 2016, 50, 43–65. [Google Scholar] [CrossRef]
- Pignatari, M.; Göbel, K.; Reifarth, R.; Travaglio, C. The production of proton-rich isotopes beyond iron: The γ-process in stars. Int. J. Mod. Phys. E 2016, 25, 1630003. [Google Scholar] [CrossRef] [Green Version]
- Adams, F.C. The Birth Environment of the Solar System. Annu. Rev. Astron. Astrophys. 2010, 48, 47–85. [Google Scholar] [CrossRef] [Green Version]
- Gritschneder, M.; Lin, D.N.C.; Murray, S.D.; Yin, Q.Z.; Gong, M.N. The Supernova Triggered Formation and Enrichment of Our Solar System. Astrophys. J. 2011, 745, 22. [Google Scholar] [CrossRef] [Green Version]
- Travaglio, C.; Gallino, R.; Rauscher, T.; Dauphas, N.; Röpke, F.K.; Hillebrandt, W. Radiogenic p-isotopes from Type Ia Supernova, Nuclear Physics Uncertainties, and Galactic Chemical Evolution Compared with Values in Primitive Meteorites. Astrophys. J. 2014, 795, 141. [Google Scholar] [CrossRef] [Green Version]
- Lugaro, M.; Pignatari, M.; Ott, U.; Zuber, K.; Travaglio, C.; Gyürky, G.; Fülöp, Z. Origin of the p-process radionuclides 92Nb and 146Sm in the early solar system and inferences on the birth of the Sun. Proc. Natl. Acad. Sci. USA 2016, 113, 907–912. [Google Scholar] [CrossRef] [Green Version]
- Chaussidon, M.; Robert, F.M.K.K.A. Lithium and Boron Isotopic Compositions of Refractory Inclusions from Primitive Chondrites: A Record of Irradiation in the Early Solar System. In Proceedings of the 32nd Annual Lunar and Planetary Science Conference, Houston, TX, USA, 12–16 March 2001; Volume 32, p. 1862. [Google Scholar]
- Chaussidon, M.; Robert, F.; McKeegan, K. Incorporation of Short-lived 7Be in One CAI from the Allende Meteorite. In Proceedings of the 33rd Annual Lunar and Planetary Science Conference, Houston, TX, USA, 11–15 March 2002; p. 1563. [Google Scholar]
- Gounelle, M.; Shu, F.H.; Shang, H.; Glassgold, A.E.; Rehm, K.E.; Lee, T. Extinct Radioactivities and Protosolar Cosmic Rays: Self-Shielding and Light Elements. Astrophys. J. 2001, 548, 1051–1070. [Google Scholar] [CrossRef]
- Goswami, J.N.; Marhas, K.K.; Sahijpal, S. Did Solar Energetic Particles Produce the Short-lived Nuclides Present in the Early Solar System? Astrophys. J. 2001, 549, 1151–1159. [Google Scholar] [CrossRef]
- Leya, I.; Halliday, A.N.; Wieler, R. The Predictable Collateral Consequences of Nucleosynthesis by Spallation Reactions in the Early Solar System. Astrophys. J. 2003, 594, 605–616. [Google Scholar] [CrossRef]
- Chaussidon, M.; Robert, F.; McKeegan, K.D. Li and B isotopic variations in an Allende CAI: Evidence for the in situ decay of short-lived 10Be and for the possible presence of the short-lived nuclide 7Be in the early solar system. Geochimica et Cosmochimica Acta 2006, 70, 224–245. [Google Scholar] [CrossRef]
- Dauphas, N.; Chaussidon, M. A Perspective from Extinct Radionuclides on a Young Stellar Object: The Sun and Its Accretion Disk. Annu. Rev. Earth Planet. Sci. 2011, 39, 351–386. [Google Scholar] [CrossRef] [Green Version]
- Zinner, E. Presolar Grains. In Treatise on Geochemistry; Elsevier: Amsterdam, The Netherlands, 2014; pp. 181–213. [Google Scholar] [CrossRef]
- Tissot, F.L.H.; Dauphas, N.; Grossman, L. Origin of uranium isotope variations in early solar nebula condensates. Sci. Adv. 2016, 2, e1501400. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Morbidelli, A.; Raymond, S.N. Challenges in planet formation. J. Geophys. Res. Planets 2016, 121, 1962–1980. [Google Scholar] [CrossRef]
- Safronov, V. Evolution of the Protoplanetary Cloud and Formation of the Earth and Planets; Nauka Press: Moscow, Russia, 1969. [Google Scholar]
- Goldreich, P.; Ward, W.R. The formation of planetesimals. Astrophys. J. 1973, 183, 1051–1062. [Google Scholar] [CrossRef]
- Wetherill, G.; Stewart, G.R. Accumulation of a swarm of small planetesimals. Icarus 1989, 77, 330–357. [Google Scholar] [CrossRef]
- Weidenschilling, S.J.; Cuzzi, J.N. Formation of planetesimals in the solar nebula. In Protostars and Planets III; Levy, E.H., Lunine, J.I., Eds.; University of Arizona Press: Tucson, AZ, USA, 1993; pp. 1031–1060. [Google Scholar]
- Lissauer, J.J. Planet Formation. Annu. Rev. Astron. Astrophys. 1993, 31, 129–172. [Google Scholar] [CrossRef]
- Cameron, A.G.W. Physics of the primitive solar accretion disk. Moon Planets 1978, 18, 5–40. [Google Scholar] [CrossRef]
- Boss, A.P. Giant Planet Formation by Gravitational Instability. Science 1997, 276, 1836–1839. [Google Scholar] [CrossRef]
- Mayer, L. Formation of Giant Planets by Fragmentation of Protoplanetary Disks. Science 2002, 298, 1756–1759. [Google Scholar] [CrossRef] [Green Version]
- Ford, E. Dynamical Instabilities in Extrasolar Planetary Systems Containing Two Giant Planets. Icarus 2001, 150, 303–313. [Google Scholar] [CrossRef] [Green Version]
- Beer, M.E.; King, A.R.; Livio, M.; Pringle, J.E. How special is the Solar system? Mon. Not. R. Astron. Soc. 2004, 354, 763–768. [Google Scholar] [CrossRef] [Green Version]
- Rice, K. The Detection and Characterization of Extrasolar Planets. Challenges 2014, 5, 296–323. [Google Scholar] [CrossRef]
- Masset, F.; Snellgrove, M. Reversing type II migration: Resonance trapping of a lighter giant protoplanet. Mon. Not. R. Astron. Soc. 2001, 320, L55–L59. [Google Scholar] [CrossRef] [Green Version]
- Kley, W. On the migration of a system of protoplanets. Mon. Not. R. Astron. Soc. 2000, 313, L47–L51. [Google Scholar] [CrossRef] [Green Version]
- Nesvorný, D. Young Solar System’s Fifth Giant Planet? Astrophys. J. 2011, 742, L22. [Google Scholar] [CrossRef] [Green Version]
- Batygin, K.; Brown, M.E.; Betts, H. Instability-driven Dynamical Evolution Model of a Primordially Five-planet Outer Solar System. Astrophys. J. Lett. 2011, 744, L3. [Google Scholar] [CrossRef] [Green Version]
- Pavlova, E. Regularities of the positioning of the planets in the solar system. Vestn. Mosk. Univ. (Herald Mosc. State Univ. Phys. Astron.) 1992, 33, 97–99. [Google Scholar]
- Tito, E.P.; Pavlov, V.I. A possible mechanism of origin of heavy elements in the solar system. arXiv 2013, arXiv:1311.4207. [Google Scholar]
- Shapiro, S.L.; Teukolsky, S.A. Black Holes, White Dwarfs, and Neutron Stars; Wiley: Hoboken, NJ, USA, 1983. [Google Scholar] [CrossRef]
- Glendenning, N.K. Compact Stars: Nuclear Physics, Particle Physics, and General Relativity, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Lattimer, J.M.; Mackie, F.; Ravenhall, D.G.; Schramm, D.N. The decompression of cold neutron star matter. Astrophys. J. 1977, 213, 225. [Google Scholar] [CrossRef]
- Eichler, D.; Livio, M.; Piran, T.; Schramm, D.N. Nucleosynthesis, neutrino bursts and γ-rays from coalescing neutron stars. Nature 1989, 340, 126–128. [Google Scholar] [CrossRef]
- Ruffert, M.; Janka, H.T.; Takahashi, K.; Schaefer, G. Coalescing neutron stars—A step towards physical models. II. Neutrino emission, neutron tori, and gamma-ray bursts. Astrophys. Astron. 1997, 319, 122–153. [Google Scholar]
- Goriely, S.; Bauswein, A.; Janka, H.T. R-Process Nucleosynthesis in Dynamically Ejected Matter of Neutron Star Mergers. Astrophys. J. 2011, 738, L32. [Google Scholar] [CrossRef] [Green Version]
- Just, O.; Bauswein, A.; Pulpillo, R.A.; Goriely, S.; Janka, H.T. Comprehensive nucleosynthesis analysis for ejecta of compact binary mergers. Mon. Not. R. Astron. Soc. 2015, 448, 541–567. [Google Scholar] [CrossRef] [Green Version]
- Tito, E.P.; Pavlov, V.I. Hot super-dense compact object with particular EoS. Astrophys. Space Sci. 2018, 363. [Google Scholar] [CrossRef] [Green Version]
- Rees, M.J. “Dead Quasars” in Nearby Galaxies? Science 1990, 247, 817–823. [Google Scholar] [CrossRef]
- Imshennik, V.S.; Popov, D. An analytic model for the evolution of a close binary system of neutron (degenerate) stars. Astron. Lett. 1998, 24, 206–221. [Google Scholar]
- Colpi, M.; Wasserman, I. Formation of an Evanescent Proto–Neutron Star Binary and the Origin of Pulsar Kicks. Astrophys. J. 2002, 581, 1271–1279. [Google Scholar] [CrossRef]
- Koposov, S.E.; Boubert, D.; Li, T.S.; Erkal, D.; Costa, G.S.D.; Zucker, D.B.; Ji, A.P.; Kuehn, K.; Lewis, G.F.; Mackey, D.; et al. Discovery of a nearby 1700 km/s star ejected from the Milky Way by Sgr A*. Mon. Not. R. Astron. Soc. 2019. [Google Scholar] [CrossRef]
- Tito, E.P.; Pavlov, V.I. Relativistic Motion of Stars near Rotating Black Holes. Galaxies 2018, 6, 61. [Google Scholar] [CrossRef] [Green Version]
- Jaqaman, H.; Mekjian, A.Z.; Zamick, L. Nuclear condensation. Phys. Rev. C 1983, 27, 2782–2791. [Google Scholar] [CrossRef]
- Karnaukhov, V.; Oeschler, H.; Avdeyev, S.; Rodionov, V.; Kirakosyan, V.; Simonenko, A.; Rukoyatkin, P.; Budzanowski, A.; Karcz, W.; Skwirczyńska, I.; et al. Spinodal decomposition, nuclear fog and two characteristic volumes in thermal multifragmentation. Nucl. Phys. A 2005, 749, 65–72. [Google Scholar] [CrossRef] [Green Version]
- Borderie, B.; Frankland, J. Liquid–Gas phase transition in nuclei. Prog. Part. Nucl. Phys. 2019, 105, 82–138. [Google Scholar] [CrossRef] [Green Version]
- Jaqaman, H.R.; Mekjian, A.Z.; Zamick, L. Liquid-gas phase transitions in finite nuclear matter. Phys. Rev. C 1984, 29, 2067–2074. [Google Scholar] [CrossRef]
- Karnaukhov, V.A. Nuclear multifragmentation and phase transitions in hot nuclei. Phys. Part. Nucl. 2006, 37, 165–193. [Google Scholar] [CrossRef]
- Cherepanov, E.A.; Karnaukhov, V. Fission and Nuclear Liquid-Gas Phase Transition. Commun. Jt. Inst. Nucl. Res. 2009, 2009, 1–9. [Google Scholar]
- Karnaukhov, V.; Avdeyev, S.; Botvina, A.; Cherepanov, E.; Karzc, W.; Kirakosyan, V.; Kuzmin, E.; Oeschler, H.; Rukoyatkin, P.; Skwirczynska, I. Properties of Hot Nuclei Produced in Relativistic Collisions. 2011. Available online: https://vfs.fias.science/d/4fdd7ba24e/files/?p=/Karna-NUFRA.pdf (accessed on 25 October 2013).
- Goodman, A.L.; Kapusta, J.I.; Mekjian, A.Z. Liquid-gas phase instabilities and droplet formation in nuclear reactions. Phys. Rev. C 1984, 30, 851–865. [Google Scholar] [CrossRef] [Green Version]
- Sil, T.; Samaddar, S.K.; De, J.N.; Shlomo, S. Liquid-gas phase transition in infinite and finite nuclear systems. Phys. Rev. C 2004, 69. [Google Scholar] [CrossRef] [Green Version]
- Sauer, G.; Chandra, H.; Mosel, U. Thermal properties of nuclei. Nucl. Phys. A 1976, 264, 221–243. [Google Scholar] [CrossRef]
- Zhang, F.S. Phase transitions, correlations and fluctuations of nuclear multifragmentation. Z. Für Phys. A Hadron. Nucl. 1996, 356, 163–170. [Google Scholar] [CrossRef]
- Csernai, L.; Kapusta, J.I. Entropy and cluster production in nuclear collisions. Phys. Rep. 1986, 131, 223–318. [Google Scholar] [CrossRef]
- Müller, H.; Serot, B.D. Phase transitions in warm, asymmetric nuclear matter. Phys. Rev. C 1995, 52, 2072–2091. [Google Scholar] [CrossRef] [Green Version]
- Bertsch, G.; Siemens, P.J. Nuclear fragmentation. Phys. Lett. B 1983, 126, 9–12. [Google Scholar] [CrossRef] [Green Version]
- Heiselberg, H.; Pethick, C.J.; Ravenhall, D.G. Instabilities in Hot Nuclear Matter: A Mechanism for Nuclear Fragmentation. Phys. Rev. Lett. 1988, 61, 818–821. [Google Scholar] [CrossRef]
- López, J.A.; Lübeck, G. Nuclear spinodal decomposition. Phys. Lett. B 1989, 219, 215–221. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E. Fluid Mechanics, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 1987. [Google Scholar]
- Chandrasekhar, S. Dynamical Friction. I. General Considerations: The Coefficient of Dynamical Friction. Astrophys. J. 1943, 97, 255. [Google Scholar] [CrossRef]
- Tito, E.P.; Pavlov, V.I. Accretion-caused deceleration of a gravitationally powerful compact stellar object moving within a dense Fermi gas. Astrophys. Space Sci. 2016, 361. [Google Scholar] [CrossRef] [Green Version]
- Pavlov, V.I.; Tito, E.P. Transition scattering in stochastically inhomogeneous media. J. Acoust. Soc. Am. 2009, 125, 676–689. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pavlov, V.I.; Sukhorukov, A.I. Emission of acoustic transition waves. Sov. Phys. Uspekhi 1985, 28, 784–802. [Google Scholar] [CrossRef]
- Pavlov, V.I.; Kharin, O.A. Emission of acoustic waves and formation of heated jet as a fast source moves through a medium with a relativistic equation of state. J. Exp. Theor. Phys. 1990, 71, 211–216. Available online: http://www.jetp.ac.ru/cgi-bin/e/index/e/71/2/p211?a=list.
- Zeldovich, Y.B.; Raizer, Y. Physics of Shock Waves and High-Temperature Hydrodynamic Phenomena; Academic Press: Cambridge, MA, USA, 1966. [Google Scholar]
- Chizhov, A.V.; Schmidt, A.A. Impact of a high-velocity drop on an obstacle. Tech. Phys. 2000, 45, 1529–1537. [Google Scholar] [CrossRef]
- Panov, I.; Kolbe, E.; Pfeiffer, B.; Rauscher, T.; Kratz, K.L.; Thielemann, F.K. Calculations of fission rates for r-process nucleosynthesis. Nucl. Phys. A 2005, 747, 633–654. [Google Scholar] [CrossRef] [Green Version]
- Panov, I.V.; Korneev, I.Y.; Rauscher, T.; Martínez-Pinedo, G.; Kelić-Heil, A.; Zinner, N.T.; Thielemann, F.K. Neutron-induced astrophysical reaction rates for translead nuclei. Astron. Astrophys. 2010, 513, A61. [Google Scholar] [CrossRef]
- Korneev, I.Y.; Panov, I.V. Contribution of fission to heavy-element nucleosynthesis in an astrophysical r-process. Astron. Lett. 2011, 37, 864–873. [Google Scholar] [CrossRef]
- Nazarewicz, W. The limits of nuclear mass and charge. Nat. Phys. 2018, 14, 537–541. [Google Scholar] [CrossRef]
- Wapstra, A.H. Criteria that must be satisfied for the discovery of a new chemical element to be recognized. Pure Appl. Chem. 1991, 63, 879–886. [Google Scholar] [CrossRef] [Green Version]
- Heenen, P.H.; Skalski, J.; Staszczak, A.; Vretenar, D. Shapes and alpha- and beta-decays of superheavy nuclei. Nucl. Phys. A 2015, 944, 415–441. [Google Scholar] [CrossRef]
- Jachimowicz, P.; Kowal, M.; Skalski, J. Adiabatic fission barriers in superheavy nuclei. Phys. Rev. C 2017, 95. [Google Scholar] [CrossRef] [Green Version]
- Goldanskh, V.I. Modes of Radioactive Decay Involving Proton Emission. Annu. Rev. Nucl. Sci. 1966, 16, 1–30. [Google Scholar] [CrossRef]
- Thoennessen, M. Reaching the limits of nuclear stability. Rep. Prog. Phys. 2004, 67, 1187–1232. [Google Scholar] [CrossRef] [Green Version]
- Giuliani, S.; Matheson, Z.; Nazarewicz, W.; Olsen, E.; Reinhard, P.G.; Sadhukhan, J.; Schuetrumpf, B.; Schunck, N.; Schwerdtfeger, P. Colloquium: Superheavy elements: Oganesson and beyond. Rev. Mod. Phys. 2019, 91. [Google Scholar] [CrossRef] [Green Version]
- National Nuclear Data Center (NuDat2), Brookhaven National Laboratory, Graphics by Wikimedia Commons/Public Domain. Half-Lives of Isotopes. Available online: https://www.nndc.bnl.gov/nudat2/ (accessed on 1 June 2012).
- Greiner, W. Nuclei: Superheavy–superneutronic–strange–and of antimatter. J. Phys. Conf. Ser. 2013, 413, 012002. [Google Scholar] [CrossRef] [Green Version]
- Afanasjev, A.; Agbemava, S.; Gyawali, A. Hyperheavy nuclei: Existence and stability. Phys. Lett. B 2018, 782, 533–540. [Google Scholar] [CrossRef]
- De Jesús Mendoza-Temis, J.; Wu, M.R.; Langanke, K.; Martínez-Pinedo, G.; Bauswein, A.; Janka, H.T. Nuclear robustness of therprocess in neutron-star mergers. Phys. Rev. C 2015, 92. [Google Scholar] [CrossRef] [Green Version]
- Shibagaki, S.; Kajino, T.; Mathews, G.J.; Chiba, S.; Nishimura, S.; Lorusso, G. Relative contributions of the weak, main and fission-recycling r-process. Astrophys. J. 2016, 816, 79. [Google Scholar] [CrossRef] [Green Version]
- Schmidt, K.H.; Jurado, B. Review on the progress in nuclear fission—experimental methods and theoretical descriptions. Rep. Prog. Phys. 2018, 81, 106301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Oganessian, Y.T.; Utyonkov, V.K. Super-heavy element research. Rep. Prog. Phys. 2015, 78, 036301. [Google Scholar] [CrossRef] [PubMed]
- San-Tsiang, T.; Zah-Wei, H.; Chastel, R.; Vigneron, L. On the New Fission Processes of Uranium Nuclei. Phys. Rev. 1947, 71, 382–383. [Google Scholar] [CrossRef]
- Perelygin, V.; Shadieva, N.; Tretiakova, S.; Boos, A.; Brandt, R. Ternary fission produced in Au, Bi, Th and U with Ar ions. Nucl. Phys. A 1969, 127, 577–585. [Google Scholar] [CrossRef]
- Oganessian, Y.T.; Sobiczewski, A.; Ter-Akopian, G.M. Superheavy nuclei: From predictions to discovery. Phys. Scr. 2017, 92, 023003. [Google Scholar] [CrossRef]
- Khuyagbaatar, J.; Yakushev, A.; Düllmann, C.; Ackermann, D.; Andersson, L.L.; Block, M.; Brand, H.; Even, J.; Forsberg, U.; Hartmann, W.; et al. Fission in the landscape of heaviest elements: Some recent examples. EPJ Web Conf. 2016, 131, 03003. [Google Scholar] [CrossRef] [Green Version]
- Schunck, N.; Robledo, L.M. Microscopic theory of nuclear fission: A review. Rep. Prog. Phys. 2016, 79, 116301. [Google Scholar] [CrossRef] [Green Version]
- Bjørnholm, S.; Lynn, J.E. The double-humped fission barrier. Rev. Mod. Phys. 1980, 52, 725–931. [Google Scholar] [CrossRef]
- Nazarewicz, W.; Bender, M.; Ćwiok, S.; Heenen, P.; Kruppa, A.; Reinhard, P.G.; Vertse, T. Theoretical description of superheavy nuclei. Nucl. Phys. A 2002, 701, 165–171. [Google Scholar] [CrossRef]
- Brodziński, W.; Skalski, J. Predictions for superheavy elements beyond Z= 126. Phys. Rev. C 2013, 88. [Google Scholar] [CrossRef]
- Bernard, R.; Goutte, H.; Gogny, D.; Younes, W. Microscopic and nonadiabatic Schrödinger equation derived from the generator coordinate method based on zero- and two-quasiparticle states. Phys. Rev. C 2011, 84. [Google Scholar] [CrossRef] [Green Version]
- Weizsacker, C.F.V. Zur Theorie der Kernmassen. Z. Phys. 1935, 96, 431–458. [Google Scholar] [CrossRef]
- Bohr, N.; Wheeler, J.A. The Mechanism of Nuclear Fission. Phys. Rev. 1939, 56, 426–450. [Google Scholar] [CrossRef]
- Bohr, A.; Mottelson, B.R. Nuclear Structure; World Scientific Publishing Co. Pte. Ltd.: Singapore, 1998. [Google Scholar]
- Mattauch, J.; Thiele, W.; Wapstra, A. Adjustment of relative atomic masses. Nucl. Phys. 1965, 1, 73–120. [Google Scholar] [CrossRef]
- Green, A.E.S.; Engler, N.A. Mass Surfaces. Phys. Rev. 1953, 91, 40–45. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E. Statistical Physics, 2nd ed.; Addison-Wesley: Boston, MA, USA, 1966. [Google Scholar]
- Rumer, Y.B.; Ryvkin, M.S. Thermodynamics, Statistical Physics and Kinetics; Fizmathgiz: Moscow, Russia, 1977; pp. 536–538. [Google Scholar]
- Barabash, A. Average and recommended half-life values for two-neutrino double beta decay. Nucl. Phys. A 2015, 935, 52–64. [Google Scholar] [CrossRef] [Green Version]
- Heeck, J.; Rodejohann, W. Neutrinoless quadruple beta decay. EPL (Europhys. Lett.) 2013, 103, 32001. [Google Scholar] [CrossRef] [Green Version]
- Goutte, H.; Panebianco, S.; Dore, D. Overview on Recent Fission Studies and Related Topics. Jpn. Phys. Soc. Conf. Proc. 2015, 6, 010025. [Google Scholar] [CrossRef] [Green Version]
- Anders, E.; Grevesse, N. Abundances of the elements: Meteoritic and solar. Geochim. Cosmochim. Acta 1989, 53, 197–214. [Google Scholar] [CrossRef]
- Guillot, T. The Interiors of Giant Planets: Models and Outstanding Questions. Annu. Rev. Earth Planet. Sci. 2005, 33, 493–530. [Google Scholar] [CrossRef]
- Vagnozzi, S. New Solar Metallicity Measurements. Atoms 2019, 7, 41. [Google Scholar] [CrossRef] [Green Version]
- Luck, R.E. Abundances in the Local Region. I. G and K Giants. Astronom. J. 2015, 150, 88. [Google Scholar] [CrossRef] [Green Version]
- Luck, R.E. Abundances in the Local Region II: F, G, and K Dwarfs and Subgiants. Astronom. J. 2016, 153, 21. [Google Scholar] [CrossRef] [Green Version]
- Luck, R.E. Abundances in the Local Region. III. Southern F, G, and K Dwarfs. Astron. J. 2018, 155, 111. [Google Scholar] [CrossRef]
- Marov, M. The Formation and Evolution of the Solar System. In Oxford Research Encyclopedia (Planetary Science); Oxford University Press: Oxford, UK, 2018; pp. 1–54. [Google Scholar] [CrossRef]
- Zinner, E. Stellar Nucleosynthesis and the Isotopic Composition of Presolar Grains from Primitive Meteorites. Annu. Rev. Earth Planet. Sci. 1998, 26, 147–188. [Google Scholar] [CrossRef]
- Mumma, M.J.; Charnley, S.B. The Chemical Composition of Comets—Emerging Taxonomies and Natal Heritage. Annu. Rev. Astron. Astrophys. 2011, 49, 471–524. [Google Scholar] [CrossRef]
- Alexander, C.M.O.; Bowden, R.; Fogel, M.L.; Howard, K.T.; Herd, C.D.K.; Nittler, L.R. The Provenances of Asteroids, and Their Contributions to the Volatile Inventories of the Terrestrial Planets. Science 2012, 337, 721–723. [Google Scholar] [CrossRef]
- Pontoppidan, K.M.; Salyk, C.; Bergin, E.A.; Brittain, S.; Marty, B.; Mousis, O.; Öberg, K.I. Volatiles in Protoplanetary Disks. In Protostars and Planets VI; Beuther, H., Klessen, R.S., Dullemond, C.P., Henning, T., Eds.; University of Arizona Press: Tucson, AZ, USA, 2014; p. 363. [Google Scholar] [CrossRef] [Green Version]
- Amelin, Y. Lead Isotopic Ages of Chondrules and Calcium-Aluminum-Rich Inclusions. Science 2002, 297, 1678–1683. [Google Scholar] [CrossRef]
- Price, D.J.; Bate, M.R. The impact of magnetic fields on single and binary star formation. Mon. Not. R. Astron. Soc. 2007, 377, 77–90. [Google Scholar] [CrossRef]
- Bürzle, F.; Clark, P.C.; Stasyszyn, F.; Greif, T.; Dolag, K.; Klessen, R.S.; Nielaba, P. Protostellar collapse and fragmentation using an MHD gadget. Mon. Not. R. Astron. Soc. 2010, 412, 171–186. [Google Scholar] [CrossRef] [Green Version]
- Boss, A.P.; Keiser, S.A. Collapse and Fragmentation of Magnetic Molecular Cloud Cores with the Enzo AMR MHD Code. I. Uniform Density Sphere. Astrophys. J. 2013, 764, 136. [Google Scholar] [CrossRef] [Green Version]
- Raghavan, D.; McAlister, H.A.; Henry, T.J.; Latham, D.W.; Marcy, G.W.; Mason, B.D.; Gies, D.R.; White, R.J.; ten Brummelaar, T.A. A Survey of Stellar Families: Multiplicity of Solar-type Stars. Astrophys. J. Suppl. Ser. 2010, 190, 1–42. [Google Scholar] [CrossRef]
- Machida, M.N.; Tomisaka, K.; Matsumoto, T.; Inutsuka, S.I. Formation Scenario for Wide and Close Binary Systems. Astrophys. J. 2008, 677, 327–347. [Google Scholar] [CrossRef] [Green Version]
- Carney, B.W.; Latham, D.W.; Stefanik, R.P.; Laird, J.B.; Morse, J.A. Spectroscopic Binaries, Velocity Jitter, and Rotation in Field Metal-poor Red Giant and Red Horizontal-Branch Stars. Astronom. J. 2003, 125, 293–321. [Google Scholar] [CrossRef]
- Beck, J.G.; Giles, P. Helioseismic Determination of the Solar Rotation Axis. Astrophys. J. 2005, 621, L153–L156. [Google Scholar] [CrossRef]
- Boss, A.P.; Goswami, J.N. Presolar Cloud Collapse and the Formation and Early Evolution of the Solar Nebula; University of Arizona Press: Tucson, AZ, USA, 2006. [Google Scholar]
- Doyle, L.R.; Carter, J.A.; Fabrycky, D.C.; Slawson, R.W.; Howell, S.B.; Winn, J.N.; Orosz, J.A.; Prša, A.; Welsh, W.F.; Quinn, S.N.; et al. Kepler-16: A Transiting Circumbinary Planet. Science 2011, 333, 1602–1606. [Google Scholar] [CrossRef] [Green Version]
- Johnson, J.A.; Aller, K.M.; Howard, A.W.; Crepp, J.R. Giant Planet Occurrence in the Stellar Mass-Metallicity Plane. PASP 2010, 122, 905. [Google Scholar] [CrossRef] [Green Version]
- Joergens, V. Binary frequency of very young brown dwarfs at separations smaller than 3AU. Astron. Astrophys. 2008, 492, 545–555. [Google Scholar] [CrossRef] [Green Version]
- Helled, R.; Bodenheimer, P.; Podolak, M.; Boley, A.; Meru, F.; Nayakshin, S.; Fortney, J.J.; Mayer, L.; Alibert, Y.; Boss, A.P. Giant Planet Formation, Evolution, and Internal Structure. In Protostars and Planets VI; University of Arizona Press: Tucson, AZ, USA, 2014. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.Y.; Banerjee, R.; Pudritz, R.E.; Jørgensen, J.K.; Shang, H.; Krasnopolsky, R.; Maury, A. The Earliest Stages of Star and Planet Formation: Core Collapse, and the Formation of Disks and Outflows. In Protostars and Planets VI; University of Arizona Press: Tucson, AZ, USA, 2014. [Google Scholar] [CrossRef] [Green Version]
- Boss, A.P. Possible Rapid Gas Giant Planet Formation in the Solar Nebula and Other Protoplanetary Disks. Astrophys. J. 2000, 536, L101–L104. [Google Scholar] [CrossRef] [PubMed]
- Pickett, B.K.; Cassen, P.; Durisen, R.H.; Link, R. The Effects of Thermal Energetics on Three-dimensional Hydrodynamic Instabilities in Massive Protostellar Disks. II. High-Resolution and Adiabatic Evolutions. Astrophys. J. 2000, 529, 1034–1053. [Google Scholar] [CrossRef]
- Boss, A. Planet Formation. Gravit. Space Biol. Bull. 2004, 17, 91–98. [Google Scholar]
- Lunine, J.; Coradini, A.; Gautier, D.; Owen, T.; Wuchterl, G. The origin of Jupiter. Jupit. Planet Satell. Magnetos. 2004, 1, 19–34. [Google Scholar]
- Cassen, P. Models for the fractionation of moderately volatile elements in the solar nebula. Meteorit. Planet. Sci. 1996, 31, 793–806. [Google Scholar] [CrossRef]
- Weidenschilling, S.J. Formation processes and time scales for meteorite parent bodies. In Meteorites and the Early Solar System; University of Arizona: Tucson, AZ, USA, 1988; pp. 348–371. [Google Scholar]
- Weidenschilling, S.J. From icy grains to comets. In Comets II; University of Arizona: Tucson, AZ, USA, 2004; pp. 97–104. [Google Scholar]
- Weidenschilling, S.J.; Cuzzi, J.N. Accretion dynamics and timescales: Relation to chondrites. In Meteorites and the Early Solar System II; University of Arizona: Tucson, AZ, USA, 2006. [Google Scholar]
- Cuzzi, J.N.; Weidenschilling, S.J. Particle-gas dynamics and primary accretion. In Meteorites and the Early Solar System II; University of Arizona: Tucson, AZ, USA, 2006. [Google Scholar]
- Dominik, C.; Tielens, A.G.G.M. The Physics of Dust Coagulation and the Structure of Dust Aggregates in Space. Astrophys. J. 1997, 480, 647–673. [Google Scholar] [CrossRef]
- Zsom, A.; Dullemond, C.P. A representative particle approach to coagulation and fragmentation of dust aggregates and fluid droplets. Astron. Astrophys. 2008, 489, 931–941. [Google Scholar] [CrossRef] [Green Version]
- Testi, L.; Birnstiel, T.; Ricci, L.; Andrews, S.; Blum, J.; Carpenter, J.; Dominik, C.; Isella, A.; Natta, A.; Williams, J.P.; et al. Dust Evolution in Protoplanetary Disks. In Protostars and Planets VI; University of Arizona Press: Tucson, AZ, USA, 2014. [Google Scholar] [CrossRef] [Green Version]
- Zsom, A.; Ormel, C.W.; Güttler, C.; Blum, J.; Dullemond, C.P. The outcome of protoplanetary dust growth: Pebbles, boulders, or planetesimals? II. Introducing the bouncing barrier. Astrophys. Astron. 2010, 513, A57. [Google Scholar] [CrossRef]
- Windmark, F.; Birnstiel, T.; Ormel, C.W.; Dullemond, C.P. Breaking through: The effects of a velocity distribution on barriers to dust growth. Astrophys. Astron. 2012, 544, L16. [Google Scholar] [CrossRef] [Green Version]
- Weidenschilling, S.J. Aerodynamics of solid bodies in the solar nebula. Mon. Not. R. Astron. Soc. 1977, 180, 57–70. [Google Scholar] [CrossRef]
- Birnstiel, T.; Fang, M.; Johansen, A. Dust Evolution and the Formation of Planetesimals. Space Sci. Rev. 2016, 205, 41–75. [Google Scholar] [CrossRef] [Green Version]
- Birnstiel, T.; Andrews, S.M. On the outer edges of protoplanetary dust disks. Astrophys. J. 2013, 780, 153. [Google Scholar] [CrossRef] [Green Version]
- Johansen, A.; Blum, J.; Tanaka, H.; Ormel, C.; Bizzarro, M.; Rickman, H. The Multifaceted Planetesimal Formation Process. In Protostars and Planets VI; University of Arizona Press: Tucson, AZ, USA, 2014. [Google Scholar] [CrossRef] [Green Version]
- Okuzumi, S.; Tanaka, H.; Kobayashi, H.; Wada, K. Rapid Coagulation of Porous Dust Aggregates Outside the Snow Line: A Pathway to Successful Icy Planetesimal Formation. Astrophys. J. 2012, 752, 106. [Google Scholar] [CrossRef]
- Kataoka, A.; Tanaka, H.; Okuzumi, S.; Wada, K. Fluffy dust forms icy planetesimals by static compression. Astron. Astrophys. 2013, 557, L4. [Google Scholar] [CrossRef] [Green Version]
- Johansen, A.; Oishi, J.S.; Low, M.M.M.; Klahr, H.; Henning, T.; Youdin, A. Rapid planetesimal formation in turbulent circumstellar disks. Nature 2007, 448, 1022–1025. [Google Scholar] [CrossRef] [Green Version]
- Cuzzi, J.N.; Hogan, R.C.; Bottke, W.F. Towards initial mass functions for asteroids and Kuiper Belt Objects. Icarus 2010, 208, 518–538. [Google Scholar] [CrossRef] [Green Version]
- Pfalzner, S.; Davies, M.B.; Gounelle, M.; Johansen, A.; Münker, C.; Lacerda, P.; Zwart, S.P.; Testi, L.; Trieloff, M.; Veras, D. The formation of the solar system. Phys. Scr. 2015, 90, 068001. [Google Scholar] [CrossRef]
- Sheppard, S.S.; Trujillo, C.A. The Size Distribution of the Neptune Trojans and the Missing Intermediate-sized Planetesimals. Astrophys. J. 2010, 723, L233–L237. [Google Scholar] [CrossRef] [Green Version]
- Bottke, W.F.; Durda, D.D.; Nesvorný, D.; Jedicke, R.; Morbidelli, A.; Vokrouhlický, D.; Levison, H. The fossilized size distribution of the main asteroid belt. Icarus 2005, 175, 111–140. [Google Scholar] [CrossRef]
- Throop, H.B.; Bally, J. Can Photoevaporation Trigger Planetesimal Formation? Astrophys. J. 2005, 623, L149–L152. [Google Scholar] [CrossRef]
- Scott, E.R.D. Handbook of Iron Meteorites. Meteorit. Planet. Sci. 1975, 48, 2608. [Google Scholar] [CrossRef] [Green Version]
- Caporali, S.; Grazzi, F.; Salvemini, F.; Garbe, U.; Peetermans, S.; Pratesi, G. Structural Characterization of Iron Meteorites through Neutron Tomography. Minerals 2016, 6, 14. [Google Scholar] [CrossRef] [Green Version]
- Plavcan, J.; Hornácková, M.; Grolmusová, Z.; Kociánová, M.; Rakovský, J.; Veis, P. Sikhote-Alin Meteorite, Elemental Composition Analysis Using CF LIBS. 2012. Available online: https://www.semanticscholar.org/paper/Sikhote-Alin-Meteorite%2C-Elemental-Composition-Using-Plavcan-Hor%C5%88%C3%A1%C4%8Dkov%C3%A1/ac8253280505eeebf41fdb388a82097eabb36095 (accessed on 1 June 2020).
- Greenberg, R.; Chapman, C.R. Asteroids and meteorites: Origin of stony-iron meteorites at mantle-core boundaries. Icarus 1984, 57, 267–279. [Google Scholar] [CrossRef]
- White, W. Geochemistry; Wiley-Blackwell: Hoboken, NJ, USA, 2013. [Google Scholar]
- Ormel, C.W.; Klahr, H.H. The effect of gas drag on the growth of protoplanets. Astron. Astrophys. 2010, 520, A43. [Google Scholar] [CrossRef] [Green Version]
- Johansen, A.; Lacerda, P. Prograde rotation of protoplanets by accretion of pebbles in a gaseous environment. Mon. Not. R. Astron. Soc. 2010. [Google Scholar] [CrossRef] [Green Version]
- Lambrechts, M.; Johansen, A. Forming the cores of giant planets from the radial pebble flux in protoplanetary discs. Astron. Astrophys. 2014, 572, A107. [Google Scholar] [CrossRef] [Green Version]
- Levison, H.F.; Kretke, K.A.; Duncan, M.J. Growing the gas-giant planets by the gradual accumulation of pebbles. Nature 2015, 524, 322–324. [Google Scholar] [CrossRef]
- Hillenbrand, L.A. On the Stellar Population and Star-Forming History of the Orion Nebula Cluster. Astronom. J. 1997, 113, 1733. [Google Scholar] [CrossRef]
- Allen, L.; Megeath, S.T.; Gutermuth, R.; Myers, P.C.; Wolk, S.; Adams, F.C.; Muzerolle, J.; Young, E.; Pipher, J.L. The Structure and Evolution of Young Stellar Clusters. In Protostars and Planets V; Reipurth, B., Jewitt, D., Keil, K., Eds.; University of Arizona Press: Tucson, AZ, USA, 2007; p. 361. [Google Scholar]
- Woosley, S.E.; Heger, A.; Weaver, T.A. The evolution and explosion of massive stars. Rev. Mod. Phys. 2002, 74, 1015–1071. [Google Scholar] [CrossRef]
- Gounelle, M.; Meibom, A. The Origin of Short-lived Radionuclides and the Astrophysical Environment of Solar System Formation. Astrophys. J. 2008, 680, 781–792. [Google Scholar] [CrossRef] [Green Version]
- Williams, J.P.; Gaidos, E. On the Likelihood of Supernova Enrichment of Protoplanetary Disks. Astrophys. J. 2007, 663, L33–L36. [Google Scholar] [CrossRef] [Green Version]
- Lewis, R.S.; Ming, T.; Wacker, J.F.; Anders, E.; Steel, E. Interstellar diamonds in meteorites. Nature 1987, 326, 160–162. [Google Scholar] [CrossRef]
- Lofgren, G.; Russell, W. Dynamic crystallization of chondrule melts of porphyritic and radial pyroxene composition. Geochim. Cosmochim. Acta 1986, 50, 1715–1726. [Google Scholar] [CrossRef]
- Desch, S.J.; Connolly, H.C. A model of the thermal processing of particles in solar nebula shocks: Application to the cooling rates of chondrules. Meteorit. Planet. Sci. 2002, 37, 183–207. [Google Scholar] [CrossRef]
- Hewins, R.; Connolly, H.; Lofgren, G.E., Jr.; Libourel, G. Experimental Constraints on Chondrule Formation. In Chondrites and the Protoplanetary Disk; Astronomical Society of the Pacific Conference Series; Krot, A.N., Scott, E.R.D., Reipurth, B., Eds.; Astronomical Society of the Pacific: San Francisco, CA, USA, 2005; Volume 341, p. 286. [Google Scholar]
- Cuzzi, J.N.; Alexander, C.M.O. Chondrule formation in particle-rich nebular regions at least hundreds of kilometres across. Nature 2006, 441, 483–485. [Google Scholar] [CrossRef] [PubMed]
- Desch, S.J.; Morris, M.A.; Connolly, H.C.; Boss, A.P. A Critical Examination of the X-Wind Model for Chondrule and Calcium-rich, Aluminum-rich Inclusion Formation and Radionuclide Production. Astrophys. J. 2010, 725, 692–711. [Google Scholar] [CrossRef] [Green Version]
- Gast, P.W. Limitations on the composition of the upper mantle. J. Geophys. Res. 1960, 65, 1287–1297. [Google Scholar] [CrossRef]
- Lodders, K.; Palme, H.; Gail, H.P. 4.4 Abundances of the elements in the Solar System. In Solar System; Springer: Berlin/Heidelberg, Germany, 2009; pp. 712–770. [Google Scholar] [CrossRef] [Green Version]
- Asplund, M.; Grevesse, N.; Sauval, A.J.; Scott, P. The Chemical Composition of the Sun. Annu. Rev. Astron. Astrophys. 2009, 47, 481–522. [Google Scholar] [CrossRef] [Green Version]
- Grevesse, N.; Scott, P.; Asplund, M.; Sauval, A.J. The elemental composition of the Sun-III. The heavy elements Cu to Th. Astron. Astrophys. 2014, 573, A27. [Google Scholar] [CrossRef] [Green Version]
- Scott, P.; Grevesse, N.; Asplund, M.; Sauval, A.J.; Lind, K.; Takeda, Y.; Collet, R.; Trampedach, R.; Hayek, W. The elemental composition of the Sun I. The intermediate mass elements Na to Ca. Astron. Astrophys. 2014, 573, A25. [Google Scholar] [CrossRef] [Green Version]
- Scott, P.; Asplund, M.; Grevesse, N.; Bergemann, M.; Sauval, A.J. The elemental composition of the Sun-II. The iron group elements Sc to Ni. Astron. Astrophys. 2014, 573, A26. [Google Scholar] [CrossRef] [Green Version]
- Serenelli, A.M.; Basu, S.; Ferguson, J.W.; Asplund, M. New Solar Composition: The Problem with Solar Models Revisited. Astrophys. J. 2009, 705, L123–L127. [Google Scholar] [CrossRef]
- Meléndez, J.; Asplund, M.; Gustafsson, B.; Yong, D. The Peculiar Solar Composition and Its Possible Relation to Planet Formation. Astrophys. J. 2009, 704, L66–L70. [Google Scholar] [CrossRef] [Green Version]
- Villante, F.L. Constraints on the Opacity Profile of the Sun from Helioseismic Observables and Solar Neutrino Flux Measurements. Astrophys. J. 2010, 724, 98–110. [Google Scholar] [CrossRef] [Green Version]
- Vagnozzi, S.; Freese, K.; Zurbuchen, T.H. Solar Models in Light of New High Metallicity Measurements from Solar Wind Data. Astrophys. J. 2017, 839, 55. [Google Scholar] [CrossRef] [Green Version]
- Asplund, M.; Grevesse, N.; Sauval, A.J. The solar chemical composition. Nucl. Phys. A 2006, 777, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Caffau, E.; Ludwig, H.G.; Steffen, M.; Freytag, B.; Bonifacio, P. Solar Chemical Abundances Determined with a CO5BOLD 3D Model Atmosphere. Sol. Phys. 2010, 268, 255–269. [Google Scholar] [CrossRef] [Green Version]
- Bahcall, J.N.; Basu, S.; Serenelli, A.M. What Is the Neon Abundance of the Sun? Astrophys. J. 2005, 631, 1281–1285. [Google Scholar] [CrossRef] [Green Version]
- Charbonnel, C. Influence of Gravity Waves on the Internal Rotation and Li Abundance of Solar-Type Stars. Science 2005, 309, 2189–2191. [Google Scholar] [CrossRef] [PubMed]
- Guzik, J.A.; Watson, L.S.; Cox, A.N. Can Enhanced Diffusion Improve Helioseismic Agreement for Solar Models with Revised Abundances? Astrophys. J. 2005, 627, 1049–1056. [Google Scholar] [CrossRef] [Green Version]
- Castro, M.; Vauclair, S.; Richard, O. Low abundances of heavy elements in the solar outer layers: Comparisons of solar models with helioseismic inversions. Astron. Astrophys. 2006, 463, 755–758. [Google Scholar] [CrossRef]
- Guzik, J.A.; Mussack, K. Exploring Mass Loss, Low-Z Accretion, and Convective Overshoot in Solar Models to Mitigate the Solar Abundance Problem. Astrophys. J. 2010, 713, 1108–1119. [Google Scholar] [CrossRef] [Green Version]
- Turck-Chièze, S.; Palacios, A.; Marques, J.P.; Nghiem, P.A.P. Seismic and Dynamical Solar Models. I. The Impact of the Solar Rotation History on Neutrinos and Seismic Indicators. Astrophys. J. 2010, 715, 1539–1555. [Google Scholar] [CrossRef] [Green Version]
- Turck-Chièze, S.; Piau, L.; Couvidat, S. The Solar Energetic Balance Revisited by Young Solar Analogs, Helioseismology, and Neutrinos. Astrophys. J. Lett. 2011, 731, L29. [Google Scholar] [CrossRef] [Green Version]
- Serenelli, A.M.; Haxton, W.C.; Peña-Garay, C. Solar Models with Accretion. I. Application to the Solar Abundance Problem. Astrophys. J. 2011, 743, 24. [Google Scholar] [CrossRef]
- Yang, W. Solar Models with New Low Metal Abundances. Astrophys. J. 2016, 821, 108. [Google Scholar] [CrossRef] [Green Version]
- Montalbán, J.; Miglio, A.; Noels, A.; Grevesse, N.; di Mauro, M.P. Solar Model with CNO Revised Abundances. In Proceedings of the SOHO 14/GONG 2004 Workshop (ESA SP-559), “Helio- and Asteroseismology: Towards a Golden Future”, New Haven, CT, USA, 12–16 July 2004. [Google Scholar]
- Drake, J.J.; Testa, P. The ‘solar model problem’ solved by the abundance of neon in nearby stars. Nature 2005, 436, 525–528. [Google Scholar] [CrossRef]
- Vincent, A.C.; Scott, P.; Trampedach, R. Light bosons in the photosphere and the solar abundance problem. Mon. Not. R. Astron. Soc. 2013, 432, 3332–3339. [Google Scholar] [CrossRef] [Green Version]
- Christensen-Dalsgaard, J.; Mauro, M.P.D.; Houdek, G.; Pijpers, F. On the opacity change required to compensate for the revised solar composition. Astron. Astrophys. 2008, 494, 205–208. [Google Scholar] [CrossRef] [Green Version]
- Villante, F.L.; Ricci, B. Linear Solar Models. Astrophys. J. 2010, 714, 944–959. [Google Scholar] [CrossRef] [Green Version]
- Villante, F.L.; Serenelli, A.M.; Delahaye, F.; Pinsonneault, M.H. The Chemical Composition of the Sun from Helioseismic and Solar Neutrino Data. Astrophys. J. 2014, 787, 13. [Google Scholar] [CrossRef] [Green Version]
- Villante, F.L.; Serenelli, A.M. A Quantitative Analysis of the Solar Composition Problem. Phys. Procedia 2015, 61, 366–375. [Google Scholar] [CrossRef] [Green Version]
- Cumberbatch, D.T.; Guzik, J.A.; Silk, J.; Watson, L.S.; West, S.M. Light WIMPs in the Sun: Constraints from helioseismology. Phys. Rev. D 2010, 82, 103503. [Google Scholar] [CrossRef] [Green Version]
- Frandsen, M.T.; Sarkar, S. Asymmetric Dark Matter and the Sun. Phys. Rev. Lett. 2010, 105, 011301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Taoso, M.; Iocco, F.; Meynet, G.; Bertone, G.; Eggenberger, P. Effect of low mass dark matter particles on the Sun. Phys. Rev. D 2010, 82, 083509. [Google Scholar] [CrossRef] [Green Version]
- Lopes, I.; Panci, P.; Silk, J. Helioseismology with Long-range Dark Matter-Baryon Interactions. Astrophys. J. 2014, 795, 162. [Google Scholar] [CrossRef] [Green Version]
- Vincent, A.C.; Scott, P.; Serenelli, A. Possible Indication of Momentum-Dependent Asymmetric Dark Matter in the Sun. Phys. Rev. Lett. 2015, 114, 081302. [Google Scholar] [CrossRef] [Green Version]
- Vincent, A.C.; Serenelli, A.; Scott, P. Generalised form factor dark matter in the Sun. J. Cosmol. Astropart. Phys. 2015, 2015, 040. [Google Scholar] [CrossRef] [Green Version]
- Vincent, A.C.; Scott, P.; Serenelli, A. Updated constraints on velocity and momentum-dependent asymmetric dark matter. J. Cosmol. Astropart. Phys. 2016, 2016, 007. [Google Scholar] [CrossRef]
- Dev, P.S.B.; Teresi, D. Asymmetric dark matter in the Sun and diphoton excess at the LHC. Phys. Rev. D 2016, 94, 025001. [Google Scholar] [CrossRef] [Green Version]
- Geytenbeek, B.; Rao, S.; Scott, P.; Serenelli, A.; Vincent, A.C.; White, M.; Williams, A.G. Effect of electromagnetic dipole dark matter on energy transport in the solar interior. J. Cosmol. Astropart. Phys. 2017, 2017, 029. [Google Scholar] [CrossRef]
- Shearer, P.; von Steiger, R.; Raines, J.M.; Lepri, S.T.; Thomas, J.W.; Gilbert, J.A.; Landi, E.; Zurbuchen, T.H. The Solar Wind Neon Abundance Observed with ACE/SWICS and Ulysses/SWICS. Astrophys. J. 2014, 789, 60. [Google Scholar] [CrossRef]
- Boss, A.P. Evolution of the Solar Nebula. IV. Giant Gaseous Protoplanet Formation. Astrophys. J. 1998, 503, 923–937. [Google Scholar] [CrossRef]
- Gloeckler, G.; Geiss, J. Measurement of the Abundance of Helium-3 in the Sun and in the Local Interstellar Cloud with SWICS on Ulysses. Space Sci. Rev. 1998, 84, 275–284. [Google Scholar] [CrossRef]
- Krankowsky, D. The Composition of Comets 1. In International Astronomical Union Colloquium; Cambridge University Press: Cambridge, UK, 1991; Volume 116, pp. 854–877. [Google Scholar]
- Wyckoff, S.; Tegler, S.C.; Engel, L. Nitrogen Abundance in Comet Halley. Astrophys. J. 1991, 367, 641. [Google Scholar] [CrossRef]
- Weaver, H.; Feldman, P.; Combi, M.; Krasnopolsky, V.; Lisse, C.; Shemansky, D. A Search for Argon and O VI in Three Comets Using the Far Ultraviolet Spectroscopic Explorer. Astrophys. J. 2002, 576. [Google Scholar] [CrossRef] [Green Version]
- Owen, T.; Mahaffy, P.; Niemann, H.; Sudhir, A.; Wong, M. Protosolar Nitrogen. Astrophys. J. 2001, 553, L77. [Google Scholar] [CrossRef]
- Owen, T.; Bar-Nun, A. Comets, Impacts, and Atmospheres. Icarus 1995, 116, 215–226. [Google Scholar] [CrossRef]
- Owen, T.; Mahaffy, P.; Niemann, H.B.; Atreya, S.; Donahue, T.; Bar-Nun, A.; de Pater, I. A low-temperature origin for the planetesimals that formed Jupiter. Nature 1999, 402, 269–270. [Google Scholar] [CrossRef]
- Pearl, J.C.; Conrath, B.J. The albedo, effective temperature, and energy balance of Neptune, as determined from Voyager data. J. Geophys. Res. 1991, 96, 18921. [Google Scholar] [CrossRef]
- Fortney, J.J.; Hubbard, W.B. Phase separation in giant planets: Inhomogeneous evolution of Saturn. Icarus 2003, 164, 228–243. [Google Scholar] [CrossRef]
- Stevenson, D.J. The Uranus-Neptune Dichotomy: The Role of Giant Impacts. In Proceedings of the Lunar and Planetary Science Conference, Houston, TX, USA, 17–21 March 1986; pp. 1011–1012. [Google Scholar]
- Podolak, M.; Helled, R. What Do We Really Know about Uranus and Neptune? Astrophys. J. 2012, 759, L32. [Google Scholar] [CrossRef] [Green Version]
- NASA Exoplanet Archive. Confirmed Planets Table. 2019. Available online: https://exoplanetarchive.ipac.caltech.edu/docs/doi.html (accessed on 1 June 2020).
- Borucki, W.J. Kepler: A Brief Discussion of the Mission and Exoplanet Results. Proc. Am. Philosoph. Soc. 2017, 161, 38–65. [Google Scholar]
- David, T.J.; Hillenbrand, L.A.; Petigura, E.A.; Carpenter, J.M.; Crossfield, I.J.M.; Hinkley, S.; Ciardi, D.R.; Howard, A.W.; Isaacson, H.T.; Cody, A.M.; et al. A Neptune-sized transiting planet closely orbiting a 5-10-million-year-old star. Nature 2016, 534, 658–661. [Google Scholar] [CrossRef] [Green Version]
- Greaves, J.; Richards, A.; Rice, W.; Muxlow, T. Enhanced dust emission in the HL Tau disc: A low-mass companion in formation? Mon. Not. R. Astron. Soc. 2008, 391, L74–L78. [Google Scholar] [CrossRef] [Green Version]
- Valencia, D.; O’Connell, R.J.; Sasselov, D. Internal structure of massive terrestrial planets. Icarus 2006, 181, 545–554. [Google Scholar] [CrossRef] [Green Version]
- Sotin, C.; Grasset, O.; Mocquet, A. Mass radius curve for extrasolar Earth-like planets and ocean planets. Icarus 2007, 191, 337–351. [Google Scholar] [CrossRef]
- Kuchner, M.J. Volatile-rich Earth-Mass Planets in the Habitable Zone. Astrophys. J. 2003, 596, L105–L108. [Google Scholar] [CrossRef] [Green Version]
- Léger, A.; Selsis, F.; Sotin, C.; Guillot, T.; Despois, D.; Mawet, D.; Ollivier, M.; Labèque, A.; Valette, C.; Brachet, F.; et al. A new family of planets? “Ocean Planets”. Icarus 2004, 169, 499–504. [Google Scholar] [CrossRef] [Green Version]




© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tito, E.P.; Pavlov, V.I. Hypothesis about Enrichment of Solar System. Physics 2020, 2, 213-276. https://doi.org/10.3390/physics2020014
Tito EP, Pavlov VI. Hypothesis about Enrichment of Solar System. Physics. 2020; 2(2):213-276. https://doi.org/10.3390/physics2020014
Chicago/Turabian StyleTito, Elizabeth P., and Vadim I. Pavlov. 2020. "Hypothesis about Enrichment of Solar System" Physics 2, no. 2: 213-276. https://doi.org/10.3390/physics2020014
APA StyleTito, E. P., & Pavlov, V. I. (2020). Hypothesis about Enrichment of Solar System. Physics, 2(2), 213-276. https://doi.org/10.3390/physics2020014




