1. Introduction
Following Bohm [
1], Griffiths [
2] and Bowman [
3] the kernel of quantum mechanics is the Schrödinger wave equation (Schrödinger [
4,
5,
6,
7,
8,
9]). Born [
10] introduced a statistical interpretation to the wave function appearing in the Schrödinger equation, to Schrödinger’s explicit disapproval (Schrödinger [
4,
5,
6,
7,
8,
9]) who preferred the wave field interpretation. Eventually the statistical approach was entrenched in quantum mechanics not only as a technical means of providing answers and solutions to sub-atomic phenomena but as a “complete” interpretation of the physical “reality” following Bohr’s and Heisenberg’s “Copenhagen interpretation” that became mainstream physics. The latter was challenged, not only by Schrödinger, but also by a large group of physicists led by Albert Einstein who claimed that the quantum mechanical description of physical reality cannot be considered complete, as shown in their famous EPR paper (Einstein, Podolsky and Rosen [
11]). They concluded their derivations by stating that “While we have thus shown that the wave function does not provide a complete description of the physical reality, we left open the question of whether or not such a description exists. We believe, however, that such a theory is possible.” Einstein did not object to the probabilistic description of sub-atomic phenomena in quantum mechanics. However, he believed that this probabilistic representation was a technique used to overcome the practical difficulties of dealing with a more complicated underlying physical reality, much in the same way he suggested earlier to deal with Brownian motion (Einstein [
12,
13]). Niels Bohr led another group of physicists, including Werner Heisenberg, Max Born, Wolfgang Pauli and others, that believed in the probabilistic interpretation of sub-atomic phenomena as being complete. Bohr’s answer [
14] to the EPR paper (Einstein et al. [
11]) was linked to the fact that the finite interaction between an object and the measuring device “entails—because of the impossibility of controlling the reaction of the object on the measuring instruments…—the necessity of a final renunciation of the classical ideal of causality and a radical revision of our attitude towards the problem of physical reality” (Bohr [
14]). The latter is linked to the concept of “complementarity” (Bohr [
14]).
Hooft [
15] has shown that several quantum mechanical models are equivalent to certain deterministic systems because “a basis can be found in terms of which the wave function does not spread”. Hooft [
16] introduces a mathematical theory for deterministic quantum mechanics by using the mathematical formalism used in quantum mechanics. “Classical, i.e., deterministic theories underlining quantum mechanics are considered, and it is shown how an apparent quantum mechanical Hamiltonian can be defined in such theories, being the operator that generates evolution in time”. Hooft [
17] shows that while “it is often claimed that the collapse of the wave function and Born’s rule to interpret the square of the norm as a probability, have to be introduced as separate axioms in quantum mechanics besides the Schroedinger equation” it is not true in certain models “where quantum behavior can be attributed to underlying deterministic equations. He argues, “that indeed the apparent spontaneous collapse of wave functions and Born’s rule are features that strongly point towards determinism underlying quantum mechanics.”
The solution to the Schrödinger equation for the complex wave-function
leads to the superposition of an infinite number of modes, while Born’s [
10] interpretation implies that
.
Whatever the interpretation, the experimental fact still shows that the wave-function collapses upon observation, i.e., as soon as experimental measurement is undertaken the wave-function collapses from the superposition of an infinite number of modes to one single mode. In quantum mechanics no reason is given for the wave function collapse. It is an experimental fact and is being used as a “postulate” in quantum mechanics (Bowman [
3]). It is this collapse of the wave function and what will be shown to be similar in natural convection in porous media that this paper focuses on. This in no way suggests a complete analogy between natural convection in porous media and quantum mechanics. It only demonstrates a similarity between the two in the experimental observation of the wave function collapse and it shows that as distinct from quantum mechanics there is a clear reason behind the wave function collapse in natural convection in porous media. It, therefore, suggests the existence of a deterministic reality behind quantum mechanical phenomena that can be further explored and possibly revealed.
Selecting natural convection in porous media to demonstrate such a wave function collapse is just an example choice, and many more such examples are available from fluid mechanics, such as natural convection in pure fluids, Taylor-Couette instability, and others.
2. Quantum Mechanics and the Collapse of the Wave Function
The Schrödinger equation has the form (Griffiths [
2])
where
is the complex wave function, and
is the position vector in Cartesian coordinates,
is time,
is a potential function, and
is the reduced Planck’s constant. The solution to the Schrödinger equation depends on the imposed potential
but, generally, has a wave solution that, in the one-dimensional finite space, takes the form
where
and
is the initial condition for the wave function. The solution (Equation (2)) to the Schrödinger equation (Equation (1)) is the linear superposition of all discrete eigen-modes.
However, upon observation via measurement at any given time
, the observed result has the form
which implies that only one mode is observed rather than the whole infinite series of the superposition of modes. The latter “phenomenon” was named “the collapse of the wave function” and has no deterministic nor causality linked explanation in quantum mechanics. The present paper shows that a similar “collapse of the wave function” occurs in natural convection in porous media where there is a definitely deterministic reason for the latter, as well as a causality linked explanation. This implies that it might be possible in using the methodology developed in analyzing natural convection in porous (or non-porous) media for the potential derivation of a deterministic quantum mechanics theory that will complement and be equivalent to the well-developed and widely accepted statistical quantum theory.
3. Natural Convection in Porous Media—Problem Formulation
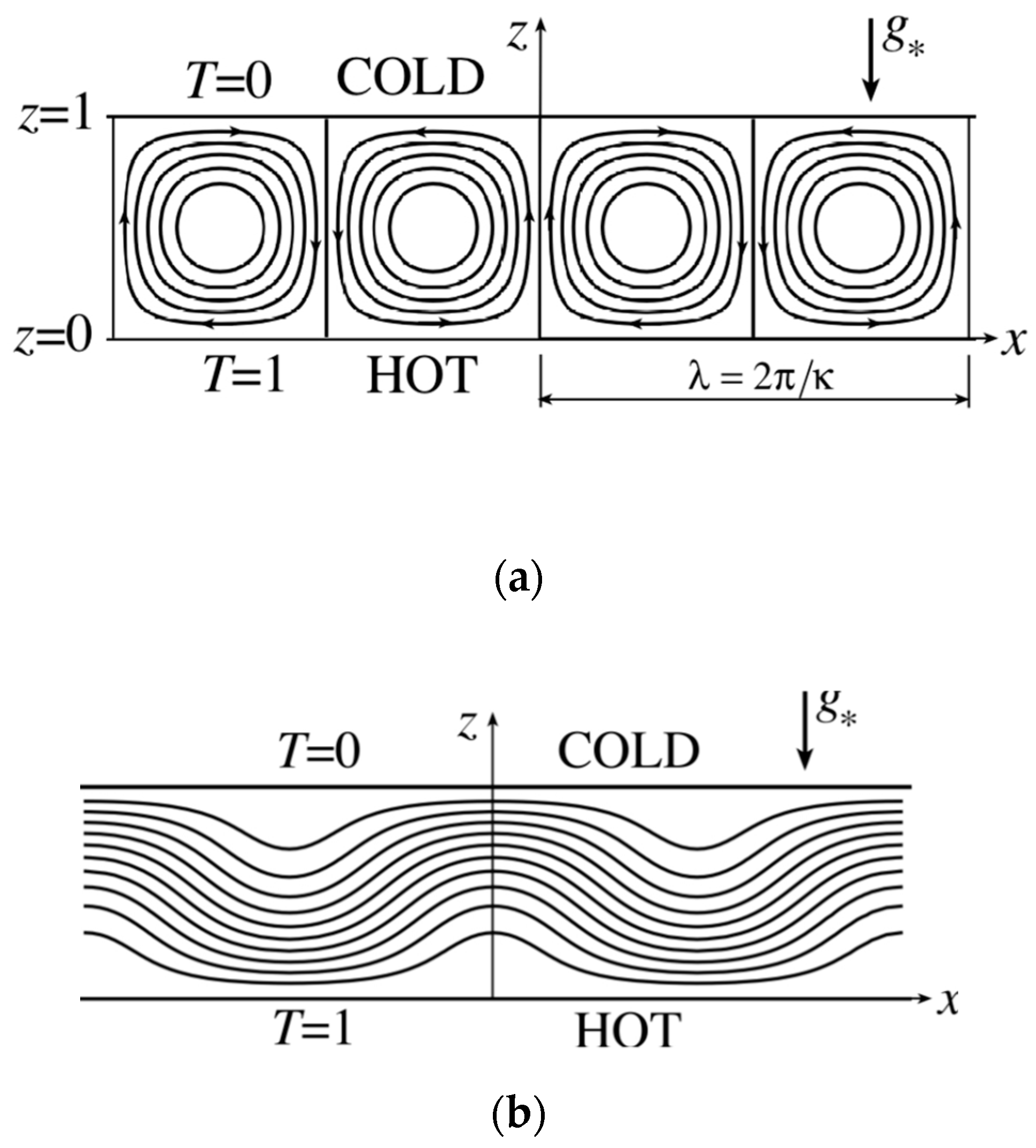
The governing equations for the natural convection in porous media (see
Figure 1) expressed in a dimensionless form (Nield and Bejan [
18], Vadasz and Braester [
19], Braester and Vadasz [
20], Vadasz et al. [
21]) are
where
is the porous media Rayleigh number,
is the dimensionless temperature,
is the dimensionless reduced pressure, and
is the filtration velocity vector. The symbols
stand for thermal expansion coefficient, characteristic temperature difference used to convert the temperature into a dimensionless form, acceleration due to gravity, the height of the porous layer, permeability, effective thermal diffusivity, and kinematic viscosity, respectively. The boundary conditions associated with natural convection in porous media as presented in
Figure 1 are
and
at
, and
and
at
.
Equations (5)–(7) accept a basic motionless solution in the form
The linear stability of this basic solution can be established via a linear stability analysis by subjecting the basic solution (Equation (8)) to small perturbations
and
in the form
where the symbol
stands only to explicitly indicate that these are very small perturbations to the basic solution. Substituting Equations (9) and (10) into the governing Equations (5)–(7) and neglecting nonlinear terms that are
or smaller yields, following the application of the curl operator
twice on Equation (6), the following set of linear partial differential equations
where
is the perturbation of the velocity component in the
direction. The boundary conditions for the perturbed Equations (11) and (12) are
,
at
and at
.
4. Natural Convection in Porous Media—Linear Stability
The solution to this set of equations is obtained via separation of variables in the form
and a similar form for
.
Substituting Equation (13) into the set of Equations (11) and (12) produces the following separate equations
where
are separation constants that will lead to a dispersion relationship linking
to
and
,
, and
is the horizontal Laplacian operator. Equation (14) yields the solution
where further analysis shows that
is a real constant, representing the relative growth rate. The two-dimensional Helmholtz equation (Equation (15)) has solutions for a Cartesian system in the form
Equation (16) subject to the boundary conditions
leads to the solution
Substituting these solutions into Equation (13) yields
that is a stationary wave function, which upon superposition of all modes of convection yields the following complete and general solutions
However, when measuring experimentally or solving numerically the original governing equations only one mode is obtained, i.e.,
(for
it implies
) and the solution has the form
These solutions represent convection rolls as the plane form, as presented in
Figure 2, although other plane forms, such as hexagons, can also be solutions. Equations (24) and (25) definitely show the collapse of the wave function upon observation, similarly as in the solution of the Schrödinger equation and the consequent observation.
As distinct from the quantum mechanics problem the reason for the collapse of the wave function in natural convection is known. It is linked to the dispersion relationship obtained from substituting the separation of variable solutions (Equations (17), (18) and (20)) into Equations (11) and (12) and takes the form
leading to
when
perturbations decay and the basic motionless solution is stable (Equations (13) and (17)). When
perturbations grow and the basic solution is unstable. At marginal stability,
and the characteristic Rayleigh number is
and by observation one concludes that the minimum value of
at marginal stability is obtained when
and when the derivative of
with respect to
in Equation (28) is zero. The graphical description of Equation (27) applicable to
is presented in
Figure 3.
Taking the derivative of
with respect to
in Equation (28) and equating it to zero yields
(
) and for
showing that only one mode survived. The corresponding critical Rayleigh number is obtained by substituting
and Equation (29) into Equation (28) to yield
The reason behind the collapse of the wave-function in natural convection in porous media is because primarily at marginal stability there is only one mode that survives. All other modes decay to zero. Beyond the marginal stability, at supercritical conditions, i.e., supercritical convection when
, (including for values of
), the weak non-linear analysis shows that the amplitude of convection is
, where
representing the relative distance from the critical point. Then, from
Figure 3, it is evident that the largest amplitude is reached at
reinforcing the reason behind the fact that the critical wave number is the dominant mode of convection, a fact that explains the collapse of the wave function in this problem.
5. Rendering Schrödinger Equation from Quantum Mechanics into Euler Equation in Fluid Dynamics
Madelung [
22] showed that the Schrödinger equation can be rendered into equations very similar to the Euler equations and is applicable to potential flow. Starting from Schrödinger equation (Equation (1)) one may represent the (complex) wave function in the form
and upon substituting Equation (32) into Equation (1) and using the notation
one obtains the following set of equations
which are very similar with the Euler equations for compressible flow
Note that
, where
is a unit vector in the direction of the acceleration due to gravity,
is a body force term in addition to gravity, and
is the position vector in Cartesian coordinates. The definition of
from Equation (33) makes this analogy applicable for potential flow only, quite a severe limitation. The relationship between the potentials in Equation (35) and specific terms in Equation (37) is opaque although they can be related to the body force term
. These components are potentials from conservative forces, such as Coulomb’s electrostatic force or similar. Vadasz [
23] showed that the Navier–Stokes equations render into an extended generalized version of the Schrödinger equation.