Integral Balance Methods for Stokes’ First Equation Described by the Left Generalized Fractional Derivative

Abstract

In this paper, the integral balance methods of the Stokes’ first equation have been presented. The approximate solution of the fractional Stokes’ first equation using the heat balance integral method has been proposed. The approximate solution of the fractional Stokes’ first equation using the double integral methods has been proposed. The generalized fractional time derivative operator has been used. The graphical representations of the cubic profile and the quadratic profile for the Stokes’ first problem have been provided. The impacts of the orders of the generalized fractional derivative in the Stokes’ first problem have been investigated. The exponent of the assumed profile for the Stokes’ first equation has been discussed.

1. Introduction

The fractional differential equation is one of the most critical fields in fractional calculus. The Stokes’ first equation is a first differential equation and has received many investigations. The Stokes’ first equation has many applications in physics and the viscoelasticity. The questions related to the determination of the analytical solution and the numerical schemes are the most important questions in the Stokes’ first equations. The Stokes’ first equation for a heated second-grade fluid is very popular in Stokes’ first problems. The Stokes’ first problems have interested many mathematicians in fractional calculus. Ref. [1] has proposed a novel method for getting the analytical solution of the Stokes’ first equation for a heated second-grade fluid. As it was done in [1], the Fourier sine transform and the Laplace transform for getting the analytical solution has been proposed. For the non-Newtonian fluids, the solutions are proposed in [2,3]. As in [4], the Laplace transform method of getting the analytical solution of the Stokes’ first equation for a flat plate second-grade fluid have been used. Recently, the fractional derivatives were introduced in the viscoelasticity problems. The most used fractional derivative operators in the viscoelasticity problems are the Riemann–Liouville fractional derivative [5,6], and the Caputo fractional derivative [5,6]. In addition, many investigations related to the Stokes’ first equation described by the fractional derivative operators exist in the literature. As it was done in [7], the analytical solution of the Rayleigh–Stokes equation described by the Riemann–Liouville fractional derivative has proposed. In [7], the Laplace transform and the Fourier sine transform of getting the analytical solution have been used. Note the use of the Laplace transform, and the Fourier sine transforms depend on the boundary conditions. In other words, the application of the method is possible when we use Dirichlet boundary conditions. It is difficult to be applied when we use Neumann boundary conditions. In [8], the Stokes’ first equation described the Caputo fractional derivative and the Rayleigh–Stokes equation described by the Caputo fractional derivative have been recalled. The analytical solutions of these equations using both the Laplace transform and the Fourier sine transform. The analytical solution of the Stokes’ first equation corresponding to the Newtonian fluids has been proposed. In [9], a new model of the Stokes’ first equation for a heated generalized second-grade fluid using the Atangana–Baleanu fractional derivative has been proposed. The analytical solution using both the Laplace transform and the Fourier sine transform has been presented. There exist some investigations related to the numerical solution of the Stokes’ first equation described by an integer order or non-integer order derivative. In [10], a numerical scheme for the Stokes’ first equation described by the variable order time fractional derivative has been proposed. In [11], the numerical solutions of the Stokes’ first and second equations for fluids have been investigated. In [12], the numerical method of the Rayleigh–Stokes problem for heated generalized second-grade fluid described by the Riemann–Liouville fractional derivative has been proposed. Many other papers related to the numerical method for the Stokes’ first problem exist in the literature.

Recently, a novel method of approaching the exact solutions for the fractional diffusion equations have been developed. The homotopy perturbation method was addressed in [13]. The variational iteration method combined with the Laplace transform method presented in [14]. The heat balance integral method and the double integral method. The HBIM and the DIM techniques are an excellent compromise of approximating the solutions of the parabolic equations [15,16,17]. These methods were developed in this last decade by Myers, Mitchell, and Hristov in many of their works [15,16,17,18]. Regarding HBIM and DIM methods in the Stokes’ first equation, in this paper, we develop the heat balance integral method and the double integral method of getting a new approximate solution of the Stokes’ first equation for a heated generalized second-grade fluid described by the generalized fractional derivative.

In Section 2, we recall the definitions of certain generalized fractional derivative operators and their Laplace transforms. In Section 3, we recall the necessary tools for the applications of the heat balance integral method and the double integral method. In Section 4, we describe the HBIM and the DIM techniques of getting the approximate solution of the Stokes’ first equation. In Section 5, we propose the exponent of the assumed profile for the Stokes’ first equation. In Section 6, we give the explicit form of the approximate solution for the Stokes’ first equation. In Section 7, we discuss the Myers criterion of getting the exponent of the assumed profile. In Section 8, we give the concluding remarks.

2. Fractional Derivative News

Let’s recall certain generalized fractional derivatives, and the Laplace transforms which we will use in this paper [19]. The generalized fractional integral for a function $f:[0,+\infty [⟶\mathbb{R}$ is defined as the following form:

$$\left(I^{\alpha ,\rho }f\right)\left(t\right)=\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_a^t{\left(\frac{t^{\rho }-s^{\rho }}{\rho }\right)}^{\alpha -1}f\left(s\right)\frac{ds}{s^{1-\rho }}.$$

(1)

The generalized fractional derivative for a function $f:[0,+\infty [⟶\mathbb{R}$ is defined as the following form:

$$\left(D^{\alpha ,\rho }f\right)\left(t\right)={\gamma }^n\left({}_a{I}^{\alpha ,\rho }f\right)\left(t\right),n=⌊\alpha ⌋+1,$$

(2)

The Caputo generalized fractional derivative for a function $f:[0,+\infty [⟶\mathbb{R}$ is defined as the following form

$$\left(D_c^{\alpha ,\rho }f\right)\left(t\right)=\left(I^{n-\alpha ,\rho }{\gamma }^{n}f\right)\left(t\right),n=⌊\alpha ⌋+1.$$

(3)

Note in the above definition that we have ${\gamma }^n=t^{1-\rho }\frac{d}{dt}$ and $\mathsf{\Gamma }(.)$ designs the Gamma function. We finish this section by recalling the Laplace transform of fractional integral, the Laplace transform of the generalized fractional derivative and the Laplace transform of the Caputo fractional derivative [19]. The generalized fractional integral of a continuous function f admits a $\rho$-Laplace transform defined as follows:

$${\mathcal{L}}_{\rho }\left\{\left(I^{\alpha ,\rho }f\right)\left(t\right)\right\}=s^{-\alpha }{\mathcal{L}}_{\rho }\left\{f\left(t\right)\right\}.$$

(4)

The generalized fractional derivative of a continuous function f admit a $\rho$-Laplace transform defined as follows:

$${\mathcal{L}}_{\rho }\left\{\left(D^{\alpha ,\rho }f\right)\left(t\right)\right\}=s^{\alpha }{\mathcal{L}}_{\rho }\left\{f\left(t\right)\right\}-\sum _{k=0}^{n-1}{s}^{n-k-1}{\gamma }^k\left(I^{n-\alpha ,\rho }f\right)\left(0\right).$$

(5)

The Caputo generalized fractional derivative of a continuous function f admit a $\rho$-Laplace transform defined as follows:

$${\mathcal{L}}_{\rho }\left\{\left(D_c^{\alpha ,\rho }f\right)\left(t\right)\right\}=s^{\alpha }{\mathcal{L}}_{\rho }\left\{f\left(t\right)\right\}-\sum _{k=0}^{n-1}{s}^{\alpha -k-1}\left({\gamma }^{k}f\right)\left(0\right).$$

(6)

There exist many other fractional derivatives such as the Riemann–Liouville fractional derivative [6,20], the Atangana–Baleanu fractional derivative [9,21,22], the Caputo–Fabrizio fractional derivative [23], the Caputo fractional derivative [6,20], and the conformable fractional derivative [24]. In differentiation and integration to non-integer order, we distinguish the fractional derivatives and the fractal derivatives. For recent advancements of the fractional derivatives, see [21,23,24] and, for the fractal derivatives, see [25,26,27,28].

3. Preliminary Results for the Integral Balance Methods

In this section, we address some preliminary calculations. They will be used later in the application of the heat balance integral method and the double integral method.

For the heat integral balance method, we use the single integral. The method consists of integrating the Stokes’ first equation between 0 to finite penetration depth $\delta$.

For the double integral method, we use the double integral. The technique consists: firstly, we integrate the Stokes’ first equation between x to finite penetration depth $\delta$. Secondly, we integrate the Stokes’ first equation between 0 to finite penetration depth $\delta$.

The application of the integral balance methods uses the following calculations. We assume the approximate solution of the Stokes’ first equation is given by $u(x,t)={\left(1-\frac{x}{\delta }\right)}^n$. We notice $u(0,t)=1$, and the Goodman conditions are defined as follows:

$$u(\delta ,t)=\frac{\partial u(\delta ,t)}{\partial x}=0,$$

(7)

$$\begin{array}{ccc}\hfill {\int }_0^{\delta }{\partial }_{t}u(x,t)dx& =& {\partial }_t{\int }_0^{\delta }{\left(1-\frac{x}{\delta }\right)}^{n}dx\hfill \\ & =& {\partial }_t{\left[-\frac{\delta }{n+1}{\left(1-\frac{x}{\delta }\right)}^{n+1}\right]}_0^{\delta }\hfill \\ & =& {\partial }_t\left[\frac{\delta }{n+1}\right]\hfill \\ & =& \frac{1}{n+1}{\partial }_t\delta ,\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill {\int }_0^{\delta }\frac{{\partial }^{2}u}{\partial x^2}dx& =& {\left[\frac{\partial u}{\partial x}\right]}_0^{\delta }\hfill \\ & =& {\frac{\partial u}{\partial x}}_{\parallel x=\delta }-{\frac{\partial u}{\partial x}}_{\parallel x=0}\hfill \\ & =& \frac{n}{\delta }{\left(1-\frac{x}{\delta }\right)}_{\parallel x=0}^{n-1}\hfill \\ & =& \frac{n}{\delta },\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill {\int }_0^{\delta }{D}_t^{\alpha ,\rho }\frac{{\partial }^{2}u}{\partial x^2}dx& =& D_t^{\alpha ,\rho }{\int }_0^{\delta }\frac{{\partial }^{2}u}{\partial x^2}dx=D_t^{\alpha ,\rho }{\left[\frac{\partial u}{\partial x}\right]}_0^{\delta }\hfill \\ & =& D_t^{\alpha ,\rho }\left[{\frac{\partial u}{\partial x}}_{\parallel x=\delta }-{\frac{\partial u}{\partial x}}_{\parallel x=0}\right]\hfill \\ & =& D_t^{\alpha ,\rho }\frac{n}{\delta }{\left(1-\frac{x}{\delta }\right)}_{\parallel x=0}^{n-1}\hfill \\ & =& D_t^{\alpha ,\rho }\frac{n}{\delta },\hfill \end{array}$$

(10)

$$\begin{array}{ccc}\hfill {\int }_0^{\delta }{\int }_x^{\delta }{\partial }_{t}u(x,t)dxdx& =& {\partial }_t{\int }_0^{\delta }{\int }_x^{\delta }{\left(1-\frac{x}{\delta }\right)}^{n}dxdx\hfill \\ & =& {\partial }_t{\int }_0^{\delta }{\left[-\frac{\delta }{n+1}{\left(1-\frac{x}{\delta }\right)}^{n+1}\right]}_x^{\delta }dx\hfill \\ & =& {\partial }_t{\int }_0^{\delta }\frac{\delta }{n+1}{\left(1-\frac{x}{\delta }\right)}^{n+1}dx\hfill \\ & =& {\partial }_t{\left[-\frac{{\delta }^2}{(n+1)(n+2)}{\left(1-\frac{x}{\delta }\right)}^{n+1}\right]}_0^{\delta }\hfill \\ & =& \frac{1}{(n+1)(n+2)}{\partial }_t{\delta }^2,\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill {\int }_0^{\delta }{\int }_x^{\delta }\frac{{\partial }^{2}u}{\partial x^2}dxdx& =& {\int }_0^{\delta }{\left[\frac{\partial u}{\partial x}\right]}_x^{\delta }dx\hfill \\ & =& -{\int }_0^{\delta }\frac{\partial u}{\partial x}dx\hfill \\ & =& u(0,t),\hfill \end{array}$$

(12)

$$\begin{array}{ccc}\hfill {\int }_0^{\delta }{\int }_x^{\delta }{D}_t^{\alpha ,\rho }\frac{{\partial }^{2}u}{\partial x^2}dxdx& =& D_t^{\alpha ,\rho }{\int }_0^{\delta }{\left[\frac{\partial u}{\partial x}\right]}_x^{\delta }dx\hfill \\ & =& -D_t^{\alpha ,\rho }{\int }_0^{\delta }\frac{\partial u}{\partial x}dx\hfill \\ & =& D_t^{\alpha ,\rho }u(0,t).\hfill \end{array}$$

(13)

4. Approximate Solutions of Stokes’ First Equation

In this section, we investigate the approximate solution of the Stokes’s first equation described by the generalized fractional derivative. We use the heat balance integral method and double integral method of getting the solution of Stokes’ equation. The fractional differential equation under consideration is defined by

$$\frac{\partial u}{\partial t}=\frac{{\partial }^{2}u(x,t)}{\partial x^2}+\eta D_t^{\alpha ,\rho }\frac{{\partial }^{2}u(x,t)}{\partial x^2},$$

(14)

with initial boundary conditions defined as

• $u(x,0)=0$ for $x>0$,
• $u(0,t)=1$ for $t>0$.

The classical heat diffusion equation is obtained when $\alpha =\rho =1$ and $\eta =0$. The question in this section consists of getting the approximate solution of the Stokes’ first equation using the heat balance integral method and the double integral method. We begin by the heat balance integral method (HBIM).

4.1. Heat Integral Balance Method

The subsection aims at investigating the solution of the Stokes’ first equation described by the generalized fractional derivative using the heat balance integral method. Firstly, we stipulate that the approximate solution of the Stokes’ first Equation (14) is defined by

$$u(x,t)={\left(1-\frac{x}{\delta }\right)}^n.$$

(15)

The problem consists of getting the finite penetration depth $\delta$. The finite penetration depth $\delta$ has a physical concept—see in [16,17]. We integrate to both sides of Equation (14) between 0 to the finite penetration depth. We have

$$\begin{array}{ccc}\hfill {\int }_0^{\delta }\frac{\partial u}{\partial t}dx& =& {\int }_0^{\delta }\frac{{\partial }^{2}u(x,t)}{\partial x^2}dx+\eta D_t^{\alpha ,\rho }{\int }_0^{\delta }\frac{{\partial }^{2}u(x,t)}{\partial x^2}dx.\hfill \end{array}$$

(16)

Using identities (8)–(10), we have the following relationships:

$$\begin{array}{ccc}\hfill \frac{1}{n+1}\frac{d\delta }{dt}& =& \frac{n}{\delta }+\eta D_t^{\alpha ,\rho }\frac{n}{\delta }.\hfill \end{array}$$

(17)

Integrating again between 0 to the penetration depth respecting the variable x, we obtain

$$\begin{array}{ccc}\hfill \frac{1}{n+1}\frac{d\delta }{dt}{\int }_0^{\delta }dx& =& \frac{n}{\delta }{\int }_0^{\delta }dx+\eta {\int }_0^{\delta }{D}_t^{\alpha ,\rho }\frac{n}{\delta }dx\hfill \\ \hfill \frac{1}{n+1}\frac{d\delta }{dt}{\int }_0^{\delta }dx& =& \frac{n}{\delta }{\int }_0^{\delta }dx+\eta D_t^{\alpha ,\rho }{\int }_0^{\delta }\frac{n}{\delta }dx\hfill \\ \hfill \frac{1}{n+1}\delta \frac{d\delta }{dt}& =& \frac{n}{\delta }\delta +\eta n{D}_t^{\alpha ,\rho }\frac{1}{\delta }\delta \hfill \\ \hfill \frac{1}{n+1}\frac{d{\delta }^2}{dt}& =& 2n+2\eta n{D}_t^{\alpha ,\rho }\left(1\right)\hfill \\ \hfill \frac{d{\delta }^2}{dt}& =& 2n(n+1)+2\eta n(n+1)D_t^{\alpha ,\rho }\left(1\right).\hfill \end{array}$$

(18)

Applying the $\rho$-Laplace transform to both sides of Equation (18), we have

$$\begin{array}{ccc}\hfill s{\overline{\delta }}^2\left(s\right)& =& \frac{2n(n+1)}{s}+2\eta n(n+1)s^{\alpha -1},\hfill \\ \hfill {\overline{\delta }}^2\left(s\right)& =& \frac{2n(n+1)}{s^2}+2\eta n(n+1)s^{2-\alpha }.\hfill \end{array}$$

(19)

Applying the inverse of $\rho$-Laplace transform to both sides of Equation (19), we have

$$\begin{array}{ccc}\hfill {\delta }^2\left(s\right)& =& 2n(n+1)\left(\frac{t^{\rho }}{\rho }\right)+\frac{2\eta n(n+1)}{\mathsf{\Gamma }(2-\alpha )}{\left(\frac{t^{\rho }}{\rho }\right)}^{1-\alpha },\hfill \\ \hfill {\delta }^2\left(t\right)& =& \left[2n(n+1)+\frac{2\eta n(n+1)}{\mathsf{\Gamma }(2-\alpha )}{\left(\frac{t^{\rho }}{\rho }\right)}^{-\alpha }\right]\left(\frac{t^{\rho }}{\rho }\right).\hfill \end{array}$$

(20)

Thus, the penetration depth of the Stokes’ first equation described by the generalized fractional derivative is given by

$$\delta \left(t\right)={\left(\frac{t^{\rho }}{\rho }\right)}^{1/2}\sqrt{2n(n+1)\left(1+\frac{\eta }{\mathsf{\Gamma }(2-\alpha )}{\left(\frac{t^{\rho }}{\rho }\right)}^{-\alpha }\right)}.$$

(21)

The penetration depth of the Stokes’ first equation for Newtonian fluid is obtained when $\alpha =\rho =1$ [15] given by

$$\delta \left(t\right)=\sqrt{t}\sqrt{2n(n+1)\left(1+\frac{\eta }{t}\right)}.$$

(22)

The penetration depth of the Stokes’ first equation when $\alpha =1$ is given by

$$\delta \left(t\right)={\left(\frac{t^{\rho }}{\rho }\right)}^{1/2}\sqrt{2n(n+1)\left(1+\frac{\eta \rho }{t^{\rho }}\right)}.$$

(23)

We observe that, when $\alpha =\rho =1$ and $\eta =0$, we recover the standard penetration depth of the classical diffusion equation [16,17] and it is in the form

$$\delta \left(t\right)=\sqrt{2n(n+1)t}.$$

(24)

The penetration depth of the Stokes’ first equation described by the Riemann–Liouville fractional derivative is given by

$$\delta \left(t\right)=\sqrt{t}\sqrt{2n(n+1)\left(1+\frac{\eta }{\mathsf{\Gamma }(2-\alpha )t^{\alpha }}\right)}.$$

(25)

4.2. Double Integral Method

In this section, we investigate the penetration depth of the Stokes’ first equation described by the left generalized fractional derivative using the double integral method. We stipulate that the approximate solution of the Stokes’ first Equation (14) is defined by

$$u(x,t)={\left(1-\frac{x}{\delta }\right)}^n.$$

(26)

The problem consists of getting the finite penetration depth $\delta$. We use double integration. Firstly, we integrate to both sides of Equation (14) between x to the finite penetration depth. Secondly, we integrate between 0 to the penetration depth as described in the next paragraph:

$$\begin{array}{ccc}\hfill {\int }_0^{\delta }{\int }_x^{\delta }\frac{\partial u}{\partial t}& =& {\int }_0^{\delta }{\int }_x^{\delta }\frac{{\partial }^{2}u(x,t)}{\partial x^2}+\eta D_t^{\alpha ,\rho }{\int }_0^{\delta }{\int }_x^{\delta }\frac{{\partial }^{2}u(x,t)}{\partial x^2}.\hfill \end{array}$$

(27)

Using the identities (11)–(13), we obtain the following relationships:

$$\begin{array}{ccc}\hfill \frac{1}{(n+1)(n+2)}{\partial }_t{\delta }^2& =& 1+\eta D_t^{\alpha ,\rho }\left(1\right),\hfill \\ \hfill \frac{d{\delta }^2}{dt}& =& (n+1)(n+2)+\eta (n+1)(n+2)D_t^{\alpha ,\rho }\left(1\right).\hfill \end{array}$$

(28)

Applying the $\rho$-Laplace transform to both sides of Equation (28), we have

$$\begin{array}{ccc}\hfill s{\overline{\delta }}^2\left(s\right)& =& \frac{(n+1)(n+2)}{s}+\eta (n+1)(n+2)s^{\alpha -1},\hfill \\ \hfill {\overline{\delta }}^2\left(s\right)& =& \frac{(n+1)(n+2)}{s^2}+\eta (n+1)(n+2)s^{\alpha -2}.\hfill \end{array}$$

(29)

Applying the inverse of $\rho$-Laplace transform to both sides of Equation (29), we have

$$\begin{array}{ccc}\hfill {\delta }^2\left(s\right)& =& (n+1)(n+2)\left(\frac{t^{\rho }}{\rho }\right)+\frac{\eta (n+1)(n+2)}{\mathsf{\Gamma }(2-\alpha )}{\left(\frac{t^{\rho }}{\rho }\right)}^{1-\alpha },\hfill \\ \hfill {\delta }^2\left(t\right)& =& \left[(n+1)(n+2)+\frac{\eta (n+1)(n+2)}{\mathsf{\Gamma }(2-\alpha )}{\left(\frac{t^{\rho }}{\rho }\right)}^{-\alpha }\right]\left(\frac{t^{\rho }}{\rho }\right).\hfill \end{array}$$

(30)

Thus, the penetration depth of the Stokes’ first equation described by the generalized fractional derivative is given by

$$\delta \left(t\right)={\left(\frac{t^{\rho }}{\rho }\right)}^{1/2}\sqrt{(n+1)(n+2)\left(1+\frac{\eta }{\mathsf{\Gamma }(2-\alpha )}{\left(\frac{t^{\rho }}{\rho }\right)}^{-\alpha }\right)}.$$

(31)

The penetration depth of the Stokes’ first equation for Newtonian fluid is obtained when $\alpha =\rho =1$, and given by

$$\delta \left(t\right)=\sqrt{t}\sqrt{(n+1)(n+2)\left(1+\frac{\eta }{t}\right)}.$$

(32)

The penetration depth of the Stokes’ first equation, obtained when $\alpha =1$, is given by

$$\delta \left(t\right)={\left(\frac{t^{\rho }}{\rho }\right)}^{1/2}\sqrt{(n+1)(n+2)\left(1+\frac{\eta \rho }{t^{\rho }}\right)}.$$

(33)

We observe that, when $\alpha =\rho =1$ and $\eta =0$, we recover the classical penetration depth of the classical diffusion equation [16,17]. We have

$$\delta \left(t\right)=\sqrt{(n+1)(n+2)t}.$$

(34)

The penetration depth of the Stokes’ first equation described by the Riemann–Liouville fractional derivative is given by

$$\delta \left(t\right)=\sqrt{t}\sqrt{(n+1)(n+2)\left(1+\frac{\eta }{\mathsf{\Gamma }(2-\alpha )t^{\alpha }}\right)}.$$

(35)

5. Exponent of the Approximate Solution of the Stokes’ First Equation

In this section, we investigate finding the exponent n of the approximate solution of the Stokes’ first equation described by the Riemann–Liouville fractional derivative. The exponent n is the subject of many investigations in the literature. The method of finding the exponent n was proposed by Myers in [16]. This method will be described later. Myers and Mitchell propose another method of finding the exponent n [16,17]. This method called “Matching method” by Hristov that consists of stipulating the penetration depth in the heat balance integral method and the double integral method are the same. This idea is reasonable and physically comprehensive:

$$\begin{array}{ccc}\hfill 2n(n+1)& =& (n+1)(n+2),\hfill \\ \hfill 2n& =& n+2,\hfill \\ \hfill n& =& 2.\hfill \end{array}$$

(36)

With this exponent $n=2$, we will describe the explicit form of the approximate solutions of the Stokes’ first equation.

6. Approximate Solution of the Stokes’ First Equation

In this section, we investigate the graphical representation of the approximate solution of the Stokes’ first equation described by the generalized fractional derivative. We use the exponent $n=2$. We stipulate that the penetration depth obtained with the HBIM and the DIM method is the same. The approximate solution of the Stokes’ first equation described by the left generalized fractional derivative is given by

$$\begin{array}{ccc}\hfill u(x,t)& =& {\left(1-\frac{x}{\delta }\right)}^n\hfill \\ & =& {\left(1-\frac{x}{{\left(\frac{t^{\rho }}{\rho }\right)}^{1/2}\sqrt{2n(n+1)\left(1+\frac{\eta }{\mathsf{\Gamma }(2-\alpha )}{\left(\frac{t^{\rho }}{\rho }\right)}^{-\alpha }\right)}}\right)}^n.\hfill \end{array}$$

With $n=2$, we have

$$\begin{array}{ccc}\hfill u(x,t)& =& {\left(1-\frac{x}{{\left(\frac{t^{\rho }}{\rho }\right)}^{1/2}2\sqrt{3\left(1+\frac{\eta }{\mathsf{\Gamma }(2-\alpha )}{\left(\frac{t^{\rho }}{\rho }\right)}^{-\alpha }\right)}}\right)}^2.\hfill \end{array}$$

(37)

Let’s analyze some special cases. In Figure 1, we depict the behavior of the approximate solution when $\alpha =1$, $t=0.5$ and $\rho \le 1$.

We notice all the curves decay in the space, by following the increase of the order $\rho \le 1$. Observing the behavior of the classical Stokes’ first equation ($\alpha =\rho =1$), we note an acceleration impact in the diffusion process when the order $\rho \le 1$. In Figure 2, we depict the behavior of the approximate solution when $\alpha =1$, $t=0.5$ and $\rho \ge 1$.

We notice all the curves decay in the space, by following the increase of the order $\rho <1$. Observing the behavior of the classical Stokes’ first equation ($\alpha =\rho =1$), we note a retardation impact in the diffusion process when the order $\rho <1$. In Figure 3, we depict the behavior of the approximate solution in the space and in the time with $\alpha =\rho =0.65$.

In Figure 4, we depict the behavior of the approximate solution in the space and the coordinate time with $\rho =1$. It corresponds to Stokes’ first equation for Newtonian fluid.

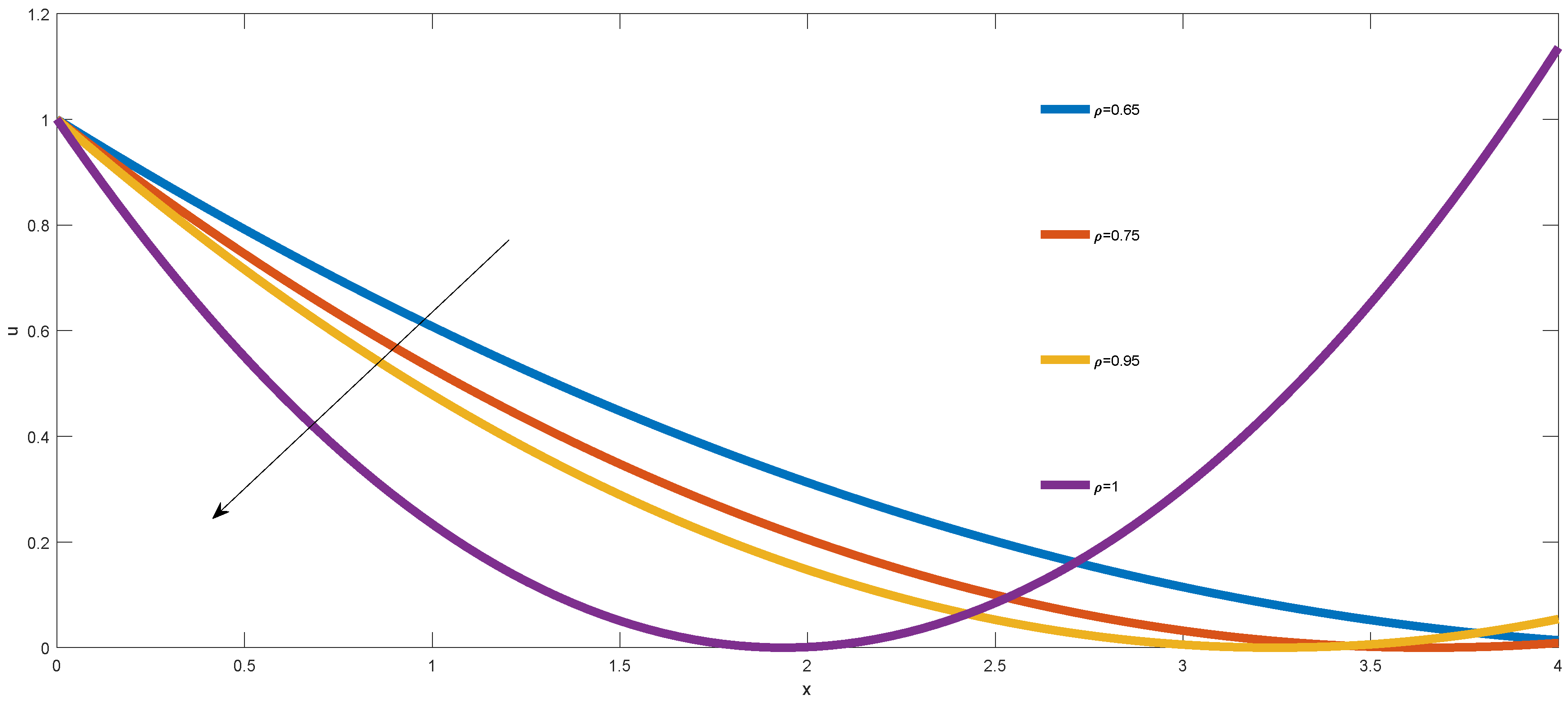
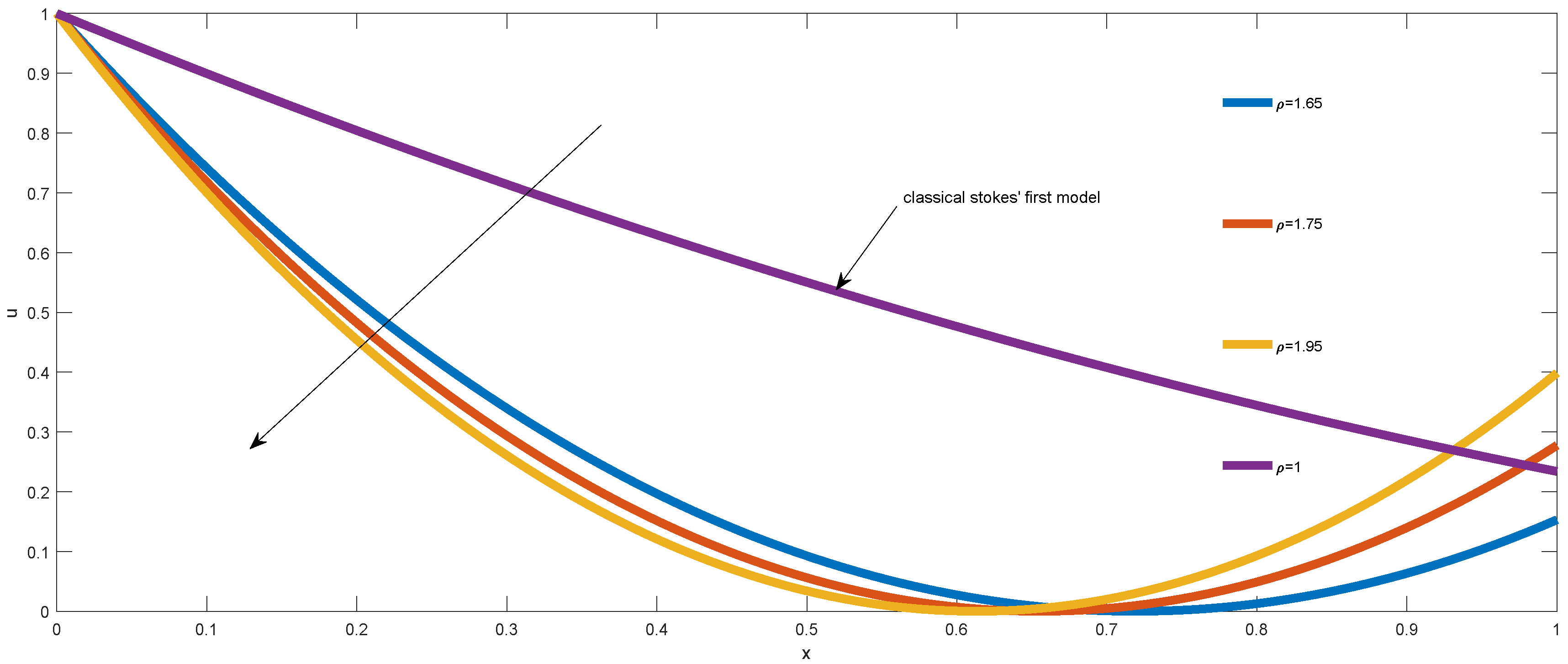
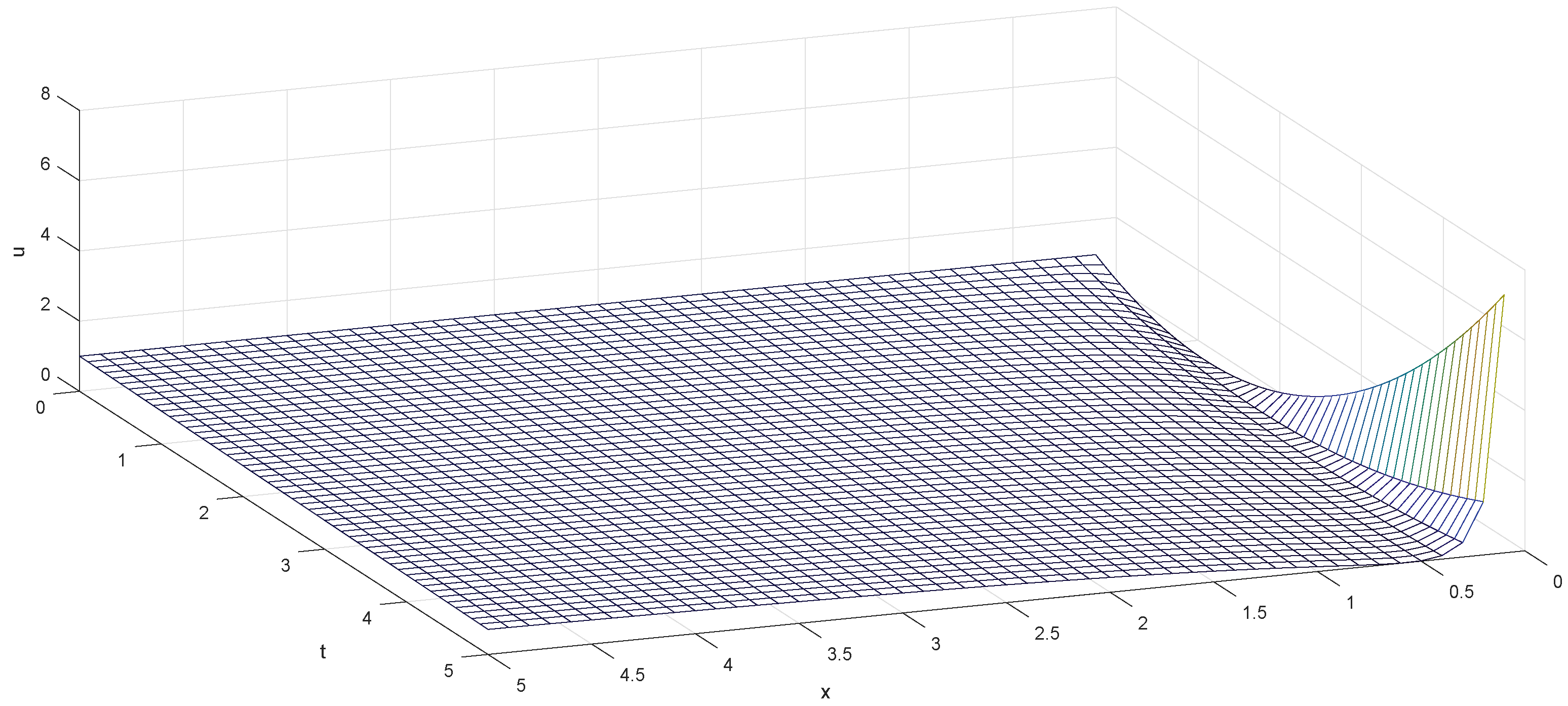
7. Physical Discussion

In this section, we describe the physical meanings of our works briefly. The physical proposition of our works is to propose the flow profile of the Stokes’ first problem. Note that the similarity variable plays an important role in the determination of the flow profiles of the physical models. Our objective in this paper is to propose the flow of the Stokes’ first problem using the penetration depth, which is a physical method, by forgetting the mathematical aspect of the model (14). In other words, the model is a mathematical equation; it can be solved using many mathematical tools; here, we forget these tools and propose the flow profile using the physical concepts. The integral balance method is a good compromise to determine the flow profile by using the similarity variable. The HBIM and DIM propose the approximate value of the penetration depth. This penetration depth is used to give the similarity variable and to deduce the form of the flow profile. In our work, the similarity variable permit to classify the Stokes’ first problem in two classes: Stokes’ first problem for Newtonian fluid and the Stokes’ first problem for generalized second-grade fluid. Let us make $\alpha =\rho =1$ and $\eta =0$; using the penetration depth Equation (23), the similarity variable is given by $x/2\sqrt{t}$ when $n=1$, which represents the similarity variable of the Stokes’ first problem for a Newtonian fluid. Using the similarity variable, the exact flow profile for Newtonian fluid is given by

$$u(x,t)=1-erf\left(\frac{x}{2\sqrt{t}}\right),$$

where $erf(\dots )$ denotes the Gaussian function. In general for a Newtonian fluid when the value of the exponent is arbitrary, the similarity variable is in the form $x/\sqrt{t}\sqrt{2n(n+1)}$. Let us have $\alpha =\rho =1$ and $\eta \ne 0$. The similarity variable of the Stokes’ first problem coincides with the similarity variable for a heated second-grade fluid, for a long time of diffusion. With classical mathematical tools, the profile of the flow is difficult to be established, and the graphical representation of the solution is not trivial. Our method proposes the following approximate flow profile for Stokes’ first problem for a heated second-grade fluid

$$u(x,t)={\left(1-\frac{x}{\sqrt{t}2\sqrt{3\left(1+\frac{\eta }{t}\right)}}\right)}^2,$$

where we stipulate the exponent $n=2$. The graphical representation of the flow is depicted in Figure 2. The above flow profile confirms Teipel works [29] on Stokes’ first equation. The similarity solution by series expansion is not possible [29]. Our observation is that, when the time of the diffusion process is very long, the similarity variable of the Stokes’ first problem can be obtained and is in the form when we use $HBIM$ $x/\sqrt{t}\sqrt{2n(n+1)}$ because the term $\frac{\eta }{\mathsf{\Gamma }(2-\alpha )}{\left(\frac{t^{\rho }}{\rho }\right)}^{-\alpha }$ converges to zero. A conclusion is that, when the time of the diffusion process is very long, we recover the similarity variable and the flow profile of the Newtonian fluid.

8. Optimization of the Residual Function

In this section, we give a brief exposition related to the Myers method of getting the exponent n of the assumed profile. Let us have the residual function of the Stokes’ first equation as

$$R\left(u_a(x,t)\right)=\frac{\partial u_a}{\partial t}-\frac{{\partial }^2{u}_a(x,t)}{\partial x^2}-\eta D_t^{\alpha ,\rho }\frac{{\partial }^2{u}_a(x,t)}{\partial x^2},$$

(38)

where $u_a$ is the approximate solution of the Stokes’ first equation. Let us define the Langford function defined by

$${\int }_0^{\delta }{R}^2\left(u_a(x,t)\right)dx⟶min.$$

(39)

Naturally by Myers, when the approximate solution $u_a$ is the exact solution or approach exact solution u, then the residual function should be zero or approach zero too. That is, $R\left(u_a(x,t)\right)=0.$ Myers criterion of getting exponent n consists of finding an optimal n that minimizes the Langford function. A trivial consequence of the Myers criterion is that the residual function should attend its minimum for certain values of the exponent $n.$ Thus, we can obtain the value of the exponent n at the boundary conditions ($x=0$ and $x=\delta$). In other words, the Goodman condition should be satisfied:

$$u_a(x,0)=\frac{\partial u_a(\delta ,t)}{\partial x}=0.$$

(40)

We begin by recalling some calculations strategical for the Residual function:

$$\frac{\partial u_a}{\partial t}=n{\left(1-\frac{x}{\delta }\right)}^{n-1}\left(\frac{x}{{\delta }^2}\right)\frac{d\delta }{dt},$$

(41)

$$\frac{{\partial }^2{u}_a}{\partial x^2}=\frac{n(n-1)}{{\delta }^2}{\left(1-\frac{x}{\delta }\right)}^{n-2}.$$

(42)

We investigate the value of the $D_t^{\alpha ,\rho }\left(\frac{{\partial }^2{u}_a}{\partial x^2}\right)$. We first recall the Taylor expansion of the function ${\left(1-\frac{x}{\delta }\right)}^{n-2}$. We have the following relation:

$${\left(1-\frac{x}{\delta }\right)}^{n-2}=1-\frac{(n-2)x}{\delta }+o\left(\frac{x}{\delta }\right).$$

(43)

Thus, we have the following relationship:

$$D_t^{\alpha ,\rho }\left(\frac{{\partial }^2{u}_a}{\partial x^2}\right)=n(n-1)D_t^{\alpha ,\rho }\left(\frac{1}{{\delta }^2}\right)-n(n-1)(n-2)x{D}_t^{\alpha ,\rho }\left(\frac{1}{{\delta }^3}\right).$$

(44)

The residual function of the Stokes’ first equation defined by Equation (14) is given by

$$\begin{array}{ccc}\hfill R\left(u_a(x,t)\right)& =& n{\left(1-\frac{x}{\delta }\right)}^{n-1}\left(\frac{x}{{\delta }^2}\right)\frac{d\delta }{dt}-\frac{n(n-1)}{{\delta }^2}{\left(1-\frac{x}{\delta }\right)}^{n-2}\hfill \\ & -& n(n-1)\eta D_t^{\alpha ,\rho }\left(\frac{1}{{\delta }^2}\right)+n(n-1)(n-2)x\eta D_t^{\alpha ,\rho }\left(\frac{1}{{\delta }^3}\right).\hfill \end{array}$$

(45)

At $x=0$, in order to satisfy the Goodman conditions, the Residual function should be zero and then we have

$$\begin{array}{ccc}\hfill R\left(u_a(0,t)\right)=-\frac{n(n-1)}{{\delta }^2}-n(n-1)\eta D_t^{\alpha ,\rho }\left(\frac{1}{{\delta }^2}\right)& =& 0,\hfill \\ \hfill n-1& =& 0,\hfill \\ \hfill n& =& 1.\hfill \end{array}$$

(46)

At $x=\delta$ and $\eta =0$, in order to satisfy the Goodman conditions, the Residual function should be zero and then we have

$$\underset{x\to \delta }{lim}\frac{n(n-1)}{{\delta }^2}{\left(1-\frac{x}{\delta }\right)}^{n-2}=0$$

when $n=2.$ Note that the exponent $n=1$ and $n=2$ found at the boundary conditions are not necessary for the optimal exponent that minimizes the Langford function. An alternative is finding n by minimizing the function

$${\int }_0^{\delta }{R}^2\left(u_a(x,t)\right)dx$$

(47)

with the residual function defined by Equation (45). The result is not trivial. In this paper, we accept the optimal exponent $n=2$ in the previous section. The method used in Section 6 is more straightforward than the Myers criterion defined in this section. In conclusion, for the Stokes’ first equation, we assume that the approximate solution is quadratic. That is,

$$u(x,t)={\left(1-\frac{x}{\delta }\right)}^2.$$

(48)

The penetration depth $\delta$ is obtained with HBIM method or the DIM method.

9. Conclusions

In this paper, we have discussed the approximate solution of the Stokes’ first equation described by the generalized fractional derivative. We have analyzed the impact of the order $\rho$ in the diffusion process. The order $\rho$ have in general a retardation or an acceleration effect in the diffusion process. Furthermore, the quadratic function is a good compromise to approach the exact solution of the Stokes’ first equation.