Entropy Production, Entropy Generation, and Fokker-Planck Equations for Cancer Cell Growth
Abstract
:1. Introduction
2. Non-Equilibrium Fokker-Planck Equations
3. Entropy Production and Fokker-Planck Equations
4. Entropy Generation and Fokker-Planck Equations
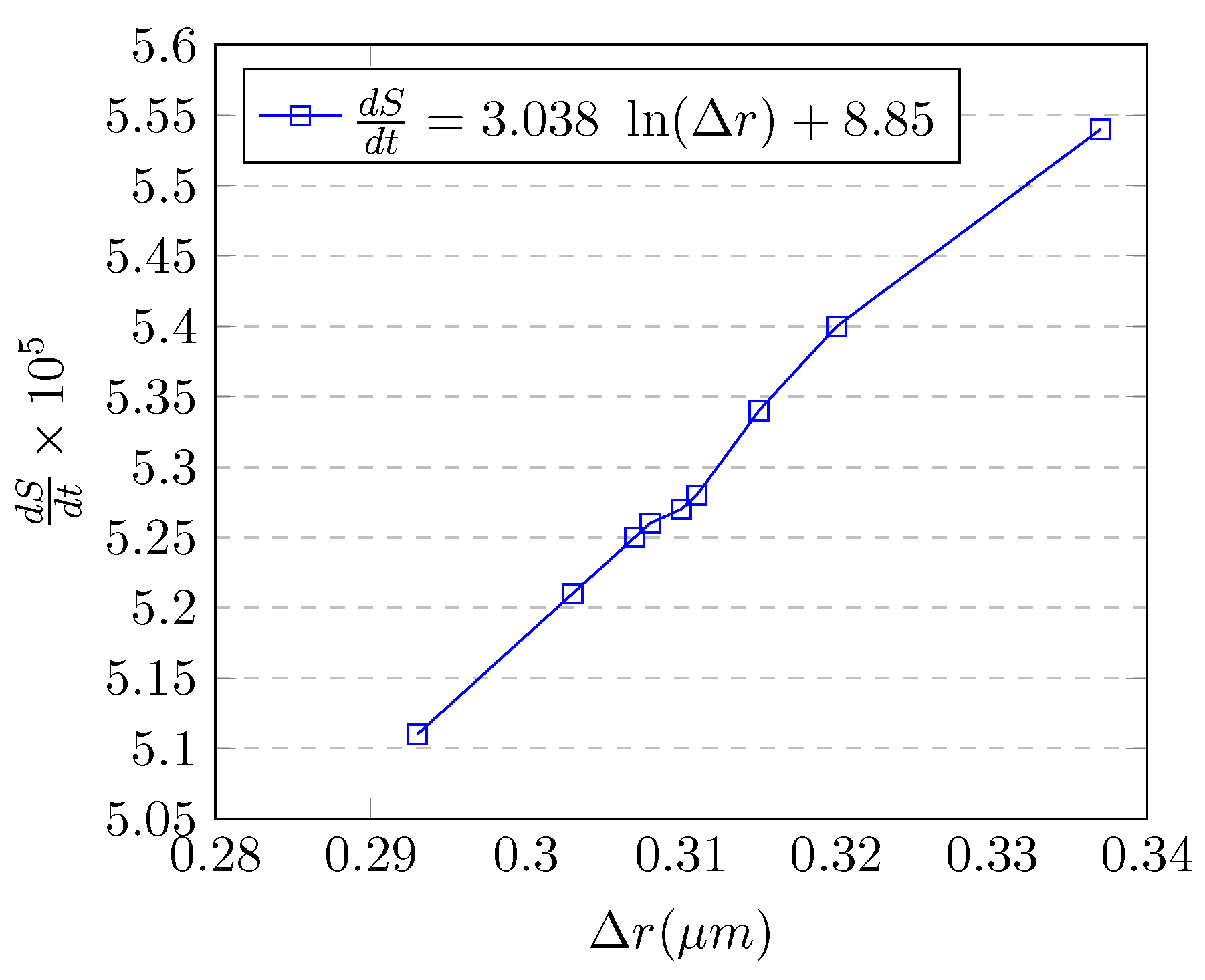
5. A Generalized Model for Cancer Growth
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Levine, H. Introduction to physics in cancer research. Cancer Res. 2014, 74, 4572. [Google Scholar] [CrossRef] [PubMed]
- Solomon, K.A. Physics and cancer. Phys. Today 2002, 55. [Google Scholar] [CrossRef]
- Klopper, A. Topics in non-equilibrium physics. Nat. Phys. Insight 2015, 11. [Google Scholar] [CrossRef]
- Jordan, R.; Kinderlehrer, D.; Otto, F. The variational formulation of the fokker-planck equation. SIAM J. Math. Anal. 1996, 29, 1. [Google Scholar] [CrossRef]
- Lucia, U. Entropy generation and the fokker-planck equation. Phys. A 2014, 393, 256. [Google Scholar] [CrossRef]
- Tome, T. Entropy production in nonequilibrium systems described by a Fokker-Planck equation. Braz. J. Phys. 2006, 36, 1285. [Google Scholar] [CrossRef]
- Nicolas, G.; Prigogine, I. Self-Organization in Nonequilibrium Systems; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Tome, T.; DeOliviera, M.J.T. Entropy production in irreversible systems described by a Fokker-Planck equation. Phys. Rev. E 2010, 82, 021120. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tome, T.; DeOliviera, M.J.T. Entropy Production in Nonequilibrium Systems at Stationary States. Phys. Rev. Lett. 2012, 108, 020601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tome, T.; DeOliviera, M.J.T. Stochastic approach to equilibrium and nonequilibrium thermodynamics. Phys. Rev. E 2015, 91, 042140. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Esposito, M.; Van den Broeck, C. Three faces of the second law. I. Master equation formulation. Phys. Rev. E 2010, 82, 011143. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Van den Broeck, C.; Esposito, M. Three faces of the second law. II. Fokker-Planck formulation. Phys. Rev. E 2010, 82, 011144. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dewar, R. Information theory explanation of the fluctuation theorem, maximum entropy production and self-organized criticality in non-equilibrium stationary states. J. Phys. A Math. Gen. 2003, 36, 631. [Google Scholar] [CrossRef]
- Lucia, U. Statistical approach of the irreversible entropy variation. Phys. A Stat. Mech. Appl. 2008, 387, 3454–3460. [Google Scholar] [CrossRef]
- Lucia, U. Irreversibility, entropy and incomplete information. Phys. A Stat. Mech. Appl. 2009, 388, 4025–4033. [Google Scholar] [CrossRef]
- Lucia, U. Maximum entropy generation and κ-exponential model. Phys. A Stat. Mech. Appl. 2010, 389, 4558–4563. [Google Scholar] [CrossRef]
- Cohen, M.; Grieblin, T.; Ahaghotu, C.; Rokhlin, O.; Ross, J. Cellular adhesion molecules in urologic malignancies. Am. J. Clin. Pathol. 1997, 107, 56–63. [Google Scholar] [CrossRef] [PubMed]
- Okegawa, T.; Pong, R.; Li, Y.; Hsieh, J.T. The role of cell adhesion molecule in cancer progression and its application in cancer therapy. Acta Biochim. Pol. 2004, 51, 445. [Google Scholar] [PubMed]
- London, F. The general theory of molecular forces. Trans. Faraday Soc. 1937, 33, 8b. [Google Scholar] [CrossRef]
- Iyer, S.; Gaikwad, R.M.; Subba-Rao, V.; Woodworth, C.D.; Sokolov, I. Atomic force microscopy detects differences in the surface brush of normal and cancerous cells. Nat. Nanotechnol. 2009, 4, 389–393. [Google Scholar] [CrossRef] [PubMed] [Green Version]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Capotosto, S.; Smoot, B.; Hallford, R.; Sharma, P. Entropy Production, Entropy Generation, and Fokker-Planck Equations for Cancer Cell Growth. Physics 2019, 1, 147-153. https://doi.org/10.3390/physics1010014
Capotosto S, Smoot B, Hallford R, Sharma P. Entropy Production, Entropy Generation, and Fokker-Planck Equations for Cancer Cell Growth. Physics. 2019; 1(1):147-153. https://doi.org/10.3390/physics1010014
Chicago/Turabian StyleCapotosto, Salvatore, Bailey Smoot, Randal Hallford, and Preet Sharma. 2019. "Entropy Production, Entropy Generation, and Fokker-Planck Equations for Cancer Cell Growth" Physics 1, no. 1: 147-153. https://doi.org/10.3390/physics1010014




