Energy Consumption Framework and Analysis of Post-Quantum Key-Generation on Embedded Devices

Abstract

The emergence of quantum computing and Shor’s algorithm necessitates an imminent shift from current public key cryptography techniques to post-quantum-robust techniques. The NIST has responded by standardising Post-Quantum Cryptography (PQC) algorithms, with ML-KEM (FIPS-203) slated to replace ECDH (Elliptic Curve Diffie-Hellman) for key exchange. A key practical concern for PQC adoption is energy consumption. This paper introduces a new framework for measuring PQC energy consumption on a Raspberry Pi when performing key generation. The framework uses both the available traditional methods and the newly standardised ML-KEM algorithm via the commonly utilised OpenSSL library.

1. Introduction

Ensuring data confidentiality relies heavily on cryptographic techniques. Whilst single-key symmetric encryption such as AES-256 [1] offers efficiency for bulk data encryption, the secure establishment and rotation of the shared keys used is critical to the success of maintaining confidentiality. A primary challenge of encryption is that keys require sharing between parties, but that the channel between them may be subject to interception and eavesdropping. Many of the activities that are carried out online, from Internet banking to commerce sites or reading the news, all now typically use secure HTTPS and encryption. If a key used for encryption were to become known, then in some applications there may be severe consequences, as it could potentially be used to impersonate either party in the transaction or to decrypt that data. Given the vast scale and dynamic combination of users and sites, it is not practical to pre-generate and distribute all cryptographic key combinations in advance, so the keys must be negotiated ad hoc: as they become required online. It is therefore critically important to ensure that encryption keys are negotiated securely and kept protected from potential adversaries.

Fortunately, cryptographic keys are typically generated and negotiated using asymmetric cryptography techniques first disclosed to the academic community by Diffie and Hellman [2]. Here, each party has its own key-pair comprising their own private and public keys, and a mathematical technique is used to combine the other party’s public key with a local secret private key to negotiate a secure channel in which only those two parties can participate. Assuming a strong method, this addresses the issues of eavesdropping and confidentiality, and also addresses a malicious actor attempting to interpose themselves into communications.

1.1. Key Generation with Hybrid Encryption

Whilst this asymmetric method can be used for data encryption, it is typically far less efficient (in time and energy resources) than for communications protected with symmetric encryption [3]. The asymmetric channel’s typical main purpose therefore becomes the secure sharing of the symmetric algorithm’s key material, with the bulk data then conveyed symmetrically and encrypted with this key. This standard approach to modern cryptography is known as ‘hybrid encryption’ [4], trading-off the characteristics of each technique for reasons of convenience, efficiency, and confidentiality.

Asymmetric key generation techniques are a critical part of current hybrid cryptography, with popular methods including RSA [5] and Elliptic Curve Cryptography (ECC) [6,7]. If these methods were to be fundamentally compromised, then access to the negotiated secret symmetric keys could be revealed, with the consequence of data decryption becoming trivial.

1.2. Quantum Computing Exploits

For some time, it has been known that the mathematical principles underpinning RSA and ECC’s security, whilst computationally intensive and difficult for a classical computer-based attack, are potentially readily solvable with quantum computing hardware. Shor’s algorithm [8] is notable in this respect, as it is able to factorise large numbers extremely efficiently. This development necessitates the creation of alternative techniques for secure key exchange in a ‘post-quantum’ world, particularly as encrypted data could be stored and recovered later using these methods. In response to this threat, the National Institute of Standards and Technology (NIST) has been a leader, initiating a competition in 2017 to identify promising post-quantum cryptography (PQC) methods [9]. These techniques rely on differing mathematical problems, believed to be resistant to both known classical and quantum computing algorithms.

1.3. Aim of the Paper

The key aim of this paper is to analyse and compare the energy efficiency of standard pre- and post-quantum NIST cryptographic key generation algorithms, as implemented in the OpenSSL 3.5 library released in April 2025 [10]. It differs from other evaluations, which have typically concentrated on time performance rather than energy performance, e.g., ‘openssl speed’ to give tables such as in [11] and from other work in the energy recording area such as Tasopoulos et al. [12]. It creates a framework for the readily available Raspberry Pi and makes use of accurate, commodity USB energy meters.

The Raspberry Pi is a popular single-board computer platform increasingly utilised in industrial process applications [13], where controllers are typically embedded with long operational lifetimes and where energy constraints can be a defining factor in design and implementation.

2. Related Literature

2.1. Energy Relating to Thermodynamic Principles

This study’s findings on the energy consumption incurred by key generation algorithms align with the fundamental thermodynamic limits of computation, notably Landauer’s principle of minimum energy dissipation [14]. Whilst the measured energy values are orders of magnitude above this theoretical bound due to the practical hardware design and inefficiencies, experimental validations of the principle by Berut et al. [15], and Bennett’s review [16] illustrated the unavoidable physical energy costs of computation in the context of information processing: here, the key generation activities.

2.2. Post-Quantum Cryptography (PQC)

The imminent emergence of quantum computing is fast becoming a problem in reality, not only for cryptographers, but also for users of cryptography. What was once purely a theoretical problem relegated to the ‘long grass’ of the future has emerged as a pressing concern within the 2020s, as Aydeger et al. outlined [17]. The potential impact of quantum computing on cryptography poses a significant threat to the existing hegemony of cryptographic standards. These techniques, including RSA [5] (from 1978), DES/3DES [18,19] (1977/1995), and more recently others including AES [1] (2001) and Elliptic Curve Cryptography (ECC), whose applicability is outlined in papers such as Koblitz [6] and Miller [7] from the late 1980s, have proven to be the bedrock of the practical protection of communications over the last decades [17].

2.2.1. In the Classical Space

The main algorithms in contemporary use are not currently known to have fundamental flaws that can be exploited by attacks based on classical computing. Whilst classical computing capabilities have risen exponentially, this increase has been largely driven by Moore’s Law [20] and the self-governed targets of the semiconductor industry, as outlined in reports such as the IEEE International Roadmap for Devices and Systems [21]. Specialised computing branches, including massively parallel GPUs, ASICs, and FPGAs, have achieved performance gains that outpaced Moore’s Law for general-purpose computing hardware, further contributing to the potential for stronger cryptographic algorithm attacks. Despite these improvements, the underlying mathematical problems on which cryptographic techniques rely have remained largely intact, with key sizes increasing to meet user expectations for security, and the required window of protection. One such mathematical characteristic is the computational hardness of large-number factorisation, a principle that protects both key exchange and the integrity of digital signatures. By using appropriately chosen cryptographic parameters, data protected by these traditional methods are expected to remain secure for decades, centuries, or even millennia, due to the time and energy required to mount a successful attack using classical computing methodologies.

2.2.2. The Rise of the ‘Quantum’ Machines

The general availability of powerful quantum computers would fundamentally alter the capability to attack existing cryptography standards, and significant progress has been made in theoretical attack vectors and the production of small-scale quantum computers. Although the progress achieved may currently seem limited, technological improvements often occur on a logarithmic scale (see Moore’s Law [20]), with seemingly slow initial progress rapidly transforming into significant advancements. Algorithms such as Shor [8] exemplify this threat, reducing what was once a logarithmically difficult factorisation problem for classical devices into one that can be solved relatively easily using sufficiently large quantum computers. Quantum computing has the capacity to perform calculations across many states simultaneously, breaking the logarithmic protection of the techniques commonly deployed including ECC and RSA. Widespread quantum computing availability in the near future poses a particular concern, as adversaries may already be engaging in ‘Store Now, Decrypt Later’ (SNDL) activities in anticipation. This is clearly a concern for sectors where long-term data confidentiality is crucial, such as the protection of proprietary information in industry and ‘top-secret’ government activities.

2.2.3. Standardisation and Governmental Response

The risks highlighted by quantum computing have focused the attention of governments, industry, and the research community, prompting a wide range of response activities. The research presented in this paper was selected to contribute to the development and validation of new post-quantum cryptography (PQC) techniques and standards, specifically examining the practical reality of energy use. PQC methods currently appear to be more resilient to both classical and potential quantum computing attacks than existing key-generation algorithms including RSA and ECC [9]. Governments worldwide are establishing timelines for the transition away from quantum-vulnerable algorithms to quantum-resistant techniques. Australia’s approach is among the most ambitious, with a target to complete the transition by 2030 [22]. Many other countries and administrative domains are also setting ambitious deadlines in the 2030s, including the UK [23], the US [24], and the EU (through individual agencies in member states) [25,26].

2.3. Vulnerabilities Exposed by Quantum Computing

Shor’s algorithm, presented in 1994 [8], poses a significant theoretical threat to traditional public-key cryptography, and is well known as a critical issue which must be addressed. Shor offers a ‘polynomial-time quantum algorithm’ for factorising large integers, a computationally hard problem for classical computers, and is the basis of many classical key exchange mechanisms. Although highly speculative, some industry estimates such as those from MITRE [27], suggest that attacks on RSA-2048 could become feasible by 2035. It is probable that ‘Store Now, Decrypt Later’ activities are already underway, anticipating quantum computing’s potential. This highlights why the subject is receiving urgent attention in critical government, military, and commercial applications, where confidentiality time-frames must be maintained beyond the prospective availability of quantum computing techniques.

Another significant quantum algorithm that threatens modern cryptography is Grover’s algorithm: ‘A fast quantum mechanical algorithm for database search’ [28] (1996). Grover’s algorithm provides a quadratic speedup for searching unsorted databases (such as the AES keyspace), effectively halving the key length of symmetric algorithms like AES [28], thus AES-256’s effective security is reduced to AES-128. Whilst this still provides a sufficient-sized window for the foreseeable future, halving the effective number of bits weakens the encryption and leaves it more vulnerable should further advances be made in this area.

Despite their theoretical nature, the increasing feasibility of quantum computing has driven significant attention to Post-Quantum Cryptography (PQC) at regulatory and governmental levels. While the extension of existing algorithms has been explored, with larger keys for example, the consensus is that practical RSA is fundamentally vulnerable to Shor’s algorithm on a sufficiently powerful quantum computer. Simply increasing the key size is not a viable long-term solution, with Bernstein et al. [29] suggesting impractical key sizes (e.g., 1 TB) would be needed for post-quantum safety. Section 3 of this paper demonstrates the exponentially increasing resource demands (time and energy) for generating larger RSA key pairs (e.g., 4096-bit). Whilst the impact of Grover algorithm’s is considered less catastrophic compared with the potential of Shor’s, the cryptographic community is also actively exploring ways to reinforce symmetric encryption security and address other limitations of algorithms like AES [30] after its 20+ years of practical use.

2.4. NIST Standardisation

In 2022, the National Institute of Standards and Technology (NIST) finalised its first set of quantum-resistant cryptographic algorithms [9] following a standardisation process initiated in 2017. This competition aimed to identify cryptographic methods resilient to both classical and quantum computer attacks. The selected algorithms were published as Federal Information Processing Standards (FIPS), establishing them as de facto standards suitable for production use [31]. NIST’s FIPS standards are widely recognised benchmarks for cryptography, making NIST’s PQC selections likely to be adopted by industry and governments internationally.

This paper primarily focuses on FIPS 203 [32], which standardises ML-KEM (formerly Kyber). ML-KEM is a Key Exchange Mechanism (KEM) that securely establishes a session between two parties using asymmetric encryption, subsequently enabling a shared secret symmetric key to be agreed and used for the secure encryption of data transfers between the parties. It employs lattice-based cryptography, relying on the mathematical difficulty of lattice problems like the Shortest Vector Problem (SVP) and Learning With Errors (LWE), believed to be hard to attack using both classical and quantum computers [31]. ML-KEM is designed to replace existing key-exchange protocols in applications, e.g., for websites and setting up other secure channels.

Whilst ML-KEM is currently the only finalised FIPS standard for post-quantum key exchange, in March 2025, the NIST further selected Hamming Quasi-Cyclic (HQC) [33] as an alternative method to move towards standardisation. For this paper’s experimentation, ML-KEM was used, owing to its integration into the OpenSSL 3.5 production library [10]. The first batch of NIST PQC standards [31] also included two digital signature algorithms: FIPS 204 [34], standardising ML-DSA (formerly Dilithium); and FIPS 205 [35], detailing SLH-DSA (formerly SPHINCS+).

Beyond the First Batch PQC Standards—Round 4

Many of the cryptographic techniques in the PQC process are based on lattice-based category methods [33], which unlike other techniques do not have a long history of use and validation nor have formal proofs attached to them. The NIST therefore sought diverse algorithm candidates, to mitigate risks associated with potential vulnerabilities in a specific category (specifically lattices), as noted on page 4 of the Round-4 NIST PQC status paper [33].

As part of the evaluation of these candidates, the Isogeny-based key exchange candidate SIKE was withdrawn after a flaw was discovered—see pp. 1, 8 and 16 of [33]. Subsequently, the NIST selected Hamming Quasi-Cyclic (HQC), as per page 18 in the same document [33], a non-lattice-based key exchange protocol utilising ‘quasi-cyclic codes’, for standardisation. This alternative will proceed towards formalisation with a designated name and FIPS standard. Having multiple standardised options also allows for easier adoption of alternatives based on the environmental requirements of the deployment, such as bounds of working memory or key length. This desire for diverse characteristics across all areas is highlighted throughout the Round 4 status paper [33].

2.5. Energy Efficiency in PQC

This section reviews studies on the energy efficiency of post-quantum cryptography (PQC) algorithms, especially within Transport Layer Security (TLS) and resource-constrained devices. Paquin et al. [36] analysed the integration of quantum-resistant cryptography into TLS. Their benchmarking quantified computational and data transfer overheads, revealing the feasibility of PQC in web communication, though some algorithms increased the overall network traffic due to larger key sizes and overheads. Notably, the lattice-based techniques showed comparable results to classical methods, suggesting deployment of PQC is practical with the careful selection of algorithms (e.g., NIST standardisation efforts).

Barton et al. [37] also examined PQC integration into TLS, specifically focusing on constrained environments (similarly to this study) and highlighting the inherent challenges. This pre-NIST standardisation work indicated potential additional PQC overheads (latency, computation, traffic) that vary with security level, compared to low-power classical cryptographic methods.

Tasopoulos et al. [12], also pre-NIST but evaluating many of its candidates, verified the resource utilisation of a complete TLS 1.3 implementation, and provided a valuable point of reference when validating the results of this paper. They found that PQC could be implemented in resource-limited settings, the with lattice-based Kyber showing favourable performance. However, some other algorithms were less energy-efficient than the classical alternatives, emphasising the importance of appropriate algorithm selection during implementation.

Schöffel et al. [38] specifically examined the energy costs of PQC Key Exchange Mechanisms (KEMs) in TLS-based low-power IoT devices. Their findings reinforced the significant energy cost variations among PQC techniques, reiterating the importance of selecting appropriate algorithms to minimise power consumption, based on both security needs and environmental constraints.

Finally, Roma et al. [39]’s analysis of PQC energy efficiency in mobile and large-scale environments showed performance variations based on vastly different architectures, but again highlighted the energy efficiency of lattice-based techniques. They concluded that algorithm selection should depend on specific requirements and platform characteristics, noting the increased significance of energy costs at scale and the impact on battery life in portable applications.

In summary, these studies collectively demonstrated the feasibility of integrating PQC in low-power devices, but consistently emphasised the need for careful algorithm and parameter selection. This is particularly the case in resource-constrained environments, to manage trade-offs in computation, memory, data transfer, and energy. Lattice-based techniques often appear efficient, aligning with early NIST selections. However, non-PQC algorithms may remain a valid choice when the implementation platform does not support post-quantum cryptography or where confidentiality or integrity are not deemed to be critical concerns and the platform can be de-prioritised based on risk.

The following section details the methodology for researching the energy efficiency of key generation algorithms on the target hardware platform.

3. Implementation

The NIST’s PQC standardisation efforts are widely regarded as the most significant globally [31], progressing through a series of competitive evaluation rounds [24]. Submissions undergo rigorous peer review and are evaluated on their technical merits before the selected algorithms progress to be finalised as standards. These are the standards incorporated in this study.

As indicated by the literature review, the field of post-quantum computing (PQC) is extensive. This paper focuses on a specific overlapping area defined by four key aspects:

• Key Exchange: A crucial component of secure communication whose traditional techniques were protected by large-number factorisation and that will be rendered vulnerable to Shor’s algorithm in quantum computing. New quantum-resistant techniques are emerging.
• Energy Consumption: A comparative evaluation of the energy used during key generation methods for both traditional and post-quantum cryptography.
• Computing Platform: The Raspberry Pi 5 was selected as the test platform, ensuring the homogeneity and repeatability of the results. Its uniform and common integration into operational technology solutions and use by hobbyists make it a relevant choice.
• Software Library: Standardised libraries were employed in the solutions, recognising the implementation complexity and verification challenges of cryptographic code. Following the established best practice in cryptography, this paper utilised the tested, peer-reviewed, and performant OpenSSL library rather than developing custom implementations.

An illustration of these four constituent parts is presented in Figure 1. This paper focused on a practical comparison of the energy consumed during key generation for newly standardised PQC algorithms against traditional methods. Experimentation was conducted on a Raspberry Pi platform, employing standardised cryptographic libraries to ensure a consistent basis for comparison. The aim was to establish a baseline for this platform, to ascertain the impact of transitioning to PQC for this specific aspect of the cryptographic suite.

3.1. Methodology and Implementation Overview

To ensure the acquisition of reliable energy utilisation data, the experimental methodology involved executing key generation algorithms across a significant number of iterations for each algorithm. Key generation was performed on the Raspberry Pi, with adjustments made for algorithms with longer key generation times to normalise each algorithm’s time-on-test. Baseline energy consumption of the Pi platform (excluding key generation) was established through extensive NULL runs, whose times were subsequently subtracted from the experimental results including the key-generation stage.

A distributed architecture was employed for the experimentation, utilising a Raspberry Pi as the device under test (DUT) and a Windows-based data acquisition system to record electrical parameters from a TC66C energy meter inline with the Pi’s power supply. A block diagram of the experimental setup is illustrated in Figure 2, with a marked-up photograph of the TC66C meter and Raspberry Pi in Figure 3.

Remote STOP/START signalling via network communication facilitated automated data collection on the Windows collector, with specific steps taken to maintain a consistent testing environment on the Pi, such as fixing the CPU clock and running the fan at 100%, as well as operating the testing over a very large number of iterations. The software measurement developed for the Windows machine featured a multi-threaded design to manage network communication and data acquisition asynchronously, to capture accurate results triggered by the signalling sent from the Pi DUT.

Aggregated full results are provided and analysed in Section 5, with practical examples of an experimental setup, including screenshots of what is visible to the user in (Appendix A). For reference, the source code, input, and results data files are located on this paper’s specific, static GitHub site [40]. Further details regarding the environment, experimental setup, system components, test procedures, and software architecture are provided in Section 4.

3.2. Data Analysis

Following each experiment, the data collected in that algorithm’s output file(s) were analysed to determine the DUT’s energy consumption characteristics.

3.2.1. Calculating Energy Used

The TC66C energy monitor returned a number of parameters across its USB serial connection to the Windows collector. Its power source was also from the Windows device, avoiding influencing the passing of power data recorded for the Pi. The software created for this paper used a TC66 software library provided by TheHWCave on GitHub [41] to set up the connection to the meter and periodically recover highly accurate data on voltage, current, wattage, and energy used.

Cumulative energy consumption was converted from milliwatt-hours (mWh) to Joules (J) as follows:

$$\mathrm{Joules}\left(\mathrm{J}\right)=\mathrm{Milliwatt}\text{-}\mathrm{hours}\left(\mathrm{mWh}\right)\times 3.6$$

The 3.6 factor is derived from there being 3600 s in an hour, and 1000 mWh in 1 Wh.

3.2.2. Result Accuracy

The TC66 unit used to gather the results in the experiments was not calibrated. However, an identical unit was tested against a calibrated Agilent lab supply in an analysis performed by TheHWCave [42]. The results of this analysis found the tested TC66C unit to be well within its 0.05% Voltage accuracy specification and the 0.1% stated accuracy for current. In the typical voltage and current window seen during experimental testing for this paper, TheHWCave’s study demonstrated the meter exhibited significantly better tolerances, typically within 0.02% accuracy for voltage and 0.05% for current.

3.3. Selection of Parameters Tested

Our experimental methodology relied on several carefully chosen parameters, which we outline below along with their selection criteria:

• Iterations: A range of experimental round sizes were implemented in the environment. These were chosen to validate the results of the tests, and the final outputs predominantly made use of ‘500,000’ key examples—with testing taking place over a period of around 24 h of operation. This iteration count was specified in the input file of the test script.
• Security Levels: A range of algorithms were chosen that covered the NIST security levels from 1 to 5, where a broad equivalence of the different algorithms under test was ensured to permit easy comparison.
• Algorithms: Three categories of algorithms were included in the testing, all were from the OpenSSL3.5 library as compiled for the Raspberry Pi device under test. The full set can be seen in

  Table 1. NIST security levels and equivalent symmetric key sizes for OpenSSL key generation protocols (based on NIST SP 800-57 Part 1 Rev. 5 (Table 2) [43] and the author’s categorisation).

  NIST Sec Level	Protocol	Category	Equiv. Bit Size
  Level 1	RSA-1024	Classic Technology	80
  Level 2	EC secp160r1	Elliptic Curve Cryptography	80
  	RSA-1536	Classic Technology	∼96
  Level 3	EC secp224r1	Elliptic Curve Cryptography	112
  	RSA-2048	Classic Technology	112
  	EC P-256 (secp256r1, FIPS 186-4)	Elliptic Curve Cryptography	128
  	ML-DSA-44	Post-quantum Technology	∼128
  	ML-KEM-512 (Kyber-512, FIPS 203)	Post-quantum Technology	∼128
  Level 4	RSA-3072	Classic Technology	128
  	EC P-384 (secp384r1, FIPS 186-4)	Elliptic Curve Cryptography	192
  	ML-DSA-65	Post-quantum Technology	∼192
  	ML-KEM-768 (Kyber-768, FIPS 203)	Post-quantum Technology	∼192
  Level 5	RSA-4096	Classic Technology	∼140
  	EC P-521 (secp521r1, FIPS 186-4)	Elliptic Curve Cryptography	256
  	ML-DSA-87	Post-quantum Technology	∼256
  	ML-KEM-1024 (Kyber-1024, FIPS 203)	Post-quantum Technology	∼256

  .
  • Elliptic Curve. Several commonly used ECC algorithms were chosen to enumerate a range of security levels. This was used to baseline the method versus other key generation categories.
  • RSA. Another classic algorithm used for key generation. RSA is a more mature solution and still commonly in use. Over the years, the key sizes used have ramped upwards to maintain security as computing power has risen. Several key sizes for RSA were selected in the analysis.
  • ML-KEM Post-Quantum Cryptography Technique. This is the currently available key generation technique standardised by the NIST as FIPS 203, and implemented in the April 2025 OpenSSL3.5 library release.
  • The ML-DSA algorithm was also included. While this is not explicitly used as a key exchange mechanism, it does perform key generation at equivalent security levels using Lattice techniques, and was therefore a useful yardstick to ensure the broad validity of the results of the ML-KEM method while awaiting the standardisation of HQC and its implementation in OpenSSL for evaluation.
• Polling Interval: This is a parameter which was chosen as part of the experimental setup. It is the frequency at which data were recovered by the Windows collector machine from the TC66C meter, and did not impact on the key generation process. The data used for the energy calculations were a cumulative value from the TC66C, so the period chosen here only defined start and stop time granularity and the update period on the screen for the user.

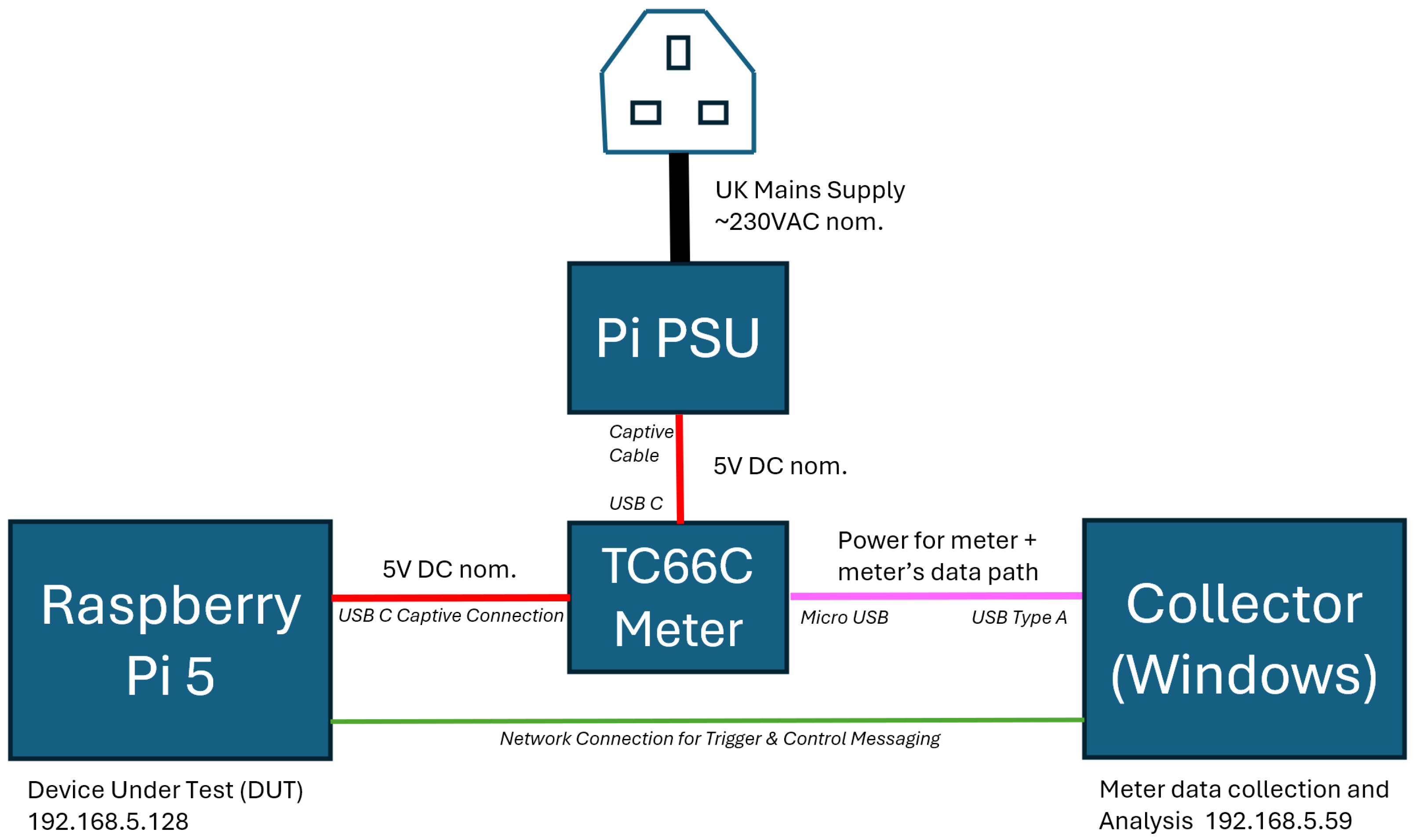
4. Methodology

The experiments were designed to record the empirical energy utilisation over a significant number of iterations, to establish a reliable baseline. Key generation for each algorithm was executed multiple times across 10,000, 100,000, and 500,000 rounds—from under an hour to over a day in total duration. Where the key generation times were considerably longer (for instance, with larger RSA key sizes), a lower iteration count was used, and the corresponding experiments were adjusted accordingly, balancing out the time on test for each algorithm.

Furthermore, multiple NULL runs were performed in between key generation runs, involving identical numbers of loop iterations but triggering a 5 ms delay instead of the OpenSSL key generation operation. The 5 ms duration of the delay was not critical; rather, these runs served to capture the baseline energy consumption of the Raspberry Pi platform (including the fan) incorporating everything other than the key generation itself. This background energy usage (averaged over multiple NULL runs) was then subtracted from the results obtained, including the actual OpenSSL key generation processes.

Software were developed to execute in the test environment, including cycling through the different key generation parameters, to trigger the start and stop of data capture from the energy meter and to provide feedback to the test operator on the status of the experiment. An example of live test runs and actual screen captures the tests can be reviewed in (Appendix A).

Specific steps taken to ensure consistent measurement included running the fan on the Pi at 100% for all experiments, fixing the CPU clock to minimise the potential for dynamic frequency and voltage scaling influencing results, and pausing several seconds before starting the experiment to ensure the environment had settled, particularly in relation to the fan speed.

The test framework was carefully designed to provide a consistent environment for each run and to ensure that accurate, repeatable experimental results could be gathered. The principle that results gathering should not impact the device under test through viewing of its status was followed to develop the solution—minimising the triggering of the ‘observer effect’, such as through reporting using a separate collection machine rather than the device under test (DUT).

4.1. Experimental Approach

The experimental setup employed a distributed architecture to benchmark the energy consumption of the process running on the DUT (Raspberry Pi). A Windows-based data acquisition system was utilised to record electrical parameters (voltage, current, power, etc.) from a Ruideng TC66 tester connected inline with the power supply of the Raspberry Pi. The experiment was controlled remotely via network communication between the Raspberry Pi and the Windows machine, with trigger messages being sent for GETREADY, START, and STOP purposes, aligning with the timing of the experiment running on the Pi.

The key system components included

• Target System—Device Under Test—(Raspberry Pi): This single-board computer executed the software which ran the experiments whose energy consumption was being benchmarked. It also hosted a network client responsible for sending control messages to accurately start and stop the energy acquisition recording.
• Data Acquisition System (Windows Machine): This system hosted the data logging software. It was connected to the TC66C energy tester that monitored the electrical utilisation characteristics of the Raspberry Pi. This system also ran a network server to receive control messages to toggle acquisition on and off for the energy data.
• USB Tester (Ruideng TC66C): An external hardware device connected between the Raspberry Pi and its power supply. It accurately measured and reported instantaneous electrical parameters such as voltage, current, and power, and cumulative totals, including the energy consumed.
• Ethernet Network: The communication medium facilitating the exchange of control messages between the Raspberry Pi and the Windows machine. This was a dedicated network with UDP messages used, without the latency and additional energy of a TCP handshake.

4.2. Experimental Procedure

A structured approach allowed for remote control and automated data collection, enhancing the efficiency and reproducibility of the energy benchmarking experiments. The experiments proceeded through the following stages, initiated and controlled via network communication (see also (Appendix A) for a practical example):

• Initialisation and Preparation (Triggered by “GETREADY” message): The Raspberry Pi, acting as the control client, sent a “GETREADY” message to the Windows data acquisition server. This message included experimental parameters (e.g., test duration, sampling frequency, experiment identifier, etc.). After receiving the “GETREADY” message, the Windows machine

  -

  Parsed the experimental parameters.

  -

  Initialised the data logging system, preparing the output file(s) with appropriate headers based on the received parameters.

  -

  Transitioned the TC66C meter to the ‘ready’ state, awaiting the “START” command.

• Data Acquisition (Triggered by “START” message): Once the process on the Raspberry Pi was ready for benchmarking (i.e., after the CPU clock had been hard set and the fans had time to spin up and settle), and immediately prior to starting the experiment, a “START” message was sent to the Windows machine. The Windows machine then

  -

  Initiated data collection from the USB tester at the specified sample rate.

  -

  Continuously recorded the measured electrical parameters (voltage, current, power, energy, etc.) along with timestamps to the designated output file(s).

  -

  Simultaneously, a subset of the data were displayed on the Windows screen for real-time monitoring by the operating user (on the Windows machines, so not impacting the DUT).

• Termination (Triggered by “STOP” message): At completion of the benchmarking process on the Raspberry Pi, it sent a ‘STOP’ message to the Windows machine. The Windows machine next

  -

  Ceased data acquisition from the USB tester.

  -

  Closed the output file(s), ensuring all data were saved.

  -

  Cleanly terminated the data logging application and network server thread.

4.3. Software Design/Architecture

The software on the Windows machine was designed with a multi-threaded architecture, to ensure responsiveness and separation of its asynchronous roles:

• Main Control Thread: This thread was responsible for coordinating the overall operation of the data acquisition. It also controlled the other threads and overall flow.
• Network Server Thread: This continuously listened for incoming network messages (“GETREADY”, “START”, “STOP”) from the Raspberry Pi, and was started and stopped by the main thread. After receiving a message, it parsed the command and any associated parameters, signalling to the main control thread to take appropriate action.
• Data Acquisition Thread: This thread was responsible for periodically reading data from the USB tester. It also wrote the data to the output file(s) and displayed pertinent information on the screen to give positive feedback to the user/operator as to the current operational state. This thread was started and stopped by the main thread based on the “START” and “STOP” messages received via the network from the Pi.

5. Evaluation

Table 1 presents a categorisation of the key generation algorithms employed by this study, mapped to their equivalent NIST Security Levels interpreted by the author from NIST SP 800-57 Part 1 Revision 5 [43]. The selection of algorithms provided coverage across all five NIST security level equivalents, encompassing established classic cryptography with RSA and Elliptic Curve Cryptography (ECC), and the emerging post-quantum cryptography standards. Module-Lattice-Based Key-Encapsulation Mechanism (ML-KEM) as specified in FIPS 203 (Kyber) was the primary algorithm on test, with the key generation part of ML-DSA used for check-and-balance purposes.

For clarity, common alternative names and relevant FIPS standards are included in brackets alongside the protocol identifier where applicable. Additionally, Table 1 provides the estimated equivalent symmetric key size in bits for each algorithm, offering a comparative measure of their current perceived security strength.

5.1. Energy Results—Key Generation

The experiments were conducted on a Raspberry Pi 5 platform under the previously outlined controlled conditions, with fixed clock speeds and 100% fan to establish a consistent baseline for the energy consumption measurements across each of the selected algorithms.

The bar chart in Figure 4 visualises the energy efficiency of the various key generation algorithms across the different NIST Security Levels. The horizontal axis represents the NIST Security Level, ranging from 1 to 5. There may be one or more algorithm in each level. The vertical axis displays the energy efficiency in Joules per 1000 key generations, using a logarithmic scale to accommodate the wide range of values, particularly relating to RSA. Each bar on the chart corresponds to a specific key generation algorithm. The colour of each bar indicates the category of that algorithm: blue represents the recently standardised post-quantum algorithms, green: elliptic curve cryptography, and orange: classic RSA technology. The name of each algorithm and its efficiency is printed above the corresponding bar for identification and comparative purposes.

5.1.1. Energy Results—Commentary

The Post-Quantum Cryptography techniques were broadly equivalent in terms of their energy utilisation when compared with the Elliptic Curve Cryptography methods at NIST Security Level 3. At NIST levels 4 and 5, the post-quantum techniques were more energy efficient for the same security level than the tested current ECC methods. Turning to RSA, as expected, the energy efficiency became exponentially worse as the key size increased. Compared with ECC, RSA was around two or more orders of magnitude less efficient at key generation as the elliptic curve equivalent, as well as generating larger keys. Comparing RSA to the PQC techniques shows an even greater offset, as the PQC was much flatter across the resources it required as the security level increased.

5.1.2. Extrapolating Potential Energy Savings

This section presents a highly speculative, order-of-magnitude estimate of the potential energy savings that could be realised by transitioning notionally from RSA-2048 key generation to ML-KEM-512 on a large scale. Due to the decentralised nature of key generation across various systems globally, the assumptions made here are necessarily quite broad. Key generation is also a comparatively low-volume cryptographic operation compared with others in the suite, and the results are accordingly small.

Several key areas where RSA key generation is prevalent are considered:

• Web Servers (HTTPS): Assuming approximately 300 million websites active globally using certificates (an estimate in Jan 2025 based on [44]), and a conservative average certificate cycle of 3 months (LetsEncrypt uses 60 days and has over 50% of the market), this equates to roughly 1.2 billion key generations per year.
• VPN Users: With an estimated 1.5 billion VPN users globally [45], assuming each host generates a new key each year, this adds another 1.5 billion key generations annually.
• Other Applications (VPN, Email, SSH): A conservative estimate for the combined key generation for secure email, SSH, and other applications is around 10% of the web server figure, supposing approximately 120 million key generations per year.

Based on these highly speculative assumptions, the total estimated RSA key generations per year could be in the order of 2.82 billion.

The experiment demonstrated (Figure 4) that the energy consumption for generating a single RSA-2048 key was approximately 1.093 Joules on the test platform. Therefore, taking this and RSA-2048 as the baseline, the total estimated annual energy consumption for key generation across these applications if performed on a Raspberry Pi 5 would be in the order of 3.082 GigaJoules.

To convert this to kilowatt-hours (kWh)

$$\mathrm{3,082,000,000}\mathrm{J}\times {\displaystyle \frac{1\mathrm{W}·\mathrm{s}}{1\mathrm{J}}}\times {\displaystyle \frac{1\mathrm{W}·\mathrm{h}}{3600\mathrm{s}}}\times {\displaystyle \frac{1\mathrm{kW}·\mathrm{h}}{1000\mathrm{W}·\mathrm{h}}}\approx 856.11\mathrm{kWh}$$

Assuming an average electricity unit price of GBP 0.26 per kWh (based on the UK average from QEP Table 2.2.4 referenced in [46]), the estimated annual cost for RSA-2048 key generation across these 2.82 billion keys would be approximately

$$856.11\mathrm{kWh}\times 0.26/\mathrm{kWh}\approx 222.59\mathrm{GBP}$$

The experiments determined the energy consumption for ML-KEM-512 (offering comparable NIST Level 3 security to RSA-2028) to be approximately 7.61 Joules per 1000 key generations, or 0.00761 Joules per key. The energy saving per key generated would therefore be $1.093-0.00761=1.09939$ Joules for each key. This suggests that less than 1% of the energy would be required for key generation using ML-KEM-512 PQC compared with RSA-2048, ∼131 times more efficient.

For NIST ‘Level 5’ security, comparing RSA-4096 (11.952 Joules per key) with ML-KEM-1024 (approximately 0.00789 Joules per key), the potential energy saving multiplier is even more significant, at around 1500 times, whereas ECC P-521 (approximately 0.003376 Joules per key) is around 350 times more energy efficient than RSA-4096. Also noted here is that ML-KEM-1024 is circa four times more efficient than EC-P521, a significant advantage for the newer quantum-robust technology.

In conclusion, while this extrapolation is based on numerous broad assumptions, it suggests that a large-scale transition from traditional key generation techniques like RSA-2048 to post-quantum alternatives such as ML-KEM could lead to substantial energy savings and reduced computational overhead, as well as protection from quantum techniques such as Shor. Whilst the work in this paper was carried out on the lower-power Raspberry Pi 5 platform, it is fully expected that there would be similar order of magnitude results on other computational architectures. Additional research with more granular usage statistics is required to further refine these estimates.

5.2. Key Generation Time Observation

Whilst not the goal of this paper, a plot of compute time was additionally created and studied, purely for academic interest. This is illustrated in Figure 5. The compute time required per 1000 key generations exhibited a broadly similar shape to the energy consumption graph (Figure 4), with RSA algorithms generally requiring significantly longer processing times, particularly at higher NIST Security Levels. PQC again performed well against the ECC category methods, outperforming them as the security level increased in comparison.

However, the relative performance in compute time between RSA and the two other categories differed. It appears that RSA consumed energy at a slower rate than the ECC and PQC techniques, resulting in a larger time multiple for RSA versus the other techniques.

A tentative conclusion is that RSA may not be fully optimised in OpenSSL3.5 on the Pi, or that it is less able to be parallelised with more serialisation portions, exhibiting Amdahl’s Law [47]. This finding is included as an observation, but is not explored further in this paper, as it is not the main purpose of the study. However, the author believes this to be an interesting observation, still worthy of note.

6. Conclusions

This paper’s experimental analysis strongly suggests that a shift towards post-quantum key generation cryptography is desirable for new deployments, due to its comparable or superior energy efficiency and inherent resilience to future quantum threats. In Figure 4, it is clear that as the NIST security level increased, the lattice-based key generation methods outperformed ECC, and significantly outperformed RSA, whilst adding resilience to known and projected post-quantum computing attacks.

6.1. RSA’s Dead-End

It is particularly apparent that RSA’s viability is increasingly challenged, even before the potential impact of quantum computing on its integrity is taken into account. Key sizes for RSA already need to be 2048–4096 bits and beyond for best practice (NIST Level 3 to Level 5), due to the impact and roadmap of classical computing progression (Moore’s Law [20]), and the cryptographic attacks this enables.

The energy used for RSA-4096 key generation was orders of magnitude greater than for NIST security level 5 ‘equivalents’ such as Elliptic Curve P521 and ML-KEM-1024 (see Figure 4). When the potential of quantum computing algorithms is taken into account, even the Level 3–Level 5 key sizes for RSA do not provide sufficient protection. Larger RSA key sizes (towards 1 TB) that offer additional resilience to PQC attacks [29] quickly become unsustainable in terms of their requirements for memory and consumption of computational resources and energy.

6.2. Use of Elliptic Curve Cryptography

From the perspective of Elliptic Curve Algorithms at NIST Level 3, the post-quantum ML-KEM methods remained close to the energy used by the classical ECC method (see Figure 4 and

Table 2. Equivalent to Figure 4 with numerics to compare instead of logarithmic bar heights. RSA was particularly resource-hungry at larger key sizes.

NIST ‘Sec’ Level	Protocol	Category	J/1000 Keygens
Level 1	RSA-1024	Classic Technology	218.64
Level 2	EC secp160r1	Elliptic Curve Cryptography	8.69
	RSA-1536	Classic Technology	828.84
Level 3	EC secp224r1	Elliptic Curve Cryptography	10.16
	EC P-256 (secp256r1, FIPS 186-4)	Elliptic Curve Cryptography	7.33
	ML-DSA-44	Post-quantum Technology	8.36
	ML-KEM-512 (Kyber-512, FIPS 203)	Post-quantum Technology	7.61
	RSA-2048	Classic Technology	1093.08
Level 4	EC P-384 (secp384r1, FIPS 186-4)	Elliptic Curve Cryptography	17.05
	ML-DSA-65	Post-quantum Technology	8.97
	ML-KEM-768 (Kyber-768, FIPS 203)	Post-quantum Technology	7.76
	RSA-3072	Classic Technology	4014.84
Level 5	EC P-521 (secp521r1, FIPS 186-4)	Elliptic Curve Cryptography	33.76
	ML-DSA-87	Post-quantum Technology	9.82
	ML-KEM-1024 (Kyber-1024, FIPS 203)	Post-quantum Technology	7.89
	RSA-4096	Classic Technology	11,952.0

). However, ML-KEM had a discernible advantage at NIST security Levels 4 and above in the tested environment. When comparing with RSA, ECC should be preferred from a purely energy-based perspective where it is still necessary to use a classical technique, and where this option is available. Use of such algorithms is likely to be prevalent for some time, especially as the NIST post-quantum standards [33] have only recently been published (2024–2025) and are not yet commonly deployed or available in mainstream hardware and software libraries [10].

6.3. Adoption of New PQC Standards

Considerable lead times will be required for the implementation and testing of libraries based on the new PQC standards for deployment. Integration into the software stacks of general-purpose computing is only just beginning (as evidenced by the April 2025 v3.5 production release of the widely-used OpenSSL library, which incorporates PQC methods [10]). It will also take some time to incorporate any methods that can be hardware-accelerated into general-purpose and application-specific processors, now that some standards have been ratified.

The PQC standards are also not static. They are still being developed, with new rounds of evaluation being led by the NIST to diversify approaches beyond lattice techniques [33]. Even once the full set of FIPS standards are finalised, a long tail of platforms to be updated will remain, particularly in the operational technology and embedded space, which have extended deployment lifetimes, prioritising availability over most other factors [48].

Governmental guidance is also relatively new in this area, outlining recommended roadmaps to quantum-safe cryptography within their jurisdictions [22,23,24,25]. It will also take some time to incorporate PQC into practice and into regulatory requirements for specific industry sectors.

6.4. Recommendations

This paper experimentally analysed the energy characteristics of classical versus PQC key generation and evaluated the results obtained in this area. The author recommends that classical key generation techniques should no longer be considered for new implementations, as the energy efficiency results are clear. Non quantum-safe methods should be phased out of existing applications and deployments as feasible, especially given that the post-quantum alternatives were shown to match or exceed the energy efficiency performance in the tested environment—by significant margins in many instances. This becomes particularly apparent as security levels rise, as illustrated in Figure 4. Given that energy consumption directly translates to operational cost, it is crucial that, alongside the selection of a cryptography algorithm to meet the required protection level, equal consideration is given to energy optimisation. This approach can saves resource by minimising both the financial burden of energy used and the indirect environmental costs of additional cooling controls.

6.5. Future Work

The recommendations above are qualified by further potential experimental work utilising this test platform and software to broaden its scope. This would enable a more comprehensive end-to-end study to be performed with more parameters and to understand the full impact of the transition to PQC compared to classical cryptographic techniques. The scope may be expanded in a number of suggested ways:

• Additional Hardware Platforms: To use and compare more than one type of hardware, for example adding Raspberry Pi 4 and another standard Intel x86/AMD64 ISA platform for comparisons. The meter used (unmodified) can capture up to 20 V with currents up to 5 A. Devices with attached batteries (e.g., laptops) are not suitable for this exercise due to the need to capture live energy utilisation directly.
• Alternative Software Libraries: To identify further suitable cryptographic libraries for comparative testing, other than OpenSSL. For example, exploring Bouncy Castle [49] and/or other potential PQC libraries as they become available. A challenge here will be ensuring comparable algorithm support and maturity across different libraries. Possible alternative sources can be found directly at asecuritysite [50], which is a cryptographic website with resources for researchers, hobbyists, and professionals in the area, including for post-quantum cryptography.
• Explore End-to-End Sessions: To expand the study to a fuller E2E lifecycle measurement across a range of scenarios:
  • On-Network Key Exchange: Measure the bidirectional energy consumption of different PQC and traditional key exchange protocols including network communication.
  • Data Transfer: Quantify the energy cost of encrypting and transmitting datasets of varying sizes using the negotiated symmetric keys derived from both PQC and traditional key exchange mechanisms (also considering the cost of the required hardening to AES-256 for all applications that Grover’s algorithm effectively mandates).
  • Digital Signatures: Evaluate the energy efficiency of generating and verifying digital signatures using standardised PQC algorithms (e.g., ML-DSA, SLH-DSA), comparing to traditional signature schemes. Isolating the energy cost of specific operations in an end-to-end scenario will be a key challenge in this potential future work.
• New Standards: To incorporate the evolution of the standards, for example to include HQC testing once this has been finalised by the NIST [33] into a FIPS standard and is incorporated into OpenSSL and other cryptographic libraries. Additional work to evaluate this algorithm could be carried out upon its availability, even whilst in Beta testing.

The experimental broadening proposed in this Future Work and how it impacts on the areas selected as the initial scope of this study is illustrated in Figure 6.

A significant portion of the work for this paper involved investing time in developing a robust methodology for capturing energy utilisation data. The setup is outlined in more detail in Section 4.3. The framework was designed to allow this study to be extended in the future to other applications that utilise similar experimental setups. Having established energy efficiency differences in key generation, future research should examine if the patterns of the results persist across all operations and end-to-end encrypted communication protocols.