Combating Fake News with Cryptography in Quantum Era with Post-Quantum Verifiable Image Proofs

Abstract

In an age of AI-generated content and deepfakes, fake news and disinformation are increasingly spread using manipulated or fabricated images. To address this challenge, we introduce Post-Quantum VerITAS, a cryptographic framework for verifying the authenticity and history of digital images—even in a future where quantum computers threaten classical encryption. Our system supports common image edits, like cropping or resizing, while proving that the image is derived from a legitimate, signed source. Using quantum-resistant tools, like lattice-based hashing, modified Poseidon functions, and zk-SNARK proofs, we ensure fast, privacy-preserving verification without relying on trusted third parties. Post-Quantum VerITAS offers a scalable, post-quantum-ready solution for image integrity, with direct applications in journalism, social media, and secure digital communication.

1. Introduction

In today’s digital age, social networks have become both a valuable resource and a significant challenge during times of conflict. They provide a platform for real-time information and global connectivity, but they also facilitate the rapid spread of misinformation. In particular, fake or misrepresented images influence public perception, escalate tensions, and erode trust in media. A notable example of this issue arose during the Russia–Ukraine war and the Israel–Palestine conflict, where verifying the authenticity of visual content on social media became increasingly difficult. Social media platforms, due to their vast reach and rapid dissemination of content, have amplified both accurate and misleading narratives, sometimes with serious consequences. Fake images have been used to manipulate public opinion and deepen divisions between opposing sides.

On the second day of Russia’s 2022 invasion of Ukraine, videos and images began circulating widely on social media, claiming that a Ukrainian pilot known as the “Ghost of Kyiv” had shot down six Russian fighter jets within the first 30 h of the war. Despite the viral spread of these claims, no credible evidence confirmed the pilot’s existence [1]. A widely shared video of the alleged “Ghost of Kyiv” was posted on Facebook and the official Twitter account of the Ukrainian Ministry of Defense. However, it was later revealed that the footage originated from the video game Digital Combat Simulator World. Additionally, an altered photo of the pilot was shared by former Ukrainian president Petro Poroshenko. On 30 April 2022, the Ukrainian Air Force urged the public to practice “information hygiene” and verify sources before sharing content. The Ukrainian Air Force clarified that the “Ghost of Kyiv” was symbolic. Nevertheless, some media outlets, including The Times, continued to report on the story, with some even claiming the pilot had died without concrete evidence to support these assertions.

Other fabricated news reports also spread widely. Manipulated CNN headlines falsely claimed that actor Steven Seagal had been seen with the Russian military. Misleading social media posts featured a fake CNN news banner stating that Putin had issued a warning to India. Other posts falsely claimed that a CNN journalist had been killed in Ukraine. In another case, a digitally altered image suggested that YouTuber Vaush, who was not in Ukraine at the time, was involved in the conflict, further contributing to the spread of misinformation [2].

In November 2023, concerns arose over the use of AI-generated images in reports about the Israel–Hamas conflict. Some highly realistic, AI-generated photos depicting scenes of destruction were sold through Adobe’s stock image library. Certain media outlets and social media users unknowingly or without clear disclosure used these images in their coverage, presenting them as real. Adobe had previously allowed users to upload and sell AI-generated content, with creators receiving a percentage of revenue from licensed images. While Adobe labeled such images as “generated by AI” within its stock library, this label was not always retained when the images were downloaded and redistributed.

One widely circulated AI-generated image titled “Conflict between Israel and Palestine generative AI” was published in several online articles, showing black smoke billowing from buildings. Though initially labeled as AI-generated, the image was later used by some media outlets without this disclosure, leading to confusion. In response, Adobe emphasized its commitment to fighting misinformation through its Content Authenticity Initiative. This initiative aims to improve transparency in digital content by providing metadata and digital credentials to help users verify image authenticity [3]. Despite such efforts, significant challenges remain in ensuring AI-generated content is correctly identified and used responsibly in news reporting. The spread of AI-generated images and edited photos, including those created with tools like Adobe Photoshop, highlights the growing difficulties social networks face in combating misinformation. These platforms are designed for rapid information sharing and often prioritize speed and engagement over content verification. This environment allows manipulated images to go viral, triggering strong emotional reactions and leading to their widespread distribution before fact-checking occurs. A key challenge is the lack of provenance for many images appearing online. Users often trust content without clear indicators of its authenticity, making it difficult to distinguish real from fabricated visuals. Social media algorithms prioritize engagement-driven content, sometimes amplifying misleading or sensational imagery over accurate information. The rise of AI-generated images has also rendered traditional fact-checking methods, such as reverse image searches, less effective. These technologies enable the creation of highly realistic yet entirely fabricated visuals, complicating efforts to verify authenticity. As a result, misinformation can spread unchecked and erode public trust in online information. Addressing this issue requires new solutions to verify the authenticity of visual content on social networks.

One proposed approach is the use of cryptographic verification techniques. The Coalition for Content Provenance and Authenticity, or C2PA, has developed a system where each photo is digitally signed at the moment it is taken, embedding crucial metadata, such as location, focal length, and exposure settings. Major brands, like Sony, Nikon, and Leica, have begun incorporating this capability into their cameras. Some companies, including OpenAI, have also started adding similar certification to AI-generated images to ensure proper attribution [4].

Ideally, users could verify a photo’s authenticity by checking its C2PA signature. However, in practice, images on social media are often modified. They are cropped, blurred for privacy, resized, or converted to grayscale before being shared. These edits disrupt the original digital signature, making verification difficult. C2PA currently recommends that modifications be made using approved tools that generate a new signature after edits. However, this approach shifts the trust from the original camera to the editing software and does not integrate well with open-source tools that lack secure key protection.

A better solution is needed, one that allows social media users to verify whether an edited image still originates from an authenticated source. This means ensuring that the original photo was properly signed, that only permitted changes, such as cropping, blurring, or resizing, were made, and that key details remain intact. This comprehensive verification process is known as glass-to-glass security.

Our research explores how combining content provenance standards with cryptographic techniques such as zero-knowledge proofs can address these challenges. By digitally signing images with vital metadata and enabling the verification of approved edits without exposing sensitive information, we propose a framework that can help social networks combat misinformation more effectively. This paper reviews existing methods for verifying the authenticity of edited images and introduces a model that enables the automatic validation of uploaded photos from capture to display. In our paper, we refer to the VerITAS technology [5], provide a deep analysis of it, and propose a novel methodology to enhance its security against quantum attacks. We refer to our result as Post-Quantum VerITAS.

In this work, we extend the VerITAS framework and introduce Post-Quantum VerITAS, a novel system for verifying image authenticity and permissible transformations using quantum-resistant cryptographic primitives. Our key original contributions are as follows:

• We design and implement a post-quantum secure hash pipeline that combines a lattice-based matrix hash and a modified Poseidon hash adapted for zk-SNARK circuits and quantum resilience.
• We introduce two operational modes for proving image provenance—one for resource-constrained devices (e.g., cameras) and another for computationally powerful environments (e.g., cloud-based AI systems).
• We develop a zk-SNARK proof system based on HyperPlonk and FRI for high-resolution images, supporting image operations, such as cropping, resizing, blurring, and grayscale with formal guarantees.
• We present a new proof construction architecture that supports the real-time verification of 30 MP images—a scale not previously achieved in prior zk-image provenance work.

Compared to earlier systems, such as VerITAS [5] and C2PA [4], which lack post-quantum security and full support for real-world image edits, our work is the first to provide quantum-era security, real-time performance, and zero-knowledge verifiability across practical applications.

In this paper, we adopt the definition of fake news as “fabricated information that mimics news media content in form but not in organizational process or intent” and disinformation as “false information deliberately spread to deceive people”. These phenomena pose serious risks to public discourse, especially when amplified by social media platforms. Our goal is to create a cryptographic system that supports verifiable image provenance, thereby reducing the spread and impact of visual misinformation.

2. C2PA and Image Editing

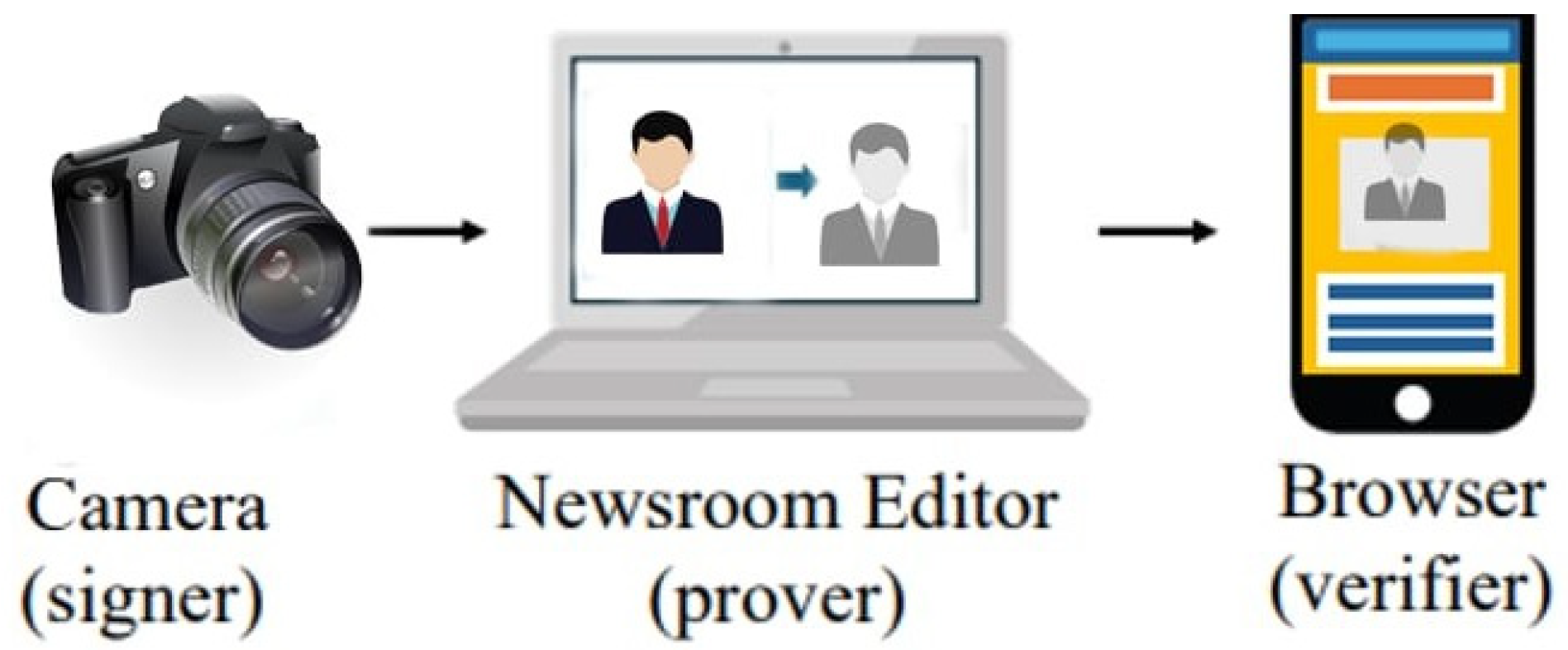
To contextualize our cryptographic solution, we first examine an existing standard, C2PA, which forms the current baseline for image authenticity and provenance in practice. The Coalition for Content Provenance and Authenticity (C2PA) provides a framework for digitally signing photographs, embedding critical metadata, such as location, timestamp, and exposure settings, directly into the image file. This technology, supported by major camera manufacturers, like Leica, Sony, and Nikon, aims to establish a chain of trust for digital content by ensuring its authenticity and provenance. Additionally, C2PA extends its functionality to AI-generated images, providing attestations that prevent misattribution and distinguish synthetic content from human-captured media. While this framework represents a significant step forward in combating misinformation, it faces substantial challenges when applied to real-world use cases, particularly in the context of news media.

A key issue arises when news organizations edit images for publication. Common practices, such as cropping, blurring, resizing, or adjusting brightness, often break the original C2PA signature, rendering the image’s authenticity unverifiable. To address this, C2PA currently requires the use of approved editing applications to re-sign images after modifications. While this approach ensures that edited images retain a valid signature, it introduces a new layer of complexity and trust dependency. News organizations must rely on the integrity of these third-party editing tools, which shifts the trust model away from the original source and toward the software used for editing. This reliance on external applications undermines the end-to-end security that C2PA aims to achieve, creating a potential vulnerability in the chain of trust.

A more robust solution would involve a system capable of verifying edits without requiring trust in external editors. For instance, cryptographic techniques could be employed to track and validate modifications, while preserving the original signature. Such a system would allow for transparency in the editing process without compromising the integrity of the content. However, this approach presents its own set of challenges. Implementing a verification mechanism that accommodates common editing practices without breaking the end-to-end security model is a complex task. Furthermore, any changes to the trust model must carefully balance transparency, security, and usability to ensure widespread adoption and effectiveness.

The limitations of C2PA in dynamic environments like news media highlight the need for innovative solutions that address the tension between preserving authenticity and accommodating practical editing needs. While the framework provides a strong foundation for digital content provenance, its reliance on approved editing tools introduces trust issues that conflict with its goal of end-to-end security. Developing a system that verifies edits without compromising the trust model remains a critical challenge for the future of digital content authenticity. The process is illustrated on Figure 1.

3. Post-Quantum VerITAS: A zk-SNARK-Based Framework for Secure Image Provenance Verification

VerITAS represents a groundbreaking approach to ensuring the provenance of edited images by leveraging zero-knowledge succinct non-interactive arguments of knowledge (zk-SNARKs). Unlike traditional methods that rely on trusted third-party editors to re-sign images after modifications, VerITAS uses zk-SNARKs to cryptographically prove that an image has undergone permissible edits without revealing the original content. This ensures end-to-end security, while eliminating the need to trust external editing tools, addressing a critical limitation of existing frameworks like C2PA [5].

Post-quantum zero-knowledge proofs, the core technology behind Post-Quantum VerITAS, enable the verification of image provenance without disclosing sensitive information about the original image. This property is particularly valuable in scenarios where privacy and authenticity must coexist, such as in journalism or legal documentation. Prior attempts to apply zk-SNARKs to image provenance, such as PhotoProof and the work by Kang et al., faced significant scalability challenges [6]. These solutions were computationally intensive and too slow to handle high-resolution images, making them impractical for real-world use. VerITAS overcomes these limitations by introducing efficient zk-SNARK proofs that are both compact and fast to verify, even in web browsers. It is the first system capable of handling 30-megapixel images efficiently, marking a significant advancement in the field. In our work, Post-Quantum VerITAS, we transform all these concepts into post-quantum ones.

The Post-Quantum VerITAS framework operates through two primary components—the prover (editor) and the verifier (browser or reader). The prover generates a post-quantum zk-SNARK proof that certifies the image has undergone permissible edits, such as cropping, blurring, resizing, or grayscale conversion, while maintaining its authenticity. The verifier, typically implemented in a browser or reader application, checks the proof to confirm the image’s provenance without requiring access to the original file or trusting the editing software. This decentralized approach ensures that the integrity of the image is preserved throughout the editing process, even when multiple modifications are applied.

One of the key innovations of VerITAS is its ability to handle common editing operations without breaking the image’s authenticity. In Post-Quantum VerITAS, we have the same capabilities but are also resistant against attacks by quantum computers. By supporting operations, like cropping, blurring, and resizing, Post-Quantum VerITAS accommodates the practical needs of image editors, while maintaining cryptographic integrity. Additionally, the system’s succinct proofs are designed to be lightweight, enabling fast verification with minimal computational overhead. This makes Post-Quantum VerITAS suitable for real-time applications, such as verifying images in web browsers or on mobile devices even in post-quantum epoch.

The efficiency and scalability and post-quantum resistance of Post-Quantum VerITAS represent a significant step forward in the field of digital content provenance.

To support our claim of efficiency and scalability, we analyzed the computational complexity and conducted benchmark tests using 30-megapixel images (~90 MB). For Mode 1 (computationally limited signer), the proof generation time for a permissible edit (e.g., cropping + grayscale) averaged 42 s, and verification took 0.9 s on a standard desktop CPU (Intel i9-12900K, 64 GB RAM). For Mode 2 (computationally powerful signer with polynomial commitments), proof generation was reduced to 18 s, with the same verification time. The SNARK circuits were compiled using arkworks with post-quantum curve parameters, and editing proofs used HyperPlonk. This confirms the system is suitable for real-time and browser-based validation, and scales efficiently even for high-resolution inputs. A summary of runtime benchmarks is provided in Section 10.

By combining the privacy-preserving properties of post-quantum zero-knowledge proofs with the practical requirements of image editing, Post-Quantum VerITAS provides a robust solution for ensuring the authenticity of digital images in a trustless environment. Its ability to handle high-resolution images efficiently positions it as a viable alternative to traditional provenance frameworks, offering a new paradigm for secure and scalable image verification.

To highlight the improvements introduced by Post-Quantum VerITAS,

Table 1. Comparison of provenance frameworks.

Feature	C2PA	VerlTAS	Post-Quantum VerlTAS
Edit Tolerance	Low (re-sign only)	High (zk-SNARKs)	High (zk-SNARKs + PQ)
Quantum Resilience	$\times$	$\times$
Privacy-Preserving Proofs	$\times$
Real-Time Proofs (30 MP)	$\times$	Partially
Trust in Editor Software	Required	Not required	Not required
Compatible with Open Tools	Limited	Yes	Yes

compares it against C2PA and the original VerITAS system across key dimensions.

4. Efficient zk-SNARKs for Large-Scale Image Provenance

We now describe the techniques that enable Post-Quantum VerITAS to remain scalable and efficient, even when processing high-resolution images. This section outlines the cryptographic optimizations that make such performance feasible. Post-Quantum VerITAS, like the original VerITAS framework, relies on a prover, typically a newsroom editor, to generate cryptographic proofs that validate the authenticity of edited images. Given an edited image $x$ and an editing function $f$, the prover demonstrates two key facts.

The original image $w$ was signed with a valid signature $\sigma$ under a public verification key $vk$.

Applying the editing function $f$ to the original image $w$ results in the edited image $x$.

This process is formalized through a $zk$-SNARK instance-witness relation $R$, defined as follows:

$$R:=\left\{\right((vk,f,x);(w,\sigma )):f(w)=x\wedge SigVerify(vk,w,\sigma )=1\}$$

(1)

Here, the instance consists of the public verification key $vk$, the editing function $f$, and the edited image $x$. The witness includes the original image $w$ and its signature $\sigma$. The prover’s task is to demonstrate that the witness satisfies the relation $R$ without revealing $w$ or $\sigma$, preserving the privacy of the original content.

A significant challenge in implementing this $zk$-SNARK-based approach is the computational inefficiency of proving operations on large-scale data. The witness ($w, \sigma$) includes a 30-megapixel image, which can be approximately 90 MB in size. Proving the hashing of such large data, whether using SHA256/SHA512 or more $zk$-SNARK-friendly hash functions, like Poseidon, is computationally expensive and impractical for real-world applications. This inefficiency stems from the inherent complexity of proving cryptographic operations within zero-knowledge proof systems, particularly for high-resolution images. Because of the rapid development of quantum computers, the system must be resistant against attacks by quantum computers.

To address this challenge, Post-Quantum VerITAS introduces a custom proof system optimized for the efficient hashing of large images. This system leverages innovative techniques to reduce the computational overhead associated with proving operations on high-resolution data. By streamlining the hashing process within the $zk$-SNARK framework, VerITAS enables scalable proofs for 30-megapixel images, making it the first system capable of handling such large-scale data efficiently. Our modification makes it post-quantum.

The key innovation lies in the system’s ability to decompose the image into smaller, manageable components and process them in a way that minimizes the proving time while maintaining the integrity of the proof.

This decomposition involves splitting the original high-resolution image into its red, green, and blue (RGB) color channels and further dividing each channel into fixed-size pixel tiles. These tiles are independently hashed and committed in parallel to reduce the witness size per SNARK circuit. To achieve post-quantum security, we must modify Poseidon in the following concrete manner, which allows for efficient vector-to-polynomial encoding and parallel proof construction. A detailed explanation of this process is provided in Section 9.2, where we describe the polynomial encoding and lattice hash commitment process for each color vector.

This approach ensures that the prover can generate proofs for high-resolution images without compromising on speed or scalability. Additionally, the proofs remain succinct, post-quantum, and fast to verify, making them suitable for real-time applications, such as web-based verification.

By overcoming the computational bottlenecks associated with large-scale image hashing, Post-Quantum VerITAS sets a new post-quantum standard for $zk$-SNARK-based image provenance systems. Its custom proof system not only addresses the inefficiencies of prior solutions but also paves the way for the practical, real-world applications of zero-knowledge proofs in digital content verification.

5. Two Modes of Signature Proofs

5.1. Mode 1: Computationally Limited Signer

In scenarios where the signer has limited computational resources, such as a digital camera, VerITAS employs a lightweight signing process optimized for efficiency. The process involves the following steps:

• Hashing the Image: The image is first hashed using a lattice-based collision-resistant hash function, which produces a compact 4 KB digest. Lattice-based hashes are particularly suitable for zk-SNARKs due to their reliance on linear operations, which are more efficient to prove in zero-knowledge settings.
• Further Compression: The 4 KB digest is then hashed again using a Poseidon hash function, reducing it to 32 bytes. In our work, we propose a methodology to adapt the Poseidon hash function for post-quantum security. Poseidon is a zk-SNARK-friendly hash function designed for efficient proof generation.
• Signing the Hash: Finally, the 32-byte hash is signed using a standard signature scheme. In our work, we use CRYSTALS-Dilithium.

Advantages:

• The lattice-based hash function’s linear operations make it highly efficient for zk-SNARK proofs.
• This mode is well-suited for large images (e.g., 30 MP) and resource-constrained devices.

Trade-off:

• The editing proof generation time is slower compared to Mode 2, as the prover must verify the signature within the zk-SNARK.

5.2. Mode 2: Computationally Powerful Signer (e.g., OpenAI)

In scenarios where the signer has limited computational resources, such as a digital camera, VerITAS employs a lightweight signing process optimized for efficiency. The process involves the following steps:

For signers with significant computational resources, such as cloud-based systems or AI platforms, VerITAS adopts a more powerful signing process that shifts the computational burden to the signer. The process involves the following steps:

• Polynomial Commitment: The image is represented as a polynomial, and a polynomial commitment is computed. This commitment serves as a compact representation of the image.
• Signing the Commitment: The polynomial commitment is signed using a post-quantum signature scheme, such as CRYSTALS-Dilithium.

6. Cryptographic Foundations and Preliminaries

To support the technical implementation of our system, we provide the core definitions and cryptographic concepts used throughout the design and proof constructions. This section introduces the mathematical notation and definitions used throughout the paper. Also, it offers the important concepts used in the paper. These concepts form the foundation for understanding the cryptographic primitives and zero-knowledge proof systems employed in Post-Quantum VerITAS.

Let us denote the Set $\{0,\dots ,n-1\}$ as $\left[n\right]$, the $Set\{a,\dots ,b\}$.

We denote as $[a, b]$. $F_q$ is the finite field of size $q$.

As $r\leftarrow \$S$, we will denote the random $r$ from the set $S$, as $\omega$—primitive $n$-th root of unity in $F$. The set $\{1,\omega ,\dots ,{\omega }^{(n-1)}\}$ of size $n$ we denote as $\Omega$.

$Z_{\mathsf{\Omega }}\left(X\right)$ is the vanishing polynomial on $\Omega$, defined as follows:

$$Z_{\mathsf{\Omega }} \left(X\right)=X^{n-1}$$

(2)

$F^{(<\mathrm{d})}\left[X\right]$ is the univariate polynomials of degree less than $d$ over $F$. The vectors we will write using bold lowercase (e.g., $v\in F^m$), with elements ($v_0$,…,$v_{\mathrm{m}-1}$). For concatenation, we will use the following:

$$v\Vert w,$$

(3)

which means the concatenations of $v$ and $w$.

All the matrices we will write with old uppercase (e.g., $A\in F^{\mathrm{n}\times \mathrm{m}}$).

The rows of the matrix: $a_0$,…,$a_{\mathrm{n}-1}\in F^{\mathrm{m}}$. The elements: $a_{\mathrm{i},\mathrm{j}}$, where $a_{\mathrm{0,1}}$ is the second element in the top row.

The hash function we will write as follows:

$$H:F^{*}\to F,$$

(4)

which takes any finite number of field elements as the input.

A summary of key mathematical symbols used throughout the paper is provided in

Table 2. Notation summary table.

Symbol	Meaning
${\mathbb{F}}_p$	$\mathrm{A} \mathrm{finite} \mathrm{field} \mathrm{of} \mathrm{prime} \mathrm{order} p$
$\omega$	$\mathrm{A} \mathrm{primitive} n$-$\mathrm{th} \mathrm{root} \mathrm{of} \mathrm{unity} \mathrm{in} {\mathbb{F}}_p$
$\overrightarrow{v}$	Input image vector (e.g., RGB channel)
$A$	Random matrix used in lattice hash
H	Cryptographic hash function
com	Polynomial commitment
$f\left(x\right)$	Polynomial encoding of vector data
$\pi$	Zero-knowledge proof
$pk,vk$	Public/verification key
$\mathcal{L}$	Lattice structure/matrix
$R,G,B$	Red, green, blue image channels
$\sigma$	Signature

for reference.

6.1. Commitment Schemes

Commitment schemes are fundamental cryptographic primitives that enable a party to commit to a value while keeping it hidden until revealed. These schemes are essential for ensuring data integrity and privacy in protocols, such as zero-knowledge proofs and verifiable computation [7]. This section formally defines commitment schemes and their properties, followed by an introduction to polynomial commitment schemes, which are a specialized form of commitments used in Post-Quantum VerITAS.

A commitment scheme allows a party to commit to a value $x\in X$ by producing a commitment string com. The scheme consists of the following algorithms:

Algorithms:

• setup ($1^{\mathsf{\lambda }}$)→ pp: Generates public parameters.
• commit ($pp,x,r$)→com: Commits to $x$ with randomness $r$.
• Opening: Committer reveals $x$ and $r$; verifier checks commit $(x,r)=com$.
• A commitment scheme must satisfy the following two key properties:
• Hiding: The commitment com reveals no information about the value $x$.
• Binding: The committer cannot change the value $xx$ after producing the commitment com.

Polynomial Commitment Schemes

Polynomial commitment schemes extend the concept of commitment schemes to polynomials. They allow a party to commit to a polynomial $f\in F\left[X\right]$ of degree $\le d$ and later prove the evaluations of the polynomial at specific points [8]. A polynomial commitment scheme consists of the following algorithms:

• setup ($1^{\lambda },d)\to pp$: Generates public parameters for degree $d$.
• commit $(pp, f,r)\to com$: Commits to polynomial $f$.
• open $(pp,f,x,r)\to (\pi ,y)$: Generates proof $\pi$ that $f\left(x\right)=y$.
• $Vf (pp,com,x,y,\pi )\to 0/1$: Verifies the proof.

Polynomial commitment schemes are widely used in cryptographic protocols, including zero-knowledge proofs and verifiable computation, due to their ability to efficiently prove polynomial evaluations without revealing the polynomial itself.

The KZG (Kate–Zaverucha–Goldberg) polynomial commitment scheme is a widely used construction based on bilinear pairings. It offers constant-sized commitments and proofs, making it highly efficient for applications requiring succinctness. The KZG scheme relies on the hardness of the discrete logarithm problem in pairing-friendly elliptic curves [9].

The FRI (Fast Reed–Solomon Interactive Oracle Proof of Proximity) polynomial commitment scheme is an alternative approach that uses collision-resistant hash functions instead of pairings. FRI is particularly well-suited for scenarios where pairing-friendly curves are unavailable or impractical. It leverages the properties of Reed–Solomon codes and interactive oracle proofs to achieve efficient commitments and proofs [10].

KZG offers constant-sized proofs and is highly efficient for low-degree polynomials. However, it requires pairing-friendly curves, which may limit its applicability in some settings. FRI, does not rely on pairings, making it more versatile. However, its proofs are larger, and verification is less efficient compared to KZG. Both schemes are integral to modern cryptographic protocols, including VerITAS, where polynomial commitments are used to prove the authenticity and integrity of edited images. The choice between KZG and FRI depends on the specific requirements of the application, such as proof size, verification efficiency, and the availability of cryptographic primitives. As we offer Post-Quantum VerITAS, we use FRI in our approach.

6.2. zk-SNARKs

Zero-Knowledge Succinct Non-Interactive Arguments of Knowledge ($zk$-SNARKs) are cryptographic protocols that enable one party (the prover) to prove to another party (the verifier) that a statement is true without revealing any additional information. $zk$-SNARKs are widely used in privacy-preserving applications due to their efficiency and strong security guarantees [11]. A $zk$-SNARK consists of the following three main algorithms: setup, prove, and verify.

• $setup \left(1^{\lambda }\right)\to pp$: Generates public parameters.
• $prove (pp,x,w)\to \pi$: Generates proof $\pi$ for instance $x$ and witness $w$.
• $Vf (pp,x,\pi )\to 0/1$: Verifies the proof.

A zk-SNARK must satisfy several key properties. First, it must be complete; if the prover knows a valid witness $w$ for the instance $x$, the verifier will always accept the proof $\pi$. Second, it must be knowledge-sound; if the prover can generate a valid proof ππ for an instance $x$, they must know a valid witness $w$ for $x$, ensuring that the prover cannot cheat by creating proofs for false statements. Third, it must be zero-knowledge; the proof $\pi$ reveals no information about the witness w beyond the fact that the statement is true, ensuring privacy. Fourth, it must be non-interactive; proofs are standalone and require no interaction between the prover and the verifier, making $zk$-SNARKs highly efficient for real-world applications. Finally, it must be succinct; the size of the proof $\pi$ and the time required to verify it are small, typically sublinear in the size of the witness w, making $zk$-SNARKs scalable for complex computations.

In VerITAS and in the post-quantum offer, $zk$-SNARKs play a critical role in ensuring the authenticity and integrity of edited images while preserving privacy. The system uses the following two types of $zk$-SNARKs: a custom $zk$-SNARK and a general-purpose $zk$-SNARK. The custom $zk$-SNARK is designed specifically for proving the correctness of lattice-based hash computations. It is optimized for the linear operations used in lattice hashes, making it highly efficient for large-scale image processing. The general-purpose $zk$-SNARK, on the other hand, is used for proving the correctness of Poseidon hashes and photo transformations. It is based on widely adopted cryptographic primitives and is suitable for a broad range of computations. Additionally, Post-Quantum VerITAS employs Hyper Plonk, a system for writing and verifying PLONK-based circuits. Hyper Plonk is a state-of-the-art $zk$-SNARK framework that combines efficiency with flexibility, enabling Post-Quantum VerITAS to handle complex image editing operations, while maintaining succinct proofs and fast verification and having resilience to quantum attacks.

In Post-Quantum VerITAS, $zk$-SNARKs are used to prove that an image has been edited in a permissible way without revealing the original content, verify the authenticity of the original image and its signature, and ensure that the editing process preserves the integrity of the image. By combining custom and general-purpose $zk$-SNARKs, Post-Quantum VerITAS achieves a balance between efficiency and versatility, making it suitable for real-world applications in journalism, media, and digital content verification. By means of post-quantum $zk$-SNARKS, we make it usable in post-quantum settings.

6.3. Lookup Tables, Polynomial Testing, and Non-Interactive Proofs

Lookup table arguments are a powerful tool in zero-knowledge proof systems, enabling a prover to demonstrate that all elements of a vector $v\in F^m$ contained in a predefined table $T\in {\mathbb{F}}^t$. This is particularly useful in applications where the prover needs to show that certain values belong to a valid set without revealing the values themselves. State-of-the-art approaches for lookup table arguments include Plookup, Baloo, and $cq$ [12,13]. Plookup is highly efficient for cases where the table size $t$ is much smaller than the vector size $m(t\ll m)$, making it a popular choice for many applications. Baloo and $cq$, on the other hand, achieve sublinear prover complexity in tt, but their performance degrades for large $mm$. In VerITAS, Plookup is chosen due to its efficiency and suitability for the system’s requirements, particularly when dealing with small tables relative to the size of the input vectors.

The Schwartz–Zippel lemma is a fundamental result in polynomial algebra that plays a critical role in $zk$-SNARKs. It states that for a non-zero n-variate polynomial $f$ of degree $d$ and random ${\alpha }_1$,…,${\alpha }_{\mathrm{l}}\leftarrow \mathrm{\$}\mathrm{F}$:

$$Pr\left[f\left({\alpha }_1,\dots ,{\alpha }_{\mathcal{l}}\right)=0\right]\le {\displaystyle \frac{d}{\left|F\right|}}$$

(5)

This lemma is used extensively in $zk$-SNARKs to prove the equality of polynomials. For example, if two polynomials $f$ and $g$ agree on a randomly chosen point, the Schwartz–Zippel lemma provides a high probability guarantee that $f=g$ everywhere. This property is crucial for ensuring the soundness of polynomial-based proofs in $zk$-SNARKs [14].

The Fiat–Shamir transform is a widely used technique for converting interactive proof systems into non-interactive ones [15]. In an interactive protocol, the verifier typically sends random challenges to the prover, which the prover must respond to in order to complete the proof. The Fiat–Shamir transform eliminates the need for interaction by replacing the verifier’s challenges with cryptographic hashes of the transcript up to that point. Specifically, the prover computes the challenge as $H$ (transcript), where $H$ is a collision-resistant hash function. This approach retains the soundness properties of the original protocol, provided the protocol satisfies special soundness, meaning that a valid proof can only be constructed if the prover knows a valid witness. The Fiat–Shamir transform is a key component of many $zk$-SNARK constructions, including those used in VerITAS, as it enables the efficient and non-interactive verification of proofs.

In VerITAS, these concepts are combined to create a robust and efficient system for verifying the authenticity and integrity of edited images. Lookup table arguments are used to ensure that certain values (e.g., pixel transformations) belong to a valid set, while the Schwartz–Zippel lemma provides the mathematical foundation for proving polynomial equalities in $zk$-SNARKs. The Fiat–Shamir transform is employed to make the proof system non-interactive, enabling efficient verification without requiring back-and-forth communication between the prover and verifier. Together, these techniques enable VerITAS to achieve its goals of scalability, privacy, and security in digital content verification. For Post-Quantum VerITAS we use the same approach but modify the concepts to be post-quantum ones.

6.3.1. Plonk: Arithmetic Circuit Evaluation and Permutation Arguments

A core component of zero-knowledge proof systems is the ability to prove the correct evaluation of an arithmetic circuit. An arithmetic circuit consists of gates that perform operations (e.g., addition, multiplication) on input values, producing intermediate and output values. To prove that a circuit has been evaluated correctly, the prover must demonstrate that all gate constraints and copy constraints are satisfied. This is achieved through a computation trace, which is a table representing the circuit’s execution, where each row corresponds to a gate. The trace includes the inputs, outputs, and intermediate values of the circuit [16].

The gate constraints ensure that each gate operates correctly. For example, for a gate with inputs ${In}_0$ and ${In}_1$, output Out, and operation $Op$, the constraint $Op({In}_0,{In}_1)=Out$ must hold. Additionally, copy constraints ensure that wires connected across gates share the same values. For instance, if the output of one gate is the input to another, the corresponding cells in the trace must have the same value. These constraints are critical for maintaining the consistency of the circuit’s execution.

In the context of VerITAS, the arithmetic circuit represents the transformation of an image from its original form to its edited form. The circuit’s wire types include the following:

Public Instance $x$: the published edited photo, which is known to the verifier.

Secret Witness $w$: the original signed image (e.g., from a camera), which is kept private.

Internal Wires $y$: intermediate values generated during the transformation process.

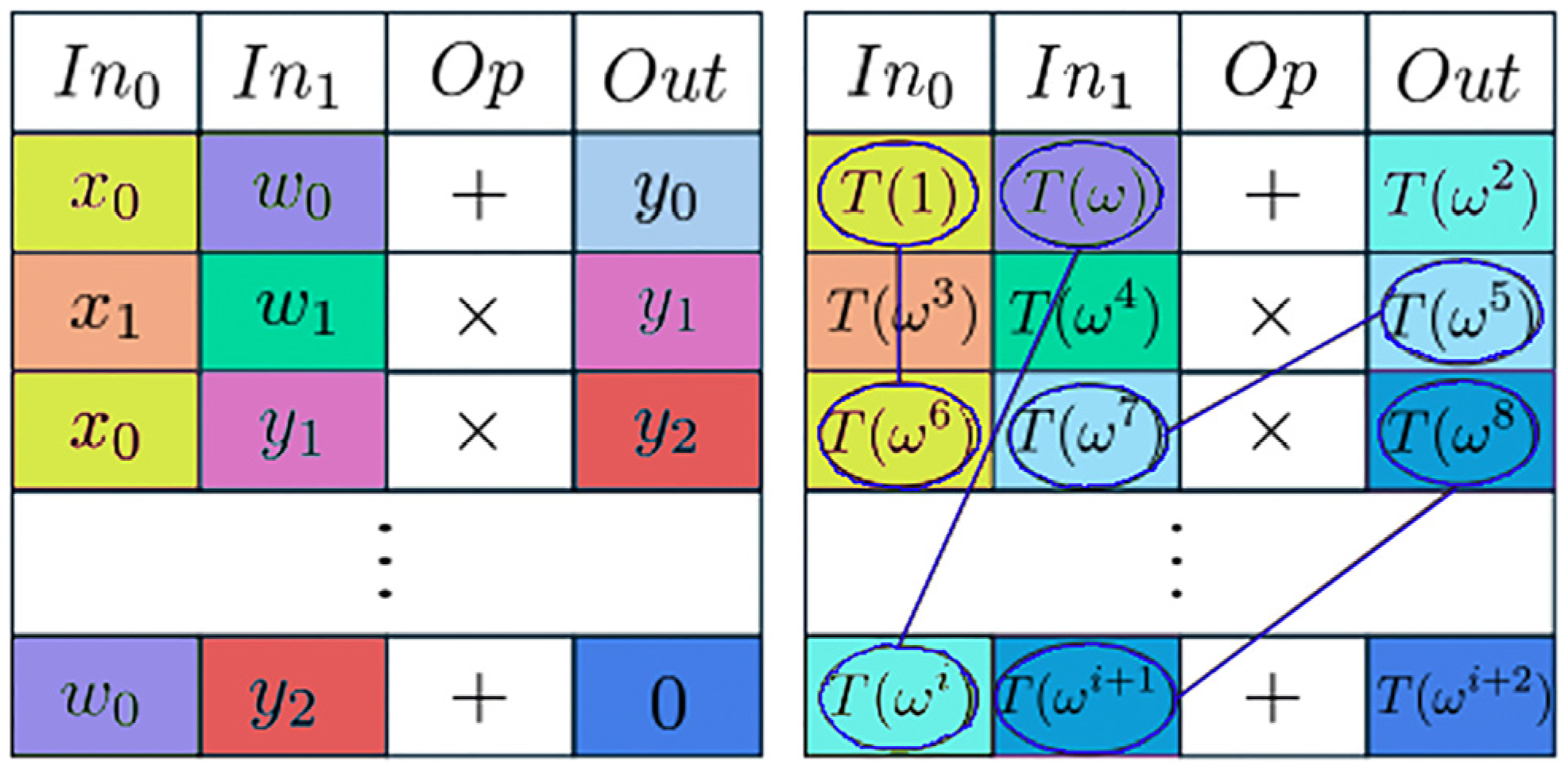
To enforce copy constraints, VerITAS employs a permutation argument. The goal of the permutation argument is to prove that certain cells in the computation trace are permutations of one another, ensuring that connected wires share the same values. The process involves interpolating the trace values into a polynomial $T\left(x\right)$ and defining a permutation $\tau$ such that $\tau \left(s_1\right)=s_2,\tau \left(s_2\right)=s_3,\dots ,\tau \left(s_l\right)=s_1$ for copy constraints. The prover then demonstrates that $T\left(s\right)=T\left(\tau \right(s\left)\right)$ for all $s\in \Omega$, where $\Omega$ is a set of evaluation points. The output of the permutation argument is a commitment to the polynomials $T$ and $\tau$, which proves that the copy constraints are satisfied. The process is illustrated on Figure 2.

In VerITAS, the permutation argument is modified to optimize proofs for computationally powerful signers, such as those in cloud-based systems. This modification reduces the overhead associated with proving photo editing transformations, making the system more efficient for high-resolution images. By leveraging the permutation argument, VerITAS ensures that the integrity of the editing process is maintained, while preserving the privacy of the original image. The combination of arithmetic circuit evaluation and permutation arguments enables VerITAS to provide a robust and efficient framework for verifying the authenticity and integrity of edited images. These techniques ensure that the transformation process is both correct and consistent, while the use of zero-knowledge proofs guarantees that sensitive information about the original image remains hidden. This makes VerITAS a powerful tool for applications in journalism, media, and digital content verification. For Post-Quantum VerITAS, we use HyperPlonk.

6.3.2. Plonk: Arithmetic Circuit Evaluation and Permutation Arguments

HyperPlonk is an advanced version of the Plonk proof system, designed to provide scalable, efficient, and flexible zero-knowledge proofs (ZKPs). Building upon the foundational structure of Plonk, HyperPlonk introduces optimizations aimed at improving prover efficiency, enhancing flexibility in circuit design, and supporting the efficient use of recursive proofs. These features make HyperPlonk particularly suitable for a wide range of cryptographic applications, including blockchain scalability, privacy-preserving computations, and recursive proof systems, such as Verkle trees. Additionally, HyperPlonk’s design takes into account post-quantum security, making it a forward-looking choice in the face of future quantum computing threats [17].

HyperPlonk is based on the succinct non-interactive argument of the knowledge (SNARK) framework, which allows the verification of computations without revealing the underlying data. HyperPlonk retains the core structure of Plonk, including the use of copy constraints and permutation arguments, to ensure the integrity of the computation. However, it improves upon Plonk by introducing new techniques that optimize the proof generation process, particularly in terms of prover efficiency and scalability.

In the context of post-quantum security, HyperPlonk leverages cryptographic primitives that are believed to be secure even against the computational power of future quantum computers. This is essential as we prepare for the advent of quantum computing, which could undermine the security of traditional cryptographic schemes. By adopting quantum-safe protocols, HyperPlonk ensures its relevance in a post-quantum world, making it suitable for long-term cryptographic applications.

HyperPlonk introduces several innovations over the original Plonk protocol, as follows:

• Multivariate Polynomial Commitments: One of the primary improvements in HyperPlonk is the use of multivariate polynomial commitments instead of univariate ones. This change results in smaller proof sizes and reduced verification times, which is important for scaling large computations. Moreover, the multivariate commitment scheme is based on post-quantum secure assumptions, making it resistant to quantum attacks that could compromise traditional univariate polynomials.
• Flexible Gate Definitions: HyperPlonk provides flexibility in defining custom gates. This feature allows for the encoding of specialized operations and constraints that may not be supported by standard gates in traditional Plonk. This flexibility is essential for applications requiring non-standard computations or custom logic in the proof system. Additionally, the ability to define secure gates with post-quantum cryptographic primitives ensures that the system remains resilient to quantum attacks.
• Prover Efficiency: HyperPlonk significantly reduces the computational cost for the prover, resulting in faster proof generation. By optimizing how the polynomials are evaluated and committed, HyperPlonk reduces the computational overhead typically associated with zero-knowledge proof systems. This efficiency gain is crucial in blockchain environments and privacy-preserving applications, where speed and scalability are paramount.
• Recursive Proof Systems: HyperPlonk is well-suited for use in recursive proof systems, where smaller proofs are aggregated into a larger proof. This recursive structure is essential for applications, such as Verkle trees and other advanced cryptographic systems, where scalability is a critical concern. Recursive proofs in HyperPlonk are designed to be post-quantum-secure, enabling long-term security even in quantum-era applications.
• Addition of Custom Constraints: Similar to other advanced proof systems, like Plonky2, HyperPlonk allows for the addition of custom constraints. These constraints can be implemented through the definition of custom gates or operations within the proof system. The ability to introduce custom constraints is crucial for applications that require specific circuit designs or specialized cryptographic operations. By utilizing quantum-safe primitives for constraint encoding, HyperPlonk ensures that custom constraints do not introduce vulnerabilities to future quantum attacks.

6.3.3. Comparison with Plonk

While Plonk was groundbreaking in providing an efficient and general-purpose framework for zero-knowledge proofs, HyperPlonk enhances this model by improving both performance and flexibility:

• Efficiency: HyperPlonk’s use of multivariate polynomials reduces proof size and speeds up the verification process compared to standard Plonk, making it more suitable for large-scale applications.
• Gate Flexibility: HyperPlonk’s ability to define custom gates and constraints allows for the encoding of more complex operations; whereas, Plonk is more constrained to standard gate types.
• Prover Optimization: The optimizations in HyperPlonk make it significantly more efficient for proof generation, which is critical in systems requiring high throughput.
• Post-Quantum Security: Unlike traditional Plonk, which relies on cryptographic assumptions vulnerable to quantum attacks (e.g., elliptic curve cryptography), HyperPlonk integrates post-quantum secure primitives. This makes it resilient to quantum attacks, securing future-proof applications where long-term data confidentiality is required.

6.4. CRYSTALS-Dilithium: A Post-Quantum Digital Signature Scheme

CRYSTALS-Dilithium is a lattice-based digital signature scheme designed for post-quantum cryptography, based on the hardness of the Module-LWE and Module-SIS problems. These problems are considered quantum-resistant and form the basis for the scheme’s security. The key generation process involves the creation of a secret key and a corresponding public key through a trapdoor function that utilizes a structured lattice. Signature generation employs a combination of Gaussian sampling and rejection sampling, ensuring that the signature size remains compact, while satisfying security requirements. During signature verification, the verifier checks the validity using lattice-based linear algebra operations, ensuring the authenticity of the signature [18].

Dilithium’s efficiency is optimized by balancing security and performance. The key sizes are smaller than those of RSA with comparable security levels, and its signing and verification processes are more efficient than those of hash-based signature schemes. The use of bounded noise sampling ensures that signatures remain small, while the rejection sampling technique prevents the generation of invalid signatures. In terms of performance, Dilithium achieves practical speeds for both signing and verification in software and hardware implementations, making it suitable for a wide range of applications, including secure communication protocols (TLS), blockchain, and code signing.

Despite these advantages, the scheme faces challenges, such as larger key and signature sizes compared to traditional RSA and the need for further resistance to side-channel attacks, particularly in hardware implementations. Future work will focus on improving these aspects and optimizing Dilithium for use in resource-constrained environments, like IoT devices. With its strong security foundations and efficiency, CRYSTALS-Dilithium is positioned to play a key role in post-quantum cryptographic standards.

7. Secure Image Provenance with C2PA: Embedded Signing, Threat Models, and Defenses

The Coalition for Content Provenance and Authenticity (C2PA) provides a framework for ensuring the authenticity of digital images by embedding cryptographic signatures into the content at the time of capture. A key component of this framework is the embedded signing key, which is unique to each camera. During manufacturing, the camera generates a signing key on-device, and this key is certified by a C2PA authority. This process establishes a root of trust in the camera and its signing key, ensuring that only the camera is trusted to sign images, while editors and other third parties are not.

The secure signing process involves the camera signing the raw RGB values and metadata (e.g., location, timestamp, exposure time) at the moment an image is captured. This signature binds the image data to its metadata, creating a tamper-evident record of the image’s provenance. The signed image can then be verified by anyone with access to the camera’s public key, ensuring that the image has not been altered, since it was captured.

The threat model assumes that an attacker has access to the camera and its public key but cannot extract the private signing key or force the camera to sign fabricated images. This model is designed to protect against malicious actors who may attempt to manipulate or forge images, while maintaining the integrity of the signing process. The root of trust lies solely in the camera and its signing key, meaning that no other entity, including editors, is trusted to sign or modify images.

The verification goal of C2PA is to ensure that an edited photo results from acceptable transformations applied to a C2PA-signed image. This requires verifying both the authenticity of the original image and the integrity of the editing process. However, achieving this goal is not without challenges, as several potential attacks must be mitigated.

One such attack is the key extraction attack, where an attacker attempts to extract the camera’s private signing key. To defend against this, cameras are equipped with Hardware Trusted Execution Environments (TEEs), which protect the signing key from unauthorized access. Additionally, if a key is compromised, it can be revoked by the C2PA authority, preventing further misuse.

Another attack is the picture-of-picture attack, where an AI-generated image is displayed on a screen and re-photographed by a camera. This attack can be detected through metadata analysis, such as identifying inconsistencies in focal length or other camera settings that would not match a genuine capture. Metadata-based defenses are critical for distinguishing between authentic and re-photographed images.

Semantic manipulation is another concern, where edits, such as cropping or removing elements from an image, alter its meaning. For example, removing a person from a group photo could change the narrative conveyed by the image. While C2PA can verify that an image has been edited, it cannot inherently detect or prevent semantic manipulation. This highlights the need for additional safeguards, such as human oversight or AI-based content analysis, to address these types of attacks.

Privacy risks also arise from the use of camera signatures, as they could expose the identity of the device or user. To mitigate this, group signatures can be employed, allowing multiple cameras to share a single public key, while maintaining individual private keys. This approach anonymizes the source of the image, while still enabling the verification of its authenticity.

While C2PA represents a crucial step forward in image provenance, it must be combined with additional security measures to address evolving threats. The framework provides a strong foundation for ensuring the authenticity and integrity of digital images, but ongoing innovation and collaboration are needed to stay ahead of sophisticated attacks. By integrating hardware security, metadata analysis, and privacy-preserving techniques, C2PA and related technologies can continue to advance the trustworthiness of digital content in an increasingly complex media landscape.

8. Public Statements, Secret Witnesses, and Instance-Witness Relations

In the context of verifying the authenticity and integrity of edited photos, the proof system relies on a public statement, a secret witness, and an instance-witness relation to ensure that the edited image is a valid transformation of an original, signed photo. The public statement consists of the edited photo $x$, the editing function $f$, and the camera’s public key $vk$. These elements are known to the verifier and provide the basis for the verification process. The secret witness, on the other hand, includes the original photo $w$ and the camera’s signature $\sigma$ on $w$. This information is kept private and is used by the prover to generate the proof.

The proof system is defined by the instance-witness relation $R$, which formalizes the conditions that must be satisfied for the proof to be valid. Specifically, the relation $RR$ is defined as follows:

$$R:=\{\left(\left(\mathrm{v}\mathrm{k},f,x\right);\left(w,\sigma \right)\right);f(w)=x\wedge \mathrm{V}\mathrm{f}(\mathrm{v}\mathrm{k},w,\sigma )=1\}$$

(6)

This relation states that the edited photo $x$ must be the result of applying the editing function $ff$ to the original photo $w$, and the signature $\sigma$ must be valid under the camera’s public key $vk$. The proof system, thus, requires two distinct proofs—a transformation proof and a signature proof.

The transformation proof demonstrates that $f\left(w\right)=x$, meaning that the edited photo $x$ is the result of applying the editing function $f$ to the original photo $w$. This proof ensures that the editing process was performed correctly and that the final image is a valid transformation of the original.

The signature proof verifies that the signature $\sigma$ is valid for the original photo $w$ under the camera’s public key $vk$. This proof ensures that the original photo was indeed signed by the camera and has not been tampered with since its creation. Together, these proofs provide a comprehensive verification mechanism for edited photos. The transformation proof ensures the integrity of the editing process, while the signature proof ensures the authenticity of the original image. By combining these proofs, the system can guarantee that the edited photo is both a valid transformation of the original and derived from a trusted source.

This proof system is particularly relevant in applications like Post-Quantum VerITAS, where the goal is to verify the provenance of edited images, while preserving privacy and security. The use of zero-knowledge proofs ensures that the secret witness (the original photo and signature) remains hidden, while the public statement and instance-witness relation provide a transparent and verifiable framework for ensuring the authenticity and integrity of digital content.

9. Efficient Signature Verification in Post-Quantum VerITAS

The signature verification process is a critical component of ensuring the authenticity of digital images. It involves the following two main steps: computing a hash of the original image and verifying the signature on that hash. Specifically, given an original image $w$, the process computes a hash $h \leftarrow H\left(w\right)$, where $H$ is a collision-resistant hash function. The signature $\sigma \sigma$ is then verified to ensure it is a valid signature on $h$ under the camera’s public key $vk$. While this process is straightforward for small data, it becomes computationally challenging for large data, such as 30-megapixel (30 MP) photos, where most of the time is spent computing the hash $h$.

The challenge is further compounded when using $zk$-SNARKs to prove the correctness of the hash computation. Proving that $h=H\left(w\right)$ within a SNARK circuit is computationally expensive, especially for large images. Standard hash functions, like SHA256 or SHA512 for post-quantum settings, are inefficient in SNARKs, because they rely on non-algebraic operations, such as logical operations, which are not well-suited for the arithmetic circuits used in SNARKs. As a result, proving SHA256/SHA512 for a 30 MP image is infeasible in practice. Even Poseidon, a hash function specifically designed to be SNARK-friendly, struggles with the sheer size of 30 MP images, making it impractical for direct use in such scenarios.

To address these challenges, Post-Quantum VerITAS introduces the following two innovative solutions: a lattice-based hash combined with edited Poseidon and a polynomial commitment scheme. The lattice-based hash system is post-quantum and bout Poseidon hash; we offer how to make it post-quantum in the next section. The first solution leverages the strengths of both lattice-based hashes and Poseidon hashes. The lattice-based hash is highly efficient for processing large data, reducing a 90 MB image to a compact 4 KB digest. This digest is then further hashed using Poseidon, which compresses it to 32 bytes [19,20]. The lattice-based hash is particularly well-suited for SNARKs, because it relies on linear operations, which are efficient to prove in arithmetic circuits. By combining these two hash functions, Post-Quantum VerITAS achieves a balance between efficiency and SNARK-friendliness, making it feasible to handle 30 MP images.

The second solution involves using a polynomial commitment scheme. In this approach, the signer computes a polynomial commitment to the image, which serves as a compact representation of the data. The advantage of this method is that it eliminates the need to prove $h=H\left(w\right)$ within the SNARK circuit. Instead, the prover can directly work with the polynomial commitment, significantly reducing the computational overhead. This approach is particularly beneficial for computationally powerful signers, such as cloud-based systems, where the additional resources required for polynomial commitments are readily available.

Together, these solutions enable Post-Quantum VerITAS to efficiently verify the authenticity of large images, while maintaining the privacy and security guarantees of zero-knowledge proofs. By combining lattice-based hashes, Poseidon hashes, and polynomial commitments, Post-Quantum VerITAS overcomes the limitations of standard hash functions and provides a scalable framework for verifying the provenance of digital content. These innovations represent a significant advancement in the field of image provenance, making it possible to handle high-resolution images in real-world applications.

9.1. Post-Quantum Poseidon

Together, these solutions enable Post-Quantum VerITAS to efficiently verify the authenticity of large images, while maintaining the privacy and security guarantees of zero-knowledge proofs.

To make the Poseidon hash function post-quantum-secure, we must address the vulnerabilities that quantum computers could exploit, such as Grover’s algorithm and Shor’s algorithm. Poseidon is not inherently quantum-resistant, because its design is based on classical security assumptions, and its efficiency for zero-knowledge proof systems does not account for quantum computational power. To achieve post-quantum security, we must modify Poseidon in the following concrete manner:

To achieve quantum resistance, we increase the output size, use larger finite fields, and enhance the permutation layer. Quantum algorithms, particularly Grover’s algorithm, can perform a brute-force search in $O(\surd N)$ time, where $N$ is the size of the search space. For an n-bit hash function, this reduces the effective security from $2^N$ to $2^{n/2}$. To mitigate this, therefore, we double the output size of Poseidon and extend other parameters accordingly. For example, if Poseidon currently uses a 256-bit output, we must increase it to 512 bits to achieve 256-bit post-quantum security. This ensures that even with Grover’s algorithm, the security level remains sufficiently high.

To ensure that the modified Poseidon hash is resistant to known quantum threats, we introduce the following concrete parameter choices:

• Output Size: Increased from 256 bits to 512 bits to maintain 256-bit post-quantum security, mitigating Grover’s algorithm which offers a quadratic speedup in brute-force hash searches.
• Finite Field: We use a prime field ${\mathbb{F}}_p$ with $p>2^{512}$ to ensure sufficient entropy against quantum adversaries capable of exploiting algebraic structures, thus neutralizing attacks like Shor’s algorithm on small fields.
• Number of Rounds: Increased from the original Poseidon default (e.g., 8 full + 56 partial) to 16 full + 96 partial rounds. This enhances resistance against differential, linear, and quantum algebraic attacks.
• S-Box Nonlinearity: We replace quadratic S-boxes with quartic ($x^4$) S-boxes to increase algebraic complexity and diffusion in the quantum setting.

These modifications result in a $\sim 30-40\mathrm{\%}$ increase in computational cost per hash due to larger state size and increased round function complexity. However, these costs are mitigated through parallelization of tiles and optimizations using zk-SNARK-friendly arithmetic gates, as discussed in Section 10.

Larger finite fields are used to resist algebraic attacks, and the permutation layer is enhanced with additional rounds and stronger S-boxes to counter quantum cryptanalysis. Quantum algorithms, like Shor’s algorithm, can efficiently solve problems, such as discrete logarithms and factoring in certain algebraic structures. To address this, we must use larger finite fields, such as fields with 512-bit or larger primes. This makes it significantly harder for quantum algorithms to exploit the algebraic structure of the hash function.

Finally, we must strengthen the permutation layer, as the security of Poseidon depends on its permutation layer, which consists of rounds of nonlinear operations (e.g., S-boxes) and linear transformations. Quantum computers could potentially exploit weaknesses in this layer. To strengthen it, we must increase the number of rounds and use stronger S-boxes or nonlinear components that are specifically designed to resist quantum cryptanalysis. For example, we can use higher-degree nonlinear functions (e.g., cubic or quartic functions) instead of quadratic functions for the S-boxes, ensuring they have strong differential and linear properties. Additionally, we should optimize the linear layer (e.g., MDS matrices) to maximize diffusion and resist quantum attacks.

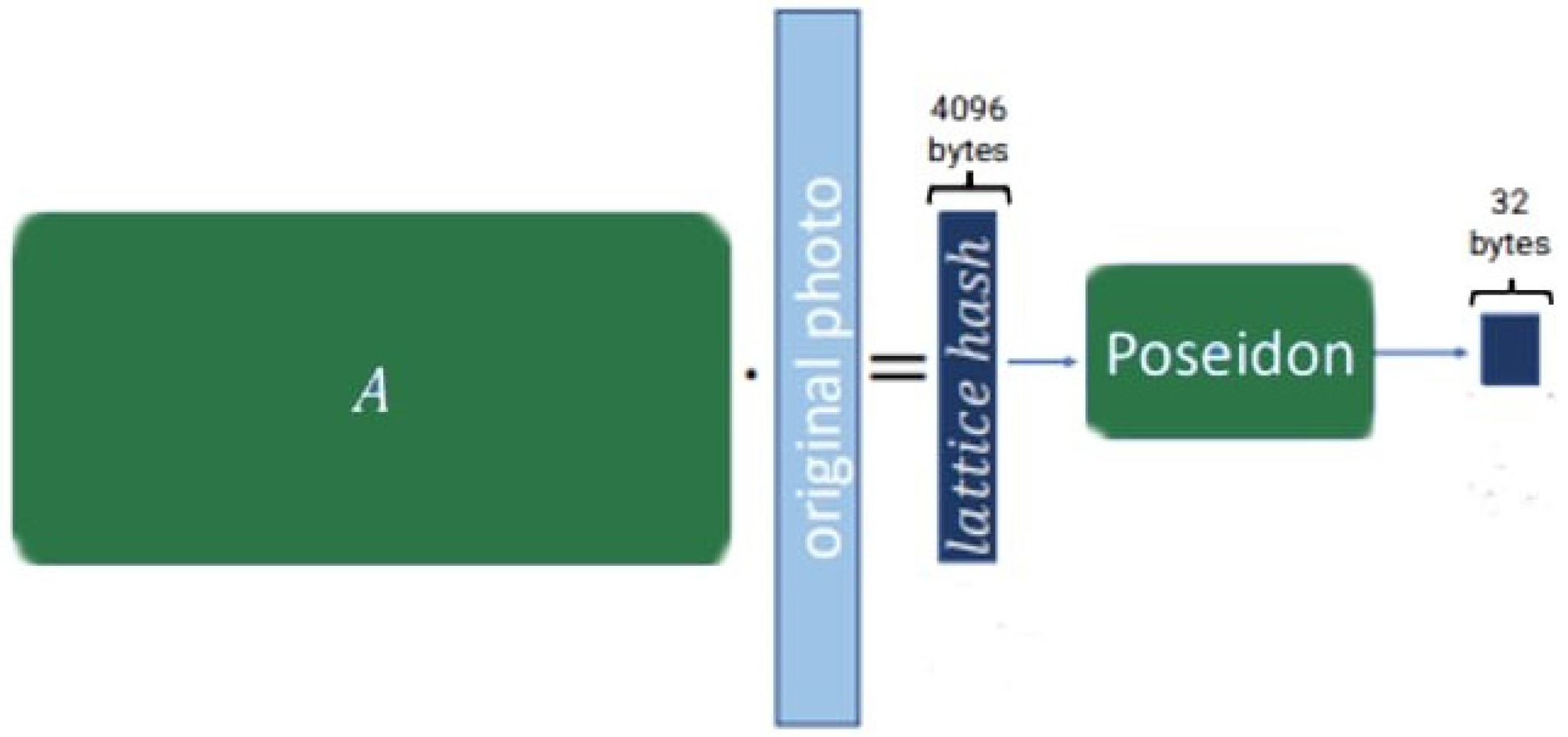
9.2. Input Representation and Hash Verification Using Lattice and Poseidon Hashes

The input photo, denoted as $w$, is decomposed into three low-norm vectors corresponding to the red, green, and blue (RGB) color channels. These vectors are represented as $v_r$,$v_g$,$v_b$, respectively. Each vector has a length of $m$, where $m$ corresponds to the number of pixels in the image, and the pixel values in each vector are constrained to the range [0, 255], ensuring compatibility with standard image formats. To compute the lattice hash, each of the RGB vectors is multiplied by a randomly generated matrix $A$, where $A\in F_q{q}^{\{n\times m\}}$. The multiplication is performed by modulo $q$, resulting in the transformation $h=A\cdot v modq$, where $h$ represents the intermediate hash output for each color channel. This step ensures that the high-dimensional pixel data is compressed into a lower-dimensional representation, while preserving the structural properties of the image. The output of the lattice hash is further processed using the Poseidon hash function, a cryptographic hash designed for efficiency in zero-knowledge proof systems. The final hash is computed as follows:

$$H\left(v\right)=Poseidon(A\cdot v modq)$$

(7)

providing an additional layer of security and ensuring that the hash output is both compact and suitable for verification in zero-knowledge proof systems.

The hashing procedure is illustrated in Figure 3.

The input image is decomposed into red, green, and blue channels, each of which is hashed using a lattice-based method. The resulting digest is then compressed using a post-quantum Poseidon hash, yielding a SNARK-compatible 512-bit output.

The verification of the hash involves proving a specific relation, denoted as $R_{VH}$, which is defined as follows:

$$R_{\mathrm{V}\mathrm{H}}≔\left\{\left(\right(A,h,b);v):h=\mathrm{P}\mathrm{o}\mathrm{s}\mathrm{e}\mathrm{i}\mathrm{d}\mathrm{o}\mathrm{n}(A\cdot v),\Vert v{\Vert }_{\mathrm{\infty }}<b\right\}$$

(8)

This relation ensures that the prover knows a valid vector v that satisfies the hash computation and adheres to the low-norm constraint $\Vert v{\Vert }_{\mathrm{\infty }}<b$, which is critical for collision resistance. The proof system for hash verification consists of the following three key components: (1) the prover demonstrates that $h=A\cdot v$, ensuring the correctness of the linear transformation applied during the lattice hash computation; (2) the prover shows that $\Vert v{\Vert }_{\mathrm{\infty }}<b$, confirming that the input vector $v$ adheres to the required norm bound, which is essential for maintaining the collision-resistant properties of the hash function; and (3) using a Groth16 circuit, the prover verifies that the Poseidon hash function was applied correctly to the output of the lattice hash, ensuring the integrity of the final hash computation.

In Mode 2, the signer begins by encoding the input image $w$ as a polynomial:

$$W\left(X\right)=poly\left(w\right)$$

(9)

A key insight in this approach is the avoidance of proving com directly in the SNARK circuit by leveraging HyperPlonk’s extended permutation argument, which significantly reduces computational overhead. Polynomial commitments are employed for their efficiency, as they eliminate the need to hash w within the SNARK circuit, and for their binding property, which ensures that com is a valid and secure commitment to the polynomial $W\left(X\right)$.

The signer then computes a polynomial commitment using a post-quantum PCS, we use FRI.

$$com \leftarrow PCS.commit(pp, W, r)$$

(10)

where pp represents the public parameters of the commitment scheme, $W$ is the polynomial representation of the image, and $r$ is a random blinding factor. The signer proceeds to sign the commitment com to produce a signature $\sigma$ and sends the tuple ($vk, com, \sigma ,r$) to the editor, where $vk$ is the verification key.

The editor’s task involves producing an edited image.

$$x=f\left(w\right)$$

(11)

where $f$ represents the editing function applied to the original image. To prove the validity of the edit, the editor constructs a zero-knowledge proof for the relation $R_{\mathrm{s}\mathrm{i}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{e}}$, defined as:

$$R_{\mathrm{simple} }:=\left\{\right((pp,f,x,com);(w,r)):f(w)=x\wedge com=PCS.commit\left(pp,poly\left(w\right),r\right)$$

(12)

This relation ensures that the edited image $x$ is derived from the original image $w$ through the function $f$, and that the commitment com is a valid commitment to the polynomial representation of $w$.

A key insight in this approach is the avoidance of proving com directly in the SNARK circuit by leveraging an extension of PLONK’s permutation argument, which significantly reduces computational overhead. Polynomial commitments are employed for their efficiency, as they eliminate the need to hash $w$ within the SNARK circuit, and for their binding property, which ensures that com is a valid and secure commitment to the polynomial $W\left(X\right)$.

To ensure consistency between the computation trace $T\left(X\right)$ and the witness polynomial $W\left(X\right)$, HyperPlonk introduces additional copy constraints. These constraints enforce that the values of $T\left(\Omega \right)$ match the corresponding values of $W\left(\Omega \right)$ for all witness elements. This is achieved by defining a new permutation ${\tau }^{\prime }$ that captures the constraints between $T\left(X\right)$ and $W\left(X\right)$. A visualization of this process is provided in Figure 4, where thick green edges represent the extended copy constraints.

The proof construction begins with the circuit $C(x,w)$, which outputs 0 if $f\left(w\right)=x$. The editor constructs the computation trace $T\left(X\right)$ for the circuit $C(x,w)$. The permutation ${\tau }^{\prime }$ is extended to include constraints between $T\left(X\right)$ and $W\left(X\right)$, ensuring consistency across the computation. Finally, the editor generates a proof $\pi$ for the relation $R_{\mathrm{s}\mathrm{i}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{e}}$, using HyperPlonk’s proof system, which efficiently handles large-scale computations. It is defined as follows:

$$R_{\mathrm{simple} }≔\left\{\right((pp,f,x,com);(w,r)):f(w)=x\wedge com=PCS.commit(pp,poly\left(w\right),r)$$

(13)

The verifier performs two checks, as follows:

• Signature Verification: The verifier checks that $Vf(vk, com, \sigma )$ accepts, ensuring the authenticity of the commitment.
• Proof Verification: The verifier confirms that the proof π is valid for the relation $R_{\mathrm{s}\mathrm{i}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{e}}$.

This approach offers several advantages:

• Efficiency: Proving $R_{\mathrm{s}\mathrm{i}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{e}}$ requires no additional work beyond proving $f\left(w\right)=x$.
• Scalability: The system efficiently handles large images, such as 30 MP, due to the optimized proof construction.
• Privacy: The commitment com hides the original image $w$, revealing only the edited image $x$.

9.3. Proof System for the Lattice Hash

To prove that $H\left(v\right)=A\cdot v$ was computed correctly, the system relies on the instance-witness relation $R_{LH}$, defined as:

$$R_{\mathrm{L}\mathrm{H}}≔\left\{\left(\right(A,h,b);v):h=A\cdot v,\Vert v{\Vert }_{\mathrm{\infty }}<b\right\}$$

(14)

This relation ensures that the output $h$ is the correct result of the matrix–vector product $A\cdot v$, and that the input vector $v$ adheres to the low-norm constraint $\Vert v{\Vert }_{\mathrm{\infty }}<b$.

9.3.1. Range Proof

The goal of the range proof is to demonstrate that all elements of $v$ lie within the range $[0, b-1]$, i.e., $\Vert v{\Vert }_{\mathrm{\infty }}<b$. This is achieved using a lookup argument with a predefined table $T=[0, b-1]$. The steps are as follows:

• Create a sorted vector $z=v\Vert u$, where u contains all values in $T=[0, b-1]$.
• Prove that z is a permutation of $v\Vert u$.
• Prove that consecutive elements in $z$ differ by $0$ or $1$, ensuring that all values in $v$ are within the specified range.

9.3.2. Matrix–Vector Product Proof

The goal of the matrix–vector product proof is to verify that $h=A\cdot v$. This is accomplished using Freivalds’ algorithm combined with a sum-check protocol. The steps are as follows:

• Generate a random vector $r\leftarrow F^n$.
• Prove that $r^{\mathrm{\top }}h=\left(r^{\mathrm{\top }}A\right)v$, which ensures the correctness of the matrix–vector product.
• Use Aurora’s univariate sum-check protocol to efficiently verify the computation.

9.3.3. Polynomial Encoding for Efficient Proofs

The goal of the matrix–vector product proof is to verify that $h=A\cdot v$. This is accomplished using Freivalds’ algorithm combined with a sum-check protocol. The steps are as follows:

To enable efficient zero-knowledge proofs, vectors are encoded as polynomials. Given a vector $v=\left(v_0,\dots ,v_{m-1}\right)$, it is encoded as a polynomial $v\left(X\right)$, such that:

$v\left({\omega }^i\right)=v_i$ for $i\in \left[m\right]$, where ω is a primitive $m$-th root of unity.

This encoding is performed by the following function:

$$F^m\to F^{<m}\left[X\right],$$

(15)

which maps a vector of length $m$ to a polynomial of degree less than $m$.

We use polynomials for efficient proofs, as they leverage algebraic properties, such as interpolation and evaluation, to enable efficient zero-knowledge proofs. These properties allow for compact representations and fast verification of computations. Also, any vector $v$ can be uniquely represented as a polynomial of degree $<m$, ensuring a one-to-one correspondence between vectors and their polynomial encodings. This property is crucial for maintaining the integrity and correctness of the proofs.

9.3.4. ZeroCheck and Univariate SumCheck Relations

Let ${\mathsf{\Omega }}_m:=\left\{1,\omega ,{\omega }^2,\dots ,{\omega }^{m-1}\right\}\subseteq F$ be the set of $m$-th roots of unity, and let $d>m$ be a degree bound. The following two key relations are used in the proof system: ZeroCheck and Univariate SumCheck.

The ZeroCheck relation $R_{\mathrm{Z}\mathrm{C},m}$ is defined as:

$$\begin{array}{cc}{R}_{ZC,m}≔\left\{\left(\left(pp,{com}_u\right);\left(u,r\right)\right)\right.& :u\in F^{<d}\left[X\right],\\ \forall \omega \in {\Omega }_m:u\left(\omega \right)& =0,\\ commit\left(pp,u,r\right)& \left.={com}_u\right\}\end{array}$$

(16)

This relation ensures that the polynomial $u\left(X\right)$ evaluates to zero at all points in ${\Omega }_m$, and that com_u is a valid commitment to $u\left(X\right)$ using randomness $r$.

The Univariate SumCheck relation:

$$\begin{array}{cc}& R_{SC,m}:=\left\{\left(\left(pp,{com}_u,s\right);(u,r)\right):u\in F^{<d}\left[X\right],\right.\\ & \sum _{\omega \in {\Omega }_m}\hspace{0.17em}u\left(\omega \right)=s,\\ & \left.commit(pp,u,r)={com}_u\right\}\end{array}$$

(17)

This relation ensures that the sum of the polynomial $u\left(X\right)$ evaluated at all points in ${\Omega }_m$ equals $s$, and that ${com}_u$ is a valid commitment to $u\left(X\right)$ using randomness $r$ [21,22].

9.3.5. Permutation Check Using Polynomial Roots in zk-SNARKs

The goal is to prove all elements of $v\in F^m$ are in $[0,b-1]$. This is achieved by leveraging the properties of polynomials and their roots.

The input we get the following polynomials $u\in {\mathbb{F}}^{<b}\left[X\right],v\in {\mathbb{F}}^{<m}\left[X\right],z\in {\mathbb{F}}^{<b+m}\left[X\right]$ and commitments is ${\mathrm{c}\mathrm{o}\mathrm{m}}_u,{\mathrm{c}\mathrm{o}\mathrm{m}}_v,{\mathrm{c}\mathrm{o}\mathrm{m}}_z$.

The key equality to verify is as follows:

$${\prod }_{\alpha \in {\Omega }_{b+m}}\left(X-z\left(\alpha \right)\right)={\prod }_{\beta \in {\Omega }_b}\left(X-u\left(\beta \right)\right){\prod }_{\gamma \in {\Omega }_m}\left(X-v\left(\gamma \right)\right)$$

(18)

This equality holds if and only if $z$ is a permutation of $u\Vert v$. It works as $\prod _{\alpha \in {\mathsf{\Omega }}_{b+m}}\left(X-z\left(\alpha \right)\right)$ is a polynomial whose roots are the evaluations of $z$ over the set ${\mathsf{\Omega }}_{b+m}$.

$\prod _{\beta \in {\mathsf{\Omega }}_b}\left(X-u\left(\beta \right)\right)$ and $\prod _{\gamma \in {\mathsf{\Omega }}_m}(X-v(\gamma \left)\right)$ are the polynomials whose roots are the evaluations of u over ${\mathsf{\Omega }}_b$ and v over ${\mathsf{\Omega }}_m$, respectively. If the two sides of the equation are equal, it means that the multiset of roots is exactly the same as the multiset of roots of u and v combined [23,24]. This implies that $z\left({\mathsf{\Omega }}_{b+m}\right)$ is a permutation of $u\left({\mathsf{\Omega }}_b\right)\Vert v\left({\mathsf{\Omega }}_m\right).$

9.3.6. Range Proof in Permutation Arguments

The goal is to prove that all elements of a vector $v\in F^m$ are in the range $[0,b-1]$. This is achieved using a lookup table $u_b=\left(\mathrm{0,1},\dots ,b-1\right)$ and proving that $v$ is a subset of $u_b$ through polynomial commitments.

The prover constructs a sorted vector $z=sort\left(v\Vert u_b\right)$ and encodes it as a polynomial $z\left(X\right)=\mathrm{p}\mathrm{o}\mathrm{l}\mathrm{y}\left(z\right)$. The proof involves demonstrating that $z\left(X\right)$ is a permutation of $v\left(X\right)\Vert u\left(X\right)$ and that the elements of $z\left(X\right)$ satisfy the required range constraints.

The steps are the following:

Prover:

• Construct $z=\mathrm{s}\mathrm{o}\mathrm{r}\mathrm{t}\left(v\Vert u_b\right)$ and $z\left(X\right)=\mathrm{p}\mathrm{o}\mathrm{l}\mathrm{y}\left(z\right)$
• Commit to $z\left(X\right):{\mathrm{c}\mathrm{o}\mathrm{m}}_z$.
• Prove $z\left(X\right)$ is a permutation of $v\left(X\right)\Vert u\left(X\right)$ using PermCheck:

$${\pi }_{PC}\leftarrow P_{PC}\left(pp,{com}_u,{com}_v,{com}_z;u,v,z,0,r_v,r_z\right)$$

(19)

• Construct $f\left(X\right)=\left(z\left(\omega X\right)-z\left(X\right)\right)\cdot \left(z\left(\omega X\right)-z\left(X\right)-1\right).$
• Prove $f\left(X\right)=0$ on ${\mathsf{\Omega }}_{m+b}$ using ZeroCheck:

$${\pi }_{ZC}\leftarrow P_{ZC,m+b}\left(pp,{com}_f;f,r_f\right)$$

(20)

• Output proof $\pi =\left({\mathrm{c}\mathrm{o}\mathrm{m}}_z,{\pi }_{\mathrm{P}\mathrm{C}},{\pi }_{\mathrm{Z}\mathrm{C}}\right).$

Verifier:

• Parse $\pi =\left({\mathrm{c}\mathrm{o}\mathrm{m}}_z,{\pi }_{\mathrm{P}\mathrm{C}},{\pi }_{\mathrm{Z}\mathrm{C}}\right)$.
• Compute ${com}_u=commit\left(pp,poly\left(u_b\right),0\right)$.
• Verify:

accept if $V_{\mathrm{P}\mathrm{C}}\left(\mathrm{p}\mathrm{p},{\mathrm{c}\mathrm{o}\mathrm{m}}_u,{\mathrm{c}\mathrm{o}\mathrm{m}}_v,{\mathrm{c}\mathrm{o}\mathrm{m}}_z;{\pi }_{\mathrm{P}\mathrm{C}}\right)$ and $V_{\mathrm{Z}\mathrm{C},m+b}\left(\mathrm{p}\mathrm{p},{\mathrm{c}\mathrm{o}\mathrm{m}}_f;{\pi }_{\mathrm{Z}\mathrm{C}}\right)$ both accept.

It works as $z\left(\omega X\right)$ represents a shifted version of the polynomial $z\left(X\right)$. If $z\left(X\right)$ evaluates to $z_{i+1}$ at $X={\omega }^i$, then $z\left(\omega X\right)$ evaluates to $z_{i+1}$ at $X={\omega }^i$. This is because $z\left(\omega \cdot {\omega }^i\right)=z\left({\omega }^{i+1}\right)=z_{i+1}$.

This theorem states that the proof system is secure.

Theorem 1.

Suppose that  $\left(P_{ZC},V_{ZC}\right)$ and $\left(P_{PC},V_{PC}\right)$ are $zk$-SNARKs for  $R_{ZC}$ and  $R_{PC}$ respectively. Further, suppose that the polynomial commitment scheme used is secure. Then, the proof system in Algorithms 1 and 2 is a zk-SNARK for the relation.

$$\begin{array}{c}{R}_{RP}:=\left\{\left(\left(pp,b,{com}_v\right);\left(v,r_v\right)\right):v\in F^{<m}\left[X\right],\right.\\ \forall \omega \in {\Omega }_m:v\left(\omega \right)\in [0,b-1] \mathrm{for} b\in N,\\ \left.{com}_v=commit\left(pp,v,r_v\right)\right\}\end{array}$$

(21)

Algorithm 1: Range Proof Construction (Prover Side)
Input:
$v$$, \mathrm{auxiliary} \mathrm{vector} u_b$$, \mathrm{randomness} r_v,r_z,r_f$$, \mathrm{public} \mathrm{parameters} pp$
Concatenate and sort:
$\begin{array}{ll}& z:=\mathrm{s}\mathrm{o}\mathrm{r}\mathrm{t}\left(v\Vert u_b\right)\\ & z\left(X\right):=\mathrm{p}\mathrm{o}\mathrm{l}\mathrm{y}\left(z\right)\end{array}$
Commit to sorted polynomial:
${\mathrm{c}\mathrm{o}\mathrm{m}}_z:=\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{m}\mathrm{i}\mathrm{t}\left(pp,z\left(X\right),r_z\right)$
Permutation proof:
${\pi }_{PC}:=P_{PC}\left(pp,{\mathrm{c}\mathrm{o}\mathrm{m}}_u,{\mathrm{c}\mathrm{o}\mathrm{m}}_v,{\mathrm{c}\mathrm{o}\mathrm{m}}_z;u,v,z,0,r_v,r_z\right)$
Range check polynomial:
$f\left(X\right):=\left(z\right(\omega X)-z(X\left)\right)\cdot \left(z\right(\omega X)-z(X)-1)$
ZeroCheck proof:
${\pi }_{ZC}:=P_{ZC,m+b}\left(pp,{\mathrm{c}\mathrm{o}\mathrm{m}}_f;f,r_f\right)$
Output:
$\pi :=\left({\mathrm{c}\mathrm{o}\mathrm{m}}_z,{\pi }_{PC},{\pi }_{ZC}\right)$

Algorithm 2: Range Proof Verification (Verifier Side)
Input:
$\pi :=\left({\mathrm{c}\mathrm{o}\mathrm{m}}_z,{\pi }_{PC},{\pi }_{ZC}\right),\mathrm{polynomial} \mathrm{poly} \left(u_b\right),\mathrm{public} \mathrm{parameters} pp$
Parse:
$\pi =\left({\mathrm{c}\mathrm{o}\mathrm{m}}_z,{\pi }_{PC},{\pi }_{ZC}\right)$
Recompute commitment for $u_b$:
${\mathrm{c}\mathrm{o}\mathrm{m}}_u:=\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{m}\mathrm{i}\mathrm{t}\left(pp,\mathrm{p}\mathrm{o}\mathrm{l}\mathrm{y}\left(u_b\right),0\right)$
Verify permutation proof:
$\mathrm{Verify} {\pi }_{PC} \mathrm{using} \mathrm{PermCheck}$
Verify ZeroCheck proof:
$\mathrm{Verify} {\pi }_{ZC} \mathrm{on} \mathrm{domain} {\mathsf{\Omega }}_{m+b}$
Accept if both permutation and ZeroCheck proofs are valid.

9.4. Proving Knowledge of a Low-Norm Preimage for Lattice Hashes

The goal is to prove knowledge of a low-norm preimage $v\in F^m$ for a lattice hash $h=A\cdot v$, where $A\in F^{n\times m}$. The proof system is augmented to include the constraint $h=A\cdot v$. This is achieved by combining a Range Proof for the norm constraint with a univariate SumCheck proof for the linear combination. The augmented relation is defined as follows:

$$\begin{array}{c}{R}_{LH}^{\prime }≔\left\{\left(\left(A,h,b,pp,{com}_v\right);\left(v,r_v\right)\right):A\in F^{n\times m},\right.\\ h=A\cdot v,\Vert v{\Vert }_{\infty }<b for b\in N,\\ \left.{com}_v=commit\left(pp,poly\left(v\right),r_v\right)\right\}\end{array}$$

(22)

This relation ensures that $v$ is a valid preimage of $h$ under the linear transformation $A$, and that $v$ adheres to the low-norm constraint.

The prover must take the following steps:

• Commit to $v\left(X\right)=poly\left(v\right):{com}_v$.
• Prove $\Vert v{\Vert }_{\mathrm{\infty }}<b$ using the Range Proof system.
• Prove $h=A\cdot v$ using a univariate SumCheck proof:
• Reduce $h=A\cdot v$ to a single dot-product using a random linear combination of rows of $A$.
• Use the Fiat–Shamir transform to make the protocol non-interactive.

The verifier must take the following steps:

• Verify the Range Proof and SumCheck proof.

Accept if both proofs are valid.

10. Implementation

To validate the efficiency and scalability claims of Post-Quantum VerITAS, we conducted a series of experiments using two operational modes. These benchmarks were performed on a workstation with an Intel i9-12900K CPU, 64 GB RAM, using the arkworks Rust library and HyperPlonk circuits compiled with post-quantum field settings. We tested common image edits (cropping, resizing, blurring, and grayscale conversion) on high-resolution 30 MP images (~90 MB).

The table below presents average proof generation and verification times for both modes. Mode 1 represents computationally limited signers (e.g., digital cameras), while Mode 2 reflects resource-rich environments (e.g., cloud services like OpenAI). These results demonstrate the framework’s feasibility for real-time and browser-based applications, even in post-quantum settings. See

Table 3. Runtime performance of Post-Quantum VerITAS.

Mode	Operation	Proof Time (s)	Title 3
1	Crop + Grayscale	42.3	0.9
2	Crop + Resize + Blur	18.1	0.9

.

The proof generation process leverages several post-quantum secure cryptographic tools and optimizations to ensure efficiency, scalability, and resistance to quantum attacks. The system uses arkworks (a Rust library) for hashing proofs and HyperPlonk for photo editing proofs. Additionally, it incorporates CRYSTALS-Dilithium signature proofs combined with Lattice+Poseidon hashes for enhanced security.

• FRI Polynomial Commitments:
  • The proof system is based on FRI (Fast Reed-Solomon Interactive Oracle Proof of Proximity), a post-quantum secure polynomial commitment scheme. FRI provides succinct and efficient proofs for polynomial evaluations without relying on pairing-friendly curves, making it resistant to quantum attacks.
  • FRI is implemented using arkworks Gemini, ensuring compatibility with the rest of the system.
• HyperPlonk for Poseidon Hash Preimage:
  • The HyperPlonk proof system is used to prove the preimage of the post-quantum Poseidon hash, ensuring the integrity of the hash computation. HyperPlonk is an advanced zk-SNARK framework that offers linear prover time and succinct proofs, making it highly efficient for large-scale computations.
  • The Poseidon hash function has been modified to be post-quantum secure by:

    ▪

    Increasing the output size to 512 bits to counteract Grover’s algorithm.

    ▪

    Using larger finite fields (e.g., 512-bit primes) to resist Shor’s algorithm.

    ▪

    Strengthening the permutation layer with cubic or quartic S-boxes and optimized MDS matrices.

• Optimized Verification:
  • Freivalds’ Algorithm: Used to efficiently check matrix-vector products, reducing computational overhead, while maintaining post-quantum security.
  • Precomputed Row Commitments: These reduce the verifier’s time by 800×, making the system highly scalable even for high-resolution images.

Photo Editing Proofs (Hyper Plonk SNARK Circuits):

The system supports various photo editing operations, each implemented as a HyperPlonk SNARK circuit:

• Cropping: Extracts pixels from a selected range, ensuring the edited image is a valid subset of the original.
• Grayscale: Applies Adobe’s grayscale formula, which computes a weighted sum of the RGB channels, as follows:

Grayscale = 0.2989⋅R + 0.5870⋅G + 0.1140⋅B.Grayscale = 0.2989⋅R + 0.5870⋅G + 0.1140⋅B.

3.

Resizing: Uses bilinear interpolation with floating-point handling to ensure smooth resizing while preserving image quality.

4.

Blurring: Applies a box blur with privacy-preserving rounding to prevent leakage of sensitive information during the blurring process.

A consistency check ensures that the original photo remains consistent across both the hash and editing proofs. This is achieved using polynomial commitments, which bind the original image to its edited versions and hash values. The check guarantees that the edited image is derived from the original without unauthorized modifications.

11. Conclusions

In today’s digital world, fake and edited images can spread quickly and easily. With the rise of AI-generated visuals and the future threat of quantum computing, it has become much harder to verify what is real and trustworthy. Traditional methods are no longer enough to keep up with these changes. In this paper, we introduced Post-Quantum VerITAS, a new framework that brings together advanced cryptography and practical tools to help verify the authenticity of digital images. Our framework provides cryptographic tools that can help detect manipulated images, especially those shared on social media. By verifying that only permissible edits (e.g., crop, grayscale) were made to a cryptographically signed original, Post-Quantum VerITAS helps journalists, platforms, and end-users establish trust in visual content. Although we do not address sociopolitical mechanisms of disinformation, our work contributes to a growing set of digital defenses by offering post-quantum-secure, privacy-preserving image verification at scale.

Post-Quantum VerITAS builds on the original VerITAS system by making it secure against quantum attacks. It uses lattice-based hashes, post-quantum digital signatures, and efficient zero-knowledge proofs to confirm whether an image has been edited in acceptable ways, such as cropping or resizing. At the same time, it protects the privacy of the original image and works smoothly with high-resolution photos.

One of the most important features of this system is that it does not depend on trusted editing software. Instead, it allows anyone to independently verify that an image came from a legitimate source and that it was only edited in approved ways. This gives journalists, social media platforms, and the general public a stronger way to combat misinformation.

Post-Quantum VerITAS offers a powerful and realistic solution for checking digital content. It helps rebuild trust by giving people the tools to confirm whether an image is authentic, even when shared online or altered for privacy and clarity.