Fault Slip Tendency Analysis for a Deep-Sea Basalt CO2 Injection in the Cascadia Basin
Abstract
1. Introduction
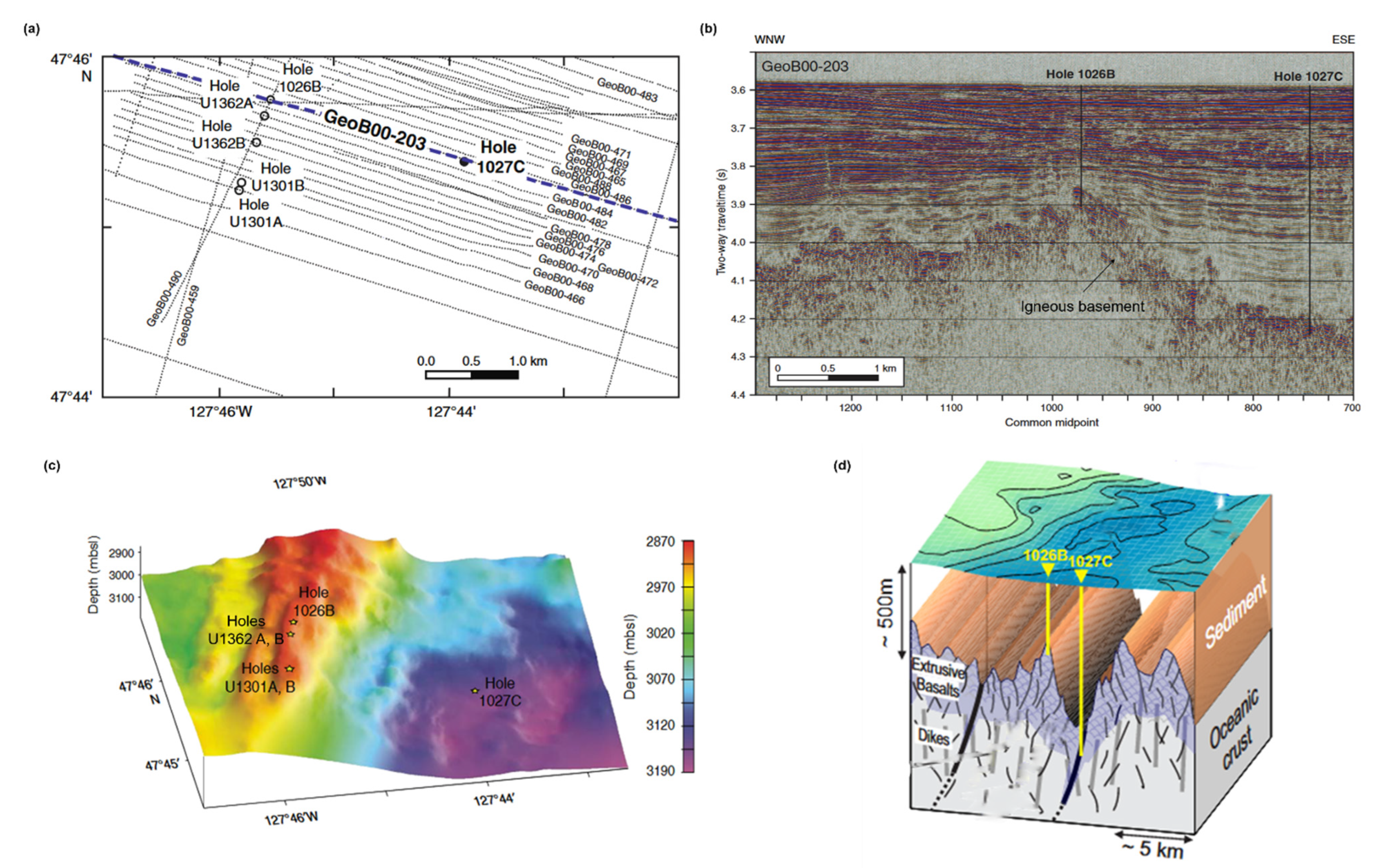
2. Geological Setting
3. Data and Methods
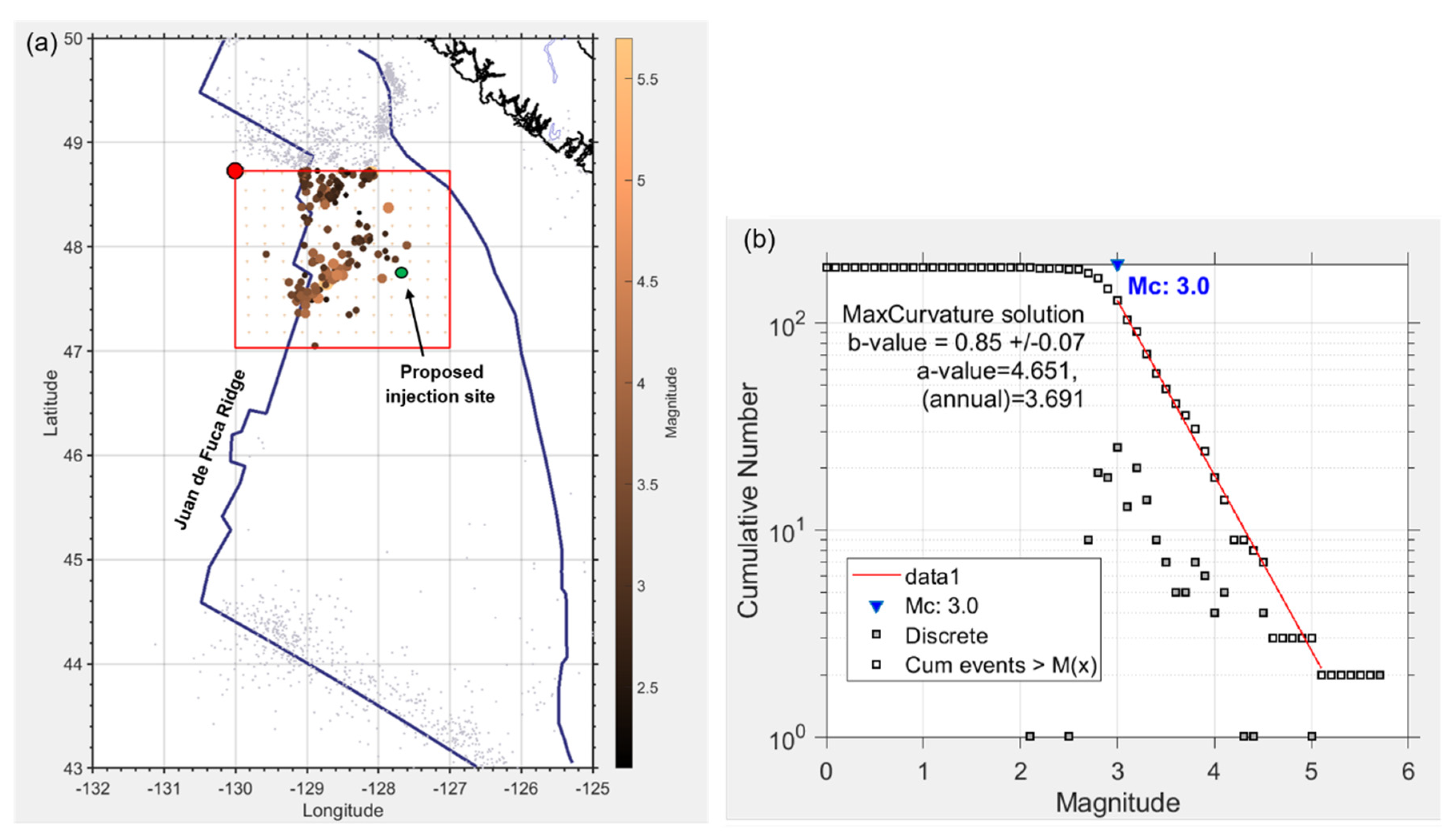
3.1. Historical Seismicity Data
3.2. Stress Data
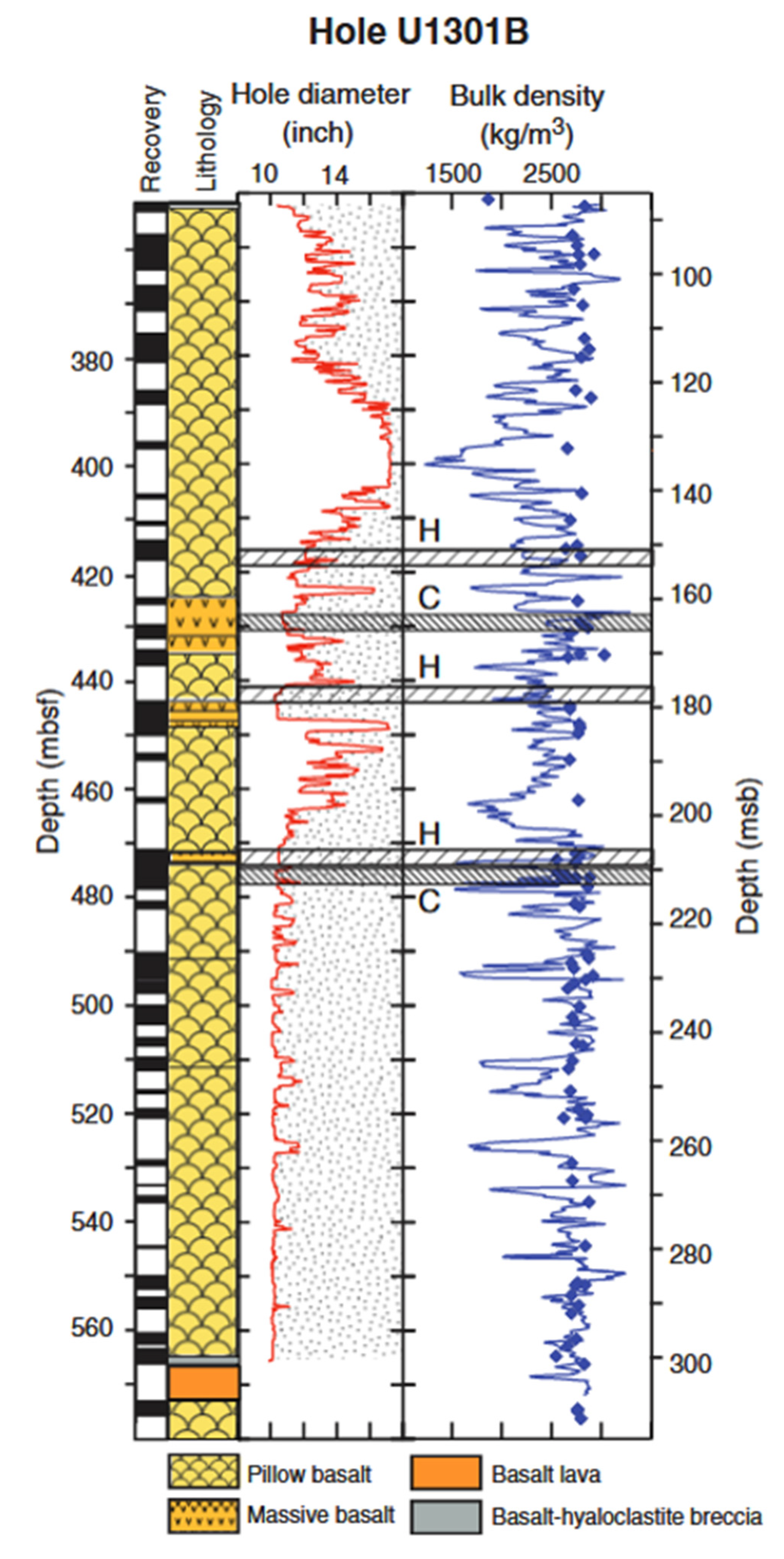
3.3. Fault Data
3.4. Mohr–Coulomb Failure Criteria
4. Frequency Magnitude Distributions
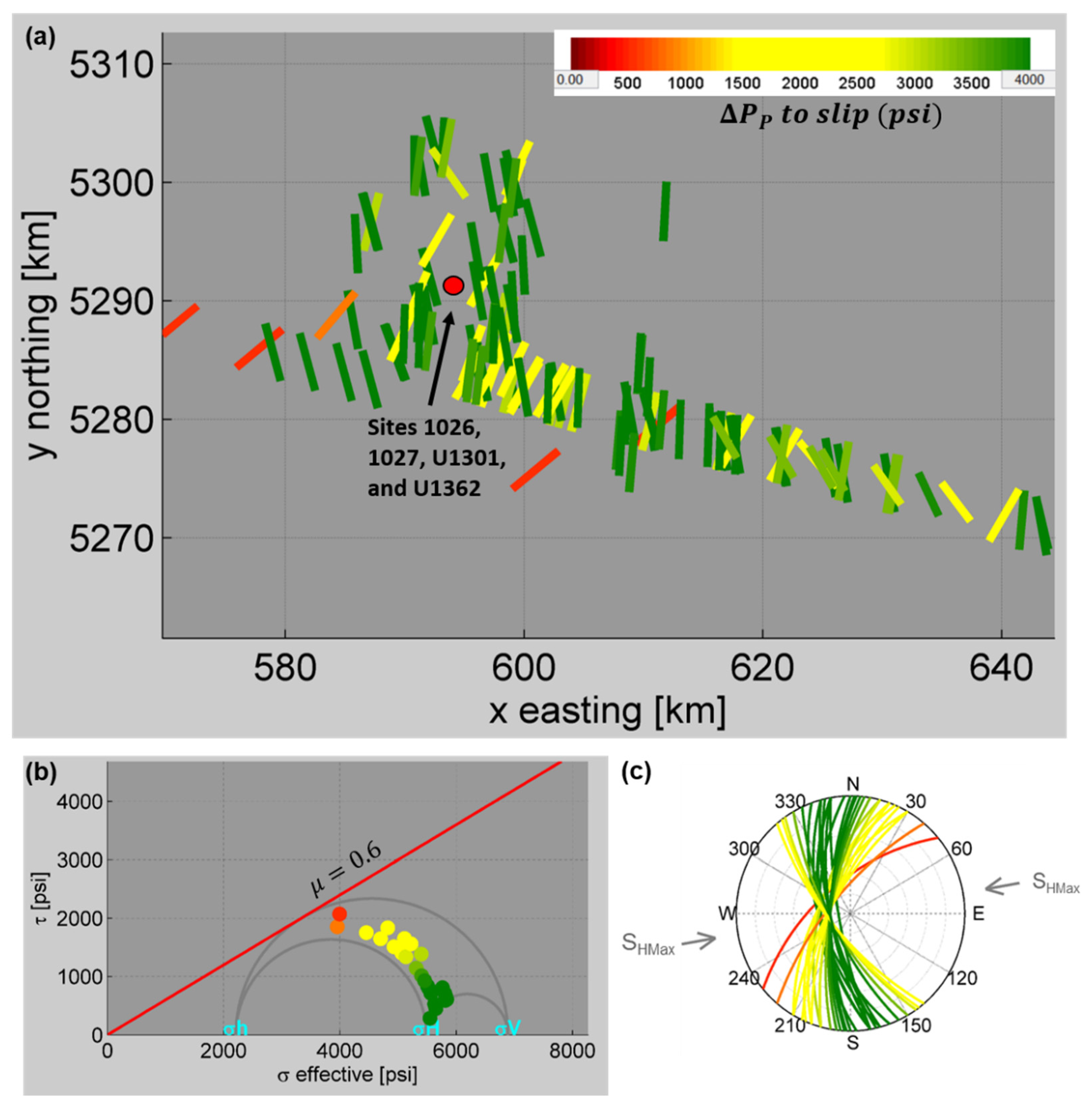
5. Fault Slip Potential Analysis
5.1. Deterministic Analysis of the Fault Slip Potential
5.2. Probabilistic Analysis of Fault Slip Potential
5.3. Fault Slip Potential Due to Fluid Injection
5.4. Assessment of the Fault Slip Potential
6. Discussion
6.1. Effect of the Stress Field and Fault Orientation on the Fault Slip Potential
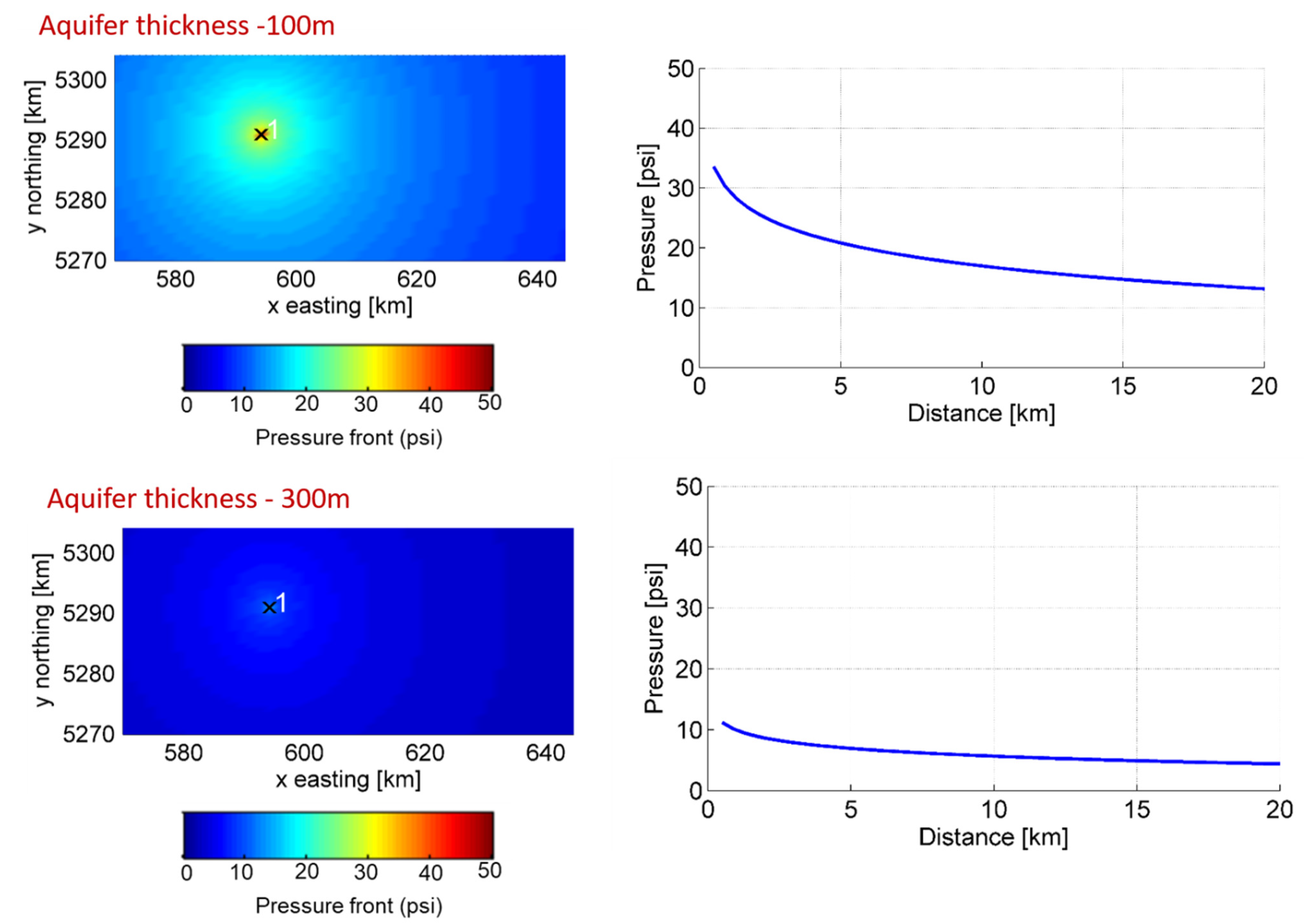
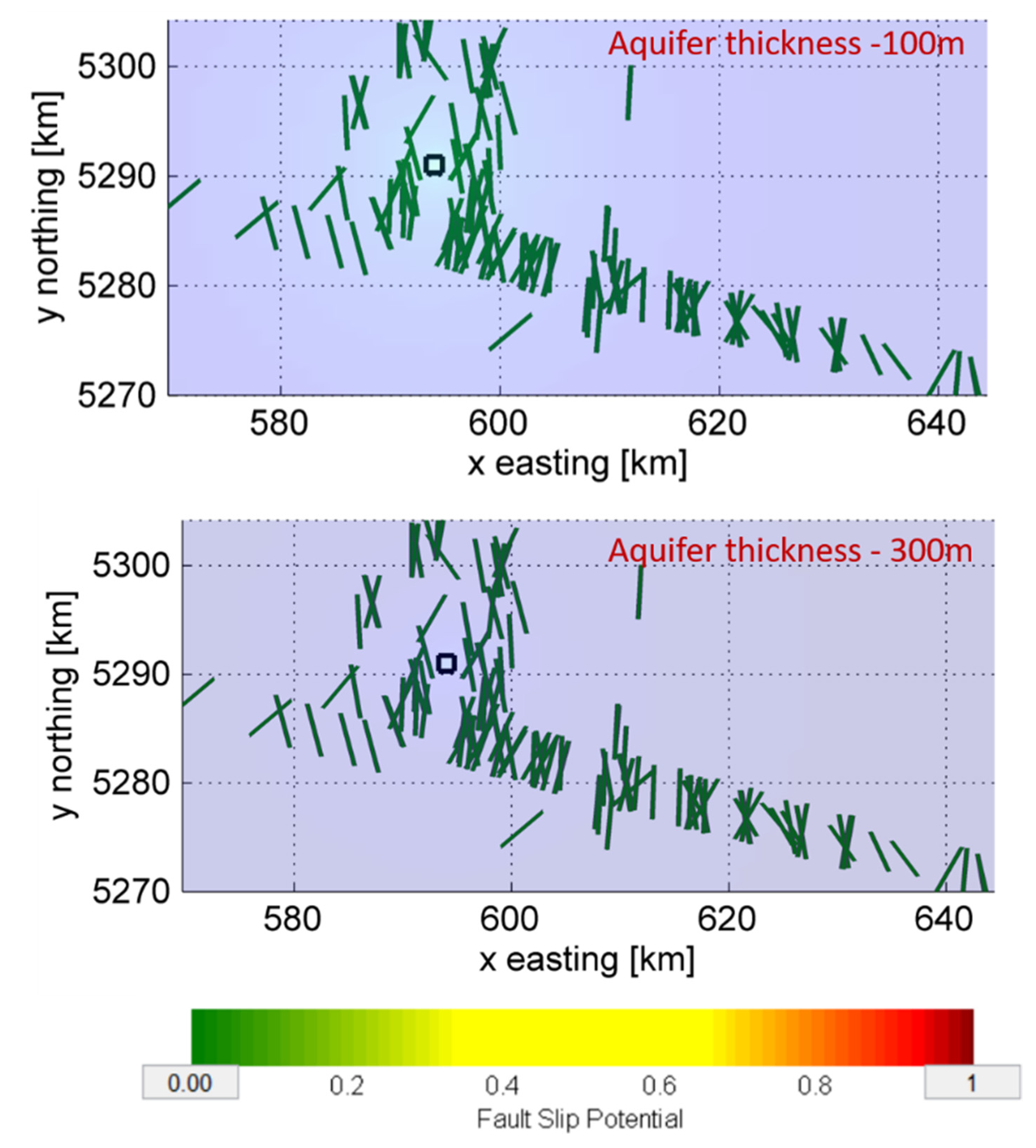
6.2. Effect of Aquifer Thickness and Injection Rate on the Fault Slip Potential
6.3. Effect of Pore Pressure Perturbations on the Fault Slip Potential
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Goldberg, D.; Aston, L.; Bonneville, A.; Demirkanli, I.; Evans, C.; Fisher, A.; Garcia, H.; Gerrard, M.; Heesemann, M.; Hnottavange-Telleen, K.; et al. Geological Storage of CO2 in Sub-Seafloor Basalt: The CarbonSAFE Pre-Feasibility Study Offshore Washington State and British Columbia. Energy Procedia 2018, 146, 158–165. [Google Scholar] [CrossRef]
- Goldberg, D.; Slagle, A.L. A Global Assessment of Deep-Sea Basalt Sites for Carbon Sequestration. Energy Procedia 2009, 1, 3675–3682. [Google Scholar] [CrossRef]
- Awolayo, A.N.; Laureijs, C.T.; Byng, J.; Luhmann, A.J.; Lauer, R.; Tutolo, B.M. Mineral Surface Area Accessibility and Sensitivity Constraints on Carbon Mineralization in Basaltic Aquifers. Geochim. Cosmochim. Acta 2022, 334, 293–315. [Google Scholar] [CrossRef]
- Ground Water Protection Council and Interstate Oil and Gas Compact Commission. Potential Induced Seismicity Guide: A Resource of Technical & Regulatory Considerations Associated with Fluid Injection, 2nd ed.; Ground Water Protection Council: Oklahoma City, OK, USA, 2021; p. 250. [Google Scholar]
- Grigoli, F.; Cesca, S.; Priolo, E.; Rinaldi, A.P.; Clinton, J.F.; Stabile, T.A.; Dost, B.; Fernandez, M.G.; Wiemer, S.; Dahm, T. Current Challenges in Monitoring, Discrimination, and Management of Induced Seismicity Related to Underground Industrial Activities: A European Perspective. Rev. Geophys. 2017, 55, 310–340. [Google Scholar] [CrossRef]
- National Research Council. Energy. In Induced Seismicity Potential in Energy Technologies; National Academies Press: Washington, DC, USA, 2013; ISBN 9780309253703. [Google Scholar]
- Ellsworth, W.L. Injection-Induced Earthquakes. Science 2013, 341, 1225942. [Google Scholar] [CrossRef]
- Eaton, D.W. Passive Seismic Monitoring of Induced Seismicity; Cambridge University Press: Cambridge, UK, 2018; ISBN 9781107145252. [Google Scholar]
- Verdon, J.P. Significance for Secure CO2 Storage of Earthquakes Induced by Fluid Injection. Environ. Res. Lett. 2014, 9, 064022. [Google Scholar] [CrossRef]
- Verdon, J.P.; Stork, A.L. Carbon Capture and Storage, Geomechanics and Induced Seismic Activity. J. Rock Mech. Geotech. Eng. 2016, 8, 928–935. [Google Scholar] [CrossRef]
- Vilarrasa, V.; Carrera, J.; Olivella, S.; Rutqvist, J.; Laloui, L. Induced Seismicity in Geologic Carbon Storage. Solid Earth 2019, 10, 871–892. [Google Scholar] [CrossRef]
- Gutenberg, B.; Richter, C.F. Frequency of Earthquakes in California. Bull. Seismol. Soc. Am. 1944, 34, 185–188. [Google Scholar] [CrossRef]
- Bonifacie, M.; Monnin, C.; Jendrzejewski, N.; Agrinier, P.; Javoy, M. Chlorine Stable Isotopic Composition of Basement Fluids of the Eastern Flank of the Juan de Fuca Ridge (ODP Leg 168). Earth Planet. Sci. Lett. 2007, 260, 10–22. [Google Scholar] [CrossRef]
- Fisher, A.T.; Harris, M. Integrated Ocean Drilling Program Expedition 327 Preliminary Report: Juan de Fuca Ridge-Flank Hydrogeology the Hydrogeologic Architecture of Basaltic Oceanic Crust: Compartmentalization, Anisotropy, Microbiology, and Crustal-Scale Properties on the Eastern Flank of Juan de Fuca Ridge, Eastern Pacific Ocean, 5 July–5 September 2010. Available online: http://publications.iodp.org/preliminary_report/327/index.html (accessed on 30 April 2021).
- Fisher, A.T.; Urabe, T.; Klaus, A. IODP Expedition 301 Installs Three Borehole Crustal Observatories, Prepares for Three-Dimensional, Cross-Hole Experiments in the Northeastern Pacific Ocean. Sci. Drill. 2005, 1, 6–11. [Google Scholar] [CrossRef]
- Zühlsdorff, L.; Hutnak, M.; Fisher, A.T.; Spiess, V.; Davis, E.E.; Nedimovic, M.; Carbotte, S.; Villinger, H.; Becker, K. Site surveys related to IODP Expedition 301: ImageFlux (SO149) and RetroFlux (TN116) expeditions and earlier studies. InProc. IODP 2005, 301, 2. [Google Scholar]
- Sun, T.; Davis, E.; Heesemann, M. Seismic Formation Fluid Pressure Observations Reveal High Anisotropy of Oceanic Crust. Geophys. Res. Lett. 2021, 48, e2021GL095347. [Google Scholar] [CrossRef]
- Riedel, M.; Malinverno, A.; Wang, K.; Goldberg, D.; Guerin, G. Horizontal Compressive Stress Regime on the Northern Cascadia Margin Inferred from Borehole Breakouts. Geochem. Geophys. Geosyst. 2016, 17, 3529–3545. [Google Scholar] [CrossRef]
- Balfour, N.J.; Cassidy, J.F.; Dosso, S.E.; Mazzotti, S. Mapping Crustal Stress and Strain in Southwest British Columbia. J. Geophys. Res. 2011, 116, B03314. [Google Scholar] [CrossRef]
- Rosenberger, A.; Davis, E.E.; Villinger, H. Data report: Hydrocell-95 and-96 single-channel seismic data on the eastern Juan de Fuca Ridge flank. InProc. ODP Sci. Results 2000, 168, 9–19. [Google Scholar]
- Davis, E.E.; Fischer, A.T.; Firth, J.V. Hydrothermal Circulation in the Oceanic Crust: Eastern Flank of the Juan de Fuca Ridge: Covering Leg 168 of the Cruises of the Drilling Vessel JOIDES Resolution, San Francisco, California, to Victoria, British Columbia, Sites 1023–1032, 20 June–15 August 1996. In Proceedings of the Ocean Drilling Program. Part A, Initial report; Ocean Drilling Program: College Station, TX, USA; pp. 3235–3240. 1997; Volume 168, Available online: https://pascal-francis.inist.fr/vibad/index.php?action=getRecordDetail&idt=397608 (accessed on 30 April 2021).
- Carbotte, S.M.; Nedimović, M.R.; Canales, J.P.; Kent, G.M.; Harding, A.J.; Marjanović, M. Variable Crustal Structure along the Juan de Fuca Ridge: Influence of On-Axis Hot Spots and Absolute Plate Motions. Geochem. Geophys. Geosyst. 2008, 9, 8. [Google Scholar] [CrossRef]
- Carbotte, S.M.; Canales, J.P.; Carton, H.; Nedimović, M.R. Multi-Channel Seismic Shot Data from the Cascadia Subduction Zone Acquired during the R/V Marcus Langseth Expedition MGL1211(2012). In Integrated Earth Data Applications; IEDA: Des Moines, IA, USA, 2014; Available online: https://www.marine-geo.org/tools/search/Files.php?data_set_uid=19000 (accessed on 30 April 2021).
- Han, S.; Carbotte, S.M.; Canales, J.P.; Nedimović, M.R.; Carton, H.; Gibson, J.C.; Horning, G.W. Seismic Reflection Imaging of the Juan de Fuca Plate from Ridge to Trench: New Constraints on the Distribution of Faulting and Evolution of the Crust prior to Subduction. J. Geophys. Res. Solid Earth 2016, 121, 1849–1872. [Google Scholar] [CrossRef]
- Rohr, K.M.M.; King, H.; Riedel, M.; Schmidt, U. From mid-plate to subduction zone: Stratigraphy of the northeast Juan de Fuca plate, offshore British Columbia. Geol. Surv. Can. Curr. Res. 2019, 4. [Google Scholar]
- Ferguson, R.; King, H.M.; Kubik, K.; Rohr, K.M.; King, L.; Lister, C.J.; Fustic, M.; Hayward, N.; Brent, T.A.; Jassim, Y. Petroleum, mineral, and other resource potential in the offshore Pacific, British Columbia, Canada. Geol. Surv. Can. 2018, 1, 1. [Google Scholar]
- Byerlee, J. Friction of Rocks. Pure Appl. Geophys. PAGEOPH 1978, 116, 615–626. [Google Scholar] [CrossRef]
- Lund Snee, J.E.; Zoback, M.D. State of stress in Texas: Implications for induced seismicity. Geophys. Res. Lett. 2016, 43, 10–208. [Google Scholar]
- Lee, H.; Ong, S.H. Estimation of in situ stresses with hydro-fracturing tests and a statistical method. Rock Mech. Rock Eng. 2018, 51, 779–799. [Google Scholar] [CrossRef]
- Zhang, S.; Ma, X. Global frictional equilibrium via stochastic, local Coulomb frictional slips. J. Geophys. Res. Solid Earth 2021, 126, e2020JB021404. [Google Scholar] [CrossRef]
- Walsh, F.R.; Zoback, M.D. Probabilistic Assessment of Potential Fault Slip Related to Injection-Induced Earthquakes: Application to North-Central Oklahoma, USA. Geology 2016, 44, 991–994. [Google Scholar] [CrossRef]
- Lund Snee, J.-E.; Zoback, M.D. Multiscale Variations of the Crustal Stress Field throughout North America. Nat. Commun. 2020, 11, 1951. [Google Scholar] [CrossRef]
- Snee, J.-E.L.; Zoback, M.D. State of Stress in the Permian Basin, Texas and New Mexico: Implications for Induced Seismicity. Lead. Edge 2018, 37, 127–134. [Google Scholar] [CrossRef]
- Simpson, R.W. Quantifying Anderson’s Fault Types. J. Geophys. Res. Solid Earth 1997, 102, 17909–17919. [Google Scholar] [CrossRef]
- Zhang, Y.; Yin, S.; Zhang, J. In Situ Stress Prediction in Subsurface Rocks: An Overview and a New Method. Geofluids 2021, 2021, 6639793. [Google Scholar] [CrossRef]
- Farrell, J.; Husen, S.; Smith, R.B. Earthquake swarm and b-value characterization of the Yellowstone volcano-tectonic system. J. Volcanol. Geotherm. Res. 2009, 188, 260–276. [Google Scholar] [CrossRef]
- Aki, K. Maximum likelihood estimate of b in the formula log N= a-bM and its confidence limits. Bull. Earthq. Res. Inst. Tokyo Univ. 1965, 43, 237–239. [Google Scholar]
- Wiemer, S.; Wyss, M. Minimum Magnitude of Completeness in Earthquake Catalogs: Examples from Alaska, the Western United States, and Japan. Bull. Seismol. Soc. Am. 2000, 90, 859–869. [Google Scholar] [CrossRef]
- Wiemer, S. A Software Package to Analyze Seismicity: ZMAP. Seismol. Res. Lett. 2001, 72, 373–382. [Google Scholar] [CrossRef]
- Mignan, A.; Woessner, J. Estimating the magnitude of completeness for earthquake catalogs. Community Online Resour. Stat. Seism. Anal. 2012, 1–45. [Google Scholar]
- Wyss, M. Towards a Physical Understanding of the Earthquake Frequency Distribution. Geophys. J. Int. 1973, 31, 341–359. [Google Scholar] [CrossRef]
- Wiemer, S.; Benoit, J.P. Mapping the B-Value Anomaly at 100 Km Depth in the Alaska and New Zealand Subduction Zones. Geophys. Res. Lett. 1996, 23, 1557–1560. [Google Scholar] [CrossRef]
- Wiemer, S.; Wyss, M. Mapping spatial variability of the frequency-magnitude distribution of earthquakes. In Advances in Geophysics; Elsevier: Amsterdam, The Netherlands, 2002; Volume 45, p. 259. [Google Scholar]
- Walsh, R.; Zoback, M.D.; Lele, S.P.; Pais, D.; Weingarten, M.; Tyrrell, T. FSP 2.0: A Program for Probabilistic Estimation of Fault Slip Potential Resulting from Fluid Injection. 2018. Available online: https://scits.stanford.edu/fault-slip-potential-fsp (accessed on 30 April 2021).
- Winslow, D.M.; Fisher, A.T. Sustainability and Dynamics of Outcrop-to-Outcrop Hydrothermal Circulation. Nat. Commun. 2015, 6, 7567. [Google Scholar] [CrossRef] [PubMed]
- Winslow, D.M.; Fisher, A.T.; Stauffer, P.H.; Gable, C.W.; Zyvoloski, G.A. Three-Dimensional Modeling of Outcrop-to-Outcrop Hydrothermal Circulation on the Eastern Flank of the Juan de Fuca Ridge. J. Geophys. Res. Solid Earth 2016, 121, 1365–1382. [Google Scholar] [CrossRef]
- Chiaramonte, L.; Zoback, M.D.; Friedmann, J.; Stamp, V. Seal Integrity and Feasibility of CO2 Sequestration in the Teapot Dome EOR Pilot: Geomechanical Site Characterization. Environ. Geol. 2007, 54, 1667–1675. [Google Scholar] [CrossRef]
- Hennings, P.H.; Lund Snee, J.; Osmond, J.L.; DeShon, H.R.; Dommisse, R.; Horne, E.; Lemons, C.; Zoback, M.D. Injection-Induced Seismicity and Fault-Slip Potential in the Fort Worth Basin, Texas. Bull. Seismol. Soc. Am. 2019, 109, 1615–1634. [Google Scholar] [CrossRef]
- Goebel, T.H.W.; Brodsky, E.E. The Spatial Footprint of Injection Wells in a Global Compilation of Induced Earthquake Sequences. Science 2018, 361, 899–904. [Google Scholar] [CrossRef] [PubMed]
- Eiken, O. Twenty Years of Monitoring CO2 Injection at Sleipner. Geophysics and Geosequestration 2019, 209–234. [Google Scholar] [CrossRef]



| Parameter | Data Sources |
|---|---|
| Vertical stress gradient | Density logs: |
| Pore pressure | |
| Maximum horizontal stress orientation | Analogs from similar oceanic settings (e.g., Nankai). |
| Maximum and minimum horizontal stress (SHmax and Shmin) | Calculated from Aϕ parameter for a normal fault stress regime. |
| Faults | Compiled from Ocean Drilling Program (ODP) Leg 168 [20,21] and from multichannel seismic data around Holes 1027 and 1026 from Cruise EW0207 [22] and Cruise MGL1211-02 [23]. |
| Porosity, permeability, and aquifer thickness | Properties are derived from [3,45,46]. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ekpo Johnson, E.; Scherwath, M.; Moran, K.; Dosso, S.E.; Rohr, K.M. Fault Slip Tendency Analysis for a Deep-Sea Basalt CO2 Injection in the Cascadia Basin. GeoHazards 2023, 4, 121-135. https://doi.org/10.3390/geohazards4020008
Ekpo Johnson E, Scherwath M, Moran K, Dosso SE, Rohr KM. Fault Slip Tendency Analysis for a Deep-Sea Basalt CO2 Injection in the Cascadia Basin. GeoHazards. 2023; 4(2):121-135. https://doi.org/10.3390/geohazards4020008
Chicago/Turabian StyleEkpo Johnson, Eneanwan, Martin Scherwath, Kate Moran, Stan E. Dosso, and Kristin M. Rohr. 2023. "Fault Slip Tendency Analysis for a Deep-Sea Basalt CO2 Injection in the Cascadia Basin" GeoHazards 4, no. 2: 121-135. https://doi.org/10.3390/geohazards4020008
APA StyleEkpo Johnson, E., Scherwath, M., Moran, K., Dosso, S. E., & Rohr, K. M. (2023). Fault Slip Tendency Analysis for a Deep-Sea Basalt CO2 Injection in the Cascadia Basin. GeoHazards, 4(2), 121-135. https://doi.org/10.3390/geohazards4020008







