Earthquake Nowcasting with Deep Learning
Abstract
:1. Introduction
2. Introduction to Earthquake Nowcasting
3. Data Description
3.1. Earthquake Data
3.2. Choice of Training and Validation Data
3.3. Earthquake Faults
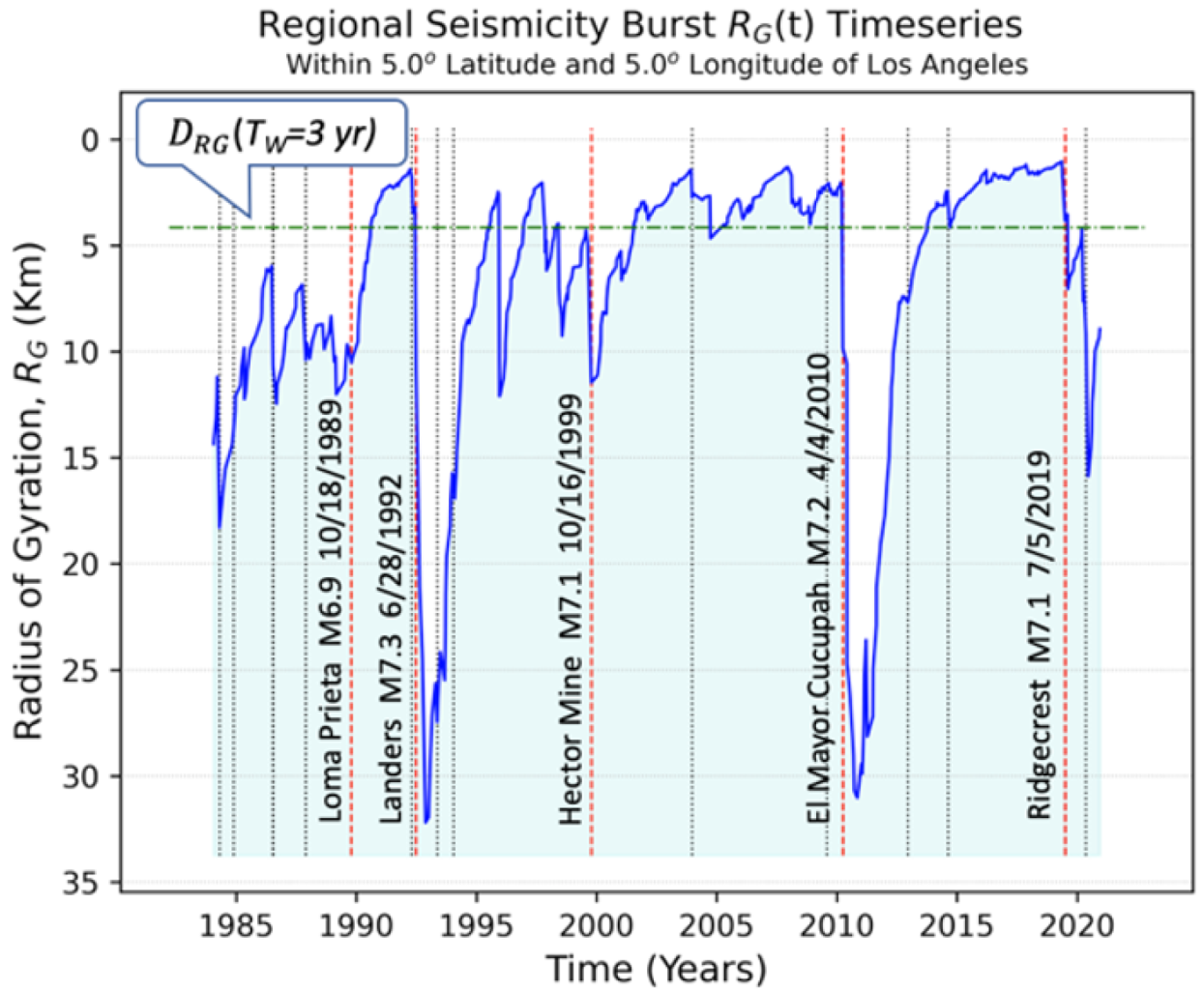
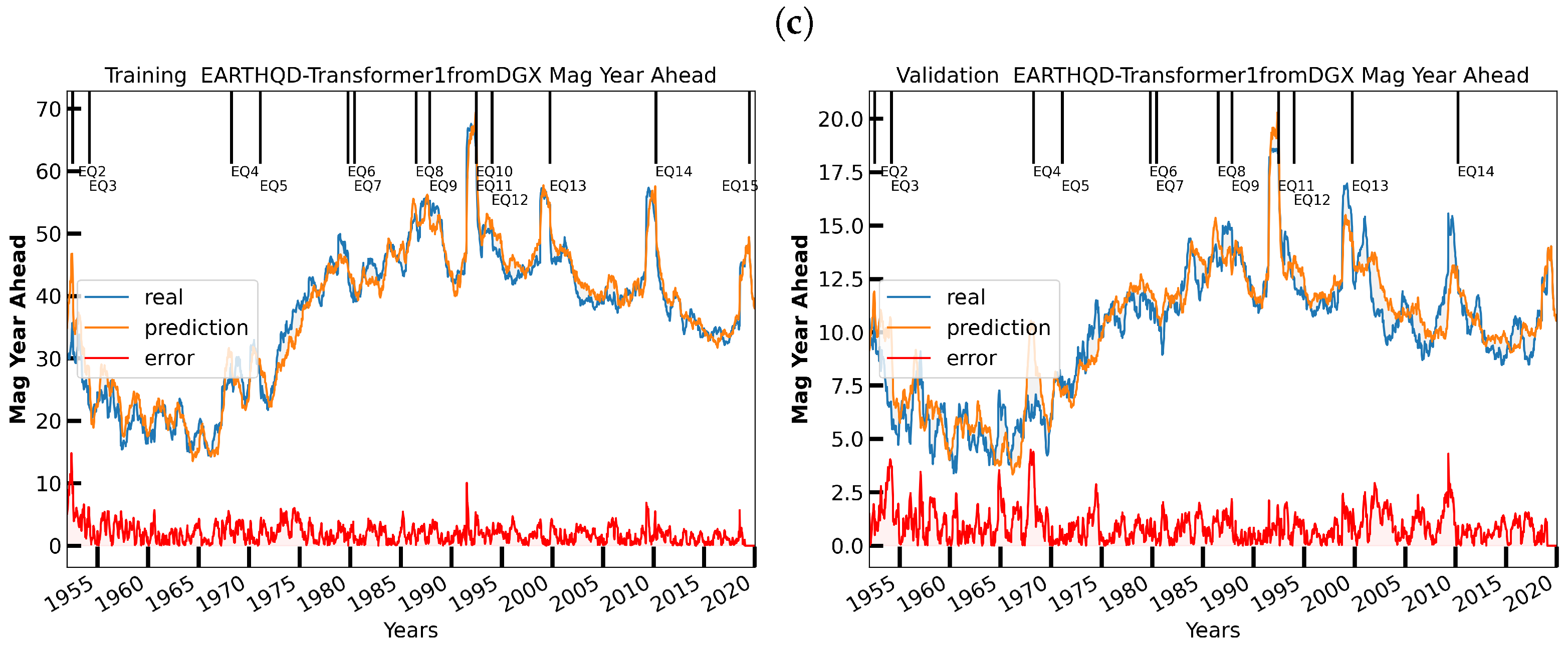
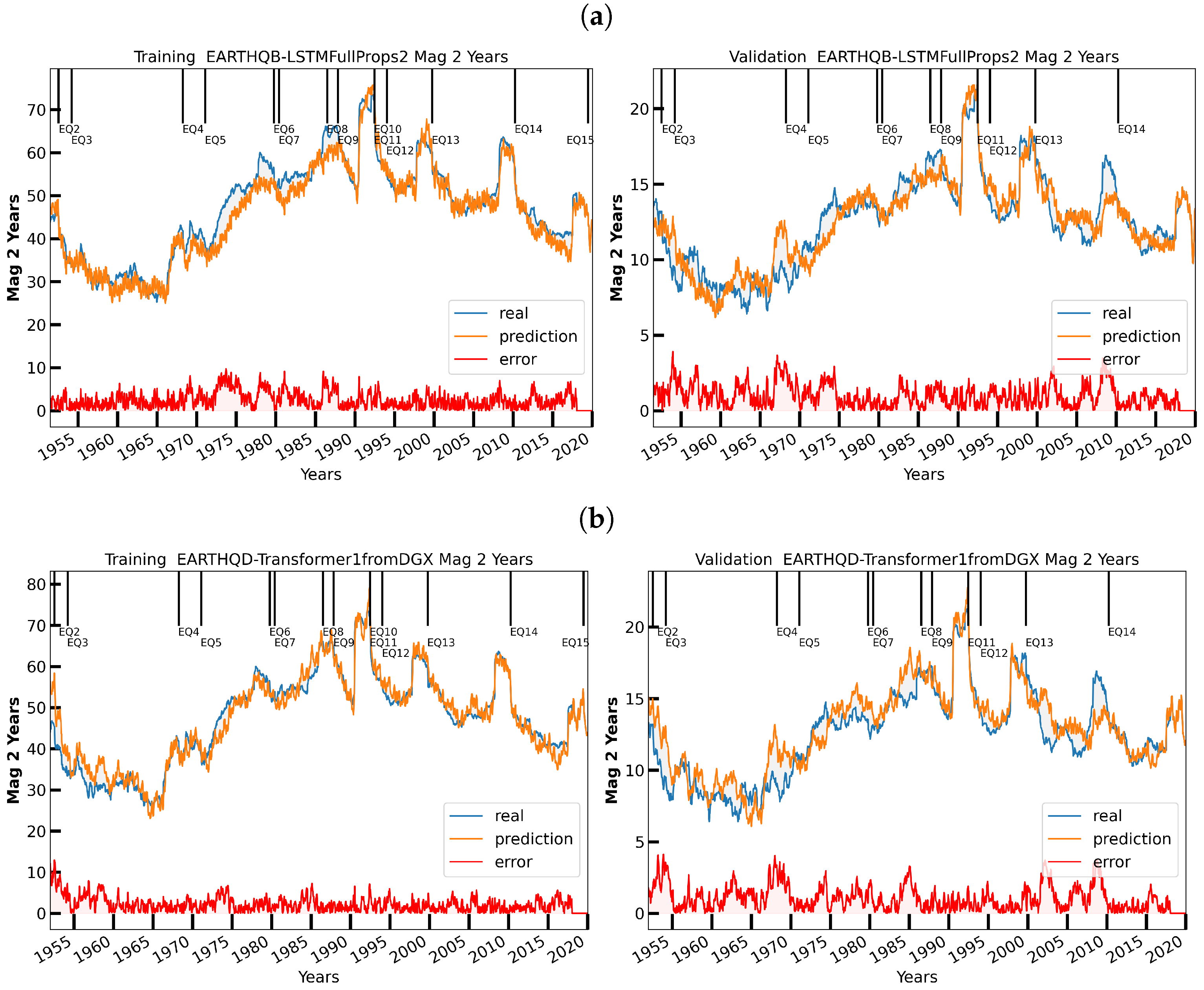
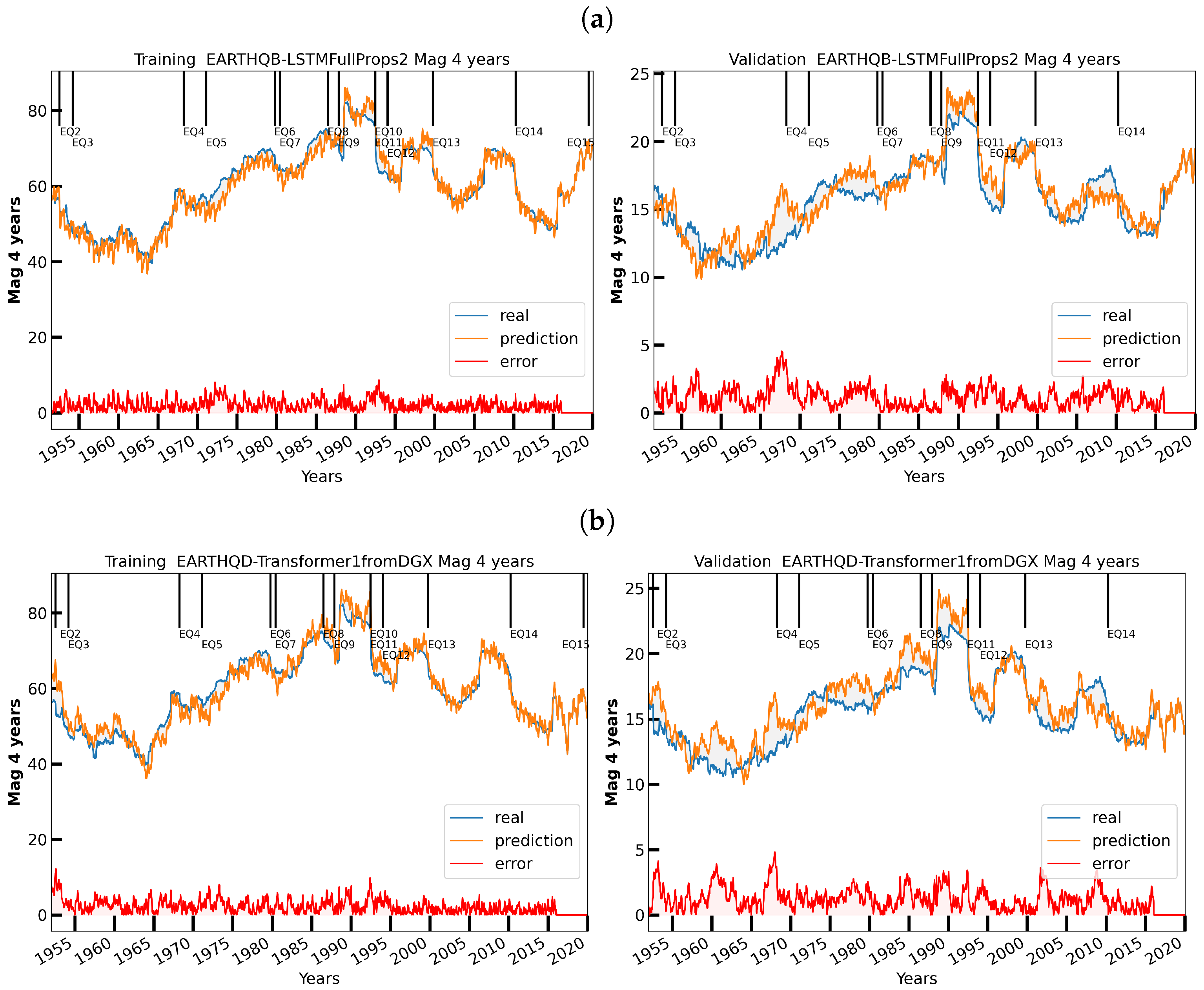
3.4. Visualizing the Data and Their Models
4. Formulation of Deep Learning for Time Series
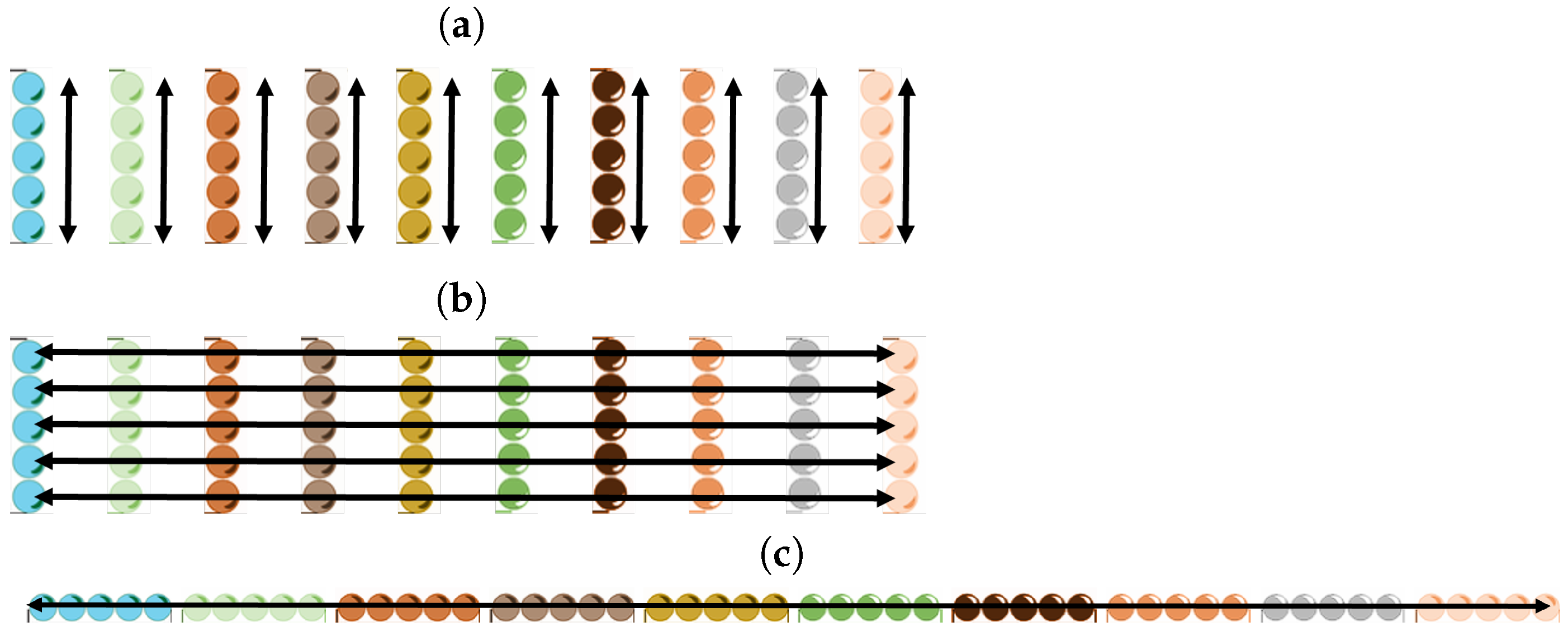
4.1. Spatial Bag Problem
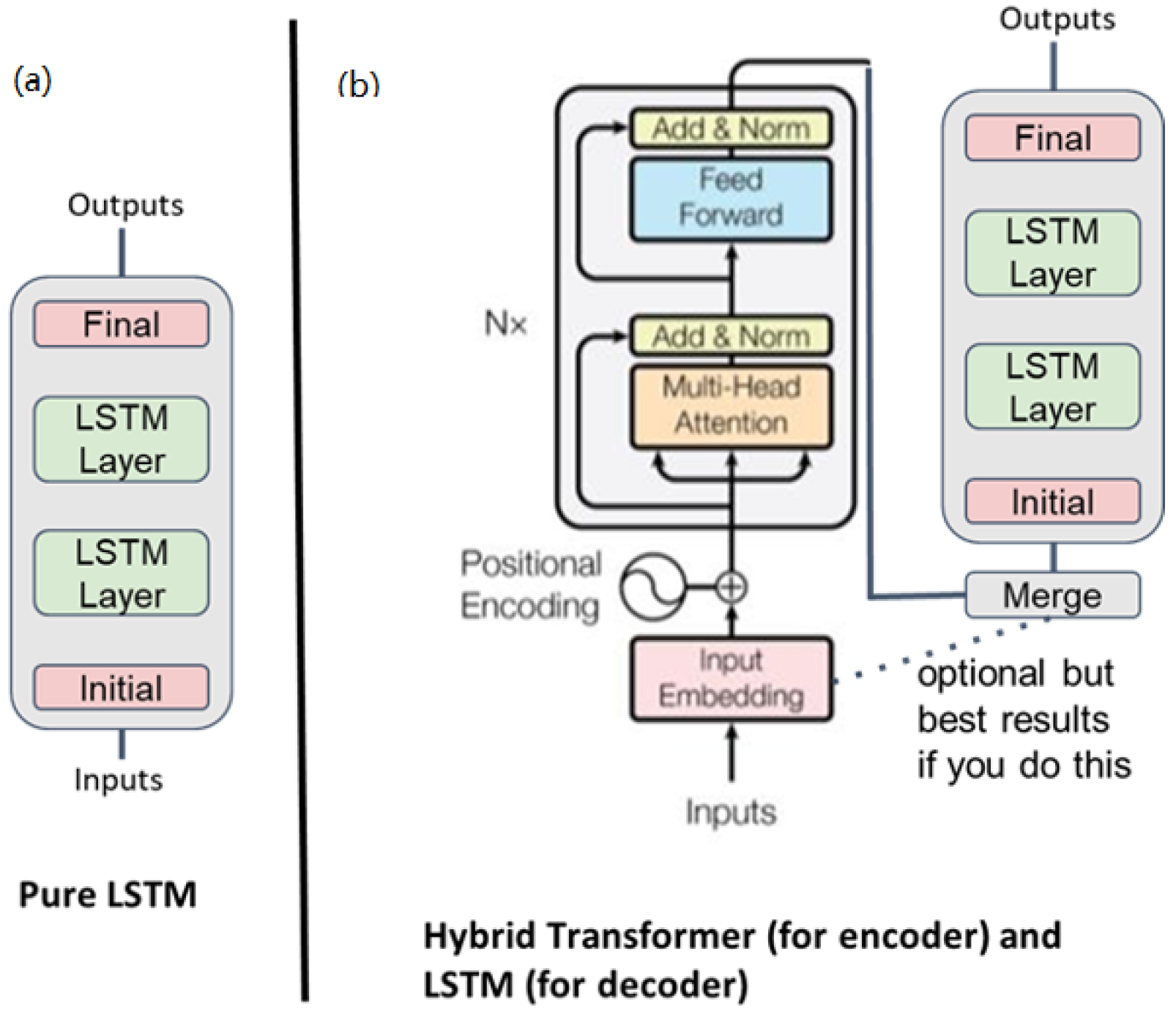
4.2. Deep Learning Implementations
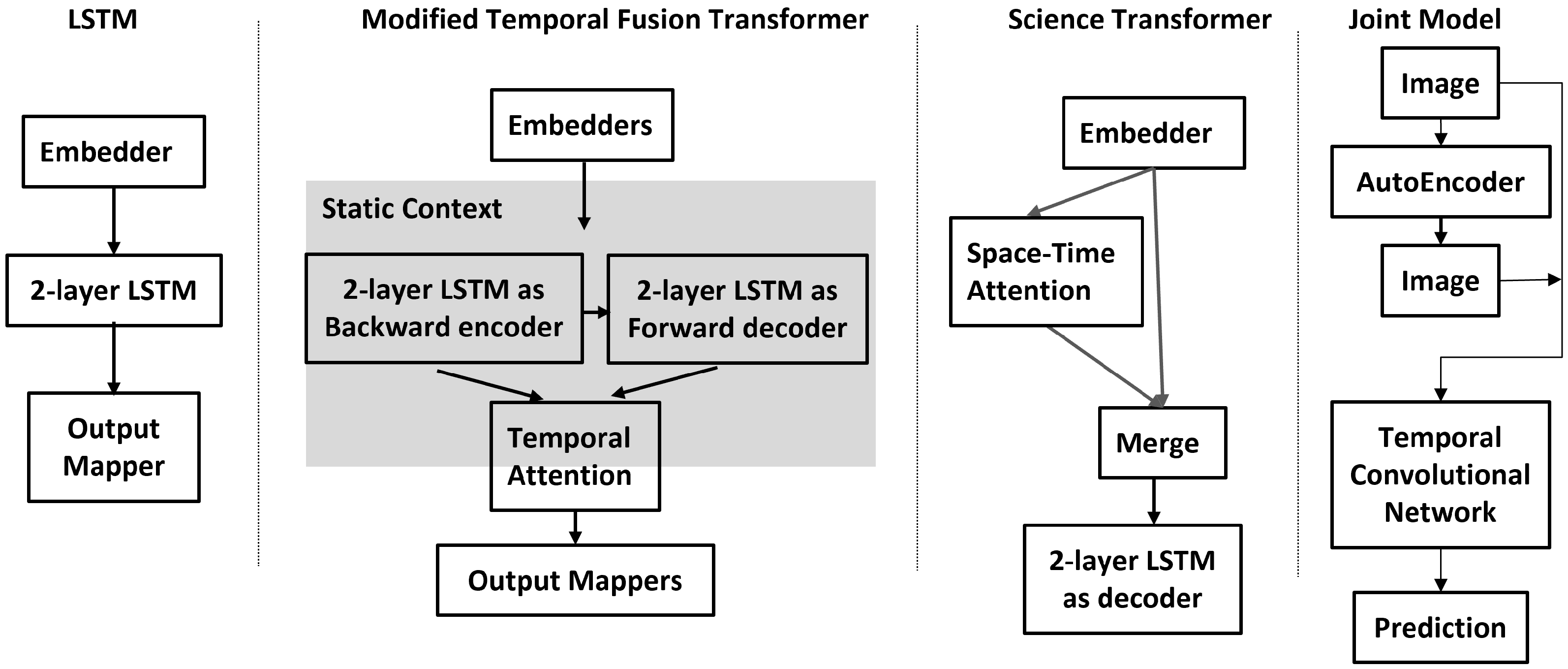
- LSTM. Pure recurrent neural network—two-layer LSTM [56].
- Science Transformer. A hybrid model that was built at the University of Virginia with a space–time transformer for the decoder and a two-layer LSTM for the encoder.
- AE-TCN Joint Model. This is an architecture that combines two models. One is an autoencoder (AE) that encodes and decodes the image-like input and output. The other is a temporal convolutional network (TCN) which takes the differences from the input and output of the autoencoder and predicts the one-step future loss which is used to nowcast immediate earthquakes in refenerces [59,60].
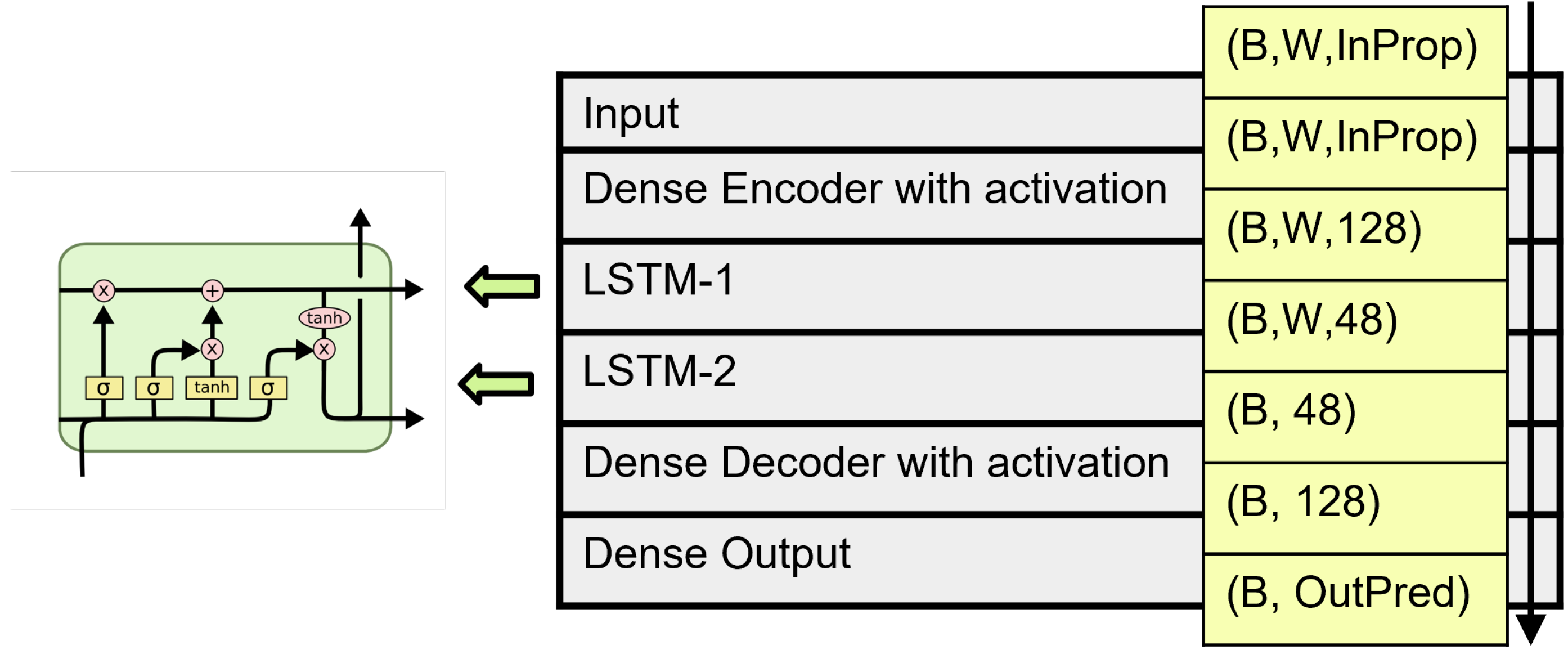
4.3. The Deep Learning Models in Detail
4.4. The Deep Learning Inputs and Outputs
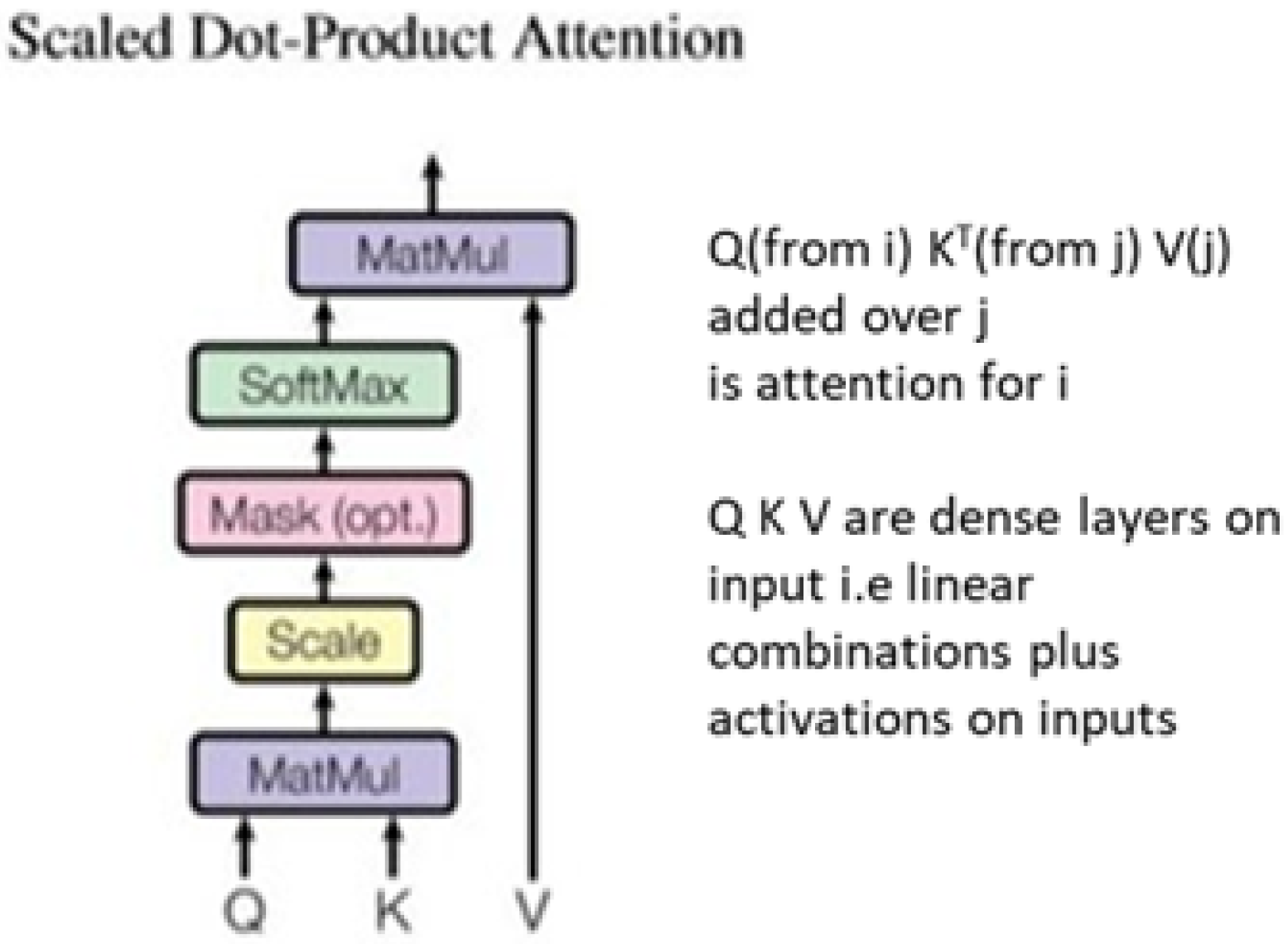
5. Transformer and Attention Technologies
5.1. Using Transformers for Spatial Bags
5.2. Scaled Dot-Product Attention and the Vectors Q K V
5.3. Choosing the Group of Items over Which Attention Is Calculated
- Temporal search: Points in sequence for fixed location.
- Spatial search: Locations for a fixed position in the sequence.
- Full search: Complete location–sequence space.
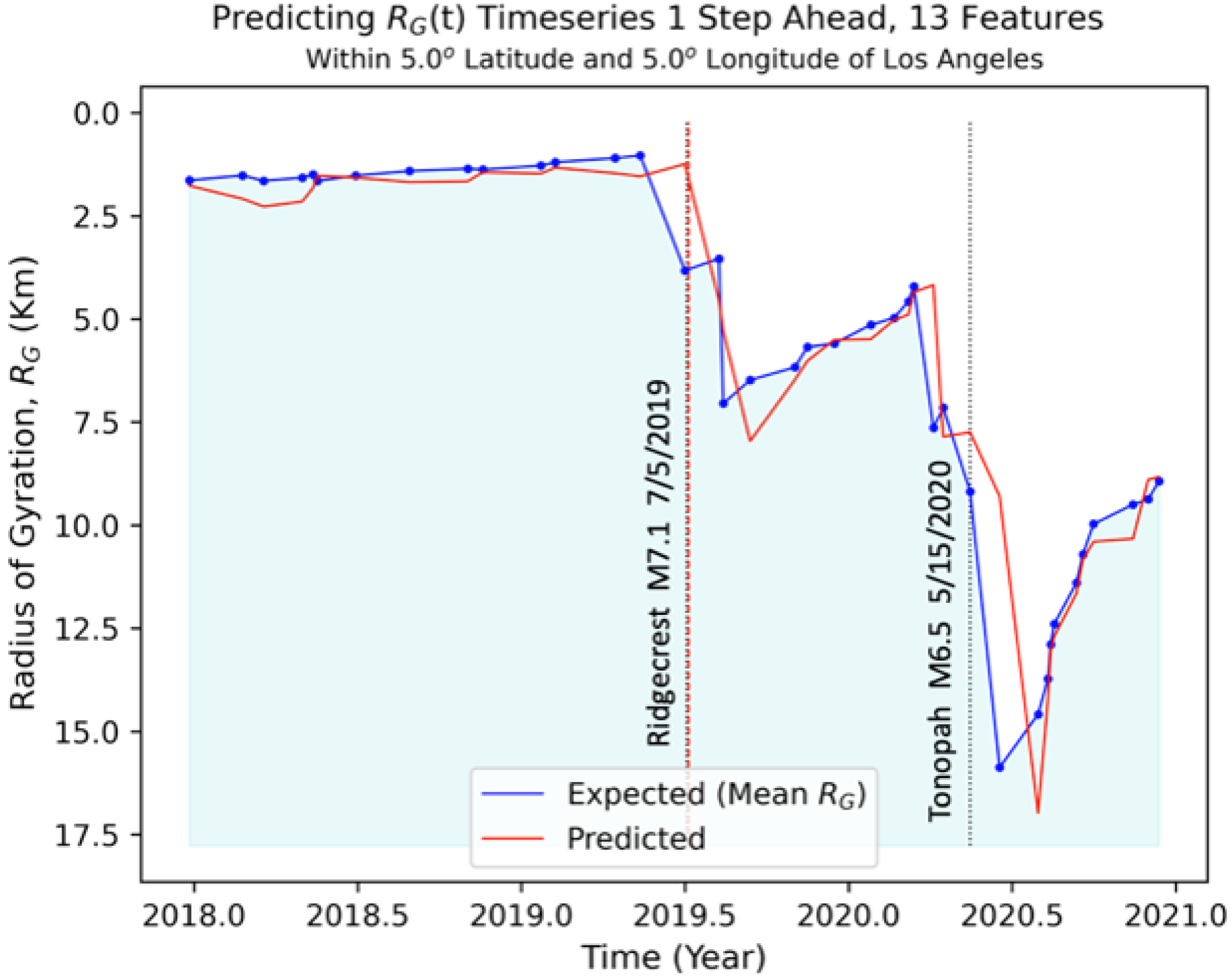
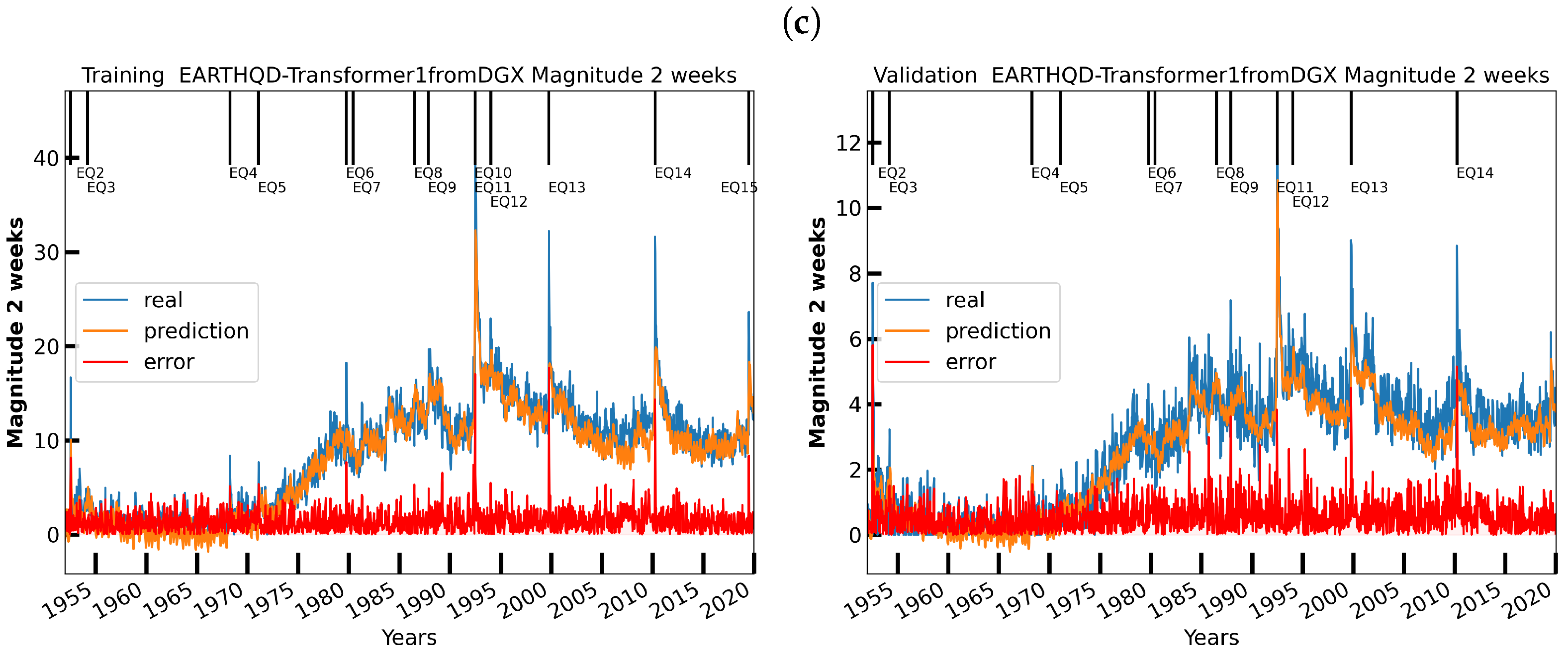
6. Initial Earthquake Nowcasting Results
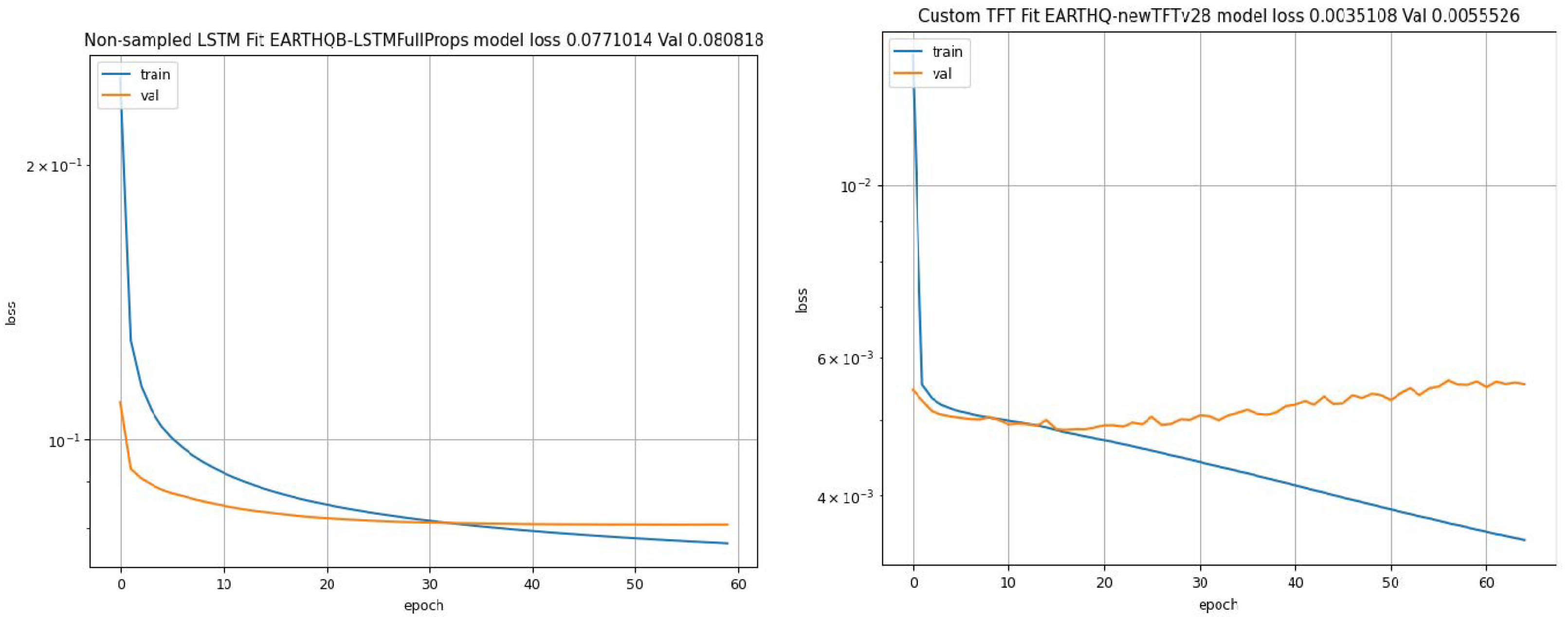
6.1. Initial Results
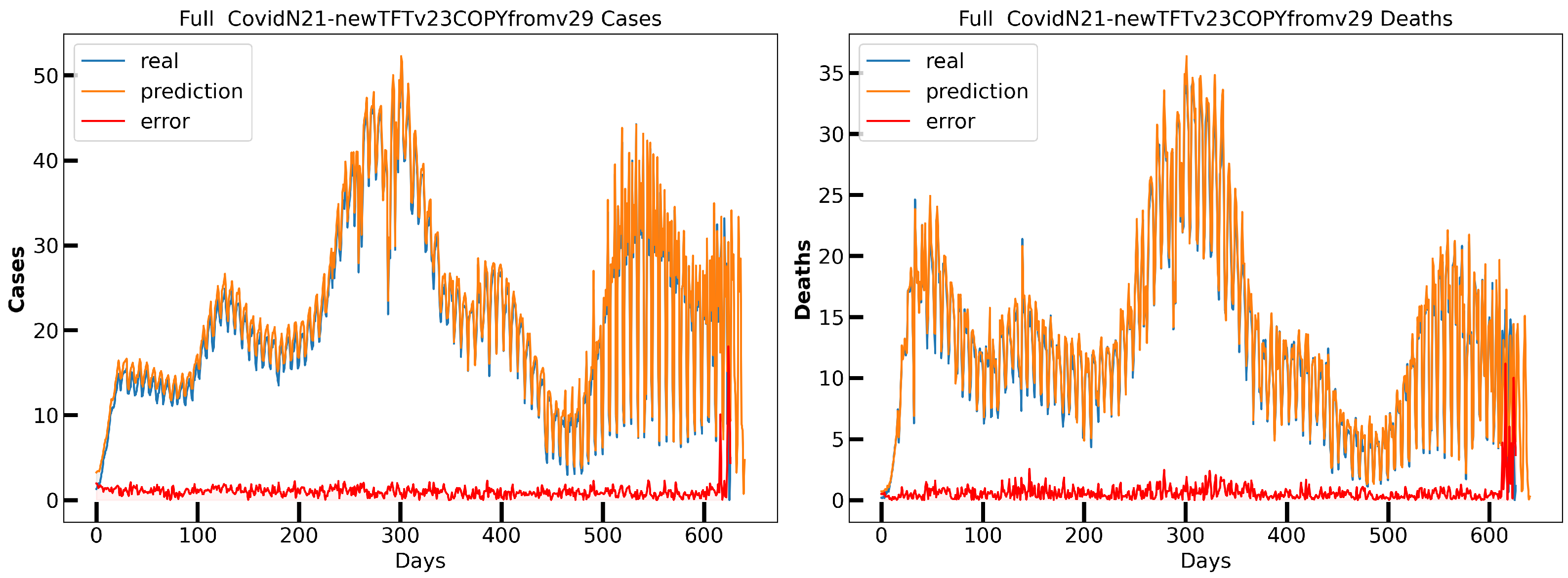
6.2. Nowcasting Extreme Events with AE-TCN Joint Model
7. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rundle, J.; Fox, G. Computational Earthquake Science. Comput. Sci. Eng. 2012, 14, 7–9. [Google Scholar] [CrossRef]
- Fox, G. FFFFWNPF-EARTHQD-Transformer1fromDGX DGX Jupyter Notebook for Science Transformer Forecast. Originally run 7 December 2021 on NVIDIA DGX but rehosted on Google Colab 15 March 2022. Available online: https://colab.research.google.com/drive/18yQ1RomlpHkCjRVwP4x5oBsyJ7WDoWwT?usp=sharing (accessed on 15 March 2022).
- Hey, T.; Trefethen, A. The Fourth Paradigm 10 Years On. Inform. Spektrum 2020, 42, 441–447. [Google Scholar] [CrossRef] [Green Version]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Advances in Neural Information Processing Systems; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Dutchess County, NY, USA, 2017; Volume 30, pp. 5998–6008. [Google Scholar]
- Laptev, N.; Yosinski, J.; Li, L.E.; Smyl, S. Time-Series Extreme Event Forecasting with Neural Networks at Uber. In International Conference on Machine Learning. 2017, Volume 34, pp. 1–5. Available online: http://www.cs.columbia.edu/~lierranli/publications/TSW2017_paper.pdf (accessed on 10 April 2022).
- Li, Y.; Yu, R.; Shahabi, C.; Liu, Y. Diffusion convolutional recurrent neural network: Data-driven traffic forecasting. In Proceedings of the ICLR 2018 Conference, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Geng, X.; Li, Y.; Wang, L.; Zhang, L.; Yang, Q.; Ye, J.; Liu, Y. Spatiotemporal multi-graph convolution network for ride-hailing demand forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 3656–3663. [Google Scholar]
- Djuric, N.; Radosavljevic, V.; Cui, H.; Nguyen, T.; Chou, F.C.; Lin, T.H.; Singh, N.; Schneider, J. Uncertainty-aware short-term motion prediction of traffic actors for autonomous driving. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Snowmass, CO, USA, 1–5 March 2020; IEEE Xplore 2020. pp. 2095–2104. Available online: https://arxiv.org/pdf/1808.05819.pdf (accessed on 7 December 2021).
- Ye, J.; Zhao, J.; Ye, K.; Xu, C. How to Build a Graph-Based Deep Learning Architecture in Traffic Domain: A Survey. IEEE Trans. Intell. Transp. Syst. 2020, 1–21. [Google Scholar] [CrossRef]
- Shen, C.; Penn State University. D2 2020 AI4ESS Summer School: Recurrent Neural Networks and LSTMs. Available online: https://www.youtube.com/watch?v=vz11tUgoDZc (accessed on 1 July 2020).
- Kratzert, F. CAMELS Extended Maurer Forcing Data. Available online: https://www.hydroshare.org/resource/17c896843cf940339c3c3496d0c1c077/ (accessed on 14 July 2020).
- Kratzert, F. Catchment-Aware LSTMs for Regional Rainfall-Runoff Modeling GitHub. Available online: https://github.com/kratzert/ealstm_regional_modeling (accessed on 14 July 2020).
- Kratzert, F.; Klotz, D.; Shalev, G.; Klambauer, G.; Hochreiter, S.; Nearing, G. Towards learning universal, regional, and local hydrological behaviors via machine learning applied to large-sample datasets. Hydrol. Earth Syst. Sci. 2019, 23, 5089–5110. [Google Scholar] [CrossRef] [Green Version]
- Addor, N.; Newman, A.J.; Mizukami, N.; Clark, M.P. The CAMELS data set: Catchment attributes and meteorology for large-sample studies. Hydrol. Earth Syst. Sci. 2017, 21, 21. [Google Scholar] [CrossRef] [Green Version]
- Sit, M.A.; Demiray, B.Z.; Xiang, Z.; Ewing, G.; Sermet, Y.; Demir, I. A Comprehensive Review of Deep Learning Applications in Hydrology and Water Resources. 2020. Available online: https://arxiv.org/ftp/arxiv/papers/2007/2007.12269.pdf (accessed on 7 December 2021).
- Liu, Y. Artificial Intelligence for Smart Transportation Video. Available online: https://slideslive.com/38917699/artificial-intelligence-for-smart-transportation (accessed on 8 August 2019).
- Yao, H.; Wu, F.; Ke, J.; Tang, X.; Jia, Y.; Lu, S.; Gong, P.; Ye, J.; Li, Z. Deep multi-view spatial-temporal network for taxi demand prediction. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; AAAI: Menlo Park, CA, USA, 2018. [Google Scholar]
- Wu, Y.; Tan, H. Short-term traffic flow forecasting with spatial-temporal correlation in a hybrid deep learning framework. arXiv 2016, arXiv:1612.01022. [Google Scholar]
- Fox, G.C. Deep Learning for Spatial Time Series. Available online: https://www.researchgate.net/publication/346012611_DRAFT_Deep_Learning_for_Spatial_Time_Series?channel=doi&linkId=5fb5c04a92851c933f3d4ef1&showFulltext=true (accessed on 17 November 2020).
- Fox, G.; Rundle, J.; Feng, B. Study of Earthquakes with Deep Learning. Frankfurt Institute for Advanced Study Seismology & Artificial Intelligence Kickoff Workshop (Virtual). 2021. Available online: https://docs.google.com/presentation/d/1nTM-poaFzrT_KBB1J7BlZdOMEIMTu-s48mcBA5DeP30/edit#slide=id.g7a25695c64_0_0 (accessed on 7 December 2021).
- Guan, H.; Mokadam, L.K.; Shen, X.; Lim, S.H.; Patton, R. FLEET: Flexible Efficient Ensemble Training for Heterogeneous Deep Neural Networks. In Proceedings of Machine Learning and Systems. 2020; pp. 247–261. Available online: https://proceedings.mlsys.org/paper/2020/hash/ed3d2c21991e3bef5e069713af9fa6ca-Abstract.html (accessed on 1 December 2021).
- Scholz, C.H. The Mechanics of Earthquakes and Faulting; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Rundle, J.B.; Stein, S.; Donnellan, A.; Turcotte, D.L.; Klein, W.; Saylor, C. The complex dynamics of earthquake fault systems: New approaches to forecasting and nowcasting of earthquakes. Rep. Prog. Phys. 2021, 84, 076801. [Google Scholar] [CrossRef]
- Rundle, J.B.; Donnellan, A. Nowcasting earthquakes in southern California with machine learning: Bursts, swarms, and aftershocks may be related to levels of regional tectonic stress. Earth Space Sci. 2020, 7, e2020EA001097. [Google Scholar] [CrossRef]
- Rundle, J.B.; Donnellan, A. Nowcasting earthquakes in southern California with machine learning: Bursts, swarms and aftershocks may reveal the regional tectonic stress. Earth Space Sci. Open Arch. 2020. [Google Scholar] [CrossRef]
- Rundle, J.B.; Donnellan, A.; Fox, G.; Crutchfield, J.P. Nowcasting Earthquakes by Visualizing the Earthquake Cycle with Machine Learning: A Comparison of Two Methods. Surv. Geophys. 2021. [Google Scholar] [CrossRef]
- Rundle, J.B.; Turcotte, D.L.; Donnellan, A.; Grant Ludwig, L.; Luginbuhl, M.; Gong, G. Nowcasting earthquakes. Earth Space Sci. 2016, 3, 480–486. [Google Scholar] [CrossRef]
- Savage, J.C. Principal component analysis of geodetically measured deformation in Long Valley caldera, eastern California, 1983-1987. J. Geophys. Res. 1988, 93, 13297–13305. [Google Scholar] [CrossRef]
- Tiampo, K.F.; Rundle, J.B.; McGinnis, S.; Gross, S.J.; Klein, W. Eigenpatterns in southern California seismicity. J. Geophys. Res. 2002, 107, ESE 8-1–ESE 8-17. [Google Scholar] [CrossRef]
- Rundle, J.B.; Donnellan, A.; Fox, G.; Crutchfield, J.P.; Granat, R. Nowcasting Earthquakes: Imaging the Earthquake Cycle in California with Machine Learning. Earth Space Sci. 2021, 8, e2021EA001757. [Google Scholar] [CrossRef]
- Kane, M.J.; Price, N.; Scotch, M.; Rabinowitz, P. Comparison of ARIMA and Random Forest time series models for prediction of avian influenza H5N1 outbreaks. BMC Bioinform. 2014, 15, 276. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. Available online: http://xxx.lanl.gov/abs/https://direct.mit.edu/neco/article-pdf/9/8/1735/813796/neco.1997.9.8.1735.pdf (accessed on 7 December 2021). [CrossRef]
- Romero, R.A.C. Generative Adversarial Network for Stock Market Price Prediction. Available online: http://cs230.stanford.edu/projects_fall_2019/reports/26259829.pdf (accessed on 9 December 2021).
- Brownlee, J. A Gentle Introduction to Generative Adversarial Networks (GANs). Available online: https://machinelearningmastery.com/what-are-generative-adversarial-networks-gans/ (accessed on 9 December 2021).
- Wikipedia. Generative Adversarial Network. Available online: https://en.wikipedia.org/wiki/Generative_adversarial_network (accessed on 9 December 2021).
- Quinlan, J.R. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef] [Green Version]
- Wikipedia. ID3 Algorithm. Available online: https://en.wikipedia.org/wiki/ID3_algorithm (accessed on 7 December 2021).
- Earthquake Hazards Program of United States Geological Survey. USGS Search Earthquake Catalog Home Page. Available online: https://earthquake.usgs.gov/earthquakes/search/ (accessed on 1 December 2020).
- Fox, G. Earthquake Data Used in Study “Earthquake Forecasting with Deep Learning”. Available online: https://drive.google.com/drive/folders/1wz7K2R4gc78fXLNZMHcaSVfQvIpIhNPi?usp=sharing (accessed on 1 December 2020).
- Field, E.H. Overview of the Working Group for the Development of Regional Earthquake Likelihood Models (RELM). Seismol. Res. Lett. 2007, 78, 7–16. [Google Scholar] [CrossRef]
- Quaternary Fault and Fold Database of the United States. Available online: https://www.usgs.gov/programs/earthquake-hazards/faults (accessed on 7 December 2021).
- Hanks, T.C.; Kanamori, H. A moment magnitude scale. J. Geophys. Res. Solid Earth 1979, 84, 2348–2350. [Google Scholar] [CrossRef]
- Benioff, H. Global strain accumulation and release as revealed by great earthquakes. GSA Bull. 1951, 62, 331–338. [Google Scholar] [CrossRef]
- Rundle, J.B.; Klein, W.; Turcotte, D.L.; Malamud, B.D. Precursory Seismic Activation and Critical-point Phenomena. In Microscopic and Macroscopic Simulation: Towards Predictive Modelling of the Earthquake Process; Mora, P., Matsu’ura, M., Madariaga, R., Minster, J.B., Eds.; Birkhäuser Basel: Basel, Switzerland, 2001; pp. 2165–2182. [Google Scholar]
- Ben-Zion, Y.; Lyakhovsky, V. Accelerated Seismic Release and Related Aspects of Seismicity Patterns on Earthquake Faults. In Earthquake Processes: Physical Modelling, Numerical Simulation and Data Analysis Part II; Matsu’ura, M., Mora, P., Donnellan, A., Yin, X.C., Eds.; Birkhäuser Basel: Basel, Switzerland, 2002; pp. 2385–2412. [Google Scholar]
- Newman, W.I.; Turcotte, D.L.; Gabrielov, A.M. log-periodic behavior of a hierarchical failure model with applications to precursory seismic activation. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 1995, 52, 4827–4835. [Google Scholar] [CrossRef] [PubMed]
- Kadupitiya, J.C.S.; Fox, G.C.; Jadhao, V. Simulating Molecular Dynamics with Large Timesteps using Recurrent Neural Networks. arXiv 2020, arXiv:2004.06493. [Google Scholar]
- CIG Computational Infrastructure for Geodynamics. Virtual Quake Model for Earthquakes (Originally Virtual California). Available online: https://geodynamics.org/resources/1614/download/vq-1.1.0.tar.gz (accessed on 13 February 2022).
- Richards-Dinger, K.; Dieterich, J.H. RSQSim Earthquake Simulator. Seismol. Res. Lett. 2012, 83, 983–990. [Google Scholar] [CrossRef]
- Gilchrist, J.J.; Jordan, T.H.; Milner, K.R. Probabilities of Earthquakes in the San Andreas Fault System: Estimations from RSQSim Simulations. 2018, p. S41D-0569. Available online: https://www.scec.org/publication/8237 (accessed on 7 December 2021).
- Meyer, H.; Reudenbach, C.; Wöllauer, S.; Nauss, T. Importance of spatial predictor variable selection in machine learning applications—Moving from data reproduction to spatial prediction. Ecol. Model. 2019, 411, 108815. [Google Scholar] [CrossRef] [Green Version]
- Nash, J.; Sutcliffe, J. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Nossent, J.; Bauwens, W. Application of a normalized Nash-Sutcliffe efficiency to improve the accuracy of the Sobol’sensitivity analysis of a hydrological model. In EGU General Assembly Conference Abstracts. 2012, p. 237. Available online: https://meetingorganizer.copernicus.org/EGU2012/EGU2012-237.pdf (accessed on 7 December 2021).
- Patil, S.; Stieglitz, M. Modelling daily streamflow at ungauged catchments: What information is necessary? Hydrol. Process. 2014, 28, 1159–1169. [Google Scholar] [CrossRef] [Green Version]
- Feng, D.; Fang, K.; Shen, C. Enhancing streamflow forecast and extracting insights using long-short term memory networks with data integration at continental scales. Water Resour. Res. 2019, 56, e2019WR026793. [Google Scholar] [CrossRef]
- Fox, G.C.; von Laszewski, G.; Wang, F.; Pyne, S. AICov: An Integrative Deep Learning Framework for COVID-19 Forecasting with Population Covariates. J. Data Sci. 2021, 19, 293–313. [Google Scholar] [CrossRef]
- Lim, B.; Arık, S.Ö.; Loeff, N.; Pfister, T. Temporal fusion transformers for interpretable multi-horizon time series forecasting. Int. J. Forecast. 2021, 37, 1748–1764. [Google Scholar] [CrossRef]
- Kafritsas, N. Temporal Fusion Transformer: Time Series Forecasting with Interpretability Google’s State-of-the-Art Transformer Has It All. Available online: https://towardsdatascience.com/temporal-fusion-transformer-googles-model-for-interpretable-time-series-forecasting-5aa17beb621 (accessed on 7 December 2021).
- Feng, B.; Fox, G.C. TSEQPREDICTOR: Spatiotemporal Extreme Earthquakes Forecasting for Southern California. arXiv 2020, arXiv:2012.14336. [Google Scholar]
- Feng, B.; Fox, G.C. Spatiotemporal Pattern Mining for Nowcasting Extreme Earthquakes in Southern California. In Proceedings of the 2021 IEEE 17th International Conference on eScience, Innsbruck, Austria, 20–23 September 2021; pp. 99–107. [Google Scholar]
- TFT For PyTorch. Available online: https://catalog.ngc.nvidia.com/orgs/nvidia/resources/tft_for_pytorch (accessed on 7 December 2021).
- Fox, G. Study of Earthquakes with Deep Learning (Earthquakes for Real); Lectures in Class on AI First Engineering. Available online: https://docs.google.com/presentation/d/1ykYnX0uvxPE-M-c-Tau8irU3IqYuvj8Ws8iUqd5RCxQ/edit?usp=sharing (accessed on 30 September 2021).
- Fox, G. Deep Learning Based Time Evolution. Available online: http://dsc.soic.indiana.edu/publications/Summary-DeepLearningBasedTimeEvolution.pdf (accessed on 8 June 2020).
- Fox, G. FFFFWNPF-EARTHQB-LSTMFullProps2 Google Colab for LSTM Forecast. Available online: https://colab.research.google.com/drive/16DjDXv8wjzNm7GABNMCGiE-Q0gFAlNHz?usp=sharing (accessed on 7 December 2021).
- Fox, G. FFFFWNPFEARTHQ-newTFTv29 Google Colab for TFT Forecast. Available online: https://colab.research.google.com/drive/12zEv08wvwRhQEwYWy641j9dLSDskxooG?usp=sharing (accessed on 7 December 2021).
- Galassi, A.; Lippi, M.; Torroni, P. Attention in Natural Language Processing. arXiv 2019, arXiv:1902.02181. [Google Scholar] [CrossRef] [PubMed]
- Kaji, D.A.; Zech, J.R.; Kim, J.S.; Cho, S.K.; Dangayach, N.S.; Costa, A.B.; Oermann, E.K. An attention based deep learning model of clinical events in the intensive care unit. PLoS ONE 2019, 14, e0211057. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gangopadhyay, T.; Tan, S.Y.; Jiang, Z.; Meng, R.; Sarkar, S. Spatiotemporal Attention for Multivariate Time Series Prediction and Interpretation. In Proceedings of the 2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021; pp. 3560–3564. [Google Scholar] [CrossRef]
- Xu, N.; Shen, Y.; Zhu, Y. Attention-Based Hierarchical Recurrent Neural Network for Phenotype Classification. In Advances in Knowledge Discovery and Data Mining; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 465–476. [Google Scholar]
- Kodialam, R.S.; Boiarsky, R.; Sontag, D. Deep Contextual Clinical Prediction with Reverse Distillation. In Proceedings of the 35th AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 2–9 February 2021; pp. 249–258. [Google Scholar]
- Gao, J.; Wang, X.; Wang, Y.; Yang, Z.; Gao, J.; Wang, J.; Tang, W.; Xie, X. CAMP: Co-Attention Memory Networks for Diagnosis Prediction in Healthcare. In Proceedings of the 2019 IEEE International Conference on Data Mining (ICDM), Beijing, China, 8–11 November 2019; pp. 1036–1041. [Google Scholar]
- Sen, R.; Yu, H.F.; Dhillon, I. Think Globally, Act Locally: A Deep Neural Network Approach to High-Dimensional Time Series Forecasting. Available online: https://assets.amazon.science/44/a7/9f453036411b93f79f1fe3e933ff/think-globally-act-locally-a-deep-neural-network-approach-to-high-dimensional-time-series-forecasting.pdf (accessed on 7 December 2021).
- Song, H.; Rajan, D.; Thiagarajan, J.J.; Spanias, A. Attend and diagnose: Clinical time series analysis using attention models. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Zeyer, A.; Bahar, P.; Irie, K.; Schlüter, R.; Ney, H. A Comparison of Transformer and LSTM Encoder Decoder Models for ASR. In Proceedings of the 2019 IEEE Automatic Speech Recognition and Understanding Workshop (ASRU), Sentosa, Singapore, 14–18 December 2019; pp. 8–15. [Google Scholar]
- Zeng, Z.; Pham, V.T.; Xu, H.; Khassanov, Y.; Chng, E.S.; Ni, C.; Ma, B. Leveraging Text Data Using Hybrid Transformer-LSTM Based End-to-End ASR in Transfer Learning. In Proceedings of the 12th International Symposium on Chinese Spoken Language Processing (ISCSLP), Piscataway Township, NJ, USA, 24–26 January 2021. [Google Scholar]
- Rhif, M.; Ben Abbes, A.; Farah, I.R.; Martínez, B.; Sang, Y. Wavelet Transform Application for/in Non-Stationary Time-Series Analysis: A Review. Appl. Sci. 2019, 9, 1345. [Google Scholar] [CrossRef] [Green Version]
- Arik, S.O.; Yoder, N.C.; Pfister, T. Self-Adaptive Forecasting for Improved Deep Learning on Non-Stationary Time-Series. arXiv 2022, arXiv:2202.02403. [Google Scholar]
- Huang, X.; Fox, G.C.; Serebryakov, S.; Mohan, A.; Morkisz, P.; Dutta, D. Benchmarking Deep Learning for Time Series: Challenges and Directions. In Proceedings of the 2019 IEEE International Conference on Big Data (Big Data), Los Angeles, CA, USA, 9–12 December 2019; pp. 5679–5682. [Google Scholar]
- Kates-Harbeck, J.; Svyatkovskiy, A.; Tang, W. Predicting disruptive instabilities in controlled fusion plasmas through deep learning. Nature 2019, 568, 526–531. [Google Scholar] [CrossRef]
- Fox, G.; Hey, T.; Thiyagalingam, J. Science Data Working Group of MLCommons. Available online: https://mlcommons.org/en/groups/research-science/ (accessed on 3 December 2020).
- MLCommons Homepage: Machine Learning Innovation to Benefit Everyone. Available online: https://mlcommons.org/en/ (accessed on 7 December 2021).



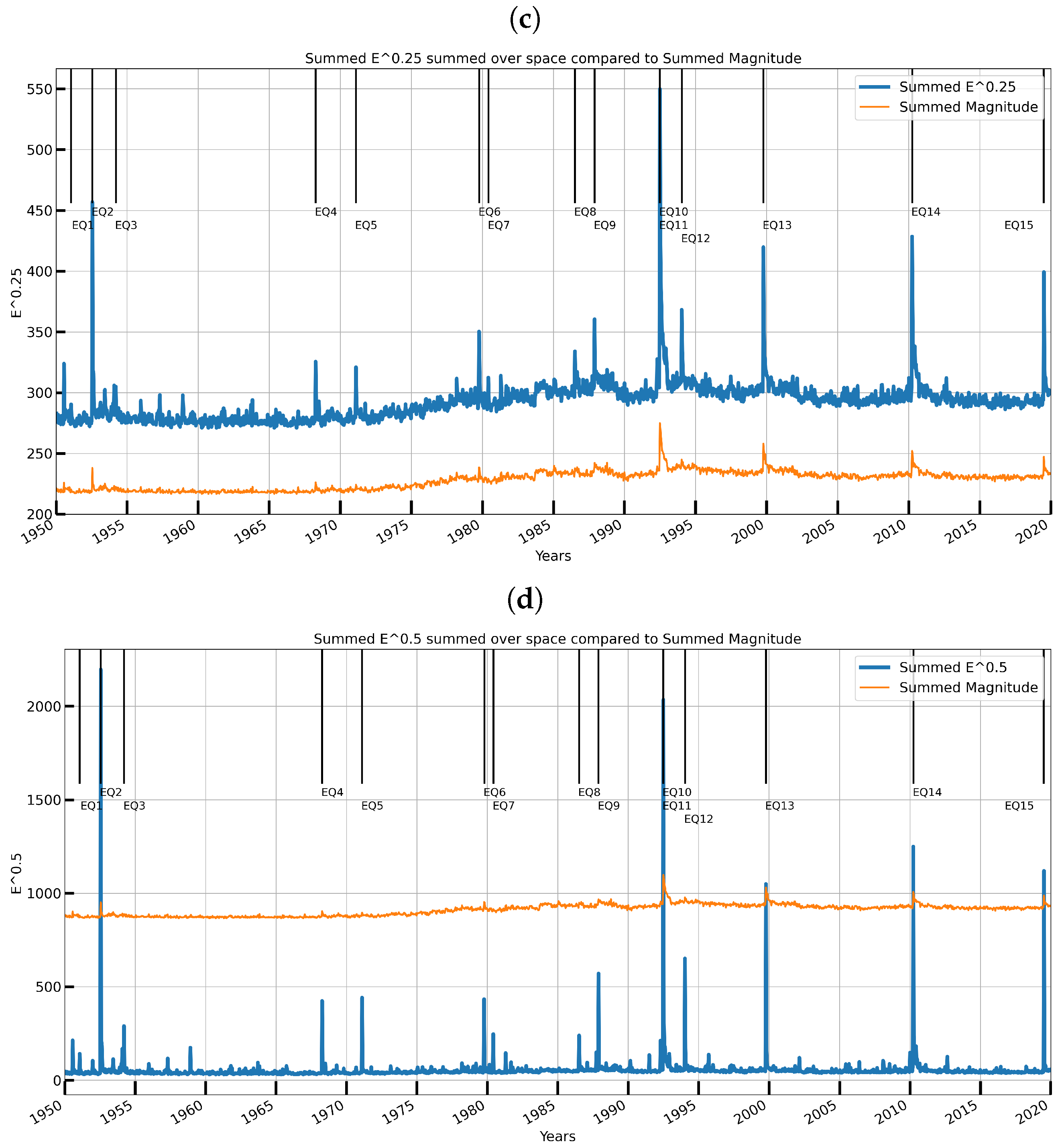

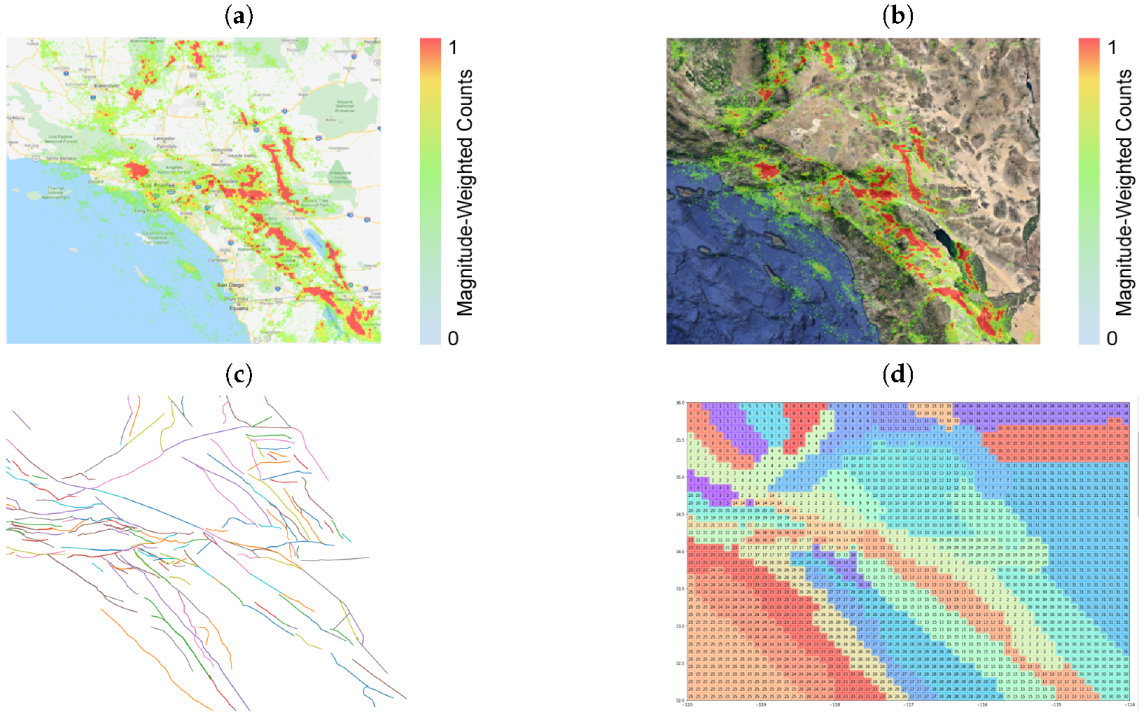




| Label | Date | Magnitude | Location |
|---|---|---|---|
| EQ1 | 24 January 1951 | 6.0 | 14 km WNW of Tecolots, B.C., MX |
| EQ2 | 21 July 1952 | 7.5 | 6 km WNW of Grapevine, CA |
| EQ3 | 19 March 1954 | 6.4 | 12 km W of Salton City, CA |
| EQ4 | 9 April 1968 | 6.6 | 5 km NNE of Ocotillo Wells, CA |
| EQ5 | 9 February 1971 | 6.6 | 10 km SSW of Agua Dulce, CA |
| EQ6 | 15 October 1979 | 6.4 | 10 km E of Mexicali, B.C., MX |
| EQ7 | 9 June 1980 | 6.3 | 5 km SE of Alberto Oviedo Mota, B.C., MX |
| EQ8 | 9 July 1986 | 6.0 | 6 km SSW of Morongo Valley, CA |
| EQ9 | 24 November 1987 | 6.6 | 22 km W of Westmorland, CA |
| EQ10 | 28 June 1992 | 7.3 | Landers, California Earthquake |
| EQ11 | 28 June 1992 | 6.3 | 7 km SSE of Big Bear City, CA |
| EQ12 | 17 January 1994 | 6.7 | 1 km NNW of Reseda, CA |
| EQ13 | 16 October 1999 | 7.1 | Hector Mine, CA Earthquake |
| EQ14 | 4 April 2010 | 7.2 | 12 km SW of Delta, B.C., MX |
| EQ15 | 4 July 2019 | 6.4 | Ridgecrest Earthquake Sequence |
| Ratio Mean/Max for Observables | Full Multiplicity | Multiplicity | |||
|---|---|---|---|---|---|
| Individual pixels | 0.11 | 0.0000046 | 0.000022 | 0.0032 | 0.000016 |
| Summed over space | 0.83 | 0.012 | 0.0079 | 0.53 | 0.025 |
| Network | # Layers | # Trainable Parameters | Window Size | Internal Label and Online Link |
|---|---|---|---|---|
| LSTM | 6 | 66,590 | 13 | EARTHQB-LSTMFullProps2 [64] |
| TFT | 73 | 8,005,334 | 26 | EARTHQ-newTFTv29 [65] |
| Science Transformer | 14 | 2,339,328 | 26 | FFFFWNPF-EARTHQD-Transformer1fromDGX [2] |
| Static Known Inputs (5) | Four space-filling curve labels of fault grouping, linear label of pixel |
| Targets (24) | for = 2, 4, 8, 14, 26, 52, 104, 208 weeks. Additionally, for skip 52 weeks and predict next 52 weeks; skip 104 weeks and predict next 104 weeks. With relative weight 0.25, all the Known Inputs and linear label of pixel |
| Dynamic Known Inputs (13) | for l = 0 to 4 for period = 8, 16, 32, 64 |
| Dynamic Unknown Inputs (9) | Energy-averaged Depth, Multiplicity, Multiplicity m > 3.29 events for = 2, 4, 8, 14, 26, 52 weeks |
| Static Known Inputs (5) | Four space-filling curve labels of fault grouping, linear label of pixel |
| Targets (4) | for = 2, 14, 26, 52 weeks. Calculated for t-52 to t for encoder and t to t + 52 weeks for decoder in 2 week intervals. One hundred and four predictions per sequence |
| Dynamic Known Inputs (13) | for l = 0 to 4 for period = 8, 16, 32, 64 |
| Dynamic Unknown Inputs (9) | Energy-averaged Depth, Multiplicity, Multiplicity m > 3.29 events for = 2, 4, 8, 14, 26, 52 weeks |
| Normalized Nash Sutcliffe Efficiency (NNSE) | ||||||
|---|---|---|---|---|---|---|
| Time Period | LSTM Train | TFT Train | Science Transformer Train | LSTM Validation | TFT Validation | Science Transformer Validation |
| 2 weeks | 0.903 | 0.915 | 0.893 | 0.868 | 0.875 | 0.856 |
| 4 weeks | 0.895 | 0.916 | 0.867 | 0.884 | ||
| 8 weeks | 0.886 | 0.913 | 0.866 | 0.881 | ||
| 14 weeks | 0.924 | 0.963 | 0.919 | 0.893 | 0.905 | 0.881 |
| 26 weeks | 0.946 | 0.956 | 0.954 | 0.897 | 0.892 | 0.896 |
| 52 weeks | 0.919 | 0.957 | 0.955 | 0.861 | 0.871 | 0.876 |
| 104 weeks | 0.923 | 0.937 | 0.853 | 0.83 | ||
| 208 weeks | 0.935 | 0.921 | 0.811 | 0.77 | ||
| Time Period | MSE | LSTM | TFT | Science Transformer | |||
|---|---|---|---|---|---|---|---|
| First Half | Second Half | First Half | Second Half | First Half | Second Half | ||
| Two weeks | Training | 0.0026 | 0.0035 | 0.0025 | 0.0035 | 0.0025 | 0.0035 |
| Validation | 0.0029 | 0.0037 | 0.0029 | 0.0037 | 0.0029 | 0.0037 | |
| One year | Training | 0.0096 | 0.0063 | 0.0070 | 0.0036 | 0.0083 | 0.0053 |
| Validation | 0.011 | 0.0073 | 0.013 | 0.0085 | 0.011 | 0.0074 | |
| Two years | Training | 0.011 | 0.0069 | N/A | N/A | 0.0095 | 0.0058 |
| Validation | 0.014 | 0.0086 | N/A | N/A | 0.016 | 0.012 | |
| Four years | Training | 0.011 | 0.0079 | N/A | N/A | 0.0095 | 0.0058 |
| Validation | 0.015 | 0.011 | N/A | N/A | 0.016 | 0.012 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fox, G.C.; Rundle, J.B.; Donnellan, A.; Feng, B. Earthquake Nowcasting with Deep Learning. GeoHazards 2022, 3, 199-226. https://doi.org/10.3390/geohazards3020011
Fox GC, Rundle JB, Donnellan A, Feng B. Earthquake Nowcasting with Deep Learning. GeoHazards. 2022; 3(2):199-226. https://doi.org/10.3390/geohazards3020011
Chicago/Turabian StyleFox, Geoffrey Charles, John B. Rundle, Andrea Donnellan, and Bo Feng. 2022. "Earthquake Nowcasting with Deep Learning" GeoHazards 3, no. 2: 199-226. https://doi.org/10.3390/geohazards3020011
APA StyleFox, G. C., Rundle, J. B., Donnellan, A., & Feng, B. (2022). Earthquake Nowcasting with Deep Learning. GeoHazards, 3(2), 199-226. https://doi.org/10.3390/geohazards3020011






