Generalized Linear Driving Force Formulas for Diffusion and Reaction in Porous Catalysts
Abstract
1. Introduction
2. Methods
- Linearization of the only nonlinear term, that is, the kinetic term, by Taylor series expansion for multivariable functions limited to the first derivatives only; this step leads to a non-homogeneous linear boundary value problem.
- Transformation of the resulted model to the Laplace domain; the problem is reduced to a set of ordinary differential equations.
- Simplification of the solution of the mass and heat balance equations by employing the well-known Damkohler relationship between the temperature and concentration and analogical relationships between concentrations of the various species; the relationships can be deduced by integrating mass and heat balance equations with the proper boundary condition. The simplification results in a set of uncoupled boundary value problems.
- Solution of the model in the Laplace domain and calculation of the average values of all variables Ci and T.
- Manipulations in the complex domain; their aim is to obtain an equation of required form.
- Inverse integral transformation.
- Transformation of linear terms into nonlinear using the same relationships as in point (a).
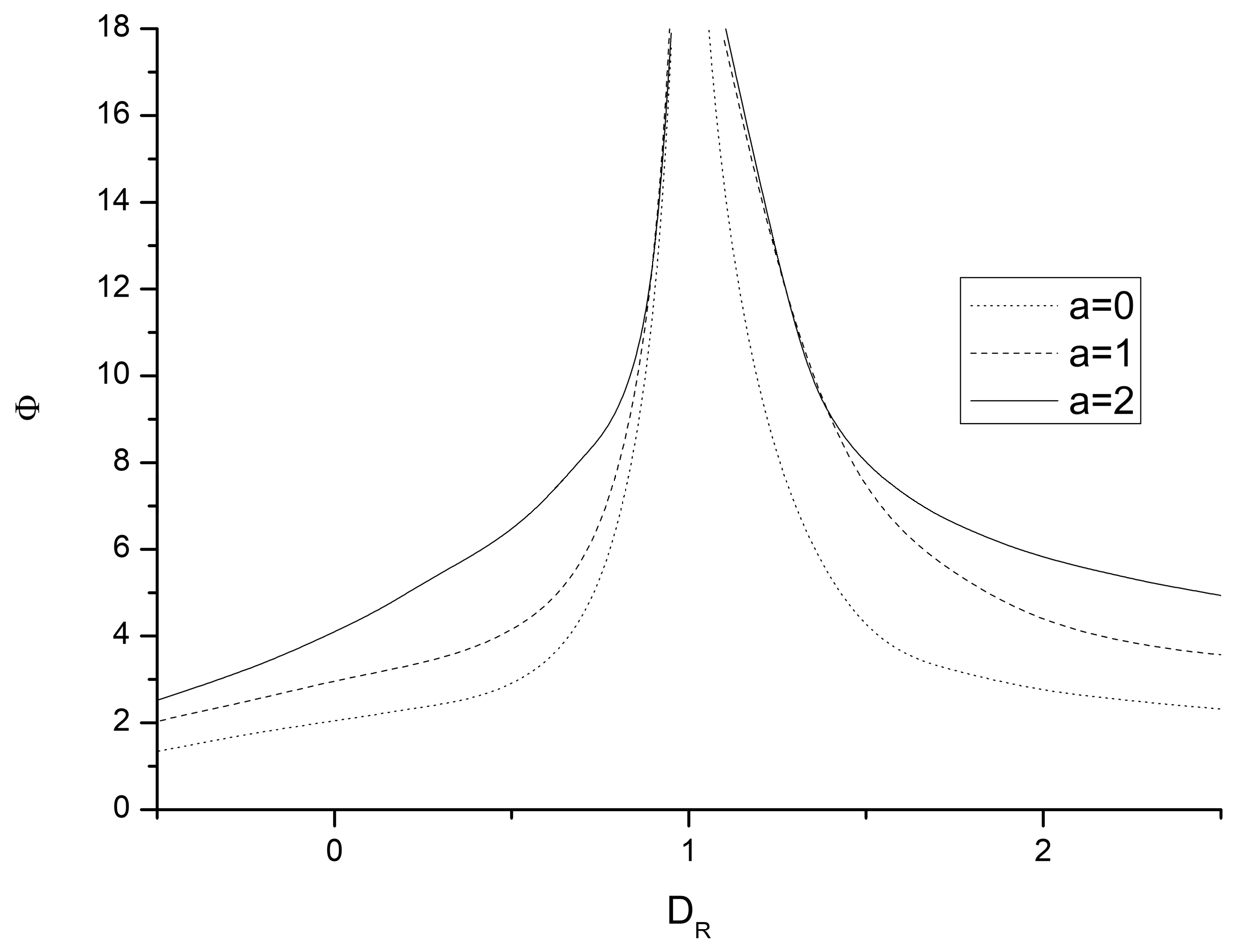
| M 1 < 0 | M = 0 | M > 0 | |
|---|---|---|---|
| Ψ0 (a = 0) | 3 | ||
| Ψ1 (a = 1) | 4 | ||
| Ψ2 (a = 2) | 5 |
3. Results
| Parameters | η | ηApM | Error |
|---|---|---|---|
| CBs = 1; CCs = 0.1; CDs = 0.1; 1/DB = 0.5; 1/DC = 1.2; 1/DD = 0.3; Φ = 0.5; ΘA = 0.05; ΘB = 0.05; ΘC = 0.05; ΘD = 0.05; DR = 1.5; (1) 1 | 0.93 | 0.93 | 0% |
| CBs = 1; CCs = 0.1; CDs = 0.1; 1/DB = 0.5; 1/DC = 1.2; 1/DD = 0.3 Φ = 3.16; ΘA = 0.05; ΘB = 0.05; ΘC = 0.05; ΘD = 0.05; DR = 1.5; (2) 1 | 0.63 | 0.63 | 0% |
| CBs = 1; CCs = 0.1; CDs = 0.1; 1/DB = 0.5; 1/DC = 1.2; 1/DD = 0.3 Φ = 10.0; ΘA = 0.05; ΘB = 0.05; ΘC = 0.05; ΘD = 0.05; DR = 1.5; (3) 1 | 0.24 | 0.26 | 8% |
| CBs = 1; CCs = 0.1; CDs = 0.1; 1/DB = 0.5; 1/DC = 1.2; 1/DD = 0.3; Φ = 0.5; ΘA = 0.3; ΘB = 0.3; ΘC = 0.3; ΘD = 0.3; DR = 1.5 | 0.95 | 0.95 | 0% |
| CBs = 1; CCs = 0.5; CDs = 0.5; 1/DB = 0.5; 1/DC = 1.2; 1/DD = 0.3; Φ = 3.16; ΘA = 0.3; ΘB = 0.3; ΘC = 0.3; ΘD = 0.3; DR = 1.5 | 0.70 | 0.70 | 0% |
| CBs = 1; CCs = 0.5; CDs = 0.5; 1/DB = 0.5; 1/DC = 1.2; 1/DD = 0.3; Φ = 10.0; ΘA = 0.3; ΘB = 0.3; ΘC = 0.3; ΘD = 0.3; DR = 1.5 | 0.29 | 0.31 | 6% |
| CBs = 1; CCs = 5; CDs = 5; 1/DB = 0.5; 1/DC = 1.2; 1/DD = 0.3; Φ = 0.5; ΘA = 0.3; ΘB = 0.3; ΘC = 0.3; ΘD = 0.3; DR = 1.5 | 0.996 | 0.996 | 0% |
| CBs = 1; CCs = 5; CDs = 5; 1/DB = 0.5; 1/DC = 1.2; 1/DD = 0.3; Φ = 3.16; ΘA = 0.3; ΘB = 0.3; ΘC = 0.3; ΘD = 0.3; DR = 1.5 | 0.96 | 0.96 | 0% |
| CBs = 1; CCs = 5; CDs = 5; 1/DB = 0.5; 1/DC = 1.2; 1/DD = 0.3; Φ = 10.0; ΘA = 0.3; ΘB = 0.3; ΘC = 0.3; ΘD = 0.3; DR = 1.5 | 0.73 | 0.72 | 1% |
| CBs = 1; CCs = 0.5; CDs = 0.5; 1/DB = 0.5; 1/DC = 1.2; 1/DD = 0.3; Φ = 0.5; ΘA = 0.05; ΘB = 0.05; ΘC = 0.05; ΘD = 0.05; DR = 1.35; (4) 1 | 0.85 | 0.85 | 0% |
| CBs = 1; CCs = 0.5; CDs = 0.5; 1/DB = 0.5; 1/DC = 1.2; 1/DD = 0.3; Φ = 3.16; ΘA = 0.05; ΘB = 0.05; ΘC = 0.05; ΘD = 0.05; DR = 1.35; (5) 1 | 0.43 | 0.44 | 2% |
| CBs = 1; CCs = 0.5; CDs = 0.5; 1/DB = 0.5; 1/DC = 1.2; 1/DD = 0.3; Φ = 10.0; ΘA = 0.05; ΘB = 0.05; ΘC = 0.05; ΘD = 0.05; DR = 1.35; (6) 1 | 0.14 | 0.16 | 14% |
| CBs = 1; CCs = 0.5; CDs = 0.5; 1/DB = 0.5; 1/DC = 1.2; 1/DD = 0.3; Φ = 0.5; ΘA = 1; ΘB = 1; ΘC = 1; ΘD = 1; DR = 1.80 | 0.99 | 0.99 | 0% |
| CBs = 1; CCs = 0.5; CDs = 0.5; 1/DB = 0.5; 1/DC = 1.2; 1/DD = 0.3; Φ = 3.16; ΘA = 1; ΘB = 1; ΘC = 1; ΘD = 1; DR = 1.80 | 0.92 | 0.92 | 0% |
| CBs = 1; CCs = 0.5; CDs = 0.5; 1/DB = 0.5; 1/DC = 1.2; 1/DD = 0.3; Φ = 10.0; ΘA = 1; ΘB = 1; ΘC = 1; ΘD = 1; DR = 1.80 | 0.59 | 0.60 | 2% |
| CBs = 0.5; CCs = 0.5; CDs = 0.5; 1/DB = 0.5; 1/DC = 1.2; 1/DD = 0.3 Φ = 0.5; ΘA = 0.05; ΘB = 0.05; ΘC = 0.05; ΘD = 0.05; DR = 2.0; (7) 1 | 0.96 | 0.96 | 0% |
| CBs = 0.5; CCs = 0.5; CDs = 0.5; 1/DB = 0.5; 1/DC = 1.2; 1/DD = 0.3 Φ = 3.16; ΘA = 0.05; ΘB = 0.05; ΘC = 0.05; ΘD = 0.05; DR = 2.0; (8) 1 | 0.74 | 0.73 | 1% |
| CBs = 0.5; CCs = 0.5; CDs = 0.5; 1/DB = 0.5; 1/DC = 1.2; 1/DD = 0.3 Φ = 10.0; ΘA = 0.05; ΘB = 0.05; ΘC = 0.05; ΘD = 0.05; DR = 2.0; (9) 1 | 0.32 | 0.335 | 5% |
| CBs = 2; CCs = 0.5; CDs = 0.5; 1/DB = 0.5; 1/DC = 1.2; 1/DD = 0.3; Φ = 0.5; ΘA = 0.05; ΘB = 0.05; ΘC = 0.05; ΘD = 0.05; DR = 1.2 | 0.95 | 0.95 | 0% |
| CBs = 2; CCs = 0.5; CDs = 0.5; 1/DB = 0.5; 1/DC = 1.2; 1/DD = 0.3 Φ = 3.16; ΘA = 0.05; ΘB = 0.05; ΘC = 0.05; ΘD = 0.05; DR = 1.2 | 0.67 | 0.67 | 0% |
| CBs = 2; CCs = 0.5; CDs = 0.5; 1/DB = 0.5; 1/DC = 1.2; 1/DD = 0.3 Φ = 10.0; ΘA = 0.05; ΘB = 0.05; ΘC = 0.05; ΘD = 0.05; DR = 1.2 | 0.26 | 0.27 | 4% |
| CBs = 1; CCs = 0.5; CDs = 0.5; 1/DB = 0.25; 1/DC = 1.2; 1/DD = 0.3; Φ = 0.5; ΘA = 0.05; ΘB = 0.05; ΘC = 0.05; ΘD = 0.05; DR = 1.4 | 0.96 | 0.96 | 0% |
| CBs = 1; CCs = 0.5; CDs = 0.5; 1/DB = 0.25; 1/DC = 1.2; 1/DD = 0.3 Φ = 3.16; ΘA = 0.05; ΘB = 0.05; ΘC = 0.05; ΘD = 0.05; DR = 1.4 | 0.72 | 0.72 | 0% |
| CBs = 1; CCs = 0.5; CDs = 0.5; 1/DB = 0.25; 1/DC = 1.2; 1/DD = 0.3 Φ = 10.0; ΘA = 0.05; ΘB = 0.05; ΘC = 0.05; ΘD = 0.05; DR = 1.4 | 0.30 | 0.315 | 5% |
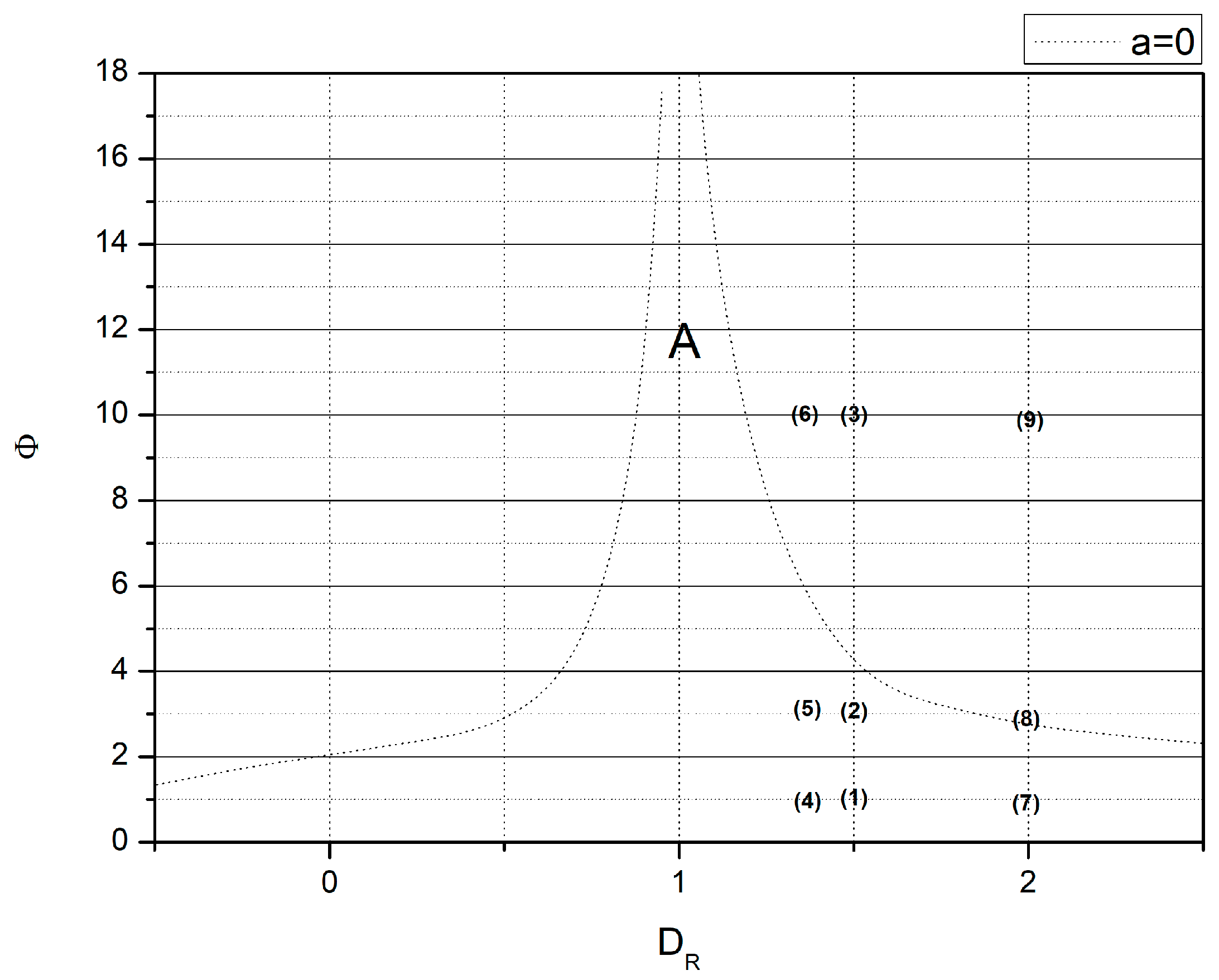
- if Φ = 0.5, then in all cases the point with coordinates (DR,Φ) lies within the validity region; see Figure 2: points (1), (4), (7);
- if Φ = , then the point with coordinates (DR,Φ) lies either in the vicinity of the border of validity region (rows no. 5 and 6) or within (remaining cases); see Figure 2: points (2), (5), (8);
- if Φ = 10, then the point with coordinates (DR,Φ) lies either in the vicinity of the border of the validity region (row no. 7) or out of it (remaining cases); see Figure 2: points (3), (6), (9).
- for Φ = 0.5, in all cases, the effectiveness factor is correctly estimated.
- For Φ = , in all cases, the effectiveness factor is estimated correctly.
- The Φ = 10 effectiveness factor is correctly estimated only for data presented in row no. 7.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Goto, M.; Hirose, T. Approximate rate equation for intraparticle diffusion with or without reaction. Chem. Eng. Sci. 1993, 48, 1912–1915. [Google Scholar] [CrossRef]
- Kim, D.H. Linear driving force formulas for diffusion and reaction in porous catalysts. AIChE J. 1989, 35, 343–346. [Google Scholar] [CrossRef]
- Goto, M.; Smith, J.M.; McCoy, B.J. Parabolic profile approximation (linear driving-force model) for chemical reactions. Chem. Eng. Sci. 1990, 45, 443–448. [Google Scholar] [CrossRef]
- Szukiewicz, M.K. New approximate model for diffusion and reaction in a porous catalyst. AIChE J. 2000, 46, 661–665. [Google Scholar] [CrossRef]
- Szukiewicz, M.K. Approximate model for diffusion and reaction in a porous catalyst with mass-transfer resistances. AIChE J. 2001, 47, 2131–2135. [Google Scholar] [CrossRef]
- Başaǧaoǧlu, H.; McCoy, B.J. Linear Driving-Force Model for Diffusion and Reaction with Interphase Partitioning. AIChE J. 2001, 47, 754–756. [Google Scholar] [CrossRef]
- Álvarez-Ramírez, J.; Valdés-Parada, F.J.; Ochoa-Tapia, J.A. Low-order models for catalyst particles: A dynamic effectiveness factor approach. AIChE J. 2005, 51, 3219–3230. [Google Scholar] [CrossRef]
- Balakotaiah, V. On the relationship between Aris and Sherwood numbers and friction and effectiveness factors. Chem. Eng. Sci. 2008, 63, 5802–5812. [Google Scholar] [CrossRef]
- Kim, D.H. Linear driving force formulas for unsteady-state diffusion and reaction in slab, cylinder and sphere catalyst. AIChE J. 2009, 55, 834–839. [Google Scholar] [CrossRef]
- Szukiewicz, M. An approximate model for diffusion and reaction in a porous pellet. Chem. Eng. Sci. 2002, 57, 1451–1457. [Google Scholar] [CrossRef]
- Reyes, E.P.; Méndez, A.R.; Escobar, G.V.; Rugerio, C.G. Approximate Solution to the Diffusion-Reaction Problem with Nonlinear Kinetics in Transient Systems. In Innovations and Advanced Techniques in Computer and Information Sciences and Engineering; Sobh, T., Ed.; Springer: Dordrecht, The Netherlands, 2007; pp. 133–138. [Google Scholar] [CrossRef]
- Szukiewicz, M.; Petrus, R. Approximate model for diffusion and reaction in a porous pellet and an effectiveness factor. Chem. Eng. Sci. 2004, 59, 479–483. [Google Scholar] [CrossRef]
- Bidabehere, C.M.; García, J.R.; Sedran, U. Transient effectiveness factor in porous catalyst particles. Application to kinetic studies with batch reactors. Chem. Eng. Res. Des. 2017, 118, 41–50. [Google Scholar] [CrossRef]
- Valencia, P.; Ibañez, F. Estimation of the effectiveness factor for immobilized enzyme catalysts through a simple conversion assay. Catalysts 2019, 9, 930. [Google Scholar] [CrossRef]
- Mary, M.L.C.; Devi, M.C.; Meena, A.; Rajendran, L.; Abukhaled, M. Mathematical modeling of immobilized enzyme in porous planar, cylindrical, and spherical particle: A reliable semi-analytical approach. React. Kinet. Mech. Catal. 2021, 134, 641–651. [Google Scholar] [CrossRef]
- Abu-Reesh, I.M. Approximation of intra-particle reaction/diffusion effects of immobilized enzyme system following reverse Michaelis–Menten (rMM) mechanism: Third degree polynomial and Akbari–Ganji methods. React. Kinet. Mech. Catal. 2023, 136, 2875–2892. [Google Scholar] [CrossRef]
- Ananthaswamy, V.; Rajendran, L. Approximate analytical solution of non-linear kinetic equation in a porous pellet. Glob. J. Pure Appl. Math. 2012, 8, 101–111. [Google Scholar]
- Gwadera, M.; Kupiec, K.; Neupauer, K. Approximate equations of mass diffusion and heat conduction with a source term. Przem. Chem. 2016, 95, 1988–1993. [Google Scholar]
- Skoneczny, S.; Cioch-Skoneczny, M. Mathematical modelling and approximate solutions for microbiological processes in biofilm through homotopy-based methods. Chem. Eng. Res. Des. 2018, 139, 309–320. [Google Scholar] [CrossRef]
- Bizon, K. Assessment of a POD method for the dynamical analysis of a catalyst pellet with simultaneous chemical reaction, adsorption and diffusion: Uniform temperature case. Comp. Chem. Eng. 2017, 97, 259–270. [Google Scholar] [CrossRef]
- Bizon, K.; Tabiś, B. Adsorption with chemical reaction in porous catalyst pellets under alternate concentration fields. Uniform temperature case. Chem. Proc. Eng. 2016, 37, 473–484. [Google Scholar] [CrossRef]
- Bizon, K.; Tabiś, B. Dynamics of an isothermal catalyst pellet with simultaneous chemical reaction and adsorption. Chem. Eng. Res. Des. 2016, 115, 221–229. [Google Scholar] [CrossRef]
- Georgiou, A. Asymptotically exact driving force approximation for intraparticle mass transfer rate in diffusion and adsorption processes: Nonlinear isotherm systems with macropore diffusion control. Chem. Eng. Sci. 2004, 59, 3591–3600. [Google Scholar] [CrossRef]
- Georgiou, A.; Kupiec, K. Nonlinear driving force approximations for intraparticle mass transfer in adsorption processes. Nonlinear isotherm systems with macropore diffusion control. Chem. Eng. J. 2003, 92, 185–191. [Google Scholar] [CrossRef]
- Szukiewicz, M.; Petrus, R. Approximate models application for modelling of fixed bed reactors. Hung. J. Ind. Chem. 2001, 29, 91–94. [Google Scholar]
- Pereira, C.S.M.; Gomes, P.S.; Gandi, G.K.; Silva, V.M.T.M.; Rodrigues, A.E. Multifunctional reactor for the synthesis of dimethylacetal. Ind. Eng. Chem. Res. 2008, 47, 3515–3524. [Google Scholar] [CrossRef]
- Bidabehere, C.M.; García, J.R.; Sedran, U. Transient effectiveness factors in the dynamic analysis of heterogeneous reactors with porous catalyst particles. Chem. Eng. Sci. 2015, 137, 293–300. [Google Scholar] [CrossRef]
- Sá Gomes, P.; Leão, C.P.; Rodrigues, A.E. Simulation of true moving bed adsorptive reactor: Detailed particle model and linear driving force approximations. Chem. Eng. Sci. 2007, 62, 1026–1041. [Google Scholar] [CrossRef]
- Pietschak, A.; Kaiser, M.; Freund, H. Tailored catalyst pellet specification for improved fixed-bed transport characteristics: A shortcut method for the model-based reactor design. Chem. Eng. Res. Des. 2018, 137, 60–74. [Google Scholar] [CrossRef]
- Skoneczny, S.; Cioch-Skoneczny, M. Approximate Models of Microbiological Processes in a Biofilm Formed on Fine Spherical Particles. Processes 2022, 10, 48. [Google Scholar] [CrossRef]
- Kumar, J.; Kukreja, V.K. Analytic solution of a diffusion dispersion model of packed bed of finite thickness. J. Interdiscip. Math. 2019, 22, 1–16. [Google Scholar] [CrossRef]
- Belfiore, L.A. Transport Phenomena for Chemical Reactor Design; John Wiley & Sons: Hoboken, NJ, USA, 2003; pp. 491–508. [Google Scholar]
- Gottifredi, J.C.; Gonzo, E.E.; Quiroga, O.D. Isothermal Effectiveness Factor I. Analytical expression for single reaction with arbitrary kinetics. Slab geometry. Chem. Eng. Sci. 1981, 36, 705–711. [Google Scholar]
| Parameters | ηA | η | ηApM | Error |
|---|---|---|---|---|
| Φ = 0.5; n = 0.5; DR = 0.5; | 0.9602 | 0.9600 | 0.9595 | 0.1% |
| Φ = 0.8; n = 0.5; DR = 0.5; | 0.9048 | 0.9000 | 0.9009 | −0.1% |
| Φ = 1.0; n = 0.5; DR = 0.5; | 0.8598 | 0.8495 | 0.8515 | −0.2% |
| Φ = 1.5; n = 0.5; DR = 0.5; | 0.7367 | 0.7062 | 0.7097 | −0.5% |
| Φ = 2.0; n = 0.5; DR = 0.5; | 0.6196 | 0.5774 | 0.5701 | 1.3% |
| Φ = 4.0; n = 0.5; DR = 0.5; | 0.3288 | 0.2890 | 0.2531 | 12% |
| Φ = 0.5; n = 1.0; DR = 1.0; | 0.9244 | 0.9242 | 0.9242 | 0.0% |
| Φ = 0.8; n = 1.0; DR = 1.0; | 0.8309 | 0.8300 | 0.8300 | 0.0% |
| Φ = 1.0; n = 1.0; DR = 1.0; | 0.7631 | 0.7616 | 0.7616 | 0.0% |
| Φ = 1.5; n = 1.0; DR = 1.0; | 0.6069 | 0.6034 | 0.6034 | 0.0% |
| Φ = 2.0; n = 1.0; DR = 1.0; | 0.4866 | 0.4820 | 0.4820 | 0.0% |
| Φ = 4.0; n = 1.0; DR = 1.0; | 0.2530 | 0.2498 | 0.2498 | 0.0% |
| Φ = 0.5; n = 1.5; DR = 1.5; | 0.8925 | 0.8926 | 0.8930 | 0.0% |
| Φ = 0.8; n = 1.5; DR = 1.5; | 0.7735 | 0.7766 | 0.7757 | 0.1% |
| Φ = 1.0; n = 1.5; DR = 1.5; | 0.6952 | 0.6996 | 0.6988 | 0.1% |
| Φ = 1.5; n = 1.5; DR = 1.5; | 0.5337 | 0.5400 | 0.5407 | −0.1% |
| Φ = 2.0; n = 1.5; DR = 1.5; | 0.4234 | 0.4313 | 0.4322 | −0.2% |
| Φ = 4.0; n = 1.5; DR = 1.5; | 0.2212 | 0.2235 | 0.2372 | −6.1% |
| Φ = 0.5; n = 2.0; DR = 2.0; | 0.8641 | 0.8644 | 0.8652 | −0.1% |
| Φ = 0.8; n = 2.0; DR = 2.0; | 0.7283 | 0.7328 | 0.7322 | 0.1% |
| Φ = 1.0; n = 2.0; DR = 2.0; | 0.6355 | 0.6525 | 0.6515 | 0.2% |
| Φ = 1.5; n = 2.0; DR = 2.0; | 0.4951 | 0.5174 | 0.4978 | 3.8% |
| Φ = 2.0; n = 2.0; DR = 2.0; | 0.3900 | 0.4022 | 0.3988 | 0.8% |
| Φ = 4.0; n = 2.0; DR = 2.0; | 0.2032 | 0.2041 | 0.2255 | −11% |
| Φ = 0.5; n = 3.0; DR = 3.0; | 0.8165 | 0.8180 | 0.8175 | 0.1% |
| Φ = 0.8; n = 3.0; DR = 3.0; | 0.6623 | 0.6641 | 0.6660 | −0.3% |
| Φ = 1.0; n = 3.0; DR = 3.0; | 0.5773 | 0.5830 | 0.5838 | −0.1% |
| Φ = 1.5; n = 3.0; DR = 3.0; | 0.4264 | 0.4324 | 0.4407 | −1.9% |
| Φ = 2.0; n = 3.0; DR = 3.0; | 0.3333 | 0.3364 | 0.3546 | −5.4% |
| Φ = 4.0; n = 3.0; DR = 3.0; | 0.1741 | 0.1757 | 0.2067 | −17% |
| Parameters | ηA | η | ηApM | Error |
|---|---|---|---|---|
| Φ = 0.1; K = 0.5; DR = 0.667; | 0.9974 | 0.9968 | 0.9977 | −0.1% |
| Φ = 0.4; K = 0.5; DR = 0.667; | 0.9658 | 0.9638 | 0.9654 | −0.2% |
| Φ = 0.8; K = 0.5; DR = 0.667; | 0.8778 | 0.8695 | 0.8716 | −0.2% |
| Φ = 1.0; K = 0.5; DR = 0.667; | 0.8232 | 0.8058 | 0.8109 | −0.6% |
| Φ = 2.0; K = 0.5; DR = 0.667; | 0.5599 | 0.5183 | 0.5133 | 1.0% |
| Φ = 5.0; K = 0.5; DR = 0.667; | 0.2276 | 0.2130 | 0.1873 | 12% |
| Φ = 0.1; K = 1.0; DR = 0.500; | 0.9983 | 0.9970 | 0.9983 | −0.1% |
| Φ = 0.4; K = 1.0; DR = 0.500; | 0.9741 | 0.9650 | 0.9735 | −0.9% |
| Φ = 0.8; K = 1.0; DR = 0.500; | 0.8969 | 0.8922 | 0.8966 | −0.5% |
| Φ = 1.0; K = 1.0; DR = 0.500; | 0.8596 | 0.8350 | 0.8426 | −0.9% |
| Φ = 2.0; K = 1.0; DR = 0.500; | 0.6179 | 0.5427 | 0.5357 | 1.3% |
| Φ = 5.0; K = 1.0; DR = 0.500; | 0.2531 | 0.2315 | 0.1775 | 23% |
| Φ = 0.1; K = 5.0; DR = 0.167; | 0.9994 | 0.9970 | 0.9994 | −0.2% |
| Φ = 0.4; K = 5.0; DR = 0.167; | 0.9912 | 0.9875 | 0.9908 | −0.3% |
| Φ = 0.8; K = 5.0; DR = 0.167; | 0.9658 | 0.9609 | 0.9592 | 0.2% |
| Φ = 1.0; K = 5.0; DR = 0.167; | 0.9475 | 0.9256 | 0.9312 | −0.6% |
| Φ = 2.0; K = 5.0; DR = 0.167; | 0.5396 | 0.6174 | 0.6170 | 0.1% |
| Φ = 5.0; K = 5.0; DR = 0.167; | 0.2322 | 0.2480 | 0.1458 | 41% |
| Parameters | ηA | η | ηApM | Error |
|---|---|---|---|---|
| Φ = 0.5; n = 0.5; m = 0.5; DR = 0.250; | 0.9419 | 0.9412 | 0.9416 | 0.0% |
| Φ = 0.8; n = 0.5; m = 0.5; DR = 0.250; | 0.8657 | 0.8648 | 0.8647 | 0.0% |
| Φ = 1.0; n = 0.5; m = 0.5; DR = 0.250; | 0.8074 | 0.8057 | 0.8055 | 0.0% |
| Φ = 1.5; n = 0.5; m = 0.5; DR = 0.250; | 0.6625 | 0.6596 | 0.6570 | 0.4% |
| Φ = 2.0; n = 0.5; m = 0.5; DR = 0.250; | 0.5408 | 0.5332 | 0.5311 | 0.4% |
| Φ = 4.0; n = 0.5; m = 0.5; DR = 0.250; | 0.2830 | 0.2799 | 0.2655 | 5.1% |
| Φ = 0.5; n = 0.5; m = 0.5; DR = 0.250; | 0.9245 | 0.9254 | 0.9249 | 0.1% |
| Φ = 0.8; n = 0.5; m = 0.5; DR = 0.250; | 0.8315 | 0.8352 | 0.8331 | 0.3% |
| Φ = 1.0; n = 0.5; m = 0.5; DR = 0.250; | 0.7629 | 0.7683 | 0.7671 | 0.2% |
| Φ = 1.5; n = 0.5; m = 0.5; DR = 0.250; | 0.6098 | 0.6153 | 0.6156 | 0.0% |
| Φ = 2.0; n = 0.5; m = 0.5; DR = 0.250; | 0.4910 | 0.4943 | 0.4987 | −0.9% |
| Φ = 4.0; n = 0.5; m = 0.5; DR = 0.250; | 0.2585 | 0.2578 | 0.2669 | −3.5% |
| Φ = 0.5; n = 0.5; m = 0.5; DR = 0.250; | 0.8927 | 0.8948 | 0.8936 | 0.1% |
| Φ = 0.8; n = 0.5; m = 0.5; DR = 0.250; | 0.7745 | 0.7797 | 0.7779 | 0.2% |
| Φ = 1.0; n = 0.5; m = 0.5; DR = 0.250; | 0.6969 | 0.7040 | 0.7024 | 0.2% |
| Φ = 1.5; n = 0.5; m = 0.5; DR = 0.250; | 0.5369 | 0.5462 | 0.5473 | −0.2% |
| Φ = 2.0; n = 0.5; m = 0.5; DR = 0.250; | 0.4263 | 0.4350 | 0.4405 | −1.3% |
| Φ = 4.0; n = 0.5; m = 0.5; DR = 0.250; | 0.2248 | 0.2263 | 0.2458 | −8.6% |
| Φ = 0.5; n = 0.5; m = 0.5; DR = 0.250; | 0.8393 | 0.8412 | 0.8406 | 0.1% |
| Φ = 0.8; n = 0.5; m = 0.5; DR = 0.250; | 0.6934 | 0.6997 | 0.6976 | 0.3% |
| Φ = 1.0; n = 0.5; m = 0.5; DR = 0.250; | 0.6094 | 0.6170 | 0.6161 | 0.1% |
| Φ = 1.5; n = 0.5; m = 0.5; DR = 0.250; | 0.4551 | 0.4631 | 0.4687 | −1.2% |
| Φ = 2.0; n = 0.5; m = 0.5; DR = 0.250; | 0.3575 | 0.3638 | 0.3774 | −3.7% |
| Φ = 4.0; n = 0.5; m = 0.5; DR = 0.250; | 0.1877 | 0.1886 | 0.2188 | −16% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szukiewicz, M.K.; Chmiel-Szukiewicz, E. Generalized Linear Driving Force Formulas for Diffusion and Reaction in Porous Catalysts. Reactions 2024, 5, 305-317. https://doi.org/10.3390/reactions5020015
Szukiewicz MK, Chmiel-Szukiewicz E. Generalized Linear Driving Force Formulas for Diffusion and Reaction in Porous Catalysts. Reactions. 2024; 5(2):305-317. https://doi.org/10.3390/reactions5020015
Chicago/Turabian StyleSzukiewicz, Mirosław K., and Elżbieta Chmiel-Szukiewicz. 2024. "Generalized Linear Driving Force Formulas for Diffusion and Reaction in Porous Catalysts" Reactions 5, no. 2: 305-317. https://doi.org/10.3390/reactions5020015
APA StyleSzukiewicz, M. K., & Chmiel-Szukiewicz, E. (2024). Generalized Linear Driving Force Formulas for Diffusion and Reaction in Porous Catalysts. Reactions, 5(2), 305-317. https://doi.org/10.3390/reactions5020015






