Abstract
Liquid organic hydrogen carriers (LOHCs) are an interesting alternative for hydrogen storage as the method is based on the reversibility of hydrogenation and dehydrogenation reactions to produce liquid and safe components at room temperature. As hydrogen storage involves a large amount of hydrogen and pure compounds, the design of a three-phase reactor requires the study of gas and liquid-phase kinetics. The gas-phase hydrogenation kinetics of LOHC γ-butyrolactone/1,4-butanediol on a copper-zinc catalyst are investigated here. The experiments were performed with data, taken from the literature, in the temperature and pressure ranges 200–240 °C and 25–35 bar, respectively, for a H2/γ-butyrolactone molar ratio at the reactor inlet of about 90. The best kinetic law takes into account the thermodynamic chemical equilibrium, is based on the associative hydrogen adsorption and is able to simulate temperature and pressure effects. For this model, the confidence intervals are at most 28% for the pre-exponential factors and 4% for the activation energies. Finally, this model will be included in a larger reactor model in order to evaluate the selectivity of the reactions, which may differ depending on whether the reaction takes place in the liquid or gas phase.
1. Introduction
The threat of climate change as well as geopolitical tensions are gradually reducing or even prohibiting the use of fossil fuels. Hydrogen, produced from renewable energy sources, is widely studied as a replacement [1]. Among the hydrogen storage technologies, the most mature are compression or liquefaction and one of the most studied is physisorption. However, they have drawbacks regarding safety, due to high compression pressures and the risk of leakage and evaporation of flammable hydrogen [2,3,4]. With regard to chemical storage of hydrogen in carrier molecules, this technology can involve a wide variety of chemical reactions and storage solutions. The most common ways involve power-to-X systems, by CO2 and/or N2 hydrogenation to fuels capable of being stored under reasonable conditions over extended periods [1]. However, these systems often lack in reversibility because hydrogen is hardly retrieved [1,5]. Another solution consists in binding hydrogen to metals under a solid state [6]. Anyway, the most promising solutions in terms of hydrogen gravimetric density are currently not reversible and the reversible ones are limited in terms of hydrogen content. Another way is the use of a liquid organic hydrogen carrier (LOHC), which involves reversible reactions, is easy to transport and stable over long periods [1,4]. Indeed, a LOHC consists in a couple of hydrogen-lean|hydrogen-rich molecules, which are respectively catalytically hydrogenated and dehydrogenated into the other molecule in order to store and release hydrogen. These organic liquids are fluids sharing similar properties with hydrocarbon fuels or common chemicals. Their stability at ambient temperature and atmospheric pressure in the liquid phase makes them compatible with the existing fuel infrastructures and thus LOHCs can be easily transported in tankers, trucks and/or pipelines [1,4,7].
Multiple LOHC systems have already been identified. The main ones highlighted in the literature are aromatics|cycloalkanes, such as toluene|methylcyclohexane (TOL|MCH), dibenzyltoluene|perhydro-dibenzyltoluene (H0-DBT|H18-DBT), benzyltoluene|perhydro-benzyltoluene (H0-BT|H12-BT) and couples based on N-heterocycles, such as N-ethylcarbazole|perhydro-N-ethylcarbazole (H0-NEC|H12-NEC). The first cycloalkane-based LOHCs were developed because of their good hydrogen capacities (5.8–6.2%), their wide availabilities and the amount of knowledge on the processes of hydrogenation and dehydrogenation. However, reaction enthalpies, which dictate how much energy is lost during the storage process, are high for these LOHCs at around 65–69 kJ·molH2−1, although NEC LOHC has a slightly lower reaction enthalpy (52 kJ·molH2−1). Safety and toxicity profiles have also been improved from the early light aromatics LOHCs to NEC, BT and DBT LOHCs, due to their higher flash points and lesser carcinogenic properties. The liquid state criterion, which is a key point for the process designs, is hardly met for some LOHCs at some conditions. For example, H12-NEC is solid at ambient conditions. Moreover, DBT LOHCs have reaction intermediates with high viscosities. NEC has also reversibility issues with high degradation when subject to harsh dehydrogenation temperatures. Finally, the use of expensive noble metal catalysts and relatively severe reaction conditions hinder the economical or environmental viability of the aromatic-based LOHCs [1,3,7,8,9,10,11,12]. CEA has recently identified a bioavailable LOHC: γ-butyrolactone|1,4-butanediol (GBL|BDO) [13]. The latter, described for the first time by Onoda et al. [14], has low reaction enthalpies of 42 kJ·molH2−1 in liquid phase and 31 kJ·molH2−1 in gas phase, thus making it the most energy efficient. Its lower cycle operating temperature range (160–220 °C), compared to that of cycloalkane-based LOHCs _(300–350 °C), makes its process less energy consuming. BDO is partly produced from biomass, by hydrogenating bio-based succinic acid into GBL or by producing BDO directly from a fermentation of sugars over microorganisms [14,15,16,17], although most of it is currently produced from acetylene and formaldehyde [15,16,17]. It has a H2 capacity of 4.5 wt%, which is lower than that of the other LOHCs. The melting point of pure BDO at 20 °C could limit its use in colder weather or regions [16], but as for the stoichiometric ratio in feed, it remains liquid at reaction operating temperature and pressure, so reaction product separation is easier. Although GBL and BDO have good safety and toxicity profiles, GBL is known as a drug precursor because of its psychotropic properties and chemical resemblance to γ-hydroxybutyric acid (GHB) [18]. They are commonly used as solvents and monomers and their uses are allowed in industrial processes in most countries. See Table S1 in Supplementary Materials for LOHC comparisons [1,16,19,20,21,22].
For all LOHCs, except for TOL|MCH, hydrogenation and dehydrogenation are performed in three-phase reactors. Although LOHCs are usually compared with respect to their mass H2 capacities, the volume H2 capacity is therefore also useful for the design of suitable reactors as it indicates the volume of hydrogen involved during the reactions. For all LOHCs, the ratio H2/LOHC is significant (613–856 LH2·L−1 LOHC) and could act as a barrier to liquid–solid transfer by forming dry zones on the surface of the catalyst pellets. Thus, the knowledge of the reaction kinetics in both the liquid and gas phases is necessary to accurately design a three-phase reactor. As the main quality of LOHCs is the perfect reversibility of their reactions, the formation of co-products in both phases and reactions must also be assessed. This study is therefore a part of a larger study on GBL|BDO. Here, the paper is focused on the kinetics of the hydrogenation in the gas phase. The kinetics of the hydrogenation in the liquid phase will be the subject of another article.
The reaction pathway describing the equilibrium between GBL and BDO has been debated within the literature. Most have studied the reaction on copper-based catalysts in the liquid phase with temperature and pressure ranging from 200 to 250 °C and from 30 to 90 bar [14,15,23,24], respectively. Two parallel reactions, resulting in a dehydration towards tetrahydrofuran (THF) and n-Butanol (BuOH), occur at high temperature and are catalyzed by acid sites present in the catalyst support [23,24,25,26,27]; however, their mechanisms are unclear. Reaction intermediates, such as 2-Hydroxytetrahydrofuran, have been proposed as they could be involved in the formation of secondary products [19,24,27]. Ichikawa et al. proposed a model taking into account its formation without measuring it [27]. Chaudhari et al. proposed a mechanism where both GBL and BDO can lead up to the formation of THF and BuOH [23]. However, no article seems to indicate that the latter are formed from intermediates, despites hydrogen imbalances between the reactants and the secondary products (except for the dehydration of BDO into THF). For instance, the experimental data in Schlander’s Ph.D. thesis [25], performed in the gas phase, seem to indicate that GBL concentrations decrease faster than those of BDO as the secondary products build up in the mixture. As for Chaudhari et al., they contend THF is likely to be formed from the hydrogenation of GBL, rather than the dehydration of BDO [23]; we have also used Schlander’s reaction pathway, shown in Figure 1, for the kinetic modeling.
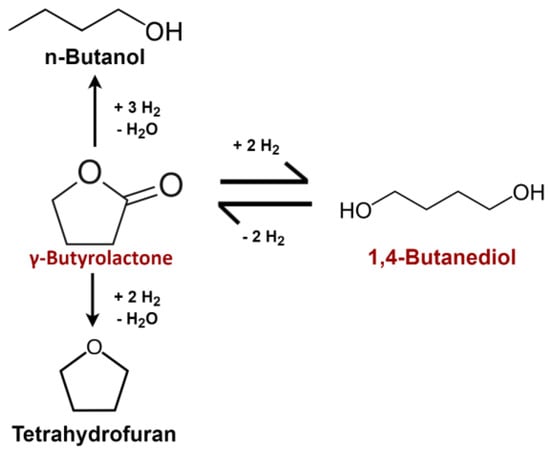
Figure 1.
Reaction scheme used for the construction of the kinetic model.
Kinetic models for the hydrogenation of GBL usually involve a simple power law model such as that proposed by Schlander [15,23,25]. However, it (Model 1 in §2.2.1) proved unable to correctly predict the experimentally described pressure effect. Hermann et al. [24] proposed a Langmuir–Hinshelwood type model because an intermediate is thought to be formed during the hydrogenation of GBL, but this approach was first ruled out because of the number of parameters needed to be estimated, giving the model too many degrees of liberty and thus making it hard to extrapolate. This is why we decided to revise the kinetic study of the GBL gas-phase hydrogenation. The aim was to build a kinetic model, able to predict the effect of temperature and pressure, to be included in a larger reactor model including all phases involved. As the data from Schlander’s works [25,26] were obtained under operating conditions that can mimic the composition of the gas phase in a trickle bed, the published data are used here to determine the appropriate kinetic law.
The GBL hydrogenation was done in gas phase on a CuZnO catalyst in an isothermal tubular reactor. The fixed bed was loaded on a reactor length of 80 mm with crushed catalyst and glass of 400 µm-diameter particles. The catalyst loading was about 8 g. The molar ratio H2/GBL at the reactor entrance was about 90. Temperature and pressure ranges from 200 to 240 °C and from 25 to 35 bar, respectively, were screened. The experimental data presented in Figure 2 are plotted as a function of the residence time tV, which is the ratio between the reactor volume VR and the total volume flow rate Q. The bimetallic catalyst was prepared by co-precipitation and contained 15 mol% Cu and 85 mol% ZnO [28]. See Section S2 in Supplementary Materials, and references [25,26,28] for further details. Regarding the potential transfer limitation, Schlander showed that the apparent kinetics could not be explained either by internal or external mass transfer (Section S3 in Supplementary Materials).
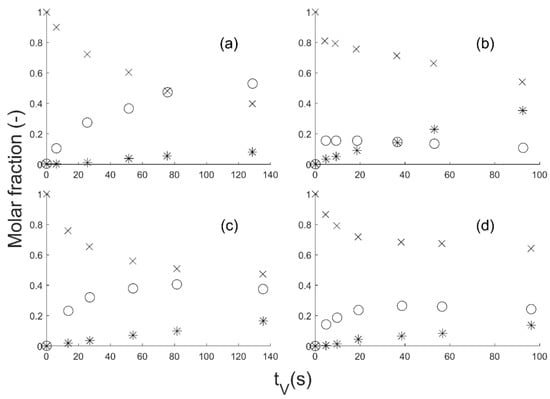
Figure 2.
GBL (times cross), BDO (circle) and side products (SP) (star) molar fraction vs. time on stream (tV): (a) 35 bar, 200 °C; (b) 25 bar, 240 °C; (c) 35 bar, 220 °C; (d) 25 bar, 220 °C. The data come from the Ph.D. thesis of J.H. Schlander [25], but were rearranged as a function of tV instead of the modified dwell time tmV.
In this paper, based on these previous bibliographic results, a reactor model was first described and then several kinetic laws were tested and kinetic parameters estimated in order to predict the effect of temperature and pressure on the gas-phase hydrogenation of GBL into BDO. The kinetic laws were established in interaction with the thermodynamics to take into account the reversibility of the reactions.
2. Materials and Methods
2.1. Reactor Model
To establish mass balance equations suitable for simulation of the experiments, some criteria were checked. GBL was highly diluted by hydrogen in the feed. As the H2/GBL molar ratio at the reactor inlet was about 90, the GBL conversion induced at most a variation of about 1.8% of the volumetric flow rate along the catalytic bed and a negligible change in the gas phase composition for all experiments considered in the kinetics. Consequently, the variation of the gas velocity along the reactor could be neglected as well as the possible temperature gradients induced by the reaction. So, the catalytic bed was considered as isothermal. Moreover, as the reactor diameter (dt) to particle diameter (dp) ratio was greater than 10 (Equation (1)), then wall effects causing a radial velocity profile resulting in deviations from plug flow could be neglected. In addition, as the reactor length (LB) to particle diameter ratio was greater than 50 (Equation (2)), the axial dispersion resulting in consequences on the residence time distribution could also be neglected.
Consequently, an isothermal plug flow model was applied. Steady state was supposed to be reached. The material balance followed the evolution of a compound within an elementary volume of catalyst :
where i is the reaction index and j is the compound index. The apparent kinetic rate is:
As the diffusion has been estimated as a non-limiting step, the efficiency factor is considered equal to 1 (See Section S3 in Supplementary Materials). Capillary condensation has also been assessed in Section S3 in Supplementary Materials.
The experimental data used the scale tV, which is the residence time. Thus
with xj is the molar fraction of condensable compound j equal to the ratio between the compound partial pressure Pj and the partial pressure of GBL at the reactor entrance PGBL,0 and rj the production rates of compound j.
2.2. Kinetic Modeling
Model 1 and Model 2 were built upon power laws with Model 2 including equilibrium constants. Model 3 and Model 4 included in addition an inhibition parameter on the hydrogen pressure. All the models were based on the reaction scheme described in Figure 1. All the models presented in this article (whether kinetic or thermodynamic) were constructed on the basis of the ideal gas hypothesis (see Section S4 in Supplementary Materials).
2.2.1. Model 1
Model 1 is a simple power law model first investigated in modeling the hydrogenation of GBL into BDO. It is the model proposed by J.H. Schlander in his thesis [25]. To avoid the interpretation bias due to the numerical methods, this model has been assessed here with the same method as used for the other models. That explains the difference between the values of the kinetic parameters estimated in this paper and given in the thesis.
Based on the reactions given in Table 1, the production rates of all active compounds are as follows:
where kj are the kinetic parameters.

Table 1.
Reaction mechanism for the construction of the first power law model: Model 1.
2.2.2. Model 2
In order to study the effect of pressure into the model, the terms of the production rates were modified to introduce the hydrogen pressure and the chemical equilibrium. kTHF and kBuOH were grouped under a single parameter kSP to better fit the single kinetic following of both side reactions. The reaction mechanism for this power law model is given in Table 2. Moreover, because of the large excess of hydrogen, the total pressure within the reactor was assumed to be the partial pressure of hydrogen. The activity of hydrogen for side reactions was neglected because of its low effect on kinetics.

Table 2.
Reaction mechanism used for the construction of the second power law model: Model 2.
2.2.3. Model 3
Model 3 is based on power law kinetics combined with an inhibition parameter added to the hydrogen partial pressure, which would describe slower kinetics due to a harder accessibility of the reactants to the active copper sites. Here, the adsorption mechanism of hydrogen is associative, meaning that each hydrogen molecule takes one site on the catalyst. The activity of hydrogen for side reactions was neglected because of its low effect on kinetics. The following reaction steps were considered for the construction of Model 3 (Table 3):

Table 3.
Reaction mechanism used for the construction of the kinetic model with inhibition of hydrogen partial pressure: Model 3.
In this model, the production rates also depend on the surface coverage of hydrogen on the catalyst as well as the surface coverage of free sites , as follows:
The production rate rSP for the side products (SP) is the same as Equation (12) of Model 2.
A steady state is assumed for the adsorption of H2 onto the catalyst and leads to expressions of the surface coverage of hydrogen on the catalyst (Equation (15)) as well as the surface coverage of free sites (Equation (16)).
Moreover, because of the large excess of hydrogen, the total pressure within the reactor is assumed to be the partial pressure of hydrogen. The production rates used for Model 3 are:
2.2.4. Model 4
Model 4 is based on Model 3, assuming a dissociative H2 sorption instead of an associative H2 sorption. For the dissociative H2 sorption, each hydrogen atom takes up one site on the catalyst. Model 4 was built similarly to Model 3. The activity of hydrogen for side reactions was neglected because of its low effect on kinetics.
The proposed reaction mechanism is given in Table 4. The induced production rates for the dissociative H2 sorption are written in Equations (19) and (20).

Table 4.
Reaction mechanism used to build the kinetic model based on a dissociative adsorption of H2: Model 4.
As for Model 3, the production rate rSP for the side products (SP) is the same as Equation (12) of Model 2 and a steady state is assumed for the adsorption of H2 onto the catalyst, and leads to the expressions of the surface coverage of hydrogen on the catalyst (Equation (21)) as well as the surface coverage of free sites (Equation (22)).
Moreover, because of the large excess of hydrogen, the total pressure within the reactor is assumed to be the partial pressure of hydrogen. The terms of production rates used for the simulation are:
2.3. Thermodynamic Equilibrium Modeling
The overall reaction equilibrium constant K is calculated through the standard Gibbs free energy change of reaction, ΔrG°:
The standard Gibbs free energy change of reaction, ΔrG°, is calculated by Hess’s law, using formation enthalpies ΔfH°j and entropies ΔfH°j for GBL and BDO. Thermodynamics properties were extracted from the NIST database and completed by the ProPhyPlus database and can be seen in Table 5.

Table 5.
Thermodynamic data used for the modeling of the equilibrium constant. Data were extracted from the databases of NIST and ProPhyPlus.
Formation enthalpies and entropies are calculated at a given temperature T according to Kirchhoff’s laws:
Finally, the heat capacities of the component Cpj are calculated according to Hess’s law, between the component and its hypothetical decomposition into elements:
2.4. Numerical Methods
All numerical operations were done using the software MATLAB. Differential equation systems were solved using a modified Rosenbrock formula of order 2 (function ode23s in MATLAB).
Parameters were estimated using a trust–region–reflective least squares algorithm (function lsqnonlin in MATLAB). The minimized objective function J(a) was the sum of gaps between the experimental data and the modeled data squared, represented through Equation (31).
For Model 1 and 2, parameters were estimated for each set of reaction conditions independently. For Model 3 and 4, parameters were estimated for the experiments at 200 and 240 °C independently and for the two experiments at 220 °C simultaneously in order to obtain kinetic constants independent of pressure conditions. For the last parameter estimation for Model 3, wherein both pre-exponential and activation energy parameters were simultaneously estimated, all the experimental data were used.
Because the uncertainties on experimental data were not available, the precision of estimated parameters only takes into account the uncertainties due to the modeling. Uncertainties on estimated parameters were calculated as follows:
The covariance matrix was calculated through the Jacobian matrix given by the function lsqnonlin of MATLAB and tN-Mp is the Student number.
3. Results and Discussion
3.1. Kinetic Model Comparison
For Model 1, the model proposed by J.H. Schlander [25], the estimated kinetic constants and their uncertainties for a 97.5% confidence interval are given in Table 6. The confidence intervals for kTHF and kBuOH show that these parameter values obviously are not significant.

Table 6.
Estimated kinetic parameters and their uncertainty for a 97.5% confidence interval for Model 1.
This is due to the very large number of parameters to be estimated compared to the amount of experimental data available. For example, kTHF and kBuOH should not be evaluated separately because all the secondary products produced by the two parallel dehydrations are drawn in a single dataset from the experiments. Moreover, kGBL and kBDO can easily be made independent of one another by a proper modeling of the reaction equilibrium, which is usually reached in the experimental section. The redundancy of kinetic constants makes the model not sensitive towards the estimated parameters, since a default in one kinetic constant can be balanced by another. This gives very large uncertainties on the estimated parameters, especially for the side reactions, thus making this model impossible to extrapolate. Moreover, the model does not take into account the effect of pressure. These unreliable results motivated the development of Model 2 (Table 7).

Table 7.
Estimated kinetic parameters and their uncertainty for a 97.5% confidence interval for Model 2.
Although we took into account the hydrogen pressure in a new model (Model 2), this model displayed a significant gap for the k kinetic parameter at 220 °C between 25 and 35 bar. Reaction rates are slower at higher pressure, which is not taken into account in that approach. Moreover, the confidence intervals for the k constant did not overlap for the experiments at 220 °C, meaning that the effect of pressure was not correctly modeled. So, it was impossible to fit an Arrhenius law for this model. Additionally, there was a non-significant k kinetic parameter at 240 °C. Indeed, uncertainties were low for every constant except for the k constant at 240 °C. This is explainable by the fact that the equilibrium was immediately reached right after the first point, and thus made the regression of this k constant happen between just the two first points. Therefore, simple power law models (Model 1 and 2) are inefficient when accounting for the drop of reaction rates as the pressure rises.
Model 3 (Table 8) was able to fit both experiments at 220 °C with a single set of constants in accordance to Arrhenius’s law where kinetic parameters were only dependent on temperatures. Parameter estimation showed that the adsorption constant was almost constant in the studied range of temperatures. This result is not surprising, considering that activation energies for adsorption constants are usually low, thus making the dependency of adsorption constants towards temperature weak.

Table 8.
Estimated kinetic parameters and their uncertainty for a 97.5% confidence interval for Model 3.
Regarding Model 4, the estimated kinetic constants and their uncertainties for a 97.5% confidence interval are given in Table 9. The estimated constants for kSP and kinetic parameters were quite similar to those of Model 3. For the k parameter, some differences in terms of value appeared for all the temperatures, while as for Model 3, the k parameter remained non-significant at 240 °C.

Table 9.
Estimated kinetic parameters and their uncertainty for a 97.5% confidence interval for Model 4.
Comparing Model 3 and 4 shows that, while kinetic constants were slightly different, the accuracy of the models was exactly the same, whether the adsorption was dissociative or associative. The model needed to slow down the reaction rates between the two pressure points of 25 and 35 bar regardless of the mathematical expression of this phenomenon. To evaluate which phenomenon, hydrogen dissociative or associative adsorption, was the limiting one taking place, further experiments with a wider range of pressures need to be performed.
3.2. Temperature Extrapolation
In order to design a LOHC process, a kinetic model able to predict the kinetics of the GBL hydrogenation into BDO at a given temperature and pressure, between 200 and 240 °C and between 25 and 35 bar, is needed. This paragraph is devoted to the extrapolation of Model 3, which was one of the only models successful in describing the slower kinetics at higher pressures. Extrapolation of Model 4 is seen to be unnecessary due to its similarity with Model 3. Extrapolation of pressures is built in the mathematical expression of the different models. For the extrapolation of temperatures, kinetic constants are modeled by Arrhenius’s law:
Pre-exponential factors Ai and activation energies Eai were re-estimated by replacing the kinetic parameters by their respective Arrhenius’s laws and using all the experimental data at once. Because of the added parameters, the problem is highly dependent on initial conditions. To find a good set of initial parameters, exponential fitting of k and kSP constants into an Arrhenius’s law were made. However, the pre-exponential factor for the k parameter given by the exponential fitting proved to be several orders of magnitude off a good initialization point. In order to find a better set of initial parameters, we noted that the uncertainty calculation on the k constant at 240 °C displayed a lot of play in the constant k, because the equilibrium was obtained right after the first point (Figure 3). Therefore, the k constant of experiment (b) was manually adjusted in order to fit perfectly into an Arrhenius’s law. This adjustment was made through an exponential fit made with the estimated k constants for 200 and 220 °C, in furtherance of calculating the k constant of experiment (b) upon the exponential fit. Initial constants found with the retrofitted k constant showed decent results in the model fitting. Exponential fitting of kSP constants into an Arrhenius’s law proved to be good enough and no adjustment was made here.
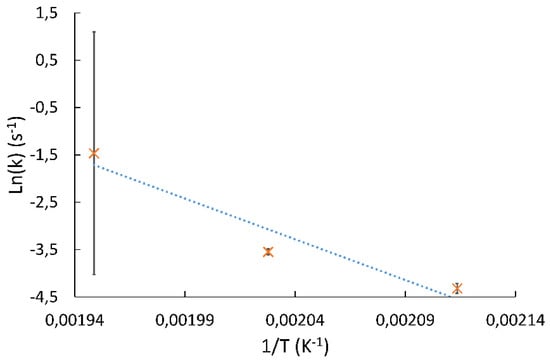
Figure 3.
Exponential fitting of k constants of Model 3 between 200 and 240 °C before adjustment.
Model testing showed that the adsorption constant was almost constant in the studied range of temperatures. Therefore, the constant was manually adjusted to 1.03 (which fitted all confidence intervals) and treated as a constant across the studied range of temperatures. Table 10 displays the initial parameters used.

Table 10.
Initial parameters used for the parameters estimation of the extrapolated Model 3.
Estimation of parameters using the aforementioned method led to a good fit of the extrapolated model to the experimental data (Figure 4).
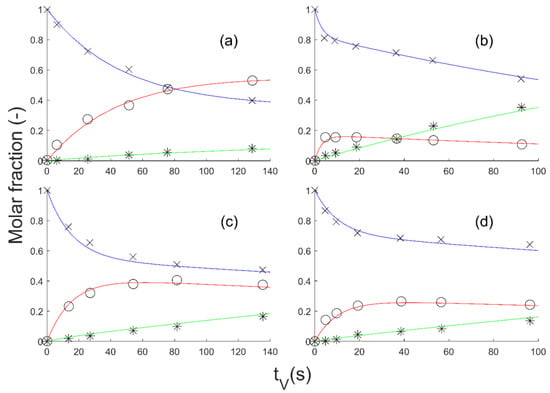
Figure 4.
Simulation of the extrapolation of Model 3 with the adjusted parameters. GBL (experimental: times cross; model: blue line), BDO (experimental: circle; model: red line) and side products (experimental: star; model: green line) molar fraction vs. time on stream (tV): (a) 35 bar, 200 °C; (b) 25 bar, 240 °C; (c) 35 bar, 220 °C; (d) 25 bar, 220 °C.
The estimated pre-exponential factors and activation energies are given in Table 11 along with parity diagrams in Figure 5. For all the parameters, the confidence intervals were narrow and showed good reliability of the parameter values.

Table 11.
Estimated parameters for Model 3 with 95% confidence intervals.
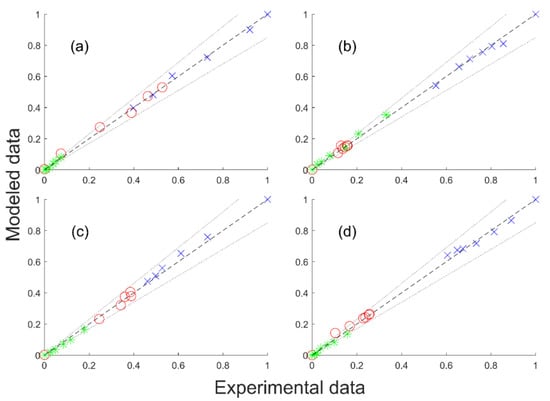
Figure 5.
Parity diagram of the extrapolation of Model 3 with the adjusted parameters. GBL (blue times cross), BDO (red circle) and side products (green star). Experimental molar fraction vs. modeled molar fraction: (a) 35 bar, 200 °C; (b) 25 bar, 240 °C; (c) 35 bar, 220 °C; (d) 25 bar, 220 °C. Dotted lines represent ± 15% deviations.
4. Conclusions
In this paper, a kinetic model has been developed for the gas-phase hydrogenation of γ-butyrolactone in the context of a hydrogen storage process. The data were gathered from experiments conducted by J.H. Schlander on the valorization of succinic acid. Indeed, several works addressing the hydrogenation of both maleic anhydride and succinic acid towards 1,4-butanediol proved to be useful to study the γ-butyrolactone–1,4-butanediol LOHC couple. The newly identified LOHC pair is definitely showing high potential of becoming a competitive LOHC system. With its much improved energy efficiency over cycloalkane-based LOHCs, and better availability than N-heterocycle LOHCs while requiring cheaper catalysts, this pair of molecules could meet the demand for a LOHC of renewable origin, readily available and with low operating costs. Currently, the γ-butyrolactone–1,4-butanediol LOHC lacks reliable kinetic models and data in the literature, thus preventing the development of efficient three-phase reactors and processes. Therefore, this paper proposes for the first time a temperature and pressure extrapolated kinetic model for the gas phase hydrogenation of this LOHC. The model will be included in a more general model for the design of a three-phase hydrogenation reactor currently under study.
Carrying out the hydrogenation of pure GBL in the liquid phase poses difficult problems such as potential dry spots on the catalyst surface. While good selectivity and conversion can be achieved with reasonable reaction conditions in the liquid phase, the presence of dry zones could lead to a drop in selectivity through the production of by-products in the gas phase, making it important to properly assess the impact of gas and liquid phase kinetics for LOHC processes.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/reactions3040033/s1. The document consists of 4 sections. Section S1: Comparison of different LOHC systems. This section contains a table with the properties of the LOHCs. Section S2: Experimental data extracted from the PhD thesis of J.H. Schlander. This section gives additional information on the data used for parameter estimation, as well as a table with the catalyst properties, a scheme of the active part of the reactor and a figure of the experimental data. Section S3: Intraparticular diffusion and capillary condensation. This section gives results and calculation methods on transfer and capillary condensation. Section S4: Ideal gas hypothesis. This section gives results and calculation methods on the thermodynamic properties of the gas phase, as well as a figure with the calculated fugacity coefficients.
Author Contributions
Conceptualization, A.C. and I.P.; methodology, A.C. and I.P.; software, V.G. and I.C.; validation, all; writing—original draft preparation, V.G.; writing—review and editing, A.C. and I.P.; funding acquisition, A.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by CEA.
Data Availability Statement
All the produced data are in the text.
Acknowledgments
The authors would like to thank the Carnot Institute for the financial support, Françoise COUENNE and Christian JALLUT (LAGEPP) for their advice on parameters estimation, as well as Sebastien THOMAS, Anne-Cécile ROGER (ICPEES) and Chaimae QASMI (CEA) for the fruitful discussions.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Abbreviation | |
| BDO | 1,4-butanediol |
| GBL | γ-butyrolactone |
| H0-BT | benzyltoluene |
| H0-DBT | dibenzyltoluene |
| H0-NEC | N-ethylcarbazole |
| H12-BT | perhydro-benzyltoluene |
| H12-NEC | perhydro-N-ethylcarbazole |
| H18-DBT | perhydro-dibenzyltoluene |
| LOHC | liquid organic hydrogen carrier |
| MCH | methylcyclohexane |
| TOL | toluene |
| Latine letters | |
| Pre-exponential factor (s−1) | |
| Set of estimated parameters | |
| Covariance matrix | |
| Specific heat capacity of elements (j: H2, O2, Cgraphite) (J·K−1·mol−1) | |
| Specific heat capacity of component j in vapour phase (j: GBL, BDO) (J·K−1·mol−1) | |
| Specific heat capacity of component j (j: GBL, BDO) (J·K−1·mol−1) | |
| Particule size of the catalyst (m) | |
| Reactor diameter (m) | |
| Activation energy (J·mol−1) | |
| Standard enthalpy of formation for component j (j: GBL, BDO) (J·mol−1) | |
| Molar flux for compound j (j: GBL, BDO, THF, BuOH) (mol·s−1) | |
| Standard Gibbs free energy of formation for component j (j: GBL, BDO) (J·mol−1) | |
| Standard Gibbs free energy change of reaction (J·mol−1) | |
| Objective function for the least-square solver (-) | |
| Equilibrium constant for the hydrogenation of GBL into BDO (Bar−2) | |
| Adsorption constant of H2 on the catalyst (Bar−1) | |
| Kinetic parameter for the hydrogenation of GBL into BDO (s−1) | |
| Kinetic parameter for side reactions (s−1) | |
| Estimated parameter | |
| Reactor length (m) | |
| Catalyst loading (kg) | |
| Number of parameters | |
| Number of experimental data points | |
| Pressure (Bar) | |
| Partial pressure of hydrogen (Bar) | |
| Gas volumetric flow rate (m3·s−1) | |
| Molar gas constant (J·K−1·mol−1) | |
| Production rate for compound j (j: GBL, BDO, THF, BuOH, side products) (s−1) | |
| Observed reaction rate for reaction i (mol·s−1·m−3catalyst) | |
| Intrinsic reaction rate for reaction i (mol·s−1·m−3catalyst) | |
| Temperature (K) | |
| Modified residence time (kgcatalyst·s·mR−3) | |
| Student factor for a degree of freedom. | |
| Residence time (s) | |
| Volume occupied by the catalyst (m3) | |
| Volume of the reactive section (m3) | |
| Molar fraction for condensable component j (j: GBL, BDO, Side products) (-) | |
| Molar fraction extracted from experimental data for a residence time k (-) | |
| Molar fraction calculated by a model for a residence time k (-) | |
| Greek letters | |
| Efficiency factor for reaction i (-) | |
| Surface coverage of hydrogen on the catalyst (-) | |
| Surface coverage of dihydrogen on the catalyst (-) | |
| Surface coverage of free sites on the catalyst (-) | |
| Stoichiometric coefficient for reaction i and for compound j (j: GBL, BDO, THF, BuOH, side products) (-) | |
References
- Aakko-Saksa, P.T.; Cook, C.; Kiviaho, J.; Repo, T. Liquid organic hydrogen carriers for transportation and storing of renewable energy—Review and discussion. J. Power Sources 2018, 396, 803–823. [Google Scholar] [CrossRef]
- Makridis, S.S. Hydrogen storage and compression. In Methane and Hydrogen for Energy Storage, 1st ed.; Rupp, C., David, S.-K.T., Eds.; IET Digital Library: Stevenage, UK, 2016; pp. 1–28. [Google Scholar] [CrossRef]
- Müller, K. Technologies for the Storage of Hydrogen Part 1: Hydrogen Storage in the Narrower Sense. ChemBioEng Rev. 2019, 6, 72–80. [Google Scholar] [CrossRef]
- Dalebrook, A.F.; Gan, W.; Grasemann, M.; Moret, S.; Laurenczy, G. Hydrogen storage: Beyond conventional methods. Chem. Commun. 2013, 49, 8735–8751. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.; Barnett, K.J.; Chada, J.P.; Brentzel, Z.J.; Xu, Z.; Dumesic, J.A.; Huber, G.W. Hydrogenation of γ-Butyrolactone to 1,4-Butanediol over CuCo/TiO2 Bimetallic Catalysts. ACS Catal. 2017, 7, 8429–8440. [Google Scholar] [CrossRef]
- Huang, Y.; Cheng, Y.; Zhang, J. A Review of High Density Solid Hydrogen Storage Materials by Pyrolysis for Promising Mobile Applications. Ind. Eng. Chem. Res. 2021, 60, 2737–2771. [Google Scholar] [CrossRef]
- Teichmann, D.; Arlt, W.; Wasserscheid, P.; Freymann, R. A future energy supply based on Liquid Organic Hydrogen Carriers (LOHC). Energy Environ. Sci. 2011, 4, 2767–2773. [Google Scholar] [CrossRef]
- He, T.; Pei, Q.; Chen, P. Liquid organic hydrogen carriers. J. Energy Chem. 2015, 24, 587–594. [Google Scholar] [CrossRef]
- Meille, V.; Pitault, I. Liquid Organic Hydrogen Carriers or Organic Liquid Hydrides: 40 Years of History. Reactions 2021, 2, 94–101. [Google Scholar] [CrossRef]
- Makaryan, I.A.; Sedov, I.V.; Maksimov, A.L. Hydrogen Storage Using Liquid Organic Carriers. Russ. J. Appl. Chem. 2020, 93, 1815–1830. [Google Scholar] [CrossRef]
- Preuster, P.; Papp, C.; Wasserscheid, P. Liquid Organic Hydrogen Carriers (LOHCs): Toward a Hydrogen-free Hydrogen Economy. Accounts Chem. Res. 2017, 50, 74–85. [Google Scholar] [CrossRef]
- Shi, L.; Qi, S.; Qu, J.; Che, T.; Yi, C.; Yang, B. Integration of hydrogenation and dehydrogenation based on dibenzyltoluene as liquid organic hydrogen energy carrier. Int. J. Hydrogen Energy 2019, 44, 5345–5354. [Google Scholar] [CrossRef]
- Chappaz, A.; Bengaouer, A. Use of Hydrogenated Organic Liquids, in Particular in Devices for Converting Energy. European Patent EP3725738, April 2020. [Google Scholar]
- Onoda, M.; Nagano, Y.; Fujita, K.-I. Iridium-catalyzed dehydrogenative lactonization of 1,4-butanediol and reversal hydrogenation: New hydrogen storage system using cheap organic resources. Int. J. Hydrogen Energy 2019, 44, 28514–28520. [Google Scholar] [CrossRef]
- Küksal, A.; Klemm, E.; Emig, G. Reaction kinetics of the liquid-phase hydrogenation of succinic anhydride on CuZnO-catalysts with varying copper-to-zinc ratios in a three-phase slurry reactor. Appl. Catal. A: Gen. 2002, 228, 237–251. [Google Scholar] [CrossRef]
- Gräfje, H.; Körnig, W.; Weitz, H.-M.; Reiß, W.; Steffan, G.; Diehl, H.; Bosche, H.; Schneider, K.; Kieczka, H.; Pinkos, R. Butanediols, Butenediol, and Butynediol. In Ullmann’s Encyclopedia of Industrial Chemistr; Wiley: Hoboken, NJ, USA, 2022; pp. 1–12. [Google Scholar] [CrossRef]
- Global and China 1,4-Butanediol (BDO) Industry Report, 2017–2021. 2017. Available online: https://www.reportlinker.com/p0318800/Global-and-China-1-4-Butanediol-BDO-Industry-Report.html (accessed on 23 April 2021).
- Satta, R.; Dimitrijevic, N.; Manev, H. Drosophila metabolize 1,4-butanediol into γ-hydroxybutyric acid in vivo. Eur. J. Pharmacol. 2003, 473, 149–152. [Google Scholar] [CrossRef]
- Schwarz, W.; Schossig, J.; Rossbacher, R.; Höke, H. Butyrolactone. In Ullmann’s Encyclopedia of Industrial Chemistr; Wiley: Hoboken, NJ, USA, 2000; pp. 1–7. [Google Scholar] [CrossRef]
- Aslam, R.; Khan, M.H.; Ishaq, M.; Müller, K. Thermophysical Studies of Dibenzyltoluene and Its Partially and Fully Hydrogenated Derivatives. J. Chem. Eng. Data 2018, 63, 4580–4587. [Google Scholar] [CrossRef]
- Davies, M.K.; Archer, A.L.; Maczek, A.O.S.; Manzanares-Papayanopoulos, A.E.; A McLure, I. Shear Viscosities of Methycyclohexane, Perfluoromethylcyclohexane, and Their Mixtures in the Vicinity of the Upper Critical Mixing Temperature. 1. Critical Isopleth and Coexistence Curve. J. Chem. Eng. Data 2006, 51, 1502–1508. [Google Scholar] [CrossRef]
- Ozokwelu, E.D.; Staff, U.B. (Eds.) Toluene. In Kirk-Othmer Encyclopedia of Chemical Technology; Wiley: Hoboken, NJ, USA, 2006; pp. 1–24. [Google Scholar] [CrossRef]
- Chaudhari, R.; Jaganathan, R.; Vaidya, S.; Chaudhari, S.; Naik, R.; Rode, C. Hydrogenation of diethyl maleate in a fixed-bed catalytic reactor: Kinetics, reactor modelling and pilot plant studies. Chem. Eng. Sci. 1999, 54, 3643–3651. [Google Scholar] [CrossRef]
- Herrmann, U.; Emig, G. Liquid Phase Hydrogenation of Maleic Anhydride and Intermediates on Copper-Based and Noble Metal Catalysts. Ind. Eng. Chem. Res. 1997, 36, 2885–2896. [Google Scholar] [CrossRef]
- Schlander, J.H. Gasphasenhydrierung von Maleinsäuredimethylester zu 1.4-Butandiol, γ-Butyrolacton und Tetrahydrofuran an Kupfer-Katalysatoren. Institut für Chemische Verfahrenstechnik. Ph.D. Thesis, Universität Karlsruhe, Karlsruhe, Germany, 2000. [Google Scholar]
- And, J.H.S.; Turek, T. Gas-Phase Hydrogenolysis of Dimethyl Maleate to 1,4-Butanediol and γ-Butyrolactone over Copper/Zinc Oxide Catalysts. Ind. Eng. Chem. Res. 1999, 38, 1264–1270. [Google Scholar] [CrossRef]
- Ichikawa, N.; Sato, S.; Takahashi, R.; Sodesawa, T.; Inui, K. Dehydrogenative cyclization of 1,4-butanediol over copper-based catalyst. J. Mol. Catal. A. Chem. 2004, 212, 197–203. [Google Scholar] [CrossRef]
- Herman, R.; Klier, K.; Simmons, G.; Finn, B.; Bulko, J.; Kobylinski, T. Catalytic synthesis of methanol from CO/H2I. Phase composition, electronic properties, and activities of the Cu/ZnO/M2O3 catalysts. J. Catal. 1979, 56, 407–429. [Google Scholar] [CrossRef]
- National Institute of Standards and Technlogy, U.S. Department of Commerce. Butyrolactone. n.d. Available online: https://webbook.nist.gov/cgi/cbook.cgi?ID=C96480&Units=SI&Mask=1#Refs (accessed on 9 June 2021).
- National Institute of Standards and Technlogy, U.S. Department of Commerce. 1,4-Butanediol. n.d. Available online: https://webbook.nist.gov/cgi/cbook.cgi?ID=C110634&Units=SI&Mask=1#Thermo-Gas (accessed on 9 June 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).