Requiem for the Rate-Determining Step in Complex Heterogeneous Catalytic Reactions?
Abstract
:1. Introduction
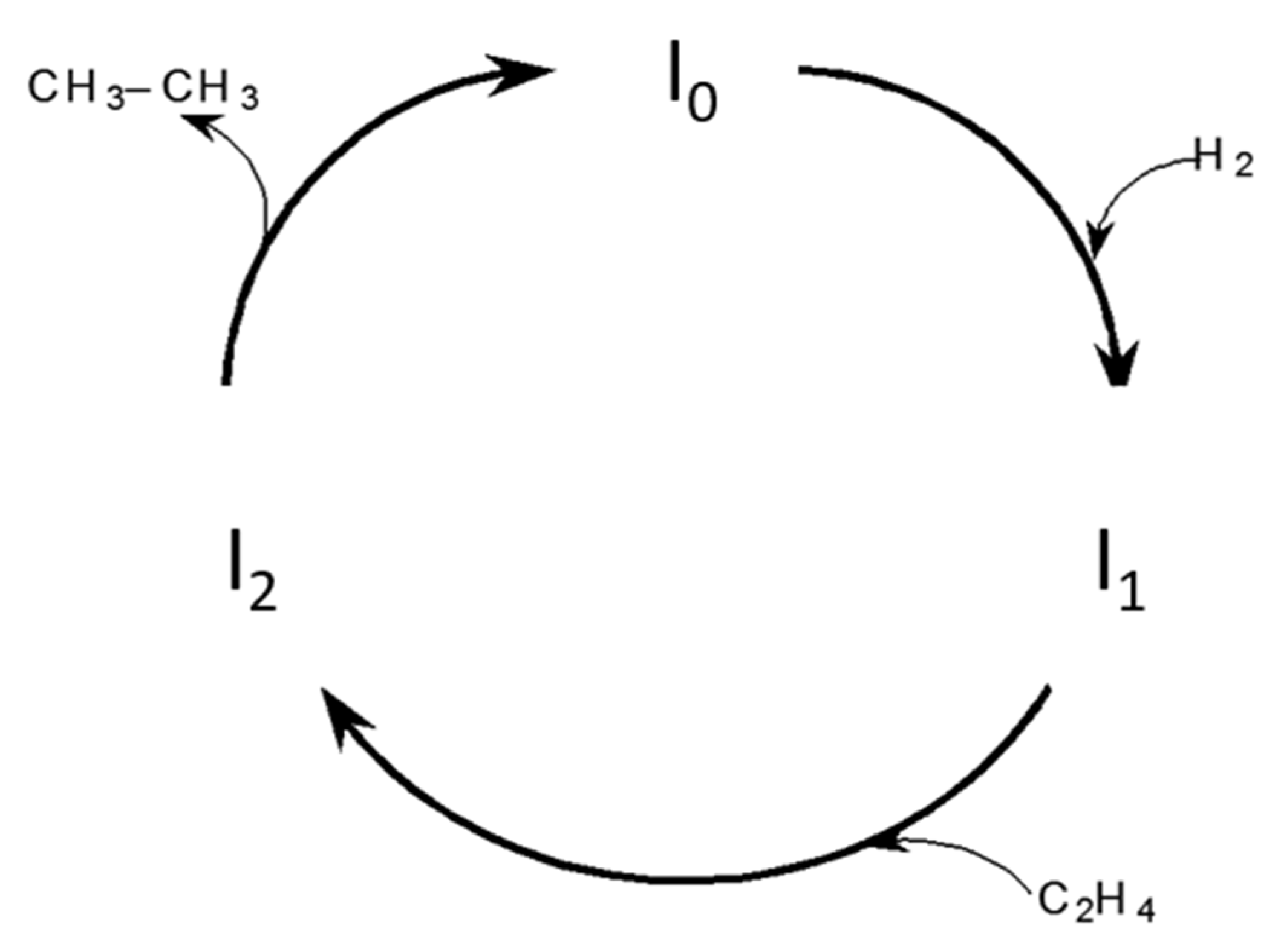
2. Three Step Sequence
3. Four Step Sequence
2.*AH2 + H2 ⇔ *AH4
3.*AH4 ⇒ *Y
3′.*Y + H2 ⇔ *B (fast)
4.*B + A Ξ *A + B
A + 3H2 = B
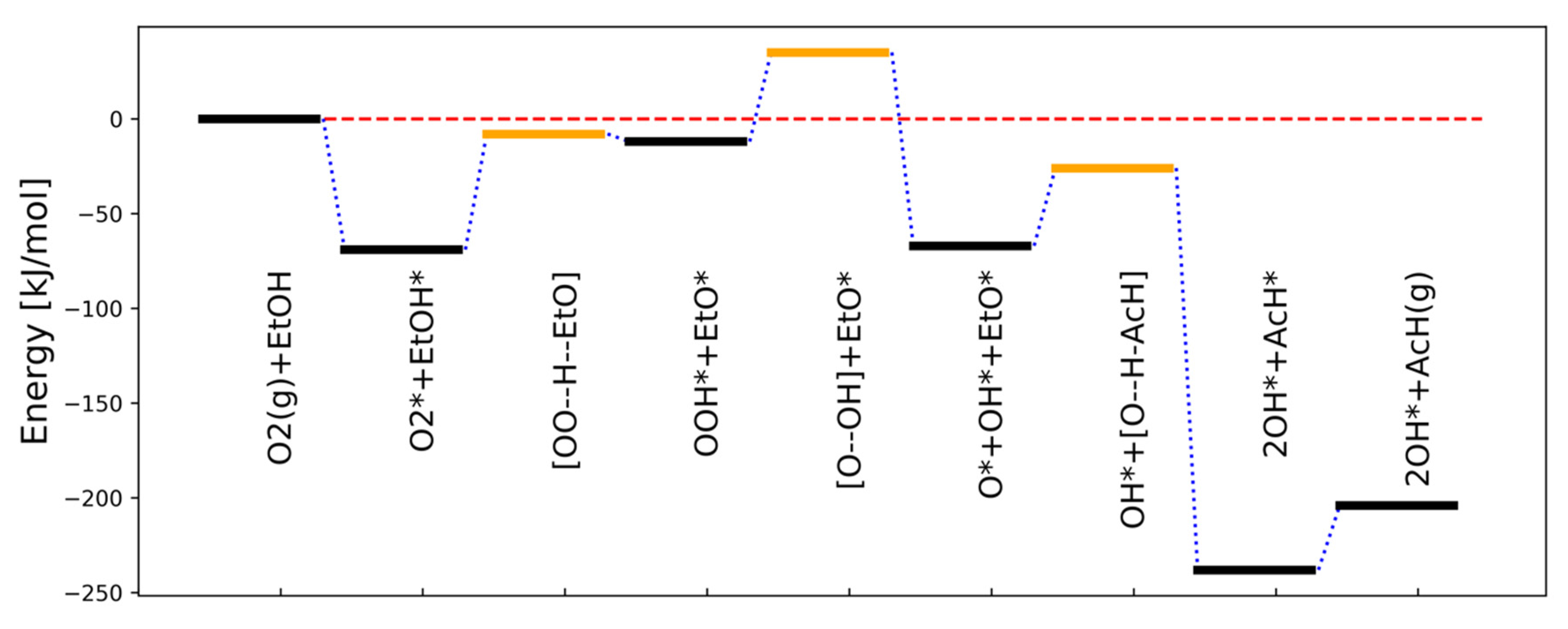
4. Oxidative Dehydrogenation of Ethanol: A Multi-Route Mechanism with Nonlinear Steps
5. Conclusions and Outlook
Funding
Conflicts of Interest
References
- Tsukamoto, M.; Gopalaiah, K.; Kagan, H.B. Equilibrium of homochiral oligomerization of a mixture of enantiomers. Its relevance to nonlinear effects in asymmetric catalysis. Phys. Chem. 2008, 112, 15361–15368. [Google Scholar] [CrossRef]
- Blackmond, D.G. Kinetic profiling of catalytic organic reactions as a mechanistic tool. Am. J. Chem. Soc. 2015, 137, 10852–10866. [Google Scholar] [CrossRef]
- Helfferich, F.G. Kinetics of Homogeneous Multistep Reactions. In Comprehensive Chemical Kinetics; Compton, R.G., Hancock, G., Eds.; Elsevier: Amsterdam, The Netherlands, 2001; Volume 38. [Google Scholar]
- Leskovac, V. Comprehensive Enzyme Kinetics; Kluwer Academic/Plenum Publishers: New York, NY, USA, 2003. [Google Scholar]
- Temkin, O.N. Homogeneous Catalysis with Metal Complexes: Kinetic Aspects and Mechanisms; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Murzin, D.Y.; Salmi, T. Catalytic Kinetics, Chemistry and Engineering, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Salmi, T.O.; Mikkola, J.-P.; Wärnå, J. Chemical Reaction Engineering and Reactor Technology; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Fogler, H.S. Elements of Chemical Reaction Engineering, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- Marin, G.; Yhablonsky, G.S. Kinetics of Chemical Reactions; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Kapteijn, F.; Berger, R.J.; Moulijn, J.A. Rate Procurement and Kinetic Modelling, Handbook of Heterogeneous Catalysis; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Blackmond, D.G. Requiem for the reaction rate equation? Catal. Lett. 2002, 83, 133–136. [Google Scholar] [CrossRef]
- Ball, L.T.; Corrie, T.J.A.; Cresswell, A.J.; Lloyd-Jones, G.C. Kinetic analysis of domino catalysis: A case study on gold-catalyzed arylation. ACS Catal. 2020. [Google Scholar] [CrossRef]
- Schmidt, O.P.; Dechert, A.-M.; Garnsey, M.; Wisniewska, H.; Blackmond, D.G. Kinetic analysis of catalytic organic reactions using a temperature scanning protocol. ChemCatChem 2019, 11, 3808–3813. [Google Scholar] [CrossRef] [Green Version]
- Gorban, A. Model reduction in chemical dynamics: Slow invariant manifolds, singular perturbations, thermodynamic estimates, and analysis of reaction graph. arXiv 2018, arXiv:1802.05745. [Google Scholar] [CrossRef] [Green Version]
- Constales, D.; Yablonsky, G.S.; D’Hooge, D.R.; Thybaut, J.W.; Marin, G.B. Physicochemical Principles of Simplifications of Complex Models, Advanced Data Analysis and Modelling in Chemical Engineering; Springer Science+Business Media: Berlin, Germany, 2017; Chapter 4; pp. 83–103. [Google Scholar]
- O’Malley, P.D.; Datta, R.; Vilekar, S.A. Ockham’s razor for paring microkinetic mechanisms: Electric analogy vs. Campbell’s degree of rate control. AIChE J. 2015, 61, 4332–4346. [Google Scholar] [CrossRef]
- Motagamwala, A.H.; Dumesic, J.A. Analysis of reaction schemes using maximum rates of constituent steps. Proc. Natl. Acad. Sci. USA 2016, 113, E2879–E2888. [Google Scholar] [CrossRef] [Green Version]
- Motagamwala, A.H.; Ball, M.R.; Dumesic, J.A. Microkinetic analysis and scaling relations for catalyst design. Ann. Rev. Chem. Biomol. Eng. 2018, 9, 413–450. [Google Scholar] [CrossRef]
- Steigelmann, C.; Andreasen, A.; Campbell, C.T. Degree of rate control: How much the energies of intermediates and transition states control rates. JACS 2009, 131, 8077–8082. [Google Scholar] [CrossRef]
- Campbell, C.T. The degree of rate control: A powerful tool for catalysis research. ACS Catal. 2017, 7, 2770–2779. [Google Scholar] [CrossRef] [Green Version]
- Wolcott, C.A.; Medford, A.J.; Studt, F.; Campbell, C.T. Degree of rate control approach to computation catalyst screening. J. Catal. 2015, 330, 197–207. [Google Scholar] [CrossRef] [Green Version]
- Mao, Z.; Campbell, C.T. Apparent activation energies in complex reaction mechanisms: A simple relationship via degrees of rate control. ACS Catal. 2019, 9, 9465–9473. [Google Scholar] [CrossRef]
- Mao, Z.; Campbell, C.T. Kinetic isotope effects: Interpretation and prediction using degrees of rate control. ACS Catal. 2020, 10, 4181–4192. [Google Scholar] [CrossRef]
- Mao, Z.; Campbell, C.T. The degree of rate control of catalyst-bound intermediates in catalytic reaction mechanisms: Relationships to site coverage. J. Catal. 2020, 381, 53–62. [Google Scholar] [CrossRef]
- Foley, B.L.; Bhan, A. Degree of rate control and De Donder relations—An interpretation based on transition state theory. J. Catal. 2020, 384, 231–251. [Google Scholar] [CrossRef]
- Vilekar, S.A.; Fishtik, I.; Datta, R. The steady-state kinetics of a catalytic reaction sequence. Chem. Eng. Sci. 2009, 64, 1968–1979. [Google Scholar] [CrossRef]
- Vilekar, S.A.; Fishtik, I.; Datta, R. The peculiar catalytic sequence of the ammonia decomposition reaction and its steady-state kinetics. Chem. Eng. Sci. 2012, 71, 333–344. [Google Scholar] [CrossRef]
- Vilekar, S.A.; Fishtik, I.; Datta, R. Topological analysis of catalytic reaction networks: Methanol decomposition on Pt (111). J. Catal. 2007, 252, 258–270. [Google Scholar] [CrossRef]
- Konsler, R.G.; Karl, J.; Jacobsen, E.N. Coperative asymmetric catalysis with dimeric salen complexes. J. Am. Chem. Soc. 1998, 120, 10780–10781. [Google Scholar] [CrossRef]
- Rosner, T.; le Bars, J.; Pfaltz, A.; Blackmond, D.G. Kinetic studies of Heck coupling reactions using palladacycle catalysts: Experimental and kinetic modelling of the role of dimer species. J. Am. Chem. Soc. 1998, 123, 1848–1855. [Google Scholar] [CrossRef]
- Noble-Teran, M.E.; Buhse, T.; Cruz, J.-M.; Coudret, C.; Micheau, J.-C. Nonlinear effects in asymmetric synthesis: A practical tool for the discrimination between monomer and dimer catalysis. ChemCatChem 2016, 8, 1836–1845. [Google Scholar] [CrossRef]
- Temkin, M. The kinetics of some industrial heterogeneous catalytic reactions. Adv. Catal. 1979, 28, 173–291. [Google Scholar]
- Horiuti, J.; Nakamura, T. On the theory of heterogeneous catalysis. Adv. Catal. 1967, 17, 1–74. [Google Scholar]
- Temkin, O.N. On Various Interconnections between Kinetics and Thermodynamics; LAP Lambert Academi Publishing: Saarbrueken, Germany, 2016; p. 119. [Google Scholar]
- Murzin, D.Y.; Touroude, R. On the rate of heterogeneous catalytic reactions with ionic intermediates. Catal. Lett. 1993, 20, 185–190. [Google Scholar] [CrossRef]
- Carucci, J.R.H.; Kurman, A.; Karhu, H.; Arve, K.; Eränen, K.; Wärnå, J.; Salmi, T.; Murzin, D.Y. Kinetics of the biofuels-assisted SCR of NOx over Ag/alumina-coated microchannels. Chem. Eng. J. 2009, 154, 34–44. [Google Scholar] [CrossRef]
- Murzin, D.Y. Interpretation of rate optima vs reaction parameters in steady state catalytic kinetics: Molecular aspects beyond concentration dependences. Mol. Catal. 2017, 433, 321–333. [Google Scholar] [CrossRef]
- Lazman, M.Z.; Yablonsky, G.S. Overall reaction rate equation of single-route complex catalytic reaction in terms of hypergeometric series. Adv. Chem. Eng. 2008, 34, 47–102. [Google Scholar]
- Laidler, K.J. Rate-controlling step: A necessary or useful concept? J. Chem. Educ. 1988, 65, 250–254. [Google Scholar] [CrossRef]
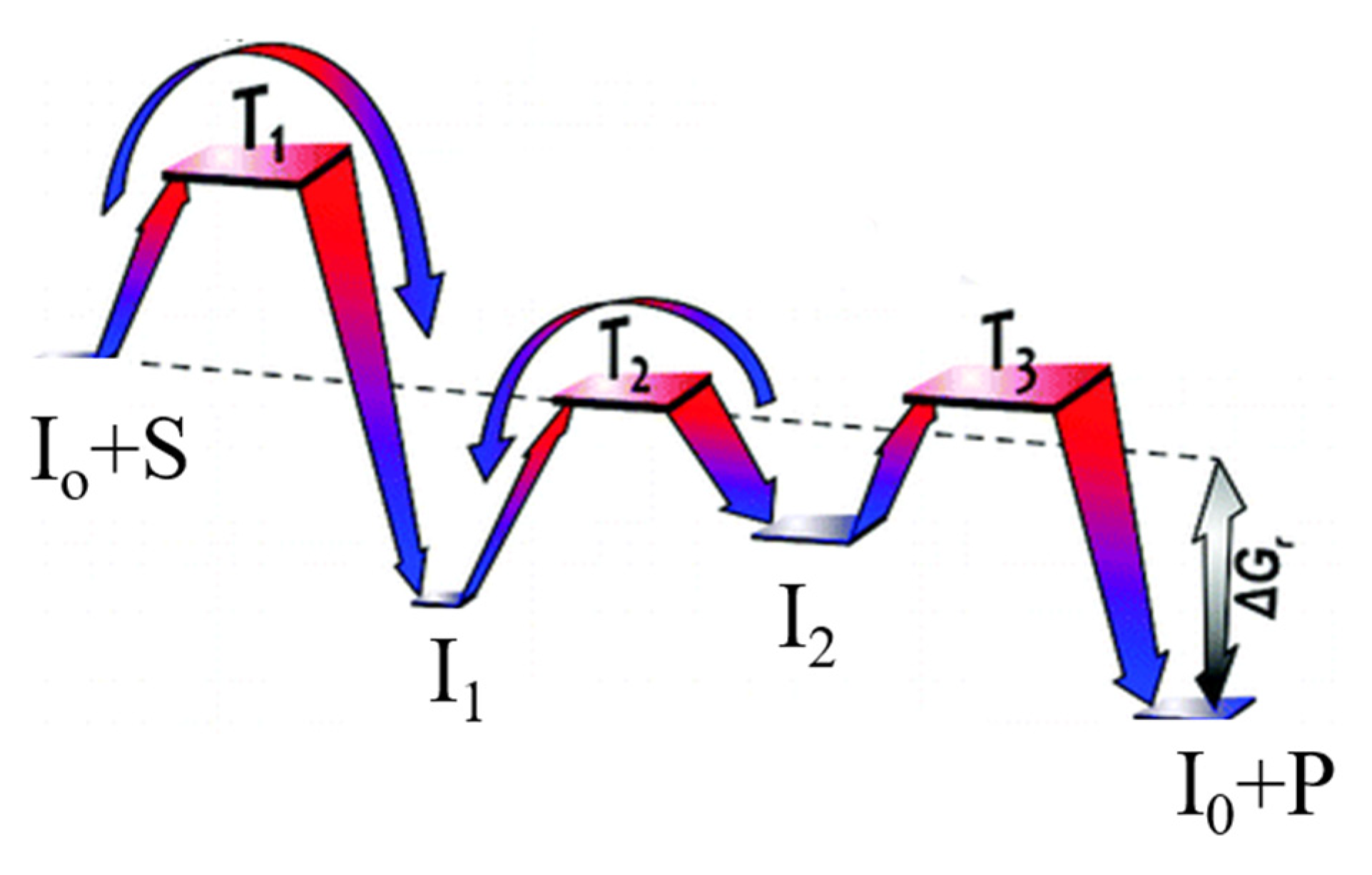
- Kozuch, S.; Shaik, S. How to conceptualize catalytic cycles? The energetic span model. Acc. Chem. Res. 2011, 44, 101–110. [Google Scholar] [CrossRef]
- Marin, G.B.; Yablonsky, G.S.; Constales, D. Kinetics of Chemical Reactions: Decoding Complexity, 2nd ed.; Wiley: Hoboken, NJ, USA, 2019. [Google Scholar]
- Temkin, M.I.; Murzin, D.Y.; Kul’kova, N.V. Kinetics and mechanism of liquid-phase hydrogenation. Doklady Akademii Nauk SSSR 1988, 303, 659–662. [Google Scholar]
- Murzin, D.Y.; Sokolova, N.A.; Kul’kova, N.V.; Temkin, M.I. Kinetics of liquid-phase hydrogenation of benzene and toluene on a nickel catalyst. Kinet. Catal. 1989, 30, 1352. [Google Scholar]
- Temkin, M.I.; Murzin, D.Y.; Kul’kova, N.V. Mechanism of liquid-phase hydrogenation of a benzene ring. Kinet. Catal. 1989, 30, 637. [Google Scholar]
- Murzin, D.Y.; Kul’kova, N.V. Kinetics and mechanism of the liquid-phase hydrogenation. Kinet. Catal. 1995, 36, 70–76. [Google Scholar]
- Murzin, D.Y.; Kul’kova, N.V. Non-equilibrium effects in the liquid-phase catalytic hydrogenation. Catal. Today 1995, 24, 35. [Google Scholar] [CrossRef]
- Behravesh, E.; Melander, M.M.; Wärnå, J.; Salmi, T.; Honkala, K.; Murzin, D.Y. Oxidative dehydrogenation of ethanol on gold: Combination of kinetic experiments and computation approach to unravel the reaction mechanism. J. Catal. 2020. [Google Scholar] [CrossRef]
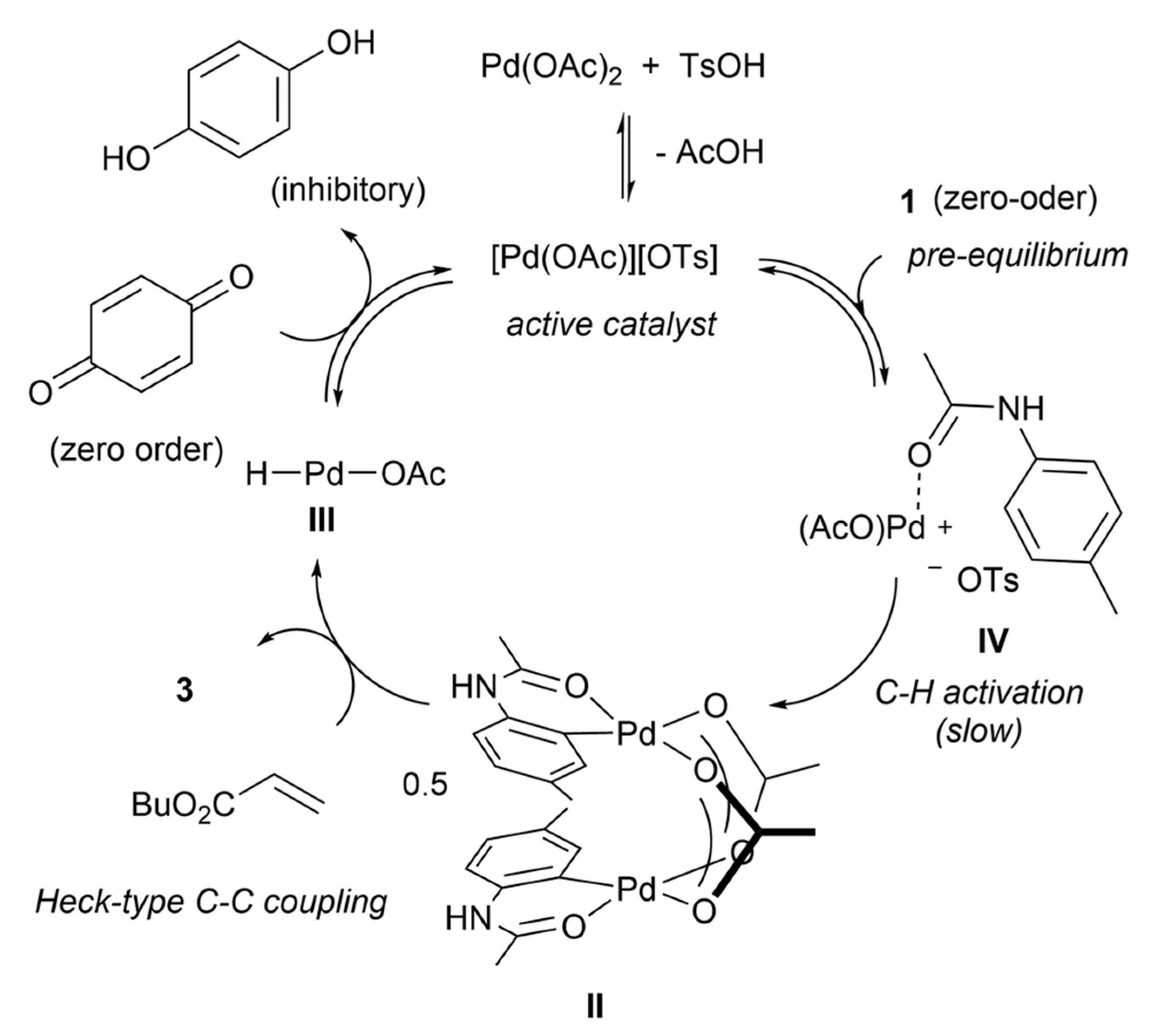
- Mulligan, C.J.; Parker, J.S.; Hii, K.K. Revisiting the mechanism of the Fujiwa-Moritani reaction. React. Chem. Eng. 2020, 5, 1104–1111. [Google Scholar] [CrossRef]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Murzin, D.Y. Requiem for the Rate-Determining Step in Complex Heterogeneous Catalytic Reactions? Reactions 2020, 1, 37-46. https://doi.org/10.3390/reactions1010004
Murzin DY. Requiem for the Rate-Determining Step in Complex Heterogeneous Catalytic Reactions? Reactions. 2020; 1(1):37-46. https://doi.org/10.3390/reactions1010004
Chicago/Turabian StyleMurzin, Dmitry Yu. 2020. "Requiem for the Rate-Determining Step in Complex Heterogeneous Catalytic Reactions?" Reactions 1, no. 1: 37-46. https://doi.org/10.3390/reactions1010004
APA StyleMurzin, D. Y. (2020). Requiem for the Rate-Determining Step in Complex Heterogeneous Catalytic Reactions? Reactions, 1(1), 37-46. https://doi.org/10.3390/reactions1010004




