Understanding Corn Production Complexity: Causal Structure Learning and Variable Ranking from Agricultural Simulations

Abstract

Corn (Zea mays L.) yield productivity is driven by a multitude of factors, specifically genetics, environment, and management practices, along with their corresponding interactions. Despite continuous monitoring through proximal or remote sensors and advanced predictive models, understanding these complex interactions remains challenging. While predictive models are improving with regard to accurate predictions, they often fail to explain causal relationships, rendering them less interpretable than desired. Process-based or biophysical models such as the Agricultural Production Systems sIMulator (APSIM) incorporate these causalities, but the multitude of interactions are difficult to tease apart and are largely sensitive to external drivers, which often include stochastic variations. To address this limitation, we developed a novel methodology that reveals these hidden causal structures. We simulated corn production under varied conditions, including different planting dates, nitrogen fertilizer amounts, irrigation rules, soil and environmental conditions, and climate change scenarios. We then used the simulation results to rank features having the largest impact on corn yield through Random Forest modeling. The Random Forest model identified nitrogen uptake and annual transpiration as the most influential variables on corn yield, similar to the existing research. However, this analysis alone provided limited insight into how or why these features ranked highest and how the features interact with each other. Building on these results, we deployed a Causal Bayesian model, using a hybrid approach of score-based (hill climb) and constraint-based (injecting domain knowledge) models. The causal analysis provides a deeper understanding by revealing that genetics, environment, and management factors had causal impacts on nitrogen uptake and annual transpiration, which ultimately affected yield. Our methodology allows researchers and practitioners to unpack the “black box” of crop production systems, enabling more targeted and effective model development and management recommendations for optimizing corn production.

1. Introduction

Corn (Zea mays L.) plays a vital role in the United States (U.S.) economy. As the largest corn producer worldwide, the U.S. produced 384.64 million metric tons of corn in the year 2024 [1]. Corn serves as the primary feed grain for livestock production, ethanol production, and raw material for numerous industrial applications, making it necessary to understand what impacts the yield for the stability of economic and food systems [2,3]. Even after rapid advancements in the monitoring of complex and multivariate agricultural ecosystems through sensors, we are limited in our ability to understand the causal mechanisms governing yield outcomes and system behavior. Corn yield, quite similar to other crops, depends on genetics (G), environment (E), and management (M), and their corresponding interactions (G × E × M), which have been a focus of study in agriculture over several decades [4].

The complexity of G × E × M interactions creates significant optimization challenges across multiple scales. Genetic factors (G), primarily cultivar selection, must be matched to anticipated environmental conditions and corresponding planting date. Environmental factors (E) create nonlinear yield responses: water deficits dramatically reduce yield (21% nationally during the 2012 drought, resulting in an average country yield of 7.7 × 10³ kg ha⁻¹ compared with the previous five years [5,6]), while excess water causes waterlogging that impedes root gas exchange, increases disease pressure, and accelerates nitrogen N runoff and leaching [6]. This nutrient loss contributes to environmental degradation and greenhouse gas emissions and could reduce yield in limited N supply. Climate change intensifies these processes by increasing weather variability and extreme events, including more frequent droughts, uneven rainfall patterns, and higher temperatures [7]. Understanding this complex agricultural ecosystem is essential to developing adaptive management strategies that can effectively balance these competing factors. Such management practices include cultivar selection with corresponding optimal planting dates, precision N fertilizer application, strategic irrigation scheduling, and integrated pest management [4,7,8].

Management decisions are conventionally based on visual inspection, guidance of extension specialists or agronomic consultants, recommendations from equipment manufacturers and dealers, or observations of neighboring farms [9]. Over the last few years, some farmers are increasingly relying on their local soil and plant conditions and electronic information from sensors (such as remote sensing or soil-based sensors) or simulation models [9,10]. However, decisions based on visual inspection or remote sensing may prove ineffective if plants do not manifest stress symptoms early or if those symptoms are not visible.

Process-based simulation models, such as Agricultural Production Systems sIMulator (APSIM) [11], Decision Support System for Agrotechnology Transfer (DSSAT) [12], and WOrld FOod STudies (WOFOST) [13], were originally designed to embody explicit causal relationships between agricultural variables and biophysical processes. These sophisticated models quantitatively define biological system behavior through accumulated understanding of cause-and-effect relationships, embedded in equations based on field experiment observations across specific G × E × M combinations. However, these biophysical models face significant limitations for large-scale applications with extrapolations due to the heterogeneity of genetic varieties, environmental conditions, and management practices. They also struggle with accurate predictions and site-specific recommendations because of uncertainties in parameterization, calibration requirements, and spatial scale constraints. To address these limitations, biophysical models are increasingly integrated with machine learning algorithms like Random Forest to generate optimized recommendations and improve predictions across various applications [14,15]. While machine learning excels at improving prediction outcomes, it is most often not interpretable, as it does not explain complex interacting causal relationships. Paradoxically, as these models have evolved to capture agricultural ecosystems more precisely, they have become increasingly sophisticated and complex, and somewhat lack interpretability due to their “black-box” nature [16]. Although each component reflects well-established causal mechanisms in biophysical or mechanistic models, their integration makes it difficult to isolate, quantify, and interpret overall system behavior.

Understanding the causal relationships between variables and predictors is crucial to achieve explainable and interpretable models and to understand why, during feature ranking, which variable receives a higher feature importance score. Causal machine learning models that encode directional relationships can complement biophysical models in making predictions and conducting “what-if” scenario analysis through counterfactuals, which is not directly possible with traditional machine learning models [17]. Causal machine learning is a data-driven method for uncovering complex cause–effect relationships that are generally unknown. Thus, integration of biophysical and causal modeling approaches can help overcome limitations in modeling complex agricultural ecosystems to inform adaptive management strategies [17]. In this study, our overall goal was to explore predictive machine learning and Causal Bayesian modeling as methods to explicate the internal mapping of APSIM by using data-driven techniques. Therefore, the specific objectives were as follows:

• Identify and rank the most influential variables impacting corn yield among N fertilizer application rates, irrigation management rules, weather conditions, climate change scenarios, planting date, soil characteristics, and cultivar types;
• Elucidate the underlying causal structure describing the interactions between yield and key G, E, and M variables to enable a deeper understanding of the corn production that can inform experimental design and support mechanistically grounded decision support systems.

2. Materials and Methods

2.1. APSIM Interface and Model Description

APSIM, an open-source, process-based, and mechanistic cropping system model platform, has been widely used to simulate the interactions of crops with soil and environment [2,18,19]. In this study, the APSIM next-generation model was used because of its modular structure and easy user interface [18]. APSIM–Maize model for maize growth simulation, SOILN model for soil carbon and N cycling, SOILWAT for the dynamics of water, along with management rules for tillage, planting, fertilization, irrigation, and harvesting, were used in this study [20,21]. APSIM–Maize module uses growing degree days (GDD) as the main driving factor for simulating phenology, leaf development and senescence, and biomass accumulation. Other than GDD, biomass accumulation depends on soil moisture, fertility, and others [19,21]. The SoilN model simulates the dynamics between the soil carbon and soil nitrogen. The SoilN model considers two different pools for soil organic matter to model mineralization in a realistic manner: one for labile soil microbial biomass, and the other for the stable organic matter. The flow between the different soil organic matter pools is a function of C:N ratio for different layers between the soil and are described in [20]. The SOILWAT model works almost on the same principle as CERES and PERFECT models, where water flow is characterized by the lower limit, saturation limit and drained upper limit water content and runs on the daily time steps [20]. Even though Indiana has a capillary rise, the SOILWAT model was used rather than the SWIM model to reduce the computational load.

2.2. Experimental Setup

To investigate the effect of diverse management practices on corn yield and environmental factors, a series of experiments were simulated using APSIM with a factorial design encompassing variations in planting dates, N fertilizer amount, irrigation protocols, climate change scenarios, weather conditions, soil types, and cultivar parameters. Similar in silico experiments have been conducted in the U.S. Midwest [22], and have proven valuable for research on nitrogen management and agricultural policy development [14,23,24].

Three different planting dates were specified for 1 April, 30 April, and 30 May, and they include the 20 April to 10 May, the optimum planting window for corn production in Indiana [25]. The 1st of April and 30th of May were used to capture the “what-if” effects, if the planting is not performed in the optimal window. The planting density was set at 8 plants per square meter, and the row spacing was set at 0.75 m following typical practice in Indiana [26]. Four different amounts of urea-N (0 kg ha⁻¹, 142 kg ha⁻¹, 190 kg ha⁻¹, and 237 kg ha⁻¹) were included in the study. The N fertilizer was applied six weeks after planting, when the corn is at the V4 to V6 growth stages, aligning with the practices commonly followed by growers in the state of Indiana. These amounts included the standard recommendation of 190 kg ha⁻¹ in Indiana [27].

Irrigation triggering (starting) and stopping points were decided based on the plant available water content (PAWC). PAWC is calculated as the difference in the drain upper limit (DUL), which is equivalent to the amount of water that remains in the soil after all the excess water at saturation has been drained out, and the crop lower limit (CLL), when the plants are not able to extract any more water from the soil [28]. Three distinct thresholds were selected for starting the irrigation based on the soil moisture level. These thresholds were when the soil moisture level reaches 0%, 50%, and 75% of PAWC. Once the irrigation event was initiated, it ended when the soil moisture was at 100% of the PAWC. Since most of Indiana’s corn is rainfed, one set of simulations did not include irrigation. Three different generic cultivars with varying maturity periods were grown at each location. To account for regional differences, cultivars were selected with relative maturity ratings appropriate for different parts of Indiana: 105 days (suitable for northern Indiana), 115 days (suitable for central Indiana), and 130 days (suitable for southern Indiana). This design allowed for comparison of how each maturity type performed across all locations, rather than limiting each cultivar to its recommended region.

Weather data from three locations representing different regions of Indiana, namely northern Indiana from Pinney Purdue Agriculture Center (PPAC) (41°27′3.61″ N, 86°56′28.51″ W), central Indiana from Agronomy Center for Research and Education (ACRE) (40°29′20.9″ N, 87°0′11.7″ W), and southern Indiana from Southeast Purdue Agriculture Center (SEPAC) (39°2′28.64″ N, 85°31′24.24″ W), were used. Soil types from these same locations were used to represent the soil characteristics of northern, central, and southern Indiana, respectively. The base case simulation used both weather and soil data from ACRE (central Indiana). To isolate the independent effects of weather and soil conditions, additional scenarios systematically varied these factors: ACRE soil was paired with weather data from northern and southern sites, while ACRE weather was paired with soil data from northern and southern sites. This factorial approach enabled assessment of how weather and soil conditions independently influence crop performance across Indiana regions. Two climate change scenarios, namely mid-century and end-century [7,29] were included. For the mid-century scenario, the precipitation increased 6%, carbon dioxide concentration increased to 550 ppm, and temperature increased by 2.5 K (2.5 °C); for the end-century scenario, these were 10%, 550 ppm, and 5.5 K (5.5 °C), respectively [29]. For a comprehensive analysis, each combination was run using 38 years of historical weather, from 1984 to 2021 [4]. The simulation operated on an annual basis, and to individualize the effects, it was reset each year with a spin-up period prior to the actual planting date.

The full factorial design involved two irrigation management strategies: irrigated and rainfed conditions. For irrigated scenarios, simulations included 3 irrigation trigger points (PAWC_trigger) and one stopping point (PAWC_stop) (100% PAWC), while rainfed scenarios used no irrigation. Each of these simulation design had (3 Cultivars) G × (3 Scenarios × 38 years × 5 (since soil and weather combinations were structured)) E × (3 Planting Dates × 4 N rates) M, resulting in a total of 82,080 (

Table 1. Summary of factorial combinations used in the APSIM simulations.

Factor	Levels
Cultivars (Genetics)	105 RM, 115 RM, 130 RM
Soil Types	North, Central, South Indiana
Weather Locations	North, Central, South Indiana
Planting Dates	1 April, 30 April, 30 May
Nitrogen Rates	0, 142, 190, 237 kg ha−1
Irrigation management	No irrigation and Irrigation Triggers (0%, 50%, 75% PAWC),
	which stops at 100%PAWC
Climate Scenarios	Historical, Mid-century (precipitation increased by 6%, ${\mathrm{CO}}_2$ to
	550 ppm, and temperature by 5.5 K), End-century (precipitation
	increased by 10%, ${\mathrm{CO}}_2$ to 650 ppm, and temperature by 5.5 K)
Years Simulated	1984–2021 (38 years)

).

2.3. Site Description and Agrometeorological Data

The historical weather data required to simulate the experiment, including solar radiation (MJ m⁻² d⁻¹) and rainfall (mm), as well as maximum and minimum air temperatures (°C), were downloaded from the NASA Prediction of Worldwide Energy Resources (POWER) (https://power.larc.nasa.gov, (accessed on 6 October 2025)) for all three locations and were converted into the APSIM readable format with .met extension. The rainfall dataset was downloaded through CHIRPS, and the monthly average for the three locations is presented in Figure 1. The soil properties required for the simulation study were directly sourced from the web soil survey, SSURGO database (https://websoilsurvey.sc.egov.usda.gov/App/WebSoilSurvey.aspx (accessed on 6 October 2025)) and are presented in

Table A1. Soil physical, chemical, and organic properties for the farm at ACRE (40°29′20.9″ N, 87°0′11.7″ W) and soil taxonomy fine-silty, mixed, superactive, mesic typic endoaquolls.

Depth (cm)	BD	AD	LL15	DUL	SAT	KS	LL	KL	XF	PAWC	pH	Carbon (%)
0–15	1.40	0.12	0.229	0.345	0.442	29.57	0.229	0.08	1	0.116	6.59	4.500
15–30	1.40	0.21	0.229	0.345	0.442	21.70	0.229	0.08	1	0.116	6.59	4.500
30–60	1.49	0.23	0.230	0.346	0.408	15.78	0.230	0.08	1	0.116	7.12	2.250
60–90	1.55	0.18	0.182	0.312	0.385	13.26	0.182	0.08	1	0.130	7.12	1.420
90–120	1.64	0.13	0.125	0.270	0.351	14.46	0.125	0.08	1	0.145	7.23	0.750
120–150	1.80	0.11	0.111	0.254	0.291	20.48	0.111	0.06	0.9	0.143	7.86	0.750
150–180	1.80	0.11	0.111	0.254	0.291	26.13	0.111	0.03	0.5	0.143	7.86	0.750

Note: BD = bulk density (g/cc), AD = air dry (mm/mm), LL15 = wilting point at 15 bars (mm/mm), DUL = drained upper limit (mm/mm), SAT = saturated water content (mm/mm), KS = saturated soil conductivity (mm/day), LL = maize lower limit (mm/mm), KL = maize water conductivity between soil layers (/day), XF = maize extinction coefficient, PAWC = maize plant available water content (mm/mm), pH = soil pH, Carbon = soil organic matter percentage.

,

Table A2. Soil physical, chemical, and organic properties for the farm at SEPAC (39°2′28.64″ N, 85°31′24.24″ W) and soil taxonomy fine-silty, mixed, active, mesic aquic fragiudalfs.

Depth (cm)	BD	AD	LL15	DUL	SAT	KS	LL	KL	XF	PAWC	pH	Carbon (%)
0–15	1.42	0.08	0.233	0.365	0.420	38.76	0.233	0.06	1.000	0.132	5.90	2.281
15–30	1.54	0.08	0.230	0.335	0.385	27.37	0.230	0.06	0.876	0.105	5.80	1.041
30–60	1.59	0.08	0.233	0.324	0.375	17.72	0.235	0.06	0.748	0.089	5.70	0.590
60–90	1.64	0.08	0.237	0.316	0.355	14.05	0.264	0.04	0.602	0.052	5.75	0.374
90–120	1.68	0.08	0.228	0.304	0.340	15.87	0.291	0.01	0.516	0.013	5.94	0.295
120–150	1.68	0.07	0.224	0.300	0.340	17.01	0.299	0.00	0.509	0.001	6.02	0.287
150–180	1.69	0.07	0.219	0.294	0.340	18.56	0.294	0.00	0.000	0.000	6.12	0.277

Note: BD = bulk density (g/cc), AD = air dry (mm/mm), LL15 = wilting point at 15 bars (mm/mm), DUL = drained upper limit (mm/mm), SAT = saturated water content (mm/mm), KS = saturated soil conductivity (mm/day), LL = maize lower limit (mm/mm), KL = maize water conductivity between soil layers (/day), XF = maize extinction coefficient, PAWC = maize plant available water content (mm/mm), pH = soil pH, Carbon = soil organic matter percentage.

and

Table A3. Soil physical, chemical, and organic properties for the farm at PPAC (41°27′3.61″ N, 86°56′28.51″ W) and soil taxonomy class as fine-loamy over sandy or sandy-skeletal, mixed, superactive, mesic typic argiaquolls.

Depth (cm)	BD	AD	LL15	DUL	SAT	KS	LL	KL	XF	PAWC	pH	Carbon (%)
0–15	1.36	0.06	0.170	0.286	0.430	77.75	0.170	0.06	1.000	1.360	6.00	3.123
15–30	1.45	0.05	0.160	0.267	0.400	73.37	0.160	0.06	1.000	1.450	5.95	1.979
30–60	1.47	0.05	0.158	0.257	0.395	69.23	0.158	0.06	1.000	1.472	5.93	1.418
60–90	1.51	0.04	0.142	0.232	0.380	73.37	0.160	0.05	1.000	0.072	6.05	0.874
90–120	1.53	0.03	0.118	0.200	0.380	90.40	0.156	0.03	1.000	0.044	6.24	0.607
120–150	1.53	0.03	0.114	0.196	0.380	96.92	0.163	0.02	1.000	0.033	6.32	0.604
150–180	1.53	0.03	0.109	0.190	0.380	105.70	0.171	0.01	1.000	0.019	6.42	0.600

Note: BD = bulk density (g/cc), AD = air dry (mm/mm), LL15 = wilting point at 15 bars (mm/mm), DUL = drained upper limit (mm/mm), SAT = saturated water content (mm/mm), KS = saturated soil conductivity (mm/day), LL = maize lower limit (mm/mm), KL = maize water conductivity between soil layers (/day), XF = maize extinction coefficient, PAWC = maize plant available water content (mm/mm), pH = soil pH, Carbon = soil organic matter percentage.

. The initial water content values were defined based on the irrigated and non-irrigated field conditions. The initial fraction of maximum available water content for the irrigated conditions was set at 26% LL15, while for non-irrigated conditions it was set to 4% of LL15 [30]. The corresponding initial water content was fixed and constant across all the scenarios under irrigated and non-irrigated management practices. At the same time, the initial N content was set as 3 ppm of ${\mathrm{NH}}_4\mathrm{N}$ and 20 ppm of ${\mathrm{NO}}_3\mathrm{N}$ and was the same for all scenarios.

2.4. Random Forest

With multiple predictors influencing the response variable (yield), interactions among these predictors can introduce non-linearity. Random Forest regression (RF) is a robust model method frequently employed to address such nonlinear problems [31]. RF is a collection of decision trees, which works on if–then–else rule, the way humans intuitively think [31]. In RF, these decision trees work on different subsets of the data and then average the predictions in those subsets. RF has been used previously for agricultural problems such as yield prediction, weed classification, and feature importance determination [3,32]. In this study, we use RF to rank the features affecting yield. RF uses a method called mean decrease in impurity (MDI) for feature importance during the training. In this method, feature importance is based on how much each feature reduces the variance in the response variable (yield) while splitting. Features that contribute to larger variance reduction across all trees receive higher importance scores. Previous studies have similarly used RF with simulation data to explore relationships among variables in APSIM outputs [14,23].

The performance of RF is dependent on its hyperparameters, including the number of trees, maximum depth, and maximum number of features per tree [3]. These hyperparameters were optimized using 3-fold cross-validation with GridSearchCV (GSCV). The search space included the number of trees ranging from 50 to 200 (step size of 10), maximum depth from 2 to 16 (step size of 2), and maximum features set to either ’sqrt’ or ’log2’. During hyperparameter tuning, GSCV trains models across all parameter combinations and selects the configuration yielding the highest cross-validation score for final RF model training [33]. For training the model, the dataset was split into an 80% training set and a 20% test set, and feature scaling was applied to ensure appropriate ranking. All analyses were performed using the ‘scikit-learn’ library in Python (version 3.11).

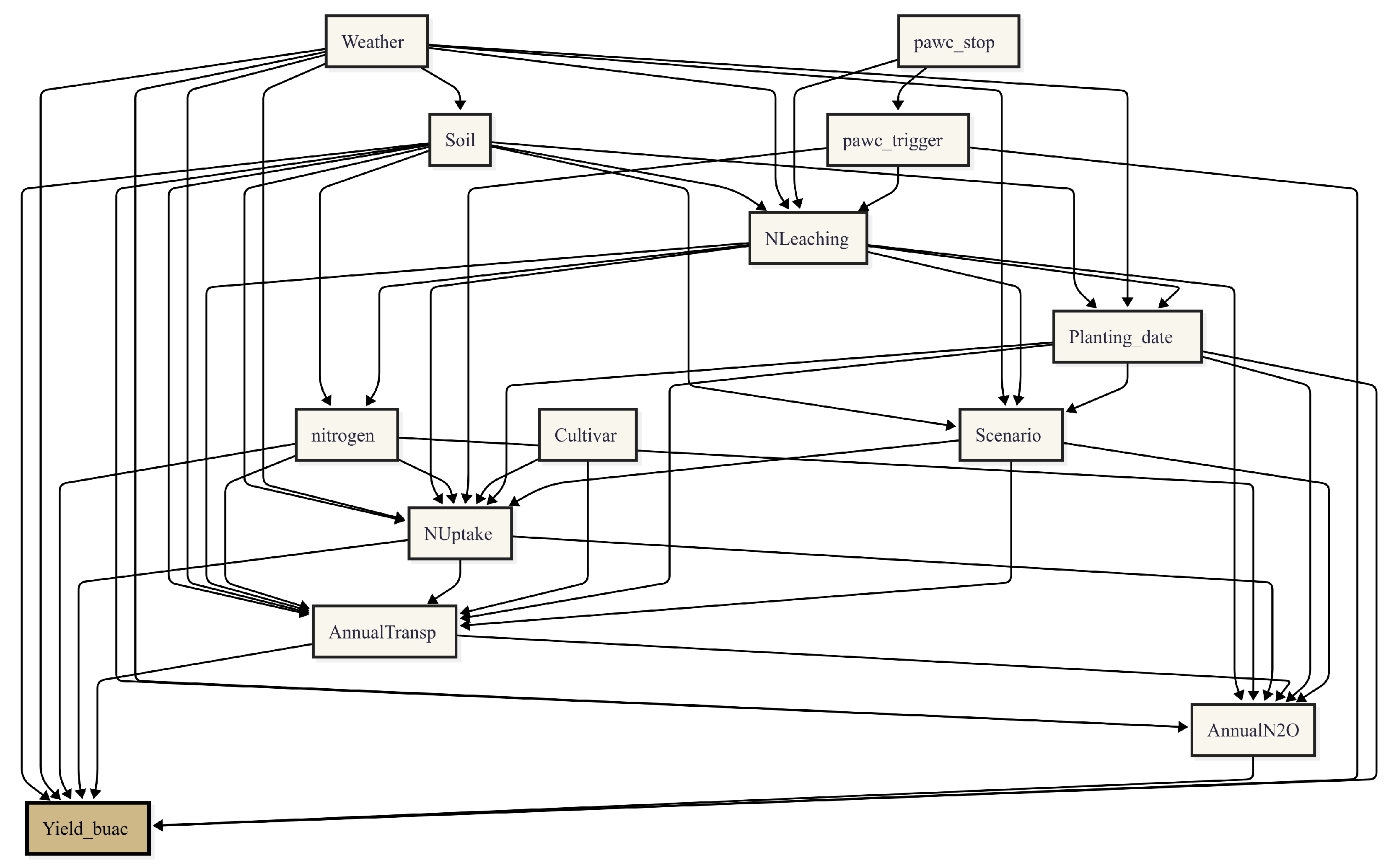
2.5. Causal Learning

Causal inference can help in understanding whether changing X will cause a change in Y, which is quite different from traditional statistical approaches that merely identify correlations or make predictions [17,34,35]. Correlation tells us that two variables tend to change together, while causal inference enables us to understand the underlying mechanisms and predict the effect of interventions. To facilitate structural learning, a causal graph, also known as a Causal Bayesian Graph, was used to represent the relationship among variables in the dataset. A causal graph is a directed acyclic graph (DAG) consisting of nodes representing a variable or component and edges illustrating causal relationships and the direction of influence among variables [36]. The directed nature of the edges encodes causal assumptions, where an arrow from A to B indicates that A has a direct causal effect on B. The acyclic constraint ensures that no variable can be its own cause through a chain of relationships, which is essential for meaningful causal interpretation [35].

These relationships between the variables and components are driven by the optimization procedure and raw data. This optimization could be conducted in two ways, namely the dependency analysis method (constraint-based) or the search and scoring method (score-based). Constraint-based methods (dependency analysis) use statistical tests to identify conditional independence relationships in the data, based on which it construct graphs [37]. Score-based methods (search and scoring) treat structure learning as an optimization problem, defining a scoring function that evaluates how well a given DAG structure explains the observed data [37]. Given that score-based methods can scale to larger datasets and construct reliable networks within reasonable time frames across diverse domains, this research employed a score-based hill climb (HC) algorithm [38]. The HC algorithm incorporated a pre-training constraint stipulating that the final response variable (yield) cannot serve as a causal factor for the predictors, a constraint also acknowledged by [39].

HC is a heuristic search method that works as a greedy search and has two phases, namely forward search and backward search [40]. In the forward search phase, the HC algorithm typically starts with an initial model, in most cases with no nodes connected via an edge. It then iteratively explores the state space of possible DAGs by performing local modifications, such as adding or reversing edges, that lead to maximizing the K2 score [41]. Meanwhile, in the backward search phase, the edges are removed to avoid overfitting and simplify the model. Given the large size of the dataset, with 82,080 rows and 14 columns, heavy computational resources were required. To reduce the computational load, the KBinsDiscretizer, widely used in existing literature with large datasets, was applied to convert all variables into discrete form, making them compatible with Bayesian Network learning algorithms [42]. After the preprocessing using the KBinDiscretizer and normalization, along with one-hot encoding, the dataset was fed into the processing model. To find the optimal number of bins in KBinDiscretizer, likelihood-based criteria, Akaike Information Criterion (AIC), and the Bayesian Information Criterion (BIC) was used with quantile strategy [43,44,45]. Five-fold cross-validation was conducted to stabilize estimates and reduce overfitting. The number of bins that minimized the AIC and BIC score was selected as the optimal discretization level for each variable. Once the bins were identified, the model was trained on the encoded dataset, and the Causal Bayesian Graph was drawn to examine the causal relationship between the variables. The learned graph was validated by domain experts. We also compared the causal graph with the APSIM documentation graph for knowledge validation.

3. Results and Discussions

3.1. Random Forest

Deploying the GSCV provided a max depth of 14, max features of ‘sqrt’, and a number of trees of 180, which were further used for training the model. As expected, predictive machine learning algorithms such as RF do not provide details about how variables interact with one another. In this research, deploying the RF algorithm on the APSIM simulated dataset helped identify which features have higher importance for yield simulations, as shown in Figure 2. However, it is important to note that a high degree of multicollinearity exists among the input variables. Therefore, a variable showing high importance does not necessarily mean that other variables are unimportant. This phenomenon is particularly common when using variables that aggregate multiple processes, such as NUptake or transpiration, which can absorb the explanatory power of more direct environmental or management variables.

Figure 2 shows NUptake as the dominant factor influencing corn yield, with a feature importance score of 0.392. In APSIM, NUptake reflects the product of final biomass and plant N concentration. Biomass consolidates many factors, such as radiation, water availability, and N availability [46]. Therefore, the dominance of NUptake is unsurprising given its composite nature, which integrates multiple underlying influences and provides more explanatory power than individual factors. All the factors that impact biomass will affect NUptake. For instance, water stress reduces biomass and, consequently, NUptake. Similarly, factors affecting N availability influence NUptake through plant N concentration and via their impact on biomass.

Following NUptake, annual transpiration was found as the second most influential variable impacting corn yield, with a feature importance score of 0.236. Like NUptake, transpiration is a composite variable that reflects multiple interacting factors influencing yield. Transpiration is closely linked to the dynamics of atmospheric water demand, soil availability, crop biomass, and physiological processes. In APSIM, biomass accumulation is strongly correlated with corn yield and is simulated based on both available water for transpiration and radiant energy, with the more limiting factor determining daily biomass accumulation [46]. Moreover, transpiration also drives crop development dynamics, seasonal length, and resource capture efficiency. These findings also align well with prior research, which indicates that higher corn yields require greater transpiration and that for every inch of evapotranspiration, corn yield can increase by about 900 kg ha⁻¹ at 15.5% moisture content (17 bu ac⁻¹) [47].

N-related variables, including Annual ${\mathrm{N}}_2\mathrm{O}$ emission (with a feature score of 0.084) and N leaching (with a feature score of 0.030), were ranked fourth and sixth, respectively. Higher ${\mathrm{N}}_2\mathrm{O}$ emissions and leaching are associated with increased N availability in the soil and greater precipitation, both factors that generally have a positive effect on yield [48]. At the same time, increased precipitation can cause more anoxic soil conditions, which promote denitrification and drive nitrate (${\mathrm{NO}}_3^{-}$) deeper into the soil profile, leading to higher N leaching. Therefore, the importance of annual ${\mathrm{N}}_2\mathrm{O}$ emissions and N leaching in predicting yield likely reflects the combined effects of N and water availability, rather than a direct influence of these two variables on yield itself.

The management decision factors of planting date and cultivar selection had a lower direct influence on the model. We believe that their effect was captured by the NUptake and annual transpiration, and these management variables did not provide additional information to the model. Planting date exhibited a feature importance score of 0.014 (ranking seventh), suggesting that while timing of planting affects crop development cycles and exposure to seasonal weather patterns, its impact was captured by previous variables. Meanwhile, cultivar selection received an importance score of 0.009 (ranking ninth). The unexpectedly low score for cultivar selection likely stems from the limited diversity of cultivars used in the simulation (only three variants with growing maturity degree days of 105, 115, and 130), which were tested across different climatic conditions in North, South, and Central Indiana. This restricted range may have artificially constrained the potential variability attributable to genetic differences. On the other hand, N fertilizer amount ranked third, with a score of 0.146, reflecting the importance of N fertilizer application amount on the corn yield. In a field experiment study [49] found that corn grain yield in high-yielding zones increased from approximately 7 × 10³ kg ha⁻¹ to 12.7 × 10³ kg ha⁻¹ as nitrogen fertilizer increased, with a particularly sharp increase at 112 kg N ha⁻¹. In low-yielding zones, yields also increased sharply at the same nitrogen level (112 kg N ha⁻¹) but then remained relatively consistent between 5.7 × 10³ kg ha⁻¹ and 6.26 × 10³ kg ha⁻¹ [49]. Despite experiencing identical weather conditions, these yield differences were attributed to variations in soil types between zones.

The feature importance score of climate change and weather conditions was surprisingly low, with values of 0.009 and 0.012, respectively, even though they both have a significant impact on corn yield in other studies. The other factors considered in this study had captured the effect of weather and climate change and summarized it better than the actual variables. For instance, ref. [50] used APSIM to simulate the corn production under the representative concentration pathway (RCP) 4.5 and RCP 8.5 scenarios, finding that corn yield declined by around 30.5% and 41.3%, respectively. They argue that this could be because the increase in temperature and precipitation decreases the growth period and yield, while an increase in ${\mathrm{CO}}_2$ concentration will alleviate some detrimental impacts on corn yield.

Soil properties, including physical, chemical, and organic traits, affect the water retention capacity, nutrient availability, and root development, which in turn affect the crop growth. Based on the RF model, soil types ranked fifth most influential variable with a feature importance score of 0.065. However, irrigation starting point (PAWC_trigger) and irrigation stopping point (PAWC_stop) had a small feature importance score of 0.002 and 0.001, respectively. This lower feature score could be due to the fact that NUptake and Annual transpiration captured their effects. The lower feature importance score of PAWC_trigger and PAWC_stop was most likely due to Indiana’s high precipitation, combined with soils with high water holding capacity, which reduces the impact of additional water on yield. The binary irrigation logic in the simulations (either no irrigation or full irrigation to 100% PAWC) as the stopping point further reduced the sensitivity of these parameters. PAWC_stop minimal score stems directly from this all-or-nothing design, which simplified irrigation decisions and limited variability in modeled outcomes.

3.2. Causal Learning

While the RF model effectively identifies the relative importance of various features for corn yield prediction using the APSIM simulation dataset, it has inherent limitations. Specifically, the RF model cannot elucidate the interdependencies among variables or their cascading effects on final corn yield. These limitations can be addressed through causal inference using the DAGs presented in Figure 3. By applying likelihood-based criteria, the numerical features, namely, N fertilizer amount, N uptake (NUptake), N leaching, Annual transpiration, Annual ${\mathrm{N}}_2\mathrm{O}$, and Yield, were discretized into five uniform bins to mitigate potential skewness and enhance consistency in model fitting. To reduce complexity, the optimal bin number identified for yield was adopted uniformly across the entire dataset. The DAG was constructed by applying a Bayesian Network with HillClimb optimization to data discretized using KBinsDiscretizer. In Figure 3, independent variables (potential predictors) are represented in light golden color, while the target variable (corn yield) is shown as a golden node. The directed edges between nodes represent causal relationships, where the variable at the arrowhead is causally influenced by the variable at the arrow’s tail. The model learned 47 edges in total, creating a comprehensive representation of corn growth with nodes representing key variables across three categories: environmental factors (weather, NLeaching, ${\mathrm{N}}_2\mathrm{O}$ emissions, scenario, soil properties), genetic variables (cultivar, AnnualTransp, Nuptake), and management factors (N application amount, irrigation rules). These variables relate either directly or indirectly to corn yield and to each other.

From Figure 3, weather emerges as the most critical variable due to its multiple outgoing connections. Weather affects soil, NUptake, annual transpiration, annual ${\mathrm{N}}_2\mathrm{O}$ emissions, yield, planting date, scenario, and N Leaching. The weather variable in this study represents the combination of maximum and minimum temperature, rainfall, and solar radiation. Based on the Figure 3, it could be seen that weather impacts the soil by impacting its water dynamics, temperature, and organic matter dynamics. Water dynamics are simulated through the SOILWAT module, which models soil water balance on a daily timestep using a cascading tipping bucket approach [46]. When rainfall occurs, the model computes infiltration, runoff, and redistribution processes [20]. Soil temperature (SoilTemp) in APSIM is simulated through EPIC and depends on mean air temperature, annual amplitude in mean air temperature, and latitude [51,52]. Soil organic matter dynamics, particularly decomposition in the SOILN module, are governed by first-order kinetic reactions dependent on moisture and temperature [20]. Additionally, both nitrification (forming nitrates from ammonium) and denitrification (forming ${\mathrm{N}}_2\mathrm{O}$ and ${\mathrm{N}}_2$ from nitrates) are first-order processes dependent on temperature and moisture. The ammonium input to soil can originate from mineralization or external inorganic fertilizers [53]. Therefore, the causal network reveals that weather, scenario, N amount, and soil collectively exert a causal impact on Annual ${\mathrm{N}}_2\mathrm{O}$ emissions.

The NUptake in APSIM is driven by plant N demand and constrained by N supply. The N supply itself is influenced by weather conditions and climate change scenarios through the coordinated action of SoilN, SoilWater, and SoilTemp modules. This relationship is reflected in Figure 3, where nodes linking Soil, Scenario, and Weather connect to NUptake [20]. As established previously, soil ammonium levels depend on externally applied inorganic fertilizers, as well as soil dynamics, and consequently, the N amount demonstrates a direct causal relationship with NUptake, as illustrated in Figure 3. Corn nitrogen demand in APSIM is determined by the plant’s growth rate and internal N concentration targets, both of which depend on the specific cultivar, which explains why Figure 3 shows that cultivar exerts a causal impact on NUptake. When N supply exceeds plant demand, the remaining soil nitrogen becomes subject to ${\mathrm{N}}_2\mathrm{O}$ emissions and leaching, where leaching depends on soil characteristics and moisture content. Therefore, Figure 3 demonstrates that Soil, PAWC_stop, and PAWC_trigger parameters impact NLeaching, similar to the weather’s rainfall component, since higher water content increases nitrogen leaching rates [54].

While N leaching represents one aspect of soil water dynamics, transpiration constitutes another critical water-related process in the soil–plant–atmosphere continuum. The APSIM MICROMET module calculates annual transpiration using weather variables (temperature, rainfall, radiation, and wind speed), crop-specific parameters (such as leaf area index and canopy height), and soil water availability [55]. Consequently, Figure 3 shows that weather, soil, scenario, and cultivar have causal relationships with AnnualTransp. Other than these factors, NUptake also had a causal impact on AnnualTransp, as it increases the leaf area index and hence above-ground biomass. In APSIM, the plant modeling framework allows for simulating the water stress, which in turn impacts the photosynthesis, leaf area expansion, stem extension, and N fixation, and hence impacts the NUptake and corresponding yield [56].

The way these simulations were set, the irrigation could be triggered on the basis of PAWC, and PAWC_stop had a causal relationship with PAWC_trigger. Stopping the irrigation earlier will bring the system closer to the triggering limit and hence opening the irrigation system, though this is not the way these relationships have been encoded, but based on practical understanding of agricultural ecosystems, this seems logical. The scenario factor mentioned above represents one of APSIM’s most powerful features for agricultural research. APSIM provides users the flexibility to construct and evaluate various agricultural scenarios, particularly those involving climate change and management practices. This capability is achieved by altering weather inputs through the ClimateControl module and management practices through the Manager module. The ClimateControl module enables users to modify ${\mathrm{CO}}_2$, daily maximum and minimum temperatures, rainfall amounts, and other parameters. Since these modifications require baseline weather conditions as a foundation, weather exerts a causal impact on scenario development in APSIM simulations.

In addition to weather and soil conditions, planting date emerges as a key variable with multiple outgoing connections. The APSIM Maize module employs an 11-stage corn phenological framework, initiating crop growth and development at the planting/sowing stage, based on thermal time accumulation [46]. Planting date establishes the environmental context throughout the growing season by determining when each phenological stage will occur, and the specific weather and soil conditions the crop will encounter. APSIM treats weather, soil, and planting date as the input variables and simulates the experiment based on the provided data, so there should not be any causal relationship between the variables. However, this experiment design includes planting dates both within and outside the optimal planting window. Therefore, the causal model might have identified systematic relationships between weather conditions and relative plant growth success for different planting dates. Planting date causally influences nitrogen uptake (NUptake), annual transpiration (AnnualTransp), scenario outcomes, annual ${\mathrm{N}}_2\mathrm{O}$ emissions, and yield. Planting date affects NUptake through several mechanistic pathways. Temperature-dependent mineralization rates vary seasonally, so earlier planting may encounter different soil thermal regimes. Additionally, phenological timing determines when peak N demands occur, while stress interactions can reduce NUptake efficiency during water-limited periods. When N supply exceeds plant demand, excess nitrogen contributes to ${\mathrm{N}}_2\mathrm{O}$ emissions. Similarly, planting date influences annual transpiration by creating distinct seasonal water use trajectories that align environmental conditions with different phenological stages. This temporal alignment between crop development and environmental resources explains the causal relationship between planting date and transpiration patterns.

Like other management practices, N fertilizer amount emerges as a key variable influencing yield. APSIM treats N fertilizer amount as a management decision and has no internal dependency on soil type and N leaching amount. However, since the causal model has no knowledge of APSIM’s design assumptions, it independently learned that soil conditions and N leaching causally impact N fertilizer amount, likely because it identified systematic patterns in how these factors correlate with fertilizer application rates across different scenarios. The model produced two particularly surprising results. First, both planting date and N Leaching appeared to causally influence the scenario, when these relationships should logically flow in the opposite direction. Second, N Leaching showed a causal impact on the planting date, which contradicts expected agricultural logic. These counterintuitive relationships may stem from the discretization process and the corresponding number of bins used, which could have influenced how the model interpreted these relationships.

Referring back to Figure 2 and Figure 3, the high ranking of NUptake and annual transpiration in the RF feature importance scores becomes clear when viewed through this causal framework, as these variables integrate effects from multiple other system components. However, Figure 3 reveals that soil properties, weather patterns, N application rates, planting date, and PAWC_trigger levels also directly influence yield outcomes.

4. Limitations and Directions for Future Work

The limitations of this study and associated possible recommendations for future work are as follows:

• This study employed a limited set of input variables and management scenarios that may not fully capture the heterogeneity of agricultural systems observed under field conditions. Future research could be expanded to larger-scale, regional simulations encompassing broader geographical regions, longer temporal periods, and more comprehensive treatment matrices. These expanded studies should include diverse cropping systems, management practices, soil types, and climatic conditions to better assist both policymakers in regional decision-making and farmers in making informed, farm-specific management decisions.
• This study employed a discretization approach using five bins with the HillClimb model. While the model struggled to map some edges correctly and occasionally reversed their direction, it successfully mapped around most edges in ways that were practical and intuitive, though not entirely identical to how those relationships were encoded in APSIM. Although these results are sensible and practically valuable, users interested in tracing causal relationships more accurately as they exist in APSIM or other crop growth models should consider several improvements. These include implementing temporal constraints (as we carried out specifically for yield, being the main focus of this study), tuning discretization hyperparameters, selecting the optimal number of bins, and exploring alternative causal discovery models.
• In most studies, including this one, spatial resolution mismatches exist between biophysical crop simulations and the weather datasets or climate change projections used to drive them [2]. Future research should quantify the effects of these scale disparities by downscaling climate projections and meteorological data to match the spatial resolution of field-scale crop models, with particular emphasis on precipitation-sensitive crops such as maize, where rainfall variability significantly affects yield outcomes [2,57].
• This study focused exclusively on the APSIM crop simulation model and aimed to elucidate the causal relationships among key variables within the model framework with yield. Future research should apply similar analytical approaches to other crop growth models to characterize their structural components, develop comprehensive model mappings, and establish evidence-based guidelines for selecting optimal models or model components for specific agricultural applications [17].

5. Conclusions

This study successfully bridges the gap between predictive and causal modeling in agriculture by leveraging APSIM simulations across diverse genetics, environmental, and management conditions, coupled with both machine learning and structural causal learning approaches. We have shown the relative importance of factors impacting corn yield, and nitrogen uptake, annual transpiration, nitrogen applied, and annual ${\mathrm{N}}_2\mathrm{O}$ had the highest feature importance scores, yet the predictive model falls short in explaining why these factors are important or providing contextual reasoning behind their rankings. Our structural causal learning approach revealed the complex causal relationships between variables, explaining why these specific factors ranked highly. The method shows feature positions within a broader causal network that serves as a foundation for using simulation-generated data to compare the internal mechanisms of different crop growth models. This causal structure of intermediate and interconnected pathways brings to light interactions and after effects that could now be a focus for experimentation. For farmers and advisors, this study demonstrates how management decisions create cascading effects throughout the agricultural system, enabling more strategic decision-making that accounts for both direct and indirect impacts on crop performance.

However, developing actual farm-specific protocols requires intervention studies and corresponding validation in real agricultural settings. While our current work focused on corn production uses score-based models with a limited set of variables and treatments, this methodology could readily be extended to different crops and incorporate a wider variety of structural learning models. In conclusion, this approach represents a significant step toward making agricultural decision support systems more transparent and mechanistically grounded, ultimately bridging the gap between complex simulation models and practical farm management.