Prediction of Soil Field Capacity and Permanent Wilting Point Using Accessible Parameters by Machine Learning
Abstract
1. Introduction
- (i)
- Determine the optimal combination of variables for FC and PWP modeling;
- (ii)
- Apply machine learning algorithms to predict the FC and the PWP from easily measurable inputs from global scale accessible data.
2. Materials and Methods
2.1. Data Source and Process
2.2. Previous PTFs and Linear Regression Algorithm
2.3. Artificial Neural Networks (ANNs)
2.4. Gene-Expression Programming (GEP)
2.5. Assessment of the Best-Fit Combination of Input Variables for ML Based Models
2.6. Rank the Input Variables for FC and PWP Modeling
3. Results and Discussion
3.1. Determination of the Best-Fit Variables
3.2. Comparison of Simulated FC and PWP by Different Models
3.3. Identification of Dominant Input Variables
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviation | Meaning |
| AE | absolute error |
| Al | altitude |
| ANN | artificial neural network |
| BPNN | backpropagation neural network |
| CEC | cation exchange capacity |
| C | clay content |
| CV | cross-validation |
| DL | deep learning |
| EC | electrical conductivity |
| FC | field capacity |
| FCANN | field capacity in ANN model |
| FCGEP | field capacity in GEP model |
| FCREG | field capacity in REG model |
| GA | gene algorithm |
| GEP | gene expression programming |
| GP | gene programming |
| i | datum order |
| k-NN | k-nearest neighbors |
| K-S test | Kolmogorov–Smirnov nonparametric test |
| La | latitude |
| Lo | longitude |
| MAE | mean absolute error |
| Max. | maximum |
| Min. | minimum |
| ML | machine learning |
| n | number of actual observations |
| NF | neuro-fuzzy |
| NRMSE | normalized root mean square error |
| OM | organic matter |
| PTF | pedotransfer functions |
| PWP | permanent wilting point |
| PWPANN | permanent wilting point in ANN model |
| PWPGEP | permanent wilting point in GEP model |
| PWPREG | permanent wilting point in REG model |
| r | correlation coefficient |
| REG | regression |
| RF | random forest |
| RMSE | root mean square error |
| R2 | coefficient of determination |
| RT | regression trees |
| S | soil textures (sand, silt, and clay content) |
| Sa | sand content |
| Si | silt content |
| SOM | soil organic matter |
| SVM | support vector machine |
| SWC | soil water content |
| WoSIS | World Soil Information Service |
| x | observed value |
| xmax | maximum observed value |
| xmin | minimum observed value |
| xnorm | normalized dimensionless variable |
| observed value in ith datum | |
| predicted value in ith datum | |
| average of the observations | |
| μ | average |
| σ | standard deviation |
| α | slope of the linear equation |
| β | intercept of the regression |
| ε | error term |
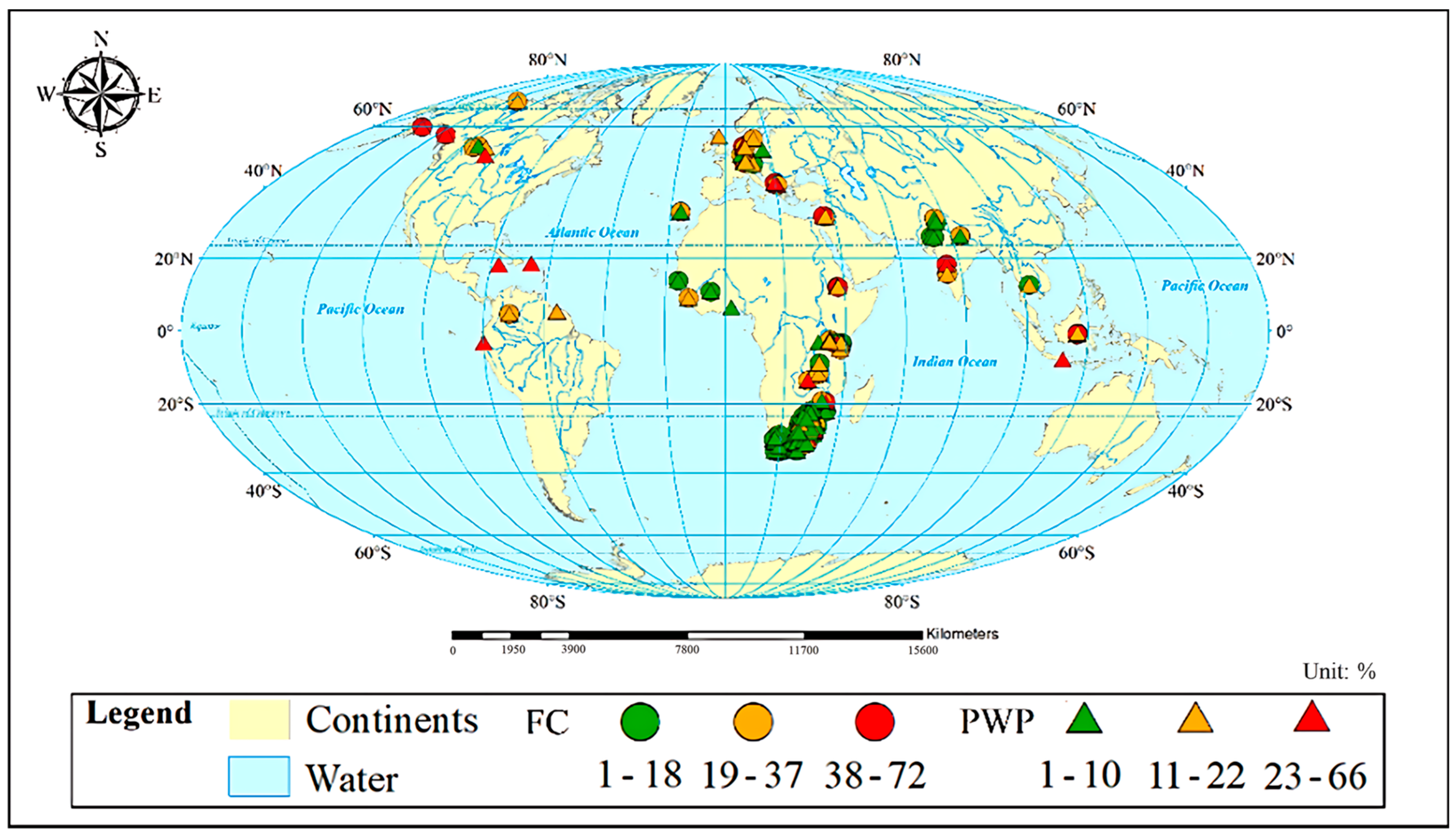
Appendix A. Soil Group and Nations of the FC and PWP Model
| Country | Target | Acrisols | Andosols | Arenosols | Calcisols | Cambisols | Chernozems | Ferralsols | Fluvisols | Kastanozems | Leptosols | Lixisols | Luvisols |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Albania | FC | 2 | |||||||||||
| PWP | 2 | ||||||||||||
| Benin | FC | ||||||||||||
| PWP | 1 | ||||||||||||
| Burkina Faso | FC | 2 | |||||||||||
| PWP | 2 | ||||||||||||
| Canada | FC | 1 | 2 | ||||||||||
| PWP | 1 | 2 | 1 | 2 | |||||||||
| Colombia | FC | 5 | |||||||||||
| PWP | 5 | ||||||||||||
| Ecuador | FC | ||||||||||||
| PWP | 1 | ||||||||||||
| Ethiopia | FC | ||||||||||||
| PWP | |||||||||||||
| Germany | FC | 10 | 1 | 5 | 1 | ||||||||
| PWP | 10 | 1 | 5 | 1 | |||||||||
| India | FC | 4 | |||||||||||
| PWP | 4 | ||||||||||||
| Indonesia | FC | 6 | |||||||||||
| PWP | 6 | 1 | |||||||||||
| Jamaica | FC | ||||||||||||
| PWP | 1 | ||||||||||||
| Jordan | FC | 1 | |||||||||||
| PWP | 1 | ||||||||||||
| Kenya | FC | 1 | 2 | ||||||||||
| PWP | 1 | 2 | |||||||||||
| Mozambique | FC | 1 | 1 | 1 | 1 | ||||||||
| PWP | 1 | 1 | 1 | 1 | |||||||||
| Poland | FC | ||||||||||||
| PWP | |||||||||||||
| Portugal | FC | 2 | 2 | 1 | |||||||||
| PWP | 2 | 2 | 1 | ||||||||||
| Puerto Rico | FC | ||||||||||||
| PWP | 1 | ||||||||||||
| Sierra Leone | FC | 1 | |||||||||||
| PWP | 1 | ||||||||||||
| South Africa | FC | 15 | 15 | 1 | 9 | 2 | 1 | 1 | 1 | 18 | 22 | ||
| PWP | 15 | 15 | 1 | 9 | 2 | 1 | 1 | 1 | 18 | 22 | |||
| Suriname | FC | ||||||||||||
| PWP | 2 | 9 | |||||||||||
| Sweden | FC | ||||||||||||
| PWP | |||||||||||||
| Thailand | FC | 1 | |||||||||||
| PWP | 1 | ||||||||||||
| UK | FC | ||||||||||||
| PWP | 1 | ||||||||||||
| Tanzania | FC | 1 | 2 | ||||||||||
| PWP | 1 | 2 | |||||||||||
| USA | FC | ||||||||||||
| PWP | |||||||||||||
| Zambia | FC | 4 | |||||||||||
| PWP | 4 | ||||||||||||
| Zimbabwe | FC | 2 | |||||||||||
| PWP | 2 | ||||||||||||
| Uncategorized | FC | 4 | |||||||||||
| PWP | 21 |
| Country | Target | Nitisols | Nitosols | Phaeozems | Planosols | Plinthosols | Podzols | Podzoluvisols | Regosols | Rendzinas | Solonetz | Vertisols | Xerosols | Yermosols |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Albania | FC | 1 | 1 | |||||||||||
| PWP | 1 | 1 | ||||||||||||
| Benin | FC | |||||||||||||
| PWP | ||||||||||||||
| Burkina Faso | FC | |||||||||||||
| PWP | ||||||||||||||
| Canada | FC | |||||||||||||
| PWP | ||||||||||||||
| Colombia | FC | |||||||||||||
| PWP | ||||||||||||||
| Ecuador | FC | |||||||||||||
| PWP | ||||||||||||||
| Ethiopia | FC | 2 | ||||||||||||
| PWP | 2 | |||||||||||||
| Germany | FC | 3 | ||||||||||||
| PWP | 3 | |||||||||||||
| India | FC | 4 | 4 | 1 | ||||||||||
| PWP | 4 | 4 | 1 | |||||||||||
| Indonesia | FC | |||||||||||||
| PWP | ||||||||||||||
| Jamaica | FC | |||||||||||||
| PWP | ||||||||||||||
| Jordan | FC | 2 | 1 | |||||||||||
| PWP | 2 | 1 | ||||||||||||
| Kenya | FC | |||||||||||||
| PWP | ||||||||||||||
| Mozambique | FC | |||||||||||||
| PWP | ||||||||||||||
| Poland | FC | |||||||||||||
| PWP | 1 | |||||||||||||
| Portugal | FC | |||||||||||||
| PWP | ||||||||||||||
| Puerto Rico | FC | |||||||||||||
| PWP | ||||||||||||||
| Sierra Leone | FC | |||||||||||||
| PWP | ||||||||||||||
| South Africa | FC | 6 | 1 | 7 | 2 | 9 | 6 | 2 | ||||||
| PWP | 6 | 1 | 7 | 2 | 9 | 6 | 2 | |||||||
| Suriname | FC | |||||||||||||
| PWP | 5 | |||||||||||||
| Sweden | FC | 1 | ||||||||||||
| PWP | 1 | |||||||||||||
| Thailand | FC | |||||||||||||
| PWP | ||||||||||||||
| UK | FC | |||||||||||||
| PWP | ||||||||||||||
| Tanzania | FC | 1 | ||||||||||||
| PWP | 1 | |||||||||||||
| USA | FC | 3 | ||||||||||||
| PWP | 4 | |||||||||||||
| Zambia | FC | 1 | ||||||||||||
| PWP | 1 | |||||||||||||
| Zimbabwe | FC | |||||||||||||
| PWP |

Appendix B. Used Parameters of Each Factor of Published PTFs
| PTFs | Target | Soil | Silt | Clay | Organic Matters | Sa × OM | C × OM | Sa × C | Si × C | 1/(OM + 1) | Si × OM’ | C × OM’ | Constant |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sa | Si | C | OM | OM’ | |||||||||
| Saxton and Rawls | FC’ | −0.251 | 0.195 | 0.011 | 0.006 | −0.027 | 0.452 | 0.299 | |||||
| FC | FC’ + (1.283(FC’)2 − 0.374(FC’) − 0.015) | ||||||||||||
| Adhikary et al. | FC | −0.51 | −0.27 | 56.37 | |||||||||
| Tóth et al. | FC | 0.00154 | 0.00453 | −0.000511 | −0.1887 | 0.00144 | 0.00087 | 0.2449 | |||||
| Saxton and Rawls | PWP’ | −0.024 | 0.487 | 0.006 | 0.005 | −0.013 | 0.068 | 0.031 | |||||
| PWP | PWP’ + (0.14(PWP’) − 0.02) | ||||||||||||
| Adhikary et al. | PWP | 0.44000 | 0.71 | ||||||||||
| Tóth et al. | PWP | −0.00084 | 0.00213 | 0.000385 | −0.0767 | 0.00095 | 0.00233 | 0.09878 | |||||
Appendix C. Model Performance and Comparisons
| Target | Model | Data | R2 | RMSE | NRMSE | MAE | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Training | CV | Testing | Training | CV | Testing | Training | CV | Testing | Training | CV | Testing | Training | CV | Testing | ||
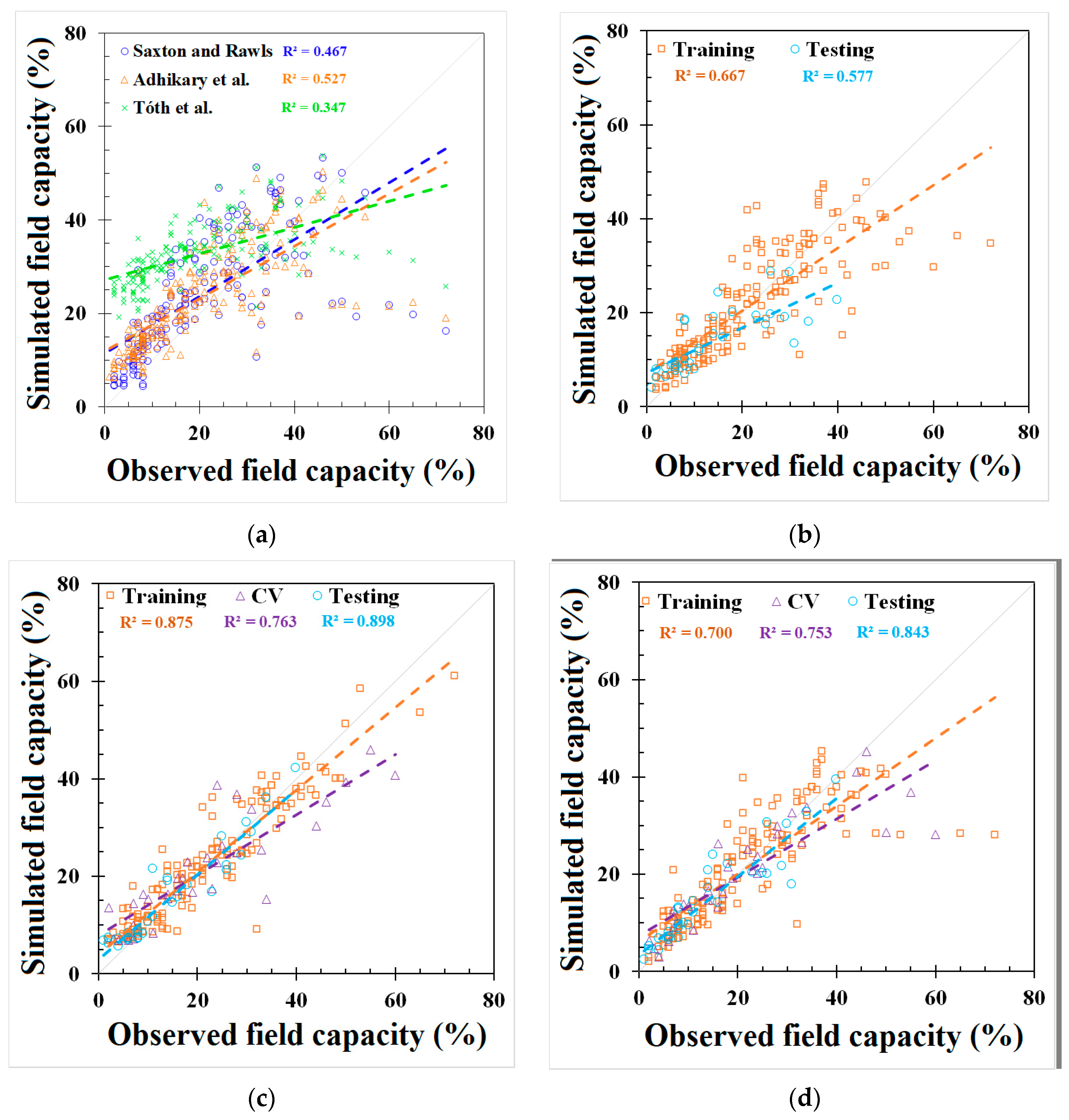
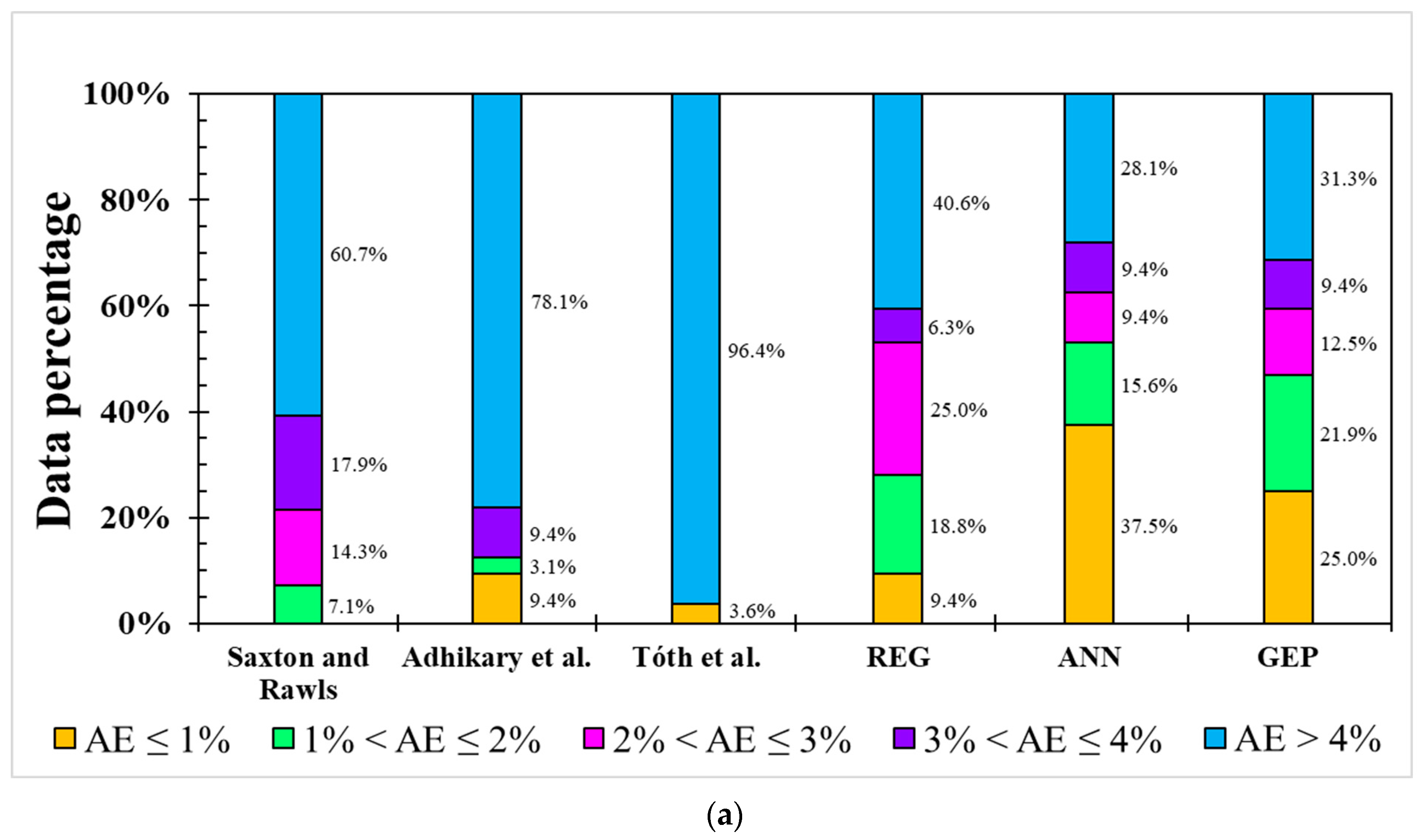
| FC | Saxton and Rawls | Total: 179 | Total: 0.467 | Total: 11.254 | Total: 55.6% | Total: 8.120 | ||||||||||
| Adhikary et al. | Total: 210 | Total: 0.527 | Total: 9.969 | Total: 49.2% | Total: 7.369 | |||||||||||
| Tóth et al. | Total: 179 | Total: 0.347 | Total: 17.225 | Total: 85.0% | Total: 15.575 | |||||||||||
| REG | 178 | - | 32 | 0.667 | - | 0.577 | 8.200 | - | 7.053 | 38.5% | - | 49.2% | 5.438 | - | 5.005 | |
| ANN | 146 | 32 | 32 | 0.875 | 0.763 | 0.898 | 4.910 | 8.013 | 4.574 | 23.2% | 36.3% | 31.9% | 3.683 | 6.022 | 3.133 | |
| GEP | 146 | 32 | 32 | 0.700 | 0.753 | 0.843 | 7.487 | 8.337 | 4.290 | 35.4% | 37.7% | 29.9% | 4.628 | 4.672 | 3.115 | |
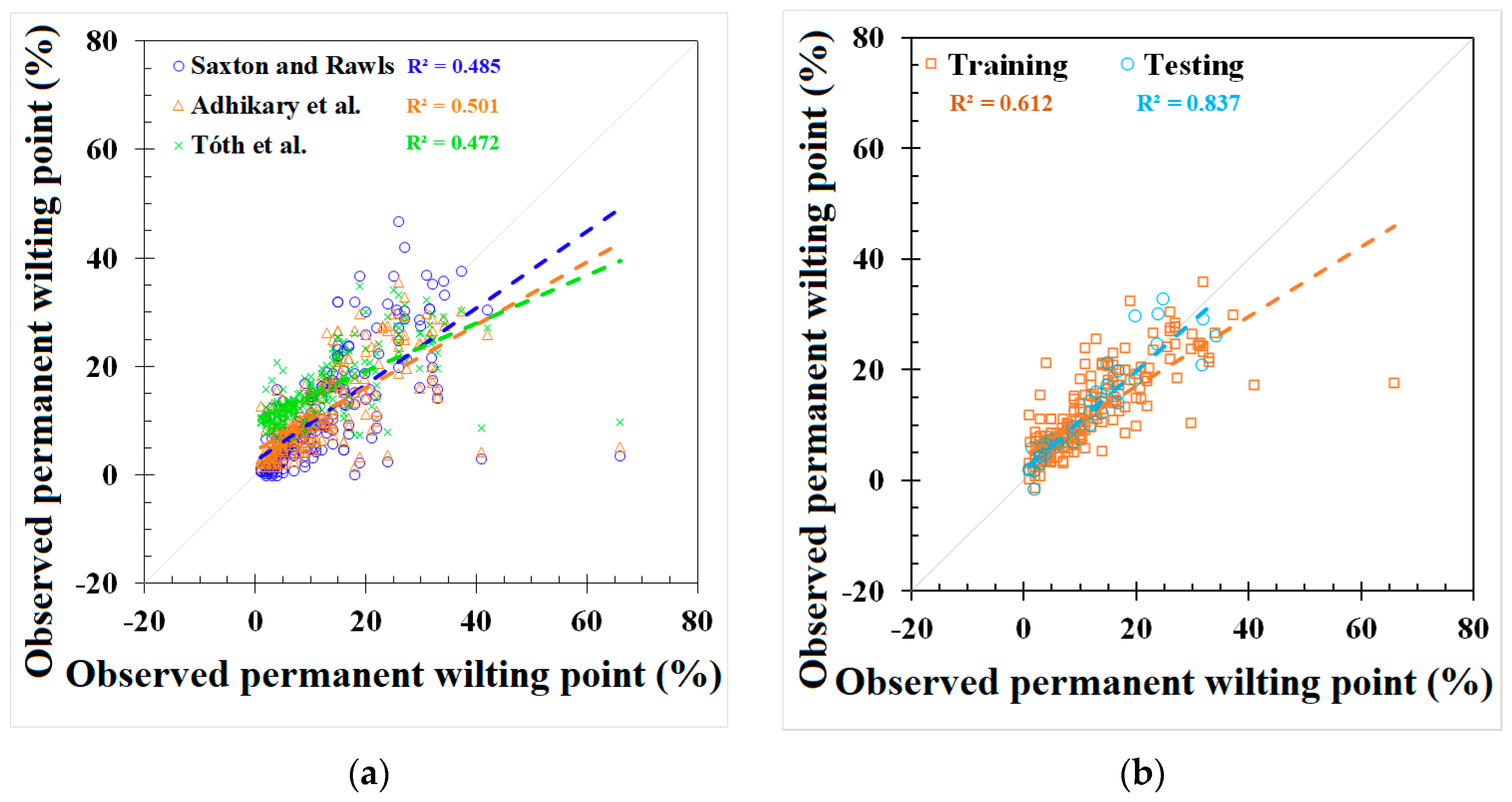
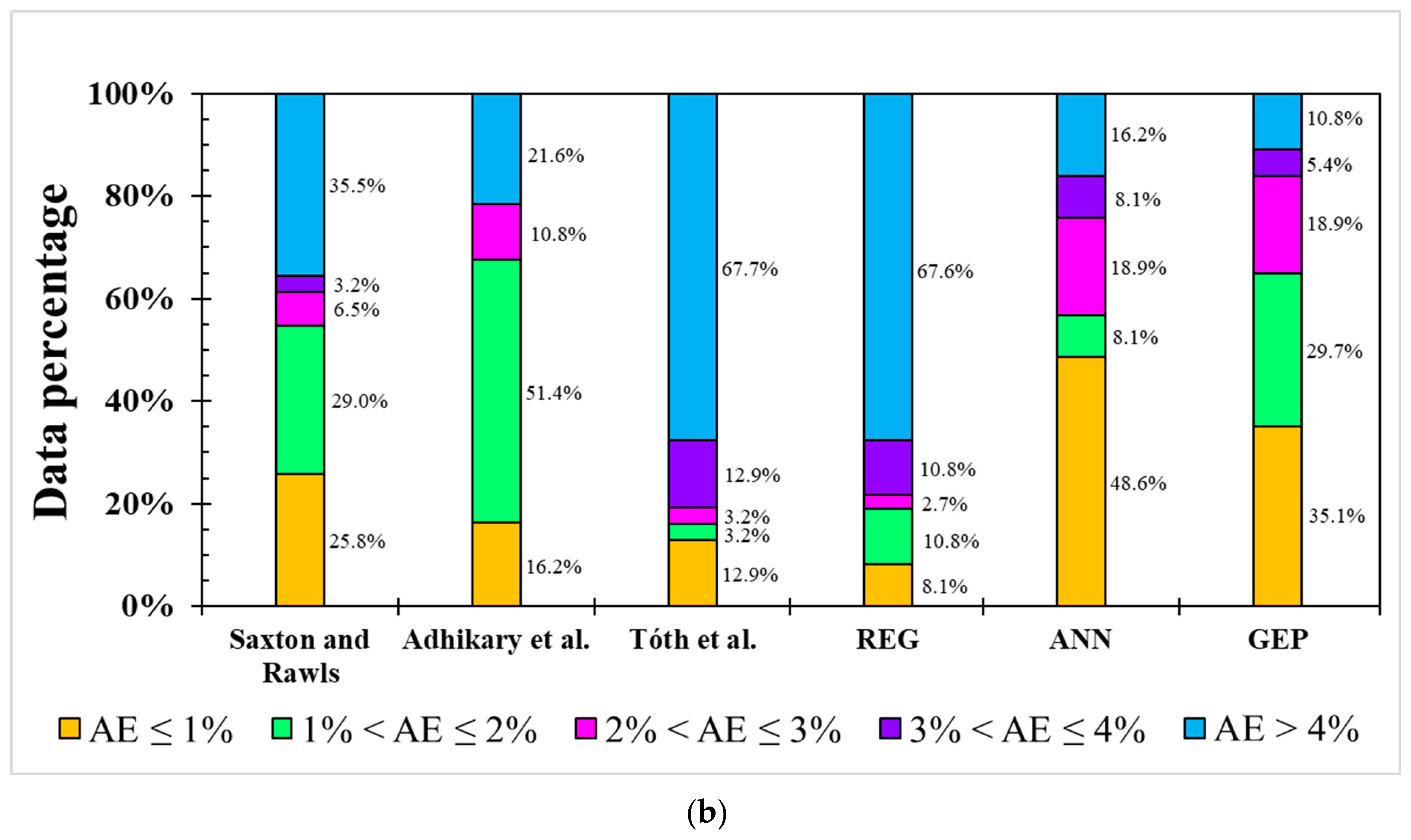
| PWP | Saxton and Rawls | Total: 221 | Total: 0.485 | Total: 18.918 | Total: 157.5% | Total: 14.392 | ||||||||||
| Adhikary et al. | Total: 254 | Total: 0.501 | Total: 17.699 | Total: 147.3% | Total: 13.494 | |||||||||||
| Tóth et al. | Total: 221 | Total: 0.472 | Total: 16.244 | Total: 135.2% | Total: 12.705 | |||||||||||
| REG | 217 | - | 37 | 0.612 | - | 0.837 | 5.836 | - | 8.475 | 49.8% | - | 69.0% | 3.531 | - | 6.122 | |
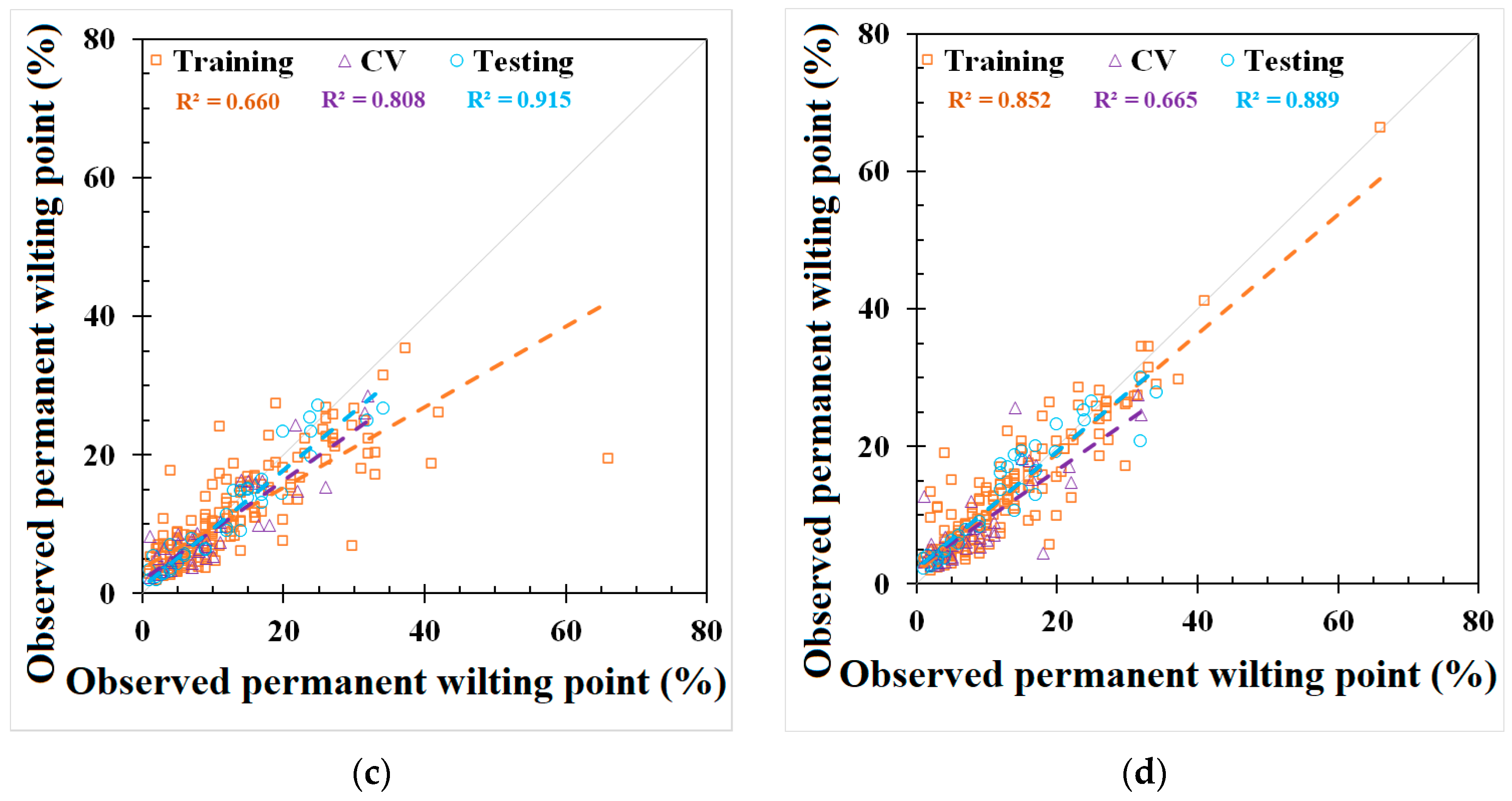
| ANN | 180 | 37 | 37 | 0.660 | 0.808 | 0.915 | 6.031 | 3.774 | 2.442 | 49.1% | 36.9% | 19.9% | 3.514 | 2.778 | 1.758 | |
| GEP | 180 | 37 | 37 | 0.852 | 0.665 | 0.889 | 3.723 | 4.551 | 2.746 | 30.8% | 46.5% | 22.3% | 2.542 | 3.083 | 2.000 | |
Appendix D. Python-Based FCGEP and PWPGEP Models
- Python-based FCGEP model
- # This model was implemented using Python 3.8. Ensure compatibility with this version.
- # Considering potential future updates to Python that may lead to compatibility issues with certain modules, the authors recommend that future users assess compatibility with the following sections when using different versions of Python.
- From math import *
- def fieldCapacity(d):
- 2.
- Python-based PWPGEP model
- # This model was implemented using Python 3.8. Ensure compatibility with this version.
- # Considering potential future updates to Python that may lead to compatibility issues with certain modules, the authors recommend that future users assess compatibility with the following sections when using different versions of Python.
- From math import *
- def permanentWiltingPoint(d):
- def gep5Rt(x):
References
- Brady, N.C.; Weil, R.R.; Weil, R.R. The Nature and Properties of Soils; Prentice Hall: Upper Saddle River, NJ, USA, 2008; Volume 13. [Google Scholar]
- Assi, A.T.; Blake, J.; Mohtar, R.H.; Braudeau, E. Soil aggregates structure-based approach for quantifying the field capacity, permanent wilting point and available water capacity. Irrig. Sci. 2019, 37, 511–522. [Google Scholar] [CrossRef]
- Hoogenboom, G.; Porter, C.; Shelia, V.; Boote, K.; Singh, U.; White, J.; Hunt, L.; Ogoshi, R.; Lizaso, J.; Koo, J. Decision Support System for Agrotechnology Transfer (DSSAT); Version 4.7; DSSAT Foundation: Gainesville, FL, USA, 2017; Available online: https://DSSAT.net (accessed on 1 March 2023).
- Pentoś, K.; Pieczarka, K.; Serwata, K. The Relationship between Soil Electrical Parameters and Compaction of Sandy Clay Loam Soil. Agriculture 2021, 11, 114. [Google Scholar] [CrossRef]
- Mohanty, B.; Gaur, N. Near Surface Soil Moisture Controls Beyond the Darcy Support Scale: A Remote Sensing Perspective. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 15–19 December 2014; p. H13D-1135. [Google Scholar]
- Tunçay, T.; Başkan, O.; Bayramın, I.; Dengız, O.; Kılıç, Ş. Geostatistical approach as a tool for estimation of field capacity and permanent wilting point in semi-arid terrestrial ecosystem. Arch. Agron. Soil Sci. 2018, 64, 1240–1253. [Google Scholar] [CrossRef]
- Jian, J.; Du, X.; Stewart, R.D. A database for global soil health assessment. Sci. Data 2020, 7, 16. [Google Scholar] [CrossRef]
- McBratney, A.B.; Santos, M.M.; Minasny, B. On digital soil mapping. Geoderma 2003, 117, 3–52. [Google Scholar] [CrossRef]
- Santra, P.; Kumar, M.; Kumawat, R.; Painuli, D.; Hati, K.; Heuvelink, G.; Batjes, N. Pedotransfer functions to estimate soil water content at field capacity and permanent wilting point in hot Arid Western India. J. Earth Syst. Sci. 2018, 127, 35. [Google Scholar] [CrossRef]
- Morgan, C.L. Assessing Soil Health: Soil Water Cycling. Crops Soils 2020, 53, 35–41. [Google Scholar] [CrossRef]
- Nourbakhsh, F.; Afyuni, M.; Abbaspour, K.C.; Schulin, R. Research note: Estimation of field capacity and wilting point from basic soil physical and chemical properties. Arid Land Res. Manag. 2004, 19, 81–85. [Google Scholar] [CrossRef]
- Taşan, S.; Demir, Y. Comparative Analysis of MLR, ANN, and ANFIS Models for Prediction of Field Capacity and Permanent Wilting Point for Bafra Plain Soils. Commun. Soil Sci. Plant Anal. 2020, 51, 604–621. [Google Scholar] [CrossRef]
- Jin, X.; Wang, S.; Yu, N.; Zou, H.; An, J.; Zhang, Y.; Wang, J.; Zhang, Y. Spatial predictions of the permanent wilting point in arid and semi-arid regions of Northeast China. J. Hydrol. 2018, 564, 367–375. [Google Scholar] [CrossRef]
- Cueff, S.; Coquet, Y.; Aubertot, J.-N.; Bel, L.; Pot, V.; Alletto, L. Estimation of soil water retention in conservation agriculture using published and new pedotransfer functions. Soil Tillage Res. 2021, 209, 104967. [Google Scholar] [CrossRef]
- Rotnitzky, A.; Wypij, D. A note on the bias of estimators with missing data. Biometrics 1994, 50, 1163–1170. [Google Scholar] [CrossRef]
- Tóth, B.; Weynants, M.; Nemes, A.; Makó, A.; Bilas, G.; Tóth, G. New generation of hydraulic pedotransfer functions for Europe. Eur. J. Soil Sci. 2015, 66, 226–238. [Google Scholar] [CrossRef]
- Tunçay, T.; Kılıç, Ş.; Dedeoğlu, M.; Dengiz, O.; Başkan, O.; Bayramin, İ. Assessing soil fertility index based on remote sensing and gis techniques with field validation in a semiarid agricultural ecosystem. J. Arid Environ. 2021, 190, 104525. [Google Scholar] [CrossRef]
- Keshavarzi, R.; Mohammadi, S. A new approach for numerical modeling of hydraulic fracture propagation in naturally fractured reservoirs. In Proceedings of the SPE/EAGE European Unconventional Resources Conference and Exhibition—From Potential to Production, Vienna, Austria, 20–22 March 2012; p. cp-285-00039. [Google Scholar]
- Mohanty, M.; Sinha, N.K.; Painuli, D.; Bandyopadhyay, K.; Hati, K.; Reddy, K.S.; Chaudhary, R. Modelling soil water contents at field capacity and permanent wilting point using artificial neural network for Indian soils. Natl. Acad. Sci. Lett. 2015, 38, 373–377. [Google Scholar] [CrossRef]
- Shiri, J.; Keshavarzi, A.; Kisi, O.; Karimi, S. Using soil easily measured parameters for estimating soil water capacity: Soft computing approaches. Comput. Electron. Agric. 2017, 141, 327–339. [Google Scholar] [CrossRef]
- Gunarathna, M.; Sakai, K.; Nakandakari, T.; Momii, K.; Kumari, M.; Amarasekara, M. Pedotransfer functions to estimate hydraulic properties of tropical Sri Lankan soils. Soil Tillage Res. 2019, 190, 109–119. [Google Scholar] [CrossRef]
- Ghorbani, M.A.; Shamshirband, S.; Haghi, D.Z.; Azani, A.; Bonakdari, H.; Ebtehaj, I. Application of firefly algorithm-based support vector machines for prediction of field capacity and permanent wilting point. Soil Tillage Res. 2017, 172, 32–38. [Google Scholar] [CrossRef]
- Yamaç, S.S.; Şeker, C.; Negiş, H. Evaluation of machine learning methods to predict soil moisture constants with different combinations of soil input data for calcareous soils in a semi arid area. Agric. Water Manag. 2020, 234, 106121. [Google Scholar] [CrossRef]
- Hateffard, F.; Dolati, P.; Heidari, A.; Zolfaghari, A.A. Assessing the performance of decision tree and neural network models in mapping soil properties. J. Mt. Sci. 2019, 16, 1833–1847. [Google Scholar] [CrossRef]
- McCutcheon, M.; Farahani, H.; Stednick, J.; Buchleiter, G.; Green, T. Effect of soil water on apparent soil electrical conductivity and texture relationships in a dryland field. Biosyst. Eng. 2006, 94, 19–32. [Google Scholar] [CrossRef]
- Frost, P.S.; van Es, H.M.; Rossiter, D.G.; Hobbs, P.R.; Pingali, P.L. Soil health characterization in smallholder agricultural catchments in India. Appl. Soil Ecol. 2019, 138, 171–180. [Google Scholar] [CrossRef]
- Corwin, D.L.; Lesch, S.M. Apparent soil electrical conductivity measurements in agriculture. Comput. Electron. Agric. 2005, 46, 11–43. [Google Scholar] [CrossRef]
- Allen, D.E.; Singh, B.P.; Dalal, R.C. Soil health indicators under climate change: A review of current knowledge. In Soil Health and Climate Change; Springer: Berlin/Heidelberg, Germany, 2011; pp. 25–45. [Google Scholar]
- Sinha, S.K.; Wang, M.C. Artificial Neural Network Prediction Models for Soil Compaction and Permeability. Geotech. Geol. Eng. 2008, 26, 47–64. [Google Scholar] [CrossRef]
- Besalatpour, A.; Hajabbasi, M.; Ayoubi, S.; Afyuni, M.; Jalalian, A.; Schulin, R. Soil shear strength prediction using intelligent systems: Artificial neural networks and an adaptive neuro-fuzzy inference system. Soil Sci. Plant Nutr. 2012, 58, 149–160. [Google Scholar] [CrossRef]
- Pham, V.-N.; Oh, E.; Ong, D.E.L. Effects of binder types and other significant variables on the unconfined compressive strength of chemical-stabilized clayey soil using gene-expression programming. Neural Comput. Appl. 2022, 34, 9103–9121. [Google Scholar] [CrossRef]
- Batjes, N.H.; Ribeiro, E.; van Oostrum, A. Standardised soil profile data to support global mapping and modelling (WoSIS snapshot 2019). Earth Syst. Sci. Data 2020, 12, 299–320. [Google Scholar] [CrossRef]
- Batjes, N.H.; Ribeiro, E.; van Oostrum, A.; Leenaars, J.; Hengl, T.; Mendes de Jesus, J. WoSIS: Providing standardised soil profile data for the world. Earth Syst. Sci. Data 2017, 9, 1–14. [Google Scholar] [CrossRef]
- Ribeiro, E.; Batjes, N.; Van Oostrum, A.J.M. World Soil Information Service (WoSIS)—Towards the Standardization and Harmonization of World Soil Data; ISRIC, World Soil Information: Wageningen, The Netherlands, 2018; Volume 166. [Google Scholar]
- Saxton, K.E.; Rawls, W.J. Soil water characteristic estimates by texture and organic matter for hydrologic solutions. Soil Sci. Soc. Am. J. 2006, 70, 1569–1578. [Google Scholar] [CrossRef]
- Adhikary, P.P.; Chakraborty, D.; Kalra, N.; Sachdev, C.; Patra, A.; Kumar, S.; Tomar, R.; Chandna, P.; Raghav, D.; Agrawal, K. Pedotransfer functions for predicting the hydraulic properties of Indian soils. Soil Res. 2008, 46, 476–484. [Google Scholar] [CrossRef]
- Liu, L.-W.; Hsieh, S.-H.; Lin, S.-J.; Wang, Y.-M.; Lin, W.-S. Rice Blast (Magnaporthe oryzae) Occurrence Prediction and the Key Factor Sensitivity Analysis by Machine Learning. Agronomy 2021, 11, 771. [Google Scholar] [CrossRef]
- Hsieh, S.-H.; Liu, L.-W.; Chung, W.-G.; Wang, Y.-M. Sensitivity analysis on the rising relation between short-term rainfall and groundwater table adjacent to an artificial recharge lake. Water 2019, 11, 1704. [Google Scholar] [CrossRef]
- Ferreira, C. Gene expression programming in problem solving. In Soft Computing and Industry; Springer: London, UK, 2002; pp. 635–653. [Google Scholar]
- Liu, L.-W.; Wang, Y.-M. Modelling reservoir turbidity using Landsat 8 satellite imagery by gene expression programming. Water 2019, 11, 1479. [Google Scholar] [CrossRef]
- Wang, X.; Liu, L.; Zhang, W.; Ma, X. Prediction of Plant Uptake and Translocation of Engineered Metallic Nanoparticles by Machine Learning. Environ. Sci. Technol. 2021, 55, 7491–7500. [Google Scholar] [CrossRef]
- Lee, C.-H.; Liu, L.-W.; Wang, Y.-M.; Leu, J.-M.; Chen, C.-L. Drone-Based Bathymetry Modeling for Mountainous Shallow Rivers in Taiwan Using Machine Learning. Remote Sens. 2022, 14, 3343. [Google Scholar] [CrossRef]
- Ferreira, C. Gene Expression Programming: Mathematical Modeling by an Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2006; Volume 21. [Google Scholar]
- Liu, L. Drone-based photogrammetry for riverbed characteristics extraction and flood discharge modeling in Taiwan’s mountainous rivers. Measurement 2023, 220, 113386. [Google Scholar] [CrossRef]
- Faloye, O.T.; Ajayi, A.E.; Ajiboye, Y.; Alatise, M.O.; Ewulo, B.S.; Adeosun, S.S.; Babalola, T.; Horn, R. Unsaturated Hydraulic Conductivity Prediction Using Artificial Intelligence and Multiple Linear Regression Models in Biochar Amended Sandy Clay Loam Soil. J. Soil Sci. Plant Nutr. 2022, 22, 1589–1603. [Google Scholar] [CrossRef]
- Lee, C.-H.; Hsu, M.-K.; Wang, Y.-M.; Leu, J.-M.; Chen, C.-L.; Liu, L. Evaluating gradient descent variations for artificial neural network bathymetry modeling and sensitivity analysis. J. Appl. Remote Sens. 2024, 18, 022204. [Google Scholar] [CrossRef]
- Jamieson, P.D.; Porter, J.R.; Wilson, D.R. A test of the computer simulation model ARCWHEAT1 on wheat crops grown in New Zealand. Field Crops Res. 1991, 27, 337–350. [Google Scholar] [CrossRef]
- Moral, F.J.; Serrano, J.M. Using low-cost geophysical survey to map soil properties and delineate management zones on grazed permanent pastures. Precis. Agric. 2019, 20, 1000–1014. [Google Scholar] [CrossRef]
- Nocco, M.A.; Ruark, M.D.; Kucharik, C.J. Apparent electrical conductivity predicts physical properties of coarse soils. Geoderma 2019, 335, 1–11. [Google Scholar] [CrossRef]
- Carter, M.R.; Gregorich, E.G. Soil Sampling and Methods of Analysis; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Topp, G.C.; Davis, J.L.; Annan, A.P. Electromagnetic determination of soil water content: Measurements in coaxial transmission lines. Water Resour. Res. 1980, 16, 574–582. [Google Scholar] [CrossRef]
- Ratcliffe, R.G.; Rengel, Z. (Eds.) Handbook of plant growth. pH as the master variable. Ann. Bot. 2003, 92, 165–166. [Google Scholar] [CrossRef]
- Tang, C.; Rengel, Z. Handbook of Soil Acidity; Marcel Dekker: New York, NY, USA, 2003; pp. 57–81. [Google Scholar]
- Liu, L.-W.; Ismail, M.H.; Wang, Y.-M.; Lin, W.-S. Internet of Things based Smart Irrigation Control System for Paddy Field. AGRIVITA J. Agric. Sci. 2021, 43, 378–389. [Google Scholar] [CrossRef]
| Target | Parameter | Input | Output | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Clay | Sand | Silt | Longitude | Latitude | Altitude | pH | EC | FC or PWP | ||
| % | % | % | Decimal | Decimal | m | - | ds/m | % | ||
| FC (n = 210) | μ | 24.314 | 53.401 | 21.405 | 23.519 | −5.726 | 834.962 | 7.345 | 3.425 | 20.257 |
| σ | 17.276 | 27.241 | 17.058 | 38.883 | 29.995 | 569.649 | 1.337 | 7.117 | 13.736 | |
| Max. | 79.000 | 98.000 | 78.000 | 116.721 | 69.433 | 2604.000 | 10.400 | 50.500 | 72.000 | |
| Min. | 2.000 | 1.000 | 0.000 | −154.850 | −33.821 | −2.000 | 3.500 | 0.000 | 1.000 | |
| r | 0.618 | −0.755 | 0.603 | −0.180 | 0.623 | −0.240 | −0.093 | −0.007 | - | |
| PWP (n = 254) | μ | 24.348 | 53.361 | 21.536 | 15.843 | −3.078 | 803.590 | 7.191 | 3.120 | 11.937 |
| σ | 17.831 | 27.677 | 16.770 | 45.224 | 28.847 | 597.034 | 1.431 | 6.728 | 9.485 | |
| Max. | 79.000 | 98.000 | 78.000 | 116.721 | 69.433 | 2604.000 | 10.400 | 50.500 | 66.000 | |
| Min. | 2.000 | 1.000 | 0.000 | −154.850 | −33.821 | −2.000 | 3.500 | 0.000 | 1.000 | |
| r | 0.706 | −0.701 | 0.424 | −0.187 | 0.410 | −0.003 | 0.048 | 0.042 | - | |
| Target | Combination | Training | CV | Testing | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | NRMSE | MAE | R2 | RMSE | NRMSE | MAE | R2 | RMSE | NRMSE | MAE | ||
| FC | L | 0.655 | 8.063 | 38.1% | 6.338 | 0.707 | 9.908 | 44.8% | 8.187 | 0.259 | 9.530 | 66.4% | 8.019 |
| S | 0.739 | 6.986 | 33.0% | 4.979 | 0.722 | 9.164 | 41.5% | 6.683 | 0.596 | 6.700 | 46.7% | 5.178 | |
| PH | 0.016 | 13.787 | 65.2% | 11.088 | 0.036 | 15.511 | 70.2% | 11.964 | 0.013 | 11.666 | 81.3% | 10.662 | |
| EC | 0.002 | 13.616 | 64.4% | 11.146 | 0.013 | 15.406 | 69.7% | 12.149 | 0.058 | 12.298 | 85.7% | 11.254 | |
| L + S | 0.722 | 7.601 | 35.9% | 5.115 | 0.777 | 9.008 | 40.8% | 5.742 | 0.716 | 6.186 | 43.1% | 4.578 | |
| PH + EC | 0.024 | 13.501 | 63.8% | 10.931 | 0.054 | 15.748 | 71.3% | 12.468 | 0.002 | 11.829 | 82.5% | 10.891 | |
| L + PH | 0.747 | 6.925 | 32.7% | 5.409 | 0.714 | 8.856 | 40.1% | 7.070 | 0.279 | 11.271 | 78.6% | 9.219 | |
| L + EC | 0.670 | 7.900 | 37.4% | 6.254 | 0.613 | 10.220 | 46.3% | 8.464 | 0.257 | 9.902 | 69.0% | 8.328 | |
| L + PH + EC | 0.598 | 8.851 | 41.8% | 7.280 | 0.707 | 10.223 | 46.3% | 7.749 | 0.386 | 8.877 | 61.9% | 7.457 | |
| S + PH | 0.775 | 6.511 | 30.8% | 4.808 | 0.722 | 8.875 | 40.2% | 6.888 | 0.575 | 7.062 | 49.2% | 5.586 | |
| S + EC | 0.750 | 6.819 | 32.2% | 5.165 | 0.696 | 8.823 | 39.9% | 6.316 | 0.575 | 7.036 | 49.1% | 4.574 | |
| S + PH + EC | 0.807 | 5.996 | 28.3% | 4.489 | 0.696 | 8.928 | 40.4% | 6.389 | 0.712 | 5.754 | 40.1% | 4.137 | |
| L + S + PH | 0.727 | 7.403 | 35.0% | 4.936 | 0.762 | 8.502 | 38.5% | 5.186 | 0.752 | 5.705 | 39.8% | 4.495 | |
| L + S + EC | 0.875 | 4.910 | 23.2% | 3.683 | 0.763 | 8.013 | 36.3% | 6.022 | 0.898 | 4.574 | 31.9% | 3.133 | |
| L + S + PH + EC | 0.791 | 6.637 | 31.4% | 4.598 | 0.698 | 9.554 | 43.2% | 5.689 | 0.819 | 4.801 | 33.5% | 3.647 | |
| PWP | L | 0.151 | 9.154 | 74.6% | 6.665 | 0.415 | 6.367 | 62.3% | 4.887 | 0.398 | 7.781 | 64.4% | 6.135 |
| S | 0.514 | 6.877 | 56.0% | 3.994 | 0.654 | 4.773 | 46.7% | 3.742 | 0.790 | 4.327 | 35.8% | 3.235 | |
| PH | 0.000 | 9.959 | 81.2% | 7.194 | 0.015 | 8.055 | 78.8% | 6.425 | 0.031 | 9.503 | 78.7% | 7.787 | |
| EC | 0.006 | 9.957 | 81.1% | 7.137 | 0.024 | 7.936 | 77.6% | 6.304 | 0.070 | 9.845 | 81.5% | 8.041 | |
| L + S | 0.639 | 5.939 | 48.4% | 3.686 | 0.727 | 4.205 | 41.1% | 3.195 | 0.834 | 3.840 | 31.8% | 2.777 | |
| PH + EC | 0.007 | 9.904 | 80.7% | 7.174 | 0.009 | 8.002 | 78.3% | 6.411 | 0.087 | 9.855 | 81.6% | 8.062 | |
| L + PH | 0.419 | 7.651 | 62.4% | 5.649 | 0.473 | 5.962 | 58.3% | 4.330 | 0.425 | 7.372 | 61.0% | 6.125 | |
| L + EC | 0.537 | 6.941 | 56.6% | 5.006 | 0.503 | 5.924 | 58.0% | 4.458 | 0.382 | 7.719 | 63.9% | 6.023 | |
| L + PH + EC | 0.487 | 7.248 | 59.1% | 5.325 | 0.557 | 5.657 | 55.3% | 4.386 | 0.370 | 7.857 | 65.1% | 6.457 | |
| S + PH | 0.723 | 5.208 | 42.4% | 3.520 | 0.697 | 4.502 | 44.0% | 3.398 | 0.777 | 4.578 | 37.9% | 3.384 | |
| S + EC | 0.535 | 6.721 | 54.8% | 3.872 | 0.672 | 4.632 | 45.3% | 3.575 | 0.785 | 4.400 | 36.4% | 3.148 | |
| S + PH + EC | 0.596 | 6.310 | 51.4% | 3.594 | 0.723 | 4.247 | 41.5% | 3.049 | 0.813 | 4.188 | 34.7% | 2.949 | |
| L + S + PH | 0.655 | 5.882 | 47.9% | 3.555 | 0.784 | 3.894 | 38.1% | 3.059 | 0.872 | 3.405 | 28.2% | 2.508 | |
| L + S + EC | 0.662 | 4.910 | 40.0% | 3.502 | 0.798 | 4.230 | 41.4% | 2.890 | 0.877 | 3.578 | 29.6% | 2.366 | |
| L + S + PH + EC | 0.660 | 6.031 | 49.1% | 3.514 | 0.808 | 3.774 | 36.9% | 2.778 | 0.915 | 2.442 | 19.9% | 1.758 | |
| Target | Model | Input Variables | Testing Dataset | R2 | RMSE | NRMSE | MAE |
|---|---|---|---|---|---|---|---|
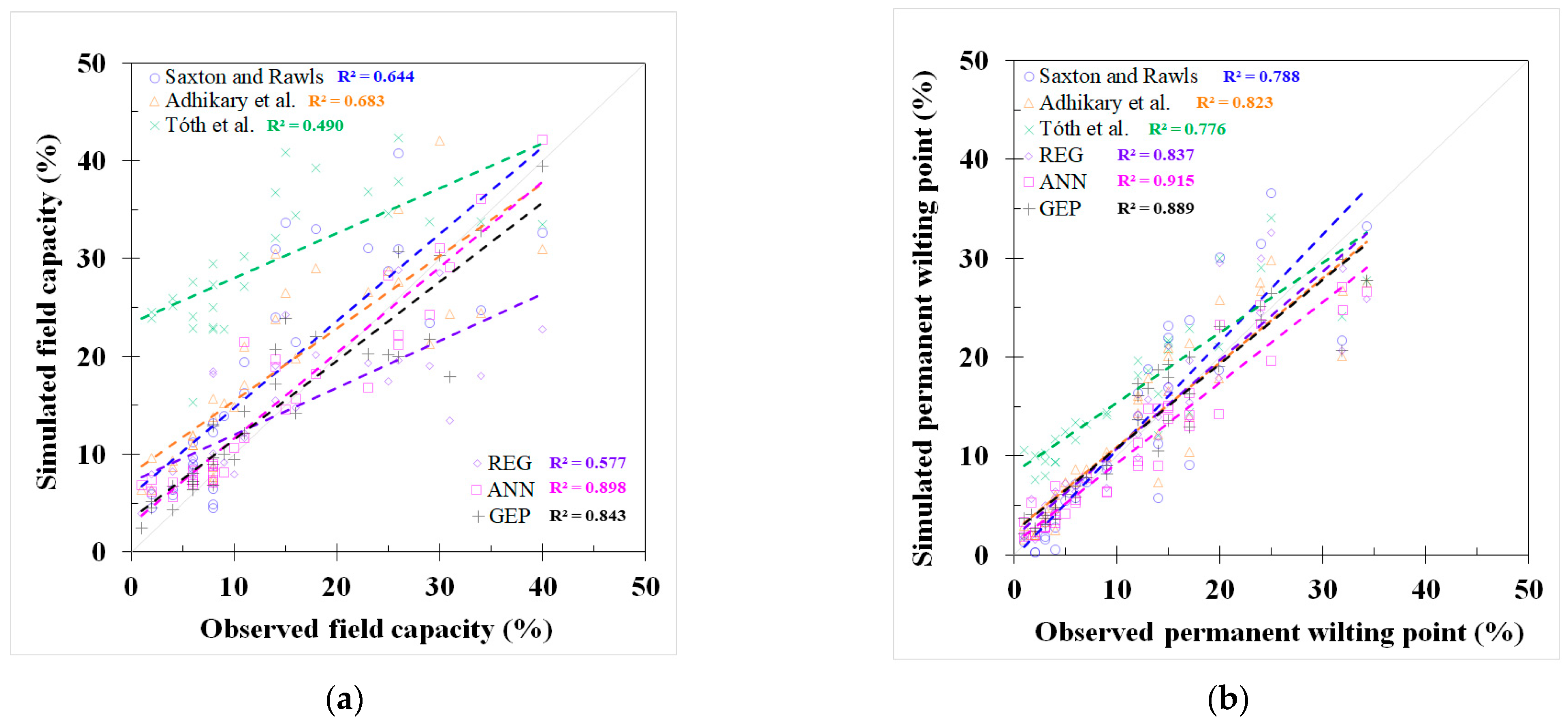
| FC | Saxton and Rawls | Sa, C, OM | 28 | 0.644 | 8.077 | 56.3% | 6.467 |
| Adhikary et al. | Sa, Si | 32 | 0.683 | 7.482 | 52.2% | 6.465 | |
| Tóth et al. | Si, C, OM | 28 | 0.490 | 17.766 | 123.9% | 16.405 | |
| REG | L, Sa, Si, C, EC | 32 | 0.577 | 7.053 | 49.2% | 5.005 | |
| ANN | L, Sa, Si, C, EC | 32 | 0.898 | 4.574 | 31.9% | 3.133 | |
| GEP | L, Sa, Si, C, EC | 32 | 0.843 | 4.290 | 29.9% | 3.115 | |
| PWP | Saxton and Rawls | Sa, C, OM | 31 | 0.788 | 5.107 | 41.6% | 3.567 |
| Adhikary et al. | C | 37 | 0.823 | 7.646 | 62.2% | 4.031 | |
| Tóth et al. | Si, C, OM | 31 | 0.776 | 4.632 | 37.7% | 4.144 | |
| REG | L, Sa, Si, C, EC, pH | 37 | 0.837 | 8.475 | 69.0% | 6.122 | |
| ANN | L, Sa, Si, C, EC, pH | 37 | 0.915 | 2.442 | 19.9% | 1.758 | |
| GEP | L, Sa, Si, C, EC, pH | 37 | 0.889 | 2.746 | 22.3% | 2.000 |
| Variable | Field Capacity | Permanent Wilting Point | ||
|---|---|---|---|---|
| p-Value | Significance | p-Value | Significance | |
| Altitude | 0.704 | 0.012 | * | |
| Sand | 0.017 | * | 0.331 | |
| Silt | 0.042 | * | 0.099 | |
| Clay | 0.042 | * | 0.331 | |
| EC | 0.545 | 0.039 | * | |
| pH | - | 0.415 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Ma, X. Prediction of Soil Field Capacity and Permanent Wilting Point Using Accessible Parameters by Machine Learning. AgriEngineering 2024, 6, 2592-2611. https://doi.org/10.3390/agriengineering6030151
Liu L, Ma X. Prediction of Soil Field Capacity and Permanent Wilting Point Using Accessible Parameters by Machine Learning. AgriEngineering. 2024; 6(3):2592-2611. https://doi.org/10.3390/agriengineering6030151
Chicago/Turabian StyleLiu, Liwei, and Xingmao Ma. 2024. "Prediction of Soil Field Capacity and Permanent Wilting Point Using Accessible Parameters by Machine Learning" AgriEngineering 6, no. 3: 2592-2611. https://doi.org/10.3390/agriengineering6030151
APA StyleLiu, L., & Ma, X. (2024). Prediction of Soil Field Capacity and Permanent Wilting Point Using Accessible Parameters by Machine Learning. AgriEngineering, 6(3), 2592-2611. https://doi.org/10.3390/agriengineering6030151












