Autonomous Driving Strategy for a Specialized Four-Wheel Differential-Drive Agricultural Rover
Abstract
1. Introduction
2. Materials and Methods
2.1. Vehicle Kinematic Model
- The vehicle consists of a rigid body; thus, all the effects related to its deformability can be ignored.
- The algorithm was developed considering a 2-D operative environment since the rover belongs to the category of land vehicles; hence, vertical movement is neglectable.
- The 2-D environment implies that the state of the vehicle is fully defined with three degrees of freedom: two translational (longitudinal and lateral movements), and one rotational (yaw) around the axis perpendicular to the movement plane.
- The 2-D environment also implies that the rolling and pitch angles can be ignored.
- The wheel–ground contact is in a condition of pure rolling.
- Lateral slip can be ignored because the rover working speed is quite low; thus, almost all the effects related to vehicle dynamics are neglectable.
- and are the angular velocities of the right and left wheels, respectively.
- v is the longitudinal speed of the vehicle.
- is the yaw speed of the vehicle.
- r is the wheel radius fixed at 0.2 m.
- l is the track width of the rover equal to 1 m.
2.2. Virtual Operative Environment Definition
- 1 in cases of the presence of an obstacle that the vehicle must avoid.
- 0 in cases of a free path.
- The number of fruit plants in a row n.
- The width w and length l of each fruit plant row, expressed in meters.
- The width L1 and length L2 of the orchard field, expressed in meters.
- The dimensional value Ys to which each fruit plant row must start, expressed in meters.
- The value of mesh refinement m, defined as the number of matrix elements contained for each square meter.

- The number of free rows N, defined as:N = n +1
- The recurring step of the fruit plant rows P, defined as:P = L1/N
- The occupied row area A, defined as the product between w and l.
- n is equal to 9; hence, N is equal to 10.
- w is equal to 2 m, and l is equal to 80 m.
- L1 and L2 are equal to 100 m; hence, P is equal to 10.
- Ys is equal to 10 m.
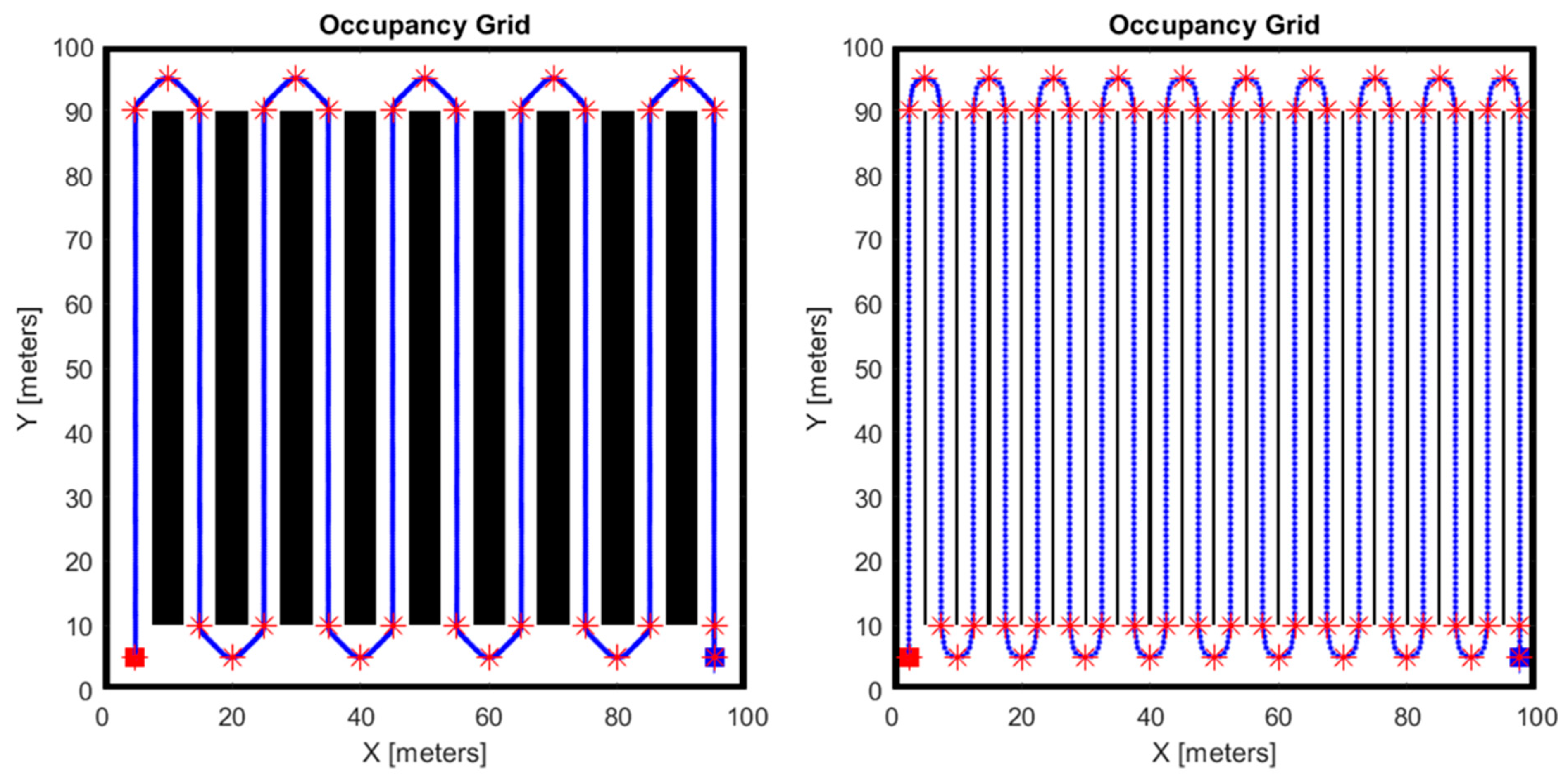
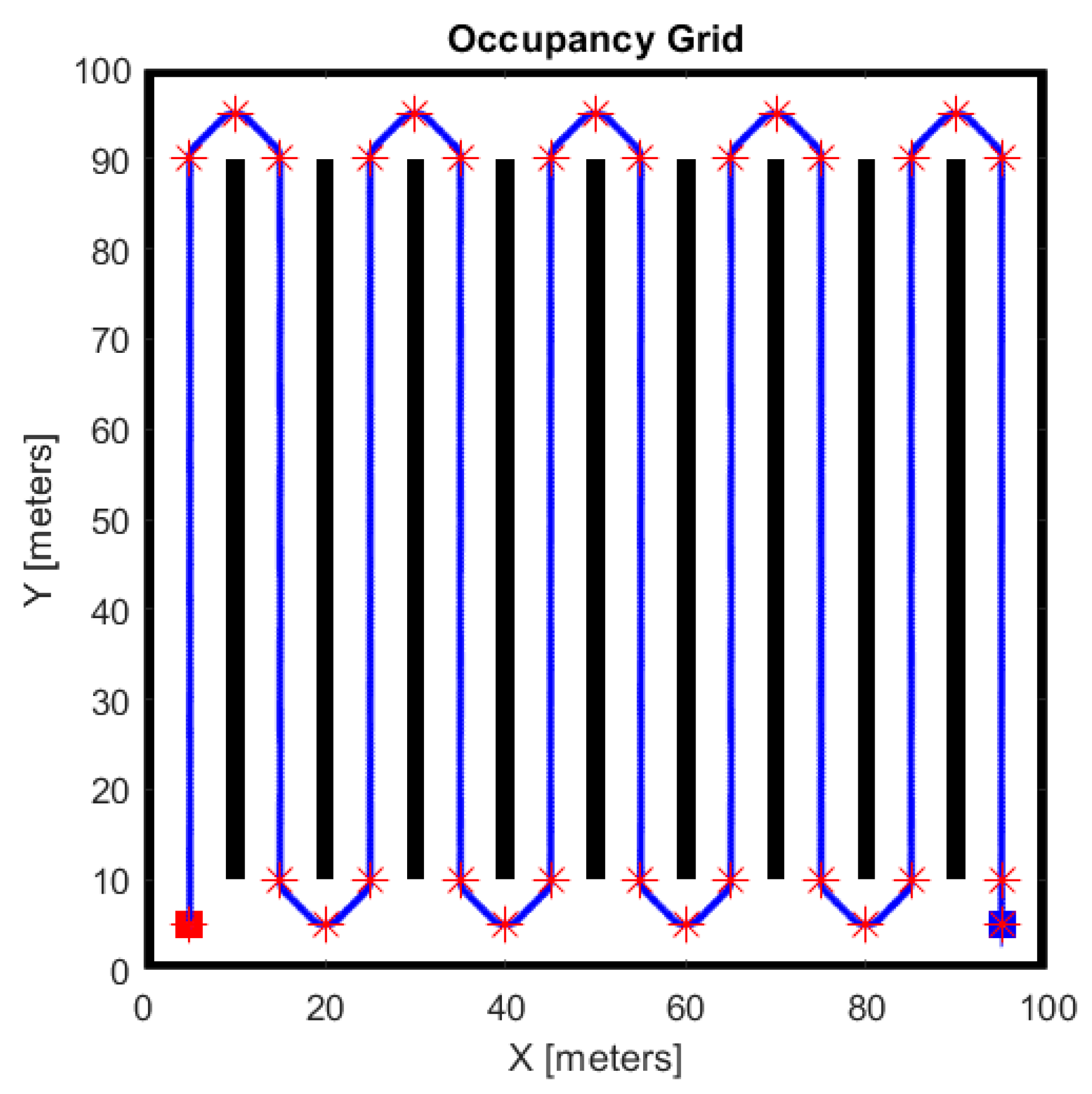
2.3. Global Path Planning
- Traveling in a straight line along the fruit plant rows.
- Executing a hairpin turn in order to exit from a free row and enter the next one.
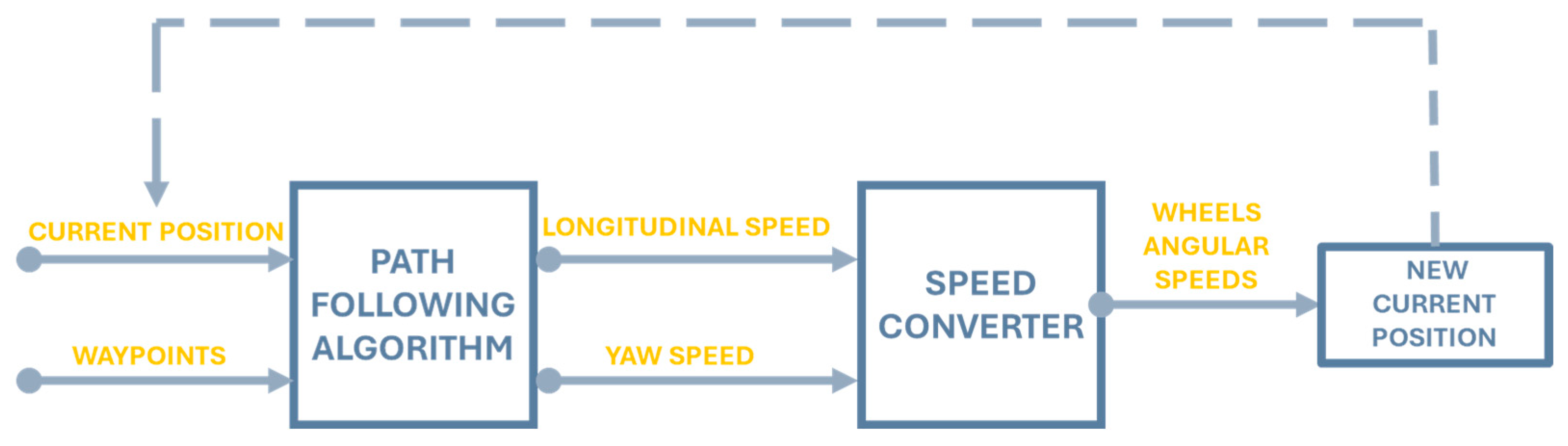
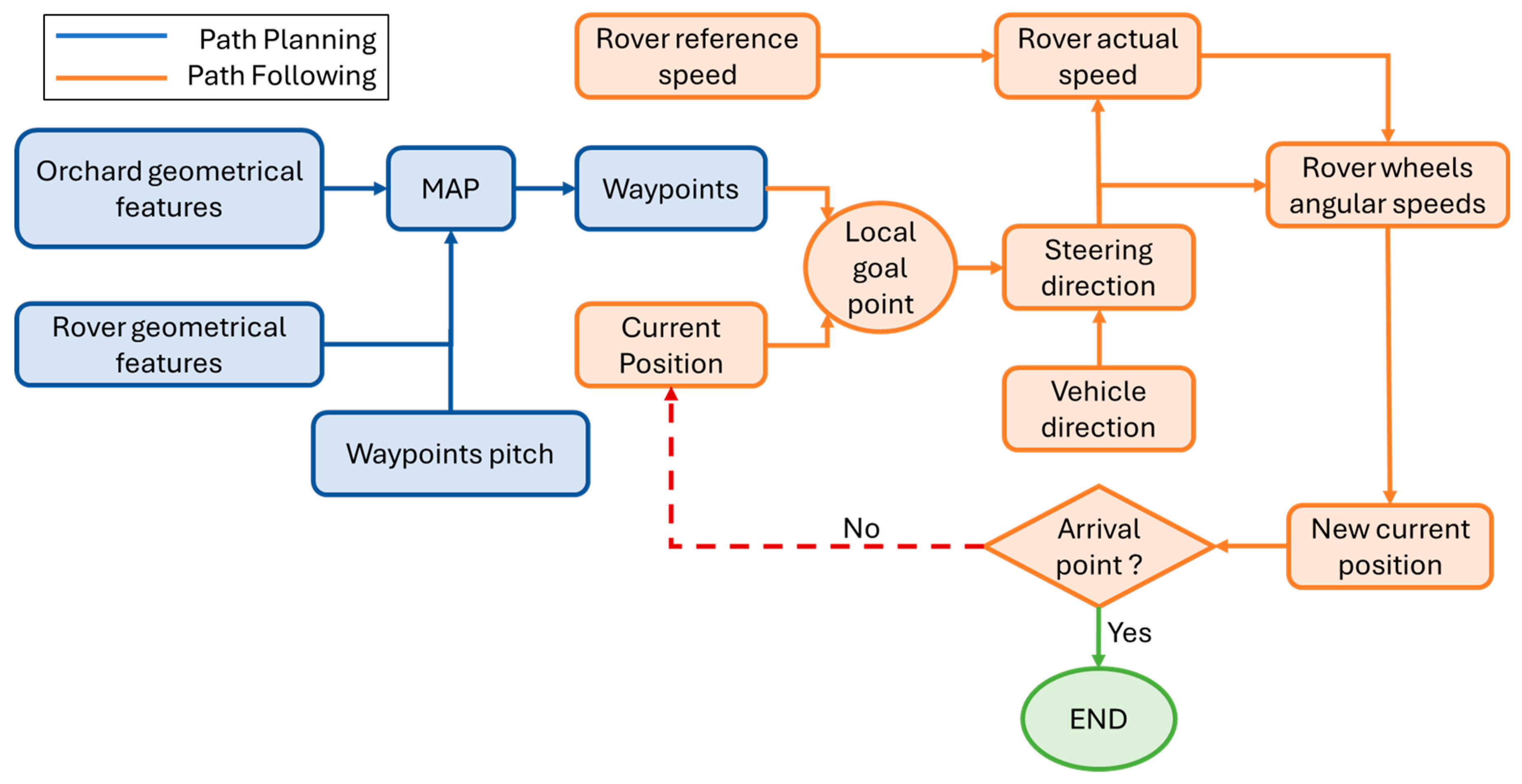
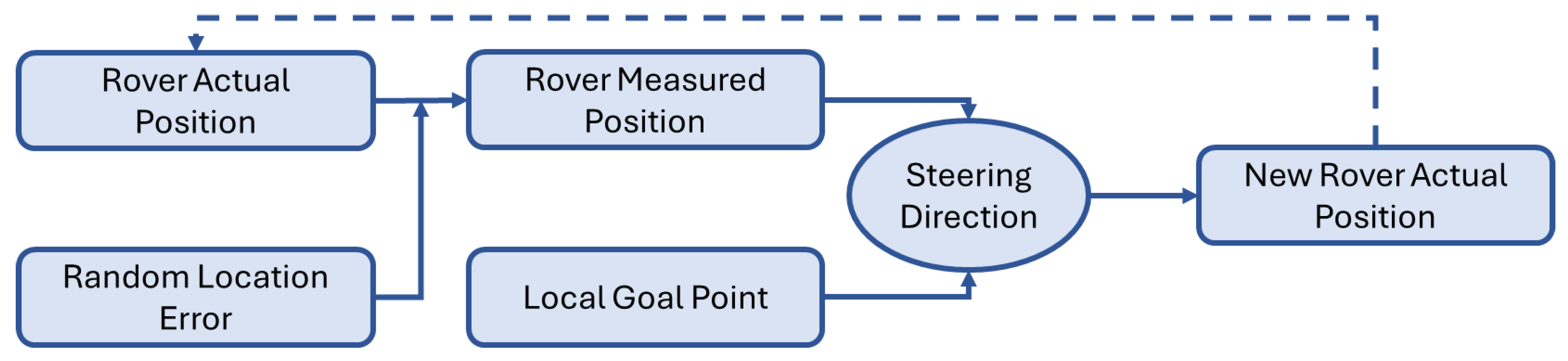
2.4. Path-Following Algorithm
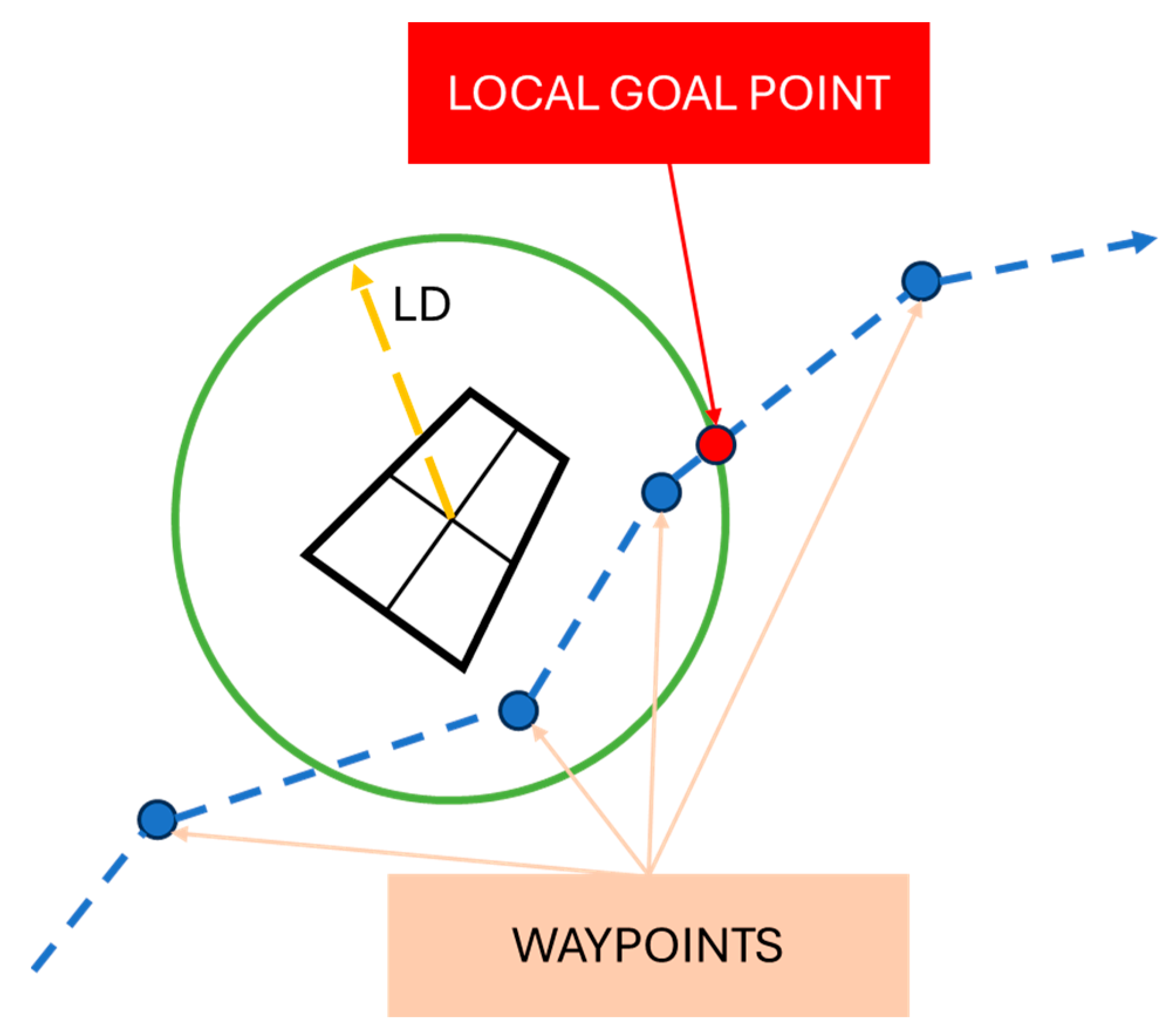
- Definition of a “local” goal point (LGP).
- Definition of the commands that must be imposed in a way that the rover can reach the goal point calculated in the previous step.
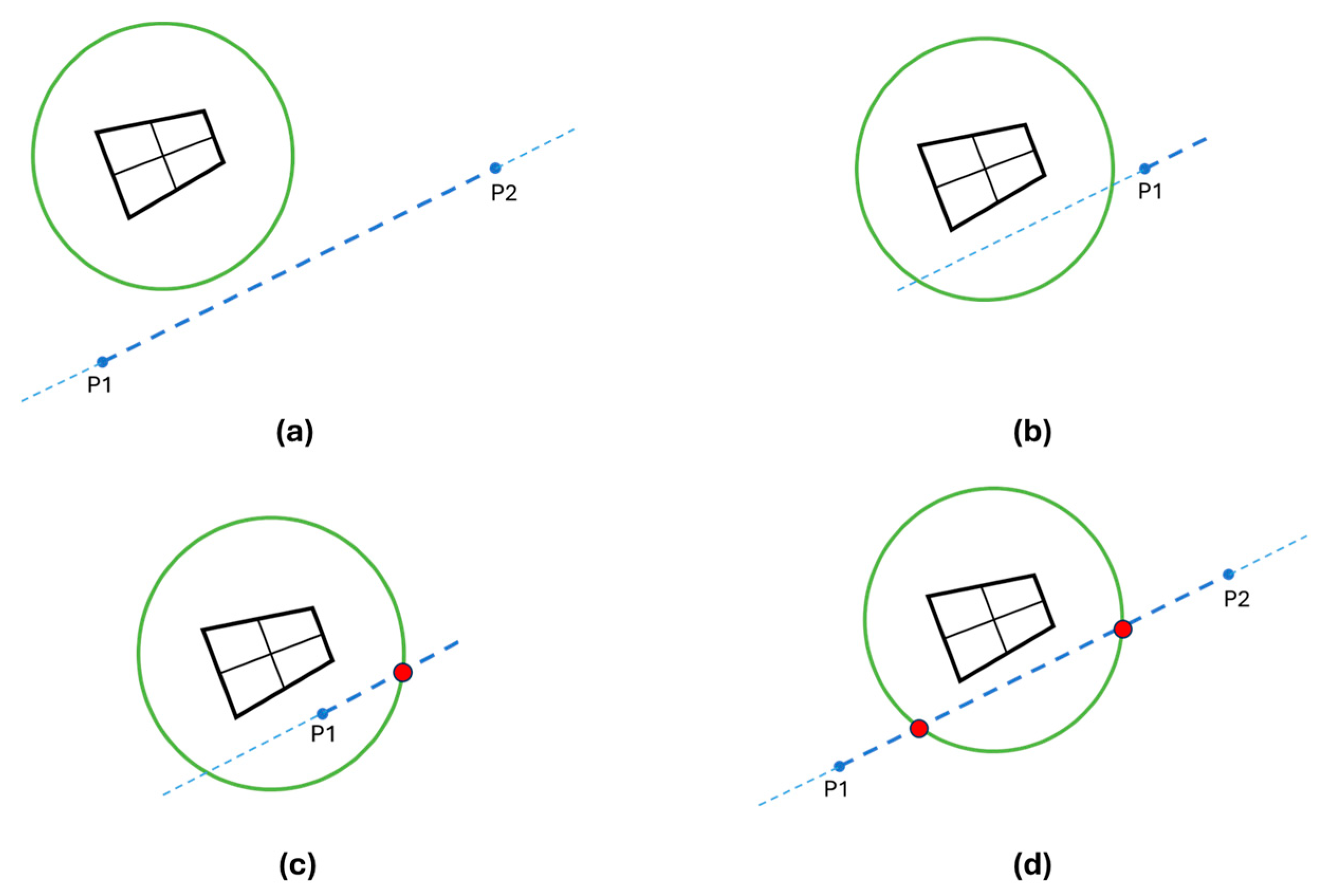
- No intersections (Figure 10a).
- Single or multiple intersections with the straight line, but the points found are not included between P1 and P2 (Figure 10b); this case is interpreted by the algorithm as the previous one.
- Single intersection: The point found corresponds to the local goal point pursued by the rover (Figure 10c).
- Multiple intersections between P1 and P2: In this case, the algorithm chooses the nearest point to the second waypoint (Figure 10d).
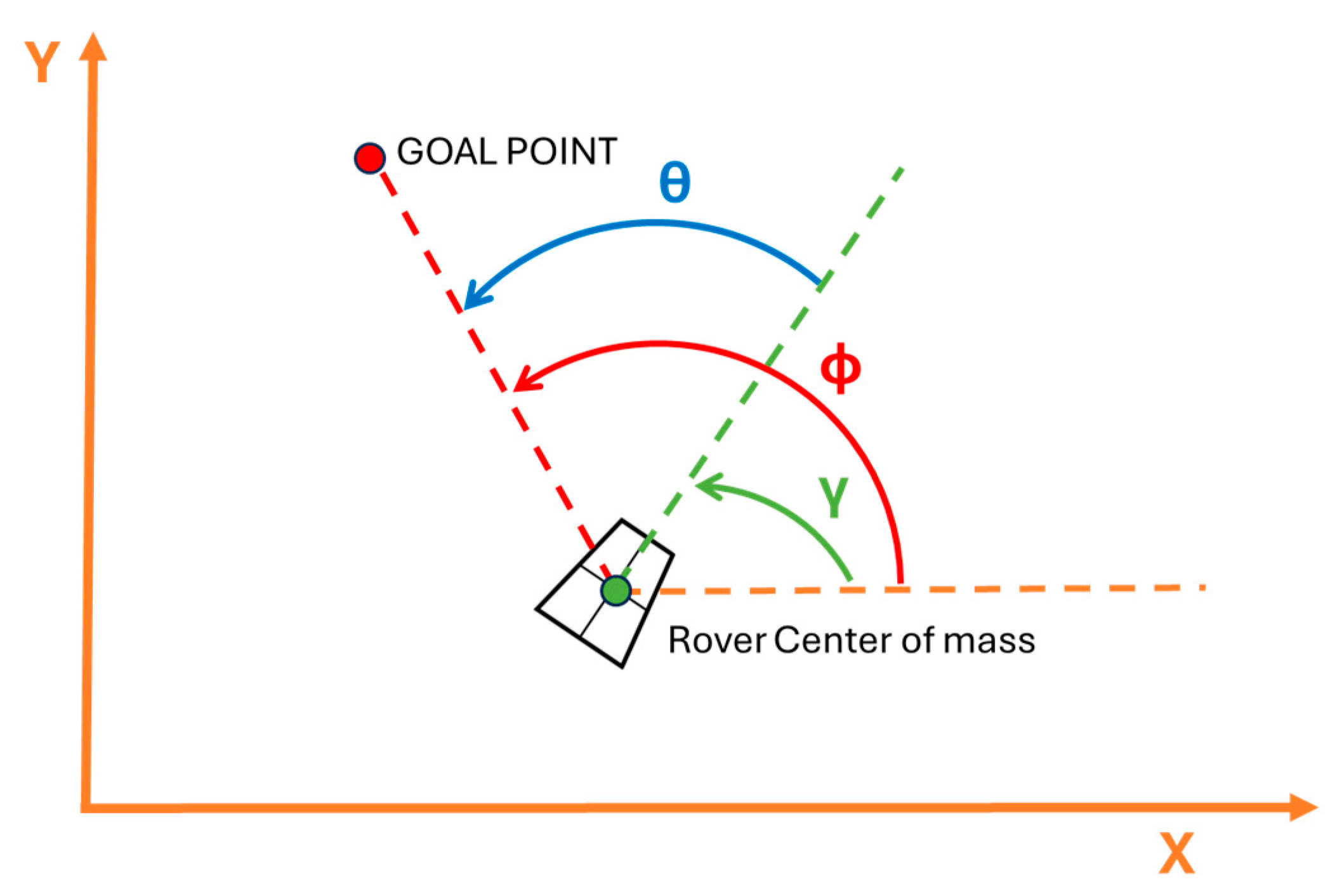
- Vehicle direction γ defines the actual rover direction.
- Goal point angle φ defines the direction of the segment, which links the goal point and the rover center of mass, with respect to the reference system adopted and calculated using the atan2 function.
- Steering angle θ.
- v is the longitudinal speed of the vehicle.
- vt is the maximum rover speed.
- θ is the steering angle.
- θmax is the maximum steering angle and set to 360° because 4-wheel differential-drive vehicles ideally can execute a pivot maneuver.
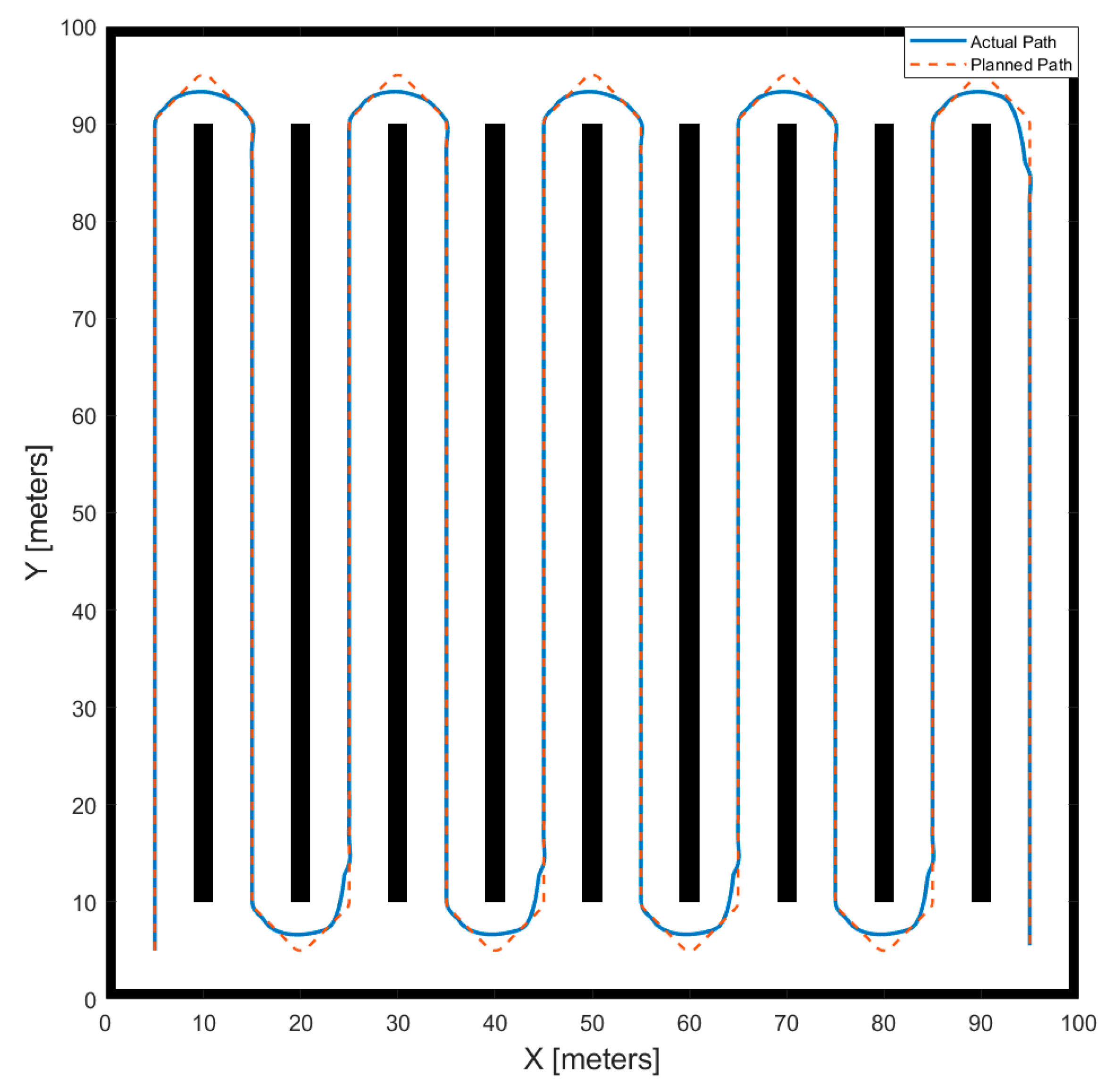
3. Results and Discussion
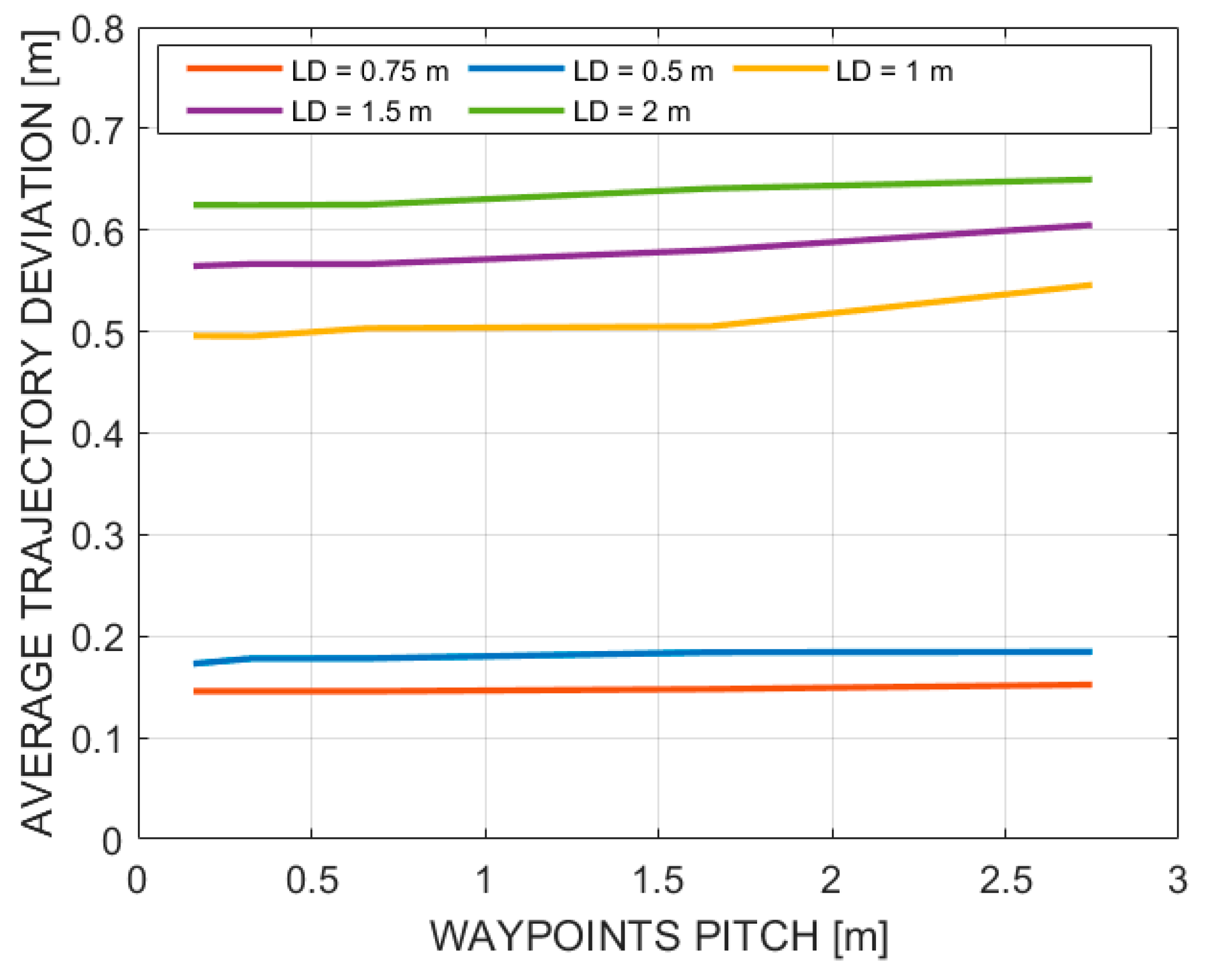
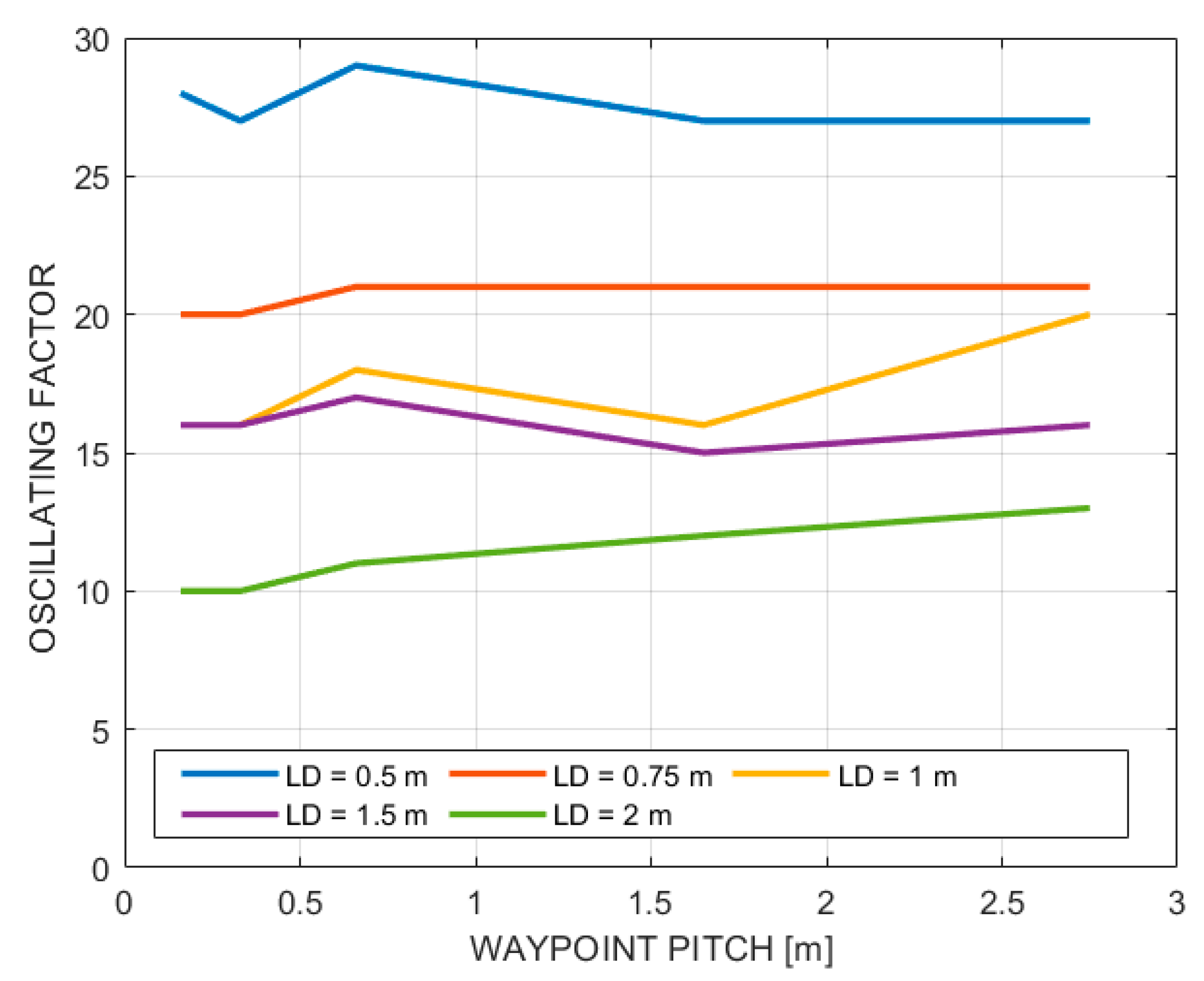
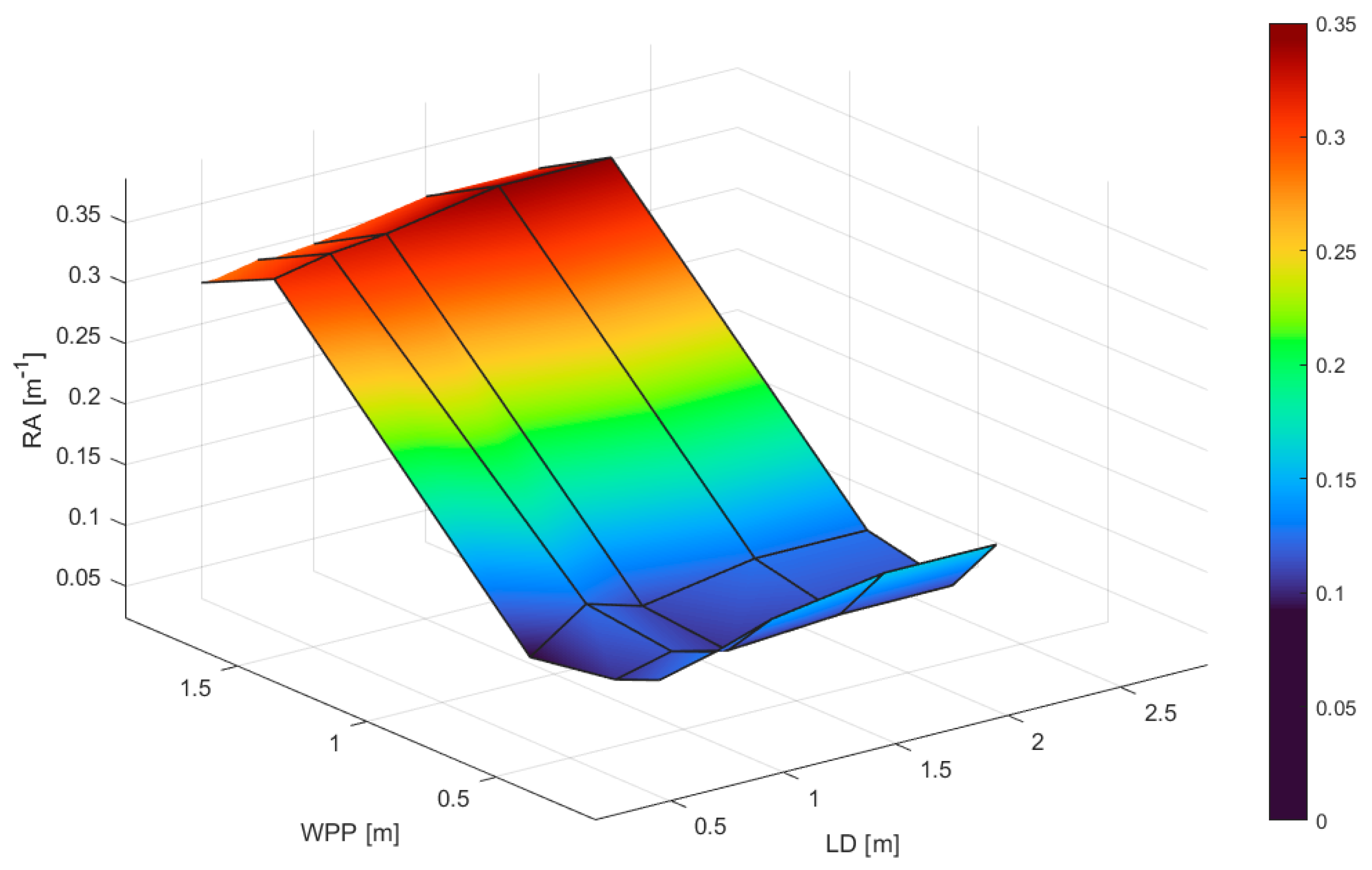
- Waypoint pitch (WPP): This indicates the distance (in meters) between two consecutive waypoints and can be obtained by splitting the total length of the planned path by the total number of waypoints.
- Lookahead distance (LD): This indicates the radius of the circumference that the vehicle uses to find the local goal point.
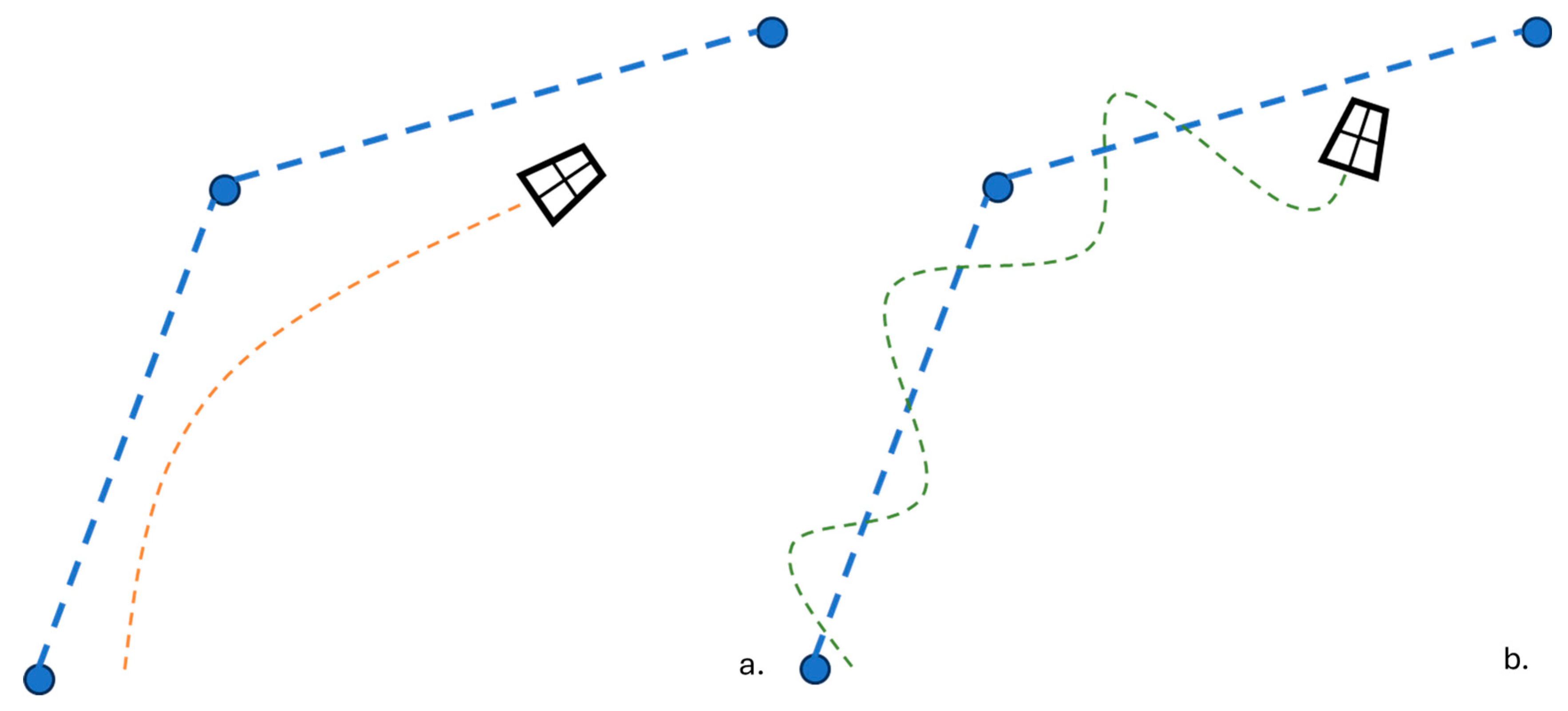
- Average trajectory deviation (ATD).
- Oscillating factor (OF).
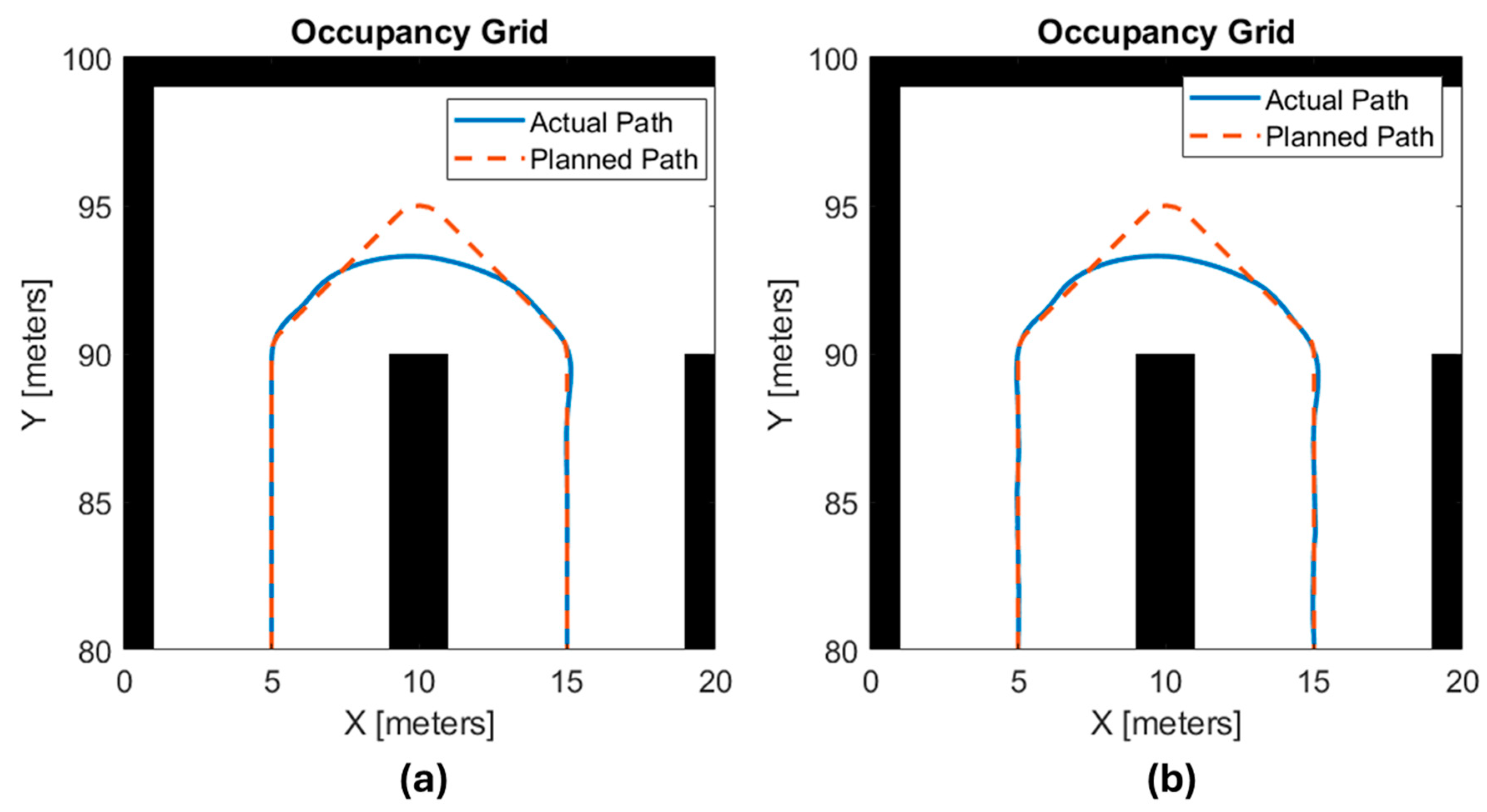
Influence of Positioning Error
4. Conclusions
- Empirical assessment of the algorithm’s reliability.
- The introduction of possible corrective coefficients linked with the dynamic behavior of the rover.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- FAO. World Food and Agriculture—Statistical Yearbook 2021; FAO: Rome, Italy, 2021; ISBN 978-92-5-134332-6. [Google Scholar]
- Prosekov, A.Y.; Ivanova, S.A. Food Security: The Challenge of the Present. Geoforum 2018, 91, 73–77. [Google Scholar] [CrossRef]
- Martelli, S.; Mocera, F.; Somà, A. Carbon Footprint of an Orchard Tractor through a Life-Cycle Assessment Approach. Agriculture 2023, 13, 1210. [Google Scholar] [CrossRef]
- Mantoam, E.J.; Romanelli, T.L.; Gimenez, L.M. Energy Demand and Greenhouse Gases Emissions in the Life Cycle of Tractors. Biosyst. Eng. 2016, 151, 158–170. [Google Scholar] [CrossRef]
- Martelli, S.; Mocera, F.; Somà, A. New Challenges towards Electrification Sustainability: Environmental Impact Assessment Comparison between ICE and Hybrid-Electric Orchard Tractor; SAE: Warrendale, PA, USA, 2023. [Google Scholar]
- Wollenberg, E.; Richards, M.; Smith, P.; Havlík, P.; Obersteiner, M.; Tubiello, F.N.; Herold, M.; Gerber, P.; Carter, S.; Reisinger, A.; et al. Reducing Emissions from Agriculture to Meet the 2 °C Target. Glob. Chang. Biol. 2016, 22, 3859–3864. [Google Scholar] [CrossRef]
- Gołasa, P.; Wysokiński, M.; Bieńkowska-Gołasa, W.; Gradziuk, P.; Golonko, M.; Gradziuk, B.; Siedlecka, A.; Gromada, A. Sources of Greenhouse Gas Emissions in Agriculture, with Particular Emphasis on Emissions from Energy Used. Energies 2021, 14, 3784. [Google Scholar] [CrossRef]
- Clerici, D.; Martelli, S.; Mocera, F.; Somà, A. Mechanical Characterization of Lithium-Ion Batteries with Different Chemistries and Formats. J. Energy Storage 2024, 84, 110899. [Google Scholar] [CrossRef]
- Platis, D.; Anagnostopoulos, C.; Tsaboula, A.; Menexes, G.; Kalburtji, K.; Mamolos, A. Energy Analysis, and Carbon and Water Footprint for Environmentally Friendly Farming Practices in Agroecosystems and Agroforestry. Sustainability 2019, 11, 1664. [Google Scholar] [CrossRef]
- Stott, P.A.; Christidis, N.; Otto, F.E.L.; Sun, Y.; Vanderlinden, J.; van Oldenborgh, G.J.; Vautard, R.; von Storch, H.; Walton, P.; Yiou, P.; et al. Attribution of Extreme Weather and Climate-related Events. WIREs Clim. Change 2016, 7, 23–41. [Google Scholar] [CrossRef]
- Patz, J.A.; Campbell-Lendrum, D.; Holloway, T.; Foley, J.A. Impact of Regional Climate Change on Human Health. Nature 2005, 438, 310–317. [Google Scholar] [CrossRef]
- Ravankar, A.; Ravankar, A.A.; Rawankar, A.; Hoshino, Y. Autonomous and Safe Navigation of Mobile Robots in Vineyard with Smooth Collision Avoidance. Agriculture 2021, 11, 954. [Google Scholar] [CrossRef]
- Liang, Y.; Zhou, K.; Wu, C. Environment Scenario Identification Based on GNSS Recordings for Agricultural Tractors. Comput. Electron. Agric. 2022, 195, 106829. [Google Scholar] [CrossRef]
- Mocera, F.; Somà, A.; Martelli, S.; Martini, V. Trends and Future Perspective of Electrification in Agricultural Tractor-Implement Applications. Energies 2023, 16, 6601. [Google Scholar] [CrossRef]
- Pascuzzi, S.; Łyp-Wrońska, K.; Gdowska, K.; Paciolla, F. Sustainability Evaluation of Hybrid Agriculture-Tractor Powertrains. Sustainability 2024, 16, 1184. [Google Scholar] [CrossRef]
- Beligoj, M.; Scolaro, E.; Alberti, L.; Renzi, M.; Mattetti, M. Feasibility Evaluation of Hybrid Electric Agricultural Tractors Based on Life Cycle Cost Analysis. IEEE Access 2022, 10, 28853–28867. [Google Scholar] [CrossRef]
- Martini, V.; Mocera, F.; Somà, A. Carbon Footprint Enhancement of an Agricultural Telehandler through the Application of a Fuel Cell Powertrain. World Electr. Veh. J. 2024, 15, 91. [Google Scholar] [CrossRef]
- Martini, V.; Mocera, F.; Somà, A. Design and Experimental Validation of a Scaled Test Bench for the Emulation of a Hybrid Fuel Cell Powertrain for Agricultural Tractors. Appl. Sci. 2023, 13, 8582. [Google Scholar] [CrossRef]
- Al-lwayzy, S.; Yusaf, T. Chlorella Protothecoides Microalgae as an Alternative Fuel for Tractor Diesel Engines. Energies 2013, 6, 766–783. [Google Scholar] [CrossRef]
- Owczuk, M.; Matuszewska, A.; Kruczyński, S.; Kamela, W. Evaluation of Using Biogas to Supply the Dual Fuel Diesel Engine of an Agricultural Tractor. Energies 2019, 12, 1071. [Google Scholar] [CrossRef]
- Baillie, C.P.; Thomasson, J.A.; Lobsey, C.R.; McCarthy, C.L.; Antille, D.L. A Review of the State of the Art in Agricultural Automation. Part I: Sensing technologies for optimization of machine operation and farm inputs. In Proceedings of the 2018 ASABE Annual International Meeting, Detroit, MI, USA, 29 July–1 August 2018; American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2018. [Google Scholar]
- Ghobadpour, A.; Boulon, L.; Mousazadeh, H.; Malvajerdi, A.S.; Rafiee, S. State of the Art of Autonomous Agricultural Off-Road Vehicles Driven by Renewable Energy Systems. Energy Procedia 2019, 162, 4–13. [Google Scholar] [CrossRef]
- Roshanianfard, A.; Noguchi, N.; Okamoto, H.; Ishii, K. A Review of Autonomous Agricultural Vehicles (The Experience of Hokkaido University). J. Terramech. 2020, 91, 155–183. [Google Scholar] [CrossRef]
- Rubio, F.; Valero, F.; Llopis-Albert, C. A Review of Mobile Robots: Concepts, Methods, Theoretical Framework, and Applications. Int. J. Adv. Robot. Syst. 2019, 16, 172988141983959. [Google Scholar] [CrossRef]
- Durmus, H.; Gunes, E.O.; Kirci, M.; Ustundag, B.B. The Design of General Purpose Autonomous Agricultural Mobile-Robot: “AGROBOT”. In Proceedings of the 2015 Fourth International Conference on Agro-Geoinformatics (Agro-Geoinformatics), Istanbul, Turkey, 20–24 July 2015; pp. 49–53. [Google Scholar]
- Califano, F.; Cosenza, C.; Niola, V.; Savino, S. Multibody Model for the Design of a Rover for Agricultural Applications: A Preliminary Study. Machines 2022, 10, 235. [Google Scholar] [CrossRef]
- Sparrow, R.; Howard, M. Robots in Agriculture: Prospects, Impacts, Ethics, and Policy. Precis. Agric. 2021, 22, 818–833. [Google Scholar] [CrossRef]
- Pedersen, S.M.; Fountas, S.; Have, H.; Blackmore, B.S. Agricultural Robots—System Analysis and Economic Feasibility. Precis. Agric. 2006, 7, 295–308. [Google Scholar] [CrossRef]
- King, A. Technology: The Future of Agriculture. Nature 2017, 544, S21–S23. [Google Scholar] [CrossRef] [PubMed]
- Yahya, N. Green Urea; Springer: Singapore, 2018; ISBN 978-981-10-7577-3. [Google Scholar]
- Martelli, S.; Mocera, F.; Somà, A. Co-Simulation of a Specialized Tractor for Autonomous Driving in Orchards; SAE: Warrendale, PA, USA, 2022. [Google Scholar]
- Han, J.; Park, C.; Jang, Y.Y.; Gu, J.D.; Kim, C.Y. Performance Evaluation of an Autonomously Driven Agricultural Vehicle in an Orchard Environment. Sensors 2021, 22, 114. [Google Scholar] [CrossRef] [PubMed]
- Ko, M.H.; Ryuh, B.-S.; Kim, K.C.; Suprem, A.; Mahalik, N.P. Autonomous Greenhouse Mobile Robot Driving Strategies From System Integration Perspective: Review and Application. IEEE/ASME Trans. Mechatron. 2015, 20, 1705–1716. [Google Scholar] [CrossRef]
- Santos, L.C.; Santos, F.N.; Solteiro Pires, E.J.; Valente, A.; Costa, P.; Magalhaes, S. Path Planning for Ground Robots in Agriculture: A Short Review. In Proceedings of the 2020 IEEE International Conference on Autonomous Robot Systems and Competitions (ICARSC), Ponta Delgada, Portugal, 15–17 April 2020; pp. 61–66. [Google Scholar]
- Han, X.; Lai, Y.; Wu, H. A Path Optimization Algorithm for Multiple Unmanned Tractors in Peach Orchard Management. Agronomy 2022, 12, 856. [Google Scholar] [CrossRef]
- Hameed, I.A. Intelligent Coverage Path Planning for Agricultural Robots and Autonomous Machines on Three-Dimensional Terrain. J. Intell. Robot. Syst. 2014, 74, 965–983. [Google Scholar] [CrossRef]
- Santos, L.; Santos, F.; Mendes, J.; Costa, P.; Lima, J.; Reis, R.; Shinde, P. Path Planning Aware of Robot’s Center of Mass for Steep Slope Vineyards. Robotica 2020, 38, 684–698. [Google Scholar] [CrossRef]
- Bochtis, D.; Griepentrog, H.W.; Vougioukas, S.; Busato, P.; Berruto, R.; Zhou, K. Route Planning for Orchard Operations. Comput. Electron. Agric. 2015, 113, 51–60. [Google Scholar] [CrossRef]
- Juman, M.A.; Wong, Y.W.; Rajkumar, R.K.; H’ng, C.Y. An Integrated Path Planning System for a Robot Designed for Oil Palm Plantations. In Proceedings of the TENCON 2017—2017 IEEE Region 10 Conference, Penang, Malaysia, 5–8 November 2017; pp. 1048–1053. [Google Scholar]
- Li, S.; Xu, H.; Ji, Y.; Cao, R.; Zhang, M.; Li, H. Development of a Following Agricultural Machinery Automatic Navigation System. Comput. Electron. Agric. 2019, 158, 335–344. [Google Scholar] [CrossRef]
- Hernandez, J.I.; Kuo, C.Y. Steering Control of Automated Vehicles Using Absolute Positioning Gps and Magnetic Markers. IEEE Trans. Veh. Technol. 2003, 52, 150–161. [Google Scholar] [CrossRef]
- Huang, P.; Luo, X.; Zhang, Z. Headland Turning Control Method Simulation of Autonomous Agricultural Machine Based on Improved Pure Pursuit Model. In Computer and Computing Technologies in Agriculture III, Proceedings of the Third IFIP TC 12 International Conference, CCTA 2009, Beijing, China, 14–17 October 2009; Springer: Berlin/Heidelberg, Germany, 2010; pp. 176–184. [Google Scholar]
- Peng, H.; Wang, W.; An, Q.; Xiang, C.; Li, L. Path Tracking and Direct Yaw Moment Coordinated Control Based on Robust MPC With the Finite Time Horizon for Autonomous Independent-Drive Vehicles. IEEE Trans. Veh. Technol. 2020, 69, 6053–6066. [Google Scholar] [CrossRef]
- Sainz-Rubio, V.; Rovira-Mas, F.; Diago, M.P.; Fernandez-Novales, J.; Barrio, I.; Cuenca, A.; Alves, F.; Valente, J.; Tardaguila, J. VINESCOUT: A Vineyard Autonomous Robot for on-the-Go Assessment of Grapevine Vigour and Water Status. Available online: https://investigacion.unirioja.es/documentos/603618dcd700765ec201af64/f/60362b47d700765ec201af65.pdf (accessed on 19 May 2024).
- Fountas, S.; Mylonas, N.; Malounas, I.; Rodias, E.; Hellmann Santos, C.; Pekkeriet, E. Agricultural Robotics for Field Operations. Sensors 2020, 20, 2672. [Google Scholar] [CrossRef]
- Gobhinath, S.; Darshini, M.D.; Durga, K.; Priyanga, R.H. Smart Irrigation with Field Protection and Crop Health Monitoring System Using Autonomous Rover. In Proceedings of the 2019 5th International Conference on Advanced Computing & Communication Systems (ICACCS), Coimbatore, India, 15–16 March 2019; pp. 198–203. [Google Scholar]
- Cornejo, J.; Magallanes, J.; Denegri, E.; Canahuire, R. Trajectory Tracking Control of a Differential Wheeled Mobile Robot: A Polar Coordinates Control and LQR Comparison. In Proceedings of the 2018 IEEE XXV International Conference on Electronics, Electrical Engineering and Computing (INTERCON), Lima, Peru, 8–10 August 2018; pp. 1–4. [Google Scholar]
- Korkmaz, M.; Durdu, A. Comparison of Optimal Path Planning Algorithms. In Proceedings of the 2018 14th International Conference on Advanced Trends in Radioelecrtronics, Telecommunications and Computer Engineering (TCSET), Lviv-Slavske, Ukraine, 20–24 February 2018; pp. 255–258. [Google Scholar]
- Gasparetto, A.; Boscariol, P.; Lanzutti, A.; Vidoni, R. Path Planning and Trajectory Planning Algorithms: A General Overview. In Motion and Operation Planning of Robotic Systems: Background and Practical Approaches; Springer: Cham, Switzerland, 2015; pp. 3–27. [Google Scholar]
- Dubins, L.E. On Curves of Minimal Length with a Constraint on Average Curvature, and with Prescribed Initial and Terminal Positions and Tangents. Am. J. Math. 1957, 79, 497. [Google Scholar] [CrossRef]
- Hameed, I.A. Coverage Path Planning Software for Autonomous Robotic Lawn Mower Using Dubins’ Curve. In Proceedings of the 2017 IEEE International Conference on Real-Time Computing and Robotics (RCAR), Okinawa, Japan, 14–18 July 2017; pp. 517–522. [Google Scholar]
- Macenski, S.; Singh, S.; Martín, F.; Ginés, J. Regulated Pure Pursuit for Robot Path Tracking. Auton. Robots 2023, 47, 685–694. [Google Scholar] [CrossRef]
- Wang, W.-J.; Hsu, T.-M.; Wu, T.-S. The Improved Pure Pursuit Algorithm for Autonomous Driving Advanced System. In Proceedings of the 2017 IEEE 10th International Workshop on Computational Intelligence and Applications (IWCIA), Hiroshima, Japan, 11–12 November 2017; pp. 33–38. [Google Scholar]
- Mocera, F.; Martini, V.; Somà, A. Comparative Analysis of Hybrid Electric Architectures for Specialized Agricultural Tractors. Energies 2022, 15, 1944. [Google Scholar] [CrossRef]
- Mekik, C.; Arslanoglu, M. Investigation on Accuracies of Real Time Kinematic GPS for GIS Applications. Remote Sens. 2009, 1, 22–35. [Google Scholar] [CrossRef]
- Ekaso, D.; Nex, F.; Kerle, N. Accuracy Assessment of Real-Time Kinematics (RTK) Measurements on Unmanned Aerial Vehicles (UAV) for Direct Geo-Referencing. Geo-Spat. Inf. Sci. 2020, 23, 165–181. [Google Scholar] [CrossRef]
- Xu, H. Application of GPS-RTK Technology in the Land Change Survey. Procedia Eng. 2012, 29, 3454–3459. [Google Scholar] [CrossRef]
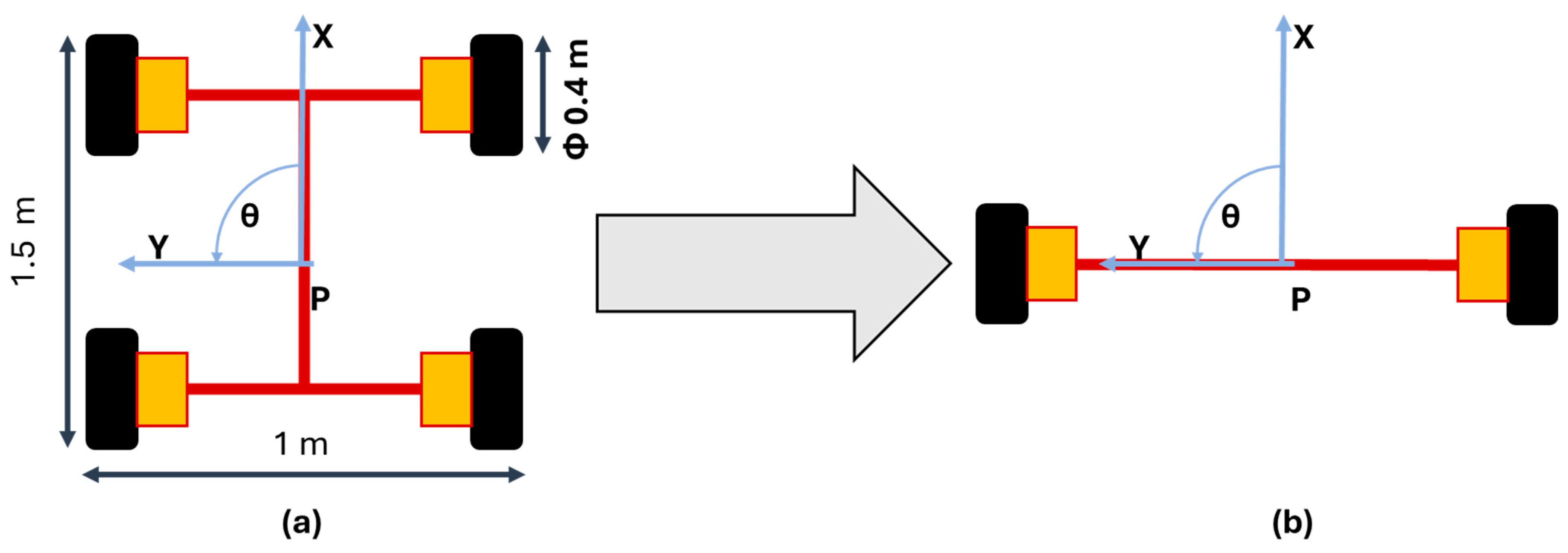





| Rover Features for Autonomous Driving Algorithm Application | |
|---|---|
| Wheelbase | 1.5 m |
| Track Width | 1 m |
| Wheel Radius | 0.2 m |
| Minimum Turning Radius | 1 m |
| Reference Rover Speed | 7 km/h |
| Accuracy (m) | RA (m−1) | ∆RA % with Respect to Baseline |
|---|---|---|
| 0 (baseline) | 0.34 | 0% |
| ±0.01 | 0.0272 | −91.77% |
| ±0.02 | 0.0317 | −90.43% |
| ±0.05 | 0.0316 | −90.45% |
| ±0.1 | 0.0273 | −91.75% |
| Accuracy (m) | RA (m−1) | ∆RA % with Respect to Baseline |
|---|---|---|
| 0 (ideal case) | 0.7232 | 118.4% |
| ±0.01 | 0.6421 | 93.92% |
| ±0.02 | 0.6219 | 87.80% |
| ±0.05 | 0.3022 | −8.74% |
| ±0.1 | 0.0601 | −81.85% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martelli, S.; Mocera, F.; Somà, A. Autonomous Driving Strategy for a Specialized Four-Wheel Differential-Drive Agricultural Rover. AgriEngineering 2024, 6, 1937-1958. https://doi.org/10.3390/agriengineering6030113
Martelli S, Mocera F, Somà A. Autonomous Driving Strategy for a Specialized Four-Wheel Differential-Drive Agricultural Rover. AgriEngineering. 2024; 6(3):1937-1958. https://doi.org/10.3390/agriengineering6030113
Chicago/Turabian StyleMartelli, Salvatore, Francesco Mocera, and Aurelio Somà. 2024. "Autonomous Driving Strategy for a Specialized Four-Wheel Differential-Drive Agricultural Rover" AgriEngineering 6, no. 3: 1937-1958. https://doi.org/10.3390/agriengineering6030113
APA StyleMartelli, S., Mocera, F., & Somà, A. (2024). Autonomous Driving Strategy for a Specialized Four-Wheel Differential-Drive Agricultural Rover. AgriEngineering, 6(3), 1937-1958. https://doi.org/10.3390/agriengineering6030113












