Abstract
Missing data and class imbalance hinder the accurate prediction of rare events such as dairy mastitis. Resampling and imputation are employed to handle these problems. These methods are often used arbitrarily, despite their profound impact on prediction due to changes caused to the data structure. We hypothesize that their use affects the performance of ML models fitted to automated milking systems (AMSs) data for mastitis prediction. We compare three imputations—simple imputer (SI), multiple imputer (MICE) and linear interpolation (LI)—and three resampling techniques: Synthetic Minority Oversampling Technique (SMOTE), Support Vector Machine SMOTE (SVMSMOTE) and SMOTE with Edited Nearest Neighbors (SMOTEEN). The classifiers were logistic regression (LR), multilayer perceptron (MLP), decision tree (DT) and random forest (RF). We evaluated them with various metrics and compared models with the kappa score. A complete case analysis fitted the RF (0.78) better than other models, for which SI performed best. The DT, RF, and MLP performed better with SVMSMOTE. The RF, DT and MLP had the overall best performance, contributed by imputation or resampling (SMOTE and SVMSMOTE). We recommend carefully selecting resampling and imputation techniques and comparing them with complete cases before deciding on the preprocessing approach used to test AMS data with ML models.
1. Introduction
Mastitis is the most costly and frequent disease in dairy farming, contributing to considerable (about EUR 125 per cow and year) and recurring costs incurred through a reduction of milk quantity and quality, as well as the reproductive performance and longevity of cows [1,2,3]. The disease affects 20–40% of lactating cows annually, leading to a potential 11 to 18% of gross margins of dairy farms. Subclinical mastitis contributes about 48% of these costs through either subsequent milk yield reduction (72%) or the subsequent culling of infected cows (25%). This disease can be caused by a wide diversity of pathogens but is dominated by only few species. The most important mastitis-causing bacterial species are Streptococcus agalactiae, Streptococcus dysgalactiae, Streptococcus uberis, Staphylococcus aureus, and Escherichia coli [2,4]. The subclinical form of mastitis, without overt symptoms, is by far more prevalent than the clinical form and causes high economic losses [2,5]. Simultaneously, subclinical mastitis is, due to the low level of symptoms, difficult to detect. Mastitis affects both the economic viability of farms and the health of dairy cows, hence impacting the viability of the dairy industry [6]. Mastitis leads to reduced milk yield, increased veterinary costs, and higher culling rates [7]. Mastitis affects both the quantity and quality of the milk produced. Infected cows produce less milk, and the milk often has altered composition, including higher somatic cell counts (SCCs) and lower levels of key components like casein [8]. This not only reduces the volume of milk available but also its suitability for processing into dairy products. The effective management of mastitis involves both preventive measures and timely treatment. Strategies include maintaining good milking hygiene, using proper milking techniques, and implementing selective dry-cow therapy to reduce the use of antibiotics. Early detection and treatment are crucial to minimize the impact of the disease [9]. Therefore, modern data analysis tools like machine leaning could help us to identify subclinical mastitis cases more often and accurately.
Managing mastitis is even a bigger challenge in large-scale dairy farms despite the use of automated milking systems (AMSs) that has steadily increased in Germany and across European countries over the last few years [10]. The AMS uses sensors to collect data such as milk yield and milk components, and through management programs, alerts are given in case of variations of either milk production (milk yield and milk flow), electric conductivity, somatic cell counts (SCCs), milk temperature, milk color or a combination of these parameters as an indication for mastitis occurrence [11,12]. The data collected at each milking, or through monthly milk recording programs, are routinely used to help farmers for better decision-making in production, reproduction and health. This is specifically the case for mastitis predictions based on milk yield, milk parameters (conductivity, SCC, blood in milk, temperature) and cow characteristics [11,13]. For this prediction purpose, several machine learning (ML) approaches have been used that aim to improve the monitoring of udder health status in general or mastitis specifically, whether subclinical or clinical. Bobbo et al. [14] compared eight ML models and achieved a prediction accuracy above 75% for all in a binary classification, with 200,000 cells/mL SCC as a threshold for positivity. Hyde et al. [15] trained random forest models to predict mastitis infection patterns in a binary classification where the predictor was contagious vs. environmental mastitis or environmental lactation vs. an environmental dry period. They obtained 98% prediction accuracy. Post et al. [16] applied ML models to a group of animals with historical records of diseases and achieved higher prediction accuracy than when the model was applied to the whole population. Findings from other studies using similar methodologies showed also high prediction accuracy [16,17]. Despite these encouraging results, the application of mastitis-prediction ML models in real-life conditions remains limited because of a discrepancy between the performance on the training and validation datasets and the actual data. The nature of data recording by sensor systems and the low occurrence of the disease appear as major reasons for the difference [18].
Indeed, farm sensor data present, in general, two types of challenges that make them difficult to handle by prediction algorithms. First, the data are often noisy, with missing values, outliers and skewed values accounting for about 30% of data loss prior to analysis. They occur because of sensor failure during signal transmission or the interruption of the milking process, e.g., by the detachment of a teat cup [19]. The missing values or wrongly recorded values fall into the type of either missing values completely at random or missing values at random. Missing values together with a clear definition of positive cases represent a major hindrance for ML algorithms trained on ‘experimental datasets’ to be used under farm conditions [20]. To handle the problem, it is common in practice to delete missing values completely or at least to apply methods such as listwise deletion, but less common is the reporting of the magnitude of missing values or the use of missing data handling methods [21]. Although working without missing values is convenient, it only produces reliable estimates in limited situations where missing values occur completely at random and only for the dependent variable. In other situations, this results in severely biased estimates, not to mention the potential waste of information in the omitted data and the low practical application of the obtained results [22]. This is of particular importance in disease prediction, where metrics obtained from the training datasets need to be applied in real-life situations [20]. Indeed, it is very common to have large amounts of missing values in sensor-generated datasets [21].
Various techniques have been developed to deal with the challenge of missing values in large datasets. The common imputation methods are simple imputation, multiple imputation and linear interpolation. The simple imputation method replaces missing values with mean, median or mode values [23]. This method is largely applied because of its computational convenience, although, in many cases, the results and conclusions are not sensible or generalizable [24]. Multiple imputation uses the MICE (multiple imputation with chained equations) algorithm, which is a Markov chain Monte Carlo method that imputes incomplete data in a variable-by-variable way, starting with a random draw of the observed data. For instance, a first regression of the first variable with missing values is applied to all other variables, provided that the rows have observations for the variable of interest. Then, missing values for the variable of interest are replaced by simulated draws from its posterior predictive distribution. The process is repeated for all other variables with missing values in turn; this is called a cycle. This process is repeated several times to generate a single imputed dataset, and the whole process is repeated three to five times to obtain stable results [25]. Although recognized for its robustness, the method suffers the limitation of a lack of theoretical rationale [23,25,26]. Linear interpolation estimates the value of the missing data based on the two data points adjacent to the missing one in a one-dimensional data sequence [27]. It is reputed to perform well on time-dependent data and on datasets with a small to moderate number of missing values between adjacent points [26].
The second major hurdle when training models on AMS data to predict mastitis is the class imbalance between positive and negative cases [18]. Although frequently observed in dairy farms, mastitis is a rare occurrence when the data resolution is increased to either a daily basis, an animal level, or both. This imbalance causes a bias when fitting standard learning classifiers, reflected in their inability to correctly predict the minority class, despite sometimes achieving high prediction accuracy [28]. Johnson and Khoshgoftaar [29] noted that the total number of the minority class is more important than the percentage of imbalance. Various methods to handle class imbalance are reported in the literature to improve disease prediction [18,28]. Johnson and Khoshgoftaar [29] categorized them into three groups: data-level methods, algorithm-level methods and hybrid methods. Data-level methods change the dataset structure by either reducing the majority class (undersampling), increasing the minority class (oversampling), or both, to achieve a more balanced class distribution [24]. Among popular resampling techniques is the Synthetic Minority Oversampling Technique (SMOTE), which produces synthetic samples by interpolating minority samples with their k-nearest neighbors. The algorithm seems to be improved by taking into consideration the minority class lying along the borderline, hence expanding the minority class area towards the side of the majority class where only few instances of majority class are found [30]. However, oversampling techniques may lead to overfitting. Random undersampling is among the first undersampling techniques developed and works by discarding random samples in the majority class. The technique has been improved with several techniques using nearest neighbors to reduce instances in the majority class. Edited Nearest Neighbors (ENN) tests every instance with the rest of the samples using k-NN and disqualifies incorrectly classified samples. Undersampling methods have the disadvantage of discarding information that may be useful. Techniques combining oversampling and undersampling have been developed to overcome the limitations of individual methods. The SMOTE-ENN technique combines SMOTE and Edited Nearest Neighbors for undersampling [28].
Studies on mastitis prediction with machine learning classifiers use the above-mentioned data (pre)processing techniques almost interchangeably, making the comparison and evaluation of effectiveness across studies more complex. Hence, starting with an analysis based on complete cases where all missing values are removed from the dataset prior to analysis, we evaluated whether the imputation techniques at three levels of complexity, namely simple imputation, multiple imputation with a chained equation, or linear interpolation would improve the performance of ML classifiers. The second of our hypotheses was to evaluate the improvement of ML classifiers’ performance when class imbalance was handled by resampling techniques of varying levels of complexity with SMOTE, SMOTEEN and SVMSMOTE, respectively. Thirdly, we compared performance metrics across models with both imputation and resampling techniques in order to decipher individual models’ suitability and robustness for mastitis prediction using data collected through automated milking systems. We used several metrics, including accuracy, F1 score, precision, recall and kappa score.
2. Materials and Methods
2.1. Data Collection
The dataset included records of 232 cows and 75,217 milking events, for which daily milk yield, electric conductivity at quarter and cow levels, and somatic cell counts were recorded. Data were collected between January 2015 and September 2017 from a dairy farm that used an AMS as well as a dairy herd management program. The Lely Astronaut system (Lely Industries N.V., Maassluis, The Netherlands) equipped with in-line sensors for electric conductivity (EC) and SCC was used to milk cows and monitor their performance. The main features used in this study were measured by the AMS (EC, SCC, daily milk yield), to which we added six engineered features representing the class-wise 7-day moving average (Ma) of SC, EC and milk yield, as well as their standard deviations. Hence, the mastitis cases used in this study referred to the alarm raised by the AMS due to changes detected in milk. Descriptions of abnormal milk (n = 54), mastitis (n = 398), high conductivity (n = 14), watery milk (n = 2) were classified as positive cases, while instances where no alarm was raised were classified as negative cases (n = 74,749). The average conductivity was 68.44 ± 3.42 µS/cm, and the average SCC was 93.86 ± 188.29 × 103 cells/mL. The dataset contained missing values for predictors, as presented in Table 1.

Table 1.
Description of the dataset.
2.2. Data Preparation
2.2.1. Libraries and Packages Used for Data Preparation and Modeling
All analyses were performed in Python, using numpy, pandas, scikit learn and imblearn libraries. The main scikit-learn modules used were preprocessing and calibration to scale the data with a standard scaler and calibrate the classifiers. The model selection module was used to split training, validation and test sets and to perform grid-search cross-validation. The fivefold cross-validation using the k-fold strategy was also performed with the GridsearchCV function to obtain optimal parameters and conduct hyperparameter tuning for each model. The impute and experimental modules were used to impute missing values with simple and multivariate imputers. Machine learning models were implemented with the linear model, tree, ensemble and neural network modules. We selected four common supervised learning models: logistic regression (LR), decision tree (DT), random forest (RF) and multilayer perceptron (MLP) [27]. We imported confusion matrix, roc_auc_score, ross_val_score, cross_val_predict, fscore, cohen_kappa_score, precision, recall roc_curve from the metrics module to compute precision metrics and plot the ROC curves. We used the oversampling and combine modules of imblearn to perform the resampling methods [28]. The plotting of ROC curves was aided by the pyplot package of matplotlib library [20]. Finally, we used the statsmodels library to compare the metrics of the models tested and determine for each model type whether resampling, imputation or both influenced the observed performance.
2.2.2. Training, Validation and Test Data Split
The dataset was loaded and checked for inconsistencies before further processing. Inconsistencies such as missing dates, missing all values across one observation, outliers that could have resulted from erroneous measurement or recording, and the corresponding data were cleaned. The data were then split into training and test sets at a ratio of 80:20. The test set was excluded from further processing and model building. This split ratio and procedure have been previously applied in studies of mastitis prediction using machine learning with a sample size comparable to that of the current study [14,18,31]. The training set was further split into training and validation sets and subjected to further processing and model evaluation.
2.3. Missing-Value Imputation
We followed two directions for further data processing. On one hand, all missing values were deleted from the dataset, meaning only complete cases (CCs) (for which no missing imputation was required) remained. On the other hand, data with missing values were processed with one of three selected imputation techniques: simple imputer (SI), multiple imputer (MI) and linear interpolation (LI). We performed the simple imputer technique with the strategy of replacing missing values with the mean. Due to the simplicity of its computation, the SI method is widely used for imputing missing values in livestock datasets used for disease prediction with machine learning. Previous studies on the prediction of several diseases in dairy cows using sensor data found this imputation method satisfactory to impute missing values where less than 20% of data for a variable were missing [9,10]. The MI works by modeling missing values of a given variable on the basis of other features in the data frame, and in an iterative process, it designates a column as the output (y) and the others as inputs (X). Then, a regressor is fit on (X, y) for the known y and used to predict the missing y. The process is repeated for the set maximum number of iterations (n = 10 for this study), and the final imputation round is returned [32]. Although the method is reputed for its robustness, it is not widely reported in disease prediction studies for dairy cows. Some use cases include the modeling of the perinatal mortality of calves and the application of machine learning to animal breeding [11,12]. The LI procedure is mostly used in cases where the pattern of missingness is associated with a time dimension (days or hours). Hence, a timewise replacement of the missing value is preferred to SI or MI. This procedure is reported for the prediction of lameness, mastitis and milk yield in dairy cows [13,14]. In the current study, we implemented the interpolate function with the linear method and the bidirectional replacement of missing values (forward and backward). Hence, two datasets—one with only complete cases and one with missing replaced values—would form the basis for data processing. They had imbalance ratios of 53.76 and 156.52, respectively (Table 2).

Table 2.
Imbalance ratio of the initial datasets.
2.4. Resampling Methods
The two sets of data were submitted to the three resampling methods described in the introduction, namely the Synthetic Minority Oversampling Technique (SMOTE), the SMOTE technique combined with Edited Nearest Neighbors (SMOTEEN) and the SMOTE technique combined with Support Vector Machine (SVM) classifier (SVMSMOTE). The SMOTE technique oversampled the minority class without altering the majority class, and we set the k neighbors to implement the oversampling at n = 5. The ‘k neighbors’ represent the neighborhood of samples used to generate the synthetic samples [30]. The SMOTEEN technique not only oversampled the minority class but also undersampled the majority class, and here, the k neighbors were set at n = 5, while for the Edited Nearest Neighbors, the undersampling was set at n = 3. The SVMSMOTE technique oversampled the minority class along the borderline and used the Support Vector Machine (SVM) classifier to predict new cases. We used n = 5 for k neighbors and n = 10 for m_neighbors, which represents the nearest neighbors used to determine if a risk of misrepresenting a minority sample exists (Table 3) [30]. The settings used for implementing the resampling methods are reported to provide the best results [31,33,34].

Table 3.
Imputed datasets without resampling and resampled with SMOTE, SMOTEEN, and SVMSMOTE methods.
2.5. Model Building, Evaluation and Parameter Tuning
We obtained 16 datasets from the implementation of resampling and imputation methods that were subjected to four common machine learning classifiers: logistic regression (LR), decision tree (DT), random forest (RF) and multilayer perceptron (MLP). The classifiers were chosen because of their different approaches of segregating classes to predict each category for a binary outcome variable. The LR is best for simple, interpretable cases where linear relationships can be drawn. It is often the first choice for simple datasets and was selected to find out how it would perform with the complexity of missingness and imbalance. Hence, the other models (DT, RF and MLP), with increasing levels of robustness and reducing levels of interpretability, were chosen to compare their performance on this type of data with the basic LR model. Hence, for each classifier, four datasets were applied to each imputation method, and there were four others for resampling techniques, while sixteen (one for each combination) were applied to the combination of resampling and imputation. The performance of the classifiers was evaluated using accuracy, precision, recall, F1 score and Cohen’s kappa score from the scikit-learn metrics. They were computed from a confusion matrix (Table 4), where the correctly classified positive and negative cases are labelled true positive (TP) and true negative (TN). Positive cases incorrectly classified as negative are labelled false negative (FN), while negative cases incorrectly classified as positive are labelled false positive (FP).

Table 4.
Representation of a confusion matrix.
Accuracy is the most commonly used metric and the starting point to evaluate the performance of classifiers. Accuracy is the proportion of correct predictions (true positive, true negative) among all examined cases [7]. The formulae to compute performance metrics are presented below:
Accuracy = (TP + TN)/(TP + FP + TN + FN)
Sensitivity, recall, true-positive rate TPR = TP/(TP + FN)
Positive predictive value, precision PPV = TP/(TP + FP)
False-positive rate FPR = FP/(FP + TN)
Specificity, true-negative rate TNR = TN/(TN + FP)
Negative predictive value NPV = TN/(TN + FN)
F1 score = 2 × TP/2 × (TP + FP + FN) = 2 × (precision × recall)/(precision + recall)
Kappa score = (p0 − pe)/(1 − pe), where p0 is the observed agreement ratio on the assigned label assigned to any sample, and pe is the expected agreement when both annotators assign labels randomly [27].
Since the accuracy score for unbalanced problems often provides an overoptimistic estimation of the classifier ability to predict the majority class [24], the use of other performance metrics and ROC plots could strengthen the obtained meaning of model performance. The ROC plots the true-positive rate and the false-positive rate at various thresholds values. The F1 score is a weighted (harmonic) mean of sensitivity and precision. The Cohen’s kappa value compares the classifier’s performance to the probability that its performance may only be based on chance. In general, predictions from models with kappa values <0.20 are considered poor; values between 0.21 and 0.40 are fair; values from 0.40 to 0.60 are moderate; and above 61 is considered substantial to almost perfect [25]. Twenty-nine out of eighty models tested for the current study had a kappa score <20, and none of the models had a kappa value >50.
Model tuning consisted of finding the best parameters for each model resulting from the imputation and resampling methods. We performed a fivefold cross-validation and a grid search of parameters to obtain the best values for each model. A full description of the parameter tuning and model fitting can be found in Supplementary File S2. In a nutshell, the grid-search cross-validation for LR models included solver (lbfgs, liblinear), penalty criteria (l2, l1, elasticnet), and C (0.1 to 100) in a fivefold cross-validation. The liblinear solver, the l2 penalty and the C value of 100 were selected for the best LR model. The C value of 0.1 was selected for all datasets except for the one from LI, whose C value was 10.
The grid-search cross-validation for DT models included the criterion (gini, entropy), max depth (None, 2–20), max features (None, sqrt, log2, 0.2 to 0.8), and splitter (best or random). The cross-validation was set to fivefold. The selected criterion was gini, the max depth was n = 8 and the splitter criteria set to best. (See Supplementary File S1).
For RF models, criterion (gini, entropy and log_loss), max depth (None, 2–20), and max features (None, sqrt, log2, 0.2–0.8) in a fivefold cross-validation were included in the grid search. The best-performing RF model was fitted with the criterion set to entropy, the max depth n = 20, max features = None and class weight = balanced.
The grid search cross-validation parameters for MLP models included activation (identity, logistic, tanh, relu), solver (lbfgs, sgd, adam), alpha (0.0001 to 0.01), learning rates (constant, invscaling, adaptive) and cross-validation (cv = 5). The best-performing MLP model was fitted with activation logistic, learning rate = invsaling, solver= lbfgs, and alpha= 0.05 (See Supplementary File S1).
Thus, we ranked the classifiers’ performance metrics first by kappa value and then by the f1 score and precision/ recall scores, regardless of the accuracy score. We also examined the ROC curves of the best models to evaluate their performance at various thresholds. Finally, we assessed the contribution of resampling or imputation techniques or both on the prediction performance of the ML classifiers using AIC values. An overview of the complete workflow performed in this study is shown in Figure 1.

Figure 1.
Data processing and analysis workflow. The figure shows how the test set was split from the original dataset. The two lines of processing with complete cases and with missing values. The data with missing values were imputed with SI, MI and LI, while the complete case analysis was without missing values. All the datasets were then submitted to resampling, creating 16 datasets that were split into training and validation sets to train and evaluate the models before testing the final model on the test set.
3. Results
3.1. Performance Metrics of ML Models Trained on Data with Different Missing-Value Imputation Techniques
The results show a concordance between performance metrics for SGD, DT, and MLP, while for LR, the accuracy and recall scores concur, and for RF, accuracy concurs with F1 and kappa scores only. Based on the kappa scores, the CC performed highest with RF (0.782). The SI performed better with LR (0.277), DT (0.668) and MLP (0.574). The precision score was highest with LI for DT, RF and MLP (precision = 0.580, 0.634 and 0.462, respectively), while it was highest with CC for SGD (0.329) and with SI for LR (0.250). Overall, RF had the highest kappa score (0.782), followed by DT (0.668), MLP (0.574), SGD (0.370) and LR (0.277), respectively (Table 5 and Table S1).

Table 5.
Performance metrics of ML models from data without missing-value imputation techniques (CC), with simple imputer (SI) linear interpolation (LI) and multiple imputer (MI). The score of the performance metrics for each imputation method represents the mean of four datasets tested for each model (n = 4).
3.2. Performance Metrics of ML Models Trained on Data with Different Resampling Techniques
The results for resampling indicate that most models had higher precision but lower recall without resampling. The F1 and kappa scores concurred with the precision score for all models except the MLP. The precision of the LR models were lowest and decreased with the complexity of the resampling methods (0.69 for no resampling, vs. 0.13, 0.12 and 0.11 for SMOTE, SMOTEEN, and SVMSMOTE). On the other hand, the recall increased from 0.46 for no resampling to 0.98 for SVMSMOTE. The RF had the overall highest performance (kappa = 0.81), of which the highest accuracy (0.99) and precision scores (0.90) were without resampling, while the highest recall was with SVMSMOTE (0.98) (Figure 2 and Table S1).
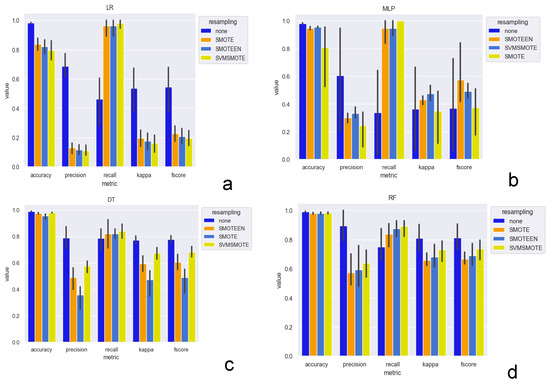
Figure 2.
Performance metrics of ML models from data with resampling techniques: Models tested were LR (a), MLP (b), DT (c) and RF (d).
3.3. Ranking of the Prediction Scores of Individual Machine Learning Models with Both Resampling and Imputation Methods*
The RF models exhibited the highest performance, with four out of the top five rankings, while LR had the lowest ranking. The top-performing classifiers did not undergo resampling, were imputed with MI for RF (kappa = 0.962), LI for DT (0.811) and SI for MLP (0.781), and for LR (0.607). The best-performing resampling methods used were SVMSMOTE and SMOTE, that produced fair to moderate kappa scores (>0.35). The best discriminative classifiers had lower kappa scores (0.239–0.607). MLP models recorded low prediction accuracy (kappa = 0.229 − 0.332) with LI, CC and MICE, both with and without resampling methods. (Table 6).

Table 6.
Performance metrics of best-ranked ML models. Top five models with kappa > 0.20 were selected for each model category. The full list of ranked models can be found in Table S1).
4. Discussion
This study demonstrated the influence of resampling and imputation techniques on the prediction performance of three machine learning models trained to detect mastitis incidences from automated milking systems data. Features included quarter and cow-level conductivity, milk yield and in-line somatic cell count, with their seven-day moving averages and standard deviations, from a conventional dairy farm in Germany. The study is based on the analysis of data collected by a milking robot and hence should be understood in the context of mastitis prediction with sensor-collected data. The sensors offer the advantage of data with high time resolution, but they bring along the issues of misrecording and missing values. Handling the latter is the purpose of the current study. Although the nature of data recording with sensors can be seen as a limitation compared to data generated in controlled conditions, it offers greater opportunities for applications in practice in dairy farms, especially because of the increasing use of automated milking systems. Three types of classifiers were evaluated: classical discriminative classifiers (LR), ensemble classifiers (DT and RF), and a neural network-based classifier (MLP). We considered the data with complete cases (without missing values) as the control or ground-truth dataset to which resampling methods were compared for each classifier. The dataset without resampling was used to control ML classifiers’ performance using resampling techniques (namely SMOTE, SMOTEEN, and SVMSMOTE). Additionally, within each case of imputation (CC, SI, MI, and LI), we evaluated the performance improvement contributed by both imputation and resampling methods.
We found that, on average, the recall scores of DT, RF and MLP classifiers subjected to CC analysis were lower than those subjected to imputation techniques. In contrast, the precision score was higher than that of imputation techniques for RF and DT only. The CC analysis was considered in this study as the reference dataset for the ones with the imputation methods. Mukaka et al. [35] argue in the same direction, stating that CC analysis can generate unbiased estimates for binary outcomes while achieving high statistical coverage. Therefore, they recommended using CC analysis to complement that with imputation techniques.
The analysis of model-specific performance revealed that ensemble models had the highest performance metrics with the lowest difference between precision and recall regardless of the imputation technique used. In contrast, the discriminative models (LR) had the highest difference between precision and recall scores. Bobbo et al. [14], comparing machine learning models for the prediction of udder health status, also reported a better performance for ensemble and neural network-based models than linear models. In our study, for instance, the RF classifier had the best performance with MI (kappa = 0.96), CC (kappa = 0.83) without resampling, and SMOTEEN resampling without imputation (kappa = 0.811). The best two DT models were with LI and SI without resampling (kappa = 0.81 and 0.79, respectively). This trend was confirmed by the ROC curves for RF and DT that had higher TPR (>90%) and lower FPR (<10%) for RF with imputation methods compared to CC (Supplement). Findings by Tiwaskar et al. [36] confirm this improvement in machine learning models’ performance with imputation techniques in a study where they tested RF models with various levels of missing values. Performance improvement was observed not only for ensemble models but also for others. Simple imputer improved the performance of LR (kappa = 0.61 vs. 0.24) compared to CC without resampling. Overall, the LR models had high recall and lower precision scores for CC than imputation techniques, leading to lower kappa scores than ensemble models. The ROC curves with higher or similar performance for CC than imputation techniques, regardless of the resampling techniques, confirm this (Supplement). Mukaka et al. [35] also found better CC analysis results than imputation techniques for binary outcomes with LR. Other authors [29,30] found the opposite and suggested that imputation was better than CC analysis. On the one hand, this can be explained by the fact that imputation techniques, especially for MI, increase the variability in the outcome values that inflates the standard error of the effect-size estimate, probably caused by a random component added to the missing outcome values [24,25,35]. On the other hand, the difference can also be attributed to the mechanisms of occurrence of missing values, for which [35] provided an in-depth analysis and suggested a thorough examination before deciding on the imputation method to apply. Hence, in-depth feature engineering with techniques such as interaction features, binning and more domain-specific transformation than only moving averages can be explored in further studies to improve ML performance with the resampling and imputation techniques presented in our study. Looking at the time-series dimension as well as applying weighted loss to discriminative classifiers such as LR may also be explored to improve their performance.
The comparison among imputation methods showed that LI performed either similarly or worse than SI or MI for all models. According to [19], this could be due to the lack of data segregation before applying linear imputation to datasets. They suggested that LI methods estimate the value of the missing data based on two adjacent data points in a dimensional sequence. Hence, for datasets where many consecutive data points still need to be included, such as in the AMS data used in the current study, the performance of LI may need to be improved. The LI imputation method relies mainly on time-dependent missing-value imputation instead of inter-attribute correlations employed by other imputation techniques [35]. For this reason, LI is incredibly efficient for time series and has been reported to improve the performance of neural network-based classifiers in other studies [36,37]. This is less of an issue for ensemble models that work by segregating data into similar packets small enough to identify their inherent patterns in the terminal nodes. For example, decision trees have two kinds of nodes and determine, for each leaf node, a class label with a majority vote of training examples reached by the leaf. Further, they treat each internal node as representing a question on features that will branch out according to the answers found. Hence, they split the leaves of a tree until questions are exhausted [38]. Therefore, these intrinsic characteristics of the ensemble models and LI led to no significant performance improvement compared to other imputation techniques or complete cases. Following the approach suggested by [27], it could be beneficial to segregate the data before submitting it to LI for better results. This data segregation may not be helpful for ensemble models, which are reputed to be robust enough to yield good performance with SI and MI and sometimes without imputing missing values, as explained above [39]. Indeed, four of the top ten models in this study were RF or DT without missing imputation.
The performance of ML models from resampled datasets showed similar behavior to that of the missing-value imputation. The RF models had the highest metrics, followed by DT, MLP and LR. Resampling improved the recall scores of all classifiers. The SVMSMOTE had the best recall score for all models and the best or comparable precision scores for DT, RF and MLP. Nithya et al. [40] similarly suggested that integrating ensemble models with SVMSMOTE allows for the more effective handling of imbalanced datasets. The SMOTE was slightly better than other resampling techniques for LR, which are reported to perform better with more balanced datasets [41,42]. The evaluation of model fit revealed that both resampling and missing-value imputation are relevant to explaining the performance of most of the tested ML models.
The MLP model performed moderately with imputed data, even without resampling. This finding aligns with reports that the method improves the performance of neural network-based models; hence, it could be applied to these ML models without resampling [36,37]. The same behavior was observed for SI and MI data fitted to DT and RF models, resulting in better performance than CCs. The SVMSMOTE for LR performed better without imputation than the data where missing values were imputed. This improvement suggests that an improvement in the class imbalance between the classes (majority and minority) is beneficial for the performance of these classifiers [41,43,44]. Indeed, some studies have applied resampling methods without imputation with satisfactory prediction performance. Random forest, DT, and, to some extent, MLP, had models with good performance without resampling or missing-value imputation [37,39,45]. These models are reported to have robust mechanisms to handle imbalances and missing values. They are sometimes used to preprocess data and predictions [46,47]. However, in the case of AMS data for mastitis prediction, it always seems reasonable to compare results from resampling/imputation techniques and those without to assess the extent of performance improvement. In this context, the data without resampling or imputation may serve as the ground truth to evaluate the preprocessing techniques.
5. Conclusions
Based on our research, the choice between missing-value imputation and resampling techniques for machine learning models depends on the specific model being used. We found that complete case analysis yielded higher kappa scores than missing-value imputation techniques for logistic regression (LR), while random forest (RF), decision tree (DT), and multilayer perceptron (MLP) performed better with imputation techniques. We also noticed significant variations between models and agreement between accuracy, F1 score, precision, and recall metrics with kappa. For ensemble models, resampling with the Synthetic Minority Oversampling Technique (SMOTE) or Support Vector Machine SMOTE (SVMSMOTE) improved classification performance using simple imputations or complete cases. In addition, linear interpolation (LI) and SMOTE resampling improved MLP classification, while LR performed better with complete cases and SVMSMOTE resampling. Therefore, we suggest using SVMSMOTE sampling for studies with similar class-imbalance problems when using LR or ensemble models for classification, and SMOTE when using an MLP classifier. However, in cases where missing values are significant, simple imputation for ensemble models and linear interpolation for MLP will enhance classifier performance. When dealing with missing-value imputation, we recommend comparing results from imputed datasets with complete cases.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/agriengineering6030195/s1, Supplementary File S1. ROC curves for resampling methods. Supplementary File S2. ROC curves for the ML models performance with resampling methods.
Author Contributions
Conceptualization: O.K., C.A. and T.K.; methodology: O.K., C.A. and L.M.; data processing and analysis: O.K.; validation: C.A., T.K., L.M., O.K., T.A., P.S.B., B.A. and M.D.; original draft preparation: O.K. and T.K.; review and editing: T.K., C.A., L.M., P.S.B., T.A., B.A. and M.D.; supervision: T.A. and B.A.; project administration: T.K., P.S.B., M.D., T.A. and B.A.; funding acquisition: T.A. and B.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Federal Ministry of Food and Agriculture (BMEL, Germany) based on a resolution of the German Bundestag. The article is funded through the project MEDICow; funding was provided by the Federal Office of Agriculture and Food (BLE, Germany) within the framework of the federal program ‘Livestock Husbandry’ (grant number: 28N206601).
Data Availability Statement
The data used to produce the results presented in this manuscript will be made available upon reasonable request. The source code used to produce the results presented in this manuscript can be availed freely at https://github.com/Okashongwe/resampling_mast.git, accessed on 26 July 2024.
Acknowledgments
The authors wish to thank the dairy farm for the support and provision of data.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Cheng, W.N.; Gu, H.S. Bovine Mastitis: Risk Factors, Therapeutic Strategies, and Alternative Treatments-A Review. Asian-Australas. J. Anim. Sci. 2020, 33, 1699–1713. [Google Scholar] [CrossRef] [PubMed]
- Egyedy, A.F.; Ametaj, B.N. Mastitis: Impact of Dry Period, Pathogens, and Immune Responses on Etiopathogenesis of Disease and its Association with Periparturient Diseases. Dairy 2022, 3, 881–906. [Google Scholar] [CrossRef]
- Hogeveen, H.; Steeneveld, W.; Wolf, C.A. Production Diseases Reduce the Efficiency of Dairy Production: A Review of the Results, Methods, and Approaches Regarding the Economics of Mastitis. Annu. Rev. Resour. Econ. 2019, 11, 289–312. [Google Scholar] [CrossRef]
- Sweeney, M.T.; Gunnett, L.; Kumar, D.M.; Lunt, B.L.; Moulin, V.; Barrett, M.; Gurjar, A.; Doré, E.; Pedraza, J.R.; Bade, D.; et al. Antimicrobial susceptibility of mastitis pathogens isolated from North American dairy cattle, 2011–2022. Vet. Microbiol. 2024, 291, 110015. [Google Scholar] [CrossRef]
- Martins, S.A.; Martins, V.C.; Cardoso, F.A.; Germano, J.; Rodrigues, M.; Duarte, C.; Bexiga, R.; Cardoso, S.; Freitas, P.P. Biosensors for On-Farm Diagnosis of Mastitis. Front. Bioeng. Biotechnol. 2019, 7, 186. [Google Scholar] [CrossRef] [PubMed]
- Tommasoni, C.; Fiore, E.; Lisuzzo, A.; Gianesella, M. Mastitis in Dairy Cattle: On-Farm Diagnostics and Future Perspectives. Animals 2023, 13, 25381. [Google Scholar] [CrossRef]
- Haxhiaj, K.; Wishart, D.S.; Ametaj, B.N. Mastitis: What It Is, Current Diagnostics, and the Potential of Metabolomics to Identify New Predictive Biomarkers. Dairy 2022, 3, 722–746. [Google Scholar] [CrossRef]
- Bernhardt, H.; Höhendinger, M.; Gräff, A.; Hijazi, O.; Höld, M.; Reger, M.; Stumpenhausen, J. Development of Automatic Milking in Germany. In Proceedings of the 2019 ASABE Annual International Meeting, Boston, MA, USA, 7 July–10 July 2019; American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2019; p. 1. [Google Scholar]
- Kaswan, S.; Chandratre, G.A.; Upadhyay, D.; Sharma, A.; Sreekala, S.M.; Badgujar, P.C.; Panda, P.; Ruchay, A. Applications of sensors in livestock management. In Engineering Applications in Livestock Production; Academic Press: Cambridge, MA, USA, 2024; pp. 63–92. [Google Scholar]
- D’Anvers, L.; Adriaens, I.; Brulle, I.V.D.; Valckenier, D.; Salamone, M.; Piepers, S.; De Vliegher, S.; Aernouts, B. Key udder health parameters on dairy farms with an automated milking system. Livest. Sci. 2024, 287, 105522. [Google Scholar] [CrossRef]
- Bonestroo, J.; van der Voort, M.; Hogeveen, H.; Emanuelson, U.; Klaas, I.C.; Fall, N. Forecasting Chronic Mastitis Using Automatic Milking System Sensor Data and Gradient-Boosting Classifiers. Comput. Electron. Agric. 2022, 198, 107002. [Google Scholar] [CrossRef]
- Bobbo, T.; Biffani, S.; Taccioli, C.; Penasa, M.; Cassandro, M. Comparison of Machine Learning Methods to Predict Udder Health Status Based on Somatic Cell Counts in Dairy Cows. Sci. Rep. 2021, 11, 13642. [Google Scholar] [CrossRef]
- Hyde, R.M.; Down, P.M.; Bradley, A.J.; Breen, J.E.; Hudson, C.; Leach, K.A.; Green, M.J. Automated Prediction of Mastitis Infection Patterns in Dairy Herds Using Machine Learning. Sci. Rep. 2020, 10, 4289. [Google Scholar] [CrossRef] [PubMed]
- Post, C.; Rietz, C.; Büscher, W.; Müller, U. Using Sensor Data to Detect Lameness and Mastitis Treatment Events in Dairy Cows: A Comparison of Classification Models. Sensors 2020, 20, 3863. [Google Scholar] [CrossRef] [PubMed]
- Fadul-Pacheco, L.; Delgado, H.; Cabrera, V.E. Exploring Machine Learning Algorithms for Early Prediction of Clinical Mastitis. Int. Dairy J. 2021, 119, 105051. [Google Scholar] [CrossRef]
- Abdul Ghafoor, N.; Sitkowska, B. MasPA: A Machine Learning Application to Predict Risk of Mastitis in Cattle from AMS Sensor Data. Agriengineering 2021, 3, 575–583. [Google Scholar] [CrossRef]
- Tian, H.; Zhou, X.; Wang, H.; Xu, C.; Zhao, Z.; Xu, W.; Deng, Z. The Prediction of Clinical Mastitis in Dairy Cows Based on Milk Yield, Rumination Time, and Milk Electrical Conductivity Using Machine Learning Algorithms. Animals 2024, 14, 427. [Google Scholar] [CrossRef]
- Hannon, F.P.; Green, M.J.; O’grady, L.; Hudson, C.; Gouw, A.; Randall, L.V. Predictive modelling of deviation from expected milk yield in transition cows on automatic milking systems. Prev. Vet. Med. 2024, 225, 106160. [Google Scholar] [CrossRef]
- Dominiak, K.N.; Kristensen, A.R. Prioritizing Alarms from Sensor-Based Detection Models in Livestock Production—A Review on Model Performance and Alarm Reducing Methods. Comput. Electron. Agric. 2017, 133, 46–67. [Google Scholar] [CrossRef]
- Van Buuren, S. Flexible Imputation of Missing Data; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Madley-Dowd, P.; Hughes, R.; Tilling, K.; Heron, J. The Proportion of Missing Data Should Not Be Used to Guide Decisions on Multiple Imputation. J. Clin. Epidemiol. 2019, 110, 63–73. [Google Scholar] [CrossRef]
- Pham, T.M.; Pandis, N.; White, I.R. Missing Data: Issues, Concepts, Methods. Semin. Orthod. 2024, 30, 37–44. [Google Scholar] [CrossRef]
- Woods, A.D.; Gerasimova, D.; Van Dusen, B.; Nissen, J.; Bainter, S.; Uzdavines, A.; Davis-Kean, P.E.; Halvorson, M.; King, K.M.; Logan, J.A.; et al. Best practices for addressing missing data through multiple imputation. Infant. Child Dev. 2024, 33, e2407. [Google Scholar] [CrossRef]
- Li, J.; Wang, Z.; Wu, L.; Qiu, S.; Zhao, H.; Lin, F.; Zhang, K. Method for Incomplete and Imbalanced Data Based on Multivariate Imputation by Chained Equations and Ensemble Learning. IEEE J. Biomed. Health Inform. 2024, 28, 3102–3113. [Google Scholar] [CrossRef] [PubMed]
- Huang, G. Missing Data Filling Method Based on Linear Interpolation and Lightgbm. Proc. J. Phys. Conf. Ser. 2021, 1754, 012187. [Google Scholar] [CrossRef]
- Khushi, M.; Shaukat, K.; Alam, T.M.; Hameed, I.A.; Uddin, S.; Luo, S.; Yang, X.; Reyes, M.C. A Comparative Performance Analysis of Data Resampling Methods on Imbalance Medical Data. IEEE Access 2021, 9, 109960–109975. [Google Scholar] [CrossRef]
- Johnson, J.M.; Khoshgoftaar, T.M. A Survey on Classifying Big Data with Label Noise. J. Data Inf. Qual. 2022, 14, 43. [Google Scholar] [CrossRef]
- Guo, J.; Wu, H.; Chen, X.; Lin, W. Adaptive SV-Borderline SMOTE-SVM algorithm for imbalanced data classification. Appl. Soft. Comput. 2024, 150, 110986. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- van Leerdam, M.; Hut, P.R.; Liseune, A.; Slavco, E.; Hulsen, J.; Hostens, M. A Predictive Model for Hypocalcaemia in Dairy Cows Utilizing Behavioural Sensor Data Combined with Deep Learning. Comput. Electron. Agric. 2024, 220, 108877. [Google Scholar] [CrossRef]
- Ghorbani, R.; Ghousi, R. Comparing Different Resampling Methods in Predicting Students’ Performance Using Machine Learning Techniques. IEEE Access 2020, 8, 67899–67911. [Google Scholar] [CrossRef]
- Lemaître, G.; Nogueira, F.; Aridas, C.K. Imbalanced-Learn: A Python Toolbox to Tackle the Curse of Imbalanced Datasets in Machine Learning. J. Mach. Learn. Res. 2017, 18, 1–5. [Google Scholar]
- Kiouvrekis, Y.; Vasileiou, N.G.C.; Katsarou, E.I.; Lianou, D.T.; Michael, C.K.; Zikas, S.; Katsafadou, A.I.; Bourganou, M.V.; Liagka, D.V.; Chatzopoulos, D.C.; et al. The Use of Machine Learning to Predict Prevalence of Subclinical Mastitis in Dairy Sheep Farms. Animals 2024, 14, 2295. [Google Scholar] [CrossRef]
- Bagui, S.S.; Mink, D.; Bagui, S.C.; Subramaniam, S. Determining Resampling Ratios Using BSMOTE and SVM-SMOTE for Identifying Rare Attacks in Imbalanced Cybersecurity Data. Computers 2023, 12, 204. [Google Scholar] [CrossRef]
- Liu, J.-J.; Yao, J.-P.; Liu, J.-H.; Wang, Z.-Y.; Huang, L. Missing data imputation and classification of small sample missing time series data based on gradient penalized adversarial multi-task learning. Appl. Intell. 2024, 54, 2528–2550. [Google Scholar] [CrossRef]
- Park, I.; Kim, H.S.; Lee, J.; Kim, J.H.; Song, C.H.; Kim, H.K. Temperature Prediction Using the Missing Data Refinement Model Based on a Long Short-Term Memory Neural Network. Atmosphere 2019, 10, 718. [Google Scholar] [CrossRef]
- Magallanes-Quintanar, R.; Galván-Tejada, C.E.; Galván-Tejada, J.I.; Gamboa-Rosales, H.; Méndez-Gallegos, S.d.J.; García-Domínguez, A. Neural Hierarchical Interpolation for Standardized Precipitation Index Forecasting. Atmosphere 2024, 15, 912. [Google Scholar] [CrossRef]
- Abidin, N.Z.; Ritahani, A.; Emran, A.N. Performance Analysis of Machine Learning Algorithms for Missing Value Imputation. ijacsa 2018, 9, 660. [Google Scholar] [CrossRef]
- Ou, H.; Yao, Y.; He, Y. Missing data imputation method combining random forest and generative adversarial imputation network. Sensors 2024, 24, 1112. [Google Scholar] [CrossRef]
- Nithya, R.; Kokilavani, T.; Beena, T.L.A. Balancing Cerebrovascular Disease Data with Integrated Ensemble Learning and SVM-SMOTE. Netw. Model. Anal. Health Inform. Bioinform. 2024, 13, 12. [Google Scholar] [CrossRef]
- Mukaka, M.; White, S.A.; Terlouw, D.J.; Mwapasa, V.; Kalilani-Phiri, L.; Faragher, E.B. Is Using Multiple Imputation Better than Complete Case Analysis for Estimating a Prevalence (Risk) Difference in Randomized Controlled Trials When Binary Outcome Observations Are Missing? Trials 2016, 17, 341. [Google Scholar] [CrossRef]
- Buabeng, A.; Simons, A.; Frempong, N.K.; Ziggah, Y.Y. A Novel Hybrid Predictive Maintenance Model Based on Clustering, Smote and Multi-Layer Perceptron Neural Network Optimised with Grey Wolf Algorithm. SN Appl. Sci. 2021, 3, 593. [Google Scholar] [CrossRef]
- Wongvorachan, T.; He, S.; Bulut, O. A Comparison of Undersampling, Oversampling, and SMOTE Methods for Dealing with Imbalanced Classification in Educational Data Mining. Information 2023, 14, 54. [Google Scholar] [CrossRef]
- Jian, C.; Gao, J.; Ao, Y. A New Sampling Method for Classifying Imbalanced Data Based on Support Vector Machine Ensemble. Neurocomputing 2016, 193, 115–122. [Google Scholar] [CrossRef]
- Tiwaskar, S.; Rashid, M.; Gokhale, P. Impact of machine learning-based imputation techniques on medical datasets-a comparative analysis. Multimed. Tools Appl. 2024, 1–21. [Google Scholar] [CrossRef]
- Upadhyay, A.; Singh, M.; Yadav, V.K. Improvised Number Identification Using SVM and Random Forest Classifiers. J. Inf. Optim. Sci. 2020, 41, 387–394. [Google Scholar] [CrossRef]
- Kaur, P.; Joshi, J.C.; Aggarwal, P. Estimation of missing weather variables using different data mining techniques for avalanche forecasting. Nat. Hazards 2024, 120, 5075–5098. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).