Optimizing Urban Public Transportation with a Crowding-Aware Multimodal Trip Recommendation System

Highlights

What are the main findings?

• A proof of concept for a multimodal public transportation recommendation system that explicitly integrates both QoS (e.g., crowding) and QoE (e.g., user preferences) for overcoming the limitations of traditional approaches in balancing load distribution of the transportation system.
• The BeT paradigm adoption to provide the architectural foundation for designing a framework to model and validate this balance effectively.

What is the implication of the main finding?

• The QoE-QoS balanced strategy enables transportation systems to reduce infrastructure stress while maintaining passenger satisfaction, demonstrating that crowd-aware recommendations can enhance both efficiency and user experience.

Abstract

Traditional multimodal public transportation recommenders often overlook in-vehicle crowding, a critical factor that causes passenger discomfort and leads to an inefficient distribution of people across the network that affects its reliability. To address this, we propose a proof of concept for a novel framework that directly integrates crowding into its optimization process, balancing it with user preferences such as travel habits, travel time, and line changes. Built on the Behavior-Enabled IoT (BeT) paradigm, our system is designed to manage the crucial QoE and QoS trade-off inherent in smart mobility. We validate our balanced strategy using real-world data from Lyon, comparing it against two baselines: a QoE-driven model that prioritizes user habits and a QoS-driven model that focuses solely on network efficiency. Our Wilcoxon-based statistical analysis demonstrates that a balanced strategy is the most effective approach for substantially mitigating public transit crowding. Our Wilcoxon-based statistical analysis demonstrates that a balanced strategy is the most effective approach for mitigating public transit crowding, since it leads to a substantial decrease in crowding. Despite a potential increase in travel times, our solution respects user habits and avoids excessive transfers, providing significant operational improvements without compromising passenger convenience.

1. Introduction

In urban areas, public transportation is a key component for improving the quality of life and alleviating crowding. However, vehicle crowding becomes a more pressing problem as public transit ridership increases.

In France, public transit use is widespread and growing, as seen in Lyon’s network (TCL), which experienced a 9.8% increase in passenger trips between 2014 and 2019 [1]. Crowding not only causes passenger discomfort and stress [2] but also leads to users actively seeking out less-congested routes or even skipping buses entirely, which results in an inefficient distribution of passenger load across the network. From an operational standpoint, crowding negatively impacts overall infrastructure performance by increasing in-vehicle time, travel times, and dwell times, ultimately reducing the reliability of the entire transit system [2,3].

A user survey, conducted with 325 users (mostly in Lyon), shows that passengers prioritize individual travel speed over comfort; however, high reported trust and a demonstrated willingness to accept slightly longer routes to avoid crowding (as in Figure 1) suggest that users are receptive to system recommendations aimed at improving collective efficiency through subtle optimization. Appendix A reports on all survey results.

TCL has been actively seeking solutions since the COVID-19 pandemic. A collaboration with Keolis, SYTRAL Mobilités, and Affluences led to a pilot project [4] in a Lyon metro station, where an AI-equipped camera system provides real-time crowding information via a color-coded light system. While early user feedback indicates that the system is highly positive and improves both comfort and efficiency, this information-based approach still relies on individual passenger choices and does not proactively manage network-wide load. This highlights the need for a more comprehensive solution.

Most of the trip-planning systems often prioritize individual user experience, but they fail to account for how those recommendations affect crowding [5,6,7,8,9,10]. When these systems do evaluate the impact of recommendations, they typically limit their analysis to road traffic congestion, and completely ignore in-vehicle crowding [11,12,13]. Other crowd-driven approaches, such as ComfRide [14] and SmartTransfer [15], often operate from a user-centric perspective, prioritizing individual satisfaction by balancing factors like travel time and perceived comfort. However, these systems have limited effectiveness in minimizing network-wide crowding because they rely on individual user preferences and lack a mechanism to distribute demand systematically. Similarly, Google Maps provides indicators to guide user choice, such as crowding, but leaves the responsibility of selecting the route entirely to the user, without addressing load balancing. Our balanced strategy addresses this shortcoming by selecting paths that minimize network crowding before offering a user-specific choice.

This work presents a proof of concept for a novel multimodal public transit system that balances the user’s Quality of Experience (QoE) with the infrastructure’s Quality of Service (QoS). Our balanced strategy addresses this by employing a two-phase selection process on the set of feasible paths. First, it identifies a curated subset of the top-k paths with the lowest crowding. From this reduced set, the system then ranks the paths based on QoE metrics and selects the one with the highest overall rank, ensuring that the solution mitigates in-vehicle crowding while still respecting key factors like station preference, travel time, and line changes. We applied the Behavior-enabled IoT(BeT) paradigm to facilitate the system’s architectural design. As a framework specifically developed to guide software architects in building smart city systems that balance QoE and QoS [16], the BeT paradigm provided a structured and effective modeling process for our proposed system.

The resulting framework, developed according to the BeT reference architecture, demonstrated that exploiting travelers’ flexibility, derived from analyzing their behaviors, improves in-vehicle crowding of the transportation system while still ensuring travelers’ satisfaction. This result was achieved by classifying the problem and mapping all the aspects identified by the BeT paradigm. This process allowed us to easily create a well-structured system that adheres to the main constraints of the paradigm’s reference architecture. We validated the framework using a real-world scenario based on extensive data from Lyon’s TCL public transportation network (https://www.tcl.fr, accessed on 10 October 2024).

To summarize, the main contributions of this paper are:

• A novel public transportation recommendation system ensuring a more efficient passenger load distribution while preserving user satisfaction, by directly integrating in-vehicle crowding metrics into the optimization process. Our balanced strategy has been compared to two baseline models: a QoE-driven baseline, which bases recommendations solely on user habits, and a QoS-driven baseline, which is “crowding-greedy” and prioritizes network efficiency over user preferences.
• The classification of the problem and the application of the BeT paradigm and the related modeling process to easily define a well-structured and validated architecture. This approach bypasses the need to create a new architecture from scratch, allowing for swift implementation. The resulting system is inherently robust because its structure is based on a proven blueprint, ensuring high confidence in its design and functionality.
• A method to infer the preferences for estimating travelers’ QoE from real-world datasets related to the transportation system of a large city. We uniquely used validation data from user subscriptions, a data source that is the primary one owned by public transportation providers but has not been utilized in previous studies.
• An extension of MnMS (https://github.com/licit-lab/MnMS, accessed on 4 November 2024) (Multimodal Network Modelling and Simulation) simulator for studying transportation systems with path choice policies based on the tradeoffs between QoE and QoS. We implemented the boarding denial mechanism and introduced additional path evaluation methods.

The rest of this work is structured as follows: Section 2 analyzes the state of the art of recommenders for transportation systems and introduces the BeT paradigm, detailing its core principles and concepts. Then, Section 3 applies the steps of the BeT modeling process to design the architecture of the proposed system and its components and present the experiments in Section 4, which include a smaller-scale validation and a real-life case study application in Lyon. Here we present and discuss the results, providing insights and analyzing the threats to the validity of the process that produced them. We outline the study’s potential limitations and threats to validity in Section 5. We conclude with a summary of contributions in Section 6, and directions for future works in Section 7.

2. Related Works and Background

2.1. Beyond Road Traffic: The Critical Gap in Public Transportation Recommendation Systems

Various systems [5,6,17] generate personalized recommendations but fail to verify their impact on network crowding. While some works, such as those by Namoun et al. [8], Ghalmane et al. [9], and the SPINE project [10], address environmental footprint by recommending greener routes, none of these systems evaluate the risk that their recommendations could lead to an undesirable redistribution of passengers, ultimately causing overcrowding in vehicles. Furthermore, a few other works that explicitly consider the congestion limit the concept to the road traffic [11,12,13]. However, some approaches introduce crowding as a factor, but with significant limitations. Comride [14] is a personalized route recommendation system for bus transit that aims to maximize user satisfaction. It achieves this objective by calculating a Route Comfort Index (RCI), a metric that combines historical data with a user’s preferences for factors like crowdedness and road quality. However, ComfRide’s approach is unilateral; its sole goal is to please the individual user. Our balanced strategy focuses on minimizing network-wide crowding to alleviate infrastructure burden. While the RCI includes crowding as a factor, its influence is dependent on user priority; therefore, the system will not effectively minimize crowdedness across the network if users do not prioritize it. Unlike ComfRide, our design involves a two-phase path selection process: we first identify and select the paths that minimize crowding, ensuring a positive impact on the network. We then offer the best choice that suits the user’s needs from the selected paths. Furthermore, while ComfRide is a unimodal system, limited to a single mode of transportation (buses), we leverage multimodality. The latter allows us to integrate different transportation options and expand the solution space, offering more flexible and optimized alternatives for the user and network sustainability and management. Like ComfRide, Google Maps operates from a user-centric perspective. Its core objective is to deliver highly specific travel advice to individuals, not to aid public transportation providers in balancing demand across their network. Furthermore, despite displaying real-time crowding data, this information does not serve as a primary decision criterion for route choice, as the platform prioritizes and ranks all route options based on the total travel time. SmartTransfer system [15] leverages a multi-task spatiotemporal learning model to predict passenger transfer volumes at different times and locations within a transportation network. First, it generates multiple candidate routes, and second, it ranks these routes based on both time costs and trip crowdedness. The system’s objective function calculates a weighted harmonic mean of crowdiness and travel time for each potential route. A user-defined weight parameter allows the system to prioritize one factor over the other, a feature that, like ComfRide’s RCI, makes the system’s effectiveness in managing network-wide crowding entirely dependent on individual user preferences. However, the study provides a proof of concept on a minimal set of routes but fails to demonstrate the system’s effectiveness at a large scale. The validation, while based on a real-world experiment, is primarily qualitative, focusing on “perceived comfort” and offering no numerical data to prove an actual reduction in crowding across the entire network. In essence, the system can balance time and comfort for a single trip, but provides no quantitative evidence of a positive impact on the overall transit system.

Table 1. Comparative Analysis of Multimodal Transport Systems.

System	QoE Metrics	QoS Metrics	Limitations
[5]	Travel time, cost, distance, weather, time, accessibility	-	Overlooks crowding implications
[6]	Travel time, cost, distance, travel habits, demographics	-	Overlooks system-wide implications; limited to taxi-bus and bus-cycle modes
[7]	Mode preferences, walking/cycling distance	-	No direct mechanism to mitigate crowding
[17]	User travel intentions	Network reliability	Does not verify any reduction in crowding
[7]	Mode preferences, walking/cycling distance, openness to new routes	Environmental friendliness, MaaS operator requirements	Lacks explicit mechanisms to mitigate crowding
[11]	Travel time, cost, and comfort	Road congestion	Exclusively focuses on car traffic congestion
[12]	Time perception and active transportation acceptability	Road congestion	Not canonical recommendation systems; exclusively focuses on car traffic congestion
[13]	Distance, travel cost	Road congestion	Exclusively focuses on car traffic congestion
[18]	Time-mode habits	Road congestion	Purely conceptual
[8]	Desired travel time, cost, carbon footprint	${\mathrm{CO}}_2$ emissions	Overlooks the risk of vehicle overcrowding.
[9]	Route distance, travel duration, safety, mode consistency, and route type	Environmental friendliness, ${\mathrm{CO}}_2$ savings	Overlooks the risk of vehicle overcrowding
[10]	Passenger satisfaction, waiting time, short waiting time, speed, parking capacity, accessibility	${\mathrm{CO}}_2$ savings	Overlooks the risk of vehicle overcrowding
[14]	RCI (weighted sum of various route features, like crowdedness and road quality)	-	Unilateral goal of maximizing a single user’s comfort, being unimodal, restricting the solution space, and failing to provide a globally optimal solution for the entire transport network
Google Maps	Travel time, travel cost, and number of transfers, road congestion, crowding	-	Prioritizes the shortest travel time; does not have mechanisms to mitigate network-wide crowding
[15]	Travel time, crowding	-	Failing to provide a globally optimal solution for the entire transport network, weak method validation
BeT-driven recommender	Station preference, travel time, line changes	In-vehicle crowding	-

reports a comprehensive comparison of examined solutions. Our work addresses this gap by proposing a proof of concept that explicitly and actively balances QoE and QoS, using in-vehicle crowding as a key metric to create a more efficient, but still comfortable, public transportation network.

2.2. Behavior Enabled IoT: Principles and Modeling Process

The Behavior-enabled IoT (BeT)paradigm [16] emerges as a solution, directly addressing these inherent limitations because it is built to deal with the QoE-QoS trade-off. Indeed, BeT distinguishes itself by explicitly considering the mutual influence between human behaviors and cyber-physical systems. By analyzing individual and collective behaviors, a BeT system dynamically adapts to improve QoE while maintaining QoS. Balancing system efficiency with user satisfaction often involves trade-offs, as their requirements may not always align. The system autonomously scales resources, adjusts configurations, and controls physical processes to optimize QoE. However, adaptive measures alone may not be sufficient when resources are limited, demand is high, or when the system cannot directly control every variable of a physical process or the surrounding environment that heavily relies on individual or crowd human actions. In such cases, strategies like user recommendations or environmental adjustments can influence behavior to achieve the desired outcomes.

A BeT system can be described as the interaction between a human agent and a system agent, mediated by a BeT Manager that handles QoE-QoS balancing (Figure 2). Each agent gathers data through a sensing interface to continuously update its behavioral model. The human agent collects data based on user interactions with the BeT system. The system agent monitors a physical process, gathering cyber-physical data. The balancer retrieves behavioral models to extract QoE and QoS constraints and data, optimizing their balance. As a result of this process, two types of outputs can be generated:

• Actuating operations modify the physical process to align with QoE requirements and are transmitted via the actuating interface.
• Suggestions for the users are sent through the recommending interface, aiming to reduce behavioral pressure on the system infrastructure. When the users accept the suggestion and change their behavior, this will affect the process we want to control.

The BeT paradigm provides a specific modeling process to support architects in designing well-structured systems that can balance QoE and QoS. The modeling process consists of three main stages that lead to defining a concrete architecture in the specific domain. Here, we briefly summarize the main steps of the process, while in the next section, we extensively describe the approach while designing the concrete architecture of the multi-modal recommendation system:

• QoE-QoS Analysis: We must clearly understand the system’s goals and constraints. It begins by identifying all relevant stakeholders, such as end-users, system operators, and infrastructure providers, and meticulously gathering their needs and expectations regarding both QoE and QoS. Next, these objectives are translated into concrete, measurable metrics and constraints. Constraints are limitations, such as maximum response time or energy consumption, minimum accuracy, or acceptable vehicle crowding. Mathematical formulations are often used to determine these metrics and constraints precisely. Finally, the phase delves into the relationship and potential trade-offs between QoE and QoS. It acknowledges that improvements in one area may impact the other and that there are often diminishing returns. This analysis helps to identify potential conflicts and develop strategies for balancing competing needs.
• Behavior Modeling and Balancing Strategy Definition: We identify observable properties and controllable resources. This involves determining what data can be collected (e.g., user location, system performance metrics) and what aspects of the system can be directly controlled (e.g., traffic signals, service schedules). Next, a behavior model is developed, integrating monitored properties, computed information, and external data sources. This model aims to simulate and predict (human or system) behavior. Then, we must develop a balancing strategy to optimize QoE and QoS. This strategy must consider defined constraints and find solutions satisfying user and system requirements. It involves determining the outputs of the strategy (e.g., recommendations, control actions), the recipients of these outputs, and the distribution channels.
• BeT Concrete System Design: This phase translates the abstract architecture into a concrete system. It involves designing individual components, defining their responsibilities, inputs, and outputs, and ensuring that they work together seamlessly. The framework has to be tailored to the specific scenario, adding necessary components to integrate data or other functionalities required by the particular application.

3. BeT-Driven Design Process and Modeling of a Multi-Modal Traveling Recommendation System

We follow the BeT modeling process to develop a BeT-driven reference architecture for the public transportation recommendation system.

3.1. QoE-QoS Analysis

The key stakeholders of a public transportation recommendation system include daily travelers and the infrastructure provider. Users seek to maximize their comfort and enjoy a smooth transition between their origin and destination, which includes avoiding crowded stations and lengthy travel paths. The infrastructure provider aims to offer the best possible service by minimizing user stress. This incentivizes subscriptions, generating revenue for infrastructure investment. The offered service should reduce the likelihood of incidents and problems and effectively redistribute crowds during such events to mitigate user discomfort and dissatisfaction.

Based on the analysis of existing solutions in literature (see Section 2), the QoE metrics can be travel time, cost, walking distance, number of transfers, and traveling habits, like mode and time preferences. Regarding QoS metrics, we can measure and forecast parameters like vehicle or station crowding and CO₂ emissions from traffic.

Generally, each individual possesses a limited set of preferred routes they tend to follow when frequently traveling to the same destination [19]. Furthermore, even when the destination changes, there is a common inclination to rely on familiar modes of transportation and solutions. An effective recommendation system must redirect users to mitigate infrastructure crowding. However, the suggested alternative should respect the user’s preferences, including their established transportation habits, and should not be excessively long or involve a significant number of transfers.

Moreover, to further enhance the system’s sophistication, it could intervene in vehicle scheduling by increasing service frequency in response to crowding. Alternatively, it could adjust traffic signal timings to manage urban traffic flow, affecting vehicles like trams or buses. Due to current constraints, these interventions are not planned for the present application case study. Nevertheless, it is advisable not to disregard this potential to establish a comprehensive recommendation architecture, as it could be realized through alternative means and in different settings.

3.2. Behavior Modeling and Balancing Strategy Definition

To compute QoE metrics such as travel time and walking distance, we require the city graph of the public transportation network to extract link lengths and the characteristics of public transportation vehicles, including speed. Additionally, knowledge of vehicle attributes (such as accessibility, air conditioning, and seat type) allows us to align these features with the QoE constraints provided by the user within their query. We require their historical location data within the network to model users’ daily travel patterns concerning time and preferred modes. For instance, in our case study, we have access to validation data provided by the public transportation operator. Similarly, other works, such as [6], obtained comparable information by extracting these features from the query history on their recommendation application. Furthermore, this information can be combined with external data, including weather conditions, seasonal factors, weekday/weekend distinctions, or national calendar events, to provide a more comprehensive understanding.

Calculating QoS metrics like traffic congestion or in-vehicle crowding necessitates knowing the vehicle capacity and having access to either a traffic congestion forecaster (ranging in sophistication) or fresh information received from edge in-vehicle nodes. Our case study simulates the latter. Therefore, it is reasonable as a QoE-QoS balancing strategy, given the k possible routes, to extract those that satisfy the QoS constraints and select the one that most closely aligns with the user’s preferences. If the users accept the suggestion, we will observe a change in the crowding distribution. This conclusion implies the necessity of a planning and evaluation phase that must be integrated with the architecture modules.

3.3. BeT Core Components’ System Design

Building upon the preceding elements, we defined a generalized architecture applicable to transportation systems, which was implemented in our case study. The BeT reference architecture modules are illustrated in Figure 3. The human agent receives the user’s Origin-Destination (OD) query, for which the user seeks a recommendation. In addition, the Sensing interface collects all user traveling data to compute the QoE metrics described in the previous steps. The human agent hosts the Human behavioral model, which captures user habits when interacting with the transportation system. At the same time, the system agent collects the public transportation network data to feed the related model. The latter uses fresh data and historical trends to estimate vehicle or station crowd levels.

The QoE-QoS balancer comprises two modules, a route planner and a route evaluator. The route planner is responsible for generating multiple candidate routes that connect the origin and destination across different modes of transportation (e.g., buses, trams, and subways). The route evaluator filters and prioritizes candidate routes by considering fresh crowding data and user preferences. The final output is a customized route suggestion to provide a comfortable and efficient journey, recommending alternative times or modes when it can help avoid crowded conditions. The suggestion is transmitted to the end-user through the recommendation interface. In the following subsections, we will delve deeper into the responsibilities of each module and explore potential methodologies for their construction.

3.3.1. Human Behavior Model

Behavioral modeling in multimodal transportation systems often uses graph-based approaches to represent users, locations, and transportation modes, learning embeddings to predict behavior like mode choice [6,20,21]. Other methods include hybrid collaborative filtering [22] and advanced statistical techniques like logit models [23,24,25,26]. Some studies also incorporate travel intention and traffic uncertainty [17] or quantify user values like comfort and safety [9,27]. All these models consider factors such as travel time, cost, and convenience. None of the examined studies have considered subscription validation data as a source. While various data, including road sensors, user clicks, smartphone data, and crowd-sourced feedback, were used for planning and validation, none of the studies mention using the specific validation data generated from public transportation user subscriptions. This highlights a gap in the current research, as public transportation providers own this primary data source and could offer unique insights into traveler behavior and preferences. Our solution specifically leverages ticket validation data to understand user movements in the absence of more granular data. This pragmatic approach allows us to implement our system using readily available information. However, our proposed framework is highly adaptable; it can be extended to use more advanced sources, such as GPS data from a user-provided app or in-vehicle sensors, enhancing the system’s accuracy and effectiveness further as new data collection technologies become available.

Our primary objective is to prove the benefits of our strategy. Therefore, we have opted for a straightforward yet effective approach to user behavior modeling. The model relies on a statistical analysis of historical public transportation usage data, which allows us to build a statistical representation of user preferences. To this end, we introduce the Behavior Index (BI), a metric that quantifies the frequency of a user’s interactions (e.g., ticket validations) within specific time intervals and locations. While this method is less complex than the machine learning or graph-based models previously mentioned, it is sufficient to demonstrate the integration of user behavior into the system’s decision-making process. Let J be the set of j-minute time intervals subdividing 24 h, and let D be the set of days d covered by our dataset. Each interval is small enough to group validations around the same time, regardless of the day, month, or year. A reasonable value might be 10 min. Let N denote the count operator and X the set of public transportation stations in the city. Within a defined j interval, we calculate the ratio of a person’s validation at a specific station x to their total number of validations across the entire dataset. The resulting ratio reflects how frequently a user enters a particular station.

The Behavior Index ($BI$) is formally defined as:

$$BI(u,x,j)={\displaystyle \frac{N(u,x,j(d\left)\right)}{{\sum }_{x\in X,j\in J,d\in D}N(u,x,j(d\left)\right)}}$$

(1)

where:

• N: the count operator.
• u: a user.
• x: a station within the set of all city stations X.
• j: j-minute time interval, which belongs to J, occurring on day d belonging to D.

The $BI$ provides a clear and concise way to understand how users’ validations are distributed across different locations and periods, offering valuable insights into their behavioral patterns.

The BI, as defined, is a static behavioral model. Because it is calculated on a one-time basis using a historical dataset, it provides a snapshot of a user’s past habits without adapting to the latest changes. This approach is sufficient for our purposes, as it guarantees data consistency for the duration of a specific simulation. However, in a complete and operational system, ensuring that the behavioral model is dynamic and continuously updated is crucial. The computational method remains the same, but the model’s inputs must be refreshed periodically to reflect a user’s evolving habits. The failure to adapt to new behaviors, such as a change in commute or the use of new routes, would quickly make the system’s recommendations obsolete and ineffective, undermining the reliability and relevance of the service. This behavior model has two main scalability challenges. The first is space complexity, as it requires significant storage to host the index for all users. The second is time complexity, which is tied to the current statistical approach. This method can be expensive because it may require recomputing all indexes whenever new validation data is registered. However, the scalability issue can be mitigated by allowing for non-consistent queries on the latest BI values, which are very fast.

Example: Consider Alice’s validation data for one month. She consistently boards a tram at Station A at 8:05 a.m. every Monday (4 times in the month). She also took the metro at Station B at 9:00 a.m. on 2 Saturdays within the last two weeks. If Alice has a total of 20 validations in the month:

• For Station A (8:00–8:10 a.m.): $N\left(\mathrm{Alice},\mathrm{Station}\mathrm{A},8:00–8:10\mathrm{a}.\mathrm{m}.\right)=4$.
• For Station B (8:00–8:10 a.m.): $N\left(\mathrm{Alice},\mathrm{Station}\mathrm{B},8:00–8:10\mathrm{a}.\mathrm{m}.\right)=2$.
• Total validations: ${\sum }_{x\in X,j\in J}N(\mathrm{Alice},x,j)=20$.

Thus, her BI values are:

• $BI\left(\mathrm{Alice},\mathrm{Station}\mathrm{A},8:00–8:10\mathrm{a}.\mathrm{m}.\right)={\displaystyle \frac{4}{20}}=0.2$
• $BI\left(\mathrm{Alice},\mathrm{Station}\mathrm{B},9:00–9:10\mathrm{a}.\mathrm{m}.\right)={\displaystyle \frac{2}{20}}=0.1$

These values reflect Alice’s habits for specific stations at particular times based on her observed travel patterns.

3.3.2. Crowding Model

Crowding significantly affects passenger comfort, travel reliability, and network performance. Models are essential for analyzing vehicle capacity and demand to optimize service. Fresh sensor data is crucial for dynamic decision-making, allowing systems to update recommendations based on current crowding levels. Several studies highlight the importance of incorporating crowding data. Tirachini et al. [2] used statistical models to show how crowding impacts travel time. Drabicki et al. [28,29] use agent-based models to analyze how providing crowding information affects passenger decisions and overall system performance. Similarly, Cats et al. [30] compare different modeling approaches, static versus dynamic simulations, to examine the effects of crowding. Both models have limitations in fully capturing the complexity of crowding, particularly as demand increases. Other works have explored various data-driven approaches, like a deep learning model with YOLOv9 to count passengers from video footage in real-time [31]; Yin et al. developed a model that fuses multiple data sources, like fare collection and weather data, to estimate passenger loads accurately [32], while the SmartTransfer system [15] uses a spatiotemporal model to forecast in-station transfer volumes. Regardless of the chosen modeling approach, this component must infer a Crowding Index (CI). This metric quantifies the level of crowding at specific stations or on vehicles at a given time. This index serves as input for the route evaluator module, which uses it to assess crowding along potential routes.

Our objective was to determine the instantaneous crowding level of each vehicle as it approached a station. This involved utilizing the MnMs simulator of the entire transportation network and user movements, fed with the necessary data to construct a multi-layer city graph. This is an agent-based dynamic traffic simulator capable of modeling large-scale urban transportation systems. It simulates the behavior of individual travelers as they make mode and route choices, considering a wide range of mobility options (car, tram, bus, metro). To simplify the simulation and isolate the effects of public transportation, we will disregard the presence of private vehicles. This means neither cars nor bicycles will be included in the simulated environment. MnMS efficiently captures traffic flow dynamics at a large scale. We have enhanced the simulator to incorporate additional features, such as vehicle capacity constraints, enabling more accurate simulations of real-world scenarios. The system now accounts for the maximum capacity of each vehicle, ensuring that users who attempt to board are appropriately managed when the capacity is exceeded. This improvement allows the simulation to identify cases where users cannot board due to overcrowding, thereby capturing displaced passengers and their subsequent travel decisions. Let X be the set of public transportation stations in the city, T be the temporal horizon, and $V_{in}$ be the set of vehicles approaching their next station. Let $N_{passengers}$ be the count operator for the passengers on each vehicle $v_{in}$. Therefore, we define the CI at time $t\in T$ for the station $x\in X$ as the ratio of passengers on board the incoming vehicle $v_{in}(x,t)$ and its capacity ($Capacity\left(v_{in}\right)$), as in Equation (2).

$$CI(x,t)=N_{passengers}\left(v_{in}(x,t)\right)/Capacity\left(v_{in}\right)$$

(2)

The crowding model faces challenges in terms of space complexity (requiring significant storage) and time complexity (potentially requiring re-computation based on new data). This scalability issue can be addressed by applying the same solution used for the behavioral model, accepting non-consistent, fast queries.

3.3.3. Route Planner

A multimodal route planner suggests various travel options combining public transportation modes like buses, trains, subways, trams, and bicycles. The system generates multiple routes to a destination, considering available transportation options and their schedules. Depending on the infrastructure, a set of bus-metro-tram-train combinations may be suggested. Using fresh data, the planner calculates the fastest or most efficient routes based on current schedules, providing users with various options. Sophisticated and ready-to-use tools, such as Google Maps (https://www.google.com/maps, accessed on 10 October 2024), Citymapper (https://citymapper.com/, accessed on 10 October 2024), and Moovit (https://www.moovitapp.com/, accessed on 10 October 2024), utilize advanced algorithms to calculate optimal routes, considering factors like travel time, distance, and modes. Additionally, city-specific route planners, such as the TCL (https://www.tcl.fr/se-deplacer/calcul-ditineraire, accessed on 10 October 2024) in Lyon, incorporate local transit data to optimize journeys based on the city’s infrastructure, schedules, and fresh information, providing tailored travel recommendations for the region. Algorithms for constructing route planners can also be found in the literature. Huang et al. [17] propose an algorithm combining public transportation schedules with carpooling. Standard routing algorithms like Dijkstra’s can be applied to the resulting graph. The Dynamic Journey Planner [7] combines unimodal routes from external APIs (Google, Here, OSRM) to create multimodal routes. The eCOMPASS project developed a multimodal route planner [33], optimizing public transportation routes based on eco-friendliness, travel time, and transfers. Gkiotsalis et al. [11] propose a mobile app prioritizing user preferences (time, cost, comfort). It finds the fastest route while respecting secondary preferences (transfers, distance), inspired by navigation systems. Zhang et al. [34] use a Mixed-Integer Programming (MIP) mathematical model, which incorporates passenger preferences into its objective function. Since solving the MIP model exactly would be too time-consuming, the authors developed a meta-heuristic approach called Adaptive Large Neighborhood Search (ALNS). This algorithm efficiently finds near-optimal solutions by iteratively “destroying” and “rebuilding” parts of a route plan. The output of the route planner should be the k shortest paths suggested for an OD query.

MnMS relies on a custom route planner named HiPoP. Given the metric one wants to minimize while traveling (e.g., travel time), HiPoP applies Dijkstra to extract the shortest path. HiPoP searches for the maximum of k shortest paths for various origin-destination service combinations. This is achieved by calling parallel C++ functions from the HiPOP library (wrapped in Python 3.10) for both non-intermodal and intermodal paths. The k-shortest path function computes multiple alternative paths between an origin and a destination in a graph by iteratively adjusting path costs. It starts by determining the shortest path using a standard graph traversal algorithm. Once the first path is found, its edges are penalized by increasing costs, ensuring that subsequent paths take different routes. The process continues until a specified number of paths are found or stopping conditions are met. To maintain diversity, new paths must not exceed a predefined cost threshold relative to the first path and must share only a limited portion of their route with previously computed paths. The process terminates early if too many attempts fail to find an acceptable alternative. This approach ensures that the computed paths are short and distinct, making them useful for transportation planning, routing optimization, and multi-modal network analysis applications. The current path extraction phase is computationally expensive, as each parallel thread maintains its own copy of the city graph with modified edge weights. A future production implementation would mitigate this by leveraging efficient, specialized. external services such as Google Maps.

3.3.4. Route Evaluator

The route evaluator in our multimodal transportation system is the module responsible for selecting the most suitable trip for users by balancing various factors such as personal preferences, network conditions, and travel costs. In systems where the route planner and evaluator are integrated into a single module [34], the user often selects their preferred option from a set of routes returned by the system. The literature provides instances where these modules are combined, with the user’s final choice acting as an implicit evaluation [8,11,17,33,35]. Existing works, even those with differing purposes, often employ the intuitive approach of path ranking [7,22,27], even applying complex machine learning recommendation models [6,9], leaving up to the user the final decision. In our defined architecture, the route evaluator must implement a scoring system to balance the identified factors and produce a route recommendation effectively. To balance QoE and QoS, our evaluator integrates both behavioral and crowding model information (BI and CI), ranking the k paths received from the route planner. The complexity of this scoring system can be adjusted as needed. The output of the route evaluator is the path that best balances QoE and QoS, i.e., the one with the highest score.

We integrated the route evaluator into the MnMS simulator, replacing its path choice mechanism with the following approach. Considering the N shortest paths generated by the route planner for each user, we propose a two-stage top-k path selection and subsequent ranking process that balances QoS and QoE criteria. Paths are ranked based on a set of criteria Q such as crowding, user preferences, travel costs, and number of line changes (such as switching from one bus to another or transferring from a bus to a tram). Therefore, we will differentiate between QoE-driven and QoS-based criteria. In our experimentation, the simulator computed up to ten paths per user ($N=10$). The considered path’s QoE-driven criteria are:

• Station preference B, considered in descending order (higher preference is better). For a given user u and a path $p\left(u\right)$, this preference is determined by summing the BI values at each line transition (node $x_i$), taking into account the expected arrival time ($t_{x_i}$) at that node. This reflects the time-dependent nature of user behavior (Equation (3)). Recall that $BI(u,x,j)$ for a user u at a station x within a specific j-minute time interval (e.g., 10-min window) represents the percentage of that user’s total validations that occurred at that station and time interval (as defined in Equation (1)). Therefore, for each node $x_i$ on the path, we consider the interval j in which $t_{x_i}$ falls to retrieve the relevant BI value.

  $$B\left(p\left(u\right)\right)=\sum _{i=1}^{\left|p\right(u\left)\right|-1}\delta (l_{i-1},l_i)·BI(u,x_i,t_{x_i})$$

  (3)
  $\begin{array}{c}\hfill \mathrm{where}:\\ & u:\mathrm{the}\mathrm{considered}\mathrm{user}\hfill \\ & p\left(u\right):\mathrm{the}\mathrm{computed}\mathrm{path}p\mathrm{for}\mathrm{the}\mathrm{user}u\hfill \\ & \delta (l_{i-1},l_i)=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}{l}_{i-1}\ne l_i\hfill \\ 0,\hfill & \mathrm{if}{l}_{i-1}=l_i\hfill \end{array}\right.\hfill \\ & t_{x_i}=\sum _{j=1}^{i-1}\tau (x_{j-1},x_j)\hfill \\ & \tau (x,y):\mathrm{Travel}\mathrm{time}\mathrm{between}\mathrm{nodes}x\mathrm{and}y\hfill \\ & x_i:i-\mathrm{th}\mathrm{node}\mathrm{in}\mathrm{path}p\hfill \\ & l_i:\mathrm{line}\mathrm{of}\mathrm{node}{x}_i\hfill \end{array}$
• Travel time C, in ascending order (lower cost is better).
• Line changes L, in ascending order (fewer line changes are better).

The QoS-driven criterion considered is the path’s crowding level $\Xi$ (Equation (5)), ranked in ascending order (lower crowding is better). Because users arrive at subsequent nodes at different times after their departure, we employ a moving average model to predict the CI at each line change in future times.

$$C{I}_{\mathrm{predicted}}(t,x_i)={\displaystyle \frac{1}{M}}\sum _{m=0}^{M-1}C{I}_{\mathrm{observed}}(t_{x_i}-m,x_i)$$

(4)

where:

• $C{I}_{\mathrm{predicted}}(t,x_i)$ is the predicted CI at time t for the station $x_i$.
• $C{I}_{\mathrm{observed}}(t_{x_i}-m,x_i)$ is the observed CI at a previous time point $t-m$ at the station $x_i$.
• M is the number of past observations included in the average (the window size of the moving average).

We calculate the path’s total crowding level by summing the predicted CI values for each line transition along that path, based on the estimated departure time from each subsequent station.

$$\Xi \left(p\right)=\sum _{i=1}^{\left|p\right|-1}\delta (l_{i-1},l_i)·C{I}_{\mathrm{predicted}}(t_{x_i},x_i)$$

(5)

$\begin{array}{c}\hfill \mathrm{where}:\\ & \delta (l_{i-1},l_i)=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}{l}_{i-1}\ne l_i\hfill \\ 0,\hfill & \mathrm{if}{l}_{i-1}=l_i\hfill \end{array}\right.\hfill \\ & t_{x_i}=\sum _{j=1}^{i-1}\tau (x_{j-1},x_j)\hfill \\ & \tau (x,y):\mathrm{Travel}\mathrm{time}\mathrm{between}\mathrm{nodes}x\mathrm{and}y\hfill \\ & x_i:i-\mathrm{th}\mathrm{node}\mathrm{in}\mathrm{path}p\hfill \\ & l_i:\mathrm{line}\mathrm{of}\mathrm{node}{x}_i\hfill \end{array}$

Each criterion’s score is calculated by summing its values at the nodes where line changes occur. In the formulas, the transition indicator $\delta (l_{i-1},l_i)$ captures this event. Specifically, this evaluates to 1 when there is a change in the line (e.g., at transfer points) and 0 when the user remains on the same line. Therefore, the criteria computation mechanism excludes intermediate stops where the user is aboard the same vehicle, focusing on the key moments where new decisions, such as handling crowding levels or adapting to user preferences, are most relevant. The first evaluated node in the formula represents the initial station where public transportation is boarded, excluding any preceding walking segments. We omit the last node in the path because it represents the final destination, where further transitions or decisions are no longer relevant. In the first stage, we select the top-k paths that perform best according to the QoS-based criterion. We prioritize the QoS in the initial stage of path selection to ensure that only pragmatically viable and efficient paths are considered from the outset.

From these top-k candidates, we evaluate each path based on multiple QoE-driven criteria in the second stage. Each criterion produces a separate ranking of the k paths, and since these metrics may vary in scale and orientation (minimization or maximization), rankings offer a fair way to compare them. The value $z(p,q)$ represents the path’s p total score based on criteria $q\in Q$.

After calculating each criterion’s score for every path, we rank the paths for each criterion, obtaining a set of ranks R. The ranking order (ascending or descending) depends on the specific criterion. For every path p and criterion $r\in R$, where R is the set of QoE-driven criteria, we compute its position in the corresponding ranking, defined as $rank(p,r)$. The final suitability score for path p, $S\left(p\right)$, is the sum of its positions across all QoE-related rankings, as shown in Equation (6). The ranking criteria for computing the suitability score no longer include QoS-driven parameters; instead, they solely reflect QoE-driven aspects. Equation (6) defines this scoring mechanism.

$$S\left(p\right)=\sum _{r\in R\left(q\right)}rank(p,r)$$

(6)

In the end, the path with the lowest total rank (i.e., highest aggregate position) is selected as the most suitable.

While multi-criteria decision-making (MCDM) methods such as explainable DEA [36], are valuable for structured evaluation, our setting fundamentally differs. Our system follows a two-stage dynamic framework: first, crowding is applied as a hard constraint to preserve network-level QoS; then, the remaining QoE factors (e.g., transfers, travel time) are ranked. This approach explicitly accounts for both operational constraints and the heterogeneity of user preferences elements that cannot be predetermined through single-weighted MCDM formulations. Moreover, unlike ex-post evaluation models, our method needs to operates in real time to dynamically generate feasible, user-acceptable itineraries.

The complexity of the route evaluation algorithm is mainly tied to the ranking algorithm. Its asymptotic complexity is $\mathcal{O}(N·\Lambda +NlogN+Q(k·\Lambda +klogk\left)\right)$, where N is the number of paths, Q is the number of QoE criteria, and $\Lambda$ is their average length. Given the nature of the implementation, which works on a limited set of pre-selected data, the execution time is practically constant.

3.4. Balancing Strategy: A Practical Example

Let’s illustrate the path selection process for Alice, traveling from Station A to D (Destination) on a Tuesday morning at 8:00 a.m. Alice’s total validations are 100.

• Alice’s BI:

  –

  $BI\left(\mathrm{Alice},\mathrm{A},08:00–08:10\right)=30/100=0.30$ (Initial boarding)

  –

  $BI\left(\mathrm{Alice},\mathrm{B},08:00–08:10\right)=20/100=0.20$

  –

  $BI\left(\mathrm{Alice},\mathrm{C},08:10–08:20\right)=5/100=0.05$

  –

  $BI\left(\mathrm{Alice},\mathrm{E},08:00–08:10\right)=15/100=0.15$

  –

  $BI\left(\mathrm{Alice},\mathrm{F},08:10–08:20\right)=8/100=0.08$

  –

  $BI\left(\mathrm{Alice},\mathrm{H},08:10–08:20\right)=2/100=0.02$

• Predicted CI at stations/times:

  –

  $C{I}_{\mathrm{predicted}}\left(08:00,\mathrm{A}\right)=0.15$

  –

  $C{I}_{\mathrm{predicted}}\left(08:05,\mathrm{B}\right)=0.80$

  –

  $C{I}_{\mathrm{predicted}}\left(08:15,\mathrm{C}\right)=0.40$

  –

  $C{I}_{\mathrm{predicted}}\left(08:08,\mathrm{E}\right)=0.10$

  –

  $C{I}_{\mathrm{predicted}}\left(08:18,\mathrm{F}\right)=0.20$

  –

  $C{I}_{\mathrm{predicted}}\left(08:20,\mathrm{H}\right)=0.60$

HiPoP generates three candidate paths, as in

Table 2. Example Candidate Paths.

Path	Route	Travel Time	Line Changes	Estimated Transition Times
P1	A $\stackrel{\mathrm{Line}\mathrm{X}}{\to }$ B $\stackrel{\mathrm{Line}\mathrm{Y}}{\to }$ C $\stackrel{\mathrm{Line}\mathrm{Y}}{\to }$ D	30 min	2	A (08:00), B (08:05)
P2	A $\stackrel{\mathrm{Line}\mathrm{Z}}{\to }$ E $\stackrel{\mathrm{Line}\mathrm{W}}{\to }$ F $\stackrel{\mathrm{Line}\mathrm{Y}}{\to }$ D	35 min	3	A (08:00), E (08:08), F (08:18)
P3	A $\stackrel{\mathrm{Line}\mathrm{K}}{\to }$ G $\stackrel{\mathrm{Line}\mathrm{K}}{\to }$ H $\stackrel{\mathrm{Line}\mathrm{M}}{\to }$ D	25 min	2	A (08:00), H (08:20)

.

• Stage 1: QoS-Based Filtering (Crowding Level $\Xi$)

We calculate the total crowding for each path by summing predicted CI values at each relevant station where a line transition occurs.

• $\Xi \left(\mathrm{P}1\right)=C{I}_{\mathrm{predicted}}\left(08:00,\mathrm{A}\right)+C{I}_{\mathrm{predicted}}\left(08:05,\mathrm{B}\right)=0.15+0.80=0.95$
• $\Xi \left(\mathrm{P}2\right)=C{I}_{\mathrm{predicted}}\left(08:00,\mathrm{A}\right)+C{I}_{\mathrm{predicted}}\left(08:08,\mathrm{E}\right)+C{I}_{\mathrm{predicted}}\left(08:18,\mathrm{F}\right)=0.15+0.10+0.20=0.45$
• $\Xi \left(\mathrm{P}3\right)=C{I}_{\mathrm{predicted}}\left(08:00,\mathrm{A}\right)+C{I}_{\mathrm{predicted}}\left(08:20,\mathrm{H}\right)=0.15+0.60=0.75$

Then, we rank the paths in ascending order according to $\Xi$, as in

Table 3. QoS Ranking (Lower $\Xi$ is Better).

Rank	Path ($\mathbf{\Xi }$)
1	P2 (0.45)
2	P3 (0.75)
3	P1 (0.95)

.

If $k=2$, P2 and P3 are selected as top candidates. P1 is discarded due to high crowding, despite its potentially favorable travel time or inherent fewer traditional transfers.

• Stage 2: QoE-Driven Evaluation (for P2 and P3)

We calculate Station Preference (B), Travel Time (C), and Line Changes (L) for the top-k paths, as in

Table 4. QoE Criteria Values for Top-k Paths.

Path	Station Preference (B)	Travel Time (C)	Line Changes (L)
P2	$BI\left(\mathrm{A}\right)+BI\left(\mathrm{E}\right)+BI\left(\mathrm{F}\right)=0.30+0.15+0.08=0.53$	35 min	3
P3	$BI\left(\mathrm{A}\right)+BI\left(\mathrm{H}\right)=0.30+0.02=0.32$	25 min	2

.

We rank the paths based on QoE criteria and compute the suitability score, as in

Table 5. QoE Ranking and Final Suitability Score ($S\left(p\right)$).

Criterion	P2 Rank	P3 Rank
Station Preference (B)	1	2
Travel Time (C)	2	1
Line Changes (L)	2	1
Total Suitability Score $S\left(p\right)=\sum rank$	5	4

.

In conclusion P3 is recommended to Alice as it has the lowest score (4).

• WhyQoS-First is Essential?

• P1, despite being shorter and having fewer line changes than P2, was eliminated early due to its high crowding ($\Xi =0.95$).
• Prioritizing CI in Stage 1 ensures that only fundamentally efficient and less congested paths proceed. This limits the variability in the candidate set, preventing the system from recommending paths that might be preferred by QoE metrics but are impractical due to severe crowding. It guarantees that Alice’s final recommended path is a balance of personal preference and system efficiency.

• Will Alice follow the recommended route?

• User acceptance is a critical aspect in the deployment of any route recommendation system. Even if technically optimal routes are suggested, passengers may reject them if they are perceived as inconvenient, for example, due to longer travel times, additional transfers, or deviations from habitual routes. This risk of rejection has been highlighted in the literature, where trust and perceived usefulness strongly influence the adoption of recommender systems in mobility contexts [37,38]. We also conducted a stated-preference survey to assess users’ willingness to accept recommended trip. The results are reported in Appendix A.
• In our approach, however, we expect a higher acceptance rate of the recommendations, since our approach explicitly balances infrastructure efficiency with user-centric factors. By integrating elements such as individual travel preferences, perceived comfort, and travel costs, the system ensures that the proposed routes are not only crowding-aware but also aligned with what users value in their daily journeys. This makes rerouting strategies less intrusive and increases the likelihood of users adopting the balanced recommendations in practice. For this reason, we expect Alice to follow the recommendation, and in the subsequent simulations, we assume that all users accept the suggested routes.

4. Experiments

All the following experiments will take place on a high-performance server equipped with two Intel(R) Xeon(R) Gold 5220 CPU @ 2.20 GHz processors and 754 G RAM. The experiments are conducted within the MnMS simulator (https://github.com/DistLab-Sannio/MnMS/tree/restyling, accessed on 9 January 2025). The simulator was extended to handle this by making vehicle capacity a core attribute. When a user tries to board a vehicle that has reached its maximum capacity, their boarding attempt fails. This triggers an automatic path rescheduling, creating a new route query for that user that starts from their current station. At each simulation step, the system collects two types of queries to be processed: those from users starting a new journey and those who could not board a full vehicle. We exploited MnMS built-in route planner, HiPoP, which has been customized to our specific needs. The standard path choice mechanism within MnMS is replaced by our custom route evaluator. For reproducibility, a critical configurable parameter is the edges multiplier cost, set at 1.1. This multiplier increases the cost of edges already used in previous path searches, making them less likely to be re-selected. This approach effectively encourages the discovery of diverse routes without overly penalizing paths that only diverge significantly later in their trajectory, unlike a larger multiplier (e.g., 10) would. The public transportation network is represented in MnMs by a multi-layer graph. This graph intricately connects bus, metro, and tram stations within their respective modes (intra-layer connections) and between different modes (inter-layer connections). Additionally, these transportation layers are linked with an origin and destination layer. Each origin or destination point specified in the demand data is mapped within MnMS to the nearest corresponding node on this layer. Furthermore, users within the grid are assumed to have a walking range of 500 m, which defines their willingness to reach a station.

We run three simulations, adequately modifying the suggested strategy implemented by the route evaluator. The first is a QoE-driven simulation trying to reproduce a user’s typical choice, similar to the implementation of classical recommendation systems. As extensively described in the previous section, we consider the user preference, the travel time, and the line changes as criteria. It is reasonable to assume that users follow their habits, but when traveling through unfamiliar areas, they prioritize travel time and the number of vehicle transfers for comfort. Moreover, travel time and line changes are considered to prevent the system from selecting an excessively long route solely because it passes through the most preferred stations. We do not extract top-k paths but include the user preference criteria in the suitability score computation. In this case, we extract the path with the highest suitability score. The second simulation is the QoE-QoS balanced, and the route evaluator follows exactly the description in Section 3.3.4. The third simulation is the QoS-driven simulation, prioritizing only infrastructure stress relief. We consider the crowding level, the travel time, and the line changes as criteria. Throughout the simulation, we log the CI for every serving vehicle at each time step. This detailed data will be used in the following post-simulation analysis to assess the impact on crowding. First, we refined the dataset to ensure that a single CI value was associated with each stop along every vehicle’s path. This step eliminated redundant CI recordings from the simulation’s per-step data logging and varying travel times between nodes.

4.1. Real Case: Lyon Transportation Network

The metropolitan area of Lyon, served by the TCL (Transports en Commun Lyonnais) public transportation network, is selected as our simulation case study. It operates a comprehensive network of 4 metro lines, 6 tram lines, and over 100 bus lines. Figure 4 shows in green the bus lines, in purple the metro lines, and in red the tram lines.

4.1.1. Data Overview

Our starting point is a monthly validation dataset provided by the TCL operator. This dataset, encompassing 2019 and 2020, contained real-world user data. The data includes non-subscriber and subscriber users, identified monthly by serial numbers. Given the monthly fluctuation of subscription IDs, we selected a single month for our analysis. November has been chosen because it provides complete validation data for all transportation modes and is expected to represent a period of typical crowding, as it is neither a holiday month nor a summer month and is unaffected by COVID-19 restrictions. Each dataset entry represents a user validation at a specific station, linked to a particular mode of transportation and recorded at a precise timestamp (see

Table 6. Lyon validation dataset.

USER ID	DATETIME	STATION ID	LAT	LON
30…29C7	1 November 2019 09:02:27	BUS-68-CITE TASE	4.928	45.758
30…29C7	1 November 2019 09:08:12	METRO-A-VAULX EN VELIN LA SOIE	4.921	45.760
30…6ED8	14 November 2019 08:51:22	TRAM-T4-GARE DE VENISSIEUX	4.887	45.705
30…6ED8	14 November 2019 09:02:41	TRAM-T4-LYCEE LUMIERE	4.861	45.736
30…6ED8	14 November 2019 09:06:24	TRAM-T4-LYCEE COLBERT	4.859	45.745

). The latitude and longitude coordinates of each station are provided.

A rigorous data-cleaning process was undertaken to ensure the robustness of our behavioral model. Reasonable heuristics were applied to mitigate the impact of anomalies and irregularities within the dataset. Specifically, rows representing multiple validations by the same user at the same station within a ten-minute interval were removed. Additionally, validations from the same user at different stations occurring within 60 s were discarded, given that the minimum frequency of the fastest mode of transportation, the metro, is two minutes between stations. From this dataset, we estimated the BI by grouping with a 10-min interval for each ’USER ID’, as defined in Section 3.2. By analyzing validation data, we estimate the maximum capacity of each metro line, determining the hourly passenger carrying capacity of each vehicle type (see

Table 7. TCL lines capacity.

Type	Capacity
Metro A, B, C, D	350
Bus Line C (Crystal)	150
Bus (Other lines)	90
Tram T1, T2, T3, T4, T5, T6	300

). This information is needed to compute the CI at every simulation step, as defined in Section 3.3.2.

4.1.2. OD Queries Generation

Upon examining the histogram of validations for November, we observed a relatively consistent pattern (see Figure 5). Consequently, we decided to concentrate our analysis on the third week. We observed that the beginning of November might have experienced reduced infrastructure pressure due to early-month holidays, school breaks, or weekend getaways. To assess the system’s impact on crowding, we simulated two hours from 07:00 a.m. to 09:00 a.m. on 19 November 2019, a Tuesday (Figure 6). This timeframe was selected to focus on the morning peak when many people typically commute from home to work or engage in morning activities. Figure 7 clearly shows that demand and origin requests are predominantly concentrated in Lyon city center, with larger point areas indicating a higher number of requests from those locations.

We used the trip chaining heuristic [39] to infer origin-destination trips to construct a demand profile that accurately reflects historical travel patterns, as our dataset was limited to entry validations (origin) and lacked exit point (destination) information.

If the time difference between two consecutive validations was less than or equal to one hour, we assumed they were part of the same trip. This means that even though the entire trip (from the first to the last validation) could last more than one hour, they were grouped as long as each pair of consecutive validations was no more than an hour apart. The first validation of each trip serves as the origin of the query, while the destination is defined as the first validation of the next user’s trip. If this method introduces inconsistencies, such as when a user is shown to depart and arrive at the exact location, a fallback procedure is triggered. In this case, the destination will be redefined as the starting station of the first subsequent trip with a different starting station. If a destination cannot be identified, we remove the query. This approach is based on the hypothesis that in many cases, users tend to travel from point A to B, spend some time at B, and later return from B to A or continue elsewhere, and it is partially based on established heuristics [40].

Table 8. Origin Destination Queries.

USER ID	DEPARTURE	ORIGIN	DESTINATION
30…686C	16:45:00	Valmy	St. Didier Eglise
30…ABA5	16:45:00	Grange Blanche	Guillotiere
30…EC87	16:45:00	Dauphine Lacassagne	Vaulx—La Soie
30…AB88	16:45:00	College Plan Du Loup	Mairie De Sainte Foy
30…5035	16:45:00	Ludovic Bonin	Grange Blanche

shows an overview of the resulting OD queries. We recorded 162,664 queries during peak hours, averaging 624 departures every 30 s.

In contrast to the preceding simplified scenario, which featured a constrained spatial domain and a limited number of OD pairs, the current analysis necessitates accounting for departures from a comprehensive distribution of locations throughout the Lyon metropolitan area. The origin-destination grid in the MnMS multi-layer graph is defined by 100 points in both the x and y directions, creating a 100 × 100 grid where the distance between points is approximately 1 km. This size provides a sufficiently granular representation of the urban area, and mapping precision naturally improves with smaller grid squares.

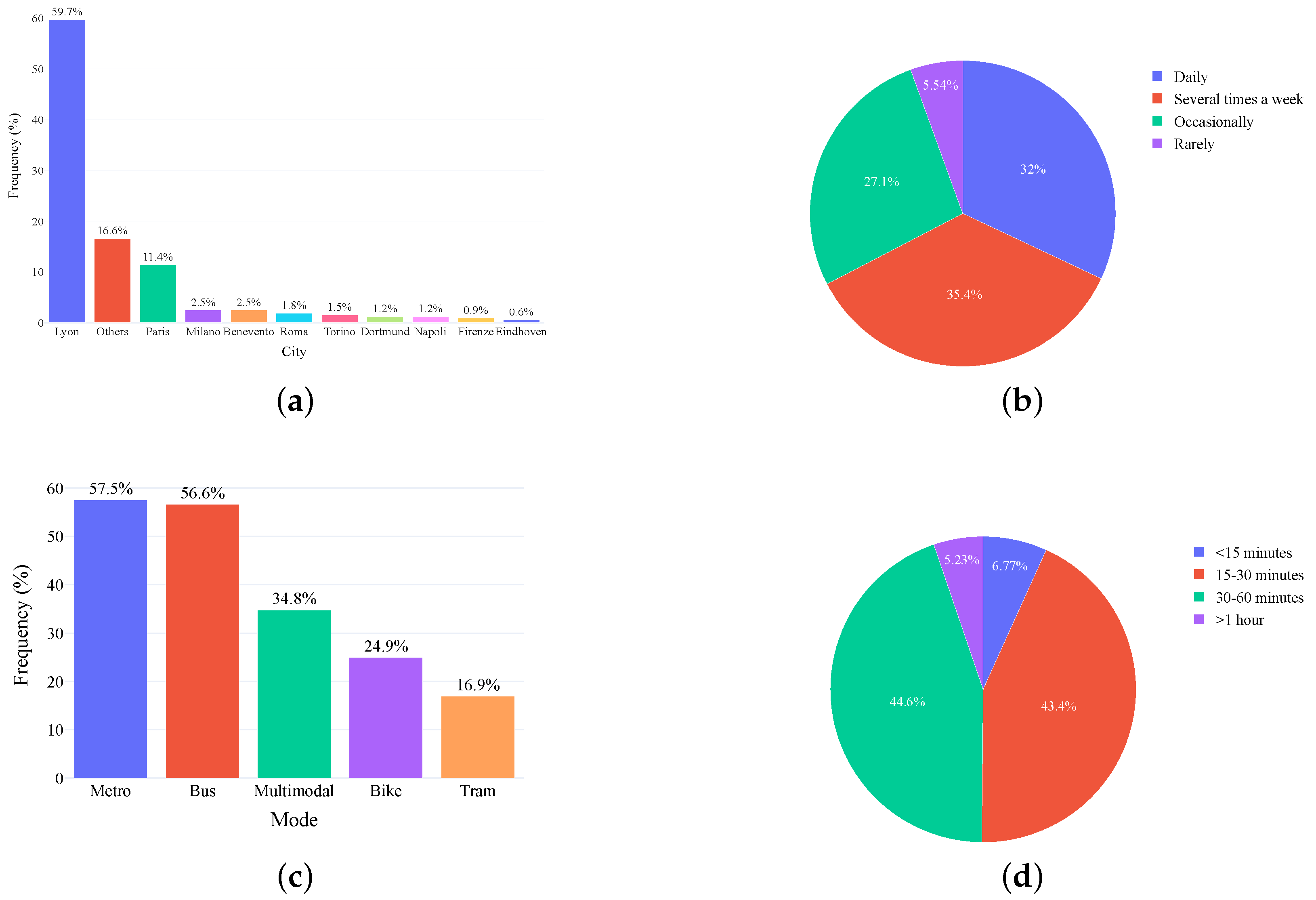
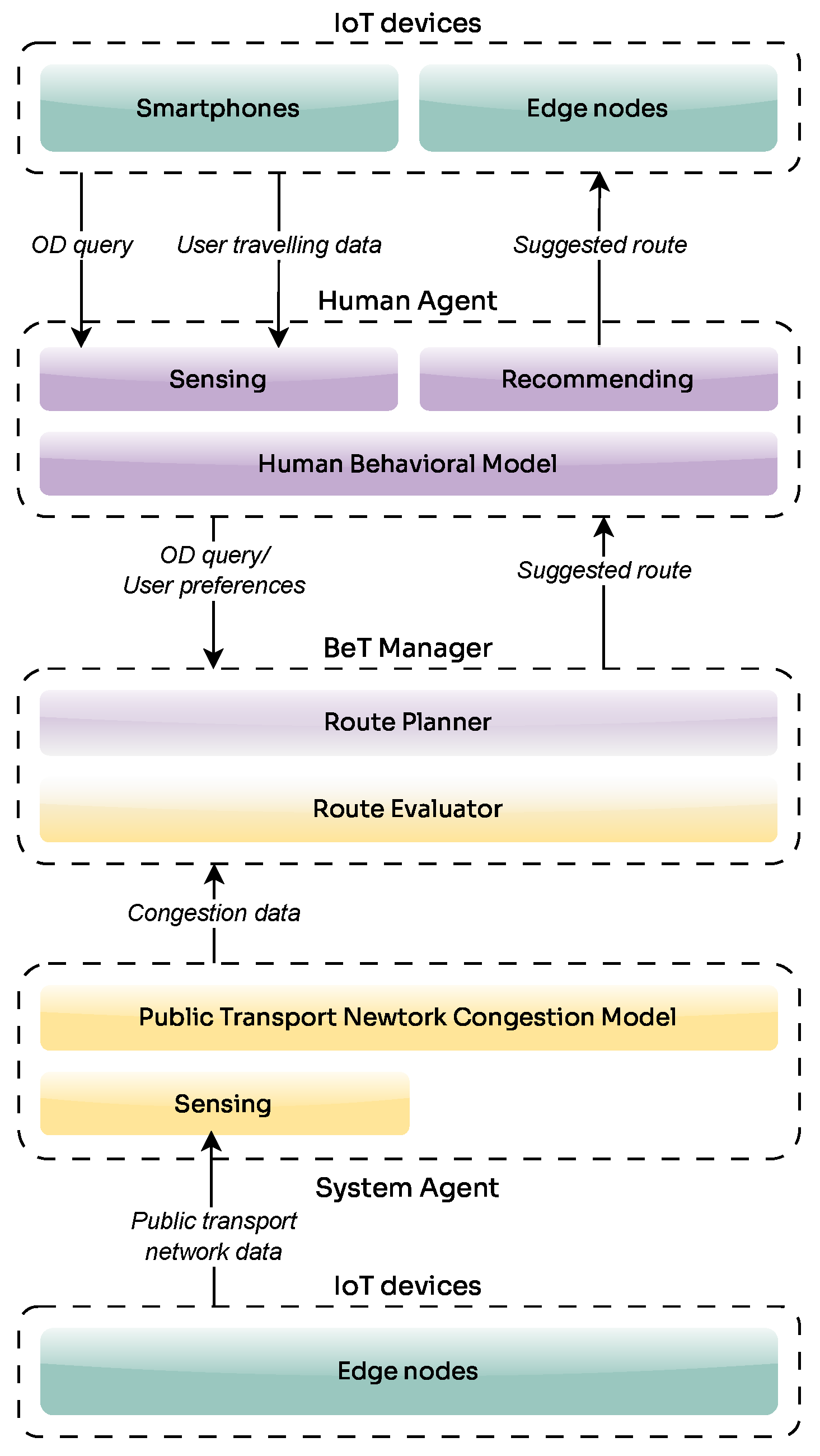
4.1.3. Results

As first evaluation, we want to confirm that our strategy effectively reduces vehicle crowding compared to the QoE-driven approach. Furthermore, we assess its alignment with a QoS-driven approach, which serves as our benchmark for achieving optimal system benefits. While the distribution of CI values provides an intuitive overview, it doesn’t allow for a direct comparison of vehicle routes, which is essential for a detailed and insightful analysis. Therefore, we’ve opted for a more robust, statistics-based analysis. Our simulation is deterministic, meaning each vehicle follows the same sequence of stops at the same times across different simulated scenarios. However, we cannot directly compare the CI at individual stops between scenarios, even with paired observations. These data points lack the statistical independence required for valid comparisons; crowding at one stop can influence the CI at all subsequent stops, creating a chain of dependency. To overcome this, we aggregate the data for each vehicle’s entire trip to obtain paired and independent values. We chose the median as the aggregation measure for two key reasons:

• It is a robust measure that is not skewed by extreme values. Unlike the mean, the median is unaffected by such outliers, providing a more stable and representative measure of a trip’s overall congestion.
• By using the median, we transform the dependent observations from a single trip into one independent data point. This single value represents the trip’s overall performance, allowing us to confidently compare these independent trip medians and perform a statistically valid assessment of different strategies. This method ensures a robust and accurate evaluation by using data points that are truly independent.

To determine which approach, j or k, performs better, we use a specialized score, ${\rho }_{j,k}$, which is fundamentally based on two measures: the p-value ($\pi$) and the effect size ($\eta$). These are derived from applying the Wilcoxon signed-rank test to our data. The Wilcoxon signed-rank test is a non-parametric statistical test used to compare two related samples to assess whether their population mean ranks differ.

Within this framework, the p-value ${\pi }_{j,k}$ reports the statistical significance of the observed difference for a two-strategy comparison, assessing whether an outcome is likely due to chance. Specifically, let s be a sample; we employ a “less than” alternative hypothesis when examining the difference between j and k approaches ($s_j-s_k$).

This means our primary aim is to discover if the approach j consistently yields lower crowding on a vehicle trip compared to approach k. However, a low p-value, while indicating statistical significance (${\pi }_{j,k}\le 0.05$), does not inherently convey the practical importance or magnitude of the observed difference. For this, we integrate the effect size ${\eta }_{j,k}$, which serves as a quantitative measure of the magnitude or strength of the observed phenomenon. This allows us to discern if a reduction in crowding is substantial enough to represent a tangible benefit to passengers, rather than being a negligible or practically irrelevant change. To compute an effect size for the Wilcoxon signed-rank test, the rank-biserial correlation [41] is employed. This measure is calculated as the difference between the sum of the favorable ranks ($W_{-}$, corresponding to negative ranks in our “less than” alternative, where j performs better) and the sum of the unfavorable ranks ($W_{+}$, corresponding to positive ranks where k performs better), normalized by the total sum of ranks $S=N(N+1)/2$ for N non-zero differences. Thus, the effect size is computed as:

$${\eta }_{j,k}={\displaystyle \frac{W_{-}-W_{+}}{S}}$$

(7)

The value of ${\eta }_{j,k}$ is bounded between −1 and 1, with its sign indicating the direction of the effect. To ensure that only statistically significant and meaningfully directed effects contribute to our overall comparison, we define a gating factor ${\gamma }_{j,k}$:

$${\gamma }_{j,k}^v=\left\{\begin{array}{cc}1\hfill & \mathrm{if}({\eta }_{j,k}>0\wedge {\pi }_{j,k}\le 0.05)\mathrm{or}({\eta }_{j,k}<0\wedge {\pi }_{j,k}\ge 0.95)\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(8)

Here, a positive effect size (${\eta }_{j,k}>0$) combined with a low p-value (${\pi }_{j,k}\le 0.05$) signifies that approach j performs significantly better than k. Conversely, if a negative effect size (${\eta }_{j,k}<0$) is observed with a high p-value (${\pi }_{j,k}\ge 0.95$, which is equivalent to 1 minus the significance level), it suggests that approach k significantly outperforms j. In all other scenarios, ${\gamma }_{j,k}$ is set to 0, filtering out non-significant or ambiguous outcomes.

To provide a single, comprehensive score representing the overall performance comparison we propose the following score ${\rho }_{j,k}$:

$${\rho }_{j,k}={\gamma }_{j,k}·{\eta }_{j,k}$$

(9)

The score, which represents the effect size of our Wilcoxon test, ranges from −1 to 1 and is only considered when statistically significant. This overall score thus represents the average statistically significant and practically meaningful effect of approach j compared to approach k across the entire fleet. The ${\rho }_{j,k}$ score is computed for each distinct pair of approaches ($j\ne k$).

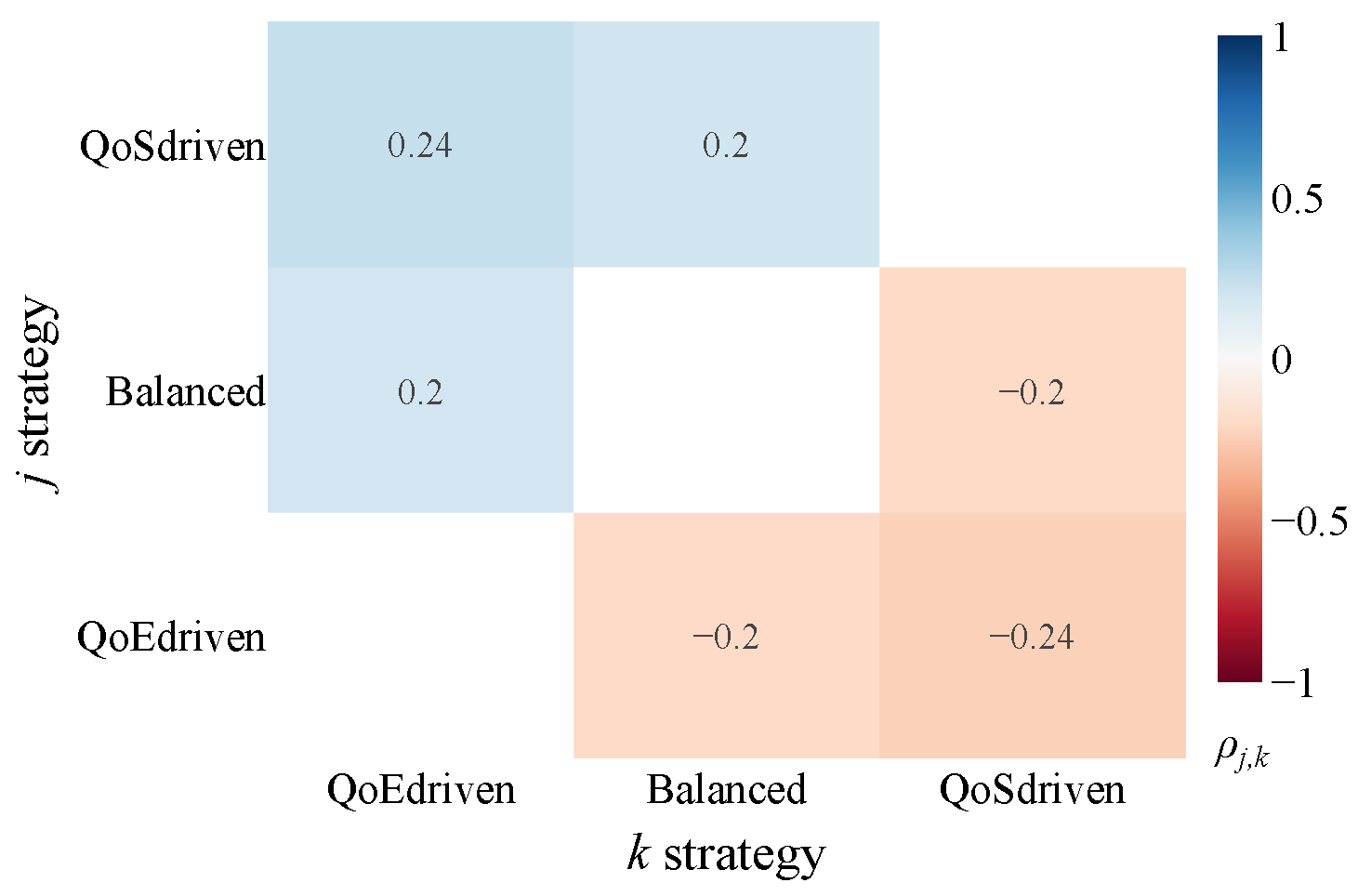
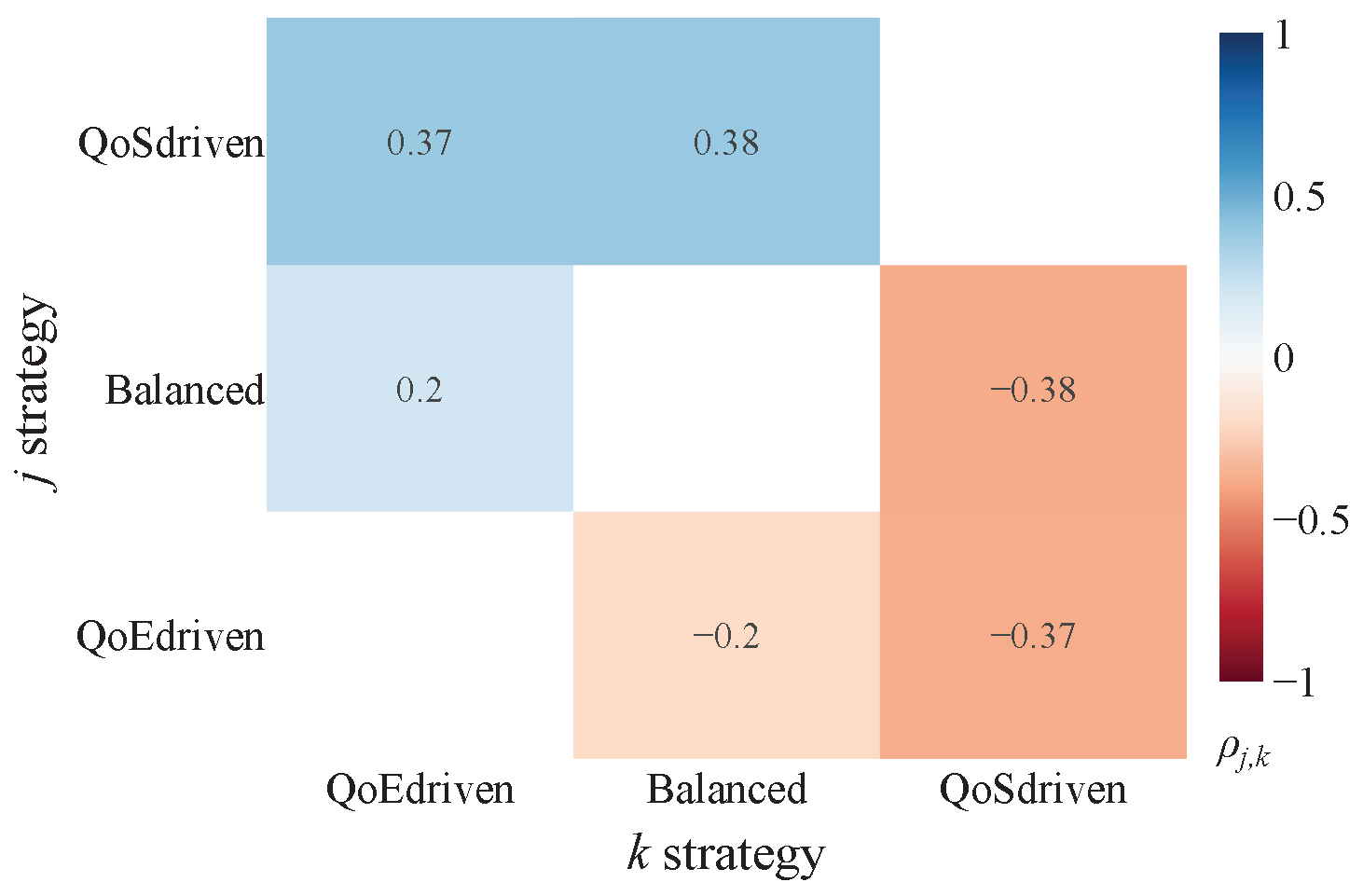
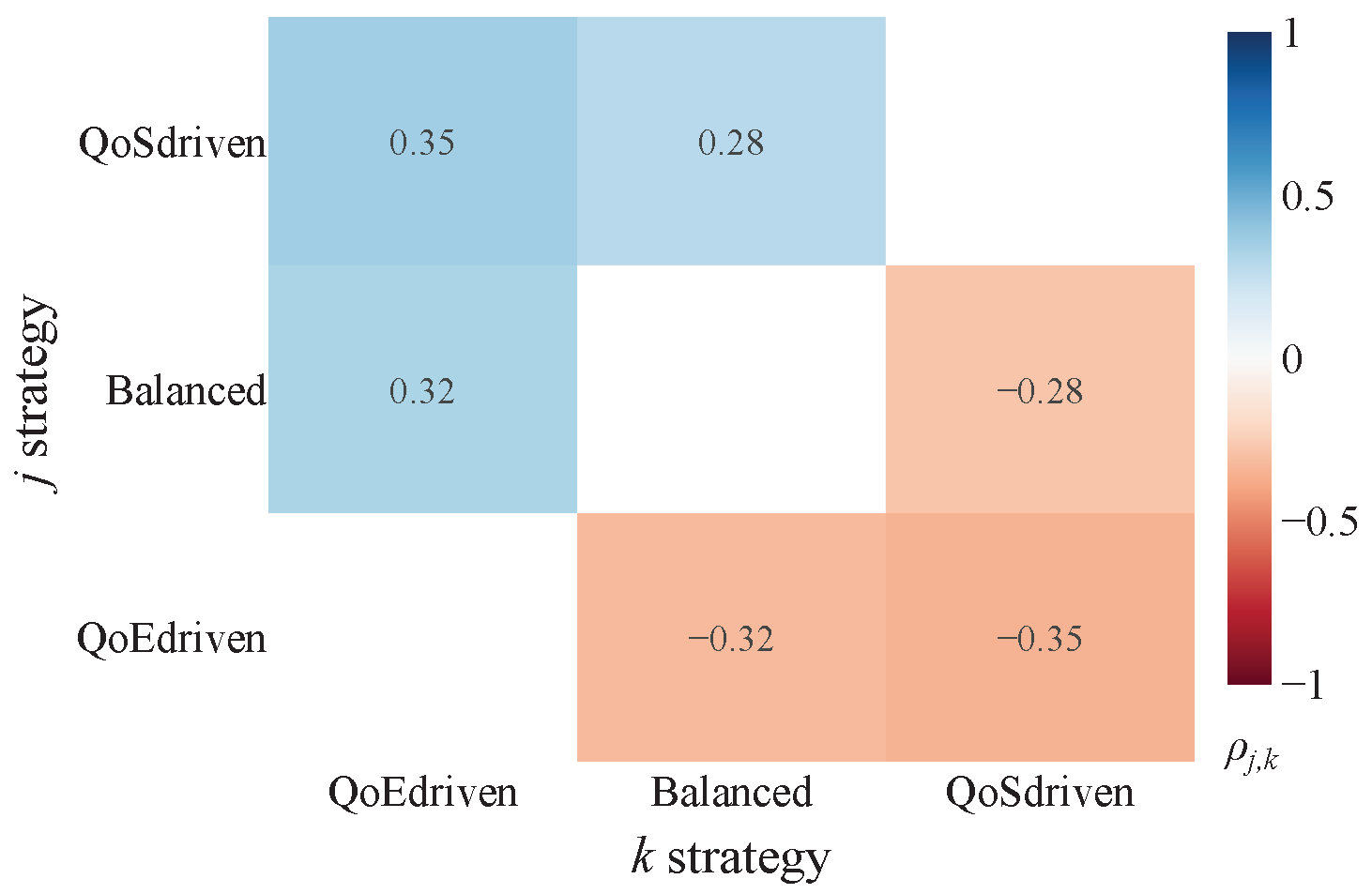
These ${\rho }_{j,k}$ scores are subsequently visualized using heatmaps for intuitive interpretation. The color gradient within these heatmaps directly indicates the comparative performance: bluer regions (tending towards +1) signify that approach j significantly and substantially reduces crowding compared to approach k, while redder regions (tending towards −1) indicate that approach j significantly increases it. The intensity of the color further reflects improvements or worsenings. Thus, the sign of ${\rho }_{j,k}$ immediately clarifies which approach yields a more favorable (lower CI) outcome.

The findings reveal that prioritizing crowding as a key metric in generating suggestions leads to a positive reduction in infrastructure stress. Unsurprisingly, the QoS-driven strategy exerts a considerable influence on the results when contrasted with the Balance approach, which, by its nature, seeks a middle ground across different considerations. This beneficial effect is most strongly observed with Tram (Figure 8b) systems, displaying the most marked improvements. The impact is also satisfactory for Metro lines (Figure 8a). However, no definitive conclusions can be drawn for buses (Figure 8c). This disparity could be attributed to the higher demand for metro services among the user base considered. 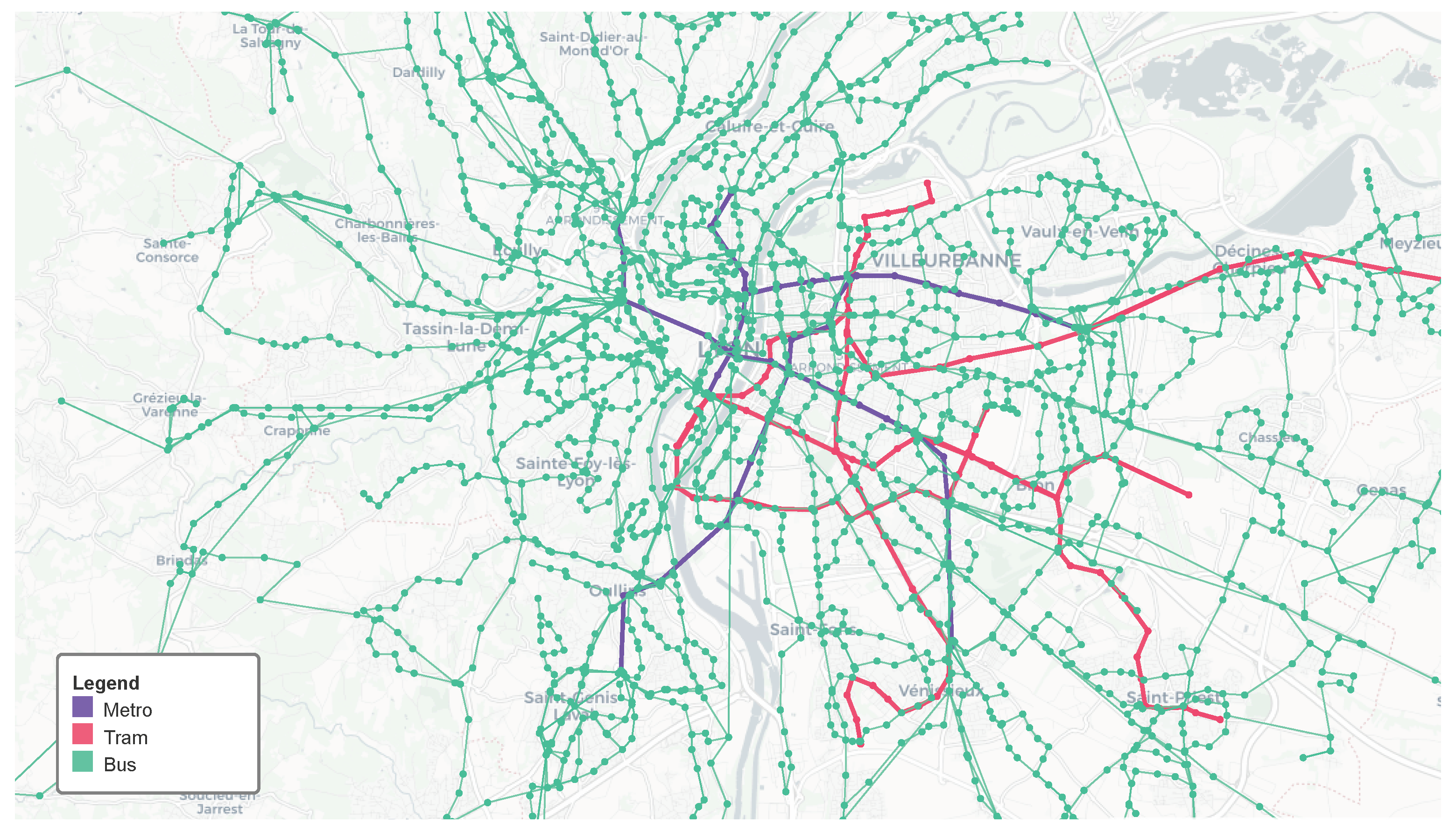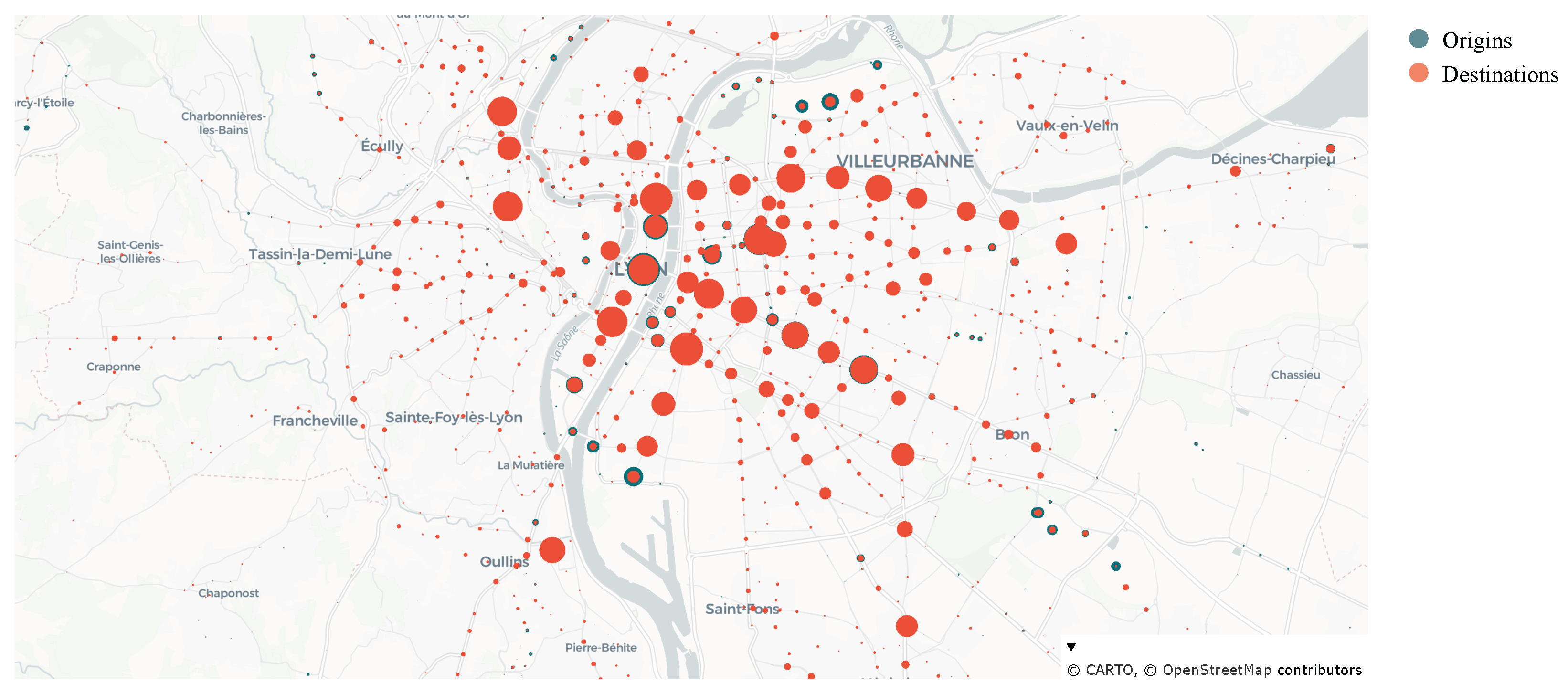Comparing Figure 4 and Figure 7, we can observe that the origins and destinations are predominantly concentrated around tram and metro stops. Additionally, while the bus network boasts a substantial number of lines, offering extensive urban and suburban coverage, this capacity is not fully utilized by the considered demand in our simulation. To delve deeper into this specific situation, we conducted further analysis, as detailed in the subsequent section. Correspondingly, the QoE-driven strategy consistently shows a higher crowding level.

To assess the model’s distributive equity, a subgroup analysis was conducted by filtering the network nodes based on their location in either urban or suburban areas. The Wilcoxon test was applied to the data for each subgroup to compare performance across distinct contexts. The findings showed that the results of the subgroup analysis were consistent across both user groups, indicating that the model’s optimization does not disproportionately favor urban users over suburban users. Furthermore, a lower level of stress was consistently observed for buses, which can likely be attributed to the limited demand for this specific mode of transport in the network studied. A full discussion of this analysis, including detailed numerical findings, is provided in the Discussion section.

4.1.4. Discussion

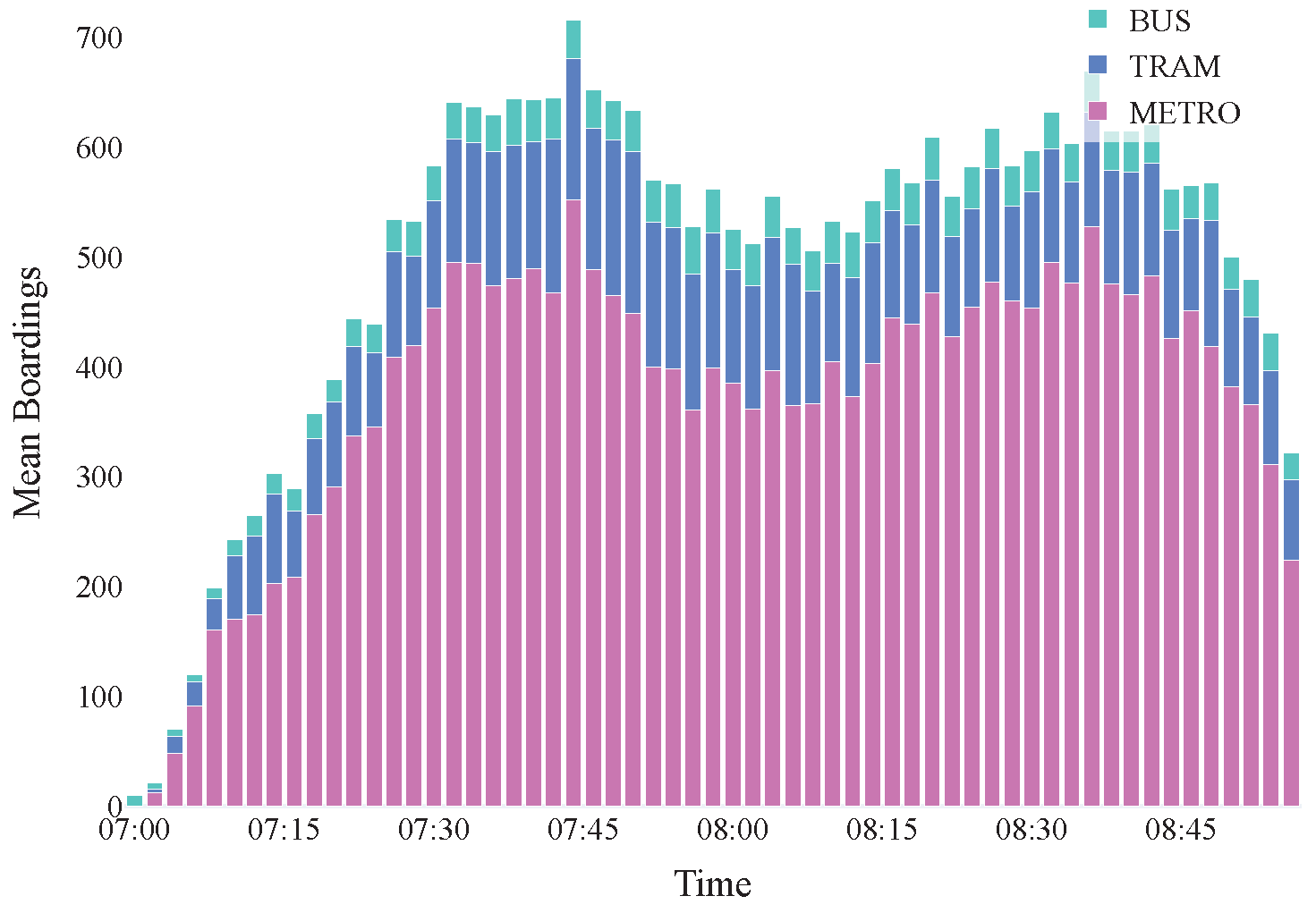
First, we tried to explain the varying outcomes across vehicle classes. To test our hypothesis about the high number of bus lines compared to service requests, we calculated the average boardings per vehicle class, $Boardin{g}_{mean}$. Let c represent the vehicle class and t denote the time bin. We define $V(c,t)$ as the set of available vehicles for class c in time bin t. Furthermore, let $b(c,t)$ be the total number of boardings and $N_{V(c,t)}$ be the count of available vehicles for class c in time bin t. To calculate $Boardin{g}_{mean}$, we first counted the boardings within each 2-min time bin. Then, we divided that sum by the number of available vehicles for that class at that specific moment.

$$Boardin{g}_{mean}(c,t)={\displaystyle \frac{{\sum }_{v\in V(c,t)}b(c,t)}{N_{V(c,t)}}}$$

(10)

As illustrated with the stacked bar plot in Figure 9, Figure 10 and Figure 11, the mean requests for buses are consistently low across all strategies when compared to metro and tram requests.This phenomenon is likely due to the vast bus network, with over 280 lines offering highly localized service across the urban area, resulting in many buses in circulation.

In addition to understanding the effects of various strategies on critical travel criteria, we evaluated their pros and cons. Given the inherent unpredictability of unfinished journeys, the analysis was limited to completed trips.

We extracted the following criteria for each users’ trip:

• Travel Times, the total time spent by a user from origin to destination, including in-vehicle time, waiting times, and possible reroutings.
• Failed Boarding Attempts, the number of times a user could not board due to capacity limits. In such cases, the user either waits for the next vehicle or is replanned on an alternative route.
• Line Changes, the number of user switches between different lines during their journey, depending on the number of different vehicles taken.
• Total Waiting Time, the cumulative waiting time incurred when a passenger’s journey is interrupted and re-calculated due to a vehicle being overcrowded, excluding any initial waiting time caused solely by the service timetable.
• Mean Station Preference. To account for the dynamic nature of path suggestions within the simulation (where a user’s journey might be interrupted and rerouted), the Mean Station Preference metric is defined as the average BI values at each line transition along a user’s actual path. It provides an insight into the average appreciation level across the sub-paths actually traversed by the user.

To ensure consistency and rigor, we applied the same scoring methodology as previously defined, utilizing a Wilcoxon signed-rank test to compare the metrics for two paired approaches. Its application is valid because the samples used are independent. Specifically, each sample represents the metric’s value for a single trip, and trips are inherently independent of one another. From this test, we extracted the p-value (${\pi }_{j,k}$) and the effect size (${\eta }_{j,k}$) for each pairwise comparison. Given that we conducted a total of 5 comparisons, we applied the Bonferroni correction to adjust the significance level and control the Type I error rate (false positives) resulting from multiple tests. The Bonferroni correction is a statistical method that lowers the significance threshold for each individual test within an analysis involving multiple comparisons. If an analysis includes m comparisons, the original significance level $\alpha$ is divided by the number of comparisons. This results in a new, more stringent significance level, ${\alpha }_{corr}$, which a p-value must meet to be considered significant. In our case, the original significance level was $\alpha =0.05$. Having conducted 5 comparisons, the new, corrected significance level is ${\alpha }_{corr}={\displaystyle \frac{\alpha }{m}}={\displaystyle \frac{0.05}{5}}=0.01$. Therefore, a p-value must be less than or equal to 0.01 to be considered statistically significant after the Bonferroni correction. We then calculated the gating factor ${\gamma }_{j,k}$ with Bonferroni correction. The final score is a simplified metric, calculated as the direct product of ${\gamma }_{j,k}$ and the effect size, ${\eta }_{j,k}$. The score ranges between −1 and 1, with the sign indicating the direction of the difference. A positive value indicates that the first approach performed better, while a negative value suggests the superiority of the second approach. This clear metric enables a consistent and immediate interpretation of the comparison across all our analyses.

Heatmaps interpretation (Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16) aligns with the one proposed in the previous section, with blue/red colors meaning that the distribution underlying the approach j is stochastically smaller/greater than k. Practically, j-sample yields smaller/greater values for the metric compared than k. A user may wish for a shorter path, no failed boarding attempts, few line changes, short waiting time, but high station preference.

In traffic theory, Wardrop’s First Principle (or user equilibrium) [42] describes a state where every individual user chooses their path based on what they perceive as the fastest or most convenient for themselves, given current traffic conditions. In this “egoistic” equilibrium, no single user can reduce travel time by unilaterally changing their route. Conversely, Wardrop’s Second Principle defines the system optimum, representing the allocation of traffic that minimizes the total travel time for everyone in the network. Our analysis of the heatmap results distinctly reveals a fundamental trade-off between individual (user-centric) and collective (system-centric) optimization, directly analogous to these two well-known concepts.

The QoE-driven strategy, inherently designed to minimize individual travel times and the number of line changes as explicitly included in its scoring criteria, prioritizes user utility. This approach directly mirrors the egoistic optimization behavior characteristic, where each user selects the optimal path for their journey. Consequently, this strategy achieves the lowest individual travel times and the fewest line changes, indicating straightforward routing. This strategy naturally guides users through habitual nodes. However, this user-centric prioritization precipitates a significant collective cost, manifesting as the highest number of failed boarding attempts and the longest waiting times for the system. This outcome precisely illustrates the “Price of Anarchy,” where individually optimal choices lead to a sub-optimal global state due to over-utilization of shared resources. Conversely, the QoS-driven strategy operates with a clear focus on system optimum, aiming to enhance overall network efficiency. This strategy effectively reduces crowding, yielding the lowest waiting times for users and ensuring more reliable boarding with less delay at stops. The system-level benefit is coupled with the highest travel times and the most frequent line changes for individual users. The strategy necessitates individual users taking less direct or less preferred paths, thereby deviating from their individual optimum to contribute to the collective good. Among these opposing priorities, the Balanced strategy emerges as a robust compromise, leveraging the capabilities of the BeT system. While it is slower than QoE-driven in terms of travel times and experiences moderate waiting times, it achieves the fewest failed boarding attempts, reducing frustration. It also presents a middle ground for leading users for line changes, being more direct than QoS-driven but involving more transfers than QoE-driven. This intermediate characteristic also extends to preserving user habits, where the Balanced strategy effectively positions itself between QoE-driven and QoS-driven. This balanced approach successfully navigates the trade-off, mitigating severe crowding points and offering a smoother boarding experience without excessively compromising individual travel efficiency.

To evaluate the model’s distributive equity, we performed a subgroup analysis on the network nodes, categorizing them as either urban or suburban. To assess this, we repeated the Wilcoxon test by filtering nodes into urban and suburban areas, allowing us to compare system performance in distinct geographic contexts. We also replicated the QoE-metric analysis by focusing on users departing from these areas. The findings showed that the results of the subgroup analysis were consistent across both user groups, indicating that the model’s optimization does not disproportionately favor urban users over suburban users. Minor variations in the effect sizes (eg., waiting time) are attributable to intrinsic structural differences between the two contexts, such as longer average trip distances and fewer transfer alternatives in suburban areas, rather than to any systematic bias in the model’s optimization process. All the results of the urban vs suburban analysis are summarized in

Table 9. Comparison of QoS ${\rho }_{j,k}$ Scores for different vehicle classes across Urban and Suburban area.

Vehicle Class	j	k	CI
			Urban	Suburban
Tram	Balanced	QoEdriven	0.72	0.57
Tram	Balanced	QoSdriven	−0.43	−0.25
Tram	QoSdriven	QoEdriven	0.60	0.38
Metro	Balanced	QoEdriven	0.25	0.25
Metro	Balanced	QoSdriven	−0.35	−0.48
Metro	QoSdriven	QoEdriven	0.37	0.52
Bus	Balanced	QoEdriven	0.07	0.17
Bus	Balanced	QoSdriven	0.17	−0.02
Bus	QoSdriven	QoEdriven	−0.15	0.06

and

Table 10. Comparison of QoE metrics ${\rho }_{j,k}$ Scores across Urban and Suburban departing user.

j	k	Urban	Suburban
Travel Time
Balanced	QoEdriven	−0.28	−0.45
Balanced	QoSdriven	0.35	0.48
QoSdriven	QoEdriven	−0.39	−0.54
Failed Boardings
Balanced	QoEdriven	0.26	0.08
Balanced	QoSdriven	−0.23	−0.16
QoSdriven	QoEdriven	0.32	0.12
Waiting Time
Balanced	QoEdriven	0.33	0
Balanced	QoSdriven	−0.41	−0.34
QoSdriven	QoEdriven	0.46	0.25
Line Changes
Balanced	QoEdriven	−0.82	−0.84
Balanced	QoSdriven	0.89	0.85
QoSdriven	QoEdriven	−0.90	−0.89
Station preference
Balanced	QoEdriven	0.37	0.26
Balanced	QoSdriven	−0.19	−0.37
QoSdriven	QoEdriven	0.31	0.38

.

The results of our experiments show that the balanced strategy achieves a more efficient distribution of demand while preserving user satisfaction. From an urban transport planning perspective, this translates into concrete support for operators. By redistributing demand across alternative routes and exploiting the multimodal nature of the transport system, the approach enables a better load balance across the network, reducing the risk of overload on critical lines. This, in turn, can directly inform scheduling adjustments and fleet allocation. In addition, the ability to generate congestion-aware recommendations highlights where additional capacity may be required, such as increasing service frequency or deploying larger vehicles, thus providing actionable insights for more resilient and adaptive public transport management. Importantly, by incorporating the BeT paradigm and related architecture, the system not only generates indicators for planners but also provides a structured way to automatically support decision making, balancing QoE and QoS in public transportation systems.

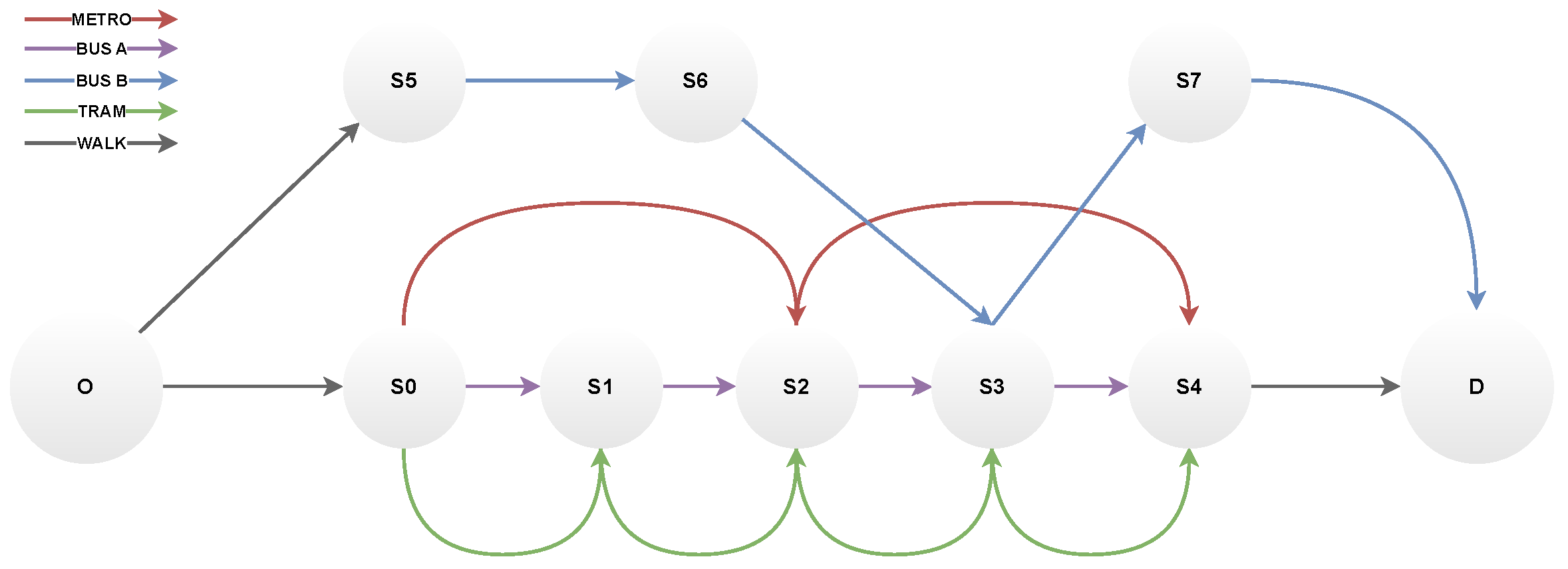
To thoroughly assess the resilience and effectiveness of our proposed system, we introduced a severe stress condition, referred to as a shock scenario, into the transportation network, simulating a critical infrastructure failure that significantly impacts user flow and system operations. Rather than applying this scenario to the full-scale Lyon network, which would have introduced excessive complexity and limited interpretability, we designed a smaller, controlled public transport graph that preserves the key structural properties of an urban public transport network (multiple intersecting lines, transfer nodes, and temporal demand peaks). The smaller graph (G) was shown in Figure 17. This network has two bus lines (A and B), one tram line, and one metro line. Buses and trams run less frequently than the metro, and have lower capacity (see

Table 11. Public means characterization.

Type	Speed	Frequency	Capacity
Bus	8.5 m/s	10 min	30
Tram	8.5 m/s	10 min	70
Metro	8.5 m/s	5 min	150

).

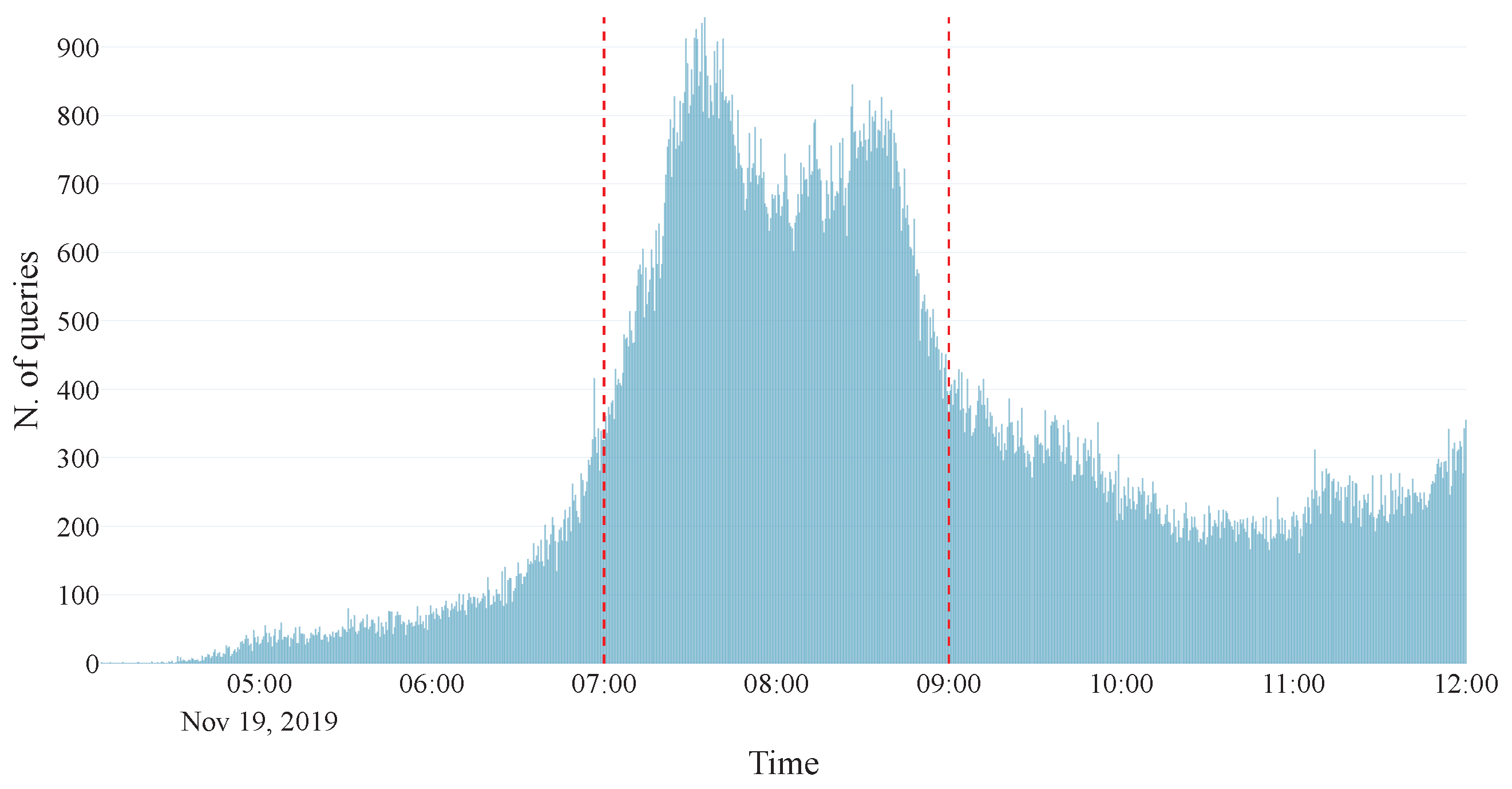
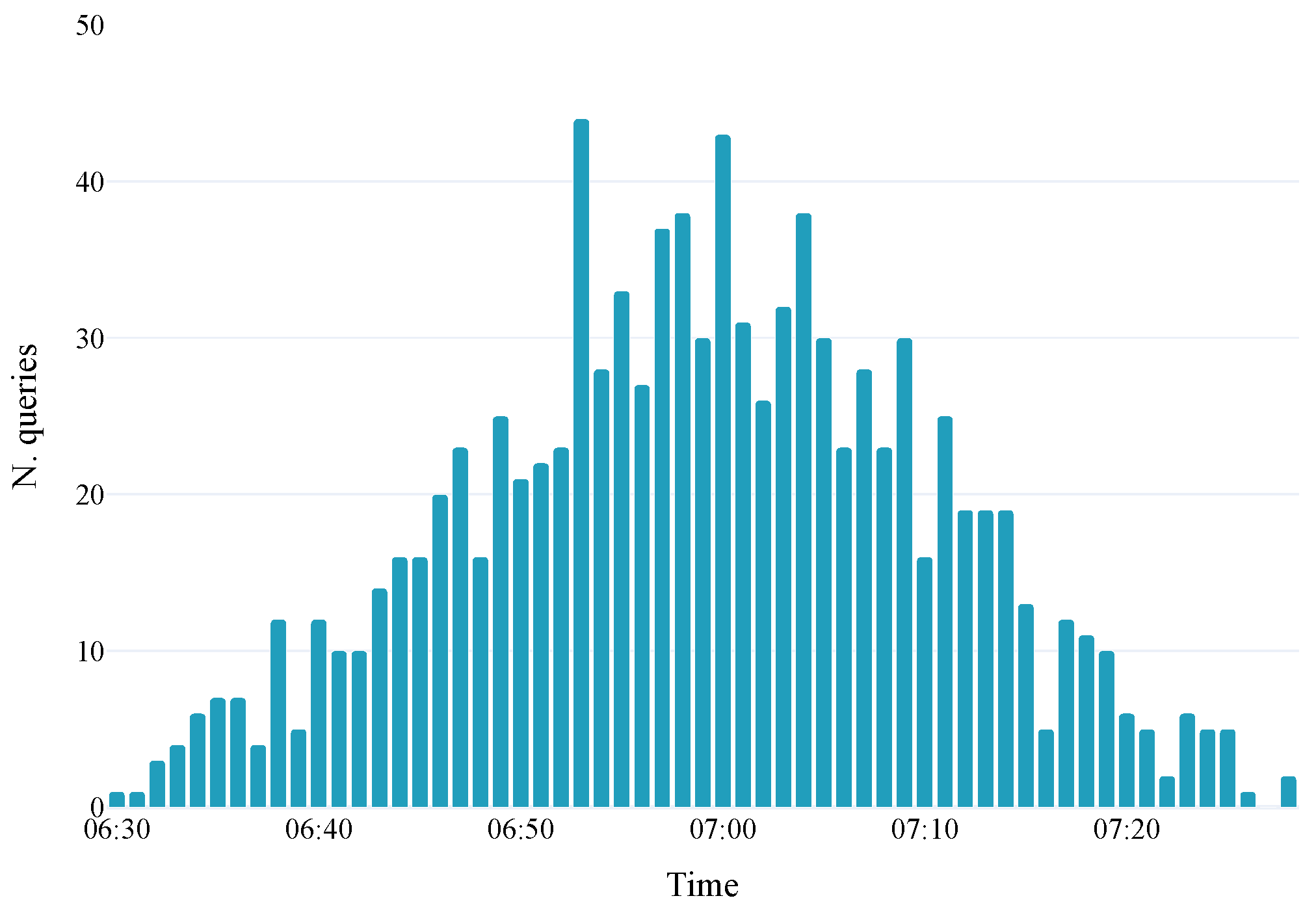
The simulation runs from 6:30 to 8:00 a.m., with departures following a Gaussian distribution peaking at 7:00 a.m. (see Figure 18). The earliest departures occur at 6:30, while the latest is at 7:30, allowing sufficient time to observe the movement of later departures within the system. The simulation step is 1 min. Users depart randomly from one of the nodes of G, and arrive at the destination node, D. The objective was not to reproduce realistic demand diversity, but to observe how the strategies react to a sudden interruption under tightly constrained conditions. Currently, 1000 users are injected into the network, with some preferring the bus and others preferring the metro. However, both are willing to take the tram as a second choice. We created a validation dataset to develop a statistical behavior model, assigning a set number of validations to each 5-min time slot. Bus-preferring users validated their trips twice at each bus station and once at each tram station, while metro-preferring users validated twice at each metro station and once at each tram station. The crowding model relies on a moving average approach, while the behavioral model is statistical, as described in Section 3.2. It is derived by dividing the number of validations at each node by the total. Crowding is predicted by employing a moving average model by analyzing a past window of 5 min.

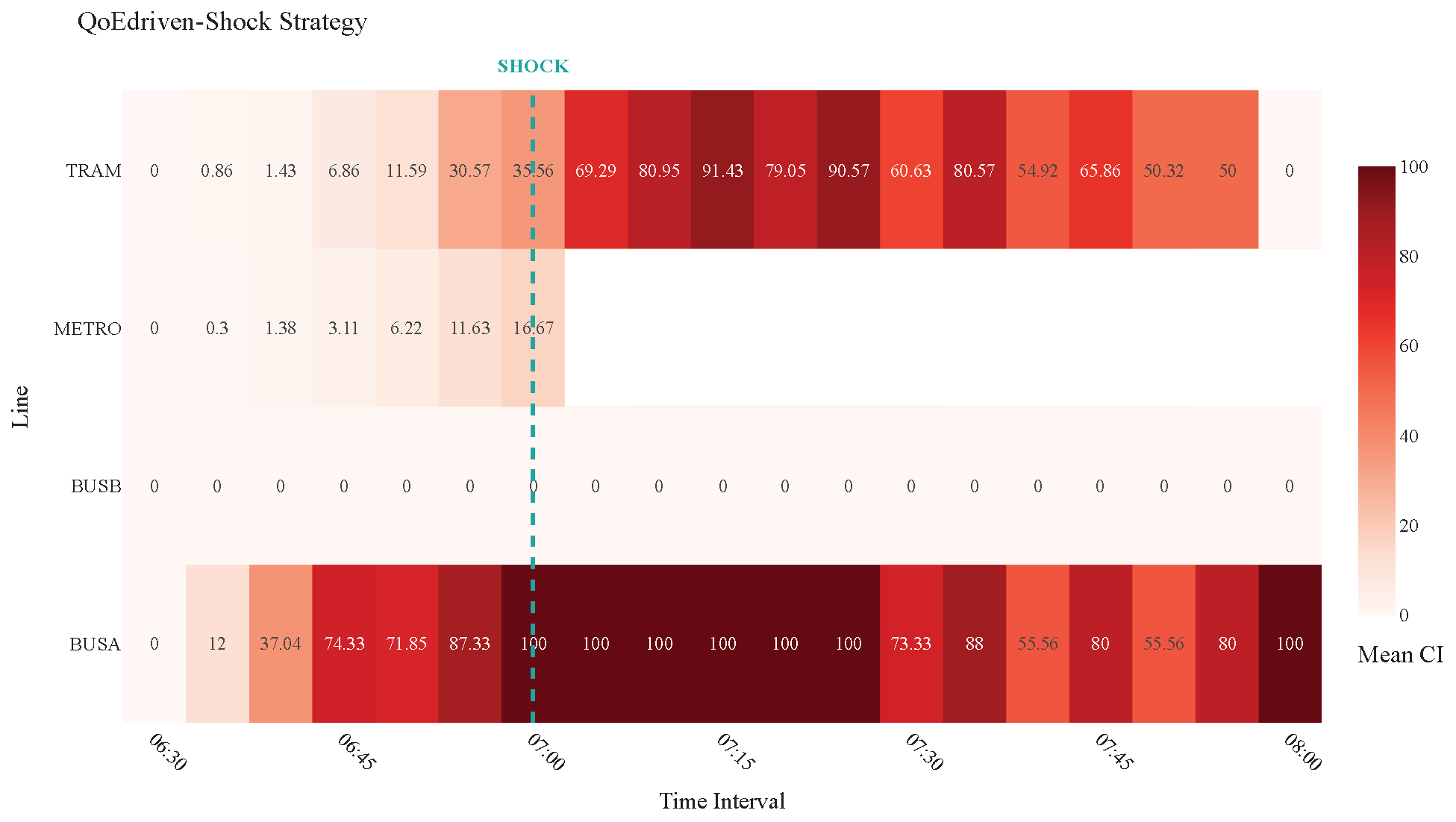
The shock is implemented by completely removing the Metro line from service starting from 7:00 a.m. This specific timing was deliberately chosen because, as established in the baseline analysis, the demand distribution is Gaussian, with the peak departure rate occurring precisely at 7:00 a.m., thus ensuring that the maximum number of users are immediately displaced, forcing a rapid re-evaluation of routes and intensifying the stress on alternative services (Bus and Tram). Furthermore, the removal of the Metro line is the most impactful single-point failure, as it is the most frequent, and highest-capacity service, providing a stringent test of the system’s ability to re-route demand effectively under heavy pressure. To study the system’s adaptive capabilities during this failure, we compare the performance under two distinct operational strategies: the Balanced-Shock Scenario and the QoE-Shock Scenario.

As shown in Figure 19 and Figure 20, although vehicles appear more crowded overall, this reflects better multimodal utilization. The Balanced strategy redistributed demand across all available modes, allowing 874 passengers to reach their destination, compared to only 687 under the QoE-driven configuration. Moreover, in the Balanced scenario, the tram and Bus A were either less crowded or remained at full capacity for shorter periods, indicating a more even temporal load distribution. This proactive redistribution prevented persistent overload and allowed a greater share of users to complete their trips. The analysis of median user criteria (

Table 12. Median user criteria under disruption scenario.

Metric	QoE-Driven	Balanced
Travel Time [s]	1926.76	1866.76
Waiting Time [s]	0	0
Line changes	1.00	1.00
Failed Boarding Attempts	1.00	1.00
Mean Station Preference	0.0042	0.0042

) further confirms comparable travel times between strategies, with the Balanced scenario showing slightly shorter median travel times, and identical values for waiting time, line changes, mean station preference, and failed boarding attempts (as defined in Section 4.1.4). Going deeper into these two scenarios, the median times spent by each user pausing for the vehicles arrival were calculated, obtaining 1317 s for QoE and 780 s for Balanced, resulting in shorter times in the proposed approach. While the user experience (QoE) remains consistent, the Balanced approach achieves this with higher throughput.

Overall, these findings suggest that, even under extreme demand conditions and infrastructure shock, the Balanced strategy enhances resilience and service continuity by dynamically distributing users across modes and mitigating persistent overcrowding.

5. Threats to Validity

This section discusses the main limitations of the proposed system and suggests directions for improvement. The following points detail key threats from simplifying assumptions and methodological choices in the system’s design.

• Assumptions about vehicle maximum capacity: We estimated vehicle capacity based on validation data, which inherently involves approximation. Consequently, discrepancies between assumed and actual capacity could impact the accuracy of crowding predictions and capacity-based routing. This limitation, however, is specific to the experimental setup. In a real-world deployment, vehicle capacity is a static parameter provided directly by the transport operator, ensuring accurate knowledge of available seats and standing room. Therefore, the limitation observed here would not apply in an operational system.
• Exclusion of motor vehicles and bicycles: The exclusion of private cars and bicycles was a deliberate design choice. The input demand used in the simulations exclusively represents Public Transport (PT) users, as the study specifically aims to enhance PT efficiency and passenger experience by mitigating on-board crowding through demand redistribution. Including private cars would shift the focus toward intermodal competition rather than optimizing public transport operations, while the simulation deliberately omits motor vehicle traffic (cars, trucks, etc.) to isolate the performance of the PT network under ideal conditions. Similarly, bicycles, even when provided through public-sharing schemes, fall outside the scope of our modeling framework. Our approach relies on vehicle-based crowding metrics that quantify occupancy and capacity at the vehicle level, whereas bicycles, even under high demand, are limited by availability rather than onboard crowding. Moreover, promoting bicycles as an alternative to crowded PT modes could reduce user acceptance, as only a minority of PT users are typically willing to switch to active modes such as cycling, particularly in urban contexts with variable weather, safety concerns, or longer travel distances. For these reasons, the study focuses on balancing passenger loads within the PT network itself, where crowding relief can be achieved without compromising user acceptance.
• Assumptions in Origin-Destination (OD) pair extraction: The derived travel demand is subject to the inherent approximations introduced by the chosen OD pair extraction technique. This approach, although approximative, is widely used in transport modeling to infer OD pairs from validation or ticketing data when direct trip records are unavailable [39,40]. In our case, this choice does not compromise the validity of the findings, as the same OD pairs were consistently used across all three tested scenarios (Balanced, QoE-driven, and QoS-driven). Thus, while the exact individual destinations may not be known, the comparative results remain robust; the observed differences in crowding and performance indicators stem solely from the routing strategies rather than from OD estimation uncertainty. Given that the public transportation infrastructure network lacks double validation (at entry and exit), a heuristic approach was necessary to derive OD pairs. Future experiments with a deployed system using real-world queries or in a real-world setting would provide valuable insights.

6. Conclusions

We proposed a multimodal public transit system as a proof of concept to minimize the impact of crowding while ensuring user-friendly recommendations based on their travel habits. We applied the BeT paradigm to design a robust, well-structured, and easily implementable architecture. This systematic process allowed us to detail all design choices and propose viable alternatives for a future production system. Our solution comprises three subsystems: a user agent, which models user preferences and habits, collects origin-destination queries, and provides recommendations; a system agent, which models public transportation crowding; and a QoE-QoS balancer, which extracts and ranks all possible routes by filtering them based on crowding levels and then selecting the route that maximizes QoE metrics (such as shortest path, user habits, and a lower number of line changes). This work uniquely utilizes the subscription validation dataset, a primary data source for public transportation providers, to offer a novel methodology for extracting a human behavior model. This study deliberately adopted simple and interpretable models for both user behavior (BI) and crowding (CI). These abstractions allowed us to validate the methodology in a controlled proof-of-concept setting. Naturally, more sophisticated behavioral models (e.g., Markov chains, Hidden Markov Models, or graph-based approaches) and advanced congestion forecasting techniques (e.g., ARIMA, Kalman filters, or spatiotemporal graph models) could provide more accurate representations of travelers’ dynamics and network interactions. The positive results obtained despite these simplifications suggest that refining the models is likely to further improve accuracy and robustness, paving the way for future research and real-world deployment.

We used a real-world dataset from TCL’s Lyon public transportation network to validate our approach. We also extended the MnMS simulator to handle boarding failures caused by crowding and to support the proposed path choice policy. To ensure a rigorous analysis, our findings were obtained using a specialized statistical score based on the Wilcoxon signed-rank test. This approach moves beyond simple crowding frequency by assessing the statistical significance and practical magnitude of differences between competing strategies. Our findings demonstrate that the balanced strategy is the most effective approach, as it successfully resolves the conflict between network efficiency and user satisfaction. The balanced approach leads to a substantial decrease in crowding, with its performance on trams nearly matching the purely QoS-driven strategy, which serves as the ideal benchmark for crowding reduction. This contrasts sharply with the QoE-driven strategy, which prioritizes individual user perception by increasing crowding, waiting times, and failed boarding attempts. While rerouting with the balanced approach may increase overall travel times, it ensures that the route remains comfortable for the user. Unlike the QoS-driven strategy, our solution respects user habits, avoids excessive transfers, and significantly improves the network’s operational conditions without compromising passenger convenience.

7. Future Works

The present work serves as a proof of concept, demonstrating that the proposed balanced strategy could support urban transportation operators and MaaS providers in dynamic crowding management while maintaining user satisfaction. As future work, we plan to extend this study by incorporating more sophisticated models. In particular, machine learning-based approaches could be employed to dynamically learn user behaviour and crowding patterns, improving the adaptability of the recommendation system to real-world conditions. This will allow the solution to evolve into a robust and deployable large-scale system. Once a real-world system allows us to elicit user-specific preferences, more advanced MCDM (multi-criteria decision-making) methods (e.g., AHP, TOPSIS) could be integrated to weight QoE factors dynamically, complementing our current two-stage framework. When deploying the system in the real world, new challenges will emerge, such as scalability and, most importantly, the users’ readiness to accept the provided recommendations. Integrating real-time data streams in a cloud/edge architecture would enhance responsiveness and scalability. Finally, the execution of perception studies to validate whether users accept rerouting strategies in practice would reinforce the robustness and practical relevance of the proposed technique.