Improved Genetic Algorithm-Based Path Planning for Multi-Vehicle Pickup in Smart Transportation
Abstract
Highlights
- This study proposes an Improved Genetic Algorithm (IGA) specifically designed for multi-vehicle path planning in large-scale and dynamic ride-hailing applications, which includes vehicle capacity constraints, incomplete station connectivity, and edge-based passenger distribution.
- Comparative experiments on four benchmark simulation environments demonstrate that the proposed IGA significantly reduces both maximum and average sub-path lengths, while improving computational efficiency relative to the classical MSTC* approach.
- The proposed IGA framework effectively addresses the operational challenges of multi-vehicle coordination in complex and intelligent transportation systems, offering a scalable and efficient solution for real-time vehicle path planning with shared-ride constraints.
- These findings provide methodological support for the development of intelligent dispatching strategies in intelligent transportation systems, with potential application in dynamic and resource-constrained urban mobility scenarios.
Abstract
1. Introduction
- We propose a novel multi-vehicle path planning model tailored for multi-passenger pickup scenarios in urban intelligent transportation systems. By extending the conventional CVRP to incorporate realistic constraints such as urban road topology and partially connected pickup stations, the proposed model significantly improves practical applicability.
- We design the IGA with a focus on accelerating convergence and enhancing global optimization capability, making it more suitable for large-scale and dynamic ride-hailing applications.
- We validate our approach using extensive simulations on four diverse maps in the Carla simulation platform. Results demonstrate significant improvements in routing quality and computational performance compared to traditional methods.
2. Related Research
2.1. Traditional Path Planning Methods
2.2. Ride-Sharing and Multi-Vehicle Task Allocation
2.3. Genetic Algorithms for Path Planning
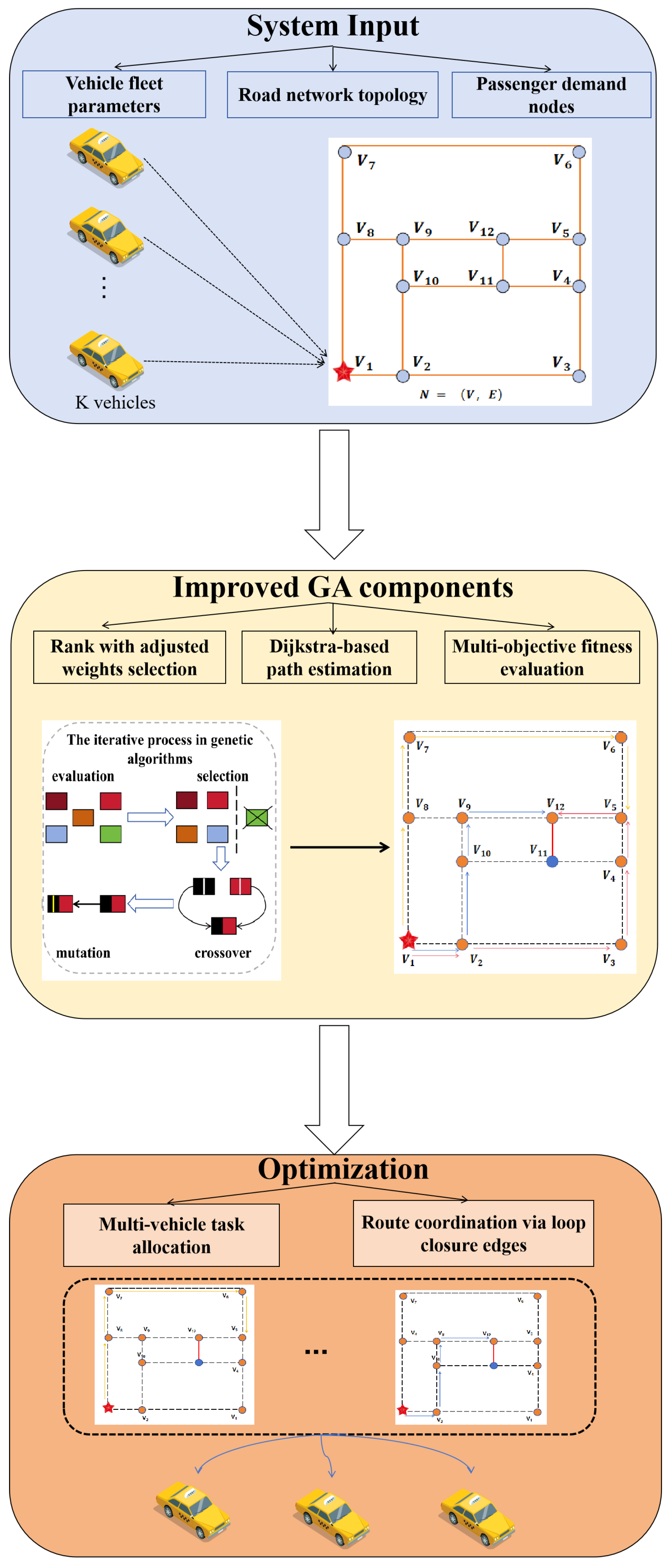
3. Modeling the Multi-Vehicle Collaborative Path Planning Problem
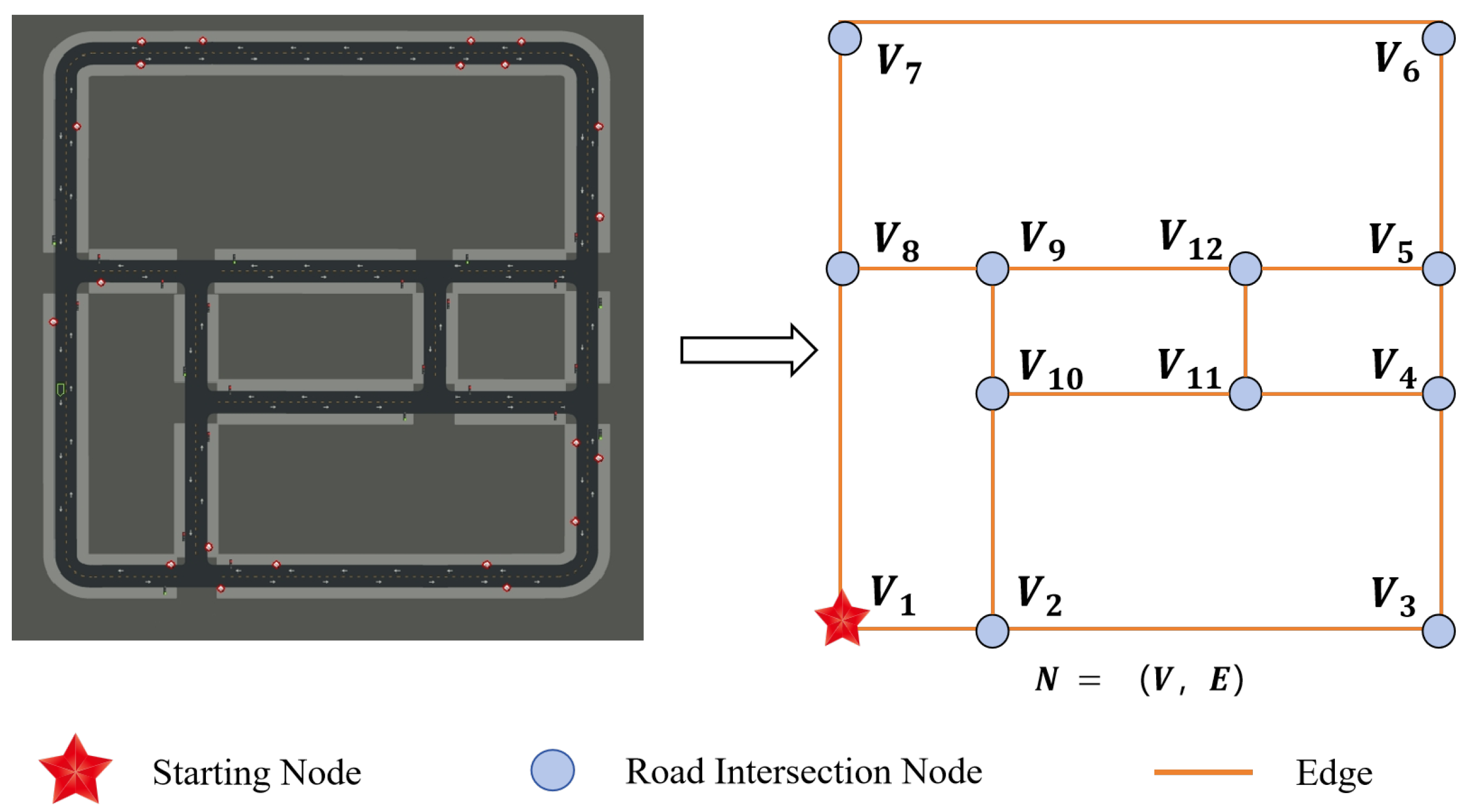
3.1. Scenario Assumptions for Pickup Path Planning
3.2. Mathematical Model
- All vehicles start from the same initial location.
- The number of vehicles is denoted by K.
- Passenger pickup requests are located along edges in the road network.
- Vehicles are initially unloaded.
- All passengers agree to shared rides.
- Vehicles are represented using a simplified kinematic model that operates along the road network graph. Dynamic aspects such as acceleration, braking forces, and tire dynamics are not explicitly modeled, as the focus of this work is on high-level path planning and task allocation.
- Constraint 1: Vehicle Capacity Constraint
- Constraint 2: Total Travel Distance Constraint
- Constraint 3: Pickup Assignment Constraint
4. Improved Genetic Algorithm Design
4.1. The Basic Framework of Genetic Algorithms
| Algorithm 1: Improved Genetic Algorithm with Repair Mechanism |
 |
4.2. Design of the Fitness Function
- Minimize the total travel distance across all vehicle routes, with a particular emphasis on reducing the length of the longest sub-path to ensure task balance and improve overall system efficiency.
- Enforce strict adherence to the vehicle capacity constraint to avoid overloading during passenger pickup.
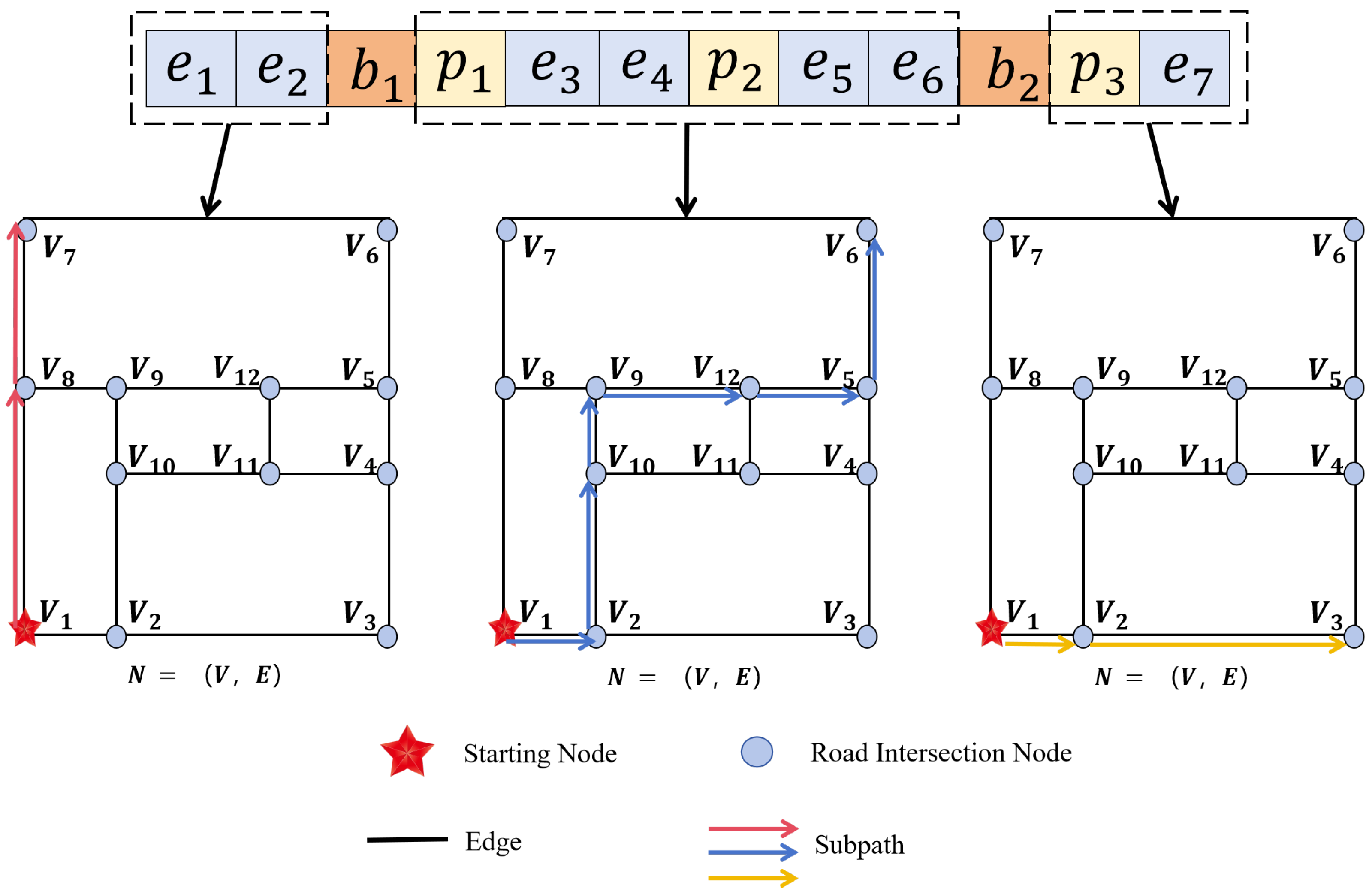
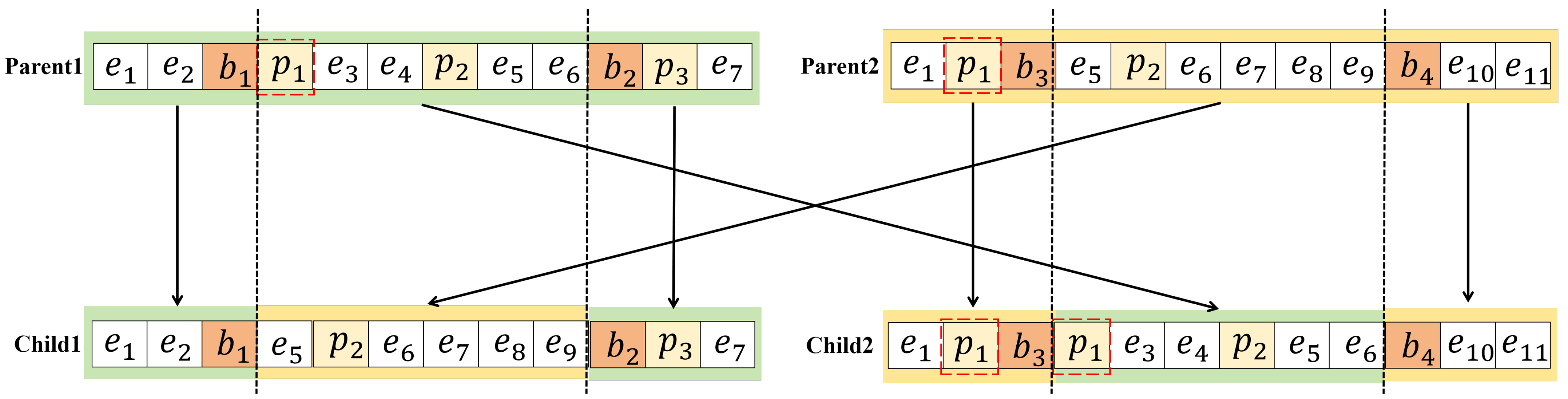
4.3. Chromosome Encoding and Genetic Operations
- Blue genes : Represent standard road edges that do not involve passenger pickups. These edges are included in the route to maintain connectivity but are not directly associated with service demands.
- Yellow genes: Represent pickup edges, i.e., road edges where passengers are waiting to be picked up. Each pickup edge has an associated demand and must be assigned to exactly one vehicle.
- Orange genes: Denote boundary markers that divide the chromosome into sub-sequences, with each sub-sequence encoding the route of a specific vehicle. These boundary genes are critical for partitioning tasks among multiple vehicles.
5. Experiments and Analysis of Results
5.1. Experimental Setup
5.2. Experimental Design, Results, and Analysis
5.2.1. Comparison of Selection Strategies in Genetic Algorithm
- Random Selection: This method selects individuals completely at random, irrespective of their fitness values. While it does not exploit any information about solution quality, it is occasionally used to maintain genetic diversity or as a baseline for comparative studies [26].
- Rank-based Selection: Individuals are ranked according to their fitness, and selection probabilities are assigned based on rank rather than absolute fitness [27]. This approach mitigates the issues associated with highly skewed fitness distributions and helps maintain selection pressure across generations.
- Rank with Adjusted Weights Selection: An extension of rank-based selection, this method assigns non-linear or custom-defined weights to different ranks, such as exponential or quadratic scaling. It enables fine-grained control over selection pressure and can be tailored to balance exploration and exploitation.
- Roulette Wheel Selection: Also known as fitness-proportional selection, this method allocates selection probability to each individual proportional to its fitness value. It is conceptually simple but can be sensitive to fitness variance, potentially causing premature convergence if a few individuals dominate the population [28].
- Tournament Selection: A subset of individuals is randomly sampled from the population to form a "tournament," and the individual with the highest fitness in the group is selected. The size of the tournament determines the selection pressure: larger tournaments favor fitter individuals more strongly.
- Truncation Selection: This method involves selecting the top-performing individuals—based on a predefined proportion or fixed number—and discarding the rest. Although it imposes strong selection pressure and accelerates convergence, it may also reduce genetic diversity and increase the risk of premature convergence [29].

5.2.2. Running Time Analysis
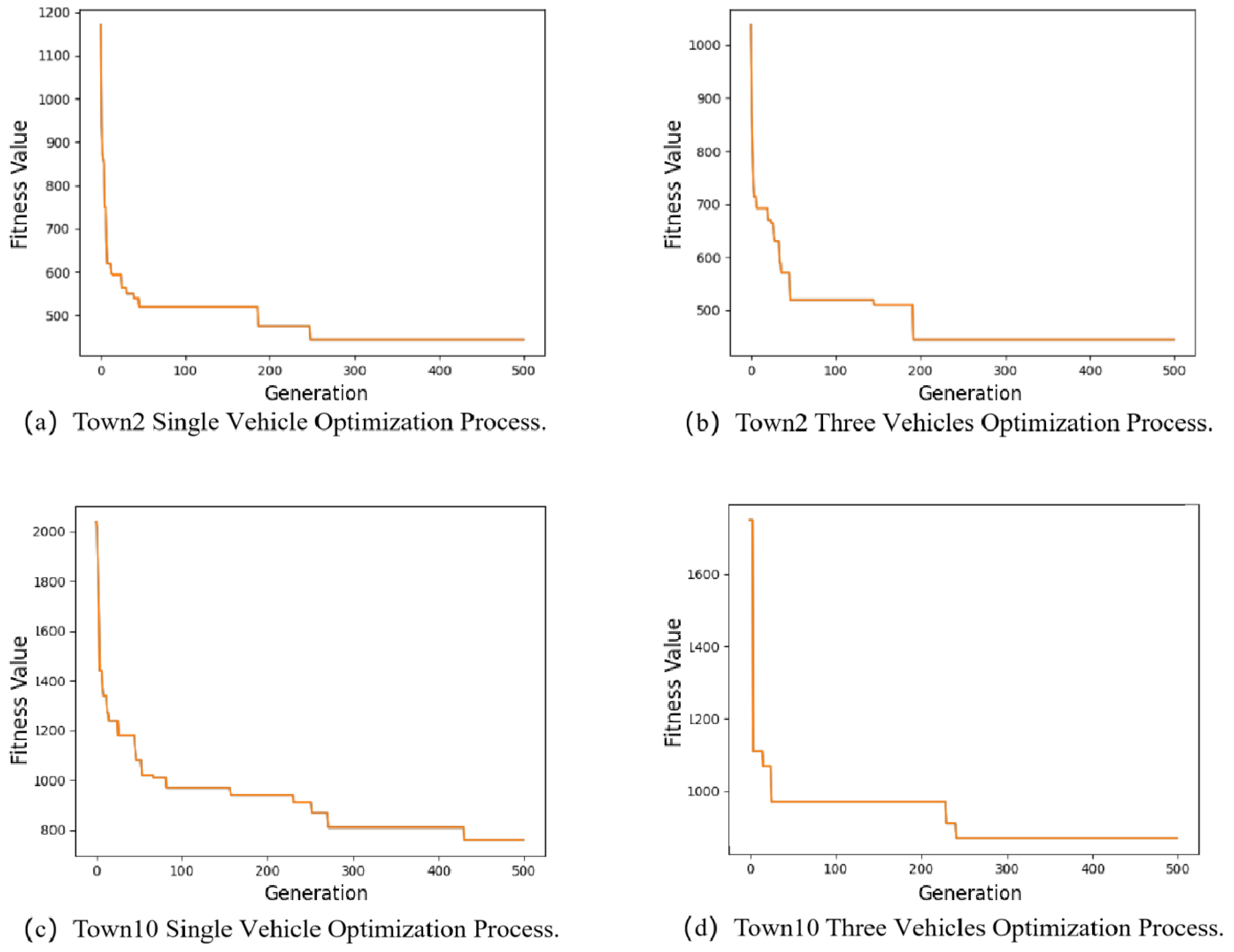
5.2.3. Single-Vehicle vs. Multi-Vehicle Performance Comparison
5.3. Comparison with MSTC*
- Minimum Spanning Tree Construction: An MST is constructed on the weighted graph to establish a globally optimal connectivity structure that minimizes the sum of edge weights.
- Path Allocation: Individual subpaths are derived from the MST and distributed among vehicles such that all nodes are visited with minimal overlap and improved efficiency.
5.3.1. Quantitative Analysis and Comparative Results
5.3.2. Algorithmic Analysis
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Elassy, M.; Al-Hattab, M.; Takruri, M.; Badawi, S. Intelligent transportation systems for sustainable smart cities. Transp. Eng. 2024, 16, 100252. [Google Scholar] [CrossRef]
- Sharma, V.; Kumar, L.; Sergeyev, S. Recent Developments and Challenges in Intelligent Transportation Systems (ITS)—A Survey. In Intelligent Computing and Communication Systems; Singh, B., Coello, C.A.C., Jindal, P., Verma, P., Eds.; Algorithms for Intelligent Systems; Springer: Singapore, 2021; pp. 37–44. [Google Scholar] [CrossRef]
- Wang, W.; Jiao, L.; Zhang, W.; Jia, Q.; Su, F.; Xu, G.; Ma, S. Delineating urban growth boundaries under multi-objective and constraints. Sustain. Cities Soc. 2020, 61, 102279. [Google Scholar] [CrossRef]
- Ahmed, H.U.; Huang, Y.; Lu, P.; Bridgelall, R. Technology Developments and Impacts of Connected and Autonomous Vehicles: An Overview. Smart Cities 2022, 5, 382–404. [Google Scholar] [CrossRef]
- Vergis, S.; Komianos, V.; Tsoumanis, G.; Tsipis, A.; Oikonomou, K. A Low-Cost Vehicular Traffic Monitoring System Using Fog Computing. Smart Cities 2020, 3, 138–156. [Google Scholar] [CrossRef]
- Dantzig, G.B.; Ramser, J.H. The Truck Dispatching Problem. Manag. Sci. 1959, 6, 80–91. [Google Scholar] [CrossRef]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Hart, P.; Nilsson, N.; Raphael, B. A Formal Basis for the Heuristic Determination of Minimum Cost Paths. IEEE Trans. Syst. Sci. Cyber. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Stentz, A. Optimal and efficient path planning for partially-known environments. In Proceedings of the 1994 IEEE International Conference on Robotics and Automation, San Diego, CA, USA, 8–13 May 1994; IEEE Computer Society Press: Los Alamitos, CA, USA, 1994; pp. 3310–3317. [Google Scholar] [CrossRef]
- Lai, G.-J.; Li, T.; Shi, B.-J. RRT-Based Optimizer: A Novel Metaheuristic Algorithm Based on Rapidly-Exploring Random Trees Algorithm. IEEE Access 2025, 13, 42744–42776. [Google Scholar] [CrossRef]
- Kavraki, L.E.; Svestka, P.; Latombe, J.-C.; Overmars, M.H. Probabilistic roadmaps for path planning in high-dimensional configuration spaces. IEEE Trans. Robot. Automat. 1996, 12, 566–580. [Google Scholar] [CrossRef]
- Chen, W.; Lin, B.; Zhang, X.; Lin, X.; Zhao, H.; Zhang, Q.; Kwok, J.T. Gradient-Based Multi-Objective Deep Learning: Algorithms, Theories, Applications, and Beyond. arXiv 2025. [Google Scholar] [CrossRef]
- Mitropoulos, L.; Kortsari, A.; Ayfantopoulou, G. A systematic literature review of ride-sharing platforms, user factors and barriers. Eur. Transp. Res. Rev. 2021, 13, 61. [Google Scholar] [CrossRef]
- Bongiovanni, C.; Kaspi, M.; Cordeau, J.-F.; Geroliminis, N. A machine learning-driven two-phase metaheuristic for autonomous ridesharing operations. Transp. Res. Part E Logist. Transp. Rev. 2022, 165, 102835. [Google Scholar] [CrossRef]
- Chen, L.; Hu, B.; Guan, Z.-H.; Zhao, L.; Shen, X. Multiagent Meta-Reinforcement Learning for Adaptive Multipath Routing Optimization. IEEE Trans. Neural Netw. Learning Syst. 2022, 33, 5374–5386. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef]
- Lambora, A.; Gupta, K.; Chopra, K. Genetic Algorithm—A Literature Review. In Proceedings of the 2019 International Conference on Machine Learning, Big Data, Cloud and Parallel Computing (COMITCon), Faridabad, India, 14–16 February 2019; pp. 380–384. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; The MIT Press: Cambridge, MA, USA, 1992. [Google Scholar] [CrossRef]
- Goldberg, D.E.; Holland, J.H. Genetic Algorithms and Learning. Mach. Learn. 1988, 3, 95–99. [Google Scholar] [CrossRef]
- Yan, F.; Dridi, M.; Moudni, A.E. Autonomous vehicle sequencing algorithm at isolated intersections. In Proceedings of the 2009 12th International IEEE Conference on Intelligent Transportation Systems, St. Louis, MO, USA, 4–7 October 2009; pp. 1–6. [Google Scholar] [CrossRef]
- Taghavi, A.; Ghanbari, R.; Ghorbani-Moghadam, K.; Davoodi, A.; Emrouznejad, A. A genetic algorithm for solving bus terminal location problem using data envelopment analysis with multi-objective programming. Ann. Oper. Res. 2022, 309, 259–276. [Google Scholar] [CrossRef]
- Wang, C.-H.; Lu, J.-Z. A hybrid genetic algorithm that optimizes capacitated vehicle routing problems. Expert Syst. Appl. 2009, 36, 2921–2936. [Google Scholar] [CrossRef]
- Blum, C. Ant colony optimization: A bibliometric review. Phys. Life Rev. 2024, 51, 87–95. [Google Scholar] [CrossRef]
- Shami, T.M.; El-Saleh, A.A.; Alswaitti, M.; Al-Tashi, Q.; Summakieh, M.A.; Mirjalili, S. Particle Swarm Optimization: A Comprehensive Survey. IEEE Access 2022, 10, 10031–10061. [Google Scholar] [CrossRef]
- Zhou, C.; Li, J.; Shi, M.; Wu, T. Multi-Robot Path Planning Algorithm for Collaborative Mapping under Communication Constraints. Drones 2024, 8, 493. [Google Scholar] [CrossRef]
- Onakpojeruo, E.P.; Uzun, B.; David, L.R.; Ozsahin, I.; Ozsahin, D.U. Selection Techniques in Genetic Algorithm. In Proceedings of the 2024 17th International Conference on Development in eSystem Engineering (DeSE), Khorfakkan, United Arab Emirates, 6–8 November 2024; pp. 411–416. [Google Scholar] [CrossRef]
- Lin, G.; Huang, C.; Zhan, S.; Lu, X.; Lu, Y. Ranking Based Selection Genetic Algorithm for Capacity Flow Assignments. In Computational Intelligence and Intelligent Systems; Cai, Z., Tong, H., Kang, Z., Liu, Y., Eds.; Communications in Computer and Information Science; Springer: Berlin/Heidelberg, Germany, 2010; Volume 107, pp. 97–107. [Google Scholar] [CrossRef]
- Lipowski, A.; Lipowska, D. Roulette-wheel selection via stochastic acceptance. Phys. A Stat. Mech. Its Appl. 2012, 391, 2193–2196. [Google Scholar] [CrossRef]
- Fang, Y.; Li, J. A Review of Tournament Selection in Genetic Programming. In Advances in Computation and Intelligence; Cai, Z., Hu, C., Kang, Z., Liu, Y., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6382, pp. 181–192. [Google Scholar] [CrossRef]
- Hazem, Z.B.; Saidi, F.; Guler, N.; Altaif, A.H. Reinforcement learning-based intelligent trajectory tracking for a 5-DOF Mitsubishi robotic arm: Comparative evaluation of DDPG, LC-DDPG, and TD3-ADX. Int. J. Intell. Robot. Appl. 2025. [Google Scholar] [CrossRef]

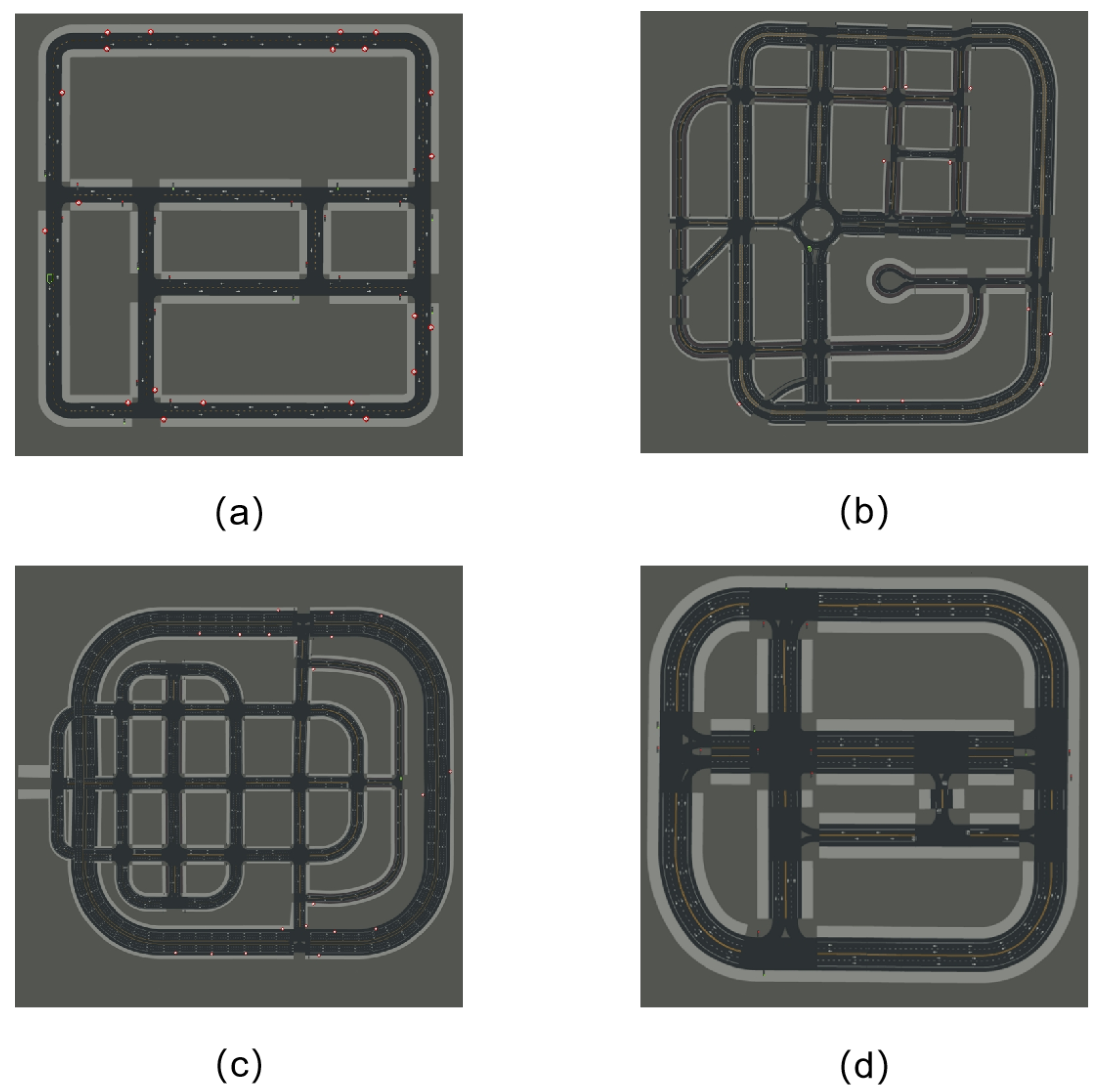
| Map | Map Size (m) | Number of Nodes | Number of Edges | Loop Closure Edges | Network Length (m) | Number of Passengers |
|---|---|---|---|---|---|---|
| Carla Town02 | 150 × 150 | 12 | 16 | 3 | 832 | 10 |
| Carla Town03 | 250 × 250 | 18 | 24 | 5 | 1450 | 15 |
| Carla Town05 | 350 × 350 | 22 | 32 | 6 | 2100 | 20 |
| Carla Town10 | 170 × 200 | 13 | 18 | 3 | 1533 | 11 |
| Selection Strategy | Final Best Fitness |
|---|---|
| Random Selection | 1380 |
| Rank-based Selection | 1910 |
| Rank with Adjusted Weights Selection | 1170 |
| Roulette Wheel Selection | 1840 |
| Tournament Selection | 1670 |
| Truncation Selection | 2200 |
| Selection Strategy | Runtime Mean (s) | Std (s) | 95% CI (s) |
|---|---|---|---|
| Random Selection | 21.36 | 0.82 | [20.96, 21.75] |
| Rank with Adjusted Weights Selection | 18.77 | 0.64 | [18.45, 19.09] |
| Rank-based Selection | 19.87 | 0.75 | [19.49, 20.25] |
| Roulette Wheel Selection | 22.04 | 0.89 | [21.61, 22.47] |
| Tournament Selection | 22.84 | 0.91 | [22.40, 23.28] |
| Truncation Selection | 22.47 | 0.88 | [22.04, 22.90] |
| Algorithm | Town | Max (m) | Avg (m) | Time (s) | ↓ Max (%) | ↓ Avg (%) | ↓ Time (%) |
|---|---|---|---|---|---|---|---|
| IGA | Town02 | 746 | 740.06 | 13.09 | 49.2 | 43.3 | 28.5 |
| Town03 | 1595 | 1566.67 | 42.62 | 24.0 | 19.7 | 12.6 | |
| Town05 | 2195 | 2181.67 | 44.22 | 23.0 | 17.7 | 15.4 | |
| Town10 | 892 | 883.06 | 18.77 | 48.3 | 39.3 | 10.8 | |
| GA | Town02 | 1100 | 980.50 | 16.75 | 25.1 | 23.6 | 7.6 |
| Town03 | 1830 | 1750.20 | 45.20 | 12.9 | 9.2 | 7.3 | |
| Town05 | 2430 | 2360.15 | 48.10 | 14.0 | 11.4 | 8.0 | |
| Town10 | 1240 | 1125.30 | 19.95 | 28.1 | 22.6 | 5.2 | |
| MSTC* | Town02 | 1468 | 1304.60 | 18.32 | - | - | - |
| Town03 | 2100 | 1950.25 | 48.75 | - | - | - | |
| Town05 | 2850 | 2650.40 | 52.30 | - | - | - | |
| Town10 | 1724.2 | 1454.30 | 21.05 | - | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Zhou, C.; Li, J.; Wang, C.; Zhang, P. Improved Genetic Algorithm-Based Path Planning for Multi-Vehicle Pickup in Smart Transportation. Smart Cities 2025, 8, 136. https://doi.org/10.3390/smartcities8040136
Liu Z, Zhou C, Li J, Wang C, Zhang P. Improved Genetic Algorithm-Based Path Planning for Multi-Vehicle Pickup in Smart Transportation. Smart Cities. 2025; 8(4):136. https://doi.org/10.3390/smartcities8040136
Chicago/Turabian StyleLiu, Zeyu, Chengyu Zhou, Junxiang Li, Chenggang Wang, and Pengnian Zhang. 2025. "Improved Genetic Algorithm-Based Path Planning for Multi-Vehicle Pickup in Smart Transportation" Smart Cities 8, no. 4: 136. https://doi.org/10.3390/smartcities8040136
APA StyleLiu, Z., Zhou, C., Li, J., Wang, C., & Zhang, P. (2025). Improved Genetic Algorithm-Based Path Planning for Multi-Vehicle Pickup in Smart Transportation. Smart Cities, 8(4), 136. https://doi.org/10.3390/smartcities8040136





