Vulnerability Assessment of Buildings: Considering the Impact of Human Engineering Activity Intensity Change

Highlights

What are the main findings?

• Inclusion of Human Engineering Activity Improves Prediction Accuracy. An ablation study demonstrates that explicitly incorporating the temporal change in human engineering activity intensity (via variations in building and road densities) significantly enhances the model’s ability to predict building vulnerability. Models without this dynamic HEAIC factor perform worse than those that include it.
• Optimal Machine Learning Configuration and Performance. Among the combinations tested, the Light Gradient Boosting Machine (LGBM) tuned with Differential Evolution and augmented via bootstrap resampling yields the best performance, achieving an RMSE of 0.3745 on the 5471-building test set, which indicates a robust, scalable vulnerability assessment for urban structures.

What is the implication of the main finding?

• Account for Anthropogenic Dynamics: By quantifying how construction and infrastructure expansion alter hazard exposure, planners obtain a more realistic, time-varying picture of which buildings are most at risk—allowing targeted mitigation (e.g., reinforcing structures in rapidly developing zones or rerouting new road projects away from unstable slopes).
• Adopt Scalable, Data-Driven Workflows: The fact that an LGBM model, when optimally tuned and augmented, achieves an RMSE of 0.3745 on over 5000 buildings shows that large-scale, machine learning-driven vulnerability assessments are both feasible and reliable. In practice, this implies that municipal authorities and disaster-management agencies can leverage existing high-resolution imagery and optimization algorithms to routinely update vulnerability maps as the city grows, rather than performing small-sample surveys that quickly become outdated.

Abstract

With accelerating urbanization, the growing density of buildings and the expansion of road networks have fundamentally reshaped the interplay between geological hazards and urban infrastructure. Traditional vulnerability assessment models for buildings (VAB) frequently overlook how human engineering activities—such as construction and city expansion—intensify disaster risk. To address this gap, we introduce VAB-HEAIC, a novel framework that integrates three dimensions of vulnerability: geological environment, building attributes, and dynamics of human engineering activity. Leveraging historical high-resolution imagery, we construct a human engineering activity intensity change indicator by quantifying variations in both road network density and building density. Nineteen evaluation factors, identified via spatial statistical analysis and field surveys, serve as model inputs. Within this framework, we evaluate four machine learning algorithms (Support Vector Regression, Random Forests, Back Propagation Neural Networks, and Light Gradient Boosting Machines), each coupled with four hyperparameter-optimization techniques (Particle Swarm Optimization, Sparrow Search Algorithm, Differential Evolution, and Bayesian Optimization), and three data augmentation strategies (feature combination, numerical perturbation, and bootstrap resampling). Applied to 5471 buildings in Dajing Town, the approach is validated using Root Mean Squared Error (RMSE). The optimal configuration—LGBM tuned with Differential Evolution and enhanced via bootstrap resampling—yields an RMSE of 0.3745. An ablation study further demonstrates that including the human engineering activity intensity change factor substantially improves prediction accuracy. These results offer a more comprehensive methodology for urban disaster risk management and planning by explicitly accounting for the role of human activity in building vulnerability.

1. Introduction

Earthquakes, landslides, and debris flows pose severe threats to urban populations and the structural integrity of buildings, particularly in densely populated, rapidly urbanizing areas [1,2]. As cities expand, interactions between infrastructure and geological processes become more complex and increase disaster risk [3,4,5]. Consequently, rigorous assessment of urban building vulnerability to geological hazards is indispensable for effective disaster risk management and informed urban planning [6,7].

Research on the vulnerability assessment of buildings (VAB) has coalesced around two scales: individual-building evaluations and cluster-level analyses [8]. At the single-building scale, methods, such as the Finite Element Method (FEM) and probabilistic analysis, are most prevalent. Mavrouli et al. developed FEM simulations for structures on various slope types (slow-moving landslides, fast-moving landslides, and rockfall-prone slopes) and applied log-normal statistical models to assess the vulnerability of single-story, reinforced concrete buildings [9]. Complementing this, Barbieri et al. used 3D FEM to study the seismic behavior of Mantua’s historic Palazzo del Capitano. They found that the longitudinal façade was poorly restrained and prone to deformation, and recommended targeted mitigation to reduce seismic risk [10]. Luo et al. applied explicit dynamic analysis in LS-DYNA to elucidate the damage processes and failure mechanisms of three-dimensional reinforced concrete frame buildings under low, medium, and high landslide impact scenarios, proposing a five-level classification scheme to characterize structural damage states [11]. Sun et al. considered uncertainties in landslide mechanics and repair processes by combining dynamic rebound calculations with FEM. Using a five-story reinforced concrete frame as a case, they applied a probability-density evolution method to estimate exceedance probabilities and quantify building vulnerability [12]. However, single-VAB alone cannot satisfy the comprehensive risk management and planning requirements of urban and rural environments. Cluster-level vulnerability evaluations encompassing larger groups of buildings offer superior insights for spatial planning and sustainable development. Traditional regional-scale methods have largely emphasized geological and environmental determinants alongside intrinsic structural attributes.

Recent advances have begun to broaden this perspective. Xing et al. used the FSA-UNet semantic segmentation model to combine satellite and street-view imagery. This approach provided a qualitative and spatially explicit view of urban buildings’ disaster-resistance characteristics [13]. Uzielli et al. assumed direction-insensitive building response and decomposed landslide flow velocities into horizontal and vertical components to perform quantitative risk assessments for 39 structures [14]. In seismic contexts, Karimzadeh et al. built a GIS-based framework to simulate a magnitude 7 event on the North Tabriz Fault. They predicted that 69.5% of buildings would be destroyed and estimated a 33% fatality rate, which was validated using observed data [15]. Ettinger et al. employed logistic regression to model flash flood damage probabilities in Arequipa, Peru, achieving over 67% predictive accuracy in 90% of test cases [2]. Saeidi et al. derived empirical vulnerability functions for underground mining-induced subsidence in the Lorraine region [16]. And Galasso et al. proposed a taxonomy to enhance flood fragility and vulnerability modelling [7]. Finally, Chen et al. (2011) combined field surveys, numerical simulation, and damage classification to assess building vulnerability during the deformation phase of the Zhao Shuling landslide [17].

In recent years, several studies have advanced vulnerability assessment of buildings (VAB) by integrating machine learning with urban and structural indicators. For instance, type-2 fuzzy logic has been applied to rapidly evaluate earthquake hazard safety for existing buildings, while regional-scale coastal hazard assessments have been proposed using vulnerability indices and spatial datasets in Cameroon. Compared to these approaches, our framework uniquely combines dynamic human activity indicators with multiple optimization and augmentation strategies to produce high-resolution, generalizable vulnerability maps under geological disaster scenarios [18]. Recent years have witnessed a growing interest in large-scale building vulnerability assessment, particularly under the influence of natural hazards such as earthquakes, landslides, and floods. Traditional methods, such as Rapid Visual Screening (RVS) and vulnerability indexing, offer practical tools for preliminary evaluation but often lack the flexibility to incorporate dynamic urban indicators and complex interactions between structural, environmental, and anthropogenic factors. In response, machine learning (ML) models have emerged as powerful alternatives capable of capturing nonlinear relationships and handling high-dimensional data inputs. Hwang et al. proposed a machine learning-based approach that integrates boosting algorithms to assess the seismic vulnerability and collapse risk of ductile, reinforced concrete frame buildings while explicitly considering modeling uncertainties at both component and system levels [19]. Zain et al. demonstrated the effectiveness of ML algorithms—particularly XGBoost and Random Forest—in predicting seismic fragility curves for RC and URM school buildings in the Kashmir region, highlighting ML’s potential in rapid, automated seismic vulnerability assessment with high accuracy and reduced computational demand [20]. Kumar et al. developed a cost-effective ML-based framework for seismic vulnerability assessment of RC educational buildings in Dhaka, demonstrating that SVR outperformed other models in predicting the Story Shear Ratio based on rapid visual assessment indicators, despite overall low explanatory power due to data complexity and limitations [21]. Elyasi et al. developed ML models to predict seismic damage classes for low-rise reinforced concrete buildings based on real-world structural and earthquake data [6]. However, integrating spatial variability and human activity dynamics into ML-based frameworks remains a significant challenge.

In large-scale seismic vulnerability assessments, especially for reinforced concrete (RC) buildings, analytical methods such as fragility curve derivation based on numerical modeling or observed damage data have been widely used [22]. For example, Perrone et al. conducted a comprehensive study on the seismic fragility of RC buildings using large-scale numerical modeling across various typologies and urban morphologies [23]. Their work demonstrates the value of high-resolution data and standardized modeling to inform regional risk assessment. While such approaches are highly informative, they often require detailed structural information and are computationally intensive.

Together, these studies have improved our understanding of regional building vulnerability. However, many rely on small sample sizes and overlook the dynamic influence of human engineering activities—such as construction and infrastructure expansion—which can significantly alter vulnerability patterns at the urban scale.

Scholars have extensively examined the factors influencing building vulnerability, primarily emphasizing structural characteristics and external environmental conditions. For example, in the Garhwal Himalayas, Singh et al. introduced a semi-quantitative landslide intensity matrix that classifies 71 buildings according to their resistance capacity under varying slide scenarios, providing a practical framework for landslide-prone regions [24]. Second, the influence of human engineering activities—such as construction and infrastructure expansion—remains largely unmeasured, even though such activities can significantly change vulnerability patterns. Third, traditional methods have difficulty handling the large and diverse datasets needed for urban-scale evaluations.

To address these gaps, this paper proposes VAB-HEAIC—an assessment framework that explicitly considers changes over time in human engineering activity intensity. By using remote sensing derived variations in building density and road network density as core indicators, our model offers a more comprehensive appraisal of urban building vulnerability to geological hazards. The key contributions are as follows:

Expanded Indicator System: We integrate geological factors, field survey data, and dynamic human engineering activity metrics, thereby extending beyond the static indicators used in prior studies

Dynamic HEAIC Metric: We construct a time-varying human engineering activity intensity change indicator by quantifying density changes in buildings and roads from historical high-resolution imagery, enabling direct linkage between anthropogenic developments and vulnerability

Integrated Optimization and Augmentation-Enhanced Machine Learning Assessment: The framework combines four machine learning models (SVR, RF, BPNN, and LGBM) with four hyperparameter optimization methods (Bayesian Optimization, Differential Evolution, Particle Swarm Optimization, and Sparrow Search Algorithm). It also integrates three data augmentation strategies: feature combination, numerical perturbation, and bootstrap resampling. Together, these components enable scalable and robust predictions for thousands of urban structures. This integration not only fine-tunes each model for maximal accuracy but also enriches and balances the training data to mitigate overfitting and improve generalization in complex urban environments.

We validate VAB-HEAIC in Dajing Town, Yueqing City, Zhejiang Province. Field surveys collected data on 1305 slope units and 5471 buildings. The results show clear improvements in prediction accuracy and provide useful insights for disaster risk management and urban planning. The remainder of this paper is organized as follows: Section 2 introduces the study area. Section 3 describes the evaluation indicators. Section 4 details the VAB-HEAIC framework. Section 5 presents experimental results and analysis, followed by a discussion in Section 6. Finally, Section 7 summarizes the conclusions.

2. Study Area

Dajing Town is located in the northeastern sector of Yueqing City, Zhejiang Province. It covers approximately 128.65 km² and administers 47 villages and two urban communities, with a registered population of 106,600. Its geographic bounds extend from 120°9′55.1″ to 121°12′28.5″ E longitude and from 28°21′51.4″ to 28°29′57.9″ N latitude, covering roughly 16.4 km in the east–west direction and 14.2 km north–south (Figure 1).

Dajing Town’s topography is shaped by tectonic erosion, forming low mountains and hills. Elevation ranges from 5 m in valley floors to 730 m at the highest peaks. Upper slopes often exceed 45° in gradient, transitioning to much gentler inclines downslope. Riparian corridors along Dajing Creek comprise alluvial and marine-alluvial plains at 5–10 m elevation with slopes below 5°, resulting in expansive, level terrain. The town has a subtropical monsoon climate with concentrated rainfall, averaging 268.6 mm per month. This rainfall supports dense subtropical evergreen broad-leaved forests. Vegetation cover exceeds 75% in most areas and is characterized by Masson pine stands interspersed with citrus orchards, bamboo groves, shrublands, and grasslands.

Geologically, Dajing Town lies on pre-Quaternary bedrock, mainly composed of Lower Cretaceous volcanic-sedimentary units from the Gao Wu, Xi Shantou, and Xiao Pingtian formations. These units are exposed in the mountainous areas. These are locally overlain by Quaternary residual slope deposits (gravelly silt clay with 10–20% clast content and thicknesses of 0.2–2.5 m) on gentler slopes. Potentially extensive volcanic intrusions—fine-grained alkali granite, rhyolitic porphyry, and related porphyritic lithologies—occur mainly near Linxi and Shuizhuizhou villages, with scattered exposures elsewhere. Collectively, the principal exposed lithologies include volcanic clastic rocks, lava flows, intrusive bodies, and unconsolidated Quaternary sediments.

By October 2022, field surveys in Dajing Town had documented 38 geological hazard sites: 28 landslides, 8 slope collapses, and 2 debris flows. Most landslides are small translational failures from the Holocene period, generally less than 5 m thick. They originate in residual slope deposits, though a few involve weathered and fragmented siltstone. Most initiate at the base of engineered cuts, where excavation destabilizes the slope toe. Collapses occur along pre-existing joint planes and intra-layer shear zones, mobilizing residual soils when artificial excavations induce stress concentrations at slope shoulders. Debris flows result from intense rainfall eroding and entraining loose slope materials and accumulated waste.

Rapid urbanization since 2004 has markedly altered Dajing Town’s built environment and infrastructure. Between 2004 and 2024, the registered population rose to 106,621. The road network expanded from 165.68 km of mostly unpaved roads in 2004 to 324.97 km of asphalted roads in 2014, and then to 347.93 km by 2024. Concurrently, building stock increased from 4019 low-rise structures (total floor area 4.86 × 106 m²) in 2004 to 5141 buildings (5.17 × 106 m²) in 2014, and 5471 buildings (5.24 × 106 m²) by 2024 (

Table 1. The statistics of road length, number of buildings, and building area in Dajing Town in 2004, 2014, and 2024.

Year	Road Length (km)	Number of Buildings	Building Area (m2)
2004	165.68	4019	4,856,211
2014	324.97	5141	5,166,633
2024	347.93	5471	5,240,970

). This intensification of construction and infrastructure underscores the growing imperative for comprehensive vulnerability assessment.

In this study, the information for all 5471 buildings in Dajing Town was acquired through a two-stage process. First, high-resolution remote sensing images from 2004, 2014, and 2024 were used to extract building footprints and estimate spatial distribution changes over time. These images were processed using supervised image interpretation techniques and validated through ground truth data.

Second, a comprehensive field survey was conducted in 2024 by a team of geotechnical and structural engineers. During this survey, detailed attributes were recorded for each building, including structural type, height classification, foundation conditions, and vulnerability indicators. Each building was georeferenced and assigned a unique identifier for integration with other spatial layers.

It is important to note that the proposed model does not assess seismic vulnerability directly. Instead, it focuses on geological hazard-related vulnerability, reflecting risks driven by topographic conditions and intensified by human engineering activities, such as infrastructure development, slope modification, and land use change.

3. Evaluation Indicators

Effective vulnerability assessment depends on a well-designed indicator system that reflects the complex nature of urban building risks under geological hazards. To achieve this, we structured evaluation metrics into three categories: geological environment indicators, slope survey indicators, and human engineering activity indicators. Each was chosen based on its relevance to local building types, terrain, and human-induced changes. By weighting and combining these indicators, our framework provides a comprehensive and quantitative assessment of building vulnerability, accounting for both natural and human-related factors.

3.1. Evaluation Indicators Derived from Geological Environment

3.1.1. Elevation

High-elevation and steep-slope areas have greater gravitational potential energy and lower overall stability. Slope failures in these zones can travel long distances with high kinetic energy, significantly increasing the exposure of buildings to landslides or collapses. Conversely, low-lying areas—such as valley bottoms, fluvial floodplains, and coastal plains—tend to accumulate surface water, exhibit shallow groundwater tables, and are susceptible to inundation, debris-flow deposition, ground liquefaction, and subsidence. Therefore, elevation reflects more than just height above sea level. It also captures various hazard-related factors, such as slope gradient, groundwater depth, and hydrodynamic forces.

In Dajing Town, elevations span from 5 m to 730 m (Figure 2a), with 5471 buildings sited within the 5–500 m band. As depicted in the elevation distribution histogram (Figure 2b), the majority of structures—4362 in total—are located between 0 m and 100 m. Of the remainder, 594 buildings lie between 100 m and 200 m, 391 between 200 m and 300 m, 83 between 300 m and 400 m, and 21 between 400 m and 500 m. This stratified distribution underscores the importance of incorporating elevation-related vulnerability gradients into our assessment framework.

3.1.2. Slope Position

The relative position on a slope exerts a profound influence on a structure’s vulnerability to geohazards. At the slope crest, buildings often sit above tension cracks and rainfall infiltration zones—common points of slope failure initiation. Once failure occurs, these ridge-top structures may be displaced together, facing the highest landslide risk. On the upper slope, steep gradients and widespread shear planes make buildings vulnerable to being swept away or hit by falling rocks. Mid-slope buildings lie in the direct path of landslide debris and falling rocks. In this zone, kinetic energy peaks, often causing the most severe structural damage. Although potential energy diminishes in the lower-slope sector, the increased thickness of deposited material can impose burial loads and lateral thrusts that undermine walls and foundations. At the slope foot—usually shaped by alluvial fans or converging flows—structures face higher risks from debris flows, floods, and liquefaction. These hazards can erode supporting soils and weaken foundations.

In Dajing Town, field surveys have delineated 1305 discrete slope units (Figure 3a), stratified by relative elevation into five zones: slope foot (0–5%), lower slope (5–35%), mid slope (35–65%), upper slope (65–95%), and slope crest (95–100%). Statistical analysis of the town’s 5471 buildings (Figure 3b) reveals that 1776 buildings (32%) lie at the slope foot, 2363 (43%) on the lower slope, 900 (16%) in the mid-slope zone, 388 (7%) in the upper slope, and 44 (1%) directly atop the ridge. This spatial distribution underscores the necessity of incorporating slope position metrics into vulnerability assessments to accurately capture hazard exposure gradients.

3.1.3. Slope

Slope gradient is a key geometric factor that affects gravitational force, water infiltration, and runoff speed. These factors in turn influence slope stability and the loads buildings may face. Slopes steeper than 30° have a larger downslope weight component, and root-soil reinforcement is usually insufficient. As a result, such terrain is more vulnerable to deep-seated landslides during heavy rainfall or earthquakes. Buildings in these areas face high risk, as they may be carried by landslides and struck by fast-moving debris. Moderately steep slopes (15–30°) are usually more stable. However, loose surface materials can still be dislodged during heavy rain, causing shallow landslides or debris flows that threaten buildings below. Slopes under 15° have low potential energy but often collect debris from upslope failures. In these areas, building foundations may experience settlement, liquefaction, or erosion from runoff.

In Dajing Town, slope gradients range from 0° to 81° (Figure 4a). Analysis of the 5471 surveyed buildings (Figure 4b) reveals that the majority—4399 structures (≈80%)—are situated on slopes under 15°. Specifically, 2550 buildings (47%) occupy very gentle slopes (0–5°), 662 (12%) on mild slopes (5–10°), and 503 (9%) on lower moderate slopes (10–15°). Buildings on steeper terrain are less common: 372 (7%) on intermediate slopes (15–20°), 232 (4%) on upper moderate slopes (20–25°), and 80 (1.5%) on notable slopes (25–30°). Only 53 buildings (1%) are located on slopes exceeding 30°, underscoring the relative scarcity of high-hazard sites but highlighting their elevated vulnerability.

3.1.4. Aspect

Slope aspect strongly influences microclimatic and geomorphic processes. It affects solar exposure, wind direction, and precipitation patterns, which in turn shape temperature, soil moisture, vegetation, and erosion rates. Slope aspect also affects water flow, soil moisture retention, and the direction of dynamic forces, such as windborne debris or rockfall. These factors directly impact a building’s vulnerability to geohazards.

In this study, slope aspect refers to the compass direction that the terrain at the building location faces, measured in degrees clockwise from north (0–360°).

In Dajing Town (Figure 5a), slope aspect analysis across 5471 structures reveals that 1024 buildings (≈19%) lie on essentially level ground (no discernible aspect). Of the remaining 4447 buildings, orientation clusters are as follows: 0–45° (northeast-facing), 325 buildings (7.3%); 45–90° (east-facing), 571 buildings (12.8%); 90–135° (southeast-facing), 814 buildings (18.3%); 135–180° (south-facing), 911 buildings (20.5%); 180–225° (southwest-facing), 913 buildings (20.5%); 225–270° (west-facing), 539 buildings (12.1%); 270–315° (northwest-facing), 251 buildings (5.6%); 315–360° (north-facing), 123 buildings (2.8%). This slope aspect distribution underscores the predominance of south- and southwest-facing exposures—zones prone to higher insolation and potentially greater thermal stress—which should be carefully considered in vulnerability modeling.

3.1.5. Lithology

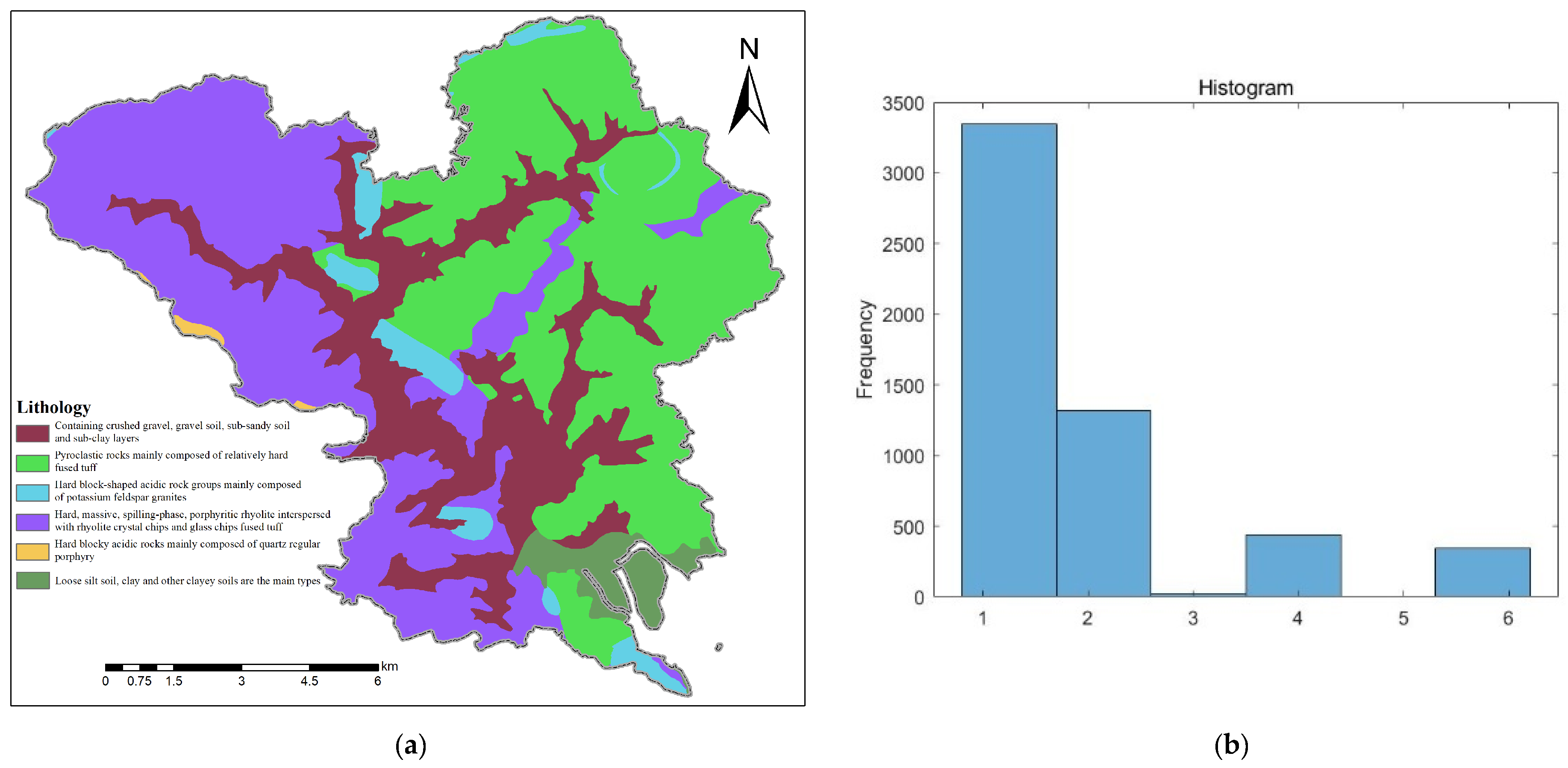
The engineering geological rock group determines the basic properties of foundations and slopes. Its lithology, structural integrity, joint patterns, and permeability influence key factors, such as shear strength, deformation modulus, and resistance to weathering. The distribution of engineering geological rock groups in Dajing Town is shown in Figure 6a, which consists of six types: (1) rock groups primarily composed of gravelly silt, sandy silt, sub-clay, and clay layers; (2) volcanic clastic rock groups mainly consisting of relatively hard welded tuff; (3) hard blocky acidic rock groups dominated by potassium (alkali) granite; (4) hard blocky flow-textured rhyolite, rhyolitic tuff, and felsic volcanic welded tuff; (5) hard blocky acidic rock groups dominated by quartz latite; and (6) loose silt, clay, and other cohesive soil rock groups.

A histogram of the distribution of engineering geological rock groups for the 5471 buildings in Dajing Town is shown in Figure 6b. Among them, 3346 buildings are located in Group 1, 1316 buildings are located in Group 2, 26 buildings are located in Group 3, 438 buildings are located in Group 4, 345 buildings are located in Group 6, and no buildings are located in Group 5.

3.1.6. Plane Curvature

Planar curvature measures how the terrain surface undulates horizontally. Positive values indicate convex features, such as ridges, while negative values represent concave forms, like valleys. A value near zero denotes a flat, planar surface. Convex slopes tend to disperse surface runoff and debris. This promotes erosion at the slope toe and cracking at the crest, potentially triggering block collapse or slope failure. Convexity may also amplify seismic wave energy, increasing the exposure of ridge-top buildings to shaking and rockfall impact. Conversely, concave zones concentrate runoff and slope detritus; during extreme precipitation events, focused infiltration elevates pore-water pressures, softening the substratum and potentially triggering deep-seated landslides or debris-flow channelization, which can inundate valley-bottom buildings through burial or lateral impact.

In Dajing Town, planar curvature computed from high-resolution elevation data spans –117.849 to 168.667 (Figure 7a). Overlay of the 5471 building footprints reveals that 1050 structures lie on nearly planar segments (curvature ≈ 0), 2589 occupy mildly concave slopes (–5 ≤ curvature < 0), and 1790 are sited on mildly convex slopes (0 < curvature ≤ 5) (Figure 7b). This distribution underscores the prevalence of low-magnitude curvature settings, with implications for targeted risk mitigation based on microtopographic controls.

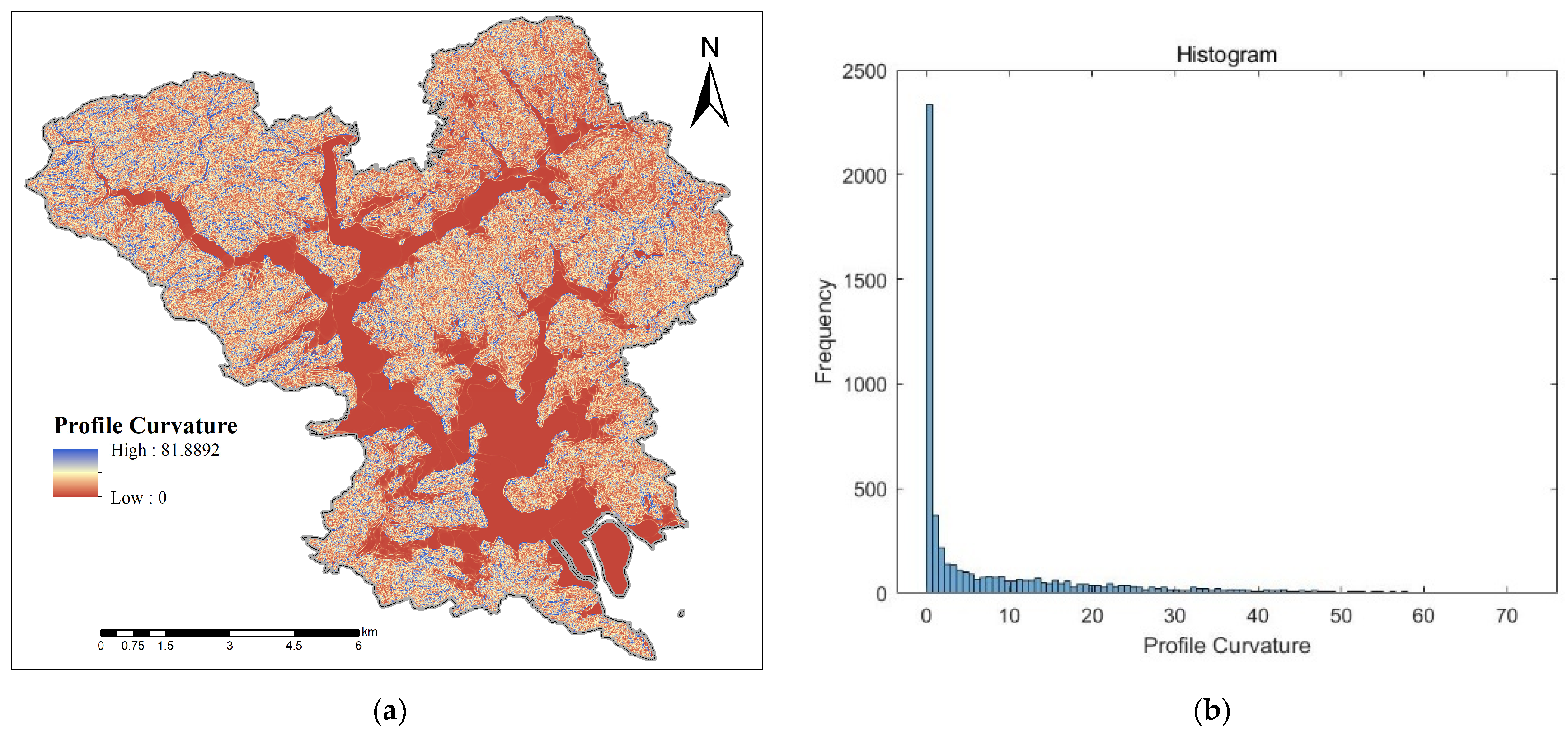
3.1.7. Profile Curvature

Profile curvature measures the longitudinal shape of a slope, defined as the curvature perpendicular to contour lines. Positive values indicate convex forms, such as ridgelines or bulging slopes. These areas concentrate gravitational and runoff-induced shear stresses at the crest and toe, which can lead to erosion, surface cracking, and shallow slope failures during intense rainfall or earthquakes. Negative values correspond to concave profiles, such as troughs or hollows. These landforms concentrate runoff and debris, which raises pore-water pressures. As a result, they are prone to deep-seated landslides or debris flows that may bury buildings in valley-bottom areas.

In Dajing Town, profile curvature derived from high-resolution elevation data spans 0 to 81.8892 (Figure 8a). When the footprints of 5471 buildings are overlaid (Figure 8b), the distribution across curvature classes is as follows: 3009 buildings (55%) on gentle convex segments (0–10); 706 buildings (13%) on moderate convexity (10–20); 404 buildings (7%) on pronounced convexity (20–30); and 450 buildings (8%) on strongly convex segments (>30). This categorization highlights that the majority of urban structures in Dajing Town are located on gently to moderately convex profiles, emphasizing the need to consider profile curvature in vulnerability assessments.

3.1.8. Terrain Ruggedness Index

The terrain ruggedness index (TRI) quantifies the vertical elevation range—i.e., the difference between the highest and lowest points—within a defined spatial unit, thereby encapsulating both the gravitational energy potential of slopes and their hydrodynamic behavior. High-ruggedness areas store greater potential energy and often experience intense toe erosion. They may also amplify seismic motions. During heavy rainfall or earthquakes, these zones are highly susceptible to landslides, slope failures, and rockfalls. Such events can entrain nearby buildings into moving debris or expose them to high-speed impacts. Conversely, low-ruggedness terrain tends to accumulate runoff and debris. This can raise groundwater levels and increase the risk of liquefaction or subsidence. Prolonged waterlogging in such areas may also weaken structural materials over time.

In Dajing Town, TRI values span from 0 to 680 (Figure 9a). When mapped against the 5471 building footprints (Figure 9b), the majority of structures—3450 buildings—fall within TRI classes of 0–1. A further 657 buildings lie in the 1–2 class, 457 in the 2–3 class, 377 in the 3–4 class, and 245 in the 4–5 class. This distribution highlights that most urban buildings occupy relatively low-ruggedness zones, while a smaller subset is exposed to higher-energy slope conditions, underscoring the importance of TRI as a vulnerability indicator.

3.2. Evaluation Indicators Derived from Slope Survey

3.2.1. Slope Cutting Height

Slope cutting height quantifies the extent of artificial excavation and consequent removal of natural lateral support. As the cut height increases, stress redistribution within the unloading zone becomes more intense. Joint apertures also widen, concentrating shear stress and displacement at the slope toe and along potential slip surfaces. These conditions become particularly hazardous under heavy rainfall or seismic loading. They can lead to tensile cracking, shear failure, or even full-scale slope detachment. Structures located on top of high-cut slopes face significantly higher risks of settlement and sliding due to weakened foundation support. Meanwhile, buildings at the slope base may be impacted by falling rocks or lateral forces from mobilized debris. Moreover, freshly exposed rock and soil surfaces accelerate weathering and enhance infiltration, further diminishing shear strength.

Field measurements in Dajing Town (Figure 10a) recorded slope cutting heights across all 1305 slope units, which were classified into five categories—1 m, 2 m, 5 m, 10 m, and 20 m. Overlaying these data with the locations of 5471 buildings yields the following distribution: 2064 buildings on 1 m cuts, 569 on 2 m cuts, 1599 on 5 m cuts, 1188 on 10 m cuts, and 51 on 20 m cuts. This distribution highlights that while most structures experience relatively minor excavation depths, a noteworthy subset is exposed to substantial slope-cutting effects with elevated vulnerability.

3.2.2. Slope Surface Morphology

Slope surface morphology refers to the overall shape of the slope face and the layout of any protective structures. It strongly influences stress distribution and subsurface water flow, which in turn affect the vulnerability of nearby buildings. Linear slopes or those with steep upper sections that suddenly shift to gentle lower segments offer limited infiltration paths during rainfall. This results in concentrated pore-water pressure and lacks a dissipative buffer zone. Once a continuous shear surface forms, these slopes become prone to sudden, large-scale failures. Buildings located at the crest are especially at risk of abrupt sliding or foundation damage.

Field surveys in Dajing Town classified 1305 slope units into four morphological types: concave (701 units), convex (599 units), linear (4 units), and flat (1 unit) (Figure 11a). Overlaying these classifications with the locations of 5471 buildings yields the distribution shown in Figure 11b: 1740 buildings (31.8%) lie on concave slopes, 1656 (30.3%) on convex slopes, 11 (0.2%) on linear slopes, and 2064 (37.7%) on essentially flat terrain. This spatial pattern highlights that over 60% of structures occupy concave or convex slope forms—settings in which slope morphology will critically influence both hydrological loading and mechanical stability and, thus, must be explicitly incorporated into vulnerability assessments.

3.2.3. Building Height

Building height significantly affects how structures respond to multiple hazards. It influences stiffness, mass distribution, and how high floors are positioned relative to potential flooding depths. Taller buildings tend to have slender columns and less lateral rigidity. These characteristics can lead to soft-story failures during earthquakes or landslides. Podium levels, like commercial arcades or elevated parking garages, are especially vulnerable. Under strong ground motion, they are prone to shear failure or overturning. Greater building height also raises the center of gravity. This increases overturning forces and instability risks, especially on uneven slopes or weak foundations.

Conversely, elevated first floor heights confer a protective advantage in pluvial and debris-flow events by positioning critical functional spaces above anticipated flood or debris levels, thereby mitigating immersion and burial hazards. Low-rise buildings with minimal clearance are especially susceptible to inundation and debris impact.

In Dajing Town, field surveys cataloged 5471 buildings by height category (Figure 12a), with 33 high-rise structures, 163 mid-rise structures, and 5275 low-rise structures, underscoring the predominance of low-rise typologies and the attendant vulnerability implications for both seismic and flood-related hazards.

3.2.4. Building Structure

The structural type of a building plays a pivotal role in determining its resilience to disaster-induced forces. Brick-concrete buildings rely mainly on masonry for compressive resistance. However, their low tensile and shear strength, along with poor ductility, makes them prone to brittle failures. These failures may include diagonal cracks or full collapse during earthquakes or landslides. In contrast, reinforced concrete frame and shear wall structures combine steel and concrete to improve strength and ductility. They dissipate energy through plastic hinges, which helps them resist moderate to severe earthquakes, debris flows, and rockfalls. However, these structures can still be unstable. Elevated first floors or concrete degradation from carbonation may cause weak-layer failures.

Field surveys in Dajing Town reveal that, of the 5471 buildings, 1899 are constructed from reinforced concrete, while 3572 are brick-concrete structures (Figure 12b). This distribution highlights the dominance of brick-concrete buildings and underscores the importance of considering structural vulnerabilities when assessing multi-hazard resilience in urban planning.

3.3. Evaluation Indicators Derived from Human Engineering Activities

Over the past two decades, Dajing Town has urbanized rapidly. This process includes more buildings, expanded roads, and intensified infrastructure construction. These changes reflect a significant increase in human activity in the area. To quantitatively assess the evolution of human activity intensity, high-resolution remote sensing images from 2004, 2014, and 2024 were analyzed, as shown in Figure 13.

In 2004, Dajing Town was mainly composed of low-rise, densely packed houses arranged in a scattered and unplanned manner. Only a few public buildings stood clustered in the town center. By 2024, there were considerable changes in building height, density, and functionality. Urbanization followed a distinct pattern summarized as: “farmland retreat, roads expand, buildings rise, and functions divide.” Roads increasingly fragmented agricultural land, and the built-up area spread outward from a compact core, expanding in a leapfrog manner. High-rise buildings replaced low-rise houses, transforming the area from a rural village into a modern town with distinct functional zones.

To measure changes in engineering activity between 2004 and 2024, we annotated remote sensing images. Key features, such as road networks and building footprints, were highlighted (Figure 13). This analysis clearly illustrates Dajing Town’s evolution and helps reveal how urbanization has affected human activity over time.

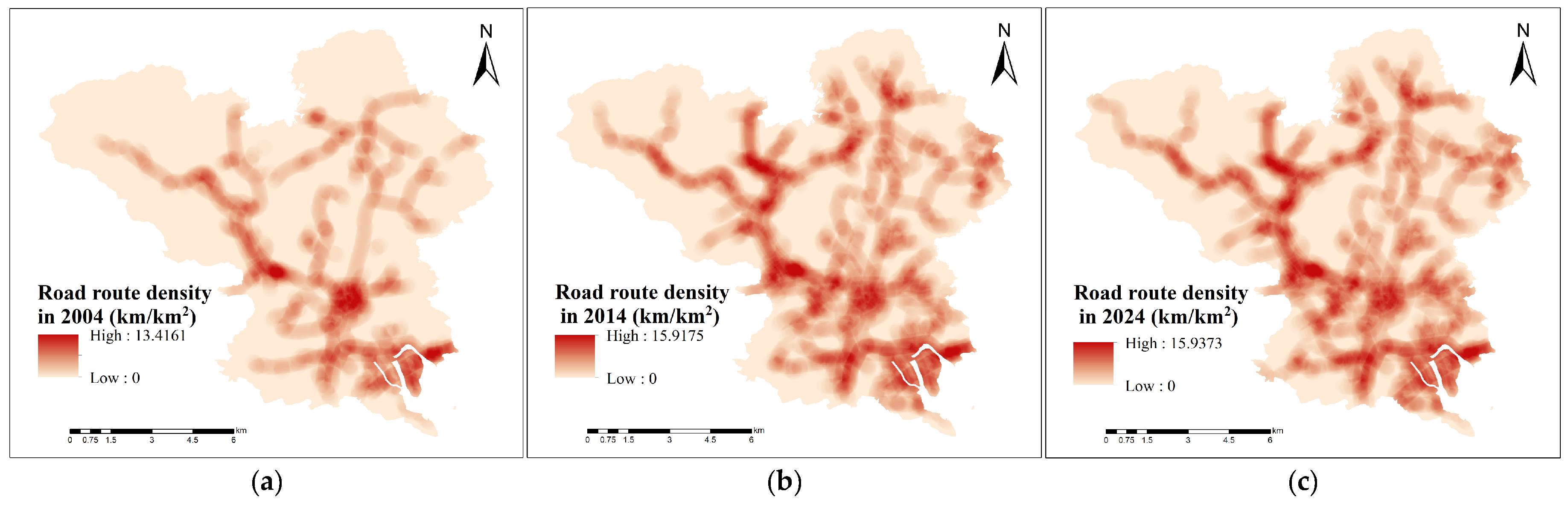
3.3.1. Road Route Density

The density of roads around buildings plays an important role in triggering geological hazards. When road density increases, activities, like excavation, slope cutting, and ditch construction, become more frequent. These actions disrupt the natural topography. These disturbances accelerate erosion at slope bases and focus groundwater infiltration. As a result, slope stability decreases, increasing the risk of landslides and collapses. Roads and drainage surfaces also speed up the concentration of rainfall runoff. This increases erosion and raises the risk of debris flows and flooding near buildings.

Figure 14 shows road route densities in Dajing Town for 2004, 2014, and 2024. The figures show that the road network has grown over time, potentially increasing building vulnerability to geological hazards. This analysis helps explain how human activity, especially infrastructure development, raises hazard exposure in the town.

3.3.2. Building Density

Building density—measured by the number or coverage of structures per unit area—can increase vulnerability to geological hazards in several ways. First, dense construction adds static loads to slopes and foundations. This increases gravitational stress and reduces overall stability. Second, impervious surfaces and crowded buildings block natural infiltration. As a result, stormwater runoff becomes more concentrated, accelerating erosion at the slope base. Figure 15 illustrates the temporal evolution of building density in Dajing Town for 2004, 2014, and 2024.

3.4. Correlation Analysis of Indicators

To better understand the interrelationships among the 19 input variables used in the VAB-HEAIC framework, a Pearson correlation analysis was conducted. The correlation matrix, visualized in the form of a heatmap (Figure 16), illustrates the pairwise linear relationships between all features.

The results reveal several noteworthy patterns. Some variables exhibit strong positive correlations, such as slope position and profile curvature (r = 0.85), as well as building density at different time intervals (e.g., BuildingDensity_2014 and BuildingDensity_2024, r = 0.98), suggesting potential redundancy or shared temporal dynamics. Similarly, RoadRouteDensity_2004 and RoadRouteDensity_014 show a strong correlation (r = 0.73), reflecting spatial continuity in infrastructure development.

Conversely, weak or near-zero correlations were observed between variables, such as building height and terrain ruggedness index or HEAIC and most terrain factors, indicating a more independent contribution to the model. Notably, HEAIC shows low linear correlation with most topographic variables (r < 0.2), suggesting that it captures a distinct aspect of human-driven changes in the environment, further justifying its inclusion as a novel variable.

This analysis supports the diversity of the selected feature set, with a mixture of correlated and uncorrelated variables enhancing the model’s capacity to capture nonlinear interactions in building vulnerability prediction. Although multicollinearity may exist in certain feature pairs, ensemble-based models, like Random Forest and LGBM, are generally robust to such issues. Nevertheless, these insights provide a useful reference for future work on feature selection or dimensionality reduction to further optimize model efficiency and reduce potential overfitting risks.

4. Machine Learning-Based Method for Building Vulnerability Assessment

The machine learning-based building vulnerability assessment flowchart, shown in Figure 17, can be divided into three parts: building data processing, model sample construction, and machine learning model prediction. The following sections will provide a detailed explanation of each part.

4.1. Building Data Processing

The first step in the machine learning-based building vulnerability assessment is processing the building data. The evaluation index system includes three main types of indicators: geological environment, slope survey, and human engineering activities.

First, obtain the elevation, slope, slope aspect, engineering geological rock groups, planar curvature, profile curvature, and terrain undulation data for Dajing Town. Spatial statistical analysis is then used to obtain the various attributes of all buildings in Dajing Town. Additionally, based on field surveys, the boundaries of slope units are defined. The attributes recorded include the slope position of the buildings, the slope cutting height of the surrounding slopes, the slope profile of the surrounding slopes, the building structure, and the building height.

High-resolution remote sensing images from 2004, 2014, and 2024 were used to interpret the historical distribution of buildings and roads in Dajing Town. Point density and line density analysis are then used to calculate the building density and road network density for Dajing Town for the years 2004, 2014, and 2024. Specifically, building and road network densities were calculated for Dajing Town for the years 2004, 2014, and 2024.

Human activity change in this study refers specifically to the intensity variation of anthropogenic engineering interventions over time, which alter the natural terrain and hydrological conditions and directly influence geohazard susceptibility. These changes are quantified through the following:

Building Density Change—Measured as the difference in structure count or built-up area per unit land from 2004 to 2024, derived from high-resolution remote sensing imagery.

Road Network Density Change—Calculated as the change in total road length per unit area across the same period, indicating increased excavation, slope cutting, and surface runoff alteration.

These two factors are integrated into a composite index named human engineering activity intensity change (HEAIC), using weighted coefficients to reflect their respective contributions to geomorphic disruption. HEAIC thus serves as a proxy to evaluate how urban expansion and infrastructure development amplify the vulnerability of buildings to geological hazards.

Construction activities, like slope cutting, for buildings and roads have triggered geological hazards in Dajing Town, threatening building safety. Therefore, it is essential to consider the intensity and changes in human engineering activities when assessing the vulnerability of buildings. The calculation of the change in human engineering activity intensity is as follows:

$$I_{eng}={\mu }_1({\displaystyle \frac{\Delta D_{building,1-2}}{\Delta t_1}}+{\displaystyle \frac{\Delta D_{building,2-3}}{\Delta t_2}})+{\mu }_2({\displaystyle \frac{\Delta D_{road,1-2}}{\Delta t_1}}+{\displaystyle \frac{\Delta D_{road,2-3}}{\Delta t_2}})$$

(1)

where ${\mu }_1$ is the weight coefficient for the change in building density. ${\mu }_2$ is the weight coefficient for the change in road network density. $\Delta t_1$ and $\Delta t_2$ are the time differences, which in this study are taken as 10 years. $\Delta D_{building,1-2}$ is the difference in building density between 2014 and 2004. $\Delta D_{building,2-3}$ is the difference in building density between 2024 and 2014. $\Delta D_{road,1-2}$ is the difference in road network density between 2014 and 2004. $\Delta D_{road,2-3}$ is the difference in road network density between 2024 and 2014. The calculation formula is as follows:

$$\begin{array}{c}\Delta D_{building,1-2}=D_{building-2014}-D_{building-2004}\\ \Delta D_{building,2-3}=D_{building-2024}-D_{building-2014}\\ \Delta D_{road,1-2}=D_{road-2014}-D_{road-2004}\\ \Delta D_{road,2-3}=D_{road-2024}-D_{road-2014}\end{array}$$

(2)

Finally, spatial statistics were used to assign changes in human engineering activity intensity to each building in Dajing Town.

4.2. Sample Construction and Model Evaluation Indicators

To meet the data requirements of machine learning models, field surveys identified 5471 buildings in Dajing Town. Among them, 210 were labeled as highly vulnerable based on expert evaluation. These samples were labeled as positive samples. The remaining samples were considered negative samples and labeled as 0. Each building received a unique ID, and together with the processed features, a vulnerability assessment dataset was constructed. Each sample includes 19 feature attributes, such as the slope of the building location, building height, and other relevant characteristics, along with the corresponding label.

To quantitatively assess the effectiveness of the VAB-HEAIC model, Root Mean Squared Error (RMSE) and the receiver operating characteristic (ROC) curve were selected for evaluation.

RMSE evaluates how closely a model’s predictions align with actual values by measuring the average prediction error. RMSE is widely used in various fields, including machine learning, statistics, and engineering, due to its simplicity and interpretability.

The RMSE is calculated by taking the square root of the mean squared error (MSE), which is the average of the squared differences between predicted and actual values. Given a set of $n$ observed values $y_i$ and their corresponding predicted values $i$, the RMSE is computed as:

$$RMSE=\sqrt{{\displaystyle \frac{1}{n}}{{\displaystyle \sum _{i=1}^n(y_i-{\widehat{y}}_i)}}^2}$$

(3)

where $y_i$ is the true value of the $i$-th data point, ${\widehat{y}}_i$ is the predicted value for the $i$-th data point, and $n$ is the number of data points.

RMSE measures the average prediction error using the same units as the original data, which makes it easy to interpret. Smaller values of RMSE indicate better model performance, as it suggests that the model’s predictions are close to the actual values. In contrast, a higher RMSE indicates greater deviation between predictions and actual values, suggesting poorer model performance.

An advantage of RMSE is its strong penalty for large errors due to the squared difference calculation, which makes it more sensitive to outliers. This is useful in applications where minimizing large errors is a priority. However, this same sensitivity can become a drawback. In datasets with many outliers, RMSE may overemphasize their impact and lead to biased model evaluations. Although RMSE is widely used, it should be considered together with other metrics such as MAE or R². RMSE alone does not reveal model bias and is sensitive to the scale of the data. In summary, RMSE is useful for evaluating the accuracy of regression models. Its clear interpretation and sensitivity to large errors make it well-suited for many real-world applications.

4.3. Machine Learning Models

In this study, four machine learning models were selected—SVR [25], RF [26], BPNN [27], and LGBM [28]—to model building vulnerability due to their distinct algorithmic foundations and complementary strengths. SVR was chosen for its ability to generalize well with limited data and its strong theoretical underpinnings in structural risk minimization. RF was selected for its robustness, interpretability, and proven performance on tabular data with heterogeneous features. BPNN, as a representative of neural networks, was included due to its ability to capture complex nonlinear mappings. LGBM, a state-of-the-art gradient boosting framework, was chosen for its high accuracy, speed, and scalability, especially suitable for large, structured datasets. The combination of these models enables a balanced evaluation and selection of the most reliable method for large-scale, data-driven vulnerability assessments.

4.3.1. SVR

Support Vector Regression (SVR) extends the Support Vector Machine (SVM) framework for regression tasks. It is designed to predict continuous outputs while preserving the robustness and generalization capabilities of SVM [29]. SVR applies structural risk minimization to fit a function that approximates the relationship between inputs and continuous targets, allowing for a predefined error margin. Based on a training dataset, SVR maps input data into a high-dimensional feature space using a weight vector and a bias term, as illustrated in Figure 18. The optimization minimizes both model complexity and prediction error beyond the ε-insensitive zone, where small errors are ignored. To address nonlinear patterns, SVR uses kernel functions—such as linear, polynomial, and RBF kernels—to transform data into higher-dimensional spaces. This approach balances complexity and accuracy, offering robustness against noise and overfitting.

4.3.2. RF

Random Forest (RF) is a widely used ensemble learning method for classification and regression. It is known for its robustness, high accuracy, and ability to manage high-dimensional data [30]. Introduced by Leo Breiman in 2001, RF combines multiple decision trees to enhance predictive performance and reduce overfitting compared to single trees [31]. During training, RF constructs a large number of decision trees. It then aggregates their predictions to produce the final output. In classification tasks, the final result is based on majority voting. For regression, it is the average of all tree outputs. Each tree is trained on a bootstrap sample randomly drawn with replacement from the original dataset. This technique, known as bagging, introduces diversity and helps reduce variance. At each split, RF selects a random subset of features. This further decorrelates the trees and improves generalization. RF performs well on large datasets with many input features. It offers internal error estimates through out-of-bag samples, enables feature importance analysis, and is robust to both noise and overfitting.

4.3.3. BPNN

Backpropagation Neural Networks (BPNNs) are popular supervised learning algorithms in artificial neural networks. They are designed to handle complex nonlinear mapping problems in classification and regression [32]. BPNN is the standard training method for multilayer perceptrons (MLPs) and is fundamental to deep learning. BPNN uses a feedforward architecture with an input layer, one or more hidden layers, and an output layer. Neurons are connected by weighted links, and data are processed using linear combinations and nonlinear activation functions. The training process includes two phases: forward propagation and backward propagation. During forward propagation, input data pass through the network to generate a prediction. The prediction error is then calculated using a loss function, such as mean squared error. In backward propagation, the error flows backward from the output to the input layer. The chain rule is used to compute gradients, and weights are updated using gradient descent or its variants to minimize the error. According to the universal approximation theorem, BPNNs can approximate any continuous function, given enough neurons and data. However, training is often computationally demanding. It may also face issues, such as local minima, slow convergence, and overfitting. To address these challenges, techniques, such as momentum, adaptive learning rates, regularization, and advanced optimizers are commonly applied.

4.3.4. LGBM

Light Gradient Boosting Machine (LGBM) is an advanced gradient boosting framework developed by Microsoft. It is designed to handle large-scale data efficiently and achieve high predictive accuracy in both classification and regression tasks. It builds an ensemble of weak learners using decision trees in a stage-wise manner [33]. LGBM introduces innovations to improve training speed and memory efficiency. One such innovation is a histogram-based decision tree algorithm, which converts continuous features into discrete bins to reduce computation and memory consumption. Unlike traditional methods, LGBM grows trees leaf-wise by splitting the leaf that yields the greatest loss reduction. This strategy often achieves lower loss and better accuracy, but it requires careful regularization to avoid overfitting. LGBM builds models by minimizing a differentiable loss function, fitting new trees at each iteration to the negative gradients of the loss function. It supports various loss functions, like logistic loss for classification and mean squared error for regression. LGBM also integrates several advanced techniques. These include feature bundling for dimensionality reduction, gradient-based one-side sampling (GOSS) for faster training, and exclusive feature bundling (EFB) for efficient handling of sparse features.

4.4. Optimization Algorithm

To enhance predictive performance and model robustness, several advanced optimization algorithms are used to fine-tune hyperparameters. Particle Swarm Optimization (PSO) [34], Sparrow Search Algorithm (SSA) [35], and Differential Evolution (DE) [36] are population-based metaheuristic methods. They explore the search space through iterative evolution and social interaction mechanisms. Bayesian Optimization (BO) [37] uses probabilistic surrogate models to guide the search efficiently. It balances exploration and exploitation to find optimal solutions. These optimization techniques help automatically identify optimal parameter settings. As a result, they improve model accuracy and convergence efficiency in the building vulnerability assessment framework.

Machine learning model performance is highly sensitive to the choice of hyperparameters, which control model complexity, learning behavior, and generalization capacity. Traditional approaches, such as grid search or manual tuning, are often computationally expensive and may fail to find optimal settings in high-dimensional spaces.

To overcome this, we integrated four intelligent optimization algorithms—PSO, SSA, DE, and BO—into our framework. These algorithms are well-suited for exploring complex, non-convex search spaces and can automatically identify high-performing hyperparameter combinations for each model. By optimizing key parameters (e.g., kernel width in SVR, depth and number of estimators in RF and LGBM), we aimed to improve model accuracy while reducing the risk of underfitting or overfitting.

4.4.1. PSO

Particle Swarm Optimization (PSO) is a population-based stochastic optimization technique introduced by Kennedy and Eberhart in 1995 [38]. It is inspired by the social behavior of bird flocking and fish schooling. It is widely used in both continuous and discrete optimization problems because of its simplicity, flexibility, and effectiveness. In PSO, particles represent potential solutions, each with a position and velocity vector. Particles move through the search space based on two factors: their own best-known position and the global best position found by the swarm. This balance helps achieve both exploration and exploitation. The velocity and position updates are controlled by inertia weight and acceleration coefficients. These parameters manage the cognitive (self-experience) and social (swarm influence) components of the search. Inertia weight usually decreases over iterations to balance global and local search, improving convergence. PSO is easy to implement, has few parameters, and can converge quickly to good solutions. PSO works well for nonlinear, non-differentiable, and multi-modal problems. However, it may suffer from premature convergence and become trapped in local optima. This issue can be mitigated by using variants, like adaptive inertia weight or hybrid algorithms.

4.4.2. SSA

The Sparrow Search Algorithm (SSA) is a nature-inspired optimization method proposed by Xue and Shen in 2020 [39]. It mimics the foraging and anti-predation behavior of sparrows. The algorithm divides the population into two groups: producers that explore the search space and scroungers that exploit known food sources. This division balances exploration and exploitation, improving optimization performance. A subset of sparrows acts as scouts. They protect the group from predators and help maintain population diversity. SSA updates the positions of sparrows based on their roles. It dynamically balances exploration and exploitation, allowing the algorithm to converge efficiently toward global optima while avoiding local traps. Compared with algorithms, like PSO and GWO, SSA achieves faster convergence and higher solution accuracy in benchmark tests. SSA has been successfully applied in various fields, including engineering optimization, machine learning parameter tuning, and energy management.

4.4.3. DE

Differential Evolution (DE) is a population-based stochastic optimization algorithm proposed by Storn and Price in 1997 [40]. It is widely used for solving nonlinear, non-differentiable, and multi-modal problems because of its simplicity and robustness. DE evolves a population of candidate solutions over successive generations. Each candidate is represented as a D-dimensional parameter vector. It uses mutation, crossover, and selection to improve the population toward the global optimum. The mutation operator generates a new vector by adding the weighted difference of two random vectors to a third base vector. The crossover step mixes the mutant and target vectors to generate a trial vector. The selection process compares the trial and target vectors and retains the one with better fitness. This process repeats until a stopping criterion is met, such as reaching a maximum number of generations or achieving a target fitness level. DE is favored for its simplicity, minimal parameter tuning, and ability to maintain population diversity, which helps prevent premature convergence.

4.4.4. BO

Bayesian Optimization (BO) is a sequential method designed to optimize expensive, non-convex, and noisy black-box functions. It is widely applied to hyperparameter tuning in machine learning and engineering tasks [41]. It models the objective function with a probabilistic surrogate, typically a Gaussian Process (GP), which offers both predictions and uncertainty estimates. At each iteration, BO uses an acquisition function—such as Expected Improvement, Probability of Improvement, or Upper Confidence Bound—to balance exploration and exploitation. Exploration targets uncertain areas, while exploitation focuses on promising ones. The acquisition function guides the search for the global optimum. BO is effective for optimizing expensive functions. It leverages past observations to guide sampling decisions more efficiently than random or grid search. However, BO can be computationally intensive. The Gaussian Process model scales cubically with the number of observations, which limits its use in high-dimensional or large-scale datasets.

4.5. Data Augmentation Model

After the original feature set is prepared, multiple data augmentation techniques are applied. These methods aim to increase the diversity and robustness of the training samples. Specifically, three augmentation strategies are used. Feature combination data augmentation (FCDA) [42] creates new features by combining existing ones. Numerical perturbation data augmentation (NPDA) [43] adds controlled noise to simulate small variations. Bootstrap resampling data augmentation (BRDA) [44] enlarges the dataset through random sampling with replacement. These augmentation techniques enrich the input space and improve the model’s generalization performance.

4.5.1. FCDA

FCDA enhances dataset diversity and robustness, especially in classification, regression, and deep learning tasks. Its primary goal is to improve model performance by generating new synthetic features from existing ones. This is particularly helpful when the dataset is small or imbalanced. The method creates new features by combining pairs or groups of existing features using operations, such as addition, subtraction, or multiplication. It can also apply advanced techniques, like polynomial transformations or interaction terms. This increases training variability and helps reduce overfitting. However, it may also raise feature dimensionality, which can increase the risk of overfitting. To control this risk, techniques, such as feature selection or dimensionality reduction, are often applied. FCDA is widely used in models, like Random Forests, XGBoost, and LGBM. It also supports deep learning by enriching data representations.

4.5.2. NPDA

NPDA enhances machine learning models’ robustness by adding controlled random variations or noise to the data. This is especially helpful for limited or imbalanced datasets. It expands the data distribution and reduces overfitting by exposing the model to more diverse inputs. The technique adds small perturbations to feature values, usually by injecting random noise. This helps the model encounter more scenarios while preserving the core data relationships. NPDA is commonly used alongside other augmentation techniques, like feature combination or resampling, to improve model performance. However, the amount of perturbation must be balanced. Excessive noise may degrade model performance, while too little may offer no benefit to generalization.

4.5.3. BRDA

BRDA improves dataset diversity by generating multiple new datasets from the original. It uses resampling with replacement to create these bootstrap samples. It is particularly useful when the dataset is small or imbalanced. In such cases, it helps improve model robustness and generalization. Bootstrap resampling selects data points randomly from the original dataset, allowing repetition. As a result, some samples may appear multiple times, while others may not appear at all. Each new sample is the same size as the original but has a different composition due to the random selection. BRDA is widely used in ensemble learning methods, such as bagging. In this approach, several models are trained on different bootstrap datasets, and their predictions are aggregated.

5. Results Analysis

5.1. Experimental Setup for VAB

In the data processing phase, spatial statistical tools are used to extract building attributes. These attributes are then normalized to standardize their statistical distribution. Four mainstream machine learning models are used: SVR, RF, BP, and LGBM. For each model, four optimization algorithms—PSO, SSA, DE, and BO—are applied to tune the model parameters. The specific parameters to be optimized vary by model: penalty, Epsilon, and Gamma for SVR; number of trees, max depth, and min samples split for RF; number of hidden-layer neurons and the momentum coefficient for BPNN; and number of trees, max depth, and learning rate ror LGBM. Many buildings in Dajing Town are located on flat ground. However, only a few were labeled as highly vulnerable during the field survey. To address this imbalance, three data augmentation methods were used: feature combination, numerical perturbation, and bootstrap resampling. Each machine learning model is tested with various optimization and augmentation methods. To balance the dataset, 230 positive samples are selected, along with 230 randomly chosen negative samples. The dataset is split into training (70%) and test (30%) sets. Each model is run 10 times, and the average RMSE is recorded as the final accuracy. Additionally, two parameters are considered when calculating human engineering activity intensity: the weight of building density change and the weight of road network density change. Their impact on the results is also analyzed.

5.2. VAB Based on Machine Learning Model

In the VAB-HEAIC framework, four machine learning models—SVR, RF, BPNN, and LGBM—were tested without data augmentation or parameter optimization. Their predictive performance, evaluated using Root Mean Squared Error (RMSE), is shown in

Table 2. The RMSE values of four machine learning models.

Machine Learning Models	RMSE
SVR	0.4564
BPNN	0.8751
RF	0.4081
LGBM	0.3967

. Lower RMSE values indicate better accuracy.

Among the models, LGBM achieved the best performance with an RMSE of 0.3967, indicating the highest prediction accuracy. RF followed closely with an RMSE of 0.4081. SVR performed moderately (RMSE: 0.4564), while BPNN showed the weakest performance, with the highest RMSE of 0.8751.

These results suggest that LGBM and RF are the most suitable for building vulnerability prediction under geological hazards, effectively capturing complex nonlinear relationships. In contrast, BPNN may be less suited for this task in its current configuration.

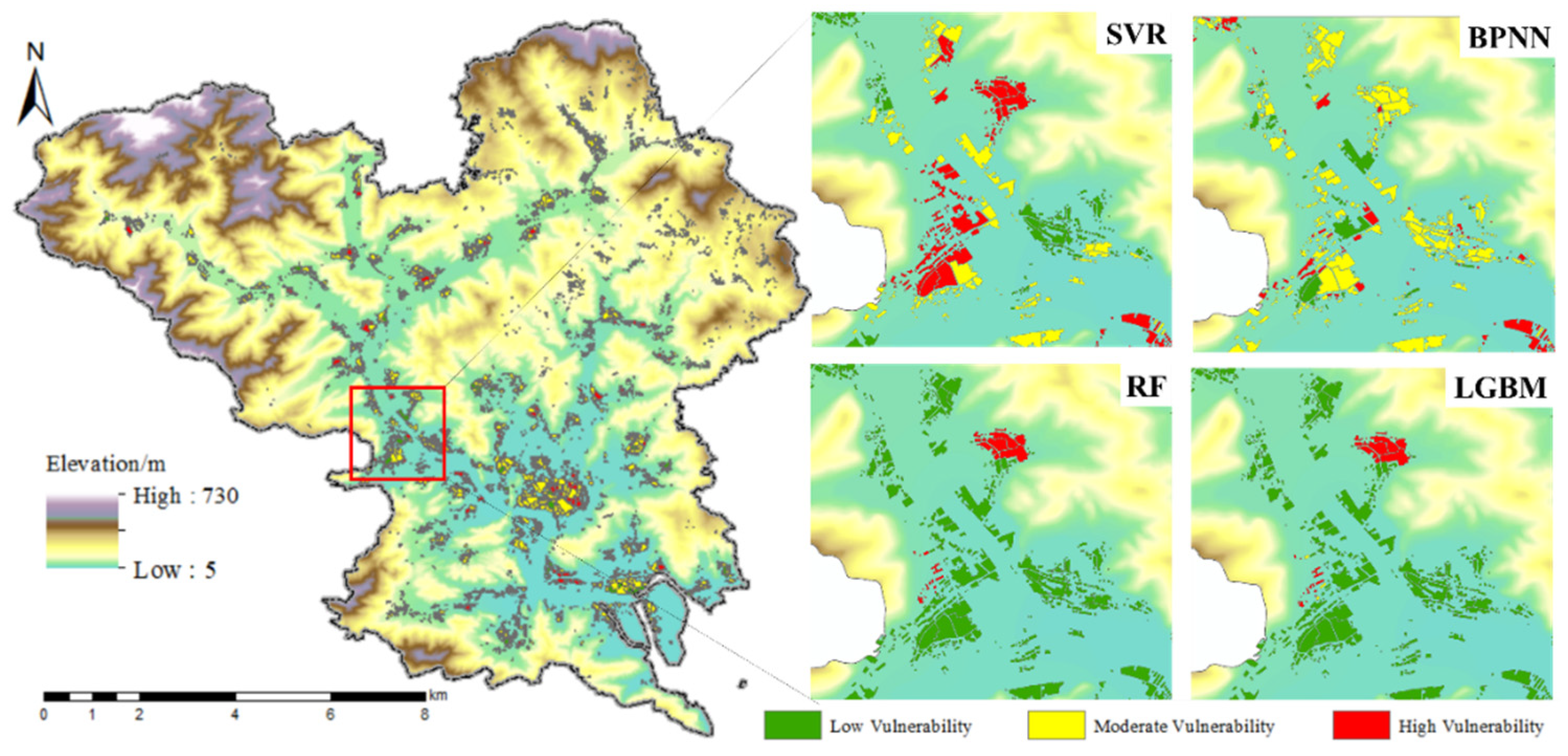
After model training, building vulnerability in the study area is predicted and classified into three levels: low, medium, and high. The spatial distributions generated by SVR, BPNN, RF, and LGBM are shown in Figure 19, overlaid on the elevation gradient (5 m to 730 m).

In general, SVR overestimates vulnerability, with scattered high-risk predictions (red and yellow) even in low-risk, gently sloping areas. This suggests high sensitivity to minor feature changes. BPNN yields smoother results than SVR, forming broader medium-risk zones but still over-labeling many mid-elevation flats as vulnerable, indicating only partial capture of actual hazard gradients. RF predictions are more focused: high-risk zones are concentrated near steep slopes or flood-prone areas, while valley floor structures are mostly labeled low risk. This reflects RF’s ability to isolate critical features. LGBM produces the most accurate and coherent pattern, with low-lying areas marked green, high-risk parcels precisely identified in steep or disturbed zones, and minimal noise. Vulnerability zones align clearly with both topographic and anthropogenic factors.

In summary, SVR and BPNN tend to over-predict vulnerability, whereas RF and especially LGBM offer more reliable and spatially coherent results, making LGBM the most suitable for risk zoning and decision-making.

5.3. VAB Based on Machine Learning Integrating Optimization Models

In the previous section, four representative machine learning models—SVR, BPNN, RF, and LGBM—were introduced and evaluated for their suitability in building vulnerability assessment under geological disasters. While these models demonstrated varying levels of predictive accuracy, their performance is inherently influenced by the choice of hyperparameters, which, if not optimally selected, may limit their predictive potential.

To further enhance the robustness and generalization capability of these models, this section integrates four widely used intelligent optimization algorithms—PSO, SSA, DE, and BO—into the training process of each machine learning model. By fine-tuning key hyperparameters through these optimization techniques, the models are expected to achieve improved prediction accuracy and stability, especially in the context of complex, multi-dimensional feature interactions, such as those introduced by changes in human engineering activity intensity.

Table 3. The RMSE values of machine learning integrating optimization models.

Machine Learning Models	No Optimization	BO	DE	SSA	PSO
SVR	0.4564	0.4840	0.4713	0.454	0.4494
BPNN	0.8751	0.5367	0.4826	0.5003	0.4889
RF	0.4081	0.4025	0.4014	0.4003	0.4002
LGBM	0.3967	0.4294	0.3852	0.3914	0.3878

presents the RMSE values of four machine learning models—SVR, BPNN, RF, and LGBM—evaluated both with and without optimization algorithms (BO, DE, SSA, and PSO). This comparison highlights the influence of optimization on model performance.

Without optimization, LGBM performs best, achieving the lowest RMSE (0.3967), followed closely by RF (0.4081). In contrast, SVR (0.4564) and especially BPNN (0.8751) show relatively poor predictive accuracy. Optimization leads to varying degrees of improvement across models: LGBM sees modest gains, particularly with PSO, reducing its RMSE to 0.3878, further enhancing its already strong baseline. RF improves slightly with SSA (0.4002) and PSO (0.4025), demonstrating its robustness and stable performance across configurations. SVR shows notable improvements, especially under SSA (0.4540) and PSO (0.4494), confirming that tuning significantly enhances its fit. BPNN benefits most from BO, with RMSE dropping from 0.8751 to 0.5367, though it still underperforms relative to the other models.

In summary, while RF and LGBM consistently deliver strong results—with or without tuning—SVR and BPNN are more sensitive to hyperparameter optimization. Among the optimization techniques, PSO and SSA generally provide the most effective improvements. These findings underscore the value of combining machine learning with intelligent optimization strategies in complex tasks, like building vulnerability assessment.

5.4. Data Enhancement Result

Building on the improvements achieved through the integration of intelligent optimization algorithms, this section further enhances the predictive accuracy and robustness of the four machine learning models—SVR, BPNN, RF, and LGBM—by introducing three complementary data augmentation strategies: feature combination data augmentation (FCDA), numerical perturbation data augmentation (NPDA), and bootstrap resampling data augmentation (BRDA). These techniques aim to expand and diversify the training dataset, thereby mitigating overfitting and improving model generalization—especially in contexts with limited or imbalanced samples.

Through the application of these augmentation methods, we assess their effects on model accuracy and stability in the task of building vulnerability assessment, accounting for the complex dynamics introduced by changes in human engineering activity intensity. The results from this comparative analysis underscore the synergistic benefits of coupling optimized machine learning algorithms with robust data augmentation techniques, offering a more reliable and adaptable framework for multi-hazard vulnerability evaluation.

5.4.1. Feature Combination Data Enhancement Results

Table 4. The RMSE values of machine learning integrating optimization models based on feature combination data enhancement.

Machine Learning Models	BO	DE	SSA	PSO
SVR	0.4959	0.4583	0.4589	0.5000
BPNN	0.6266	0.5002	0.5127	0.6887
RF	0.4084	0.4068	0.4045	0.4214
LGBM	0.4153	0.3784	0.3793	0.3807

presents the RMSE values of four machine learning models—SVR, BPNN, RF, and LGBM—combined with different optimization algorithms (BO, DE, SSA, PSO) under feature combination data augmentation. These results highlight how feature augmentation and optimization together influence model accuracy. Among the models, LGBM consistently achieves the best performance. With SSA optimization, its RMSE drops to 0.3793, followed closely by 0.3807 under PSO. These results suggest that LGBM, when combined with feature combination data enhancement and SSA optimization, achieves superior predictive accuracy compared to the other models.

RF also performs strongly, particularly with BO (RMSE: 0.4084) and SSA (RMSE: 0.4045), confirming its robustness under feature combination enhancement—especially when optimized via SSA. In contrast, SVR and BPNN show higher RMSE values than LGBM and RF, suggesting they gain less from feature combination augmentation. For example, SVR shows an RMSE of 0.4959 under BO and 0.5000 under PSO, while BPNN has an RMSE of 0.6266 with BO and 0.6887 with PSO, suggesting these models are less sensitive to the augmentation technique.

Among the optimization algorithms, SSA consistently yields the best performance—especially for LGBM and RF—highlighting its strength in boosting model accuracy. However, for SVR, DE performs slightly better, yielding an RMSE of 0.4583, indicating a possible optimization advantage for this model under certain conditions. On the other hand, PSO generally yields less optimal results, especially for SVR, where the RMSE increases to 0.5000, possibly due to overfitting or instability in this model.

In summary, combining feature combination data augmentation with optimization—especially the pairing of LGBM and SSA—substantially enhances model accuracy and robustness. This is particularly true in evaluating building vulnerability influenced by human engineering activity intensity changes. LGBM emerges as the most effective model for this task, benefiting greatly from feature combination data enhancement and optimization.

5.4.2. Numerical Perturbation Data Augmentation Results

Table 5. The RMSE values of machine learning integrating optimization models based on numerical perturbation data augmentation.

Machine Learning Models	BO	DE	SSA	PSO
SVR	0.4843	0.4496	0.4526	0.5000
BPNN	0.8041	0.4704	0.4762	0.4689
RF	0.3925	0.3912	0.388	0.3869
LGBM	0.4228	0.3826	0.3762	0.3733

shows the RMSE values of four machine learning models—SVR, BPNN, RF, and LGBM—combined with various optimization algorithms (BO, DE, SSA, PSO) and enhanced by numerical perturbation data augmentation. This augmentation technique significantly improves model performance—especially for RF and LGBM—by reducing RMSE more effectively than previous methods.

LGBM performs the best across all optimizers, achieving RMSEs as low as 0.3733 (PSO), 0.3762 (SSA), and 0.3826 (DE)—making it the most accurate model overall. This indicates that LGBM is highly robust in its predictive accuracy when combined with numerical perturbation data augmentation and optimization algorithms.

RF also maintains strong performance, with RMSE consistently below 0.45 across all optimizations. The best result is achieved under SSA optimization, with an RMSE of 0.388, reflecting a slight improvement over other optimization methods. RF proves to be a reliable model when integrated with numerical perturbation data augmentation, especially in the context of optimization.

In contrast, SVR and BPNN yield higher RMSEs, with BPNN showing instability and peaking under SSA optimization. Notably, SSA optimization significantly reduces the RMSE for SVR, improving it to 0.4526 from 0.4843 under BO. This highlights that SSA optimization has a particularly beneficial effect on SVR.

In conclusion, numerical perturbation data augmentation proves to be an effective technique for enhancing model robustness and predictive accuracy, especially when combined with advanced optimization algorithms, such as DE and SSA. The integration of this augmentation method with LGBM and RF models leads to exceptional performance, making them ideal choices for accurately assessing building vulnerability under the impact of human engineering activity intensity changes.

5.4.3. Bootstrap Resampling Data Augmentation

Table 6. The RMSE values of machine learning integrating optimization models based on bootstrap resampling data augmentation.

Machine Learning Models	BO	DE	SSA	PSO
SVR	0.4847	0.4706	0.4675	0.4713
BPNN	0.6659	0.4921	0.506	0.4909
RF	0.385	0.4009	0.4276	0.4024
LGBM	0.4213	0.3745	0.3800	0.3912

presents the RMSE values of four machine learning models—SVR, BPNN, RF, and LGBM—optimized with BO, DE, SSA, and PSO under bootstrap resampling data augmentation. The results demonstrate how this technique enhances predictive accuracy in building vulnerability assessment.

LGBM delivers the best performance across all optimizers. Its lowest RMSE of 0.3745 occurs under DE, followed closely by 0.3800 under SSA, indicating that LGBM benefits significantly from bootstrap resampling, especially when paired with strong optimizers. RF also performs well, consistently maintaining RMSEs below 0.41. Its best result, 0.4024, is achieved with PSO, highlighting RF’s robustness, though it remains slightly less accurate than LGBM. In contrast, SVR and BPNN show higher RMSEs, indicating weaker performance. However, SVR sees meaningful improvement with SSA, reducing RMSE to 0.4675. Meanwhile, PSO yields the worst results for both SVR (0.4713) and BPNN (0.4909), suggesting limited effectiveness for these models under this optimizer.

Overall, bootstrap resampling effectively improves model robustness and generalization, particularly for ensemble models like LGBM and RF. When coupled with advanced optimization algorithms, such as DE and SSA, it significantly enhances accuracy, making these approaches especially suitable for modeling vulnerability under dynamic human engineering activity intensities.

5.5. Analysis of the Importance of HEAIC

To clarify the role of human engineering activity intensity change (HEAIC) in building vulnerability assessment, this section removes the HEAIC factor from model inputs in an ablation study. The study compares model performance with and without HEAIC to show its importance in capturing complex vulnerability factors. This approach provides robust evidence of the contribution of human engineering activities to the overall assessment framework, reinforcing the necessity to incorporate HEAIC for comprehensive vulnerability evaluation.

Table 7. Comparison of RMSE with and without HEAIC.

Machine Learning Models	FCDA	NPDA	BRDA	No Optimization	FCDA	NPDA	BRDA	No Optimization
LGBM	\	\	\	0.3967	\	\	\	0.5262
LGBM_BO	0.4153	0.4228	0.4213	0.4294	0.4863	0.5509	0.5597	0.4998
LGBM_DE	0.3784	0.3826	0.3745	0.3852	0.4883	0.4915	0.5015	0.4988
LGBM_SSA	0.3793	0.3762	0.3800	0.3914	0.4746	0.4896	0.4994	0.4964
LGBM_PSO	0.3807	0.3733	0.3912	0.3878	0.4898	0.4998	0.5011	0.4981
BP	\	\	\	0.8751	\	\	\	0.6071
BPNN_BO	0.6266	0.8041	0.6659	0.5367	0.6777	0.6035	0.6431	0.5268
BPNN_DE	0.5002	0.4704	0.4921	0.4826	0.6362	0.4858	0.4885	0.4803
BPNN_SSA	0.5127	0.4762	0.5060	0.5003	0.500	0.4846	0.4841	0.4355
BPNN_PSO	0.6887	0.4689	0.4909	0.4889	0.5073	0.4893	0.5001	0.4849
RF	\	\	\	0.4081	\	\	\	0.5023
RF_BO	0.4084	0.3925	0.3850	0.4025	0.4835	0.5066	0.5017	0.5007
RF_DE	0.4068	0.3912	0.4009	0.4014	0.4838	0.5008	0.4901	0.4897
RF_SSA	0.4045	0.3880	0.4276	0.4003	0.4853	0.4911	0.4888	0.4007
RF_PSO	0.4214	0.3869	0.4024	0.4002	0.4960	0.4967	0.4848	0.4870
SVM	\	\	\	0.4564	\	\	\	0.5567
SVM_BO	0.4959	0.4843	0.4847	0.4840	0.500	0.6406	0.6008	0.5000
SVM_DE	0.4583	0.4496	0.4706	0.4713	0.4945	0.4956	0.4848	0.4842
SVM_SSA	0.4589	0.4526	0.4675	0.4540	0.4925	0.4819	0.4842	0.4838
SVM_PSO	0.5000	0.5000	0.4713	0.4494	0.6690	0.500	0.4913	0.4826

presents the RMSE results of the ablation experiment, with the results on the left considering the HEAIC factor and those on the right eliminating the HEAIC factor. The ablation results show how including or excluding HEAIC affects the RMSE of different machine learning models. The models tested include LGBM, BPNN, RF, and SVR, optimized with techniques, such as BO, DE, SSA, and PSO. The models were evaluated with three data augmentation methods: FCDA, NPDA, and BRDA.

The results reveal that LGBM performs the best overall, particularly when HEAIC is included. For instance, LGBM_BO achieves an RMSE of 0.4153 with HEAIC, which rises to 0.4863 when HEAIC is removed. The performance is similarly strong across all augmentation methods when HEAIC is present, demonstrating the model’s sensitivity to the inclusion of this factor. Other variants of LGBM, such as LGBM_DE and LGBM_SSA, also show a reduction in RMSE with HEAIC.

In contrast, BPNN performs worse than LGBM, with the BPNN_PSO variant showing the highest RMSE of 0.6887 with HEAIC, improving to 0.5073 without it. This suggests that BP’s performance is more reliant on the HEAIC factor. However, certain BPNN variants, such as BPNN_BO and BPNN_DE, perform better with HEAIC, indicating mixed results across the different BPNN models.

For RF, the results are more stable, with only slight improvements in certain variants when HEAIC is excluded. For example, the RF_PSO model shows an RMSE of 0.4214 with HEAIC, which reduces slightly to 0.3962 without it. Similarly, RF_BO and RF_DE show minimal improvements when HEAIC is included, indicating that the factor has less of an impact on RF compared to other models.

SVM generally performs worse than LGBM but shows improvement with the inclusion of HEAIC in some variants. The SVM_PSO model achieves an RMSE of 0.5000 with HEAIC, which decreases to 0.4494 without it. However, other SVM variants, such as SVM_DE and SVM_BO, show better performance with HEAIC, especially SVM_DE, which achieves an RMSE of 0.4583 with HEAIC, compared to 0.4496 without it.

In terms of data augmentation, FCDA generally results in the best performance, with LGBM_BO showing the lowest RMSE of 0.4153 with FCDA, compared to 0.4228 with NPDA and 0.4213 with BRDA. The use of FCDA consistently enhances the performance of LGBM, BP, and SVM models, suggesting its importance in improving model accuracy. On the other hand, NPDA and BRDA yield mixed results, with NPDA performing better for BP and RF, while BRDA benefits models, like BP_BPNN_BO.

In conclusion, LGBM benefits the most from the inclusion of HEAIC, showing consistent improvement in performance, particularly with FCDA. BP and SVM models exhibit more variability, with some variants performing better when HEAIC is excluded, while others perform better with it. RF shows relatively stable performance with small improvements when HEAIC is excluded. FCDA is found to be the most effective data augmentation technique, improving the RMSE across all models.

In the ablation experiment without the HEAIC factor, the BP_SSA model achieved the highest accuracy with an RMSE of 0.4255. When the HEAIC factor was included, the LGBM_DE_BRDA model performed best, with an RMSE of 0.3745. To compare the two models more clearly, the vulnerability index of all buildings was predicted and shown in Figure 20. As shown on the right (without HEAIC), more buildings were predicted as low vulnerability, with fewer classified as moderate or high. This result differs from field observations. In contrast, the LGBM_DE_BRDA model (left) clearly distinguishes high and low vulnerability buildings.

In addition to RMSE, we also evaluated model performance using MAE and R² metrics to offer a more comprehensive performance assessment. RMSE emphasizes large errors, MAE provides a more direct interpretation of average error magnitude, and R² quantifies how well the predicted outcomes capture the variance in the actual data.

As shown in

Table 8. The RMSE values, MAE values and R² of the four models.

Machine Learning Models	RMSE	MAE	R2
SVR_SSA_NPDA	0.4526	0.3471	0.6923
BPNN_BO_BRDA	0.4909	0.3715	0.6580
RF_PSO_NPDA	0.3880	0.3012	0.8034
LGBM_DE_BRDA	0.3745	0.2963	0.8317

, the best-performing model configuration (LGBM + DE + BRDA) achieved an RMSE of 0.3745, an MAE of 0.2963, and an R² of 0.8317. These results confirm that the model not only reduces error magnitude but also explains a high proportion of variance in building vulnerability outcomes.

To further evaluate the predictive accuracy of the optimal model configuration (LGBM_DE_BRDA), we visualized its output using scatter and residual plots, as shown in Figure 21.

Figure 21a presents a scatter plot comparing predicted values against true class labels (Class 0: low to medium vulnerability, Class 1: high vulnerability). The predicted values are tightly grouped around their corresponding true labels, demonstrating a clear separation between the two classes and indicating strong model discrimination performance. Figure 21b displays the residuals for each class using a boxplot format. The residuals for Class 0 are concentrated around zero with a slight negative bias, while those for Class 1 show a slightly broader distribution, reflecting the increased variability in predicting highly vulnerable buildings. Nonetheless, both distributions remain relatively compact, with no significant outliers, suggesting a well-calibrated model with minimal systematic error.

6. Discussion

6.1. Analysis of Intensity Parameters of Human Engineering Activities

In Equation (1), HEAIC is mainly controlled by two parameters, ${\mu }_1$ and ${\mu }_2$. Therefore, it is necessary to discuss the reasonable value ratio of these two parameters to describe the ratio of the road route density to the building density in the HEAIC factor. In this article, the values of ${\mu }_1$ to ${\mu }_2$ are selected from five ratios: 3:1, 2:1, 1:1, 1:2, and 1:3.

Table 9. The RMSE results under different parameter ratios.

The Ratio of Parameters ${\mathit{\mu }}_1$ and ${\mathit{\mu }}_2$	RMSE
3:1	0.3781
2:1	0.3745
1:1	0.3885
1:2	0.4052
1:3	0.4482

presents the RMSE (Root Mean Squared Error) results for different ratios of two parameters, ${\mu }_1$ and ${\mu }_2$. The results show that the 2:1 ratio yields the best performance, with the lowest RMSE of 0.3745, indicating that this specific ratio optimizes the model’s performance. The 3:1 ratio also performs well, with an RMSE of 0.3781, slightly higher than the 2:1 ratio but still among the top performers. As the ratio moves towards 1:1, the RMSE increases to 0.3885, indicating a slight decline in performance. The ratios with more imbalance, such as 1:2 and 1:3, show progressively higher RMSE values, with 1:3 producing the highest RMSE of 0.4482. This suggests that extreme imbalances between ${\mu }_1$ and ${\mu }_2$ degrade the model’s performance. In summary, the 2:1 ratio proves to be the most effective for minimizing RMSE, offering the best balance between the two parameters.

6.2. Analysis of Model Limitations

While traditional approaches, such as Rapid Visual Screening (RVS) or vulnerability index methods, have proven effective in many seismic risk studies, they may be limited in handling complex interactions and large-scale, high-dimensional datasets. In this study, the availability of labeled data, detailed geospatial indicators, and the goal of generalizable, scalable modeling motivated the use of machine learning techniques. Compared to static scoring, ML models dynamically learn relationships from data and yield higher predictive accuracy, especially when nonlinearity and inter-feature dependencies are present.

While the proposed machine learning-based vulnerability assessment model demonstrates strong predictive performance, several limitations and potential issues must be acknowledged.

First, the performance of the model is highly sensitive to the choice of hyperparameters, and despite our use of optimization techniques, some parameters may still influence the model’s results. Different initialization methods or parameter ranges could lead to variations in performance, which may affect the model’s generalizability across different datasets. Additionally, while we have conducted thorough hyperparameter optimization, there may still be unexplored parameter interactions that could further improve model accuracy if better tuned. Second, the accuracy and granularity of remote sensing data used in this study are limited by the spatial and spectral resolution of the imagery. Lower-resolution data may fail to capture subtle but important features relevant to building vulnerability, especially in dense or heterogeneous urban environments. Third, while the model has been validated in the context of Dajing Town, Yueqing City, further testing in other geographic locations or urban environments is essential to assess its generalizability and robustness. The model’s performance may vary in regions with different urban planning characteristics, disaster risks, or data availability, which necessitates additional validation across diverse contexts.

Lastly, although the optimization techniques used (such as Bayesian Optimization, Differential Evolution, and Particle Swarm Optimization) help minimize prediction error, there is always a risk of overfitting to the training data, especially in cases of high-dimensional features. Continued development of regularization techniques and further exploration of parameter sensitivity are necessary to ensure that the model remains effective in the face of these challenges.

6.3. Relationship Between Vulnerability and Potential Losses

While the proposed VAB-HEAIC framework focuses on classifying building vulnerability into low, medium, and high categories, it does not explicitly estimate physical, economic, or human losses. However, the predicted vulnerability levels inherently reflect the relative likelihood and severity of damage from geological hazards. For example, high vulnerability buildings are more likely to suffer major structural damage or collapse under triggering events, such as landslides, debris flows, or seismic shaking.

These vulnerability levels can thus be interpreted as proxies for potential loss intensity. In future research, we plan to integrate our vulnerability outputs with hazard intensity data and building exposure information (e.g., building use, occupancy, economic value) to derive more quantitative loss estimates. This could involve applying established risk assessment frameworks, such as Risk = Hazard × Vulnerability × Exposure.

In addition to this, the expected outcomes of the VAB-HEAIC framework underscore its practical value in large-scale vulnerability analysis. The use of machine learning models enables a data-driven, scalable approach to assess vulnerability patterns across thousands of structures with high spatial granularity. By integrating dynamic human engineering activity indicators—such as changes in road network density and building footprint density—the framework effectively captures how anthropogenic factors evolve over time and influence exposure to geohazards.

Furthermore, the framework is designed to be flexible and generalizable. With appropriate data preprocessing and local parameter calibration, the VAB-HEAIC approach can be transferred to other regions, particularly those facing rapid urban expansion or significant infrastructure development. The model structure allows for the incorporation of new indicators, updated imagery, and regional hazard profiles, making it suitable for decision support in urban planning, disaster mitigation, and resilience assessment.

As urban environments continue to grow in complexity, the integration of high-resolution spatial data, intelligent optimization algorithms, and data augmentation strategies—such as those demonstrated in this study—can support more robust and proactive management of vulnerability across different temporal and spatial scales.

7. Conclusions

This study proposed a comprehensive framework—VAB-HEAIC—for building vulnerability assessment. It integrates spatial statistics, four machine learning models (SVR, RF, BPNN, LGBM), four optimization algorithms (PSO, SSA, DE, BO), three data augmentation techniques, and a novel HEAIC factor.

The framework also normalizes attributes, balances samples, and uses 10× RMSE averaging to evaluate model performance. This enables systematic exploration of hyperparameter tuning and data enhancement effects. Our results show that, without optimization or augmentation, LGBM achieved the lowest RMSE (0.3967), followed by RF (0.4081). SVR and BPNN performed worse (0.4564 and 0.8751). With optimization, model accuracy improved further. PSO and SSA reduced RMSE for SVR and BPNN (down to 0.4494 and 0.4889), while LGBM–PSO improved to 0.3878. Among augmentation strategies, LGBM performed best with SSA + feature combination (RMSE = 0.3793), PSO + numerical perturbation (RMSE = 0.3733), and DE + bootstrap resampling (RMSE = 0.3745). These results show that LGBM is robust and highly compatible with data enhancement and optimization. The ablation study shows that HEAIC is indispensable. Including it consistently improved model accuracy. The best result (LGBM_DE_BRDA) had an RMSE of 0.3745 compared to 0.4863 without HEAIC. Sensitivity analysis of HEAIC weights shows that a 2:1 ratio (road network change to building density change) yields the lowest RMSE (0.3745). This suggests the ratio best reflects human engineering impacts.

The framework is designed to be forward-compatible with evolving urban landscapes. As new buildings are constructed or older ones modified, spatial attributes can be re-extracted using the same data processing pipeline (e.g., from updated remote sensing imagery), and predictions can be made using the pre-trained model. This enables periodic reassessment without re-collecting all field data. Furthermore, retraining the model with updated samples, when necessary, enhances long-term applicability under continuous urbanization.

Overall, the VAB-HEAIC framework offers a powerful data-driven method for fine-grained vulnerability assessment. Future work will expand the framework by adding environmental and socio-economic features, integrating real-time monitoring, and validating it across different regions to enhance generalization and practical use.