Highlights
What are the main findings?
- CO pollution in Jubail shows strong diurnal and moderate weekly patterns, with local sources dominating spatial variation.
- Ensemble machine learning models, especially Extreme Gradient Boosting (XGBoost) and Categorical Boosting (CatBoost), achieved highly accurate CO forecasts (R2 > 0.95).
What is the implication of the main finding?
- Predictive analytics enable proactive air quality management in smart cities, improving public health outcomes.
- Identifying pollution hotspots and weather interactions supports targeted interventions and smarter urban planning.
Abstract
Effectively managing carbon monoxide (CO) pollution in complex industrial cities like Jubail remains challenging due to the diversity of emission sources and local environmental dynamics. This study analyzes spatiotemporal CO patterns and builds accurate predictive models using five years (2018–2022) of data from ten monitoring stations, combined with meteorological variables. Exploratory analysis revealed distinct diurnal and moderate weekly CO cycles, with prevailing northwesterly winds shaping dispersion. Spatial correlation of CO was low (average 0.14), suggesting strong local sources, unlike temperature (0.92) and wind (0.5–0.6), which showed higher spatial coherence. Seasonal Trend decomposition (STL) confirmed stronger seasonality in meteorological factors than in CO levels. Low wind speeds were associated with elevated CO concentrations. Key predictive features, such as 3-h rolling mean and median values of CO, dominated feature importance. Spatiotemporal analysis highlighted persistent hotspots in industrial areas and unexpectedly high levels in some residential zones. A range of models was tested, with ensemble methods (Extreme Gradient Boosting (XGBoost) and Categorical Boosting (CatBoost)) achieving the best performance () and XGBoost producing the lowest Root Mean Squared Error (RMSE) of 0.0371 ppm. This work enhances understanding of CO dynamics in complex urban–industrial areas, providing accurate predictive models () and highlighting the importance of local sources and temporal patterns for improving air quality forecasts.
1. Introduction
In a rapidly growing urban world, air quality is a key factor in public health and sustainable development. In many cities, people go about their lives unaware of how fluctuating pollution levels affect their well-being. Managing this pollution is not only a technical challenge but also a public necessity. Smart cities use data-driven systems to turn environmental data into actionable insights [1]. At the heart of this effort are multi-site datasets that track gases like carbon monoxide (CO), temperature, and wind speed and direction. However, working with these datasets is difficult. They are complex across space and time and often messy, with missing values, inconsistencies, and variations between sensors [2].
Good decisions start with good data. In smart cities, reliable environmental data allow decision makers to spot issues early, respond faster, and plan more effectively [3]. That process begins with strong data management: cleaning, error correction, handling of missing entries, and merging of data sources. This is especially important for time-series data, which form the backbone of many air quality systems. If the foundation is weak, even the most advanced analytics will fall short [4]. Our earlier work [5] addressed this problem by cleaning and improving multi-location environmental data through outlier detection and imputation. That gave us a dependable dataset to build on. This study takes the next step by combining historical analysis with predictive modeling, helping smart cities not only understand air quality but also anticipate it.
This research has three main goals. First, we use descriptive analytics to explore historical CO patterns and their connections to weather conditions. This helps uncover seasonal cycles, long-term trends, and environmental drivers of pollution. Second, we apply predictive analytics using machine learning models such as Random Forest [6] and Long Short-Term Memory (LSTM) networks [7] to forecast future CO levels. These forecasts enable cities to act before pollution spikes occur. Third, we conduct spatiotemporal analysis to examine how gas concentrations vary across locations and over time. This helps detect anomalies and identify pollution hotspots that need targeted responses.
Taken together, these analytical approaches allow the research to address critical real-world challenges. By analyzing spatial and temporal patterns in environmental data, we can identify pollution sources and understand how weather influences air quality. Descriptive analytics provide insight into the past, while predictive analytics offer a view of what is coming next. Together, they enable cities to shift from reactive measures to proactive planning. This combined approach supports smarter urban development and better public health outcomes.
This study focuses on CO due to its acute health implications and strong link to mobile and industrial sources, offering a clear signal for evaluating spatiotemporal pollution dynamics. While other gases were recorded, CO provides the most interpretable foundation for predictive modeling in this context.
The practical impact is significant. Detecting sudden pollution events allows cities to act quickly. Predictive capabilities help them prepare ahead of time. This study connects analysis to action, giving decision makers the tools they need to improve air quality and reduce health risks.
In this paper, we present a spatiotemporal analysis of gas and weather data from multiple locations. We develop predictive models to forecast pollution trends and provide decision-support tools for policy makers. By combining historical patterns with forward-looking predictions, the goal is to help cities monitor air quality, anticipate changes, and respond effectively. This supports broader goals of sustainability and environmental resilience.
The paper is organized as follows. Section 2 reviews related work. Section 3 describes the dataset. Section 4 explains the methodology. Section 5 presents the results, and Section 6 discusses the findings, limitations, and future directions. Finally, Section 7 concludes the paper.
As smart cities continue to grow and evolve, environmental analytics will play a central role in shaping policies and managing the risks associated with air pollution. This research contributes to that future by offering data-driven insights that support cleaner, healthier urban environments.
2. Previous Work
Machine learning and deep learning have become key tools in air quality prediction, especially for smart city planning and the protection of public health [8]. Many studies have explored environmental data for air quality monitoring and weather forecasting but most focused on either spatiotemporal analysis or predictive modeling, not both [9]. Few offer integrated insights tailored to urban decision makers [8]. Despite progress in environmental analytics, gaps remain, including the limited combination of historical (descriptive) and predictive modeling and the underuse of large, multi-location datasets with diverse variables [9].
In this section, we highlight key related studies, outlining their methods, contributions, and limitations. We then show how our approach bridges these gaps. Specifically, our work uses a clean, high-resolution dataset collected over five years from multiple sensors, integrating detailed meteorological parameters. By linking historical trends with predictive insights, we provide more interpretable, accurate, and actionable information designed for smart city decision making.
2.1. Descriptive Analytics
Cesario [10] explores big data analytics in smart cities, covering applications like crime prediction, mobility, and epidemic tracking. While the study demonstrates how analytics can guide urban decisions, it does not focus on air quality or the integration of environmental and meteorological data. It also emphasizes predictive methods, with limited discussion of historical trends. Our research builds on Cesario’s work by targeting air quality specifically. We use several years of high-resolution data from multiple sensors, covering pollutants and detailed weather metrics (temperature and wind speed and direction). By combining descriptive and predictive analytics, our approach provides deeper insight into how pollution changes over time and space. The findings support more informed urban planning.
Osman and Elragal [11] propose a general big data analytics framework to support decision making across smart city domains. Their design emphasizes features like interchangeable results and persistent analytics. However, the study remains broad and does not address environmental data or predictive modeling in depth. It leans toward descriptive analytics and does not explore spatiotemporal variation. In contrast, our work focuses specifically on air quality, using detailed sensor data and meteorological inputs. We combine descriptive and predictive methods to provide a clearer, more granular understanding of air pollution and its implications. Our study expands Osman and Elragal’s ideas by offering a practical, domain-specific framework with improved interpretability and forecasting power.
Malhotra et al. [12] provided a systematic review of AI techniques for air pollution prediction. They assessed various machine learning and deep learning methods, highlighting strengths and shortcomings. Key limitations include weak integration of meteorological data, inadequate handling of spatiotemporal patterns, and a strong focus on accuracy over interpretability. While the review identified major challenges, it did not propose a unified framework. Our work directly responds to these gaps. We use five years of hourly data from ten sensors per pollutant and include comprehensive meteorological variables. We combine historical analysis with predictive modeling to produce actionable insights. This practical approach addresses the core concerns raised by Malhotra et al., improving interpretability and real-world usability.
Essamlali et al. [13] reviewed supervised machine learning techniques for the prediction of pollutants like PM, NOx, CO, and O3 in smart cities. Most studies they examine used one-year datasets, often aggregated at the daily or monthly level, with a single sensor per pollutant. Few incorporated meteorological variables such as temperature or wind. The focus was mainly on prediction, not description. Our work addresses these limitations by using five years of sensor-level data from ten sensors per pollutant, including full meteorological coverage. This supports both descriptive and predictive analytics, providing a fuller picture of urban air quality dynamics.
Together, these studies show growing interest in data-driven environmental analysis, but they also reveal key gaps. Most fall short in combining descriptive and predictive views and in using long-term, high-resolution data.
2.2. Predictive Analytics
Zareba et al. [14] proposed a machine learning pipeline for the forecasting of smog events in Krakow, using hourly data from 52 sensors over one year. Their framework includes preprocessing, feature engineering, and both linear and deep learning models, mostly focusing on PM2.5. While wind direction is included as a cyclic variable, other meteorological factors are absent. Our study builds on this by analyzing five years of multi-pollutant data from ten sensors per gas, with full weather variables. Zareba et al.’s finding that simple models can outperform complex ones in certain cases informs our model comparisons.
Kok et al. [15] developed a deep learning model for air quality forecasting using data from the CityPulse EU FP7 Project. Their dataset includes 17,568 samples across eight features at five-minute intervals. Their LSTM model outperformed support vector regression, especially in predicting critical pollution levels. However, they did not incorporate weather data, and their analysis focused mainly on ozone and nitrogen dioxide. Our research expands on theirs by using a broader range of pollutants, a longer time span, more sensors, and full meteorological integration. We also pair prediction with historical analysis for a more rounded view.
Jaisharma et al. [16] introduced the NTDP deep learning model to forecast toxic gas emissions in smart cities, using AIQ India data from 2015 to 2020. They predicted 2021 gas levels using BiLSTM and attention mechanisms, supported by daily air quality and weather reports. Although they included meteorological factors, their data were aggregated and did not reflect sensor-level detail. Our study differs by working with hourly, sensor-level data across multiple gases and incorporating a descriptive component.
Swamynathan et al. [17] aimed to forecast the Air Quality Index (AQI) using machine learning. Their multi-year dataset includes key pollutants but provides little detail on how weather data are used. Models such as Naive Bayes and SVM were employed, with a focus on prediction. In contrast, we work with detailed, sensor-level data and explicitly integrate weather variables, enabling both prediction and trend analysis.
Tsokov et al. [18] presented a hybrid deep learning model using CNN and LSTM to forecast PM2.5 in Beijing. Their approach includes imputation, spatial modeling, and hyperparameter tuning via genetic algorithms. While their results are promising, their study focused narrowly on PM2.5, lacking a descriptive component. Our research expands on this by covering multiple gases, integrating weather, and including historical trend analysis.
Simsek et al. [19] introduced CepAIr, a fog-based air quality monitoring system using deep learning and Support Vector Regression (SVR). Their dataset spans 60 days, with five-minute readings from a single sensor per gas. Meteorological data are not included. The study focused on prediction alone. Our approach uses a broader temporal scope, more sensors, and full weather integration to provide a deeper understanding.
Binu [20] outlined an AI–Internet of Things (IoT) system for one-year air pollution monitoring. It includes real-time data and anomaly detection but does not fully integrate weather data or use multi-year analytics. Our work extends this by covering five years, using multiple sensors per pollutant, and analyzing both current patterns and long-term trends.
Kotlia et al. [21] applied Random Forest and XGBoost to classify AQI levels in Uttarakhand using one year of data. Their data are aggregated and lack meteorological input. Our study differs by using hourly data, full weather integration, and a dual descriptive–predictive approach.
Overall, most prior studies have used short-term or aggregated datasets, lacking detailed weather data and focusing solely on prediction. Some researchers, like Jaisharma et al. and Swamynathan et al., have used multi-year data but without fully leveraging their resolution or combining them with descriptive analytics. Reviews by Malhotra et al. and Essamlali et al. highlight similar shortcomings across the field. Our study addresses these issues by using five years of hourly data from ten sensors per gas and incorporating full meteorological variables. By combining descriptive and predictive analytics, we offer deeper insights and more practical tools for decision makers managing urban air quality.
3. Data Description
Monitoring air quality in smart cities depends on accurate, high-resolution data. This study uses a unique dataset from Jubail Industrial City, Saudi Arabia, a region that includes both industrial and residential zones (see Figure 1). Jubail is an ideal case study because its pollution sources vary by location, driven by both industrial activity and traffic emissions. The dataset includes hourly gas and meteorological measurements from ten monitoring stations, offering a strong foundation for improving data quality and supporting better environmental decisions.
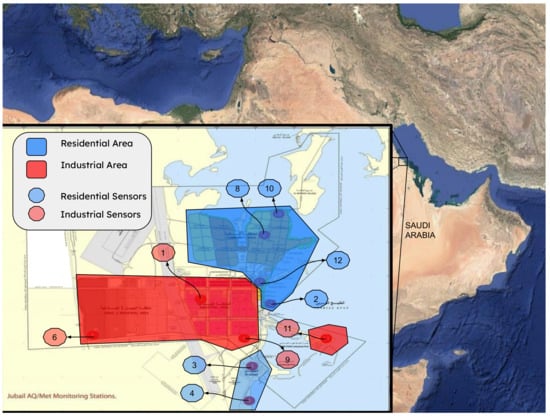
Figure 1.
Location of the ten air quality monitoring sensors in Jubail Industrial City. Red markers indicate sensors in industrial zones; blue markers are in residential areas.
The dataset spans 60 months, from January 2018 to December 2022, with hourly sampling. This provides a detailed temporal view that captures seasonal cycles, long-term trends, and unusual pollution events. The high-frequency, continuous nature of the data supports robust descriptive analytics, forecasting models, and spatiotemporal analysis.
The data collection process was not part of this study. Since we do not own the data, we were unable to independently verify the calibration status of the sensors. Our analysis assumes that the data were collected following standard operational procedures, and all results should be interpreted in the context of the reliability of the original measurements.
3.1. Key Environmental Variables
The dataset includes hourly readings of gas pollutants and meteorological conditions, allowing us to explore pollution patterns and the environmental factors that influence them. While multiple pollutants were recorded, this study focuses on carbon monoxide (CO) because of its relevance to urban health and its close ties to traffic and industrial emissions.
Other recorded gases include hydrogen sulfide (H2S), sulfur dioxide (SO2), nitric oxide (NO), nitrogen dioxide (NO2), oxides of nitrogen (NOX), ammonia (NH3), non-methane hydrocarbons (NMHC), total hydrocarbons (THC), benzene, ethyl benzene, m/p-xylene, o-xylene, and toluene. These pollutants are important for broader air quality research, especially when studying secondary pollutants or specific emission sources. Although they are part of the dataset, they are not analyzed in this paper and are left for future work.
In addition to gas pollutants, the dataset includes weather variables that affect how pollutants spread and accumulate. These include atmospheric temperature, relative humidity, pressure, solar radiation, and wind speed and direction measured at three heights (10 m, 50 m, and 90 m). For this study, we focus on three key variables: temperature, wind speed (10 m), and wind direction (10 m). Temperature influences chemical reactions and seasonal pollution levels. Wind speed affects how quickly pollutants disperse. Wind direction determines where pollutants travel and how emissions from industrial zones impact residential areas. Including these variables helps us interpret pollution patterns in their environmental context.
3.2. Data Preparation
The dataset includes missing values and outliers, which are common in real-world environmental sensor data. To ensure the reliability of the analysis, it was cleaned and preprocessed across all core variables: carbon monoxide, temperature, wind speed, and wind direction. This process included handling missing data, removing extreme outliers, and smoothing irregular fluctuations where appropriate. A complete description of the preprocessing steps, with particular focus on carbon monoxide, is provided in our previous work [5] and summarized in Section 4. Key steps included outlier detection, missing value imputation, and unit consistency. As with many sensor networks, the raw data showed occasional issues. Some CO readings were zero, which is not physically realistic. Temperature values of 100 degrees Celsius indicated likely sensor errors. In contrast, zero values in wind direction were valid and did not require correction, as they indicate wind from the north. Once cleaned, the data were organized into separate CSV files for each variable (e.g., CO.csv and Wind Speed.csv), making them easier to analyze.
This five-year, multi-location dataset, focused on CO and supported by weather data, forms the basis for the analyses that follow. The next sections explore historical patterns, predict future pollution levels, and examine how CO levels vary across space and time in Jubail.
4. Methodology
This study used a step-by-step method to look at air quality patterns and predict pollution levels in Jubail Industrial City. The method had several steps, starting with data preprocessing and descriptive analytics, to confirm the expected and discover the unexpected by fully exploring and understanding the dataset. First, we conducted descriptive analytics, including exploratory data analysis (EDA), to find historical trends, links between variables (like CO and weather), and seasonal patterns. Based on these findings, we then used feature engineering to create useful features for the models. This included techniques like normalization and transformation to prepare the data better. Next, we used predictive analytics methods with advanced models and algorithms to predict pollution levels using these created features. Finally, spatiotemporal analysis combines these features to provide reliable and useful results. Each step follows logically from the one before it. This creates an organized, data-based method to help manage air quality well and support decision making in smart cities. An overview of this complete analytical process is presented in Figure 2, which visually illustrates the sequential steps from data collection to model validation.

Figure 2.
Visual representation of the structured analytical framework employed in this study, outlining the sequential steps from data collection to validation.
4.1. Data Processing
During data cleaning, duplicate records were removed, ensuring each observation represented a unique measurement. Units of measurement were standardized across variables: gas concentrations were converted to parts per million (ppm), and temperatures were standardized to degrees Celsius (°C). Timestamps were aligned to a uniform hourly frequency, revealing 217 missing timestamps (less than 0.02% of the total expected timestamps). These missing timestamps were inserted as placeholders (Not a Number (NaN) values) to maintain the integrity of the time-series data for subsequent imputation.
Before addressing missing values and outliers, we performed initial data cleaning to correct known sensor-specific biases. Specifically, we observed that sensor 2 recorded temperature values reaching 100 °C, which is physically implausible for the monitored environment and significantly exceeds the maximum temperature of 52 °C observed across the other nine sensors. These erroneous readings were likely due to a sensor malfunction or calibration issue. To correct this, we removed these implausible temperature readings from sensor 2 and subsequently treated them as missing values to be imputed using the methods described in the following section.
As in our previous work [5], we employed a multi-stage approach to handle missing values, prioritizing methods that preserve the temporal characteristics of the data. We first assessed the suitability of linear interpolation for short gaps (less than 2 h). Linear interpolation is suitable for hourly time-series data because it assumes a linear relationship between consecutive data points, which is a reasonable approximation for short-term fluctuations in environmental variables. For gaps where linear interpolation was deemed appropriate, it was applied. For more extensive missingness or where linear interpolation was not suitable, we leveraged the methods detailed in our previous work, including (in order of application) Piecewise Cubic Hermite Interpolating Polynomial (PCHIP) interpolation [22] (chosen for its ability to preserve data shape), k-Nearest Neighbors (KNN) [23] imputation, and the Multivariate Imputation by Chained Equations (MICE) algorithm [24]. The specific parameters and implementation details for KNN and MICE are consistent with those described in our previous work [5].
We utilized a combination of statistical methods and domain knowledge to identify and address outliers, building upon the methods described in our previous work [5]. While we initially employed methods such as Interquartile Range (IQR) analysis [25], Z-score [26] detection, and rolling window statistics [27] (as detailed in [5]), our primary reliance for anomaly detection was on Isolation Forest [28], with a contamination parameter of 0.05. Isolation Forest is particularly effective at identifying data points that are easily isolated in the feature space, making it well-suited for detecting unusual pollution events or sensor malfunctions. The identified anomalies, which included the previously addressed unrealistic temperature readings from sensor 2, were removed from the dataset.
We further examined the distribution of CO concentrations. For example, we observed that 95% of the CO readings from sensor 1 fell below 0.82 ppm, while isolated instances reached values as high as 7.67 ppm. These extremely high, infrequent values, lacking any corresponding meteorological or known event-based explanation, were considered to be inconsistent with the overall data distribution and likely attributable to transient sensor errors. Because the precise cause of these sporadic extreme values was beyond the scope of this study and because they significantly deviated from the typical data patterns, they were also treated as outliers and removed. We did not apply a fixed numerical threshold for CO removal beyond the anomalies identified by Isolation Forest; instead, we relied on the algorithm’s ability to identify points that were statistically isolated in the multi-dimensional feature space, combined with our review of the data distribution. Imputed values were not capped at a specific threshold but were constrained by the inherent characteristics of the imputation methods that leverage the relationships within the valid data to generate plausible replacements.
4.2. Descriptive Analytics
Descriptive analytics provide essential insights into air quality trends, helping to understand variations in pollution levels and the influence of meteorological conditions. To examine the distribution and temporal patterns of CO concentrations, along with their relationships to meteorological variables, descriptive analyses were conducted using Python 3.9 with the pandas, statsmodels, and scipy libraries. A detailed description of the dataset can be found in Section 3. Data preprocessing involved a multi stage imputation approach, beginning with linear interpolation for short gaps, followed by advanced imputation methods such as PCHIP, KNN, or MICE for longer gaps. Outlier detection was primarily conducted using the Isolation Forest algorithm, supplemented by the IQR method described in our previous work. No additional scaling or transformation was applied to the data before conducting the descriptive analysis.
First, we calculated summary statistics for CO concentrations, temperature, wind speed, and wind direction. These included the mean, median, standard deviation, minimum, maximum, and percentiles (5th, 25th, 50th, 75th, and 95th). We computed these statistics for the entire dataset and individually for each of the ten monitoring locations to understand overall patterns and variations specific to each site. We created violin and box plots to visualize the distribution of each variable.
Second, we applied time-series decomposition to the CO concentration data at each location to separate the time series into its main components: trend, seasonality, and residuals. This decomposition helps us better understand the data structure by breaking it down into interpretable parts. Specifically, we used a classical additive decomposition model represented by the following equation:
where is the observed CO concentration at time t; is the trend component representing long-term changes; is the seasonal component capturing recurring patterns (such as annual or daily cycles); and is the residual component, which reflects random or irregular fluctuations not explained by the trend or seasonality.
To estimate the seasonal component, we used a moving average with a window size of 8760 data points, corresponding to one full year of hourly measurements (24 h * 365 days (Using 365 days simplifies the window calculation; accounting for leap years would use approximately 365.24 days)). We chose an additive model instead of a multiplicative model because seasonal fluctuations in CO concentrations appeared relatively stable over time rather than changing proportionally to the trend. This decomposition clarifies long term trends, highlights regular seasonal patterns, and isolates irregular or unexpected variations. To visualize these patterns, we generated line plots of the original data and its decomposed components (trend, seasonality, and residuals) for each location.
Third, we assessed the relationship between CO concentrations and meteorological variables (temperature, wind speed, and wind direction) using correlation matrices and Pearson’s correlation coefficient. We conducted this analysis separately for each location to consider site-specific differences. We calculated correlation coefficients using the pearsonr function from the scipy.stats [29] module and visualized these results with heat maps. In addition, we calculated correlations between CO concentrations at different sensor locations to investigate spatial relationships in pollution levels.
4.3. Feature Engineering and Selection
To prepare the data for input into the Prophet forecasting model and to maximize predictive accuracy while maintaining model parsimony, we undertook a two-stage process of feature engineering and feature selection. Feature engineering involved the creation of new variables based on temporal, spatial, and meteorological relationships within the data. Feature selection then employed the XGBoost algorithm to identify and retain only the most informative predictors for the final model.
4.3.1. Feature Engineering
Feature engineering is central to our approach to air quality forecasting, transforming raw, unprocessed data into a structured set of meaningful inputs that drive our predictive models. Far from a routine technical task, this process uncovers the latent patterns and relationships within air quality data, patterns influenced by temporal, spatial, and meteorological dynamics. Our feature engineering methodology systematically integrates insights from descriptive analytics and domain knowledge, yielding a robust collection of features organized into three key categories: temporal, spatial, and meteorological features. These meticulously crafted features enhance the accuracy and reliability of our predictive models, laying the foundation for improved air quality management.
To provide a clear overview of our feature engineering strategy, we begin with Table 1. This table serves as a roadmap, summarizing the main feature categories, along with their respective subfeatures. The subsequent sections explore each category in detail, elucidating the rationale behind every feature, its derivation, and its specific contribution to model performance. This structured presentation clarifies our methodology while illustrating how each feature captures the complexities of air quality dynamics.

Table 1.
Summary of engineered features, categorized by type, with representative examples and their purpose in enhancing model performance and interpretability for the air pollution dataset.
This step is crucial for our research, enabling our models to interpret the multifaceted factors driving CO concentrations, including temporal trends (historical pollution levels), spatial relationships (distances between monitoring stations), and meteorological influences (wind speed). By doing so, we strengthen our capacity to deliver accurate and actionable forecasts, a key objective of this study. Ultimately, this rigorous feature engineering process supports our goal of facilitating proactive decision making and policy development in smart cities, contributing to enhanced air quality management and improved public health outcomes.
Temporal Features
We extracted detailed temporal information by decomposing timestamps into their constituent components: hour of the day, day of the week, day of the month, month of the year, and year. To capture the cyclical nature of time and ensure smooth transitions (e.g., from December to January or from Sunday to Monday), we applied sine–cosine encoding to the hour, day of the week, day of the month, and month of the year features using the following formulas:
where x is the original time component and T is the period of the cycle. Specifically, we used for the hour of the day, for the day of the week, for the day of the month (using a fixed value to represent the average month length), and for the month of the year. The year was treated numerically without cyclic encoding, as it represents linear temporal progression rather than cyclic seasonal variation.
We further created two sets of granular time-of-day features: an 8-interval scheme dividing the day into three-hour blocks (0–3, 3–6, …, 21–24), and a 4-interval scheme dividing the day into six-hour blocks (0–6, 6–12, 12–18, and 18–24). These interval features were also cyclically encoded. Cyclic encoding was preferred over ordinal encoding to avoid artificial discontinuities (e.g., treating 23:59 and 00:00 as unrelated).
Granular Time of Day: We created two time-of-day features to capture daily patterns. One divides the day into eight three-hour intervals, and the other groups the day into four broader periods (morning, afternoon, evening, and night). To account for the cyclical nature of time, both features were encoded using sine and cosine transformations. Additionally, we included a binary “Night” flag that equals 1 for hours before 6 a.m. or at/after 8 p.m. (and 0 otherwise).
Rolling Window and Lag Features: Rolling window statistics (mean, median, standard deviation, minimum, and maximum) were computed for CO, temperature, and wind speed using window sizes of 3, 6, 12, 24, 72, and 168 h, capturing both short-term dynamics and longer-term trends. Lag features were generated for CO, temperature, and wind speed over lag periods of 1, 3, 6, 12, and 24 h, incorporating autocorrelation.
Difference-Based Features: Difference-based features, quantifying immediate fluctuations, were calculated as follows:
where denotes the value of the series k steps before time t, while measures the absolute change between consecutive observations. The percentage change rescales this difference by the previous value, expressing the relative magnitude of the shift in percent. These features allow the model to detect both the direction and the strength of short-term movements in the data.
Relative Difference Features: For each sensor column and for each specified rolling window size (3, 6, 12, 24, 72, and 168 h), the code creates several features:
These difference-based features are particularly valuable for rapidly identifying anomalous spikes and shifts in pollutant concentrations.
These temporal features significantly enhance the sensitivity of our models to daily, weekly, and seasonal variations, directly benefiting both descriptive analyses of historical trends and predictive accuracy. Temporal features improve forecasting accuracy by explicitly modeling recurring environmental patterns identified through historical analyses.
Spatial Features
Sensor Grouping: We grouped sensors based on spatial location into residential and industrial categories, determined by using local zoning data and land use maps. Residential zones were further categorized into Upper, Mid, and Lower zones based on their geographical location along a north–south axis, reflecting a gradient of decreasing proximity to the primary industrial area, as well as their distance from each other (less than 5 km). Industrial zones were categorized as Close or Far based on their distance from the center of the industrial zone, with a threshold of 8 km; Close industrial zones are those within 8 km of the center of the industrial zone, while Far zones are beyond this radius. This categorization allows us to capture the influence of different land use types and proximity to pollution sources on observed pollutant levels. Figure 3 shows the industrial zone and the residential zone, as well as the subgroups that were extracted.
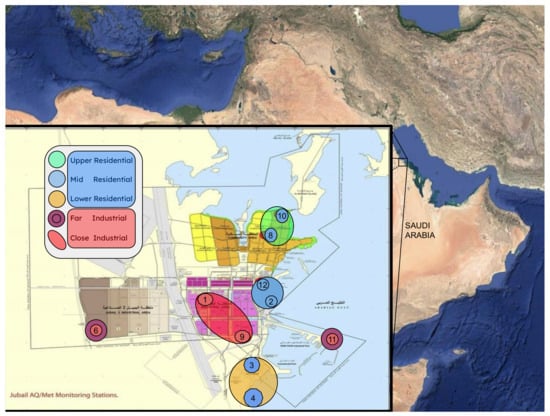
Figure 3.
Map showing the sensor groups with respect the residential and industrial zones.
Table 2 presents the calculated distances, in kilometers, between each pair of air quality monitoring sensors deployed across Jubail Industrial City. These distances are critical for understanding the spatial relationships among sensor locations, which, in turn, influence the spatial component of pollution dispersion patterns and are integral to the spatiotemporal modeling phase of this study. By quantifying how far apart the sensors are, this table provides foundational information for spatial interpolation techniques, spatial correlation analysis, and other geostatistical methods used later in the analytical workflow.

Table 2.
Distance in kilometers between the sensors in the monitoring stations.
Relative Difference Features (CO Sensor Differences): We computed relative differences between a reference sensor (S1) and other sensor stations (S2, S3, S4, S6, S8, S9, S10, S11, and S12), where S1 was chosen as the reference sensor due to its central location within the sensor network and its position in the middle of the industrial area. The following features were created:
where is a small constant (set to 0.00001) added for numerical stability to prevent division by zero and i represents each of the other sensor stations. All spatially derived features are standardized or normalized based on the machine learning preprocessing steps to maintain balanced scales. These spatially informed features strengthen our ability to model and predict location-specific pollution dynamics, which is essential for targeted environmental management. Spatial features enhance local predictive accuracy by capturing geographic variability, enabling targeted interventions.
Meteorological Features
Wind Direction Encoding: For each identified wind direction column, the wind direction values (assumed to be in degrees) were first converted to radians using np.deg2rad(). Two new features were created: a sine-transformed feature (<original_col>_sin) and a cosine-transformed feature (<original_col>_cos). Wind direction encoding using sine and cosine transformations was critical because it maintains the cyclic continuity inherent in directional data, ensuring that wind directions near 0° and 360° are treated equivalently.
These engineered meteorological features ensure accurate modeling of complex environmental interactions and cyclic behaviors, substantially enhancing predictive capability. Meteorological features provide predictive models with critical non-linear interactions and environmental context, significantly boosting prediction reliability.
Overall Impact on Modeling Outcomes
The incorporation of meticulously engineered features spanning temporal, spatial, and meteorological categories forms a robust analytical framework. This framework facilitates the precise modeling of intricate interactions and patterns within environmental datasets, thereby improving the accuracy of predictive outcomes. The resulting models are well positioned to inform evidence-based decision making in urban air quality management, directly supporting the overarching objectives of enhancing public health and promoting environmental sustainability.
4.3.2. Feature Selection
Our feature engineering step (the result generated in Section 4.3.1) produced a large set of features—2218 in total. These features were derived from time-based transformations, weather variables, gas measurements, and spatial context. While this high-dimensional feature space offered rich information, it also introduced challenges.
To address this, we applied feature selection to improve forecasting accuracy, reduce overfitting, boost computational efficiency, and enhance model interpretability. Among various methods, we selected XGBoost (Extreme Gradient Boosting) [30] for this task. XGBoost was chosen for its strong performance in handling high-dimensional data. It ranks features by assigning importance scores based on reductions in the model’s objective function—in this case, squared error. It also captures complex non-linear relationships and is naturally resistant to multicollinearity. While we considered alternatives like Recursive Feature Elimination (RFE) and Lasso regression, these methods are either more limited in capturing non-linear relationships or more sensitive to multicollinearity. In contrast, XGBoost offers robustness in high-dimensional settings, effectively models non-linear dependencies, and provides readily interpretable feature importance scores, making it the most suitable choice.
To train the XGBoost model effectively, we first split the dataset temporally. The first 80% of the time-ordered data were used for training, while the remaining 20% were reserved for testing. This approach preserved the time-series structure and prevented data leakage.
We then conducted a grid search combined with 5-fold TimeSeriesSplit cross-validation to tune the model’s hyperparameters. This form of cross-validation respects the chronological order of data, ensuring that each fold is trained on past data and validated on future data, which is crucial for time-series forecasting. The grid search explored hyperparameters including max_depth (values: 4, 6, 8), learning_rate (values: 0.01, 0.05, 0.1), and n_estimators (values: 100, 500, 1000). We also applied early stopping with a patience of 20 rounds, monitoring the validation root mean squared error (RMSE) to halt training before overfitting.
The best-performing model was selected based on the lowest average RMSE across the five folds. This final XGBoost model was implemented using the xgboost package in Python with the following parameters: objective = reg:squarederror, learning_rate = 0.05, max_depth = 6, subsample = 0.8, colsample_bytree = 0.8, and random_state = 42. A max_depth of 6 allowed the model to capture moderately complex interactions without overfitting. A learning_rate of 0.05 encouraged stable learning, while subsample and colsample_bytree values of 0.8 added randomness to help generalize better.
After training, we extracted feature importance scores. These scores reflect how much each feature contributed to reducing the squared-error loss across all trees. We retained only the features with an importance score of at least 0.01. This threshold was selected based on a sharp drop-off in importance values observed around this point. In the end, this process resulted in the selection of 10 features out of the original 2218, reinforcing the significant dimensionality reduction achieved through feature selection.
4.4. Predictive Analytics
Predictive modeling plays a crucial role in air quality forecasting, enabling the development of robust machine learning models that can forecast CO concentrations based on historical data and relevant features. This subsection explores the methodologies used to achieve accurate and reliable predictions, focusing on the predictive models employed, their optimization, and the validation strategies used. Given the complexity of air quality data, which involve non-linear relationships, temporal dependencies, and high-dimensional feature sets, a variety of advanced models were employed. Each model was chosen for its specific strengths in handling these challenges. To provide a clear and concise overview, Table 3 below summarizes the models, their key strengths, and the validation methods used to assess their performance. This table serves as a quick reference for readers to compare the approaches and understand their applicability to air quality forecasting.

Table 3.
Summary of predictive models, their validation strategies, and types. The Type column identifies the underlying approach: machine learning, deep learning, statistical (traditional time-series forecasting), or hybrid (combining multiple methodologies).
4.4.1. Model Selection and Validation
A variety of machine learning models were selected to address forecasting challenges, each offering unique strengths for different aspects of time-series data [6,7,30,31,32,33]. These models fall into four main categories:
- Tree-Based Ensembles: Random Forest [6], XGBoost [30], and CatBoost [33] handle non-linear relationships effectively and are robust to noisy, high dimensional data. They also provide feature importance metrics for interpretability. XGBoost and CatBoost can yield higher accuracy but typically require more computational resources than Random Forest.
- Specialized Time-Series Models: Prophet [31], developed by Facebook, is designed for data with strong seasonality and trend components, incorporating holiday effects and user-defined change points. It trains quickly and produces interpretable decompositions of trend and seasonality.
- Deep Learning Models: Long Short-Term Memory (LSTM) networks [7] capture long-range temporal dependencies but tend to be more computationally intensive and less interpretable.
- Comparative Modeling Framework: The Darts library [32] provides a unified environment for testing both classical statistical methods (Autoregressive Integrated Moving Average (ARIMA)) and deep learning models, simplifying side-by-side comparisons.
We performed hyperparameter optimization for all models using grid search, systematically exploring parameter values to maximize accuracy. For tree-based ensembles (XGBoost, Random Forest, and CatBoost), we employed TimeSeriesSplit cross-validation, a variation of K-fold cross-validation specifically designed for time-series data. Unlike standard K-fold cross-validation, which randomly splits the data into subsets without considering temporal order [34], TimeSeriesSplit preserves the chronological sequence by progressively training on earlier periods and testing on later ones, thereby mitigating data leakage [35].
Walk-forward validation, utilized for Prophet, LSTM, and models within Darts, sequentially expands the training set forward in time, continually validating predictions on the immediate future [36]. This method maintains temporal integrity and is particularly advantageous when forecasting accuracy over continuous time horizons is critical. Standard K-fold cross-validation is typically avoided in time-series contexts due to its inherent assumption of independent and identically distributed observations, a condition not met by sequential temporal data [37].
Although methods like SHapley Additive exPlanations (SHAP) [38] and Local Interpretable Model-agnostic Explanations (LIME) [39] can help explain how complex models make decisions, we did not use them here. Instead, we relied on simpler measures built directly into tree-based models (like feature importance scores) and Prophet’s clearly interpretable components. This approach provided a good balance between being understandable and making accurate predictions.
4.4.2. Model Evaluation
Model performance was evaluated using metrics such as mean absolute error (MAE), mean squared error (MSE), root mean squared error (RMSE), mean absolute percentage error (MAPE), and the coefficient of determination (R2 Score).
The MAE measures the average absolute difference between predicted and actual values, directly interpretable in the original units; lower values indicate better predictive accuracy.
where n is the total number of observations, is the true value at index i, and is the corresponding model prediction.
The MSE penalizes large errors more heavily than small ones; lower values indicate superior predictive accuracy.
where all variables are as defined above.
The RMSE is the square root of the MSE, expressed in the original units of the target variable, facilitating intuitive interpretation. A lower RMSE signifies higher prediction quality and a greater penalty on large forecasting errors.
where n, , and are as defined above.
The MAPE expresses the average error as a percentage of the true value and is useful for comparing predictive accuracy across models or datasets with differing scales.
where n, , and are as defined above and we assume for all i.
The score indicates the proportion of variance in the target variable that is explained by the model. Values approaching 1 imply a highly accurate model, whereas values near 0 or negative values imply poor predictive performance.
where is the mean of the true values and all other variables are as defined above.
Together, these metrics provided a comprehensive evaluation of model forecasting performance, demonstrating improvements resulting directly from effective feature selection.
Additionally, validation strategies were tailored to the characteristics of each predictive method. TimeSeriesSplit cross-validation was applied to ensemble models like XGBoost, Random Forest, and CatBoost, while a temporal validation approach, walk-forward validation, was implemented for Prophet, LSTM, and models built using Darts. This ensured chronological consistency, avoided data leakage, and provided more realistic performance assessments for sequential data.
Given the need for efficient, real-time forecasting in smart city applications, computational efficiency was a key consideration. For example, XGBoost was favored for its balance of accuracy and speed, unlike the more resource-intensive LSTM, which requires significant computational power for training and inference.
Through these diverse methodologies, predictive modeling aimed to achieve accurate and reliable forecasting of air quality indicators, ultimately enhancing decision-making processes within smart city contexts.
4.5. Overview of Predictive Modeling Approaches
4.5.1. Gradient Boosting with XGBoost
This model handles non-linear relationships effectively and typically offers high accuracy on tabular data. A simplified version of the XGBoost objective function is expressed as follows:
where is the loss (e.g., mean squared error) and penalizes model complexity.
Key hyperparameters included the following:
- learning_rate (eta): Step size shrinkage to prevent overfitting (optimal value: 0.01)
- max_depth: Maximum depth of each tree (optimal value: 3)
- n_estimators: Number of boosting rounds (optimal value: 500)
- subsample: Fraction of training instances sampled for each tree (optimal value: 0.7)
- colsample_bytree: Fraction of features sampled for each tree (optimal value: 0.8)
- min_child_weight: Minimum sum of instance weights needed in a child node (optimal value: 4)
- reg_alpha: L1 regularization term (Lasso) on weights (optimal value: 0.1)
- reg_lambda: L2 regularization term (Ridge) on weights (optimal value: 1.0)
These optimal values were identified via grid search over predefined ranges (e.g., max_depth , learning_rate, etc.).
Validation: We employed TimeSeriesSplit cross-validation to assess generalization and reduce overfitting risk. Each fold produced error metrics such as RMSE and MAE; the best hyperparameter set was chosen based on mean validation performance.
4.5.2. Time-Series Forecasting with Prophet
Prophet decomposes time data series into trend, seasonality, and holiday effects:
where models trend, accounts for seasonality, handles holiday or event effects, and is an error term.
Key Prophet hyperparameters and their optimized values used in this study include the following:
- changepoint_prior_scale: Controls the flexibility of the trend component (optimal value: 0.0005);
- seasonality_prior_scale: Manages the flexibility of seasonal variations (optimal value: 15);
- holidays_prior_scale: Adjusts the strength of holiday effects (optimal value: 10);
- seasonality_mode: Determines whether seasonality is modeled as additive or multiplicative (optimal mode: multiplicative);
- daily_seasonality: Enables capture of daily seasonal patterns (set to True);
- weekly_seasonality: Enables capture of weekly seasonal patterns (set to True);
- yearly_seasonality: Enables capture of yearly seasonal patterns (set to True);
- n_changepoints: Specifies the number of potential change points in the model (optimal value: 25).
These hyperparameters were determined through systematic tuning and validation procedures to enhance forecasting accuracy.
Validation: We used walk-forward validation to preserve temporal ordering and avoid data leakage. For each training window, Prophet was fitted, and forecasts were generated for the subsequent validation period. The process was repeated until all folds were evaluated.
4.5.3. Ensemble Learning with Random Forest
Random Forest aggregates multiple decision trees, each trained on a bootstrapped sample of the data. The ensemble prediction is typically the mean of individual tree outputs:
where is the prediction of the b-th tree in the forest.
Main hyperparameters used in the Random Forest model include the following:
- n_estimators: Number of trees in the forest (optimal value: 500);
- max_depth: Maximum depth of each tree (optimal value: 15);
- max_features: Number of features considered when splitting a node (optimal value: sqrt, meaning square root of total features);
- min_samples_leaf: Minimum number of samples required in a leaf node (optimal value: 5);
- random_state: Ensures reproducibility of the results (set to 42).
These hyperparameters were identified and optimized via grid search, balancing predictive performance and computational efficiency.
Validation: We, again, employed TimeSeriesSplit cross-validation to average out the performance across multiple folds, mitigating variance due to any single data split.
4.5.4. Gradient Boosting with CatBoost
This framework is designed to natively handle categorical features, reducing the need for manual encoding. It shares the general gradient-boosting objective:
where is the loss (e.g., mean squared error) and penalizes model complexity.
The optimized hyperparameters employed for CatBoost are the following:
- iterations: Number of boosting iterations (optimal value: 1000);
- learning_rate: Shrinkage parameter controlling step size (optimal value: 0.0057);
- depth: Maximum depth of each tree (optimal value: 4);
- subsample: Fraction of data instances used for fitting of each tree (optimal value: 0.8774);
- l2_leaf_reg: L2 regularization coefficient (optimized through tuning);
- random_seed: Ensures reproducibility of results (set to 42);
- loss_function: Objective function optimized during training (RMSE).
These parameters were identified through a systematic grid search and validation.
Validation: We employed TimeSeriesSplit cross-validation, ensuring consistency with other tree-based methods. Each fold’s performance was evaluated using metrics such as RMSE, and MAE, and hyperparameters were selected based on optimal average validation performance.
4.5.5. Deep Learning Forecasting with Darts
Darts [32] is an open-source library that unifies various forecasting models, including classical statistical approaches (e.g., ARIMA) and deep learning architectures (e.g., RNNs (Recurrent Neural Networks) and CNNs (Convolutional Neural Networks)). It enables straightforward comparison of multiple models on the same dataset.
Implementation Details: We experimented with several pre-built models (e.g., ARIMA, ExponentialSmoothing, and RNNModel within Darts) to gauge performance under different assumptions. Hyperparameter tuning was applied individually for each model via grid search or built-in Darts utilities.
Validation: Consistent with time-series practice, we used walk-forward validation for each model to avoid temporal leakage. Models were retrained on each new fold, and forecast accuracy was recorded for a holdout period.
4.5.6. Time-Series Forecasting with LSTM
An LSTM-based model was implemented to capture long-term temporal dependencies in CO data. LSTM networks use memory cells and gating mechanisms (forget, input, and output) to propagate information across time steps, defined as follows:
where
- is the forget gate, deciding what information should be removed from the previous cell state;
- is the input gate, determining what new information should be added to the cell state;
- represents the candidate values to update the cell state;
- is the updated cell state, combining old and new information;
- is the output gate, controlling the information output from the cell state;
- is the hidden state (cell output) at the current time step;
- denotes the sigmoid activation function;
- tanh denotes the hyperbolic tangent activation function;
- , , , and are the weight matrices for each respective gate;
- , , , and are the biases for each respective gate;
- is the input vector at time step t;
- and are the hidden state and cell state, respectively, from the previous time step; and
- ⊙ denotes the element-wise (Hadamard) product.
Preprocessing and Windowing: Data were scaled to via min–max normalization. We then reshaped the series into overlapping windows with a length of 24 h, feeding sequences of 24 data points to predict the next time step.
Model Architecture and Hyperparameters: We stacked two LSTM layers with 80 and 50 units, respectively, followed by a dense layer with ReLU activation. L1–L2 regularization was applied with and to reduce overfitting. The network was trained via the Adam optimizer (learning rate = 0.001) for 40 epochs, with a batch size of 64.
Validation: Walk-forward validation was employed to align with time-series best practices, training on an expanding window and testing on the next step. Performance was measured via RMSE, MAE, and .
This mixture of traditional statistical, machine learning, and deep learning models ensures comprehensive exploration of predictive performance and addresses various aspects of data complexity, from seasonal fluctuations to long-term dependencies. The chosen model and hyperparameter configurations were ultimately selected based on combined statistical accuracy and alignment with domain objectives.
4.6. Spatiotemporal Analysis
To analyze the spatial distribution of CO concentrations and their relationship to meteorological factors, the following spatiotemporal analysis techniques were employed:
- Delaunay Triangulation and Visualization: Delaunay triangulation was applied to spatially interpolate CO concentrations across the study area using data from ten monitoring stations. This interpolation technique was selected due to its effectiveness in handling irregular sensor spacing and its ability to minimize interpolation artifacts. The computational implementation was performed using the scipy.spatial.Delaunay function in Python, which generated a triangulated mesh visualized as a heat map. This visualization approach facilitated the analysis of spatial patterns and concentration gradients.Delaunay triangulation was chosen over alternative interpolation methods, including inverse distance weighting (IDW) and kriging, because it better accommodates irregularly distributed sensors and minimizes computational complexity. Although boundary effects and elongated triangles occasionally appeared near the edges of the study area, careful evaluation confirmed that these minor issues did not significantly affect the accuracy or interpretation of the spatial analysis.
- Integration with Meteorological Data: Wind vectors, representing hourly wind speed and direction, were overlaid on the CO concentration heat maps. This integration was performed to allow for a visual assessment of the relationship between wind patterns and pollution dispersion.
- Spatial Clustering and Sensor Grouping: Sensors were grouped based on spatial location and proximity to industrial and residential zones, as detailed in Section 4.1. This categorization was informed by local zoning data and land use maps. Residential zones were further subdivided into Upper, Mid, and Lower categories along a north–south axis, reflecting their distance from the primary industrial area and each other (with a separation of less than 5 km). Industrial zones were categorized as Close (within 8 km of the industrial zone’s center) or Far (beyond 8 km) to allow for analysis of the influence of proximity to pollution sources.
- Hotspot Identification: A hotspot identification procedure was implemented using the interpolated CO values from the Delaunay triangulation. Areas were classified as potential hotspots if the interpolated CO concentration exceeded the 95th percentile of all interpolated CO values for at least three consecutive hours. This temporal persistence criterion was included to minimize the influence of short-term fluctuations and identify sustained periods of elevated CO.Using the 95th percentile threshold effectively identified persistent high CO emission events. Alternative thresholds (e.g., 90th or 98th percentiles) could also be effective. However, the 95th percentile balanced identifying significant pollution events and excluding short-term variations. Future studies should explore how varying this threshold affects hotspot characterization.
We began our methodological journey by exploring historical CO data. We used statistics and visualizations to understand past CO levels and examined how temperature, wind speed, and wind direction related to CO. This exploration revealed key temporal patterns, such as seasonal changes in CO concentrations and the influence of wind direction on pollution over time. We then analyzed the spatial dimension of pollution to identify areas with the highest CO concentrations. We applied Delaunay triangulation to generate CO concentration heat maps from our sensor data. To see how weather affected these patterns, we overlaid wind direction and speed onto the heat maps, which helped us observe how wind dispersed pollutants. To better analyze local effects, we grouped sensors based on their location in industrial or residential zones, further dividing residential areas by their position north or south of the industrial zone. This grouping allowed us to compare pollution exposure across regions. We also used the spatial maps to detect persistent pollution hotspots, areas with high CO levels lasting several hours. These time and space insights were essential. We used them to engineer new features for our predictive models, capturing seasonal trends, temperature effects, and wind patterns. Finally, we applied time-series forecasting and machine learning techniques, using all this knowledge to predict future CO concentrations accurately.
5. Results
This section presents the key findings from the descriptive and predictive analyses. First, the results of the exploratory data analysis are detailed, highlighting patterns in historical CO concentrations and their relationship with meteorological factors. Subsequently, the performance of the predictive models developed using engineered features is evaluated.
5.1. Preprocessing Data
We began by examining the raw meteorological data, including temperature, wind speed, wind direction, and CO concentration. During this process, we identified data quality issues, such as physically implausible values and missing data caused by sensor malfunctions or communication errors. For example, sensor S2 recorded a temperature of 100 °C, which is not physically plausible (Figure 4a,b). We found that missing values accounted for 2.42% of temperature readings, 3.11% of wind speed data, 2.91% of wind direction data, and 2.85% of CO concentration data, all of which were below our predefined 4% threshold. We describe our detailed methods for handling missing values and outliers in [5].
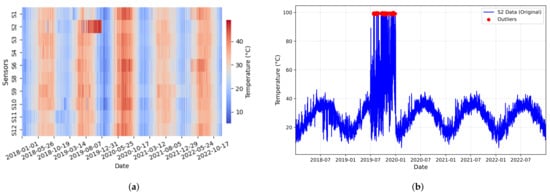
Figure 4.
Temperature outliers in sensor S2 (2018–2022) data. (a) Raw temperature readings with erroneous measurements above 52 °C in 2019; (b) the annual trend with a significant outlier at 100 °C.
We used time-series plots to confirm that we had eliminated anomalies caused by unit inconsistencies and duplicate records. Figure 5 shows the result for the year 2020, and Figure 6 shows the effects of outlier handling across the full 5-year period (2018–2023). We applied anomaly detection methods to identify outliers and removed them carefully to preserve the original data distribution.
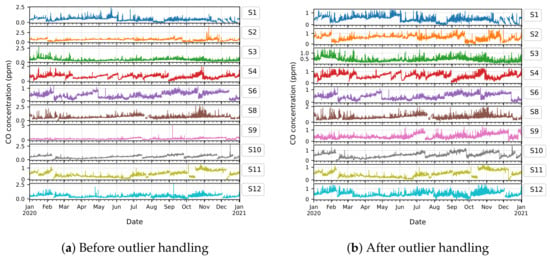
Figure 5.
Time-series plots of CO concentrations across all ten sensors in Jubail Industrial City. (a) Before outlier removal; (b) after outlier handling. The plots show the period from January 2020 to December 2020, illustrating the removal of erroneous high values and the resulting improvement in data consistency. Note the clarity of the pattern after deleting the outlier in (b).
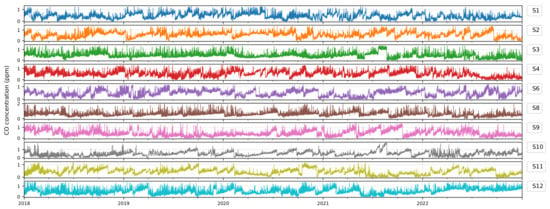
Figure 6.
Time-series plots of CO concentrations across all ten sensors in Jubail Industrial City after outlier handling. The plots show the period from January 2018 to December 2022, illustrating the removal of erroneous high values and the resulting improvement in data consistency.
Figure 7 highlights these outliers with red markers in the CO measurements from sensor 10. We completed these preprocessing steps, including imputing missing values and managing outliers rigorously, to improve the dataset’s accuracy and reliability, making it suitable for further analysis, such as descriptive analytics and predictive modeling.
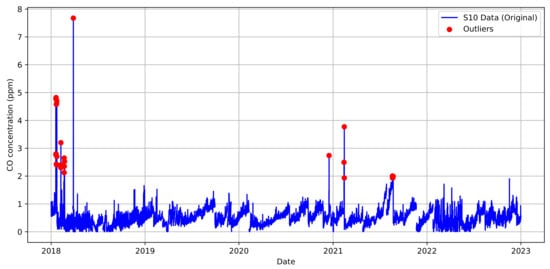
Figure 7.
Outlier and anomaly detection for CO in the sensor 10 dataset (2018-2022).
We observed a pronounced diurnal cycle in CO concentrations. Figure 8 illustrates this pattern. CO levels tend to rise in the early morning, peaking around 6 a.m.–8 a.m.This increase likely results from morning traffic and industrial start-ups. Levels then decline around mid-day. In the late evening, after about 8 p.m., concentrations rise again. This pattern suggests renewed emission sources or reduced atmospheric dispersion overnight. Figure 9 shows moderate variability in CO levels across the week. We noticed slightly higher average concentrations on weekdays, especially from Monday through Wednesday. In contrast, weekends showed lower values. These patterns likely reflect changes in traffic volume and industrial activity. Sensor S8 consistently recorded the highest CO levels. Other sensors, such as S11, reported lower concentrations overall.
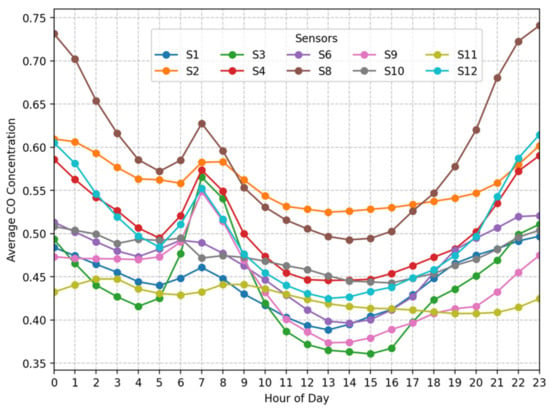
Figure 8.
Time-series plots of average CO concentrations (ppm) for all sensors by hour of the day.
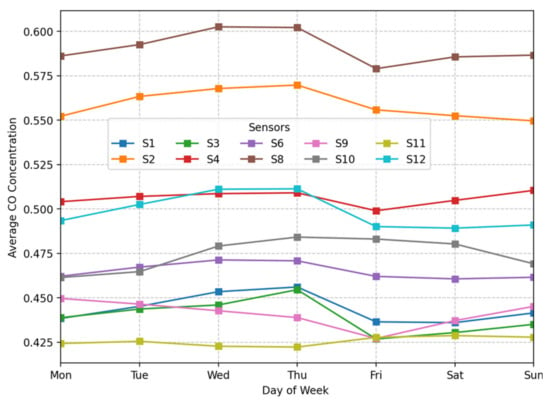
Figure 9.
Time-series plots of average CO concentrations (ppm) for all sensors by day of the week.
5.2. Descriptive Analysis
In this section, we present the results of the descriptive analysis of CO concentration, temperature, wind speed, and wind direction data collected from the ten monitoring stations. We focus on characterizing the distributions, identifying key trends and patterns, and examining the relationships between these variables. We show the results both before and after handling outliers to highlight the impact of this preprocessing step. This descriptive analysis provides the foundation for the predictive modeling that follows.
5.2.1. CO Concentrations
We present summary statistics for CO concentrations before and after outlier treatment in Table 4 and Table 5, respectively. Figure 10 visualizes the distributions of CO concentrations after removing outliers.

Table 4.
Statistical summary of CO concentrations before outlier treatment (ppm).

Table 5.
Statistical summary of CO concentrations after outlier treatment (ppm).
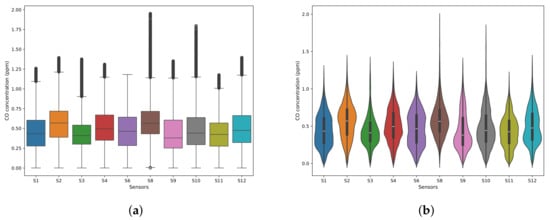
Figure 10.
Distribution of CO concentrations (ppm) across all ten sensors after outlier handling. The box plots (a) show the interquartile range and outliers, while the violin plots (b) show the density distribution.
Before treating outliers (Table 4), we found that the mean CO concentrations across the ten sensors ranged from 0.422 ppm at S11 to 0.584 ppm at S8. S8 had the highest average, likely due to its location within the industrial zone (see Figure 1). We observed a right-skewed distribution overall. In many locations, the maximum values were much higher than the 95th percentile. For example, at S10, the maximum reached 7.675 ppm, while the 95th percentile was only 0.914 ppm. This pattern indicates infrequent but extreme CO concentration events, possibly caused by specific industrial releases or weather conditions.
After we removed the outliers (Table 5), the maximum values dropped significantly. This brought them closer to the general distribution of the data. We also observed a slight decrease in standard deviations at most locations, suggesting fewer extreme values. Figure 10a shows box plots that visualize the interquartile range and any remaining outliers. Figure 10b displays violin plots that represent the density distribution of CO concentrations after outlier handling. These plots highlight the central tendencies and spread of the cleaned data.
5.2.2. Temperature
We present summary statistics for temperature before and after outlier treatment in Table 6 and Table 7, respectively. Before removing outliers (Table 6), we observed that mean temperatures across the ten sensors ranged from 26.7 °C at S11 to 29.6 °C at S2. Sensor S2 recorded a maximum temperature of 100 °C. This extreme value was a clear outlier, most likely caused by a sensor malfunction. After outlier handling (Table 7), the maximum temperature at S2 dropped to 49.0 °C. This adjustment brought the reading in line with values from other sensors. It also significantly reduced the standard deviation at that location. The mean temperatures across all sensors showed only small differences. This pattern suggests that temperature remained relatively uniform across the study area. Any localized variations likely stemmed from microclimatic conditions or differences in sensor placement.

Table 6.
Statistical summary of temperature before outlier treatment (°C).

Table 7.
Statistical summary of temperature after outlier treatment (°C).
5.2.3. Wind Speed
We present summary statistics for wind speed before and after outlier treatment in Table 8 and Table 9, respectively. Before handling outliers (Table 8), we observed that mean wind speeds ranged from 1.7 m/s at S3 to 5.4 m/s at S6. This range shows considerable variation in wind conditions across the monitoring network. Several sensors recorded high maximum wind speeds, such as 19.7 m/s at S6 and 17.5 m/s at S4. These values suggest the presence of strong wind gusts. After outlier treatment (Table 9), we found that the overall distributions, as well as the maximum and minimum values, did not change much. This stability occurred because we imputed the data based on each sensor. Figure 11a,b show box plots and violin plots of the wind speed data after outlier handling. These visualizations highlight the interquartile ranges, any remaining outliers, and the overall density distributions.

Table 8.
Statistical summary of wind speed before outlier treatment (m/s).

Table 9.
Statistical summary of wind speed after outlier treatment (m/s).
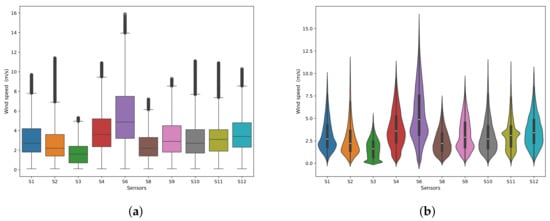
Figure 11.
Distribution of wind speed (m/s) across all ten sensors after outlier handling. The box plots (a) show the interquartile, while the violin plots (b) show the density distribution.
5.2.4. Wind Direction
Figure 12 shows wind rose diagrams for sensor S8 (Figure 12a) and sensor S9 (Figure 12b). These diagrams illustrate the distribution of wind direction and speed. Figure 13a displays a heat map that represents the frequency of wind directions across all sensors combined. The wind roses and the combined heat map reveal that the prevailing wind direction in Jubail Industrial City comes from the northwest (NW). The wind roses also indicate that the highest wind speeds usually occur with NW winds. This pattern suggests that NW winds strongly influence how pollutants disperse and move in the area. Sensor S9 shows a slightly different pattern than the average wind direction in Figure 13b. It has a more noticeable wind component from the southwest. This variation may affect local CO concentrations near that sensor.
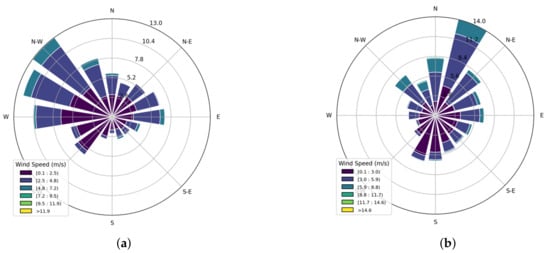
Figure 12.
Wind rose diagrams showing wind direction and speed (m/s). (a) Sensor S8; (b) sensor S9.
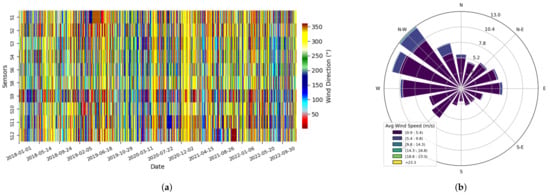
Figure 13.
The wind rose diagram shows that NW is the most frequent wind direction with the highest speed. (a) Heat map showing the frequency distribution of wind directions across all sensors. Sensor S9 shows different behavior than other sensors. (b) Wind rose diagram showing wind direction and speed (ppm) (average of all sensors).
5.2.5. Correlation Analysis
Figure 14 shows correlation matrices for temperature, CO concentrations, wind speed, and wind direction across all sensors (S1–S10). Each heat map presents pairwise Pearson correlation coefficients. Darker blue indicates stronger positive correlations. Darker red indicates stronger negative correlations. Lighter colors reflect weaker correlations.
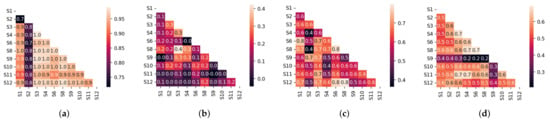
Figure 14.
Correlation matrices for (a) temperature, (b) CO concentrations, (c) wind speed, and (d) wind direction across all sensors (S1–S12). Each heat map illustrates pairwise Pearson correlation coefficients. Darker blue indicates stronger positive correlation, darker red indicates stronger negative correlation, and lighter colors indicate weaker correlation.
Temperature (Figure 14a)
We observed a strong average correlation of 0.92 for temperature across sensors. This indicates that temperature fluctuations remain consistent across the study area. However, sensor S2 shows weaker correlations, ranging from 0.72 to 0.80. This finding aligns with the earlier sensor issues and outlier treatment we discussed. It suggests that S2 may not represent broader regional temperature patterns well.
CO Concentrations (Figure 14b)
We found a much lower average correlation of 0.14 for CO concentrations. This very weak correlation shows that CO levels vary significantly across locations. Local CO sources, such as traffic and industrial activity, likely explain this variation. Local ventilation and dispersion differences may also play a role.
Wind Speed (Figure 14c)
The average wind speed correlation across sensors is 0.61, showing a moderate positive relationship. Wind speeds appear somewhat consistent regionally. However, local factors, such as topography, sensor height, and sheltering, likely cause the observed differences.
Wind Direction (Figure 14d)
We observed an average wind direction correlation of 0.53 across sensors. This moderate correlation suggests that large-scale weather patterns shape wind direction. Still, local terrain and urban structures introduce noticeable variation over short distances.
5.2.6. Time-Series Decomposition
We performed STL decomposition on data from all 10 sensors, each measuring different environmental parameters. To keep the explanation clear and concise, we present detailed results for two representative sensors: sensor S2 (temperature) and sensor S8 (CO concentration). These examples highlight key features, such as seasonal patterns, trends, and residual anomalies, found across the dataset.
Figure 15 shows the STL decomposition of temperature readings from sensor S2 between 2018 and 2022. The observed time series (top panel) reveals a clear seasonal cycle. Temperatures rise in the summer and fall in the winter. The trend component (second panel) displays a smooth, cyclical pattern over time. However, we observed a noticeable disruption in 2019. This aligns with a period of sensor error and data imputation. The seasonal component (third panel) remains stable, showing an annual amplitude of about 20 °C from peak to peak. The residual component (bottom panel) is relatively small. Still, some fluctuations around 2019 suggest that imputation did not fully capture the true temperature behavior.
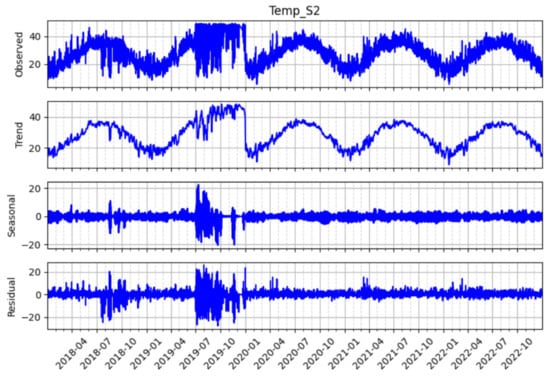
Figure 15.
STL decomposition of temperature readings at sensor S2, showing the original time series (Temp_S2), trend, seasonal, and residual components.
Figure 16 shows the STL decomposition for CO concentrations at sensor S8. The observed series (top panel) ranges from 0.1 ppm to 2.0 ppm and shows significant variation. The trend component (second panel) follows a loose two-year cycle but does not indicate a strong overall increase or decrease. We also observed a dip around 2020. The seasonal component (third panel) shows a consistent yearly cycle. CO concentrations typically peak by about 0.5 ppm during the winter months (December–February). The residual component (bottom panel) stays small, suggesting that the STL model captures most systematic variation. However, we saw larger residuals in early 2019, which may reflect anomalies or unmodeled events.
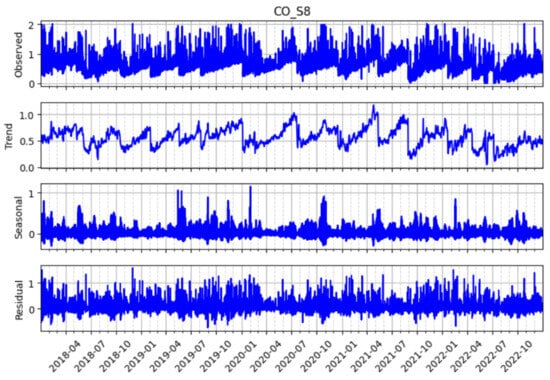
Figure 16.
STL decomposition of carbon monoxide (CO) readings at sensor S8 which, showing the original time series as well as its trend, seasonal, and residual components.
These examples from sensors S2 and S8 demonstrate how STL decomposition separates long-term trends, seasonal patterns, and residuals, even when data includes imputed values or anomalies. We observed similar patterns in the data from other sensors. Table 10 summarizes the percentage of variance explained by the seasonal component for each variable and sensor. The table shows that seasonality plays a larger role in temperature and wind patterns than in CO concentrations. For temperature, the seasonal component explains between 4.73% (S11) and 18.44% (S6) of the total variance. Wind speed shows a stronger seasonal effect, ranging from 18.26% (S11) to 47.64% (S1). Wind direction also reflects strong seasonality, with contributions ranging from 22.17% (Wind direction in sensor S11) to 44.38% (Wind direction in sensor S9). In contrast, CO concentrations show the weakest seasonal influence. The seasonal component explains only 1.80% (S11) to 12.67% (S8) of the total variance. This suggests that while CO levels have some seasonal structure, other influences, like local emissions and short-term weather conditions, contribute more to their overall variability.

Table 10.
Percentage of variance explained by the seasonal component in STL decomposition.
5.3. Feature Selection Results
Table 11 shows the top 10 features and their importance scores. We used an XGBoost model trained to predict CO concentrations at sensor S1 (CO_S1) to identify these features. The rolling mean of CO_S1 over a 3-h window (CO_S1_rolling_mean_3h) ranked as the most important feature. It had an importance score of 0.589457. The rolling median over a 3-h window (CO_S1_rolling_median_3h) followed as the second most important feature, with a score of 0.242463. The remaining features all had importance scores below 0.02. This drop indicates that the top two features carried much more predictive weight than the others. The rest included several ratio and difference features related to CO_S1, along with rolling maximum, minimum, and difference from median values.

Table 11.
Top 10 features selected by XGBoost for CO_S1 prediction.
5.4. Anomalies and Outliers
Figure 17 shows the relationship between wind direction and CO concentration at sensor 10. We used box plots categorized by season to highlight important patterns and anomalies in CO levels. Spring consistently recorded the lowest CO concentrations across almost all wind directions. Median values in spring remained well below those in winter, summer, and fall. This seasonal pattern may result from meteorological factors like increased wind dispersion or reduced industrial activity. Spring also showed a narrow interquartile range (IQR) and fewer high outliers. These characteristics suggest that CO levels during spring are both low and stable. Winter and fall displayed higher variability and elevated CO levels. This was especially true when winds came from the south, southwest, and northwest. These wind directions may align with nearby pollution sources, such as traffic or industrial areas. We also observed more outliers during these seasons, indicating frequent CO spikes. These spikes may be linked to specific environmental or human activities. Summer showed moderate CO levels. It fell between spring and winter in terms of concentration. We noted a noticeable number of outliers, particularly when winds blew from the northwest and north. These anomalies and outliers offer valuable insights into pollution dynamics. The results suggest that wind direction and seasonal variation play key roles in shaping the spread and intensity of CO pollution events.
Figure 17.
Box plot of CO concentration (ppm) versus wind direction, categorized by season, for sensor 10. Each group shows the distribution of CO levels for a specific wind direction and season.
5.5. Predictive Model Performance
Table 12 summarizes the predictive performance of six forecasting models. The evaluation is based on five key metrics: RMSE, MSE, MAE, MAPE, and . Lower values for RMSE, MSE, MAE, and MAPE indicate better predictive accuracy. A higher reflects stronger explanatory power in terms of data variance.

Table 12.
Performance comparison of forecasting models.
Among all test models, XGBoost showed the strongest overall performance. It achieved the lowest RMSE (0.0371 ppm), MSE (0.0015 ppm2), and MAE (0.0155 ppm), along with the highest value (0.9665). Despite this excellent absolute accuracy, XGBoost recorded a relatively high MAPE of 22.60%. This suggests that, while the model performs well in absolute terms, its predictions may vary more in percentage terms, especially when actual values are small.
Prophet and LSTM demonstrated excellent relative accuracy, achieving the lowest MAPE scores: 9.64% for Prophet and 9.49% for LSTM. Prophet is well-suited for modeling seasonality and trends, offering consistent predictions. However, its absolute errors were slightly higher (RMSE = 0.0392 ppm and MAE = 0.0239 ppm). LSTM also performed well in capturing temporal dependencies but showed higher absolute errors (RMSE = 0.0559 ppm and MAE = 0.0342 ppm). These results indicate that Prophet and LSTM are ideal when minimizing percentage error is more important than absolute precision.
CatBoost provided balanced performance. It reported an RMSE of 0.0394 ppm, MAE of 0.0257 ppm, and a solid of 0.9508. Across all metrics, CatBoost ranked near the top and outperformed Random Forest. Its MAPE of 19.44% suggests a moderate level of relative accuracy, making it a dependable choice when a balance between absolute and relative performance is needed.
Random Forest had the weakest performance overall. It showed the highest RMSE (0.0535 ppm), the highest MSE (0.0029 ppm2), and the lowest (0.9310). Still, its MAPE of 16.44% was moderate. This implies that, while it lacks precision in magnitude, it can still be used in situations where identifying general trends is sufficient.
The Darts (Neural Basis Expansion Analysis for Time-Series forecasting, N-BEATS) model performed similarly to LSTM in terms of absolute accuracy. It recorded an RMSE of 0.0553 ppm and an MAE of 0.0328 ppm. However, its was lower (0.9031), indicating less explanatory power. Its MAPE of 16.25% was close to that of Random Forest, reflecting moderate relative accuracy.
In summary, no single forecasting model excelled in all evaluation metrics. XGBoost is the best option for those seeking high absolute accuracy and strong variance explanation. Prophet and LSTM are better suited for applications where minimizing relative errors is critical, such as budgeting or resource allocation. CatBoost offers a reliable middle ground, delivering balanced and consistent performance across both absolute and relative measures.
5.6. Predictive Insight
The forecasting results offer meaningful insights into the behavior and structure of air quality data in the studied urban setting. The strong performance of tree-based models, especially XGBoost and CatBoost, suggests that pollutant concentrations are influenced by complex, non-linear relationships. These may include interactions between weather patterns, emission sources, and time-based features. The ability of these models to explain a large portion of the variance indicates that much of the pollution dynamics can be learned from historical trends and engineered features.
In contrast, the low percentage errors achieved by Prophet and LSTM highlight the presence of consistent seasonal and temporal patterns. This suggests that pollution levels follow predictable cycles such as daily traffic peaks or weekly industrial activity. While these models had slightly higher absolute errors, their strength in capturing recurring patterns makes them valuable for forecasting relative changes over time. These differences in model behavior reveal multiple layers of predictability within the data. High absolute accuracy shows that general pollution levels can be reliably estimated. Meanwhile, strong relative accuracy indicates that fluctuations across a range of values can also be forecasted with confidence. This distinction is important. For example, XGBoost’s consistent performance is well-suited for tasks like triggering air quality alerts when thresholds are exceeded. On the other hand, LSTM or Prophet may be better for comparing pollution trends across locations or time periods. The weaker performance of models like Random Forest and N-BEATS suggests that model success depends on how well the structure aligns with the data. Random Forest’s averaging nature may oversimplify localized variations. N-BEATS, while designed for time-series forecasting, may require more tuning or longer input sequences to fully capture hourly fluctuations in air quality.
In summary, model behavior reflects deeper patterns in the data. These patterns can guide both model selection and real-world applications. Understanding how different models interpret the same dataset helps in designing better monitoring systems; interpreting sensor outputs more clearly; and supporting timely, data-informed decisions for urban air quality management.
5.7. Spatiotemporal Analysis
To analyze the spatial distribution of CO concentrations and their relationship to meteorological factors, the following spatiotemporal analysis techniques were employed.
5.7.1. Delaunay Triangulation and Visualization
We analyzed spatial and temporal patterns in CO concentrations using Delaunay triangulation and hotspot identification. Delaunay triangulation is a geometric technique that connects nearby sensor points to form triangles in such a way that no point lies inside the circumcircle of any triangle. This results in a mesh that adapts naturally to the spatial distribution of the sensors, allowing us to interpolate values across the area more effectively. By applying this method, we were able to visualize pollutant gradients between sensors and capture how CO levels varied across different zones. This analysis not only confirmed expected spatial relationships, such as higher concentrations in industrial zones, but also uncovered unexpected patterns in the pollutant distribution that were not aligned with zoning classifications. We report findings related to interpolation accuracy, clarity of spatial visualizations, zone-specific CO averages, and hotspot locations. Together, these results both provide validation of known spatial trends and reveal new insights into air quality dynamics in the city.
In Figure 18, we show the triangulation network created to represent the spatial arrangement of sensors. We observed that the figure clearly reflects the expected proximity and structure of the monitoring stations. Most sensor connections followed anticipated spatial relationships, supporting the quality of the network design. However, we noted a few exceptions. Sensor S2 (temperature) exhibited significantly lower spatial coverage within the triangulation. This limited representation likely resulted from its location or sparse connectivity to nearby sensors, which reduced its contribution to the interpolation mesh. We also found that Sensor S9 (wind direction) displayed wind patterns that differed from surrounding sensors. While this observation is not directly visualized in the triangulation network shown in Figure 18, it raised questions about local atmospheric influences or sensor placement. We observed unique patterns in other sensors as well. Sensor S6, located in the middle of the desert, recorded stable but distinct results, possibly due to minimal interference from human activity. Sensor S11 sits offshore, near a port area. We suspect that emissions transported by ships or industrial discharge may influence its readings. Other than these specific observations, we did not observe any unusual long or short connections between sensors. This consistency confirmed that the triangulation network provided good spatial coverage and an accurate basis for further spatiotemporal analyses. Figure 19 highlights hotspots, mainly located in the central industrial area. The strongest hotspot appeared in the triangle formed by sensors S1, S8, and S9. This area aligns with known industrial emission zones. We also analyzed how CO concentrations spread outward from this hotspot. The gradients extended into nearby residential and natural areas, further supporting the hotspot definition we used in this study.
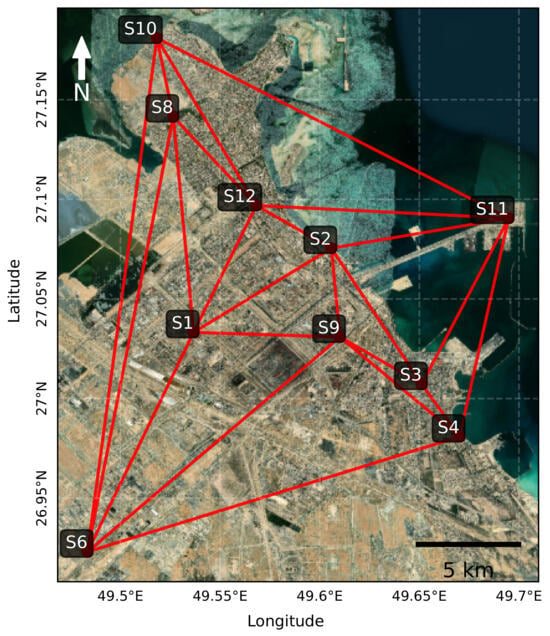
Figure 18.
Delaunay triangulation and spatial interpolation of CO monitoring stations across Jubail.
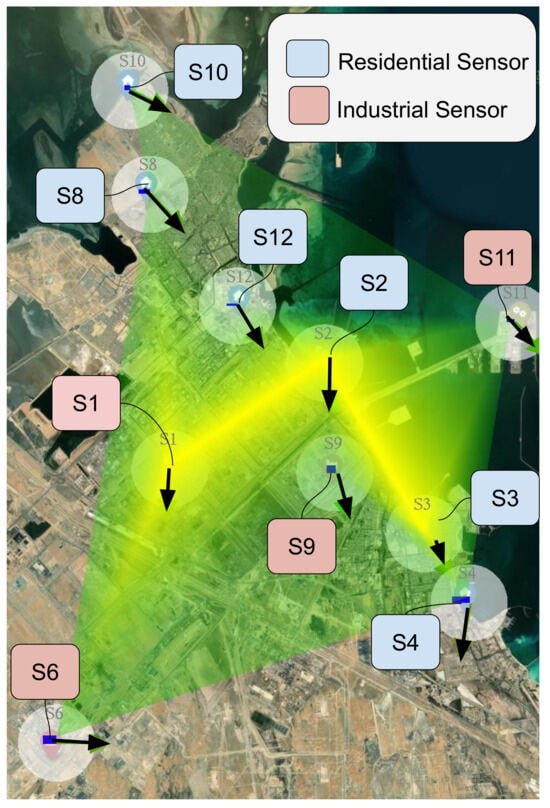
Figure 19.
Identified CO hotspots based on visualization and interpolated values exceeding the 95th percentile.
We observed that average CO levels were higher in residential zones compared to industrial zones. Specifically, upper residential areas recorded a mean concentration of 0.533 ppm, mid-residential areas recorded a mean concentration of 0.529 ppm, and lower residential areas recorded a mean concentration of 0.473 ppm. In contrast, close industrial zones showed a mean of 0.442 ppm, while far industrial zones averaged 0.445 ppm. This pattern was unexpected, given the proximity of industrial zones to known emission sources.
We also noticed a slight discrepancy within the industrial zones. The far industrial zone (sensors S6 and S11) showed slightly higher CO averages than the close industrial zone (sensors S1 and S9). This result stood out because we had anticipated closer zones to exhibit higher concentrations due to their proximity to the industrial center.
We found that hotspots identified using the 95th percentile threshold appeared frequently. These hotspots typically lasted for several consecutive hours. This persistence suggested that the elevated CO levels were due to sustained emissions rather than short-term spikes. The results provide insight into the temporal dynamics of pollution events across the monitored area.
5.7.2. Integration with Meteorological Data
In Figure 20, we show the relationship between CO concentrations at sensor S12, wind direction, and wind speed categories. The box plots reveal clear patterns. CO levels tend to decrease as wind speeds increase. We observed the highest median CO concentrations during very low wind-speed conditions. These occurred when winds came from the west (W), southwest (SW), and northwest (NW). This pattern suggests either local emission sources or reduced pollutant dispersion from these directions. In contrast, CO concentrations were lower when winds came from the east (E) and southeast (SE), especially under moderate to high wind speeds. This pattern suggests effective dispersion from those directions.
Figure 20.
CO concentrations at sensor 12 categorized by wind direction (i.e., where the wind came from) and wind speed. The box plots illustrate variations in pollutant concentrations with directional influences and wind speed intensity.
Figure 21 shows how CO concentrations at sensor 10 vary with wind speed and temperature. We consistently observed elevated CO levels during very low and low wind-speed conditions. This finding highlights the role of wind in pollutant buildup. Temperature also influenced CO concentrations. We observed higher median values during hotter periods, up to 55 °C, when wind speeds were low. We also saw elevated CO levels under colder conditions (below 15 °C), when wind speeds were very low. These results suggest that temperature affects atmospheric dispersion or reflects seasonal emission changes. Moderate to high wind speeds consistently led to lower CO concentrations across all temperature categories. This confirms that stronger winds help dilute and disperse pollutants more effectively.
Figure 21.
CO concentrations at sensor 10 categorized by wind speed and temperature conditions. The box plots highlight interactions between wind speed and temperature categories influencing local CO levels.
In summary, the analyses revealed distinct temporal and spatial patterns in CO concentrations, identified key predictive features based on recent CO history, and demonstrated varying performance across the tested forecasting models. These results provide the basis for the discussion presented in the next section.
6. Discussion
6.1. Preprocessing
This research supports decision making in smart cities by relying on accurate, consistent environmental data. The preprocessing steps, including standardization and outlier removal, are fully detailed in Section 4.1. Figure 4 and Figure 22 show how anomalies like the 100 °C reading from sensor S2 and further issues in summer 2019 were handled. These steps ensured a clean foundation for analysis. As noted in [26,40], both broad data standardization and precise anomaly detection are essential for working with real-world sensor data.
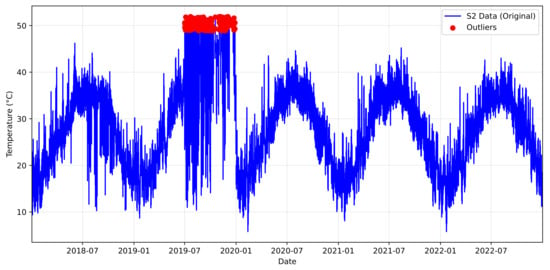
Figure 22.
Temperature readings at sensor S2 in 2019 after initial outlier removal, highlighting the remaining anomalous temperature pattern during the second half of the year.
Figure 5 and Figure 6 show the overall effectiveness of our outlier removal approach across the full study period and in 2020 specifically. Figure 7 highlights targeted CO outlier removal in sensor 10, where removed values were clearly flagged while preserving distribution patterns. These steps helped prevent erroneous data from distorting the analysis. This preprocessing strategy improved data quality by reducing bias and ensuring consistency, enabling more accurate and trustworthy analytics for smart city management. Errors at this stage risk propagating through the analysis and misleading decision makers. Still, imputation and outlier removal involve trade-offs. Imputation may smooth out short-term variations, and outlier filters might discard rare but real events. Future research could assess how sensitive the results are to these choices by testing different thresholds or using imputation methods designed to retain finer detail. In short, preprocessing strengthens both model accuracy and the decisions based on those models. A high-quality dataset is essential for meaningful visual and predictive analytics.
6.2. Descriptive Analytics
- CO Analysis
Sensor S8 recorded the highest average CO levels, likely due to traffic exposure and prevailing winds (Figure 1), consistent with previous findings near major roads [5,41]. Sensor S10 showed a right-skewed distribution, with peaks up to 7.675 ppm, possibly caused by episodic emissions or sudden weather shifts [42]. Removal of these outliers (Table 5) clarified baseline concentrations and followed standard cleaning practices [26]. Post-cleaning data (Figure 10) showed most CO levels remained under 1 ppm, but occasional spikes underline the need for real-time monitoring in areas with unstable patterns [43]. Industrial sensors (S1 and S9) had morning and evening peaks tied to operations and traffic (Figure 8), while residential sensors (S8 and S10) reflected commuter influence, likely intensified by windborne transport [44]. CO levels at southern sensors (S3 and S4) were slightly lower, suggesting dispersion over distance. Coastal sensor S11 showed wind-driven variation, and desert-based S6 recorded low baselines with occasional spikes from wind shifts or dust. Weekly trends (Figure 9) confirmed higher workday concentrations, especially near industrial zones. These findings support the need for local air quality strategies that account for emissions, wind patterns, and urban layout [45].
- Temperature Analysis
Summary statistics for temperature before and after outlier treatment appear in Table 6 and Table 7. Initially, as shown in Table 6, mean temperatures ranged from 26.7 °C (S11) to 29.6 °C (S2). Notably, sensor S2 recorded an exceptionally high maximum of 100 °C. Such a high value strongly suggests a sensor malfunction. Our previous work also identified similar anomalies that pointed toward instrument error [5]. After addressing outliers (Table 7), the maximum temperature at S2 decreased to 49.0 °C. This adjustment not only aligned S2’s measurements with those of other sensors but also reduced its standard deviation. Overall, the mean temperatures across all sensors varied only slightly. This suggests a relatively uniform temperature distribution that is mainly influenced by minor microclimatic conditions or sensor placement differences [41]. A plausible explanation for S2’s anomalously high reading is an instrument error. No other sensor recorded temperatures near 100 °C, and field observations did not indicate any heat-related damage. In addition, S2 exhibited an abrupt temperature drop in the middle of summer, pointing to possible inconsistencies in its data. Similar abrupt changes have been reported in sensor calibration studies, where they often indicate a malfunction [46]. Although S2 provided reasonable temperature values at other times of the year, the evidence strongly supports the hypothesis of a sensor malfunction. Nonetheless, localized environmental factors cannot be entirely ruled out. Further calibration or on-site investigation would be needed to confirm the exact cause of these unusual readings [5,46].
- Wind Speed Analysis
The wind speed summaries before and after outlier treatment (Table 8 and Table 9, respectively) clarify the variability in local wind conditions. Initially, as shown in Table 8, mean wind speeds ranged from 1.7 m/s at S3 to 5.4 m/s at S6. This range indicates that wind conditions differ significantly across monitoring sites. In addition, several sensors recorded high wind gusts, such as 19.7 m/s at S6 and 17.5 m/s at S4. These high values suggest that occasional strong wind events occur, which may play a key role in pollutant dispersion. Previous studies have shown that strong wind gusts can enhance the mixing of pollutants and affect their spatial distribution [44]. After outlier removal, the distributions and extreme values remained largely unchanged (Table 9). This outcome suggests that most original wind speed measurements were within expected ranges. We imputed missing data based on individual sensor characteristics, which helped preserve the natural variability of the wind speeds. In Figure 11, the box plots and violin plots reveal stable wind conditions overall, with only minor outliers remaining. Our previous work [5] supports this finding, demonstrating that careful data handling can maintain the integrity of meteorological measurements. The overall consistency in wind speed measurements is important. It helps explain how pollutants disperse and accumulate in different areas. Reliable wind data are critical for accurate dispersion modeling and air quality assessment [41].
- Wind Direction Analysis
The wind rose diagrams (Figure 12a,b) clearly show a predominance of northwest (NW) winds. This finding has important implications for understanding pollutant dispersion in the study area. In fact, previous studies have demonstrated that dominant wind directions strongly influence pollutant transport [44]. Moreover, our analysis indicates that the highest wind speeds are associated with NW winds, suggesting that these winds play a critical role in transporting pollutants. The industrial area is located to the south of Jubail Industrial City. Consequently, sensors S3 and S4, situated in residential areas to the southeast (SE), are positioned directly downwind from the industrial sources when NW winds prevail. Based solely on wind direction, one would expect these sensors to record higher CO concentrations during NW winds [41]. However, our observations tell a different story. Figure 23 shows that NW winds coincide with the lowest CO concentrations at sensor S3. The box plot in Figure 23a illustrates that both the median and interquartile ranges for CO under NW winds are lower than those under other wind directions. Similarly, the violin plot in Figure 23b confirms that high CO concentrations are less frequent during NW winds. This unexpected result suggests that a barrier or other mitigating factor may be present between the industrial source and sensor S3, reducing pollutant transport during NW conditions. In contrast, the highest CO levels at S3 occur during southwest (SW) winds, which may indicate either a different emission source or a more complex circulation pattern [47].
Figure 23.
Distribution of CO concentrations at sensor S3, grouped by wind direction. The plots show that NW winds are associated with the lowest CO concentrations, contrary to expectations based solely on wind direction and sensor location relative to the industrial area. (a) Box plot; (b) violin plot.
A similar phenomenon is observed at sensors S8 and S10. Although these sensors are located in residential areas to the northeast (NE) of the industrial zone, where lower CO concentrations might be expected during NW winds, Figure 24 reveals that the highest CO levels occur with winds from the southwest (SW), south (S), and southeast (SE) directions. Both the box plot (Figure 24a) and the violin plot (Figure 24b) support this finding. These observations challenge the simplistic view of downwind dispersion and suggest that localized emissions, complex terrain, or unaccounted wind circulation patterns influence the measured CO concentrations.
Figure 24.
Distribution of CO concentrations at sensor S8, grouped by wind direction. The plots show that the highest CO concentrations are associated with winds from the SW, S, and SE. (a) Box plot; (b) violin plot.
Overall, these findings highlight the complexity of pollutant dispersion in the study area. They emphasize that relying solely on prevailing wind directions is insufficient for accurately predicting CO levels. Further research including spatial analysis, back-trajectory modeling, detailed emission inventories, and topographical studies is needed to fully understand these dynamics [43]. Nonetheless, the consistent link between higher wind speeds and NW winds underscores the importance of incorporating detailed wind pattern analysis into air quality management strategies.
6.2.1. Correlation Analysis
Figure 14a shows clear differences in spatial coherence across variables. Temperature had the highest correlation (average 0.92), indicating regional uniformity, consistent with prior studies [5,41]. Sensor S2 showed notably lower values, likely due to calibration issues or local microclimates such as shading or heat island effects [46]. CO correlations were much lower (average of 0.14), reflecting the strong influence of local sources like traffic and industry. This aligns with previous research emphasizing the need for dense sensor networks to detect pollution hotspots [43]. Wind speed and direction had moderate correlations (0.61 and 0.53), suggesting a mix of regional weather influences and local disruptions caused by topography or urban form [44]. These patterns highlight the need for strategic sensor placement. While temperature can support broad regional analysis, pollutants like CO require site-specific monitoring. Wind variability further complicates dispersion modeling and should be integrated into management strategies [45].
6.2.2. STL Decomposition
Sensor S2 displayed a clear seasonal temperature pattern with a major disruption in 2019. During this period, it recorded unrealistically high values not seen at other sensors, suggesting sensor error [5]. In contrast, the unusually low temperatures observed in summer may reflect genuine microclimatic variation, as similar values appeared elsewhere in the dataset [41]. Residual inconsistencies remained after imputation, indicating that more advanced methods may be needed to recover accurate trends [48]. CO concentrations followed a roughly two-year cycle, possibly linked to periodic industrial or meteorological changes. Higher winter CO levels were consistent with heating emissions and stagnant air conditions [43]. However, irregular spikes in early 2019 were not well captured by the STL model, suggesting the presence of outlier events beyond standard seasonality. STL decomposition was effective in separating seasonal and trend components for both variables [48]. Still, its accuracy depends heavily on input quality. The residual patterns during periods with imputed or anomalous data underline the need for rigorous preprocessing to support reliable time-series analysis.
6.3. Feature Selection
Table 11 shows that short-term temporal features dominate CO prediction at sensor S1. The 3-h rolling mean and median received importance scores of 0.59 and 0.24, respectively, confirming a strong autocorrelative structure [5,35]. Scores for remaining features dropped below 0.02. Some ratio and difference metrics related to CO at sensor S1 still appear among the top ten, suggesting that the rate of change adds predictive value, though less than the raw rolling statistics. This pattern underscores the site-specific nature of CO variation at S1. Adding meteorological or spatial features may improve the model and clarify whether similar patterns apply at other locations [43].
6.4. Predictive Analysis
The comparative evaluation of forecasting models highlights important trade-offs between absolute accuracy, relative error, and model complexity. XGBoost emerged as the most effective model in terms of absolute error metrics, achieving the lowest RMSE, MSE, and MAE and the highest (0.9665). These results reflect its strong capability in capturing complex, non-linear relationships and high-order interactions across meteorological and pollutant data. The model’s gradient-boosted architecture, combined with regularization and efficient handling of missing values, likely contributed to its robustness and high explanatory power.
This makes XGBoost especially suitable for applications that prioritize minimizing absolute error, such as operational planning or environmental risk mitigation, where even small deviations in predicted pollutant levels could lead to meaningful outcomes in cost savings or public health protection. However, its relatively high MAPE (22.60%) suggests that its percentage-based errors are larger when actual values are small. This limits its effectiveness in scenarios where proportional accuracy is critical, such as comparative analysis across locations or pollutants with varying scales. In contrast, Prophet and LSTM achieved the lowest MAPE values (9.64% and 9.49%, respectively), indicating strong performance in relative accuracy. Prophet’s strength lies in its ability to model trend and seasonality components, which is especially useful for cyclical patterns in air quality data. LSTM, designed to capture temporal dependencies through its memory-based architecture, also performed well in this regard. However, both models showed higher absolute errors, suggesting occasional larger deviations from true values, particularly when pollutant levels are high. This trade-off implies that Prophet and LSTM are preferable when forecasting applications require reliable percentage predictions, even if the exact magnitudes are slightly off.
The Darts (N-BEATS) model yielded comparable results to LSTM in terms of absolute accuracy but showed a lower value (0.9031), indicating reduced ability to explain overall variance. Its MAPE (16.25%) positioned it between the tree-based and sequence-based models, suggesting moderate performance in both absolute and relative terms. Given its architectural design for long-term forecasting, N-BEATS may require further tuning or longer historical sequences to realize its full potential in hourly air quality prediction.
CatBoost offered a balanced outcome across metrics. With an RMSE of 0.0394, MAE of 0.0257, and , it consistently ranked near the top. Its MAPE (19.44%) was lower than that of XGBoost but higher than that of Prophet and LSTM. These results make CatBoost a reliable all-rounder when forecasting scenarios demand a trade-off between absolute accuracy and relative consistency.
Random Forest showed the weakest performance in both absolute error and variance explanation. It recorded the highest RMSE (0.0535) and lowest (0.9310). Nonetheless, its MAPE (16.44%) suggests that it still delivers acceptable results in terms of proportional accuracy. This indicates potential value in simpler or less-critical forecasting scenarios, especially where computational simplicity or interpretability is favored.
These findings are drawn from a specific urban location using a fixed set of sensors, a five-year time window, and a consistent data preprocessing pipeline. As such, model performance may vary under different conditions, including other pollutant types, cities with different topographies, or alternative seasonal cycles. LSTM’s underperformance in absolute terms, for example, could be attributed to the relatively short training sequences or hourly data granularity. Likewise, Prophet’s additive structure may have limited its ability to model abrupt fluctuations, despite its success in identifying seasonal trends. The high absolute accuracy achieved by XGBoost suggests it is particularly valuable for short-term pollutant forecasting to support operational decisions, such as issuing health advisories or dynamically adjusting transportation infrastructure. Meanwhile, models like Prophet and LSTM, with their strong relative performance, are better suited for cross-site evaluations, longitudinal comparisons, or forecasting pollutants with varying baseline concentrations. CatBoost and Random Forest occupy a middle ground. CatBoost, in particular, provides competitive accuracy without the higher computational costs of deep learning models. Its consistent performance across metrics makes it an attractive option for applications where both types of accuracy—absolute and relative—are important but not critical.
In summary, model selection should align with the specific objectives of the forecasting task. XGBoost is recommended for scenarios demanding precise, magnitude-based predictions. Prophet and LSTM are better suited for percentage-based evaluations across varying data scales. CatBoost offers a dependable compromise when priorities are mixed. While Random Forest lags in performance, it remains useful for baseline comparisons or scenarios with limited computational resources.
6.5. Delaunay Triangulation and Visualization
This discussion interprets key outcomes of the CO interpolation and hotspot analysis. The objective is to understand both expected and unexpected patterns and to evaluate methodological decisions, including the choice of interpolation methods, sensor grouping, and hotspot thresholds. These factors shaped the observed trends and revealed areas that warrant further investigation. As highlighted in earlier sections, future studies should integrate meteorological, environmental, and activity-based data to improve interpretability [5,41]. A notable unexpected result was that residential zones showed higher average CO levels than industrial areas. This may be due to localized emissions from traffic and domestic heating or wind-driven transport from nearby industrial zones. Sensor altitude and the built environment may also affect readings. Similar counterintuitive patterns have been reported in previous urban air quality studies [41,43]. In the analysis of the industrial zone, sensors S6 and S9 (far industrial) had higher CO levels than sensors S1 and S9 (close industrial). This likely reflects a grouping issue, as sensor S9 appears in both categories. Overlapping classifications make direct comparisons difficult and underscore the need for clearly defined, non-overlapping sensor groupings [5].
6.6. Integration with Meteorological Data
Figure 20 and Figure 21 support the link between meteorological factors and CO distribution. CO levels were higher during periods of low wind speeds, consistent with pollutant accumulation under stagnant conditions [41,44]. Elevated concentrations under western and northwestern winds suggest nearby upwind emission sources, pointing to the need for targeted analysis of land use and emissions in those directions [43]. At sensor 10, temperature effects showed two distinct behaviors. Higher CO levels during warm periods may reflect increased industrial and traffic activity [5], while colder periods may see elevated CO due to reduced atmospheric mixing or domestic heating. This pattern highlights the complex interaction between emissions and meteorology, reinforcing the importance of detailed weather integration in air quality analysis [41].
6.7. Connecting Historical and Predictive Analytics
Integrating descriptive and predictive analytics created a strong foundation for effective decision making in urban environments. Through descriptive analytics, we identified historical patterns, meteorological influences, spatial variability, and critical data quality issues. These insights directly informed our predictive modeling strategy. For example, recognizing the strong autocorrelation in CO concentrations led us to include rolling mean and median features in our models, which significantly improved predictive accuracy [5,35]. Observations from our descriptive analysis, such as the low spatial correlation of CO levels, indicated that localized factors strongly influence pollutant concentrations. This knowledge guided us to focus on site-specific features rather than general regional trends [41]. In addition, the complex interactions observed between meteorological conditions and CO concentrations underscored the need to include weather-related variables in the model. These insights helped explain why rolling statistics emerged as dominant predictors, with the recent past consistently providing the strongest signals for current CO levels. Recent advances in integrated urban air quality analytics further support our approach. For instance, studies have shown that combining descriptive and predictive analytics can enhance the understanding of pollutant dynamics and improve model performance [49]. Performing a detailed descriptive and spatiotemporal analysis before predictive modeling provided multiple benefits. It allowed us to carefully choose relevant features and select models suited to the identified data characteristics. This comprehensive approach not only enabled more accurate predictions but also highlighted specific challenges, such as the handling of data anomalies and localized variations [43]. Moreover, the iterative feedback between descriptive and predictive analytics ensured continuous improvement and model adaptability. Ultimately, this integration supports urban planners in implementing timely and targeted strategies. Such strategies include managing industrial activities, initiating pollution control measures, and issuing timely public advisories, thereby enhancing urban environmental management [45].
6.8. Implications
6.8.1. Implications for Decision Making
The seasonal patterns identified in Figure 17 highlight the importance of considering temporal context in air pollution analysis. We observed consistently low CO levels during spring across all wind directions. This pattern likely results from favorable dispersion conditions. For instance, stronger and more consistent winds during spring, combined with reduced emissions, promote pollutant dilution. Such seasonal dispersion characteristics have been noted in previous studies [41]. In contrast, frequent high-CO outliers in winter and fall suggest that pollutants tend to accumulate during periods of stagnant atmospheric conditions. Temperature inversions and reduced wind activity during these seasons can trap emissions near the ground. Notably, these high-CO events were especially prominent when winds came from the southwest and northwest. This observation indicates potential upwind pollution sources, supporting the idea that seasonal wind patterns interact closely with emission sources to shape local air quality [43]. Our results offer several practical implications for urban planners, environmental agencies, industrial managers, and public health officials in Jubail Industrial City. For air quality management, authorities could consider targeted emission controls during seasons or wind conditions known to exacerbate pollution. Urban planners might use these insights when designing zoning strategies, such as locating residential or sensitive facilities away from known hotspots and prevailing wind pathways. Public health officials could benefit by issuing timely advisories when forecasted conditions predict elevated pollutant concentrations [45]. Furthermore, our predictive models hold significant operational potential. By accurately forecasting high-concentration events, these models enable proactive mitigation measures and effective resource allocation. Continued refinement and validation of these predictive tools will further enhance their reliability and practical utility in maintaining urban air quality and protecting public health.
6.8.2. Implications for Smart Cities
The findings from this study have significant implications for air quality management and smart city initiatives in Jubail Industrial City. For example, the low spatial correlation of CO concentrations highlights the importance of maintaining a dense sensor network. A detailed network can accurately assess public exposure and identify localized pollution hotspots [41,43]. Moreover, the unexpected relationship between wind direction and CO levels at certain sensors underscores the complexity of urban air quality. This finding reveals the limitations of relying solely on simple dispersion models [44]. Our detailed spatiotemporal analysis supports data-driven environmental governance by enabling precise targeting of pollution control measures and efficient resource allocation [5,45].
The predictive models developed in this study can be seamlessly integrated into smart city platforms. These models could provide real-time air quality forecasts and timely alerts, benefiting both citizens and city managers. For instance, forecast information may trigger dynamic traffic management measures that reduce pollutant emissions during peak events [49]. Furthermore, this analysis demonstrates the value of sensor network infrastructure as a key Internet of Things (IoT) component for environmental monitoring in smart cities. Sensor data reveal complex interactions between meteorological conditions, emission sources, and pollutant distribution. Such insights can optimize the positioning of mobile monitoring units, enhance targeted interventions, and guide urban planning decisions [11,45].
Finally, our research suggests that integrating air quality data with other smart city data streams, such as traffic flow or energy consumption, could yield deeper insights. This comprehensive integration would enable more effective and comprehensive environmental strategies, ultimately contributing to Jubail’s environmental management, operational efficiency, and citizen well-being [10].
6.9. Future Directions
Future research should extend sensor coverage to improve spatial resolution and fill gaps in under-represented areas. Incorporating detailed emissions data, such as industrial activity, traffic volume, and port operations, will support more accurate attribution of observed CO patterns [43]. Enhancing calibration and maintenance procedures can reduce measurement uncertainty and improve overall data reliability [46].
Further analysis of temporal patterns at individual sensors and hotspots could reveal daily or seasonal emission cycles linked to industrial or traffic behavior [5,41]. Sensor-specific anomalies, including irregular temperature readings at sensor S2 and zone classification inconsistencies at sensor S9, should be addressed to improve data quality and consistency.
Additional variables should be integrated to strengthen environmental interpretations. Correlating CO levels with wind speed, wind direction, temperature, and humidity will clarify how meteorological conditions influence pollutant concentrations [44]. Including vertical profiles of meteorological and pollutant data would improve the analysis of atmospheric mixing and dispersion dynamics [35].
Expanding the pollutant scope beyond CO to include NOx, PM2.5, and ozone will offer a more comprehensive view of air quality and allow for the exploration of compound effects [45]. Studying pollutant interactions under varying environmental and operational conditions can reveal patterns not captured by single-pollutant analysis.
Future work should also refine data preprocessing strategies. Sensitivity analyses on hotspot thresholds, imputation methods, and outlier handling can test the robustness of findings. Adopting more advanced imputation techniques may help preserve short-term variability while reducing bias.
From a modeling perspective, future studies should explore algorithms that better capture spatiotemporal dependencies and non-linear relationships. Deep learning architectures such as N-BEATS and the Temporal Fusion Transformer may enhance long-term forecasting performance and feature representation. Integrating smart city datasets, including energy use, transport patterns, or public health indicators, can help generate insights that support broader urban decision making.
Extending model validation across different cities, pollutants, and time frames will also be important. This will help ensure generalizability and strengthen the case for deploying predictive models in varied urban environments. Together, these future directions can enhance environmental data analytics and support more effective planning, pollution mitigation, and public health protection for cities like Jubail.
7. Conclusions
This study investigated carbon monoxide (CO) pollution dynamics in Jubail Industrial City. We aimed to understand spatiotemporal patterns and develop predictive models using five years of environmental monitoring data (2018–2022).
We identified clear diurnal and weekly patterns in CO concentrations. These patterns were strongly influenced by meteorological conditions. Low wind speeds consistently led to higher CO levels. CO showed significant spatial variability, with low inter-sensor correlation (average of 0.14). This highlighted the importance of local emission sources and micro-environmental influences. In contrast, temperature displayed high spatial coherence. Time-series decomposition revealed seasonal patterns for meteorological variables. However, CO did not follow a strong seasonal trend. This suggests that non-seasonal local drivers play a larger role. Spatiotemporal analysis confirmed expected industrial hotspots. Surprisingly, residential zones showed higher average CO concentrations than industrial areas. Our feature selection process revealed that short-term temporal history, especially 3 h rolling statistics, provided the most predictive information for CO forecasting. Among several tested models, XGBoost achieved the lowest prediction errors, demonstrating the effectiveness of the selected features and modeling approach. These results provide a deeper understanding of CO dynamics in a complex urban–industrial environment. Local factors, wind speed, and recent CO history emerged as key drivers. The finding of elevated CO in residential zones has direct public health implications and deserves further study. Our integrated analytics approach provides city decision makers with both explanatory insights and predictive tools, which can improve proactive air quality management in urban areas. This study has a few limitations. These include the spatial resolution of the monitoring network and the reliance on imputed data for some periods. Future research should include more detailed emission data and expand analysis to other pollutants, like NOX and PM2.5. Investigating the causes of high CO levels in residential zones is also important.
This research improves our understanding of CO behavior in Jubail. It supports smart city goals by providing tools for better environmental monitoring and decision making. The integration of high-quality data and advanced analytics lays the groundwork for future real-time forecasting and visual analytics platforms.
Author Contributions
Conceptualization, A.S.A. and M.B.; methodology, A.S.A.; software, A.S.A.; validation, A.S.A. and M.B.; formal analysis, A.S.A.; investigation, A.S.A.; resources, A.S.A.; data curation, A.S.A.; writing—original draft preparation, A.S.A.; writing—review and editing, A.S.A. and M.B.; visualization, A.S.A.; supervision, M.B.; project administration, M.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The dataset used in this study was provided explicitly for research purposes and pertains solely to the specific dataset analyzed. This dataset is owned by the Royal Commission and is not publicly available.
Acknowledgments
We would like to express our sincere gratitude to the Royal Commission for Jubail and Jubail Industrial City, Saudi Arabia, for providing the valuable dataset used in this research. Their support in granting access to comprehensive gas and weather measurements was instrumental in facilitating this study. The availability of high-quality data significantly contributed to the development and evaluation of data quality techniques, enabling deeper insights into environmental conditions. We appreciate their commitment to data transparency and scientific research, which greatly benefited this work.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results. All data used in this research were provided explicitly for research purposes and pertain solely to the specific dataset used in the study. This dataset is owned by the Royal Commission.
References
- Shahid, S.; Brown, D.J.; Wright, P.; Khasawneh, A.M.; Taylor, B.; Kaiwartya, O. Innovations in Air Quality Monitoring: Sensors, IoT and Future Research. Sensors 2025, 25, 2070. [Google Scholar] [CrossRef] [PubMed]
- Ameer, S.; Shah, M.A.; Khan, A.; Song, H.; Maple, C.; Islam, S.U.; Asghar, M.N. Comparative Analysis of Machine Learning Techniques for Predicting Air Quality in Smart Cities. IEEE Access 2019, 7, 128325–128338. [Google Scholar] [CrossRef]
- Comai, A. Decision-Making Support: The Role of Data Visualization in Analyzing Complex Systems. World Future Rev. 2014, 6, 477–484. [Google Scholar] [CrossRef]
- Amović, M.; Govedarica, M.; Radulović, A.; Janković, I. Big Data in Smart City: Management Challenges. Appl. Sci. 2021, 11, 4557. [Google Scholar] [CrossRef]
- AlSalehy, A.S.; Bailey, M. Improving Time Series Data Quality: Identifying Outliers and Handling Missing Values in a Multilocation Gas and Weather Dataset. Smart Cities 2025, 8, 82. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Mahalingam, U.; Elangovan, K.; Dobhal, H.; Valliappa, C.; Shrestha, S.; Kedam, G. A Machine Learning Model for Air Quality Prediction for Smart Cities. In Proceedings of the 2019 International Conference on Wireless Communications, Signal Processing and Networking (WiSPNET), Chennai, India, 21–23 March 2019; pp. 452–457. [Google Scholar] [CrossRef]
- Hadj Sassi, M.S.; Chaari Fourati, L. Comprehensive Survey on Air Quality Monitoring Systems Based on Emerging Computing and Communication Technologies. Comput. Netw. 2022, 209, 108904. [Google Scholar] [CrossRef]
- Cesario, E. Big data analytics and smart cities: Applications, challenges, and opportunities. Front. Big Data 2023, 6, 1149402. [Google Scholar] [CrossRef]
- Shahat Osman, A.M.; Elragal, A. Smart Cities and Big Data Analytics: A Data-Driven Decision-Making Use Case. Smart Cities 2021, 4, 286–313. [Google Scholar] [CrossRef]
- Malhotra, M.; Walia, S.; Lin, C.C.; Aulakh, I.K.; Agarwal, S. A Systematic Scrutiny of Artificial Intelligence-Based Air Pollution Prediction Techniques, Challenges, and Viable Solutions. J. Big Data 2024, 11, 142. [Google Scholar] [CrossRef]
- Essamlali, I.; Nhaila, H.; El Khaili, M. Supervised Machine Learning Approaches for Predicting Key Pollutants and for the Sustainable Enhancement of Urban Air Quality: A Systematic Review. Sustainability 2024, 16, 976. [Google Scholar] [CrossRef]
- Zareba, M.; Cogiel, S.; Danek, T.; Weglinska, E. Machine Learning Techniques for Spatio-Temporal Air Pollution Prediction to Drive Sustainable Urban Development in the Era of Energy and Data Transformation. Energies 2024, 17, 2738. [Google Scholar] [CrossRef]
- Kök, İ.; Şimşek, M.U.; Özdemir, S. A deep learning model for air quality prediction in smart cities. In Proceedings of the 2017 IEEE International Conference on Big Data (Big Data), Boston, MA, USA, 11–14 December 2017; pp. 1983–1990. [Google Scholar] [CrossRef]
- Jaisharma, K.; Deepa, N.; Devi, T. Monitoring AI-Based Processing for Predicting Poisonous Gas Emissions in Smart Cities Using Novel Temporal Dynamics Prediction Model. In Proceedings of the 2024 Second International Conference on Data Science and Information System (ICDSIS), Hassan, India, 17–18 May 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Swamynathan, S.; Sneha, N.; Ramesh, S.P.; Niranjana, R.; Ponkumar, D.D.N.; Saravanakumar, R. A Machine Learning Approach for Predicting Air Quality Index in Smart Cities. In Proceedings of the 2024 International Conference on IoT Based Control Networks and Intelligent Systems (ICICNIS), Bengaluru, India, 17–18 December 2024; pp. 1609–1615. [Google Scholar] [CrossRef]
- Tsokov, S.; Lazarova, M.; Aleksieva-Petrova, A. A Hybrid Spatiotemporal Deep Model Based on CNN and LSTM for Air Pollution Prediction. Sustainability 2022, 14, 5104. [Google Scholar] [CrossRef]
- Şimsek, M.U.; Kök, İ.; Özdemir, S. Cepair: An AI-powered and fog-based predictive CEP system for air quality monitoring. Clust. Comput. 2024, 27, 9107–9121. [Google Scholar] [CrossRef]
- Binu, C.A. AI-Driven IoT Solutions for Urban Pollution Monitoring. Smart Internet Things 2024, 1, 226–243. [Google Scholar]
- Kotlia, P.; Lohani, M.C.; Pant, J. Applying Machine Learning for Predictive Analysis for Air Quality Assessment across different Districts in Uttarakhand. In Proceedings of the 2024 First International Conference on Innovations in Communications, Electrical and Computer Engineering (ICICEC), Davangere, India, 24–25 October 2024; pp. 1–7. [Google Scholar] [CrossRef]
- Fritsch, F.; Carlson, R. Monotone Piecewise Cubic Interpolation. SIAM J. Numer. Anal. 1980, 17, 238–246. [Google Scholar] [CrossRef]
- Batista, G.; Monard, M. An analysis of k-nearest neighbor as an imputation method. In Proceedings of the 2003 Brazilian Symposium on Artificial Intelligence, Ribeirão Preto, Brazil, 23–28 November 2003; pp. 125–130. [Google Scholar]
- Azur, M.J.; Stuart, E.A.; Frangakis, C.; Leaf, P.J. Multiple imputation by chained equations: What is it and how does it work? Int. J. Methods Psychiatr. Res. 2011, 20, 40–49. [Google Scholar] [CrossRef]
- Tukey, J.W. Exploratory Data Analysis; Addison-Wesley: Boston, MA, USA, 1977. [Google Scholar]
- Barnett, V.; Lewis, T. Outliers in Statistical Data, 3rd ed.; Wiley: Hoboken, NJ, USA, 1994. [Google Scholar]
- Brockwell, P.J.; Davis, R.A. Introduction to Time Series and Forecasting, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Liu, F.T.; Ting, K.M.; Zhou, Z.H. Isolation Forest. In Proceedings of the 2008 Eighth IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008; pp. 413–422. [Google Scholar] [CrossRef]
- Rojas, S.J.; Christensen, E.A.; Blanco-Silva, F.J. Learning SciPy for Numerical and Scientific Computing; Packt Publishing Ltd.: Birmingham, UK, 2015. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Taylor, S.J.; Letham, B. Forecasting at scale. Am. Stat. 2018, 72, 37–45. [Google Scholar] [CrossRef]
- Herzen, J.; Lässig, F.; Piazzetta, S.G.; Neuer, T.; Tafti, L.; Raille, G.; Van Pottelbergh, T.; Pasieka, M.; Skrodzki, A.; Huguenin, N.; et al. Darts: User-friendly modern machine learning for time series. J. Mach. Learn. Res. 2022, 23, 1–6. [Google Scholar] [CrossRef]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased boosting with categorical features. Adv. Neural Inf. Process. Syst. 2018, 31, 6639–6649. [Google Scholar]
- Ruppert, D. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. J. Am. Stat. Assoc. 2004, 99, 567. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice, 2nd ed.; hlOTexts: Melbourne, Australia, 2018. [Google Scholar]
- Bergmeir, C.; Benítez, J.M. On the use of cross-validation for time series predictor evaluation. Inf. Sci. 2012, 191, 192–213. [Google Scholar] [CrossRef]
- Bergmeir, C.; Hyndman, R.J.; Koo, B. A note on the validity of cross-validation for evaluating autoregressive time series prediction. Comput. Stat. Data Anal. 2018, 120, 70–83. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 4765–4774. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why should I trust you?”: Explaining the predictions of any classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1135–1144. [Google Scholar] [CrossRef]
- Kachhoria, R.; Mahalle, P.N.; Bhagwat, S. Data Collection and Preprocessing for Environmental Monitoring Using Wireless Sensor Networks. In Machine Learning for Environmental Monitoring in Wireless Sensor Networks; IGI Global: Hershey, PA, USA, 2025; pp. 39–52. [Google Scholar] [CrossRef]
- Chen, W.; Tang, H.; Zhao, H. Diurnal, Weekly and Monthly Spatial Variations of Air Pollutants and Air Quality of Beijing. Atmos. Environ. 2015, 119, 21–34. [Google Scholar] [CrossRef]
- Lee, S.J.; Hajat, S.; Steer, P.J.; Filippi, V. A Time-Series Analysis of Any Short-Term Effects of Meteorological and Air Pollution Factors on Preterm Births in London, UK. Environ. Res. 2008, 106, 185–194. [Google Scholar] [CrossRef]
- Parrish, D.D.; Kuster, W.C.; Shao, M.; Yokouchi, Y.; Kondo, Y.; Goldan, P.D.; de Gouw, J.A.; Koike, M.; Shirai, T. Comparison of Air Pollutant Emissions among Mega-Cities. Atmos. Environ. 2009, 43, 6435–6441. [Google Scholar] [CrossRef]
- Huang, Y.D.; Hou, R.W.; Liu, Z.Y.; Song, Y.; Cui, P.Y.; Kim, C.N. Effects of Wind Direction on the Airflow and Pollutant Dispersion inside a Long Street Canyon. Aerosol Air Qual. Res. 2019, 19, 1152–1171. [Google Scholar] [CrossRef]
- Gulia, S.; Shiva Nagendra, S.M.; Khare, M.; Khanna, I. Urban Air Quality Management—A Review. Atmos. Pollut. Res. 2015, 6, 286–304. [Google Scholar] [CrossRef]
- Nalakurthi, N.V.S.R.; Abimbola, I.; Ahmed, T.; Anton, I.; Riaz, K.; Ibrahim, Q.; Banerjee, A.; Tiwari, A.; Gharbia, S. Challenges and Opportunities in Calibrating Low-Cost Environmental Sensors. Sensors 2024, 24, 3650. [Google Scholar] [CrossRef]
- Liu, Y.; Su, H.; Gu, J.; Tian, Z.; Li, K. Quantifying Multiple Effects of Industrial Patterns on Air Quality: Evidence from 284 Prefecture-Level Cities in China. Ecol. Indic. 2022, 145, 109722. [Google Scholar] [CrossRef]
- Cleveland, R.B.; Cleveland, W.S.; McRae, J.E.; Terpenning, I. STL: A Seasonal-Trend Decomposition Procedure Based on Loess. J. Off. Stat. 1990, 6, 3–73. [Google Scholar]
- Govea, J.; Gaibor-Naranjo, W.; Sanchez-Viteri, S.; Villegas-Ch, W. Integration of Data and Predictive Models for the Evaluation of Air Quality and Noise in Urban Environments. Sensors 2024, 24, 311. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).