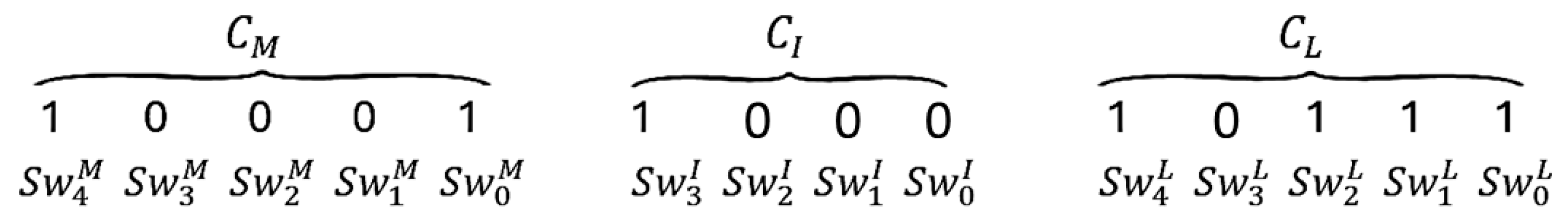Universal Digital Calibration of Mismatched DACs: Enabling Sub-0.02 mm² Area with Redundancy and Segmented Correction

Abstract

This paper presents a novel methodology for the design and calibration of ultra-compact digital-to-analog converters (DACs), integrating architectural redundancy and a digital calibration algorithm. The proposed calibration approach generates pre-distortion codes that correct both positive and negative nonlinearity errors, even in designs with severe mismatch or relaxed layout constraints. This enables the use of aggressively scaled devices while maintaining high linearity and spectral fidelity. The algorithm is architecture-agnostic and compatible with resistor-string, current-steering, and hybrid DAC structures. It operates with minimal memory, low latency, and supports both foreground and background calibration modes. The method is validated through simulation and silicon measurement of three 14-bit DAC architectures fabricated in TSMC 180 nm CMOS. Post-calibration results demonstrate linearity within ±0.5–1.2 LSB, ENOB up to 13.8 bits, and significant improvements in SNR, SFDR, and THD. The compact layouts—occupying as little as 0.0169 mm²—highlight the scalability of the proposed method for applications such as analog AI accelerators and high-density mixed-signal SoCs.

1. Introduction

Digital-to-Analog Converters (DACs) are indispensable components in mixed-signal integrated circuits, serving as the critical interface between digital computation and the analog world. They are foundational to systems requiring precise analog waveforms, including audio and video processing, instrumentation, communication systems, and sensor interfaces [1]. As the backbone of signal generation and control, DACs must balance competing demands of resolution, linearity, speed, power, and silicon area [2,3,4,5,6].

Popular DAC architectures—such as resistor-string, R-2R ladder, current-steering, and capacitive DACs—are selected based on application-specific trade-offs [7]. In emerging domains such as the Internet-of-Things (IoT) and edge artificial intelligence (AI), the trend toward integrating thousands of DACs on a single chip has heightened the need for ultra-compact, energy-efficient designs [8]. For instance, in analog neural networks and in-memory computing platforms, DACs are deployed to modulate weights stored as charge, conductance, or current. A notable example is the phase-change memory-based AI accelerator published in [9], where on-chip DACs played a pivotal role in determining computational precision and power efficiency.

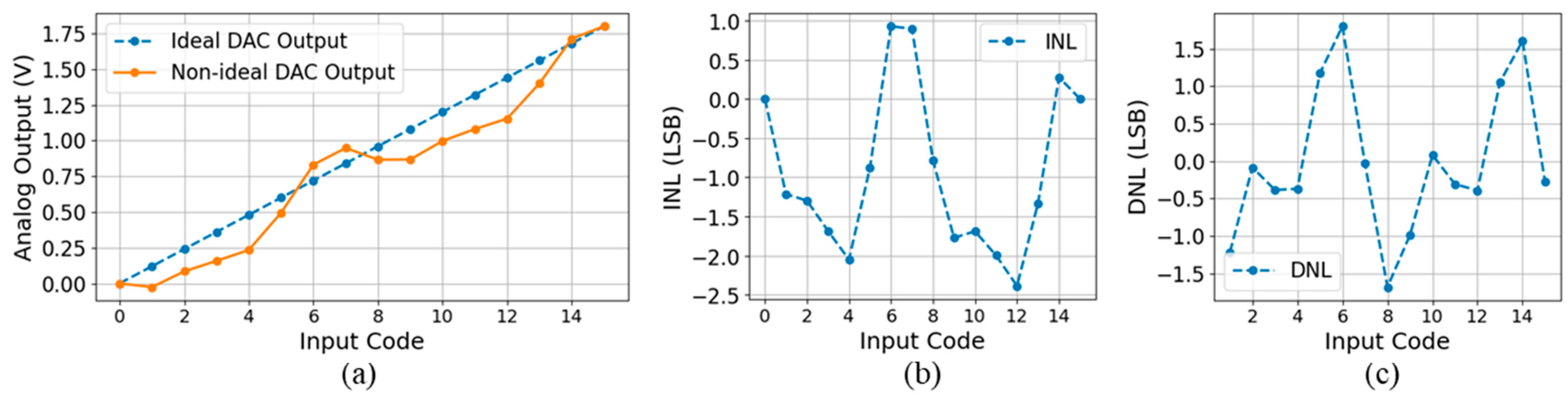
Similarly, in applications like ultrasound imaging, LiDAR, or MEMS control, DACs are required at the channel or pixel level for biasing or actuation [10]. Scaling such systems to hundreds or thousands of channels demands DACs that are ultra-compact and energy-efficient. However, aggressive area reduction typically exacerbates mismatch and compromises linearity, resulting in deviation of the DAC transfer function from its ideal behavior (Figure 1a). These deviations are quantitatively characterized by integral nonlinearity (INL) and differential nonlinearity (DNL). INL measures the deviation of each output level from an ideal linear reference, which is typically defined by a straight line connecting the first and last output codes of the DAC, this line iscommonly referred to as the end-point fit. The expression for this ideal linear voltage is given in Equation (1).

$$V_{fit}\left(k\right)=\left({\displaystyle \frac{V_{out}\left(k_{Last}\right)-V_{out}\left(k_{First}\right)}{2^n}}\right)\times k$$

(1)

where $k_{First}$ and $k_{Last}$ denote the first and last digital input codes, respectively, and n represent the resolution of the DAC in bits. The INL at each code is given in Equation (2) as illustrated in Figure 1b. The overall INL of the DAC is then defined as the maximum absolute value of the code-level INLs, as expressed in Equation (3).

$$\mathrm{I}\mathrm{N}\mathrm{L}\left(\mathrm{k}\right)=V_{out}\left(k\right)-V_{fit}\left(k\right)$$

(2)

$$\mathrm{I}\mathrm{N}\mathrm{L}=\max \left(\left|\mathrm{I}\mathrm{N}\mathrm{L}\left(\mathrm{k}\right)\right|\right)$$

(3)

DNL quantifies the deviation of each output step from the ideal step size. It is mathematically defined in Equation (4) and graphically illustrated in Figure 1c. DNL captures irregularities in step size that may result in missing codes or non-uniform output transitions. The overall DNL is typically expressed as the maximum of the absolute values of DNL(k), as defined in Equation (5). The ideal LSB, denoted as $LS{B}_{ideal}$ is defined as $V_{FS}/(2^n-1)$, where $V_{FS}$ is the full-scale output voltage and $n$ is the resolution of the DAC.

$$\mathrm{D}\mathrm{N}\mathrm{L}\left(\mathrm{k}\right)={\displaystyle \frac{V_{out}\left(k\right)-V_{out}\left(k-1\right)}{LS{B}_{ideal}}}-1$$

(4)

$$\mathrm{D}\mathrm{N}\mathrm{L}=\max \left(\left|\mathrm{D}\mathrm{N}\mathrm{L}\left(\mathrm{k}\right)\right|\right)$$

(5)

It should be noted that If $\mathrm{D}\mathrm{N}\mathrm{L}<1LSB$ or $\mathrm{I}\mathrm{N}\mathrm{L}<0.5LSB$ the transfer characteristic of the DAC is monotonic [11]

Traditional DACs achieve high linearity through meticulous device matching [12], laser trimming [13], or the use of large components [14]—techniques that, while effective, result in significant silicon area overhead. To overcome this trade-off between linearity and area, we introduce a redundancy-based design methodology. The central concept is to design the DAC with relaxed matching constraints by employing smaller, mismatch-prone components to save area, and subsequently restore accuracy through digital calibration. This approach ensures the final DAC achieves near-ideal performance with minimal area cost, enabling aggressive area reduction without sacrificing linearity. 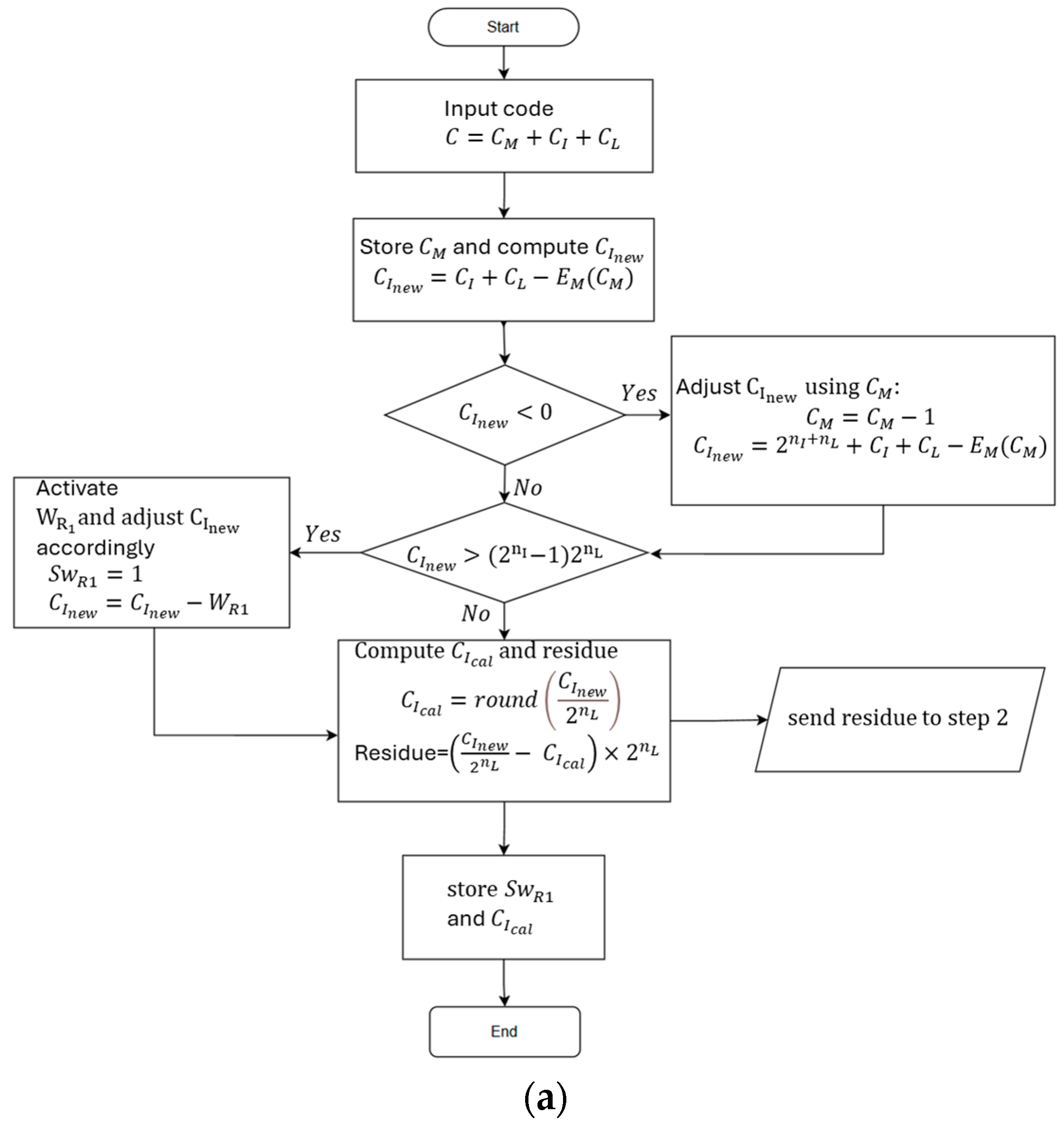Figure 2 show a simplified flow chart of our proposed design methodology.

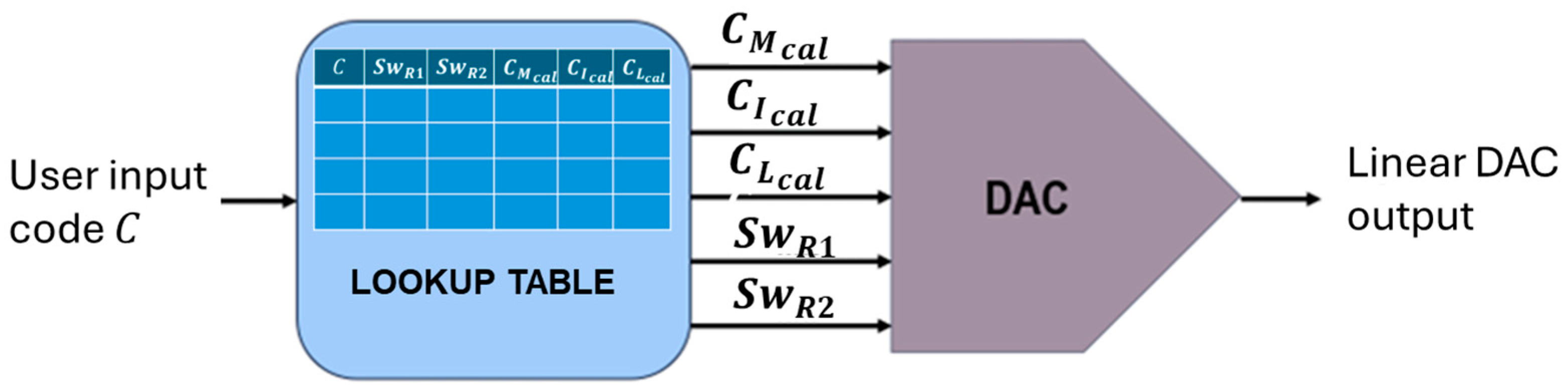
We begin by designing a compact DAC architecture with relaxed matching constraints, while ensuring that specific conditions are met to make the DAC calibratable. The fabricated DAC is subsequently tested, and the integral nonlinearity (INL) at major code transitions is measured and stored in memory. These INL measurements are then used to generate a predistortion or calibration code that linearizes the DAC output. Depending on system requirements, the predistortion code may be applied directly as they are generated or stored in a lookup table (LUT). During normal operation, the LUT maps user input codes to their corresponding calibration codes, thereby ensuring a linear output response.

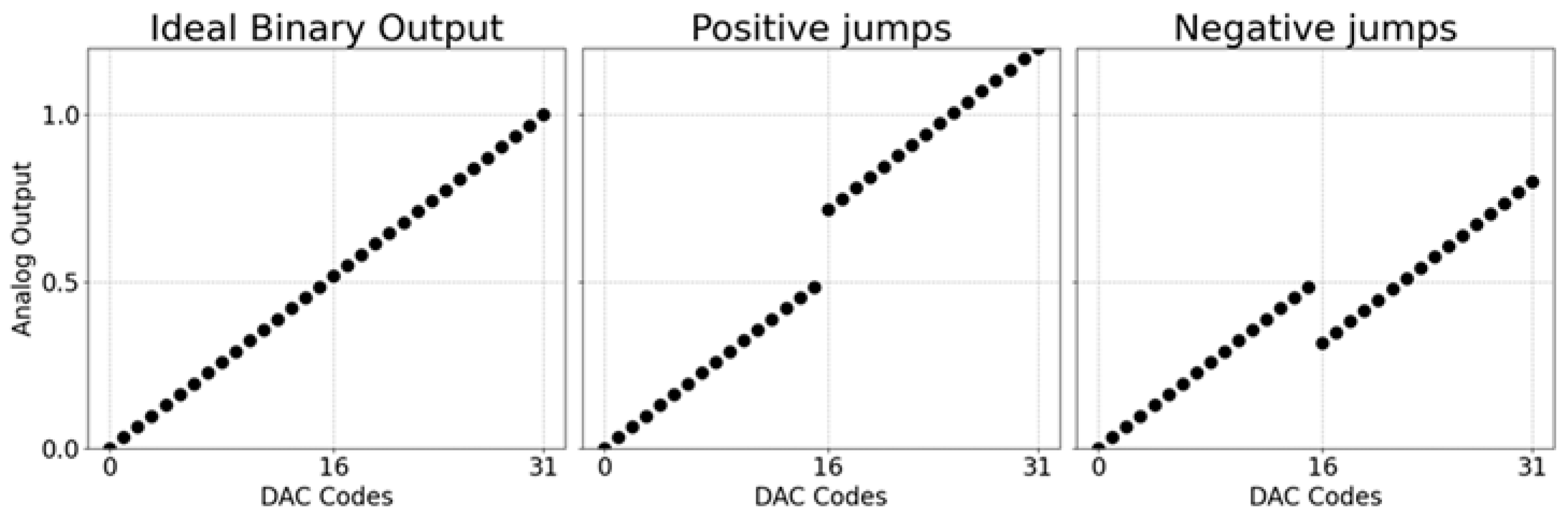
Importantly, our proposed digital calibration algorithm addresses both negative and positive INL jumps in the transfer function. Negative INL jumps—representing a scenario where the output voltage for a given code is substantially less than that of the previous code—are typically calibratable. However, positive INL jumps—a scenario in which the output voltage corresponding to a given input code increases abruptly relative to its preceding code—may render intermediate output levels unreachable, leading to non-recoverable errors, Figure 3 illustrates this.

While negative jumps can be corrected by existing codes, positive jumps necessitate redundancy. By introducing redundant bits and switching schemes, we create additional degrees of freedom in the DAC transfer function, enabling smooth interpolation of previously unreachable voltage levels (Figure 4).

As shown in Figure 4a, the non-ideal DAC transfer function exhibits a discontinuity marked by a large positive jump—specifically, the output voltage abruptly increases from approximately 0.95 V to 1.5 V between two adjacent digital input codes. This creates a 0.55 V gap in the output range, where no intermediate code can generate a valid output voltage. Such missing regions are particularly problematic because they represent non-recoverable linearity errors, rendering portions of the analog output space unreachable.

Figure 4b demonstrates the application of a redundancy-based technique to eliminate this discontinuity. By activating a redundant bit, a controlled offset is introduced into the transfer function, effectively bridging the output gap. This approach ensures complete output coverage across the full-scale range. The redundant bit does not modify the core DAC architecture or its nominal transfer function. Instead, it enables small, precise shifts in the output that, when combined with calibration, allow alternate input codes to reconstruct the missing output levels. This synergy between redundancy and calibration significantly improves overall linearity without architectural disruption.

Existing calibration techniques such as Dynamic Element Matching (DEM) [15] work by randomizing mismatch errors across conversions. While effective in reducing static mismatch, DEM is often inadequate for high-speed or highly mismatched systems due to its non-deterministic nature and limited effectiveness in dynamic conditions.

Ref. [16] presented a low-complexity calibration algorithm that leverages segmentation alongside Successive Approximation Register (SAR) logic and a high-resolution comparator. While this approach offers the benefit of tracking temperature variations and component parameter drift, it suffers from several limitations. Notably, the reliance on multiple feedback loops increases the overall circuit complexity and introduces additional latency due to the time required for loop convergence. This makes the algorithm less suitable for rapidly changing conditions. Furthermore, the presence of multiple feedback paths raises the risk of instability, particularly under aggressive correction gains or noisy operating environments. Other approaches, including digital foreground calibration techniques presented in [17,18], proposed a set of switching-based calibration algorithms tailored primarily for unary or segmented DAC architectures. While effective at reducing static nonlinearity due to random mismatch, their approach exhibits limited capability in correcting systematic errors such as gradient-induced mismatches. Additionally, the method also introduces non-trivial digital control complexity due to the required folding and reordering of switching sequences, and its applicability is largely restricted to unary DACs, limiting its generalizability across broader DAC architectures.

Compared to the methods presented above, the proposed calibration algorithm offers a more general, robust, and scalable solution. It is applicable to a broad range of DAC architectures, including those where the superposition principle holds (e.g., R-2R ladders) as well as those where it does not (e.g., segmented resistor-string DACs). Unlike prior approaches that are restricted to foreground-only calibration and unary configurations, the proposed algorithm supports both foreground and background calibration. In particular, an integrated ADC can periodically monitor the DAC output for deviations, enabling adaptive recalibration of correction codes over time. This approach effectively compensates for both random and systematic errors through a combination of hierarchical redundancy and deterministic digital correction, thereby maintaining high linearity and ensuring reliable performance throughout the DAC’s operational lifespan. Overall, the proposed method achieves high resolution, low latency, and robust operation under process, voltage, temperature, and aging variations, making it well-suited for modern, high-performance, and deeply scaled mixed-signal systems.

This article is a revised and expanded version of the following three conference papers [8,19,20].

The remainder of this paper is organized as follows. Section 2 introduces the conceptual DAC design. Section 3 describes the proposed redundancy-based calibration algorithm. Section 4 presents several representative design examples. Section 5 reports the simulation and measurement results, while Section 6 compares the proposed work with state-of-the-art DACs. Finally, Section 7 concludes the paper.

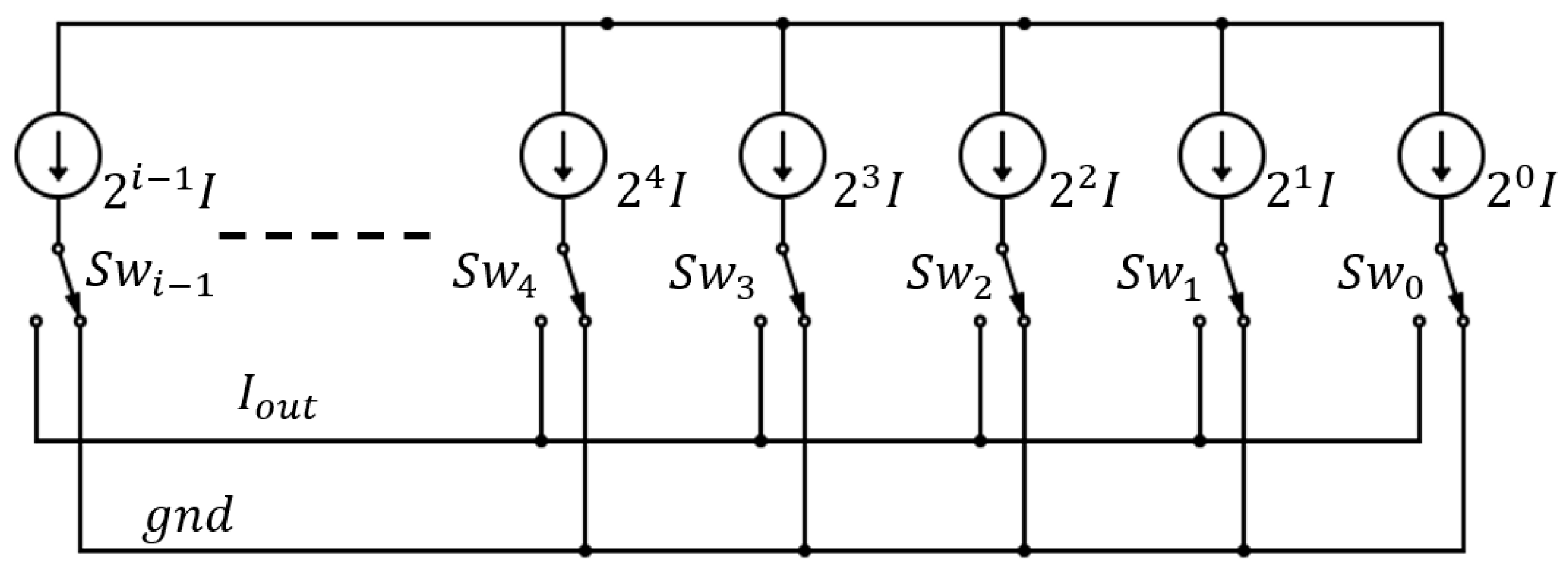
2. Conceptual Design of the DAC

Figure 5 presents the conceptual block diagram of the proposed DAC architecture. At its core lies a segmented DAC structure, which may be implemented using any conventional topology—resistor-string, capacitive (CDAC), or current-steering—depending on the application requirements. The architecture is partitioned into three segments: the Most Significant Bit (MSB), Intermediate Significant Bit (ISB), and Least Significant Bit (LSB). In addition to the core analog segments, the system includes a digital controller, an embedded memory unit, and a redundant bit segment. To achieve substantial area savings, the DAC is deliberately designed with relaxed matching constraints—particularly in the MSB and ISB segments—while preserving precise matching only in the LSB segment. This relaxed matching requirement led to significant area savings leveraging the rule of thumb that each 1-bit ENOB increase requires approximately 4 times area growth. This area-efficient design inherently introduces nonlinearities at the major code transitions of the MSB and ISB segments, resulting in deviations from the ideal transfer function. These non-idealities are modeled as deterministic code dependent error functions $E_M\left(C_M \right)$, and $E_I\left(C_I \right)$, where $C_M$ and $C_I$, respectively, represent the code for the MSB and ISB segments. These error values or INL, recorded during a post-fabrication testing phase, are stored in a local memory.

The extracted INL data are processed by a digital controller, which computes accurate calibration codes that linearize the DAC output during normal operation. When activated, the corresponding calibration code triggers additional control logic—including redundant bit segments—to selectively compensate for nonlinearity in the MSB and ISB segments.

The proposed algorithm can be operated in two different modes depending on its application which include the inline calibration mode, and a full lookup table calibration mode; in the inline calibration mode, the user input code is processed in real time by a digital controller, which computes the corresponding calibrated code that is then sent to the nonlinear DAC to generate a linearized output. In this calibration mode, memory requirements are minimized by storing only key segment-level error terms: $2^{n_M}$ entries of $E_M\left(C_M\right)$, $2^{n_I}$ entries of $E_I\left(C_I\right)$, and a single gain error term. For a 14-bit DAC with segmentation $n_M=5$, $n_I=4$ and $n_L=5$, this results in a total of only 32 + 16 + 1 = 49 stored error values. Assuming the calibration error terms are stored in a 49-entry lookup table with 8-bit resolution, and the SRAM is implemented using the TSMC 180 nm technology node (with a reported 6T bit-cell size of 4.4–4.65 μm² [21,22]), the total core memory capacity is 49 × 8 = 392 bits. This corresponds to an estimated core cell area of approximately 392 bits × 4.4 μm² ≈ 1724.8 μm². Accounting for an additional 30–100% peripheral overhead, the overall memory area is projected to be in the range of 2248 μm² to 3449.6 μm². This area can be substantially reduced by migrating to more advanced technology nodes. For instance, in the TSMC N2 (2 nm) node, which has a projected 6T SRAM bit-cell area of 0.0199 μm² [23,24] the same 392-bit memory would occupy only about 392 × 0.0199 μm² ≈ 7.8 μm², and including the same peripheral overhead, the total area would be expected to fall within 10.14 μm² to 15.6 μm². While this approach is highly memory-efficient, it introduces additional latency due to real-time computation and increases power consumption due to the active digital processing logic required during operation. In latency-sensitive applications, a lookup table (LUT)-based calibration mode is preferable. In this approach, calibration codes are precomputed and stored in memory during a one-time calibration phase. During normal operation, each user input code is directly remapped to its calibrated output through a simple memory fetch. This method significantly reduces both latency and runtime power consumption, as it eliminates the need for real-time computation and involves minimal combinational logic. The primary trade-off is an increased memory requirement to store all calibrated codes, with an estimated area within $0.748267 \mathrm{m}{\mathrm{m}}^2$ and $1.1 \mathrm{m}{\mathrm{m}}^2$ when implemented in the TSMC 180 nm Process, and within $0.002603 \mathrm{m}{\mathrm{m}}^2$ and $0.005206 \mathrm{m}{\mathrm{m}}^2$ when implemented in the TSMC N2 technology. Nevertheless, the overall power overhead remains low, and the method avoids the use of feedback loops or toggling of analog circuitry. This is demonstrated in Figure 6.

For high-density systems such as analog AI accelerators or large-scale mixed-signal SoCs, both power consumption and memory requirements can be significantly reduced through calibration reuse strategies. DACs exhibiting similar mismatch profiles—resulting from symmetric layout placement or shared environmental conditions—can share a common calibration profile. In scenarios where chip-to-chip variation is minimal, a single calibration instance can be reused across multiple identical DACs, effectively minimizing calibration overhead. Moreover, the proposed architecture is inherently compatible with modern System-on-Chip (SoC) platforms. The digital controller and memory required for calibration can be implemented using existing on-chip computational resources, eliminating the need for external calibration circuitry. In large-scale AI accelerators, embedded processors can autonomously execute the calibration algorithms—including those augmented by machine learning techniques—to dynamically correct for analog non-idealities. This self-correcting capability enhances system linearity, yield, and robustness while incurring minimal area and power overhead per DAC cell.

3. Proposed Digital Calibration

To illustrate the proposed DAC calibration concept, we consider an n-bit binary-weighted current-steering DAC, as shown in Figure 7. In this structure, the total output current is formed by summing the contributions from digitally controlled, binary-weighted current sources.

$$I_{out}=\sum _{i=0}^{n}S{w}_i{2}^{i}I$$

(6)

where $S{w}_i\in \left\{\mathrm{0,1}\right\}$ denotes the binary state of the switch controlling the $Ith$ current source, and $I$ is the unit current. Ideally, when selected, the $i^{th}$ current source contributes an output current of exactly $2^{i}I.$ However, due to device mismatch and process variations, the actual output current deviates from this nominal value, introducing conversion errors. As shown in

Table 1. Ideal DAC Output.

Design Weight (LSB)	8192	4096	2048	1024	512	256	128	64	32	16	8	4	2	1	Output (LSB)
Actual Weight (LSB)	8011	4140	2000	1040	500	250	124	68	31	16	8	4	2	1
DAC code	1	0	0	0	1	0	0	0	1	1	0	1	1	1	8573
Calibrated code	1	0	0	0	1	0	1	1	1	1	1	0	0	1	8759

Expected output: 8759 LSB.

, these non-idealities can cause the actual DAC output (8573 LSB) for a given input code to differ from the expected (8759 LSB) output.

To mitigate this, a calibration algorithm is employed to compute an alternative input code that compensates for the mismatched current sources by intelligently reconfiguring the switch states. This calibrated code, when applied to the same non-ideal current sources, restores the output to its intended value. The following section describes the methodology used to generate these calibrated input codes. It is important to point out that in this example, no redundant bit has been activated.

3.1. Calibration Algorithm

To achieve a linear output from a highly compact segmented DAC, we propose a calibration algorithm that corrects mismatch-induced errors through digital code remapping and the activation of redundant bits. The DAC is partitioned into three segments: an $n_M$-bit MSB segment, an $n_I$-bit ISB segment, and an $n_L$-bit LSB segment as in [25], such that the total resolution is $n=n_M+n_I+n_L$. A user-supplied $n$-bit digital input code $C$ (e.g., $n=14$) is decomposed into its segment components as expressed in Equation (7), where $C_M,C_I,$ and $C_L$ represent the MSB, ISB, and LSB codes, respectively.

$$C=C_M\times 2^{n_I+n_L}+C_I\times 2^{n_L}+C_L$$

(7)

This code can be mapped to the various switch controls in the MSB, ISB, and LSB segments as illustrated in Figure 8. Where $S{w}_i^M, S{w}_i^I,$ and $S{w}_i^L$ represent the switch control of the $i^{th}$ switch in the MSB, ISB, and LSB segments, respectively.

To correct for nonlinearity or error introduced in the MSB segment $E_M\left(C_M\right)$, the ISB code is updated as in Equation (8), with both redundant bit switch control initially set to 0.

$$C_{I_{new}}=C_I\times 2^{n_L}+C_L-E_M\left(C_M\right)$$

(8)

If $C_{I_{new}}<0$, we decrement $C_M$ by 1, and increase $C_{I_{new}}$ by the corresponding weight $2^{\left(n_I+n_L\right)}$ as shown in Equation (9).

$$If C_{I_{new}}<0:\left\{\begin{array}{c}{C}_M\to \left(C_M-1\right)\\ C_{I_{new}}\to \left(2^{\left(n_I+n_L\right)}+C_I\times 2^{n_L}+C_L-E_M\left(C_M\right)\right)\end{array}\right.$$

(9)

Next if $C_{I_{new}}$ exceeds the maximum value, ${(2}^{{\mathrm{n}}_{\mathrm{I}}}-1)2^{{\mathrm{n}}_{\mathrm{L}}}$, for the ISB segment, a redundant bit $R1,$ is activated by activating its switch control ${Sw}_{R1}$ and its weight $W_{R1}$ is subtracted as shown in Equation (10) The calibrated ISB code is then computed Equation (11).

$$if C_{I_{new}}>{(2}^{{\mathrm{n}}_{\mathrm{I}}}-1)2^{{\mathrm{n}}_{\mathrm{L}}}:\left\{\begin{array}{c}{Sw}_{R1}\to 1\\ C_{I_{new}}\to (C_{I_{new}}-W_{R1})\end{array}\right.$$

(10)

$$C_{I_{cal}}=round\left({\displaystyle \frac{C_{I_{new}}}{2^{n_L}}}\right)$$

(11)

The LSB code is adjusted based on the fractional residue and the ISB segment error ${\mathrm{E}}_{\mathrm{I}}\left(C_{I_{cal}}\right)$, as formulated in Equation (12).

$$C_{L_{new}}=\left({\displaystyle \frac{C_{I_{new}}}{2^{n_L}}}-C_{I_{cal}}\right)\times 2^{n_L}-{\mathrm{E}}_{\mathrm{I}}\left(C_{I_{cal}}\right)$$

(12)

If the updated LSB code $C_{L_{new}}$ is less than zero, the calibrated ISB code $C_{I_{cal}}$ is decremented, and $C_{L_{new}}$ is adjusted accordingly, as described in Equation (13).

$$if C_{L_{new}}<0:\left\{\begin{array}{c}{C}_{I_{cal}}\to \left(C_{I_{cal}}-1\right)\\ C_{L_{new}}\to \left(2^{n_L}+\left({\displaystyle \frac{C_{I_{new}}}{2^{n_L}}}-C_{I_{cal}}\right)\times 2^{n_L}-{\mathrm{E}}_{\mathrm{I}}\left(C_{I_{cal}}\right)\right)\end{array}\right.$$

(13)

To handle saturation in the LSB segment, the LSB segment gain error is first computed as described in Equation (14). When the new LSB segment code $C_{L_{new}}$ exceeds the threshold ${\displaystyle \frac{{(2}^{n_L}-1)}{G_e}},$ the second redundant bit control switch ${Sw}_{R2} \mathrm{i}\mathrm{s} \mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{d}. \mathrm{I}\mathrm{n} \mathrm{t}\mathrm{h}\mathrm{i}\mathrm{s} \mathrm{c}\mathrm{a}\mathrm{s}\mathrm{e}, \mathrm{i}\mathrm{t}\mathrm{s} \mathrm{a}\mathrm{s}\mathrm{s}\mathrm{o}\mathrm{c}\mathrm{i}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{d} \mathrm{w}\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t} W_{R2}$ is subtracted from the output, as illustrated in Equation (15). The final calibrated output voltage, incorporating this correction, is expressed in Equation (16). The complete calibration logic flow is depicted in the flowchart shown in Figure 9.

$$G_e={\displaystyle \frac{2^{n_L}-1}{\left(2^{n_L}-1\right)+E_L\left(2^{n_L}-1\right)}}$$

(14)

$$If C_{L_{new}}>{\displaystyle \frac{{(2}^{n_L}-1)}{G_e}}:\left\{\begin{array}{c}{Sw}_{R2}\to 1\\ C_{L_{cal}}=(C_{L_{new}}-W_{R2})\end{array}\right. \mathrm{e}\mathrm{l}\mathrm{s}\mathrm{e} C_{L_{cal}}=C_{L_{new}}$$

(15)

$$Vout=V_{DAC}\left(C_{cal}\right)=V_{DAC}\left(C_M\times 2^{\left(n_I+n_L\right)}+C_{I_{cal}}\times 2^{n_L}+C_{L_{cal}}+{Sw}_{R1}{W}_{R1}+{Sw}_{R2}{W}_{R2}\right)$$

(16)

The flow chat in Figure 9 describes the calibration process and will be applied to different design examples with subtle changes.

3.2. Summary of the DAC Design Methodology

• Define the Matching Requirement:
  To ensure accurate DAC calibration, the minimum matching level must meet or exceed the resolution requirements of the LSB segment.
• Segment the Architecture and Assign Redundant Bits:
  Begin with a two-segment DAC structure. If the worst-case mismatch error from a higher-order segment (e.g., the MSB segment) exceeds the correction range of the lower-order segment (e.g., LSB), an intermediate segment should be introduced. For a design with $n_s$ segments, the number of redundant bits required is $n_R=n_s-1$. Designs with tighter matching constraints may require only one redundant bit, whereas architectures with relaxed matching typically necessitate multiple redundant bits. While binary-weighted and current-steering DACs offer flexibility in segmentation and redundancy insertion, some architectures—such as segmented resistor-string DACs—impose fixed segmentation due to inherent structural constraints. The resolution of each segment is chosen to achieve the overarching goal of ensuring that the DAC remains calibratable. To achieve this, specific rules must be followed when partitioning the DAC. Starting with the LSB segment, the relaxed matching requirements of the DAC must be greater than or equal to the resolution of the LSB segment. This constraint influences the minimum achievable area—smaller LSB resolution allows for reduced matching requirement and consequently area. Importantly, because the LSB segment is responsible for absorbing the residual error from the ISB segment plus the error residue from the MSB segment, the aggregate weight of the LSB segment must exceed both of these errors combined. Similarly, the total weight of the ISB segment must be sufficient to absorb the error from the MSB segment. These hierarchical weight relationships are essential to enable accurate and bounded digital correction across segments.
• Size Core Components Based on Matching Targets:
  Key elements—such as resistors, capacitors, and transistors—should be sized using Pelgrom’s law or other mismatch models to achieve the desired matching performance. In advanced CMOS nodes, area-efficient sizing is critical to meet integration and cost constraints.
• Size Redundant Bits:
  Redundant bits must be sized to compensate for worst-case errors within their corresponding segments. Specifically, their weight should exceed the maximum expected INL contribution from the segment they are intended to correct. Also, for effective calibration, the redundant bit responsible for correcting ISB segment errors must have a weight less than the total weight of the LSB segment. Similarly, the redundant bit used to correct MSB segment errors must have a weight less than the total weight of the ISB segment.
• Perform Calibration:
  Implement a hierarchical, segment-wise calibration strategy. Redundant bits are used to correct mismatch-induced errors from the immediately higher-order segment. For instance, a redundant bit placed in the ISB segment is responsible for calibrating MSB segment errors, while the LSB segment’s redundant bit corrects ISB segment errors, and so forth.

4. Design Examples

To show the universality of our design methodology we demonstrate using three design examples, all MOSFET R2R DAC, Three Segment Interpolating Resistor String DACs and a hybrid Current Source Capacitor DAC. All three cases are 14-bit architectures with $n_M=5; n_I=4; n_L=5$ each structure also incorporate two additional redundant bits.

4.1. All MOSFET DAC

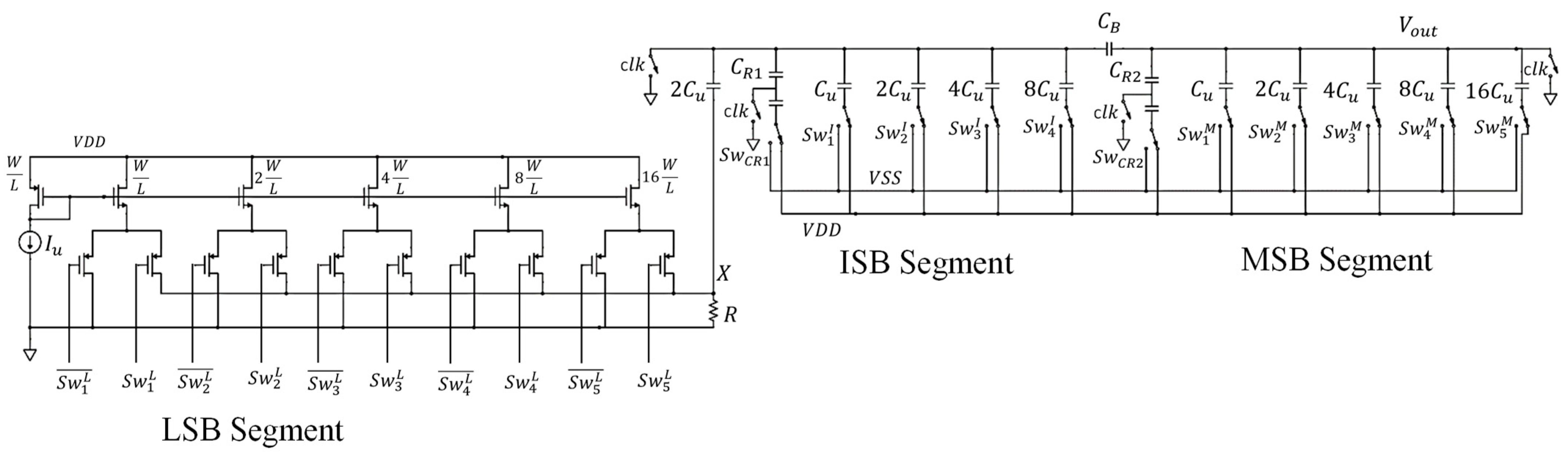
Figure 10 depicts the schematic circuit of the modified all MOSFET R-2R current steering DAC with redundant bits. The core structure, as illustrated in Figure 10a, is a 14-bit all MOSFET R-2R structure previously introduced in [26]. The MOSFET structure operates based on the linear current division principle. It divides an input current $I_{in}$ into two equal currents: $I_1 \mathrm{a}\mathrm{n}\mathrm{d} I_2$. $I_1$ passes through $M_1$ and is switched between $I_{out+} \mathrm{a}\mathrm{n}\mathrm{d} I_{out-}$, which represent the differential outputs of the DAC. Meanwhile, $I_2$ passes through $M_2$ and is equally divided into $I_3$ and $I_4$, and so on. This configuration results in an R-2R structure, where $M_1$ and $M_3$ or $M_4$ form the 2R part depending on which one is activated, while $M_2$ constitutes the R part. In addition to the core structure, which comprises a 14-bit all MOSFET R-2R ladder, the proposed design incorporates two extra redundant bits, as depicted in Figure 10b.

The DAC design process consists of two key stages. The first involves determining the minimum MOSFET area required to achieve adequate matching in the LSB segment. The second focuses on sizing the redundant bit to ensure it can correct the worst-case INL.

To determine the minimum required MOSFET area for an $n_L$-bit matching, the standard deviation of the relative current mismatch, ${\sigma }_{{\displaystyle \frac{∆\mathrm{I}}{I_{NOM}}}}$ is first estimated using Monte Carlo simulation, as described in [27]. This mismatch is directly related to the transistor gate area WL, as expressed in Equation (17), and is further linked to the target resolution $n$ and the standard deviation of INL, as shown in Equation (18). Where $A_{\beta }^2=A_{\mu }^2+A_{Cox}^2$, and $A_{VTO},{ A}_{\mu }^2, A_{Cox}^2$ are Pelgrom mismatch coefficients, and $V_{EB}$ is excess bias voltage.

$${\sigma }_{{\displaystyle \frac{∆\mathrm{I}}{I_{NOM}}}}={\displaystyle \frac{1}{\sqrt{WL}}}\sqrt{A_{\beta }^2+{\displaystyle \frac{4}{V_{EB}^2}}{A}_{VTO}^2}$$

(17)

$${\sigma }_{IN{L}_K-MAX } ={\sigma }_{{\displaystyle \frac{∆\mathrm{I}}{I_{NOM}}} }\left[{\displaystyle \frac{\sqrt{N}}{2}}\right], N=2^n$$

(18)

Using Equations (17) and (18), we can estimate the required MOSFET area for a desired INL or, conversely, predict the maximum achievable INL for a given area as expressed in Equation (19).

$${\sigma }_{IN{L}_K-MAX} ={\displaystyle \frac{1}{2}}\sqrt{{\displaystyle \frac{2^n}{WL}}\left(A_{\beta }^2+{\displaystyle \frac{4}{V_{EB}^2}}{A}_{VTO}^2\right)}$$

(19)

For high yield we will size the redundant bits weights as three times this standard deviation, ensuring they can correct errors from both the MSB and ISB segments.

The first redundant bit $W_{R1}$ is sized to correct the worst-case cumulative error $E_{M_{\mathrm{m}\mathrm{a}\mathrm{x}} }$ from the MSB segment, estimated in Equation (20).

$$E_{M_{\mathrm{m}\mathrm{a}\mathrm{x}} }={\displaystyle \frac{3}{2}}\sqrt{{\displaystyle \frac{2^{\left(n_M+n_I+n_L\right)}}{WL}}\left(A_{\beta }^2+{\displaystyle \frac{4}{V_{EB}^2}}{A}_{VTO}^2\right)}$$

(20)

The second redundant bit $W_{R_2}$ is sized to cover both the worst case cumulative ISB error $E_{I_{\mathrm{m}\mathrm{a}\mathrm{x}}}$ and the quantization residue from the MSB segment as in Equation (21). Where $Q_e$ represents the quantization residue with a maximum value of $2^{n_L-1}$.

$$E_{I_{\mathrm{m}\mathrm{a}\mathrm{x}}}+Q_e={\displaystyle \frac{3}{2}}\sqrt{{\displaystyle \frac{2^{\left(n_I+n_L\right)}}{WL}}\left(A_{\beta }^2+{\displaystyle \frac{4}{V_{EB}^2}}{A}_{VTO}^2\right)}+2^{n_L-1}$$

(21)

Equations (20) and (21) define the lower bounds for $W_{R1}$ and $W_{R2}$. The upper bounds are defined by the maximum output current that can be produced by the ISB and LSB segments. Hence the redundant bits must satisfy the conditions in Equations (22) and (23) below.

$$E_{M_{\mathrm{m}\mathrm{a}\mathrm{x}} }<W_{R1}<2^{n_L}\left(2^{n_I}-1\right)$$

(22)

$$E_{I_{\mathrm{m}\mathrm{a}\mathrm{x}}}+Q_e<W_{R2}<2^{n_L}-1$$

(23)

If the weight of a redundant bit is too small, it will be insufficient to bridge large integral nonlinearity (INL) gaps, rendering calibration ineffective. Conversely, if the weight is too large, it may lead to overcorrection or create unusable code regions. To ensure the redundant bit weight remain within this range even when subjected to mismatch, each redundant bit is conservatively sized as the average of its respective lower and upper bounds. Additionally, the area of the core DAC is sized such that the range of acceptable redundant bit weights is larger than the worst-case variation in the redundant bits due to mismatch. This design strategy ensures that, even under mismatch, the actual (measured) weight of the redundant bit remains within the predefined calibratable range. The calibration algorithm then uses this measured weight during calibration code generation/remapping. As long as the redundant bit’s weight remains within the valid range, the DAC remains fully calibratable.

The required MOSFET gate area WL to ensure adequate matching in the LSB segment is given by Equation (24). For high yield it is important to maintain $3{\sigma }_{IN{L}_K-MAX}\le 0.5LSB$.

$$WL={\displaystyle \frac{2^{n_L}}{4{\sigma }_{IN{L}_K-MAX}^2}}\left(A_{\beta }^2+{\displaystyle \frac{4}{V_{EB}^2}}{A}_{VTO}^2\right)=9\times 2^{n_L}\left(A_{\beta }^2+{\displaystyle \frac{4}{V_{EB}^2}}{A}_{VTO}^2\right)$$

(24)

The overall DAC transfer function is thus expressed as in Equation (25). Where the first term represents the ideal current contribution from the MSB segment, combined with the error due to device mismatch, denoted as $E_M\left(C_M\right)$. The second term corresponds to the ISB segment, including its mismatch-induced error $E_I\left(C_I\right)$. The third term is the contribution from the LSB segment, which may be subject to a gain error $G_E$. The final two terms represent the current contributions from redundant bits, used to facilitate digital calibration. The digital calibration algorithm described in Section 3 is then employed to compensate for the mismatch and gain errors in the MSB, ISB, and LSB segments, thereby restoring DAC linearity.

$$I_{out}=\left(C_M\times 2^{\left(n_I+n_L\right)}{I}_u+E_M\left(C_M\right)\right)+\left(C_I\times 2^{n_L}{I}_u+E_I\left(C_I\right)\right)+C_L{G}_E{I}_u+S{w}_{R1}{W}_{R1}{I}_u+S{w}_{R2}{W}_{R2}{I}_u$$

(25)

4.2. Three Segment String DAC

Figure 11 illustrates a modified three-segment resistor-string DAC with redundancy [19]. The architecture consists of three cascaded resistor ladders, labeled from left to right as the MSB, ISB, and LSB segments. Each segment is responsible for generating coarse, intermediate, and fine voltage levels, respectively. To minimize area and power consumption, the buffers which are traditionally used to isolate adjacent segments are removed, at the cost of increased susceptibility to loading effects. To further minimize area, the unit resistor is sized to meet the matching requirement for the LSB segment using Equations (26)–(28). Where ${\sigma }_{{\displaystyle \frac{R}{R_N}}}$ represent the standard deviation of resistor mismatch, $A_R^2$ is the resistor mismatch coefficient, and A represent the area of unit Resistor. For high yield, the design targets $3{\sigma }_{IN{L}_K-MAX }<0.5LSB$ for the LSB segment.

$${\sigma }_{IN{L}_K-MAX }={\sigma }_{{\displaystyle \frac{R}{R_N}}}\times {\displaystyle \frac{\sqrt{2^{n_L}}}{2}}$$

(26)

$${\sigma }_{{\displaystyle \frac{R}{R_N}}}^2={\displaystyle \frac{A_R^2}{A}}$$

(27)

$$A={\displaystyle \frac{A_R^2{2}^n}{4{\sigma }_{IN{L}_K-MAX }^2}}=9\times 2^{n_L} A_R^2$$

(28)

Although this relaxed resistor sizing approach reduces area, it, along with the removal of inter-segment buffers, introduces nonlinearity in the DAC output due to mismatch and increased segment loading effects. To introduce redundancy and compensate for these errors, an additional resistor is added to the MSB segment, increasing the total number of resistors in the MSB segment ($N_M$) to $2^{n_M}+1$. Furthermore, the tap voltages $V_{I_H}$ and $V_{I_L}$ in the ISB segment are connected across two MSB resistors instead of one, deviating from the conventional configuration. As a result, $2^{n_I+1}$ resistors are distributed across two MSB resistors. This modification effectively doubles the voltage span across the ISB segment, providing an additional $2^{n_I}$ LSB of redundancy. These extra codes enable correction of the mismatch-induced errors $E_M\left(C_M\right), { E}_I\left(C_I\right)$ and $G_e$ in the MSB, ISB and LSB segments, respectively, as well as errors arising from segment loading.

The overall DAC transfer function which is the sum of the contributions from the MSB, ISB, and LSB segments, is expressed in Equation (29), where $V_{Out, M}$, $V_{Out, I}$, and $V_{Out,L}$ are defined in Equations (30), (31) and (32), respectively.

$${V_{Out}=V}_{Out, M}+V_{Out, I}+V_{Out,L}$$

(29)

$$V_{Out, M}={\displaystyle \frac{S_w^{M}R}{{(D}_M-2)R+R_{eff}^M}}{V}_{ref}+E_M\left(S_w^M\right)$$

(30)

$$V_{Out, I}={\displaystyle \frac{S_w^{I}R}{{(D}_I-1)R+R_{eff}^I}}{\displaystyle \frac{R_{eff}^M}{{(D}_M-2)R+R_{eff}^M}}{V}_{ref}+{\displaystyle \frac{S_w^{I}R}{{(D}_I-1)R+R_{eff}^I}}\left(E_M\left(S_w^M+2\right)-E_M\left(S_w^M\right)\right)+E_I\left(S_w^I\right)$$

(31)

$$\begin{array}{c}{V}_{Out,L}={\displaystyle \frac{S_w^{L}R}{D_{L}R}}\times {\displaystyle \frac{R_{eff}^I}{{(D}_I-1)R+R_{eff}^I}}\times {\displaystyle \frac{R_{eff}^M}{{(D}_M-2)R+R_{eff}^M}}{V}_{ref}+{\displaystyle \frac{S_w^{L}R}{D_{L}R}}\times {\displaystyle \frac{R_{eff}^I}{{(D}_I-1)R+R_{eff}^I}}\left(E_M\left(S_w^M+2\right)-E_M\left(S_w^M\right)\right)\\ +{\displaystyle \frac{S_w^{L}R}{D_{L}R}}\left(E_I\left(S_w^I+1\right)-E_I\left(S_w^I\right)\right)+E_L\left(S_w^L\right)\end{array}$$

(32)

In Equations (30)–(32), the first term denotes the nominal voltage contribution of the MSB, ISB, and LSB segments, respectively. The second term in Equation (30) captures the MSB-segment mismatch error, which propagates to the ISB and LSB outputs, as reflected by the second terms of Equations (31) and (32). The third term in Equation (31) represents mismatch-plus-loading error in the ISB segment; this error similarly manifests in the LSB output, as shown by the third term in Equation (32). The final term in Equation (32) corresponds to LSB-segment mismatch error, which remains below ±0.5 LSB.

$S_w^M, { S}_w^I$ and $S_w^L$ represent the switch position of the MSB, ISB and LSB segment. $D_M$, $D_I$ and $D_L$ is defined in Equation (33). $R_{eff}^I$ is the effective resistance of the ISB tap resistor due to the loading effect of the LSB segment, similarly $R_{eff}^M$ is the effective resistance of the two MSB tap resistors due to the combined loading ISB and LSB segments. These relationships are quantified in Equation (34).

$$D_M=2^{n_M}+1; D_I=2^{n_I}; D_L=2^{n_L};$$

(33)

$$R_{eff}^I=D_{L}R||R={\displaystyle \frac{D_{L}R}{D_L+1}}; R_{eff}^M=\left[{(D}_I-1)R+R_{eff}^I\right]||2R={\displaystyle \frac{2R\left({(D}_L+1)\left(D_I-1\right)+D_L\right)}{{(D}_L+1)\left(D_I-1\right)+D_L+2(D_L+1)}}$$

(34)

Given the additional $2^{n_I}$ LSBs of redundancy in the ISB segment, errors originating from both mismatch and loading effects can be effectively compensated during calibration by adjustments within the ISB segment. A decoder is however necessary to map $S_w^M, { S}_w^I$ and $S_w^L$ to $C_M, { C}_I,$ and $C_L.$

4.3. Current Source Capacitor DAC

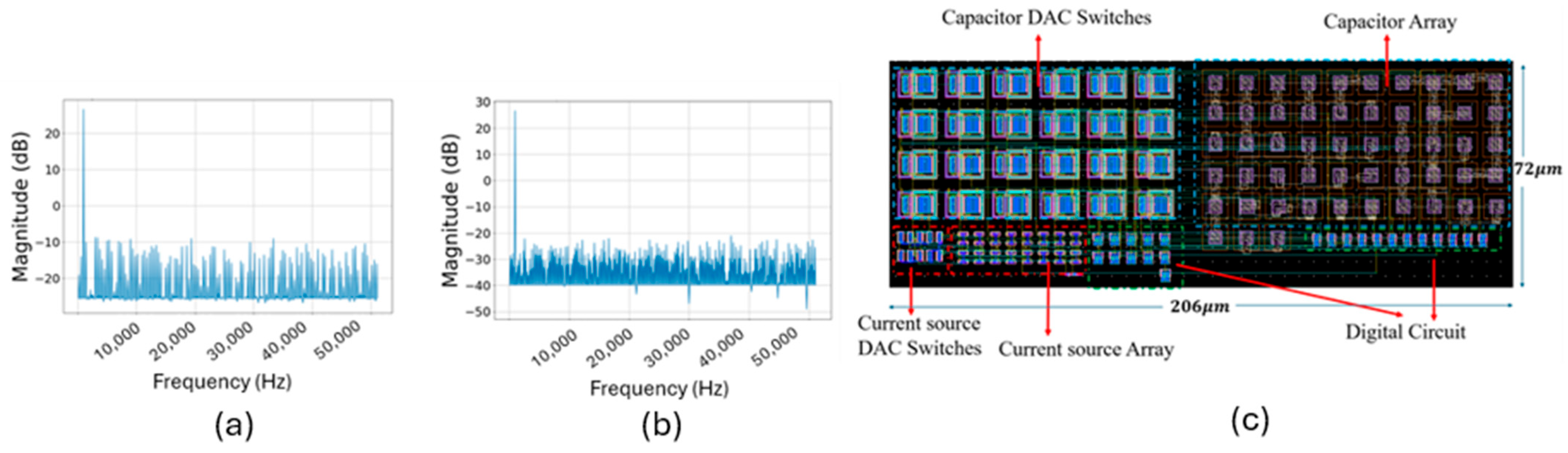
Figure 12 illustrates the schematic of a proposed current source–CDAC (Capacitive DAC) architecture with redundancy. The DAC is implemented as a two-segment CDAC, comprising an $n_M$-bit Most Significant Bit (MSB) segment, an $n_I$-bit Intermediate Significant Bit (ISB) segment, and an $n_L$-bit Least Significant Bit (LSB) segment, which utilizes a binary-weighted switched current source DAC.

A bridge capacitor $C_B$ which connects the MSB and ISB segments is used to minimize the capacitance spread. In the LSB segment, current from the switched current sources is steered between node X and ground based on the input LSB code. This current develops a voltage $V_X$ across a resistor R, which then charges the LSB capacitor (sized as $2C_u$). This configuration constrains the maximum voltage $V_{X, max}$ to $V_{REF}/2$, ensuring adequate voltage headroom to keep all MOS devices in saturation.

To minimize channel length modulation, the lengths of all MOS transistors are set to at least twice the minimum feature length defined by the process. To reduce quiescent power consumption in the LSB current source DAC, the unit current $I_u$ is minimized and the resistor R is chosen to have a high value. The unit current is given in Equation (35).

$$I_u={\displaystyle \frac{V_{REF}}{2^{n_L+1}}}\times {\displaystyle \frac{1}{\mathrm{R}}}$$

(35)

Given $I_u$, the transistor dimensions W/L and node voltages can be determined. Starting with the diode-connected transistor and the unit current source transistor $M_C^0$, the overdrive voltage $V_{ov}$ is selected to mitigate threshold voltage variation, enhancing current matching. From the square-law model Equation (36) we can find W/L.

$$I_u={\mu }_n{C}_{ox}{\displaystyle \frac{W}{L}}{\left(V_{ov}\right)}^2$$

(36)

The widths of subsequent current sources in the DAC are binary-scaled relative to that of $M_C^0$. The drain-source voltage $V_{ds}$ of $M_C^0$ is set to 1.5 $V_{ov}$, yielding a drain voltage $V_{cd}$ given by $VDD-V_{ds}$. For the differential pair transistors $M_{d,1}^0$ and $M_{d,2}^0$ the overdrive voltage is set to half that of $M_C^0$, and their widths four times that of $M_C^0$. The common-mode input gate voltage $V_{ic}$ is therefore given in Equation (37).

$$V_{ic}=V_{cd}-\left({|V}_{ov}|+\left|V_{th}\right|\right)$$

(37)

To ensure saturation of all transistors as $V_X$ approaches $V_{X, max}$, the input differential voltage must satisfy:

$$V_{L, min}\ge V_{ic}-V_{X,max} +\left|V_{th}\right|$$

To analytically determine the required area for accurate matching in the $n_L$-bit LSB segment, we refer to Equation (24). The redundant bits, with weights $W_{R1}$ and $W_{R2}$, are designed to correct for mismatch-induced errors originating from the ISB and MSB segments, which are collectively formed by the CDAC. Therefore, the sizing of $W_{R1}$ and $W_{R2}$ must be based on the worst-case mismatch in these segments. Specifically, their values are determined using the standard deviation of the unit capacitor mismatch, ${\sigma }_{C_u}/C_u$ as defined in Equation (38).

$${\displaystyle \frac{{\sigma }_{C_u}}{C_u}}={\displaystyle \frac{K_{\sigma }}{\sqrt{2A}}}$$

(38)

where $K_{\sigma }$ is the capacitor matching coefficient and $A$ is the unit capacitor area. Assuming a metal-insulator-metal (MIM) implementation, the worst-case integral nonlinearity (INL) is given by:

$${\sigma }_{INL,MAX}=\sqrt{2^{n-2}}{\displaystyle \frac{{\sigma }_{C_u}}{C_u}}LSB=K_{\sigma }\sqrt{{\displaystyle \frac{K_C\left(2^{n-2}\right)}{C_u\times 2}}}$$

(39)

where $K_C$ is the capacitor density and $C=K_C·A$. To ensure high yield, the redundant weights must exceed three times the worst-case INL in their respective segments. This imposes the constraints in Equations (40) and (41).

$$K_{\sigma }\sqrt{{\displaystyle \frac{3K_C\left(2^{n_M+n_I+n_L-2}\right)}{C_u\times 2}}}<W_{R1}<2^{n_L}\left(2^{n_I}-1\right)$$

(40)

$$K_{\sigma }\sqrt{{\displaystyle \frac{{3K}_C\left(2^{n_I+n_L-2}\right)}{C_u\times 2}}}<W_{R2}<2^{n_L}$$

(41)

The transfer function of the DAC is therefore defined in Equation (42). Where $S{w}_i^M$, $S{w}_i^I$, $S{w}_i^L$ represent the binary switch state of the $i^{th}$ switch in the MSB, ISB, and LSB segments. $C_{R1}$ and $C_{R2}$ denote the redundant bit capacitor, while ${Sw}_1^R$ and ${Sw}_2^R$ denote the redundant bit switches. The first four terms define the ideal contributions from the CDAC (MSB, ISB, and redundant bits), while the last term represents the LSB current-source DAC contribution. $E_M\left(S{w}_i^M\right)$ and $E_I\left(S{w}_i^I\right)$ represent the error in the MSB and ISB segment, $G_e$ represent the gain error in the LSB segment.

$$V_{out}={\displaystyle \frac{\left(\left(\sum _{i=0}^{n_M-1}{2}^i{C}_{u}S{w}_i^M+E_M\left(S{w}_i^M\right)\right)+\frac{1}{2^{n_I}}{\sum }_{i=0}^{n_I-1}{2}^i{C}_u{Sw}_i^I+E_I\left(S{w}_i^I\right)+G_e{Sw}_1^R{C}_{R1}+\frac{{Sw}_2^R{C}_{R2}}{2^{n_I}}\right)V_{ref}+\frac{2C_u}{2^{n_I}}R{\sum }_{i=0}^{n_L-1}\left(S{w}_i^L{2}^i{I}_u\right)}{2^{n_M}{C}_u+C_{R1}+\frac{1}{2^{n_I}}\left(C_u+C_{R2}\right)}}$$

(42)

5. Results

In accordance with the method described in Section 4, The area allocation was performed to give each DAC a 5-bit matching. To validate our analysis, the various DAC architectures described in Section 4 were implemented using the TSMC 180 nm CMOS process and simulated in Cadence Spectre, version 14.1.0.804.isr12, Calibration was implemented in Python, version 3.11.10. To assess the effectiveness of the proposed calibration algorithm, 200 Monte Carlo simulations were performed, incorporating process variation and mismatch. The detailed results for each DAC architecture are presented below.

5.1. All Mosfet DAC

Figure 13a,b present the post-calibration INL and DNL, which were reduced to 0.65 LSB and 1 LSB, respectively. In comparison, the uncalibrated INL and DNL reached 83.48 LSB and 127.94 LSB, as shown in Figure 13c,d. These results highlight the proposed calibration algorithm’s ability to correct large nonlinearity errors, outperforming conventional dynamic element matching techniques.

Figure 14 shows the calibration’s robustness under process variation and mismatch through 200 Monte Carlo simulations. Spectral analysis before and after calibration is shown in Figure 15a,b, indicating significant performance gains: SNR improved from 54.41 dB to 84.91 dB, SFDR from 54.16 dB to 108.39 dB, THD from −52.42 dB to −103.47 dB, and ENOB from 8.75 to 13.81 bits.

Each MOSFET in the core DAC structure was carefully sized to occupy an area of $0.25 \mathsf{\mu }{\mathrm{m}}^2 (500 \mathrm{n}\mathrm{m}\times 500 \mathrm{n}\mathrm{m})$. The complete DAC layout occupies 0.016895 mm², as illustrated in Figure 15c, demonstrating exceptional area efficiency.

5.2. Three Segment Resistor String DAC

Post-calibration results, shown in Figure 16a,b, indicate a substantial linearity improvement, achieving INL/DNL of ±0.6/±1 LSB—compared to the uncalibrated values of ±35 LSB, as shown in Figure 16c,d. This corresponds to a gain of approximately 6 effective bits. The robustness of the calibration algorithm under process and mismatch variations is validated through 200 Monte Carlo simulations (Figure 17).

Spectral analysis (Figure 18a,b) further confirms significant enhancements in signal fidelity and linearity, with a marked reduction in spurious tones and harmonic distortion. Following calibration, key performance metrics improved as follows: SNR increased from 56.01 dB to 83.04 dB, SFDR from 68.27 dB to 100.60 dB, THD from −66.44 dB to −110.11 dB, and ENOB from 9.01 to 13.50 bits.

Each unit resistor in the DAC core was precisely sized to 98.616 μm². The complete layout, shown in Figure 18c, occupies only 0.108 mm²—demonstrating exceptional compactness for a resistor-string DAC architecture.

5.3. Current Source CDAC

Post-calibration results (Figure 19a,b) demonstrate significant linearity improvements, with INL and DNL reduced to ±0.8 LSB and ±1.2 LSB, respectively—compared to pre-calibration values of 15 LSB and 17.5 LSB (Figure 19c,d). This corresponds to an ENOB improvement of approximately 5 bits. Robustness against process and mismatch variations was verified through 200 Monte Carlo simulations (Figure 20).

Each unit current source was designed to occupy 0.32 μm², with a total static current of 30.38 μA. Unit capacitors in the CDAC were sized at 33.45 fF, occupying 16 μm². The complete DAC layout, shown in Figure 21c, measures $0.01483 \mathrm{m}{\mathrm{m}}^2$, demonstrating excellent compactness. Further area reduction is achievable by increasing $n_L$, albeit at the cost of higher current consumption.

5.4. Measurement Result

To validate the performance of our DAC architecture in real-world conditions, we fabricated and experimentally tested one implementation: the three-segment resistor-string DAC. Resistor-string DACs are known for their excellent monotonicity and linearity, but their inherent drawback is the exponential growth in resistor count—and thus area—with increasing resolution. This characteristic tends to limit their practical use to low-resolution applications. Given these constraints, we selected the resistor-string DAC architecture to demonstrate the effectiveness of our proposed calibration and segmentation techniques under area-constrained scenarios.

The performance of the fabricated DAC prototype was evaluated through direct measurements using a laboratory testbench, as shown in Figure 22a. The measurement setup comprises two HEWLETT PACKARD E3631A triple-output DC power supplies (0–6 V, 5 A/0–±25 V, 0.1 A), a low-dropout regulator (LDO) for voltage stabilization, two HEWLETT PACKARD 34401A precision digital multimeters, and a PC interface for code loading and data acquisition. The DAC was programmed using an Arduino-based interface, and output voltages were recorded to extract static performance metrics such as INL and DNL. All measurements were conducted in a laboratory environment maintained at 25 ± 2 °C. No external shielding was employed; however, no significant power supply ripple or electromagnetic interference (EMI) was observed during testing.

Figure 22a,b present the measured INL and DNL across the full digital input range after calibration. The results show that the DAC achieves INL and DNL within ±1.6 LSB, confirming strong linearity and monotonicity. These values closely match the simulated post-layout performance, thereby validating the effectiveness of the proposed architecture and digital calibration algorithm under real-world conditions.

Figure 22d,e show the measured INL and DNL before calibration. The pre-calibrated INL reaches ±30 LSB, while the DNL spans ±40 LSB, indicating substantial nonlinearity and segment mismatch. The reduction from ±30 LSB to ±1.6 LSB INL corresponds to an approximate 4.5-bit improvement in effective number of bits (ENOB).

Figure 23 summarizes the INL_MAX, INL_MIN, DNL_MAX, and DNL_MIN values across eight measured chips, both before and after calibration. The results confirm that the DAC achieves high resolution and accuracy with minimal deviation from ideal behavior. Moreover, the absence of large spurious discontinuities in the DNL plot suggests that the layout and switching logic are free from significant mismatch or glitching issues.

Overall, the experimental results highlight the robustness, scalability, and practical viability of the proposed DAC architecture and its associated calibration methodology.

6. Discussion

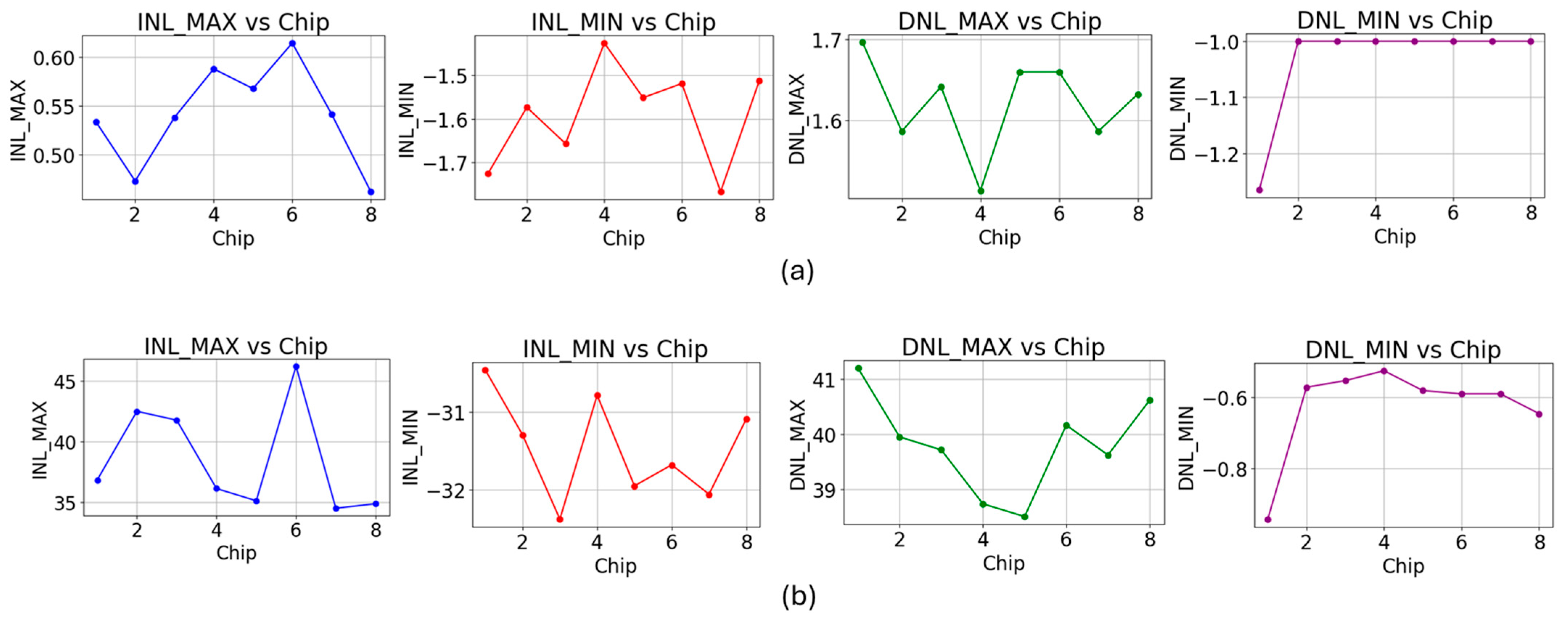
Table I benchmarks the three prototype DACs presented in this work against four representative state-of-the-art designs reported in JSSC’03 [27], T-VLSI’12 [28], ESSCIRC’10 [29], and JSSC’07 [30]. Taken together, the data highlight three main advantages of the proposed redundancy-based calibration strategy: superior linearity at higher resolution, dramatic area savings, and architecture-agnostic robustness.

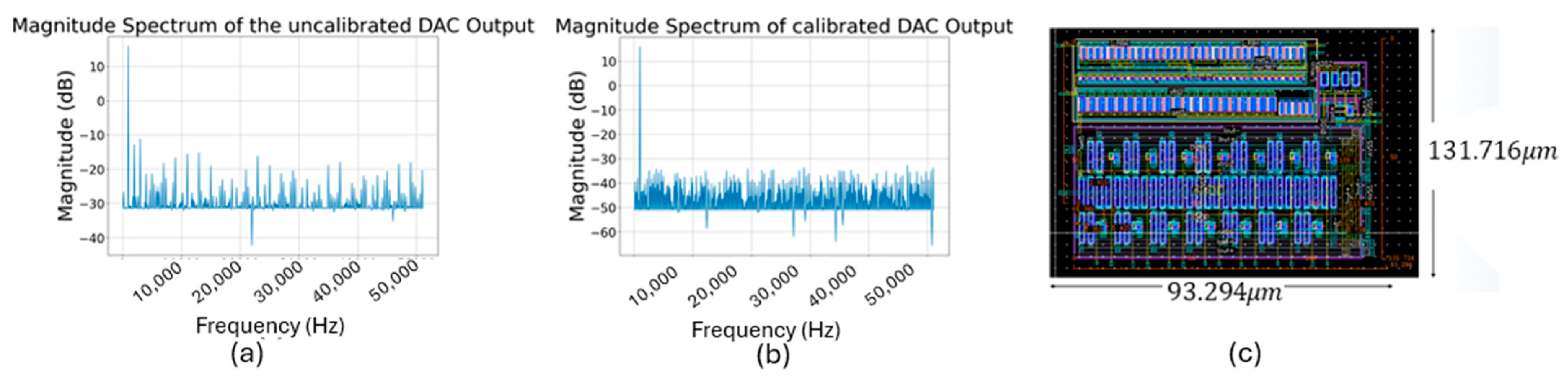
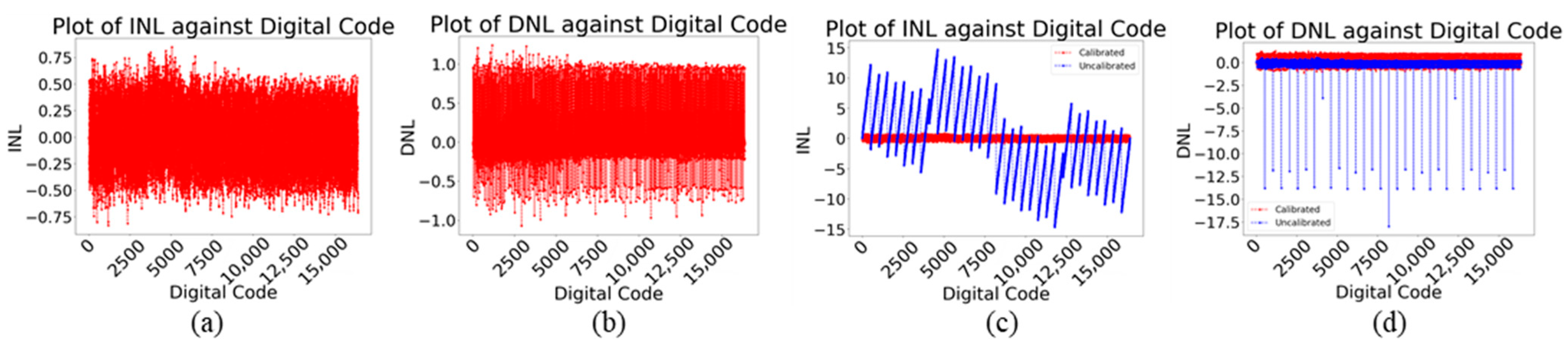
First, the proposed designs achieve high linearity despite being fabricated in an older 180 nm process. The 14-bit All-MOS R-2R DAC exhibits an INL of 0.6 LSB and a DNL of 1 LSB—surpassing the 12-bit linearity of the current-steering DACs in [27,28,29] and outperforming the 14-bit DAC in [30] by more than 2× in terms of INL. The three-segment resistor-string DAC, validated in silicon, achieves ±1.6 LSB INL and DNL, offering two extra bits of resolution compared to [27,28,29], with comparable or better static performance. Although the INL/DNL of the resistor-string DAC is slightly larger than the best-reported 12-bit performance, the gain in resolution and area efficiency remains substantial. Similarly, the hybrid current-source CDAC achieves 0.8 LSB INL and 1.2 LSB DNL, verifying that the proposed calibration method generalizes well across diverse architectures.

Second, the proposed designs demonstrate unprecedented area efficiency. The All-MOS DAC occupies just 0.017 mm², more than 60× smaller than the 1.04 mm² DAC in [27] and over 10× smaller than the 0.18 mm² design in [28], despite offering two more bits of resolution. The silicon-verified resistor-string DAC requires only 0.108 mm², a 28× reduction in area compared to the 3 mm² design in [30]. Remarkably, the current-source CDAC achieves the smallest footprint at 0.015 mm², making it the most compact entry in the table. These savings stem from the use of minimal-sized devices, with linearity restored digitally using the proposed redundancy-assisted predistortion strategy.

Third, because the calibration operates purely in the digital domain and leverages redundant weights embedded in each segment, it is inherently deterministic and architecture-agnostic. Unlike dynamic-element-matching methods, which randomize rather than correct mismatch, the present approach remaps input codes to cancel both positive and negative INL jumps. Silicon measurements of the resistor-string prototype confirm close agreement with Monte-Carlo predictions, underscoring the method’s robustness to process variation and mismatch.

Overall, the comparison presented in

Table 2. Performance comparison of the proposed DAC architectures with redundancy and prior state-of-the-art designs. The proposed architectures achieve comparable INL/DNL performance with substantially reduced die area, demonstrating high linearity and compactness enabled by redundancy and digital calibration.

	JSSC’ 03 [28]	T-VLSI’12 [29]	ESSCIRC’1 [30]	JSSC’07 [31]	All MOS DAC	3-Seg-RES-String	3-Seg-RES-String	Current-Src CDAC
Technology ($\mathsf{\mu }\mathrm{m}$)	0.13	0.09	0.18	0.18	0.18	0.18	0.18	0.18
Architecture	Current steering	Current steering	Current steering	Current steering	Current steering	Resistor	Resistor	Hybrid
Measurement ($\mathsf{\mu }\mathrm{m}$)	Yes	Yes	Yes	Yes	No	No	Yes	No
Resolution	12	12	12	14	14	14	14	14
Output Range	1.5	1.2	1.8	1.8	1.8	1.8	1.8	1.8
INL (LSBs)	0.43	0.4	0.5	1.37	0.6	0.6	1.6	0.8
DNL (LSBs)	0.6	0.3	0.5	0.76	1	1	1.6	1.2
With calibration	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes
Die Area (mm2)	1.04	0.18	0.8	3	0.017	0.108	0.108	$0.015$

demonstrates that the proposed methodology allows designers to trade costly analog device matching for inexpensive and scalable digital logic—a trade-off that becomes increasingly advantageous as CMOS technology continues to scale. As technology nodes shrink, device mismatch worsens due to increased process variability. However, this trend has minimal impact on our design methodology, which requires precise matching only in the LSB segment. The redundant bits are appropriately sized to compensate for mismatch in the upper segments, ensuring calibratability without relying on precise analog layout techniques.

At the same time, digital resources—such as logic and memory—become smaller, faster, and more cost-effective at advanced nodes. Our redundancy-assisted digital calibration framework is designed to exploit this trend, making it particularly well-suited for sub-65 nm technologies. Moreover, as maintaining analog precision becomes increasingly costly and area-intensive in deeply scaled processes, digital correction techniques such as predistortion offer a highly scalable and energy-efficient alternative. This makes the proposed architecture an attractive option for modern mixed-signal and system-on-chip (SoC) designs targeting advanced CMOS nodes.

Ongoing work focuses on fully integrating the calibration controller and lookup table on-chip, scaling the technique to support ≥16-bit resolution and update rates exceeding 1 GS/s. The approach is also being ported to sub-65 nm CMOS nodes, where mismatch becomes more pronounced, yet the relative cost of digital logic is significantly reduced. While the current algorithm primarily addresses static nonlinearity, efforts are underway to extend its capabilities to dynamic nonlinearity correction. Additionally, future work will explore regression-based models and neural network techniques for predictive estimation of INL and DNL.

7. Conclusions

This paper introduced a compact, scalable DAC design and calibration methodology that leverages redundancy and digital correction to achieve high linearity in area-constrained applications. The proposed algorithm corrects both positive and negative INL discontinuities with low complexity and is applicable across a range of DAC architectures. Simulations and measurements on three 14-bit designs demonstrate its effectiveness, with post-calibration INL/DNL within ±0.5–1.2 LSB, ENOB up to 13.81, and significant improvements in SNR and SFDR. Layouts as small as 0.0169 mm² were achieved, underscoring the suitability of this method for highly integrated mixed-signal systems. This work paves the way for efficient, high-resolution DACs in next-generation edge AI and precision analog applications.