Performance of G3-PLC Channel in the Presence of Spread Spectrum Modulated Electromagnetic Interference
Abstract
1. Introduction
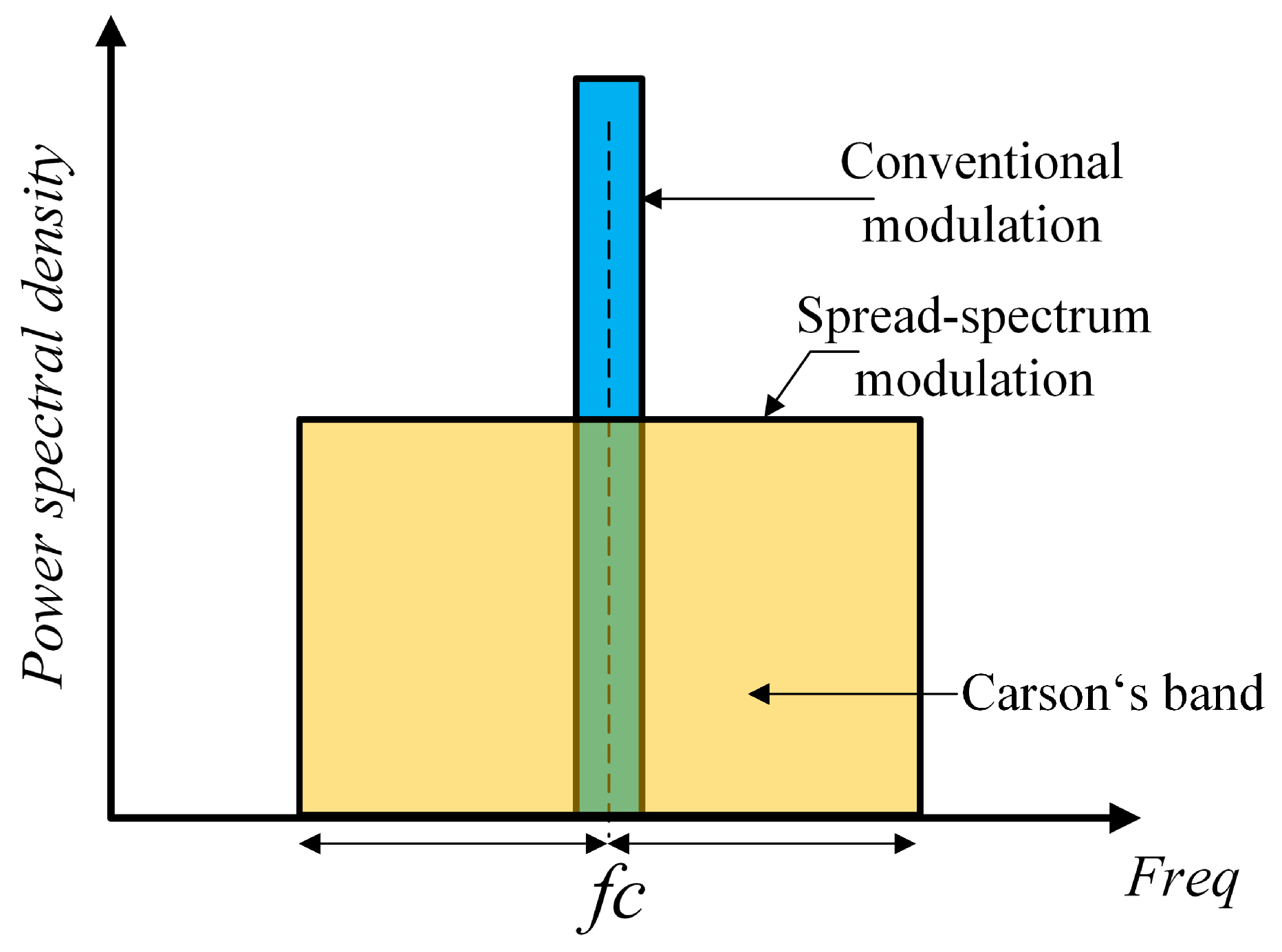
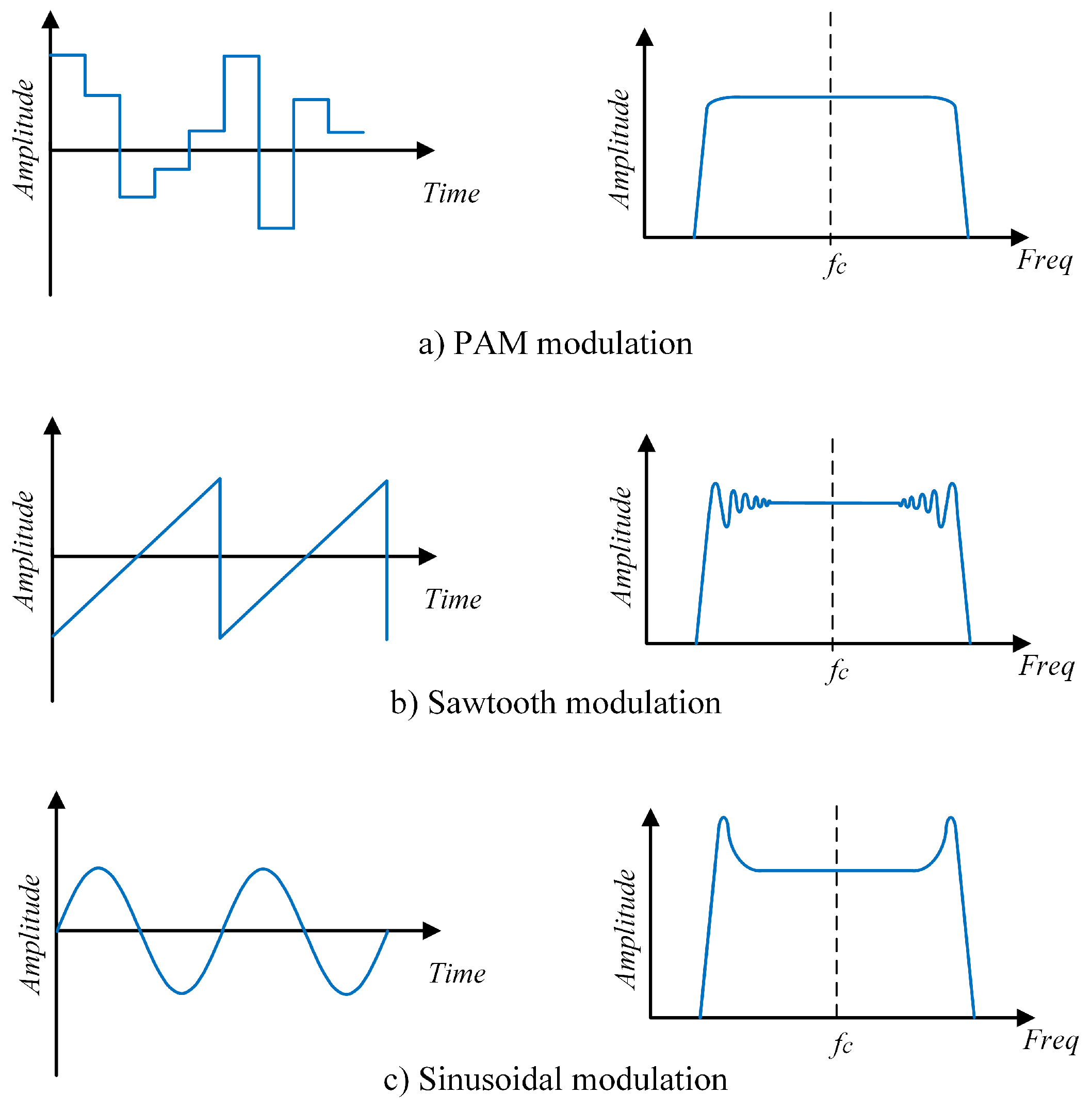
2. Converter Modulation
3. Power Line Communication Systems
4. Experimental Setup
5. Experimental Results
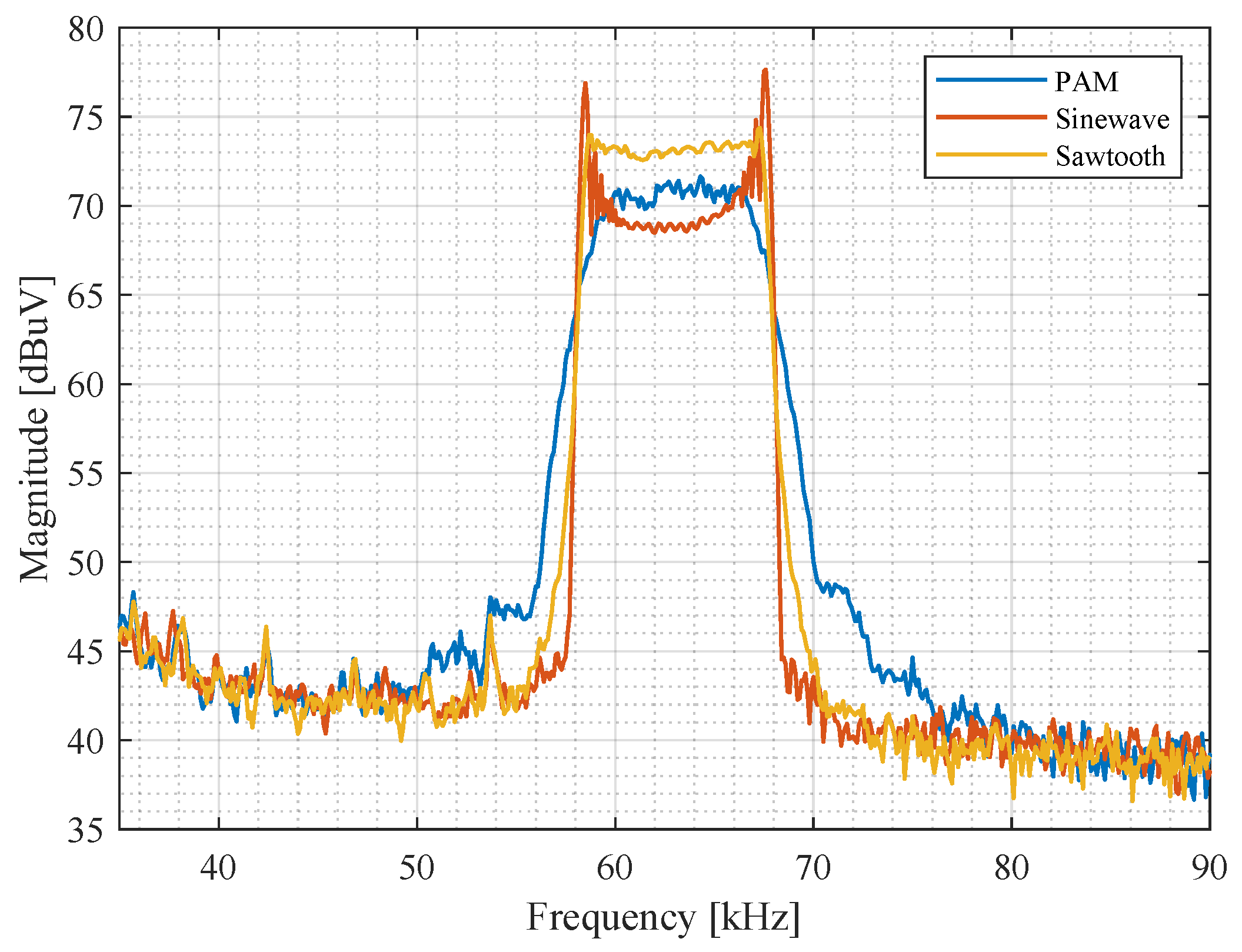
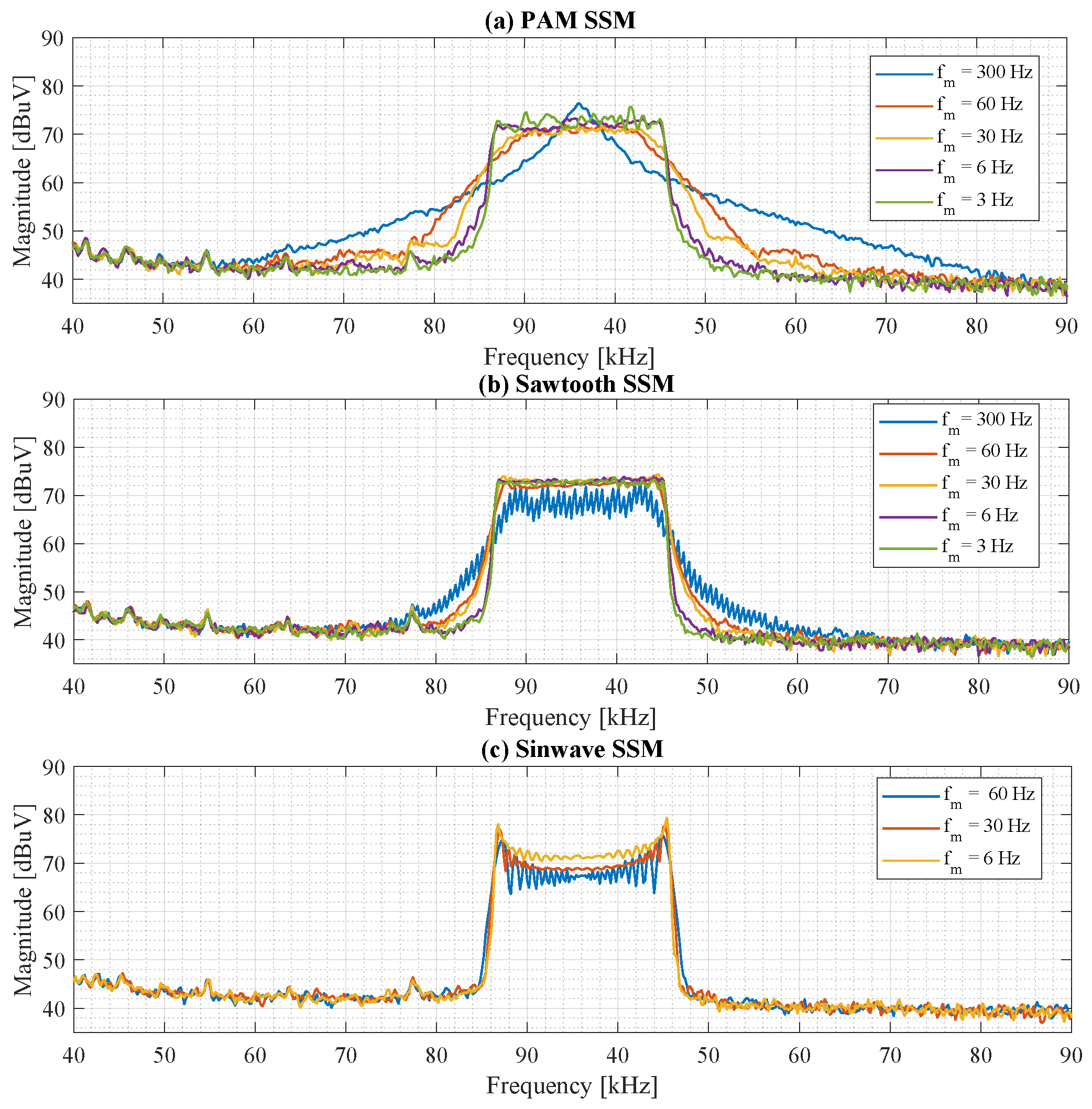
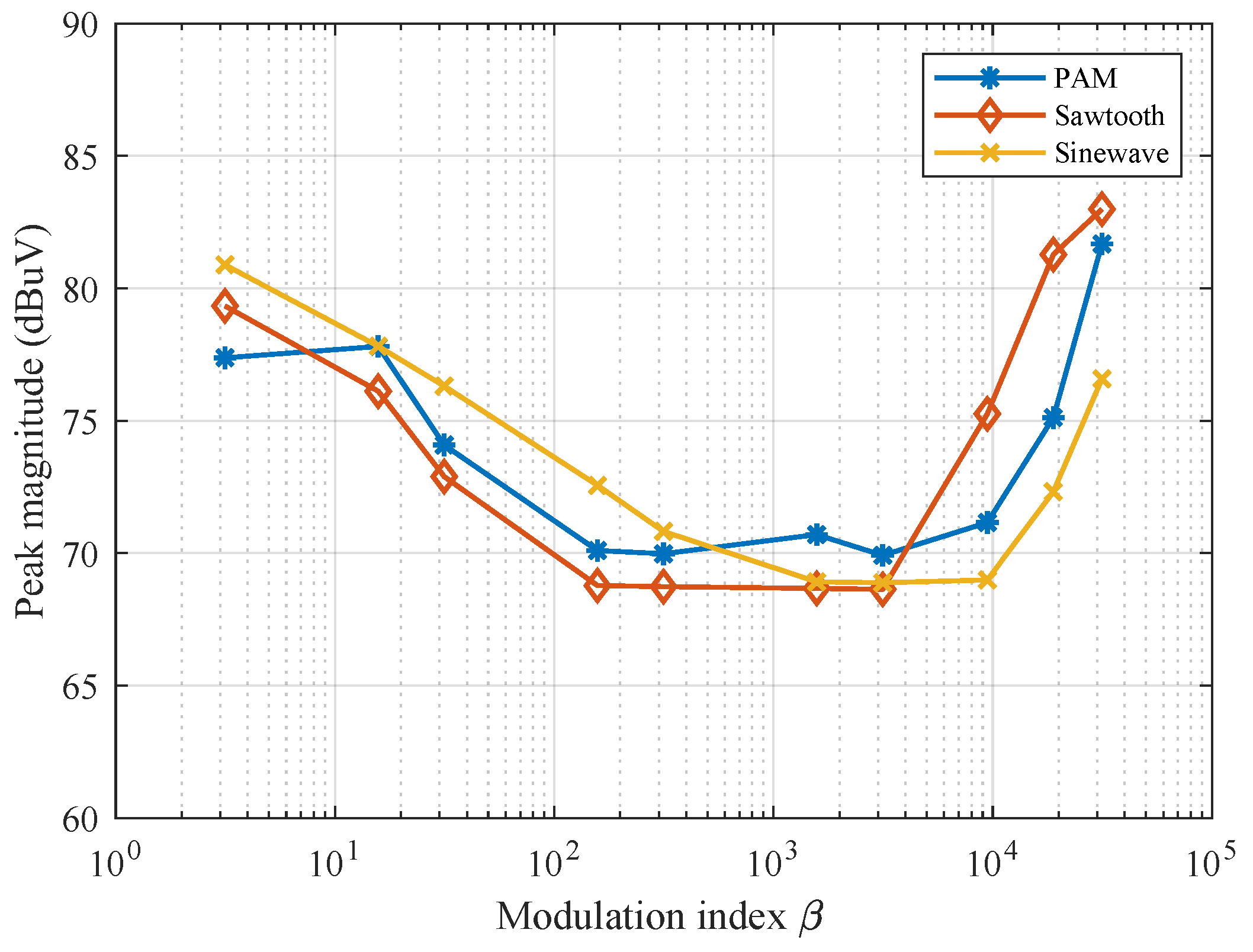
5.1. EMI Spectrum Measurements
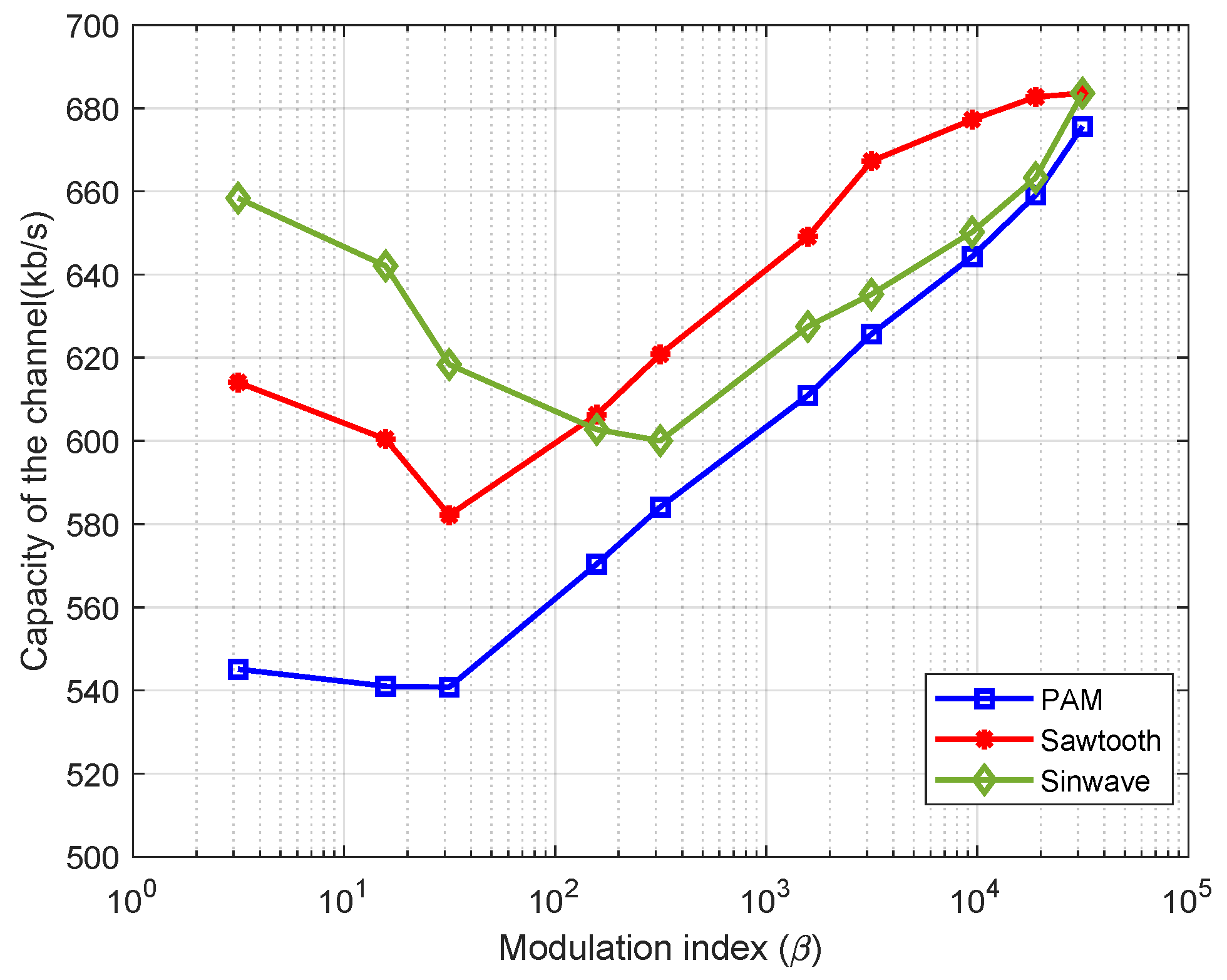
5.2. Channel Capacity Analysis
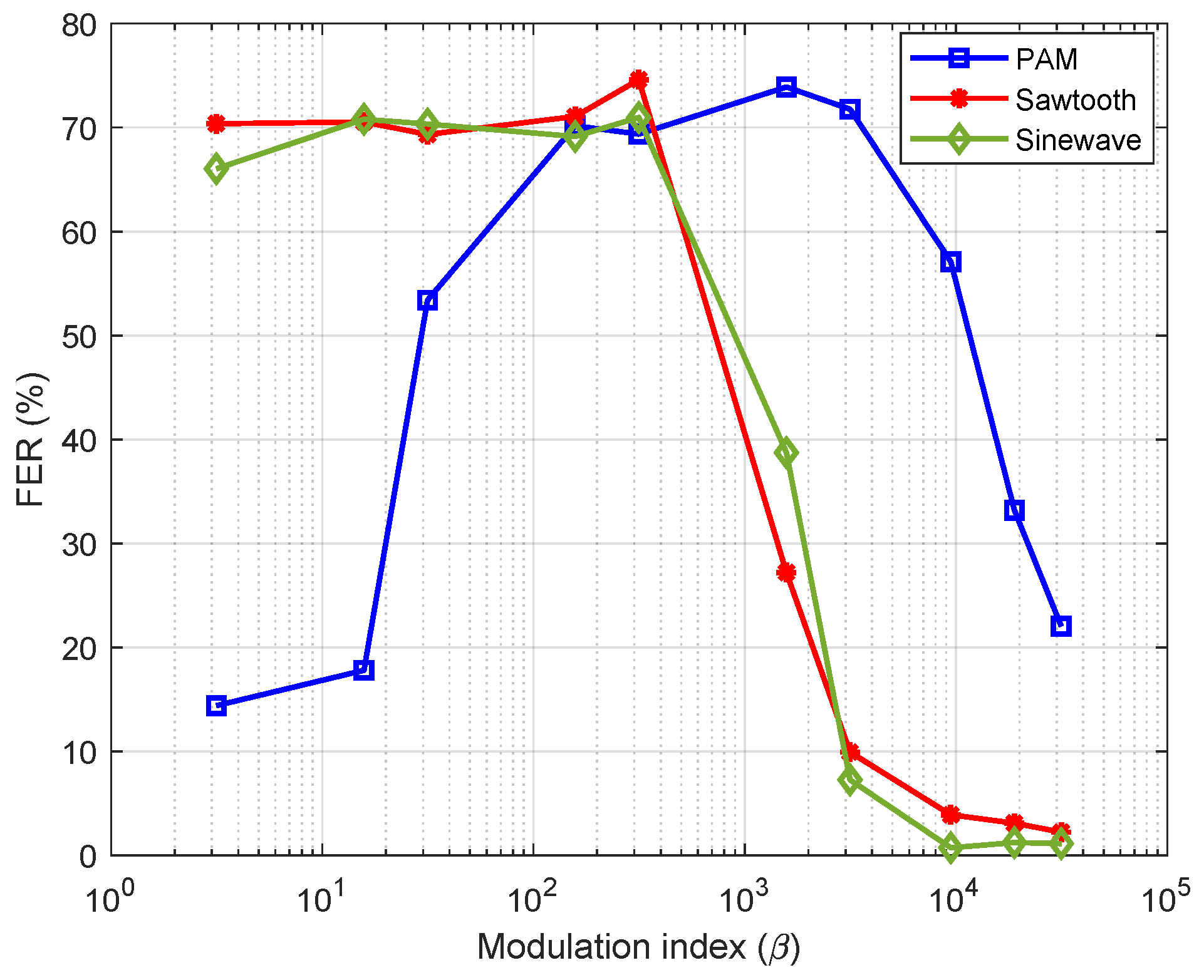
5.3. The PLC Performance in the Presence of EMI
5.4. Statistical Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AV | Average detector |
| AWGN | Additive White Gaussian Noise |
| EMC | Electromagnetic Compatibility |
| EMI | Electromagnetic Interference |
| EN | European Norm |
| FCC | Federal Communications Commission |
| FEC | Forward Error Correction |
| FER | Frame Error Rate |
| GSM | Global System for Mobile |
| IF | Intermediate Frequency |
| IFBW | Intermediate Frequency Band Width |
| LED | Light Emitted Diode |
| LISN | Line Impedance Stabilization Network |
| OFDM | Orthogonal Frequency Division Multiplexing |
| PAM | Pulse Amplitude Modulation |
| PLC | Power Line Communication |
| PRIME | Power line Related Intelligent Metering Evolution |
| PWM | Pulse Width Modulation |
| QP | Quasi Peak detector |
| RBW | Resolution Bandwidth |
| RCFMFD | Random Carrier Frequency Modulation with Fixed Duty cycle |
| RCFMVD | Random Carrier Frequency Modulation with Variable Duty cycle |
| RPPM | Random Pulse Position Modulation |
| RPWM | Random Pulse Width Modulation |
| SCENT | Smart Cities EMC Network for Training |
| SSM | Spread Spectrum Modulation |
| TI | Texas Instrument |
References
- Chung, D.D.L. Materials for electromagnetic interference shielding. Mater. Chem. Phys. 2020, 255, 123587. [Google Scholar] [CrossRef]
- Musolino, F.; Crovetti, P.S. Interference of Spread-Spectrum Modulated Disturbances on Digital Communication Channels. IEEE Access 2019, 7, 158969–158980. [Google Scholar] [CrossRef]
- Wang, Y.; Wen, H.; Hou, X.; Tang, H.; Sun, H.; Zheng, K.; Li, S. Comparison of Differential-Mode and Mixed-Mode Conducted Emission for Household Appliances in Power-Line Communication System. IEEE Trans. Electromagn. Compat. 2017, 59, 2023–2028. [Google Scholar] [CrossRef]
- Wibisono, M.A.; Moonen, N.; Leferink, F. Interference of LED Lamps on Narrowband Power Line Communication. In Proceedings of the 2020 IEEE International Symposium on Electromagnetic Compatibility & Signal/Power Integrity (EMCSI), Reno, NV, USA, 27–31 July 2020; pp. 219–221. [Google Scholar] [CrossRef]
- Nia, M.S.S.; Shamsi, P.; Ferdowsi, M. EMC Modeling and Conducted EMI Analysis for a Pulsed Power Generator System including an AC-DC-DC Power Supply. IEEE Trans. Plasma Sci. 2020, 48, 4250–4261. [Google Scholar] [CrossRef]
- Tounquet, F.; Alaton, C. Benchmarking Smart Metering Deployment in EU-28; Europeon Commission: Brussels, Belgium, 2019; ISBN 978-92-76-17295-6. [Google Scholar] [CrossRef]
- Korki, M.; Hosseinzadeh, N.; Member, S.; Moazzeni, T. Performance Evaluation of a Narrowband Power Line Communication for Smart Grid with Noise Reduction Technique. IEEE Trans. Consum. Electron. 2011, 57, 1598–1606. [Google Scholar] [CrossRef]
- Hoch, M. Comparison of PLC G3 and PRIME. In Proceedings of the 2011 IEEE International Symposium on Power Line Communications and Its Applications, ISPLC 2011, Udine, Italy, 3–6 April 2011; pp. 165–169. [Google Scholar] [CrossRef]
- Cheng, C.H.; Wu, T.L. A Common-Mode Filter with Three Alterable and Designable Transmission Zeroes. In Proceedings of the IEEE International Symposium on Electromagnetic Compatibility, Singapore, 14–17 May 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 429–432. [Google Scholar] [CrossRef]
- Shirai, R.; Wada, K.; Shimizu, T. Failure protection method for CAN communication against EMI noise generated by switched-mode power supplies. IEEE J. Emerg. Sel. Top Power Electron. 2021, 9, 6152–6160. [Google Scholar] [CrossRef]
- Lai, Y.-S.; Chang, Y.-T.; Chen, B.-Y. Novel Random-Switching PWM Technique with Constant Sampling Frequency and Constant Inductor Average Current for Digitally Controlled Converter. IEEE Trans. Ind. Electron. 2013, 60, 3126–3135. [Google Scholar] [CrossRef]
- Chen, J.; Jiang, D.; Sun, W.; Shen, Z.; Zhang, Y. A Family of Spread-Spectrum Modulation Schemes Based on Distribution Characteristics to Reduce Conducted EMI for Power Electronics Converters. IEEE Trans. Ind. Appl. 2020, 56, 5142–5157. [Google Scholar] [CrossRef]
- Pareschi, F.; Rovatti, R.; Setti, G. EMI reduction via spread spectrum in DC/DC converters: State of the art, optimization, and tradeoffs. IEEE Access 2015, 3, 2857–2874. [Google Scholar] [CrossRef]
- Pareschi, F.; Setti, G.; Rovatti, R.; Frattini, G. Practical optimization of EMI reduction in spread spectrum clock generators with application to switching DC/DC converters. IEEE Trans. Power Electron. 2014, 29, 4646–4657. [Google Scholar] [CrossRef]
- Park, H.; Kim, M.; Jung, J.-H. Spread-Spectrum Technique Employing Phase-Shift Modulation to Reduce EM Noise for Parallel–Series LLC Resonant Converter. IEEE Trans. Power Electron. 2019, 34, 1026–1031. [Google Scholar] [CrossRef]
- Yu, M.; Shi, M.; Hu, W.; Yi, L. FPGA-Based Dual-Pulse Anti-Interference Lidar System Using Digital Chaotic Pulse Position Modulation. IEEE Photonics Technol. Lett. 2021, 33, 757–760. [Google Scholar] [CrossRef]
- Peyghambari, A.; Dastfan, A.; Ahmadyfard, A. Selective Voltage Noise Cancellation in Three-Phase Inverter Using Random SVPWM. IEEE Trans. Power Electron. 2016, 31, 4604–4610. [Google Scholar] [CrossRef]
- Loschi, H.; Lezynski, P.; Smolenski, R.; Nascimento, D.; Sleszynski, W. FPGA-Based System for Electromagnetic Interference Evaluation in Random Modulated DC/DC Converters. Energies 2020, 13, 2389. [Google Scholar] [CrossRef]
- Bojarski, J.; Smolenski, R.; Lezynski, P.; Sadowski, Z. Diophantine equation based model of data transmission errors caused by interference generated by DC-DC converters with deterministic modulation. Bull. Pol. Acad. Sci. Tech. Sci. 2016, 64, 575–580. [Google Scholar] [CrossRef]
- Beshir, A.H.; Wan, L.; Grassi, F.; Crovetti, P.S.; Liu, X.; Wu, X.; El Sayed, W.; Spadacini, G.; Pignari, S.A. Electromagnetic Interference of Power Converter with Random Modulation on the Power Line Communication System. Electronics 2021, 10, 2979. [Google Scholar] [CrossRef]
- Auinger, B.; Deutschmann, B.; Winkler, G. Elimination of Electromagnetic Interference in Communication Channels by Using Spread Spectrum Techniques. In Proceedings of the 2017 International Symposium on Electromagnetic Compatibility—EMC EUROPE, Angers, France, 4–7 September 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Sayed, W.E.; Crovetti, P.; Moonen, N.; Lezynski, P.; Smolenski, R.; Leferink, F. Electromagnetic Interference of Spread-Spectrum Modulated Power Converters in G3-PLC Power Line Communication Systems. IEEE Lett. Electromagn. Compat. Pract. Appl. 2021, 3, 118–122. [Google Scholar] [CrossRef]
- Bendicks, A.; Frei, S.; Hees, N.; Wiegand, M. Systematic Reduction of Peak and Average Emissions of Power Electronic Converters by the Application of Spread Spectrum. IEEE Trans. Electromagn. Compat. 2018, 60, 1571–1580. [Google Scholar] [CrossRef]
- Mukherjee, R.; Patra, A.; Banerjee, S. Impact of a frequency modulated pulsewidth modulation (PWM) switching converter on the input power system quality. IEEE Trans. Power Electron. 2010, 25, 1450–1459. [Google Scholar] [CrossRef]
- Li, H.G.; Cai, W.Y.; Gong, S.D. Chaotic spread spectrum for EMI reduction in DC-DC converter. In Proceedings of the 2017 IEEE 6th Asia-Pacific Conference on Antennas and Propagation, APCAP 2017—Proceeding, Xi’an, China, 16–19 October 2018; pp. 1–3. [Google Scholar]
- Callegari, S.; Rovatti, R.; Setti, G. Spectral properties of chaos-based FM signals: Theory and simulation results. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2003, 50, 3–15. [Google Scholar] [CrossRef]
- Cano, C.; Pittolo, A.; Malone, D.; Lampe, L.; Tonello, A.M.; Dabak, A. State of the art in Power Line Communications: From the Applications to the Medium. IEEE J. Sel. Areas Commun. 2016, 34, 1935–1952. [Google Scholar] [CrossRef]
- Matanza, J.; Alexandres, S.; Rodriguez-Morcillo, C. Performance evaluation of two narrowband PLC systems: PRIME and G3. Comput. Stand Interfaces 2013, 36, 198–208. [Google Scholar] [CrossRef]
- Sayed, W.E.; Lezynski, P.; Smolenski, R.; Moonen, N.; Thomas, D.W.P. The Effect of EMI Generated from Spread-Spectrum-Modulated SiC-Based Buck Converter on the G3-PLC Channel. Electronics 2021, 10, 1416. [Google Scholar] [CrossRef]
- Elsayed, W.W.S. The Effect of Spread–Spectrum Modulated EMI on the Power Line Communication Systems. Ph.D. Thesis, University of Zielona Gora, Zielona Góra, Poland, 2024. [Google Scholar]
- Lambros, S.; Athanasiou, D.I.; Fotiadis, L.K. (Eds.) Michalis, Propagation of Segmentation and Imaging System Errors. In Michalis, Atherosclerotic Plaque Characterization Methods Based on Coronary Imaging; Academic Press: Cambridge, MA, USA, 2017; pp. 151–166. ISBN 9780128047347. [Google Scholar] [CrossRef]


| The central switching frequency | 63 kHz |
| Duty cycle | 50% |
| Modulating signal | PAM, sawtooth, and sinusoidal |
| Modulating signal sampling frequency | Varies from 30 Hz to 60 kHz |
| Modulating signal frequency | Varies from 0.3 to 600 Hz |
| Spreading factor () | 15% |
| Modulating Signal | Correlation Factor |
|---|---|
| Sawtooth | −0.954 |
| Sine wave | −0.6551 |
| RandomPAM | 0.07009 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
ElSayed, W.; Madi, A.; Lezynski, P.; Smolenski, R.; Crovetti, P. Performance of G3-PLC Channel in the Presence of Spread Spectrum Modulated Electromagnetic Interference. Signals 2025, 6, 33. https://doi.org/10.3390/signals6030033
ElSayed W, Madi A, Lezynski P, Smolenski R, Crovetti P. Performance of G3-PLC Channel in the Presence of Spread Spectrum Modulated Electromagnetic Interference. Signals. 2025; 6(3):33. https://doi.org/10.3390/signals6030033
Chicago/Turabian StyleElSayed, Waseem, Amr Madi, Piotr Lezynski, Robert Smolenski, and Paolo Crovetti. 2025. "Performance of G3-PLC Channel in the Presence of Spread Spectrum Modulated Electromagnetic Interference" Signals 6, no. 3: 33. https://doi.org/10.3390/signals6030033
APA StyleElSayed, W., Madi, A., Lezynski, P., Smolenski, R., & Crovetti, P. (2025). Performance of G3-PLC Channel in the Presence of Spread Spectrum Modulated Electromagnetic Interference. Signals, 6(3), 33. https://doi.org/10.3390/signals6030033








