Interpretability of Methods for Switch Point Detection in Electronic Dance Music
Abstract
1. Introduction
2. Related Work
2.1. Methods for MSA
2.1.1. Checkerboard Kernel (CK)
2.1.2. Structural Feature (SF)
2.1.3. Fusion Method (CK and SF)
2.1.4. Spectral Clustering (SC)
2.1.5. Ordinal Linear Discriminant Analysis (OLDA)
2.2. Methods for Switch Point Detection
2.3. Datasets
- A switch point is always located on the downbeat at the start of a period.
- A switch point marks a position of high novelty in features such as rhythmic density, loudness, instrumental layers, and/or harmony.
- Switch points are located in the initial portion of the track that precedes the first point of salience.
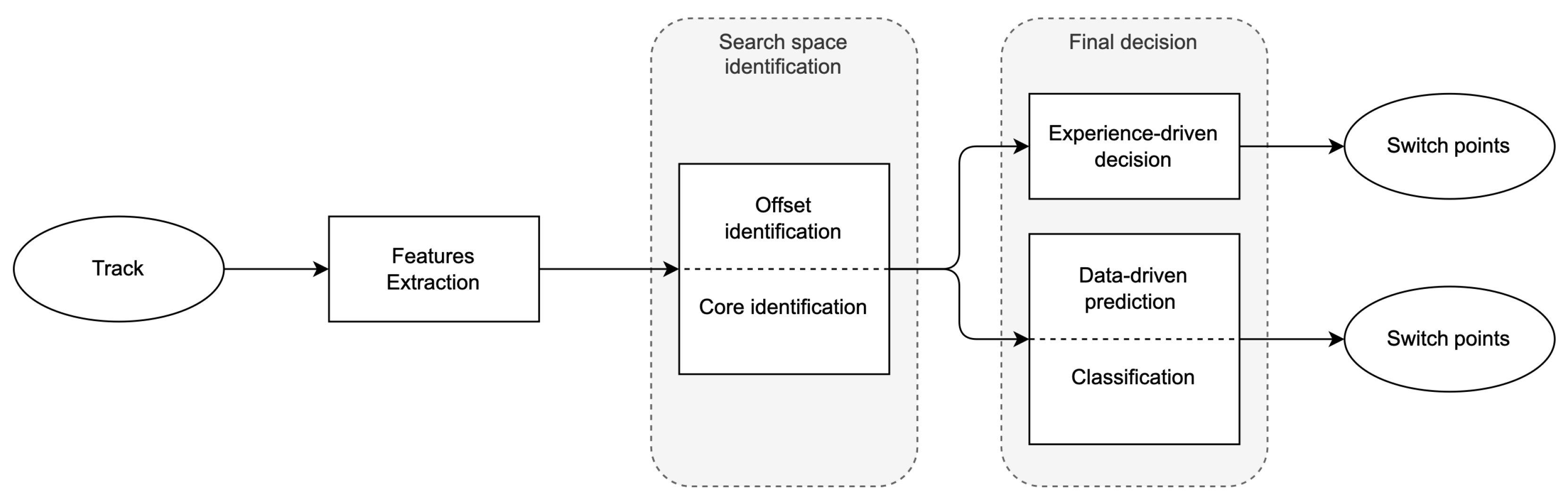
3. Methods
3.1. Search Space Identification
3.1.1. Regularity
3.1.2. Predictability
3.2. Final Decision
3.3. Experience-Driven
3.4. Data-Driven
3.4.1. Deep Learning (DL)
3.4.2. Linear Classification—Linear Discriminant Analysis (LC-LDA)
3.4.3. Nonlinear Classification—Decision Tree (NLC-DT)
3.4.4. Nonlinear Classification—Gradient Boosting Decision Trees (NLC-GBDTs)
4. Evaluation
4.1. Evaluation Metrics
4.2. Experience-Driven Approach
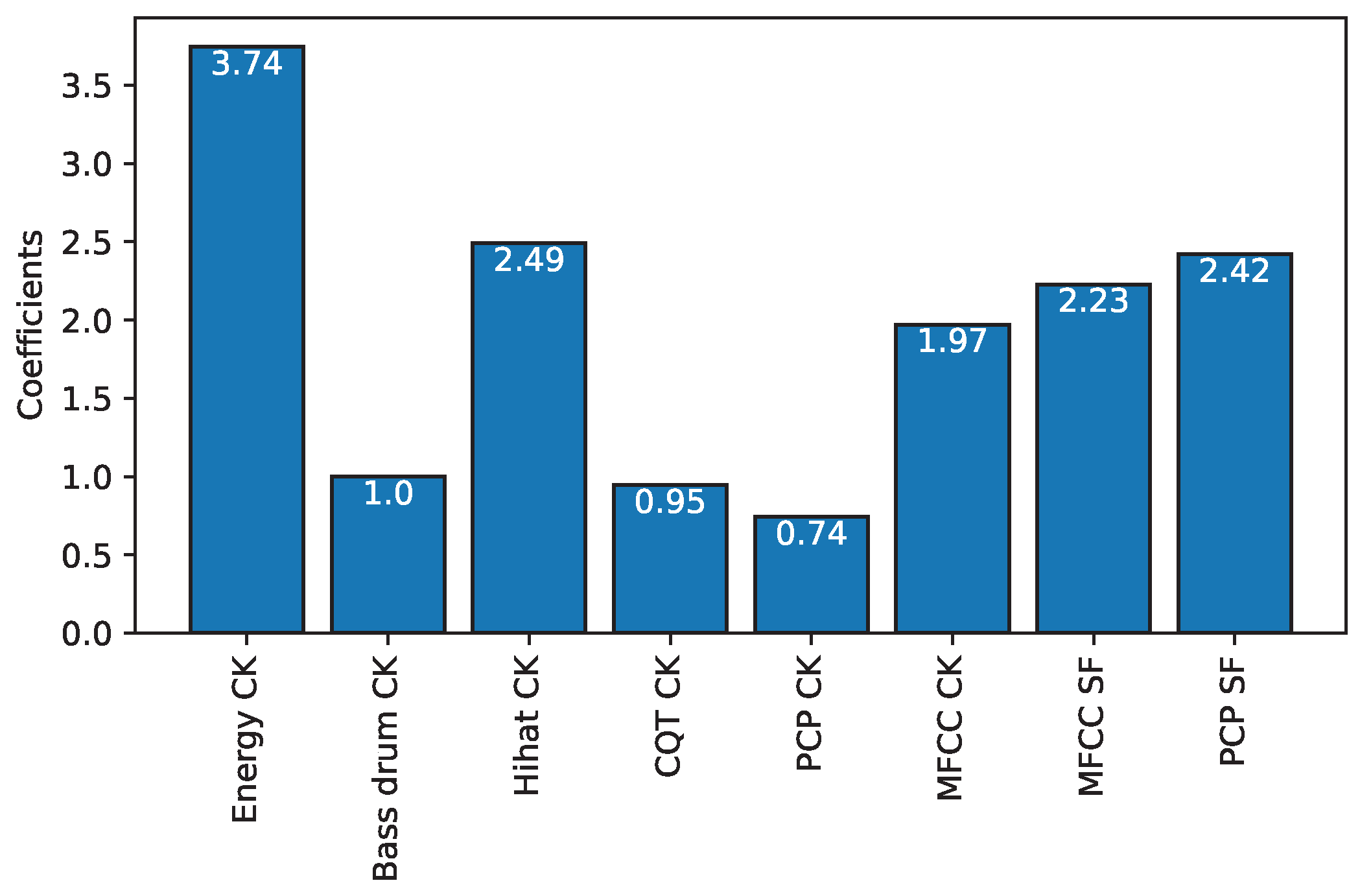
4.3. LC-LDA
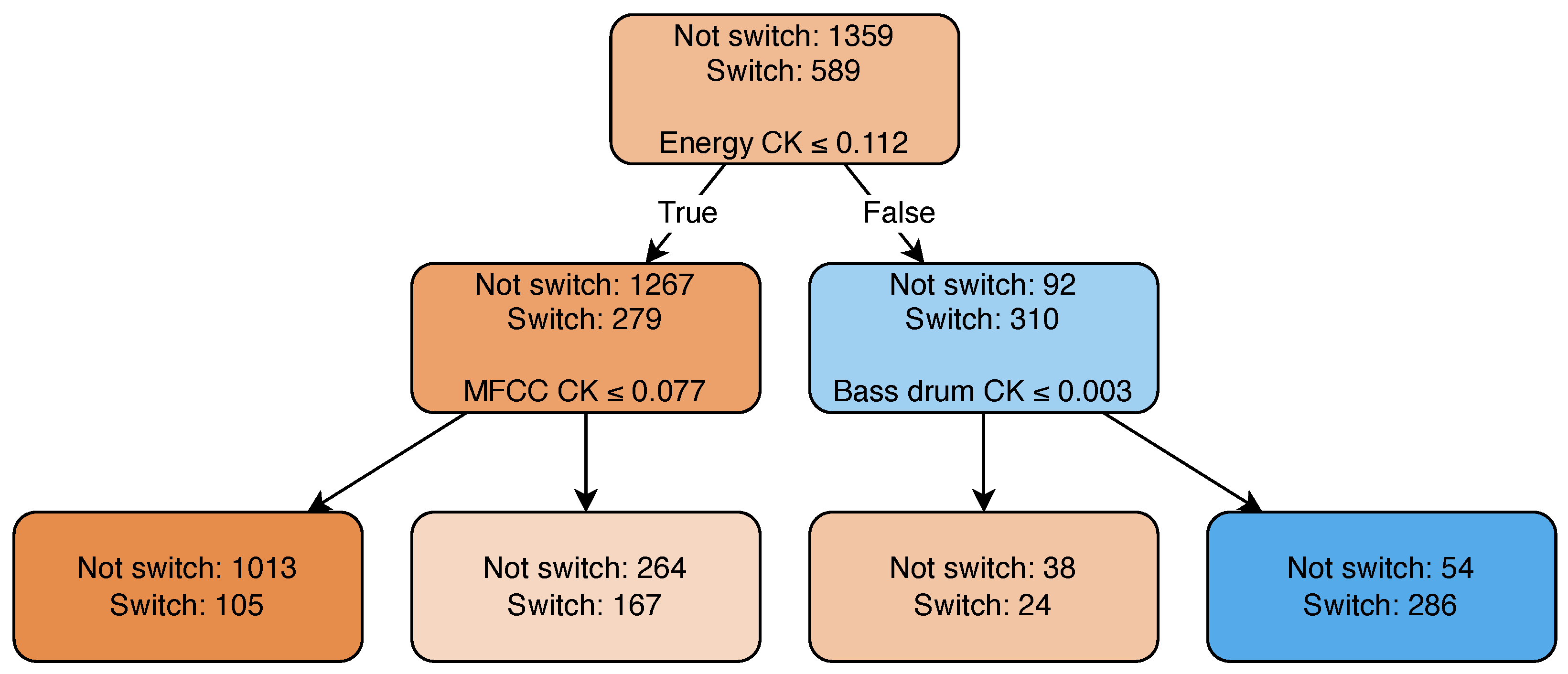
4.4. NLC-DT
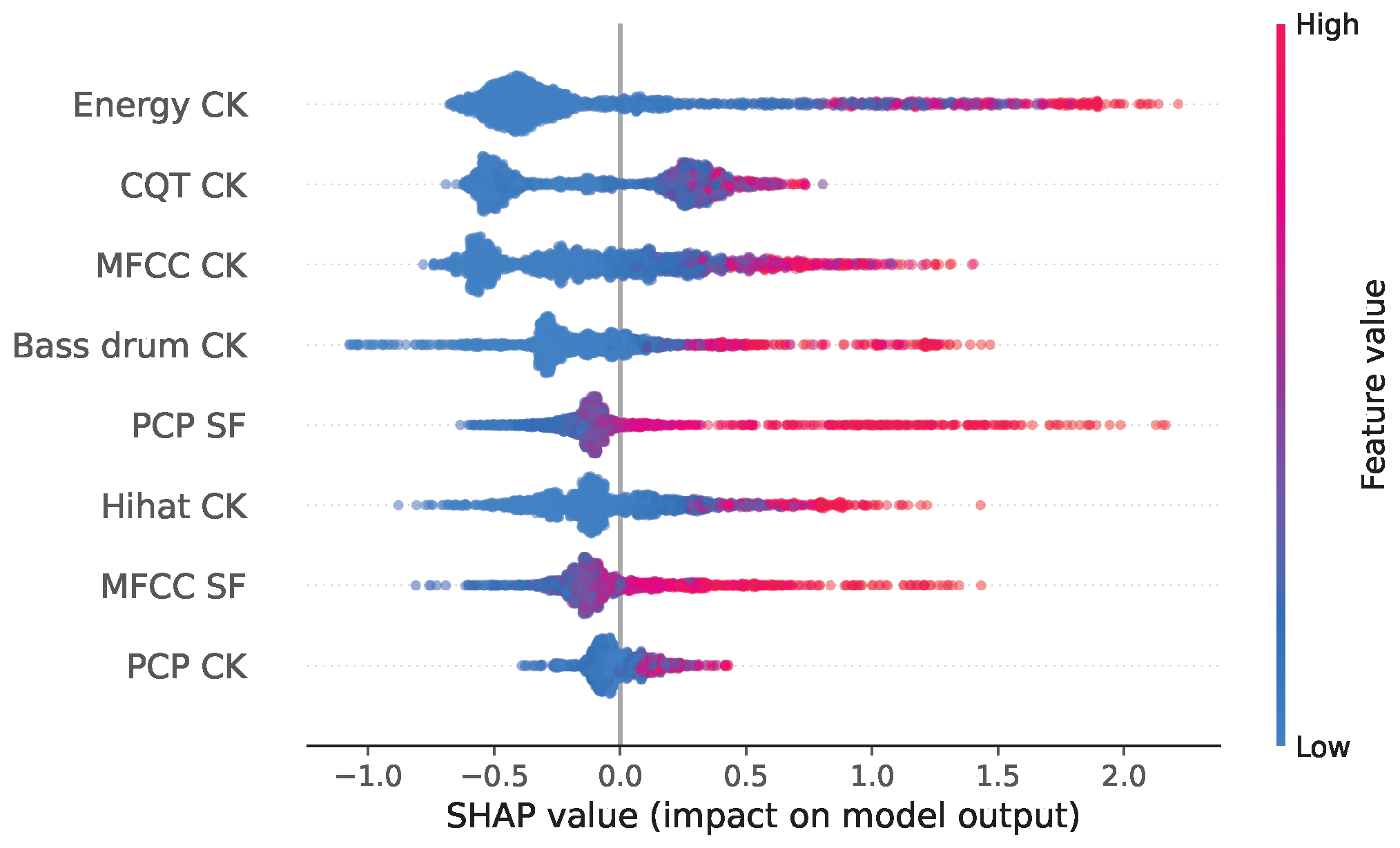
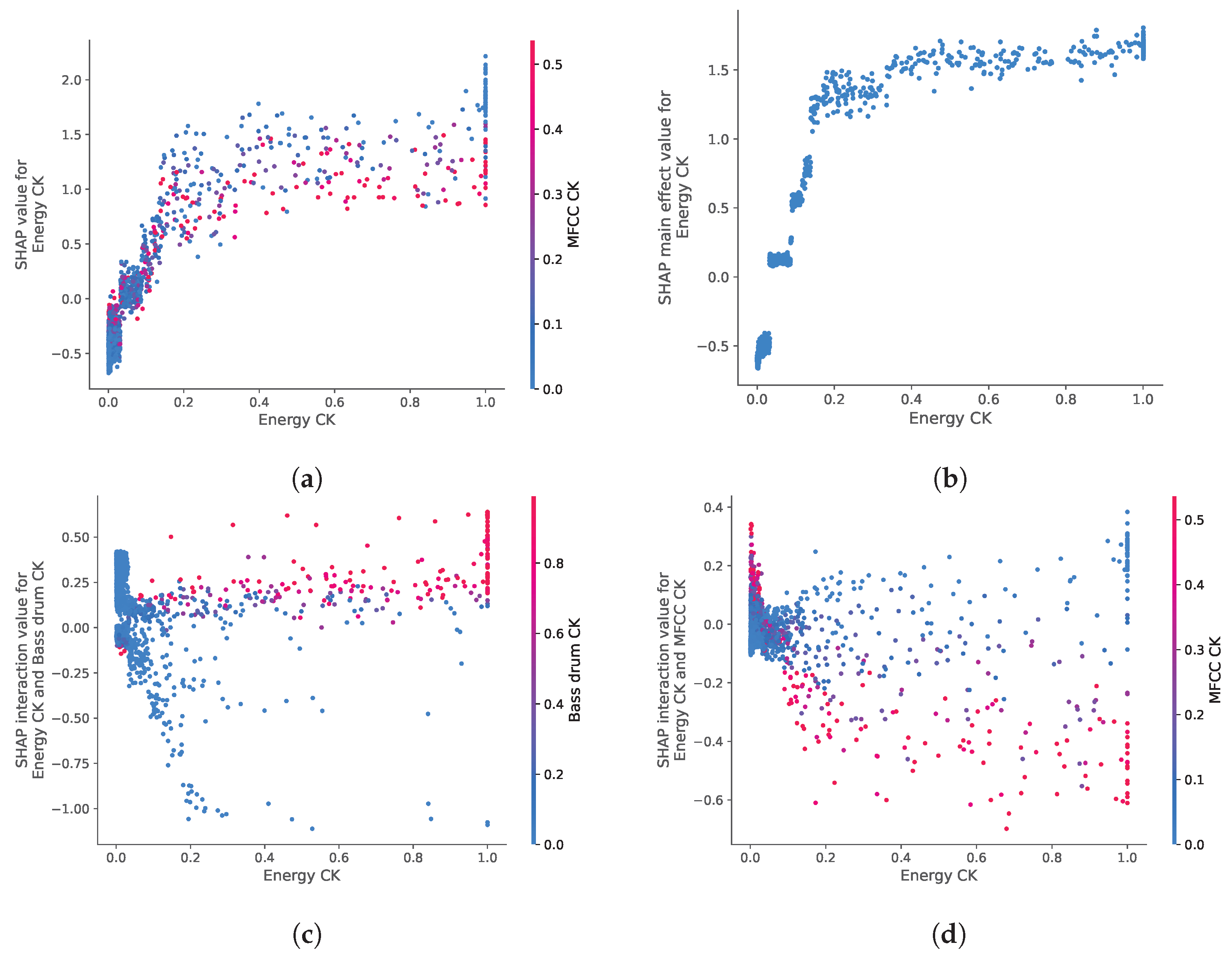
4.5. NLC-GBDT
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Butler, M.J. Unlocking the Groove: Rhythm, Meter, and Musical Design in Electronic Dance Music. Ph.D. Thesis, Indiana University, Bloomington, IN, USA, 2003. [Google Scholar]
- Zehren, M.; Alunno, M.; Bientinesi, P. Automatic Detection of Cue Points for the Emulation of DJ Mixing. Comput. Music. J. 2022, 46, 16. [Google Scholar] [CrossRef]
- Kell, T.; Tzanetakis, G. Empirical Analysis of Track Selection and Ordering in Electronic Dance Music using Audio Feature Extraction. In Proceedings of the 14th International Society for Music Information Retrieval Conference, ISMIR 2013, Curitiba, Brazil, 4–8 November 2013; pp. 505–510. [Google Scholar]
- Kim, T.; Choi, M.; Sacks, E.; Yang, Y.H.; Nam, J. A Computational Analysis of Real-World DJ Mixes using Mix-To-Track Subsequence Alignment. In Proceedings of the 21st International Society for Music Information Retrieval Conference, Virtual, 11–16 October 2020; pp. 764–770. [Google Scholar]
- Bittner, R.M.; Gu, M.; Hernandez, G.; Humphrey, E.J.; Jehan, T.; McCurry, P.H.; Montecchio, N. Automatic Playlist Sequencing and Transitions. In Proceedings of the 18th International Society for Music Information Retrieval Conference, Suzhou, China, 23–27 October 2017; pp. 472–478. [Google Scholar]
- Paulus, J.; Klapuri, A. Audio-based music structure analysis. In Proceedings of the 11th International Society for Music Information Retrieval, Utrecht, The Netherlands, 9–13 August 2010; pp. 625–636. [Google Scholar]
- Wang, J.C.; Smith, J.B.L.; Lu, W.T.; Song, X. Supervised Metric Learning for Music Structure Features. In Proceedings of the 22th International Society for Music Information Retrieval Conference, Online, 7–12 November 2021; pp. 730–737. [Google Scholar]
- Foote, J. Automatic audio segmentation using a measure of audio novelty. In Proceedings of the IEEE International Conference on Multimedia and Expo, New York, NY, USA, 30 July–2 August 2000; Volume 1, pp. 452–455. [Google Scholar] [CrossRef]
- Serra, J.; Muller, M.; Grosche, P.; Arcos, J.L. Unsupervised Music Structure Annotation by Time Series Structure Features and Segment Similarity. IEEE Trans. Multimed. 2014, 16, 1229–1240. [Google Scholar] [CrossRef]
- Kaiser, F.; Peeters, G. A simple fusion method of state and sequence segmentation for music structure discovery. In Proceedings of the 14th International Society for Music Information Retrieval Conference, Curitiba, Brazil, 4–8 November 2013. [Google Scholar]
- McFee, B.; Ellis, D.P.W. Analyzing song structure with spectral clustering. In Proceedings of the 15th International Society for Music Information Retrieval Conference, Taipei, Taiwan, 27–31 October 2014; pp. 405–410. [Google Scholar]
- Nieto, O.; Mysore, G.J.; Wang, C.i.; Smith, J.B.L.; Schlüter, J.; Grill, T.; McFee, B. Audio-Based Music Structure Analysis: Current Trends, Open Challenges, and Applications. Trans. Int. Soc. Music Inf. Retr. 2020, 3, 246–263. [Google Scholar] [CrossRef]
- McFee, B.; Ellis, D.P. Learning to segment songs with ordinal linear discriminant analysis. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 5197–5201. [Google Scholar] [CrossRef]
- Nieto, O.; Bello, J.P. Systematic exploration of computational music structure research. In Proceedings of the 17th International Society for Music Information Retrieval Conference, New York City, NY, USA, 7–11 August 2016; pp. 547–553. [Google Scholar]
- Rocha, B.; Bogaards, N.; Honingh, A. Segmentation and Timbre Similarity in Electronic Dance Music. In Proceedings of the 10th Sound and Music Computing Conference, Stockholm, Sweden, 30 July–2 August 2013; pp. 754–761. [Google Scholar]
- Vande Veire, L.; De Bie, T. From raw audio to a seamless mix: Creating an automated DJ system for Drum and Bass. EURASIP J. Audio Speech Music Process. 2018, 2018, 13. [Google Scholar] [CrossRef]
- Davies, M.E.P.; Hamel, P.; Yoshii, K.; Goto, M. AutoMashUpper: Automatic Creation of Multi-Song Music Mashups. IEEE/ACM Trans. Audio Speech Lang. Process. 2014, 22, 1726–1737. [Google Scholar] [CrossRef]
- Yadati, K.; Larson, M.; Liem, C.C.S.; Hanjalic, A. Detecting Drops in Electronic Dance Music: Content based approaches to a socially significant music event. In Proceedings of the 15th International Society for Music Information Retrieval Conference, Taipei, Taiwan, 27–31 October 2014; pp. 143–148. [Google Scholar]
- Schwarz, D.; Schindler, D.; Spadavecchia, S. A Heuristic Algorithm for DJ Cue Point Estimation. In Proceedings of the Sound and Music Computing (SMC), Limassol, Cyprus, 4–7 July 2018. [Google Scholar]
- McCallum, M.C. Unsupervised Learning of Deep Features for Music Segmentation. In Proceedings of the ICASSP 2019—2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019. [Google Scholar] [CrossRef]
- Salamon, J.; Nieto, O.; Bryan, N.J. Deep Embeddings and Section Fusion Improve Music Segmentation. In Proceedings of the 22th International Society for Music Information Retrieval Conference, Online, 7–12 November 2021; p. 8. [Google Scholar]
- Ullrich, K.; Schlüter, J.; Grill, T. Boundary Detection in Music Structure Analysis using Convolutional Neural Networks. In Proceedings of the 15th International Society for Music Information Retrieval Conference, Taipei, Taiwan, 27–31 October 2014. [Google Scholar]
- Grill, T.; Schluter, J. Music boundary detection using neural networks on spectrograms and self-similarity lag matrices. In Proceedings of the 2015 23rd European Signal Processing Conference (EUSIPCO), Nice, France, 31 August–4 September 2015; pp. 1296–1300. [Google Scholar] [CrossRef]
- Wang, J.C.; Hung, Y.N.; Smith, J.B.L. To Catch A Chorus, Verse, Intro, or Anything Else: Analyzing a Song with Structural Functions. In Proceedings of the ICASSP 2022—2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 23–27 May 2022; pp. 416–420. [Google Scholar] [CrossRef]
- Peeters, G. The Deep Learning Revolution in MIR: The Pros and Cons, the Needs and the Challenges. In Perception, Representations, Image, Sound, Music; Kronland-Martinet, R., Ystad, S., Aramaki, M., Eds.; Series Title: Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2021; Volume 12631, pp. 3–30. [Google Scholar] [CrossRef]
- Schwarz, D.; Fourer, D. Methods and Datasets for DJ-Mix Reverse Engineering. In Perception, Representations, Image, Sound, Music; Kronland-Martinet, R., Ystad, S., Aramaki, M., Eds.; Springer: Cham, Switzerland, 2021; pp. 31–47. [Google Scholar]
- McFee, B.; Raffel, C.; Liang, D.; Ellis, D.; McVicar, M.; Battenberg, E.; Nieto, O. librosa: Audio and Music Signal Analysis in Python. In Proceedings of the SciPy, Austin, TX, USA, 6–12 July 2015; pp. 18–24. [Google Scholar] [CrossRef]
- Vogl, R.; Widmer, G.; Knees, P. Towards multi-instrument drum transcription. In Proceedings of the 21th International Conference on Digital Audio Effects (DAFx-18), Aveiro, Portugal, 4–8 September 2018. [Google Scholar]
- Böck, S.; Krebs, F.; Widmer, G. Joint Beat and Downbeat Tracking with Recurrent Neural Networks. In Proceedings of the 17th International Society for Music Information Retrieval Conference, New York City, NY, USA, 7–11 August 2016; pp. 255–261. [Google Scholar]
- Hosmer, D.W.; Lemeshow, S. Applied Logistic Regression, 2nd ed.; Wiley Series in Probability and Statistics; Wiley: New York, NY, USA, 2000. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer Series in Statistics; Springer: New York, NY, USA, 2009. [Google Scholar]
- Raffel, C.; McFee, B.; Humphrey, E.J.; Salamon, J.; Nieto, O.; Liang, D.; Ellis, D.P.W. mir_eval: A transparent implementation of common MIR metrics. In Proceedings of the 15th International Society for Music Information Retrieval Conference (ISMIR), Taipei, Taiwan, 27–31 October 2014; pp. 367–372. [Google Scholar]
- Cawley, G.C.; Talbot, N.L.C. On Over-fitting in Model Selection and Subsequent Selection Bias in Performance Evaluation. J. Mach. Learn. Res. 2010, 11, 2079–2107. [Google Scholar]
- Molnar, C. Interpretable Machine Learning: A Guide for Making Black Box Models Explainable, 2nd ed.; Independently Published; 2022; Available online: https://christophm.github.io/interpretable-ml-book/index.html (accessed on 24 September 2024).
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.I. From local explanations to global understanding with explainable AI for trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef] [PubMed]


| Work | Features | Decision Rules |
|---|---|---|
| [15] | MFCC with CK | PP and period quantization |
| [17] | (Semitone) PCP with CK | PP and period quantization |
| [18] | (Harmonic) PCP with SF | PP |
| [5] | CQT and MFCC | SC |
| [16] | MFCC and energy with CK | PP and period quantization |
| [19] | Timbre and PCP with fusion (CK and SF) | PP and loudness and position |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zehren, M.; Alunno, M.; Bientinesi, P. Interpretability of Methods for Switch Point Detection in Electronic Dance Music. Signals 2024, 5, 642-658. https://doi.org/10.3390/signals5040036
Zehren M, Alunno M, Bientinesi P. Interpretability of Methods for Switch Point Detection in Electronic Dance Music. Signals. 2024; 5(4):642-658. https://doi.org/10.3390/signals5040036
Chicago/Turabian StyleZehren, Mickaël, Marco Alunno, and Paolo Bientinesi. 2024. "Interpretability of Methods for Switch Point Detection in Electronic Dance Music" Signals 5, no. 4: 642-658. https://doi.org/10.3390/signals5040036
APA StyleZehren, M., Alunno, M., & Bientinesi, P. (2024). Interpretability of Methods for Switch Point Detection in Electronic Dance Music. Signals, 5(4), 642-658. https://doi.org/10.3390/signals5040036






