Learning with Errors: A Lattice-Based Keystone of Post-Quantum Cryptography

Abstract

The swift advancement of quantum computing devices holds the potential to create robust machines that can tackle an extensive array of issues beyond the scope of conventional computers. Consequently, quantum computing machines create new risks at a velocity and scale never seen before, especially with regard to encryption. Lattice-based cryptography is regarded as post-quantum cryptography’s future and a competitor to a quantum computer attack. Thus, there are several advantages to lattice-based cryptographic protocols, including security, effectiveness, reduced energy usage and speed. In this work, we study the learning with errors (LWE) problem and the cryptosystems that are based on the LWE problem and, in addition, we present a new efficient variant of LWE cryptographic scheme.

1. Introduction

The evolution of quantum computing involves a convergence of advancements in quantum theory, hardware engineering, algorithm development and interdisciplinary research. The field continues to progress rapidly, and while large-scale, fault-tolerant quantum devices suitable for broad applications may be some years away, the steady evolution suggests promising future potential for quantum technologies in various domains, like cryptography, economy, drug development, geology and others. The institutionalization by law of the United States’ government in the 2018 National Quantum Initiative Act, “to accelerate quantum research and development for the economic and national security of the United States” [1], is indicative of this potential.

Quantum computing uses quantum physics properties to process information in ways that classical computers cannot [2]. The foundations of quantum devices lie in the principles of quantum mechanics, such as qubits—the equivalent of the bit in a classical computer—superposition and entanglement. With the development of quantum algorithms, quantum machines process vast amounts of information simultaneously, providing potential speedups for highly interconnected and parallel computations [3]. Quantum computers have immense potential to revolutionize various fields, like cryptography, and optimize complex systems more efficiently than classical algorithms, offering speedups for certain types of tasks.

Since antiquity, cryptography has played a crucial role in everyday life, ensuring the confidentiality, integrity and authenticity of information exchanged over communication channels or devices [4]. Cryptographic schemes encompass various methodologies, algorithms and protocols to protect information and secure data. A principal issue in cryptography is the secure process of sharing cryptographic keys between communicating parties to enable encrypted data. Key exchange ensures that both parties establish a shared secret key without exposing it to potential eavesdroppers or adversaries, and great progress has been made in this field with the evolution of quantum cryptography. Since its initial presentation in 1982 [5], the term “quantum cryptography” has drawn the attention, investigation and financial support of academics, governments and businesses. In 1984, C. Bennett and G. Brassard introduced the first quantum key distribution protocol [6], a groundbreaking concept that paved the way for the appearance and development of other protocols [7,8]. Quantum cryptography, nevertheless, continues to be a pressing matter under investigation, with promising solutions in the fields of quantum key distribution, quantum encryption [9,10] and quantum digital signatures [11]. The above recent advances in the quantum key distribution process and quantum encryption procedure have improved the secret key rate and the signature rate and offer security advantages over typical schemes.

However, with the introduction of a sufficiently large quantum computer, there is no longer any security in present encryption systems. Shor’s algorithm discovery demonstrated that a quantum computer, if realized at scale, could solve certain problems significantly faster than classical computers, like the integer factorization problem and the discrete logarithm problem [12]. The potential impact of Shor’s algorithm on cryptography is major, as it poses a threat to the security of widely used cryptographic schemes, such as RSA and elliptic curve cryptography (ECC). So, this impact has spurred interest in post-quantum cryptography, which aims to develop encryption algorithms and cryptographic protocols that are resistant to quantum attacks.

As the development of quantum computing progresses, post-quantum cryptography aims to develop encryption algorithms and cryptographic protocols that remain secure even in the presence of quantum computers. Some techniques and approaches that are used involve code-based cryptography, multivariate polynomial cryptography, hash-based cryptography and lattice-based cryptography [13].

Early discussions of lattices can be found in the 18th century in the works of mathematicians such as C.F. Gauss and J.L. Lagrange, and in the late 19th and early 20th centuries, H. Minkowski played a pivotal role in advancing the study of lattices and their geometrical properties [14]. The field of lattice theory, as a branch of abstract algebra and order theory, gained momentum in the mid-20th century with the contributions of G. Birkoff [15] and G.C. Rota [16]. It was not until the early 21st century that lattice-based cryptography emerged as a post-quantum cryptographic solution. The hardness of certain lattice problems, such as the shortest vector problem (SVP), the closest vector problem (CVP) and the learning with errors (LWE) problem, formed the basis for developing cryptographic schemes resistant to quantum attacks.

The learning with errors (LWE) cryptosystem is critically important for post-quantum cryptography and is regarded as one of the leading candidates for creating cryptographic schemes resilient to attacks from both classical and quantum computers. It is based on the namesake LWE problem, which is a fundamental problem in lattice-based cryptography. The LWE cryptographic scheme is a cornerstone of many cryptographic protocols whose security is founded on the belief that solving LWE on a classical or quantum computer is computationally difficult, even for quantum computers, thus providing resistance to attacks from powerful quantum algorithms, like Shor’s algorithm. Various cryptographic primitives crucial for post-quantum security, both encryption and digital signature schemes, exploit the complexity of solving LWE to offer security guarantees in a post-quantum setting. These schemes are characterized by their efficiency and practicality and undergo rigorous analysis and scrutiny to ensure their viability and security.

Ongoing research focuses on refining LWE-based cryptographic constructions, optimizing their efficiency and exploring new variants to enhance security further. This active research aims to strengthen and improve the practicality of LWE-based schemes. In this sense, we introduce a variant of the learning with errors cryptographic protocol without modification of its original structure by adding an extra step in the procedure of key generation in the algorithm. In this manuscript, we present a variation of the LWE cryptosystem by introducing a transformation to the protocol’s key generation procedure. This extra phase preserves the security and efficiency of the protocol without increasing its complexity because the operations added to it are simply matrix additions and multiplications and thus do not interact with the remaining parts of the LWE algorithm’s structure. After selecting a specific transformation mapping f, we provide discrete implementations in small dimensions and propose specific cases of our variation.

The rest of the paper is organized as follows. In Section 2, we denote the main definitions and the essential mathematical background, while in Section 3, the basic lattice theory and the computational problems in lattices are presented. In Section 4, we introduce the most widely known and analyzed lattice-based cryptosystems, and in Section 5, we present the learning with errors problem and the original LWE cryptosystem, and we propose a new efficient variant of it. Finally, Section 6 concludes this work, and some future work directions are given.

2. Preliminaries

Firstly, some standard notations are included, and therefore some basic definitions are adduced.

For a positive integer q, let ${\mathbb{Z}}_q=\mathbb{Z}/q\mathbb{Z}$ denote the finite ring of integers modulo q and ${\mathbb{Z}}_q^n$ denote the vector space of dimension n over ${\mathbb{Z}}_q$.

Definition 1. 

The n-dimensional cube of side length ${\rho }_n$ is defined by

$$B_n=\{x_n\in {\mathbb{R}}^n|\forall i\in \{1,\dots n\}:-\frac{{\rho }_n}{2}\le x_i\le \frac{{\rho }_n}{2}\}$$

Definition 2. 

The n-dimensional ball of radius $n^{-c}$ is defined by

$$S_n=\{x\in {\mathbb{R}}^n|\parallel x\parallel \le n^{-c}\}$$

for any positive integer c.

Definition 3. 

For any positive integer n and real positive number s, which is taken to be $s=1$ when omitted, the Gaussian function ${\rho }_s:{\mathbb{R}}^n\to {\mathbb{R}}^{+}$ with width s is defined as

$${\rho }_s\left(x\right):={exp(-\pi \parallel x\parallel }^2/s^2)=\rho (x/s).$$

Definition 4. 

The Gaussian distribution $D_s$ with parameter s over ${\mathbb{R}}^n$ is defined as

$$f\left(x\right):={\rho }_s\left(x\right)/{\int }_{{\mathbb{R}}^n}{\rho }_s\left(z\right)dz={\rho }_s\left(x\right)/s^n.$$

Definition 5. 

For any countable set A and positive parameter s, the discrete Gaussian probability distribution $D_{A,s}$ is defined as

$$D_{A,s}\left(x\right):=\frac{{\rho }_s\left(x\right)}{{\rho }_s\left(A\right)},\forall x\in A.$$

Definition 6. 

For a lattice coset $c+\mathcal{L}\subset {\mathbb{R}}^n$ and positive parameter s, the discrete Gaussian probability distribution $D_{c+\mathcal{L},s}$ is defined as the Gaussian distribution restricted to the coset

$$D_{c+\mathcal{L},s}\left(x\right)\propto \left\{\begin{array}{cc}{\rho }_s\left(x\right)\hfill & ifx\in c+\mathcal{L}\hfill \\ 0\hfill & otherwise\hfill \end{array}\right.$$

Definition 7. 

For $\alpha \in {\mathbb{R}}^{+}$, the distribution ${\mathsf{\Psi }}_{\alpha }$ is the distribution on $\mathbb{T}$ obtained by sampling from a normal variable with mean 0 and standard deriviation $\frac{\alpha }{\sqrt{2\pi }}$ and reducing the result modulo 1,

$$\forall r\in [0,1),{\mathsf{\Psi }}_{\alpha }\left(r\right):=\sum _{k=-\infty }^{\infty }\frac{1}{\alpha }·exp\left(-\pi {\left(\frac{r-k}{\alpha }\right)}^2\right).$$

3. Lattices

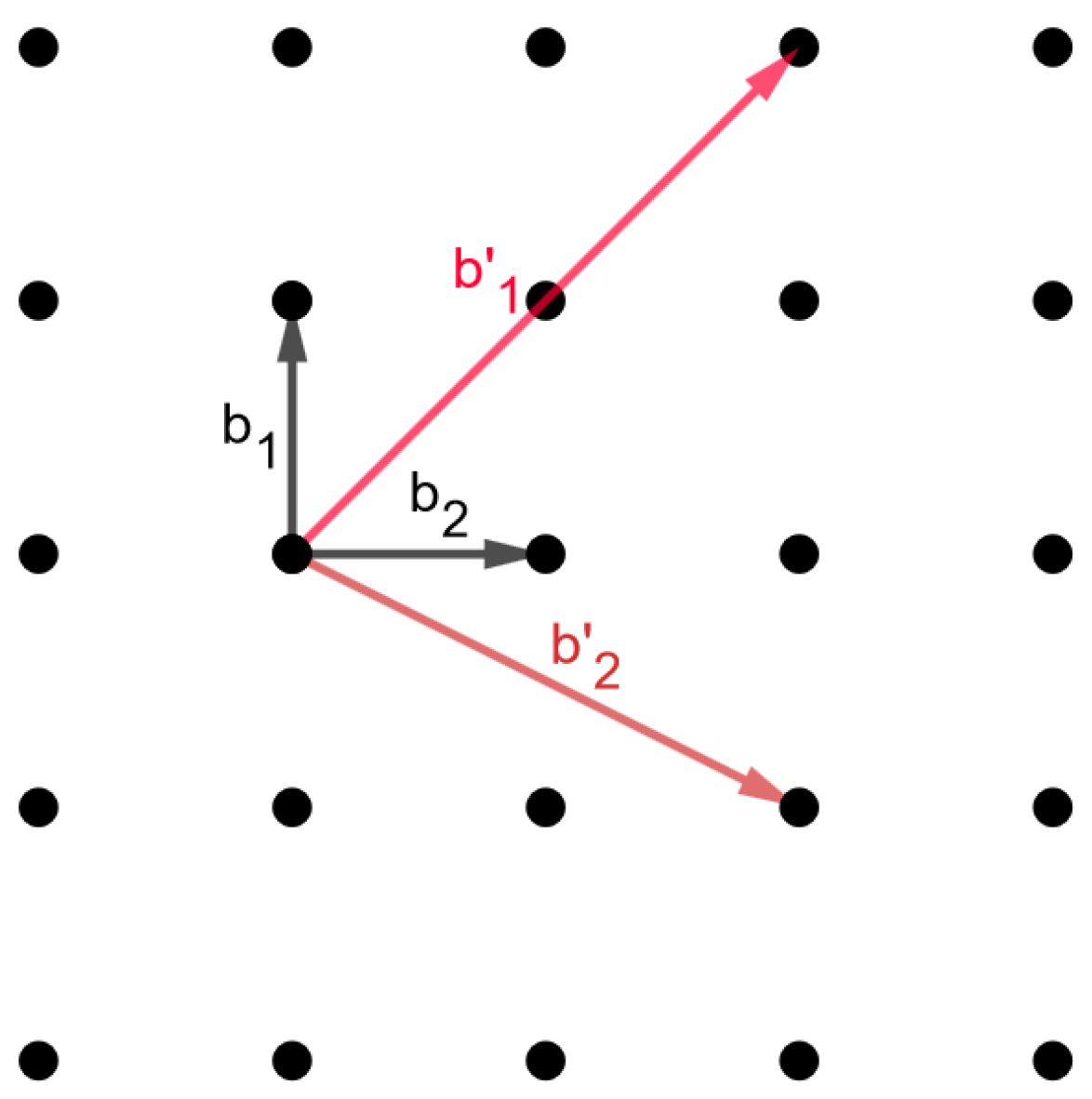
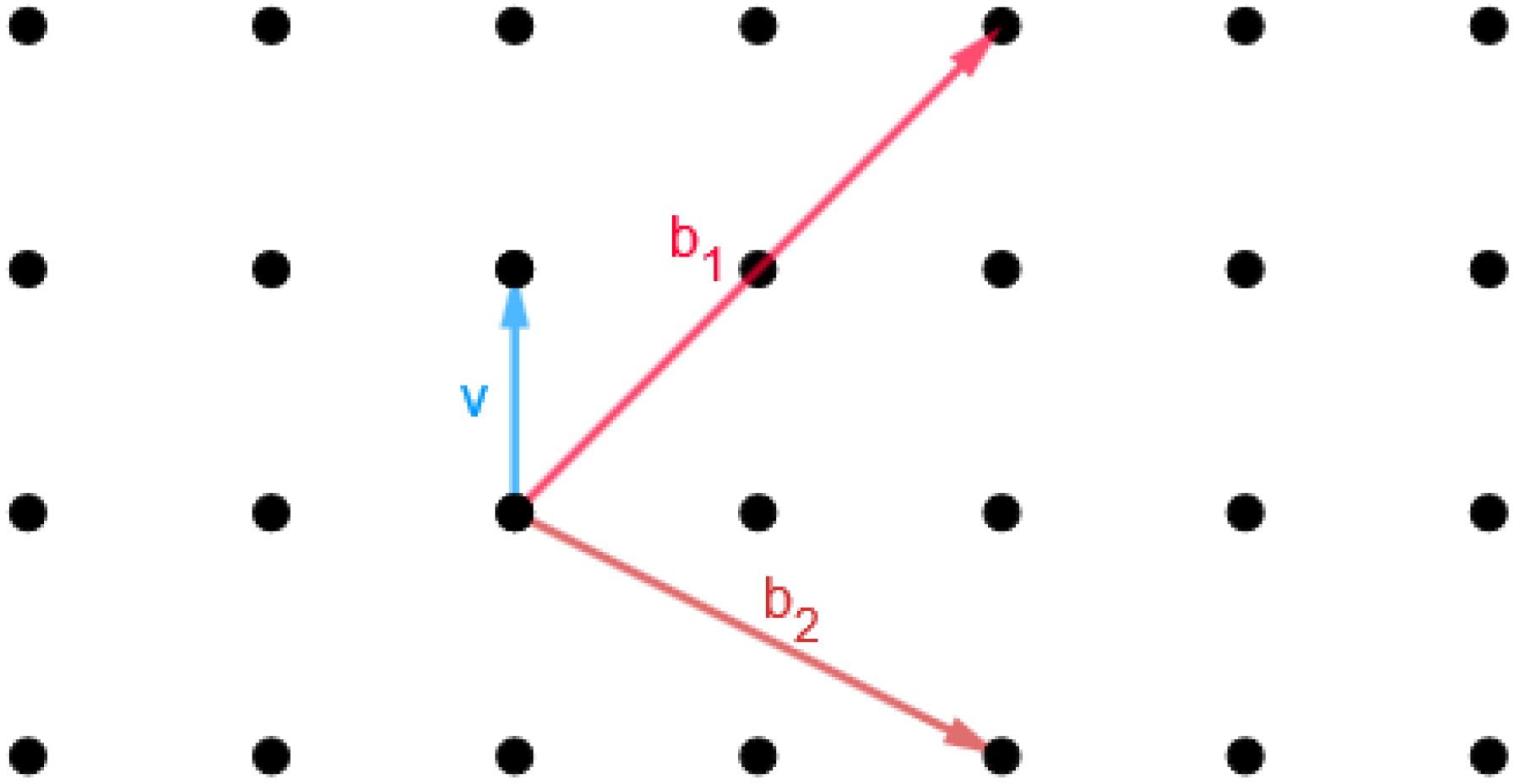
3.1. Basic Definitions

Although lattices have been studied for centuries, mostly because of their associations with quadratic forms and algebraic number theory, interest in their algorithmic aspect began in the 1980’s and since then has become a well-thought-out and crucial tool in the science of cryptology.

An n-dimensional lattice $\mathcal{L}$ can be viewed as an additive, discrete subgroup of ${\mathbb{R}}^n$ possessing a periodic structure. There are certain lattices with particular significance, like the integer lattice, which is a subgroup of ${\mathbb{Z}}^n$, or the scaled lattice $a\mathcal{L}$ for a real number a and a lattice $\mathcal{L}$. Each lattice is generated and described by a set of linearly independent vectors, its basis.

Definition 8. 

A set of vectors $\{b_1,b_2,\dots ,b_m\}\in {\mathbb{R}}^n$ is linearly independent if the equation

$${\lambda }_1{b}_1+{\lambda }_2{b}_2+\cdots +\lambda b_m=0,\mathit{where}{\lambda }_i\in \mathbb{R}$$

accepts only the trivial solution ${\lambda }_1={\lambda }_2=\cdots ={\lambda }_m=0$.

Definition 9. 

Given n linearly independent vectors $b_1,b_2,\dots ,b_m\in {\mathbb{R}}^n$, the lattice generated by them is defined as the set

$$\mathcal{L}(b_1,b_2,\dots ,b_m)=\{\sum _i{x}_i{b}_i:x_i\in \mathbb{Z},1\le i\le n\}$$

The set of the vectors $\{b_1,b_2,\dots ,b_m\}$ is called a basis of the lattice $\mathcal{L}$.

Let B denote the $n\times m$ matrix with columns $b_1,b_2,\dots ,b_m$, then a lattice can be written as

$$\mathcal{L}\left(B\right)=\mathcal{L}(b_1,b_2,\dots ,b_m)=\left\{Bx\right|x\in {\mathbb{Z}}^n\}$$

where $Bx$ is the usual matrix-vector multiplication.

Definition 10. 

The same number, $dim\mathcal{L}$, of elements of all the bases of a lattice $\mathcal{L}$ is called the rank of the lattice since it matches the dimension of the vector subspace spanned by $\mathcal{L}$.

We call m the rank of the lattice and n the dimension. If $n=m$, the lattice $\mathcal{L}$ is called a full-rank lattice.

A lattice $\mathcal{L}$ can be generated by different bases; for example, ${\mathbb{Z}}^2$ has as its basis the vectors $b_1={(1,0)}^T,b_2={(0,1)}^T$ but also the vectors $b_1={(1,1)}^T,b_2={(2,1)}^T$. A lattice generated by two different bases is demonstrated in Figure 1.

This is generalized with the help of the unimodular matrix.

Definition 11. 

A matrix $U\in {\mathbb{Z}}^{n\times n}$ is called unimodular if $detU=\pm 1$.

Theorem 1. 

For a basis B of a lattice $\mathcal{L}$ and any unimodular matrix $U\in {\mathbb{Z}}^{n\times n}$, $B·U$ is also a basis of $\mathcal{L}\left(B\right)$ due to the fact that $U·{\mathbb{Z}}^n={\mathbb{Z}}^n$.

Besides that fact, n independent linear vectors are not necessarily a basis of ${\mathbb{R}}^n$ or ${\mathbb{Z}}^n$; for example, ${(2,0)}^T$ and ${(1,1)}^T$ are not a basis of ${\mathbb{Z}}^2$.

Definition 12. 

Let $\mathcal{L}$ be a lattice with dimension n and $B=\{b_1,b_2,\dots ,b_n\}$ a basis of the lattice. We define the fundamental parallelepiped of $\mathcal{L}$ to be the set

$$\mathcal{P}\left(\mathcal{B}\right)=\left\{Bx\right|x\in {\mathbb{R}}^n,\forall i:0\le x_i<1\}.$$

Definition 13. 

Let $\mathcal{L}=\mathcal{L}\left(\mathcal{B}\right)$ be a lattice of rank n and B a basis of $\mathcal{L}$. The determinant of $\mathcal{L}$ denoted by $det\left(\mathcal{L}\right)$ is the n-dimensional volume of $\mathcal{P}\left(\mathcal{B}\right)$.

The determinant can be written as

$$det\left(\mathcal{L}\left(\mathcal{B}\right)\right)=vol\left(\mathcal{P}\right)\mathrm{and}\mathrm{also}det\left(\mathcal{L}\right)=\sqrt{det\left(B^{T}B\right)}.$$

Definition 14. 

For any lattice $\mathcal{L}=\mathcal{L}\left(\mathcal{B}\right)$, we define the minimum distance of $\mathcal{L}$ as the smallest distance between any two lattice points:

$${\lambda }_1\left(\mathcal{L}\right)=inf\{\parallel x-y\parallel :x,y\in \mathcal{L},x\ne y\}.$$

Clearly, the minimum distance can equivalently be denoted as the length of the shortest nonzero lattice vector:

$${\lambda }_1\left(\mathcal{L}\right)=min\{\parallel v\parallel :v\in \mathcal{L}\setminus \left\{0\right\}\}.$$

where $\left|\right|·\left|\right|$ denotes the Euclidean norm. Generalizing, the ith successive minimum ${\lambda }_i\left(\mathcal{L}\right)$ can be defined as the smallest r such that the lattice $\mathcal{L}$ has i linear independent vectors of norm at most r. The minimum length of a set of independent vectors of a lattice $\mathcal{L}$ is denoted as ${\lambda }_n\left(\mathcal{L}\right)$, where the length of a set is defined as the length of the longest vector in the set.

Definition 15. 

Let V be an arbitrary vector space over a lattice $\mathcal{L}$. An inner product on V is a function $\langle ,\rangle :V\times V\to \mathcal{L}$, which satisfies

1. 

$\langle x,x\rangle \ge 0$ $\forall x\in V$ and $\langle x,x\rangle =0$ iff $x=0$

2. 

$\langle x+y,z\rangle =\langle x,z\rangle \vee \langle y,z\rangle$ $\forall x,y,z\in V$

3. 

$\langle ax,y\rangle =a\langle x,y\rangle$ $\forall x,y\in V$ and $a\in \mathcal{L}$

4. 

$\langle x,y\rangle =\langle y,x\rangle$, $\forall x,y\in V$.

Definition 16. 

Given a lattice $\mathcal{L}\subset {\mathbb{R}}^n$, we define the dual of $\mathcal{L}$ as the set

$${\mathcal{L}}^{*}=\{u:\langle u,\mathcal{L}\rangle \subseteq \mathbb{Z}\}.$$

It is obvious that the dual of a lattice is the set of points whose inner products with the vectors in the lattice $\mathcal{L}$ are integer numbers. Furthermore, the dual of a lattice, ${\mathcal{L}}^{*}$, is also a lattice.

3.2. Computational Lattice Problems

The structure of lattices makes them preferable in cryptography, and some lattices’ problems are believed to be effortless while others are considered intractable. For example, given a set of vector $\{u_1,u_2,\dots ,u_n\}\in {\mathbb{R}}^n$, which generates a lattice L, it is straightforward with an algorithm to compute a basis $\{b_1,b_2,\dots ,b_n\}\in {\mathbb{R}}^n$ of L.

Another undemanding problem is assessing if a given vector u belongs to the lattice L. On the other hand, there are problems in lattice theory, that are believed to be hard.

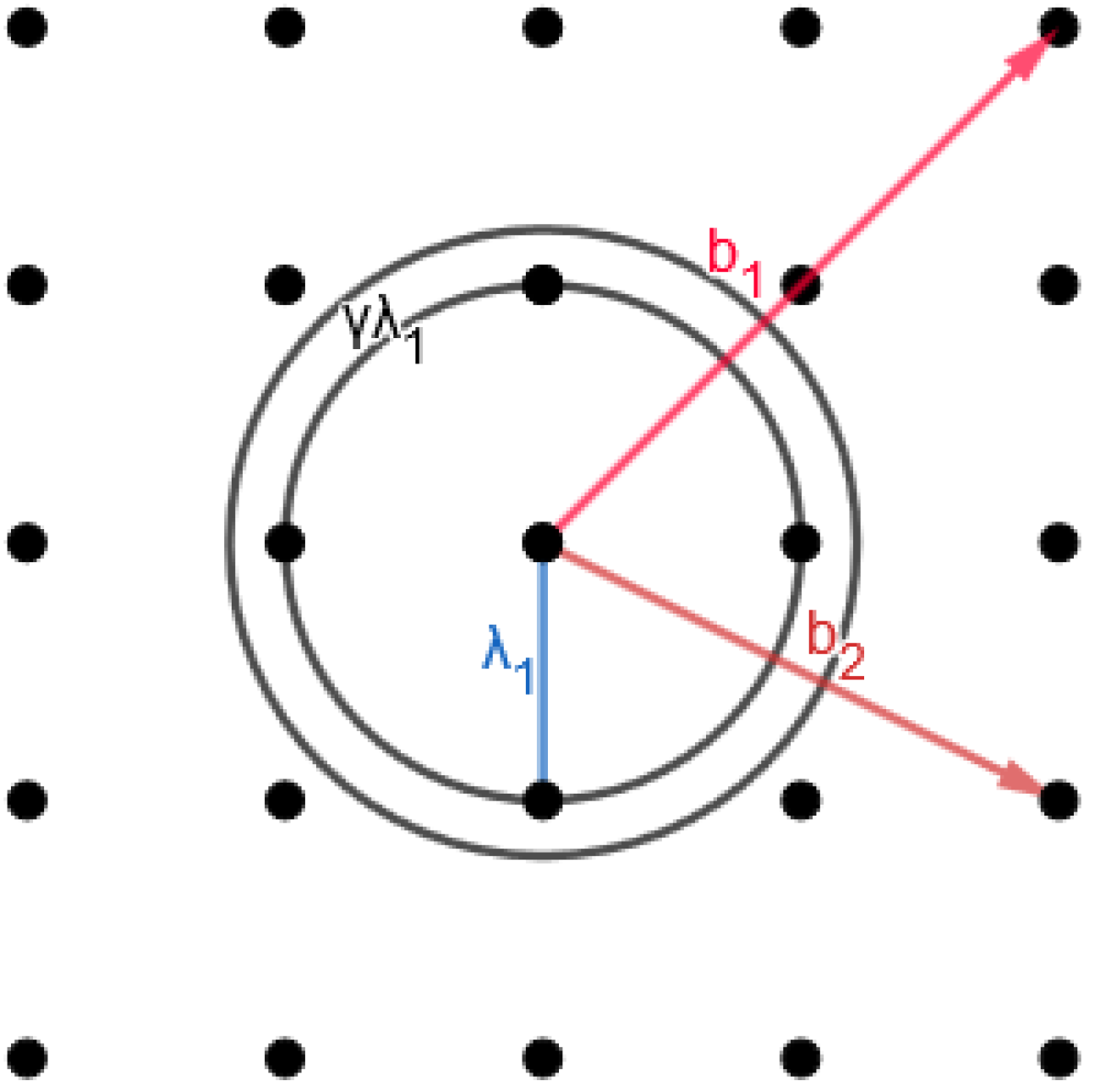
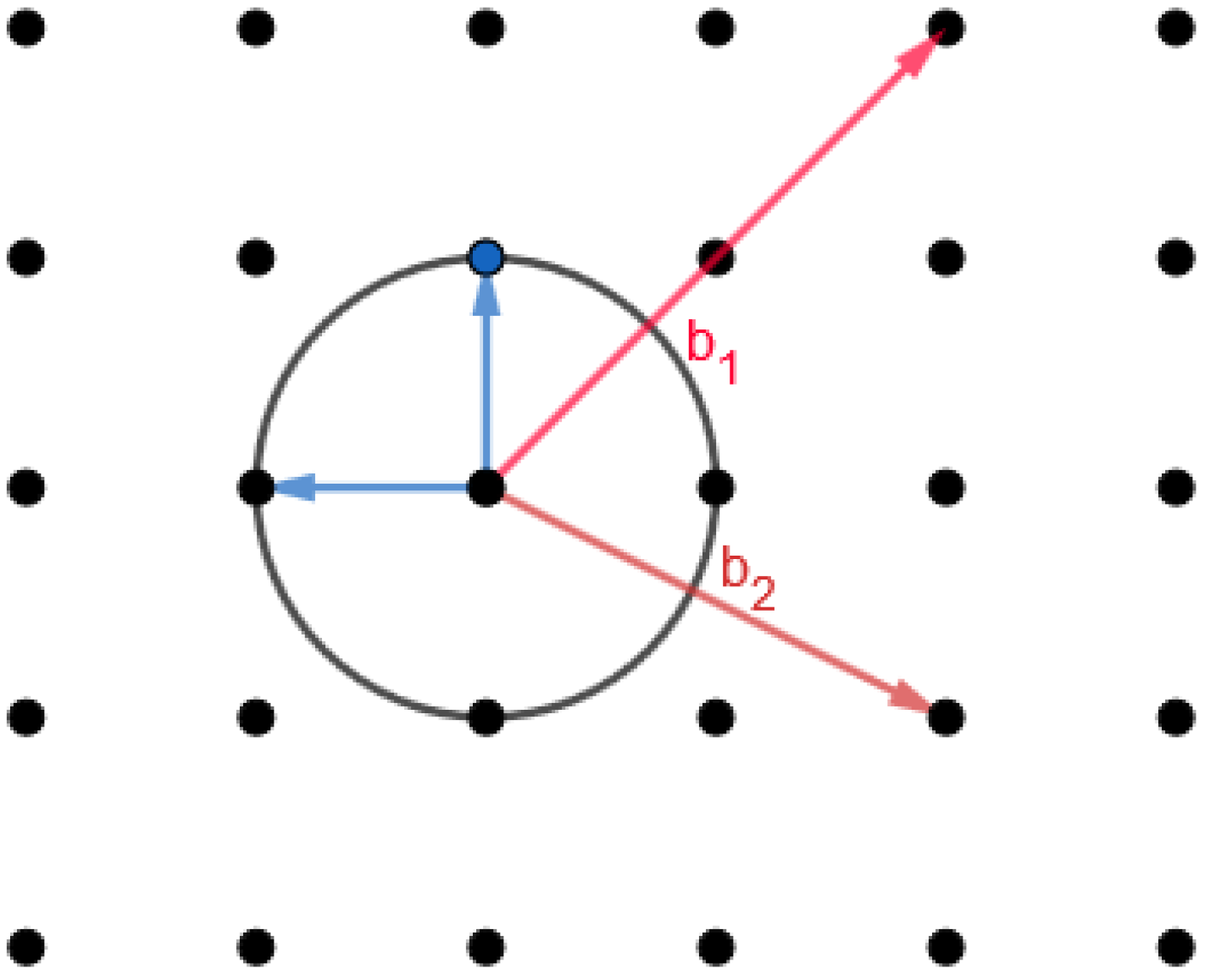
3.2.1. Shortest Vector Problem (SVP)

A computationally challenging lattice problem that has been widely researched over the years is the shortest vector problem (SVP). Renowned mathematicians, like C. F. Gauss, studied lattices and developed algorithms for locating the shortest nonzero vector in two-dimensional lattices. Given a lattice $\mathcal{L}$, the problem of finding the shortest vector in the lattice is a crucial question in lattice theory and is called the shortest vector problem.

Therefore, the requested issue can be considered a search problem. The SVP is defined as follows.

Definition 17. 

(Shortest Vector Problem). Given a basis $B=\{b_1,b_2,\dots ,b_n\}$ of a lattice $\mathcal{L}\left(B\right)$, find the nonzero shortest vector v, i.e., find $v\in \mathcal{L}$ for which $\parallel v\parallel ={\lambda }_1\left(\mathcal{L}\right)$.

Therefore, we search for the nonzero vector v with the minimum norm, i.e., the vector with the minimum distance from the origin, as is shown in Figure 2. Calculating the length of the shortest nonzero vector in the lattice $\mathcal{L}$ without necessarily locating the vector, is a variation of the shortest vector problem. The following theorem is considered one of the most important in lattice theory.

Theorem 2. 

Minkowski’s first theorem. The shortest nonzero vector in any n-dimensional lattice $\mathcal{L}$ has a length, at most, of ${\gamma }_{n}det{\left(\mathcal{L}\right)}^{1/n}$, where ${\gamma }_n$ is an absolute constant (approximately equals to $\sqrt{n}$) that only depends only on the dimension n and $det\left(\mathcal{L}\right)$ is the determinant of the lattice.

Moreover, the same problem can be examined from another perspective, as a decision problem: given a fixed norm, determine if there is a vector with a length less than or equal to this norm. The decision version of the shortest vector problem is denoted as GAPSVP.

For this instance of SVP, we denote $\gamma =\gamma \left(n\right)\ge 1$ as an approximate factor, and we want to determine if there is a vector whose norm is less than a certain norm multiplied by $\gamma \left(n\right)$. This version of the problem can be visualized in Figure 3.

Definition 18. 

(${G\mathit{AP}\mathit{SVP}}_{\gamma }$). Let $\mathcal{L}$ be an n-dimensional lattice and d a positive number; an instance of ${G\mathit{AP}\mathit{SVP}}_{\gamma }$ is given. In YES instances, ${\lambda }_1\left(\mathcal{L}\right)\le d$, whereas in NO instances, ${\lambda }_1\left(\mathcal{L}\right)>\gamma \left(n\right)·d$.

The shortest vector problem is regarded as a challenging mathematical issue, and its hardness is a continuous subject of study. In 1996, M. Ajtai proved that the SVP is NP-hard for a random class of lattices [17], and two years later, D. Micciancio proved that GAPSVP_γ is NP-hard for an approximation factor inferior to $\sqrt{2}$, using the Euclidean norm [18]. The relation between the approximation factor and the hardness of the decisional problem has been studied and improved upon in recent years [19].

Due to that fact, the SVP serves as a building block for cryptographic techniques that can be proven to be safe, such as lattice-based encryption.

3.2.2. Closest Vector Problem (CVP)

Another computational lattice problem that is important for cryptography and is closely related to the shortest vector problem is the closest vector problem (CVP). The CVP asks to find the lattice point of a lattice closest to a given target point.

Let $\mathcal{L}$ be a lattice and a fixed point $t\in {\mathbb{R}}^n$, the distance is defined as follows:

$$d(t,\mathcal{L}):mi{n}_{x\in \mathcal{L}}\parallel x-t\parallel .$$

Definition 19. 

(Closest Vector Problem). Given a basis $B=\{b_1,b_2,\dots ,b_n\}$ of a lattice $\mathcal{L}\left(B\right)$ and a target vector t, not necessarily in the lattice, find the lattice point $v\in \mathcal{L}\left(B\right)$ closest to t.

Therefore, the requested nonzero vector $v\in \mathcal{L}$ is the one for which $\parallel t-v\parallel$ is minimal, i.e., $\parallel v\parallel =d(t,\mathcal{L})$, as presented in Figure 4.

Another useful variation of the CVP calculates the target’s distance from the lattice without determining the lattice’s closest vector, as many applications just require the determination of a lattice vector that is reasonably close to the target, not necessarily the closest one.

For the approximate factor $\gamma =\gamma \left(n\right)\ge 1$, the $\gamma$-approximate closest vector problem (${\mathrm{CVP}}_{\gamma }$) is defined as follows.

Definition 20. 

(${\mathit{CVP}}_{\gamma }$). Given a basis $B=\{b_1,b_2,\dots ,b_n\}$ of a lattice $\mathcal{L}\left(B\right)\subset {\mathbb{R}}^n$ and a point $t\in {\mathbb{R}}^n$, find a $v\in \mathcal{L}$ such that $\parallel t-v\parallel \le \gamma \left(n\right)·dist(t,\mathcal{L})$.

Likewise, the ${\mathrm{CVP}}_{\gamma }$ asks to find a vector of the lattice coset $t+\mathcal{L}$ having norm at most $\gamma \left(n\right)·\lambda (t+\mathcal{L})$, where

$$\lambda (t+\mathcal{L}):=\underset{x\in t+\mathcal{L}}{min}\parallel x\parallel =dist(t,\mathcal{L}).$$

In 1986, L. Babai presented the first approximate polynomial time algorithm to solve the closest vector problem [20] and, in addition, other algorithms have been proposed. One of them is the embedding technique, thanks to Kannan [21] and the Micciancio–Voulgaris algorithm, that solves the closest vector problem in $2^{\mathcal{O}\left(n\right)}$ space and time [22].

The closest vector problem is assumed to be roughly NP-hard to solve within any constant factor [23]. In addition to being an open topic in lattice theory, the task of developing a suitable CVP approximation method with approximation factors that grow as a polynomial in the lattice’s dimension finds many applications in computer science. For all these facts, numerous lattice cryptography systems, in which the decryption process equates to a CVP computation, are based on the CVP.

A similar problem to the approximate closest vector problem ${\mathrm{CVP}}_{\gamma }$ is the bounded-distance decoding problem ${\mathrm{BDD}}_{\gamma }$.

Definition 21. 

(${\mathit{BDD}}_{\gamma }$). Given a basis $B=\{b_1,b_2,\dots ,b_n\}$ of an n-dimensional lattice $\mathcal{L}\left(B\right)$ and a target point $t\in {\mathbb{R}}^n$, for which stands $dist(t,\mathcal{L})<d={\lambda }_1\left(\mathcal{L}\right)/\left(2\gamma \left(n\right)\right)$, find the unique vector v of the lattice $\mathcal{L}$ such that $\parallel t-v\parallel <d$.

This problem is a principal basis in modern cryptosystems, and an average-case of BBD has been employed in innumerable cryptographic schemes, including those that share a lattice among multiple users. The bounded distance decoding problem is proven to be NP-hard, and in 2020, H. Bennett and C. Peikert proved its hardness on lattices in $l_p$ norms under randomized reductions [24].

3.2.3. Shortest Independent Vector Problem (SIVP)

An additional significant computational problem in lattices that has great significance in cryptography is the shortest independent vector problem (SIVP). The main question in this problem is how to minimize the length of the longest vector of the basis. Viewing it from a different angle, the basic task is to find a new basis that generates the same lattice and has the ability to minimize the length of the longest vector. This problem can be visualized in Figure 5.

Definition 22. 

Shortest independent vector problem (SIVP). Given a basis $B=\{b_1,b_2,\dots ,b_n\}$ of a lattice $\mathcal{L}$, find n linearly independent vectors $\{v_1,v_2,\dots ,v_n\}$ that belong to the lattice such that $\parallel v_i\parallel \le {\lambda }_n$ for $1\le i\le n$.

The approximate shortest independent vector problem (${\mathrm{SIVP}}_{\gamma }$) is presented below.

Definition 23. 

(${\mathit{SIVP}}_{\gamma }$). Given a basis $B=\{b_1,b_2,\cdots ,b_n\}$ of a full-rank lattice $\mathcal{L}$, output a set $V=\left\{v_i\right\}\subset \mathcal{L}$ of n linearly independent lattice vectors, such that $\parallel v_i\parallel \le \gamma \left(n\right)·\lambda \left(n\right)\left(\mathcal{L}\right)$ for all i.

This problem has been studied and proven to be NP-hard by a reduction from the closest vector problem to the shortest independent vector problem [25].

3.3. Computational Lattice Problems and Complexity

These lattice problems have all been extensively researched and they are of great importance as they are believed to be difficult aside from having very large approximate factors. A critical issue is finding an interesting, practical and useful basis of a lattice that, from a mathematical perspective, satisfies sufficiently strong features. In 1982, L. Lovasz, A. Lenstra and H. Lenstra proposed a polynomial time algorithm for basis reduction, LLL [26], which approximates, in small dimensions, the solution of the SVP. The LLL algorithm resolves lattice problems within exponential approximation factors $\gamma \left(n\right)$.

Various efforts have tried to improve the LLL algorithm; therefore, there are some variants of it in the literature [27]. Another famous lattice reduction algorithm is the blockwise Korkin–Zolotarev (BKZ) algorithm proposed by C.P. Schnorr and M. Euchner in 1991 [28]. The BKZ algorithm is widely used, frequently found in software libraries and utilized in the majority of lattice record computations as well as cryptanalysis.

The famous lattice problems, SVP, CVP and SIVP, cannot be solved in polynomial time, and the well-known algorithms that use polynomial factors $poly\left(n\right)$, or even better, approximate factors, need superexponential $2^{\mathsf{\Theta }(nlogn)}$ time or exponential $2^{\mathsf{\Theta }\left(n\right)}$ space and time. An important fact is the existence of time–approximation tradeoffs that interpolate between these classes of outcomes to obtain $\gamma =2^k$ approximation factors in $2^{\tilde{\mathsf{\Theta }}(n/k)}$ time, which symbolizes the most advanced quantum algorithms.

Moreover, a cryptosystem whose security depends on the fact that no polynomial time algorithm can solve a given problem may become insecure if, for instance, a quasi-polynomial time solution for that problem is able to run quickly enough. So, in terms of complexity, various computational lattice problems are considered to be NP-hard and the cryptographic protocols that are based in lattice theory use polynomial approximation factors $\gamma \left(n\right)\ge n$.

3.4. Quantum Computers and Lattices

Lattice problems are thought to be difficult, and there are outstanding questions in this branch of study. Indicative of this fact is the existence and operation of the web page https://www.latticechallenge.org/ (accessed on 13 March 2008), which presents sample instances for evaluating algorithms that resolve the shortest vector problem. So, lattices provide one of the most well-known methods for performing post-quantum cryptography, as there are no known algorithms for certain computational lattice problems, and many attempts to devise them have failed.

Conversely, lattices have provided us with means of resolving basic issues in quantum computing and cryptography, such as producing a verifiable stream of truly random coins, creating classical protocols that verify that a quantum computer is operating as intended, and creating a quantum money system. In 1994, P. Shor proposed a polynomial time quantum algorithm for solving the integer factorization and discrete logarithm problems. Current quantum computer technology does not yet allow these problems to be solved with large integers [29]. The quantum routine adopted in Shor’s algorithm, which uses periodicity, does not seem to be suitable for lattice problems. Thus, it leads to the below conjecture that justifies the significance of lattice-based cryptographic schemes for post-quantum cryptography [30].

Conjecture 1. 

There is no polynomial time quantum algorithm that approximates lattice problems within polynomial factors.

The development of quantum algorithms has no impact on our comprehension of lattice difficulties, but there are a few highly interesting connections between quantum algorithms and lattice problems, even though genuine quantum algorithms for lattice problems are unknown. The first instance of this purpose was made by O. Regev in 2004 [31], when Regev showed the connection between lattice problems and quantum computing. In this work, a solution to the unique shortest vector problem was proposed based on the assumption of the existence of an algorithm that solves the hidden subgroup problem in the set-sampling bipartite group. Moreover, the following theorem of Regev was proven, and therefore, a quantum reduction algorithm from $\mathsf{\Theta }\left(n^{2.5}\right)$-unique-SVP to the average case subset sum problem was obtained.

Theorem 3. 

If there is a solution to the dihedral coset problem with failure parameter f, then there exists a quantum algorithm that solves the $\mathsf{\Theta }\left(n^{\frac{1}{2}+2f}\right)$-unique-SVP.

However, quantum algorithms can be helpful to solve certain problems in lattice theory. Suppose there exists an oracle that, given an input of a lattice $\mathcal{L}$ and a target point t, which is close to the lattice, outputs the closest lattice point to t, and if the point t is far from the lattice, the output oracle is unspecified. While in a typical model, this appears to be useless, in a quantum environment, it is different.

Moreover, in recent years, there have been developments in the theory of lattice field applications of quantum computing. Quantum computing presents the possibility of simulating lattice field theories in parameter regimes, such as the sign-problem-plagued regimes of finite baryon density, topological terms and out-of-equilibrium dynamics, which are essentially inaccessible using the traditional Monte Carlo approach [32]. However, quantum computing can be advantageous even in situations where classical and quantum computations are competitive, such as specific parameter regimes of lattice field theory or, more broadly, reduced energy consumption. More importantly, a modest quantum step translates into a huge classical leap whenever one tackles an exponentially challenging classical problem. For example, computations of (3+1)-dimensional lattice gauge theories, including Lattice QCD, require many incremental steps to improve both quantum hardware and quantum algorithms in order to simulate out-of-equilibrium dynamics, where the errors of the best-known classical algorithms grow exponentially in time [32].

In 2023, thirty years after P. Shor, O. Regev proposed a faster algorithm for factorization in a completely new way [33]. Regev’s algorithm decreases the quantity of gates, or logical processes, required to factor extremely large numbers. In theory, this may allow a larger machine to decode the encryption keys more quickly or a smaller quantum computer to discover the hidden keys. This is the first algorithm to enhance the correlation between the number of quantum operations needed to factor a given number and its magnitude. Internet encryption may have progressed to a point where quantum computing is ready to use Regev’s or Shor’s approach to find prime factors. Security chiefs and federal agencies are already switching to substitutes, such as lattice cryptography, which is impervious to quantum hacking.

4. Lattice-Based Cryptography

Although lattices have been studied for centuries, lattice-based cryptographic protocols are considered to be one of the most modern and futuristic tools in the science of cryptology. One of the main arguments for this fact is that lattice-based protocols are considered to be resistant algorithms under quantum attacks and have immediately become a choice for post-quantum cryptography, as we discussed above. However, there are several reasons why lattice-based cryptography is widely studied and preferred over other forms of cryptography.

An additional factor supporting the preference for lattice-based cryptography is the main structure of a lattice-based protocol. The majority of these algorithms are efficient and parallelizable. Moreover, they are characterized by simplicity, and their operations are uncomplicated as they are based on linear and simple operations on matrices and vectors modulo nearly small integers.

Another important feature of lattice-based cryptographic algorithms is the variety of applications in the field of encryption. Lattice-based protocols can successfully perform fully homomorphic encryption, i.e., the computation of encrypted data or ciphertext without revealing any information about the data. Consequently, lattice-based cryptographic schemes are flexible, versatile and powerful for encryption, digital signatures, key transport and authenticated key exchange. In recent years, significant steps have been taken in the construction of this type of cryptosystem based on lattice theory, though it remains an open field of research [34].

The cryptographic schemes that are based on lattices’ structure offer strong security guarantees. They are based on the hypothesis that some mathematical problems in lattice structures are difficult. The security of lattice-based cryptography depends on the worst-case hardness assumptions of the lattice problems. Lattice-based cryptographic schemes will continue to provide a solid basis for safe communication and data protection in a post-quantum world if these certain computational problems are still difficult to resolve, even for quantum computing devices.

Lattice cryptography is gaining the interest of scientists and cryptographers because of the interesting and practical properties of lattices. The development of lattice cryptography has been significant and fundamental to the art of encryption. As a result of this evolution, various cryptosystems have been introduced that are now considered cornerstones for post-quantum cryptography. Subsequently, we present some primitive, well-known and performed constructions of lattice-based cryptography.

In 1996, M. Ajtai proposed the first cryptographic primitive based on lattices and gave the worst-case reduction [17], and in 1997, Ajtai and Dwork introduced a lattice-based asymmetric key cryptosystem that is performed in ${\mathbb{R}}^n$ [35]. This work attracted a lot of interest because of its unexpected security proof that was predicated on the worst-case assumptions [35].

Ajtai’s brilliant idea inspired numerous researchers to turn their academic interest to lattice-based cryptosystems. Although the presented work is indeed amazing, it is regarded as impractical and inefficient due to its long-lasting key generation process, sluggish encryption and large key sizes in larger dimensions. The cryptosystem is not at all functional in dimensions where the lattice problems given in the security proof are hard to solve.

Around the same time, in 1996, J.H. Silverman, J. Pipher and J. Hoffstein proposed another public key cryptographic scheme that can be explained via specially constructed lattices, the NTRU cryptosystem [36]. The NTRU is one of the fastest public key cryptography systems and is based on the shortest vector problem in lattices. It uses polynomial rings to encrypt and decrypt data, as the operations of the cryptographic protocol take place in the ring of polynomials. The NTRU is more efficient than other existing cryptosystems such as RSA and is thought to be immune to threats of a quantum computer, making it a prominent post-quantum cryptosystem. Although the NTRU is a 28-year-old cryptographic scheme, it remains a fundamental lattice-based cryptosystem and a current subject of research. NTRU has been updated several times since its conception to adapt to cryptanalytic developments. During the standardization process of the National Institute of Standards and Technology (NIST) for post-quantum cryptography, several concrete encryption-key encapsulation mechanism (KEM) and NTRU-based signature techniques were presented [37]. Concerning the KEM, two candidates, NTRUEncrypt and NTRU-HRSS-KEM, were fused to form a scheme known as “NTRU”. The system is relatively simple to be performed in constant time and has a high performance rate, allowing it to be used in production. Moreover, Falcon, an NTRU-based signature scheme, also reached the final round of standardization, as it is distinguished by extremely quick execution and small key sizes [37]. Other characteristics that made it stand out are its compactness, scalability, flexibility, memory economy and, of course, security.

The McEliece cryptographic scheme [38] was the ancestor of the cryptographic scheme introduced by O. Goldreich, S. Goldwasser and S. Halevi in 1997, the GGH cryptosystem [39]. Inspired by the McEliece cryptosystem, in which the private and public keys are representations of a linear code, GGH enables us to understand well the use of lattices in cryptography.

The basic idea of constructing the cryptosystem is to have a “good basis” of a lattice, representing the private key, and a “bad basis” of the same lattice, representing the public key. In both cryptographic schemes, the plaintext is added with a noise vector, and the result of their addition is the ciphertext. The fundamental difference between these two cryptographic systems is that the domains in which the operations take place are distinct. A discrete implementation of GGH, NTRU and the cryptosystem presented below in this work, LWE, was introduced in [40].

According to its three creators, the increase in the key size of the GGH cryptosystem compensates for the decrease in computational time. A few years later, D. Micciancio proposed a simple way to minimize both the key size and the ciphertext without reducing the level of security [41,42].

Several attacks have been performed [43,44,45] that demonstrated the fragility and vulnerability of the GGH cryptosystem, so many researchers then considered GGH useless. Despite being regarded as one of the most prominent lattice-based cryptosystems and maintaining theoretical relevance, it is not recommended for practical application due to security flaws. GGH is inefficient in comparison to other stronger and more efficient lattice-based cryptosystems like NTRU and learning with errors (LWE) due to its weakness to these preformed attacks [40].

Besides encryption and decryption cryptographic schemes, one important cryptographic primitive used in electronic data transfer is digital signatures, which ensure the authenticity of the messages transmitted. The high-level concepts for lattice-based signatures are similar to the previous digital signature schemes, but the technical details are far more complicated. The main source of difficulty is the distinct algebraic structure of the hard one-way function that underpins lattice cryptography.

Typically, mathematical operations are performed inside a lattice structure in a lattice-based digital signature protocol. Certain lattice problems, such as the learning with errors (LWE) problem, which will be analyzed below, and the short integer solution (SIS) problem, that are assumed to be hard, form the basis for the security of these schemes. The digital signature algorithms based on lattices offer certain benefits, including their ability to withstand quantum attacks and their potential for effective implementation. All operations performed are on a lattice, and the security of the cryptographic scheme is based on the hardness of the computational lattice problems.

The first digital signature protocol based on lattices was introduced in 1997, with ideas comparable to those of the GGH cryptographic scheme [39]. In 2003, another digital signature using the NTRU lattice, NTRUSIGN [46], was proposed, and other proposals were additionally introduced, such as the Ring-LWE signature scheme [47] and the BLISS signature scheme [48].

During the NIST Post-Quantum Cryptography Standardization Process [37], various cryptographic protocols were submitted for evaluation, and three of the four potential candidates for post-quantum cryptography were lattice-based digital signature schemes. CRYSTALS-Dilithium, SPHINCS+ and Falcon are cryptographic schemes that stood out for their efficiency, compactness, speed, flexibility and strong security guarantees against both classical and quantum attacks.

5. Learning with Errors (LWE)

An astonishing flexible foundation for lattice-based cryptographic protocols was introduced in 2005 by computer scientist O. Regev, the learning with errors (LWE) cryptosystem [49]. Regev was awarded the Godel Prize in 2018 for his work, which was considered suitable for building secure cryptosystems, even for post-quantum cryptography.

The difficulty of solving hard lattice problems is as hard as solving the LWE problem [49] and that fact makes the LWE cryptosystem and its variants a candidate for the quantum era. Learning with errors is characterized by security and efficiency; it is a high probabilistic algorithm and has emerged as one of the most cutting-edge and innovative research subjects in both cryptography and computer science. After the development of the LWE cryptosystem, many variations and optimizations were created, as it constitutes a cornerstone of modern cryptography.

5.1. The Learning with Errors Problem

The Gauss elimination algorithm is efficient in solving a system of m equations, finding $s=(s_1,s_2,\dots ,s_n)$ in the following form:

$$\begin{array}{c}{a}_{11}{s}_1+a_{12}{s}_2+\dots +a_{1n}{s}_n=b_1\\ a_{21}{s}_1+a_{22}{s}_2+\dots +a_{2n}{s}_n=b_2\\ ⋮\\ a_{m1}{s}_1+a_{m2}{s}_2+\dots +a_{mn}{s}_n=b_m\end{array}$$

An example of the above system of equations in matrix form, given a $m\times n$ matrix A, a $n\times 1$ matrix s and a $n\times 1$ matrix b, would be like $A·s=b$, where

$$A=\left(\begin{array}{cccc}11& 2& \cdots & 3\\ 1& 4& \cdots & 1\\ ⋮& \ddots & ⋮\\ 5& 3& \cdots & 9\end{array}\right),s=\left(\begin{array}{c}{s}_1\\ s_2\\ ⋮\\ s_n\end{array}\right),b=\left(\begin{array}{c}8\\ 13\\ ⋮\\ 2\end{array}\right)$$

It is obvious that by adding a matrix $n\times 1$ matrix e to the product $A·s$, even with small values, the equation system becomes

$$\begin{array}{c}\hfill A·s+e=b\end{array}$$

(1)

The LWE problem states that, given a secret vector $s=(s_1,s_2,...,s_n)\in {\mathbb{Z}}^n$ with coefficient integer numbers and m linear equations, such that

$$\begin{array}{c}{a}_{11}{s}_1+a_{12}{s}_2+\dots +a_{1n}{s}_n\approx b_1\\ a_{21}{s}_1+a_{22}{s}_2+\dots +a_{2n}{s}_n\approx b_2\\ ⋮\\ a_{m1}{s}_1+a_{m2}{s}_2+\dots +a_{mn}{s}_n\approx b_m\end{array}$$

adding a small error to each equation recovers s. The symbol “≈” is used to claim that, within a certain error, the value approaches the actual response.

This problem becomes hard for the Gauss elimination algorithm, and it gives no information from the resulting equations. This problem is considered to be a hard problem as the addition and multiplication of the rows increases the number of errors in each equation, thus the response will be far from the true value and the final row reduced state will be meaningless.

Occasionally, short solutions to Equation (1) are required. Therefore, the solution is asked to lie in a subset $S\subset {\mathbb{Z}}_q^m$, where S can be a subset such that $S=\{0,1\}$ or, in general, the set of all solutions $S={[-C,\dots ,C]}^m$, and each coordinate takes an absolute value bounded by some number $C\ll q/2$. Another option of the set is the Euclidean ball of a small radius r, $S=Bal{l}_r^2$. The above problem is defined as the short integer solution (SIS) problem, which was first presented in 1996 by M. Ajtai [17].

Definition 24. 

(Short integer solution problem). The short integer solution problem states that, given m uniformly random vectors $a_i\in {\mathbb{Z}}_q^n$ forming the columns of a matrix $A\in {\mathbb{Z}}_q^{n\times m}$, find a nonzero integer vector $z\in {\mathbb{Z}}^m$ of norm $\parallel z\parallel \le \beta$, such that

$$f_A\left(z\right):=Az=\sum _i{a}_i{z}_i=0\in {\mathbb{Z}}_q^n.$$

In terms of a lattice problem, the SIS problem states that, given a lattice $\mathcal{L}$ generated by A, find a vector v on the scaled (by q) dual lattice of $\mathcal{L}$, i.e., it expresses an average-case SVP on the lattice

$$\mathcal{L}=\{u\in {\mathbb{Z}}_q^m|uA\equiv 0modq\}.$$

The LWE problem is regarded as an analog of the SIS problem, and for its comprehension and the construction of the LWE cryptosystem, some basic definitions are given below.

Definition 25. 

Let $s\in {\mathbb{Z}}_q^n$ be a secret vector and χ a given distribution on ${\mathbb{Z}}_q$. The LWE distribution $A_{s,n,q,\chi }$ generates a sample $(a,b)\in {\mathbb{Z}}_q^n\times {\mathbb{Z}}_q$ or $(A,b)\in {\mathbb{Z}}_q^{m\times n}\times {\mathbb{Z}}_q^m$, where $a\in {\mathbb{Z}}_q^n$ is uniformly distributed, and $b=\langle a,s\rangle +e$, where $e\leftarrow \chi$ and $\langle a,s\rangle$ is the inner product of a and s in ${\mathbb{Z}}_q$. If $b\in {\mathbb{Z}}_q$ is uniformly distributed, then it is called the uniform LWE distribution.

Definition 26. 

Fix a size parameter $n\ge 1$, $q\ge 2$ and an error probability distribution χ on ${\mathbb{Z}}_q$. Let $A_{s,\chi }$ on ${\mathbb{Z}}_q^n\times {\mathbb{Z}}_q$ be the probability distribution choosing a vector $a\in {\mathbb{Z}}_q$ uniformly at random, choosing $e\in {\mathbb{Z}}_q$ according to χ, and outputting $(a,\langle a,s\rangle +e)$ where additions are performed in ${\mathbb{Z}}_q$. An algorithm solves the LWE problem with modulus q and error distribution χ if for any $s\in {\mathbb{Z}}_q^n$, vector with n coefficients, and given enough samples from $A_{s,\chi }$, it outputs s with high probability.

Definition 27. 

(search-LWE problem). The search-LWE problem, with parameters $n,q,\chi ,m$, states that, given m independent samples $(a_i,b_i)\in {\mathbb{Z}}_q^n\times {\mathbb{Z}}_q$ derived from a uniformly random $s\in {\mathbb{Z}}_q^n$ and fixed for all samples, find s.

The above problem can become a decision problem where the question is which distribution to use.

Definition 28. 

(decision-LWE problem). The decision-LWE problem with parameters $n,q,\chi ,m$ states that, given m independent samples $(a_i,b_i)\in {\mathbb{Z}}_q^n\times {\mathbb{Z}}_q$, where there is a way to generate samples from $A_{s,\chi }$ as above and also generate uniformly random distributed samples of $(a_i,b_i)$ from ${\mathbb{Z}}_q^n\times {\mathbb{Z}}_q$ (uniform distribution U), determine whether the samples are generated from $A_{s,\chi }$ or U.

Definition 29. 

A function $f\left(n\right)$ is defined as a negligible function in n, if ${lim}_{n\to \infty }{n}^{c}f\left(n\right)=0$ for any positive constant c.

Definition 30. 

If ϕ denotes an arbitrary real-valued function on lattices, an instance of the discrete Gaussian sampling (DGS) problem, $DG{S}_{\varphi }$, is given by an n-dimensional lattice $\mathcal{L}$ and a number $r>\varphi \left(\mathcal{L}\right)$. The task is to extract a sample from $D_{\mathcal{L}},r$.

Definition 31. 

For positive real $ϵ>0$ and an n-dimensional lattice $\mathcal{L}$, the smoothing parameter ${\eta }_{ϵ}\left(L\right)$ is defined to be the smallest s such that ${\rho }_{1/s}(L^{*}\setminus \left\{0\right\})\le ϵ$.

Theorem 4 

(Regev). Let $ϵ=ϵ\left(n\right)$ be some negligible function of n. Also, let $p=p\left(n\right)$ be some integer and $a=a\left(n\right)\in (0,1)$ such that $ap>2\sqrt{n}$. Assume that we have access to an oracle W that solves $LW{E}_{p,{\mathsf{\Psi }}_a}$ given a polynomial number of samples. Then, there exists an efficient quantum algorithm for $DG{S}_{\sqrt{2n}·{\eta }_{ϵ}\left(L\right)/a}$.

The following theorem was proven by O. Regev [49] and connects the worst-case lattice problems to the LWE problem, providing a robust indication that the LWE problem is hard. For a real positive a, ${\overline{\mathsf{\Psi }}}_a$ denotes the distribution on ${\mathbb{Z}}_q$ by sampling a normal variable with mean 0 and standard deviation $aq/\sqrt{2\pi }$, where the result is rounded to the nearest integer and reduced modulo q.

Theorem 5 

(Regev). Assume that we have access to an oracle that solves the LWE problem with parameters $n,m,q,{\overline{\mathsf{\Psi }}}_a$, where $ap>2\sqrt{n}$, $q\le poly\left(n\right)$ is prime and $m\le poly\left(n\right)$. Then, there exists a quantum algorithm running in time $poly\left(n\right)$ for solving the (worst-case) lattice problems $SIV{P}_{\tilde{O}(n/a)}$ and (the decision variant of) $SV{P}_{\tilde{O}(n/a)}$ in any lattice of dimension n.

5.2. The LWE Cryptosystem

The LWE cryptosystem is initially parameterized by the integer n, which denotes the security parameter and expresses the lattice dimension, the integers m and q, which express the number of equations and the modulus, respectively, and a real positive a, denoting the noise parameter. Assume that $\chi$ is a given probability distribution on ${\mathbb{Z}}_q$ and the LWE distribution $A_{s,\chi }$ is as described above.

The accuracy and security of the cryptographic scheme are determined by the parameters, so they must be chosen carefully. Choose q to be a prime number such that $n^2\le q\le 2n^2$, $m=(1+ϵ)(n+1)logq$ for some arbitrary constant $ϵ>0$ and $a=1/\left(\sqrt{n}{log}^{2}n\right)$.

The LWE cryptosystem has a conventional cryptographic scheme structure, and its steps are as follows.

• Private key. A uniformly random vector $s\in {\mathbb{Z}}_q^n$ is chosen.
  s is the private key.
• Public key. m vectors $a_1,a_2,\dots ,a_m\in {\mathbb{Z}}_q^n$ are selected independently from the uniform distribution.
  There are elements (error offsets) chosen independently, $e_1,e_2,\dots ,e_m\in {\mathbb{Z}}_q^n$, according to $\chi$.
  The public key of the cryptosystem is ${(a_i,b_i)}_{i=1}^m$, where $b_i=\langle a_i,s\rangle +e_i$.
• Encryption. To be able to encrypt a bit, a random set S is chosen uniformly among all $2^m$ subsets of $\left[m\right]$.
  The encryption holds $({\sum }_{i\in S}{a}_i,{\sum }_{i\in S}{b}_i)$ if the bit is 0 and $({\sum }_{i\in S}{a}_i,\lfloor \frac{q}{2}\rfloor +{\sum }_{i\in S}{b}_i)$ if the bit is 1.
• Decryption. The decryption of a pair $(a,b)$ is 0 if $b-\langle a,s\rangle$ is closer to 0 than to $\lfloor \frac{q}{2}\rfloor$ modulo q. Otherwise, the decryption is 1.

The LWE cryptographic scheme serves as the foundation of various protocols, particularly the cryptographic schemes used in post-quantum cryptography. Due to the fact that the LWE problem is considered a challenging mathematical problem, cryptosystems built around it also enjoy extreme security.

The following algorithm, Algorithm 1, presents the latest version of the LWE cryptosystem [30] and can be visualized in Figure 6.

Both the private and public keys are denoted in matrix form. The size of the private key changes, and so do the parameters $t,l$. A function f maps the message space ${\mathbb{Z}}_q^l$ to the message space ${\mathbb{Z}}_q^l$ by multiplying each coordinate by $q/t$ and rounding to the nearest integer. It is crucial to define an inverse mapping, $f^{-1}$, that maps an element of ${\mathbb{Z}}_q^l$ to an element of ${\mathbb{Z}}_q^l$, dividing each coordinate by $q/t$ [30].

Algorithm 1: LWE

Private key. A matrix $S\in {\mathbb{Z}}_q^{n\times l}$ is chosen uniformly at random. S is the private key.  Public key. A matrix $A\in {\mathbb{Z}}_q^{m\times n}$ is chosen uniformly at random and a matrix $E\in {\mathbb{Z}}_q^{m\times l}$ is chosen, whose each element entries are according to ${\overline{\mathsf{\Psi }}}_a$. The public key is $(A,P=AS+E)\in {\mathbb{Z}}_q^{m\times n}\times {\mathbb{Z}}_q^{m\times l}$.  Encryption. Given a message $v\in {\mathbb{Z}}_t^l$ and the public key $(A,P)$, a vector $a\in {\{-r,-r+1,\dots ,r\}}^m$ is chosen uniformly at random. The output is the ciphertext $(u=A^{T}a,c=P^{T}a+f\left(v\right))\in {\mathbb{Z}}_q^n\times {\mathbb{Z}}_q^l$.  Decryption. Given the private key $S\in {\mathbb{Z}}_q^{n\times l}$ and the ciphertext $(u,c)\in {\mathbb{Z}}_q^n\times {\mathbb{Z}}_q^l$, recover the plaintext $f^{-1}(c-S^{T}u)$.

LWE is believed to be an exceedingly secure cryptosystem. This cryptographic scheme is based on lattices and depends on the assumed difficulty of specific lattice problems, namely the problem of locating the closest lattice point in the presence of random noise. Since LWE-based cryptography is immune to quantum attacks, it has attracted interest as a potential solution for post-quantum cryptography. Its security, as with any cryptographic system, depends on the specific parameters chosen and the method used.

LWE is a legitimate and well-studied cryptographic concept within the field of lattice-based cryptography. As an ongoing and dynamic field of study, the security of LWE cryptographic algorithms is continuously and consistently investigated and evaluated. Many cryptographic primitives and schemes, including encryption and digital signatures, have been constructed using the assumptions provided by LWE, so it remains a prominent area of study and is considered a promising candidate for the future of computing science.

There are several variants and extensions of the LWE problem, each offering different performance properties and security implications that find applications in the field of lattice-based cryptography. Among these variants are Ring-LWE, Binary-LWE, Dual-LWE and Multilineal-LWE [50,51,52]. Module-LWE [53] has recently received particular attention as a candidate of NIST [37] chosen in the third round of the competition; it is a key-encapsulation mechanism with a security that relies on the hardness assumptions over module lattices [54].

5.3. An Efficient Variant of LWE

Since the introduction of the LWE cryptographic scheme, numerous diverse cryptosystems have been proposed and studied because it is one of the most commonly used and researched lattice-based protocols.

The cryptographic scheme we introduce bears a strong resemblance to the original proposed cryptosystem of Oded Regev [49]. The main new idea is the existence of a map $f:K\to L$, $K,L\subseteq {\mathbb{R}}^k$, where $1\le k\le n$ (e.g., a multilinear map) is the construction of the cryptosystem in the key generation step of the cryptographic algorithm. It is important that the mapping f satisfy certain conditions, such as the dimension of the spaces $K,L$.

This step does not affect the security of the cryptographic scheme, as its safety is based on the LWE assumption but maintains the efficiency of the protocol. Since the procedure of key generation becomes increasingly intricate, the cryptographic scheme remains secure and the risks of an algebraic-analytical attack under the hardness LWE assumption do not increase.

Our variation cryptographic scheme supports addition and multiplication, and the key idea is that, by using a transform f and its matrix, the elements of the product of the secret key S and the random matrix A in the second step of the LWE algorithm are mapped to new elements. This procedure is ineffective for the complexity of the algorithm since the operations of addition and multiplication correspond to matrices’ and vectors’ addition and multiplication, which inherently offer opportunities for parallelism. Additionally, key generation involves matrix operations and sampling from distributions, which can be parallelized to some extent; therefore, parallelism is achieved. The error vector is added after matrix operations, so our scheme is also secure due to the underlying LWE hardness assumption.

The LWE cryptographic scheme can be visualized, as in Figure 7, where a lattice is generated by the public matrix A and the lattice point $(S,AS)$. As shown, the public point $t=(0,B)$ is distinct from the lattice point $(S,AS)$) and the vector $(S,“$-$E”)$ separates it from the point. With our transformation, we are changing this public point to improve both efficiency and security.

Our variant of the LWE cryptosystem is described below. The parametrization is the same as that of LWE, and all operations are performed over ${\mathbb{Z}}_q$. T is the function that maps the message space ${\mathbb{Z}}_p^l$ to the space ${\mathbb{Z}}_p^l$. Let $v\in {\mathbb{Z}}_p$ be a message vector, and we define $t\left(v\right)=\lfloor v·\frac{q}{p}\rceil \in {\mathbb{Z}}_q$.

• Private key. Choose a matrix $S\leftarrow {\mathbb{Z}}_q^{n\times l}$ uniformly at random.
  S is the private key.
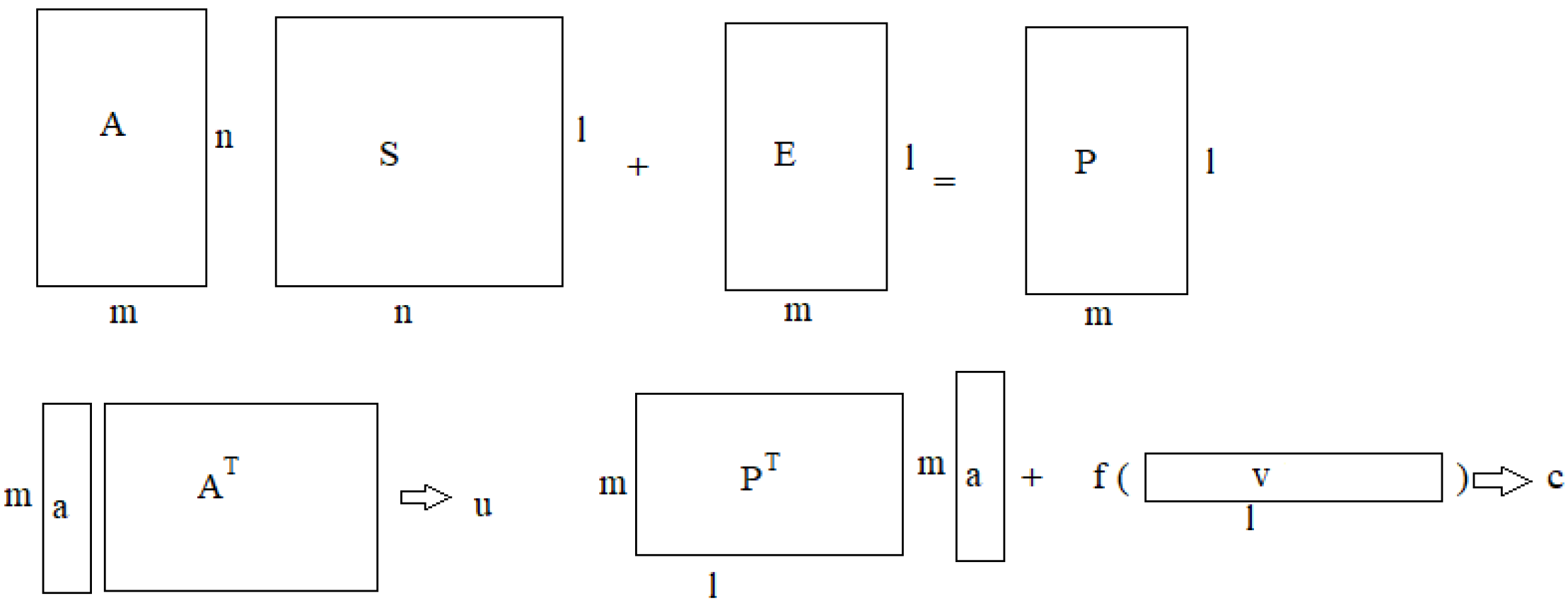
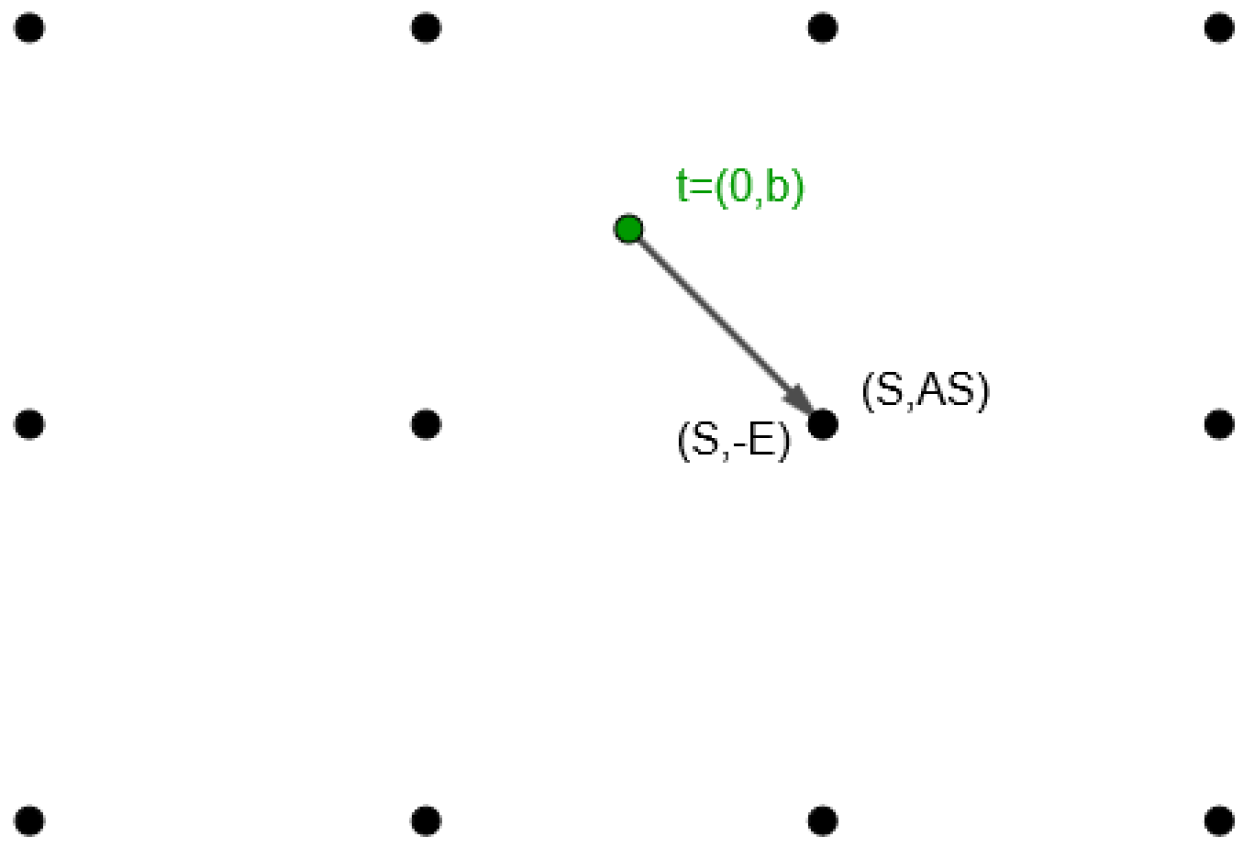
• Public key. Choose a matrix $A\leftarrow {\mathbb{Z}}_q^{m\times n}$ uniformly at random and compute the matrix product $AS$.
  Choose a suitable mapping $f:K\to L$, $K,L\subseteq {\mathbb{R}}^k$, where $1\le k\le n$ transforms the elements of the matrix $AS=C$ and maps them to elements of a matrix D, i.e., f is a suitable correspondence. D is the matrix product $CF$, where F is the matrix transformation of f.
  Choose an error matrix $E\in {\mathbb{Z}}_q^{m\times l}$, where each entry $x_{i,j}\leftarrow \chi$ is chosen independently from an error distribution $\chi$.
  The public key is $(A\leftarrow {\mathbb{Z}}_q^{m\times n},P=D+E\in {\mathbb{Z}}_q^{m\times l})$. The $(i,j)th$ entry of P is $p_{ij}=d_{ij}+x_{ij}$, where $d_{ij}$ is the element of the matrix D yielding the linear transformation and the matrix C.
• Encryption. To encrypt a message $v\in {\mathbb{Z}}_p^l$, define the vector $t=t\left(v\right)\in {\mathbb{Z}}_p^l$ by applying $t(·)$ coordinate-wise to v.
  Choose a vector $a\leftarrow {\{0,1\}}^m\subset {\mathbb{Z}}_q^m$ uniformly at random.
  The pair $(u,c)=(A^{T}a,P^{T}a+t)\in {\mathbb{Z}}_q^n\times {\mathbb{Z}}_q^l$ is the resulting ciphertext.
• Decryption. Given a ciphertext $(u,c)\in {\mathbb{Z}}_q^n\times {\mathbb{Z}}_q^l$ and the private key $S\leftarrow {\mathbb{Z}}_q^{n\times l}$, compute $m=c-S^{T}u\in {\mathbb{Z}}_q^l$. Output the plaintext $v\in {\mathbb{Z}}_p^l$, where each $v_i$ is such that $m_i-t\left(v_i\right)\in {\mathbb{Z}}_q$ is closest to $0modq$.

Efficiency. Our construction is relatively simple to implement, as it only requires addition and multiplication operations modulo q, and parallelization can be achieved. The parameters are chosen as in [30]. For the message space, the integer p is chosen to be $p=poly\left(n\right)\ge 2$ and $l=poly\left(n\right)\ge 1$. If p is chosen to be a power of two, converting an input message to an element of the message space is simpler.

It is assumed that the security parameter of the system is $\lambda$ and the parameters of the Gaussian parameters are $s,\sigma$ for the distribution $\chi =D_{\mathbb{Z},s}$, as defined above. Assuming that the output is less than $b=s\sqrt{\lambda }$, the distribution is negligibly affected.

Correctness. The decryption algorithm of our construction computes the vector

$$m=c-S^{T}u=(S^{T}A+E)a+t-S^{T}Aa=Ea+t\in {\mathbb{Z}}_q^l$$

where S is the secret key chosen uniformly at random, $(A,P=D+E)$ is the public key, with A being arbitrary and E being chosen according to the distribution we described above. Remember that $(u,c)=(A^{T}a,P^{T}a+t)$ is the ciphertext, where $a\in {\{0,1\}}^m$ and $t=t\left(v\right)$ for the message vector v.

For each coordinate $j\in \left[l\right]$, the value ${\left(Ea\right)}_j$ determines the distance from $d_j$ to $t_j$ (modulo q) and is at most $q/4p$ away from 0 (modulo q), so $d_j$ is nearest to $t\left(v_j\right)$.

Security. Oded Regev proved that the search-LWE problem is at least as hard as worst-case lattice problems [49] for the appropriate parameters, i.e., $aq\ge \sqrt{n}$. The above variant of LWE is also considered secure against possible attack under the assumption that the decision-LWE problem with variants $n,q,\chi ,m$ is hard for the same parameters’ choice.

The proof of security is similar to the proof presented by Regev [49].

First, the public key $(A,P)$ is chosen uniformly at random from ${\mathbb{Z}}_q^{m\times n}\times {\mathbb{Z}}_q^{m\times l}$. Therefore, if the parametrization of the system is such that the LWE problem is hard, the public keys generated by the cryptosystem are indistinguishable from pairs chosen uniformly at random. Second, for an arbitrary public key $(A,P)$ chosen at random with c an encryption of a fixed bit $\mu$, it is indistinguishable for $\mu =0,1$, i.e., the result gives us no information about the encrypted message.

So, the task is to prove that the LWE problem remains hard by using $a_j$ public vectors multiplied with secret vectors $s_i$ corresponding to $d_i$ vectors and $x_i$ independent error vectors for each sample, which works following a similar argument to [49,55].

Assume that we have hybrid distributions $H_0,H_1,\dots H_l$ for the public key $(A,P)$, which operate as follows: in the distribution $H_k$, the matrix A and the k rows of the matrix P are uniform, and the remaining rows of P are generated according to the key generation of our variant, using $s_i$ secret vectors and error terms $x_{ij}$ for all $i>k$ and $j\in \left[m\right]$. Therefore, $H_0$ is the distribution yielded by the key generation algorithm, $H_l$ is completely uniform and we prove that the random $H_{k-1}$ and $H_k$ are computationally indistinguishable.

Suppose for any $k\in \left[l\right]$ that there is a simulator algorithm $X^{\mathcal{O}}$ that, having an oracle $\mathcal{O}$, returns samples from either the distribution $A_s,\chi$, where $s\in {\mathbb{Z}}_q^n$ or from the uniform distribution ${\mathbb{Z}}_q^n\times {\mathbb{Z}}_q$.

In the first step, the simulator X makes m queries to $\mathcal{O}$ with outcome $(a_j,b_j)$, where $j\in \left[m\right]$, and furthermore, for each $i\in \left[m\right]$, X chooses $s_{ij}\leftarrow {\mathbb{Z}}_q^n$ and errors $x_{ij}\leftarrow \chi$.

The simulator X outputs $(A,P)$ as follows: the jth column of matrix A is vector $a_j$, and the entries of matrix P are $p_{ij}=d_{ij}+x_{ij}$, where $d_{ij}$ is the entries of the D matrix. The entries of D result from the multiplication of $AS$ and the transformation matrix defined in each case. Hence, for all columns $j<k$ and for all $i\in \left[m\right]$, X selects independent error terms $x_{ij}$ from the distribution $\chi$ and for all columns $j>k$ and for all $i\in \left[m\right]$, X chooses uniform independent error terms from ${\mathbb{Z}}_q^n\times {\mathbb{Z}}_q$.

It is obvious that if the oracle $\mathcal{O}$ generates samples from $A_{s,\chi }$, the output of the simulator is distributed according to the hybrid distribution $H_{k-1}$, while if the oracle generates samples from the uniform distribution, the output is distributed according to $H_k$. Thus, under the assumption that LWE with parameters $q,\chi$ is hard, the above distributions are indistinguishable, and consequently, the distributions $H_{k-1}$, $H_k$ are indistinguishable.

5.4. Certain Instances of the Variant

The choice of the correspondence f is critical to the structure of our cryptographic scheme. The key idea is to replace the matrix product $AS=C$ with the matrix of a transformation, so with the help of the additional step, the cryptographic scheme can be used in applications that utilize hard encryption. Matrix addition and multiplication are equivalent when encodings are added and multiplied, so our construction is as hard as the LWE cryptographic scheme and remains flexible and secure. Below certain instances of our scheme are introduced in the key generation process, and the key generation algorithm for each instance is presented. The selection of each function was made in such a way as not to increase the complexity of the algorithm too much, i.e., not to increase the operations and the time of its implementation too much.

5.4.1. The Sum of Two Entries

In the first version of the LWE cryptographic protocol, the secret vector s is an element of $Z_q^n$. So, the main idea was to choose a secret vector $s\in Z_q^{n\times 2}$, i.e., to add an additional column in the matrix S and choose a linear transformation f that maps the elements of $f:{\mathbb{Z}}_p^2$ to ${\mathbb{Z}}_p$ without interfering with the remaining structure of the system.

For $l=2$, we choose the map $f:{\mathbb{Z}}_p^2\to {\mathbb{Z}}_p$ defined by $d(c_{i1},c_{i2})=c_{i1}+c_{i2}$ for each pair $(c_{i1},c_{i2})$, $i=1,\dots ,m$ of each row of C, and the result is vector $d=(d_1,\dots d_m)$, where $d_i=c_{i1}+c_{i2},i=1,\dots m$. Graphically, the sum of two vectors is the vector representing the diagonal of the parallelogram starting from the intersection of the tails.

In $Z_q^2$, Algorithm 2 is executed.

Algorithm 2: KeyGen(1): Key Generation 1

1: $q,n,m,l,\chi \leftarrow params\left(\lambda \right)$   2: $S\leftarrow {\mathbb{Z}}_q^{n\times 2}$   3: for $i\in 1\to m$ do   4:     $x_i\leftarrow \chi$   5:     $a_i\leftarrow {\mathbb{Z}}_q^n$   6:     $c_i\leftarrow {\mathbb{Z}}_q^{mx2}$   7:     $d_i\leftarrow c_{i1}+c_{i2}\in {\mathbb{Z}}_q^m$   8:     $p_i\leftarrow d_i+x_i$   9: end for 10: return $(pk=a_i,p_i)$ {$pk$ stands for public key}

    Discrete Implementation: Let the chosen parameters for this particular implementation be n = 4, m = 3 and q = 13.

• The private key is chosen uniformly at random and is such that

  $$S=\left(\begin{array}{cc}2& 3\\ 5& 0\\ 0& 4\\ 6& 2\end{array}\right)$$
• It is selected

  $$A=\left(\begin{array}{cccc}1& 8& 6& 2\\ 0& 5& 1& 3\\ 7& 1& 6& 3\end{array}\right)$$
  Compute the product $C=AS$, such that

  $$C=\left(\begin{array}{cccc}1& 8& 6& 2\\ 0& 5& 1& 3\\ 7& 1& 6& 3\end{array}\right)\left(\begin{array}{cc}2& 3\\ 5& 0\\ 0& 4\\ 6& 2\end{array}\right)=\left(\begin{array}{cc}2& 5\\ 4& 10\\ 11& 12\end{array}\right)$$
• With the aid of the linear map $f\in {\mathbb{Z}}_q^2\to \in {\mathbb{Z}}_q,f:(x,y)=x+y$ and the matrix transformation

  $$F=\left(\begin{array}{c}1\\ 1\end{array}\right)$$

  compute the matrix product $D=CF$, such that

  $$D=\left(\begin{array}{c}7\\ 1\\ 10\end{array}\right)$$
• Select matrix

  $$E\in {\mathbb{Z}}_q^3=\left(\begin{array}{c}1\\ 0\\ -1\end{array}\right)$$
  The public key is

  $$(A,P=D+E)=\left(\left(\begin{array}{cccc}1& 8& 6& 2\\ 0& 5& 1& 3\\ 7& 1& 6& 3\end{array}\right),\left(\begin{array}{c}8\\ 1\\ 9\end{array}\right)\right).$$

5.4.2. The Cantor Pairing Function

Based on the first version of the LWE cryptosystem and on the same idea, i.e., to map the elements of a $Z_q^2$ in $Z_q$, in this case, the Cantor pairing function is chosen. The set of nonnegative integers is denoted as ${\mathbb{N}}_0=\{0,1,2,\dots \}$. The Cantor pairing function, introduced by Cantor in 1878, maps ${\mathbb{N}}_0\times {\mathbb{N}}_0$ injectively onto ${\mathbb{N}}_0$.

Definition 32. 

The Cantor pairing function is a quadratic bijection, such that

$$C(x,y)=\frac{1}{2}(x+y)(x+y+1)+y$$

Using the Cantor pairing function, we present Algorithm 3 and the function graphically plots $c_{i1}$ on the x-axis and $c_{12}$ on the y-axis.

Algorithm 3: KeyGen(2): Key Generation 2

1: $q,n,m,l,\chi \leftarrow params\left(\lambda \right)$   2: $S\leftarrow {\mathbb{Z}}_q^{n\times 2}$   3: for $i\in 1\to m$ do   4:     $x_i\leftarrow \chi$   5:     $a_i\leftarrow {\mathbb{Z}}_q^n$   6:     $c_i\leftarrow {\mathbb{Z}}_q^{mx2}$   7:     $d_i\leftarrow (c_{i1}+c_{i2})(c_{i1}+c_{i2}+1)/2+c_{i2}\in {\mathbb{Z}}_q^m$   8:     $p_i\leftarrow d_i+x_i$   9: end for 10: return $(pk=a_i,p_i)$ {$pk$ stands for public key}

5.4.3. An Inverse Transformation

In general, a linear map $f:{\mathbb{Z}}_q^m\to {\mathbb{Z}}_q^m$ is chosen, which is an isomorphism with $m\times m$ matrix F and inverse $m\times m$ matrix $F^{-1}$. In this case, we choose $m=l$. In our implementation, we choose $m=3$.

For $l=3$, we choose the linear isomorphism $f:(x,y,z)=(2x,4x+y,2x+3y+z)$.

In $Z_q^3$, we run Algorithm 4.

Algorithm 4: KeyGen(3): Key Generation 3

1: $q,n,m,l,\chi \leftarrow params\left(\lambda \right)$   2: $S\leftarrow {\mathbb{Z}}_q^{n\times 3}$   3: for $i=1\to m$ do   4:     $x_i\leftarrow \chi$   5:     $a_i\leftarrow {\mathbb{Z}}_q^n$   6:     $c_i\leftarrow {\mathbb{Z}}_q^{mx3}$   7:     $d_{i,1}\leftarrow 2c_{i1}$   8:     $d_{i,2}\leftarrow 4c_{i1}-c_{i2}$   9:     $d_{i,3}\leftarrow 2c_{i1}+3c_{i2}-c_{i3}$ 10:     $p_i\leftarrow d_i+x_i$ 11: end for 12: return $(pk=a_i,p_i)$ {$pk$ stands for public key}

    Discrete implementation

The chosen parameters for this particular implementation are: n = 4, m = 3 and q = 13.

• The private key is chosen uniformly at random and is such that

  $$S=\left(\begin{array}{ccc}2& 3& 1\\ 0& 5& 4\\ 1& 4& 0\\ 0& 1& 3\end{array}\right)$$
• The parameter is $m=3$, so the public key is generated with the help of the uniformly at random $A\in {\mathbb{Z}}_q^{3\times 4}$.
  It is chosen

  $$A=\left(\begin{array}{cccc}1& 8& 6& 2\\ 0& 2& 1& 3\\ 7& 1& 6& 4\end{array}\right)$$
  Compute the product $C=AS$, such that

  $$C=\left(\begin{array}{cccc}1& 8& 6& 2\\ 0& 2& 1& 3\\ 7& 1& 6& 4\end{array}\right)\left(\begin{array}{ccc}2& 3& 1\\ 0& 5& 4\\ 1& 4& 0\\ 0& 1& 3\end{array}\right)=\left(\begin{array}{ccc}8& 4& 0\\ 1& 4& 4\\ 7& 2& 10\end{array}\right)$$
  With the aid of the linear map $f\in {\mathbb{Z}}_q^3\to \in {\mathbb{Z}}_q^3,f:(x,y,z)=(2x,4x+y,2x+3y+z)$, with matrix transformation

  $$F=\left(\begin{array}{ccc}2& 0& 0\\ 4& 1& 0\\ 2& 3& 1\end{array}\right)$$

  compute the matrix product $D=CF$, such that

  $$D=\left(\begin{array}{ccc}6& 4& 0\\ 0& 3& 4\\ 3& 6& 10\end{array}\right)$$
  Select matrix $E\in {\mathbb{Z}}_q^{3\times 3}$, each entry of which is selected according to ${\overline{\mathsf{\Psi }}}_a$.
  Compute

  $$P=D+E\left(\begin{array}{ccc}6& 4& 0\\ 0& 3& 4\\ 3& 6& 10\end{array}\right)+\left(\begin{array}{ccc}-1& 0& 0\\ 1& 0& 0\\ 0& 1& -1\end{array}\right)=\left(\begin{array}{ccc}5& 4& 0\\ 1& 4& 4\\ 3& 7& 9\end{array}\right)$$
  The public key is $(A,P=D+E)\in {\mathbb{Z}}_q^{3\times 4}\times {\mathbb{Z}}_q^{3\times 3}$.

We wish to decrypt the message

$$v=\left(\begin{array}{ccc}0& 1& 1\end{array}\right)$$

and

$$t=\left(\begin{array}{ccc}0& 3& 3\end{array}\right)$$

respectively, for $q=13,p=4$.

For

$$a=\left(\begin{array}{ccc}1& 0& 0\end{array}\right)$$

we compute

$$u=A^{T}a=\left(\begin{array}{ccc}1& 0& 7\\ 8& 2& 1\\ 6& 1& 6\\ 2& 3& 4\end{array}\right)\left(\begin{array}{c}1\\ 0\\ 0\end{array}\right)=\left(\begin{array}{cccc}8& 9& 7& 6\end{array}\right)$$

Moreover, we compute

$$c=P^{T}a+t=\left(\begin{array}{ccc}5& 1& 3\\ 4& 4& 7\\ 0& 4& 9\end{array}\right)\left(\begin{array}{c}1\\ 0\\ 0\end{array}\right)+t=\left(\begin{array}{ccc}0& 3& 3\end{array}\right)=\left(\begin{array}{ccc}8& 11& 9\end{array}\right)+\left(\begin{array}{ccc}0& 3& 3\end{array}\right)=\left(\begin{array}{ccc}8& 11& 12\end{array}\right)$$

The ciphertext is the pair

$$(u,c)=\left(\left(\begin{array}{cccc}8& 9& 7& 6\end{array}\right),\left(\begin{array}{ccc}8& 11& 12\end{array}\right)\right).$$

Given the above ciphertext $(u,v)$ and the secret key S, we compute

$$m=c-S^{T}u=\left(\begin{array}{ccc}8& 11& 12\end{array}\right)-\left(\begin{array}{cccc}2& 0& 1& 0\\ 3& 5& 4& 1\\ 1& 4& 0& 3\end{array}\right)\left(\begin{array}{c}8\\ 9\\ 7\\ 6\end{array}\right)=\left(\begin{array}{ccc}8& 11& 12\end{array}\right)-\left(\begin{array}{ccc}10& 12& 10\end{array}\right)=\left(\begin{array}{ccc}11& 12& 2\end{array}\right).$$

So, the plaintext is

$$v=\left(\begin{array}{ccc}0& 1& 1\end{array}\right)\in Z_4^3$$

where each coordinate $v_i$ is such that $m_i-t\left(v_i\right)$ is closest to $0mod13$.

Our construction could be appropriate and suitable for heavily based applications to hard encryption, such as file storage services that encrypt data both in transit and at rest, or operating systems that offer the option of full hard disk encryption. Moreover, applications that use strong encryption techniques are those that use end-to-end encryption to secure conversations, e.g., platforms like Signal or WhatsApp. Additionally, email encryption in some services uses end-to-end encryption, and this type of encryption is also widely used on platforms like Zoom, whose main use is the proceedings of meetings, file sharing and communication channels that must maintain the security of sensitive personal information. Sensitive personal data are also required to be protected in financial and banking applications, like online payment methods and electronic transactions.

5.5. Attacks and Threats

Cryptanalysis involves studying and analyzing the weaknesses of the underlying problem of a cryptographic scheme in order to decrypt ciphertexts and codes or obtain hidden information. The LWE problem is based on the hardness of finding a unique solution to a system of linear equations in the presence of some random errors. It is believed to be secure because solving these systems of equations is considered to be computationally hard, even for quantum computers. However, many attempts have been made to find vulnerabilities or attacks carried out on cryptographic systems based on this problem, especially now that the LWE cryptosystem and its variants are regarded as candidates for secure communication in the post-quantum era.

Due to the fact that the LWE cryptographic scheme is based on lattices, lattice reduction attacks remain an active field of research. These types of attacks attempt to find short lattice vectors and can be applied to break certain instances of LWE, especially when the parameters are not selected properly. Given n samples, $(a_i,b_i)$ is created by an $n\times m$ matrix A with rows and vectors $a_i$, and a lattice $\mathcal{L}$ is being formed by b, the columns of the matrix A and certain parameters. In these types of attacks, the secret s is recovered by locating the shortest vector in the above lattice $\mathcal{L}$. M. Albrect et al. presented a study in 2015, where the hardness of LWE was analyzed and the running times of algorithms, such as the LLL and BKZ algorithms, were calculated [56].

A strategy to solve the LWE problem is by solving the SIS problem, i.e., finding a short vector v in the scaled dual lattice $\mathcal{L}=\{w\in {\mathbb{Z}}_q^m|wA\equiv 0modq\}$. Assuming that we have m samples $(A,c)$, either from ${\mathcal{L}}_{s,\chi }$ satisfying $c=As+e$ or c is uniformly random, the main aim is to find a short vector v with $v·A=0$. With this strategy, an eavesdropper solves the distinguishing LWE problem, i.e., a sample is an LWE instance $(A,t=A^{t}s+e)$ or it comes from a uniform distribution at random [30]. In this method, the adversary locates a nonzero short vector v such that $Av=0modq$, and examines if the inner product $\langle v,t\rangle$ is near to zero modulo q. In the case that t is uniform, there is a probability of $\frac{1}{2}$ of the test’s acceptance. In the case that $t=A^{t}s+e$, where e comes from a Gaussian distribution with parameter s, it states $\langle v,t\rangle =\langle v,e\rangle modq$, which is a Gaussian with parameter $\parallel v\parallel ·s$. When the value of this parameter is less than q, the uniform distribution could be distinguished from the Gaussian with an advantage near to ${exp(-\pi ·(\parallel v\parallel ·s/q)}^2)$. Finding a short vector in the dual lattice is necessary for the dual attack to succeed, but this may not always be possible, particularly for carefully selected parameters that defy lattice reduction strategies.

The choice of parameters, such as the modulus and lattice dimension, influences how hard it is to solve this problem. The problem becomes more complex with higher dimensions and greater noise distributions. A. Pouly and Y. Shen introduced a simple analysis of a dual attack [57], which is presented below and described in Algorithm 5.

Assuming an LWE sample $(A,b)$ is given and $s\in {\mathbb{Z}}_q^n$ is a secret, such that $b=As+e$ for an unknown $e\in {\mathbb{Z}}_q^m$. In the dual attack, in its most basic variation, the secret s is divided into two parts, $s_{guess}\in {\mathbb{Z}}_q^{n_{guess}}$ and $s_{dual}\in {\mathbb{Z}}_q^{n_{dual}}$, where $n=n_{guess}+n_{dual}$.

Consequently, the matrix $A\in {\mathbb{Z}}_q^{m\times n}$ is seperated into two parts $A=\left[A_{guess}{A}_{dual}\right]$. So, we have

$$b=As+e=\left(\begin{array}{cc}{A}_{guess}& A_{dual}\end{array}\right)\left(\begin{array}{c}{s}_{guess}\\ s_{dual}\end{array}\right)=A_{guess}{s}_{guess}+A_{dual}{s}_{dual}+e$$

The algorithm makes an effort to guess ${\tilde{s}}_{guess}\in {\mathbb{Z}}_q^{n_{guess}}$ on the value of $s_{guess}$ and if this guess holds true.

Assume we have the lattice

$$L_q^{*}\left(A_{dual}\right)=\{x\in {\mathbb{Z}}^m:x^T{A}_{dual}=0modq\}$$

and the inequality $det\left(L_q^{*}\left(A_{dual}\right)\right)\le q^{n_{dual}}$ holds true.

Thus, for every $x\in L_q^{*}\left(A_{dual}\right)$, we have

$$x^{T}b=x^T{A}_{guess}{s}_{guess}+x^T{A}_{dual}{s}_{dual}+x^{T}e=x^T{A}_{guess}{s}_{guess}+x^{T}e(modq)$$

So,

$$x^T(b-A_{guess}{\tilde{s}}_{guess})=x^T(A_{guess}(s_{guess}-{\tilde{s}}_{guess})+x^{T}e(modq)$$

At this point, the basic remark is that if the algorithm’s guess is correct, i.e., ${\tilde{s}}_{guess}=s_{guess}$, then $x^T(b-A_{guess}{\tilde{s}}_{guess})=x^{T}e(modq)$ comes from a Gaussian distribution. Otherwise, if the algorithm’s guess is wrong, then $x^T(b-A_{guess}{\tilde{s}}_{guess})=x^{T}e(modq)$ follows a uniform distribution. This results from the fact that $x\ne 0$ and A was chosen uniformly at random.

Let q be a prime power, $\delta >0$, $N\in \mathbb{N}$ and LWE samples $(A^{\left(i\right)},b^{\left(i\right)}),1\le i\le N$.

Algorithm 5: Dual Attack

1: Input: $q,m,\delta ,N,n=n_{guess}+n_{dual}$   2: Input: list of $(A^{\left(1\right)},b^{\left(1\right)}),\dots ,(A^{\left(N\right)},b^{\left(N\right)})$   3: Output: the first $n_{guess}$ coordinates of the secret or ⊥   4: for $j=1$ to N do   5:     Compute a basis of $L_q^{*}\left(A^{\left(j\right)}\right)$   6:     Compute a short vector $x_j\in L_q^{*}\left(A^{\left(j\right)}\right)$   7: end for   8: for ${\tilde{s}}_{guess}\in {\mathbb{Z}}_q^{n_{guess}}$ do   9:     Compute the list $y_1,\dots ,y_N$ where $y_j=x_j^T(b^{\left(j\right)}-A_{guess}^{\left(j\right)}{\tilde{s}}_{guess})$ 10:     $S\leftarrow {\sum }_{j=1}^{N}cos(2\pi y_j/q)$ 11:     if $S\ge N\delta$ then 12:         return ${\tilde{s}}_{guess}$ 13:     end if 14: end for 15: return ⊥

In 2010, R. Lindner and C. Peikert performed a new type of attack, optimizing the simple distinguishing attack and solving the LWE problem by solving the BBD problem [58].

Another important type of attack against LWE is the dual attack, which tries to recover the secret key by working in the dual lattice space and works best against LWE instances where the plaintext messages are small. The dual attack mathematically attempts to solve the short integer solution (SIS) problem in a dual lattice by performing a lattice reduction algorithm to find short vectors. Typically, dual attacks rely on taking advantage of flaws or structures in the LWE-based schemes’ implementation or particular parameters. They may not work with every example of LWE-based cryptography and frequently require fine-tuning of parameters. One popular example of a dual attack is the dual reconciliation attack. This is an attack that targets particular parameter sets where a certain sublattice of the dual lattice is located near the secret key [59]. More effectively than a direct attack on the LWE problem itself, it attempts to recover the secret key by taking advantage of this proximity.

Hybrid attacks are attacks that leverage multiple vulnerabilities or combine different techniques to compromise LWE-based systems. To undermine the security assumptions of LWE, a hybrid attack, for example, might combine lattice reduction techniques with algebraic property exploitation [60]. Moreover, hybrid attacks could involve analyzing the statistical properties of the error distribution in LWE instances while simultaneously applying computational methods, like lattice reduction, to exploit potential biases or weaknesses.

Exploring the effectiveness of combining multiple attack techniques, such as lattice reduction, algebraic methods, statistical analyses, and potentially quantum algorithms, to create stronger attacks against LWE-based schemes is an active scientific area. The exploration of novel combinations or variations of these attacks remains an open field of study. Continuing efforts are being made to strengthen security proofs for LWE-based cryptographic schemes. Researchers are working on refining parameter selection guidelines to ensure robustness against known attacks and provide higher levels of security assurance. LWE is considered one of the leading candidates for post-quantum cryptography, so preventing attacks on learning with errors and its variations involves implementing robust cryptographic schemes and making informed choices in parameters and implementations. Some of the well-studied and recommended strategies are careful parameter selection, such as using larger parameters, randomness in error generation vectors, the implementation of appropriate techniques to resist lattice reduction attacks, and, as expected, continuous evaluation and updates.

6. Conclusions and Future Research

Lattice theory, originating from diverse mathematical inquiries into geometry, number theory and abstract algebra, has evolved into a foundational concept in modern cryptography, particularly in the context of post-quantum cryptography. Recent advances in quantum computing necessitate the evolution of cryptographic practices that anticipate the emergence of powerful quantum computers and the potential threat they pose to existing cryptographic algorithms. LWE is pivotal in post-quantum cryptography due to its fundamental role in creating cryptographic schemes resilient to attacks from both classical and quantum computers. For the science of cryptography and computer science, the importance of LWE is why it has been a constant subject of study, research and analysis since its inception.

In this paper, we introduced a variant of the LWE cryptographic scheme, adding to the key generation step of the protocol a transformation that changes the elements of the product matrix of the secret key S and the uniformly random chosen matrix A. Avoiding interference with the rest of the structure of the LWE algorithm, this additional step maintains the efficiency and security of the protocol without scaling up the complexity, as the operations added into the protocol are additions and multiplications of matrices. We discussed certain instances of our variant, choosing a particular transformation mapping f, and presented discrete implementations in small dimensions. The main advantage of our variant is the addition of a transformation in the key generation algorithm, which has both an algebraic and a geometric interpretation into a lattice. Moreover, our variant is regarded as a primitive for applications that employ robust encryption, and our future work aims to implement the protocol both generally and to certain applications.

Due to its potential security features, LWE has attracted a lot of attention lately, especially in light of the concerns posed by quantum computing. Even though LWE and its variants are widely studied and performed and have been advanced significantly, there are still a number of open issues and creative uses that merit further investigation. The computational expense of lattice-based encryption in comparison to more conventional cryptographic techniques is one of its primary drawbacks. The goal of ongoing research is to make lattice-based primitives more efficient in terms of computing complexity and usefulness across a range of platforms. Blockchain technology and cryptocurrencies may benefit from the use of lattice-based cryptography, which can improve privacy, scalability and resilience to quantum attacks. Additionally, there are still open questions about the best approaches for standardization. Investigating lattice-based consensus methods, signature protocols and privacy-boosting strategies for blockchain networks may result in novel blockchain systems with improved security features. This covers factors like compatibility across various implementations and the proper parameter selection for security and performance trade-offs.

Although our LWE-based cryptographic scheme is reasonably flexible, efficient and secure, improvements and optimizations can be made. Optimizing LWE cryptosystems requires a multidisciplinary approach that combines mathematical research, algorithmic advances, hardware breakthroughs and a thorough understanding of both theoretical and practical aspects of cryptography. Ongoing research focuses on the implementation and comparison of the proposed variant, the key size of cryptosystems to improve their complexity and security, and the investigation of potential vulnerabilities to strengthen them against possible attacks.